New Fault-Tolerant Sensorless Control of FPFTPM Motor Based on Hybrid Adaptive Robust Observation for Electric Agricultural Equipment Applications
Abstract
1. Introduction
2. Sensorless Control Methods for FPFTPM Motor Drive
2.1. Conventional SMO-Based Sensorless Control
2.2. Conventional HF Injection Method
3. Analysis of Fault-Tolerant Sensorless Control
3.1. Universal Fault-Tolerant Control
3.2. Problems’ Description
- Traditional signum-function-based SMOs necessitate the use of LPFs for chattering reduction and delay compensation to mitigate LPF-induced phase delays, complicating the SMO architecture and degrading dynamic estimation accuracy in FPFTPM motor systems.
- During the fault operation, the FPFTPM motor system will be operated in an asymmetric state. Meanwhile, the normal phase currents are severely distorted. Then, according to the above introduction of the fault-tolerant control method, it can be seen that when the FPFTPM motor has a single-phase open-circuit fault, the fault-tolerant control can be realized in the dq axis coordinate system by the reduced-order transformation. However, the use of the reduced-order transformation matrix makes the control system different between normal operation and fault operation, which will greatly increase the complexity of the sensorless drive control system, and the estimated performance under fault conditions will be degraded.
- The problem 1 will further aggravate the problem 2.
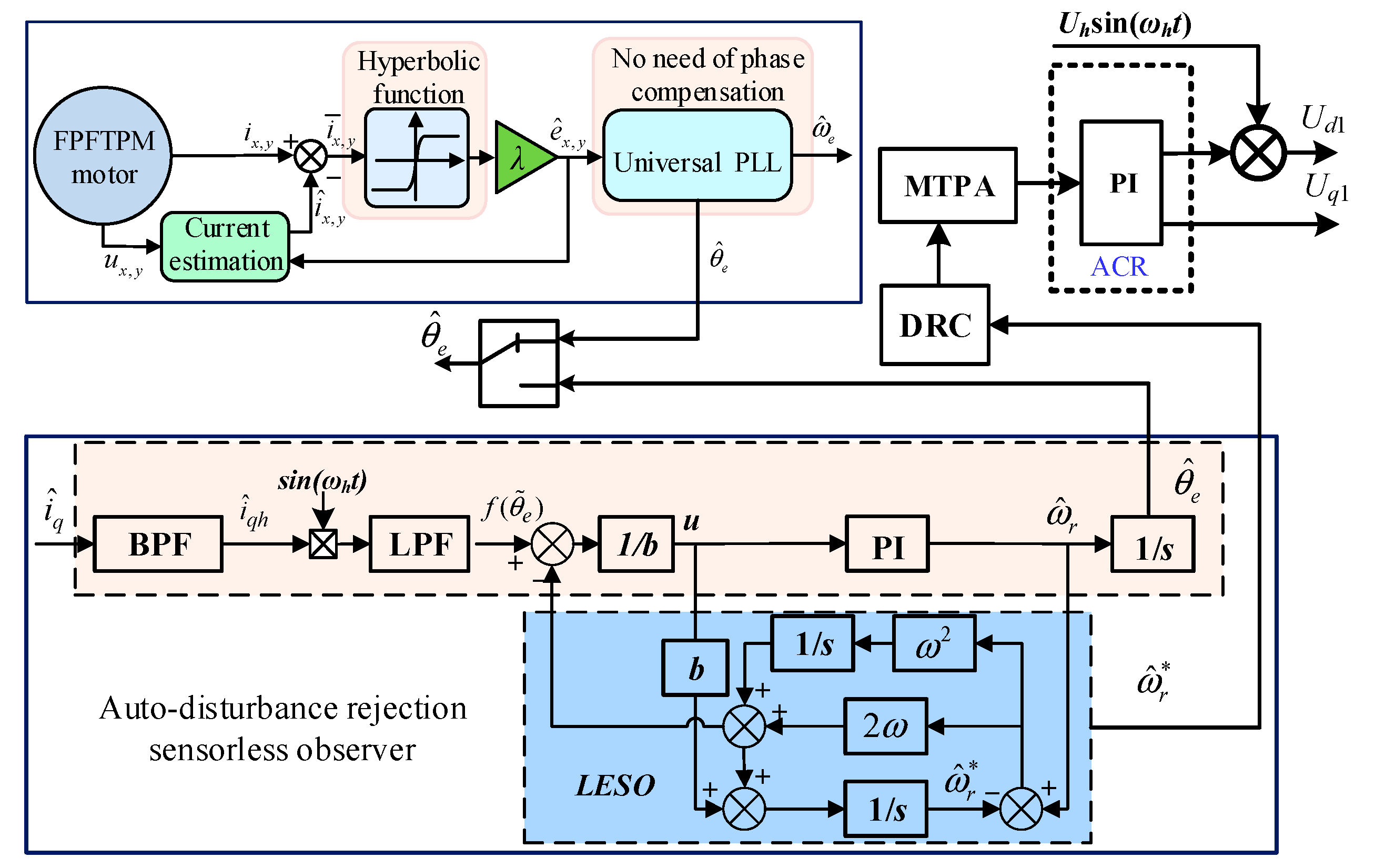
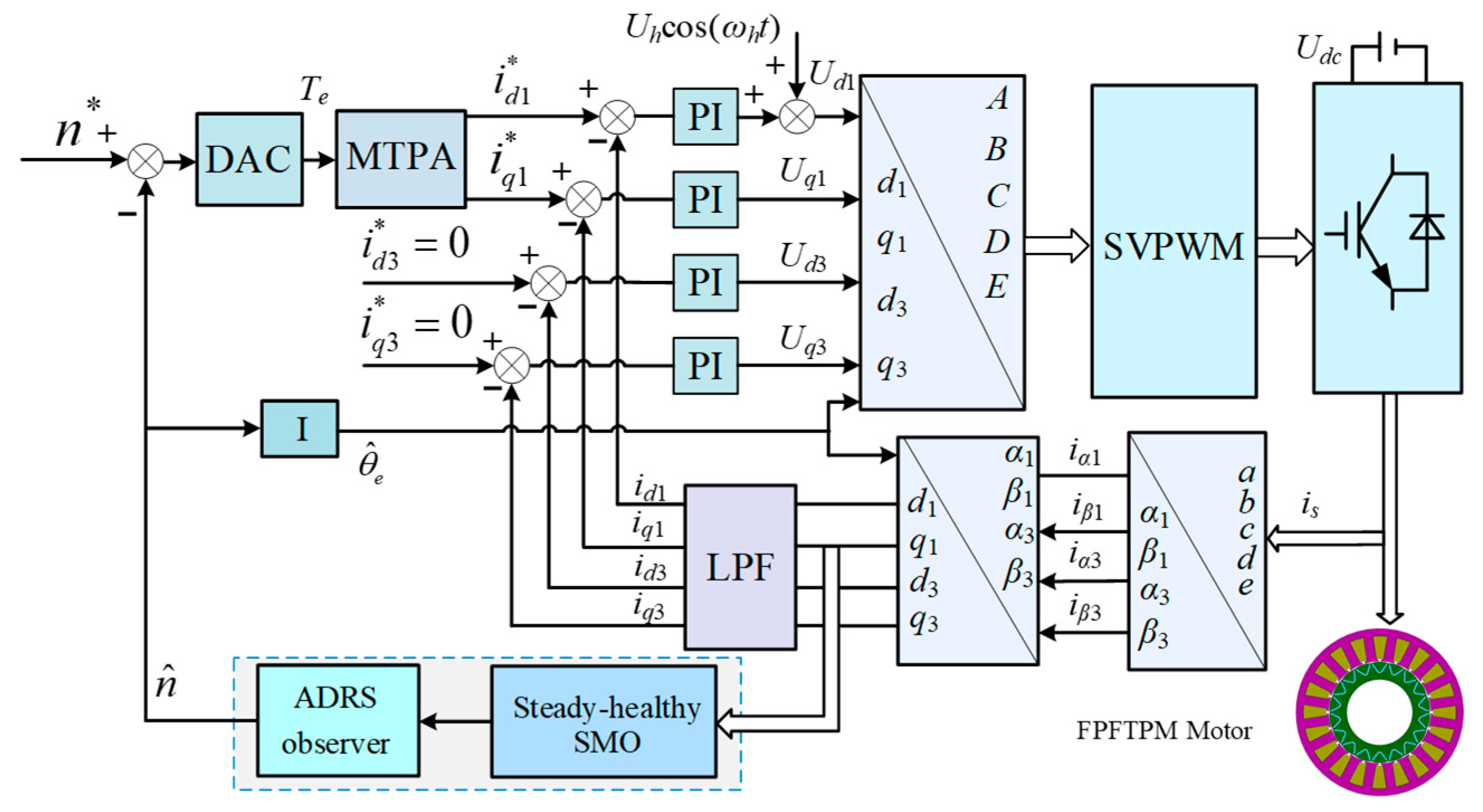
4. Fault-Tolerant Sensorless Control Based on HARO Scheme
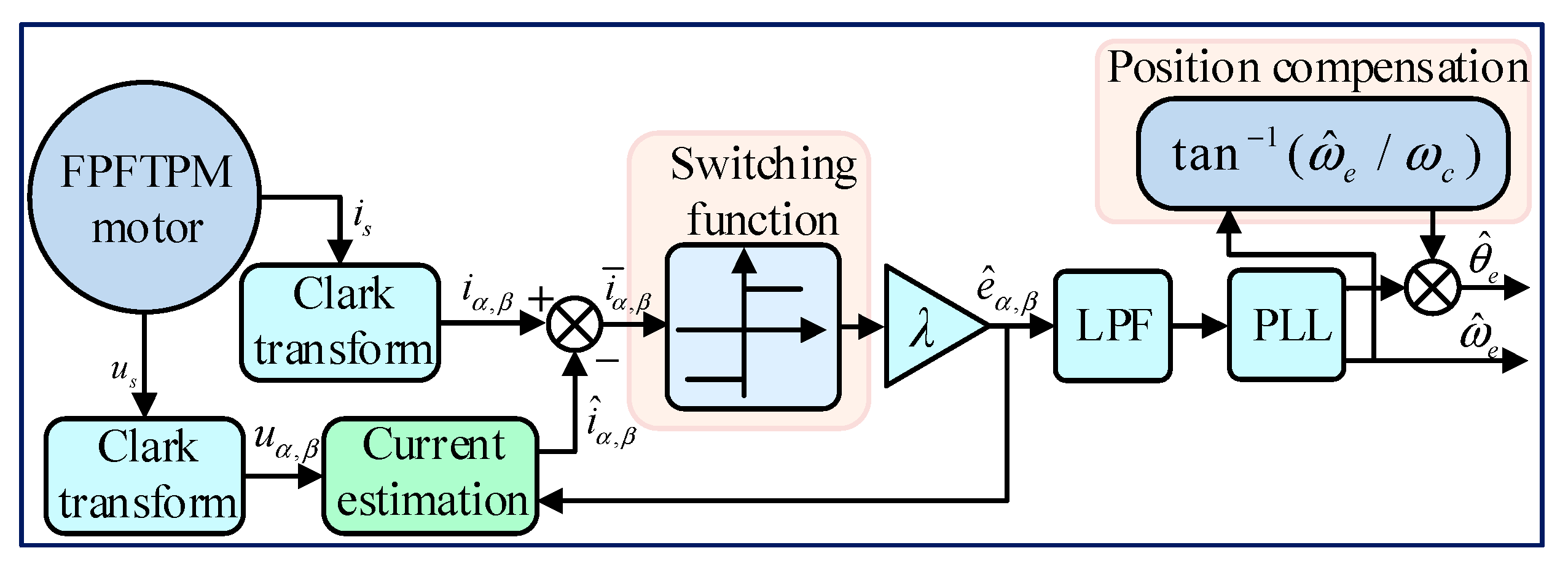
4.1. Steady-Healthy SMO for Medium/High-Speed Operation
4.2. DAC Architecture for Zero/Low-Speed Operation
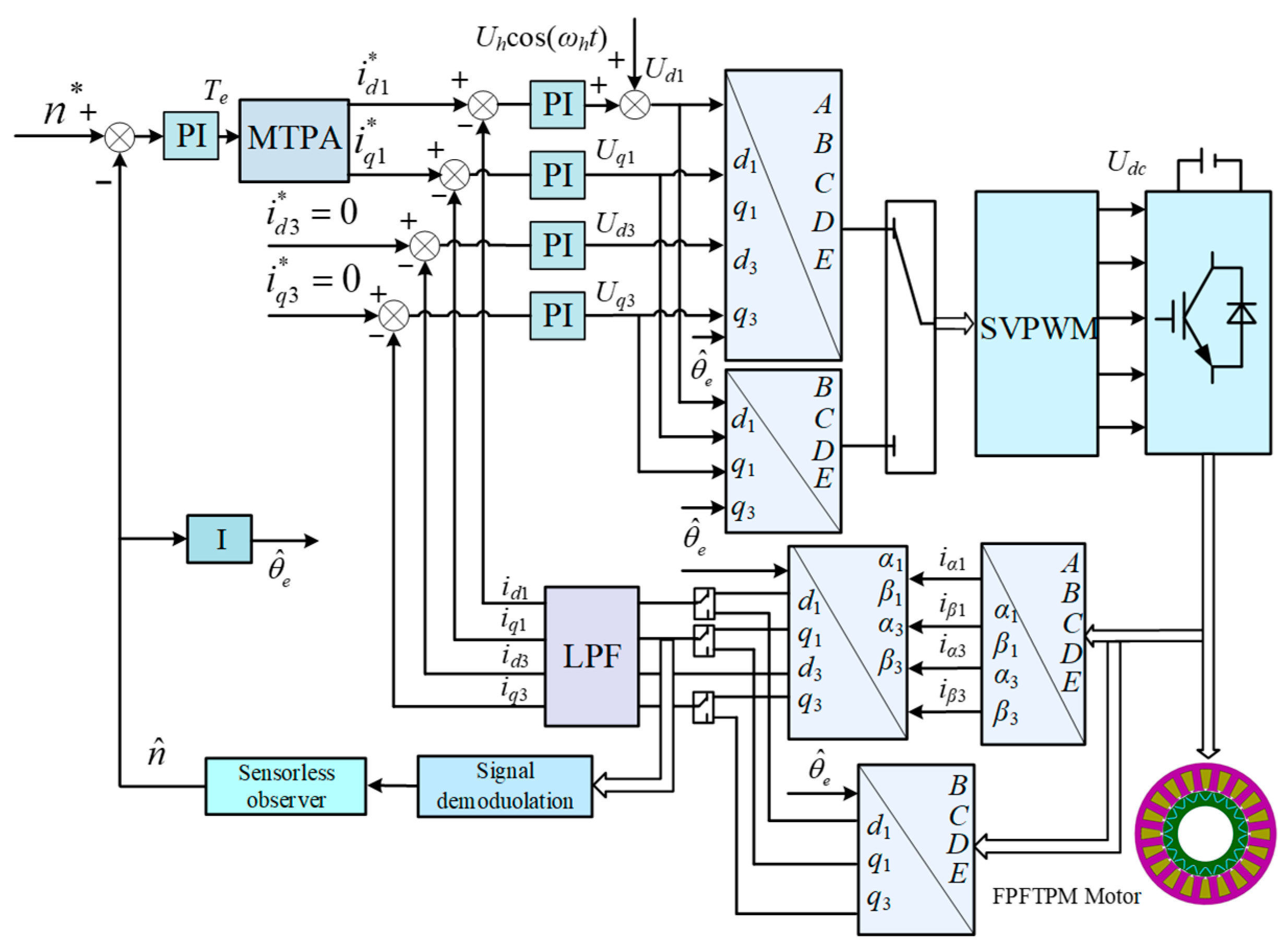
5. FPFTPM Motor Sensorless Control Drive System
6. Verification Results
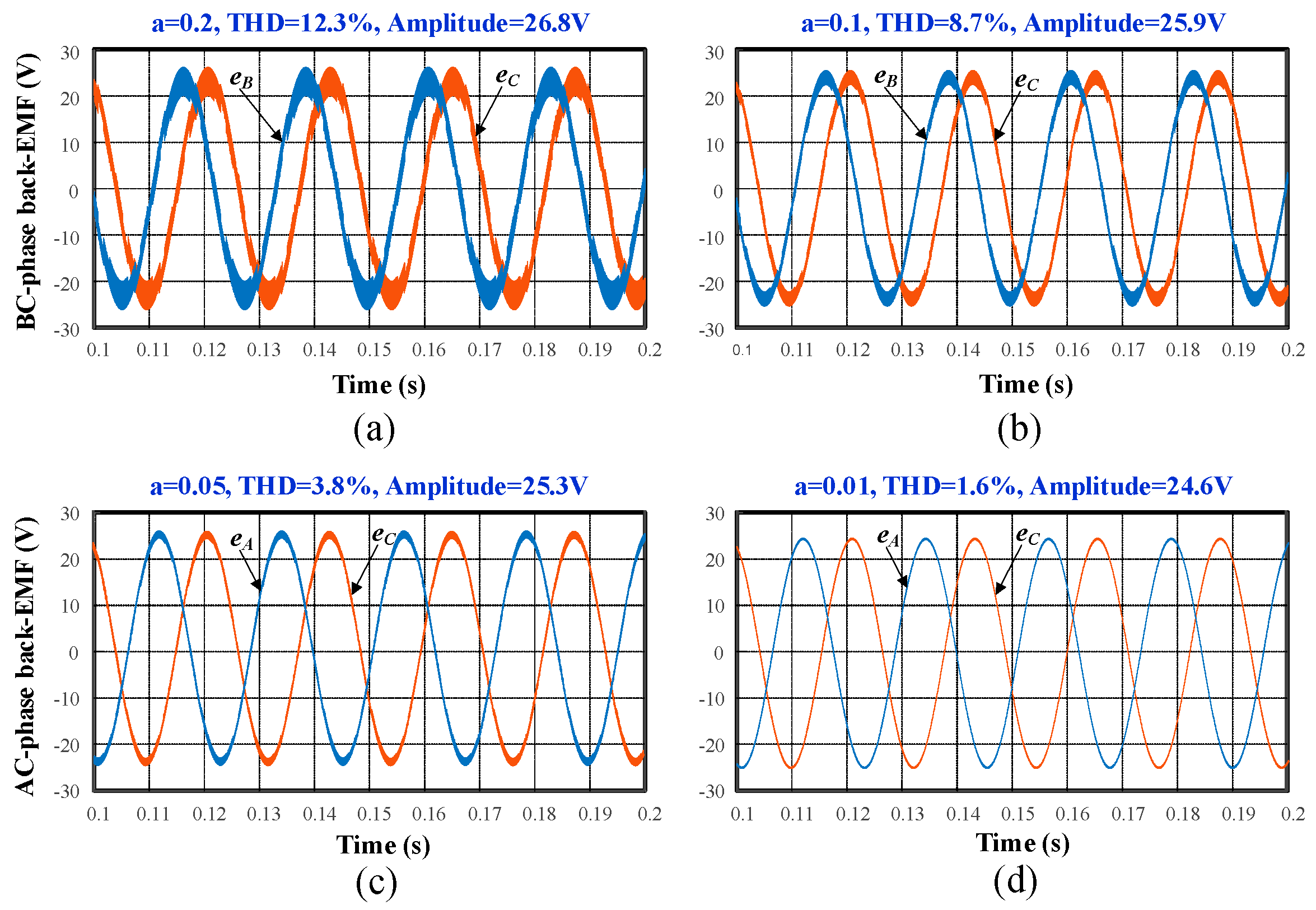
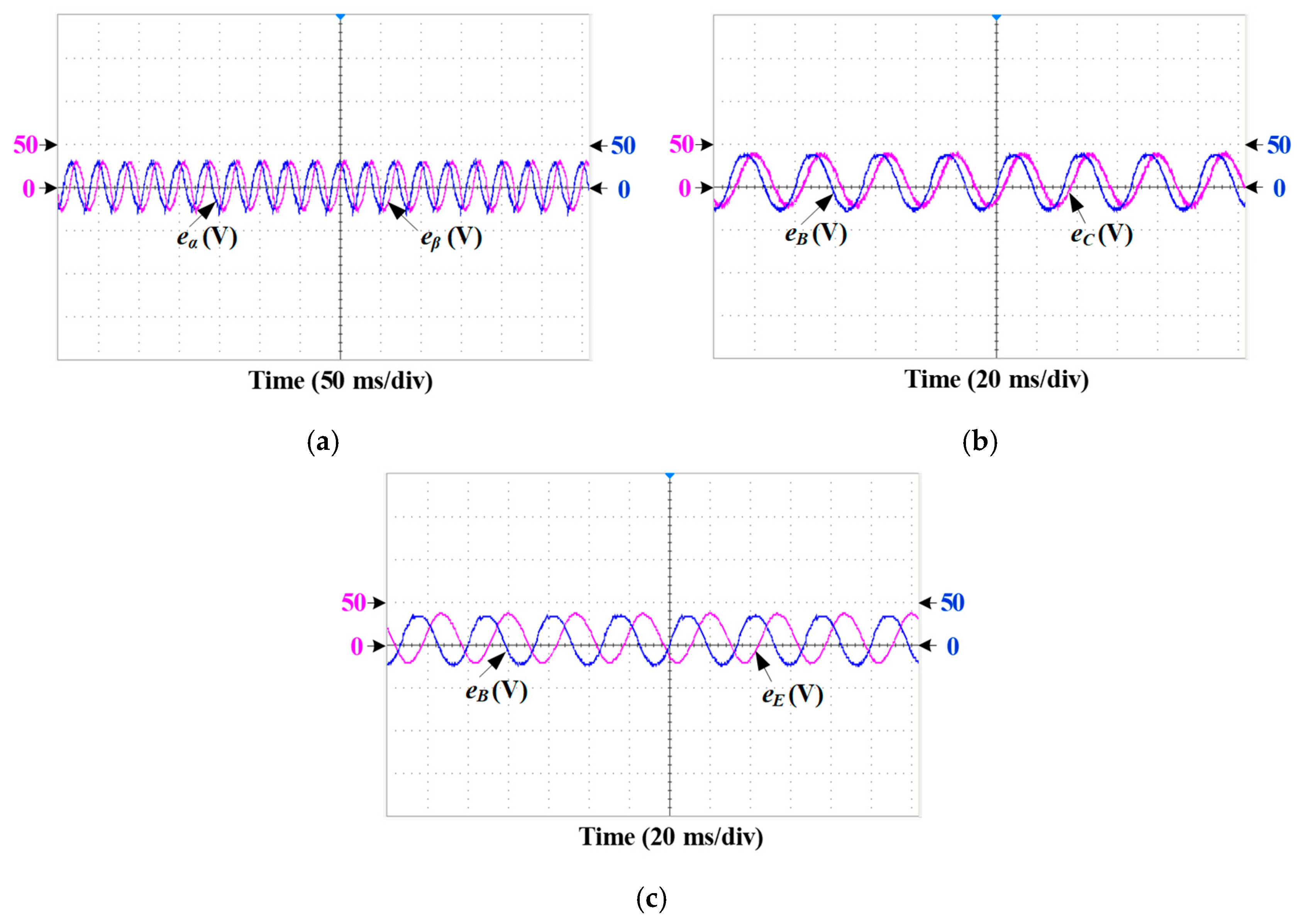
6.1. Steady-State Performance
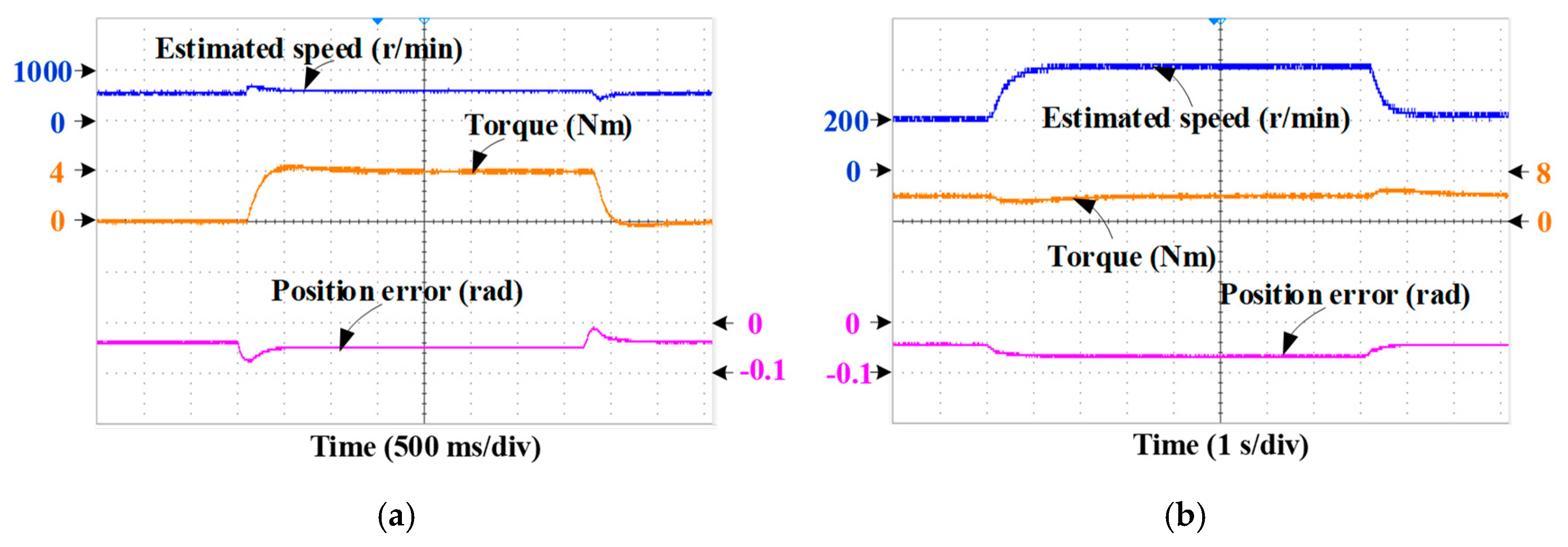
6.2. Dynamic-State Performance
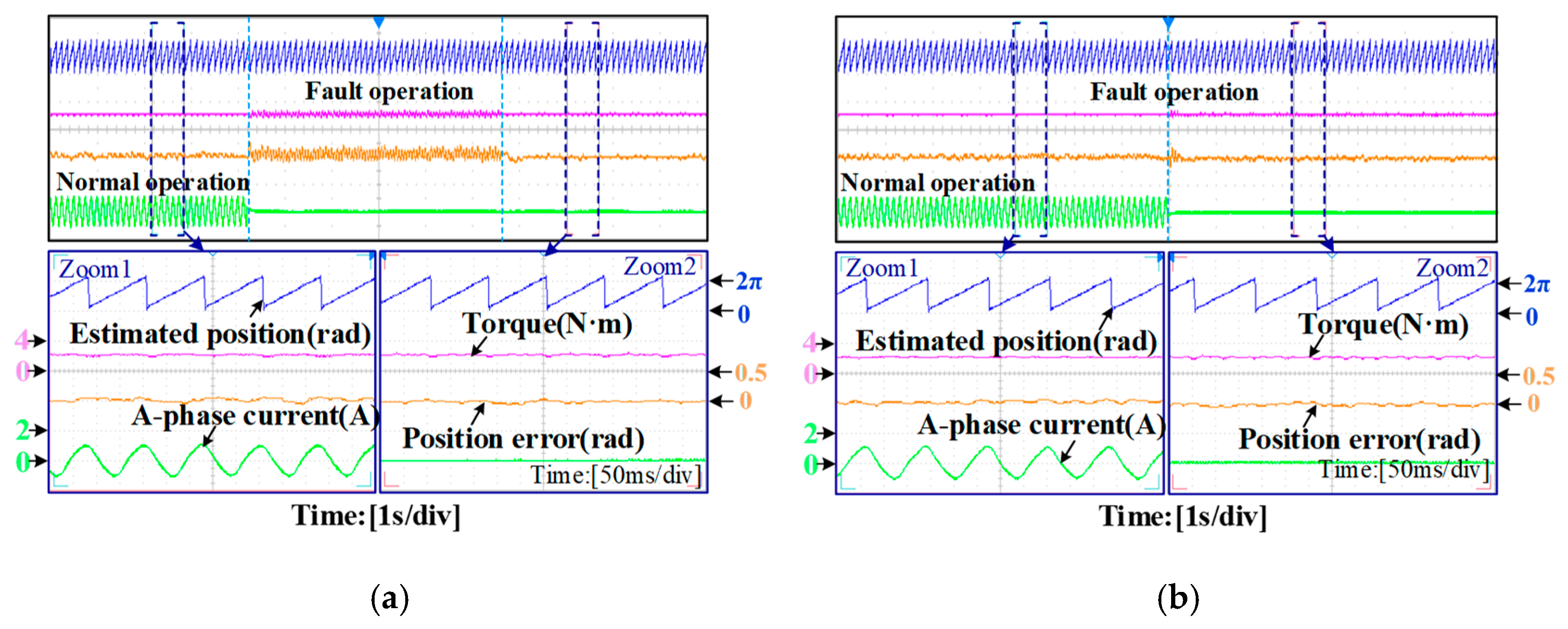
6.3. Fault Operating Performance
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhu, Z.; Chai, X.; Xu, L.; Quan, L.; Yuan, C.; Tian, S. Design and performance of a distributed electric drive system for a series hybrid electric combine harvester. Biosyst. Eng. 2023, 236, 160–174. [Google Scholar] [CrossRef]
- Li, H.; Chen, L.; Zhang, Z. A Study on the Utilization Rate and Influencing Factors of Small Agricultural Machinery: Evidence from 10 Hilly and Mountainous Provinces in China. Agriculture 2023, 13, 51. [Google Scholar] [CrossRef]
- Han, J.; Wang, F. Design and Testing of a small orchard tractor driven by a power battery. Eng. Agric. 2023, 43, e20220195. [Google Scholar]
- Yuan, J.; Ji, W.; Feng, Q. Robots and Autonomous Machines for Sustainable Agriculture Production. Agriculture 2023, 13, 1340. [Google Scholar] [CrossRef]
- Hu, J.; Zhao, X.; Liu, W.; Yao, M.; Zhao, J. Development of a Seeding Control Method Based on Seed Height in the Hopper of a Precision Wheat Drill. Appl. Eng. Agric. 2021, 37, 1131–1138. [Google Scholar] [CrossRef]
- Zhu, Q.; Zhu, Z.; Zhang, H.; Gao, Y.; Chen, L. Design of an Electronically Controlled Fertilization System for an Air-Assisted Side-Deep Fertilization Machine. Agriculture 2023, 13, 2210. [Google Scholar] [CrossRef]
- Li, J.; Shang, Z.; Li, R.; Cui, B. Adaptive Sliding Mode Path Tracking Control of Unmanned Rice Transplanter. Agriculture 2022, 12, 1225. [Google Scholar] [CrossRef]
- Lu, E.; Xue, J.; Chen, T.; Jiang, S. Robust Trajectory Tracking Control of an Autonomous Tractor-Trailer Considering Model Parameter Uncertainties and Disturbances. Agriculture 2023, 13, 869. [Google Scholar] [CrossRef]
- Cui, B.; Cui, X.; Wei, X.; Zhu, Y.; Ma, Z.; Zhao, Y.; Liu, Y. Design and Testing of a Tractor Automatic Navigation System Based on Dynamic Path Search and a Fuzzy Stanley Model. Agriculture 2024, 14, 2136. [Google Scholar] [CrossRef]
- Shi, J.; Hu, J.; Li, J.; Liu, W.; Yue, R.; Zhang, T.; Yao, M. Design and Experiment of Planting Mechanism of Automatic Transplanter for Densely Planted Vegetables. Agriculture 2024, 14, 1357. [Google Scholar] [CrossRef]
- Shi, Q.; Liu, D.; Mao, H.; Shen, B.; Li, M. Wind-induced response of rice under the action of the downwash flow field of a multi-rotor UAV. Biosyst. Eng. 2021, 203, 60–69. [Google Scholar] [CrossRef]
- Shi, Y.; Lorenz, R.D.; Valenzuela, A.M. New developments in loss minimizing control for drives without compromising torque dynamics. IEEE Trans. Ind. Appl. 2016, 6, 5327–5335. [Google Scholar] [CrossRef]
- Li, X.L.; Wang, X.Y.; Yu, S.Y. Design and analysis of a novel transverse-flux tubular linear switched reluctance machine for minimizing force ripple. IEEE Trans. Ind. Electron. 2020, 7, 741–753. [Google Scholar] [CrossRef]
- Yang, S.; Zhai, C.; Gao, Y.; Dou, H.; Zhao, X.; He, Y.; Wang, X. Planting Uniformity Performance of Motor-Driven Maize Precision Seeding Systems. Int. J. Agric. Biol. Eng. 2022, 15, 101–108. [Google Scholar] [CrossRef]
- Yu, Y.; Hao, S.; Guo, S.; Tang, Z.; Chen, S. Motor Torque Distribution Strategy for Different Tillage Modes of Agricultural Electric Tractors. Agriculture 2022, 12, 1373. [Google Scholar] [CrossRef]
- Liu, J.; Xia, C.; Jiang, D.; Sun, Y. Development and testing of the power transmission system of a crawler electric tractor for greenhouses. Appl. Eng. Agric. 2020, 36, 797–805. [Google Scholar] [CrossRef]
- Liu, H.; Yan, S.; Shen, Y.; Li, C.; Zhang, Y.; Hussain, F. Model predictive control system based on direct yaw moment control for 4WID self-steering agriculture vehicle. Int. J. Agric. Biol. Eng. 2021, 14, 175–181. [Google Scholar] [CrossRef]
- Li, J.; Wu, Z.; Li, M.; Shang, Z. Dynamic Measurement Method for Steering Wheel Angle of Autonomous Agricultural Vehicles. Agriculture 2024, 14, 1602. [Google Scholar] [CrossRef]
- Sun, J.; Wang, Z.; Ding, S.; Xia, J.; Xing, G. Adaptive disturbance observer-based fixed time nonsingular terminal sliding mode control for path-tracking of unmanned agricultural tractors. Biosyst. Eng. 2024, 246, 96–109. [Google Scholar] [CrossRef]
- Lu, E.; Ma, Z.; Li, Y.M.; Xu, L.Z.; Tang, Z. Adaptive backstepping control of tracked robot running trajectory based on real-time slip parameter estimation. Int. J. Agric. Biol. Eng. 2020, 13, 178–187. [Google Scholar] [CrossRef]
- Zhu, Z.; Yang, Y.; Wang, D.; Cai, Y.; Lai, L. Energy Saving Performance of Agricultural Tractor Equipped with Mechanic-Electronic-Hydraulic Powertrain System. Agriculture 2022, 12, 436. [Google Scholar] [CrossRef]
- Zhang, B.; Bai, T.; Wu, G.; Wang, H.; Zhu, Q.; Zhang, G.; Meng, Z.; Wen, C. Fatigue Analysis of Shovel Body Based on Tractor Subsoiling Operation Measured Data. Agriculture 2024, 14, 1604. [Google Scholar] [CrossRef]
- Zhu, Y.; Cui, B.; Yu, Z.; Gao, Y.; Wei, X. Tillage Depth Detection and Control Based on Attitude Estimation and Online Calibration of Model Parameters. Agriculture 2024, 14, 2130. [Google Scholar] [CrossRef]
- Ahmed, S.; Qiu, B.; Ahmad, F.; Kong, C.W.; Xin, H. A state-of-the-art analysis of obstacle avoidance methods from the perspective of an agricultural sprayer UAV’s operation scenario. Agronomy 2021, 11, 1069. [Google Scholar] [CrossRef]
- Zhang, L.; Li, X.Q.; Zhu, X.Y.; Zhang, C.H. Design and Optimization of a Five-Phase Reverse-Salient Fault-Tolerant Permanent Magnet Motor for Electric Vehicles. IEEE. Trans. Ind. Electron 2024. early access. [Google Scholar] [CrossRef]
- Wu, H.; Zhang, J.; Ding, S.; Huang, Y.; Hua, W. Cost function-based open-phase fault diagnosis for PMSM drive system with model predictive current control. IEEE Trans. Power Electron. 2021, 36, 2574–2583. [Google Scholar] [CrossRef]
- Zhang, L.; Fan, Y.; Lorenz, R.D.; Nied, A.; Cheng, M. Design and comparison of three-phase and five-phase FTFSCW-IPM motor open-end winding drive systems for electric vehicles applications. IEEE Trans. Veh. Technol. 2018, 67, 385–396. [Google Scholar] [CrossRef]
- Zhang, L.; Fan, Y.; Cui, R.H.; Lorenz, R.D.; Cheng, M. Fault-tolerant direct torque control of five-phase FTFSCW-IPM motor based on analogous three-phase SVPWM for electric vehicle applications. IEEE Trans. Veh. Technol. 2018, 67, 910–919. [Google Scholar] [CrossRef]
- Tang, L.; Wang, W.; Zhang, C.; Wang, Z.; Ge, Z.; Yuan, S. Linear Active Disturbance Rejection Control System for the Travel Speed of an Electric Reel Sprinkling Irrigation Machine. Agriculture 2024, 14, 1544. [Google Scholar] [CrossRef]
- Gao, Y.; Feng, K.; Yang, S.; Han, X.; Wei, X.; Zhu, Q.; Chen, L. Design and Experiment of an Unmanned Variable-Rate Fertilization Control System with Self-Calibration of Fertilizer Discharging Shaft Speed. Agronomy 2024, 14, 2336. [Google Scholar] [CrossRef]
- He, Y.; Zhu, Q.; Fu, W.; Luo, C.; Cong, Y.; Qin, W.; Meng, Z.; Chen, L.; Zhao, C.; Wu, G.J. Design and experiment of a control system for sweet potato seedling-feeding and planting device based on a pre-treatment seedling belt. J. Agric. Eng. 2022, 53, 187–196. [Google Scholar]
- Dai, D.; Chen, D.; Wang, S.; Li, S.; Mao, X.; Zhang, B.; Wang, Z.; Ma, Z. Compilation and Extrapolation of Load Spectrum of Tractor Ground Vibration Load Based on CEEMDAN-POT Model. Agriculture 2023, 13, 125. [Google Scholar] [CrossRef]
- Chen, Y.; Chen, L.; Wang, R.; Xu, X.; Shen, Y.; Liu, Y. Modeling and test on height adjustment system of electrically-controlled air suspension for agricultural vehicles. Int. J. Agric. Biol. Eng. 2016, 9, 40–47. [Google Scholar]
- Li, Y.; Xu, L.; Lv, L.; Shi, Y.; Yu, X. Study on Modeling Method of a Multi-Parameter Control System for Threshing and Cleaning Devices in the Grain Combine Harvester. Agriculture 2022, 12, 1483. [Google Scholar] [CrossRef]
- Gao, Y.; Yang, Y.; Fu, S.; Feng, K.; Han, X.; Hu, Y.; Zhu, Q.; Wei, X. Analysis of Vibration Characteristics of Tractor–Rotary Cultivator Combination Based on Time Domain and Frequency Domain. Agriculture 2024, 14, 1139. [Google Scholar] [CrossRef]
- Ding, Z.; Tang, Z.; Zhang, B.; Ding, Z. Vibration Response of Metal Plate and Shell Structure under Multi-Source Excitation with Welding and Bolt Connection. Agriculture 2024, 14, 816. [Google Scholar] [CrossRef]
- Xu, Y.; Wang, Y.; Iida, R.; Lorenz, R.D. Extending low-speed self-sensing via flux tracking with volt-second sensing. IEEE Trans. Ind. Appl. 2018, 54, 4405–4414. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, M.; Zhu, X.Y.; Pei, Z.F.; Chen, X. Space Decoupling Sensorless Control of Five-Phase Flux-Intensifying PM Motor Based on AFCCF-SMO Considering Flux-Weakening Operation. IEEE Trans. Ind. Electron. 2024. early access. [Google Scholar] [CrossRef]
- Xu, S.; Wang, D.; Wang, B.; Wang, X.; Miao, W.; Wang, X. Sideband electromagnetic vibrations in interior PMSM with high frequency pulsating injection sensorless control. IEEE Trans. Energy Convers. 2024, 39, 1919–1929. [Google Scholar] [CrossRef]
- Zhu, Z.; Zeng, L.; Chen, L.; Zou, R.; Cai, Y. Fuzzy Adaptive Energy Management Strategy for a Hybrid Agricultural Tractor Equipped with HMCVT. Agriculture 2022, 12, 1986. [Google Scholar] [CrossRef]
- Yue, R.; Yao, M.; Zhang, T.; Shi, J.; Zhou, J.; Hu, J. Design and Experiment of Dual-Row Seedling Pick-Up Device for High-Speed Automatic Transplanting Machine. Agriculture 2024, 14, 942. [Google Scholar] [CrossRef]
- Green, S.; Atkinson, D.J.; Jack, A.G.; Mecrow, B.C.; King, A. Sensorless operation of a fault tolerant PM drive. IEE Proc.—Electr. Power Appl. 2003, 150, 117–125. [Google Scholar] [CrossRef]
- Zhang, L.; Fan, Y.; Li, C.X.; Nied, A.; Cheng, M. Fault-tolerant sensorless control of five-phase FTFSCW-IPM motor based on a wide-speed strong-robustness sliding mode observer. IEEE Trans. Energy Convers. 2018, 33, 87–95. [Google Scholar] [CrossRef]
- Xu, J.; Du, Y.; Zhang, B.; Fang, H.; Guo, H.; Chen, Y. Sensorless fault tolerant control with phase delay compensation for aerospace FTPMSM drives with phase open-circuit and short-circuit faults. IEEE Trans. Ind. Electron. 2020, 68, 4576–4585. [Google Scholar] [CrossRef]
- Gaeta, A.; Scelba, G.; Consoli, A. Sensorless vector control of pm synchronous motors during single-phase open-circuit faulted conditions. IEEE Trans. Ind. Appl. 2013, 48, 1968–1979. [Google Scholar] [CrossRef]
- Saleh, K.; Sumner, M. Sensorless control of Fault Tolerant PMSM drives in case of single-phase open circuit fault. In Proceedings of the 2016 International Symposium on Power Electronics, Electrical Drives, Automation and Motion (SPEEDAM) 2016, Capri, Italy, 22–24 June 2016; pp. 528–534. [Google Scholar]
- Saghafinia, A.; Ping, H.W.; Uddin, M.N.; Gaeid, K.S. Adaptive fuzzy sliding-mode control into chattering-free IM drive. IEEE Trans. Ind. Appl. 2015, 51, 692–701. [Google Scholar] [CrossRef]
- Zhang, L.; Zhu, X.Y.; Xu, L.; Fan, D.Y. Sturdy Design of New Five-Phase Flux-Intensifying Fault-Tolerant Permanent-Magnet Motor Drive System for Healthy and Fault-Tolerant Sensorless Operation. IEEE Trans. Ind. Appl. 2023, 59, 1699–1708. [Google Scholar] [CrossRef]
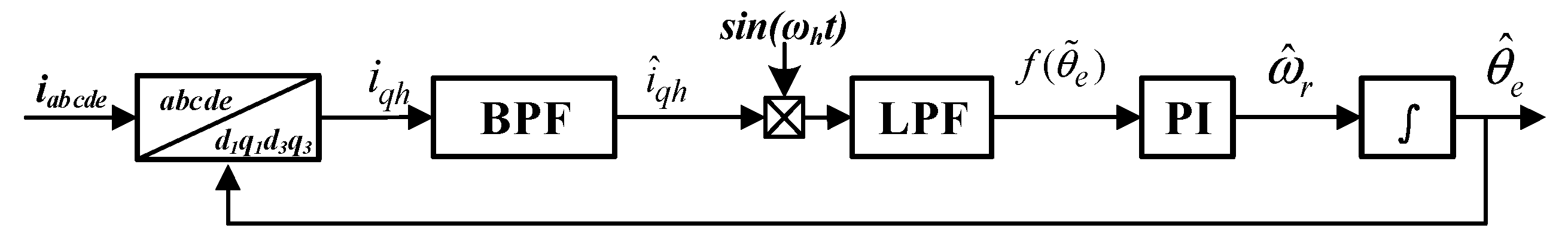








| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Rated power | 2 kW | PM flux-linkage | 0.089 Wb |
| Rated phase current | 4.75 A | Stator resistance | 0.5 Ω |
| Number of rotor pole-pair | 9 | d-axis inductance | 13.5 mH |
| Number of stator slot | 20 | q-axis inductance | 14.7 mH |
| Operating Condition | Torque Ripple | Speed Error | Position Error | |
|---|---|---|---|---|
| Medium/high speed | Conventional | 1.25% | 5 rpm | 0.2 rad |
| Proposed SMO | 1% | 2 rpm | 0.07 rad | |
| Zero/low speed | Conventional | 2.25% | 20.2 rpm | 0.642 rad |
| DAC strategy | 1.5% | 15.4 rpm | 0.325 rad | |
| Fault-tolerant | Conventional | 8.5% | 21 rpm | 0.12 rad |
| HARO strategy | 2.5% | 4 rpm | 0.04 rad | |
| varying parameters | Before parameters change | 1% | 2 rpm | 0.08 rad |
| After parameters change | 1.5% | 4 rpm | 0.1 rad | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pei, Z.; Zhang, L.; Fu, H.; Wang, Y. New Fault-Tolerant Sensorless Control of FPFTPM Motor Based on Hybrid Adaptive Robust Observation for Electric Agricultural Equipment Applications. Energies 2025, 18, 1962. https://doi.org/10.3390/en18081962
Pei Z, Zhang L, Fu H, Wang Y. New Fault-Tolerant Sensorless Control of FPFTPM Motor Based on Hybrid Adaptive Robust Observation for Electric Agricultural Equipment Applications. Energies. 2025; 18(8):1962. https://doi.org/10.3390/en18081962
Chicago/Turabian StylePei, Zifeng, Li Zhang, Haijun Fu, and Yucheng Wang. 2025. "New Fault-Tolerant Sensorless Control of FPFTPM Motor Based on Hybrid Adaptive Robust Observation for Electric Agricultural Equipment Applications" Energies 18, no. 8: 1962. https://doi.org/10.3390/en18081962
APA StylePei, Z., Zhang, L., Fu, H., & Wang, Y. (2025). New Fault-Tolerant Sensorless Control of FPFTPM Motor Based on Hybrid Adaptive Robust Observation for Electric Agricultural Equipment Applications. Energies, 18(8), 1962. https://doi.org/10.3390/en18081962





