Abstract
The increasing integration of resources with limited flexibility, such as solar power, electric vehicles (EVs), and other renewable energy sources, has raised significant concerns regarding power system stability. The stability of power systems is constantly threatened, particularly in cases where renewable energy is supplied to areas near generators, as transmission capacity constraints may lead to severe stability issues. The impact of renewable energy integration on system stability can be analyzed using transient stability and phase-angle stability theories. This study proposes a methodology to quantify the effects of renewable energy integration on transient stability. A power-phase angle curve is plotted using the Thevenin impedance calculation technique, and an improved equal-area method index is utilized to evaluate transient stability issues caused by renewable energy penetration. The proposed transient stability discrimination index (TSDI) is used to assess system stability in real-time conditions. Simulation results demonstrate that the proposed method achieves an accuracy of over 90% in ranking transient stability compared to conventional offline stability analysis. Furthermore, a correlation coefficient of 0.85 is observed between the proposed TSDI and the existing wide-area voltage stability index (WAVI), confirming the reliability of the method. These findings suggest that, when real-time Phasor Measurement Unit (PMU) data are available, the proposed approach can be effectively applied to practical power systems for enhanced stability assessment.
1. Introduction
Currently, in Korea, several new technology facilities, such as HVDC and FACT, have been installed and operated in response to the continuous increase in renewable energy and transmission volume. The uncertainty about the operation of power systems is increasing because of the uncertainty from rigid power sources, such as renewable energy, and the complex operation of new technology facilities. As a countermeasure, research on the monitoring and control of the systems using real-time data is continuously conducted; however, research on the Jeju system has not been as actively conducted as that on the land system. Jeju Island is the most active area in Korea for the expansion and supply of renewable energy; however, the load of the system is small, and it is an independent system linked to HVDC with land. In this study, to resolve the uncertainty of the current and future operation of the Jeju power system, an index is proposed to determine transient stability in real time using the Thevenin impedance calculation technique. As mentioned earlier, for special and complex systems such as the Jeju system, the Thevenin impedance of the power system can be estimated based on real-time data, and the transient stability can be determined. This could contribute to the stable operation of the power system by expanding it in the future and reflecting it in the operation of the land system.
According to the recently announced KOREA 10th power supply and demand plan, the solar and wind facility plans for 2024 are 324 and 581 MW, respectively. However, solar and wind facility plans for 2036 are expected to increase by approximately seven times to approximately 2345 and 1586 MW, respectively [1]. Therefore, approximately 3 GW of renewable energy will be added over the next 10 years. However, when renewable energy is connected to a power system, it has numerous advantages, as well as fatal disadvantages. Unlike conventional generators, renewable energy sources have rigid power characteristics and cannot actively control active and reactive power. In addition, because these sources do not provide sufficient rotational inertia, transient stability problems may arise in the event of large-scale disturbances, such as generator dropouts and transmission line faults.
In addition, because the rotator does not provide sufficient inertial energy, problems with transient stability may arise in the event of large-scale disturbances, such as generator dropouts and track drops [2]. If renewable energy access continues to increase, the impact of the transient stability problems that may arise on the power system must be considered. Unexpected situations can occur in a power system, such as sudden increases in load, track drops, or generator drops. Stability can be interpreted from several perspectives. Among them, the stability interpretation that is typically considered is phase-angle stability. The phase-angle stability was also reclassified to include transient and small signal stability [3,4,5,6]. In particular, transient stability is a phenomenon that significantly affects the stability of a power system and refers to an unexpected situation or an unstable reaction state in which the power system shows interference for a short time. A power system consists of various components such as power plants, electric wires, and substations, and power flows such as voltage, current, and frequency are generated between them [7,8,9]. In this case, the possibility of a transient stability problem may increase if the dynamic interaction between components is not stably controlled. When a generator drops or a track accident occurs, the frequency decreases, and the voltage becomes unstable, resulting in synchronous degeneration in serious cases. This is often associated with transient stability. Transient stability can also be expressed as the ability to maintain and recover synchronization. Failure to maintain synchronization in a power system can lead to major disturbances and cause an imbalance between the power supply and demand [10,11,12].
Currently, many substations and power plant systems have a Phasor Measurement Unit (PMU) installed at key points. A PMU is a device that can measure the key variables of a power system in real time with high resolution; thus, it is possible to accurately grasp and monitor the state of the power system. Numerous studies have been conducted owing to these advantages. One of the methods for evaluating the voltage stability using a PMU is the wide-area voltage stability index (WAVI). The WAVI is a method for determining voltage stability using the maximum transmission law by dividing the system into power generation and load areas using real-time phasor information of the voltage and current acquired from the PMU [13,14,15,16,17]. In addition, research is underway to calculate the Thevenin impedance using the PMU data and plot a power-phase angle curve. Thus, an area method such as determining the transient stability using the power-phase difference angle curve may also be used [18,19].
In the past, methods for determining transient stability using Korean power system data were primarily used. Many studies have used static data rather than real-time data. Representative methods include determining the transient stability using the difference in the phase angle of the generator by eliminating the generator from the system. Each real generator has its inertia. After an accident, if it does not immediately stabilize as soon as it moves to a new equilibrium point of inertia, the phase difference angle fluctuates around the equilibrium point for a certain period. In this situation, synchronous degeneration occurs when the magnitude of the phase-difference angle exceeds the unstable range above the transient stable extreme power. Accordingly, the kinetic energy and effective power change rates of the generators were reviewed. The effective power change rate was that if a failure occurred near the power generation stage in the system, the electricity produced by the generator could not be effectively transferred, resulting in the release of significantly less electrical energy compared to the mechanical energy in the generator. Using the energy action that accelerates the rotation of the generator, the degree of influence of the generator was examined by observing the rate of change in the tide flowing through the transmission line when the generator was dropped. In addition, based on the kinetic energy, the greater the rotational kinetic energy among the generators experiencing degeneration in the event of a failure, the greater the energy reduction effect in the event of a generator dropout, which was used to analyze the transient stability [20,21,22,23,24]. In addition, a method was proposed for confirming that the electrical output of the equivalent generator increased and the mechanical output decreased after reconstructing the stability index for the maximum export (SIME) analysis after shutting off the generator [25,26,27].
In this study, the Thevenin impedance was estimated using real-time data, unlike the previously studied voltage stability monitoring index and transient stability monitoring methods. Using this approach, an index was presented to determine transient stability through the improved equal-area method by plotting a power-phase angle curve. The proposed index can determine the current degree of transitional stability in real time for possible future failures. This is an index that can visually provide the transient stability level to the system operator. In the future, a method will be presented for determining changes in transient stability due to continuous renewable energy connections.
The core research question addressed in this study is as follows:
“How can transient stability be assessed in real time with limited system-wide data, particularly in the presence of high renewable energy penetration?”
To answer this question, a novel real-time transient stability assessment method is proposed. Unlike conventional approaches that require extensive offline simulations and full system information, this method utilizes only real-time Phasor Measurement Unit (PMU) data to determine transient stability. The key innovations of this study include the following:
- Thevenin Impedance-Based Stability Assessment
The proposed method estimates Thevenin equivalent impedance dynamically using PMU measurements, allowing for real-time stability monitoring without requiring detailed system modeling.
- b.
- Integration of an Improved Equal Area Criterion (EAC)
While the Equal Area Criterion (EAC) is traditionally applicable only to a single-machine infinite bus (SMIB) system, this study reinterprets EAC by introducing a new reference bus, enabling its application to complex multi-machine power systems.
- c.
- Introduction of a Transient Stability Discrimination Index (TSDI)
A new transient stability discrimination index (TSDI) is introduced, which provides a stability ranking rather than an exact critical clearing time (CCT), making it a computationally efficient tool for real-time grid operations.
This study differs from previous research in the following key aspects:
- Real-Time Application:
Conventional transient stability assessment methods rely on full system modeling and offline simulations, whereas the proposed method enables real-time assessment using only PMU data and Thevenin impedance estimation.
- b.
- Practicality for Renewable Energy-Dominant Grids:
Traditional methods often assume synchronous machine dynamics, which do not fully account for the increasing presence of inverter-based renewable energy sources (RESs).
The proposed method provides a generalized approach that can be applied to modern grids with high RES penetration, where conventional synchronous-based approaches may no longer be effective.
- c.
- Computational Efficiency:
The proposed method does not require solving complex time-domain simulations, significantly reducing computational overhead, and making it feasible for real-time control center applications.
Section 2 explains the process of calculating the Thevenin impedance, which is a parameter for determining transient stability, using the Thevenin impedance calculation technique. Section 3 introduces the transient stability and equal-area methods. In Section 4, the parameters required by the equal-area method mentioned in Section 3 are measured and calculated using case studies. In Section 5, the future development prospects of the discrimination theory are briefly presented along with a review of the results.
2. Estimating the Thevenin Impedance Method
This technique is more efficient when installed in all power plants or PMU loads, which are real-time data. However, in the current situation, the PMUs are not installed on the entire bus assuming that the real-time data of the PMU were acquired. This study proposed a Thevenin impedance estimation technique using off-line data. Thevenin impedance should replace the connection between complex bus lines of the power system in the form of a Thevenin equivalent circuit from the perspective of an electrical circuit as shown in Figure 1. Based on this, Thevenin impedance with VL, VTh, ZL, ZTh could be configured.
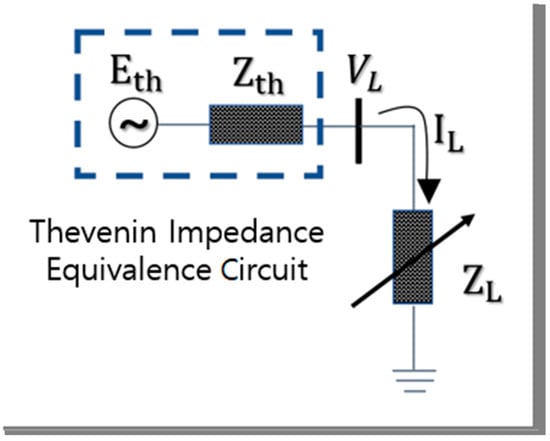
Figure 1.
Conceptual diagram of Thevenin impedance abbreviation.
Subsequently, the load bus with the installed PMU was opened, and the Thevenin voltage (VTh) was calculated using the PSS/E load flow calculation; the impedance of the open load bus is denoted by ZL. The voltage of the bus is VL, and the power of the connected load is denoted by the SL complex power
In the above equation, the load current IL is acquired using PMU data. The Thevenin impedance ZTh is calculated using the Thevenin equivalent circuit method used in electric circuits.
The complex power is
Based on the above equation, the load impedance ZL was assumed as follows:
The parameters of the Thevenin equivalent circuit can be obtained using the assumed data and calculation formula. The Thevenin impedance is calculated as follows:
3. Equal-Area Method for Determining Transient Stability
Introduction to Equal-Area Method
Transient stability is the ability of a power system to operate normally and maintain stability in the event of a temporary overload or accident. When the phase angle widens, the power system attempts to regain synchronization while reducing the difference in the phase angle by slowing down the operation of the generator to return to a normal state. In this way, the transient stability is determined from the phase angle and phase angle curves using the Thevenin impedance. With the phase angle and phase difference angle curves, the equal-area method can be used.
The equal-area method generates three types of curves based on the power angle of the difference-angle curve. In addition, the mechanical input (Pm) and electrical output (Pe) of the generator are balanced, and the generator becomes smaller than the mechanical input (Pm) owing to the decrease in the electrical output (Pe) of the generator caused by the occurrence of a one-line failure while driving at δ0. When the fault line is removed by the operation of the circuit breaker in δ1 during acceleration, the output of the generator increases from Pm, decelerates, converges to a new balance point, and operates stably.
To determine the stability, it is necessary to compare it with the specified areas. Areas A, B, and C in Figure 2, are defined as the acceleration, deceleration, and transient stability margins, respectively. If A area < (B + C) area, it is restored to a stable operating state, and if the ratio of the area in the opposite situation is A area > (B + C) area, it can be defined as unstable. Therefore, if the blocking speed is low, area A increases, and the stability margin gradually decreases or becomes unstable.
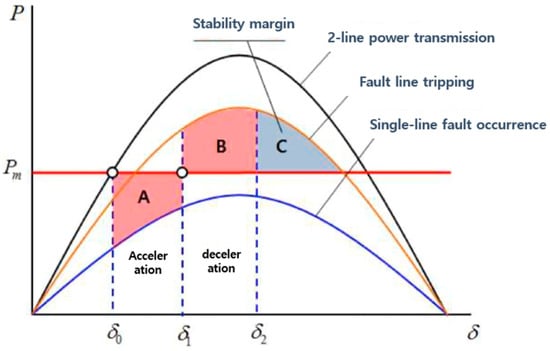
Figure 2.
Power-angle difference based on differential angle curve.
4. Case Study
Renewable energy is clean energy with low water consumption and sustainable power generation; however, large volatility and unpredictable uncertainty in the output negatively affect the operation of the power system. To confirm this, the transient stability was determined by comparing the area change according to the connection between renewable energy and the power system.
In this section, the accident scenario is selected using the PSS/E204_OFF_Peak Jeju system data provided by KEPCO to obtain the normal load voltage (VL), total voltage (VTh), load impedance (ZL), and Thevenin impedance (ZTh) values. Recently, there have been many accidents in which HVDC has failed temporarily. The cause of occurrence is the cooling system components, such as controller component defects. Accordingly, a failure scenario was used for a track with a large current on the Jeju–Jindo HVDC bus line. The first step was to determine the transitional stability using the scenario. The transitional stability determination index Sindex was used to determine the transitional stability, using the area ratio of the equal-area method. Second, the rate of renewable energy use continues to increase owing to climate change and new energy projects. If Korea’s 10th electricity supply and demand plan is reflected, it is projected that by 2036, approximately 30% of Jeju Island’s renewable energy facilities will be installed. However, if renewable energy, which is inertial and weather-affected, is added without connection to the system stability, it will be a problem for the power system. Therefore, by installing additional renewable energy in the scenario, the transient stability was compared using a system that increased the current and renewable energy by 30%.
Third, to determine the accuracy using previously applied results, the accuracy was verified by comparison with the voltage stability index (WAVI). The difference between the Sindex and WAVI is that Sindex determines the stability using the area of the equal-area method, whereas the WAVI is determined using the load impedance and Thevenin impedance. Compared to WAVI, Sindex has the advantage of being able to check stability and visualize parameters in real time. In addition, it is one of the advantages of critical clearing time (CCT) through visualization time.
4.1. Measurement and Calculation of Bus VL, VTh, ZTh, ZL
Through PSS/E Bird calculation analysis, the voltage and phase angle of the parameters required for the transient stability determination index of the steady state and the state after the failure was eliminated were measured using the line failure connected to the HVDC bus. In addition, the voltage and impedance values of the failure state were assumed to be zero and infinite, respectively. This is because the impedance was assumed to be infinite because the accident state was caused by a three-phase short circuit that forced the voltage and current to drop instantaneously. The load bus was measured and calculated using 12 Jeju system data points.
The Thevenin impedance was calculated using VL and VTh using the Thevenin impedance calculation method described in Section 2. The complex power (SL) values were calculated using the active and reactive powers of the load installed on the load bus.
4.2. Define and Calculate Transient Stability Discrimination Index
The transient stability determination index Sindex uses the equal-area method. Therefore, power is required before and after failure elimination. The equation for plotting the power-phase angle curve using the parameters shown in Table 1, Table 2, Table 3, Table 4, Table 5, Table 6 and Table 7 is as follows:

Table 1.
Pre-fault load bus voltage (VL) and total voltage (VTh).

Table 2.
Load bus voltage (VL), and total voltage (VTh) after fault elimination.

Table 3.
Load bus active and reactive power.

Table 4.
Contextual Thevenin impedance.

Table 5.
SA and SB of the mother lines.

Table 6.
Sindex calculation values by mother line.

Table 7.
Calculated values of Sindex by bus after installing additional renewable energy facilities.
Using these parameters, the power-phase angle curve can be obtained using the phase angle curve equation.
As shown in Figure 3, area A is represented by SA, and areas B and C are represented by SB to calculate the two values and use the ratio of the areas to determine the transient stability discrimination index Sindex. To calculate the area, the mechanical input (Pm), lead angle (θ), lead angle difference (∆θ), premise voltage (VTh), load voltage (VL), and Thevenin impedance (ZTh) were required. This area was obtained using integrals. However, because there was no integral symbol in the equation, and thus no power-lead angle curve during failure, the mechanical input (Pm), i.e., the generator input, could be assumed vertically, and the lead angle difference (∆θ) horizontally, enabling calculation using the formula for the area of a rectangle. Furthermore, each lead angle (θ) was defined using a number, where θ0 represented the lead angle at the point of failure, θ1 represented the lead angle at the point of recovery, and θ2 was defined as the lead angle at which maximum critical operation was possible. Based on Figure 3 above, the equation for calculating the area using the equal-area method was as follows:
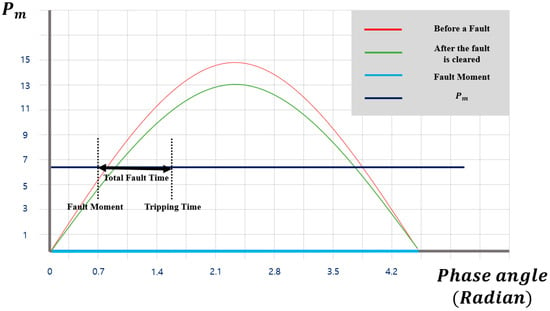
Figure 3.
BUS 150 HANLIM-CC phase angle curve example.
During failure, because the state was a three-phase short-circuit state, VTh = 0, the part in Equation (8) written with the integral symbol may be omitted. Therefore, from Equation (8), SA can be expressed as follows.
The SA and SB areas were calculated using the equations above. Table 5 presents the SA and SB area calculations.
The transient stability determination index Sindex could be defined using the calculated values of SA and SB areas. Sindex was used for the deceleration, acceleration, and transient stability margin areas using the area theory of the equal-area method. As mentioned in Section 3, the acceleration area was defined as SA, and the area obtained by adding the deceleration area and transient stability margin area was defined as SB. After an accident occurs in the power system, the critical part that can block the accident is in a critical state when the SA area and SB area are similar. If the SB area is larger than the SA area, it can be deduced that the transient stability is inadequate. In the opposite case, it can be deduced that the transitional stability is good. Based on this, Sindex can be defined by Equation (11). In conclusion, if Sindex is less than “1”, it can be inferred that the transient stability is stable, and if it is greater than “1”, it can be expected that the transient stability is unstable. Figure 4 shows the critical state in which the SA and SB areas are the same. In Figure 5, because the SA area was larger than the SB area, the transient stability state was a stable curve.
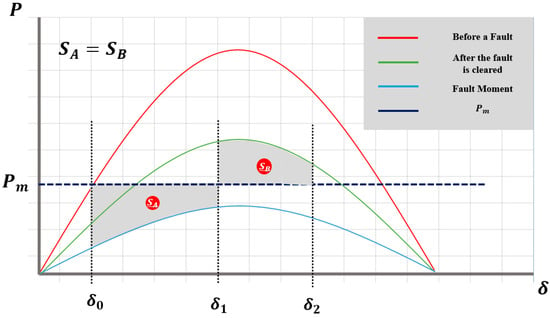
Figure 4.
Sindex = 1 power per person—phase difference angle curve.
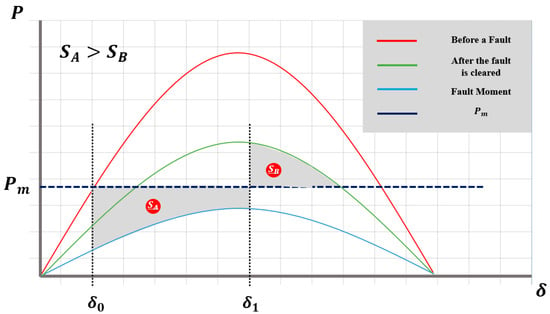
Figure 5.
Sindex < 1 power per person—phase difference angle curve.
Based on Equation (11), the transient stability discrimination index value was defined using the areas of SA and SB. Table 6 shows the Sindex for each bus line substituted into Equation (11) using these parameters.
Based on Table 6, the Sindex values, which are the transient stability discrimination indices, are not greater than “1”; therefore, it can be concluded that there is room for transient stability in the current Jeju system. Thus, it is expected that even if additional renewable energy facilities are installed, they will not significantly affect the transition stability. However, if renewable energy that does not exist in inertia is added to the land system, which has more power supply and demand than the Jeju system, it is expected that the generator input operating point will increase more than before, the SA will increase, and the SB will decrease; thus, the transient stability may not be good.
4.3. Calculation of Sindex Index Based on Additional Renewable Energy Facilities
This section examines the process of precisely analyzing and calculating the effects of introducing additional renewable energy facilities on the Sindex index. The Sindex value of the transient stability determination index according to the introduction of the additional renewable energy installation confirms the margin of transient stability compared to that before the additional installation. In particular, calculating the transient stability discrimination index to evaluate the efficiency and stability of renewable energy can be used to quantitatively determine the stability of an energy system following the introduction of new facilities.
The value of an additional renewable energy facility depends on the generator input. According to the 10th plan for the supply and demand of electricity in Korea, the current generator input value was 563.4 [MW] as of 2024, and there is a plan to increase the installation of an additional 30% renewable energy facilities in the future. Based on this, the renewable energy ratio of the system was increased by 30%, and the generator input value was selected as 733.55 [MW]. The table below lists the Sindex calculation values according to the additional installation energy.
Later, when renewable energy facilities were connected to the system, the transient stability was determined using the equal-area method. The Sindex values presented in Table 6 and Table 7 show the area change and transient stability discrimination index. It is confirmed that there was a change in the area, but the margin of the transient stability decreased; however, it did not have a significant effect. Renewable energy is highly volatile because it depends on the weather conditions. In addition, it is necessary to monitor power generation and supply power effectively in real time; however, renewable energy resources are inertial, and the power supply is not constant. If additional renewable energy facilities are installed, the transitional stability will inevitably be poor.
4.4. Verification of the Accuracy of Transient Stability Discriminant Sindex
In this study, the Sindex was defined according to the equal-area method using the perturbation equation theory, and the accuracy of the transient stability discrimination index was verified using the WAVI [5] index. WAVI is a voltage stability monitoring index that uses the Thevenin and load impedance data measured and calculated in this system. WAVI is a technique that can determine the voltage stability through information measured in the installation area without system information and can estimate the state of the system according to the system change. The maximum power that an equivalent power source can transmit to a load occurs when the Thevenin impedance equals the load impedance. When the maximum power-transfer law is applied to the power system, the limit value of the power that can be supplied to the load bus is the load power when the Thevenin impedance is equal to the load impedance. Thus, the positive voltage instability phenomenon on the impedance plane can be explained by the impedance ratio, and the stable conditions for the voltage stability can be defined by the following equation:
Using Equation (12), the WAVI was calculated using the system load impedance and Thevenin impedance of the system as of 2024 and a system whose renewable energy ratio increased by 30% in the future. The table below shows the calculated WAVI values.
According to Table 8, because the WAVI did not exceed “1”, it was inferred that there was no problem with the transitional stability in the system. It can be concluded that there was no problem in determining the index by area and the transitional stability using the equal-area method. However, because the WAVI and Sindex indices for the data with additional renewable energy facilities installed were larger, the transition stability was less stable than that of the existing system [10,11,12,13,14]. Based on this, it can be confirmed that the transient stability was reduced if renewable energy was additionally installed in the system. Moreover, the WAVI, the existing voltage stability index, and Sindex values using the theory of the equal-area method were considered to have no problems with accuracy, because the margin of the transient stability decreased when renewable energy was connected.

Table 8.
WAVI value by bus.
5. Discussion
- Key Findings and Contributions
This study introduces a real-time transient stability assessment method that utilizes Thevenin impedance estimation and an improved Equal Area Criterion (EAC) to provide stability rankings using limited PMU data. The key contributions of the proposed method are as follows:
- Minimal Data Requirement: Unlike conventional methods requiring full system parameters, this approach estimates transient stability using only real-time PMU data.
- Computational Efficiency: The method eliminates the need for time-domain simulations, allowing real-time implementation.
- Practical Application to Renewable Energy Systems: The method effectively evaluates transient stability in high RES-penetrated grids, where traditional inertia-based approaches may not be suitable.
- b.
- Comparison with Conventional Methods
Traditional transient stability assessment methods, such as time-domain simulations (TDS) and direct methods based on Lyapunov energy functions, require detailed system modeling and extensive computation time. These methods are well suited for offline studies but may not be feasible for real-time grid operations.
The proposed method provides a real-time alternative by utilizing Thevenin impedance estimation and a stability discrimination index. While a direct comparison with full offline simulations is difficult, results show that the proposed method provides stability rankings comparable to the wide-area voltage stability index (WAVI). This validates the method’s ability to assess transient stability efficiently using real-time data.
- c.
- Limitations and Future Work
Despite its advantages, the proposed method has some limitations:
- Approximate Stability Assessment: Unlike TDS, which determines precise critical clearing times (CCTs), the proposed method focuses on stability ranking, which may not provide exact fault tolerance margins.
- Impact of RES Dynamics Not Fully Modeled: The study assumes that renewable energy sources behave as constant power injections, which simplifies analysis but does not fully capture fast inverter dynamics. Future work will incorporate detailed inverter-based modeling to improve accuracy.
- Limited Validation with Real System Data: Further case studies and testing on actual power grids will strengthen the method’s applicability for industry use.
- d.
- Practical Implications
The proposed method provides a fast, real-time tool for grid operators to assess transient stability and take preventive actions before system instability occurs. As power systems move toward higher renewable energy penetration, real-time assessment techniques such as this will become increasingly important to ensure secure operation without relying on traditional synchronous machine-based stability models.
6. Conclusions
In this study, the Thevenin impedance of the Jeju abbreviated system was estimated based on real-time data. The area was calculated by applying the equal-area method and plotting a power-phase angle curve. According to the results of determining the transient stability in the Jeju reduced system, which was performed in 2024, there was no significant problem with the stability at that point. However, according to the 10th power supply plan, the renewable energy ratio is expected to increase by approximately 30% by 2036, which is expected to increase by approximately 200 MW compared to the existing generator input; thus, the transitional stability of the situation was determined. Consequently, if renewable energy was continuously connected, the possibility that the transient stability may deteriorate depending on the area using the equal-area method was confirmed. In addition, WAVI was used to confirm the index and stability of the area to verify the discrimination of the transient stability. According to the WAVI and Sindex, the index from the continuous connection of renewable energy was found to be unstable, and the transient stability decreased when the renewable energy was continuously connected. However, there was always a limit to the perfect discrimination of the transient stability using only the index. To increase the accuracy of the index, verification of the land system and an in-depth verification based on the actual system are required. To alleviate transitional stability in the future, facilities capable of increasing stability, such as power electronics facilities including the Flexible AC Transmission System (FACTS), frequential-response energy storage system (FR_ESS), and GS Energy Storage System (GS-ESS), must be introduced. In the future, there will be a need to solve problems to prepare for the continuous increase in renewable energy.
Author Contributions
Methodology, S.K.; Software, D.S. and J.L.; Validation, D.S. and J.L.; Formal analysis, S.K. and J.L.; Investigation, S.K. and S.H.; Resources, J.L. and D.L.; Data curation, D.S. and D.L.; Writing—original draft, S.K.; Writing—review & editing, S.H. and D.L.; Visualization, D.S.; Supervision, S.H.; Project administration, S.H.; Funding acquisition, D.L. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported (in part) by Glocal University Project of Mokpo National University in 2025 and Korea Institute of Energy Technology Evaluation and Planning: No. 20214000000060.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding authors.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
| PMU | Phasor Measurement Unit |
| WAVI | Wide-Area Voltage Stability Index |
| TSDI | Transient Stability Discrimination Index |
| EAC | Equal Area Criterion |
| HVDC | High Voltage Direct Current |
| FACTS | Flexible AC Transmission System |
| CCT | Critical Clearing Time |
| RES | Renewable Energy Source |
| SMIB | Single-Machine Infinite Bus |
References
- Korea Institute of Energy Research. In Proceedings of the 10th Basic Plan for Electricity Supply, January 2023. Available online: https://www.motie.go.kr/kor/article/ATCLc01b2801b/68162/view (accessed on 13 March 2025).
- Li, Y.; Chi, Y.; Wang, X.; Tian, X.; Jianqing, J. Practices and Challenge on Planning with Large-Scale Renewable Energy Grid Integration. In Proceedings of the 3rd Conference on Energy Internet and Energy System Integration, Changsha, China, 8–10 November 2019; Volume EI2, pp. 118–121. [Google Scholar] [CrossRef]
- Kundur, P.; Paserba, J.; Vitet, S. Overview on Definition and Classification of Power System Stability. In Proceedings of the CIGRE/IEEE PES International Symposium Quality and Security of Electric Power Delivery Systems, Montreal, QC, Canada, 8–10 October 2003; pp. 1–4. [Google Scholar] [CrossRef]
- Li, D.; Zhao, B.; Wu, Z.; Zhang, X.; Zhang, L. An Improved Droop Control Strategy for Low-Voltage Microgrids Based on Distributed Secondary Power Optimization Control. Energies 2017, 10, 1347. [Google Scholar] [CrossRef]
- Zhang, D.; Han, X.; Deng, C. Review on the Research and Practice of Deep Learning and Reinforcement Learning in Smart Grids. CSEE J. Power Energy Syst. 2018, 4, 362–370. [Google Scholar] [CrossRef]
- Hatziargyriou, N.; Milanovic, J.; Rahmann, C.; Ajjarapu, V.; Canizares, C.; Erlich, I.; Hill, D.; Hiskens, I.; Kamwa, I.; Pal, B.; et al. Definition and Classification of Power System Stability—Revisited & Extended. IEEE Trans. Power Syst. 2021, 36, 3271–3281. [Google Scholar] [CrossRef]
- Kundur, P.; Balu, N.J.; Lauby, M.G. Power System Stability and Control, 2nd ed.; McGraw-Hill Education: Columbus, OH, USA, 2020. [Google Scholar]
- Huda, M.; Koji, T.; Aziz, M. Techno Economic Analysis of Vehicle to Grid (V2G) Integration as Distributed Energy Resources in Indonesia Power System. Energies 2020, 13, 1162. [Google Scholar] [CrossRef]
- Yuan, Y.; Zhu, N.; Zhou, H.; Wang, H. A New Model Predictive Control Method for Eliminating Hydraulic Oscillation and Dynamic Hydraulic Imbalance in a Complex Chilled Water System. Energies 2021, 14, 3608. [Google Scholar] [CrossRef]
- Julian, D.E.; Schulz, R.P.; Vu, K.T.; Quaintance, W.H.; Bhatt, N.B.; Novosel, D. Quantifying Proximity to Voltage Collapse Using the Voltage Instability Predictor (VIP). In Proceedings of the 2000 Power Engineering Society Summer Meeting (Cat. No.00CH37134), Seattle, WA, USA, 16–20 July 2000; pp. 931–936. [Google Scholar] [CrossRef]
- Huo, W.; Ma, Y.; Ma, Y.; Li, X.; Xiong, L. Design and Implementation of Power Data Security and Compliance Management Framework. In Proceedings of the 2024 4th International Signal Processing, Communications and Engineering Management Conference (ISPCEM), Montreal, QC, Canada, 28–30 November 2024; pp. 614–618. [Google Scholar]
- Almeida, M.L.S.; Peres, L.M.; Santos, G.G. Air-core dry-type shunt reactor protection based on an alternative current alpha plane. IET Gener. Transm. Distrib. 2021, 15, 34–44. [Google Scholar] [CrossRef]
- Gómez-Expósito, A.; Conejo, A.J.; Cañizares, C.A. Electric Energy Systems: Analysis and Operation, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Wang, L.; Gong, W.; Hu, B.; Lin, A.; Li, H.; Zou, L. Modeling and analysis of the spatiotemporal variations of photosynthetically active radiation in China during 1961–2012. Renew. Sustain. Energy Rev. 2015, 49, 1019–1032. [Google Scholar] [CrossRef]
- Zhang, K.; Xie, J.; Liu, N. Hybrid Knowledge and Data-Driven Hydrogen Trading for Renewable-Dominated Hydrogen Refueling Stations. IEEE Trans. Ind. Appl. 2025, 61, 1658–1674. [Google Scholar] [CrossRef]
- Anand, M.P.; Bagen, B.; Rajapakse, A. Reliability oriented distribution system analysis considering electric vehicles and hybrid energy resources. Int. J. Electr. Power Energy Syst. 2022, 137, 107500. [Google Scholar] [CrossRef]
- Cheng, L.; Yan, J.; Yao, J.; Yang, S.; Yu, F.; Li, F. Power System Security Boundary Identification and Rules Extraction based on Tighten Weighted Oblique Decision Tree. In Proceedings of the 2023 IEEE 7th Conference on Energy Internet and Energy System Integration (EI2), Hangzhou, China, 15–18 December 2023; pp. 2806–2812. [Google Scholar] [CrossRef]
- Zhang, X.; Huang, Y.; Hu, S.; Dou, C.; Hong, Y. The Application of the New Generation of Artificial Intelligence Technology in Modern Electrical Power Systems: Models, Algorithms, and Challenges. In Proceedings of the 2023 IEEE 7th Conference on Energy Internet and Energy System Integration (EI2), Hangzhou, China, 15–18 December 2023; pp. 4897–4903. [Google Scholar] [CrossRef]
- Senyuk, M.; Odinaev, I.; Pichugova, O.; Ahyoev, J. Methodology for Forming a Training Sample for Power Systems Emergency Control Algorithm Based on Machine Learning. In Proceedings of the 2023 Belarusian-Ural-Siberian Smart Energy Conference (BUSSEC), Ekaterinburg, Russia, 25–29 September 2023; pp. 54–59. [Google Scholar] [CrossRef]
- Janeiro, F.M.; Ramos, P.M. A Comparative Analysis Between Genetic Algorithms and Complex Nonlinear Least Squares on Electrical Impedance Characterization. IEEE Trans. Instrum. Meas. 2016, 65, 1103–1110. [Google Scholar] [CrossRef]
- Su, H.-Y.; Liu, T.-Y. Robust Thevenin Equivalent Parameter Estimation for Voltage Stability Assessment. IEEE Trans. Power Syst. 2018, 33, 4560–4568. [Google Scholar] [CrossRef]
- Zhang, T.; Zhang, X.; Iu, H.; Fernando, T. Long-term Monthly Energy and Peak Demand Forecasting Based on Sequential-XGBoost. In Proceedings of the 2023 IEEE 5th International Conference on Power, Intelligent Computing and Systems (ICPICS), Shenyang, China, 14–16 July 2023; pp. 157–162. [Google Scholar] [CrossRef]
- Jeong, I.; Oh, S.; Song, J.; Ku, H.; Bae, M.; Kwak, E.-S.; Min, J.-H.; Shin, J. A Study on Analysis of Margin of Transient Stability and Calculation of Power Generation Constraints According to Renewable Energy Sources in the East Coast. Trans. Korean Inst. Electr. Eng. 2022, 71, 1564–1570. [Google Scholar] [CrossRef]
- Li, L.; Li, H.; Tseng, M.-L.; Feng, H.; Chiu, A.S.F. Renewable Energy System on Frequency Stability Control Strategy Using Virtual Synchronous Generator. Symmetry 2020, 12, 1697. [Google Scholar] [CrossRef]
- Das, K.; Guo, F.; Nuño, E.; Cutululis, N. Frequency Stability of Power System with Large Share of Wind Power Under Storm Conditions. J. Mod. Power Syst. Clean Energy 2020, 8, 219–228. [Google Scholar] [CrossRef]
- Yang, J.-Y.; Song, Y.H.; Kook, K.S. Critical Inertia Calculation Method of Generators Using Energy Balance Condition in Power System. Energies 2024, 17, 1097. [Google Scholar] [CrossRef]
- Son, D.B.; Kim, S. Estimation of Thevenin Impedance Assuming Real-Time Information and Application to Transient Stability Evaluation of Jeju System in South Korea. In Proceedings of the International Conference on Electrical Engineering (ICEE), Hong Kong, 2–6 July 2023. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).