An Analysis of the Characteristics of Internal Flow Losses of Seawater Circulation Pumps in Nuclear Power Plants Based on the Entropy Production Theory
Abstract
:1. Introduction
2. Numerical Simulation Methods and Experimental System
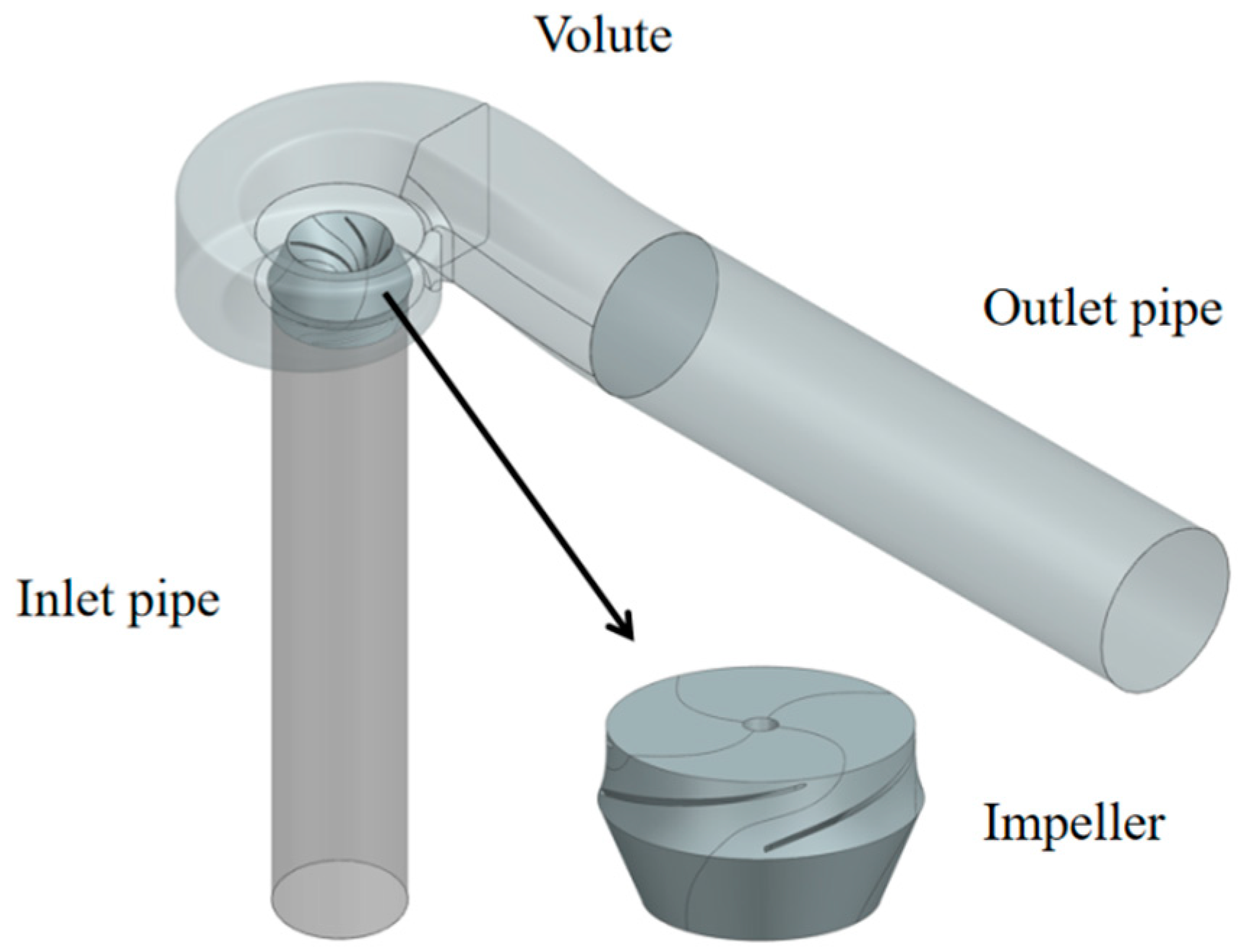
2.1. Three-Dimensional Pump Modeling
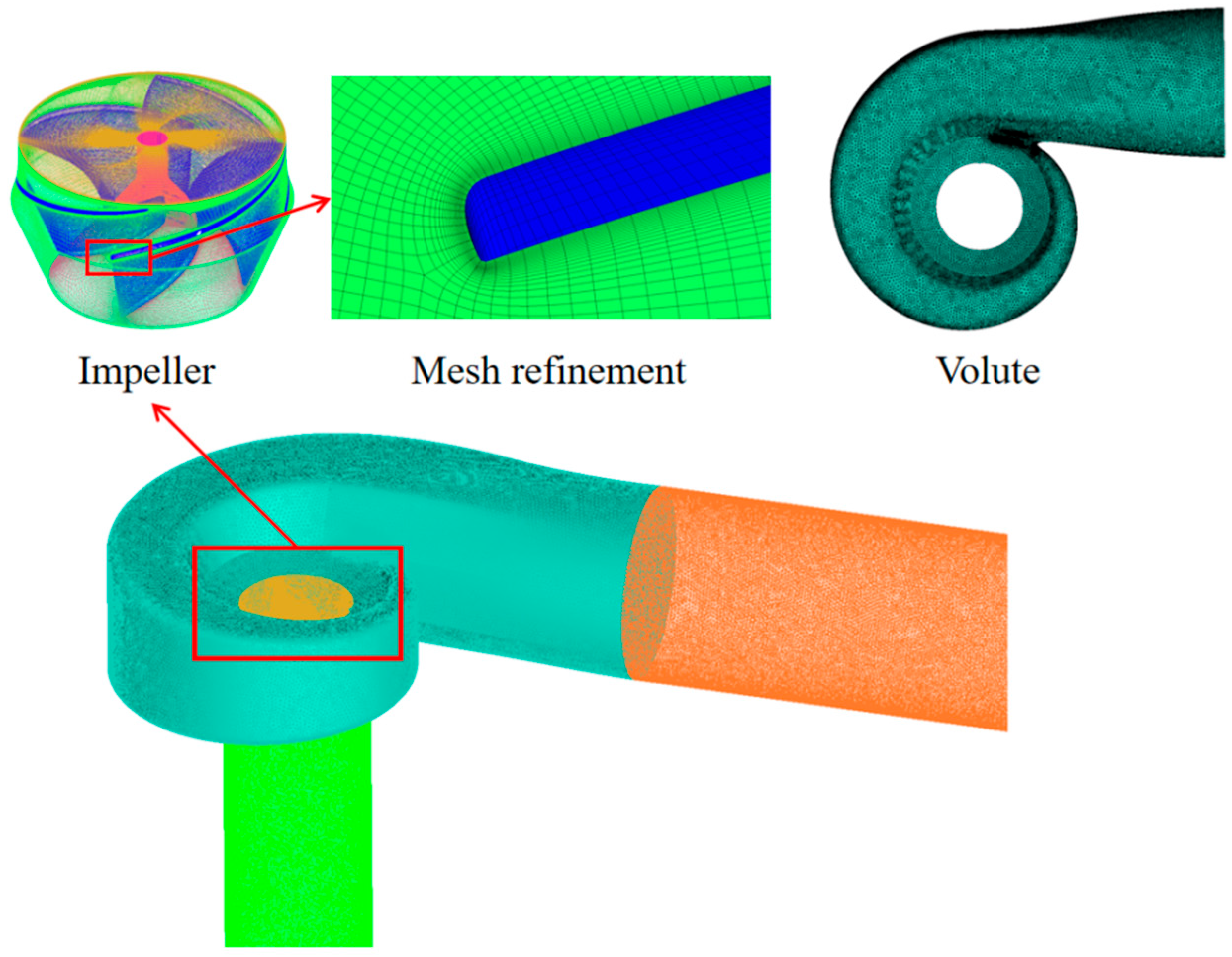
2.2. Mesh Generation
2.3. Boundary Conditions
2.4. Entropy Production Theory
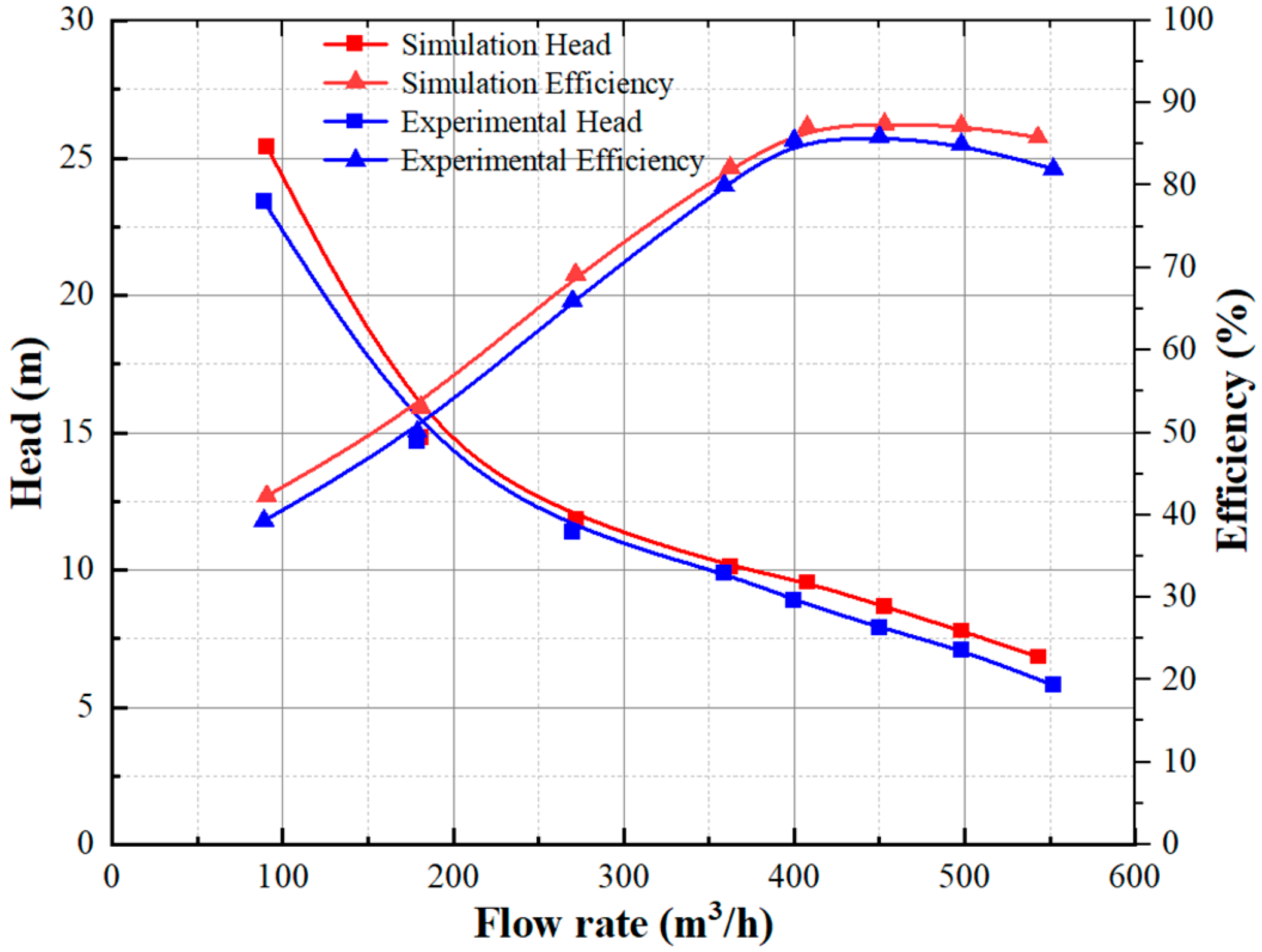
2.5. Experimental Verification
3. Results and Discussion
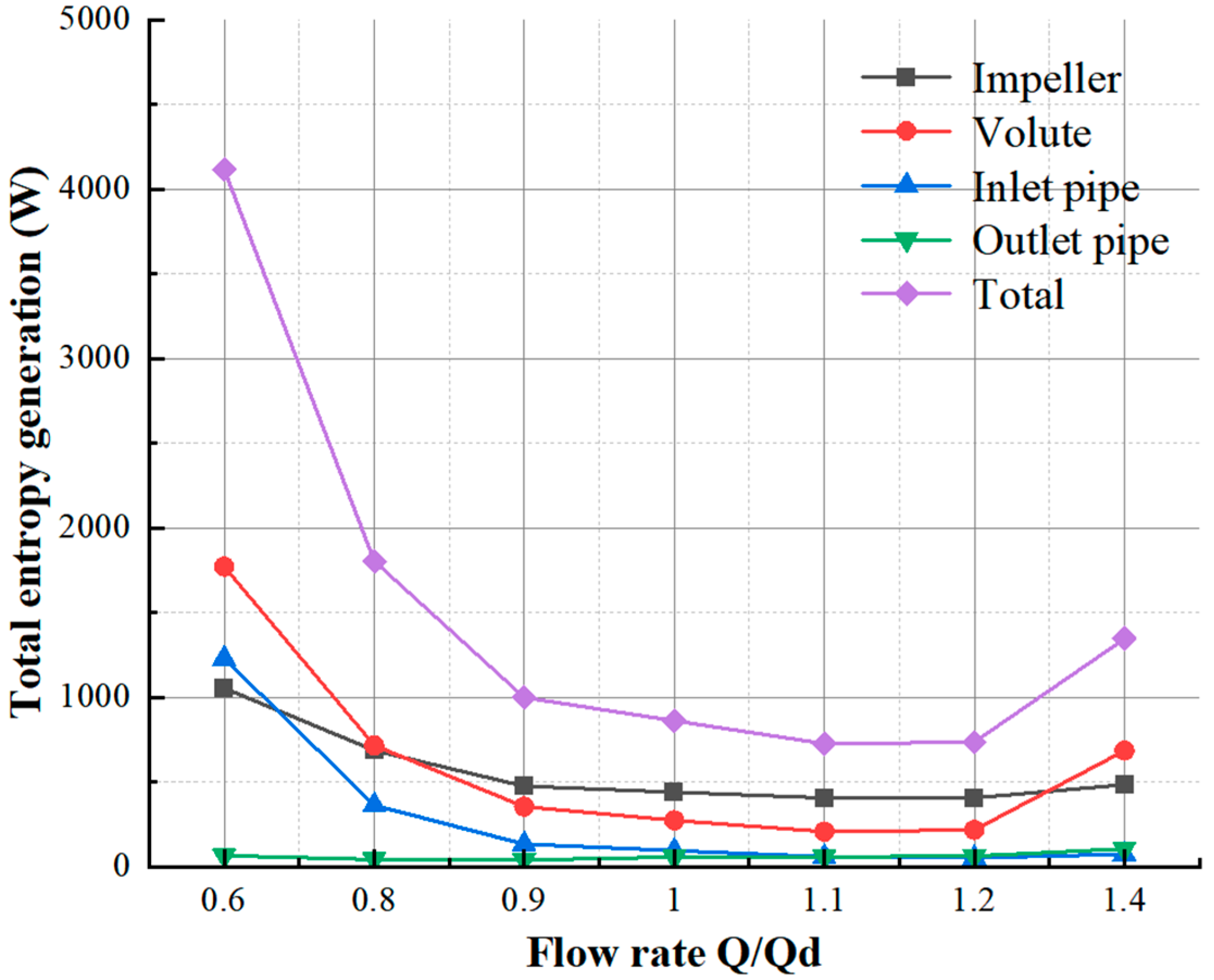
3.1. Analysis of Entropy Production Variation with Flow Rate
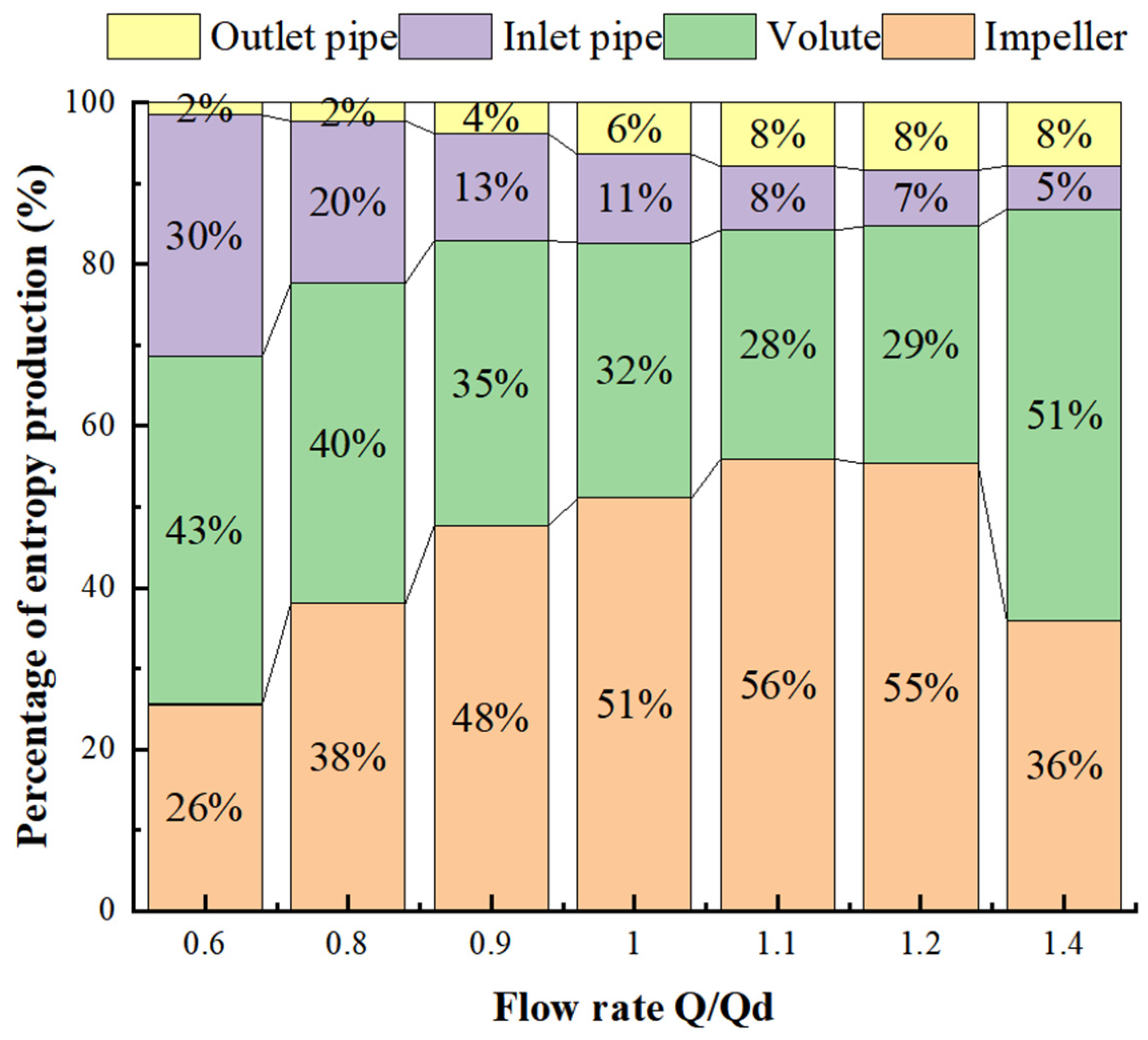
3.2. Entropy Production Proportion of Different Flow Passage Components
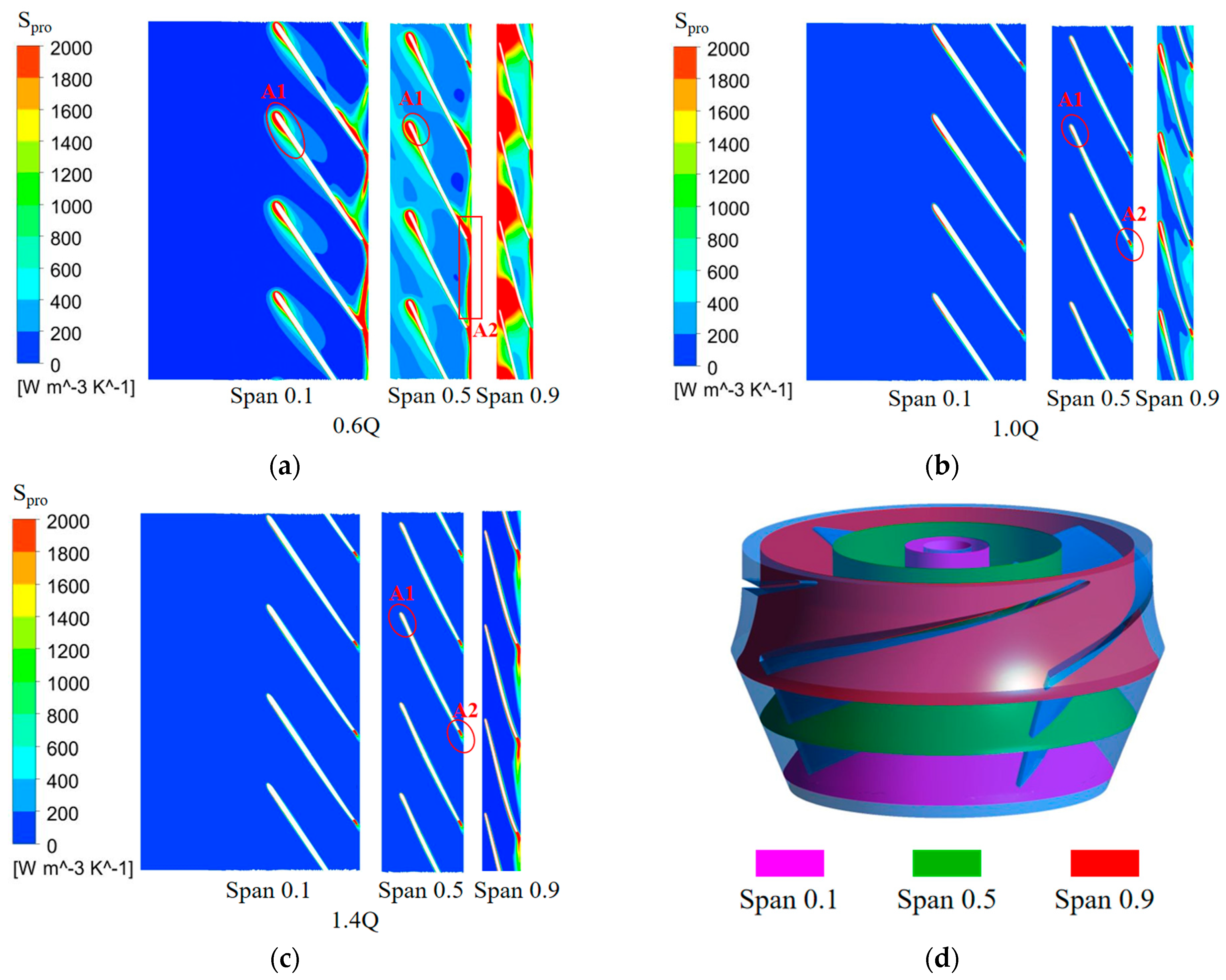
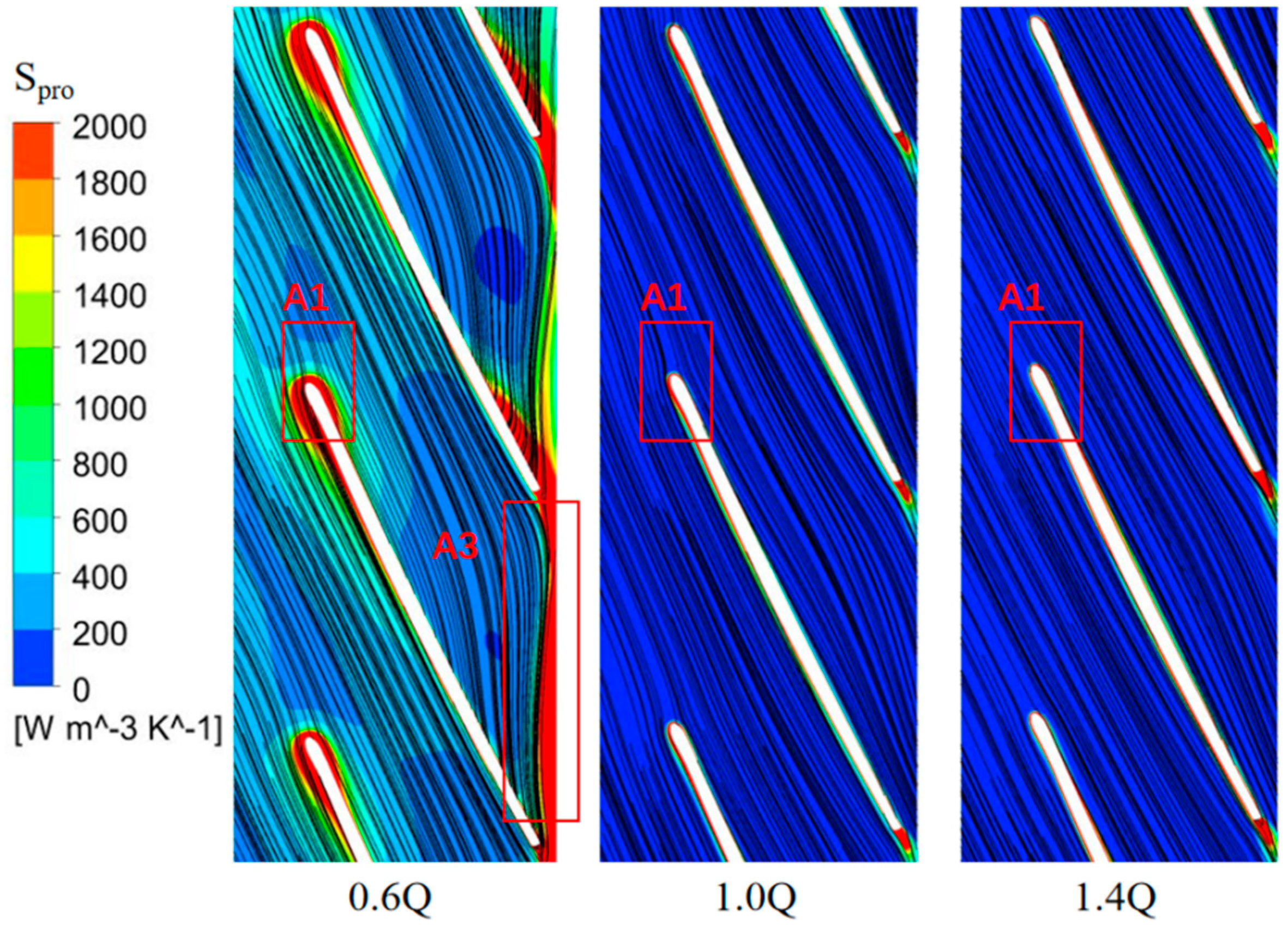
3.3. Analysis of Internal Flow and Entropy Production in Impeller
3.4. Analysis of Internal Flow and Entropy Production in Volute
4. Conclusions
- (1)
- The total entropy production of the seawater circulating pump first decreases and then increases with the flow rate, reaching the lowest value near the design working condition. The impeller and the volute account for the largest proportion of entropy production. The proportion of entropy production of the impeller reaches its maximum value near the design working condition and decreases when deviating from the design working condition; the proportion of entropy production of the volute is opposite to that of the impeller, reaching the minimum value near the design working condition and increasing after deviating from the design working condition.
- (2)
- The regions of the leading edge, trailing edge, and front shroud of the blades of the seawater circulating pump become the main areas where entropy production occurs in the impeller due to reasons such as excessive incidence angles and circulation flows.
- (3)
- The entropy production of the volute is mainly concentrated in the throat area, and relatively high entropy production occurs due to reasons such as circulation flows and vortices, which increase energy losses.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kerr, R.A. Global warming is changing the world. Science 2007, 316, 188–190. [Google Scholar] [CrossRef] [PubMed]
- Hansen, J.; Ruedy, R.; Sato, M.K.I.; Lo, K. Global warming continues. Science 2002, 295, 275. [Google Scholar] [CrossRef] [PubMed]
- Pang, Y.; Tang, P.; Li, H.; Marinello, F.; Chen, C. Optimization of sprinkler irrigation scheduling scenarios for reducing irrigation energy consumption. Irrig. Drain. 2024, 73, 1329–1343. [Google Scholar] [CrossRef]
- Song, M.; Wang, S.; Yu, H.; Yang, L.; Wu, J. To reduce energy consumption and to maintain rapid economic growth: Analysis of the condition in China based on expended IPAT model. Renew. Sustain. Energy Rev. 2011, 15, 5129–5134. [Google Scholar] [CrossRef]
- González-Gil, A.; Palacin, R.; Batty, P.; Powell, J.P. A systems approach to reduce urban rail energy consumption. Energy Convers. Manag. 2014, 80, 509–524. [Google Scholar] [CrossRef]
- Ulucak, R.; Erdogan, S. The effect of nuclear energy on the environment in the context of globalization: Consumption vs production-based CO2 emissions. Nucl. Eng. Technol. 2022, 54, 1312–1320. [Google Scholar]
- Mahmood, N.; Wang, Z.; Zhang, B. The role of nuclear energy in the correction of environmental pollution: Evidence from Pakistan. Nucl. Eng. Technol. 2020, 52, 1327–1333. [Google Scholar] [CrossRef]
- Horvath, A.; Rachlew, E. Nuclear power in the 21st century: Challenges and possibilities. Ambio 2016, 45, 38–49. [Google Scholar] [CrossRef] [PubMed]
- Lu, J.; Yao, X.; Zheng, H.; Yan, X.; Liu, H.; Wu, T. Analysis of Unsteady Internal Flow and Its Induced Structural Response in a Circulating Water Pump. Water 2024, 16, 1294. [Google Scholar] [CrossRef]
- Dai, C.; Kong, F.-Y.; Dong, L. Study on Pressure Fluctuations of Unsteady Flow in a Circulating Water Pump. Adv. Sci. Lett. 2012, 9, 50–55. [Google Scholar] [CrossRef]
- Bing, H.; Tan, L.; Cao, S.; Lu, L. Prediction method of impeller performance and analysis of loss mechanism for mixed-flow pump. Sci. China Technol. Sci. 2012, 55, 1988–1998. [Google Scholar] [CrossRef]
- Li, W.; Ji, L.; Li, E.; Shi, W.; Agarwal, R.; Zhou, L. Numerical investigation of energy loss mechanism of mixed-flow pump under stall condition. Renew. Energy 2021, 167, 740–760. [Google Scholar] [CrossRef]
- Chen, L.; Yang, Y.; Song, X.; Zhang, X.; Gong, Y. Integrated optimization design of multiphase pump based on adaptive sparse grid method. Ocean Eng. 2024, 29, 117235. [Google Scholar] [CrossRef]
- Pei, J.; Shen, J.; Wang, W.; Yuan, S.; Zhao, J. Evaluating hydraulic dissipation in a reversible mixed-flow pump for micro-pumped hydro storage based on entropy production theory. Renew. Energy 2024, 225, 120271. [Google Scholar] [CrossRef]
- Wang, H.; Wang, C.; Zhou, L.; Ji, L.; Yang, Y.; Shi, W.; Agarwal, R.K. An entropy efficiency model and its application to energy performance analysis of a multi-stage electric submersible pump. Energy 2024, 288, 129741. [Google Scholar]
- Zhou, R.; Liu, H.; Dong, L.; Ooi, K.T.; Dai, C.; Shao, C.; Zhao, Y. Energy loss assessment of a two-stage pump under natural flow in the marine cooling system based on entropy production theory. Therm. Sci. Eng. Prog. 2023, 43, 101976. [Google Scholar] [CrossRef]
- Kan, K.; Zhang, Q.; Xu, Z.; Zheng, Y.; Gao, Q.; Shen, L. Energy loss mechanism due to tip leakage flow of axial flow pump as turbine under various operating conditions. Energy 2022, 255, 124532. [Google Scholar] [CrossRef]
- Kock, F.; Herwig, H. Local entropy production in turbulent shear flows: A high-Reynolds number model with wall functions. Int. J. Heat Mass Transf. 2003, 47, 2205–2215. [Google Scholar] [CrossRef]
- Yang, F.; Li, Z.; Hu, W.; Liu, C.; Jiang, D.; Liu, D.; Nasr, A. Analysis of flow loss characteristics of slanted axial-flow pump device based on entropy production theory. R. Soc. Open Sci. 2022, 9, 211208. [Google Scholar] [CrossRef] [PubMed]
- Bejan, A.; Herwig, J. Entropy generation through heat and fluid flow. Appl. Mech. 1983, 50, 475. [Google Scholar] [CrossRef]
- Ji, L.; Li, W.; Shi, W.; Chang, H.; Yang, Z. Energy characteristics of mixed-flow pump under different tip clearances based on entropy production analysis. Energy 2020, 199, 117447. [Google Scholar] [CrossRef]
- Ji, L.; Li, W.; Shi, W.; Tian, F.; Agarwal, R. Effect of blade thickness on rotating stall of mixed-flow pump using entropy generation analysis. Energy 2021, 236, 121381. [Google Scholar] [CrossRef]
- Fei, Z.; Zhang, R.; Xu, H.; Feng, J.; Mu, T.; Chen, Y. Energy performance and flow characteristics of a slanted axial-flow pump under cavitation conditions. Phys. Fluids 2022, 34, 035121. [Google Scholar] [CrossRef]
- Li, D.; Qin, Y.; Wang, J.; Zhu, Y.; Wang, H.; Wei, X. Optimization of blade high pressure edge to reduce pressure fluctuations in pump turbine hump region. Renew. Energy 2022, 181, 24–38. [Google Scholar] [CrossRef]
- Kock, F.; Herwig, H. Entropy production calculation for turbulent shear flows and their implementation in CFD codes. Int. J. Heat Fluid Flow 2005, 26, 672–680. [Google Scholar] [CrossRef]


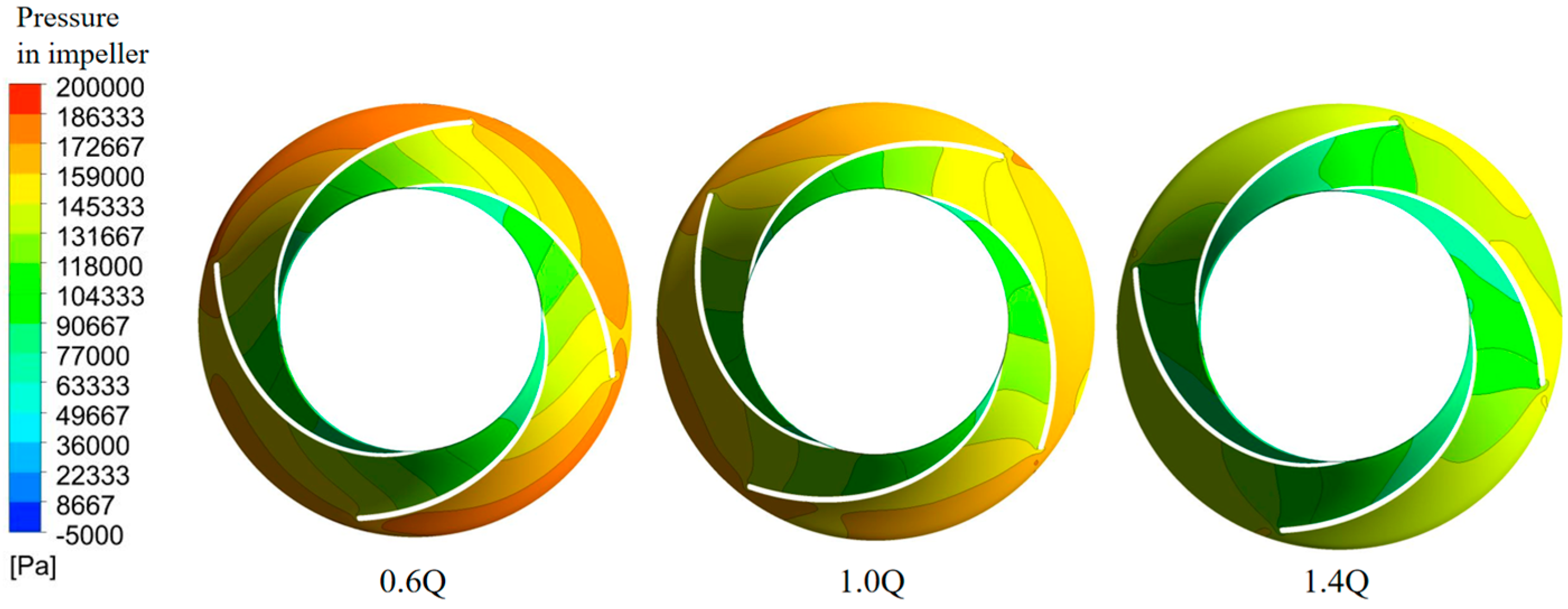



| Parameters | Value |
|---|---|
| Nominal flow rate | 453 m3/h |
| Design head | 8 m |
| Nominal rotating speed | 1450 r/min |
| Impeller blade number | 4 |
| Impeller hub number | 26.6 mm |
| Inlet diameter | 300 mm |
| Outlet diameter | 350 mm |
| Apparatus | Purpose | Range | Accuracy |
|---|---|---|---|
| Pressure Transmitter | Inlet pressure | −0.1~1.6 (Mpa) | ±0.1% |
| Pressure Transmitter | Outlet pressure | 0~0.5 (Mpa) | ±0.1% |
| Electromagnetic Flowmeter | Flow rate | 0~4000 (m3/h) | ±0.3% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhi, Y.; Huang, Q.; Su, H.; Li, H.; Chen, H.; Ke, Q.; Fu, Q. An Analysis of the Characteristics of Internal Flow Losses of Seawater Circulation Pumps in Nuclear Power Plants Based on the Entropy Production Theory. Energies 2025, 18, 1909. https://doi.org/10.3390/en18081909
Zhi Y, Huang Q, Su H, Li H, Chen H, Ke Q, Fu Q. An Analysis of the Characteristics of Internal Flow Losses of Seawater Circulation Pumps in Nuclear Power Plants Based on the Entropy Production Theory. Energies. 2025; 18(8):1909. https://doi.org/10.3390/en18081909
Chicago/Turabian StyleZhi, Yifan, Qian Huang, Haonan Su, Huairui Li, Huazheng Chen, Qidi Ke, and Qiang Fu. 2025. "An Analysis of the Characteristics of Internal Flow Losses of Seawater Circulation Pumps in Nuclear Power Plants Based on the Entropy Production Theory" Energies 18, no. 8: 1909. https://doi.org/10.3390/en18081909
APA StyleZhi, Y., Huang, Q., Su, H., Li, H., Chen, H., Ke, Q., & Fu, Q. (2025). An Analysis of the Characteristics of Internal Flow Losses of Seawater Circulation Pumps in Nuclear Power Plants Based on the Entropy Production Theory. Energies, 18(8), 1909. https://doi.org/10.3390/en18081909






