Real-Time Estimation of the State of Charge of Lithium Batteries Under a Wide Temperature Range
Abstract
1. Introduction
- In light of the variations in environmental temperature, a second-order equivalent circuit model was developed, and a parameter identification approach based on the CSO algorithm for optimizing the Kalman filter (CSO-KF) was put forward;
- An environmental temperature battery database was constructed based on the parameter identification results that incorporated temperature variations. By means of mathematical relations, the correlations among the parameters at the current moment, the SOC values, and the temperature were introduced, thus enabling the acquisition of accurate parameter values within variable-temperature environments;
- A real-time SOC estimation method based on the CSO–DKF algorithm was proposed. The parameter filter and the state filter operated alternately, and the accuracy of SOC estimation was verified under three variable-temperature environments.
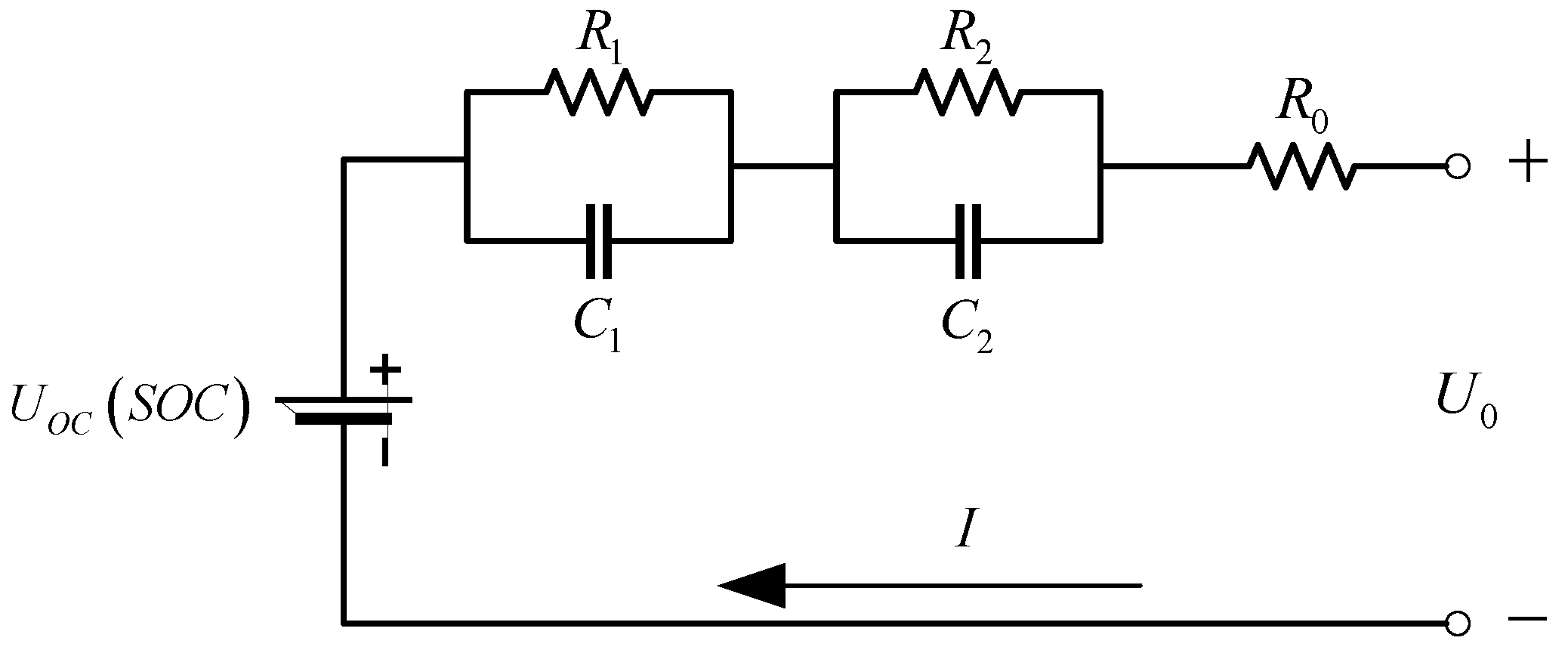
2. Battery Model
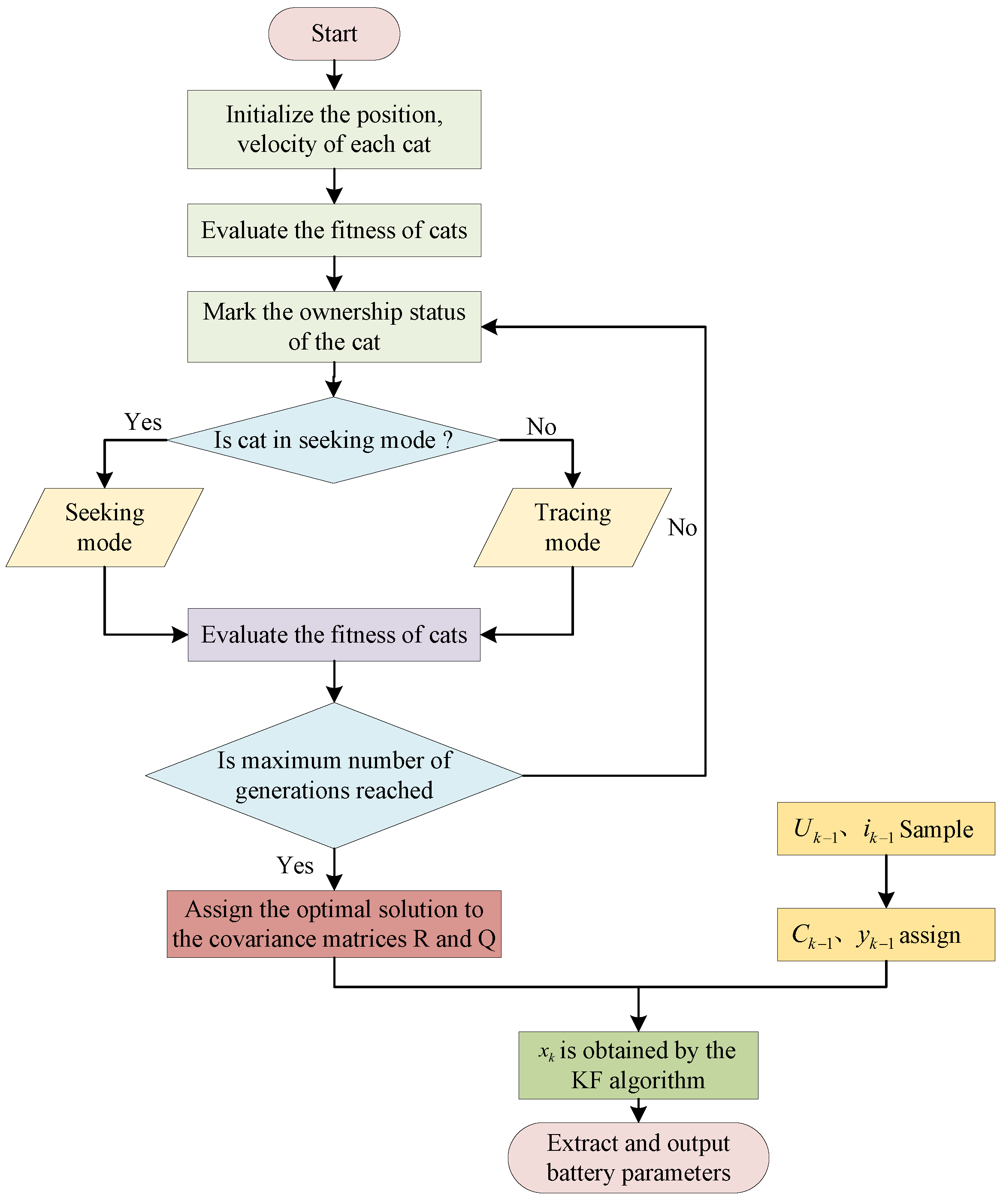
3. Dynamic Parameter Identification Method Based on Optimizing Kalman Filter with Cat Swarm Optimization Algorithm
3.1. Cat Swarm Optimization
- Generate M copies of its own position and store them in the memory pool, where M denotes the size of the memory pool;
- Perform random perturbations on the original positions of each individual within the memory pool in accordance with the variations in dimensions and ranges, thereby obtaining a new position to substitute the previous one;
- Compute the fitness function values of all the new positions in the memory pool and utilize these values as the criteria for optimization;
- In the memory pool, relocate the cat to the position with the highest fitness function value, thereby accomplishing the update of the cat’s position.
- The velocity of cat is updated via the following formula:In the formula, the value range of d is from 1 to the total number of dimensions. represents the velocity of the cat in the d dimension at time t before the update, and represents the speed of the cat in the dimension after the update. is the position of the cat with the optimal fitness function value in the d dimension, represents the position of the cat in the d dimension, c is a constant, and r is a random value within the range of [0, 1];
- Update the new position of the cat based on its current position and velocity:In the formula, represents the position of the cat in the d dimension at time t prior to the update, and represents the position of the cat in the d dimension subsequent to the update;
- To avoid out-of-bounds scenarios, if the position in a particular dimension exceeds the defined boundary, it will be adjusted to the corresponding boundary value. By implementing the aforementioned two modes, the positions of each cat are iteratively updated, gradually approaching and ultimately attaining the global optimum. Once the program satisfies the termination criteria, the algorithm concludes.
3.2. Kalman Filtering Algorithm
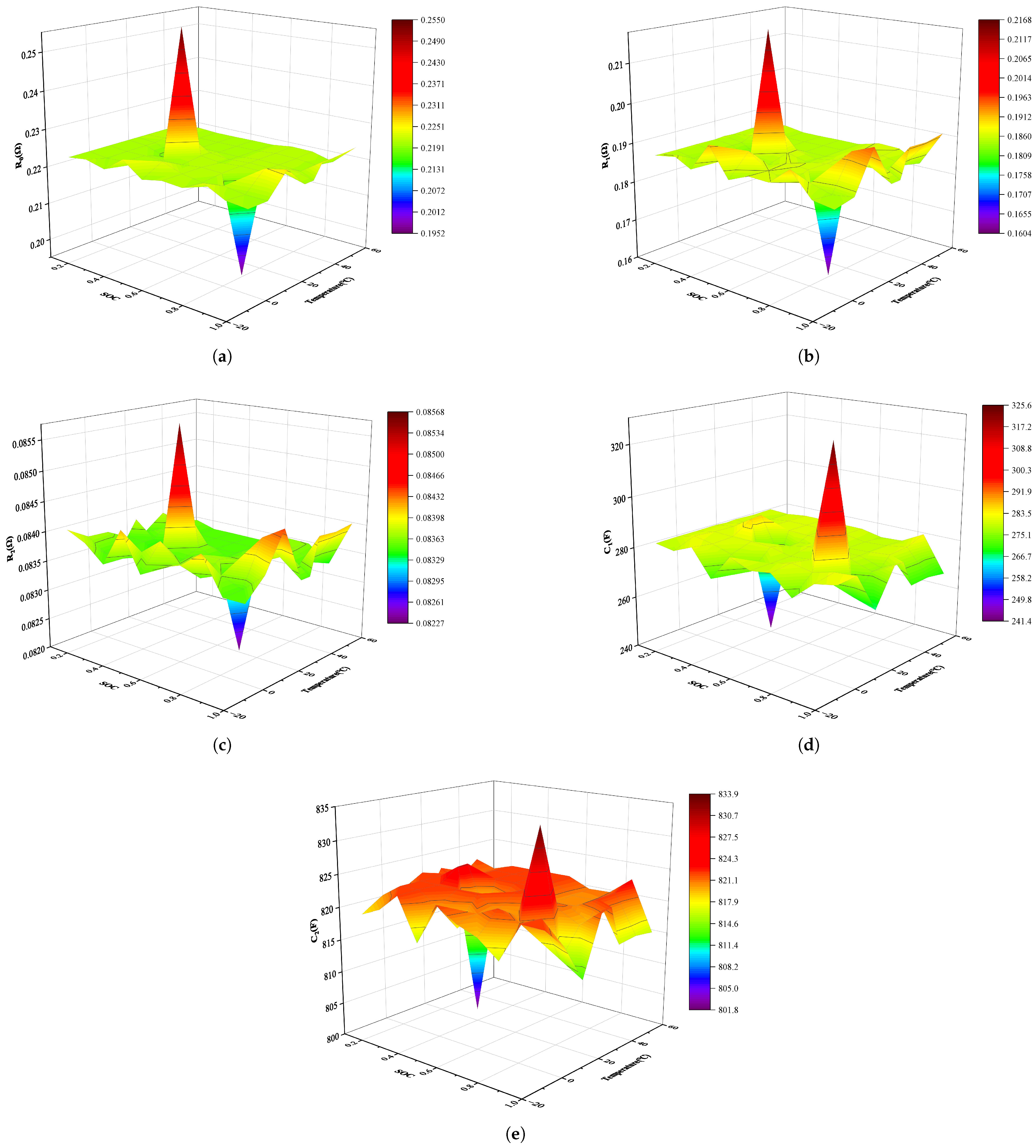
3.3. Parameter Identification
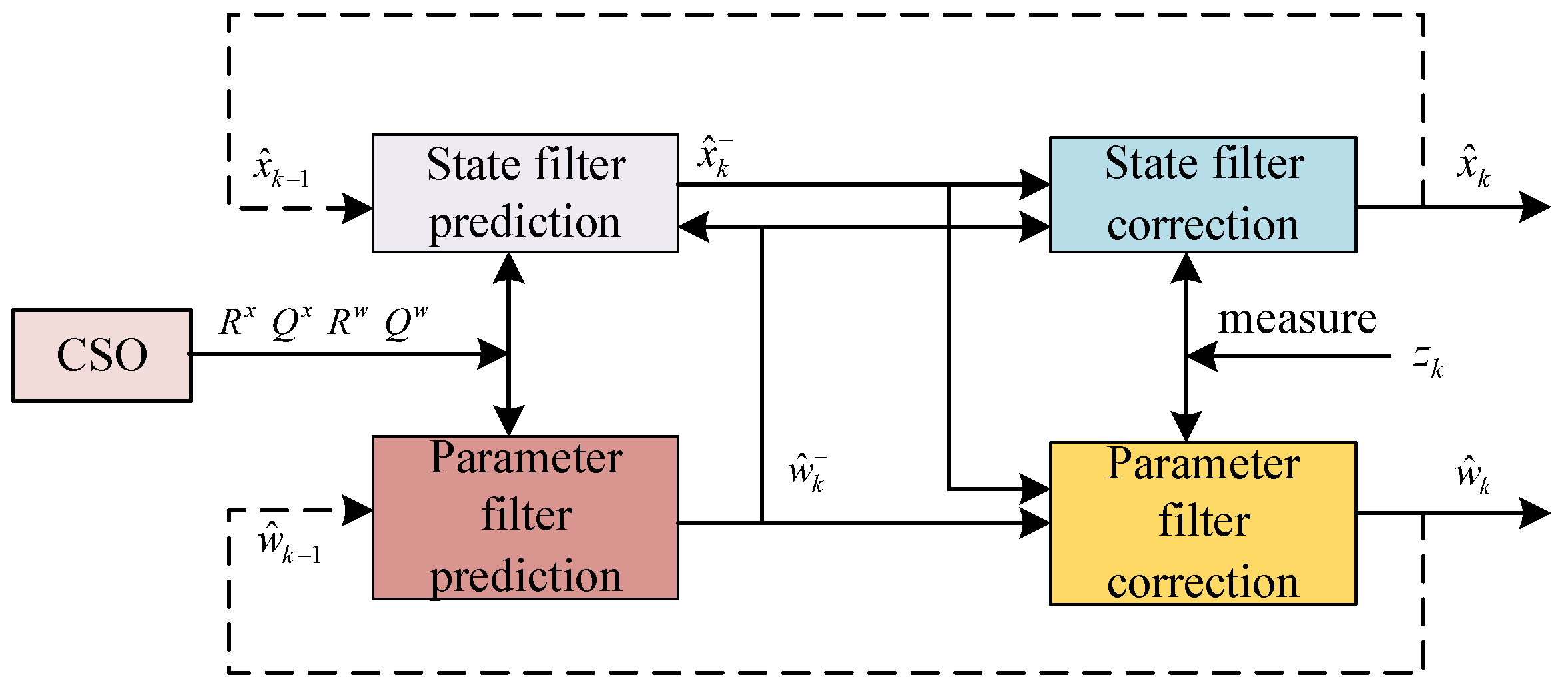
4. Real-Time SOC Estimation Method Based on Dual Kalman Filter Optimized by Cat Swarm Optimization Algorithm
4.1. Extended Kalman Filtering Algorithm
4.2. Real-Time Estimation of SOC
- Variable initialization:
- The CSO algorithm yields the optimal solutions for the noise covariance matrices , , , and ;
- Parameter prediction update:
- State variable prediction update:
- State variable correction update:
- Parameter correction update:
- Output the optimal estimated value of the state variable: .
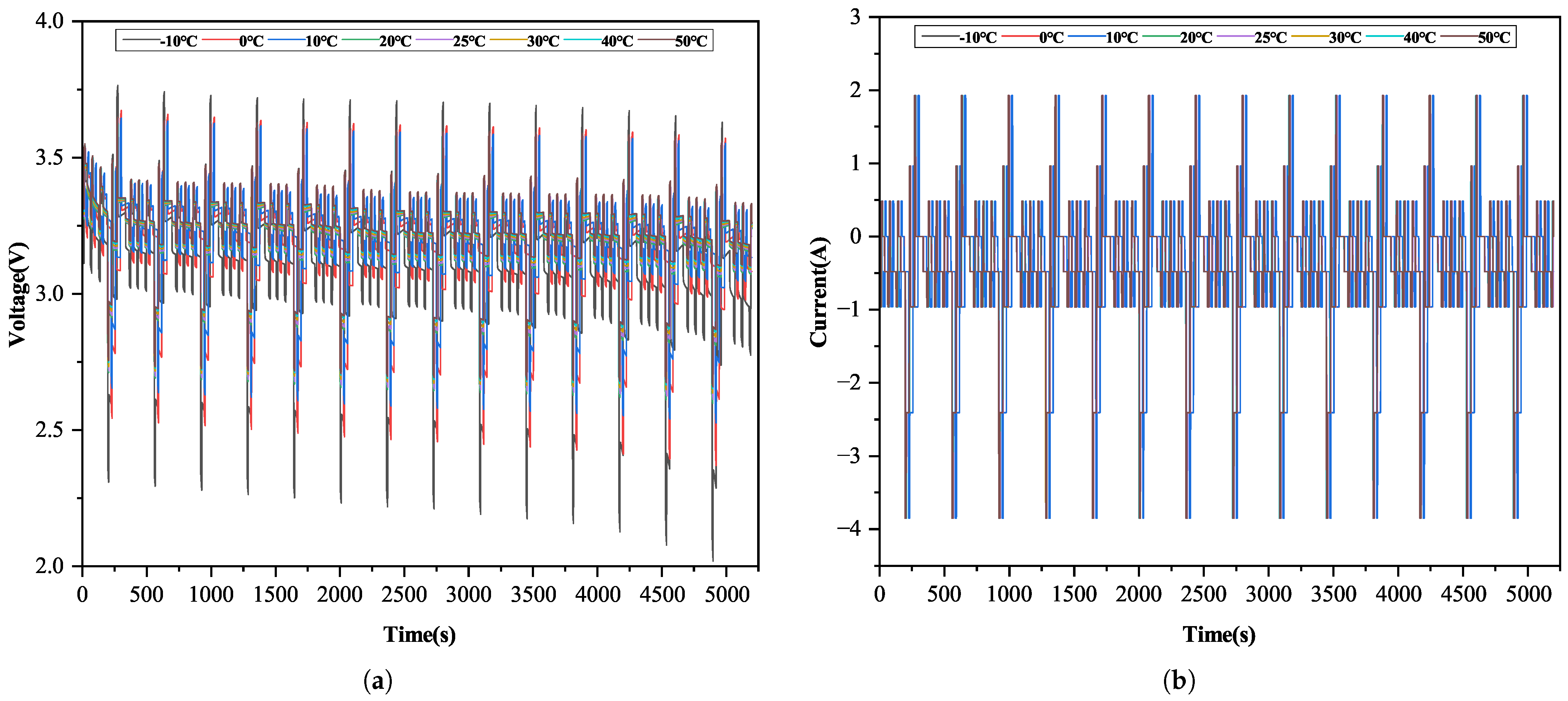
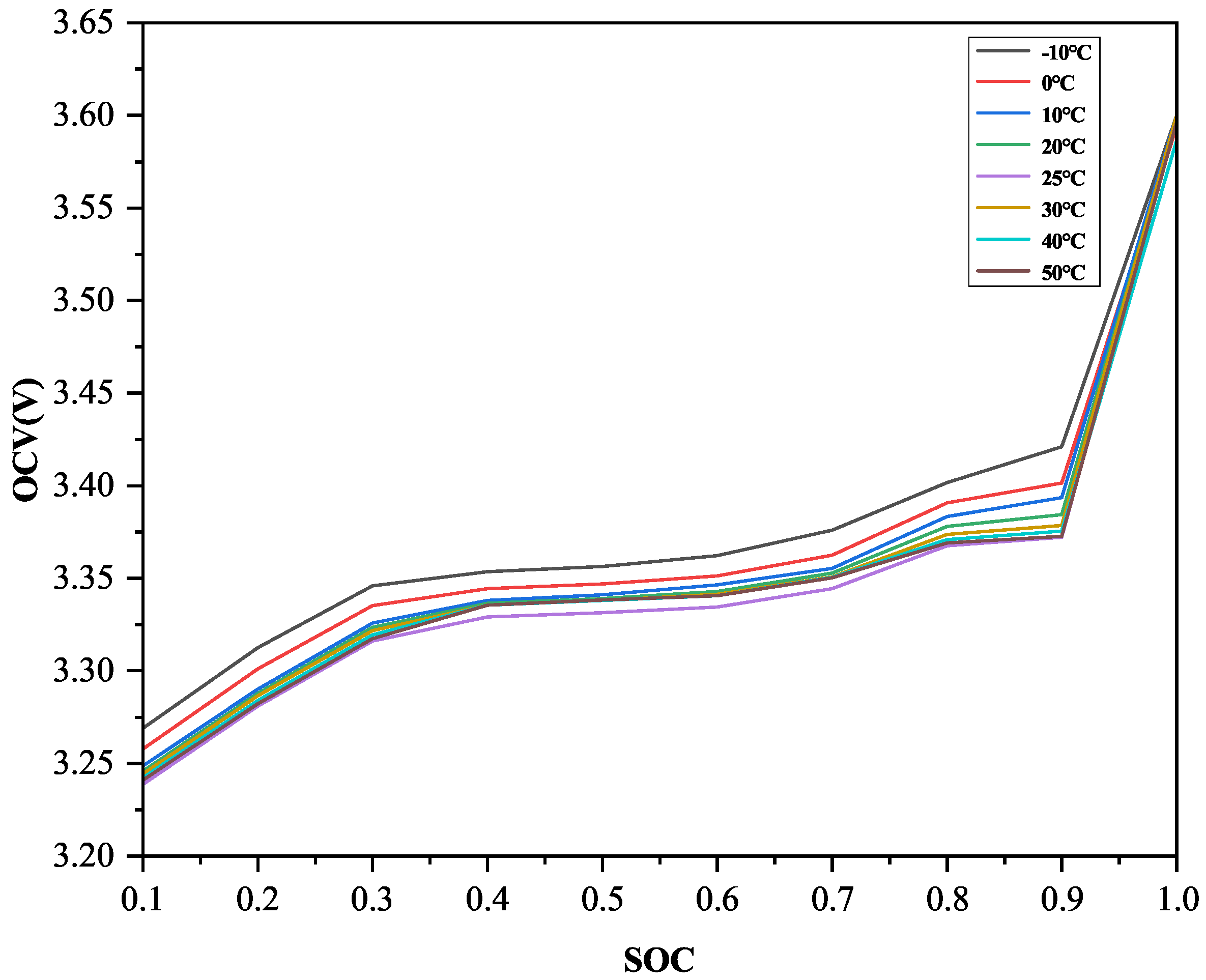
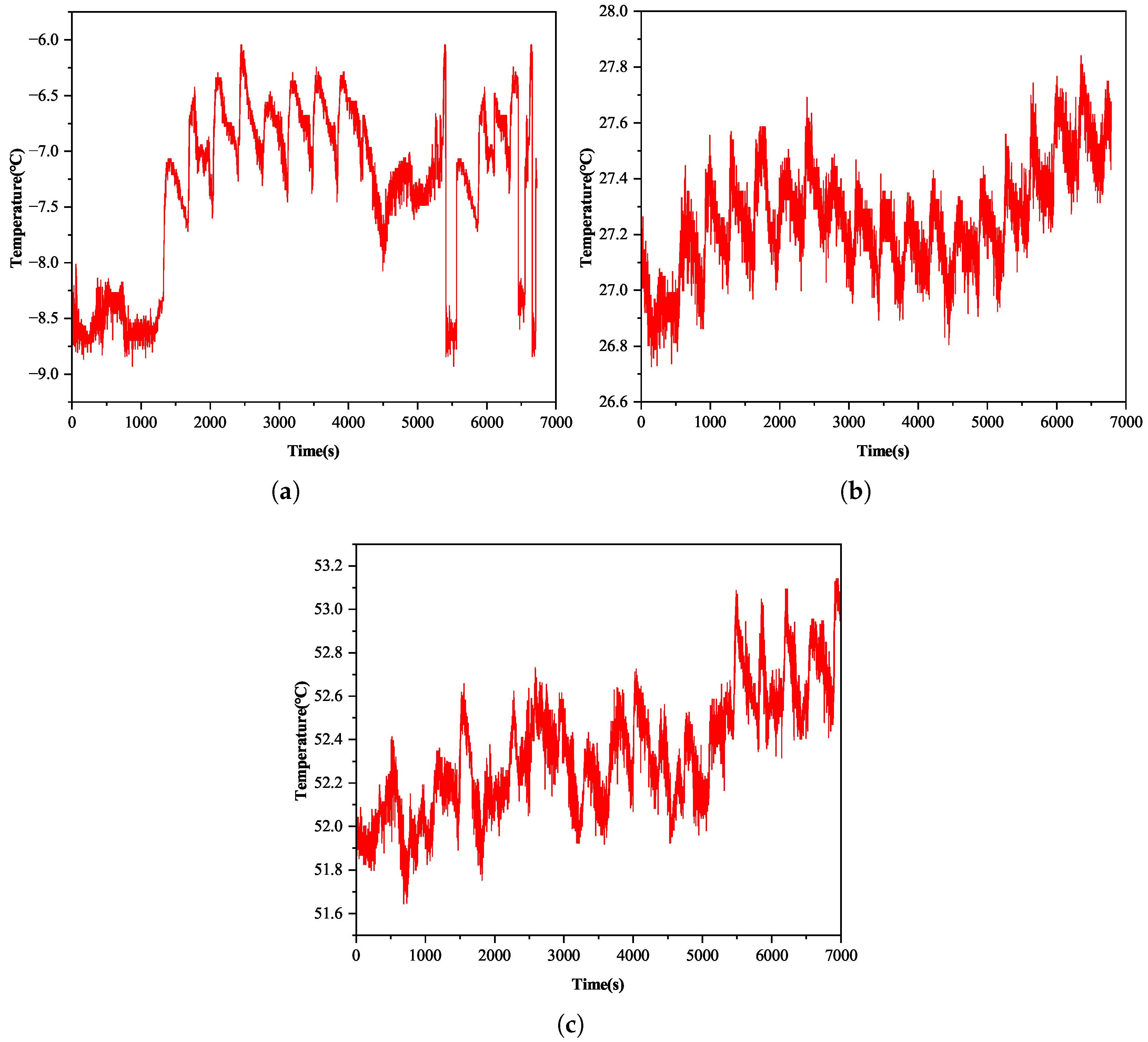
5. Experimental Validation and Analysis
6. Conclusions
- A second-order equivalent circuit model was constructed. Dynamic parameter identification was carried out by leveraging the CSO algorithm to optimize the KF, thereby determining the model parameters. Subsequently, the accuracy of the proposed model was verified under low-temperature ( °C), ambient-temperature ( °C), and high-temperature ( °C) conditions. The verification results demonstrated that the model is capable of providing favorable accuracy and exhibits robust performance with respect to temperature variations;
- An environmental temperature battery database was established based on the parameter identification results obtained at different temperatures and various SOC stages. Through mathematical expressions, the relationships among the parameters at the current moment, temperature, and SOC values were established, thus facilitating the introduction of the temperature variable during the joint estimation of dynamic parameter identification and real-time SOC;
- Building upon this foundation, the CSO algorithm was utilized to optimize the DKF for real-time SOC estimation. The state filter and the parameter filter were employed alternately. The accuracy of SOC estimation and the optimization effect of the CSO were verified within three temperature variation intervals, namely variable low temperature, variable ambient temperature, and variable high temperature. The results revealed that, under varying temperatures, this system can ensure commendable accuracy in real-time SOC estimation, thereby providing a viable approach for estimating the state of charge of lithium-ion batteries in variable-temperature environments.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Demirci, O.; Taskin, S.; Schaltz, E.; Demirci, B.A. Review of battery state estimation methods for electric vehicles-Part I: SOC estimation. J. Energy Storage 2024, 87, 111435. [Google Scholar]
- Su, L.; Zhou, G.; Hu, D.; Liu, Y.; Zhu, Y. Research on the state of charge of lithium-ion battery based on the fractional order model. Energies 2021, 14, 6307. [Google Scholar] [CrossRef]
- Wang, L.; Zhao, X.; Deng, Z.; Yang, L. Application of electrochemical impedance spectroscopy in battery management system: State of charge estimation for aging batteries. J. Energy Storage 2023, 57, 106275. [Google Scholar]
- Zheng, F.; Xing, Y.; Jiang, J.; Sun, B.; Kim, J.; Pecht, M. Influence of different open circuit voltage tests on state of charge online estimation for lithium-ion batteries. Appl. Energy 2016, 183, 513–525. [Google Scholar]
- Pattipati, B.; Balasingam, B.; Avvari, G.V.; Pattipati, K.R.; Bar-Shalom, Y. Open circuit voltage characterization of lithium-ion batteries. J. Power Sources 2014, 269, 317–333. [Google Scholar]
- Shrivastava, P.; Naidu, P.A.; Sharma, S.; Panigrahi, B.K.; Garg, A. Review on technological advancement of lithium-ion battery states estimation methods for electric vehicle applications. J. Energy Storage 2023, 64, 107159. [Google Scholar]
- Ghaeminezhad, N.; Ouyang, Q.; Wei, J.; Xue, Y.; Wang, Z. Review on state of charge estimation techniques of lithium-ion batteries: A control-oriented approach. J. Energy Storage 2023, 72, 108707. [Google Scholar]
- Xu, C.; Zhang, E.; Jiang, K.; Wang, K. Dual fuzzy-based adaptive extended Kalman filter for state of charge estimation of liquid metal battery. Appl. Energy 2022, 327, 120091. [Google Scholar]
- Wang, L.; Gao, K.; Han, J.; Zhao, X.; Liu, L.; Pan, C.; Li, G.; Wang, Y. Battery pack SOC estimation by Noise Matrix Self Adjustment-Extended Kalman Filter algorithm based on cloud data. J. Energy Storage 2024, 84, 110706. [Google Scholar]
- Miao, Y.; Gao, Z. Estimation for state of charge of lithium-ion batteries by adaptive fractional-order unscented Kalman filters. J. Energy Storage 2022, 51, 104396. [Google Scholar]
- Qian, W.; Li, W.; Guo, X.; Wang, H. A switching gain adaptive sliding mode observer for SoC estimation of lithium-ion battery. Energy 2024, 292, 130585. [Google Scholar]
- Chen, L.; Guo, W.; Lopes, A.M.; Wu, R.; Li, P.; Yin, L. State-of-charge estimation for lithium-ion batteries based on incommensurate fractional-order observer. Commun. Nonlinear Sci. Numer. Simul. 2023, 118, 107059. [Google Scholar]
- Chen, Z.; Zhou, J.; Zhou, F.; Xu, S. State-of-charge estimation of lithium-ion batteries based on improved H infinity filter algorithm and its novel equalization method. J. Clean. Prod. 2021, 290, 125180. [Google Scholar]
- Wang, Q.; Sun, C.; Gu, Y. Research on SOC estimation method of hybrid electric vehicles battery based on the grey wolf optimized particle filter. Comput. Electr. Eng. 2023, 110, 108907. [Google Scholar]
- Hannan, M.A.; Lipu, M.H.; Hussain, A.; Mohamed, A. A review of lithium-ion battery state of charge estimation and management system in electric vehicle applications: Challenges and recommendations. Renew. Sustain. Energy Rev. 2017, 78, 834–854. [Google Scholar]
- Zhang, G.; Xia, B.; Wang, J. Intelligent state of charge estimation of lithium-ion batteries based on LM optimized back-propagation neural network. J. Energy Storage 2021, 44, 103442. [Google Scholar]
- Zhang, G.; Xia, B.; Wang, J.; Ye, B.; Chen, Y.; Yu, Z.; Li, Y. Intelligent state of charge estimation of battery pack based on particle swarm optimization algorithm improved radical basis function neural network. J. Energy Storage 2022, 50, 104211. [Google Scholar]
- Korkmaz, M. A novel approach for improving the performance of deep learning-based state of charge estimation of lithium-ion batteries: Choosy SoC Estimator (ChoSoCE). Energy 2024, 294, 130913. [Google Scholar]
- Korkmaz, M. SoC estimation of lithium-ion batteries based on machine learning techniques: A filtered approach. J. Energy Storage 2023, 72, 108268. [Google Scholar]
- Liu, B.; Wang, H.; Tseng, M.L.; Li, Z. State of charge estimation for lithium-ion batteries based on improved barnacle mating optimizer and support vector machine. J. Energy Storage 2022, 55, 105830. [Google Scholar]
- Hu, J.; Hu, J.; Lin, H.; Li, X.; Jiang, C.; Qiu, X.; Li, W. State-of-charge estimation for battery management system using optimized support vector machine for regression. J. Power Sources 2014, 269, 682–693. [Google Scholar]
- Li, W.; Fan, Y.; Ringbeck, F.; Jöst, D.; Han, X.; Ouyang, M.; Sauer, D.U. Electrochemical model-based state estimation for lithium-ion batteries with adaptive unscented Kalman filter. J. Power Sources 2020, 476, 228534. [Google Scholar]
- Lotfi, N.; Landers, R.G.; Li, J.; Park, J. Reduced-order electrochemical model-based SOC observer with output model uncertainty estimation. IEEE Trans. Control Syst. Technol. 2016, 25, 1217–1230. [Google Scholar]
- Koseoglou, M.; Tsioumas, E.; Panagiotidis, I.; Papagiannis, D.; Jabbour, N.; Mademlis, C. A lithium-ion battery equivalent circuit model based on a hybrid parametrization approach. J. Energy Storage 2023, 73, 109051. [Google Scholar]
- Huang, Z.; Best, M.; Knowles, J.; Fly, A. Adaptive piecewise equivalent circuit model with SOC/SOH estimation based on extended Kalman filter. IEEE Trans. Energy Convers. 2022, 38, 959–970. [Google Scholar]
- Deng, Q.; Qiu, D.; Xie, Z.; Zhang, B.; Chen, Y. Online SOC estimation of supercapacitor energy storage system based on fractional-order model. IEEE Trans. Instrum. Meas. 2023, 72, 1–10. [Google Scholar]
- Guha, A.; Routh, B.; Velivela, N.P. Adaptive Extended Kalman Filtering based State-of-Charge and Voltage Estimation of a Lithium-ion Battery using a Fractional Order Model. IEEE Sens. J. 2024, 24, 26225–26234. [Google Scholar]
- Xiong, R.; Tian, J.; Shen, W.; Sun, F. A novel fractional order model for state of charge estimation in lithium ion batteries. IEEE Trans. Veh. Technol. 2018, 68, 4130–4139. [Google Scholar]
- Huang, J.; Asteris, P.G.; Manafi Khajeh Pasha, S.; Mohammed, A.S.; Hasanipanah, M. A new auto-tuning model for predicting the rock fragmentation: A cat swarm optimization algorithm. Eng. Comput. 2022, 38, 2209–2220. [Google Scholar]
- Lin, Q.; Li, X.; Tu, B.; Cao, J.; Zhang, M.; Xiang, J. Stable and accurate estimation of SOC using eXogenous Kalman filter for lithium-ion batteries. Sensors 2023, 23, 467. [Google Scholar] [CrossRef]
- Sepasi, S.; Ghorbani, R.; Liaw, B.Y. A novel on-board state-of-charge estimation method for aged Li-ion batteries based on model adaptive extended Kalman filter. J. Power Sources 2014, 245, 337–344. [Google Scholar]

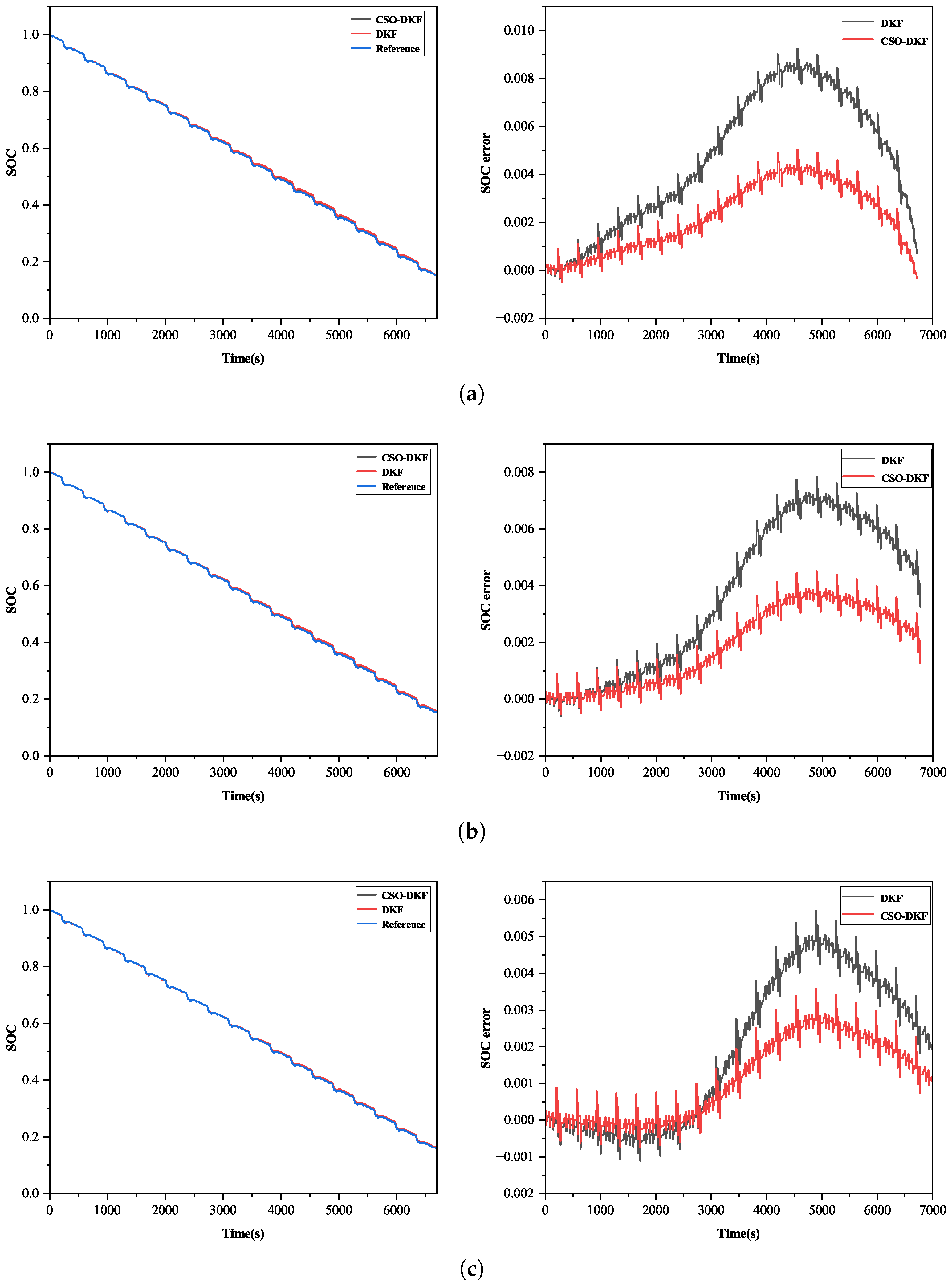
| RMSE (Variable Low Temperature) | RMSE (Variable Ambient Temperature) | RMSE (Variable High Temperature) | |
|---|---|---|---|
| CSO–DKF | 0.30% | 0.24% | 0.36% |
| DKF | 0.93% | 0.88% | 0.97% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, D.; Liu, L.; Yue, C.; Gao, X.; Zhu, Y. Real-Time Estimation of the State of Charge of Lithium Batteries Under a Wide Temperature Range. Energies 2025, 18, 1866. https://doi.org/10.3390/en18071866
Li D, Liu L, Yue C, Gao X, Zhu Y. Real-Time Estimation of the State of Charge of Lithium Batteries Under a Wide Temperature Range. Energies. 2025; 18(7):1866. https://doi.org/10.3390/en18071866
Chicago/Turabian StyleLi, Da, Lu Liu, Chuanxu Yue, Xiaojin Gao, and Yunhai Zhu. 2025. "Real-Time Estimation of the State of Charge of Lithium Batteries Under a Wide Temperature Range" Energies 18, no. 7: 1866. https://doi.org/10.3390/en18071866
APA StyleLi, D., Liu, L., Yue, C., Gao, X., & Zhu, Y. (2025). Real-Time Estimation of the State of Charge of Lithium Batteries Under a Wide Temperature Range. Energies, 18(7), 1866. https://doi.org/10.3390/en18071866






