Abstract
In Europe and elsewhere in the world, current ambitious decarbonization targets push towards a gradual decommissioning of all fossil-fuel-based dispatchable electrical generation and, at the same time, foster a gradual increase in the penetration of Renewable Energy Sources (RES). Moreover, considerations tied to decarbonization as well as to the security of supply, following recent geo-political events, call for a gradual replacement of gas appliances with electricity-based ones. As RES generation is characterized by a variable generation pattern and as the electric carrier is characterized by scarce intrinsic flexibility, and since storage capabilities through electrochemical batteries, as well as demand-side flexibility contributions, remain rather limited, it is quite natural to think of other energy carriers as possible service providers for the electricity system. Gas and heat networks and, in the future, hydrogen networks could provide storage services for the electricity system. This could allow increasing the amount of RES penetration to be managed safely by the electric system without incurring blackouts and avoiding non-economically motivated grid reinforcements to prevent the curtailment of RES generation peaks. What is explained above calls for a new approach, both in electricity network dispatch simulations and in grid-planning studies, which extends the simulation domain to other carriers (i.e., gas, heat, hydrogen) so that a global optimal solution is found. This simulation branch, called multi-energy or multi-carrier, has been gaining momentum in recent years. The present paper aims at describing the most important approaches to static ME modeling by comparing the pros and cons of all of them with a holistic approach. The style of this paper is that of a tutorial aimed at providing some guidance and a few bibliographic references to those who are interested in approaching this theme in the next years.
1. Introduction
In recent years, decarbonization has become one of the most important imperatives in the energy sector. The European Union, as well as many other countries in the world, have set very ambitious climate-neutrality targets for the mid-to-long term [1]. In the electricity sector, this has produced an important increase in the deployment pace for so-called Renewable Energy Sources (RES), most notably wind and solar. At the same time, more traditional big generators based on fossil fuels are being decommissioned because they are out-of-merit-order in electricity markets and are no longer compliant with the environmental targets. This trend has been reinforced and even further accelerated in the last years due to important geo-political events stressing the necessity to ensure the security of supply and to make the energy system independent from the purchase of fuels from politically unstable or critical nations. However, for the electricity system, characterized by very limited intrinsic flexibility (as electrochemical batteries can provide only limited storage capabilities and demand-side involvement stays rather limited), substantially increasing the penetration of RES, typically characterized by variable generation patterns, entails the need to procure more and more services for congestion management, frequency control, etc. RES power generation is characterized by evident generation peaks and valleys, and reinforcing electricity transmission and distribution networks to host such peaks without causing congestion would call for very expensive grid refurbishment actions, against, maybe, a very limited number of hours during the year in which such expanded grids would be fully utilized. In these cases, grid expansion would prove to be economically unjustified.
The same decarbonization targets mentioned above also push in the direction of overall electrification of power consumption in the industrial sector, as well as for energy end-uses. However, not all industrial processes can easily be electrified, and some industrial sectors (cement, paper) are hardly electrifiable with the present technologies, or, in other cases (steel), could be electrified only by completely replacing the present production technologies by carrying out huge investments. These sectors, usually called hard-to-abate, alongside the heavy transport sector, although not easily electrifiable, could be fed with other energy vectors, most notably hydrogen. As a matter of fact, hydrogen [2] is imposing itself as one of the most promising decarbonization “tiles” of future energy policies. However, green hydrogen is produced through electrolyzers, which, in turn, use electricity in great quantities, hence again the need to expand the electricity grid.
To cope with the very limited storage capability of the electricity system, other carriers could prove very helpful. Natural gas is characterized by very high compressibility (this phenomenon is called linepack) and there is a wide range of admissible operative pressures. Thus, the entire gas network, tightly coupled to the electricity network, could be exploited to provide flexibility to the electricity vector itself, forming a huge, distributed storage system. Hydrogen storage is itself very promising, both for short-term storage (able to compensate for daily peaks in RES electric generation) and even long-term storage (able to compensate for important seasonal generation differences in wind and solar power plants). Hydrogen storage and flow batteries are seen as the only presently mature technologies for long-term storage.
Finally, heat networks show an important flexibility potential too: thermal systems, be they for small-scale swimming pools [3] or much larger ones for district heating [4], can guarantee acceptable levels of comfort if water temperatures are held within given wide operative ranges, and this flexibility can, again, be exploited to the advantage of the electricity carrier to which services can be provided.
Table 1 summarizes the most typical interactions between energy carriers and the devices (“units”) where the energy conversion processes between carriers take place.

Table 1.
Typical interactions between energy carriers (source [5]).
All the above reasons motivate an extension of the traditional scenario simulations and planning studies for the electric system by including other carriers (natural gas, hydrogen, district-heating) with which the electricity system is (and will be more and more in the future) interconnected. Regarding dispatch scenario studies, the addition of the other interconnected carriers can help to achieve a more optimized equilibrium and a better quantification of the interdependences between the different carriers. Concerning planning studies, considering the mutual interdependency of the different sectors can help to exploit synergies and limit refurbishment costs, which are economically unjustified. Additionally, electric grids expansion meets more and more opposition from public opinion, and this leads to very long approval times, which heavily contrast with the rapidity needed to deploy all that is needed to comply with current decarbonization targets and deadlines. Thus, reducing the number of grid refurbishment interventions by exploiting synergies between carriers in a holistic approach is also a way to ease and speed up the realization of the needed electric grid upgrades.
The above considerations clarify the need to adopt a Multi-Energy (ME) approach in the simulation of the energy grids [6]. In particular, in this paper, the focus is on static multi-energy models, useful either for calculating the network flows once the injected and withdrawn powers are known (load flow analysis) or for optimizing the system dispatch or the planning of new grid infrastructure. All such models have in common the static description of the different carriers (as opposed to the one oriented towards studying transient phenomena) and the fact that very often they imply either the solution of a system of equations (for load–flow analysis) or the resolution of optimization systems that minimize operative system expenditures (OPEX, very often in the sense of pure dispatching costs) or the total system expenditures (TOTEX, meant as the sum of OPEX and CAPEX, capital expenditures) for investing in new assets to be deployed. The peculiarity of these models, if applied in an ME context instead of a single energy carrier, is that the dimension of the problem is considerably larger. This means that particular attention should be paid on one side to finding out the simplest schematization of the single components of each carrier (e.g., preserving the linearity of the models becomes nearly imperative) and on the other side to utilizing opportune solving algorithms fit for managing very large systems, and most likely utilizing modern decomposition techniques (like Benders’ decomposition [7]).
Static ME models can be very useful for the system operators of the different grids to analyze the efficacy of flexibility measures across the energy carriers, and for the national regulatory authorities to assess the possible technical–economic impact of new regulatory provisions. The importance of adopting a Multi-Energy (ME) approach in dispatch scenarios and planning studies is also reflected in numerous policy documents, which clearly call for the adoption of a multi-carrier approach. Just to mention a couple of them, at the European Union level, the European Commission [8] published in 2020 the Communication “Powering a climate neutral economy: an EU Strategy for energy system integration” [9]. In this document, we find “Energy system integration—the coordinated planning and operation of the energy system ‘as a whole’, across multiple energy carriers, infrastructures, and consumption sectors—is the pathway towards an effective, affordable and deep decarbonisation of the European economy”. The more recent document “Electricity infrastructure development to support a competitive and sustainable energy system—2024 Monitoring Report” [10] published by the European Union Agency for the Cooperation of Energy Regulators (ACER, [11]) invites grid developers “to extend the use of multi-vector scenarios to grid development planning at the national level and ensure consistency between EU TYNDP and national scenarios”. Finally, the European Network of Transmission System Operators for Electricity (ENTSO-E, [12]) and the European Network of Transmission System Operators for Gas (ENTSOG, [13]) have recently started to publish joint electricity–gas scenarios to support the vision of the Ten-Year-Network-Development-Plan 2024. These scenarios are publicly available on the web [14]. While introducing such scenarios, ENTSO-E and ENTSOG declare “The scenarios evaluate the interactions between the gas, hydrogen and electricity systems, vital to delivering the best assessment of the infrastructure from an integrated system perspective”.
This paper aims to highlight which modeling issues have to be taken into account in order to build up an ME static model. By contrast, it does not provide details on algorithms and techniques fitted to solving the very large mathematical models generated in this way. After this introduction, the second chapter describes in synthesis the most significant modeling aspects for the main components of the carriers to be typically considered in an ME model: electricity, gas, hydrogen and heat. The third chapter deals with the most typical techniques for joining the different carriers in one simulation model. Here, the goal is not to be exhaustive by quoting every single paper that has been produced in the last years (it would be nearly impossible), but, rather, to single out the most typical approaches and to outline the peculiarities of each of them. The last section introduces the most typical numerical concepts and issues. Finally, the conclusive chapter provides a comparison of the different approaches and some advice for those interested in ME modeling. The paper’s style is that of a tutorial aimed at providing some guidance and a few bibliographic references to those who are interested in a first approach to ME modeling.
2. Energy Carriers Static Modeling Approaches
Before discussing the most common ME modeling approaches, it is a good idea to carry out an analysis of the mathematic models of the main components of each carrier. In this analysis we are going to start from the general approaches and then indicate which simplifications can be useful to make the model fit for simulating large-scale systems (i.e., networks with a few thousand nodes for each carrier). To this end, the most important factors to be preserved are model convexity and model linearity. Model convexity [15] ensures that an optimization problem has one only solution, and it is thus not subject to local minima, which may typically constitute a serious problem, making numerical convergence more difficult to achieve and potentially making solutions found for subsequent time instants not mutually comparable. Linear optimization models are also convex. Linearity is an essential prerequisite to the application of algorithms like the interior point [16], which are both very fast and powerful in dealing with large-scale systems. Bearing in mind that planning problems are typically modeled as mixed integer (investments are typically associated to binary variables—see, e.g., the model developed by the FlexPlan European research project [17]), the solving of Mixed Integer Linear Problems (MILP [18]) brings huge advantages with respect to solving Mixed Integer Non-Linear Problems (MINLP).
In general, and for Multi-Energy Systems (MES) even more, model complexity is a function of the detail adopted in the representation of each system component. More detail on components’ behaviors implies a more complex mathematical description. So, it is of paramount importance to understand which is the best compromise between the completeness of the mathematical representation of the system and the complexity of the resulting problem (which implies the kind of solver that can be used and the time of resolution or, in many cases, just whether the problem is numerically tractable with the present hardware and software or not). From this point of view, ref. [19] provides an interesting classification of the mathematical representation (and complexity) associated with the different modeling details treated in ME models. ME models are divided into seven categories (Figure 1). Table 2 shows the typical modeling criticalities of each category.
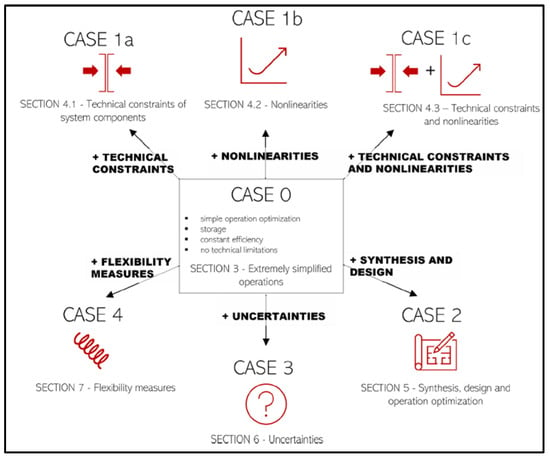
Figure 1.
Classification of ME models (source: [19]).

Table 2.
Categorization of ME models (re-elaborated from [19]).
As is evident when examining Table 2, mathematical complexity increases with the realism of the model and the number of included details (components of non-linearity, technical constraints, uncertainty, flexibility and ancillary services) and considerably changes with the aim of the model (only dispatch variables for the optimization of short-term system operation, also investment variables, which are typically integer ones, for long-term grid design and planning).
The following sections will examine the main peculiarities of the static models describing the components of different carriers (electricity networks, compressible fluid networks and heat networks). Among them, compressible fluids networks, which can represent either natural gas or hydrogen networks, and heat networks are the most complicated cases, because the relevant equations are not easily linearized without committing important approximations and because the approaches for static modeling are less established than those for the electricity networks. Although simplifications are carried out in nearly all approaches to model multi-carrier networks, it is important to have a look at the general case and analyze the meanings of the different approximations to be brought in order to get to a linear model. For this reason, the section dedicated to compressible fluid networks is much longer than the ones dedicated to the other two carriers.
2.1. Electricity Networks Modeling
Electricity networks are included in plenty of simulation tools and applications, and the relevant modeling approach necessary for each domain of simulation (planning, operation, contingency analysis, etc.) is well known. There also exist some very well-known open-access libraries, which can be used as a basis to build simulation tools; just to mention some of the most well-known ones, we can cite MATPOWER [22] for the MATLAB programming language [23] and PowerModels [24] for the Julia programming language [25]. Nonetheless, the brief introduction provided by the present section is necessary both for the sake of completeness with respect to what is written for the other energy carriers and to provide an overview of the most common modeling choices with specific reference to static models. For a more complete introduction to the modeling of the electric networks, the reader is directed to dedicated books (a few bibliographic references can be found in [26]).
Starting from electrical lines, active and reactive power can be calculated for each branch of the network by utilizing the following simplified formulation (after neglecting the shunt part of the π model, see Figure 2):
where phk is the active power of the branch between nodes h and k, qhk is the reactive power between the same nodes, Vh and Vk are the voltage modules for the two nodes h and k, and θh and θk are the voltage angles for the same nodes; ghk and bhk are, respectively, the real part and the imaginary part of the admittance yhk of the branch between nodes h and k.
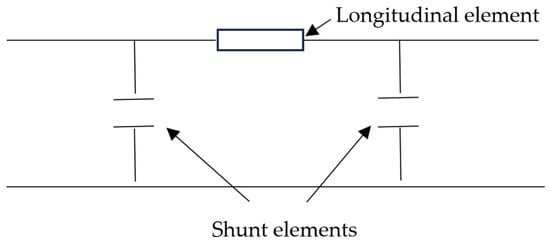
Figure 2.
Typical π model used to represent an electrical line.
The equations system constituted by (1) and (2) is non-linear, and this can be an important drawback in executing studies over big networks (even bigger if other carriers are added) and over long-term time intervals (which is typical, e.g., for grid planning analyses). On the other hand, the longitudinal reactance of the transmission networks lines is usually much bigger than the relevant resistance (for 150 kV networks, this ratio can be around 1.7, whereas for 380 kV networks, the same can increase up to 10). In this hypothesis, since the transversal (shunt) impedances of the reactive type, they do not influence active power transits, and the expressions for active and reactive power calculation are decoupled. Thus, considering only Equation (1) for active power calculation, it becomes:
where xhk is the reactance between nodes h and k. Moreover, as reactive flows are not of interest, the voltage modules at the two extremes of the line can be considered equal and are approximated with their nominal value Vn. Finally, the difference (θh − θk) is typically small, and thus the sine is approximately equal to its argument. Hence:
which is a linear expression that can be put into matrix form and solved with the customary numerical algorithms in order to calculate the system’s load flow once active power injections are known. This linearized representation is usually denominated the direct current approximation of the load flow equations.
For distribution networks, the hypothesis that the longitudinal reactance of lines is usually much bigger than the relevant resistances does not hold, and thus, a direct current approximation cannot be made. However, for distribution networks, the DISTFLOW approach can be adopted. Such an approach retains an approximate calculation of reactive power alongside active power by applying opportune approximations so that the final solving system stays linear (for details, see [17,27]).
As an alternative to applying the direct current approximation, a different kind of linear representation can be adopted. This representation is based on the so-called Power Transfer Distribution Factors (PTDF), defined as the incremental change in the active power that flows in a transmission line l due to an active power injection in a given node n of the network. PTDF factors provide a linearized description of the modalities by which flows on the transmission lines change in response to extra injections into the system. The most important information they synthetize is how active power flows split among parallel branches of a meshed transmission network as an effect of the different impedances of the branches themselves. In a meshed transmission network, PTDF factors can take any value between zero and one, the former meaning that an injection into node n does not affect line l at all, and the latter that the entire flow injected into n transits through l. Of course, the PTDF factors of distribution networks, having a tree topological structure, can only be equal to zero or to one. PTDFs are usually collected into a bidimensional matrix with so many rows as the number of lines and as many columns as the number of nodes. Theoretically, the PTDF matrix can be calculated starting from the inverse of the impedance matrix [28]. However, typically, PTDF factors are calculated by running sensitivity simulations on the studied system scenarios. Once the PTDF matrix is calculated, PTDF factors are used in the system constraint that enforces the transit limits for each line:
where Iml and IMl are, respectively, the minimum and maximum limits for active power in line l, pg and Cc are the generic generator and load in node n, and σln is the PTDF factor between node n and line l.
Regarding the PTDF representation, it must be noted that it works well if the topology of the system to be studied is fixed (e.g., to calculate system dispatch, e.g., electric markets outcome). By contrast, this representation cannot be easily applied to grid planning studies, since including more lines modifies the ratios between the impedances of the single lines, and thus the relevant PTDF factors.
Electrochemical batteries are important components of present electrical grids. The simplest way to model them is through the following equation:
where Et and Et+1 are the amount of energy stored in the battery at time t and t + 1, Δt is the time interval between t and t + 1, Ptabs and Ptinject are the amounts of power absorbed and injected at time t, ηabs and ηinj are the efficiencies in absorption and injection and ξt is a possible exogenous term (e.g., a self-discharge factor).
This kind of equation is an integral constraint, binding the energy (state variable) at time t + 1 with energy at time t. Integral constraints increase the number of non-zeros in the Jacobian matrix [29] and make simulations more numerically demanding.
The model written in (6) can be made much more complex: extra constraints can be introduced to represent maximum charge, maximum power ramp-up and down, capacity reduction of the equipment as a result of the number of charge-discharge cycles it has been subjected to [30], and others. Usually, a compromise between completeness and realism must be sought in order to ensure numerical tractability while including the effects that are important for the study to be accomplished. Very large models for planning studies suggest reducing to the minimum the number of treated constraints, while ensuring that the resulting model, yet maybe including integer variables, stays linear.
2.2. Compressible Fluids Modelling
Natural gas networks are tightly connected to electrical networks (gas-fired thermoelectrical plants consume natural gas to produce electricity; synthetic gas blended into gas networks is produced using electricity; gas linepack can provide flexibility to the electricity sector) and future hydrogen networks will be closely connected as well (green hydrogen is produced with electrolyzers that consume electricity; fuel cells convert hydrogen storage into electricity). This justifies modeling the two carriers together and, as concerns grid planning studies, even putting in competition the planning policies of the two networks. However, as already pointed out, natural gas networks modeling (or, in general, compressible fluids flow modeling) is rather complicated and non-linear. Nonetheless, linearization procedures can be adopted as well.
As the elementary building block of a gas network, we will limit ourselves to describing the modeling of an isothermal pipeline, as can be found in [31], i.e., adopting the hypothesis that the gas temperature is constant throughout the duct and equal to the external one (T(x,t) = TE, where x is an abscissa along the length of the pipeline and t is the temporal coordinate). A much more complicated modeling approach [32] removes this simplification and explicitly models the exchange of energy with the external environment though the pipeline metal structure; this model is, however, relevant only for transient studies. Further assumptions to be made when modelling an isothermal pipeline include the following:
- Turbulent motion in the pipeline (this is always verified for gas transport pipelines at a distance equal to some multiples of the diameter from the beginning and from the end of the duct). This allows us to adopt a mono-dimensional description for the fluid motion equations (otherwise, the Navier–Stokes [33] fluid dynamics laws should be used);
- The pipeline is regular—there are neither changes of section along x nor sharp changes of direction (curves). Such cases are usually modeled through concentrated losses (i.e., a pressure reduction proportional to the square of the fluid speed through a coefficient depending on the type of irregularity);
- The perfect gas law holds, stating that
In these hypotheses, the mass and momentum conservation laws become:
where A is the pipe section, W is the gas mass flow rate, g is the gravity constant, θ is the line slope with respect to horizontal, Cf is the friction coefficient and D is the pipe diameter. By setting the time derivatives as zero, one gets the following:
- W(x) = constant, i.e., mass flow rate constant throughout the pipeline;
- The expression for pressure drops calculation:
This relationship, usually called the Weymouth equation, is the most typically used one in the modeling of pressure drops along gas pipelines in steady state, disregarding the gravitational effect (customary hypothesis when simulating large gas networks). Equation (12) is not linear, but linearization procedures can be applied, as described in [34,35].
The Weymouth equation is useful for calculating pressure drops in the pipelines of a gas network. However, another important aspect, which is the delay due to the limited propagation speed of perturbation in a gas duct, is not considered by the above steady state equation. This aspect is not negligible, especially when considering the very long gas lines crossing the whole of Europe. In order to consider this, we must re-elaborate the non-stationary equation set, including (9) and (10). The most common approach is constituted by the so-called method of the characteristics. In order to derive such a method, let us create a linear combination of Equation (9), denominated as L1, and (10), denominated as L2:
In order to be able to interpret the two quantities in square brackets as the total time derivatives of, respectively, W and P, the following equalities must hold:
By placing (14) into (13), we obtain two systems of differential equations, which must be satisfied at the same time,
By integrating these two systems, we obtain the following two relationships:
These equations must be satisfied at the same time: Equation (16) along the line with slope +C and Equation (17) along a line with slope −C (the two characteristic lines); see Figure 3. Once the W and p values are calculated for time t, for each couple of grid points A and B, the same quantities can be calculated at time t + Δt, e.g., for point P, by solving the system of Equations (16) and (17).
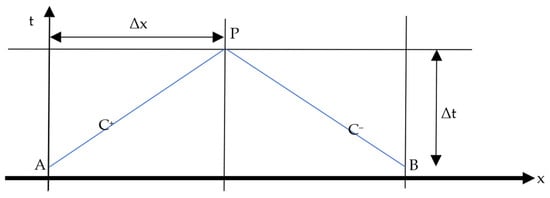
Figure 3.
Characteristic lines layout (sources: [31,32]).
The method of the characteristics is, apart the integral constraints representing storage systems, the only non-static model described in the present paper (sometimes, ME models that are not specifically dedicated to transient calculations but include storage constraints plus other effects that do not reach a steady state within one simulation time step are defined as “quasi-static” [36]). It might seem a contradiction to employ a non-static methodology in a static context. However, this is the only way to model time delays in the propagation of a pressure wave generated by a step change either in the gas injected at the pipeline inlet or in the amount extracted at the pipeline outlet. As gas networks are characterized by important spatial extensions (e.g., embracing entire Europe), the effects of a decoupling between injection and availability for the consumer is particularly evident (this is, by contrast, not the case for district heating networks, which are significantly reduced in their geographical extension).
The method of the characteristics is convergent (“stable”) provided that the spatial grid points and the discretization of the time axis are chosen so that the Friedrichs–Courant–Lewy [37,38] equation is satisfied:
The intuitive interpretation of this relationship is that, after splitting the length of the pipeline into equally spaced grid points at distance Δx, the equally spaced time steps spacing Δt must be chosen so that it is not bigger than the time taken by progressive and regressive waves (along, respectively, C+ and C−) to cover the distance Δx.
The method of characteristics, i.e., solving the set of Equations (16) and (17), allows us to calculate mass flow rate and pressure drops along a pipeline with a very good level of approximation (the isothermal duct hypothesis, which is true except for fast transients, is the only important applied precondition). However, these relationships are strongly non-linear, and the Friedrichs–Courant condition (18) imposes a very tight time discretization. On top of that, the values at time t + 1 are iteratively calculated only once all values at time t have already been calculated; in the case of an optimization process (e.g., for planning models), this means that all equations for all points of the discretized spatial grid and along the entire time horizon of the simulation must be written and solved altogether. All these issues limit the concrete possibility to apply this methodology to large static models, which, usually, just use the Weymouth equation in Formulation (12) or its linearized version.
Linearized formulations for solving the gas flow problem in Equations (9) and (10) do exist. One of the most interesting ones can be found in [39]. It applies a finite differences method to a pre-determined spatial–temporal grid and a Taylor series linear approximation in order to derive a linear discretized model. However, this model does not guarantee to preserve the speed of propagation of pressure waves (since the spatial–temporal grid is selected without caring about the slope of the characteristic curves C+ and C−). Additionally, the values in (x + Δx, t + Δt) are iteratively calculated by taking as known all values at the previous time step as well as those at the present time step for the spatial points that precede the one being calculated. So, as this was the case for the methodology of the characteristics, this means that, in an optimization process (e.g., for planning models), the full equations set must be written and solved altogether, for all points of the discretized spatial grid and along the entire time horizon of the simulation. This makes this model somewhat unsuitable for large static models.
Apart from the non-linear modeling of gas pipelines, other two important components, centrifugal compressors and regulation valves, show non-linear behaviors, and this must be seriously accounted for, especially when dealing with large static models and large optimization procedures (e.g., for grid planning).
Compressor stations are installed along gas networks to boost pressure and thus ensure proper delivery. Compressor stations are pumping stations consisting of multiple compressor units, a scrubber, cooling facilities, emergency shutdown systems, and an on-site computerized flow control and dispatch system that maintains the operation of the system. These stations are usually coupled with gas turbines that consume part of the transported gas for operation. It is estimated [40] that such stations consume 3–5% of the gas and constitute 20% of the total operating cost. The equation describing the functioning of a gas centrifugal compressor is (see [41])
where H is the compressor prevalence, z is the gas compressibility factor, RG is the gas constant, k is the isentropic exponent [41], and pd and ps are, respectively, the discharge and suction pressures. Prevalence H and the mechanical power P required to compress the gas in the compressor are bound by:
where W is the gas mass flow rate and ηis is the thermodynamical efficiency.
Compressors have to operate within established limits, which are plate data of each device. A natural way to characterize the performance of centrifugal compressors is in terms of the inlet volumetric flow rate, speed, adiabatic head, and adiabatic efficiency. The relationships between these quantities are usually represented by performance maps (see Figure 4), which are plots of H, and as a function of Q (volumetric flow rate) at different speeds. These performance maps can be approximated by cubic polynomial functions with constant coefficients, fitted by using the least squares method [42],
where Qs is the volume flow rate at surge and ω is the rotational speed (to be limited between minimum and maximum values).
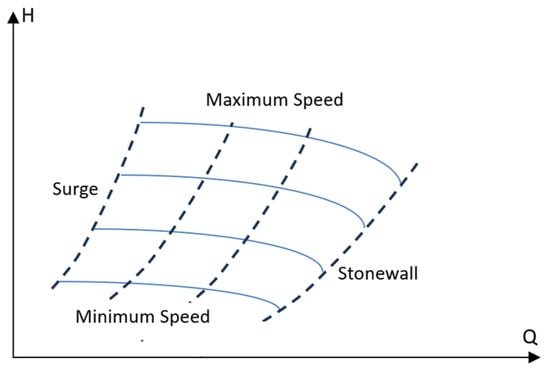
Figure 4.
Centrifugal compressors’ performance maps (the blue curves represent compressor characteristics for different speeds; “surge” and “stonewall” limits define the operative region).
Regulation valves are another important element of gas networks, and they show a strongly non-linear behavior [32] too. They are constituted by a convergent section followed by a divergent section. In the convergent section, the laws of the conservation of momentum (written by ignoring the terms of accumulation, friction and gravity) and mass are valid. Furthermore, the transformation is considered isentropic. Velocity increases in the convergent but can at most reach sonic speed. The relationship between mass flow rate (W) and the initial and final pressures in the convergent (respectively, p1 and p2) is
where rc is the pressure ratio in the sonic case, ρ1 is the upstream fluid density, and the isentropic coefficient Ast is the smallest section area. The function is defined as follows:
where αA is the ratio between the smallest section area and the entrance area, and γ is the isentropic coefficient.
In the divergent, dissipative phenomena occur, and a part of the kinetic energy is not transformed back into pressure. A recovery coefficient is defined (experimentally obtained),
where pv is the downstream pressure. This is a strongly non-linear relationship. Only under sonic conditions does the relationship become linear, and it depends only on upstream pressure,
Gas storage units are modeled similarly to electrochemical batteries:
where p is the gas pressure in the storage tank, V is its volume, z is the gas compressibility factor, RG is the gas constant, TE is the external temperature, and WI and WO are, respectively, the gas input and output mass flow rates at time t, while is the time interval between t and t + 1. Formally, this is the same equation as (6), which was already written for electrochemical batteries. As is the case for (6), Equation (27) is an integral constraint binding pressure (state variable) at time t + 1 with pressure at time t.
2.3. Heat Networks Modeling
Distribution networks are becoming a complex entity. What used to be a radial set of lines used to distribute the generation among a set of medium–low-voltage loads is now becoming active, with the presence of distributed generation. In particular, the wide penetration of photo-voltaic (PV) installations in distribution grids makes it important to discuss of local flexible means to compensate PV variability. This can be done by resorting to flexible load or small-scale storage, or by exploiting the inertia of important thermal systems connected to distribution systems, be it the case of a significant set of swimming pools connected to the electric grid (as in the case of Denmark [3]) or of big district heating systems.
District heating systems are connected to distribution grids and, due to the fact that there is a wide range of admissible temperatures for distributing water, they can be considered as a flexible load, able to provide flexibility to the electric system. Hence the interest in modeling heat and electric (distribution) systems together to investigate which synergies can arise.
Referring to the schematization in [5], the steady state behavior of a district heating pipeline can be described by means of the following equations:
- The Weymouth Equation (12), describing pressure drops in the pipeline. It has the same formulation as for compressible fluids (additionally, as for gas pipelines, mass flow rate is constant under steady-state conditions);
- An equation describing heat propagation along the pipeline—this equation can be written, by considering an infinitesimal volume along the pipeline (see Figure 5), as
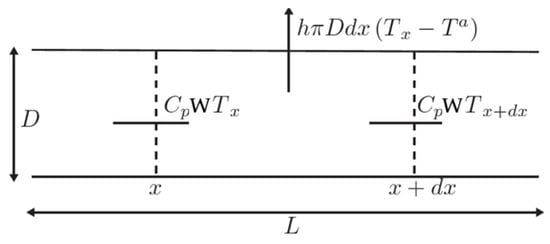 Figure 5. Heat networks’ modeling (source: [5]).
Figure 5. Heat networks’ modeling (source: [5]).
By integrating Equation (28), we derive
where T1 and T2 are the temperatures at the two extremes of the pipeline.
Equation (29) is a static representation of a district heating pipeline. While modeling thermal transients is not necessary in static system simulations due to the reduced spatial extension of the district heating systems and to the large timesteps typically adopted for this kind of simulation (hourly or bigger), in order to simulate the flexibility contribution that a district heating system can bring to the electric system, its ability to accumulate thermal energy has to be modeled. To do so, Equation (29) must be replaced with an energy balance in lumped form for the pipeline (this is an integral constraint, as it is the case for all storage system representations in this paper),
where W is the water mass flow rate in the pipeline, hi and ho are the inlet and outlet enthalpies, Ti and To are the inlet and outlet temperatures, Q is the energy exchanged with the external environment along the pipeline, Text is the external temperature, Cp is the specific heat, E = M Cp T = ρ V Cp T is the internal thermal energy of the system, M is the water mass in the pipeline, ρ is the fluid density, V is the volume, and T is the temperature of the water in the pipeline (state variable).
Heat loads are the elements of a heating system where heat is injected into and taken out of the system. Heat loads are generally modeled as heat exchangers. A basic model for a heat exchanger expresses the total exchanged heat power Δφ of a heat load as the change in the heat power between directly before and directly after the heat exchanger. Since a heat load is a connection between the supply and the return line of the heating system, the equation describing this process is
where Δφ is the thermal power of the heat load, cp is the specific heat, W is the mass flow rate of the water circulating through the heat exchanger and Tr and Ts are, respectively, the temperatures of the supply and return lines of the heat network.
Further information on the technical aspects concerning the different approaches adopted for modeling heat networks and the relevant tools can be found in two extensive review papers [43,44].
3. Typical ME Approaches
The previous section dealt with different approaches to model single energy carriers (electricity, gas or, more in general, compressible fluids, heat). The interest there was to highlight the pros and cons of different approaches useful for building up very large static ME models. This chapter introduces the most typical modeling approaches to be used for the simulation and optimization of MES, including equations and factors describing the energy transformation between the different carriers.
The optimization system (32), an extension of the approach described in [45], provides the most general formulation for an ME optimization system useful for the co-optimization of the planning of all the considered energy carriers.
The target function minimizes total system costs (TOTEX) as a sum of total dispatching costs (OPEX, first two terms) and investment costs for new infrastructure (CAPEX, last term). The nested sums are referred to by the following indices:
- c—energy carrier
- s—probabilistic scenario of RES production and load, and is the probability associated to each single scenario
- y—time horizon considered for the planning problem (typically a few years or decades, see e.g., [45] where three decades are considered—2030, 2040 and 2050)
- t—time horizon considered to calculate the system dispatch (e.g., one year)
- i—index enumerating each equipment in the system (e.g., electric lines). is the generic equipment item, and the integer variable associated with its investment.
If a sheer optimization of the dispatch (OPEX) is considered instead, all the parts of the objective function where the planning candidates are included must be omitted (these parts are easy to spot because they are multiplied by the investment integer variables α) as well as the summation over the planning time horizon (index y).
Finally, in cases where a load flow is what is sought, the objective function is completely omitted, and only the equations defining the set of constraint for all the carriers as well as the conversion equations between carriers should be considered.
The following sections will detail how the constraints equations must be written for each of the considered carriers. Three modeling representations will be considered in detail (energy hub, graph and self-consumption-based model). Then, a further approach will be hinted at, which includes a joint planning of electricity and hydrogen networks, also contemplating the possibility that hydrogen is transported in lumped quantities by means of cylinder trucks. A synthetic presentation of other recent modeling representations will complete this overview.
3.1. Energy Hub Representation
The energy hub (EH) representation was first introduced in [46]. Here, an EH is identified as a unit that provides energy conversion and the storage of multiple energy carriers. Thus, the EH represents a generalization or extension of a network node of the electrical system. The whole energy supply infrastructure can be considered as a system of interconnected energy hubs (Figure 6).
Figure 6.
One EH (left), interconnection of EHs (right) (source: [46]).
Let us consider a single converter device, which converts energy carrier α into carrier β. Input and output power flows are coupled through the following relationship:
where Pα and Lβ are the steady-state input and output power of the conversion process and cαβ is a factor expressing the efficiency of the conversion.
In the case of a converter cluster (Figure 7) where multiple inputs are converted into multiple outputs either by a single device or by a combination of multiple converters, this can be represented analytically as:
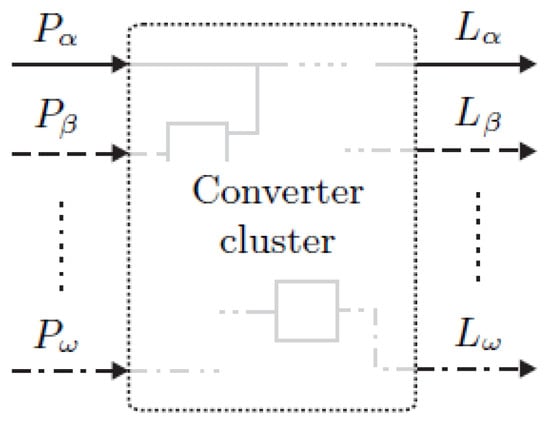
Figure 7.
Converter cluster (source: [46]).
The total input of one energy carrier may be split up between several converters at input junctions (see Figure 8). For this, the so-called dispatch factors ν are introduced, as follows:
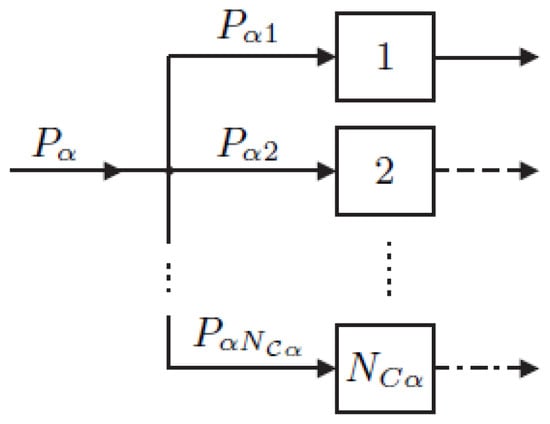
Figure 8.
Dispatch factors (source: [46]).
Storage units’ interfaces can be modeled as if they were converter devices (Figure 9 left),
where and represent, respectively, the amount of energy actually stored, and the amount of energy fed for storage; and represent the storage efficiency parameters for charge and discharge; is the stored energy.
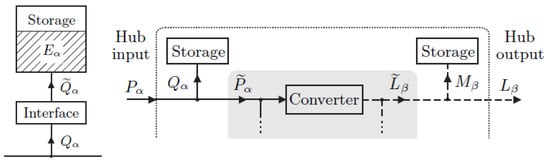
Figure 9.
Storage systems and EH (source: [46]).
Considering the layout of Figure 9, storage units located upstream and downstream with respect to the converter can be represented as only one equivalent storage device located downstream of the energy conversion:
Generalizing this, we derive:
Putting together (34) and (38), we get:
EHs are interconnected (Figure 10) through branches. Each branch is characterized by one or more components that are modeled according to the modalities described in chapter 2. The steady state of the overall system is described by a set of nodal balances and line equations (see also the graph notation introduced in the subsequent section), which, generally, creates a system of nonlinear equations. EH input and output power contributions are included into such system as nodal injections.
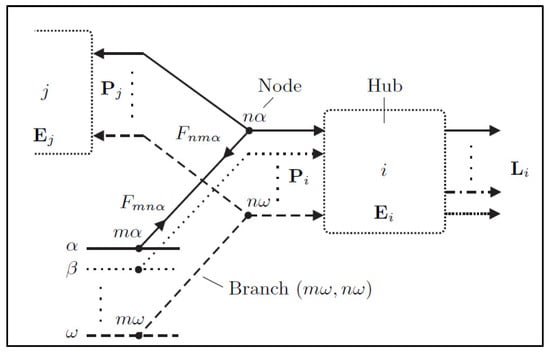
Figure 10.
Interconnection between EH (source: [46]).
3.2. Graph Representation
Dissertation [5] and paper [47] present a graph-based [48] framework for load–flow and optimization analyses of MESs that consist of gas, electricity and heat. The framework is based on interconnecting single-carrier networks through heterogeneous coupling nodes and homogeneous dummy links to form a connected multi-carrier network.
Load–flow equations consist of conservation equations written in a consistent way for all carriers, according to the following two principles:
- First law—conservation of mass or energy for each node;
- Second law—the sum of potential differences over each loop is zero.
The graph representation for each carrier is schematized in Figure 11, as follows:

Figure 11.
Graphs and variables for each carrier (source: [5]).
- Green color for gas networks. Variables: pressures (p) and mass flow rates (W);
- Red color for electricity networks. Variables: active powers (P), reactive powers (Q), voltages (V), angles (δ), currents (I);
- Blue color for heat networks (the return line is not explicitly represented). Variables: pressures (p), thermal flows (φ), supply temperature (Ts) return temperature (Tr), water flows (W).
Single carriers are coupled by introducing fictitious coupling nodes (Figure 12). In every coupling node (i.e., energy conversion node), one or more coupling equations (i.e., energy conversion equations) hold. No variables are associated with a coupling node, because it does not belong to any of the single-carrier networks. Therefore, links representing physical components cannot be connected to a coupling node. For instance, a link representing a gas pipe cannot be connected, since the flow model associated with the link requires both the start and end node to have a nodal pressure p. Therefore, a dummy link is introduced to couple a coupling node to any other single carrier node. Dummy links do not represent any physical component; they merely show a connection between nodes. If a dummy link connects a coupling node and a single-carrier node, the dummy link is of the same carrier as the single-carrier node. As such, it has the same variables associated with it as any other link of that carrier. These variables are shown in the figure at the side of the coupling node only. Although dummy links do not represent a physical component, they can be seen as lossless pipes or lines, conserving electrical energy across the line.
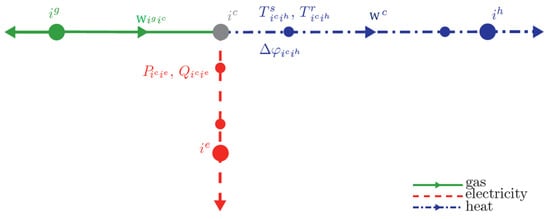
Figure 12.
Coupling nodes (source: [5]).
Provided energy injections and withdrawals are known for the whole ME system, a load flow analysis determines the flow of energy for each carrier. Typically, single-carrier networks have more variables than equations. Therefore, some variables are assumed as known. Usually, border conditions are placed on a (terminal) node, usually called a slack node, or on its terminal link. A node type is assigned to every node based on the variables that are locally (un)known (Table 3).

Table 3.
Typical node qualifications for the energy carriers (source [5]).
In a multi-carrier system, a carrier coupling model introduces more unknowns than equations. Additional equations or boundary conditions are needed for the total system to be solvable. A possible choice is that some or all the energy flows to or from the couplings are assumed known as additional border conditions. However, this decouples the integrated system into a set of separate single-carrier parts, so that the flexibility provided by coupling energy systems is not fully used. Therefore, [5] assumes all coupling (energy) flows are unknown and the additionally required border conditions are imposed elsewhere in the single-carrier parts. However, this must be done carefully, since not all combinations of load flow equations and border conditions for such integrated energy systems (consisting of gas, electricity, and heat) lead to well-posed problems.
Starting from the full set of conservation equations, written for nodes and loops of the ME graph, the mathematical system that solves the load flow problem can be easily put in matrix form (see [5]). Otherwise in the case of a planning or dispatch problem, an optimization problem should be solved, with the same load flow equations as problem constraints.
3.3. Self-Consumption-Based Representation
Report [49] illustrates an interesting model aimed at optimizing the dispatch of MES. Here, we limit ourselves to describing the overall model setting, leaving the details for a detailed reading of the report.
As shown in Figure 13, the multi-vector system described here is composed from several EHs connected as follows:
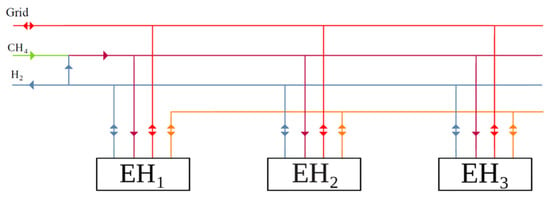
Figure 13.
Coupling nodes (source: [49]).
- To the electric vector (in red), which can both buy and sell electricity;
- To the thermal vector (in orange) with which the EHs can exchange heat;
- To the hydrogen vector (in blue), which can be exchanged between the EHs;
- To the gas network (in green), where natural gas is purchased—natural gas can be used in its pure form or mixed with hydrogen (mixture, in magenta) potentially up to 20% to serve the EHs.
The main modeling hypothesis is that each EH works via a self-consumption priority model, i.e., first satisfying its own energy demand, and then eventually reselling the surplus produced. Therefore, the developed algorithm is based on two separate mathematical models, as follows:
- The first model focuses on the single EH;
- The second model describes the multi-vector system, which is represented as a set of EHs, connected to each other through the three energy vectors.
First, the functioning of each EH is optimized separately, in order to incentivize self-consumption as much as possible, and then the residual flows are optimized by incentivizing the exchange between EH, thus simulating a local market.
The first optimization minimizes system costs over the entire considered time period. More precisely, this concerns the sum of production costs, purchase costs from the network, and revenues from sales to the network, adopting the following constraints:
- Limiting the values of the variables relating to generation and storage to a range between a minimum and a maximum value;
- Satisfying the balances of electricity, heat and gas in the network for each time period;
- Calculating the amount of energy stored in the storage systems for each instant (minimum storage at time t = 0);
- Determining the amounts of energy produced by each type of technology at any given moment;
- Limiting the operating region for the cogeneration plant;
- Making it so that the gas storage system cannot both supply and store gas at the same time (a few binary variables are introduced);
- Imposing (as binary variables):
- ○
- That the battery cannot supply and store electricity at the same time;
- ○
- That the heat storage system cannot supply and store heat at the same time;
- ○
- That the EH cannot sell and buy heat at the same time;
- ○
- That the EH cannot sell and buy gas at the same time.
The second optimization (see conceptual scheme in Figure 14) optimizes the residual flows of the three energy vectors by incentivizing the exchange between EHs. The basic idea is to consider the multi-vector system as a graph. Each EH can be identified by a node i, while each transmission line between nodes i and j can be described by an arc (i, j). Since the system is composed of three different energy vectors, there are actually three distinct graphs, one for each energy vector. For each one of the three graphs, a transmission cost is defined between each couple of EHs.
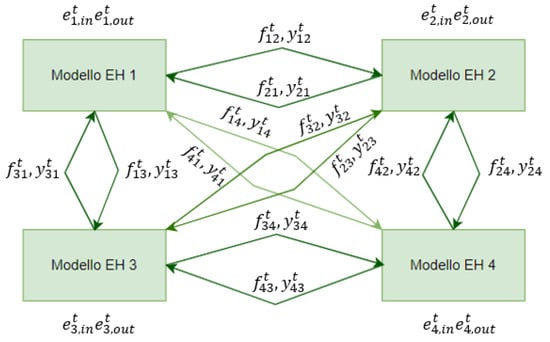
Figure 14.
Optimization of residual flows exchanged between EH − ein, eout = residual flows, fij = energy flows between EHs, yij = binary variables associated to the oriented arcs (source: [49]).
Furthermore, for each node i at each instant of time t, the residual flows of the three energy vectors are given as input data as a result of the previous optimization step.
The objective function minimizes the transmission costs of the multi-vector system over the entire considered time period T. These costs are calculated on the basis of the flows transmitted in each period between the nodes. The optimization constraints are as follows:
- Flow balances of the electric vector;
- Flow balances of the heat vector;
- Flow balances of the gas vector;
- Limitation between 0 and max of energy flows between EHs of the three vectors;
- Weymouth Equation (12) to describe gas flows, linearized according to [34].
The rigid division between the two optimizations introduces a sub-optimum in the optimization process, and the underlying hypothesis of self-consumption prioritization is not rigorously true. Additionally, the flow model applied to the second optimization stage as depicted in Figure 14 does not strictly adhere to the laws of physics (yet being still acceptable for a local market in a small geographical extension). Nonetheless, this approach is interesting because it shows an attempt to define a rationale for setting up a decoupling of the solution mechanism to help retain the numerical tractability of big ME models.
3.4. Joint Planning of Electricity and Hydrogen Transportation
In the context of the present decarbonization policies implemented in Europe and elsewhere, hydrogen is possibly the most promising vector to be utilized in the future for heavy transport, as well as in the so-called hard-to-abate industry sectors [2]. Hydrogen produced by electrolyzers (“green hydrogen”) can be sent to the utilizers through a dedicated transport infrastructure. The costs of creating such infrastructure can be reduced by reutilizing (“repurposing”) part of the existing gas pipelines. However, until hydrogen demand, which is expected to gradually increase, can attain a specific economic value justifying the buildup of a dedicated infrastructure, the most convenient way to transport it will remain the use of gas cylinder trucks. We can also think of an intermediate scenario, in which demand will start to be satisfied with hydrogen coming from a dedicated network, but part will still be supplied with trucks. This is the situation that the modeling approach described in [50] refers to.
The paper proposes a joint grid planning approach for both power and hydrogen grids, which simultaneously optimizes investments and operation for the two networks. Both a deterministic optimization approach and robust planning under uncertainty [21] are tested. Three hydrogen modeling aspects are specifically addressed and combined: truck routing, pipeline transportation and storage. We will provide a conceptual introduction to the approach, leaving the in-depth analysis to a careful reading of the paper.
Regarding the truck transportation network, the hydrogen quantity in charged and empty trucks in each zone changes according to the departure and arrival schedules, as well as the charging and discharging behaviors, of trucks. The quantity etruk,z,s,d represents the hydrogen quantity in charged trucks with transportation technology k in zone z at the end of day d in scenario s. Travel time delay is taken into account. If charged trucks with qtruk,m,n,s,d hydrogen quantity leave at the end of day d from zone m to zone n, when accounting for a time delay of Tk,m,n days, the same quantity of hydrogen arrives in zone n at the beginning of day d + Tk,m,n. Empty trucks can also be transported between any two zones, and the transportation of empty capacity is modeled too. The total amount of full and empty truck capacity in all zones during day d is calculated as the total amount staying in each zone at the end of the previous day plus the amount just arrived at the beginning of day d.
To preserve numerical tractability, a simplified linear model is adopted for hydrogen pipeline networks. The linepack storage dynamics of each pipeline are represented too.
Hydrogen and electric storage are fully modeled. Conventional electric storage, such as pumped storage and battery storage, are considered as operated in daily or weekly cycles. In each storage cycle, time periods are considered as sequential.
As both power and hydrogen systems are incorporated in the proposed planning approach, system components with distinctive physical characteristics need to be modeled in different time scales. In hydrogen systems, hydrogen storage usually has seasonal cycles, and truck transportation takes a few days to travel between two zones. In power systems, steady-state models in planning problems usually have an hourly resolution, as electric demand and renewable energy output fluctuate in a relatively short time frame. Thus, different resolutions are applied for resources with different timescales; hydrogen system components are modeled at a daily resolution, while power system components are modeled at an hourly resolution.
The objective function is the sum of the investment and operation costs for the truck and pipeline, hydrogen transportation, hydrogen production, hydrogen storage, as well as electric power generation and transmission. Among the optimization constraints, we can list the following:
- For hydrogen:
- ○
- Zonal hydrogen quantity balance constraints;
- ○
- Hydrogen production limits for the electrolyzers.
- For the electric system:
- ○
- Electric power balance for each bus;
- ○
- Limits for renewable power output;
- ○
- Power output and ramp rate for conventional generators;
- ○
- Branch flow for existing transmission lines (direct current approach);
- ○
- Flow-angle relations and flow limits for candidate lines.
3.5. Other Approaches
The PlaMES research project [51] aims at developing an integrated planning tool for MES at a European scale. The PlaMES model considers the coupling of different energy sectors (electricity, heat, mobility and gas) and calculates a cost-optimal energy mix for the future European energy system (e.g., up to 2050) compliant with the climate goals. These modeling requirements lead to writing a large mixed-integer (non-linear) optimization problem. Aside from generation and storage systems, transmission and distribution grids are also considered in the planning and operation stage in an integrated way. The complete modeling approach is described in deliverable D2.2 [52]. It contemplates the use of six tools (see Figure 15) each carrying out a single-stage optimization procedure. These tools can also be used separately, but the procedure foresees their coordinated usage to cope with the complete planning procedure. The focus is on the electricity carrier, the other ones being modeled only for their interactions with the electricity carrier.
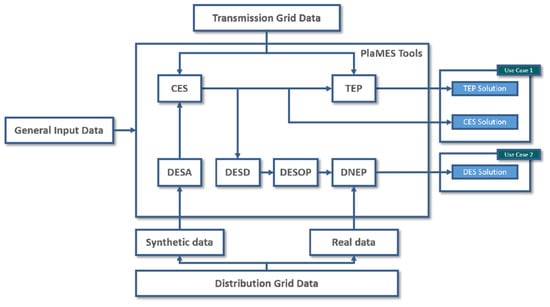
Figure 15.
Modeling framework of the PlaMES project (source [52]).
The six tools perform the following tasks:
- DESA (Decentral Energy System Aggregation) derives costs for each decentral network area by performing distribution grid expansion planning for various supply tasks depending on the integration of technologies in the respective areas. The result of this model can then be used in central planning;
- In a fully linearized approach, CES regards the Central Energy System, taking data from DESA and the transmission grid into account;
- The result of the CES will then be given to the TEP (Transmission Expansion Planning) module, which focuses on a detailed expansion planning approach analyzing different expansion technologies and congestion management interventions;
- DESD (Decentral Energy System Disaggregation) undertakes the placing of renewable energy sources and other assets that have been centrally planned in CES for a Decentral Energy System (DES);
- The operation of a DES can be performed by the DESOP (Decentral Energy System Operational Planning) module and can be enriched by information from the CES;
- The DNEP (Distribution Network Expansion Planning) module implements an optimization approach to develop the distribution network expansion plan.
As shown above, the PlaMES approach is strongly fragmented into sub tasks. If this helps, on one side, to tackle high-dimensionality problems by reducing them to tractable numerical optimizations, on the other side, there is a high risk of calculating a sub-optimal solution. Additionally, detailed planning approaches implemented in the last steps might suffer the consequences of important approximations taken to calculate the former steps, which provide the latter with input data.
An interesting approach to optimizing the participation of in energy and ancillary services markets is adopted by the MAGNITUDE project [4], which aims to develop business and market mechanisms as well as supporting coordination tools to provide flexibility to the European electricity system, by increasing and optimizing synergies between electricity, gas and heat systems. As described in [53], the MAGNITUDE project develops a novel modeling framework and an associated optimization methodology for short-term operational planning that can improve MES flexibility, with applications in district energy systems and participation in energy and Frequency Control Ancillary Services (FCAS). The approach is based on the concept of ME lattice, which models MESs by splitting them into several energy layers (see Figure 16), each one associated with a specific energy carrier. There are multiple services that can be associated with an energy carrier. Each service can be for “import”, for “export”, or “dual-mode”. The import services require an increase in the import (or decrease in the export) of an energy carrier, while export services require an increase in the export (or decrease in the import) of an energy carrier, and dual-mode may require both directions of energy flows. Figure 17 provides a simple example of application in a Combined Heat and Power plant (CHP, [54]).
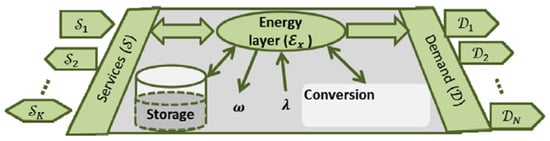
Figure 16.
An energy lattice layer: ω = losses λ = demand-shedding (source [53]).
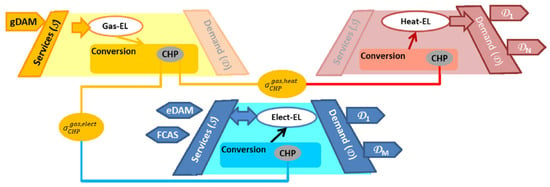
Figure 17.
An example of the ME lattice for a gas CHP plant (source [53]).
The MAGNITUDE project defines different kinds of flexibility to be provided by MES and associates each of them with the relevant services they can provide (see Figure 18):
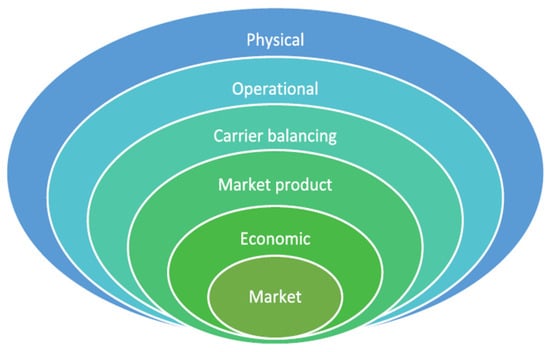
Figure 18.
Types of flexibility provided by an MES (source [53]).
- Physical. Maximum flexibility within the energy vector, quantified by its operational range;
- Operational. Modulation capability for an energy carrier that an MES can provide with respect to (starting from) a given operating point. The operational flexibility of a device is divided into two components—upward and downward;
- Carrier-balancing. Operational flexibility for an energy carrier, reduced by the constraints imposed by the other energy carriers through conversion nodes. The energy vectors of MES are coupled and cannot be viewed independently. The operational flexibility available to an energy vector is also impacted by the constraints of other energy vectors;
- Market product. Carrier-balancing flexibility is subject to market product constraints, e.g., maximum allowed activation time and minimum service duration, which further limit the flexibility that can be provided by a cluster of resources;
- Economic. Flexibility that the MES operator can offer at a given cost for a specific service and accounting for MES economic objectives (to be optimized). A device will only participate in a given service if the revenues are greater than the cost of delivering that service;
- Market. Economic flexibility cleared and accepted by the market given the market requirements and other offers.
The energy market is modeled as a simplification of the standard market design implemented in many European countries and elsewhere, schematized as in Figure 19. Stage 1 optimizes the participation of the MES in various energy markets while fulfilling multi-carrier demand(s) requirements. The decision variables obtained from the first stage of the methodology are then provided as input parameters to the second stage, which optimizes FCAS participation. The outcome of the second stage is the optimal scheduling of the resources in the ancillary service market.

Figure 19.
FCAS markets schematization by MAGNITUDE (source [53]).
Two further on-going European research projects, iDesignRES [55] and MOPO [56], are dedicating their efforts to creating advanced tools using multi-energy modeling.
Some further papers discuss modeling approaches related to the expansion of large ME systems [57,58,59,60,61,62] or smaller district heating systems joined to an electricity distribution network [63]. Such studies, while not bringing about significantly new modeling aspects with respect to the already explained ones, are nonetheless interesting because they show the different contexts in which ME models have been applied in the last few years.
Finally, it is worth mentioning that the Los Alamos National Laboratory’s Advanced Network Science Initiative ANSI [64] has recently developed a few interesting open access and open source libraries for modeling infrastructure networks [65]. In particular, the library GasPowerModels.jl (using the Julia programming language [25]) is dedicated to the joint optimization of power and natural gas transmission networks.
3.6. Computational Complexity, Convergence, Scalability and Robustness
This paper does not aim at delving into details on the most opportune techniques for solving the very large optimization problems typically generated in the study of real multi-energy models, which usually include networks of some thousands of nodes for each carrier. However, as this is a very significant problem with which one is confronted once the solving problem is defined, this section aims at providing the most important criteria to define numerical efficiency, and to sketch a discussion about how the methodologies introduced in the present paper perform with respect to them.
First, let us start with some definitions.
- The computational complexity of an algorithm can be defined as the amount of resources required to run it. A particular focus should be placed on computation time (generally measured by the number of elementary operations required) and memory storage requirements;
- Convergence of an iterative algorithm occurs when, as the iterations proceed, the output gets closer and closer to some specific value. More precisely, no matter how small an error range you choose, if you continue long enough, the target function will eventually stay within that error range around the final value;
- The scalability of an algorithm regards its ability to handle increasing amounts of data or complexity without compromising its performance or efficiency;
- The robustness of an algorithm can be broadly defined as the change in the performance of a computational system in the face of changes in the nature of the environment in which that system operates, or in the task that the system is meant to perform. In other terms, it defines sensitivity to a change in the parameters defining the system to be simulated—if small changes in one parameter can create great changes in the calculated solution, this can be a symptom of the limited reliability of the results obtained in this way.
The larger is the model, the bigger the computational time requested to solve it. As already clarified, simulating real systems demands considering some thousands of nodes for each carrier, and the number of variables can easily be in the order of magnitude of hundreds of thousands. Thus, it matters a lot that the modelling is kept as “light” as possible, by covering only those aspects that are really important for the study. For example, in the choice between the method of the characteristics and the simple equation of Weymouth, one should understand that the former involves two strongly non-linear equations to be solved together for each grid point and each simulation time, whereas the latter involves a single equation that can also be linearized. However, using the equation of Weymouth means that transport delay times along a gas pipeline cannot be represented in an adequate manner. This aspect should be considered when the final results are then obtained. As already mentioned, model linearity is an absolute prerequisite to be able to solve models with significant dimensionality. Staying in the linear domain, the interior point technique, or variations of it, can be applied, and this helps not only to speed up the simulation but also to increase the maximum system dimension that is numerically tractable, i.e., that can provide results in a reasonable amount of time as well as avoid possible problems bound with the existence of local minima (in fact, a linear optimization problem is also convex, and thus has only one optimum point). Here, the term “reasonable amount of time” depends a lot on the system to be studied—a market algorithm that must be solved every 5 min has particular numeric pre-requisites, whereas a planning problem that can afford to receive results in a few days is less demanding. The fact that planning (and other) problems are usually defined as a mixed integer further complicates the solution algorithm and lengthens the time required to solve the problem; typically, a branch-and-bound technique must be applied, which implies that the linear problem must be solved several times. Fortunately, some recent techniques, like Benders’ decomposition, can help in splitting the problem into an iteration among several problems of smaller sizes. As computational complexity is typically an exponential function of the dimension of the problem, this approach typically proves very helpful. The hardware configuration is also an important co-factor in defining the required computational time; the greater the amount of data that can be retained in the RAM memory without the requirement of frequent “swaps” between memory pages and disk, the faster an algorithm can go. Finally, the order of equations and variables also contributes a lot to speeding up the calculation. The more similar the Jacobian matrix is to a diagonal one, the easier it is to find the solution for the problem (but here, it must be said that all modern commercial solvers carry out a preliminary pre-conditioning action, swapping variables and equations so as to get a matrix that is the closest possible to a diagonal one). In this respect, all integral constrains (like the ones of storage systems we have met in the previous chapters) make the solution more difficult, because they bind the system state at time t + 1 with the one at the previous simulation time steps, thus filling the respective row of the Jacobian matrix with non-zero elements. So, the presence of storage systems must be carefully considered and, whenever possible, setting a bigger storage equivalent of some smaller ones can speed up the finding of the solution. Finally, the presence of big numbers alongside smaller ones creates “stiff” systems, and this can make the solution more complicated to calculate and the precision of the results lower (one has always to consider that computers use floating point arithmetic, with a finite number of significant digits).
Regarding convergence, for some algorithms, there are important constraints to respect (e.g., the Friedrichs–Courant relationship for the characteristics method of gas pipelines). These relationships must be attentively considered, and they can make the solution more complicated, e.g., increase the number of grid time steps over which the solution must be calculated. This, in turn, impacts computational complexity.
Scalability is an important property that is tied with computational complexity and numerical tractability. The scale of a problem must always be kept to the minimum possible while remaining compatible with the significance of results. Equivalents for the parts of the system that are not strictly relevant to obtaining results should always be introduced. However, sometimes, there is a problem regarding where to set the system border conditions so that they will be significant. For instance, when simulating a grid (be it an electrical or gas one), setting border conditions in a strongly meshed area can be a problem. Also, the fixing of energy flows at the border of the studied system must be done attentively so as not to impose artificial conditions that are not consistent with the reality (better to establish border conditions based on intensive variables, like voltages or pressures). Sometimes, it can be helpful to first simulate a broader system with less modeling details in order to be able to fix border conditions and derive a much more detailed model from a subsystem of it. In any case, any algorithm must be at least scalable in order to simulate a system with the dimensions of the real one.
Finally, regarding robustness, i.e., sensitivity to small parameter changes, what matters more is that the system modeling is well posed, e.g., that the model is not stiff. In such a case, an opportune normalization of the model variables can eliminate the problem (this is regularly applied to the modeling of the electric systems). What matters is to preserve an adequate number of significant digits in the floating-point representation of the computer.
All the above considerations should make it clear that creating a good model that can be numerically solved and is able to provide significant results is not an easy task and requires much experience. Again, we want to underline that there are no off-the-shelf solutions, but the necessary simplifications must be evaluated by considering the peculiarities of the system to be solved. In this regard, Table 4 presents some considerations related to the numerical complexity of the typical ME problems related to static models.

Table 4.
Comparison of numerical complexity of different problems.
4. Conclusions
The above sections of this paper have introduced some of the most typical approaches described in today’s technical literature to setting up static models of MES, resulting in either equation systems to solve load–flow problems or optimization systems to calculate optimal dispatch or grid planning or market allocation. ME problems require a very large number of variables in order to describe all the implemented carriers with a reasonable level of detail. Often, integer variables are implied as well (e.g., for optimal planning investment problems), making the optimization problem a MILP problem, solved by using branch-and-bound techniques, and possibly simplified by adopting some decomposition technique. The most typical one is Benders’ decomposition, which has proven particularly convenient for implementations based on parallel computing platforms and programming languages, allowing the user to distribute computation over parallel processors, as is the case for the most recent high-level languages, like MATLAB and Julia. In this context, as stated several times, deriving linear or linearized modeling for the represented MES components is of paramount importance to ensure system convexity and to allow the use of fast linear system solving techniques.
The first part of this paper was devoted to separately analyzing the components of each single carrier—electric, compressible fluids (gas/hydrogen) and heat networks. While the linearization brought about by the direct current’s approximation is often acceptable for static studies of electric networks, most components of gas and heat networks (long elements, compressors, regulation valves) have non-linear mathematical descriptions. However, linearization techniques do exist, which should be utilized whenever this is acceptable. The required modeling approach strongly depends on the type of study to be carried out: grid planning, operational optimization, the optimization of the services that the MES can provide, etc. It must also be noted that comparatively few articles in the literature deal with modeling for ME planning. Grid planning has strong peculiarities (it might require fewer modeling details on the individual components, but the number of variables is much higher, as it has to simulate much broader time horizons and include extra variables related to investments).
The second part of the paper was devoted to describing approaches to the joint representation of the different MES carriers. Energy hubs and graphs, two classic modelling tools for MES, were first introduced. Then, other approaches have been presented, including an interesting one allowing us to also model cylinder truck-transported hydrogen. The chapter was completed with a short section devoted to analyzing numeric issues and providing an overview of the typical techniques adopted to make the solution of large optimization problems numerically tractable.
As already clarified, analyzing the best way to implement the current decarbonization targets for electricity generation implies assessing the possibility to move from the current electric generation mix towards a 100% RES-based system. Such assessments should be based on an in-depth investigation of the flexibility that other carriers can provide to the electric grid. Additionally, many other fields of analysis tied to the implementation of the decarbonization targets for the energy system require the simulation of MES, including, among others, the following:
- Hybrid energy storage systems [66], which are diverse storage technologies coupled together in order to improve both transient speed and total amount of storable energy, so as to provide better services to the electric system;
- Digital twins [67], which are virtual modeling clones of entire network grids or parts of them, often coupled with Artificial Intelligence methodologies;
- The implementation of demand-side management [68] programs, which aim at providing flexibility to the electric system and parallel the effect that coupling with other carriers can provide;
- Industrial complexes, which are hard-to-abate industries [2] like steel mills where both electricity and other carriers (like hydrogen) can play a key role;
- Smart cities [69] and microgrids [70], where the interplay between electric systems and other carriers (like district heating) can allow for maximizing the efficiency and reducing the costs of electric distribution networks.
For all these cases, resorting to ME models can significantly improve the quality and reliability of the studies.
Data interoperability between Transmission System Operators (TSOs) is a further important point with modeling and numerical implications. Usually, each carrier is managed by a distinct national TSO (one for electricity, one for gas and, in the future, one for hydrogen). Up to now, each TSO has been required to provide a separate planning document. Presently, as seen when illustrating the evolution of the European regulation, TSOs are requested to elaborate joint scenarios. In the future, it will be a requirement to elaborate a joined planning strategy, so that the global minimum cost strategy is implemented. However, an important problem lies in the availability of data for setting up an overall planning model—every TSO has responsibility for the privacy of its own data, and the exchange of information is not so easy to implement. In this regard, it can be profitable to set up algorithms aimed at coordinating the different planning models (one per carrier) by means of a supervisor process allowing an exchange of data at the border between the carriers. This kind of algorithm has already been experimented at the border between electric transmission and distribution networks (see [71]) and could be profitably extended to MES. Furthermore, this approach would allow to decouple the solutions of the optimization problems for different carriers while retaining coordination between them. This would possibly result in a reasonable sub-optimum but, by contrast, would help to retain numerical tractability for bigger MES problems.
As highlighted in the introduction of the present paper, the decarbonization pathway also goes through an evaluation of the support that other carriers can provide to enhance the typically very limited flexibility of the electric system. ME models can help providing the relevant techno-economic assessments and thus promise to become a key ingredient for all future scenario analyses. ME models can be very useful in helping the system operators of the different grids to analyze the efficacy of flexibility measures across the energy carriers, and for the national regulatory authorities to assess the possible technical–economic impacts of new regulatory provisions. In this framework, the main contribution of the present paper is in providing a synthetic and complete review of the current modeling techniques for the different components of the most important energy carriers, and of the most typical techniques used to join them to create MES simulation models. However, it must be admitted that, as already clarified in Section 3.6, matching a numerically tractable technique to the solution of a very large MES (like the most general one described by (31)) is still a daunting task and an important field of research; numerical techniques are gradually being adapted to the steadily improving performances of computer hardware and software. However, in this regard, the introduction of cloud computing [72] has recently brought about new horizons of possibility.
Funding
This work was financed by the Research Fund for the Italian Electrical System under the Three-Year Research Plan 2025–2027 (MASE, Decree n.388 of 6 November 2024), in compliance with the Decree of 12 April 2024.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- European Commission. 2050 Long-Term Strategy. Striving to Become the World’s First Climate-Neutral Continent by 2050. Available online: https://climate.ec.europa.eu/eu-action/climate-strategies-targets/2050-long-term-strategy_en (accessed on 29 January 2025).
- Migliavacca, G.; Carlini, C.; Domenighini, P.; Zagano, C. Hydrogen: Prospects and Criticalities for Future Development and Analysis of Present EU and National Regulation. Energies 2024, 17, 4827. [Google Scholar] [CrossRef]
- Results of Pilot B. Report D5.2 of the SmartNet Project. 2019. Available online: https://smartnet-project.eu/wp-content/uploads/2019/05/D5.2.pdf (accessed on 29 January 2025).
- Project MAGNITUDE Web Site. Available online: https://www.magnitude-project.eu (accessed on 29 January 2025).
- Markensteijn, A.S. Mathematical Models for Simulation and Optimization of Multi-Carrier Energy Systems. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 2021. Available online: https://research.tudelft.nl/en/publications/mathematical-models-for-simulation-and-optimization-of-multi-carr (accessed on 6 February 2025).
- Mancarella, P. MES (multi-energy systems): An overview of concepts and evaluation models. Energy 2014, 65, 1–17. Available online: https://www.sciencedirect.com/science/article/abs/pii/S0360544213008931 (accessed on 27 February 2025).
- Shahidehpour, M.; Fu, Y. Tutorial: Benders Decomposition in Restructured Power Systems. Available online: http://motor.ece.iit.edu/ms/benders.pdf (accessed on 29 January 2025).
- European Commission Official Web Site. Available online: https://commission.europa.eu/index_en (accessed on 29 January 2025).
- Communication from the Commission to the European Parliament, the Council, the European Economic and Social Committee and the Committee of the Regions: Powering a Climate-Neutral Economy: An EU Strategy for Energy System Integration, 2020 COM (2020) 299 Final. Available online: https://eur-lex.europa.eu/legal-content/EN/TXT/PDF/?uri=CELEX:52020DC0299 (accessed on 29 January 2025).
- ACER. Electricity Infrastructure Development to Support a Competitive and Sustainable Energy System—2024 Monitoring Report. 2024. Available online: https://www.acer.europa.eu/monitoring/MMR/electricity_infrastructure_2024#:~:text=2024%20Monitoring%20Report,and%20competitive%20EU%20energy%20system (accessed on 29 January 2025).
- ACER. Official Web Site. Available online: https://www.acer.europa.eu/the-agency/about-acer (accessed on 29 January 2025).
- ENTSO-E. Official Web Site. Available online: https://www.entsoe.eu/ (accessed on 29 January 2025).
- ENTSO-G. Official Web Site. Available online: https://www.entsog.eu/ (accessed on 29 January 2025).
- ENTSO-E ENTSOG TYNDP Scenarios. Pathways to Carbon Neutrality in 2050. 2024. Available online: https://www.entsos-tyndp-scenarios.eu/ (accessed on 29 January 2025).
- Eiselt, H.A.; Sandblom, C.L. Operations Research; Springer Nature: Berlin/Heidelberg, Germany, 2022; Available online: https://link.springer.com/book/10.1007/978-3-030-97162-5?source=shoppingads&locale=en-it&gad_source=1&gclid=CjwKCAiA5pq-BhBuEiwAvkzVZWgiCUQdSosPFPw_u-Qq0ERV4PpFL1Rm35q6tlEcw6u7zet-g9NkxBoCG7EQAvD_BwE (accessed on 4 March 2025).
- Terlaky, T. Interior Point Methods of Mathematical Programming; Springer Nature: Berlin/Heidelberg, Germany, 1996; Available online: https://link.springer.com/book/10.1007/978-1-4613-3449-1 (accessed on 4 March 2025).
- Deliverable 1.2 of the FlexPlan Project. Probabilistic Optimization of T&D Systems Planning with High Grid Flexibility and Its Scalability. Available online: https://flexplan-project.eu/wp-content/uploads/2022/08/D1.2_20220801_V2.0.pdf (accessed on 29 January 2025).
- Wolsey, L.A. Integer Programming; Wiley: Hoboken, NJ, USA, 2020; Available online: https://www.wiley.com/en-us/Integer+Programming%2C+2nd+Edition-p-9781119606536 (accessed on 4 March 2025).
- Mancò, G.; Tesio, U.; Guelpa, E.; Verda, V. A review on MES modelling and optimization. Appl. Therm. Eng. 2024, 236, 121871. Available online: https://www.sciencedirect.com/science/article/pii/S1359431123019002 (accessed on 30 January 2025).
- Ntaimo, L. Computational Stochastic Programming; Springer Nature: Berlin/Heidelberg, Germany, 2024; Available online: https://link.springer.com/book/10.1007/978-3-031-52464-6?source=shoppingads&locale=en-it&gad_source=1&gclid=CjwKCAiA5pq-BhBuEiwAvkzVZZWzpqfKgMylS50_gPl--H9x_b0zaww_6zyoqLsj5EImbURbtoa2KRoCI0cQAvD_BwE (accessed on 4 March 2025).
- Ben-Tal, A.; El Ghaoui, L.; Nemirovski, A. Robust Optimization; Princeton Series in Applied Mathematics; Princeton University Press: Princeton, NJ, USA, 2009; Available online: https://www.amazon.it/Robust-Optimization-Aharon-Ben-Tal/dp/0691143684 (accessed on 4 March 2025).
- Official Site of the MATPOWER Library. Available online: https://matpower.org/ (accessed on 3 February 2025).
- Official Site of the MATLAB Programming Language. Available online: https://mathworks.com/products/matlab.html (accessed on 3 February 2025).
- PowerModels Library on the GitHub Repository. Available online: https://lanl-ansi.github.io/PowerModels.jl/stable/ (accessed on 3 February 2025).
- Official Site of the Julia Programming Language. Available online: https://julialang.org/ (accessed on 3 February 2025).
- Milano, F. Power flow analysis. In Chapter Part of the Book: Power System Modelling and Scripting of the Same Author; Springer Nature: Berlin/Heidelberg, Germany, 2010; Available online: https://link.springer.com/chapter/10.1007/978-3-642-13669-6_4 (accessed on 4 March 2025).
- Gan, L.; Low, S.H. Convex relaxations and linear approximation for optimal power flow in multiphase radial networks. In Proceedings of the 2014 Power Systems Computation Conference, Wroclaw, Poland, 18–22 August 2014; pp. 1–9. Available online: https://authors.library.caltech.edu/records/1fcqw-beg37 (accessed on 3 February 2025).
- Glover, J.D.; Sarma, M.S.; Overbye, T.J. Power System Analysis and Design, 5th ed.; Cengage Learning: Boston, MA, USA, 2012. [Google Scholar]
- Jacobian Matrix Definition in Microfluidics: Modelling, Mechanics and Mathematics. 2017. Available online: https://www.sciencedirect.com/topics/engineering/jacobian-matrix#definition (accessed on 4 March 2025).
- Johnen, M.; Pitzen, S.; Kamps, U.; Kateri, M.; Dechent, P.; Sauer, D.U. Modeling long-term capacity degradation of lithium-ion batteries. J. Energy Storage 2021, 34, 102011. Available online: https://www.sciencedirect.com/science/article/abs/pii/S2352152X20318466 (accessed on 3 February 2025).
- Wylie, E.B.; Streeter, V. Fluid Transients (Chapter 15); Mc. Graw Hill: New York, NY, USA, 1978. [Google Scholar]
- Migliavacca, G. Simulazione di Reti per il Trasporto di Fluido Comprimibile. Master’s Thesis, Politecnico di Milano, Milan, Italy, 1991. (In Italian; Available upon Request). [Google Scholar]
- Kollmann, W. Navier-Stokes Turbulence. In Theory and Analysis; Springer Nature: Berlin/Heidelberg, Germany, 2024; Available online: https://link.springer.com/book/10.1007/978-3-031-59578-3?source=shoppingads&locale=en-it&gad_source=1&gclid=CjwKCAiA5pq-BhBuEiwAvkzVZdKf5txHlQM7fvmvoRBzwt79DixQDehMuwJBnt0ZcN6DKgjOHpGekhoC9XcQAvD_BwE (accessed on 4 March 2025).
- Asghari, M.; Fathollahi-Fard, A.M.; Mirzapour Al-e-hashem, S.M.J.; Dulebenets, M.A. Transformation and Linearization Techniques in Optimization: A State-of-the-Art Survey. Mathematics 2022, 10, 283. [Google Scholar] [CrossRef]
- Yang, J.; Zhang, N.; Botterud, A.; Kang, C. Situation awareness of electricity-gas coupled systems with a multi-port equivalent gas network model. Appl. Energy 2020, 258, 114029. Available online: https://www.sciencedirect.com/science/article/abs/pii/S0306261919317167 (accessed on 18 March 2025).
- Dancker, J.; Wolter, M. A joined quasi-linear-state power flow calculation for integrated energy systems. IEEE Access 2022, 10, 33586–33601. [Google Scholar] [CrossRef]
- Courant, R.; Fredrichs, K.O.; Lewy, H. Uber die Differenzengleichungen der Mathematischen Physik. Math. Ann. 1928, 100, 32. Available online: https://gdz.sub.uni-goettingen.de/id/PPN235181684_0100 (accessed on 5 February 2025).
- Courant, R.; Friedrichs, K.; Lewy, H. Über die partiellen Differenzengleichungen der mathematischen Physik. Math. Ann. 1928, 100, 32–74. Available online: https://link.springer.com/article/10.1007/BF01448839 (accessed on 4 March 2025).
- Hafsi, Z.; Ekhtiari, A.; Ayed, L.; Elaoud, S. The linearization method for transient gas flows in pipeline systems revisited: Capabilities and limitations of the modelling approach. J. Nat. Gas Sci. Eng. 2022, 101, 104494. Available online: https://www.sciencedirect.com/science/article/abs/pii/S1875510022000853 (accessed on 6 February 2025).
- Demissie, A.; Zhu, W.; Taye Belachew, C. A multi-objective optimization model for gas pipeline operations. Comput. Chem. Eng. 2017, 100, 94–103. Available online: https://www.sciencedirect.com/science/article/abs/pii/S009813541730073X (accessed on 6 February 2025). [CrossRef]
- Gallagher, J.E. Isentropic Exponent Definition in Natural Gas Measurement Handbook; Elsevier: Amsterdam, The Netherlands, 2006; Available online: https://www.sciencedirect.com/topics/engineering/isentropic-exponent#:~:text=The%20isentropic%20exponent%20(%CE%BA)%20is,V%2Dcone%2C%20pitot) (accessed on 4 March 2025).
- Wolberg, J. Data Analysis Using the Method of Least Squares. In Extracting the Most Information from Experiments; Springer: Berlin/Heidelberg, Germany, 2006; Available online: https://link.springer.com/book/10.1007/3-540-31720-1 (accessed on 4 March 2025).
- Brown, A.; Foley, A.; Laverty, D.; McLoone, S.; Keatley, P. Heating and cooling networks: A comprehensive review of modelling approaches to map future directions. Energy 2022, 261, 125060. Available online: https://www.sciencedirect.com/science/article/pii/S0360544222019557 (accessed on 6 February 2025).
- Kuntuarova, S.; Licklederer, T.; Huynh, T.; Zinsmeister, D.; Hamacher, T.; Peri’c, V. Design and simulation of district heating networks: A review of modeling approaches and tools. Energy 2024, 305, 132189. Available online: https://www.sciencedirect.com/science/article/pii/S0360544224019637 (accessed on 6 February 2025).
- Migliavacca, G.; Rossi, M.; Siface, D.; Marzoli, M.; Ergun, H.; Rodriguez-Sanchez, R.; Hanot, M.; Leclercq, G.; Amaro, N.; Egorov, A.; et al. The Innovative FlexPlan Grid-Planning Methodology: How Storage and Flexible Resources Could Help in De-Bottlenecking the European System. Energies 2021, 14, 1194. Available online: https://www.mdpi.com/1996-1073/14/4/1194 (accessed on 7 February 2025). [CrossRef]
- Geidl, M. Integrated Modeling and Optimization of Multi-Carrier Energy Systems. Ph.D. Thesis, ETH Zurich, Zurich, Switzerland, 2007. No. 17141. Available online: https://www.research-collection.ethz.ch/handle/20.500.11850/123494 (accessed on 7 February 2025).
- Markensteijn, A.S.; Romate, J.E.; Vuik, C. A graph-based model framework for steady-state load flow problems of general multi-carrier energy systems. Appl. Energy 2020, 280, 115286. Available online: https://www.sciencedirect.com/science/article/pii/S0306261920307984 (accessed on 27 February 2025).
- Diestel, R. Graph Theory; Springer Nature: Berlin/Heidelberg, Germany, 2025; Available online: https://link.springer.com/book/10.1007/978-3-662-70107-2?source=shoppingads&locale=en-it&gad_source=1&gclid=CjwKCAiA5pq-BhBuEiwAvkzVZQi3LQ9C0B63G5KCCUtSWiBUJD5QM92GDIHP-G6pOwURxMjtagxHuhoCJtsQAvD_BwE (accessed on 4 March 2025).
- Simmini, F.; Cordieri, S.A. Modello Integrato del Sistema Energetico Locale; Report PORH2 D4.1.4.2. Milano, Italy 2024 (manuscript in preparation) (In Italian, available upon request).
- Wang, S.; Bo, R. Joint planning of electricity transmission and hydrogen transportation networks. IEEE Trans. Ind. 2022, 58, 2887–2897. Available online: https://ieeexplore.ieee.org/ielaam/28/9733857/9573477-aam.pdf (accessed on 11 February 2025).
- PlaMES. Project Web Site. Available online: https://plames.eu/ (accessed on 12 February 2025).
- PlaMES. Project Deliverable 2.2. Mathematical Formulation of the Model. 2020. Available online: https://plames.eu/wp-content/uploads/2020/11/20200630_Plames_D2.2_final.pdf (accessed on 12 February 2025).
- Corsetti, E.; Riaz, S.; Riello, M.; Mancarella, P. Modelling and deploying ME flexibility: The energy lattice framework. Adv. Appl. Energy 2021, 2, 100030. Available online: https://www.sciencedirect.com/science/article/pii/S2666792421000238 (accessed on 12 February 2025).
- Breeze, P. Combined Heat and Power; Elsevier: Amsterdam, The Netherlands, 2017; Available online: https://shop.elsevier.com/books/combined-heat-and-power/breeze/978-0-12-812908-1 (accessed on 4 March 2025).
- iDesignRES. Project Web Site. Available online: https://idesignres.eu/ (accessed on 13 February 2025).
- MOPO. Project Web Site. Available online: https://www.tools-for-energy-system-modelling.org/ (accessed on 13 February 2023).
- Sundar, K.; Misray, S.; Zlotniky, A.; Bent, R. Robust Gas Pipeline Network Expansion Planning to Support Power System Reliability. In Proceedings of the 2021 American Control Conference (ACC), New Orleans, LA, USA, 25–28 May 2021; Available online: https://ieeexplore.ieee.org/document/9483249 (accessed on 27 February 2025).
- Zhang, X.; Shahidehpour, M.; Alabdulwahab, A.S.; Abusorrah, A. Security-Constrained Co-Optimization Planning of Electricity and Natural Gas Transportation Infrastructures. IEEE Trans. Power Syst. 2015, 30, 2984–2993. Available online: https://ieeexplore.ieee.org/document/6987368 (accessed on 27 February 2025).
- Wald, G.; Sundar, K.; Sherwin, E.; Zlotnik, A.; Brandt, B. Optimal gas-electric energy system decarbonization planning. Adv. Appl. Energy 2022, 6, 100086. Available online: https://www.sciencedirect.com/science/article/pii/S266679242200004X (accessed on 27 February 2025).
- Birati, F.; Seifi, H.; Sepasian, M.S.; Nateghi, A.; Shafie-khah, M.; Catalao, J.P.S. Multi-Period Integrated Framework of Generation, Transmission, and Natural Gas Grid Expansion Planning for Large-Scale Systems. IEEE Trans. Power Syst. 2015, 30, 2527–2537. Available online: https://ieeexplore.ieee.org/document/6942215 (accessed on 27 February 2025).
- Thie, N.; Franken, M.; Schwaeppe, H.; Böttcher, L.; Müller, C.; Moser, A. Requirements for Integrated Planning of Multi-Energy Systems. In Proceedings of the 2020 6th IEEE International Energy Conference (ENERGYCON), Gammarth, Tunisia, 28 September–1 October 2020; Available online: https://ieeexplore.ieee.org/document/9236466 (accessed on 27 February 2025).
- Tangi, M.; Amaranto, A. Designing integrated and resilient multi-energy systems via multi-objective optimization and scenario analysis. Appl. Energy 2025, 382, 125281. Available online: https://www.sciencedirect.com/science/article/pii/S030626192500011X (accessed on 27 February 2025).
- Mostafa, M.; Vorwerk, D.; Heise, J.; Povel, A.; Sanina, N.; Babazadeh, D. Integrated Planning of Multi-energy Grids: Concepts and Challenges. In Proceedings of the NEIS 2022; Conference on Sustainable Energy Supply and Energy Storage Systems, Hamburg, Germany, 26–27 September 2022; Available online: https://ieeexplore.ieee.org/document/10048077 (accessed on 27 February 2025).
- Los Alamos National Laboratory’s Advanced Network Science Initiative. Available online: https://lanl-ansi.github.io/ (accessed on 13 February 2025).
- ANSI. Open Access Infrastructure Networks Simulation Libraries. Available online: https://lanl-ansi.github.io/software/ (accessed on 13 February 2025).
- Bocklisch, T. Hybrid energy storage systems for renewable energy applications. Energy Procedia 2015, 73, 103–111. Available online: https://www.sciencedirect.com/science/article/pii/S1876610215013508 (accessed on 25 February 2025). [CrossRef]
- Sifat, M.; Choudhury, S.M.; Das, S.K.; Ahamed, H.; Muyeen, S.M.; Hasan, M.; Ali, F.; Tasneem, Z.; Islam, M.; Islam, R.; et al. Towards electric digital twin grid: Technology and framework review. Energy AI 2023, 11, 100213. Available online: https://www.sciencedirect.com/science/article/pii/S2666546822000593 (accessed on 25 February 2025). [CrossRef]
- Gupta, P. Demand side management. In An Approach to Peak Load Smoothing; Scholar’s Press: London, UK, 2013; Available online: https://www.amazon.com/Demand-Side-Management-Approach-Smoothing/dp/3639511298 (accessed on 4 March 2025).
- Mishra, P.; Singh, G. Sustainable Smart Cities. In Enabling Technologies, Energy Trends and Potential Applications; Springer: Berlin/Heidelberg, Germany, 2023; Available online: https://link.springer.com/book/10.1007/978-3-031-33354-5 (accessed on 4 March 2025).
- Chowdhury, S.; Chowdhury, S.P.; Crossley, P.P. Microgrids and Active Distribution Networks; IET: London, UK, 2009; Available online: https://digital-library.theiet.org/doi/book/10.1049/pbrn006e (accessed on 4 March 2025).
- Rossini, M.; Rossi, M.; Siface, D. A surrogate model of distribution networks to support transmission network planning. In Proceedings of the 27th International Conference on Electricity Distribution, Rome, Italy, 12–15 June 2023; Available online: https://ieeexplore.ieee.org/document/10267731 (accessed on 18 March 2025).
- Mahmood, Z.; Puttini, R.; Erl, T. Cloud Computing: Concepts, Technology & Architecture; Pearson: London, UK, 2013. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).