Accurate Measurement Method for Distribution Parameters of Four-Circuit Transmission Lines with the Same Voltage Considering Earth Resistance
Abstract
1. Introduction
- A novel measurement method is proposed for the distribution parameters of four-circuit transmission lines with the same voltage, explicitly considering the impact of earth resistance, which has been largely neglected in previous studies.
- A phase-mode transformation matrix for four-circuit lines is derived, effectively decoupling the twelve-order parameter matrix and enabling a more efficient computation of voltage and current relationships.
- The proposed method is validated through numerical simulations in PSCAD/EMTDC, demonstrating its accuracy and applicability for various line lengths and voltage levels.
- A comparative analysis is conducted between the proposed method, traditional methods, and improved traditional methods, illustrating the superiority of the proposed approach in terms of measurement accuracy and computational efficiency.
2. Three-Phase Parallel Line Model Considering Earth Return
2.1. Physical Model of Transmission Lines
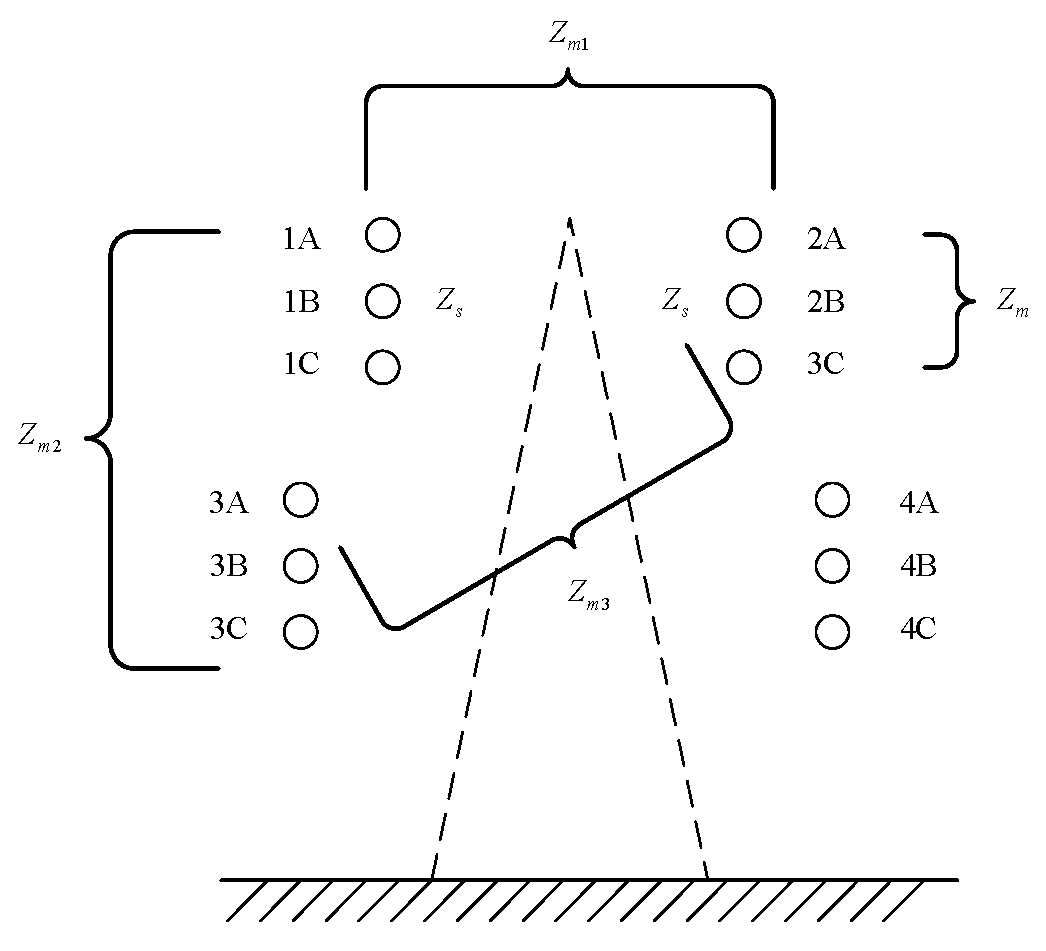
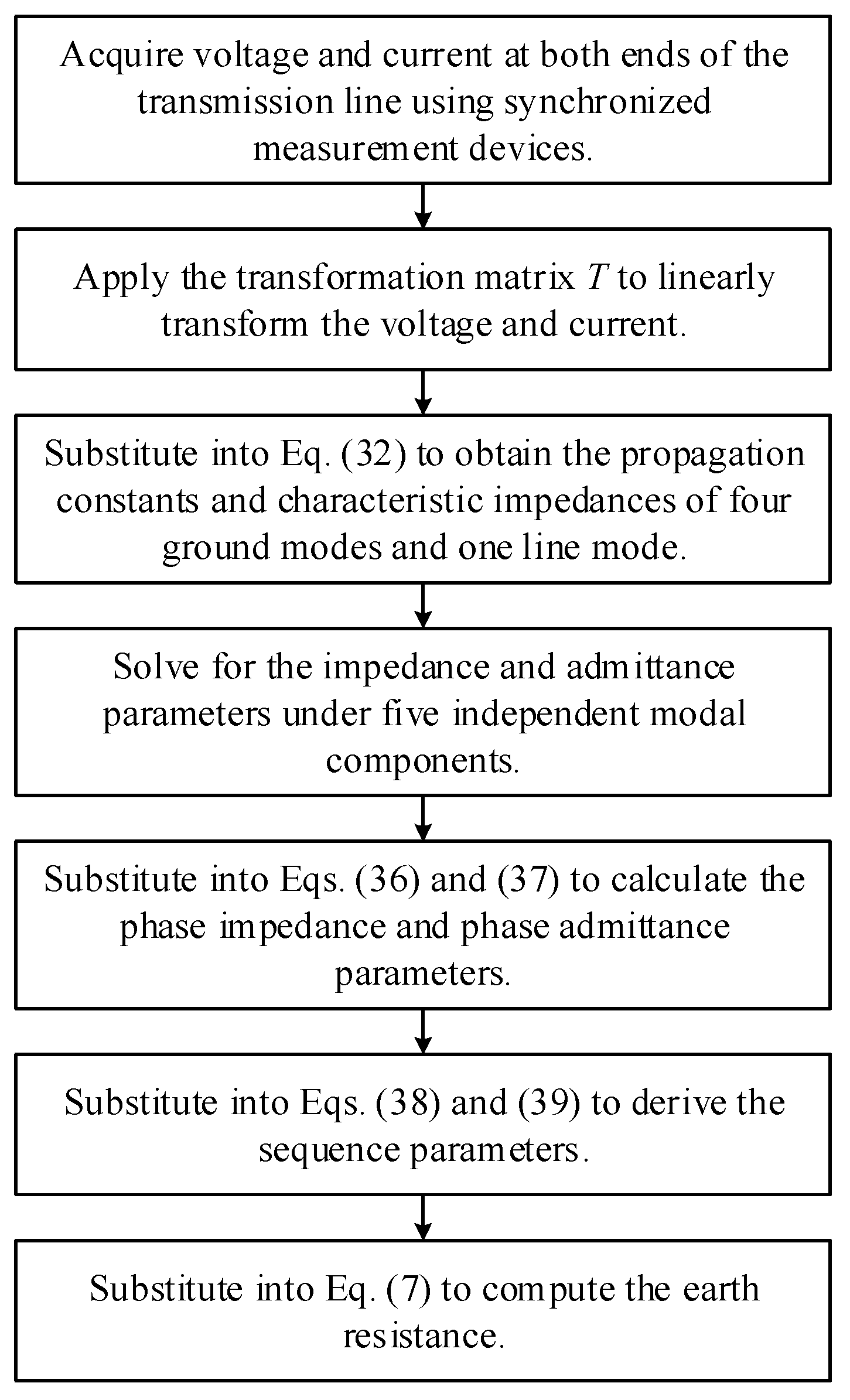
2.2. Distribution Parameter Measurement Method for Four-Circuit Parallel Lines with Same Voltage
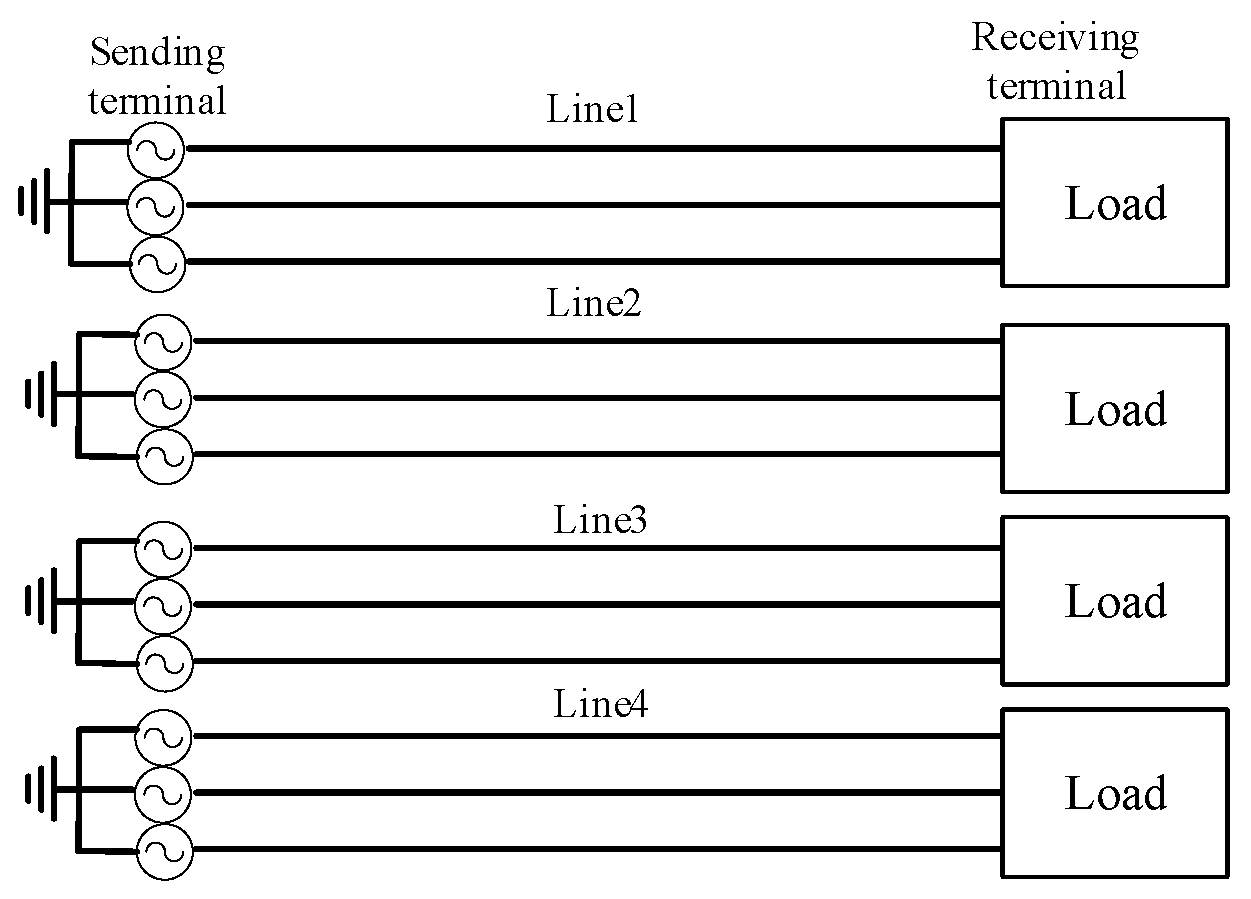
3. Simulation Example Analysis
3.1. PSCAD Simulation Model of Four-Circuit Parallel Lines with Same Voltage Level
3.2. Simulation Analysis of the Proposed Method
3.2.1. Investigating the Effect of Line Length on the Measurement Accuracy of the Proposed Method
3.2.2. Comparison of the Proposed Method with Other Methods
- Comparison with Traditional Methods
- 2.
- Comparison with the Improved Traditional Method
3.3. Discussion and Prospect
3.3.1. Discussion of Results
- High Measurement Accuracy. The proposed distributed parameter measurement method maintains high accuracy across different transmission line lengths. Unlike traditional methods, which rely on single-ended measurements and neglect distributed effects, this approach incorporates the full transmission equation and phase-mode transformation, ensuring precise parameter extraction. The measurement errors remain below 2% for resistance, inductance, and capacitance, representing a significant improvement over conventional methods.
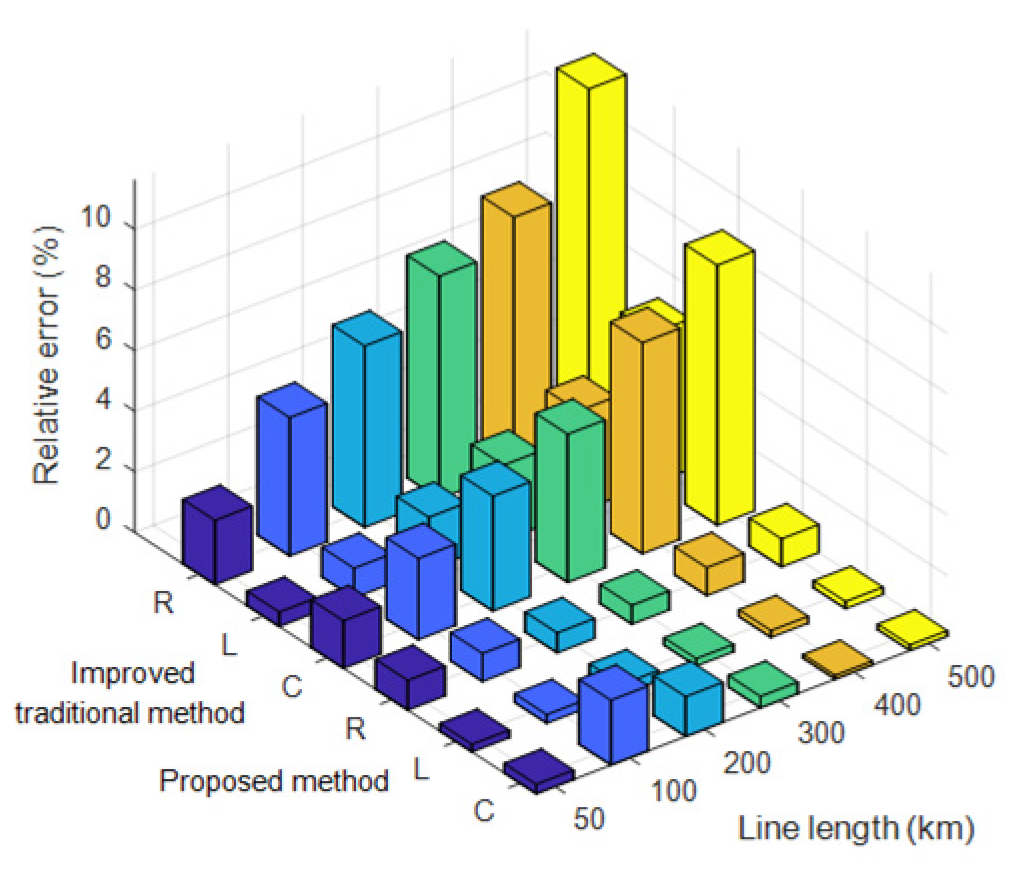
- Improved Performance Compared to Traditional Methods. The proposed method provides a cost-effective and practical solution for measuring the distributed parameters of four-circuit transmission lines. It achieves high accuracy and reliability by fully considering the distributed characteristics of transmission lines, unlike traditional methods that rely on lumped parameter models and exhibit increasing errors with longer line lengths. Additionally, the proposed method requires only a single measurement for full parameter estimation, significantly enhancing efficiency compared to traditional methods (requiring 10 measurements) and improved methods (requiring 5 measurements). It utilizes standard measurement devices such as voltage and current transformers, data acquisition systems, and GPS/BeiDou receivers, eliminating the need for specialized equipment and complex calibration procedures.
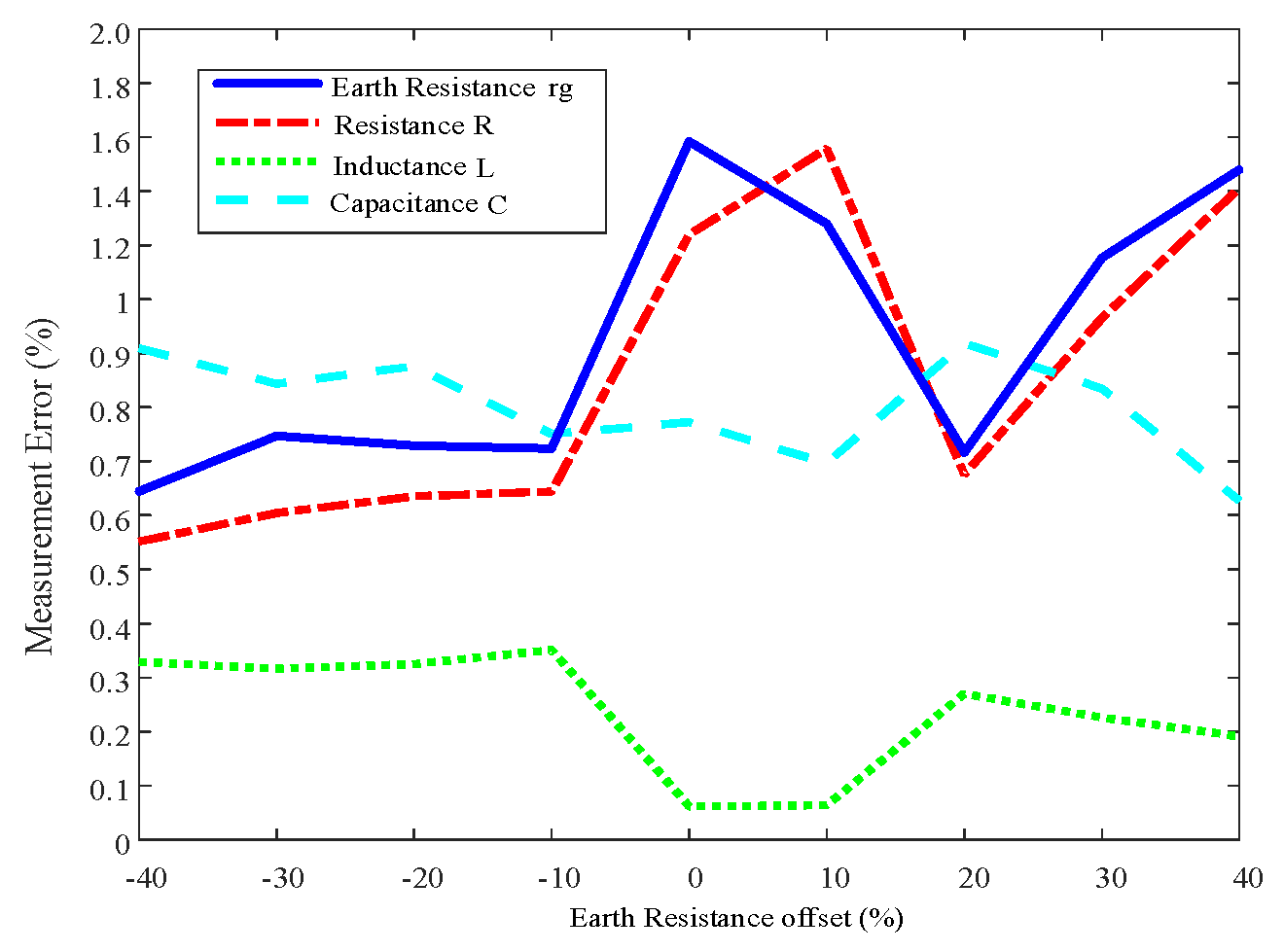
- Practical Applicability and Challenges. Although the proposed method has been validated through simulations, real-world implementation may present challenges. Factors such as external disturbances, environmental conditions, and equipment inaccuracies can affect measurement accuracy. Furthermore, precise synchronization of measurements at both ends of the line is necessary, which can be achieved using GPS or BeiDou satellite systems. The method also demonstrates strong adaptability to variations in ground resistance parameters, maintaining high testing accuracy. Future research should explore advanced filtering techniques and error compensation models to enhance robustness under practical conditions.
3.3.2. Assumptions and Limitations
- Ideal Measurement Conditions. The method assumes minimal external interference and uniform soil resistivity along the transmission line. However, it does not fully account for the complex electromagnetic interference that may occur in field measurements, which could introduce additional uncertainties. In practice, variations in soil conditions and electromagnetic disturbances may introduce measurement uncertainties.
- Simulation-Based Validation. The evaluation of the proposed method is primarily based on simulations. While the results confirm theoretical effectiveness, real-world applications may encounter additional issues such as sensor calibration errors, signal distortion, and operational constraints.
- Influence of Environmental Factors. The method’s performance may be affected by environmental factors such as glaze accumulation, humidity, and extreme weather conditions. These effects were not fully modeled in the simulations, and future work should consider integrating adaptive compensation techniques to mitigate their impact.
4. Conclusions
- The proposed method can simultaneously measure all 16 distributed parameters of four parallel transmission lines under the same voltage, including ground resistance. This ensures a more comprehensive and precise parameter extraction compared to traditional methods.
- By incorporating the full transmission equation and phase transformation, the proposed method eliminates approximation errors, maintaining high accuracy across different transmission line lengths and voltage levels.
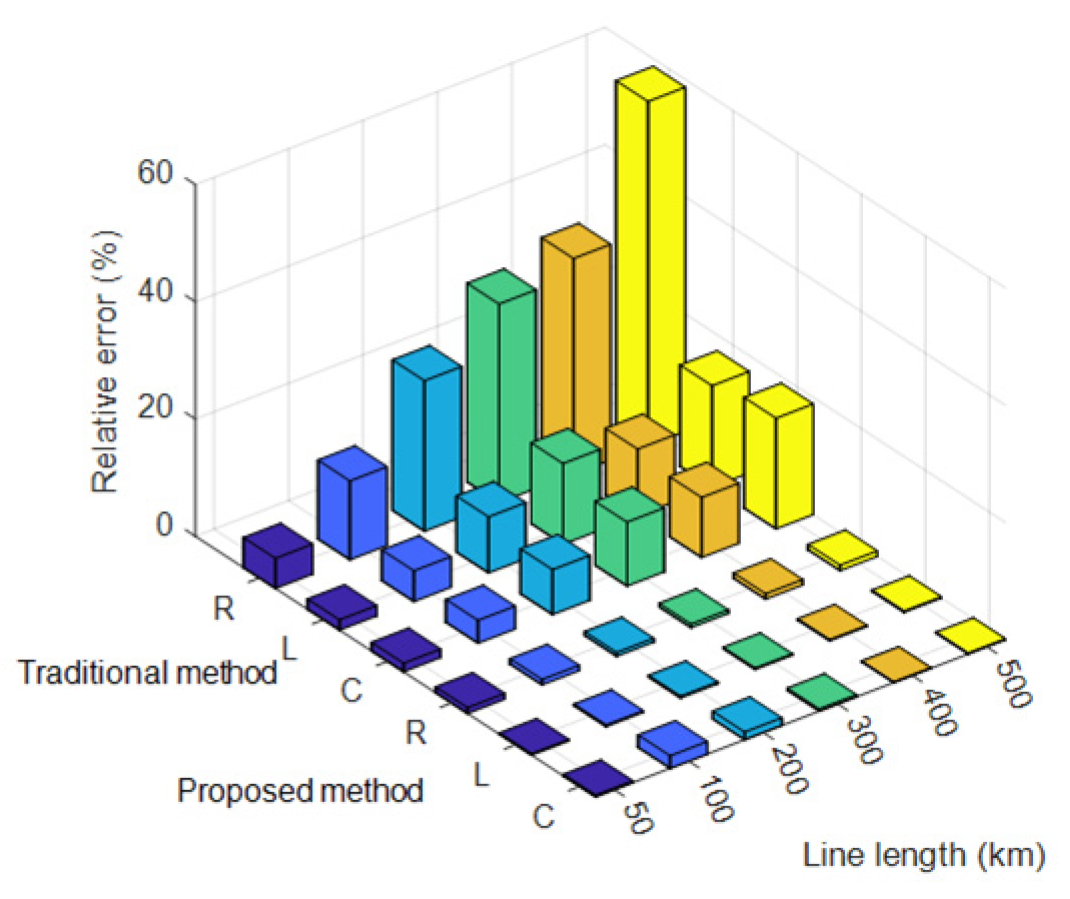
- Traditional measurement approaches rely on single-ended data and approximate the other end, leading to accuracy degradation, especially for long lines. The proposed method fully considers distributed effects along the line, significantly improving reliability.
- The method requires only a single measurement to obtain all distributed parameters, whether the line is de-energized or energized. In contrast, traditional and improved methods require 10 and 5 independent measurements, respectively, making the proposed approach much more efficient.
- The proposed method is suitable for both de-energized and energized transmission lines, making it adaptable to a wide range of practical applications in power system operation and maintenance.
- While the method has been validated through simulations, practical deployment may face challenges such as measurement synchronization, environmental influences, and equipment calibration. Future work should focus on real-world verification and improving robustness under operational conditions.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yuan, K.; Zhang, T.; Xie, X.; Du, S.; Xue, X.; Abdul-Manan, A.F.N.; Huang, Z. Exploration of Low-Cost Green Transition Opportunities for China’s Power System Under Dual Carbon Goals. J. Clean. Prod. 2023, 414, 137590. [Google Scholar] [CrossRef]
- Liu, S.; Lin, Z.; Jiang, Y.; Zhang, T.; Yang, L.; Tan, W.; Lu, F. Modelling and Discussion on Emission Reduction Transformation Path of China’s Electric Power Industry Under “Double Carbon” Goal. Heliyon 2022, 8, e10497. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Xia, Y.; Luo, Y.; Xiong, J. Research on the Development of a New Power System Under the “Dual Carbon” Goals. In Proceedings of the 2024 Boao New Power System International Forum—Power System and New Energy Technology Innovation Forum (NPSIF), Boao, China, 8–10 December 2024; pp. 758–762. [Google Scholar]
- Tong, J.; Liu, W.; Mao, J.; Ying, M. Role and Development of Thermal Power Units in New Power Systems. IEEE J. Radio Freq. Identif. 2022, 6, 837–841. [Google Scholar] [CrossRef]
- Song, Y.; Yang, S.; Li, H. Research on Transmission Scheme of Large-Scale Renewable Energy Transmitted Through Series Hybrid DC System. In Proceedings of the 2022 IEEE 6th Conference on Energy Internet and Energy System Integration (EI2), Chengdu, China, 11–13 November 2022; pp. 363–368. [Google Scholar]
- Tong, D.; Farnham, D.J.; Duan, L.; Zhang, Q.; Lewis, N.S.; Caldeira, K.; Davis, S.J. Geophysical Constraints on the Reliability of Solar and Wind Power Worldwide. Nat. Commun. 2021, 12, 6146. [Google Scholar] [CrossRef] [PubMed]
- Luo, J.; Liu, Y.; Cui, Q.; Zhong, J.; Zhang, L. Single-Ended Time Domain Fault Location Based on Transient Signal Measurements of Transmission Lines. Prot. Control Mod. Power Syst. 2024, 9, 61–74. [Google Scholar] [CrossRef]
- Panahi, H.; Zamani, R.; Sanaye-Pasand, M.; Mehrjerdi, H. Advances in Transmission Network Fault Location in Modern Power Systems: Review, Outlook and Future Works. IEEE Access 2021, 9, 158599–158615. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, B.; Zheng, X.; Lu, D.; Fu, M.; Tai, N. Fault Location Algorithm for Non-Homogeneous Transmission Lines Considering Line Asymmetry. IEEE Trans. Power Deliv. 2020, 35, 2425–2437. [Google Scholar] [CrossRef]
- Feng, X.; Qi, L.; Pan, J. A Novel Fault Location Method and Algorithm for DC Distribution Protection. IEEE Trans. Ind. Appl. 2017, 53, 1834–1840. [Google Scholar] [CrossRef]
- Liang, J.; Jing, T.; Niu, H.; Wang, J. Two-Terminal Fault Location Method of Distribution Network Based on Adaptive Convolution Neural Network. IEEE Access 2020, 8, 54035–54043. [Google Scholar] [CrossRef]
- Peng, Z.; Zhang, W.; Chen, P.; Gong, X.; Wang, L.; Liu, F. Model and Unbalance Analysis of Double-Circuit Transmission Lines on the Same Tower. In Proceedings of the 2022 IEEE 2nd International Conference on Electronic Technology, Communication and Information (ICETCI), Changchun, China, 27–29 May 2022; pp. 65–69. [Google Scholar]
- Hu, Z.; Xiong, M.; Li, C.; Tang, P. New Approach for Precisely Measuring the Zero-Sequence Parameters of Long-Distance Double-Circuit Transmission Lines. IEEE Trans. Power Deliv. 2016, 31, 1627–1635. [Google Scholar] [CrossRef]
- Liang, Y.; Guo, J.; Wang, G. Parameter Self-Adaptive Fault Location of Four-Parallel Transmission Lines on the Same Tower. In Proceedings of the 2011 4th International Conference on Electric Utility Deregulation and Restructuring and Power Technologies (DRPT), Weihai, China, 6–9 July 2011; pp. 881–884. [Google Scholar]
- Sima, W.; Wang, R.; Yang, M.; Yang, Q.; Yuan, T. Secondary Arc Current of Ultra-High Voltage Transmission Line with a Mixed Voltage of 1000/500 kV on a Single Tower. IET Gener. Transm. Distrib. 2015, 9, 686–693. [Google Scholar] [CrossRef]
- Hu, Z.; Chen, Y. New Method of Live Line Measuring the Inductance Parameters of Transmission Lines Based on GPS Technology. IEEE Trans. Power Deliv. 2008, 23, 1288–1295. [Google Scholar] [CrossRef]
- Tan, B.; Dong, X.; Liu, M.; Bi, S.; Yang, J.; Tong, X.; Wang, X. Configuration Method and Test Verification for Equalizing Resistance of HVDC Earth Electrode Considering Anisotropy of Soil Resistivity Distribution. High Volt. Appar. 2021, 57, 0144–0150. [Google Scholar] [CrossRef]
- Dong, Q.; Shao, P. Error analysis and improvement measures of single-phase power supply method to measure the impedance parameters of single-circuit asymmetric line. Electr. Meas. Instrum. 2018, 55, 15–19+30. [Google Scholar] [CrossRef]
- Apostolopoulos, C.A.; Korres, G.N. A Novel Fault-Location Algorithm for Double-Circuit Transmission Lines Without Utilizing Line Parameters. IEEE Trans. Power Deliv. 2011, 26, 1467–1478. [Google Scholar] [CrossRef]
- Xiao, Y.; Deng, J.; Xia, G.; Yang, X.; Zhang, J. A Novel Distributed Parameters Measurement Method of HVDC Transmission Line. Proc. CSEE 2015, 35, 5375–5383. [Google Scholar] [CrossRef]
- Xiao, Y.; Fan, Y.; Cheng, L.; Deng, J. A Parameter Measurement Theory of Single and Double Circuit AC Transmission Lines. Proc. CSEE 2016, 36, 5515–5522+5727. [Google Scholar] [CrossRef]
- Xiao, Y.; Deng, J.; Fan, Y.; Cheng, L. Decoupling Measurement of Zero Sequence Parameters for Four-Circuit AC Transmission Lines on Same Tower. South. Power Syst. Technol. 2016, 10, 54–59. [Google Scholar] [CrossRef]
- Yan, T.; Tan, Y.; Li, H.; Gao, M.; Hu, Z. Anti-Interference Measurement Method of Zero Sequence Capacitance of Transmission Lines Based on Harmonic Component. In Proceedings of the 2022 4th Asia Energy and Electrical Engineering Symposium (AEEES), Chengdu, China, 25–28 March 2022; pp. 674–679. [Google Scholar]
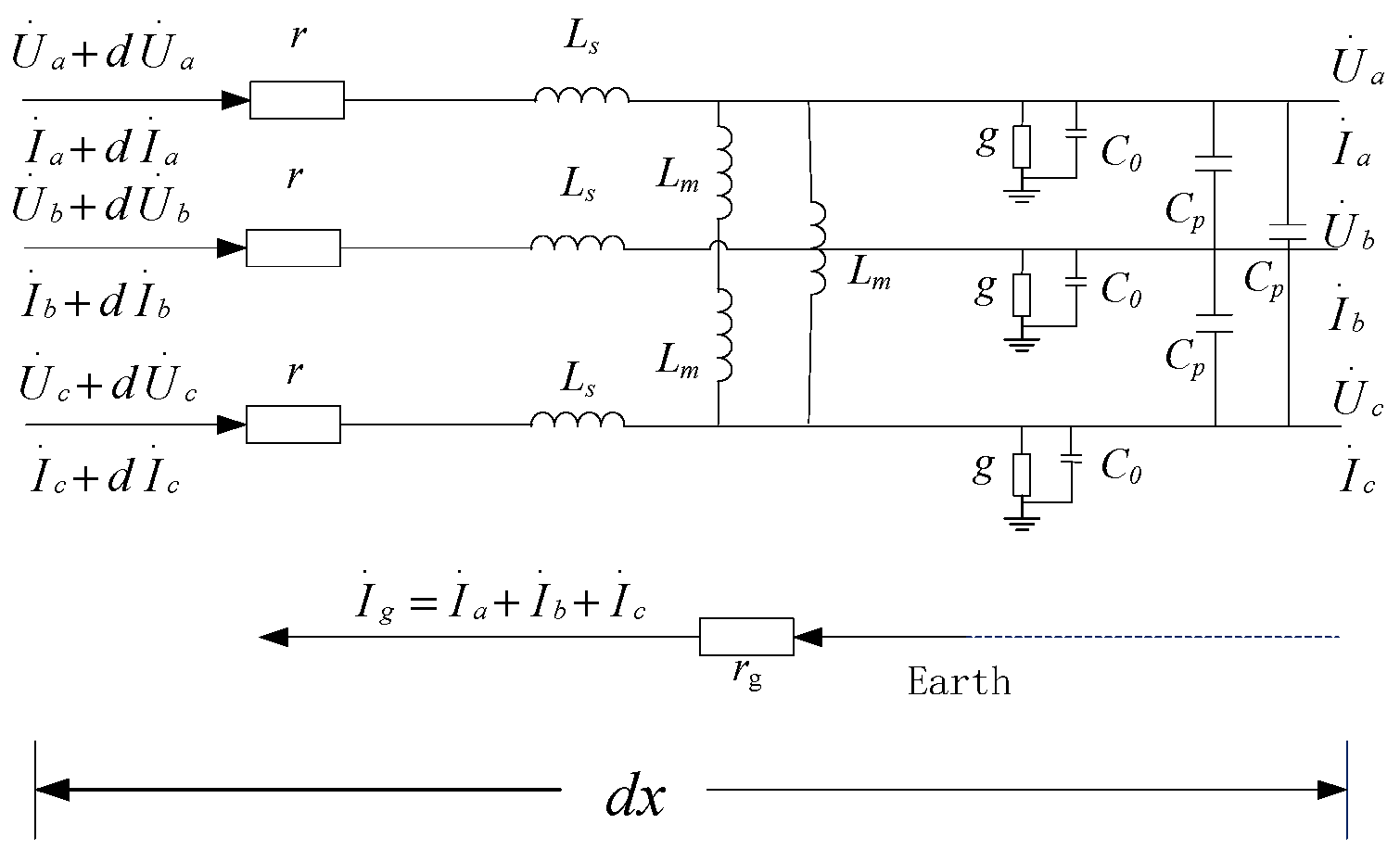

| R0 (Ω/km) | R012 (Ω/km) | R013 (Ω/km) | R014 (Ω/km) | R1 (Ω/km) |
| 0.1686 | 0.1577 | 0.1553 | 0.1553 | 0.0110 |
| L0 (mH/km) | L012 (mH/km) | L013 (mH/km) | L014 (mH/km) | L1 (mH/km) |
| 2.6620 | 1.7903 | 1.5366 | 1.4737 | 0.6975 |
| C0 (nF/km) | C012 (nF/km) | C013 (nF/km) | C014 (nF/km) | C1 (nF/km) |
| rg (Ω/km) | ||||
| 0.0525 | ||||
| Line Length (km) | 50 | 100 | 200 | 300 | 400 | 500 | |
|---|---|---|---|---|---|---|---|
| rg | Measurement Error (%) | 0.9832 | 0.9243 | 0.6607 | 0.6237 | 0.9210 | 0.9267 |
| R0 | Measurement Error (%) | 1.0717 | 0.9465 | 0.7037 | 0.6465 | 0.8483 | 0.8851 |
| R012 | Measurement Error (%) | 1.0534 | 1.2822 | 0.7536 | 0.7475 | 1.2784 | 0.9763 |
| R013 | Measurement Error (%) | 1.1404 | 1.1858 | 0.7580 | 0.7875 | 1.1163 | 0.9638 |
| R014 | Measurement Error (%) | 1.1333 | 1.1098 | 0.7606 | 0.7778 | 1.0164 | 0.9480 |
| R1 | Measurement Error (%) | 2.3387 | 1.2644 | 1.3189 | 0.9719 | 0.1923 | 0.2896 |
| L0 | Measurement Error (%) | 0.1189 | 0.1888 | 0.1806 | 0.1275 | 0.1102 | 0.1291 |
| L012 | Measurement Error (%) | 0.1889 | 0.2334 | 0.2692 | 0.1964 | 0.1811 | 0.1887 |
| L013 | Measurement Error (%) | 0.2489 | 0.2871 | 0.3288 | 0.2437 | 0.2233 | 0.2369 |
| L014 | Measurement Error (%) | 0.2620 | 0.2967 | 0.3400 | 0.2566 | 0.2280 | 0.2464 |
| L1 | Measurement Error (%) | 0.0724 | 0.0241 | 0.0117 | 0.0417 | 0.0915 | 0.0280 |
| C0 | Measurement Error (%) | 2.7997 | 1.7436 | 0.0591 | 0.1694 | 0.0395 | 0.0024 |
| C012 | Measurement Error (%) | 0.2931 | 0.7778 | 0.1861 | 0.0151 | 0.0389 | 0.0938 |
| C013 | Measurement Error (%) | 3.1217 | 1.8721 | 0.3754 | 0.0322 | 0.0837 | 0.0444 |
| C014 | Measurement Error (%) | 0.3105 | 2.1407 | 1.3148 | 0.3791 | 0.1255 | 0.1834 |
| C1 | Measurement Error (%) | 2.1929 | 1.6372 | 0.4876 | 0.7867 | 0.7181 | 0.6259 |
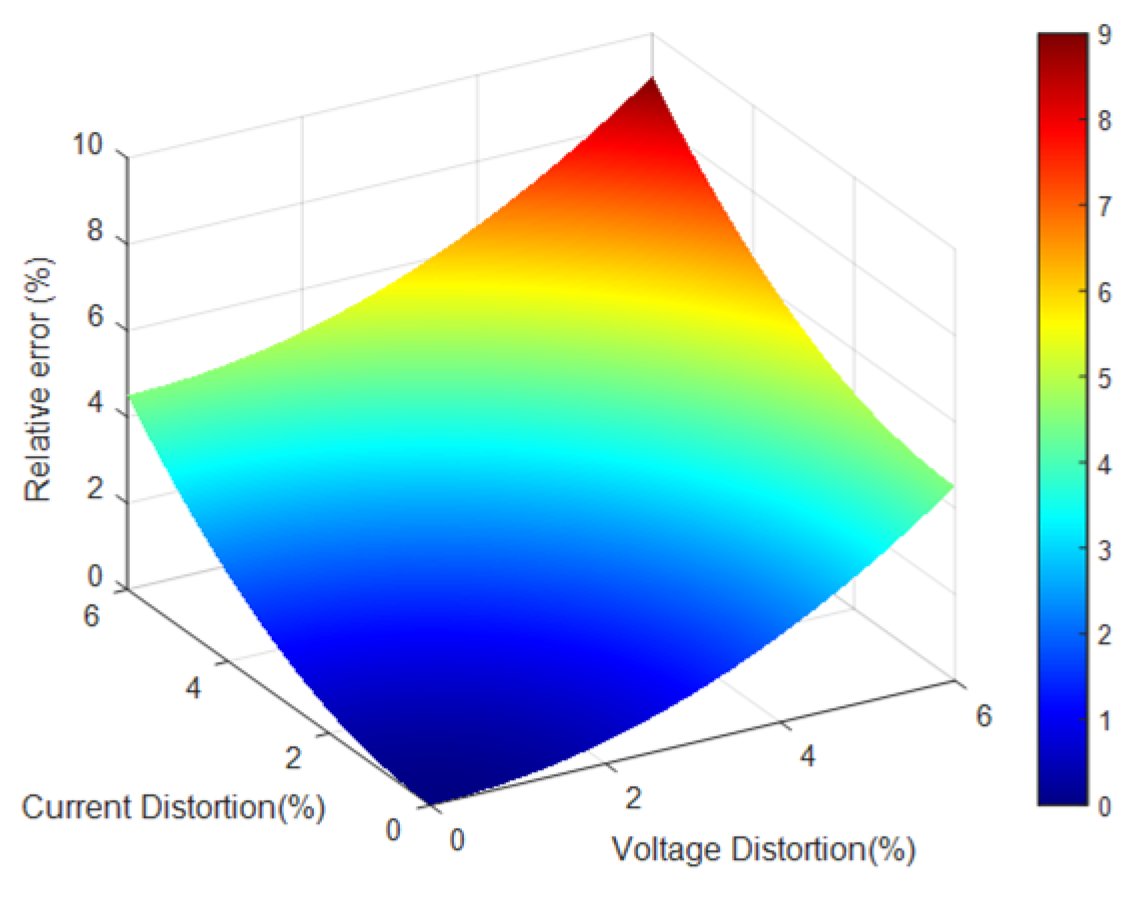
| 0 | 50 | 100 | 150 | 200 | |
|---|---|---|---|---|---|
| R (%) | 0.7220 | 1.4870 | 3.698 | 5.9090 | 8.1240 |
| L (%) | 0.5831 | 0.5715 | 1.7270 | 2.8850 | 4.0430 |
| C (%) | 0.8556 | 1.7620 | 4.3820 | 7.0040 | 9.6280 |
| Line Length (km) | 50 | 100 | 200 | 300 | 400 | 500 | |
|---|---|---|---|---|---|---|---|
| rg | Measurement Error (%) | 5.1234 | 13.4567 | 25.6789 | 33.8901 | 36.7807 | 58.6987 |
| R0 | Measurement Error (%) | 4.2345 | 11.5678 | 22.7890 | 30.9012 | 34.8272 | 55.5088 |
| R012 | Measurement Error (%) | 4.3456 | 11.6789 | 23.0123 | 31.1234 | 34.7384 | 55.2544 |
| R013 | Measurement Error (%) | 4.5678 | 12.8901 | 24.3456 | 32.4567 | 36.5562 | 58.3499 |
| R014 | Measurement Error (%) | 4.6789 | 13.0123 | 24.6789 | 32.7890 | 36.5721 | 58.4843 |
| R1 | Measurement Error (%) | 2.0123 | 6.3456 | 10.6789 | 14.8901 | 11.8627 | 17.2690 |
| L0 | Measurement Error (%) | 1.7456 | 5.2345 | 9.5678 | 13.7890 | 11.3772 | 17.3043 |
| L012 | Measurement Error (%) | 2.2567 | 6.1234 | 10.9012 | 15.0123 | 13.7779 | 21.0682 |
| L013 | Measurement Error (%) | 2.4678 | 6.5678 | 11.3456 | 16.4567 | 15.4273 | 23.6507 |
| L014 | Measurement Error (%) | 2.5789 | 6.8901 | 11.7890 | 16.8901 | 15.8255 | 24.2799 |
| L1 | Measurement Error (%) | 1.0456 | 2.8901 | 5.3456 | 7.9012 | 5.4285 | 7.9759 |
| C0 | Measurement Error (%) | 1.4567 | 3.9012 | 7.6789 | 10.9012 | 10.2419 | 18.8847 |
| C012 | Measurement Error (%) | 2.0678 | 5.1234 | 9.7890 | 13.9012 | 14.0023 | 18.2471 |
| C013 | Measurement Error (%) | 2.1789 | 5.4567 | 10.1234 | 14.3456 | 16.2844 | 23.6490 |
| C014 | Measurement Error (%) | 2.1012 | 5.3456 | 9.9012 | 14.1234 | 15.4723 | 24.8934 |
| C1 | Measurement Error (%) | 1.3678 | 3.4567 | 6.7890 | 9.5678 | 10.9535 | 18.0262 |
| Line Length (km) | 50 | 100 | 200 | 300 | 400 | 500 | |
|---|---|---|---|---|---|---|---|
| rg | Measurement Error (%) | 2.1234 | 4.5678 | 5.9876 | 7.3456 | 8.3461 | 11.6332 |
| R0 | Measurement Error (%) | 1.9876 | 4.2345 | 5.6789 | 6.9012 | 7.9876 | 11.1283 |
| R012 | Measurement Error (%) | 2.1012 | 4.3456 | 5.8901 | 7.1234 | 8.3263 | 11.5668 |
| R013 | Measurement Error (%) | 2.1012 | 4.3456 | 5.8901 | 7.1234 | 8.3263 | 11.5668 |
| R014 | Measurement Error (%) | 2.1234 | 4.5678 | 5.9876 | 7.3456 | 8.3426 | 11.6916 |
| R1 | Measurement Error (%) | 0.8765 | 1.9012 | 2.3456 | 3.0123 | 2.9459 | 3.9526 |
| L0 | Measurement Error (%) | 0.3842 | 0.8265 | 1.4523 | 2.0156 | 2.4577 | 3.6330 |
| L012 | Measurement Error (%) | 0.4637 | 0.9521 | 1.6849 | 2.4378 | 3.2565 | 4.8364 |
| L013 | Measurement Error (%) | 0.4478 | 0.9134 | 1.6257 | 2.3019 | 3.2565 | 4.8364 |
| L014 | Measurement Error (%) | 0.4765 | 0.9783 | 1.7132 | 2.4861 | 3.3282 | 4.9500 |
| L1 | Measurement Error (%) | 0.3579 | 0.7426 | 1.2890 | 1.8643 | 2.2936 | 3.8602 |
| C0 | Measurement Error (%) | 1.2345 | 2.3456 | 3.4567 | 4.5678 | 4.8935 | 6.3605 |
| C012 | Measurement Error (%) | 1.5678 | 2.6789 | 3.7890 | 4.8901 | 6.9652 | 8.5748 |
| C013 | Measurement Error (%) | 1.8901 | 2.9012 | 4.0123 | 5.1234 | 7.9518 | 9.2278 |
| C014 | Measurement Error (%) | 1.3456 | 2.4567 | 3.5678 | 4.6789 | 4.9647 | 6.7766 |
| C1 | Measurement Error (%) | 1.0123 | 2.1234 | 3.2345 | 4.3456 | 4.0147 | 5.1626 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Yang, Y.; Chen, H.; He, Y.; Yue, J.; Mai, J.; Wang, Z.; Hu, Z. Accurate Measurement Method for Distribution Parameters of Four-Circuit Transmission Lines with the Same Voltage Considering Earth Resistance. Energies 2025, 18, 1805. https://doi.org/10.3390/en18071805
Liu Y, Yang Y, Chen H, He Y, Yue J, Mai J, Wang Z, Hu Z. Accurate Measurement Method for Distribution Parameters of Four-Circuit Transmission Lines with the Same Voltage Considering Earth Resistance. Energies. 2025; 18(7):1805. https://doi.org/10.3390/en18071805
Chicago/Turabian StyleLiu, Yu, Yong Yang, Haobin Chen, Yinsheng He, Jingpeng Yue, Junjia Mai, Zequn Wang, and Zhijian Hu. 2025. "Accurate Measurement Method for Distribution Parameters of Four-Circuit Transmission Lines with the Same Voltage Considering Earth Resistance" Energies 18, no. 7: 1805. https://doi.org/10.3390/en18071805
APA StyleLiu, Y., Yang, Y., Chen, H., He, Y., Yue, J., Mai, J., Wang, Z., & Hu, Z. (2025). Accurate Measurement Method for Distribution Parameters of Four-Circuit Transmission Lines with the Same Voltage Considering Earth Resistance. Energies, 18(7), 1805. https://doi.org/10.3390/en18071805






