MPPT-Based Chaotic ABC Algorithm for a Photovoltaic Power System Under Partial Shading Conditions
Abstract
1. Introduction
2. Modeling of a PV Module
2.1. I-V Characteristics and Equivalent Circuit
2.2. Effect of Irradiance and Temperature
2.3. P-V Characteristics and Maximum Power Point
2.4. Impact of Partial Shading and Mitigation Strategies
2.4.1. Electrical Effects of Partial Shading
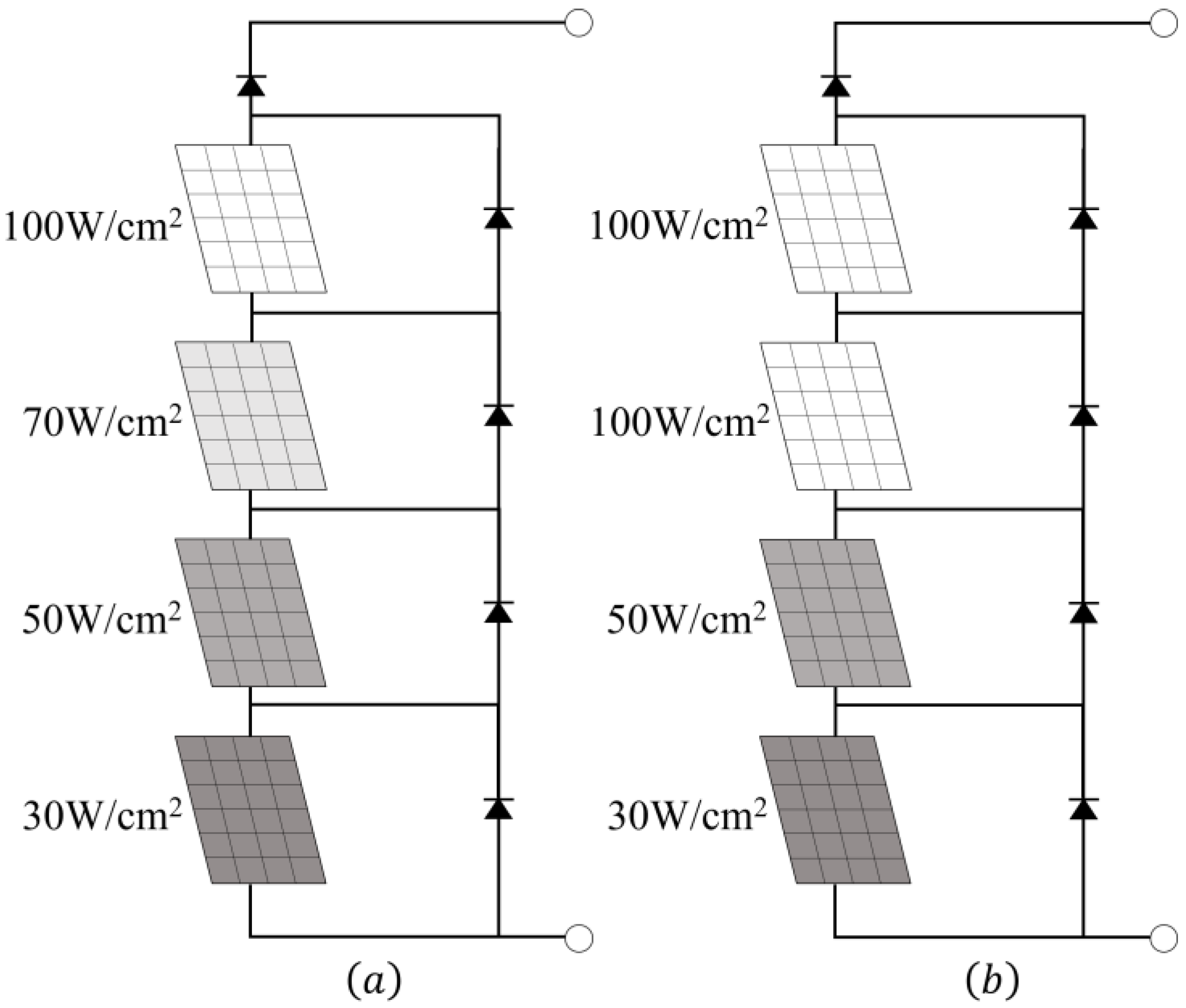
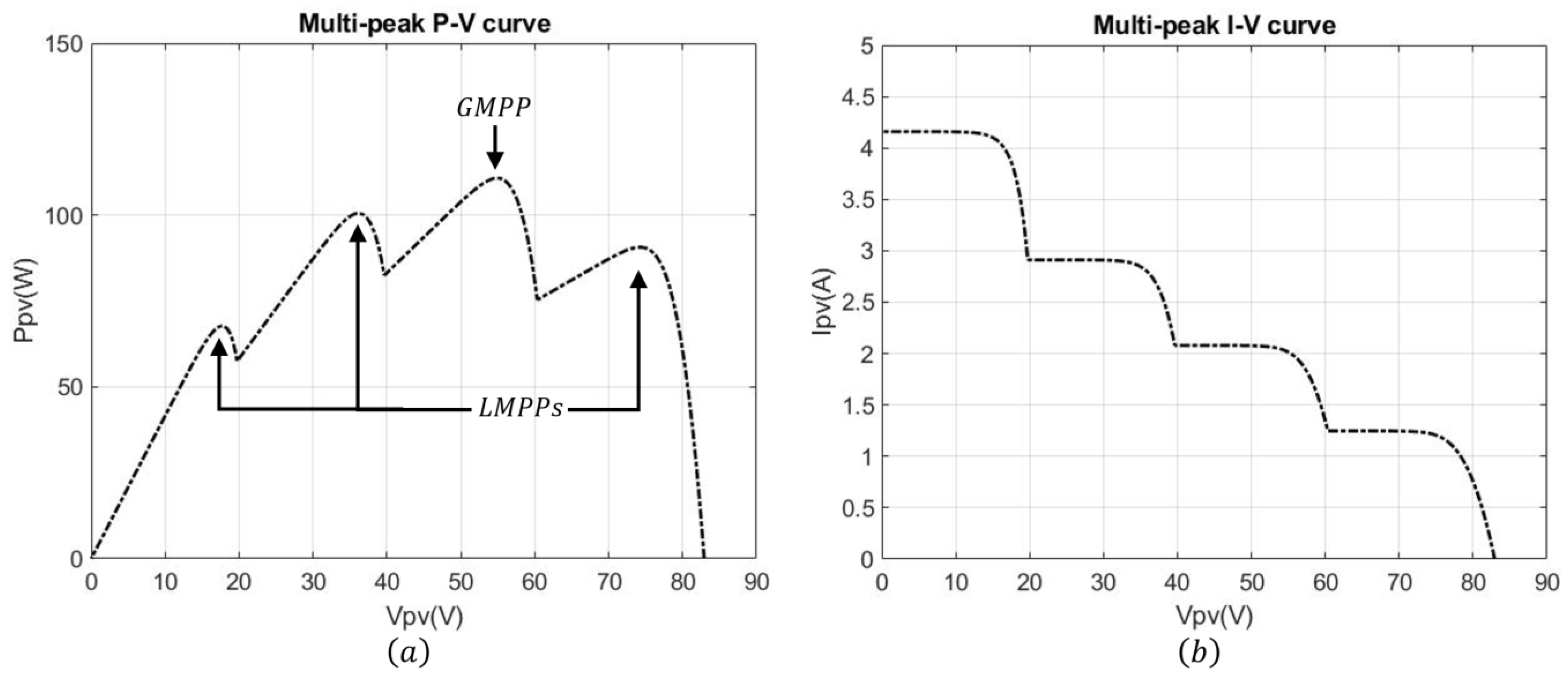
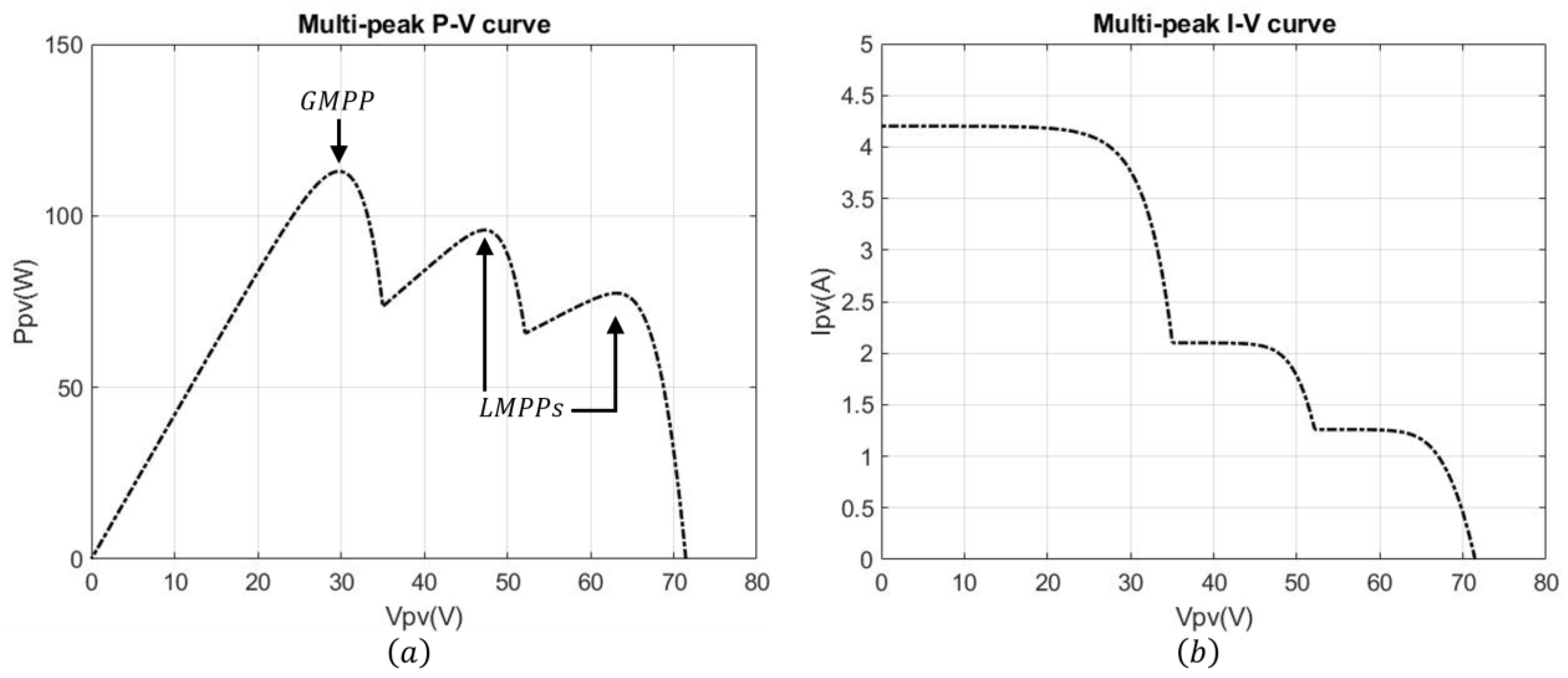
2.4.2. Multi-Peak PV Characteristics Under Partial Shading
3. Chaotic ABC Algorithm-Based MPPT for a PV Power System
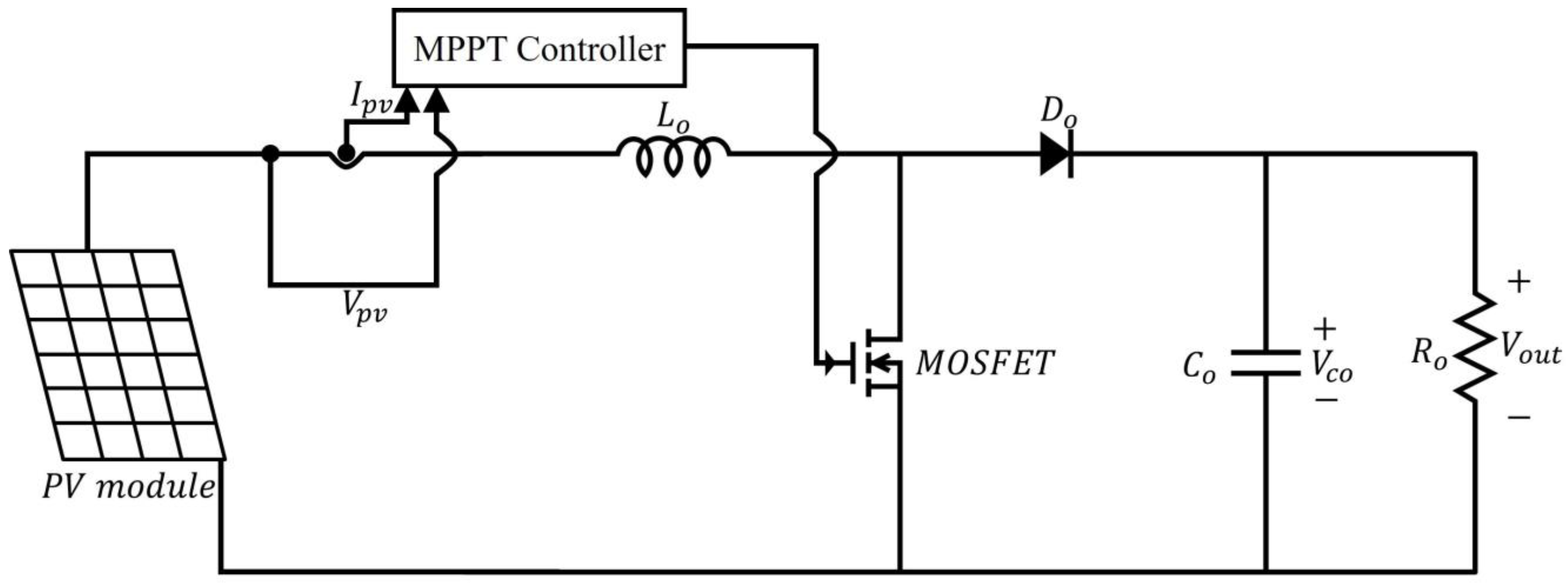
3.1. MPPT Implementation with a Boost Converter
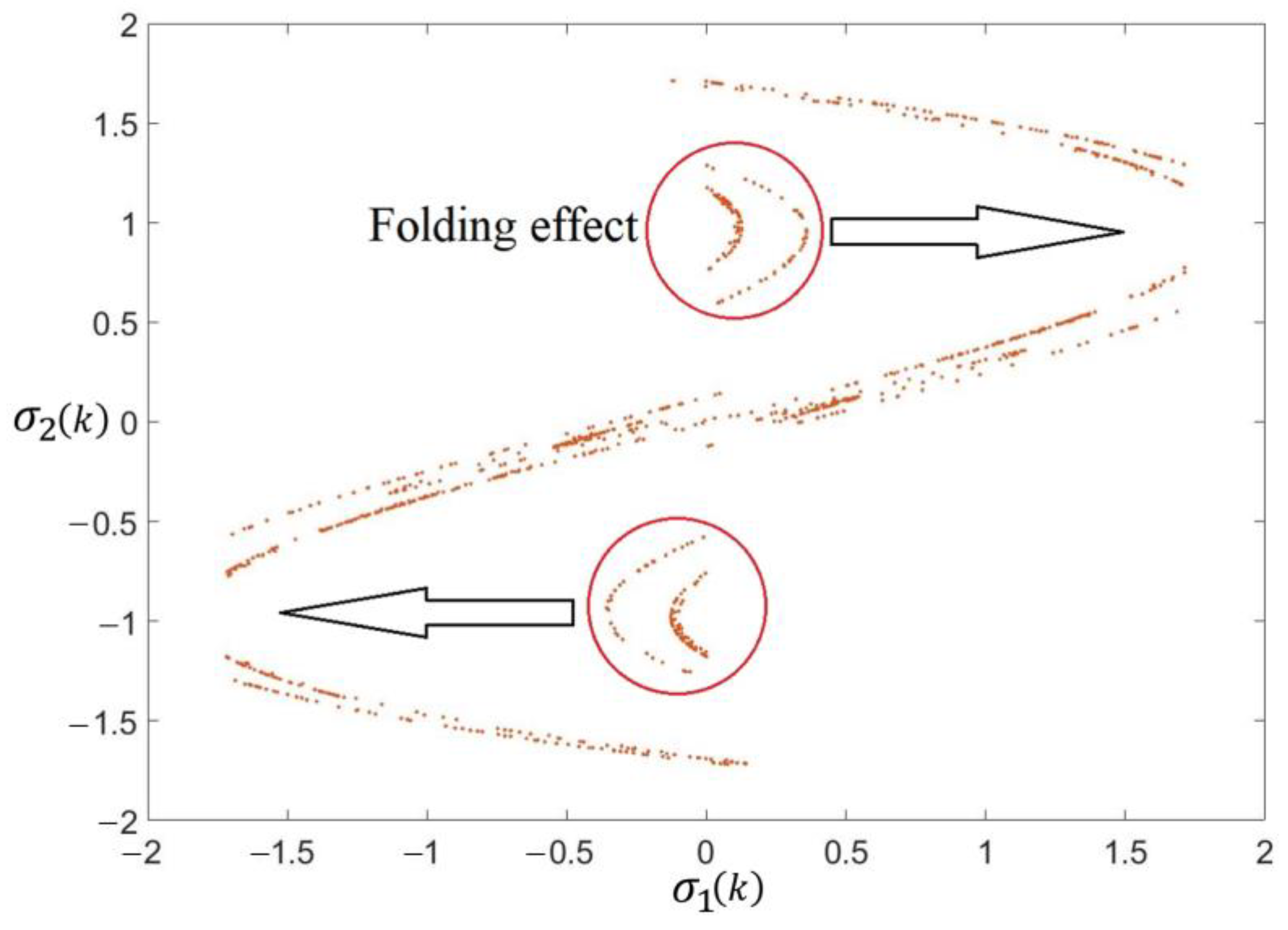
3.2. Chaotic ABC Algorithm Based MPPT
- Step 1.
- Initialization
- Step 2.
- Chaotic Employed Bee Mode
- Step 3.
- Onlooker Bee Mode
- Step 4.
- Scout Bee Mode
- Step 5.
- The algorithm defines the nectar source location with the highest nectar yield as the optimal solution.
- Step 6.
- If either of the termination criteria (the iteration exceeding or ) are met, the optimal solution is returned; otherwise, the process returns to Step 2. Note here that represents the current best duty cycle; represents the previous best duty cycle; and denotes the error tolerance.
4. Simulation Results
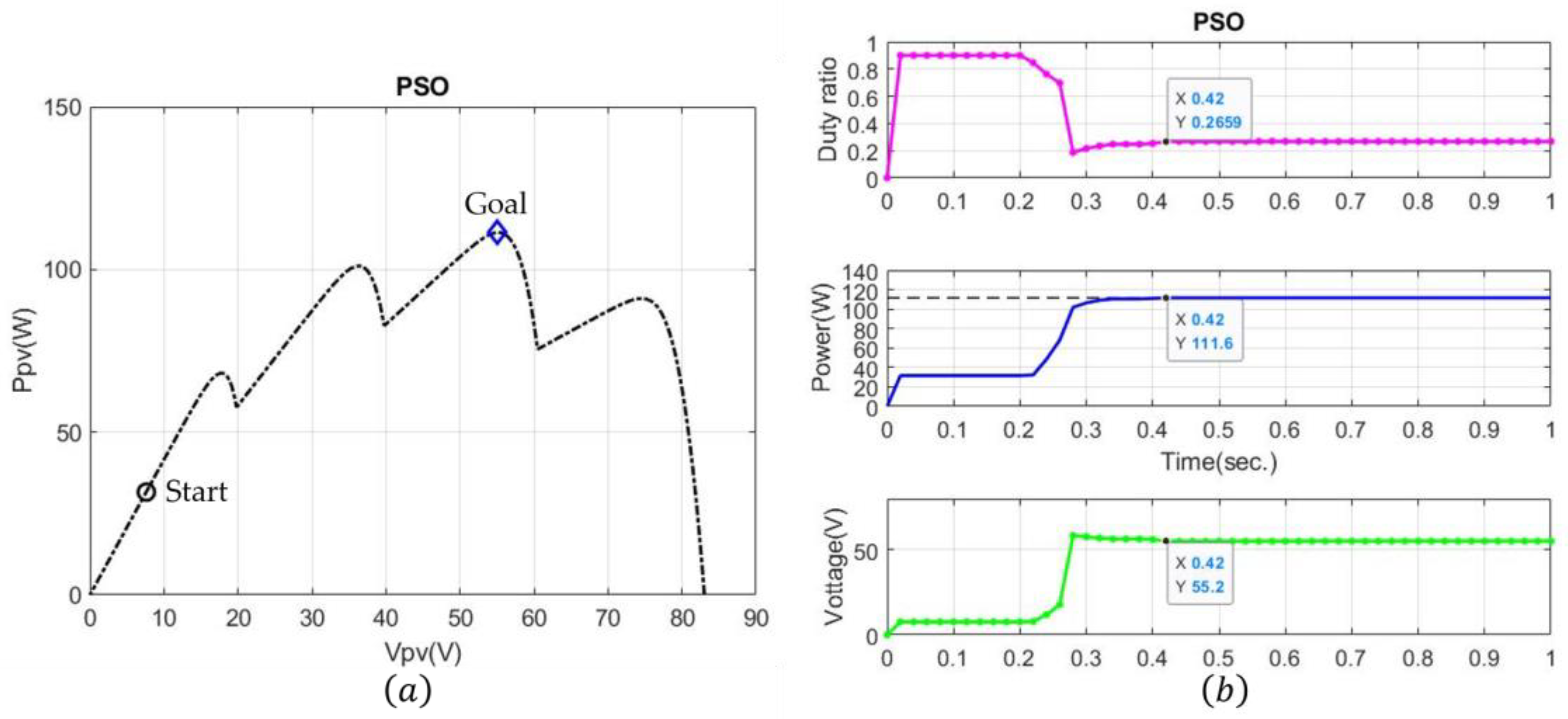
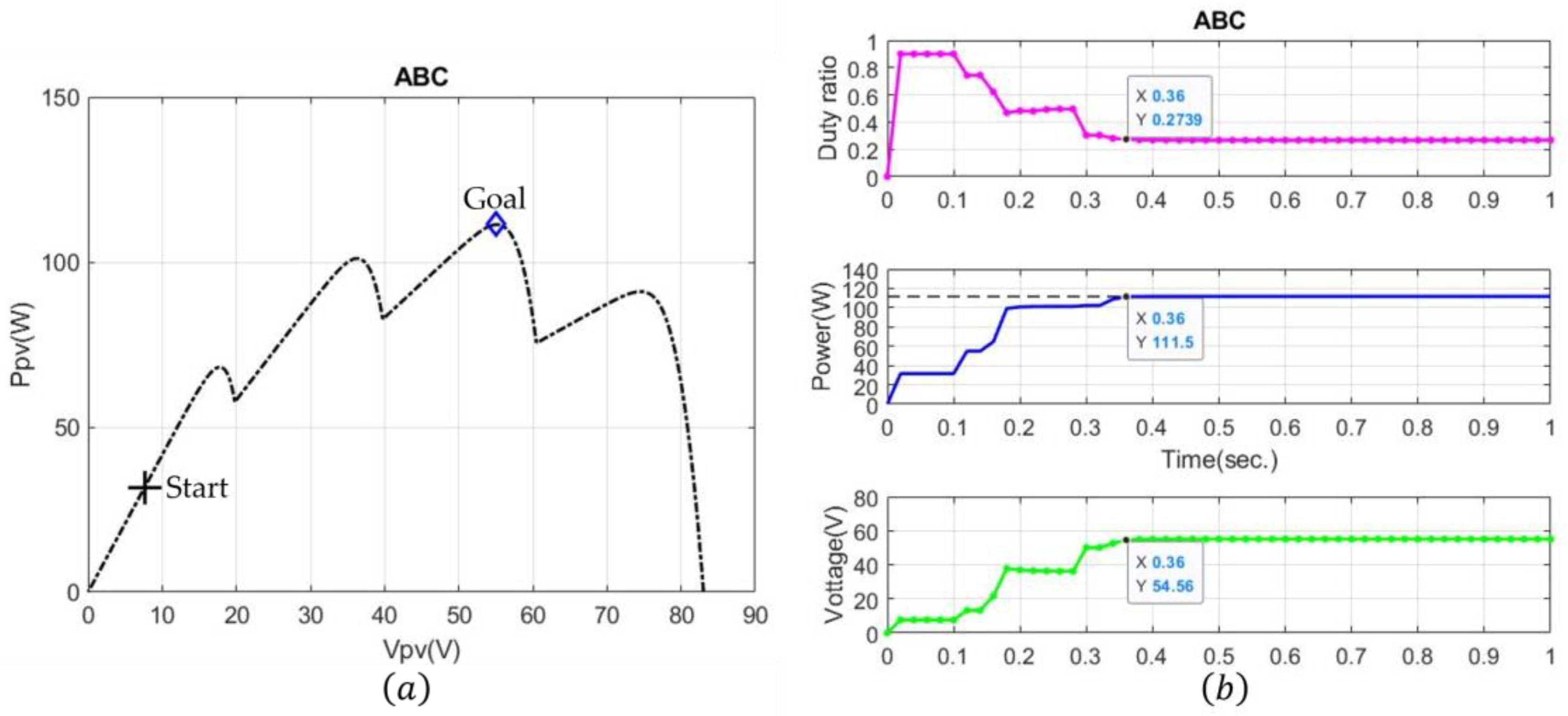
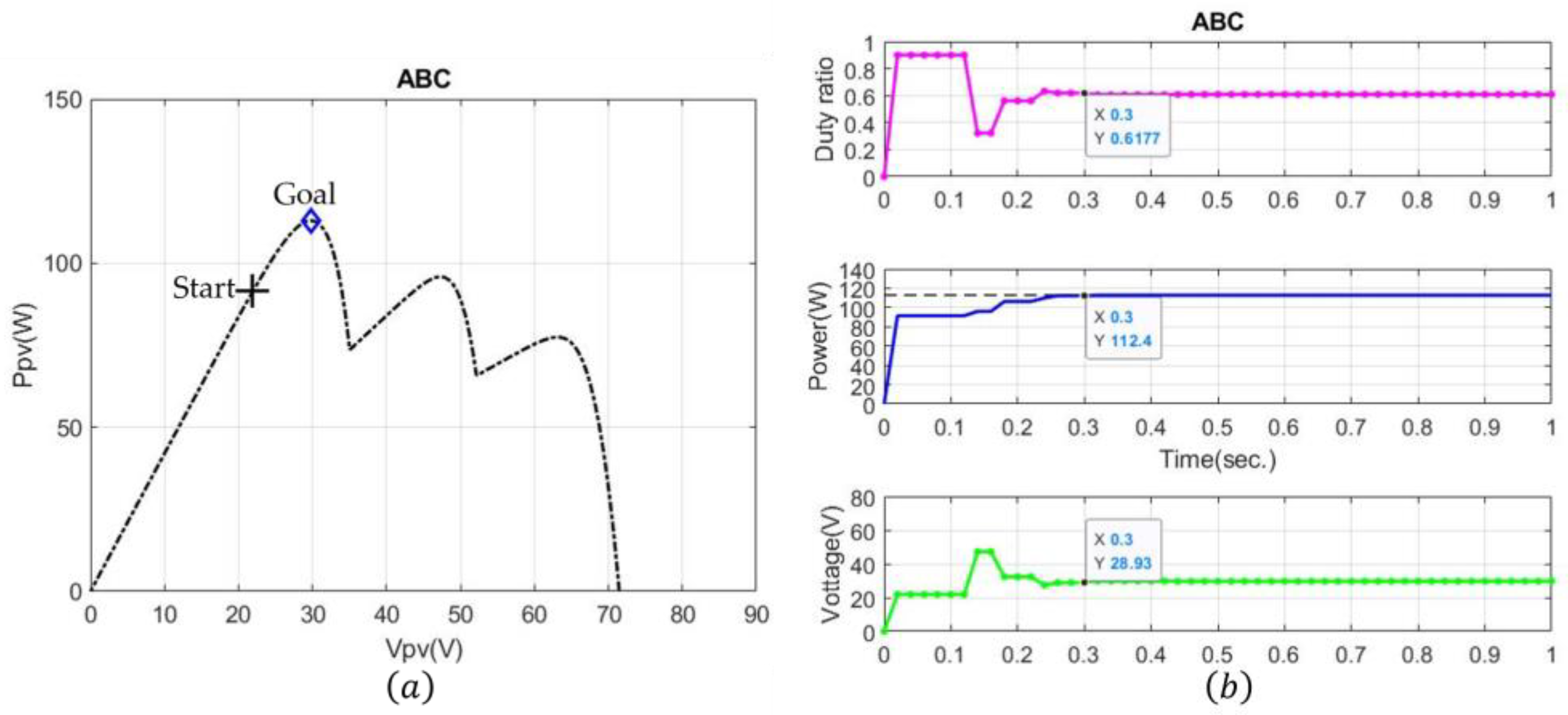
4.1. Case 1: Four-Peak Performance Under Partial Shading
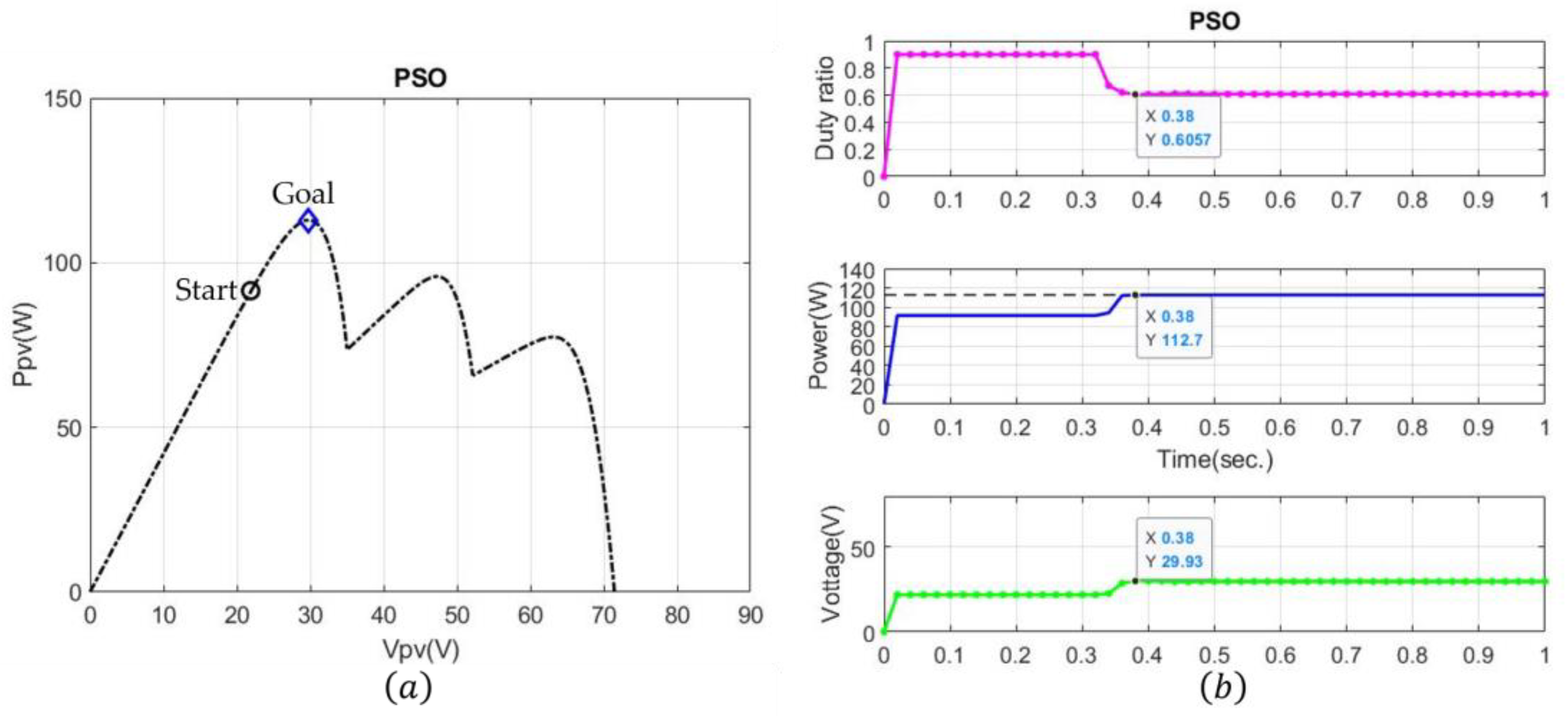
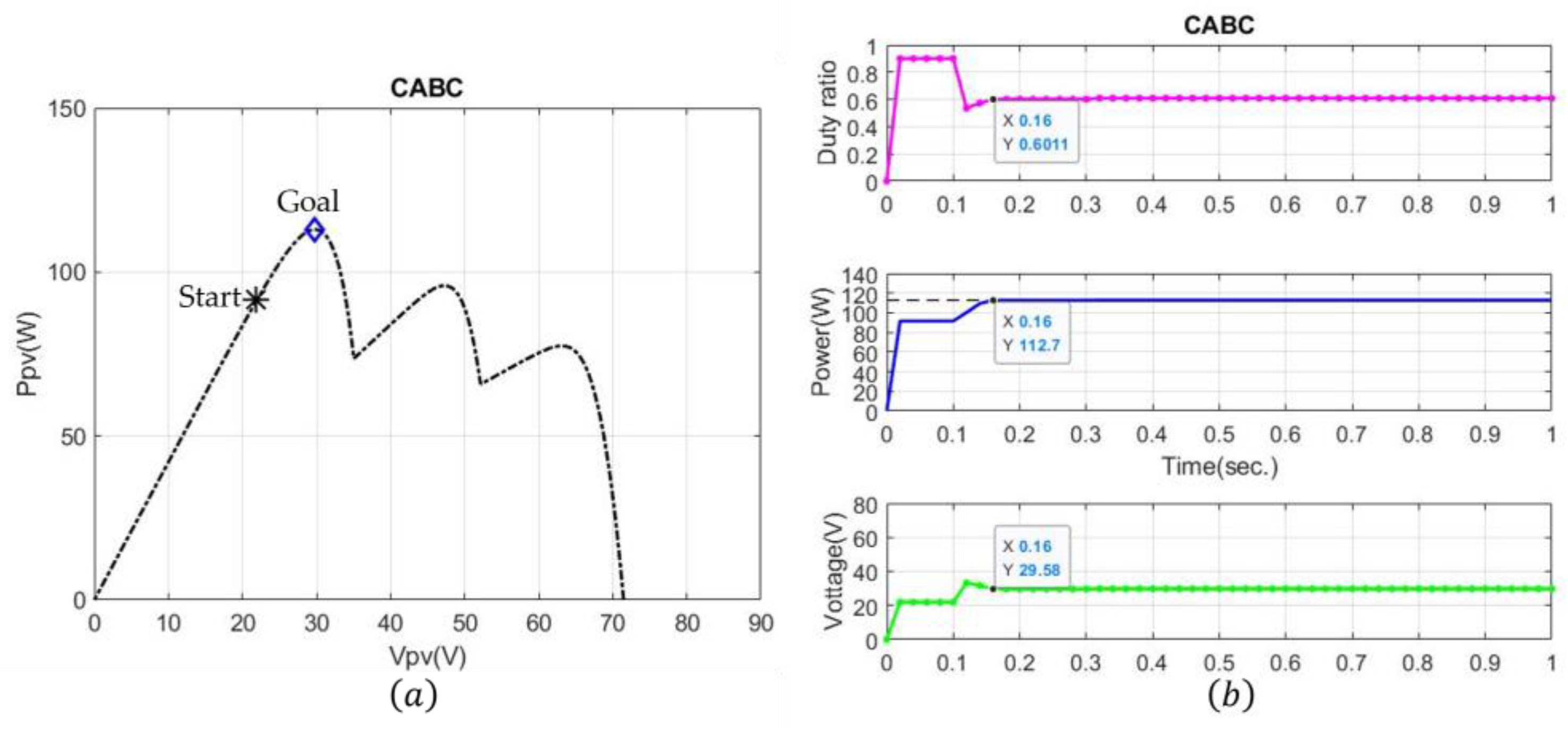
4.2. Case 2: Three-Peak Performance Under Partial Shading
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Katche, M.L.; Makokha, A.B.; Zachary, S.O.; Adaramola, M.S. A Comprehensive Review of Maximum Power Point Tracking (MPPT) Techniques Used in Solar PV Systems. Energies 2023, 16, 2206. [Google Scholar] [CrossRef]
- Manna, S.; Singh, D.K.; Akella, A.K.; Kotb, H.; AboRas, K.M.; Zawbaa, H.M.; Kamel, S. Design and implementation of a new adaptive MPPT controller for solar PV systems. Energy Rep. 2023, 9, 1818–1829. [Google Scholar]
- Kiran, S.R.; Basha, C.H.H.; Singh, V.P.; Dhanamjayulu, C.; Prusty, B.R.; Khan, B. Reduced Simulative Performance Analysis of Variable Step Size ANN Based MPPT Techniques for Partially Shaded Solar PV Systems. IEEE Access 2022, 10, 48875–48889. [Google Scholar]
- Kishore, D.K.; Mohamed, M.R.; Sudhakar, K.; Peddakapu, K. Swarm intelligence-based MPPT design for PV systems under diverse partial shading conditions. Energy 2023, 265, 126366. [Google Scholar]
- Refaat, A.; Ali, Q.A.; Elsakka, M.M.; Elhenawy, Y.; Majozi, T.; Korovkin, N.V.; Elfar, M.H. Extraction of maximum power from PV system based on horse herd optimization MPPT technique under various weather conditions. Renew. Energy 2024, 220, 119718. [Google Scholar]
- Hussain, M.T.; Sarwar, A.; Tariq, M.; Urooj, S.; BaQais, A.; Hossain, M.A. An Evaluation of ANN Algorithm Performance for MPPT Energy Harvesting in Solar PV Systems. Sustainability 2023, 15, 11144. [Google Scholar] [CrossRef]
- Sarwar, S.; Javed, M.Y.; Jaffery, M.H.; Arshad, J.; Ur Rehman, A.; Shafiq, M.; Choi, J.-G. A Novel Hybrid MPPT Technique to Maximize Power Harvesting from PV System under Partial and Complex Partial Shading. Appl. Sci. 2022, 12, 587. [Google Scholar] [CrossRef]
- Abo-Khalil, A.G.; El-Sharkawy, I.I.; Radwan, A.; Memon, S. Influence of a Hybrid MPPT Technique, SA-P&O, on PV System Performance under Partial Shading Conditions. Energies 2023, 16, 577. [Google Scholar] [CrossRef]
- Jabbar, R.I.; Mekhilef, S.; Mubin, M.; Mohammed, K.K. A modified perturb and observe MPPT for a fast and accurate tracking of MPP under varying weather conditions. IEEE Access 2023, 11, 76166–76176. [Google Scholar] [CrossRef]
- Harrison, A.; Alombah, N.H.; de Dieu Nguimfack Ndongmo, J. A New Hybrid MPPT Based on Incremental Conductance-Integral Backstepping Controller Applied to a PV System under Fast-Changing Operating Conditions. Int. J. Photoenergy 2023, 2023, 9931481. [Google Scholar]
- Stephen, A.A.; Musasa, K.; Davidson, I.E. Modelling of Solar PV under Varying Condition with an Improved Incremental Conductance and Integral Regulator. Energies 2022, 15, 2405. [Google Scholar] [CrossRef]
- Ahmed, E.M.; Norouzi, H.; Alkhalaf, S.; Ali, Z.M.; Dadfar, S.; Furukawa, N. Enhancement of MPPT controller in PV-BES system using incremental conductance along with hybrid crow-pattern search approach based ANFIS under different environmental conditions. Sustain. Energy Technol. Assess. 2022, 50, 101812. [Google Scholar] [CrossRef]
- Awad, M.; Ibrahim, A.M.; Alaas, Z.M.; El-Shahat, A.; Omar, A.I. Design and analysis of an efficient photovoltaic energy-powered electric vehicle charging station using perturb and observe MPPT algorithm. Front. Energy Res. 2022, 10, 969482. [Google Scholar] [CrossRef]
- Ouissaaden, F.I.; Dlimi, S.; Kamel, H.; El Khaldi, S.; Elmourabit, F.; Khoukh, A. Effect of Partial Shading on a PV System. In Proceedings of the 2024 International Conference on Circuit, Systems and Communication (ICCSC), Fes, Morocco, 28–29 June 2024; pp. 1–6. [Google Scholar]
- Xu, H.; Zhao, M.; Xue, F.; Zhang, X.; Sun, L. An Improved Mayfly Algorithm With Shading Detection for MPPT of Photovoltaic Systems. IEEE Access 2023, 11, 110827–110836. [Google Scholar] [CrossRef]
- Alshareef, M.J. An Effective Falcon Optimization Algorithm Based MPPT Under Partial Shaded Photovoltaic Systems. IEEE Access 2022, 10, 131345–131360. [Google Scholar] [CrossRef]
- Balaji, V.; Fathima, A.P. Hybrid algorithm for MPPT tracking using a single current sensor for partially shaded PV systems. Sustain. Energy Technol. Assess. 2022, 53, 102415. [Google Scholar] [CrossRef]
- Sharma, A.K.; Pachauri, R.K.; Choudhury, S.; Minai, A.F.; Alotaibi, M.A.; Malik, H.; Márquez, F.P.G. Role of Metaheuristic Approaches for Implementation of Integrated MPPT-PV Systems: A Comprehensive Study. Mathematics 2023, 11, 269. [Google Scholar] [CrossRef]
- Moghassemi, A.; Ebrahimi, S.; Padmanaban, S.; Mitolo, M.; Holm-Nielsen, J.B. Two fast metaheuristic-based MPPT techniques for partially shaded photovoltaic system. Int. J. Electr. Power Energy Syst. 2022, 137, 107567. [Google Scholar] [CrossRef]
- Hassan, A.; Bass, O.; Masoum, M.A. An improved genetic algorithm based fractional open circuit voltage MPPT for solar PV systems. Energy Rep. 2023, 9, 1535–1548. [Google Scholar] [CrossRef]
- Dagal, I.; Akın, B.; Akboy, E. MPPT mechanism based on novel hybrid particle swarm optimization and salp swarm optimization algorithm for battery charging through simulink. Sci. Rep. 2022, 12, 2664. [Google Scholar] [CrossRef]
- Refaat, A.; Khalifa, A.E.; Elsakka, M.M.; Elhenawy, Y.; Kalas, A.; Elfar, M.H. A novel metaheuristic MPPT technique based on enhanced autonomous group Particle Swarm Optimization Algorithm to track the GMPP under partial shading conditions-Experimental validation. Energy Convers. Manag. 2023, 287, 117124. [Google Scholar]
- Brahmi, M.; Regaya, C.B.; Hamdi, H.; Zaafouri, A. Comparative Study of P&O and PSO Particle Swarm Optimization MPPT Controllers for Photovoltaic Systems. In Proceedings of the 2022 8th International Conference on Control, Decision and Information Technologies (CoDIT), Istanbul, Turkey, 17–20 May 2022; pp. 1608–1613. [Google Scholar]
- Koh, J.S.; Tan, R.H.; Lim, W.H.; Tan, N.M. A Modified Particle Swarm Optimization for Efficient Maximum Power Point Tracking Under Partial Shading Condition. IEEE Trans. Sustain. Energy 2023, 14, 1822–1834. [Google Scholar]
- Chao, K.-H.; Li, J.-Y. Global Maximum Power Point Tracking of Photovoltaic Module Arrays Based on Improved Artificial Bee Colony Algorithm. Electronics 2022, 11, 1572. [Google Scholar] [CrossRef]
- Mensah, A.A.; Chen, H.; Otuo-Acheampong, D.; Mbuzi, T. Solar Power Generation System Based on Signal Search Artificial Bee Colony Optimization Algorithm for Maximum Power Point Tracking. In Proceedings of the 2022 12th International Conference on Power and Energy Systems (ICPES), Guangzhou, China, 23–25 December 2022; pp. 912–916. [Google Scholar]
- Pushpalatha, N.; Palpandian, P.; Banu, G.; Thirunavukkarasu, S.; Kokilavani, T.; Devi, B.P. AI Based Tagging the Optimal Power Point of a Solar Photovoltaic Using Artificial Bee Colony (ABC) Optimization Algorithm. In Proceedings of the 2023 10th IEEE Uttar Pradesh Section International Conference on Electrical, Electronics and Computer Engineering (UPCON), Gautam Buddha Nagar, India, 1–3 December 2023; pp. 1428–1432. [Google Scholar]
- Qi, P.; Xia, H.; Cai, X.; Yu, M.; Jiang, N.; Dai, Y. Novel Global MPPT Technique Based on Hybrid Cuckoo Search and Artificial Bee Colony under Partial-Shading Conditions. Electronics 2024, 13, 1337. [Google Scholar] [CrossRef]
- Mendez-Flores, E.; Ortiz, A.; Macias, I.; Molina, A. Experimental Validation of an Enhanced MPPT Algorithm and an Optimal DC–DC Converter Design Powered by Metaheuristic Optimization for PV Systems. Energies 2022, 15, 8043. [Google Scholar] [CrossRef]
- Watanabe, R.B.; Ando Junior, O.H.; Leandro, P.G.M.; Salvadori, F.; Beck, M.F.; Pereira, K.; Brandt, M.H.M.; de Oliveira, F.M. Implementation of the Bio-Inspired Metaheuristic Firefly Algorithm (FA) Applied to Maximum Power Point Tracking of Photovoltaic Systems. Energies 2022, 15, 5338. [Google Scholar] [CrossRef]
- Gupta, J.; Beryozkina, S.; Aljaidi, M.; Singla, M.K.; Safaraliev, M.; Gupta, A.; Nijhawan, P. Application of hybrid chaotic particle swarm optimization and slime mould algorithm to optimally estimate the parameter of fuel cell and solar PV system. Int. J. Hydrogen Energy 2024, 83, 1003–1023. [Google Scholar]
- Pandikumar, M.; Jenisha, K.J.; Baskar, M.; Swathi, M.; Rayaguru, N.K.; Baskaran, S. Optimized Power Quality Enhancement in PV-Integrated UPQC Systems Using Chaotic PSO-Based MPPT Algorithm. In Proceedings of the 2024 International Conference on Advancement in Renewable Energy and Intelligent Systems (AREIS), Thrissur, India, 5–6 December 2024; pp. 1–6. [Google Scholar]
- Fu, D.; Tang, L.; Ran, W.; Shi, Q.; Fu, M.; You, D. Application of Chaotic Particle Swarm Optimization to Maximum Power Point Tracking of Photovoltaic Arrays under Partial Shading Conditions. In Proceedings of the 2023 3rd International Conference on Energy Engineering and Power Systems (EEPS), Dali, China, 28–30 July 2023; pp. 430–438. [Google Scholar]



| Description | Value |
|---|---|
| Maximum output power | |
| Maximum operating current | |
| Maximum operating voltage | |
| ) | |
| ) | |
| ) | |
| ) | |
| P-N junction parameter (n) |
| Environment | Algorithm | Time to MPP (s) |
|---|---|---|
| Case1 | PSO | 0.42 |
| ABC | 0.36 | |
| CABC | 0.24 | |
| Case2 | PSO | 0.38 |
| ABC | 0.3 | |
| CABC | 0.16 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chiu, C.-S.; Chen, Y.-T. MPPT-Based Chaotic ABC Algorithm for a Photovoltaic Power System Under Partial Shading Conditions. Energies 2025, 18, 1710. https://doi.org/10.3390/en18071710
Chiu C-S, Chen Y-T. MPPT-Based Chaotic ABC Algorithm for a Photovoltaic Power System Under Partial Shading Conditions. Energies. 2025; 18(7):1710. https://doi.org/10.3390/en18071710
Chicago/Turabian StyleChiu, Chian-Song, and Yu-Ting Chen. 2025. "MPPT-Based Chaotic ABC Algorithm for a Photovoltaic Power System Under Partial Shading Conditions" Energies 18, no. 7: 1710. https://doi.org/10.3390/en18071710
APA StyleChiu, C.-S., & Chen, Y.-T. (2025). MPPT-Based Chaotic ABC Algorithm for a Photovoltaic Power System Under Partial Shading Conditions. Energies, 18(7), 1710. https://doi.org/10.3390/en18071710





