Input Power Quality Enhancement in Controlled Single-Phase AC to DC Converter
Abstract
1. Introduction
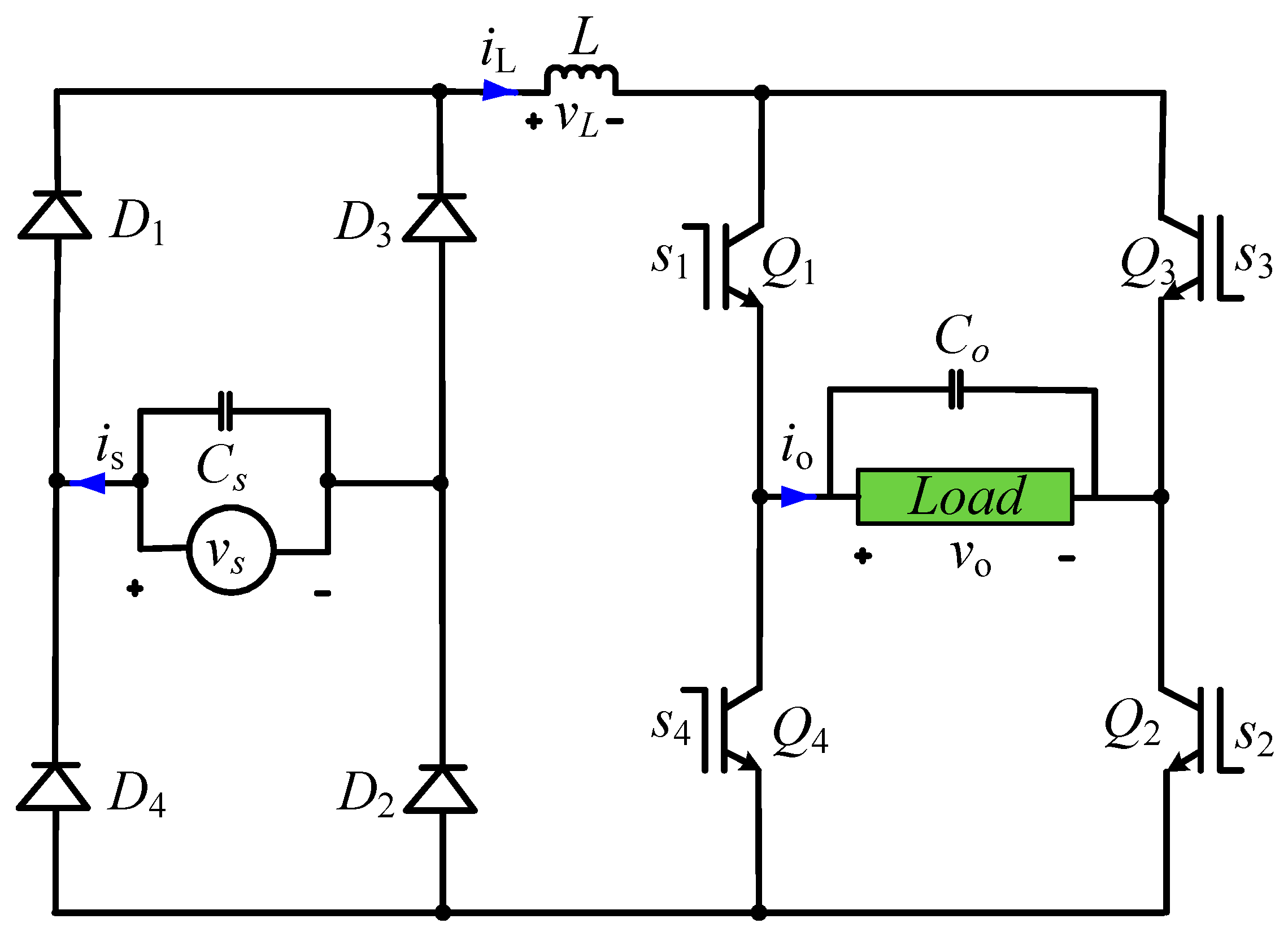
2. Operating Principle of the Tested Circuit
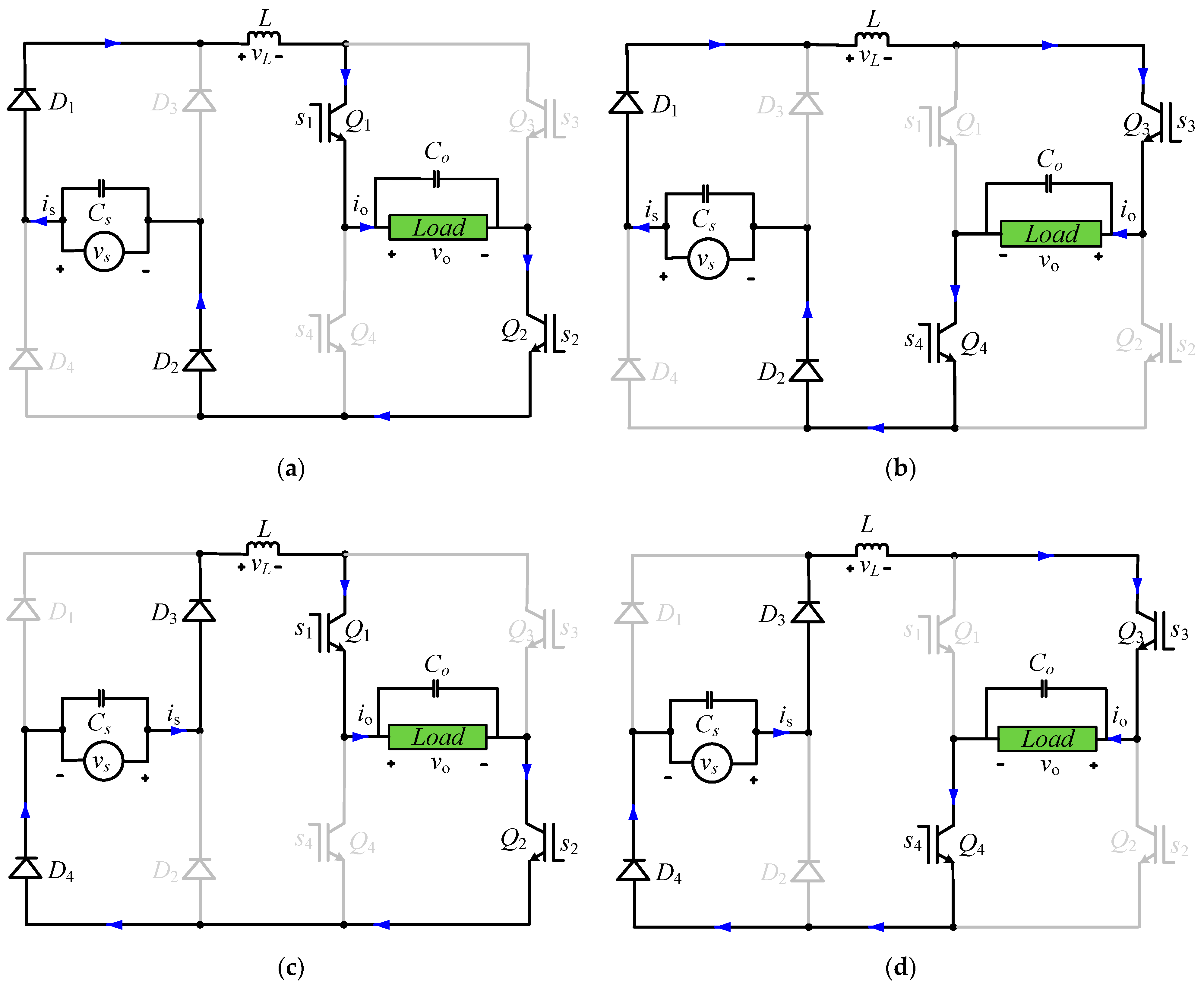
2.1. Equivalent Circuit Loops for Voltage Step-Down Operation
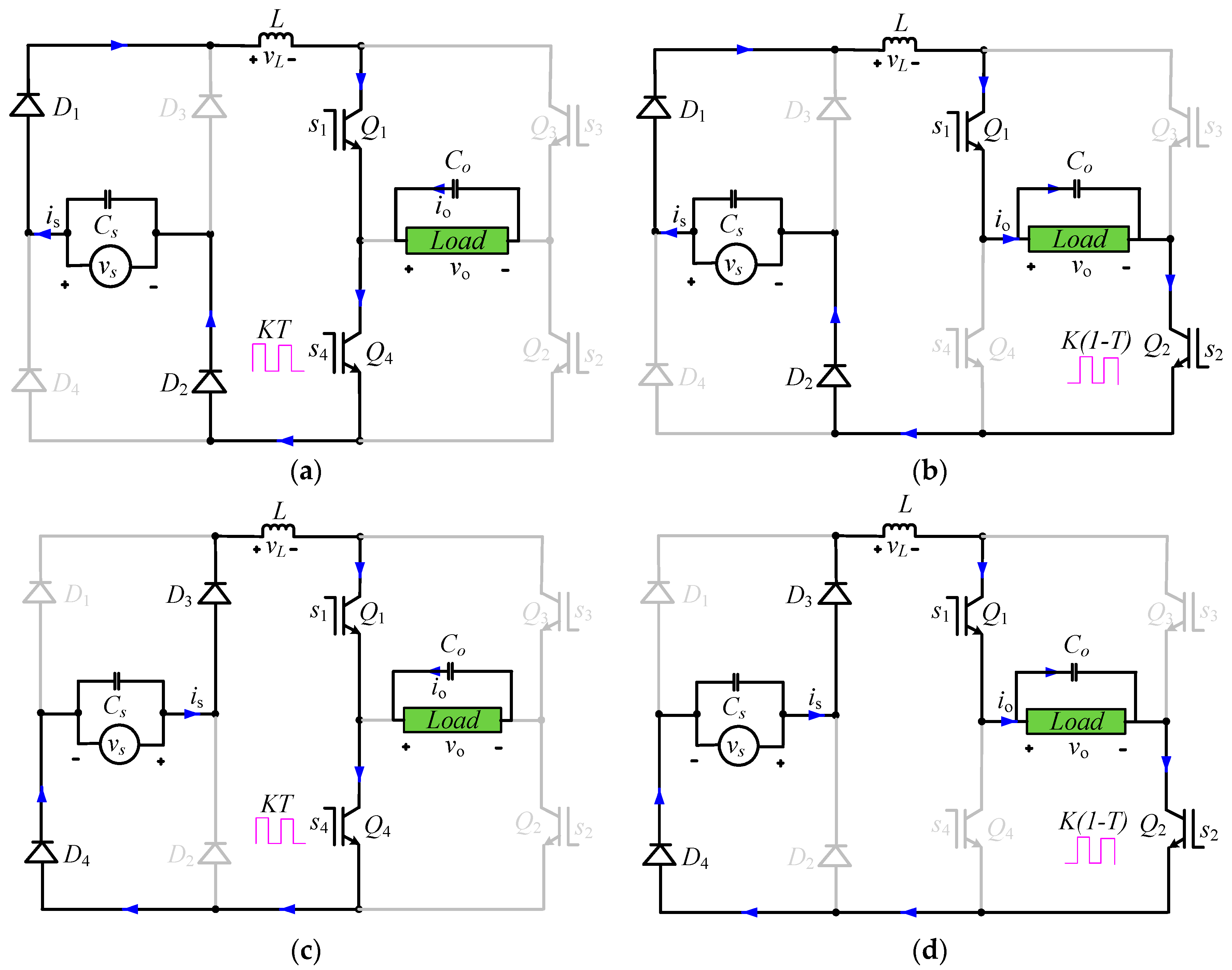
2.2. Equivalent Circuit Loops for Voltage Step-Up Operation
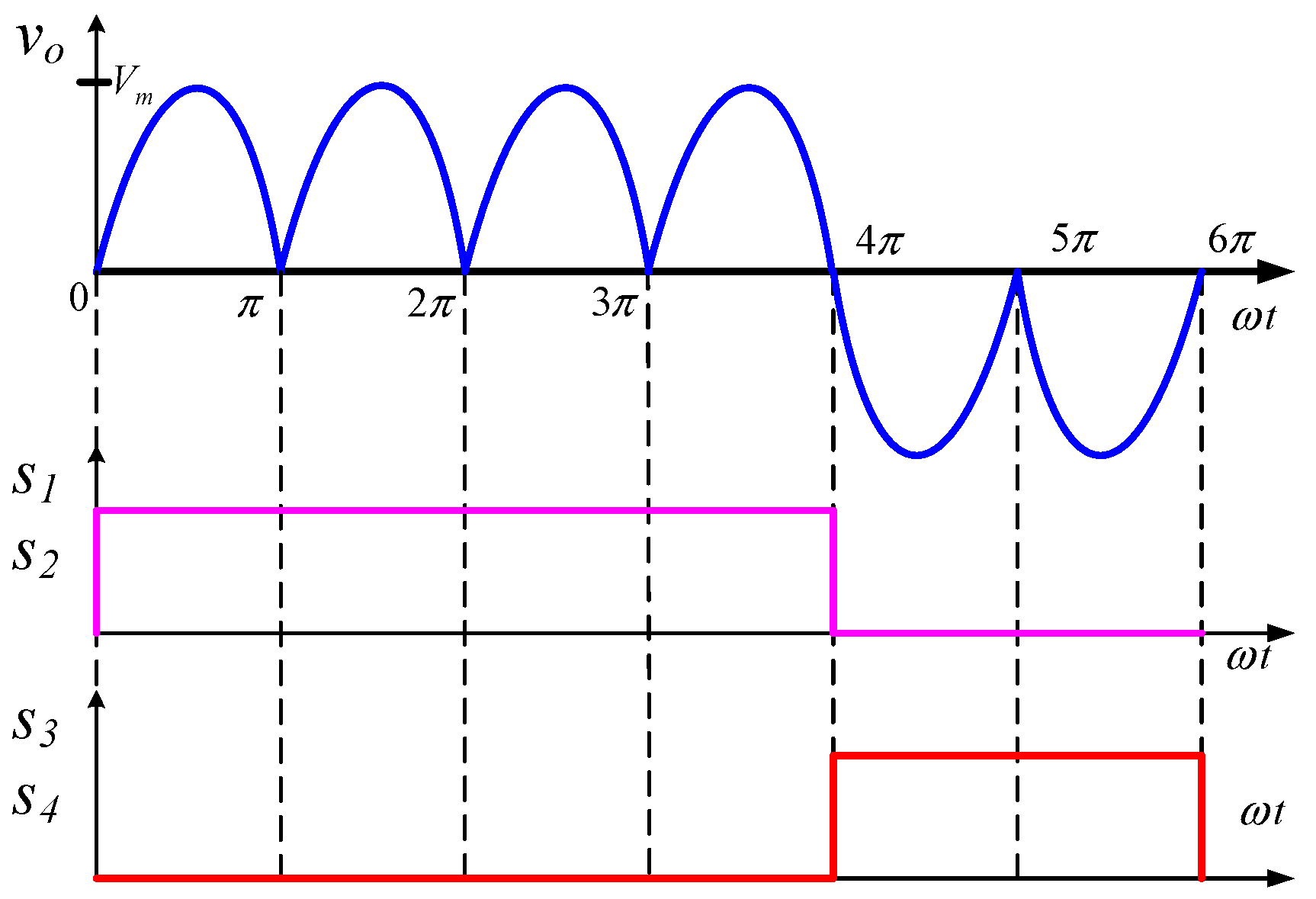
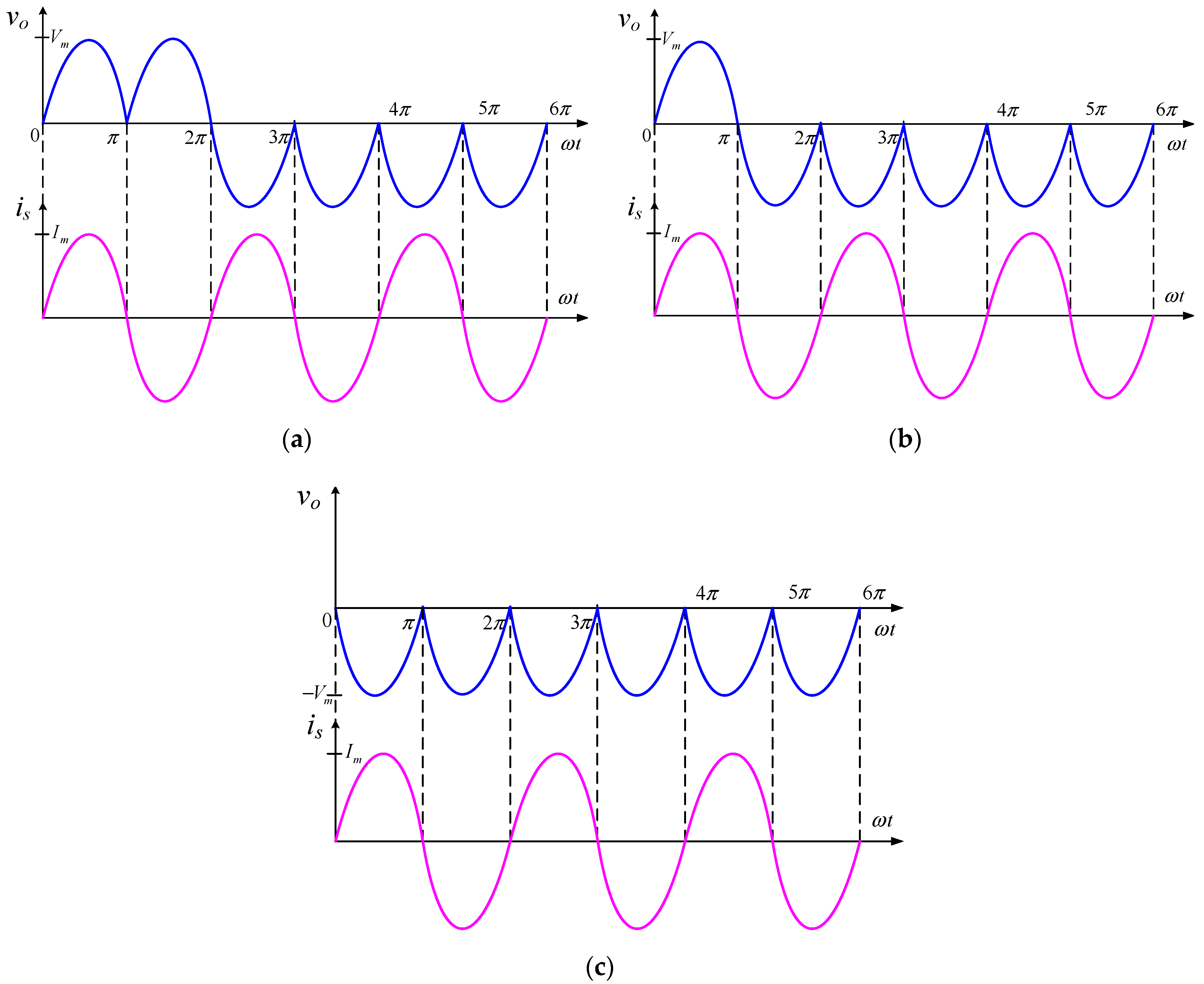
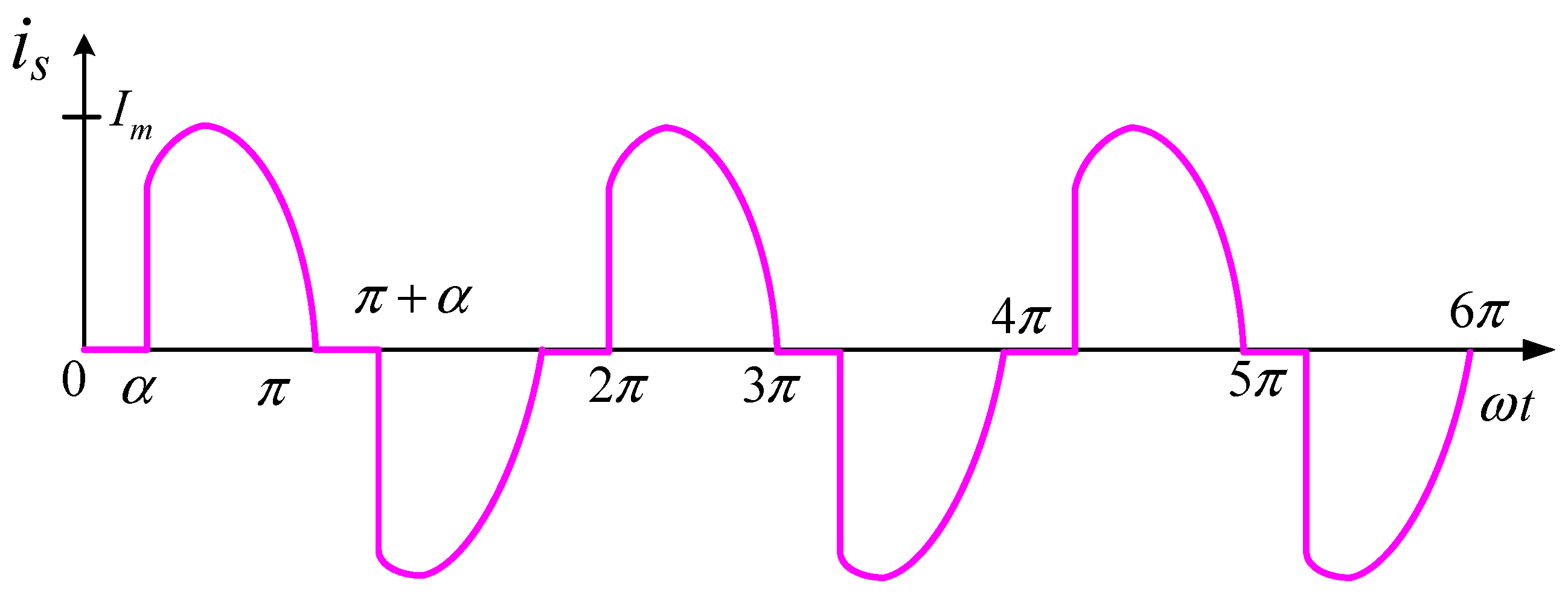
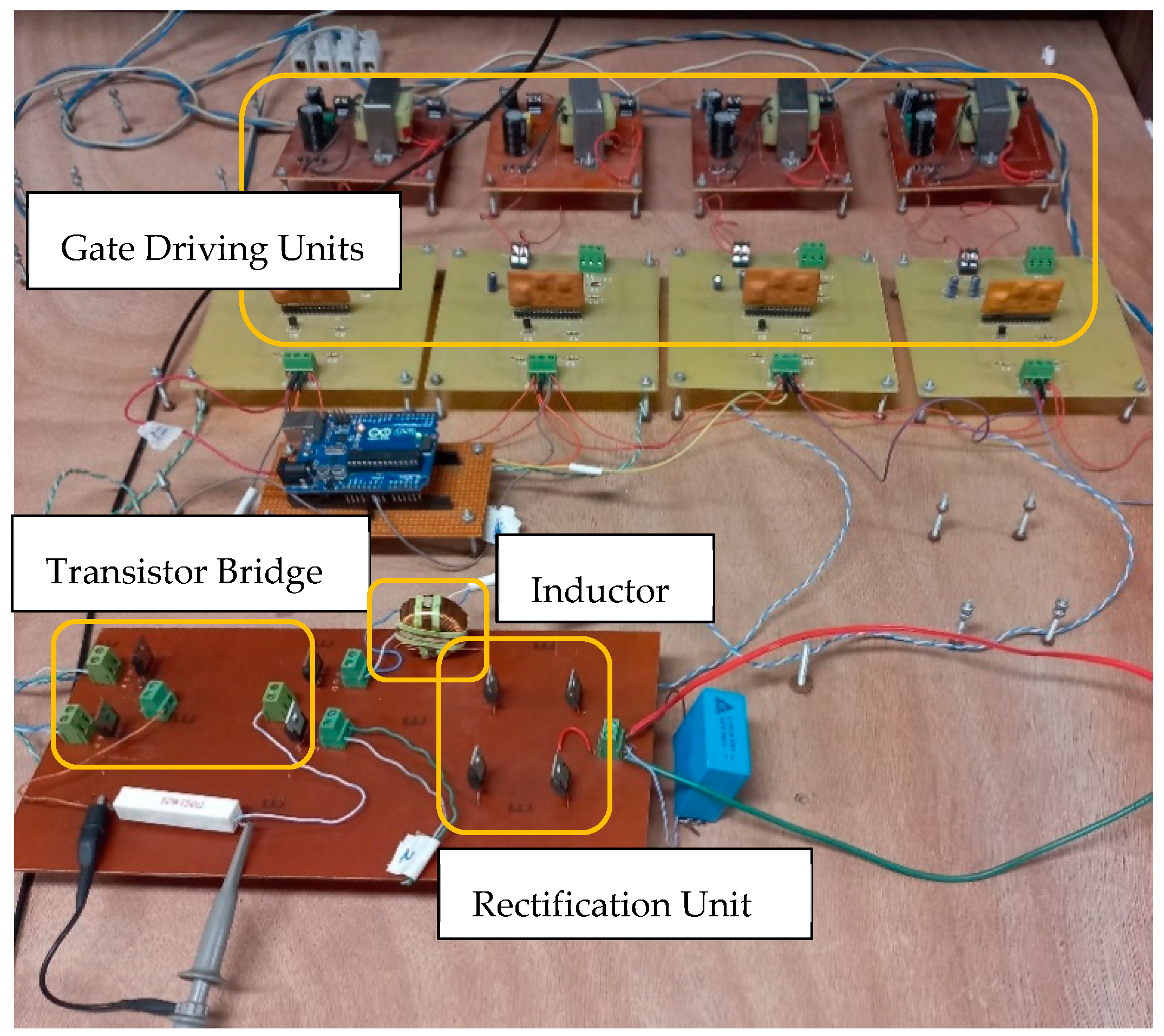
3. Evaluation and Examination
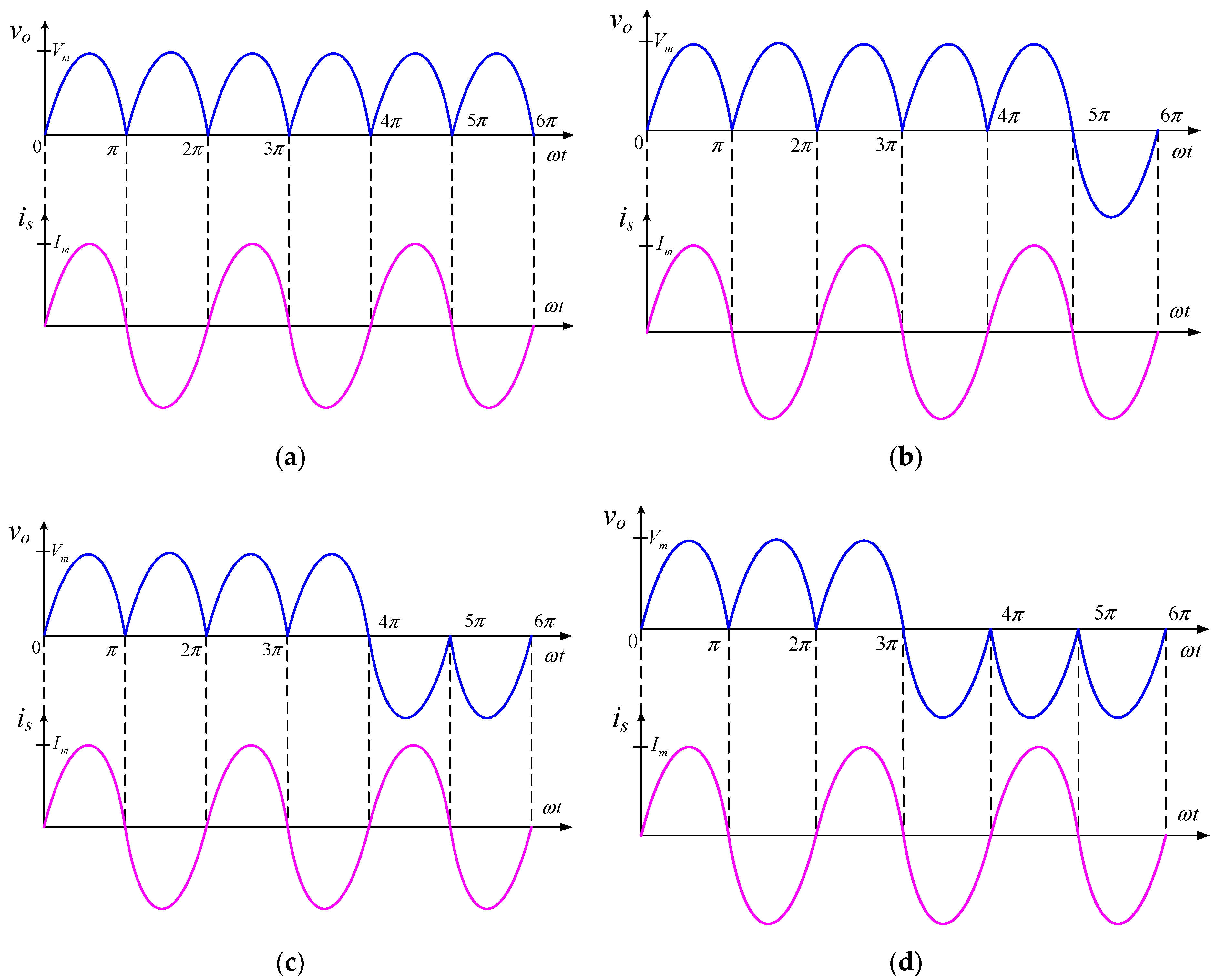
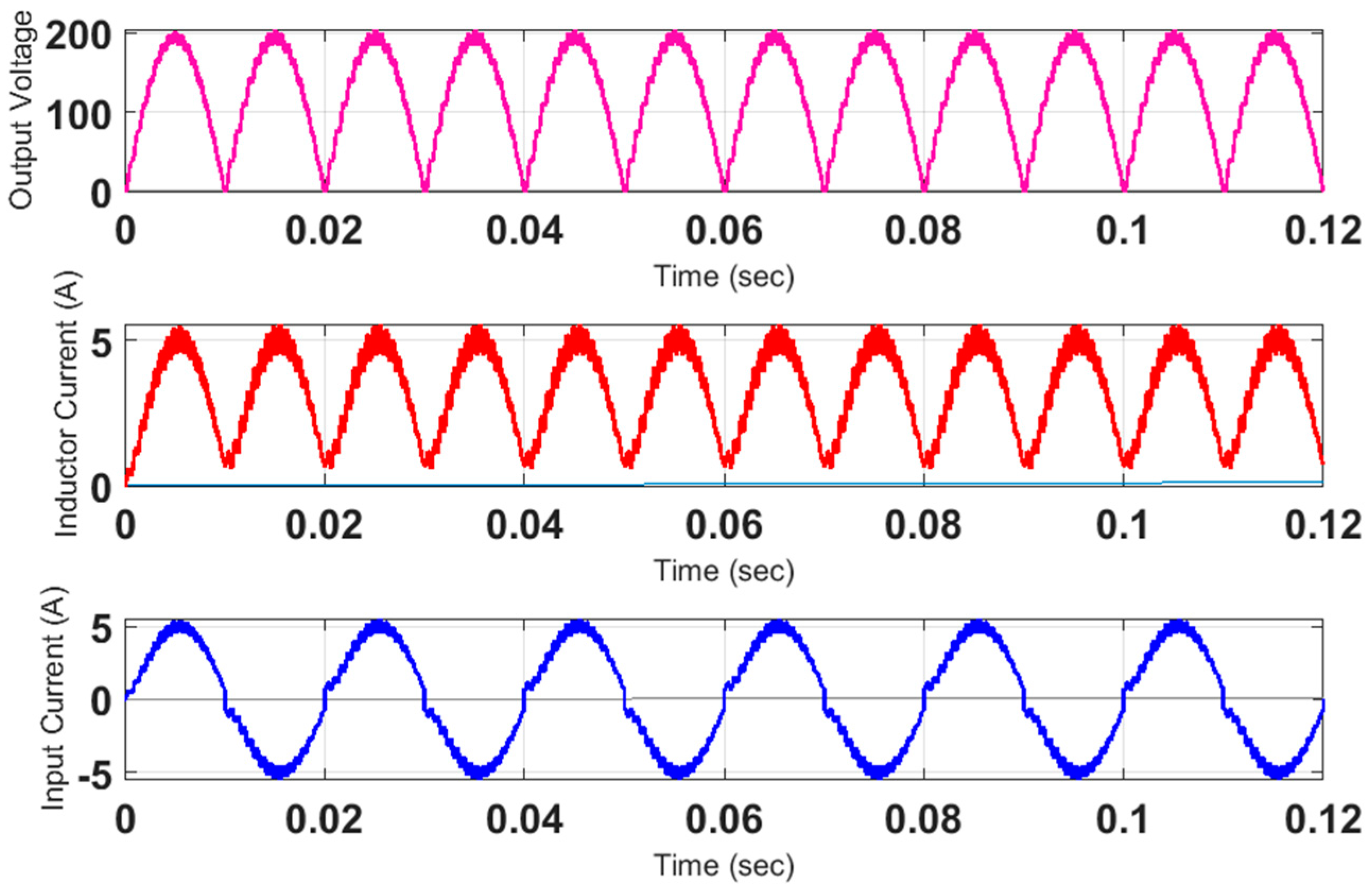
4. Results and Argument
4.1. Discussion Based on Simulation Results
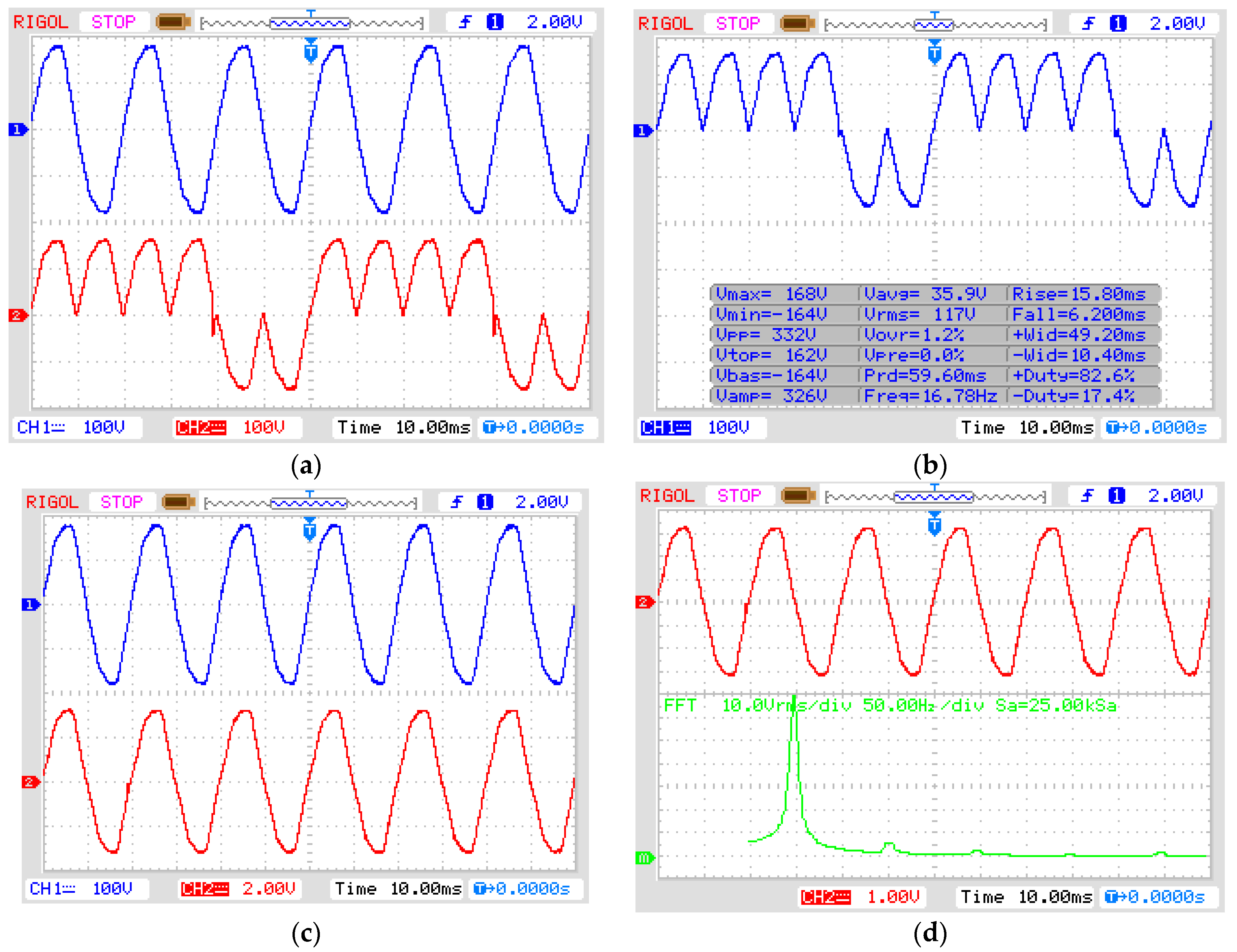
4.2. Discussion Based on Practical Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bajaj, M.; Singh, A.K. Grid integrated renewable DG systems: A review of power quality challenges and state-of-the-art mitigation techniques. Int. J. Energy Res. 2020, 44, 26–69. [Google Scholar] [CrossRef]
- Singh, B.; Singh, S.; Chandra, A.; Al-Haddad, K. Comprehensive Study of Single-Phase AC-DC Power Factor Corrected Converters with High-Frequency Isolation. IEEE Trans. Ind. Inform. 2011, 7, 540–556. [Google Scholar]
- Sharifi, S.; Monfared, M.; Nikbahar, A. Highly Efficient Single-Phase Direct AC-to-AC Converter with Reduced Semiconductor Count. IEEE Trans. Ind. Electron. 2021, 68, 1130–1138. [Google Scholar] [CrossRef]
- Sayed, S.S.; Massoud, A.M. Review on State-of-the-Art Unidirectional Non-Isolated Power Factor Correction Converters for Short-/Long-Distance Electric Vehicles. IEEE Access 2022, 10, 11308–11340. [Google Scholar]
- Vardani, B.; Tummuru, N.R. A Single-Stage Bidirectional Inductive Power Transfer System with Closed-Loop Current Control Strategy. IEEE Trans. Transp. Electrif. 2020, 6, 948–957. [Google Scholar]
- Baek, J.; Kim, J.-K.; Lee, J.-B.; Park, M.-H.; Moon, G.-W. A New Standby Structure Integrated with Boost PFC Converter for Server Power Supply. IEEE Trans. Power Electron. 2019, 34, 5283–5293. [Google Scholar]
- Wei, Y.; Luo, Q.; Alonso, J.M.; Mantooth, A. A Magnetically Controlled Single-Stage AC–DC Converter. IEEE Trans. Power Electron. 2020, 35, 8872–8877. [Google Scholar]
- Ponce-Silva, M.; Salazar-Pérez, D.; Rodríguez-Benítez, O.M.; Vela-Valdés, L.G.; Claudio-Sánchez, A.; De León-Aldaco, S.E.; Cortés-García, C.; Saavedra-Benítez, Y.I.; Lozoya-Ponce, R.E.; Aquí-Tapia, J.A. Flyback Converter for Solid-State Lighting Applications with Partial Energy Processing. Electronics 2020, 10, 60. [Google Scholar] [CrossRef]
- Dini, P.; Saponara, S. Modeling and Control Simulation of Power Converters in Automotive Applications. Appl. Sci. 2024, 14, 1227. [Google Scholar] [CrossRef]
- Sadeghian, O.; Oshnoei, A.; Mohammadi-ivatloo, B.; Vahidinasab, V.; Anvari-Moghaddam, A. A comprehensive review on electric vehicles smart charging: Solutions, strategies, technologies, and challenges. J. Energy Storage 2022, 54, 105241. [Google Scholar]
- Zhang, L.; Yin, Q.; Zhu, W.; Lyu, L.; Jiang, L.; Koh, L.H.; Cai, G. Research on the orderly charging and discharging mechanism of electric vehicles considering travel characteristics and carbon quota. IEEE Trans. Transp. Electrif. 2023, 10, 3012–3027. [Google Scholar] [CrossRef]
- Amin, A.; Tareen, W.U.K.; Usman, M.; Ali, H.; Bari, I.; Horan, B.; Mekhilef, S.; Asif, M.; Ahmed, S.; Mahmood, A. A Review of Optimal Charging Strategy for Electric Vehicles under Dynamic Pricing Schemes in the Distribution Charging Network. Sustainability 2020, 12, 10160. [Google Scholar] [CrossRef]
- Li, C.; Xu, D. Family of Enhanced ZCS Single-Stage Single-Phase Isolated AC–DC Converter for High-Power High-Voltage DC Supply. IEEE Trans. Ind. Electron. 2017, 64, 3629–3639. [Google Scholar] [CrossRef]
- Ashraf, N.; Abbas, G.; Abbassi, R.; Jerbi, H. Power Quality Analysis of the Output Voltage of AC Voltage and Frequency Controllers Realized with Various Voltage Control Techniques. Appl. Sci. 2021, 11, 538. [Google Scholar] [CrossRef]
- Ibrahim, M.E.; Abd-Elhady, A.M. Power frequency AC voltage measurement based on double wound Rogowski coil. High Volt. 2017, 2, 129–135. [Google Scholar] [CrossRef]
- Ashraf, N.; Izhar, T.; Abbas, G.; Yasin, A.R.; Kashif, A.R. Power quality analysis of a three phase ac-to-dc controlled converter. In Proceedings of the 2017 International Conference on Electrical Engineering (ICEE), Lahore, Pakistan, 2–4 March 2017; pp. 1–6. [Google Scholar]
- Friedli, T.; Hartmann, M.; Kolar, J.W. The Essence of Three-Phase PFC Rectifier Systems—Part II. IEEE Trans. Power Electron. 2014, 29, 543–560. [Google Scholar] [CrossRef]
- Jain, A.; Gupta, K.K.; Jain, S.K.; Bhatnagar, P. A Bidirectional Five-Level Buck PFC Rectifier with Wide Output Range for EV Charging Application. IEEE Trans. Power Electron. 2022, 37, 13439–13455. [Google Scholar] [CrossRef]
- Yang, X.; Zhang, Z.; Xu, M.; Li, S.; Zhang, Y.; Zhu, X.F.; Ouyang, X.; Alù, A. Digital non-Foster-inspired electronics for broadband impedance matching. Nat. Commun. 2024, 15, 4346. [Google Scholar] [CrossRef]
- Ghanayem, H.; Alathamneh, M.; Yang, X.; Seo, S.; Nelms, R.M. Enhanced Three-Phase Shunt Active Power Filter Utilizing an Adaptive Frequency Proportional-Integral–Resonant Controller and a Sensorless Voltage Method. Energies 2024, 18, 116. [Google Scholar] [CrossRef]
- Boopathi, R.; Indragandhi, V. Enhancement of power quality in grid-connected systems using a predictive direct power controlled based PV-interfaced with multilevel inverter shunt active power filter. Sci. Rep. 2025, 15, 7967. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Yang, X.; Zhang, Z. High-Efficiency Broadband Electroacoustic Energy Conversion Using Non-Foster-Inspired Circuit and Adaptively Switched Capacitor. IEEE Trans. Ind. Electron. 2025. [Google Scholar] [CrossRef]
- Ashraf, N.; Abbas, G.; Ullah, N.; Alahmadi, A.A.; Awan, A.B.; Zubair, M.; Farooq, U. A Simple Two-Stage AC-AC Circuit Topology Employed as High-Frequency Controller for Domestic Induction Heating System. Appl. Sci. 2021, 11, 8325. [Google Scholar] [CrossRef]





| Parameters | Proposed Strategy | Existing Strategy |
|---|---|---|
| Output DC Voltage | Equal | Equal |
| Output RMS Voltage | Input RMS Voltage | Input RMS Voltage |
| Bipolar Voltage Facility | Yes | No |
| Displacement Power factor | High | Low |
| Total Power Factor | High | Low |
| Total Harmonic Factor | Low | High |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ashraf, N.; Abbas, G.; Yazdan, T. Input Power Quality Enhancement in Controlled Single-Phase AC to DC Converter. Energies 2025, 18, 1674. https://doi.org/10.3390/en18071674
Ashraf N, Abbas G, Yazdan T. Input Power Quality Enhancement in Controlled Single-Phase AC to DC Converter. Energies. 2025; 18(7):1674. https://doi.org/10.3390/en18071674
Chicago/Turabian StyleAshraf, Naveed, Ghulam Abbas, and Tanveer Yazdan. 2025. "Input Power Quality Enhancement in Controlled Single-Phase AC to DC Converter" Energies 18, no. 7: 1674. https://doi.org/10.3390/en18071674
APA StyleAshraf, N., Abbas, G., & Yazdan, T. (2025). Input Power Quality Enhancement in Controlled Single-Phase AC to DC Converter. Energies, 18(7), 1674. https://doi.org/10.3390/en18071674









