Harmonic Current Effect on Vibration Characteristics of Oil-Immersed Transformers and Their Experimental Verification
Abstract
1. Introduction
2. Theory and Modeling Method for Multi-Physical Field Simulation
2.1. Theory of Electromagnetic-Structural Force Field Coupling
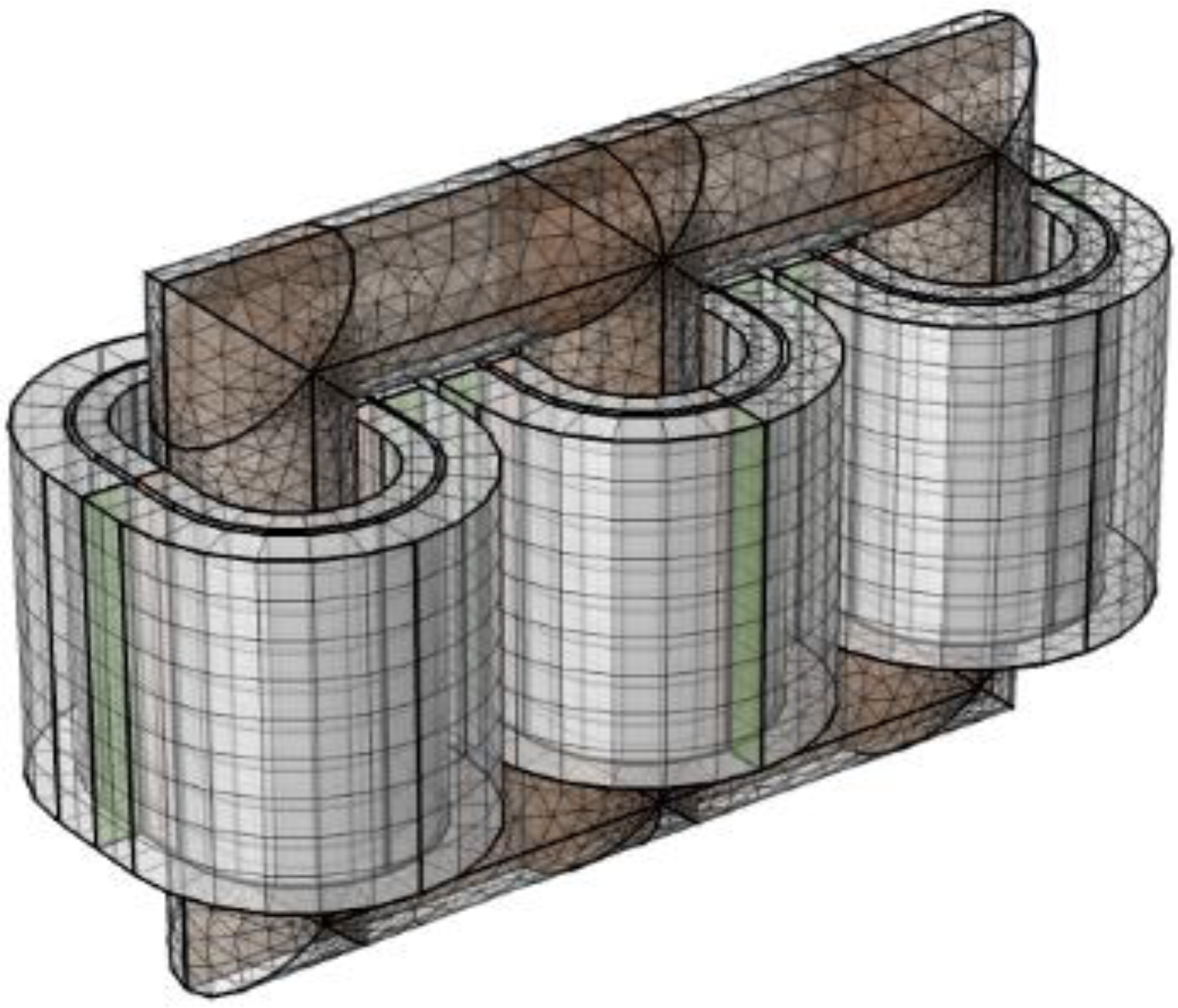
2.2. Development of the Three-Dimensional Model of the Oil-Immersed Transformer
- (1)
- The air gap between the laminated silicon steel sheets of the transformer core is minimal, and core vibration primarily arises from the magnetostrictive action. Consequently, the core is seen as a singular entity, and the interdependence among the silicon steel sheets is disregarded. Simultaneously, to more effectively simulate and analyze the comprehensive dynamic response of the transformer under harmonic stimulation, the HV and LV windings are each represented as a singular entity. The size of the core and the winding correspond accurately to the actual measurements of the transformer.
- (2)
- Structures including clamping pieces, cushion blocks, and cooling devices are excluded. Fixed constraints are applied to the iron core and windings to simulate the fixing effects of the clamping pieces and buffer components on the iron core and windings.
3. Simulation Analysis of Transformer Vibration Characteristics Under Harmonic Currents
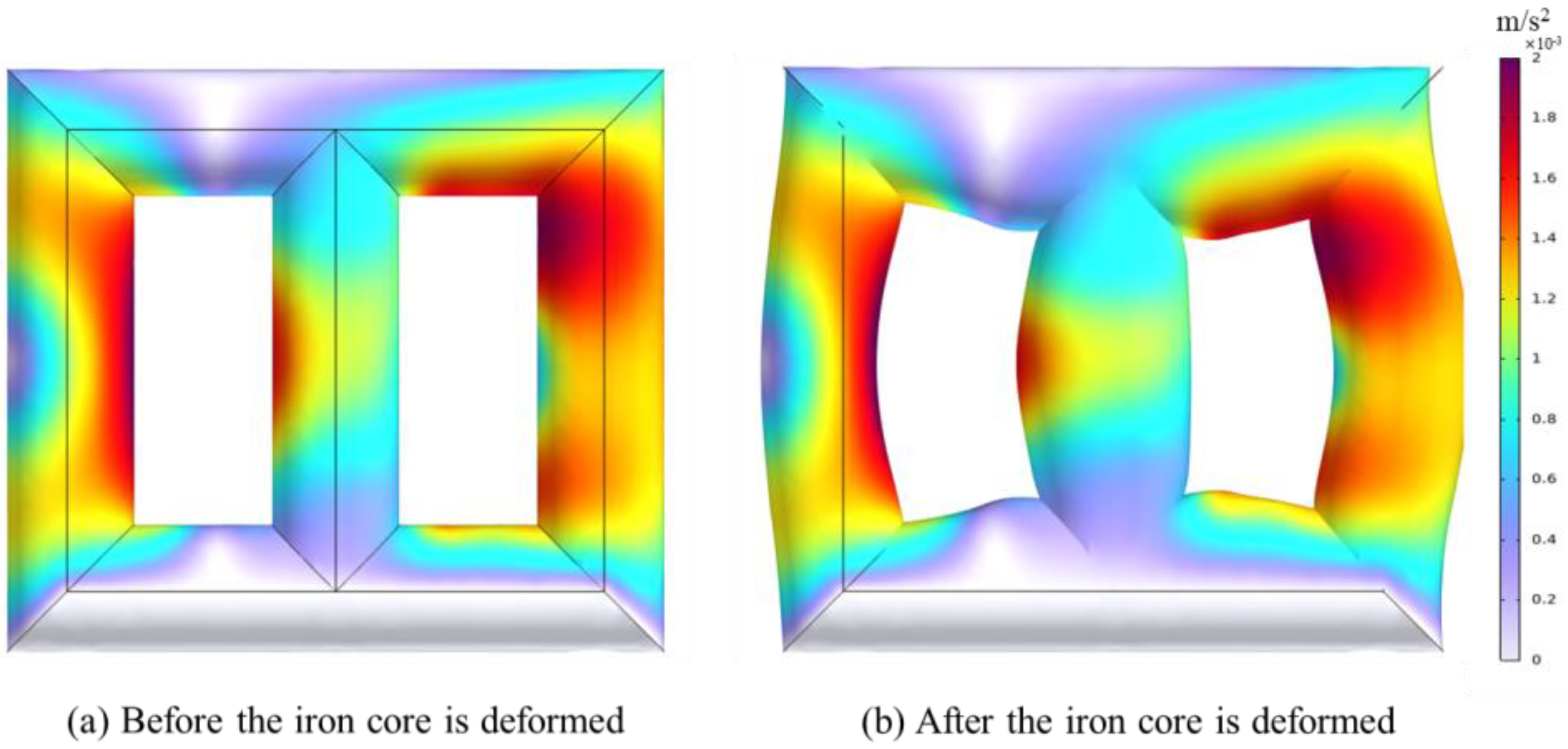
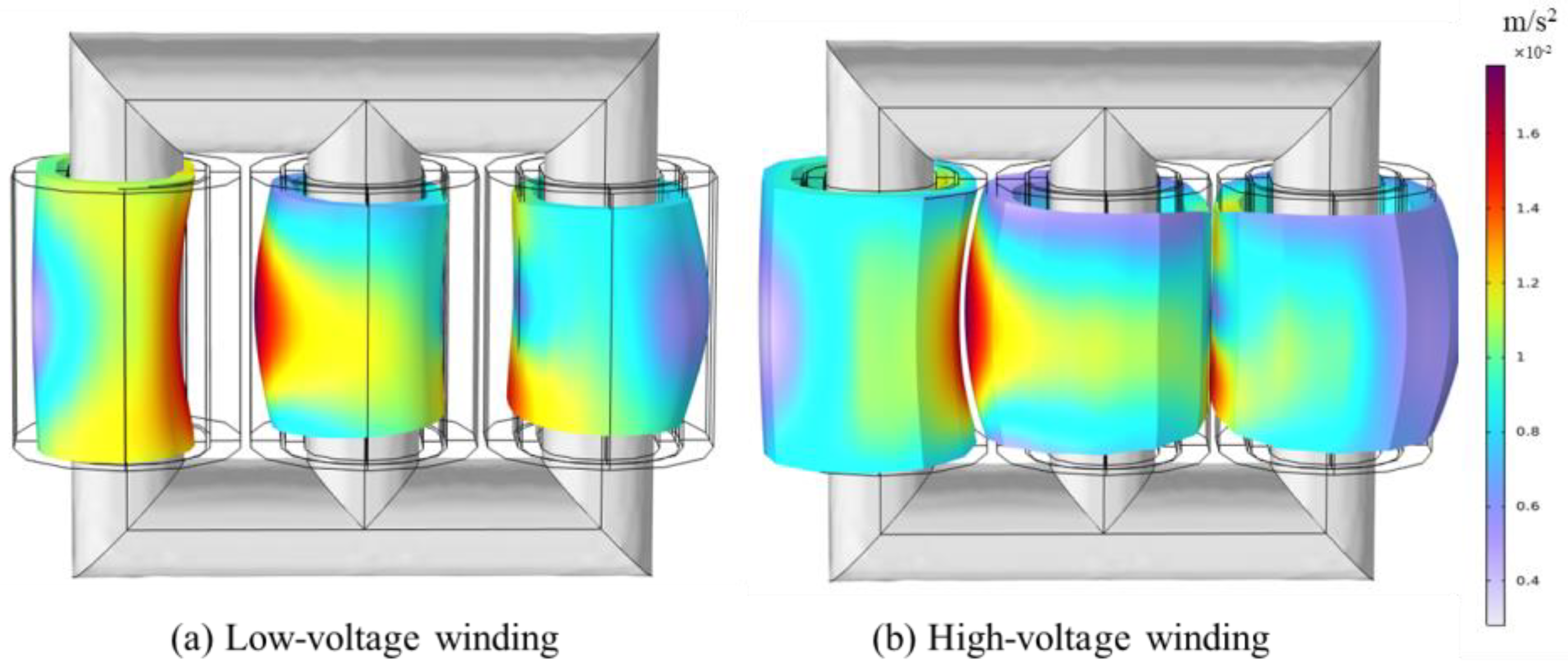
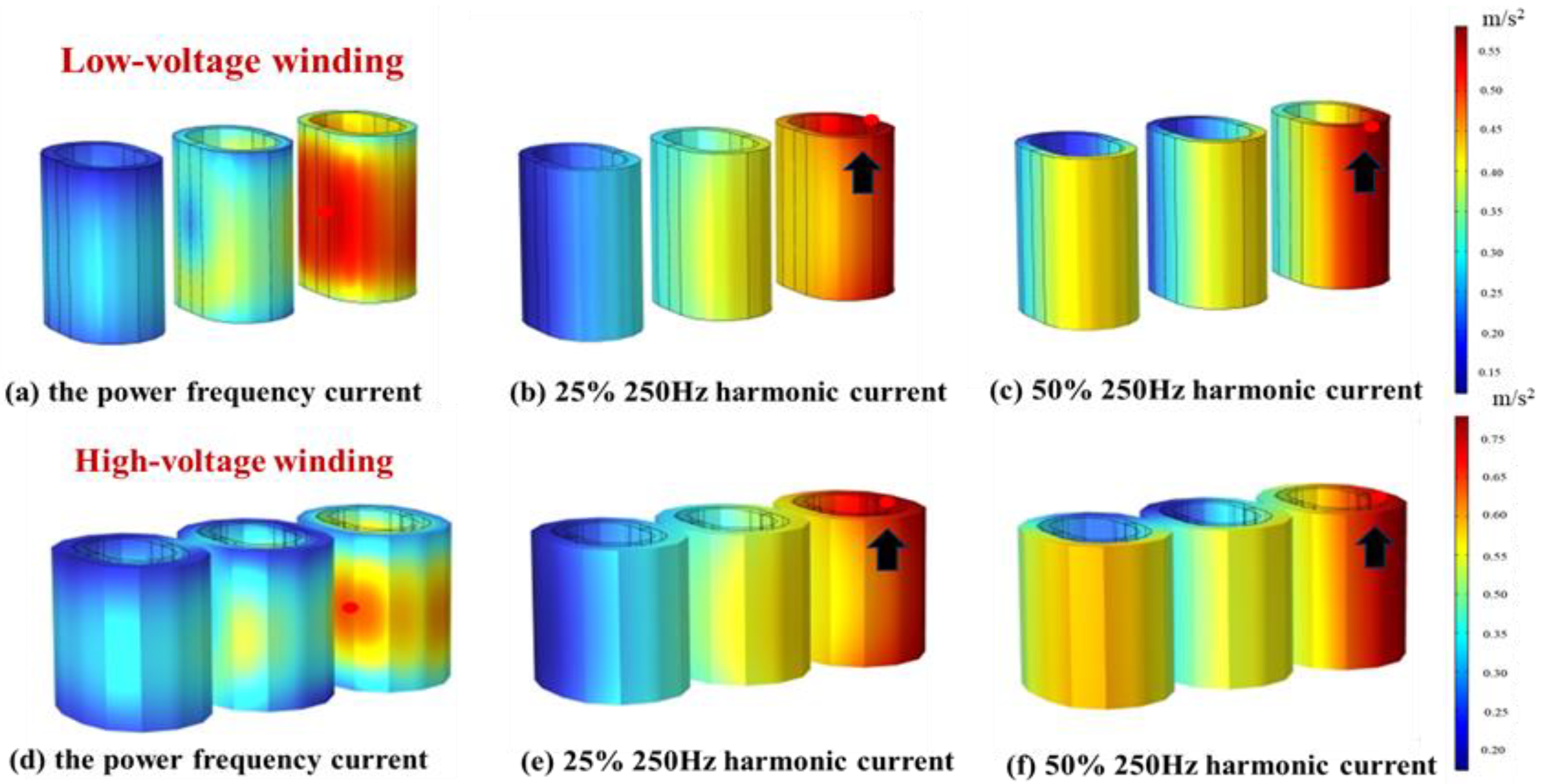
3.1. Analysis of Transformer Vibration Characteristics Under Power Frequency Current
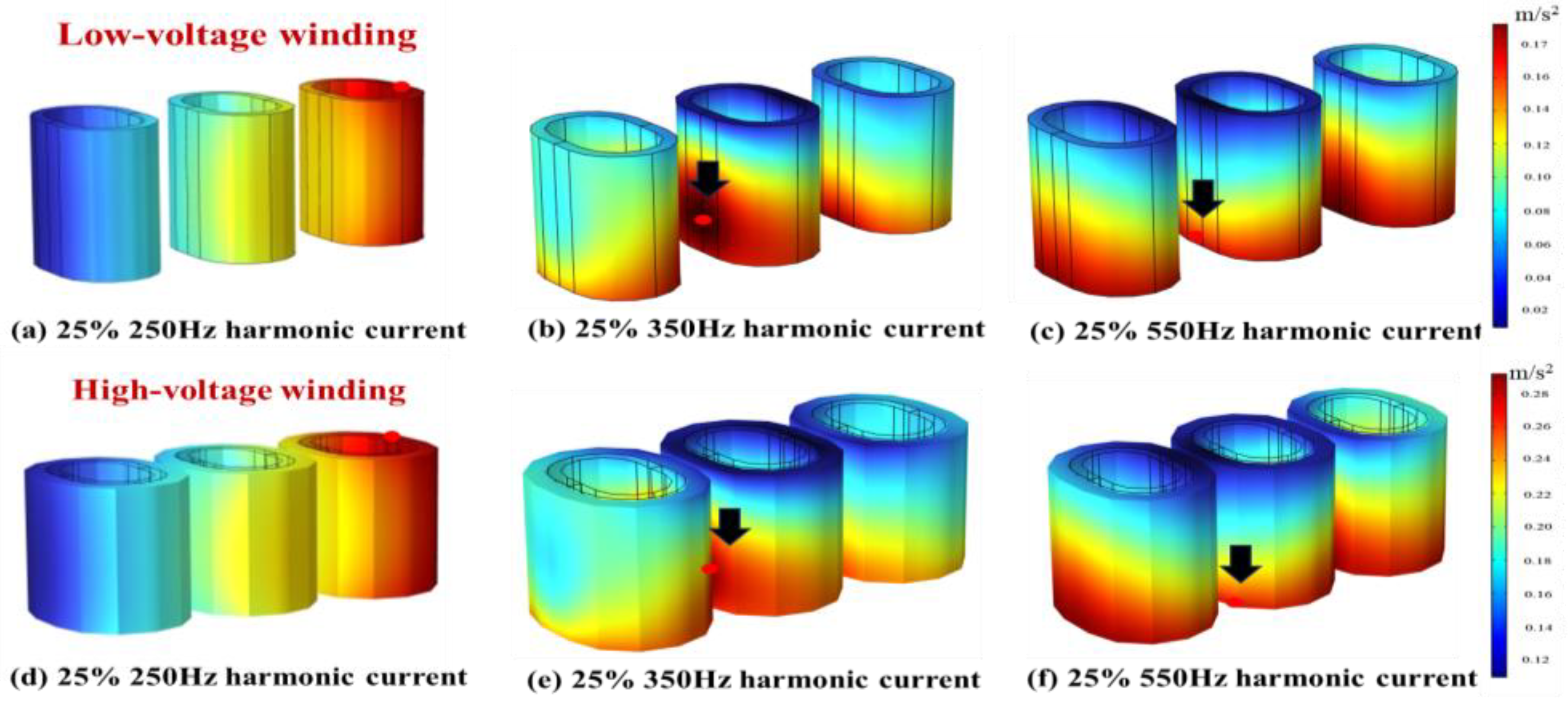
3.2. Analysis of Transformer Vibration Characteristics Under Different Harmonic Currents
4. Experimental Design and Validation
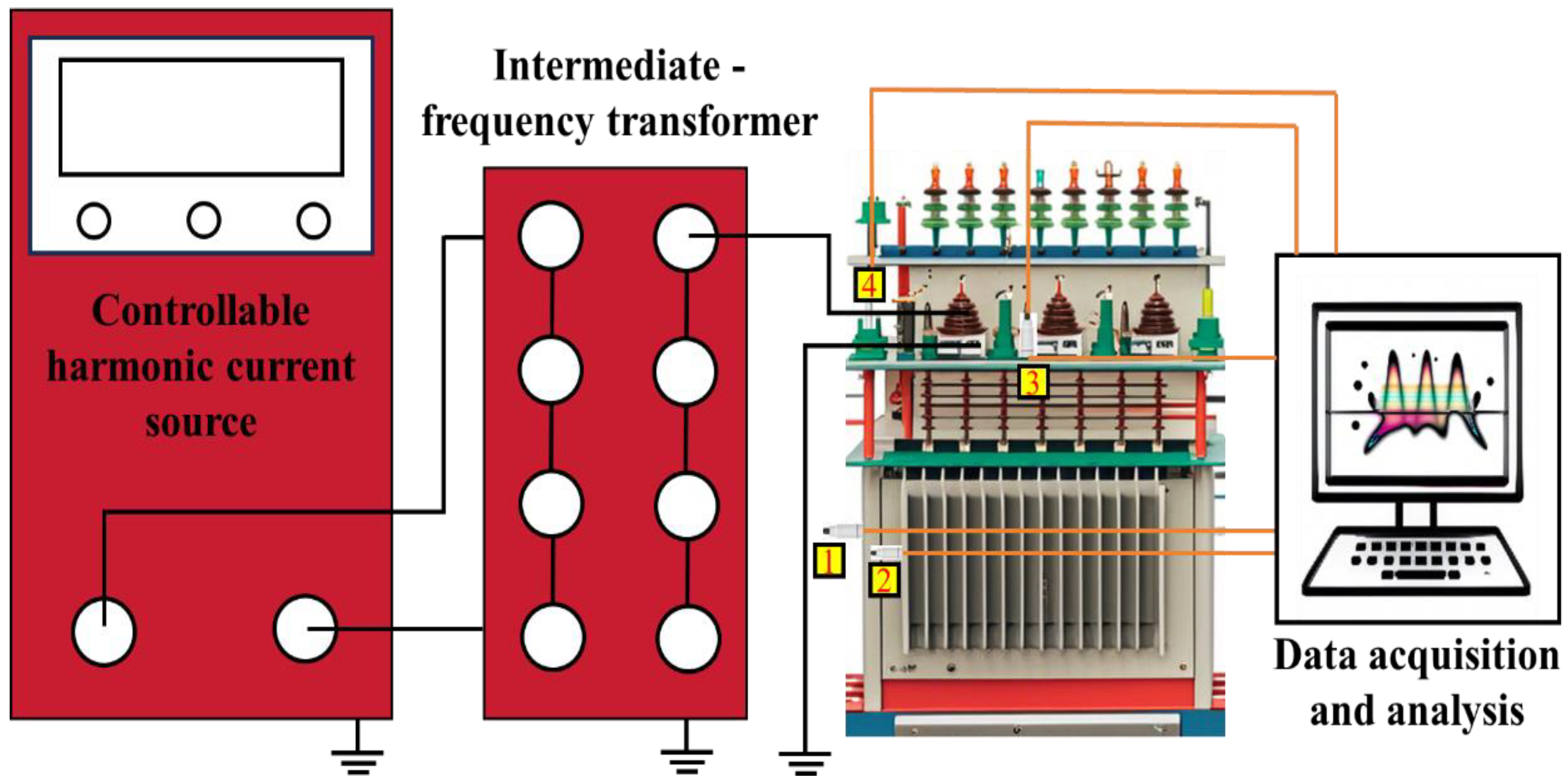
4.1. Vibration Testing Platform for the Oil-Immersed Transformer
4.2. Comparative Analysis Between Simulation and Experimentation
5. Analysis of the Characteristic Parameters of Transformer Vibration Under Harmonic Currents
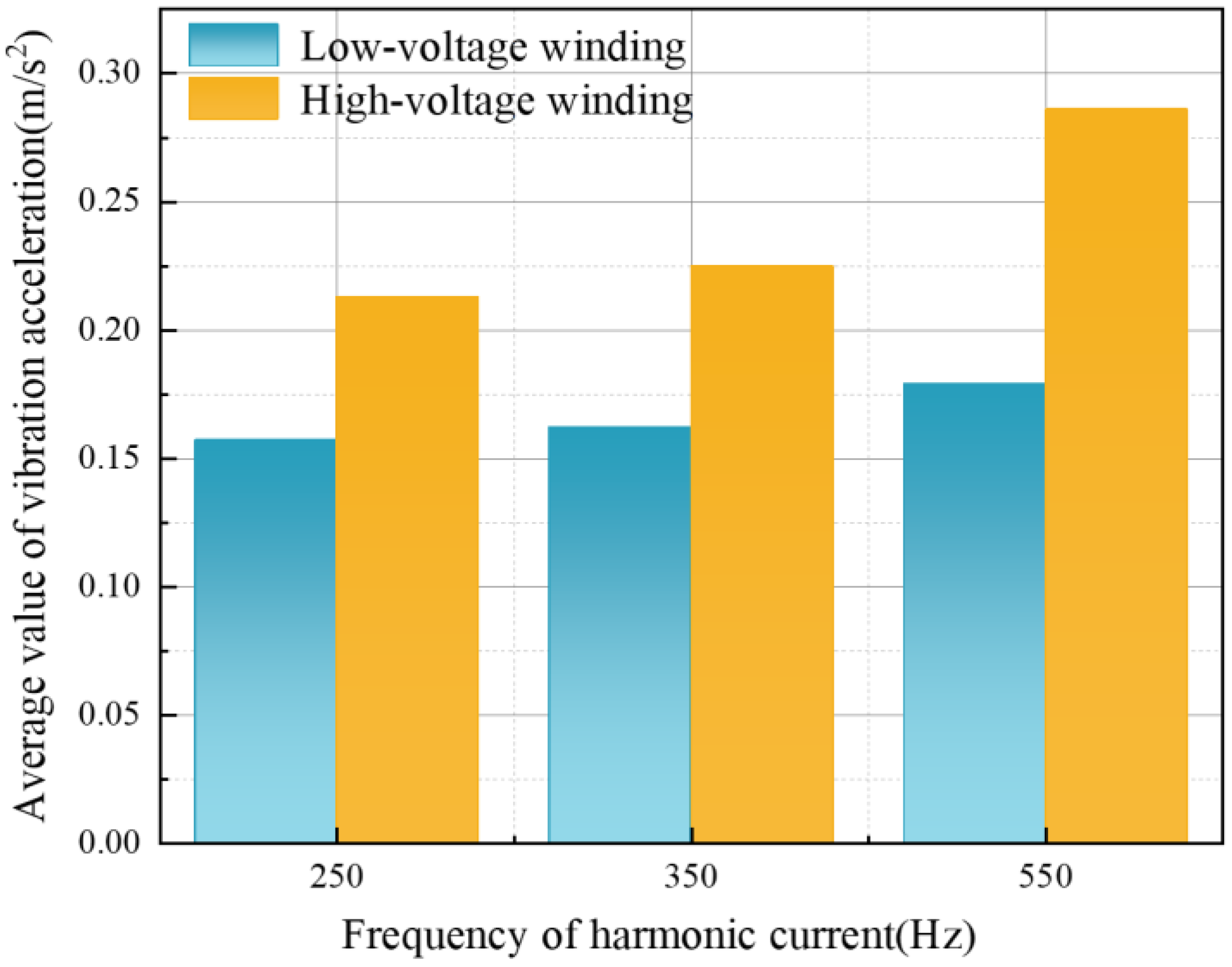
5.1. Analysis of Transformer Vibration Properties at Various Harmonic Current Frequencies
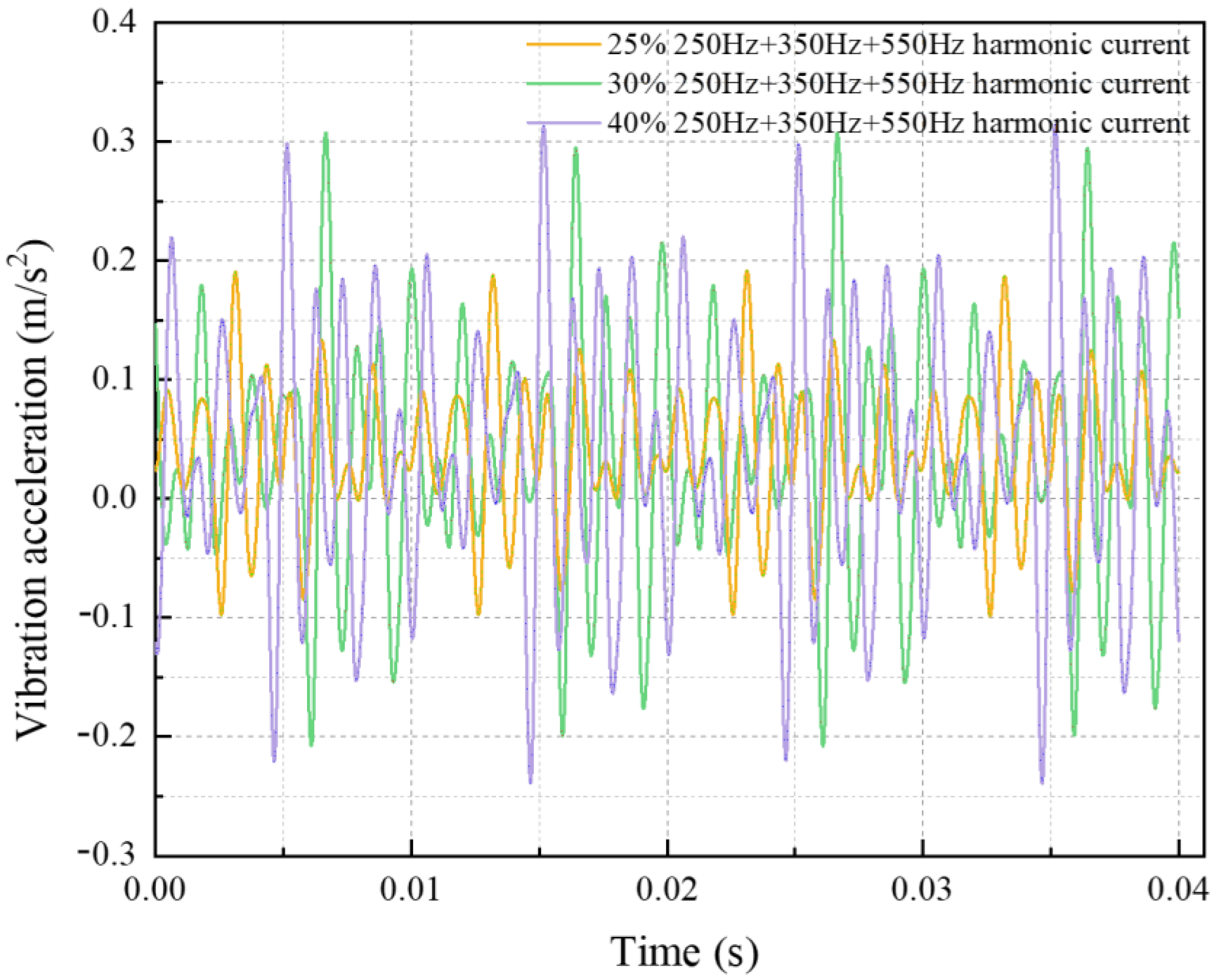
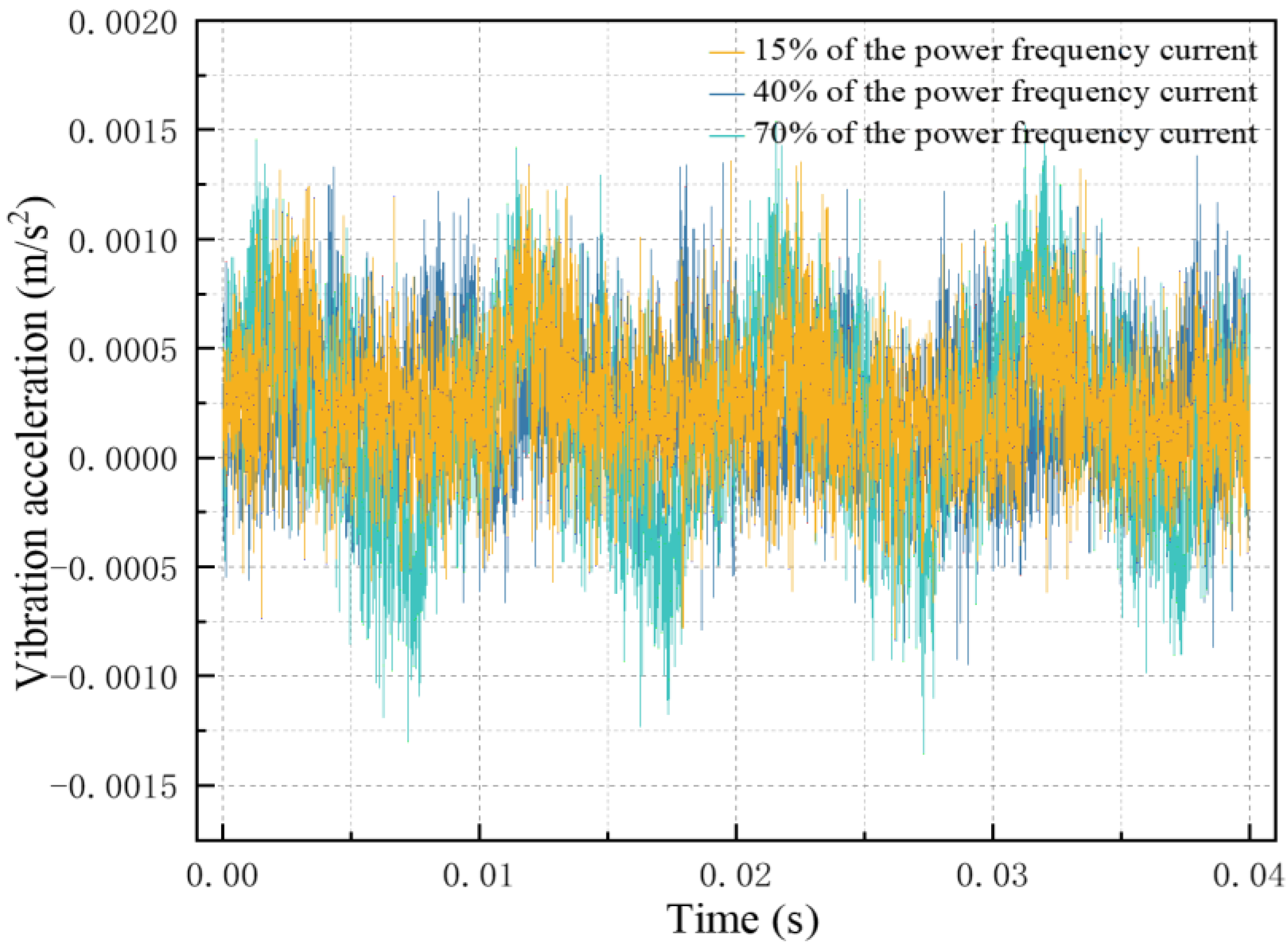
5.2. Analysis of Transformer Vibration Characteristics Under Different Harmonic Current Contents
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Alawasa, K.M.; Al-Badi, A.H. Investigation and Analysis of the Power Quality in an Academic Institution’s Electrical Distribution System. Energies 2024, 17, 3998. [Google Scholar] [CrossRef]
- Arranz-Gimon, A.; Zorita-Lamadrid, A.; Morinigo-Sotelo, D.; Duque-Perez, O. A review of total harmonic distortion factors for the measurement of harmonic and interharmonic pollution in modern power systems. Energies 2021, 14, 6467. [Google Scholar] [CrossRef]
- Taghvaie, A.; Warnakulasuriya, T.; Kumar, D.; Zare, F.; Sharma, R.; Vilathgamuwa, D.M. A comprehensive review of harmonic issues and estimation techniques in power system networks based on traditional and artificial intelligence/machine learning. IEEE Access 2023, 11, 31417–31442. [Google Scholar] [CrossRef]
- Qian, M.; Yin, F.; Yuan, Y.; Jiang, P.; Wang, L.; Zhao, L. Vibration characteristics of ± 800 kV converter transformers part I: Under no-load conditions. Int. J. Electr. Power Energy Syst. 2024, 159, 110060. [Google Scholar] [CrossRef]
- Qian, M.; Yin, F.; Yuan, Y.; Jiang, P.; Wang, L.; Zhao, L. Vibration characteristics of ± 800 kV converter transformers part II: Under load conditions. Int. J. Electr. Power Energy Syst. 2024, 159, 110026. [Google Scholar] [CrossRef]
- Liu, C.; Hao, J.; Liao, R.; Yang, F.; Li, W.; Li, Z. High proportion and large value harmonic current influence on the magnetic field, loss and temperature distribution for ultrahigh voltage converter transformer. IET Electr. Power Appl. 2024, 18, 208–225. [Google Scholar] [CrossRef]
- Dao, T.; Phung, B.T. Effects of voltage harmonic on losses and temperature rise in distribution transformers. IET Gener. Transm. Distrib. 2018, 12, 347–354. [Google Scholar] [CrossRef]
- Yaghoobi, J.; Alduraibi, A.; Martin, D.; Zare, F.; Eghbal, D.; Memisevic, R. Impact of high-frequency harmonics (0–9 kHz) generated by grid-connected inverters on distribution transformers. Int. J. Electr. Power Energy Syst. 2020, 122, 106177. [Google Scholar] [CrossRef]
- Kumar, I.; Bakshi, A. Effects of axial sticks and proof stress of conductor material on the buckling strength of transformer inner winding. IEEE Trans. Power Deliv. 2022, 11, 5465–5468. [Google Scholar] [CrossRef]
- Hu, Z.; Han, Y.; Zalhaf, A.S.; Zhou, S.; Zhao, E.; Yang, P. Harmonic sources modeling and characterization in modern power systems: A comprehensive overview. Electr. Power Syst. Res. 2023, 218, 109234. [Google Scholar] [CrossRef]
- Jiang, M.; Sha, Z.; Zhao, Y.; Chen, W.; Zhang, Q.; Wen, T. Strongly Coupled Circuit-Magnetic-Structural Effect on Winding Vibration Process of Power Transformer. IEEJ Trans. Electr. Electron. Eng. 2024, 19, 1147–1155. [Google Scholar] [CrossRef]
- Xu, J.; Hao, J.; Zhang, N.; Liao, R.; Feng, Y.; Liao, W.; Cheng, H. Simulation study on converter transformer windings stress characteristics under harmonic current and temperature rise effect. Int. J. Electr. Power Energy Syst. 2025, 165, 110505. [Google Scholar] [CrossRef]
- Xiong, J.; Luo, Y.; Ren., S.; Lu, S.; Pei, X.; Zha, X.; Zhou, W. Simulation and Experimental Study on Vibration and Noise of Power Transformer Under Load. In Proceedings of the 2023 4th International Symposium on Insulation and Discharge Computation for Power Equipment (IDCOMPU 2023), Wuhan, China, 26–28 May 2023. [Google Scholar] [CrossRef]
- Jiang, P.; Zhang, Z.; Dong, Z.; Yang, Y.; Pan, Z.; Deng, J. Axial and radial electromagnetic-vibration characteristics of converter transformer windings under current harmonics. High Volt. 2023, 8, 477–491. [Google Scholar] [CrossRef]
- Amir Esmaeili, M.; Hamed Nezhad, S. Analysis of Power Transformer Vibration Modes. J. Power Eng. 2024, 10, 45–55. [Google Scholar]
- Anthony, J.; Philip, A.; Teeraphon, P. Localized Surface Vibration and Acoustic Noise Emitted from Laboratory-Scale Transformer Cores Assembled From Grain-Oriented Electrical Steel. IEEE Trans. Magn. 2016, 52, 1–15. [Google Scholar] [CrossRef]
- Jin, M.; Chen, W.; Zhao, Y.; Wen, T.; Wu, J.; Wu, X.; Zhang, Q. Coupled magnetic-structural modeling of power transformer for axial vibration analysis under short-circuit condition. IEEE Trans. Magn. 2022, 58, 1–9. [Google Scholar] [CrossRef]
- Sun, C.; Zhu, L.; Qian, G.; Dai, W.; Hong, Z.; Wang, S.; Xu, J.; Wang, J. Study on the Effect of Harmonic Current on the Vibration Characteristics of Oil-Immersed Transformer. In Proceedings of the 2023 IEEE International Conference on Power Science and Technology (ICPST), Kunming, China, 5–7 May 2023. [Google Scholar] [CrossRef]



| Parameter | Rated Voltage (V) | Phase Current (A) | Number of Coil Turns |
|---|---|---|---|
| LV Winding | 400 | 144.3 | 104 |
| HV Winding | 10000 | 3.3 | 2364 |
| Parameter | Magnetic Permeability (H/m) | Electrical Conductivity (S/m) | Density (kg/m³) | Elastic Modulus (Pa) | Thermal Conductivity (W/(m·K)) | Poisson’s Ratio |
|---|---|---|---|---|---|---|
| Core | 5000 | 2 × 106 | 7500 | 1.8 × 1011 | 45 | 0.24 |
| Winding | / | 5.8 × 107 | 8900 | 1.2 × 1011 | 380 | 0.33 |
| Parameter Name | Value |
|---|---|
| Rated Capacity (kVA) | 240 |
| Rated Input Voltage (V) | 340 |
| Rated Input Current (A) | 705.88 |
| Rated Output Voltage (V) | 12 × 600 |
| Rated Output Current (A) | 12 × 34 |
| Operating Frequency (Hz) | 50–2500 |
| Current Composition | Simulated Value (m/s2) | Increase Amplitude (%) | Test Value (m/s²) | Increase Amplitude (%) | Error (%) |
|---|---|---|---|---|---|
| 75% 50 Hz/25% 350 Hz | 0.589 | / | 0.218 | / | / |
| 75% 50 Hz/25% 550 Hz | 0.653 | 10.87% | 0.239 | 9.63% | 1.24% |
| 75% 50 Hz/25% 250 Hz | 0.664 | 12.73% | 0.256 | 12.8% | 0.07% |
| 60% 50 Hz/40% 250 Hz | 0.805 | 36.67% | 0.298 | 36.7% | 0.03% |
| 50% 50 Hz/50% 250 Hz | 0.902 | 53.14% | 0.334 | 53.2% | 0.06% |
| Feature Name | Calculation Formula | |
|---|---|---|
| Time Domain Feature | Root Mean Square Value | |
| Absolute Average Value | ||
| Peak-to-Peak Value | ||
| Frequency Domain Feature | Mean Frequency | |
| Random Coefficient | ||
| Centroid Frequency |
| 250 Hz | 350 Hz | 550 Hz | |
|---|---|---|---|
| RMS Value | 0.085 | 0.074 | 0.091 |
| Absolute Average Value | 0.072 | 0.057158443 | 0.097 |
| Peak-to-Peak Value | 0.374176 | 0.397119 | 0.498 |
| Mean Frequency | 8.18 × 10−5 | 7.51 × 10−5 | 9.14 × 10−5 |
| Random Coefficient | 1390.010 | 1203.685 | 1204.277 |
| Centroid Frequency | 2422.362 | 2569.912 | 2382.367 |
| 25% | 30% | 35% | 40% | 50% | |
|---|---|---|---|---|---|
| RMS Value | 0.031 | 0.074 | 0.089 | 0.091 | 0.107 |
| Absolute Average Value | 0.023 | 0.056 | 0.068 | 0.070 | 0.082 |
| Peak-to-Peak Value | 0.167 | 0.412 | 0.494 | 0.498 | 0.593 |
| Mean Frequency | 3.81 × 10−7 | 2.18 × 10−6 | 3.16 × 10−6 | 3.31 × 10−6 | 4.6 × 10−6 |
| Random Coefficient | 914.628 | 1091.872 | 1180.066 | 1204.277 | 1244.019 |
| Centroid Frequency | 2152.368 | 2382.367 | 2391.157 | 2586.288 | 4571.565 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zou, D.; Hao, J.; Dai, W.; Qian, G.; Sun, H.; Xu, J. Harmonic Current Effect on Vibration Characteristics of Oil-Immersed Transformers and Their Experimental Verification. Energies 2025, 18, 1673. https://doi.org/10.3390/en18071673
Zou D, Hao J, Dai W, Qian G, Sun H, Xu J. Harmonic Current Effect on Vibration Characteristics of Oil-Immersed Transformers and Their Experimental Verification. Energies. 2025; 18(7):1673. https://doi.org/10.3390/en18071673
Chicago/Turabian StyleZou, Dexu, Jian Hao, Weiju Dai, Guochao Qian, Haoruo Sun, and Jing Xu. 2025. "Harmonic Current Effect on Vibration Characteristics of Oil-Immersed Transformers and Their Experimental Verification" Energies 18, no. 7: 1673. https://doi.org/10.3390/en18071673
APA StyleZou, D., Hao, J., Dai, W., Qian, G., Sun, H., & Xu, J. (2025). Harmonic Current Effect on Vibration Characteristics of Oil-Immersed Transformers and Their Experimental Verification. Energies, 18(7), 1673. https://doi.org/10.3390/en18071673






