Prediction of Transformer Residual Flux Based on J-A Hysteresis Theory
Abstract
1. Introduction
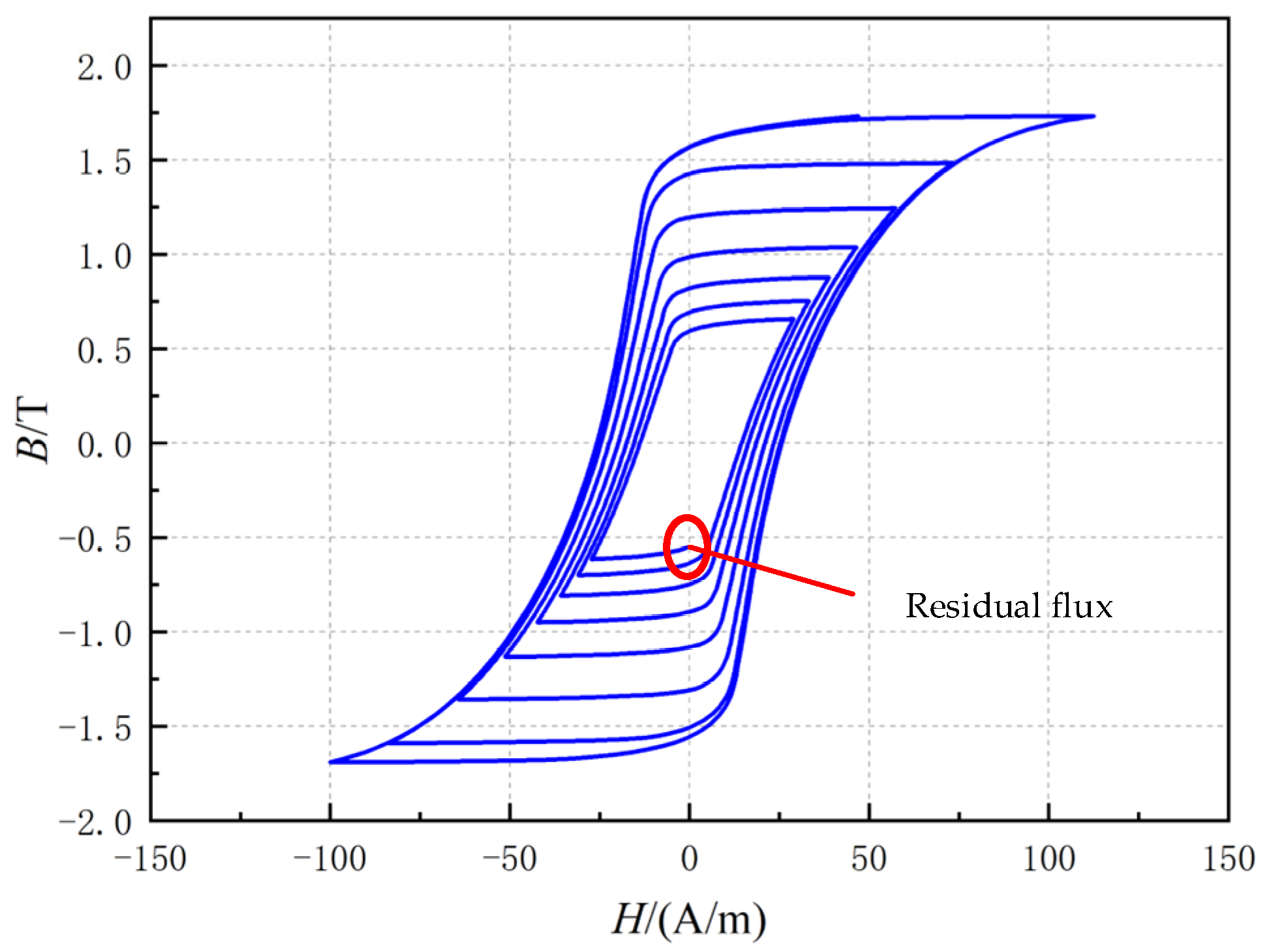
2. J-A Hysteresis Model
3. Parameter Identification Method
3.1. Standard PSO Algorithm
3.2. Improved Algorithm
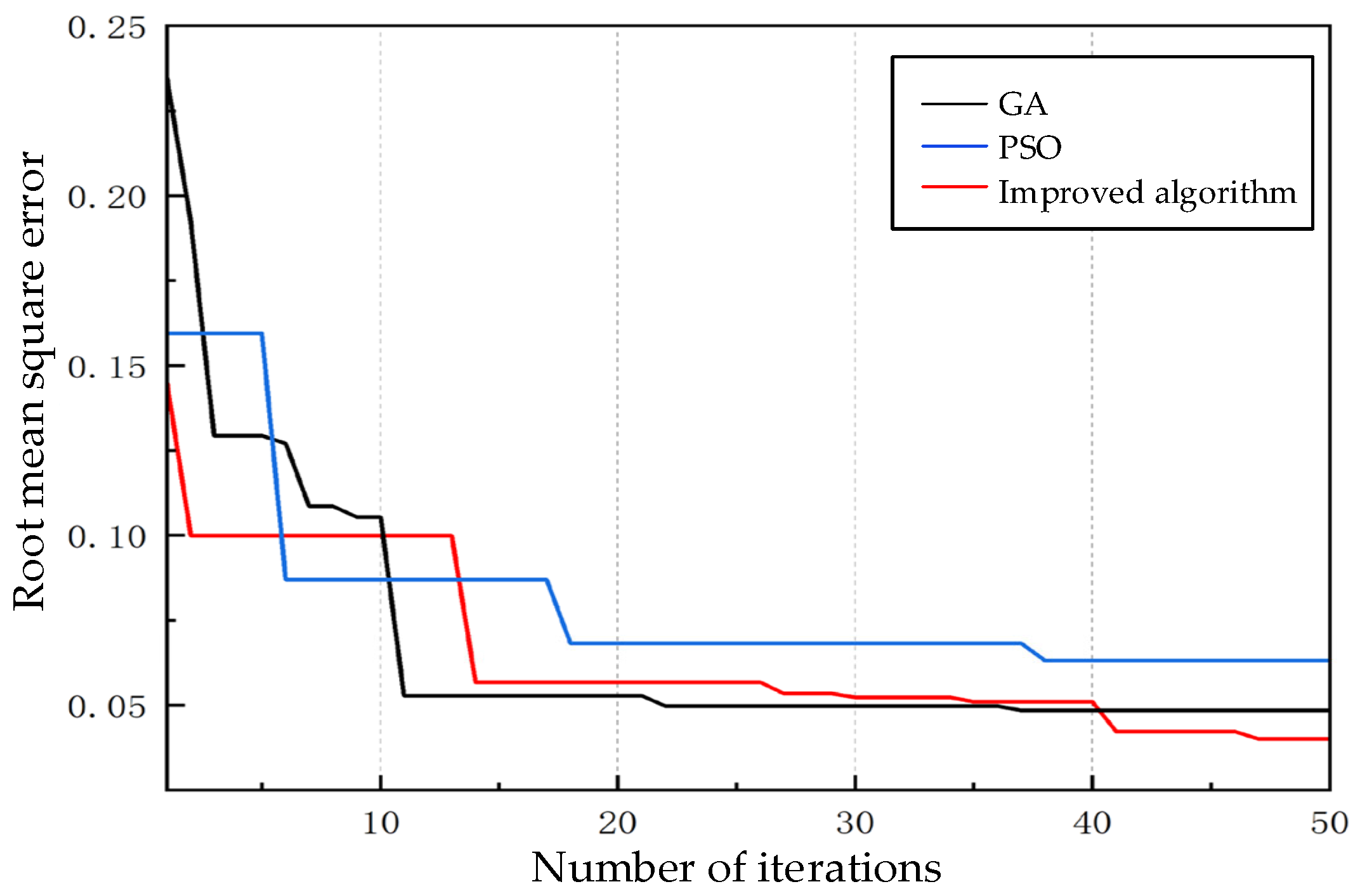
4. Algorithm Feasibility Validation
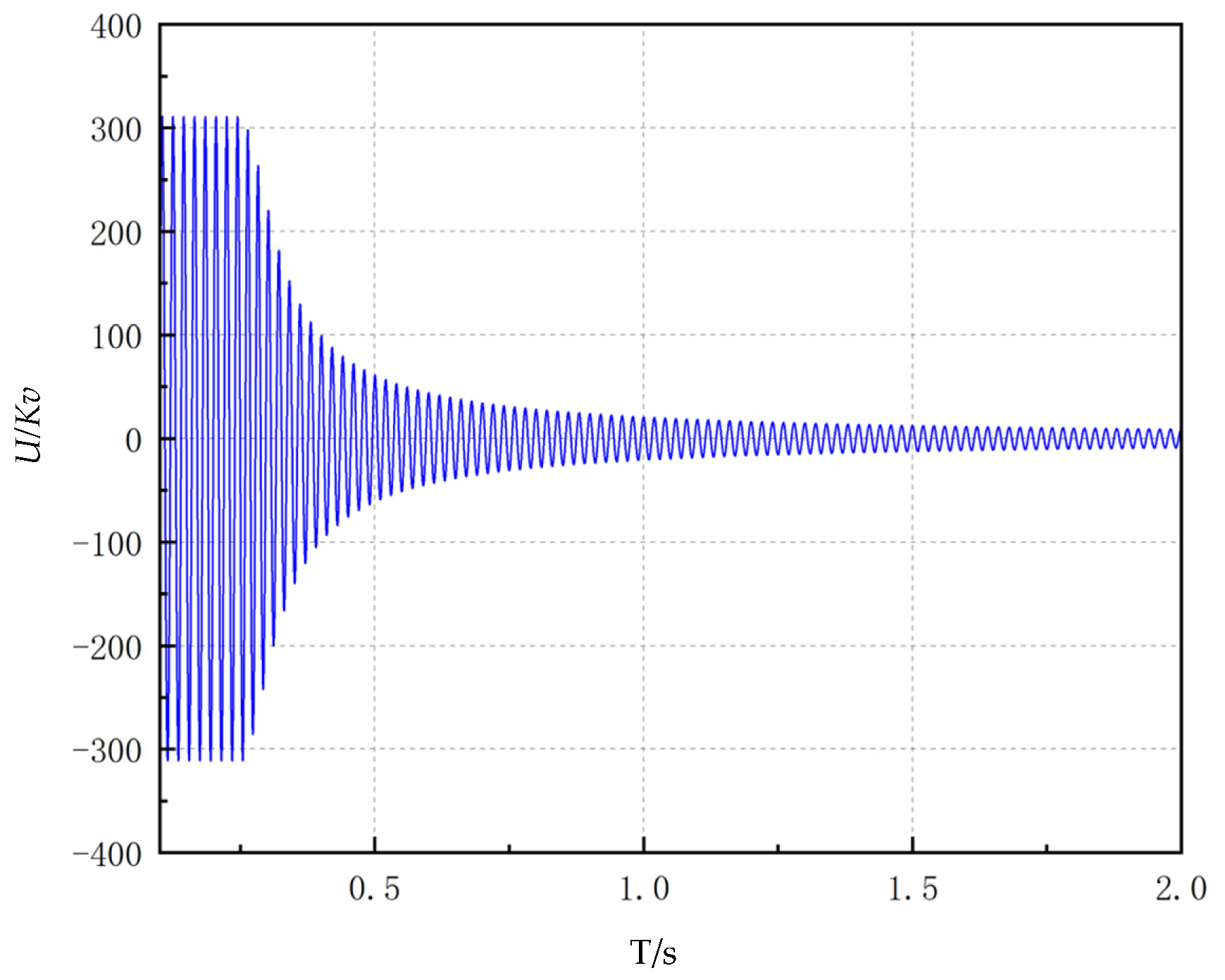
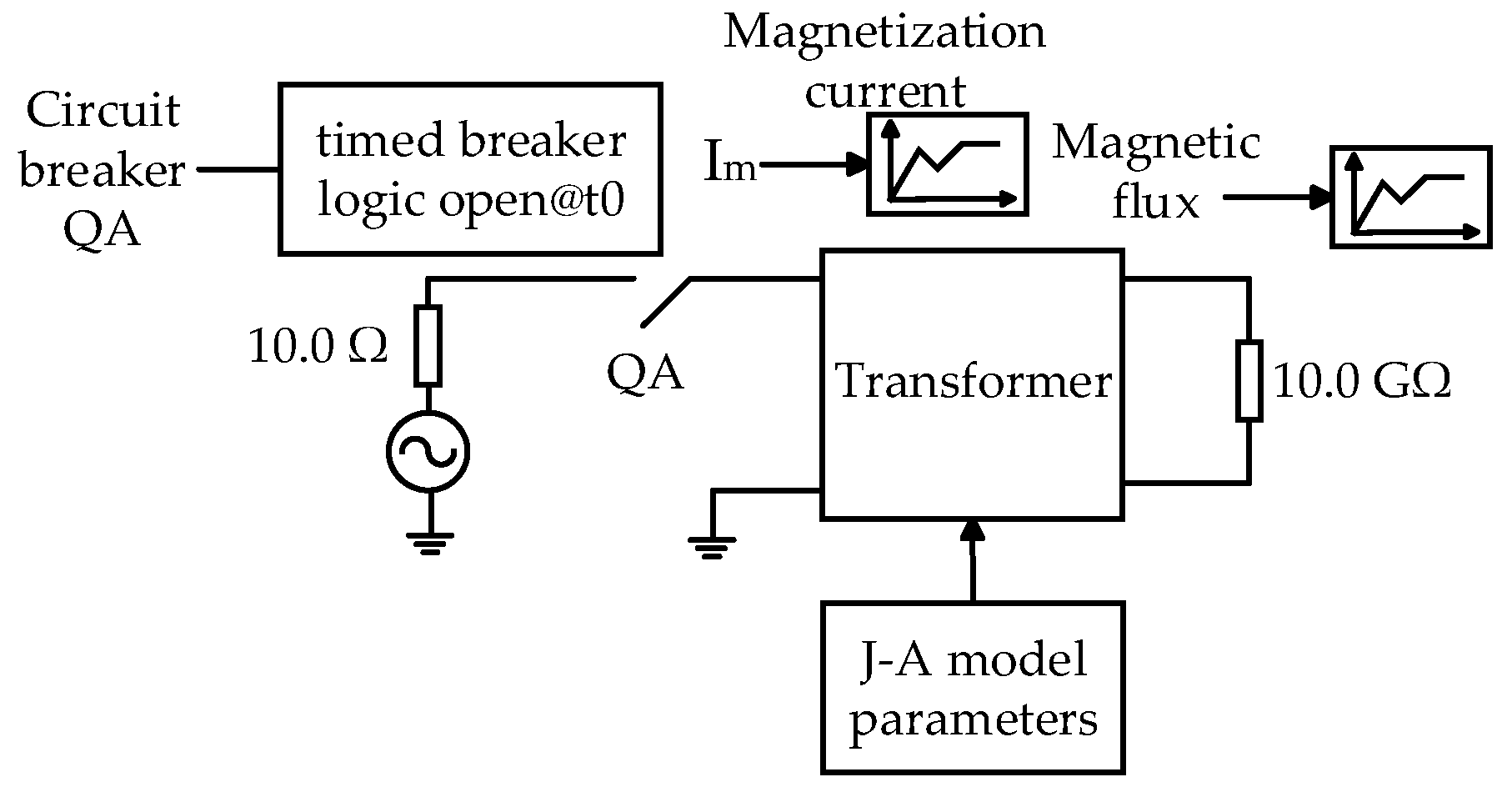
5. Residual Flux Prediction Based on the J-A Model
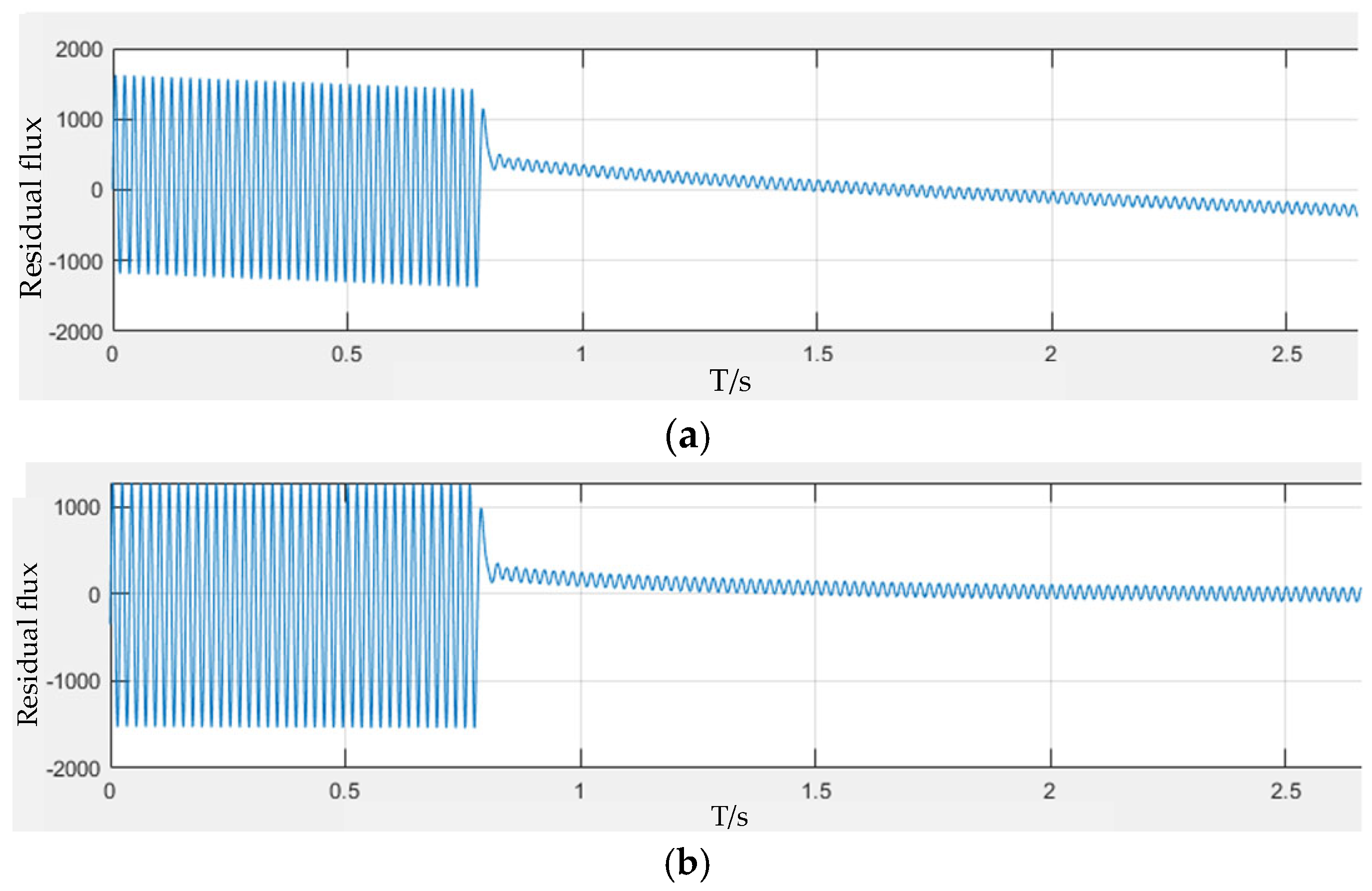
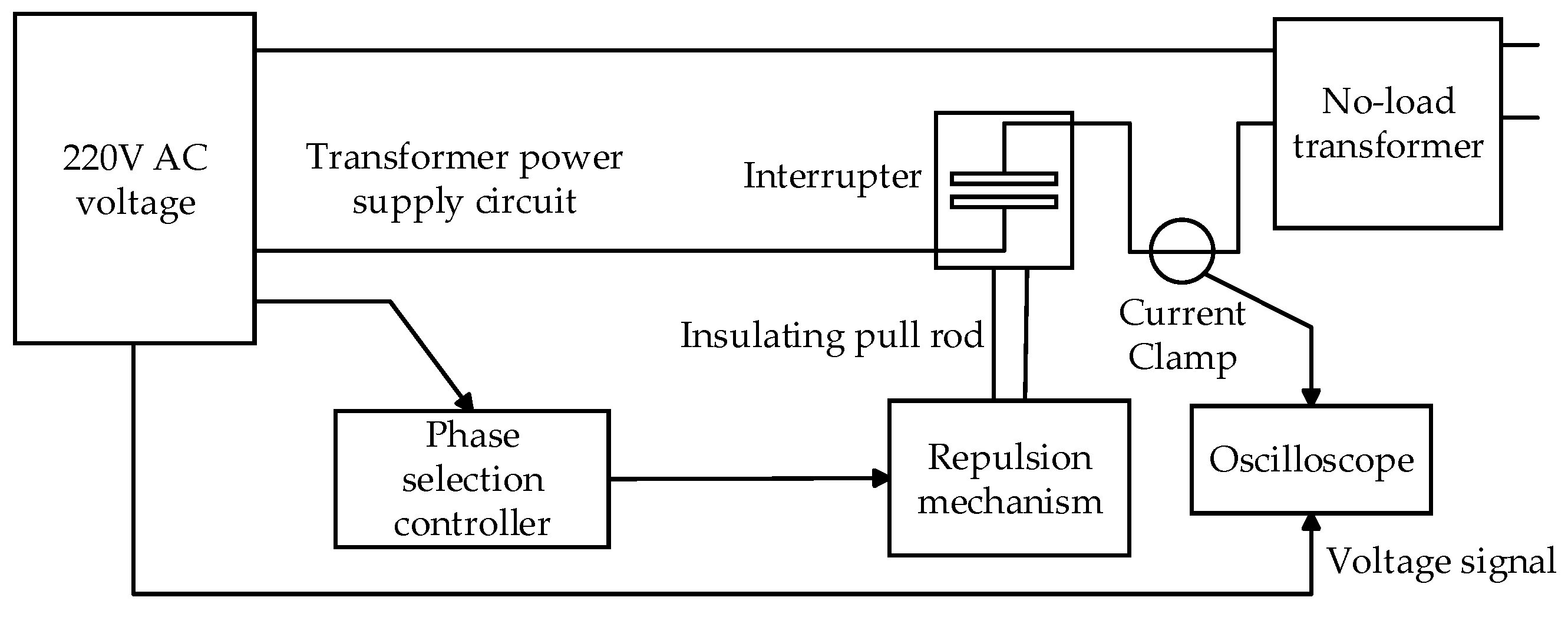
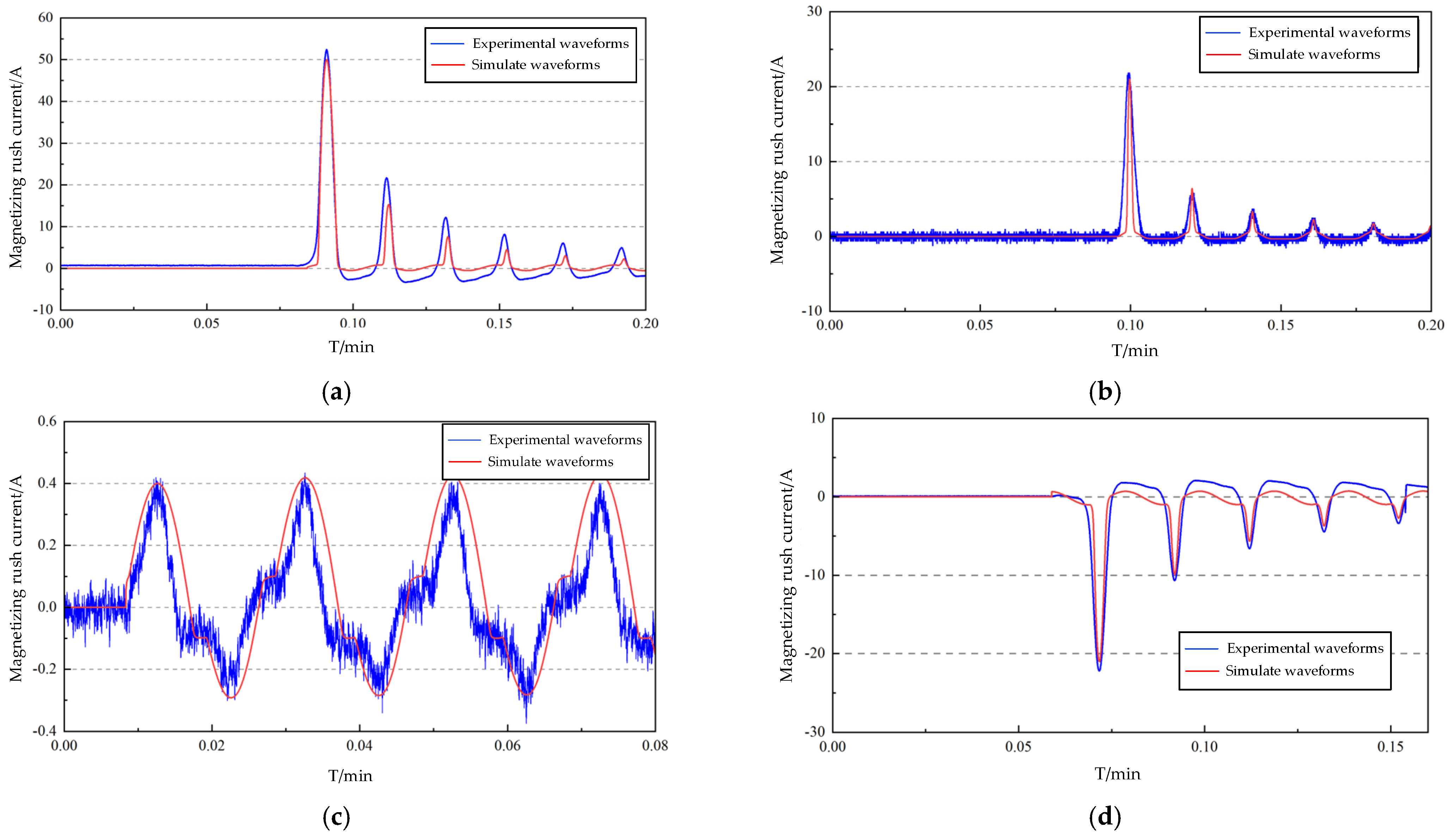
6. Model Simulation and Experimental Validation
7. Conclusions and Future Studies
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Nasution, M.F.; Mustafa, F.; Shaulgara, S. Case studies of magnetizing inrush current effect on differential & REF transformer protection. In Proceedings of the 2019 2nd International Conference on High Voltage Engineering and Power Systems (ICHVEPS), Denpasar, Indonesia, 1–4 October 2019; pp. 1–6. [Google Scholar]
- Zhijiang, L.; Xuehua, L.; ShuYong, L.; Libin, H. Study on the excitation inrush suppression strategy of phase-selective switching converter with closing resis-tor switch considering dispersion. In Proceedings of the 2022 China International Conference on Electricity Distribution (CICED), Changsha, China, 7–8 September 2022; pp. 1280–1285. [Google Scholar]
- Sung, B.C.; Kim, S. Accurate transformer inrush current analysis by controlling closing instant and residual flux. Electr. Power Syst. Res. 2023, 223, 109638. [Google Scholar] [CrossRef]
- Hamilton, R. Analysis of transformer inrush current and comparison of harmonic restraint methods in transformer protection. IEEE Trans. Ind. Appl. 2013, 49, 1890–1899. [Google Scholar] [CrossRef]
- Komarzyniec, G. Calculating the inrush current of superconducting transformers. Energies 2021, 14, 6714. [Google Scholar] [CrossRef]
- Yonezawa, R. Development of a reversible transformer model for the calculation of inrush currents energizing from higher and lower voltage windings. Electr. Eng. Jpn. 2022, 215, e23365. [Google Scholar] [CrossRef]
- Xie, W.; Xiao, F.; Tu, C.; Zheng, Y.; Peng, Z.; Guo, Q. Suppression strategy for the inrush current of a solid-state transformer caused by the reclosing process. Prot. Control Mod. Power Syst. 2023, 8, 53. [Google Scholar] [CrossRef]
- Ge, Y.; Zheng, J.; Ren, X.; Chen, S.; Kong, X.; Wang, C. Preventing maloperation scheme for saturation protection of converter transformers based on waveform prediction of magnetizing inrush current. Electr. Eng. 2024, 1–14. [Google Scholar] [CrossRef]
- Guoying, L.; Qiang, S.; Lingyun, W.; Dingqu, Z.; Feng, P. A hybrid algorithm based on fish swarm and simulated annealing for parameters identification of modified JA model. In Proceedings of the 2017 13th IEEE International Conference on Electronic Measurement & Instruments (ICEMI), Yangzhou, China, 20–22 October 2017; pp. 483–488. [Google Scholar]
- Zhu, X.; Shen, S.; Zhang, G.; Wang, Z. An Improved Method for Parameter Identification of JA Models. In Proceedings of the 2024 7th International Conference on Electronics Technology (ICET), Chengdu, China, 17–20 May 2024; pp. 1151–1155. [Google Scholar]
- Das, S.; Santra, T.; Choudhury, A.B.; Roy, D.; Yamada, S. Transient modeling and performance analysis of a passive magnetic fault current limiter considering JA hysteresis model. Electr. Power Compon. Syst. 2019, 47, 396–405. [Google Scholar] [CrossRef]
- Lu, H.-l.; Wen, X.-s.; Lan, L.; An, Y.-z.; Li, X.-p. A self-adaptive genetic algorithm to estimate JA model parameters considering minor loops. J. Magn. Magn. Mater. 2015, 374, 502–507. [Google Scholar]
- Zhang, D.; Sha, D.; Gao, C.; Liu, X.; Long, H.; Tang, G.; Zhao, Y.; Gao, Y. A Closed-Loop Soft Startup Strategy to Suppress Inrush Current for Full-Bridge Modular Multilevel Converters. IEEE Trans. Power Electron. 2024, 39, 14787–14799. [Google Scholar]
- Key, S.; Son, G.-W.; Nam, S.-R. Deep Learning-Based Algorithm for Internal Fault Detection of Power Transformers during Inrush Current at Distribution Substations. Energies 2024, 17, 963. [Google Scholar] [CrossRef]
- Pham, M.-T.; Zhang, D.; Koh, C.S. Multi-guider and cross-searching approach in multi-objective particle swarm optimization for electromagnetic problems. IEEE Trans. Magn. 2012, 48, 539–542. [Google Scholar] [CrossRef]
- Coelho, L.d.S.; Guerra, F.A.; Leite, J.V. Multiobjective exponential particle swarm optimization approach applied to hysteresis parameters estimation. IEEE Trans. Magn. 2012, 48, 283–286. [Google Scholar] [CrossRef]
- Zhang, Q.; Xie, Z.; Lu, M.; Ji, S.; Liu, D.; Xiao, Z. Optimization of Hydropower Unit Startup Process Based on the Improved Multi-Objective Particle Swarm Optimization Algorithm. Energies 2024, 17, 4473. [Google Scholar] [CrossRef]
- Mohammadpour, H.; Dashti, R.; Shaker, H.R. A new practical approach for discrimination between inrush currents and internal faults in power transformers. Technol. Econ. Smart Grids Sustain. Energy 2020, 5, 5. [Google Scholar]
- Sima, W.; Zou, M.; Yang, M.; Peng, D.; Liu, Y. Saturable reactor hysteresis model based on Jiles–Atherton formulation for ferroresonance studies. Int. J. Electr. Power Energy Syst. 2018, 101, 482–490. [Google Scholar]
- Cardelli, E.; Faba, A.; Tissi, F. Prediction and control of transformer inrush currents. IEEE Trans. Magn. 2015, 51, 1–4. [Google Scholar] [CrossRef]
- Li, C.; Yang, Y.; Li, W.; Li, H. A soft-start-based method for active suppression of magnetizing inrush current in transformers. Electronics 2023, 12, 3114. [Google Scholar] [CrossRef]
- Yu, S.; Li, Y.; Yu, Z.; Wang, X.; Li, P. Calculation of Transformer Reclosing Short Circuit Strength Considering the Influence of Remanent Magnetism. In Proceedings of the 2023 IEEE International Conference on Applied Superconductivity and Electromagnetic Devices (ASEMD), Tianjin, China, 27–29 October 2023; pp. 1–2. [Google Scholar]
- Łukaniszyn, M.; Majka, Ł.; Baron, B.; Kulesz, B.; Tomczewski, K.; Wróbel, K. Measurement Verification of a Developed Strategy of Inrush Current Reduction for a Non-Loaded Three-Phase Dy Transformer. Energies 2024, 17, 5368. [Google Scholar] [CrossRef]
- Zhou, P.; Xiang, Z.; Wang, D.; Ban, L.; Ding, L.; Wei, W. Methods for Obtaining Excitation Curves and Residual flux of Transformers by De-energizing and Energizing Test. In Proceedings of the 2019 IEEE 3rd International Electrical and Energy Conference (CIEEC), Beijing, China, 7–9 September 2019; pp. 716–720. [Google Scholar]
- Gbadega, P.A.; Saha, A.K. Impact of incorporating disturbance prediction on the performance of energy management systems in micro-grid. IEEE Access 2020, 8, 162855–162879. [Google Scholar] [CrossRef]
- García, D.; Herrera, M.; Camacho, O. A Comparative Evaluation of Metaheuristic Optimization Methods for Control Applications. In Proceedings of the 2023 IEEE Seventh Ecuador Technical Chapters Meeting (ECTM), Ambato, Ecuador, 10–13 October 2023; pp. 1–6. [Google Scholar]




| Parameters | Residual Flux | Coercivity | Coercivity Susceptibility | Hysteresis Loop Area | Maximum Magnetization |
|---|---|---|---|---|---|
| Ms increase | Increase | Remain | Increase | Remain | Increase |
| α increase | Increase | Remain | Increase | Remain | Remain |
| a increase | Decrease | Remain | Decrease | Remain | Remain |
| k increase | Increase | Increase | Remain | Increase | Remain |
| c increase | Decrease | Decrease | Remain | Decrease | Remain |
| Algorithm | k | α | a | Ms | c |
|---|---|---|---|---|---|
| Theoretical Value | 50 | 8 × 10−5 | 30 | 1.53 × 106 | 0.7 |
| GA | 69.6979 | 5.208 × 10−5 | 13.992 | 1.485 × 106 | 0.561 |
| PSO | 66.593 | 1 × 10−4 | 46.767 | 1.586 × 106 | 0.513 |
| Improved Algorithm | 54.765 | 9.422 × 10−5 | 35.473 | 1.576 × 106 | 0.622 |
| Parameter | Numerical Value |
|---|---|
| Rated capacity (VA) | 200 |
| Input/Output voltage root mean square (V) | 200/160 |
| Copper loss (p.u.) | 0.5 |
| Operating frequency (HZ) | 50 |
| Eddy-current loss (p.u.) | 0.03 |
| Leakage reactance (p.u.) | 0.1 |
| Exciting Inrush Current Peak | 30° | 60° | 90° | 120° |
|---|---|---|---|---|
| Simulation results (A) | 50.006 | 20.961 | 0.400 | −20.972 |
| Experimental results (A) | 52.422 | 21.818 | 0.420 | −22.183 |
| Relative error (%) | 4.8 | 3.9 | 4.8 | 5.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Long, Q.; Yang, X.; Jiang, K.; Zhang, C.; Hou, M.; Xin, Y.; Xiong, D.; Duan, X. Prediction of Transformer Residual Flux Based on J-A Hysteresis Theory. Energies 2025, 18, 1631. https://doi.org/10.3390/en18071631
Long Q, Yang X, Jiang K, Zhang C, Hou M, Xin Y, Xiong D, Duan X. Prediction of Transformer Residual Flux Based on J-A Hysteresis Theory. Energies. 2025; 18(7):1631. https://doi.org/10.3390/en18071631
Chicago/Turabian StyleLong, Qi, Xu Yang, Keru Jiang, Changhong Zhang, Mingchun Hou, Yu Xin, Dehua Xiong, and Xiongying Duan. 2025. "Prediction of Transformer Residual Flux Based on J-A Hysteresis Theory" Energies 18, no. 7: 1631. https://doi.org/10.3390/en18071631
APA StyleLong, Q., Yang, X., Jiang, K., Zhang, C., Hou, M., Xin, Y., Xiong, D., & Duan, X. (2025). Prediction of Transformer Residual Flux Based on J-A Hysteresis Theory. Energies, 18(7), 1631. https://doi.org/10.3390/en18071631





