Effect of Air Pressure on the Aging and Lifetime of Electrical Insulation in Winding Wires

Abstract

This paper presents the issues related to aging studies of electrical insulation in winding wires, which are widely used in electrical machines. Insulating materials in electrical machines are subjected to various stress factors, particularly electrical stress. The proper design of such insulation systems requires an understanding of the behavior of individual system components under specific operating conditions. This knowledge enables the optimization of insulation design, which can contribute to extending the operational lifespan of electrical machines. In this study, the results of experimental investigations on twisted-pair winding wires with different geometric dimensions, subjected to electrical stress (a square voltage waveform in the kilohertz frequency range) under different pressure conditions, are presented. The experimental research is supplemented by simulation-based calculations of the electric field intensity in the examined twisted-pair winding wire samples.

1. Introduction

Insulating materials used in electrical machines undergo aging processes due to various operational stresses. These include electrical stress, caused by the electric field, and thermal stress, resulting from heating due to operating current. Environmental stress comes from contaminants and chemicals, while mechanical stress is caused by centrifugal forces, mechanical shocks, and dynamic forces from short-circuit currents. One of the critical electrical factors affecting the durability of insulation systems is the development of modern motor power supply methods using inverters. Pulse–width modulation (PWM) waveforms generated by inverters, depending on the type of electronic switches used, exhibit rise times in the range of tens of nanoseconds and switching frequencies reaching several tens of kilohertz. Although this technology offers numerous advantages, it also increases electrical stress [1], which can negatively affect the operational lifespan of insulation systems in inverter-fed machines [2]. An essential aspect, both from a safety perspective and in terms of insulation durability, is the influence of air pressure on the initiation and occurrence of partial discharges (PDs) within the insulation systems of electric machines. This factor is particularly significant when electric motors powered by inverters are used in aviation applications. In the aerospace sector, where aircraft operate at high altitudes under significantly reduced pressure conditions (e.g., at 10–11 km [3], where air pressure is around 0.3 bar [4]), this becomes a crucial consideration in the design of insulation systems. Lower air pressure increases the likelihood of PD initiation [5]. Experimental and simulation studies are currently being conducted to evaluate the impact of operational stress on the degradation mechanisms and aging processes of insulation systems [2,3,6,7,8,9,10,11].

At the design stage, it is very important to consider the previously discussed stresses and their impact on the aging processes of insulation systems. In power engineering applications, the key stress factor is the electric field. The operational electric field intensity, $E_R$, can reach significant values, particularly in the insulation systems of power cables. For instance, in power cables utilizing polymeric insulation, the working field intensity at the conductor surface typically ranges from 2 ÷ 6 kV/mm [12]. Even higher values of $E_R$, reaching up to $14\mathrm{kV}/\mathrm{mm}$, are encountered in high-voltage cables [12]. This imposes demanding requirements on the insulating materials used in such designs. The primary function of an insulation system is to endure these stresses throughout the entire operational lifespan, as they are intrinsic to the device’s operation. Therefore, it is essential to anticipate these stresses during the design phase. Selecting appropriate materials and technologies will help ensure the reliability and longevity of insulation systems over many years of operation.

This study presents the results of experimental investigations on twisted pairs of stranded wires with varying geometric dimensions and different insulation thicknesses, which are essential for determining the lifetime of the samples. The samples were subjected to square-wave voltages in the kilohertz frequency range under different pressure conditions.

2. Aging Studies

One of the methods that can be used to investigate the durability of insulation systems under operational stress factors is aging testing. These tests involve subjecting the insulation system to conditions of increased intensity, such as increased electric field strength, higher temperature [13], etc. In aging studies of insulation systems or models thereof, two approaches are used:

• Investigation of the time it takes for the insulation system to fail under a constant but increased electric field intensity (compared to the operational field strength).
• Testing the dielectric breakdown voltage of the sample, which fails as a result of exceeding the dielectric strength of the insulation material (determination of the breakdown voltage).

In both of the above approaches, it is necessary to apply appropriate statistical analysis to the test results. It has been observed that the probability statistical analysis describing the failure of electrical insulation does not follow a normal distribution. In [14,15], the Weibull distribution is recommended [16], as it best describes the aging phenomena of insulation. As a result of efforts by the IEEE, the IEEE 930-2004 standard was created and later adopted as IEC-62539 [17]. This standard describes the methodology for determining the parameters of the Weibull distribution. The standard strictly concerns aging tests of insulation systems. The methodology described in the IEC-62539 [17] standard, which focuses on testing electrical strength, can also be applied to other fields of engineering, such as mechanical strength, material aging, and fatigue resistance.

3. Statistical Analysis of the Test Results

For statistical analysis in aging studies of winding wire insulation samples, a two-parameter Weibull distribution, as described by Equation (1), is used, in accordance with the recommendations of the standard given in [14,17]:

$$P\left(x\right)=1-exp\left[-{\left({\displaystyle \frac{x}{\alpha }}\right)}^{\beta }\right]$$

(1)

where x is the time to breakdown of the sample (the samples are subjected to increased exposure to an electric field), $P\left(x\right)$ is the probability of sample failure, $\alpha$ is the scale parameter (always positive), and $\beta$ is the shape parameter (always positive) [17]. The scale parameter $\alpha$ has the same dimension as the variable x. For the purposes of this study, x is measured in units of time. In the Weibull distribution, the scale parameter $\alpha$ defines the time at which the probability of sample failure is 0.632 (this corresponds to the value of $1-1/e$). By analogy, the scale parameter $\alpha$ of the Weibull distribution is the counterpart of the mean value in the normal distribution. The parameter $\alpha$ is called the lifetime or characteristic time, which means that 62.3% of the samples should not fail by this time. The shape parameter $\beta$ is a measure of spread of the breakdown times, and it is the counterpart of the inverse of the standard deviation for the normal distribution. A larger value of $\beta$ corresponds to a narrower distribution of the measurement results.

In aging studies of insulation samples, censored data are encountered, meaning that there is a certain time limit for the experiment, beyond which the last sample fails and no further results can be obtained. The process of fitting distributions can be problematic due to the limited number of samples in aging experiments, leading to insufficient statistical power. Aging tests sometimes take a long time, and the number of results is insufficient (at most a few dozen samples). Various methods have been developed in the literature to fit Weibull distributions to datasets with limited sample sizes. The White method, recommended by the standard given in [17], is considered to provide the best results. This method never yields poor results [14], and typically performs better than other methods (along with the maximum likelihood method and the least squares linear regression method). The White method is an extension of the least squares linear regression method, incorporating weighting factors. A more detailed description of this method can be found in the papers by White [18] and Montanari [14,15], as well as in the IEC 62539 standard [17].

4. Research Methodology

The study examined winding samples of electrical machines manufactured in accordance with the recommendations of the standard [19]. Model samples of the random wire machine’s insulation system [20] were prepared in the form of a twisted pair (TP) configuration, according to standard [21]. The samples were twisted using winding wires with conductor diameters of 0.5 mm, 0.8 mm, and 1.0 mm, with the number of twists specified in [21], amounting to 12, 10, and 8 twists, respectively.

The requirements of the standard given in [19] regarding the geometric dimensions of the winding wires are presented in

Table 1. Requirements of PN-EN 60317-13:2010 [19] standard regarding geometrical dimensions of Grade 1 winding wires used in aging tests.

${\mathit{d}}_{\mathit{n}}$ [mm]	$\mathbf{\Delta }{\mathit{d}}_{\mathit{min}}$ [mm]	${\mathit{d}}_{\mathit{max}}$ [mm]	a [mm]
0.5	0.024	0.544	0.0200
0.8	0.030	0.855	0.0232
1.0	0.034	1.062	0.0178

, where $d_n$ is the nominal diameter of the winding wire, $\Delta d_{min}$ represents the minimum increase in the conductor diameter resulting from the application of a polymeric insulation layer, and $d_{max}$ denotes the maximum allowable outer diameter of the conductor, including the thickness of insulation. Table 1 also includes the measured insulation thickness a of the wires tested in the experiment.

Twisted pairs of conductors, in order to maintain the geometry of the samples, were mounted on a base made of an insulating material. An exemplary TP sample is shown in Figure 1. The prepared samples were then placed in a vacuum chamber, as depicted in Figure 2b. The lid of the vacuum chamber, made of insulating material (PMMA), was equipped with bushings that allowed voltage to be applied to one of the winding wires (one wire was energized, while the other was grounded).

The aging stress was a square-wave voltage with a peak-to-peak value of 2.8 kV and a duty cycle of 50%. The frequency of the applied voltage was 3 kHz, which is similar to the frequencies commonly used in power electronic converters such as inverters and voltage converters. The waveform of the aging voltage is shown in Figure 3. The intensity of partial discharges depends on the switching time [2]: the transition from the negative voltage of $-1.4$ kV to its positive value of $+1.4$ kV. The measured switching time is approximately 2.5 $\mu$s, as illustrated in Figure 3b. The frequency of voltage switching influences the aging time: the higher the frequency, the faster the aging process occurs.

5. Results

Aging tests were conducted in a vacuum chamber (Figure 2), where the pressure could be adjusted. Air was removed from the chamber using a vacuum pump; however, vacuum conditions were not applied in the experiments, but rather a specific level of reduced pressure. Voltage was supplied to the samples inside the chamber through bushings installed in the cover, which was made of a PMMA polycarbonate plate.

During the single aging process, either two or four samples were subjected to stress, depending on the load imposed on the square-wave voltage generator by the samples. The result of the experiment was the time $t_b$ until dielectric breakdown. In each test, at least 14 samples underwent the aging process.

White’s method is recommended [14,15,17] for determining the Weibull distribution parameters for a series of 5 ÷ 20 samples, although some authors try to calculate the Weibull distribution parameters based on just 5 [13,22] or (better yet) 10 specimens [3]. In this study, it was decided that the number of tested samples would be 16. Additionally, results with extreme breakdown times were discarded—particularly very short $t_b$ values, for which there was a suspicion that they resulted from mechanical weakening of the insulation layer during the twisting process of the sample. As a result of the conducted experiment, the obtained lifetimes of the samples (denoted in

Table 2. Results of Weibull statistical analysis of breakdown times of samples.

Air Pressure	d = 0.5 mm	d = 0.8 mm	d = 1.0 mm
−0.7 bar	$\alpha$ = 1001	$\alpha$ = 2447	$\alpha$ = 1104
	$\beta$ = 6.73	$\beta$ = 8.79	$\beta$ = 2.56
−0.8 bar	$\alpha$ = 898	$\alpha$ = 1977	$\alpha$ = 944
	$\beta$ = 3.27	$\beta$ = 6.04	$\beta$ = 3.48
−0.9 bar	$\alpha$ = 750	$\alpha$ = 1814	$\alpha$ = 636
	$\beta$ = 4.76	$\beta$ = 4.98	$\beta$ = 2.59

as $\alpha$) were determined. As expected, the diameter of the winding wire has a significant impact on the determined lifetime of the sample [12]. However, the most influential parameter affecting the breakdown voltage of TP samples is the thickness of the wire insulation.

As shown in Table 1, the winding wires used in the experiment were covered with insulation of varying thicknesses (the applied Grade 1 wires met the requirements set by the standard given in [19]). The wire with a diameter of 0.8 mm had the thickest insulation layer, whereas, in contrast, the insulation thickness of the 1 mm diameter wire was approximately 1.3 times thinner than that of the aforementioned 0.8 mm wire. The differences in insulation thickness are permitted by the standard given in [19] and primarily depend on the viscosity of the insulating enamel used during wire production. The thickness of the conductor itself also influences the mechanism of enamel application.

The results of the statistical analysis obtained from the aging tests are presented in Table 2. For each sample series, the statistical lifetime $\alpha$ and the scale parameter $\beta$ were calculated. This parameter is analogous to the standard deviation in the normal distribution, meaning that the larger the $\beta$, the more the samples are concentrated around the value of $\alpha$ (see Table 2 and Figure 4 for comparison). Based on the statistical analysis of the aging test results, the following conclusions can be drawn:

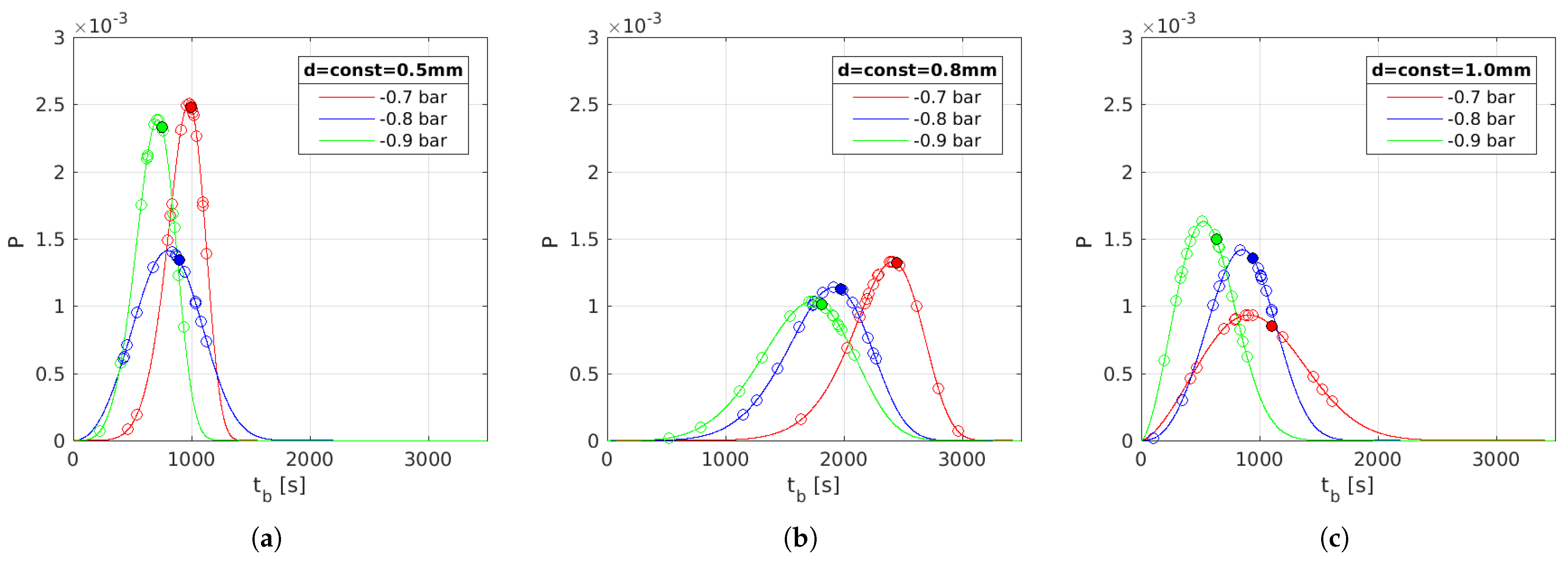
• The conductor thickness affects the dispersion of the results. It is clearly visible that in the case of the thinnest sample (Figure 4a), the experimental result regarding the dispersion is the smallest.
• The influence of air pressure on the sample lifetime $\alpha$ is evident. In each case, the sample lifetime decreases as the air pressure in the chamber is reduced.
• The higher the air pressure and the larger the wire diameter, the greater the dispersion of the breakdown time $t_b$ results ($\beta$ is smaller). At the same time, no clear pattern of lifetime $\alpha$ variation was observed.
• It was observed that the insulation thickness of the conductor had a significant impact on the experimental results (Figure 4b). The wire with $d=0.8\mathrm{mm}$ had the thickest insulation, a measuring 0.0232 mm, which was considerably thicker than in the other samples. This could explain the significantly longer lifetime $\alpha$ of these samples compared to the others.

For the purpose of analyzing the experimental results, simulations of the electric field intensity distribution in TP samples were conducted. The simulations were carried out in model described in Figure 5a.

Two stranded copper wires (1), insulated by enamel (2), are positioned side by side. The X-axis of the model passes through the centers of the conductors. The electric field strength was calculated both in the insulation and in the airspace between the wires. The finite element method was used, focusing on the electric field distribution along the Y-axis, as shown in Figure 5b. The simulations were performed under the following assumptions:

• The simulations were conducted at a voltage corresponding to the aging voltage applied to the samples (peak-to-peak value of 2.8 kV).
• The nominal diameter of the conductor $d_n$ and the insulation enamel a were assumed as specified in Table 1.
• It was assumed that the conductors were in contact with each other, not at a single point, but over an area of contact.
• A single winding wire consists of two materials: a conductor and an insulating material with a relative permittivity of ${\epsilon }_r=4.2$ [12].

In Figure 5b and Figure 6, regions with extremely high electric field intensity can be observed, reaching values close to 120 kV/mm. Similar electric field intensity values in TP samples are reported in the literature [10,23]. Such high values of electric stress exist in the air surrounding the contact area. First of all, the electric field in the enamel, where the wires are in contact, does not exceed 40 kV/mm. However, at the point where the enamel parts lose contact with each other, the electric field rapidly rises to values around 100 kV/mm. These values significantly exceed the dielectric strength of air. For such small insulation gaps, Paschen’s law is applicable, and the phenomena occurring in this region can be described by Paschen’s law characteristics [24]. In this part of the insulation system of TP sample, intense partial discharges and intensive ionization of the air occur. Additionally, the air is under reduced pressure, which leads to the formation of glow discharges and the generation of elevated temperatures.

6. Conclusions

The results of the aging tests are presented in Table 2 and graphically in Figure 4. Analyzing the results of the aging tests, simulations, and the parameters of the conductors (conductor diameter d and insulation thickness a), the following conclusions can be drawn from the conducted experiment.

• The air pressure in the chamber influences the sample lifetime $\alpha$; in all cases, the lifetime decreases as the air pressure is reduced. This effect occurs because a decrease in air pressure leads to a lower electrical breakdown strength. In an insulation system with dimensions as small as those in the TP samples, Paschen’s law applies [24]. As the breakdown strength of air decreases, the intensity of partial discharges increases, leading to insulation degradation.
• The insulation thickness of winding wires significantly affects the dispersion of measurement results (in the context of a normal distribution, dispersion is characterized by the standard deviation $\sigma$, while for the Weibull distribution, it is described by the shape parameter $\beta$, where a higher $\beta$ indicates lower variability in the experimental results). In Table 2, the influence of insulation thickness is noticeable for samples with $d=0.8$ mm, where the insulation thickness was $a=0.0232$ mm. This parameter still meets the standard requirements [19]; see Table 1.

7. Discussion

The synergy of the aforementioned erosive effects, combined with the non-uniform insulation thickness of conductors, leads to the following conclusions:

• Under certain environmental conditions, accelerated degradation of electrical machine insulation systems may occur. Such conditions are particularly relevant in aviation, where modern aircraft commonly utilize PWM converters that control electric motors driving various mechanisms.
• The insulation thickness of conductors is not constant and depends on various factors, such as the thickness d of the enameled wire and the viscosity of the liquid enamel in which the conductor is immersed, among others. These factors influence not only the final insulation thickness but also its electrical strength and aging resistance.

Based on the research results presented in this paper, it can be concluded that the insulation systems of electrical machines operated with frequency converters, such as voltage inverters, are subjected to a series of stress factors that contribute to a reduction in their service life. This degradation process can be further accelerated by reduced air pressure. The thickness of the winding wire insulation significantly affects the longevity of insulation systems in which these wires are applied.

In future research, the authors will focus on phase-resolved PD imaging, which will be recorded at various stages of the aging process. Similar experiments have been successfully conducted in the past [12,25].