Abstract
In DC urban rail transit, stray current causes unneglectable electrochemical corrosion to metallic structures near running rails. In view of the low-frequency and non-stationary distribution of dynamic stray current due to multiple trains in lines, its signal characteristic is significant for the corrosion degree prediction and mitigation performance evaluation. While zero-resistance converter system (ZRCS) is introduced for stray current mitigation, further evaluation of its mitigation performance is essential to field application. Considering that the Fourier transform processing non-stationary signals cannot estimate its frequency-domain features accurately, this paper introduces S-transform to extract the time–frequency characteristics of dynamic stray current in ZRCS. Moreover, the dynamic stray current mitigation performance of ZRCS is verified through time–frequency analysis results.
1. Introduction
With the rapid development of urban rail transit, the cumulative operation mileage has reached over 43,400 km in the world as of 2023 [1,2]. In DC traction power supply system, running rails are generally employed as the return path for traction current, which causes unneglectable rail potential and stray current issues [3,4,5], as illustrated in Figure 1. Stray current may flow into the surrounding buried metallic structures, such as gas or oil pipelines, and produce electrochemical corrosion in the anode region of metals, threatening the normal operation of power supply equipment or other infrastructure [6,7,8,9]. The Faraday electrolysis law has proven that one ampere of static DC stray current may corrode 20 pounds of steel or 23 pounds of copper per year [10]. However, due to the frequent start and stop of multiple trains in lines, stray current shows non-stationary characteristic, making it challenging to predict the corrosion degree with Faraday electrolysis law [11]. Accordingly, it is necessary to further study the stray current signal characteristics.
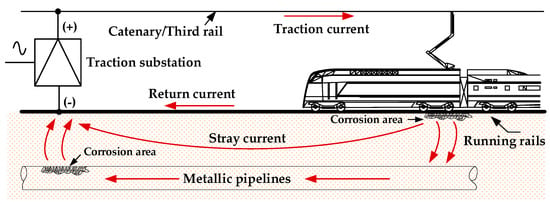
Figure 1.
Generation of rail potential and stray current.
The Fourier transform method has the defects of spectral leakage and fence phenomenon when dealing with non-stationary signals, and it cannot accurately extract its spectral distribution pattern. Hence, stray current signal should be analyzed in both time and frequency domains due to its non-stationary characteristics. Based on Fourier transform, typical time–frequency analysis methods such as short-time Fourier transform (STFT), continuous wavelet transform (CWT), and S-transform are evolved [12,13]. Nonetheless, STFT shows a fixed width of window function, making it impossible to obtain good time and frequency resolution simultaneously. Similarly, the selected wavelet basis in CWT cannot combine high- and low-frequency resolution, whereas S-transform introduces a Gaussian window whose width is inversely proportional to frequency and has better time-frequency characteristics [14]. Therefore, this paper investigates the time–frequency characteristics of dynamic stray current based on S-transform.
As for the stray current mitigation measures, there are three typical categories, i.e., reducing the magnitude of return current in running rails, suppressing the leakage of rail current, and protecting buried metal [9]. To reduce the magnitude of return current in running rails, typical measures include increasing the system voltage level and shortening the distance between traction substations [15,16]. But these measures are only suitable for newly constructed lines. To reduce the leakage of rail current, stray current drainage networks and coating materials are adopted. But the effect decays over time [17,18]. To protect the buried metallic structures, the cathodic protection is generally employed to inhibit the corrosion, but it is only limited to the protected object and cannot eliminate the negative impact of stray current like inducing harmonics or transformer DC bias in AC power system [19,20,21]. Compared with the above traditional solutions, zero-resistance converter system (ZRCS) mitigates rail potential and stray current by constructing zero-resistance loops through the cooperation of negative resistance converters (NRCs) and switch units (SUs), and then transfers return current from running rails to the specific return cable [22,23].
This paper introduces the time–frequency analysis method of stray current based on S-transform and verifies the stray current mitigation performance of ZRCS under frequency domain. The rest of this paper is organized as follows. Section 2 introduces the traction power supply system and ZRCS. In Section 3, the time–frequency analysis method is discussed in detail. Subsequently, Section 4 and Section 5 present the results of the time–frequency analysis of stray current. Finally, Section 6 summarizes the conclusion.
2. Traction Power Supply System and ZRCS
2.1. Traction Power Supply System
Figure 2 illustrates the DC traction power supply system in urban rail transit. The trains consume power supplied by traction substations through catenary or third rail, and the running rails generally serve as the return path of traction current at the same time.
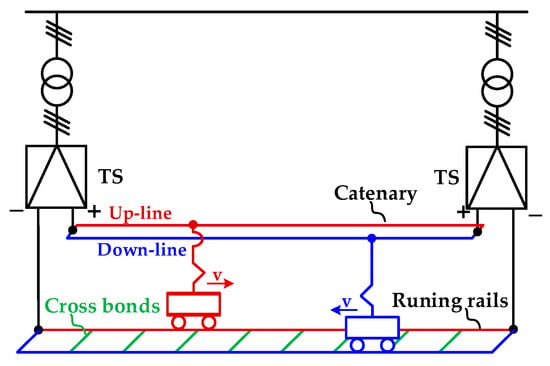
Figure 2.
DC traction power supply system.
To simplify analysis, traction substations are equivalent to voltage sources and the trains are equivalent to current sources. Moreover, all metals are considered uniform and not considering the cross-zone power supply of traction substation [24].
Figure 3 shows the equivalent circuit of DC traction power supply system, where Rt is the longitudinal resistance of catenary, Rr is the longitudinal resistance of running rails, Rg is the rail-to-earth resistance, Rs is the equivalent internal resistance of traction substation (TS), and iL1 or iL2 is the traction current of train.
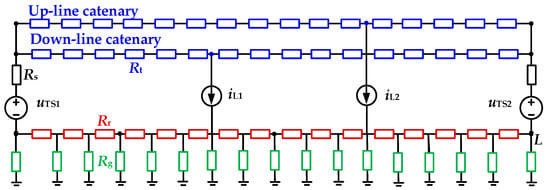
Figure 3.
Equivalent circuit of traction power supply system.
The differential model in Figure 4 is adopted to model the rail potential and rail current along running rails. The rail current ir(x) and rail potential ur(x) can be expressed as
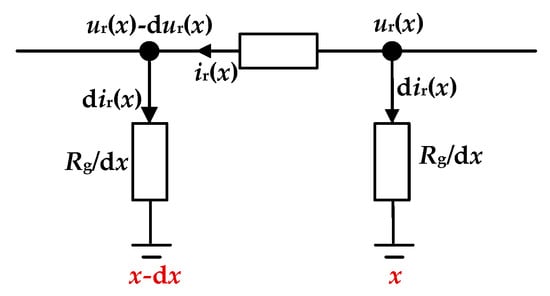
Figure 4.
Differential circuit of running rails.
Then, the rail current ir(x) and rail potential ur(x) can be derived as
where C1 and C2 are coefficients determined by the boundary rail current and rail potential, which can be derived as Equation (3), assuming that the rail potential and rail current at boundary point L are UrL and IrL.
2.2. Configuration and Control Strategy of ZRCS
Figure 5 shows the typical configuration of ZRCS under bilateral power supply, including two negative resistance converters (NRCs), (N − 1) switch units (SUs) and return cables (RCAs) installed in parallel with the existing conventional traction power supply system (CON-TPS). Among them, NRC is a power electronic device with bipolar output capability installed at TS; SU is a controllable bidirectional switch constructed at rail-to-rail cross bonds in tunnels; and RCAs are parallel cables laid along running rails employed as connections between NRCs and SUs. Accordingly, ZRCS can be parallel installed into CON-TPS without modifying trains, rails, or tunnels.
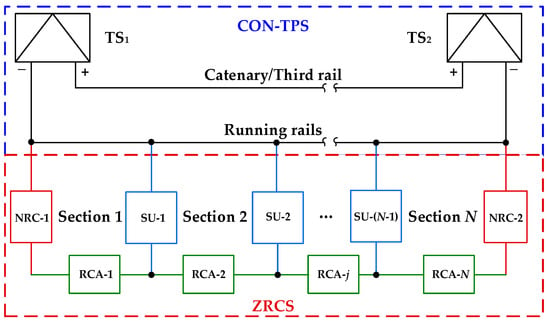
Figure 5.
Configuration of ZRCS.
Running rails are divided into N sections by two NRCs at TSs and (N − 1) SUs along running rails. During train operation, SUs at both ends of the section where the train is running are turned on. The output voltages of NRCs are controlled to counteract the voltage across RCAs and turned-on SUs to establish zero-resistance loops. Therefore, the return loop of traction current along running rails is shortened to mitigate the rail potential and stray current.
Figure 6 shows the establishment of zero-resistance loops when rail-section-k (k = 2~N − 1) carries the largest current. SU-(k − 1) and SU-k switch on. The rail current is mainly transferred to zero-resistance loops through SU-(k − 1) and SU-k. The voltages of zero-resistance loops can be expressed as
where uzeroloop_1 and uzeroloop_2 are generally controlled to be zero ideally. Based on this concept, ZRCS establishes the zero-resistance loops by transferring rail current to the external return cables, thus reducing rail potential and stray current of the line from source.
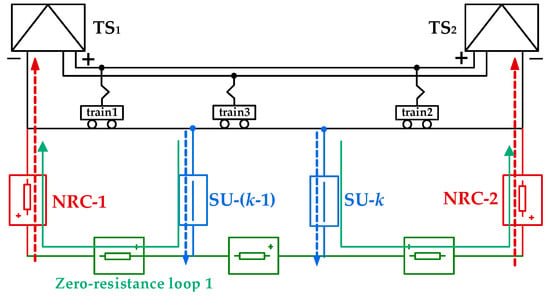
Figure 6.
The establishment of zero-resistance loops.
3. Time–Frequency Analysis of Stray Current
There are often multiple trains running at the same time in the lines, while their start-stop conditions are frequently changed, making stray current a low-frequency non-stationary signal [20]. However, the spectral distribution obtained by Fourier transform method is related to the sampling time, and some defects such as spectral leakage and fence phenomenon. In order to extract both time-domain and frequency-domain characteristics, this paper introduces a time–frequency analysis method based on S-transform to analyze stray current signal.
S-transform assumes that the signal is stationary within a window function of variable time width, and then the local spectrum of the signal is obtained by Fourier transform, after that the window function is continuously shifted on the time axis to obtain the time-varying characteristics of the signal. The S-transform of u(t) is defined as
where S(τ, f) is the time–frequency spectrum matrix. Its column vector contains the signal amplitude and phase information of different frequency points, and the row vector contains the signal amplitude and phase information at different moments of a certain frequency. By contrast, ω(τ − t, f) is a window function that varies continuously with frequency, allowing S-transform to obtain a high temporal resolution in the high frequency band and a high frequency resolution in the low-frequency band.
Moreover, due to the lossless reversibility of S-transform, signal u(t) can be reconstructed by S(τ, f) as
Based on Equation (6), the energy content E of the signal is obtained from S-transform as [25]
Thus, the total energy can be defined as
Based on Equations (7) and (8), the energy distribution of the signal at different frequencies can be obtained. Since the AC component of the stray current is meanly concentrated in the ultra-low-frequency range, this paper will conduct spectral analysis by frequency bands.
Considering that the stray current cannot be measured directly in field, the polarization potential offset value of the buried metal is often used as an indirect indicator to evaluate the interference and corrosion of the stray current. The polarization potential magnitude is directly affected by rail potential which is relatively easy to be collected. Moreover, TS is the return point of leaking stray current. Therefore, this paper characterizes stray current by the rail potential at TS to carry out time–frequency analysis.
4. Evaluation of Rail Potential and Stray Current
To evaluate the mitigation performance of ZRCS, system parameters are listed in Table 1. NRC-1 and TS1 are located at x = 0 km. NRC-2 and TS2 are located at x = 5 km. SU-1, SU-2 and SU-3 are located at x = 1.25 km, x = 2.5 km and x = 3.75 km, respectively, which divide the running rails into four sections.

Table 1.
System parameters.
Figure 7 presents typical operation curves under multiple-train condition. To simplify analysis, assuming that there are three stations between two TSs, located at x = 0 km, x = 2.5 km and x = 5 km, respectively. Train 1 runs from TS1 to the intermediate station after train 3 enters the station. Train 2 runs from the intermediate station to TS2 30 s after train 3 departs, and train 3 runs from TS1 to the intermediate station and stops 30 s before running to TS2.
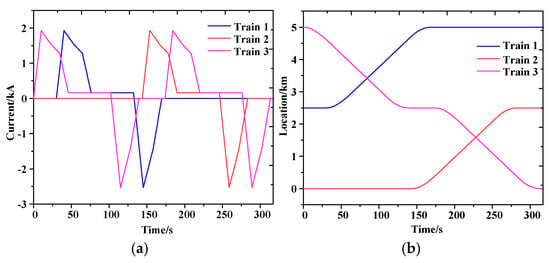
Figure 7.
Train operation curves. (a) Traction current—time; (b) Location—time.
The rail potential distribution of CON-TPS and ZRCS are shown in Figure 8. The rail potential fluctuates between −16 V and +16 V in CON-TPS, while −4 V and +4 V in ZRCS. In CON-TPS, the peak rail potential occurs at x = 0 km near TS1 at 115 s, with an amplitude of 15.3 V. In ZRCS, the peak rail potential occurs at x = 1.95 km near TS1 at 217 s, with an amplitude of 3.9 V, which is 72.76% lower than that of CON-TPS.
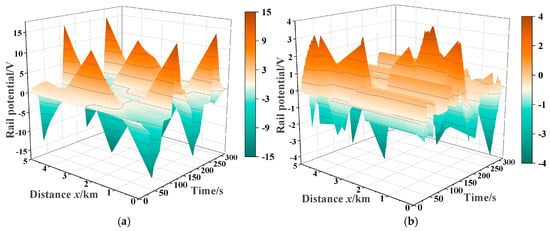
Figure 8.
Rail potential distribution. (a) CON-TPS; (b) ZRCS.
Consider that the rail potential magnitudes at TS1 and TS2 in CON-TPS are similar, to simplify stray current characterization while preserving generality, the rail potential at TS1 is therefore selected to characterize stray current.
Shown as Figure 9 and Table 2, the rail potential at TS1 fluctuates significantly when trains are accelerating or braking, and it remains stable when trains are in coasting stage. As for CON-TPS, the maximum rail potential at TS1 is 15.13 V and the minimum value is −14.19 V; for ZRCS, the corresponding value is 1.12 V and −2.59 V. The maximum value is reduced by 92.59%, and the minimum value by 81.74%.
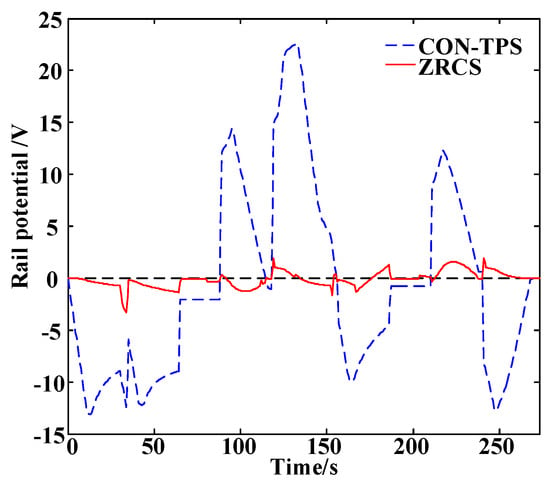
Figure 9.
Rail potential at TS1.

Table 2.
The simulation results.
Based on Equations (6)–(8), stray current signal can be reconstructed by S(τ, f) as the time–frequency spectrum shown as Figure 10. It is noted that the signal intensity is concentrated in the band of 0 to 1 Hz. The maximum amplitude of CON-TPS is 4.02 V at t = 149.2 s, with f = 0.0063 Hz, while the maximum amplitude of ZRCS is 0.326 V at t = 199.1 s, with f = 0.0063 Hz. The maximum amplitude of ZRCS is 91.89% lower than that of CON-TPS.
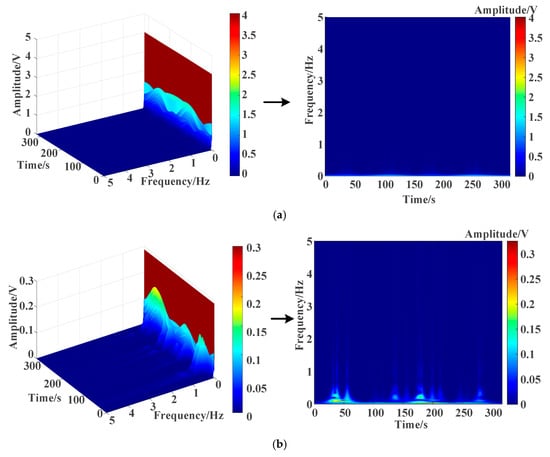
Figure 10.
Time–frequency spectrum of stray current. (a) CON-TPS; (b) ZRCS.
Figure 11 and Table 2 show the energy distribution of stray current. It is noted that DC component accounts for 2.983% in CON-TPS, while the AC components with frequencies greater than 1 Hz accounts for only 0.007%. Energy in the 0 to 0.03 Hz accounts for 88.70%. It means that the AC component of the stray current is primarily concentrated in the ultra-low-frequency bands. On the other hand, ZRCS decreases the energy in the band of 0 to 0.03 Hz from 88.70% to 35.04%, whereas the proportion of energy in the remaining frequency bands increases correspondingly. Accordingly, the main energy of dynamic stray current in ZRCS is concentrated in higher frequency bands, which effectively mitigates stray current corrosion.
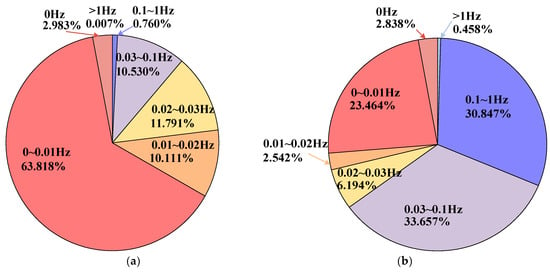
Figure 11.
Energy distribution. (a) CON-TPS; (b) ZRCS.
The rail potential mitigation percentage ηRP and stray current mitigation percentage ηSC are defined as
where ur_CON is rail potential of CON-TPS and ur_ZRCS is rail potential of ZRCS; SC_CON is the average value of each frequency of stray current under CON-TPS and SC_ZRCS is the average value of specific frequency of stray current under ZRCS.
Compared to CON-TPS, ZRCS reduces rail potential by 80% to 95% for most of the time as shown in Figure 12. In the blank areas, the ηRP is relatively poor because ur_CON is low, almost close to zero, while ur_ZRCS is higher than ur_CON.
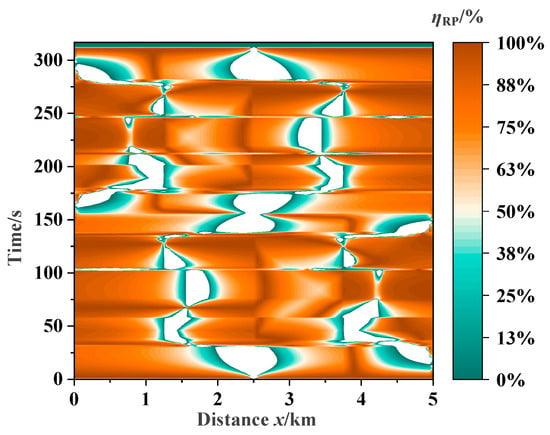
Figure 12.
Mitigation efficiency of rail potential.
Figure 13 presents the comparison of the average amplitude across each frequency band. The overall amplitude tends to decrease with increasing frequency. Notably, within the frequency band of 0–0.03 Hz, which accounts for over 70% of the total energy, the mitigation efficiency ηSC can reach 84.87% to 97.50%.
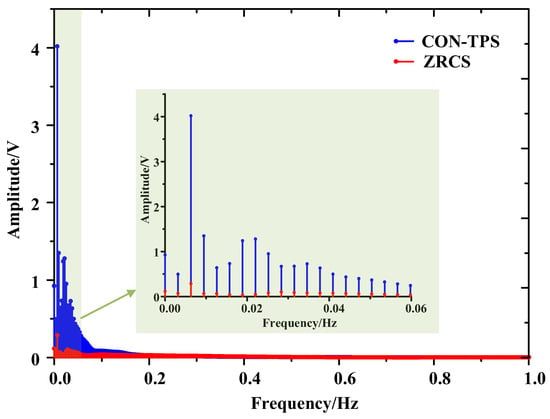
Figure 13.
Average amplitude comparison.
In summary, ZRCS can effectively reduce the rail potential and mitigate the stray currents in different frequency bands, with an optimal mitigation efficiency of over 95%. In addition, not only the amplitude of stray current in ZRCS is effectively reduced, but the main energy is concentrated in relatively higher frequency bands, which can effectively alleviate stray current corrosion.
5. Experimental Verifications
To verify the above analysis, a simplified experimental platform for ZRCS and CON-TPS is shown in Figure 14. The equivalent circuit diagram of the experimental platform is shown in Figure 14a, and the hardware prototype is shown in Figure 14b. Experimental platform of CON-TPS is a resistance network, which is composed of running rails resistance Rr, equivalent internal resistance of TS Rs, and rail-to-earth resistance Rg. Experimental platform of ZRCS consists of two NRCs, three SUs and RCA resistance RRCA, which are paralleled to CON-TPS. The two NRCs are powered by two voltage sources. The three SUs divide the resistance network into four parts. A DC current source is used as a train load. In both systems, the rail potential is measured at the 29 test points on the entire running rails. The rail potential data measured three times are averaged, and the resulting average value is then analyzed using S-transform. The specific parameters of each device of the experimental platform are shown in Table 3. To simply analysis, the catenary resistance is removed.
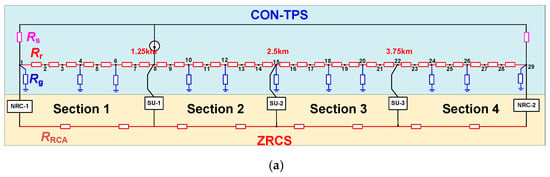
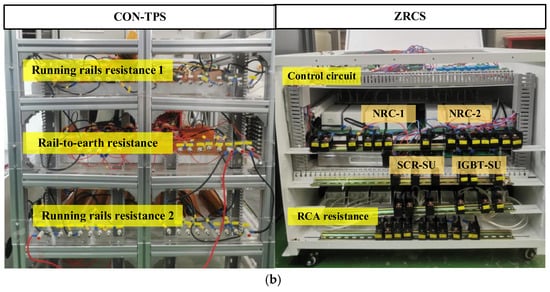
Figure 14.
Experimental platforms. (a) Equivalent circuit. (b) Hardware prototype.

Table 3.
System parameters of experimental platforms.
Figure 15 shows the simplified train operation curve. Since the resistive network is a linear system, linear interpolation can be used to estimate the rail potential at intermediate time steps.
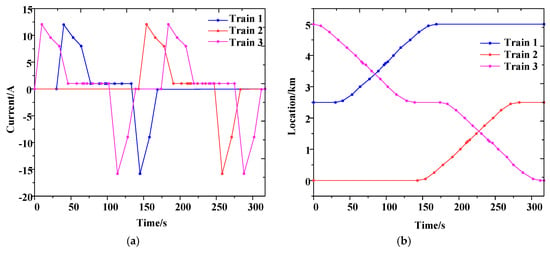
Figure 15.
Simplified train operation curves. (a) Traction current—time; (b) Location—time.
The experimental results of rail potential at TS1 are shown in Figure 16 and Table 4. As for CON-TPS, the peak rail potential at TS1 is 14.03 V and the minimum value is −13.37 V, while for ZRCS the corresponding value is 1.66 V and −1.27 V. The peak value is reduced by 88.16%, and the minimum value by 90.50%.
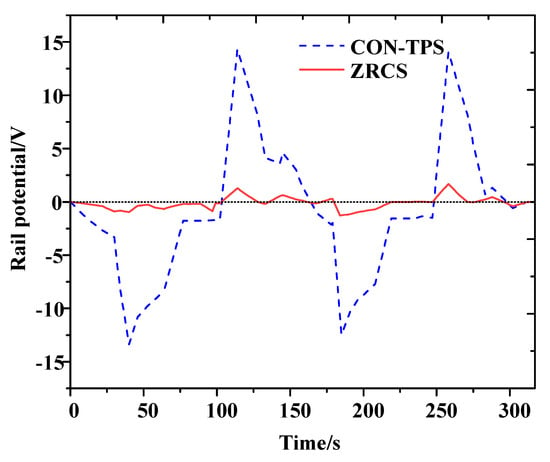
Figure 16.
Experimental results of rail potential at TS1.

Table 4.
The experimental results.
In CON-TPS experiments, the peak rail potential at TS1 is 7% lower than the simulation result, while the minimum value is 6% higher. In ZRCS experiments, the peak rail potential at TS1 is 48% higher than the simulation result, and the minimum value is 51% higher.
Figure 17 shows the time–frequency spectrum of stray current signal in experiment. The signal intensity is concentrated in the band of 0 to 1 Hz. The maximum amplitude of CON-TPS is 3.72 V at t = 126.5 s, with f = 0.0063 Hz, while the maximum amplitude of ZRCS is 0.27 V at t = 204.1 s, with f = 0.0063 Hz. The maximum amplitude of ZRCS is 92.78% lower than that of CON-TPS.
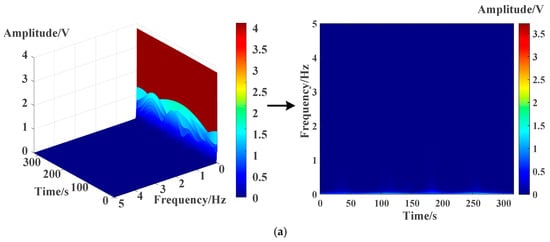
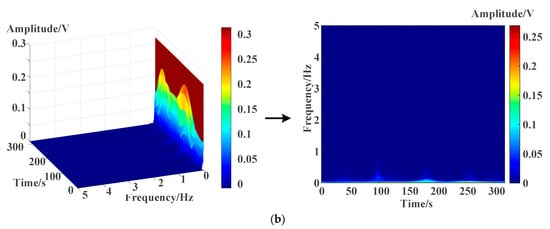
Figure 17.
Time–frequency spectrum of stray current in the experiment. (a) CON-TPS; (b) ZRCS.
In CON-TPS experiments, the maximum amplitude of the stray current signal is 7% lower than the simulation result. Similarly, in ZRCS experiments, the maximum amplitude is also 7% lower than the simulation result.
Figure 18 and Table 4 show the energy distribution of stray current in the experiment. It is noted that, in CON-TPS, energy in the 0 to 0.03 Hz band accounts for 86.49%. In contrast, ZRCS reduces the energy in this band from 86.49% to 61.48%. Similar to the simulations, the mean energy of dynamic stray current in ZRCS is concentrated in higher frequency bands.
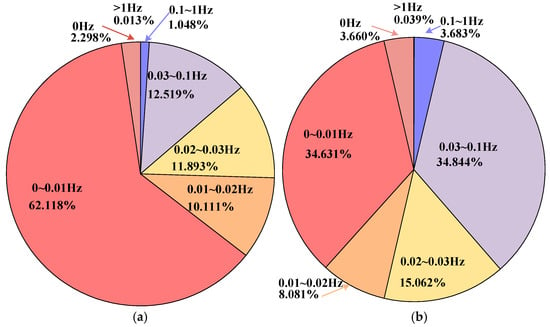
Figure 18.
Energy distribution in experiment. (a) CON-TPS; (b) ZRCS.
Table 5 compares simulation and experimental energy distributions. For CON-TPS, the simulation and experimental results of energy distribution across all frequency bands were in close agreement, with a maximum difference of 2.21% occurring in the 0–0.03 Hz frequency band. For ZRCS, the simulation and experimental results of energy distribution in the 0–0.01 Hz frequency band differed by 26.44%. This divergence may be attributed to the simplifications made in the experiment. Thus, the effect of energy distribution optimization in the experiment is less pronounced than that in the simulations.

Table 5.
Comparison of energy distribution between simulation and experiment.
Figure 19 shows the ηRP of experiment. These experimental results match the simulation results. As shown in Equation (7), the suppression rate is calculated with CON-TPS as the benchmark. In Figure 19, the suppression rate in most areas exceeds 80%. In the areas where the ηRP is relatively poor, the ur_CON is almost close to zero, while ur_ZRCS is higher than ur_CON. The experimental results are consistent with the simulation results.
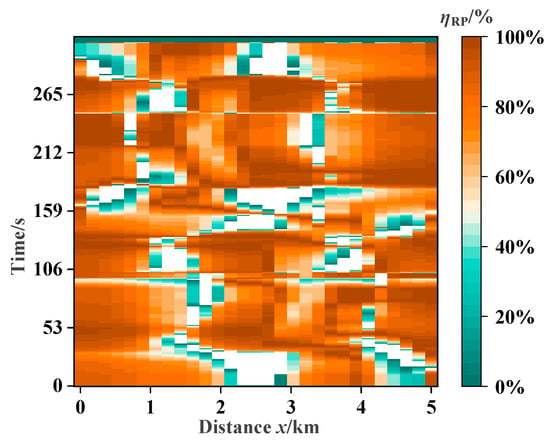
Figure 19.
Mitigation efficiency of rail potential in the experiment.
Figure 20 shows the comparison of the average amplitude across each frequency band with and without ZRCS. With the frequency increase, the average amplitude decreases in both CON-TPS and ZRCS. Furthermore, ZRCS reduces the average amplitude across all frequency bands. According to Equation (7), the stray current mitigation efficiency exceeds 80%. Within the dominant 0–0.03 Hz frequency band, the stray current mitigation efficiency ηSC achieves values ranging from 80.66% to 92.76%.
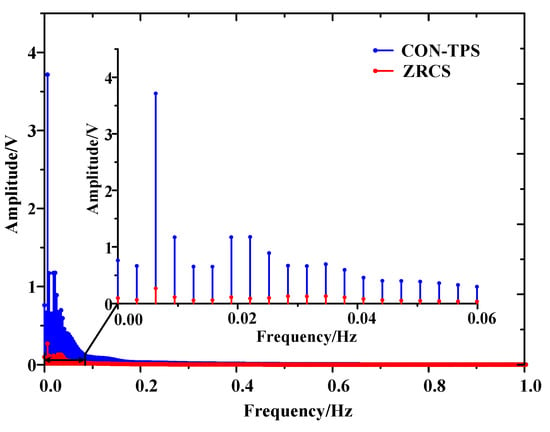
Figure 20.
Average magnitude comparison.
6. Conclusions
This paper studies the time–frequency characteristics of stray current in urban rail transit based on S-transform. The time–frequency analysis shows that stray current behaves as a low-frequency non-stationary signal, whose spectral energy is concentrated in the band of 0–1 Hz, of which 0–0.01 Hz accounts for the largest percentage. This distinctive frequency characteristics is intrinsically linked to the frequent starting and stopping of multiple trains in lines. The stray current mitigation performance of ZRCS is verified through the simulation and experimental studies. Firstly, with the operation of ZRCS, rail potential under multi-train condition can be reduced significantly and stray current under different frequencies can be effectively mitigated. In addition, the frequency-domain analysis reveals that ZRCS further mitigates stray current corrosion by driving the frequency-domain characteristics of stray current to higher frequency bands.
Author Contributions
X.S.: Conceptualization, methodology, software, validation, formal analysis, writing—original draft, writing—review and editing; X.Y.: Conceptualization, validation, resources, writing—review and editing, supervision, project administration, funding acquisition; R.Z.: Validation, visualization; Z.W.: Validation, data curation; M.C.: Software, writing—review and editing; T.Q.Z.: Funding acquisition. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by Beijing Natural Science Foundation under Grant 3222054, and in part by the Key Program of National Natural Science Foundation of China under Grant 51737001.
Data Availability Statement
The authors confirm that all data used in this study are openly available within the article. Further inquiries can be directed to the corresponding authors.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Han, B.; Yu, Y.; Xi, Z.; Sun, Y.; Lu, F.; Li, S.; Li, Z.; Huang, S.; Hu, J.; Sang, Y.; et al. Statistical Analysis of Urban Rail Transit Operations Worldwide in 2023: A Review. Urban Rapid Rail Transit 2024, 37, 1–9. [Google Scholar]
- Hu, J.; Yang, M.; Zhen, Y. A Review of Resilience Assessment and Recovery Strategies of Urban Rail Transit Networks. Sustainability 2024, 16, 6390. [Google Scholar] [CrossRef]
- Dolara, A.; Foiadelli, F.; Leva, S. Stray Current Effects Mitigation in Subway Tunnels. IEEE Trans. Power Deliv. 2012, 27, 2304–2311. [Google Scholar] [CrossRef]
- Yang, X.; Wang, M.; Zheng, T.Q.; Sun, X. Modelling and Simulation of Stray Current in Urban Rail Transit—A Review. Urban Rail Transit 2024, 10, 189–199. [Google Scholar] [CrossRef]
- Zaboli, A.; Vahidi, B.; Yousefi, S.; Hosseini-Biyouki, M.M. Evaluation and Control of Stray Current in DC-Electrified Railway Systems. IEEE Trans. Veh. Technol. 2017, 66, 974–980. [Google Scholar] [CrossRef]
- Chen, Z.; Koleva, D.; van Breugel, K. A review on stray current-induced steel corrosion in infrastructure. Corros. Rev. 2017, 35, 397–423. [Google Scholar] [CrossRef]
- Du, G.; Wang, J.; Jiang, X.; Zhang, D.; Yang, L.; Hu, Y. Evaluation of Rail Potential and Stray Current with Dynamic Traction Networks in Multitrain Subway Systems. IEEE Trans. Transp. Electrif. 2020, 6, 784–796. [Google Scholar] [CrossRef]
- Ogunsola, A.; Sandrolini, L.; Mariscotti, A. Evaluation of Stray Current From a DC-Electrified Railway with Integrated Electric-Electromechanical Modeling and Traffic Simulation. IEEE Trans. Ind. Appl. 2015, 51, 5431–5441. [Google Scholar] [CrossRef]
- Wang, M.; Yang, X.; Zheng, T.Q.; Ni, M. DC Autotransformer-Based Traction Power Supply for Urban Transit Rail Potential and Stray Current Mitigation. IEEE Trans. Transp. Electrif. 2020, 6, 762–773. [Google Scholar] [CrossRef]
- Stray Current Corrosion in Electrified Rail Systems—Final Report. Available online: https://rosap.ntl.bts.gov/view/dot/13213 (accessed on 17 February 2025).
- Qin, H.; Du, Y.; Lu, M.; Meng, Q. Effect of dynamic DC stray current on corrosion behavior of X70 steel. Mater. Corros. -Werkst. Und Korros. 2020, 71, 35–53. [Google Scholar] [CrossRef]
- Darowicki, K.; Zakowski, K. A new time-frequency detection method of stray current field interference on metal structures. Corros. Sci. 2004, 46, 1061–1070. [Google Scholar] [CrossRef]
- Mujezinovic, A.; Martinez, S. Application of the Continuous Wavelet Cross-Correlation Between Pipe-to-Soil Potential and Pipe-to-Rail Voltage Influenced by Dynamic Stray Current from DC Train Traction. IEEE Trans. Power Deliv. 2021, 36, 1015–1023. [Google Scholar] [CrossRef]
- Stockwell, R.G.; Mansinha, L.; Lowe, R.P. Localization of the complex spectrum: The S transform. IEEE Trans. Signal Process. 1996, 44, 998–1001. [Google Scholar] [CrossRef]
- Wang, Y.-Q.; Li, W.; Yang, X.-F.; Ye, G.; Fan, Q.-G.; Zhang, L.-P. Study on the Distribution and Computer Simulation of Metro Rail Potential. In Proceedings of the International Conference on Informatics, Cybernetics, and Computer Engineering (ICCE2011), Cybernetics, MEL, Australia, 19–20 November 2011; pp. 185–192. [Google Scholar]
- Vranesic, K.; Bhagat, S.; Mariscotti, A.; Vail, R. Measures and Prescriptions to Reduce Stray Current in the Design of New Track Corridors. Energies 2023, 16, 6252. [Google Scholar] [CrossRef]
- Ha, T.H.; Bae, J.H.; Lee, H.G.; Ha, Y.C.; Kim, D.K. Rapid potential-controlled rectifier for securing the underground pipeline under electrolytic interference. In Proceedings of the International Conference on Power System Technology (POWERCON 2004), Singapore, 21–24 November 2004; pp. 537–541. [Google Scholar]
- Trykoz, L.; Kamchatnaya, S.; Borodin, D.; Atynian, A.; Tkachenko, R. Protection of railway infrastructure objects against electrical corrosion. Anti-Corros. Methods Mater. 2021, 68, 380–384. [Google Scholar] [CrossRef]
- Wang, A.; Lin, S.; Hu, Z.; Li, J.; Wang, F.; Wu, G.; He, Z. Evaluation Model of DC Current Distribution in AC Power Systems Caused by Stray Current of DC Metro Systems. IEEE Trans. Power Deliv. 2021, 36, 114–123. [Google Scholar] [CrossRef]
- Machczyñski, W. Simulation model for drainage protection of earth-return circuits laid in stray currents area. Electr. Eng. 2002, 84, 165–172. [Google Scholar] [CrossRef]
- Rossouw, E.; Doorsamy, W. Predictive Maintenance Framework for Cathodic Protection Systems Using Data Analytics. Energies 2021, 14, 5805. [Google Scholar] [CrossRef]
- Gu, J.; Yang, X.; Zheng, T.Q.; Xia, X.; Zhao, Z.; Chen, M. Rail Potential and Stray Current Mitigation for Urban Rail Transit with Multiple Trains Under Multiple Conditions. IEEE Trans. Transp. Electrif. 2022, 8, 1684–1694. [Google Scholar] [CrossRef]
- Chen, M.; Yang, X.; Zheng, T.Q.; Zhao, Z.; Xia, X.; Gu, J. Improved control strategy of zero-resistance converter system for rail potential and stray current mitigation. Int. J. Rail Transp. 2023, 11, 248–266. [Google Scholar] [CrossRef]
- Zakowski, K.; Sokolski, W. 24-hour characteristic of interaction on pipelines of stray currents leaking from tram tractions. Corros. Sci. 1999, 41, 2099–2111. [Google Scholar] [CrossRef]
- Samantaray, S.R.; Tripathy, L.N.; Dash, P.K. Differential energy based relaying for thyristor controlled series compensated line. Int. J. Electr. Power Energy Syst. 2012, 43, 621–629. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).