Beyond the First Generation of Wind Modeling for Resource Assessment and Siting: From Meteorology to Uncertainty Quantification
Abstract
1. Introduction
An Exceptional Multi-Disciplinary Problem
2. Some Wind Energy Meteorology
2.1. Describing the Parameter Space for Wind
- ABL Rossby number [21];
2.2. First Applications of Meteorology in Wind Energy
2.3. Meteorology Beyond the Surface-Layer
2.4. Modeling Advancements and Their Consequences
2.4.1. RANS Modeling
2.4.2. Mesoscale Modeling
3. Appropriate Statistical Characterization, from Theory to Practice
3.1. Rational Averaging Implicit in Classic WRA
3.2. Refined Modeling and Consequent Sampling Issues
3.3. Averaging Issues Arising with Time Series Use or Comparisons
4. Uncertainty Quantification
Uncertainty in the Complex ABL System
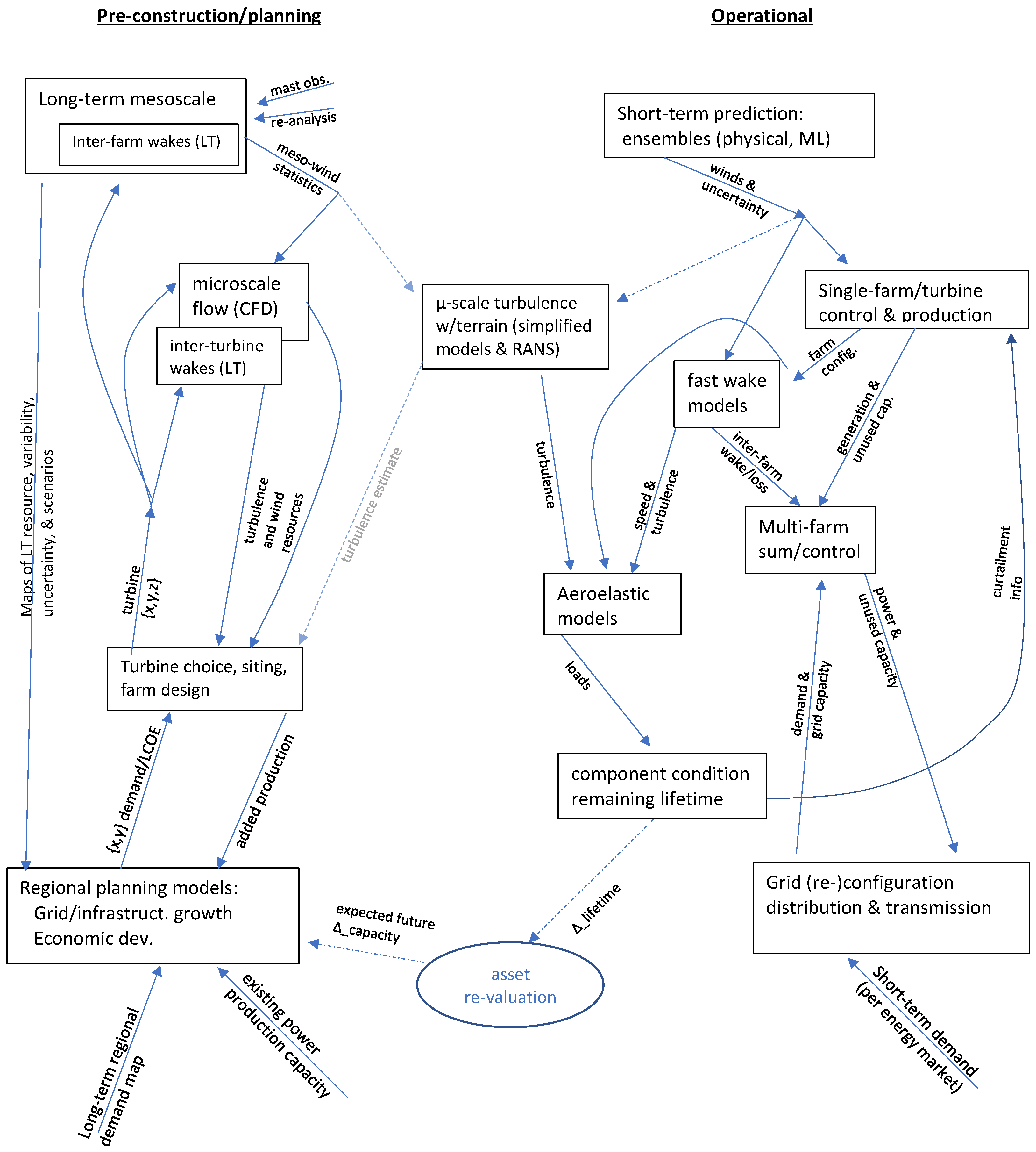
5. Industrial Application
5.1. Wind Resources
5.1.1. Wind Uncertainty Components
- Measurement
- Long-Term Correction
- Flow Modeling and Horizontal Extrapolation
- Vertical Extrapolation
- Year-to-Year Project Variability
- Wakes and Blockage
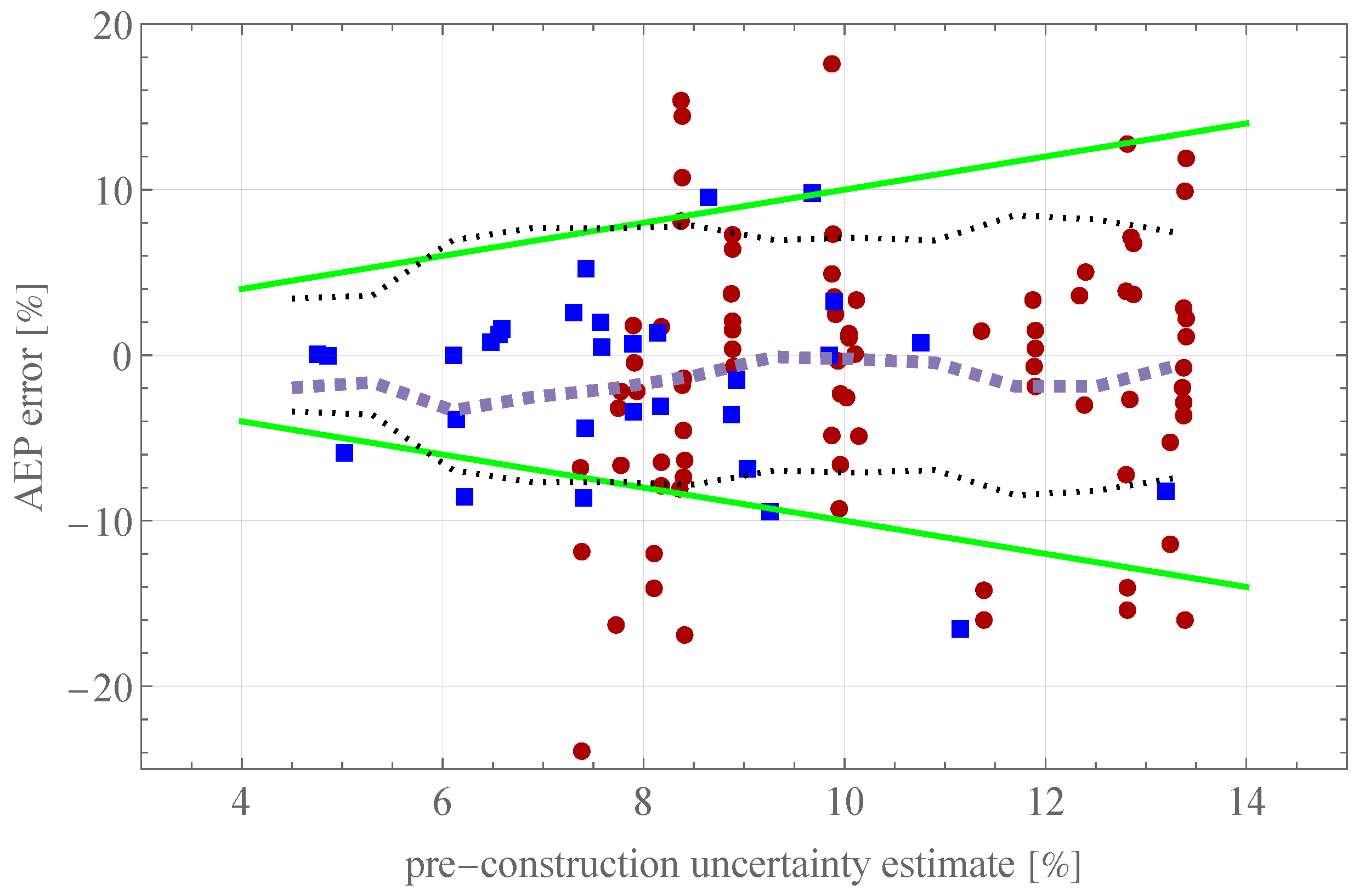
5.1.2. Combination of Uncertainty Components
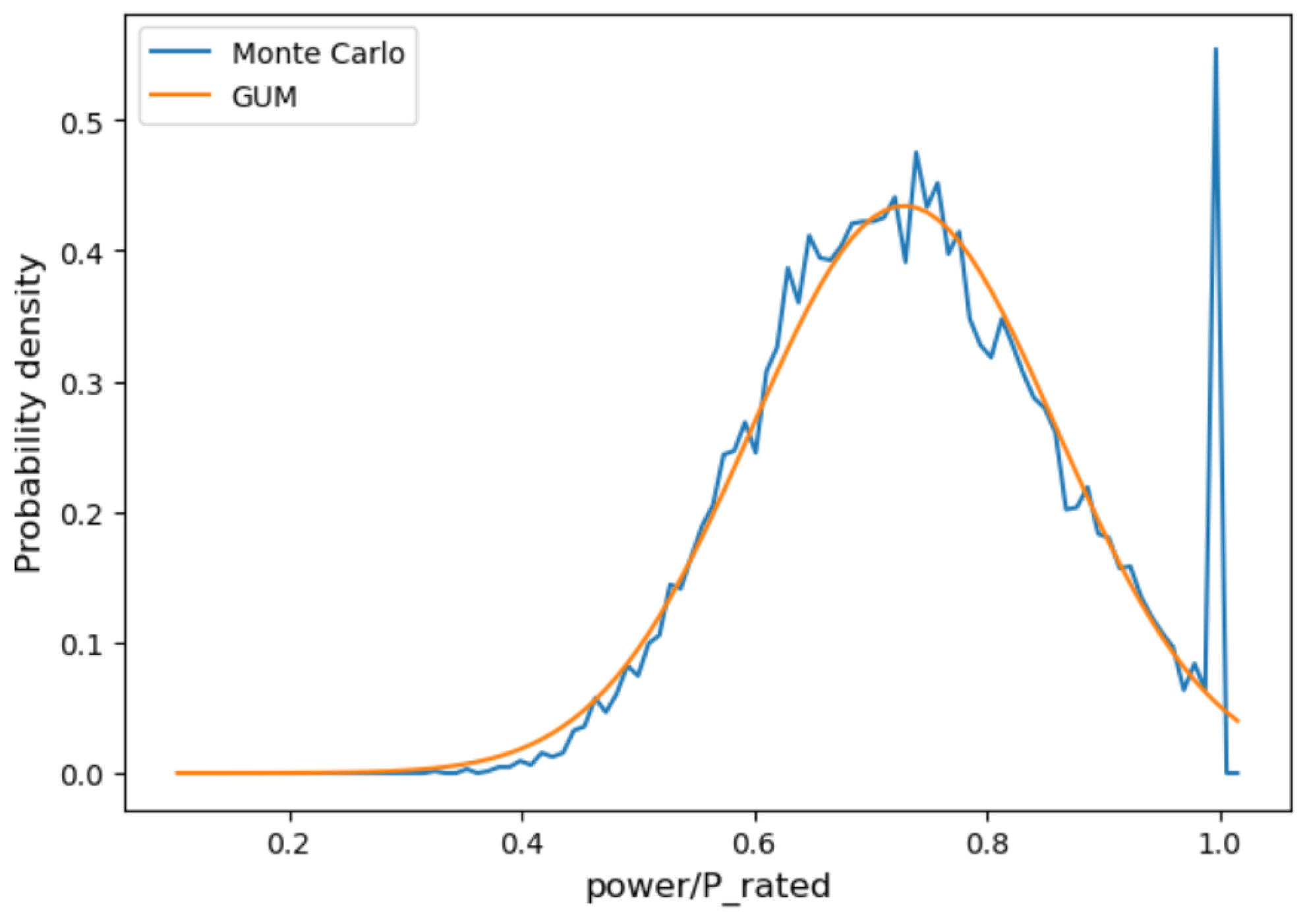
5.1.3. From Wind to Energy
5.2. Forecasting
5.3. Wind Atlases and Assessments Without Measurements
5.4. Siting, Design, and Standards
5.5. Distinction from Risk
6. Summary
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ABL | Atmospheric boundary layer. |
| AEP | Annual energy production. |
| ASL | Atmospheric surface layer. |
| CFD | Computational Fluid Dynamics. |
| EWA | European wind atlas (method). |
| EYA | Energy yield assessment. |
| GDL | Geostrophic drag law. |
| GWA | Global wind atlas. |
| HE | Horizontal extrapolation. |
| IBL | Internal boundary layer (due to surface roughness changes). |
| LES | Large-eddy simulation. |
| LT | Long term. |
| LTC | Long-term correction. |
| ML | Machine learning. |
| M-O | Monin-Obukhov (similarity theory) |
| NWP | Numerical weather prediction. |
| PBL | Planetary boundary layer (for NWP models). |
| Probability density function. | |
| PIRT | Phenomenon identification and ranking table. |
| RANS | Reynolds-averaged Navier–Stokes. |
| UQ | Uncertainty quantification. |
| VE | Vertical extrapolation. |
| V&V | Validation and verification. |
| WRA | Wind resource assessment. |
| WRF | Weather research and forecasting model. |
References
- Emeis, S. Wind Energy Meteorology—Atmospheric Physics for Wind Power Generation; Springer: Dordrecht, The Netherlands, 2013; 150p. [Google Scholar]
- Landberg, L. Meteorology for Wind Energy: An Introduction; John Wiley & Sons Ltd.: Chichester, UK, 2016; 210p. [Google Scholar]
- Watson, S. Handbook of Wind Resource Assessment; John Wiley & Sons Ltd., 2023; 320p. [Google Scholar] [CrossRef]
- Wyngaard, J.C. Turbulence in the Atmosphere; Cambridge University Press: Cambridge, UK, 2010; 393p. [Google Scholar]
- Zilitinkevich, S.S.; Tyuryakov, S.A.; Troitskaya, Y.I.; Mareev, E.A. Theoretical models of the height of the atmospheric boundary layer and turbulent entrainment at its upper boundary. Izv. Atmos. Ocean. Phys. 2012, 48, 133–142. [Google Scholar] [CrossRef]
- Dimitrov, N.; Kelly, M.; Vignaroli, A.; Berg, J. From wind to loads: Wind turbine site-specific load estimation using databases with high-fidelity load simulations. Wind Energy Sci. 2018, 3, 767–790. [Google Scholar] [CrossRef]
- IEC Standard 61400-15-2; Wind Energy Generation Systems—Part 15-2: Framework for Assessment and Reporting of the Wind Resource and Energy Yield. International Electrotechnical Comission: Geneva, Switzerland, 2025.
- Zilitinkevich, S.; Baklanov, A. Calculation of the Height of the Stable Boundary Layer in Practical Applications. Bound.-Layer Meteorol. 2002, 105, 389–409. [Google Scholar] [CrossRef]
- Bohren, C.F.; Albrecht, B.A. Atmospheric Thermodynamics; Oxford University Press: New York, NY, USA, 1998; 402p. [Google Scholar]
- Evans, J.H. Dimensional Analysis and the Buckingham Pi Theorem. Am. J. Phys. 1972, 40, 1815–1822. [Google Scholar] [CrossRef]
- Barenblatt, G.I. Scaling, Self-Similarity, and Intermediate Asymptotics; Cambridge University Press: Cambridge, UK, 1996. [Google Scholar] [CrossRef]
- Oppenheimer, M.W.; Doman, D.B.; Merrick, J.D. Multi-scale physics-informed machine learning using the Buckingham Pi theorem. J. Comput. Phys. 2023, 474, 111810. [Google Scholar] [CrossRef]
- Sathe, A.S.; Giometto, M.G. Impact of the numerical domain on turbulent flow statistics: Scalings and considerations for canopy flows. J. Fluid Mech. 2024, 979. [Google Scholar] [CrossRef]
- Csanady, G.T. On the “Resistance Law” of a Turbulent Ekman Layer. J. Atmos. Sci. 1967, 24, 467–471. [Google Scholar] [CrossRef]
- Fiedler, F.; Panofsky, H.A. The geostrophic drag coefficient and the ‘effective’ roughness length. Q. J. R. Meteorol. Soc. 1972, 98, 213–220. [Google Scholar] [CrossRef]
- Troen, I.; Petersen, E.L. European Wind Atlas; Risø National Laboratory: Roskilde, Denmark, 1989; 656p. [Google Scholar]
- Rossby, C.G.; Montgomery, R.B. The Layer of Frictional Influence in Wind and Ocean Currents. Pap. Phys. Oceanogr. Meteorol. 1935, 3, 1–101. [Google Scholar]
- Obukhov, A.M. Turbulence in an atmosphere with a non-uniform temperature. Bound.-Layer Meteorol. 1971, 2, 7–29. [Google Scholar] [CrossRef]
- Foken, T. 50 Years of the Monin–Obukhov Similarity Theory. Bound.-Layer Meteorol. 2006, 119, 431–447. [Google Scholar] [CrossRef]
- Yano, J.; Wacławczyk, M. Nondimensionalization of the Atmospheric Boundary-Layer System: Obukhov Length and Monin–Obukhov Similarity Theory. Bound.-Layer Meteorol. 2022, 182, 417–439. [Google Scholar] [CrossRef]
- van der Laan, M.P.; Kelly, M.; Floors, R.; Peña, A. Rossby number similarity of an atmospheric RANS model using limited-length-scale turbulence closures extended to unstable stratification. Wind Energy Sci. 2020, 5, 355–374. [Google Scholar] [CrossRef]
- Kazanskii, A.; Monin, A. Dynamic interaction between atmosphere and surface of earth. Akad. Nauk SSSR Izv. Seriya Geofiz. 1961, 24, 786–788. [Google Scholar]
- Smith, F.B. The relation between Pasquill stability p and Kazanski-Monin stability μ (In neutral and unstable conditions). Atmos. Environ. 1979, 13, 879–881. [Google Scholar] [CrossRef]
- Arya, S.P.S. Geostrophic drag and heat transfer relations for the atmospheric boundary layer. Quart. J. Roy. Meteor. Soc. 1975, 101, 147–161. [Google Scholar]
- Shen, Z.; Liu, L.; Lu, X.; Stevens, R.J.A.M. The global properties of nocturnal stable atmospheric boundary layers. J. Fluid Mech. 2024, 999, A60. [Google Scholar] [CrossRef]
- Zilitinkevich, S.; Johansson, P.E.; Mironov, D.V.; Baklanov, A. A similarity-theory model for wind profile and resistance law in stably stratified planetary boundary layers. J. Wind. Eng. Ind. Aerodyn. 1998, 74–76, 209–218. [Google Scholar] [CrossRef]
- Zilitinkevich, S.S.; Esau, I.N. On integral measures of the neutral barotrophic planetary boundary layer. Bound.-Layer Meteor. 2002, 104, 371–379. [Google Scholar]
- Narasimhan, G.; Gayme, D.F.; Meneveau, C. Analytical Model Coupling Ekman and Surface Layer Structure in Atmospheric Boundary Layer Flows. Bound.-Layer Meteorol. 2024, 190, 16. [Google Scholar] [CrossRef]
- Goger, B.; Rotach, M.W.; Gohm, A.; Stiperski, I.; Fuhrer, O.; de Morsier, G. A New Horizontal Length Scale for a Three-Dimensional Turbulence Parameterization in Mesoscale Atmospheric Modeling over Highly Complex Terrain. J. Appl. Meteorol. Climatol. 2019, 58, 2087–2102. [Google Scholar] [CrossRef]
- Kelly, M.; Cavar, D. Effective roughness and ‘displaced’ mean flow over complex terrain. Bound.-Layer Meteor. 2023, 186, 93–123. [Google Scholar] [CrossRef]
- Arya, S.P.S.; Wyngaard, J.C. Effect of Baroclinicity on Wind Profiles and the Geostrophic Drag Law for the Convective Planetary Boundary Layer. J. Atmos. Sci. 1975, 32, 767–778. [Google Scholar] [CrossRef]
- Floors, R.R.; Kelly, M.; Troen, I.; Peña, A.; Gryning, S.-E. Wind profile modelling using WAsP and “tall” wind measurements. In Proceedings of the 15th EMS Annual Meeting & 12th European Conference on Applications of Meteorology (ECAM) 2015, Sofia, Bulgaria, 7–11 September 2015; European Meteorological Society. 2015. [Google Scholar]
- Larsen, G.C.; Madsen, H.A.; Thomsen, K.; Larsen, T.J. Wake meandering: A pragmatic approach. Wind Energy 2008, 11, 377–395. [Google Scholar] [CrossRef]
- Larsen, G.C.; Machefaux, E.; Chougule, A. Wake meandering under non-neutral atmospheric stability conditions—Theory and facts. J. Physics: Conf. Ser. 2015, 625, 012036. [Google Scholar] [CrossRef]
- Hodgson, E.L.; Madsen, M.H.A.; Andersen, S.J. Effects of turbulent inflow time scales on wind turbine wake behavior and recovery. Phys. Fluids 2023, 35, 095125. [Google Scholar] [CrossRef]
- Andersen, S.J.; Sørensen, J.N.; Mikkelsen, R.F. Turbulence and entrainment length scales in large wind farms. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2017, 375, 20160107. [Google Scholar] [CrossRef]
- Syed, A.H.; Mann, J.; Platis, A.; Bange, J. Turbulence structures and entrainment length scales in large offshore wind farms. Wind Energy Sci. 2023, 8, 125–139. [Google Scholar] [CrossRef]
- Hodgson, E.L.; Troldborg, N.; Andersen, S.J. Impact of freestream turbulence integral length scale on wind farm flows and power generation. Renew. Energy 2025, 238, 121804. [Google Scholar] [CrossRef]
- Strickland, J.M.I.; Gadde, S.N.; Stevens, R.J.A.M. Wind farm blockage in a stable atmospheric boundary layer. Renew. Energy 2022, 197, 50–58. [Google Scholar] [CrossRef]
- Gomez, M.S.; Lundquist, J.K.; Mirocha, J.D.; Arthur, R.S. Investigating the physical mechanisms that modify wind plant blockage in stable boundary layers. Wind Energy Sci. 2023, 8, 1049–1069. [Google Scholar] [CrossRef]
- Liu, S.; Liang, X.Z. Observed Diurnal Cycle Climatology of Planetary Boundary Layer Height. J. Clim. 2010, 23, 5790–5809. [Google Scholar] [CrossRef]
- Regner, P.; Gruber, K.; Wehrle, S.; Schmidt, J. Explaining the decline of US wind output power density. Environ. Res. Commun. 2023, 5, 075016. [Google Scholar] [CrossRef]
- Jackson, P.S.; Hunt, J.C. Turbulent Wind Flow over a Low Hill. Quart. J. Roy. Meteor. Soc. 1975, 101, 929–955. [Google Scholar] [CrossRef]
- Troen, I. A high-resolution spectral model for flow in complex terrain. In Proceedings of the Ninth symposium on Turbulence and Diffusion, Roskilde, Denmark, 30 April–3 May 1990; Jensen, N.O., Kristensen, L., Larsen, S., Eds.; American Meteorological Society: Boston, MA, USA, 1990; pp. 417–420. [Google Scholar]
- Sempreviva, A.M.; Larsen, S.E.; Mortensen, N.G.; Troen, I. Response of neutral boundary layers to changes in roughness. Bound.-Layer Meteor. 1990, 50, 205–225. [Google Scholar] [CrossRef]
- Kelly, M.; Troen, I. Probabilistic stability and “tall” wind profiles: Theory and method for use in wind resource assessment. Wind Energy 2016, 19, 227–241. [Google Scholar] [CrossRef]
- Kelly, M.; Troen, I.; Jørgensen, H.E. Weibull-K Revisited: ‘tall” Profiles Height Var. Wind Stat. Bound.-Layer Meteor. 2014, 152, 107–124. [Google Scholar] [CrossRef]
- Kelly, M.; Larsen, G.; Dimitrov, N.K.; Natarajan, A. Probabilistic Meteorological Characterization for Turbine Loads. J. Phys. Conf. Ser. 2014, 524, 012076. [Google Scholar] [CrossRef]
- Kelly, M.; van der Laan, M.P. From Shear to Veer: Theory, Statistics, and Practical Application. Wind Energy Sci. 2023, 8, 975–998. [Google Scholar] [CrossRef]
- Carl, D.M.; Tarbell, T.C.; Panofsky, H.A. Profiles of Wind and Temperature from Towers over Homogeneous Terrain. J. Atmos. Sci. 1973, 30, 788–794. [Google Scholar] [CrossRef]
- Kelly, M.; Gryning, S.E. Long-Term Mean Wind Profiles Based on Similarity Theory. Bound.-Layer Meteor. 2010, 136, 377–390. [Google Scholar]
- Gryning, S.E.; Batchvarova, E.; Brümmer, B.; Jørgensen, H.; Larsen, S. On the extension of the wind profile over homogeneous terrain beyond the surface boundary layer. Bound.-Layer Meteor. 2007, 124, 371–379. [Google Scholar]
- Kelly, M.; Cersosimo, R.A.; Berg, J. A universal wind profile for the inversion-capped neutral atmospheric boundary layer. Q. J. R. Meteorol. Soc. 2019, 145, 982–992. [Google Scholar] [CrossRef]
- Liu, L.; Gadde, S.N.; Stevens, R.J. Universal Wind Profile for Conventionally Neutral Atmospheric Boundary Layers. Phys. Rev. Lett. 2021, 126, 104502. [Google Scholar] [CrossRef] [PubMed]
- Floors, R.; Peña, A.; Troen, I. Using observed and modelled heat fluxes for improved extrapolation of wind distributions. Bound.-Layer Meteorol. 2023, 188, 75–101. [Google Scholar] [CrossRef]
- Ghannam, K.; Bou-Zeid, E. Baroclinicity and directional shear explain departures from the logarithmic wind profile. Q. J. R. Meteorol. Soc. 2021, 147, 443–464. [Google Scholar] [CrossRef]
- Floors, R.; Pena, A.; Gryning, S.E. The effect of baroclinity on the wind in the Planetary boundary layer. Quart. J. Roy. Meteor. Soc. 2015, 141, 619–630. [Google Scholar]
- Narasimhan, G.; Gayme, D.F.; Meneveau, C. Analytical Wake Modeling in Atmospheric Boundary Layers: Accounting for Wind Veer and Thermal Stratification. J. Physics Conf. Ser. 2024, 2767, 092018. [Google Scholar] [CrossRef]
- Lanzilao, L.; Meyers, J. A parametric large-eddy simulation study of wind-farm blockage and gravity waves in conventionally neutral boundary layers. J. Fluid Mech. 2024, 979, A54. [Google Scholar] [CrossRef]
- Ott, S.; Nielsen, M. Developments of the Offshore Wind Turbine Wake Model Fuga; Technical Report E-0046; Danish Technical University: Roskilde, Denmark, 2014. [Google Scholar]
- Pedersen, M.M.; Forsting, A.M.; van der Laan, P.; Riva, R.; Alcayaga Romàn, L.A.; Criado Risco, J.; Friis-Møller, M.; Quick, J.; Schøler Christiansen, J.P.; Valotta Rodrigues, R.; et al. PyWake: An Open-Source Wind Farm Simulation Tool; Online Manual & Documentation; Danish Technical University: Roskilde, Denmark, 2025; Available online: https://topfarm.pages.windenergy.dtu.dk/PyWake/ (accessed on 24 February 2025).
- Sauer, J.A.; Muñoz-Esparza, D. The FastEddy® Resident-GPU Accelerated Large-Eddy Simulation Framework: Model Formulation, Dynamical-Core Validation and Performance Benchmarks. J. Adv. Model. Earth Syst. 2020, 12, e2020MS002100. [Google Scholar] [CrossRef]
- Olsen, B.T. Mesoscale to Microscale Coupling for Determining Site Conditions in Complex Terrain. Ph.D. Thesis, Danish Technical University, Risø Campus/National Lab, Roskilde, Denmark, 2018. [Google Scholar] [CrossRef]
- Temel, O.; Porchetta, S.; Bricteux, L.; van Beeck, J. RANS closures for non-neutral microscale CFD simulations sustained with inflow conditions acquired from mesoscale simulations. Appl. Math. Model. 2018, 53, 635–652. [Google Scholar] [CrossRef]
- Castorrini, A.; Gentile, S.; Geraldi, E.; Bonfiglioli, A. Increasing spatial resolution of wind resource prediction using NWP and RANS simulation. J. Wind Eng. Ind. Aerodyn. 2021, 210, 104499. [Google Scholar] [CrossRef]
- Çengel, Y.A.; Cimbala, J.M. Fluid Mechanics: Fundamentals and Applications, 4th ed.; McGraw-Hill Education: New York, NY, USA, 2018. [Google Scholar]
- Finnigan, J.; Ayotte, K.; Harman, I.; Katul, G.; Oldroyd, H.; Patton, E.; Poggi, D.; Ross, A.; Taylor, P. Boundary-Layer Flow Over Complex Topography. Bound.-Layer Meteorol. 2020, 177, 247–313. [Google Scholar] [CrossRef]
- Bou-Zeid, E.; Gao, X.; Ansorge, C.; Katul, G.G. On the role of return to isotropy in wall-bounded turbulent flows with buoyancy. J. Fluid Mech. 2018, 856, 61–78. [Google Scholar] [CrossRef]
- Sullivan, P.P.; Patton, E.G. The Effect of Mesh Resolution on Convective Boundary Layer Statistics and Structures Generated by Large-Eddy Simulation. J. Atmos. Sci. 2011, 68, 2395–2415. [Google Scholar] [CrossRef]
- Ortiz, A.V.; Koloszar, L. RANS thermal modelling of a natural convection boundary layer at low Prandtl number. Comput. Fluids 2023, 254, 105809. [Google Scholar] [CrossRef]
- Kelly, M.; Barlas, E.; Sogachev, A. Statistical prediction of far-field wind-turbine noise, with probabilistic characterization of atmospheric stability. J. Renew. Sustain. Energy 2018, 10, 013302. [Google Scholar] [CrossRef]
- Lazeroms, W.M.J.; Svensson, G.; Bazile, E.; Brethouwer, G.; Wallin, S.; Johansson, A.V. Study of Transitions in the Atmospheric Boundary Layer Using Explicit Algebraic Turbulence Models. Bound.-Layer Meteorol. 2016, 161, 19–47. [Google Scholar] [CrossRef]
- Baungaard, M.; Wallin, S.; van der Laan, M.P.; Kelly, M. Wind turbine wake simulation with explicit algebraic Reynolds stress modeling. Wind Energy Sci. 2022, 7, 1975–2002. [Google Scholar] [CrossRef]
- Skamarock, W.C.; Klemp, J.B.; Dudhia, J.; Gill, D.O.; Barker, D.M.; Duda, M.G.; Huang, X.Y.; Wang, W.; Powers, J.G. A Description of the Advanced Research WRF Version 3; Technical Note NCAR Tech. Note NCAR/TN-475+STR; National Center for Atmospheric Research (NCAR): Boulder, CO, USA, 2008. [Google Scholar] [CrossRef]
- Pielke, R.A. Mesoscale Meteorological Modeling, 3rd ed.; International Geophysics series; Elsevier/Academic Press: Cambridge, MA, USA, 2013; 726p. [Google Scholar] [CrossRef]
- Jiménez, P.A.; Dudhia, J. Improving the Representation of Resolved and Unresolved Topographic Effects on Surface Wind in the WRF Model. J. Appl. Meteorol. Climatol. 2012, 51, 300–316. [Google Scholar] [CrossRef]
- Pronk, V.; Bodini, N.; Optis, M.; Lundquist, J.K.; Moriarty, P.; Draxl, C.; Purkayastha, A.; Young, E. Can reanalysis products outperform mesoscale numerical weather prediction models in modeling the wind resource in simple terrain? Wind Energy Sci. 2022, 7, 487–504. [Google Scholar] [CrossRef]
- Vincent, C.L.; Badger, J.; Hahmann, A.N.; Kelly, M. The response of mesoscale models to changes in surface roughness. Geophysical Research Abstracts. In Proceedings of the European Geophysical Union (EGU) General Assembly, Vienna, Austria, 7–12 April 2013; Volume 15, p. 8548. [Google Scholar]
- Kelly, M.; Volker, P. WRF idealized-roughness response: PBL scheme and resolution dependence. In Proceedings of the 16th EMS Annual Meeting & 11th European Conference on Applied Climatology (ECAC), European Meteorological Society, Trieste, Italy, 12–16 September 2016. number EMS2016-389. [Google Scholar]
- Draxl, C.; Hahmann, A.N.; Peña, A.; Giebel, G. Evaluating winds and vertical wind shear from Weather Research and Forecasting model forecasts using seven planetary boundary layer schemes. Wind Energy 2014, 17, 39–55. [Google Scholar] [CrossRef]
- Haupt, S.E.; Jiménez, P.A.; Lee, J.A.; Kosović, B. Principles of meteorology and numerical weather prediction. In Renewable Energy Forecasting: From Models to Applications; Kariniotakis, G., Ed.; Woodhead: Cambridge, UK, 2017; Chapter 1; pp. 3–28. [Google Scholar] [CrossRef]
- Badger, J.; Frank, H.; Hahmann, A.N.; Giebel, G. Wind-Climate Estimation Based on Mesoscale and Microscale Modeling: Statistical-Dynamical Downscaling for Wind Energy Applications. J. Appl. Meteorol. Climatol. 2014, 53, 1901–1919. [Google Scholar] [CrossRef]
- Hahmann, A.N.; Vincent, C.L.; Peña, A.; Lange, J.; Hasager, C.B. Wind climate estimation using WRF model output: Method and model sensitivities over the sea. Int. J. Climatol. 2015, 35, 3422–3439. [Google Scholar] [CrossRef]
- Dörenkämper, M.; Olsen, B.T.; Witha, B.; Hahmann, A.N.; Davis, N.N.; Barcons, J.; Ezber, Y.; García-Bustamante, E.; González-Rouco, J.F.; Navarro, J.; et al. The Making of the New European Wind Atlas—Part 2: Production and evaluation. Geosci. Model Dev. 2020, 13, 5079–5102. [Google Scholar] [CrossRef]
- Davis, N.N.; Badger, J.; Hahmann, A.N.; Hansen, B.O.; Mortensen, N.G.; Kelly, M.; Larsén, X.G.; Olsen, B.T.; Floors, R.; Lizcano, G.; et al. The Global Wind Atlas: A High-Resolution Dataset of Climatologies and Associated Web-Based Application. Bull. Am. Meteorol. Soc. 2023, 104, E1507–E1525. [Google Scholar] [CrossRef]
- Hahmann, A.N.; Sīle, T.; Witha, B.; Davis, N.N.; Dörenkämper, M.; Ezber, Y.; García-Bustamante, E.; González-Rouco, J.F.; Navarro, J.; Olsen, B.T.; et al. The making of the New European Wind Atlas—Part 1: Model sensitivity. Geosci. Model Dev. 2020, 13, 5053–5078. [Google Scholar] [CrossRef]
- Mortensen, N.G.; Landberg, L.; Rathmann, O.; Frank, H.P.; Troen, I.; Petersen, E.L. Wind Atlas Analysis and Application Program (WAsP); Report; Risø National Laboratory: Roskilde, Denmark, 2001. [Google Scholar]
- Hahmann, A.N.; Lennard, C.; Badger, J.; Vincent, C.L.; Kelly, M.; Volker, P.J.; Argent, B.; Refslund, J. Mesoscale Modeling for the Wind Atlas of South Africa (WASA) Project; Technical Report DTU Wind Energy E-0050(EN); Wind Energy Department, Risø Lab/Campus, Danish Technical University (DTU): Roskilde, Denmark, 2015. [Google Scholar]
- Kelly, M.; Ribaudo, S.; Karagali, I.; Hahmann, A.N. Offshore wind uncertainty: ASCAT satellite data versus predictions from common WRF configurations over the North Sea. In Proceedings of the WindEurope2021: Technology Workshop on Resource Assessment & Analysis of Operating Wind Farms, Online, 8–10 September 2021; Available online: https://windeurope.org/tech2021/proceedings/ (accessed on 24 February 2025).
- Gaumond, M.; Réthoré, P.; Ott, S.; Peña, A.; Bechmann, A.; Hansen, K.S. Evaluation of the wind direction uncertainty and its impact on wake modeling at the Horns Rev offshore wind farm. Wind Energy 2014, 17, 1169–1178. [Google Scholar] [CrossRef]
- JCGM 100:2008; Evaluation of Measurement Data—Guide to the Expression of Uncertainty in Measurement. Joint Committee for Guides in Metrology: Sèvres, France, 2008; 120p. [CrossRef]
- JCGM 101:2008; Evaluation of Measurement Data—Supplement 1 to the “Guide to the Expression of Uncertainty in Measurement”—Propagation of Distributions Using a Monte Carlo Method. Joint Committee for Guides in Metrology: Sèvres, France, 2008; 82p. [CrossRef]
- JCGM 102:2011; Evaluation of Measurement Data—Supplement 2 to the “Guide to the Expression of Uncertainty in Measurement”—Extension to Any Number of Output Quantities. Joint Committee for Guides in Metrology: Sèvres, France, 2011; 72p. [CrossRef]
- JCGM GUM-1:2023; Guide to the Expression of Uncertainty in Measurement—Part 1: Introduction. Joint Committee for Guides in Metrology: Sèvres, France, 2023; 11p. [CrossRef]
- JCGM GUM-6:2020; Guide to the Expression of Uncertainty in Measurement—Part 6: Developing and Using Measurement Models. Joint Committee for Guides in Metrology: Sèvres, France, 2020; 95p. [CrossRef]
- Coleman, H.W.; Steele, W.G. Experimentation, Validation, and Uncertainty Analysis for Engineers; Wiley: Hoboken, NJ, USA, 2018; Available online: https://onlinelibrary.wiley.com/doi/book/10.1002/9781119417989 (accessed on 24 February 2025). [CrossRef]
- Huard, D.; Mailhot, A. A Bayesian perspective on input uncertainty in model calibration: Application to hydrological model “abc”. Water Resour. Res. 2006, 42. [Google Scholar] [CrossRef]
- Murcia Leon, J.P. Uncertainty Quantification in Wind Farm Flow Models. Ph.D Dissertation, Danish Technical University, Risø Campus, Roskilde, Denmark, 2017. [Google Scholar]
- Forbes, A.B. Approaches to evaluating measurement uncertainty. Int. J. Metrol. Qual. Eng. 2012, 3, 71–77. [Google Scholar] [CrossRef]
- Bich, W. Revision of the ‘Guide to the Expression of Uncertainty in Measurement’. Why and how. Metrologia 2014, 51, S155–S158. [Google Scholar] [CrossRef]
- Efremova, N.Y.; Chunovkina, A.G. Development of the Concept of Uncertainty in Measurement and Revision of Guide to the Expression of Uncertainty in Measurement. Part 1. Reasons and Probability-Theoretical Bases of the Revision. Meas. Tech. 2017, 60, 317–324. [Google Scholar] [CrossRef]
- Efremova, N.Y.; Chunovkina, A.G. Development of the Concept of Uncertainty in Measurement and Revision of the Guide to the Expression of Uncertainty in Measurement. Part 2. Comparative Analysis of Basic Provisions of the Guide and Their Planned Changes. Meas. Tech. 2017, 60, 418–424. [Google Scholar] [CrossRef]
- Hills, R.G.; Maniaci, D.C.; Naughton, J.W. V & V Framework; Technical Report SAND2015-7455; Sandia National Laboratories, Albequerque, NM, USA; Livermore, CA, USA, 2015. [CrossRef]
- ASME. Standard for Verification and Validation in Computational Fluid Dynamics andHeat Transfer; The American Society of Mechanical Engineers: New York, NY, USA, 2009. [Google Scholar]
- Mortensen, N.G.; Jørgensen, H.E.; Anderson, M.; Hutton, K. Comparison of resource and energy yield assessment procedures. In Proceedings of the EWEA 2012—European Wind Energy Conference & Exhibition, EWEA, Copenhagen, Denmark, 16–19 April 2012. [Google Scholar]
- Mortensen, N.G.; Jørgensen, H.E. Comparison of resource and energy yield assessment procedures (CREYAP), Part II. In Proceedings of the EWEA Technology Workshop: Resource Assessment, EWEA, Dublin, Ireland, 25–26 June 2013. [Google Scholar]
- Mortensen, N.G.; Nielsen, M.; Jørgensen, H.E. Comparison of resource and energy yield assessment procedures 2011–2015: What have we learned and what needs to be done? In Proceedings of the EWEA Annual Event and Exhibition 2015, European Wind Energy Association (EWEA), Paris, France, 17–20 November 2015; 10p.
- Fischereit, J.; Hansen, K.S.; Larsén, X.G.; van der Laan, M.P.; Réthoré, P.E.; Leon, J.P.M. Comparing and validating intra-farm and farm-to-farm wakes across different mesoscale and high-resolution wake models. Wind Energy Sci. 2022, 7, 1069–1091. [Google Scholar] [CrossRef]
- van der Laan, M.P.; García-Santiago, O.; Kelly, M.; Forsting, A.M.; Dubreuil-Boisclair, C.; Seim, K.S.; Imberger, M.; Peña, A.; Sørensen, N.N.; Réthoré, P.E. A new RANS-based wind farm parameterization and inflow model for wind farm cluster modeling. Wind Energy Sci. 2023, 8, 819–848. [Google Scholar] [CrossRef]
- Mortensen, N.G.; Nielsen, M.; Jørgensen, H.E. First Offshore Comparative Resource and Energy Yield Assessment Procedures (CREYAP). In Proceedings of the EWEA Offshore, EWEA, Frankfurt, Germany, 19–21 November 2013. [Google Scholar]
- Mortensen, N.G.; Nielsen, M.; Jørgensen, H. Offshore CREYAP Part 2 – final results. In Proceedings of the EWEA Technology Workshop: Resource Assessment, European Wind Energy Association, Helsinki, Finland, 2–3 June 2015. [Google Scholar]
- Badger, J.; Cavar, D.; Nielsen, M.; Mortensen, N.G.; Hansen, B.O. CREYAP 2021. In Proceedings of the WindEurope Technology Workshop 2021: Resource Assessment & Analysis of Operating Wind Farms, EWEA, Online (Pandemic-Accomodation), Naples, Italy, 8–10 September 2021. [Google Scholar]
- Maniaci, D.; Naughton, J.; Haupt, S.; Jonkman, J.; Robertson, A.; Churchfield, M.; Johnson, N.; Hsieh, A.; Cheung, L.; Herges, T.; et al. Offshore Wind Energy Validation Experiment Hierarchy. J. Phys. Conf. Ser. 2024, 2767, 062039. [Google Scholar] [CrossRef]
- Ramezani, M.; Choe, D.E.; Heydarpour, K.; Koo, B. Uncertainty models for the structural design of floating offshore wind turbines: A review. Renew. Sustain. Energy Rev. 2023, 185, 113610. [Google Scholar] [CrossRef]
- Dimitrov, N.K.; Kelly, M.; McWilliam, M.; Guiton, M.; Cousin, A.; Joulin, P.A.; Mayol, M.L.; Munoz-Zuniga, M.; Franceschini, L.; Lovera, A.; et al. End-to-end wind turbine design under uncertainties: A practical example. J. Physics: Conf. Ser. 2024, 2767, 082017. [Google Scholar] [CrossRef]
- Rafiee, A.; Repalle, N. Harnessing Uncertainty: A Generalized Polynomial Chaos Approach to Mooring Load Analysis in Offshore Floating Wind Turbines. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering (OMAE), ASME, Singapore, 9–14 June 2024; Volume 7. [Google Scholar] [CrossRef]
- Stadtmann, F.; Rasheed, A.; Kvamsdal, T.; Johannessen, K.A.; San, O.; Kölle, K.; Tande, J.O.; Barstad, I.; Benhamou, A.; Brathaug, T.; et al. Digital Twins in Wind Energy: Emerging Technologies and Industry-Informed Future Directions. IEEE Access 2023, 11, 110762–110795. [Google Scholar] [CrossRef]
- IEC Standard 61400–50; Wind Turbine Generator Systems—Part 50: Wind Measurement—Overview. International Electrotechnical Comission: Geneva, Switzerland, 2022.
- IEC Standard 61400–50-1; Wind Turbine Generator Systems—Part 50-1: Wind Measurement—Application of Meteorological Mast, Nacelle and Spinner Mounted Instruments. International Electrotechnical Comission: Geneva, Switzerland, 2022.
- IEC Standard 61400–50-2; Wind Turbine Generator Systems—Part 50-2: Wind Measurement—Application of Ground-Mounted Remote Sensing Technology. International Electrotechnical Comission: Geneva, Switzerland, 2022.
- IEC Standard 61400–50-3; Wind Turbine Generator Systems—Part 50-3: Use of Nacelle-Mounted Lidars for Wind Measurements. International Electrotechnical Comission: Geneva, Switzerland, 2022.
- IEC Standard 61400–12; Wind Turbine Generator Systems—Part 12: Power Performance Measurements of Electricity Producing Wind Turbines—Overview. International Electrotechnical Comission: Geneva, Switzerland, 2021.
- IEC Standard 61400–12-1; Wind Turbine Generator Systems—Part 12-1: Power Performance Measurements of Electricity Producing Wind Turbines. International Electrotechnical Comission: Geneva, Switzerland, 2022.
- IEC Standard 61400–12-2; Wind Turbine Generator Systems—Part 12-2: Power Performance Measurements of Electricity Producing Wind Turbines Based on Nacelle Anemometry. International Electrotechnical Comission: Geneva, Switzerland, 2022.
- IEC Standard 61400–12-3; Wind Turbine Generator Systems—Part 12-3: Power Performance—Measurement Based Site Calibration. International Electrotechnical Comission: Geneva, Switzerland, 2022.
- IEC Standard 61400–12-6; Wind Turbine Generator Systems—Part 12-6: Measurement Based Nacelle Transfer Function of Electricity Producing Wind Turbines. International Electrotechnical Comission: Geneva, Switzerland, 2022.
- MEASNET. Anemometer Calibration Procedure, version 3; Technical Report; Measuring-Network of Wind Energy Institutes: Madrid, Spain, 2020; Available online: https://www.measnet.com/documents/ (accessed on 24 February 2025).
- Clerc, A.; Anderson, M.; Stuart, P.; Habenicht, G. A systematic method for quantifying wind flow modelling uncertainty in wind resource assessment. J. Wind Eng. Ind. Aerodyn. 2012, 111, 85–94. [Google Scholar] [CrossRef]
- Troen, I.; Bechmann, A.; Kelly, M.; Sørensen, N.N.; Réthoré, P.E.; Cavar, D.; Ejsing Jørgensen, H. Complex terrain wind resource estimation with the wind-atlas method: Prediction errors using linearized and nonlinear CFD micro-scale models. In Proceedings of the 2014 EWEA Conference, Barcelona, Spain, 10–13 March 2014. [Google Scholar]
- Kelly, M.; Kersting, G.; Mazoyer, P.; Yang, C.; Fillols, F.H.; Clark, S.; Matos, J.C. Uncertainty in Vertical Extrapolation of Measured Wind Speed via Shear; Technical Report DTU Wind Energy E-0195(EN); Wind Energy Department, Risø Lab/Campus, Danish Technical University (DTU): Roskilde, Denmark, 2019. [Google Scholar] [CrossRef]
- Triviño, C.; Leask, P.; Ostridge, C. Validation of Vertical Wind Shear Methods. J. Phys. Conf. Ser.-Conf. Sess. 2 2017, 926. [Google Scholar] [CrossRef]
- Kelly, M. Uncertainty in Vertical Extrapolation of Wind Statistics: Shear-Exponent and WAsP/EWA Methods; Technical Report DTU Wind Energy E-0121(EN); Wind Energy Department, Risø Lab/Campus, Danish Technical University (DTU): Roskilde, Denmark, 2016. [Google Scholar]
- Pryor, S.C.; Barthelmie, R.J.; Bukovsky, M.S.; Leung, L.R.; Sakaguchi, K. Climate change impacts on wind power generation. Nat. Rev. Earth Environ. 2020, 1, 627–643. [Google Scholar] [CrossRef]
- Jung, C.; Schindler, D. A review of recent studies on wind resource projections under climate change. Renew. Sustain. Energy Rev. 2022, 165, 112596. [Google Scholar] [CrossRef]
- Yan, J.; Möhrlen, C.; Göçmen, T.; Kelly, M.; Wessel, A.; Giebel, G. Uncovering wind power forecasting uncertainty sources and their propagation through the whole modelling chain. Renew. Sustain. Energy Rev. 2022, 165, 112519. [Google Scholar] [CrossRef]
- Möhrlen, C.; Bessa, R.J.; Fleischhut, N. A decision-making experiment under wind power forecast uncertainty. Meteorol. Appl. 2022, 29, e2077. [Google Scholar] [CrossRef]
- Lenschow, D.H.; Mann, J.; Kristensen, L. How long is long enough when measuring fluxes and other turbulence statistics? J. Atmos. Ocean Technol. 1994, 11, 661–673. [Google Scholar] [CrossRef]
- MEASNET. Evaluation of Site-Specific Wind Conditions, version 3; Technical Report; Measuring-Network of Wind Energy Institutes: Madrid, Spain, 2022; Available online: https://www.measnet.com/documents/ (accessed on 24 February 2025).
- IEC Standard 61400–15-1; Wind Energy Generation Systems—Part 15-1: Site Suitability Input Conditions for Wind Power Plants. International Electrotechnical Comission: Geneva, Switzerland, 2025.
- der Kiureghian, A.; Ditlevsen, O. Aleatory or epistemic? Does it matter? Struct. Saf. 2009, 31, 105–112. [Google Scholar] [CrossRef]
- Kelly, M.; Jørgensen, H.E. Statistical characterization of roughness uncertainty and impact on wind resource estimation. Wind Energy Sci. 2017, 2, 189–209. [Google Scholar] [CrossRef]
- Hale, E. The Uncertainty of Uncertainty. In Proceedings of the NREL 3rd Wind Energy Systems Engineering Workshop, Boulder, CO, USA, 14 January 2015; Available online: https://www.nrel.gov/wind/systems-engineering-workshop-2015.html (accessed on 24 February 2025).
- Lee, J.C.; Jason Fields, M. An overview of wind-energy-production prediction bias, losses, and uncertainties. Wind Energy Sci. 2021, 6, 311–365. [Google Scholar] [CrossRef]

| Component (bold) or subcomponent (italic) |
| Measurement Uncertainty |
| Wind speed measurement |
| Wind direction measurement/rose |
| Other atmospheric parameters |
| Data integrity and documentation |
| Historical Wind Resource (LTC) |
| Representativeness of long-term reference period |
| Reference data consistency |
| Long-term correction method |
| On-site gap-filling/synthesis |
| Representativeness of measured data |
| Wind distribution fit |
| Horizontal Extrapolation and flow modeling |
| Model inputs |
| Model “stress” (deviation from operational envelope) |
| Model appropriateness |
| Vertical (power-law) Extrapolation |
| Model representativeness † |
| Excess uncertainty propagated by VE-model |
| Project Evaluation Period Variability |
| Interannual variability (IAV) of wind speed |
| Climate change |
| (IAV of plant performance) ‡ |
| Plant Performance |
| Turbine interaction/wake and blockage effects |
| (Non-wind elements) ‡ |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kelly, M. Beyond the First Generation of Wind Modeling for Resource Assessment and Siting: From Meteorology to Uncertainty Quantification. Energies 2025, 18, 1589. https://doi.org/10.3390/en18071589
Kelly M. Beyond the First Generation of Wind Modeling for Resource Assessment and Siting: From Meteorology to Uncertainty Quantification. Energies. 2025; 18(7):1589. https://doi.org/10.3390/en18071589
Chicago/Turabian StyleKelly, Mark. 2025. "Beyond the First Generation of Wind Modeling for Resource Assessment and Siting: From Meteorology to Uncertainty Quantification" Energies 18, no. 7: 1589. https://doi.org/10.3390/en18071589
APA StyleKelly, M. (2025). Beyond the First Generation of Wind Modeling for Resource Assessment and Siting: From Meteorology to Uncertainty Quantification. Energies, 18(7), 1589. https://doi.org/10.3390/en18071589






