Assessment of Risks of Voltage Quality Decline in Load Nodes of Power Systems
Abstract
1. Introduction
2. Materials and Methods
3. Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hovorov, P.; Kindinava, A.; Hovorov, V.; Abdelrhim, O. Control of Modes of Power Supply and Lighting Systems of Cities Based on the Concept of Smart-Grid. In Proceedings of the 2022 IEEE 8th International Conference on Energy Smart Systems (ESS), Kyiv, Ukraine, 12–14 October 2022; pp. 21–25. [Google Scholar] [CrossRef]
- Prokhorova, V.; Budanov, M.; Budanov, P. Devising an integrated methodology for energy safety assessment at an industrial power-generating enterprise. East.-Eur. J. Enterp. Technol. 2024, 130, 118–131. [Google Scholar] [CrossRef]
- Lezhniuk, P.; Rubanenko, O.; Komar, V.; Sikorska, O. The Sensitivity of the Model of the Process Making the Optimal Decision for Electric Power Systems in Relative Units. In Proceedings of the 2020 IEEE KhPI Week on Advanced Technology (KhPIWeek), Kharkiv, Ukraine, 5–10 October 2020; pp. 247–252. [Google Scholar] [CrossRef]
- Zharkin, A.F.; Novskiy, V.O.; Popov, V.A.; Yarmoliuk, O.S. Improving the Efficiency of Distribution Network Control Under the Conditions of Application of Distributed Sources Generation of Electrical Energy and Means of Its Accumulation. Tech. Electrodyn. 2021, 2021, 37–43. [Google Scholar] [CrossRef]
- Zharkin, A.; Pazieiev, A. Analysis of dynamic instability of output voltage in active power factor correctors. In Proceedings of the 2020 IEEE KhPI Week on Advanced Technology (KhPIWeek), Kharkiv, Ukraine, 5–10 October 2020; pp. 411–414. [Google Scholar] [CrossRef]
- Zharkin, F.; Palachov, S.O.; Pazieyev, A.G.; Malakhatka, D.O. Determination of optimal characteristics of devices for voltage unbalance reducing in low voltage electric networks. Tech. Electrodyn. 2020, 2020, 43–46. [Google Scholar] [CrossRef]
- Alhelou, H.H.; Hamedani-Golshan, M.E.; Njenda, T.C.; Siano, P. A survey on power system blackout and cascading events: Research motivations and challenges. Energies 2019, 12, 682. [Google Scholar] [CrossRef]
- Sun, H.; Guo, Q.; Qi, J.; Ajjarapu, V.; Bravo, R.; Chow, J.; Li, Z.; Moghe, R.; Nasr-Azadani, E.; Tamrakar, U.; et al. Review of Challenges and Research Opportunities for Voltage Control in Smart Grids. IEEE Trans. Power Syst. 2019, 34, 2790–2801. [Google Scholar] [CrossRef]
- Sovacool, B.K.; Furszyfer Del Rio, D.D. Smart home technologies in Europe: A critical review of concepts, benefits, risks and policies. Renew. Sustain. Energy Rev. 2020, 120, 109663. [Google Scholar] [CrossRef]
- Ahmad, T.; Zhu, H.; Zhang, D.; AlGhamdi, A.S.; Alshamrani, S.S. Energetics Systems and artificial intelligence: Applications of industry 4.0. Energy Rep. 2022, 8, 334–361. [Google Scholar] [CrossRef]
- Hovorov, P.; Hovorov, V.; Kindinova, A. Modeling of processes in a voltage-boosting transformer as an element of Smart-Grid power systems. In Proceedings of the 2021 IEEE 62nd International Scientific Conference on Power and Electrical Engineering of Riga Technical University (RTUCON), Riga, Latvia, 15–17 November 2021; pp. 1–4. [Google Scholar] [CrossRef]
- Scheiter, M.; Valentine, A.; Sambridge, M. Upscaling and downscaling Monte Carlo ensembles with generative models. Geophys. J. Int. 2022, 230, 916–931. [Google Scholar] [CrossRef]
- Trishch, R.; Cherniak, O.; Zdenek, D.; Petraskevicius, V. Assessment of the occupational health and safety manage-ment system by qualimetric methods. Eng. Manag. Prod. Serv. 2024, 16, 118–127. [Google Scholar] [CrossRef]
- Jeevith, H.; Børge, R. Applications of machine learning methods for engineering risk assessment—A review. Saf. Sci. 2020, 122, 104492. [Google Scholar] [CrossRef]
- Cherniak, O.; Trishch, R.; Ginevičius, R.; Nechuiviter, O.; Burdeina, V. Methodology for Assessing the Processes of the Occupational Safety Management System Using Functional Dependencies. In Integrated Computer Technologies in Mechanical Engineering—2023. ICTM 2023; Lecture Notes in Networks and Systems; Springer: Cham, Switzerland, 2024; Volume 996, pp. 3–13. [Google Scholar] [CrossRef]
- Hrinchenko, H.; Trisch, R.; Burdeina, V.; Chelysheva, S. Algorithm of technical diagnostics of the complicated damage to the continued resource of the circulation pipeline of the nuclear power plant. Probl. At. Sci. Technol. 2019, 120, 104–110. [Google Scholar] [CrossRef]
- Khomiak, E.; Trishch, R.; Zabolotnyi, O.; Cherniak, O.; Lutai, L.; Katrich, O. Automated Mode of Improvement of the Quality Control System for Nuclear Reactor Fuel Element Shell Tightness. In Information Technology for Education, Science, and Technics, ITEST 2024; Lecture Notes on Data Engineering and Communications Technologies; Emil, F., Yurii, T., Tero, V., Olena, D., Maksym, B., Constantine, B., Grygoriy, Z., Eds.; Springer: Cham, Switzerland, 2024; Volume 221, pp. 79–91. [Google Scholar] [CrossRef]
- Khomiak, E.; Burdeina, V.; Cherniak, O.; Olesia, N.; Bubela, T. Improving the Method of Quality Control of the Fuel Element Shell in Order to Improve the Safety of a Nuclear Reactor. In Integrated Computer Technologies in Mechanical Engineering—2023. ICTM 2023; Lecture Notes in Networks and Systems; Springer: Cham, Switzerland, 2024; Volume 1008, pp. 351–360. [Google Scholar] [CrossRef]
- Markulik, Š.; Šolc, M.; Blaško, P. Use of Risk Management to Support Business Sustainability in the Automotive Industry. Sustainability 2024, 16, 4308. [Google Scholar] [CrossRef]
- Dyadyura, K.; Slyuz, A.; Vysotsky, I.Y.; Bubela, T.; Cherniak, O. Decision Support Algorithm at the Life Cycle Stages of Medical Devices Based on the Application of Markov Process. In Integrated Computer Technologies in Mechanical Engineering—2023. ICTM 2023; Lecture Notes in Networks and Systems; Nechyporuk, M., Pavlikov, V., Krytskyi, D., Eds.; Springer: Cham, Switzerland, 2024; Volume 996, pp. 87–97. [Google Scholar] [CrossRef]
- Kumar, M.; Epiphaniou, G.; Maple, C. Comprehensive Threat Analysis in Additive Manufacturing Supply Chain: A Hybrid Qualitative and Quantitative Risk Assessment Framework. Prod. Eng. Res. Devel 2024, 18, 955–973. [Google Scholar] [CrossRef]
- Kupriyanov, O.; Trishch, R.; Dichev, D.; Kupriianova, K. A General Approach for Tolerance Control in Quality Assessment for Technology Quality Analysis. In Grabchenko’s International Conference on Advanced Manufacturing Processes; Lecture Notes in Mechanical Engineering; Springer: Cham, Switzerland, 2023; pp. 330–339. [Google Scholar] [CrossRef]
- Riabchykov, M.; Alexandrov, A.; Trishch, R.; Nikulina, A.; Korolyova, N. Prospects for the Development of Smart Clothing with the Use of Textile Materials with Magnetic Properties|Možnosti za razvoj pametnih oblačil z uporabo tekstilnih materialov z magnetnimi lastnostmi. Tekstilec 2022, 65, 36–43. [Google Scholar] [CrossRef]
- Mahmud, K.; Sahoo, A.K.; Fernandez, E.; Sanjeevikumar, P.; Holm-Nielsen, J.B. Computational Tools for Modeling and Analysis of Power Generation and Transmission Systems of the Smart Grid. IEEE Syst. J. 2020, 14, 3641–3652. [Google Scholar] [CrossRef]
- Ahmad, T.; Zhang, D.; Huang, C. Methodological framework for short-and medium-term energy, solar and wind power forecasting with stochastic-based machine learning approach to monetary and energy policy applications. Energy 2021, 231, 120911. [Google Scholar] [CrossRef]
- Huang, C.; Zhang, H.; Song, Y.; Wang, L.; Ahmad, T.; Luo, X. Demand Response for Industrial Micro-Grid Considering Photovoltaic Power Uncertainty and Battery Operational Cost. IEEE Trans. Smart Grid 2021, 12, 3043–3055. [Google Scholar] [CrossRef]
- Ahmad, T.; Zhang, D. Using the internet of things in smart energy systems and networks. Sustain. Cities Soc. 2021, 68, 102783. [Google Scholar] [CrossRef]
- Suman, S. Artificial intelligence in nuclear industry: Chimera or solution. J. Clean. Prod. 2021, 278, 124022. [Google Scholar] [CrossRef]
- Kiran, P.; Chandrakala, K.V. New interactive agent based reinforcement learning approach towards smart generator bidding in electricity market with micro grid integration. Appl. Soft Comput. 2020, 97, 106762. [Google Scholar] [CrossRef]
- Chang, C.-L.; McAleer, M.; Wang, Y.A. Herding behaviour in energy stock markets during the Global Financial Crisis, SARS, and ongoing COVID-19. Renew. Sustain. Energy Rev. 2020, 134, 110349. [Google Scholar] [CrossRef] [PubMed]
- Garcia, C.I.; Grasso, F.; Luchetta, A.; Piccirilli, M.C.; Paolucci, L.; Talluri, G. A comparison of power quality disturbance detection and classification methods using CNN, LSTM and CNN-LSTM. Appl. Sci. 2020, 10, 6755. [Google Scholar] [CrossRef]
- Mahela, O.P.; Khan, B.; Alhelou, H.H.; Tanwar, S. Assessment of power quality in the utility grid integrated with wind energy generation. IET Power Electron. 2020, 13, 2917–2925. [Google Scholar]
- Kharrazi, A.; Sreeram, V.; Mishra, Y. Assessment techniques of the impact of grid-tied rooftop photovoltaic generation on the power quality of low voltage distribution network—A review. Renew. Sustain. Energy Rev. 2020, 120, 109643. [Google Scholar]
- Martinez, R.; Castro, P.; Arroyo, A.; Manana, M.; Galan, N.; Moreno, F.S.; Bustamante, S.; Laso, A. Techniques to Locate the Origin of Power Quality Disturbances in a Power System: A Review. Sustainability 2022, 14, 7428. [Google Scholar] [CrossRef]
- Ciontea, C.I.; Iov, F. A Study of Load Imbalance Influence on Power Quality Assessment for Distribution Networks. Electricity 2021, 2, 77–90. [Google Scholar] [CrossRef]
- Adewumi, O.B.; Fotis, G.; Vita, V.; Nankoo, D.; Ekonomou, L. The Impact of Distributed Energy Storage on Distribution and Transmission Networks’ Power Quality. Appl. Sci. 2022, 12, 6466. [Google Scholar] [CrossRef]
- Toopshekan, A.; Yousefi, H.; Astaraei, F.R. Technical, economic, and performance analysis of a hybrid energy system using a novel dispatch strategy. Energy 2020, 213, 118850. [Google Scholar] [CrossRef]
- Ledesma, J.J.G.; do Nascimento, K.B.; de Araujo, L.R.; Penido, D.R.R. A two-level ANN-based method using synchronized measurements to locate high-impedance fault in distribution systems. Electr. Power Syst. Res. 2020, 188, 106576. [Google Scholar] [CrossRef]
- Badiei, A.; Akhlaghi, Y.G.; Zhao, X.; Shittu, S.; Xiao, X.; Li, J.; Fan, Y.; Li, G. A chronological review of advances in solar assisted heat pump technology in 21st century. Renew. Sustain. Energy Rev. 2020, 132, 110132. [Google Scholar] [CrossRef]
- Ali, M.; Prasad, R.; Xiang, Y.; Deo, R.C. Near real-time significant wave height forecasting with hybridized multiple linear regression algorithms. Renew. Sustain. Energy Rev. 2020, 132, 110003. [Google Scholar] [CrossRef]
- Bracale, A.; Caramia, P.; De Falco, P.; Hong, T. A Multivariate Approach to Probabilistic Industrial Load Forecasting. Electr. Power Syst. Res. 2020, 187, 106430. [Google Scholar] [CrossRef]
- Ramirez, A.D.; Boero, A.; Rivela, B.; Melendres, A.M.; Espinoza, S.; Salas, D.A. Life cycle methods to analyze the environmental sustainability of electricity generation in Ecuador: Is decarbonization the right path. Renew. Sustain. Energy Rev. 2020, 134, 110373. [Google Scholar] [CrossRef]
- Shi, Z.; Yao, W.; Li, Z.; Zeng, L.; Zhao, Y.; Zhang, R.; Tang, Y.; Wen, J. Artificial intelligence techniques for stability analysis and control in smart grids: Methodologies, applications, challenges and future directions. Appl. Energy 2020, 278, 115733. [Google Scholar] [CrossRef]
- Kaya, S.K.; Erginel, N. Futuristic airport: A sustainable airport design by integrating hesitant fuzzy SWARA and hesitant fuzzy sustainable quality function deployment. J. Clean. Prod. 2020, 275, 123880. [Google Scholar] [CrossRef]
- Matemilola, S.; Fadeyi, O.; Sijuade, T. Paris Agreement. In Encyclopedia of Sustainable Management; Idowu, S., Schmidpeter, R., Capaldi, N., Zu, L., Del Baldo, M., Abreu, R., Eds.; Springer: Cham, Switzerland, 2020. [Google Scholar] [CrossRef]
- Atitallah, S.B.; Driss, M.; Boulila, W.; Ghézala, H.B. Leveraging Deep Learning and IoT big data analytics to support the smart cities development: Review and future directions. Comput. Sci. Rev. 2020, 38, 100303. [Google Scholar] [CrossRef]
- Aly, H.H. A novel deep learning intelligent clustered hybrid models for wind speed and power forecasting. Energy 2020, 213, 118773. [Google Scholar] [CrossRef]
- Yun, J.; Jayababu, N.; Kim, D. Self-powered transparent and flexible touchpad based on triboelectricity towards artificial intelligence. Nano Energy 2020, 78, 105325. [Google Scholar] [CrossRef]
- Tushar, W.; Saha, T.K.; Yuen, C.; Smith, D.; Ashworth, P.; Poor, H.V.; Basnet, S. Challenges and prospects for negawatt trading in light of recent technological developments. Nat. Energy 2020, 5, 834–841. [Google Scholar] [CrossRef]
- Bienvenido-Huertas, D.; Farinha, F.; Oliveira, M.J.; Silva, E.M.; Lança, R. Comparison of artificial intelligence algorithms to estimate sustainability indicators. Sustain. Cities Soc. 2020, 63, 102430. [Google Scholar] [CrossRef]
- Chen, L.; Wu, J.; Wu, F.; Tang, H.; Li, C.; Xiong, Y. Energy flow optimization method for multi-energy system oriented to combined cooling, heating and power. Energy 2020, 211, 118536. [Google Scholar] [CrossRef]
- Adjerid, H.; Maouche, A.R. Multi-Agent system-based decentralized state estimation method for active distribution networks. Comput. Electr. Eng. 2020, 86, 106652. [Google Scholar]
- Ruhnau, O.; Hennig, P.; Madlener, R. Economic implications of forecasting electricity generation from variable renewable energy sources. Renew. Energy 2020, 161, 1318–1327. [Google Scholar] [CrossRef]
- Nguyen, M.T.; Truong, L.H.; Tran, T.T.; Chien, C.F. Artificial intelligence based data processing algorithm for video surveillance to empower industry 3.5. Comput. Ind. Eng. 2020, 148, 106671. [Google Scholar] [CrossRef]
- Hsu, C.Y.; Chen, W.J.; Chien, J.C. Similarity matching of wafer bin maps for manufacturing intelligence to empower Industry 3.5 for semiconductor manufacturing. Comput. Ind. Eng. 2020, 142, 106358. [Google Scholar] [CrossRef]
- Xu, Z.; Zheng, Z.; Gao, X. Energy-efficient steelmaking-continuous casting scheduling problem with temperature constraints and its solution using a multi-objective hybrid genetic algorithm with local search. Appl. Soft Comput. 2020, 95, 106554. [Google Scholar] [CrossRef]
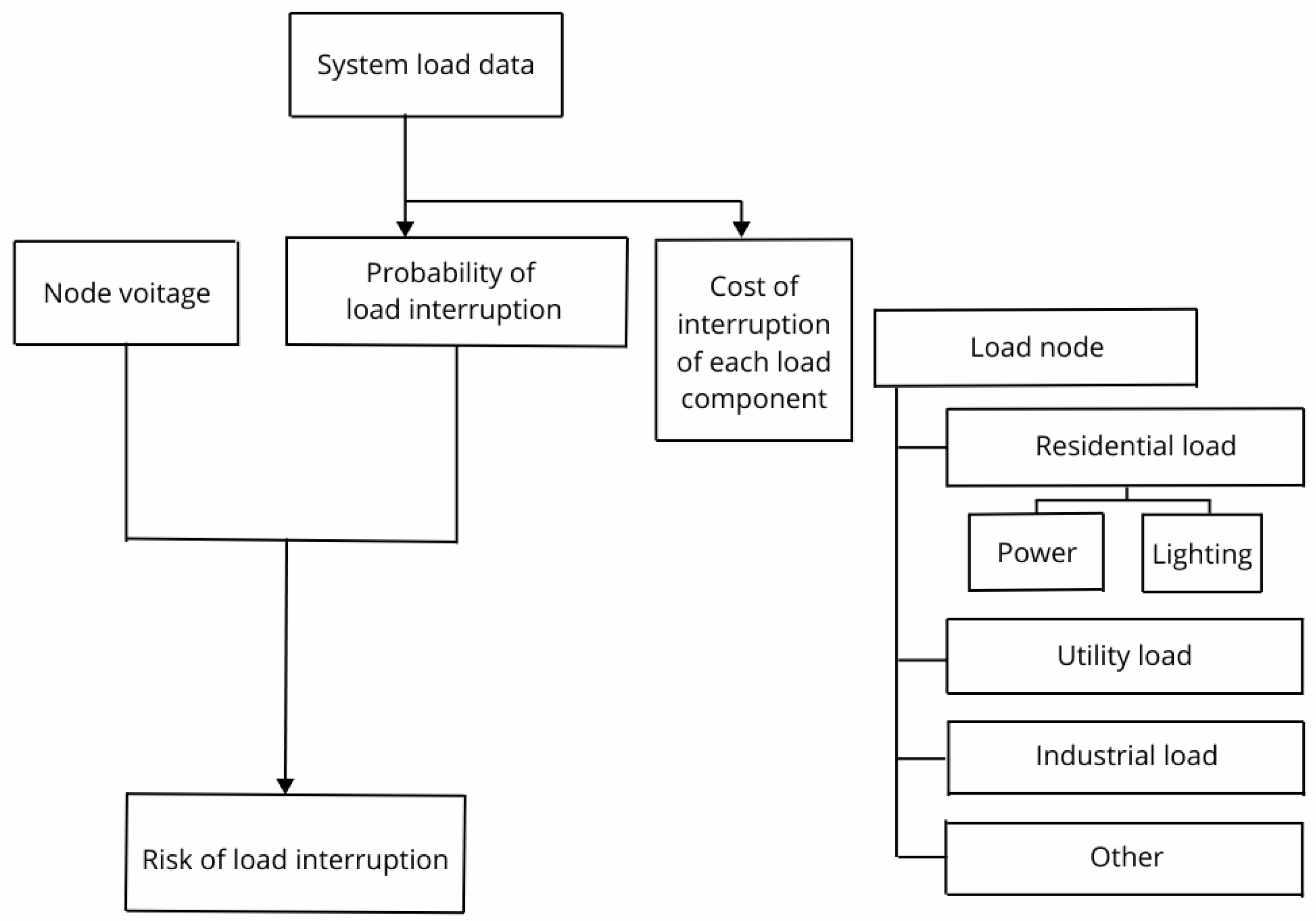
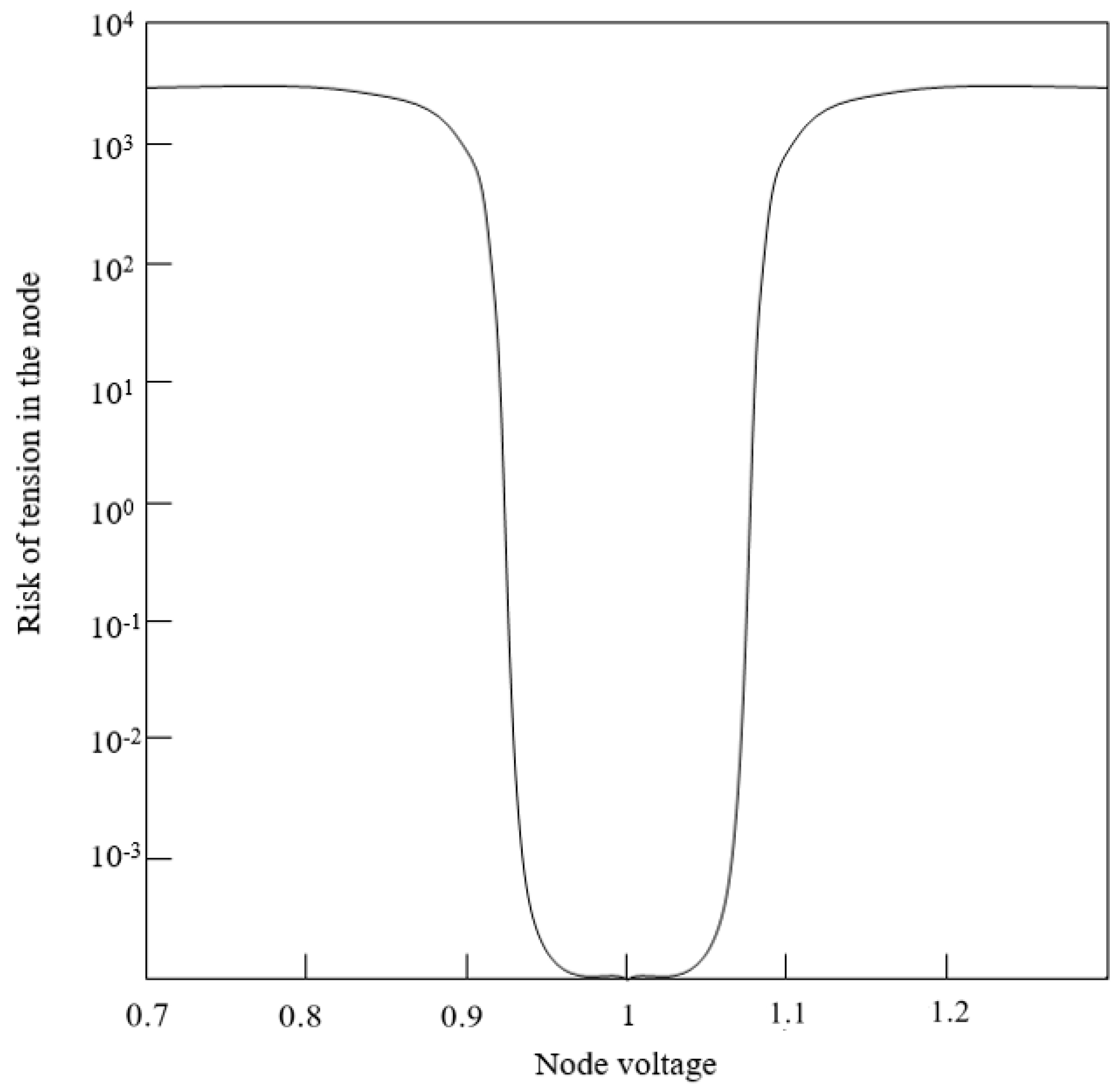
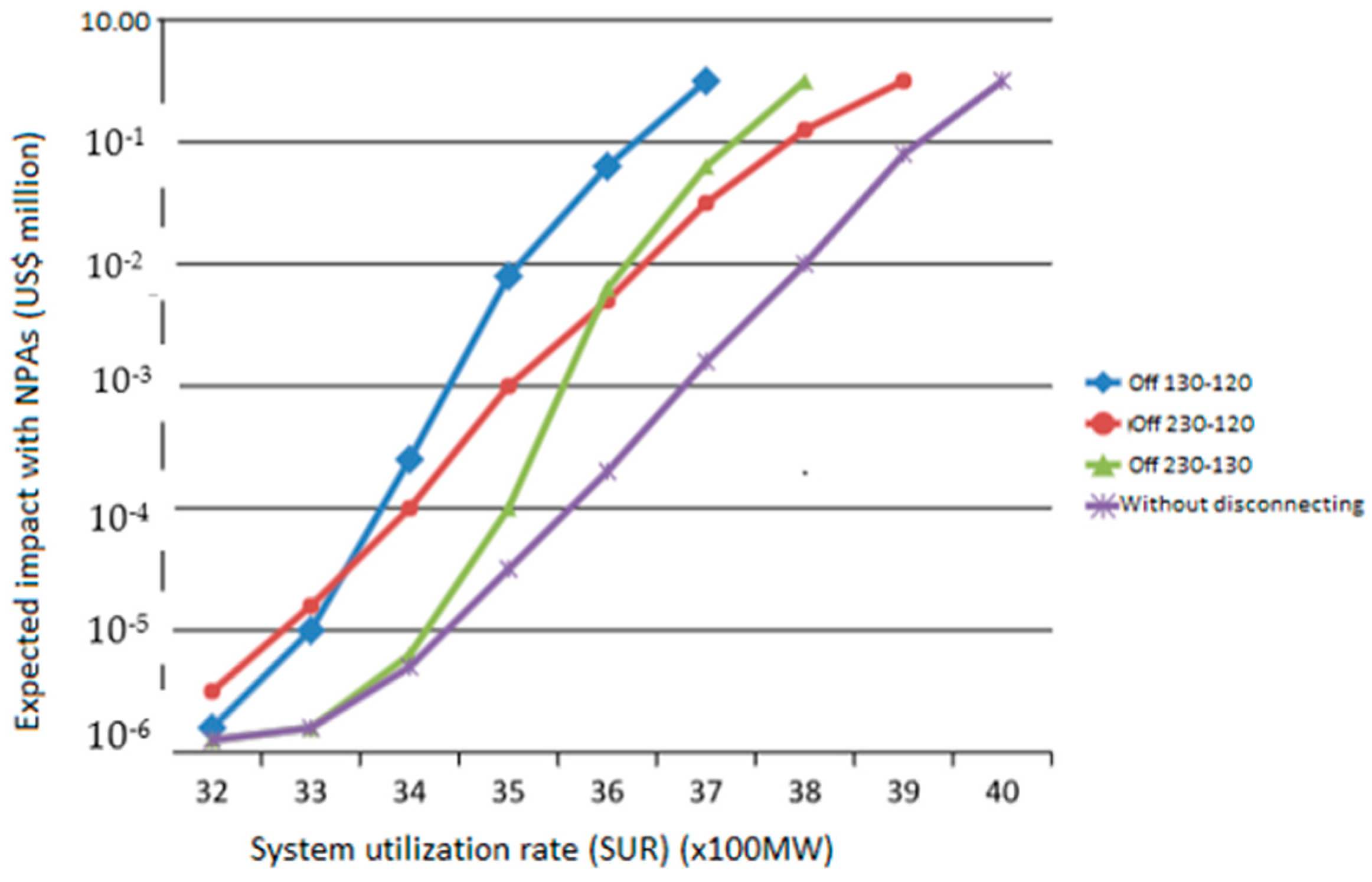
| Device | Voltage Level |
|---|---|
| Communication equipment | ±5% |
| Computers, data processing equipment | ±10% |
| Motor starters | |
| Lighting | from −15% to +10% |
| Luminescent | −10%, +25% |
| Incandescent lamp | =18% |
| Motors, standard starting | ±10% |
| Resistive loads, furnaces, heaters, etc. | Hesitates |
| Other | Hesitates |
| Emergency Situation | Probability of Occurrence | Capacity Load (×100 MW) |
|---|---|---|
| No irregularities in operation | 0.9999 | 40.70 |
| Disorderly conduct 130-120 | 4.58 × 10−5 | 39.14 |
| Disorderly conduct 230-130 | 4.58 × 10−5 | 37.32 |
| Disorderly conduct 230-120 | 4.58 × 10−5 | 36.89 |
| Emergency Situation | Probability of Occurrence | Expected Load ×100 MW | Standard Deviation ×100 MW |
|---|---|---|---|
| No irregularities in operation | 0.9999 | 40.70 | 0.3839 |
| No irregularities in operation 130-120 | 4.58 × 10−5 | 39.14 | 0.4179 |
| No irregularities in operation 230-130 | 4.58 × 10−5 | 37.32 | 0.3970 |
| No irregularities in operation 230-120 | 4.58 × 10−5 | 36.89 | 0.3353 |
| Emergency Situation | Probability of Occurrence | Expected Load ×100 MW | Standard Deviation ×100 MW |
|---|---|---|---|
| No irregularities in operation | 4.70 | 0.8160 | 4.3 × 10−9 |
| No irregularities in operation 130-120 | 3.14 | 0.8325 | 8.0 × 10−5 |
| No irregularities in operation 230-130 | 1.32 | 0.8225 | 0.0547 |
| No irregularities in operation 230-120 | 0.89 | 0.7942 | 0.1306 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hovorov, P.; Trishch, R.; Ginevičius, R.; Petraškevičius, V.; Šuhajda, K. Assessment of Risks of Voltage Quality Decline in Load Nodes of Power Systems. Energies 2025, 18, 1579. https://doi.org/10.3390/en18071579
Hovorov P, Trishch R, Ginevičius R, Petraškevičius V, Šuhajda K. Assessment of Risks of Voltage Quality Decline in Load Nodes of Power Systems. Energies. 2025; 18(7):1579. https://doi.org/10.3390/en18071579
Chicago/Turabian StyleHovorov, Pylyp, Roman Trishch, Romualdas Ginevičius, Vladislavas Petraškevičius, and Karel Šuhajda. 2025. "Assessment of Risks of Voltage Quality Decline in Load Nodes of Power Systems" Energies 18, no. 7: 1579. https://doi.org/10.3390/en18071579
APA StyleHovorov, P., Trishch, R., Ginevičius, R., Petraškevičius, V., & Šuhajda, K. (2025). Assessment of Risks of Voltage Quality Decline in Load Nodes of Power Systems. Energies, 18(7), 1579. https://doi.org/10.3390/en18071579







