An Evaluation of the Power System Stability for a Hybrid Power Plant Using Wind Speed and Cloud Distribution Forecasts
Abstract
1. Introduction
1.1. Background
1.2. The Objective and Method
2. Prediction of the Photovoltaic Power
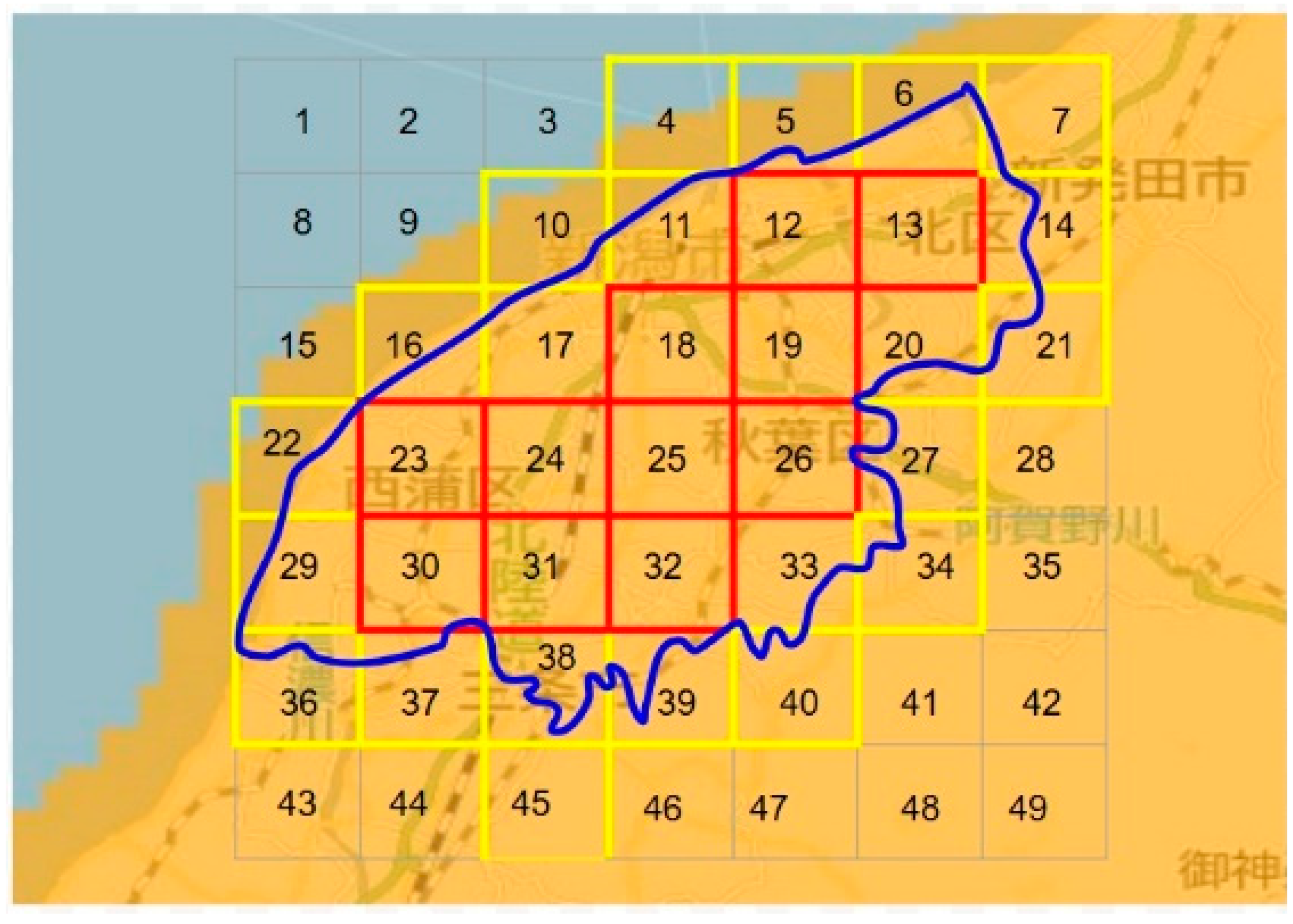
2.1. Mesh Design for PV Power Estimation
- *
- The picture is taken from the CDF data and Google Maps;
- *
- A mesh is designed on the picture to cover Niigata City.
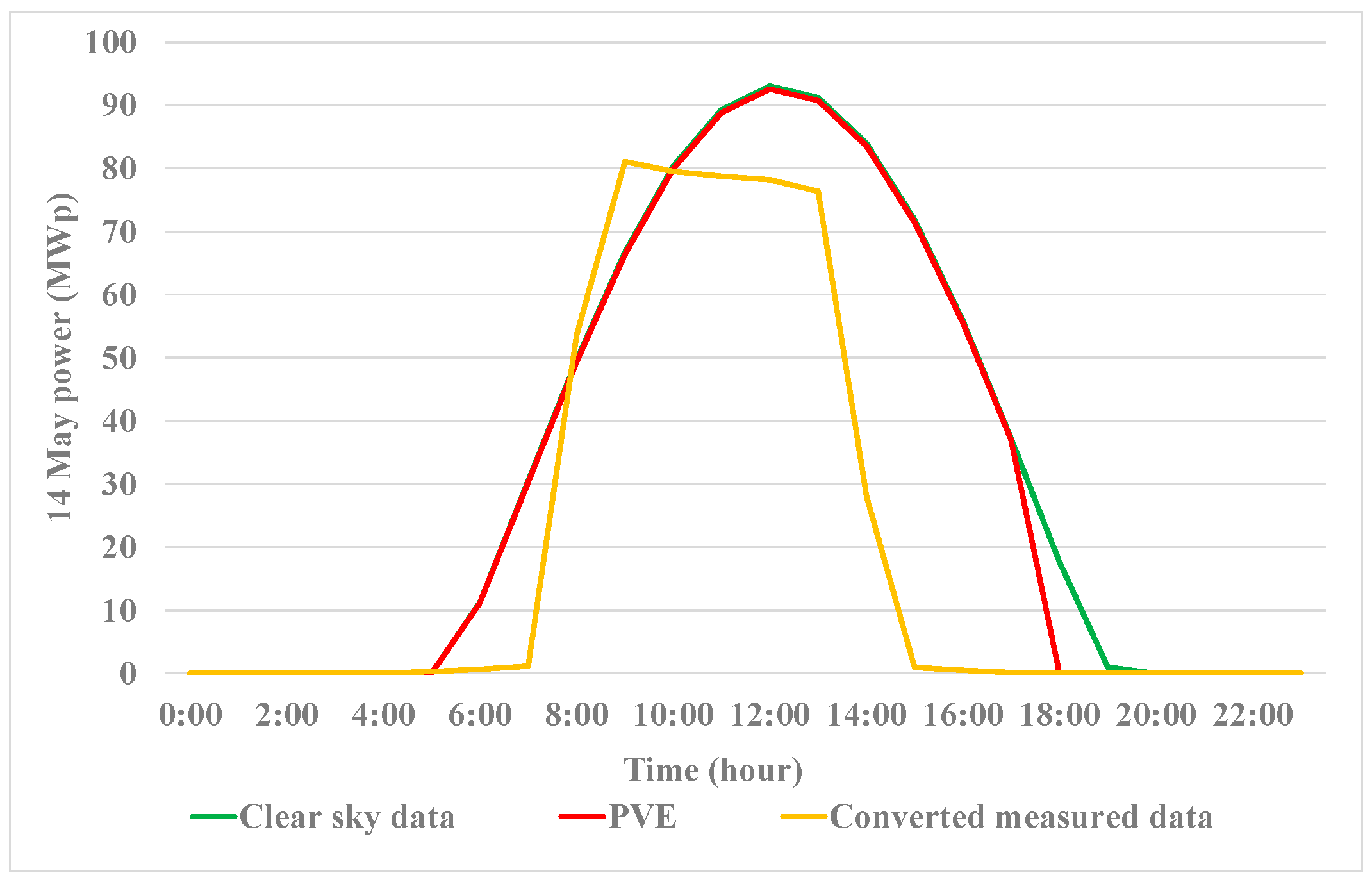
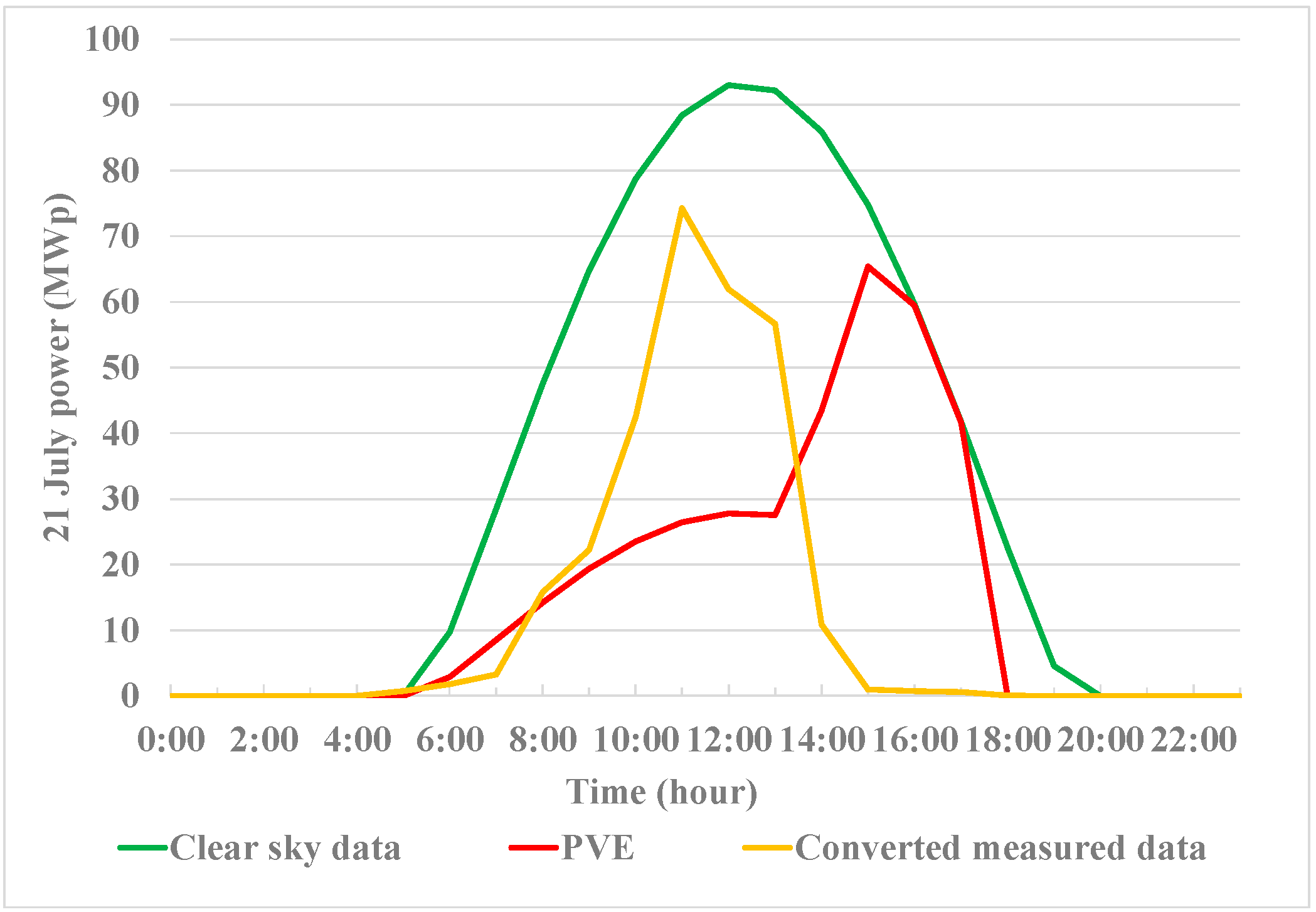
2.2. Daily Power Curve for Niigata City
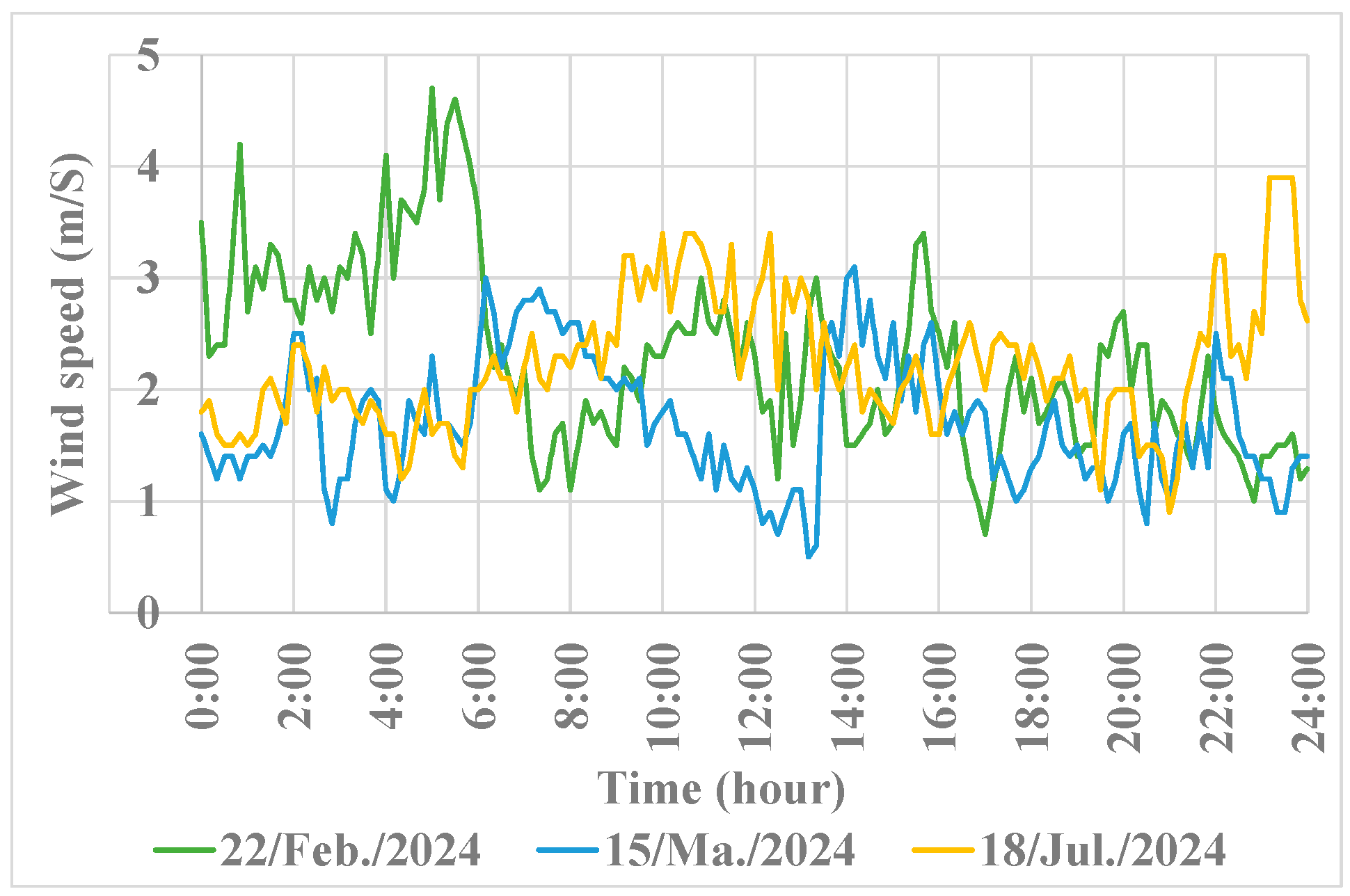
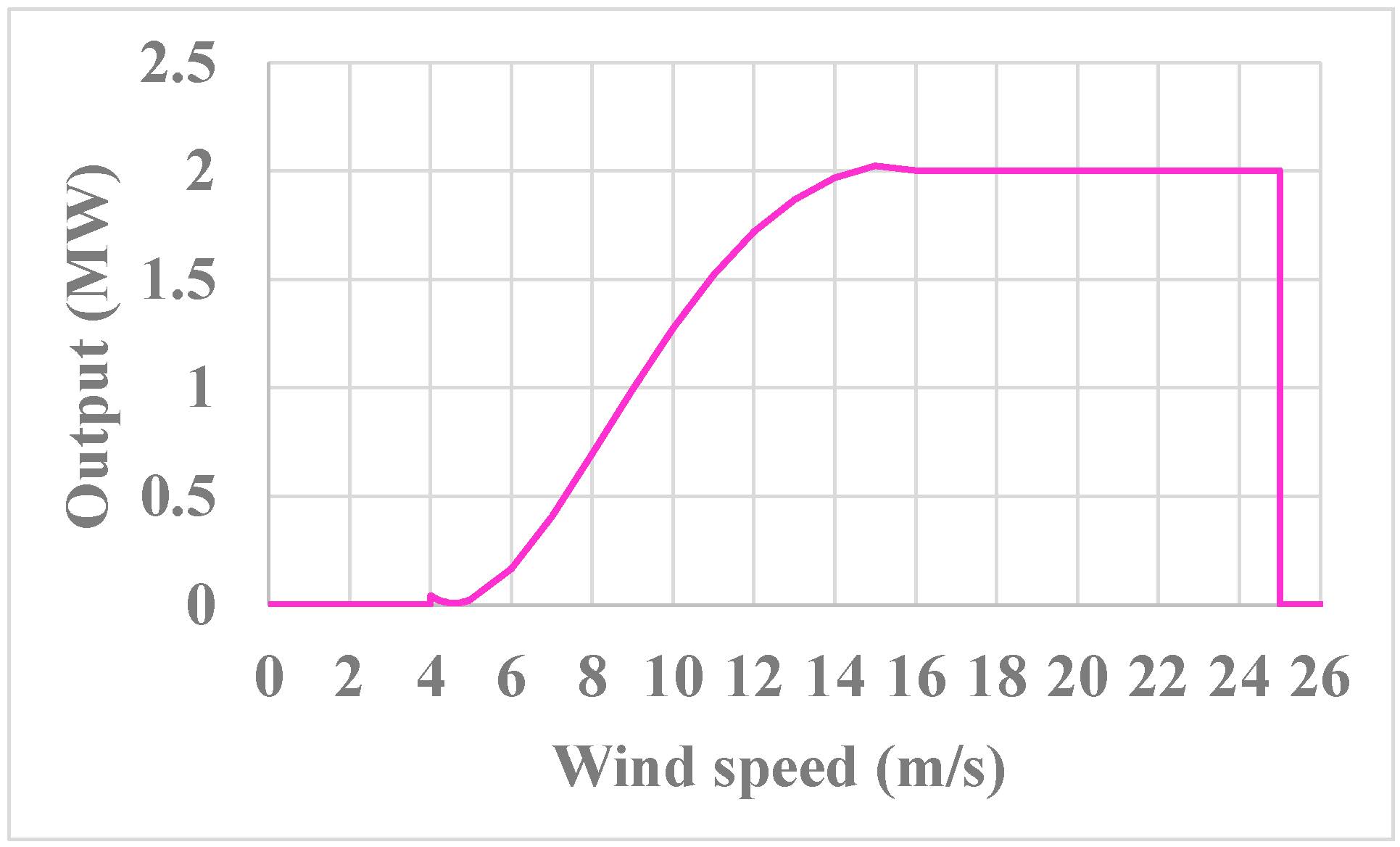
3. Prediction of the Wind Power
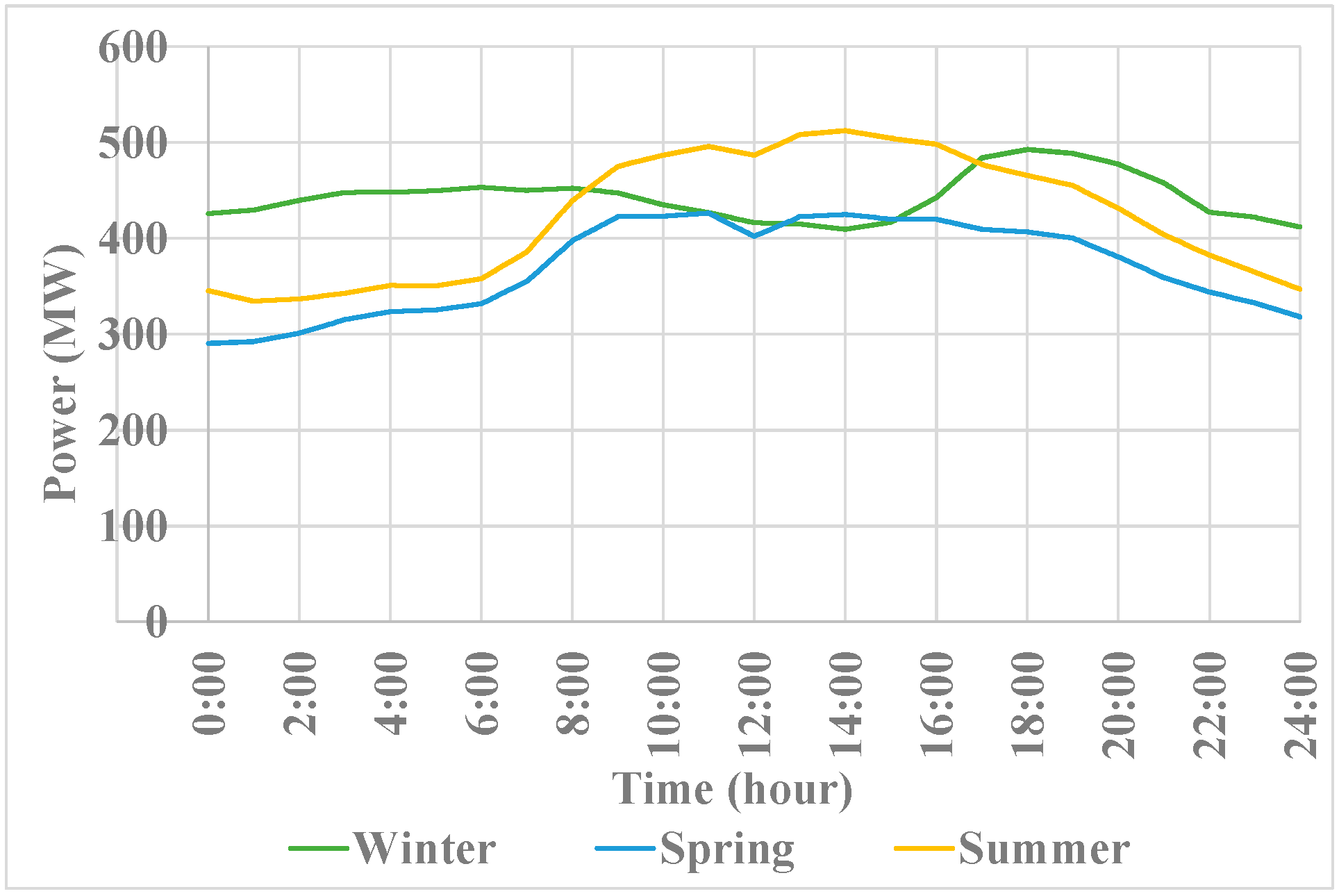
4. Power Balance Simulation
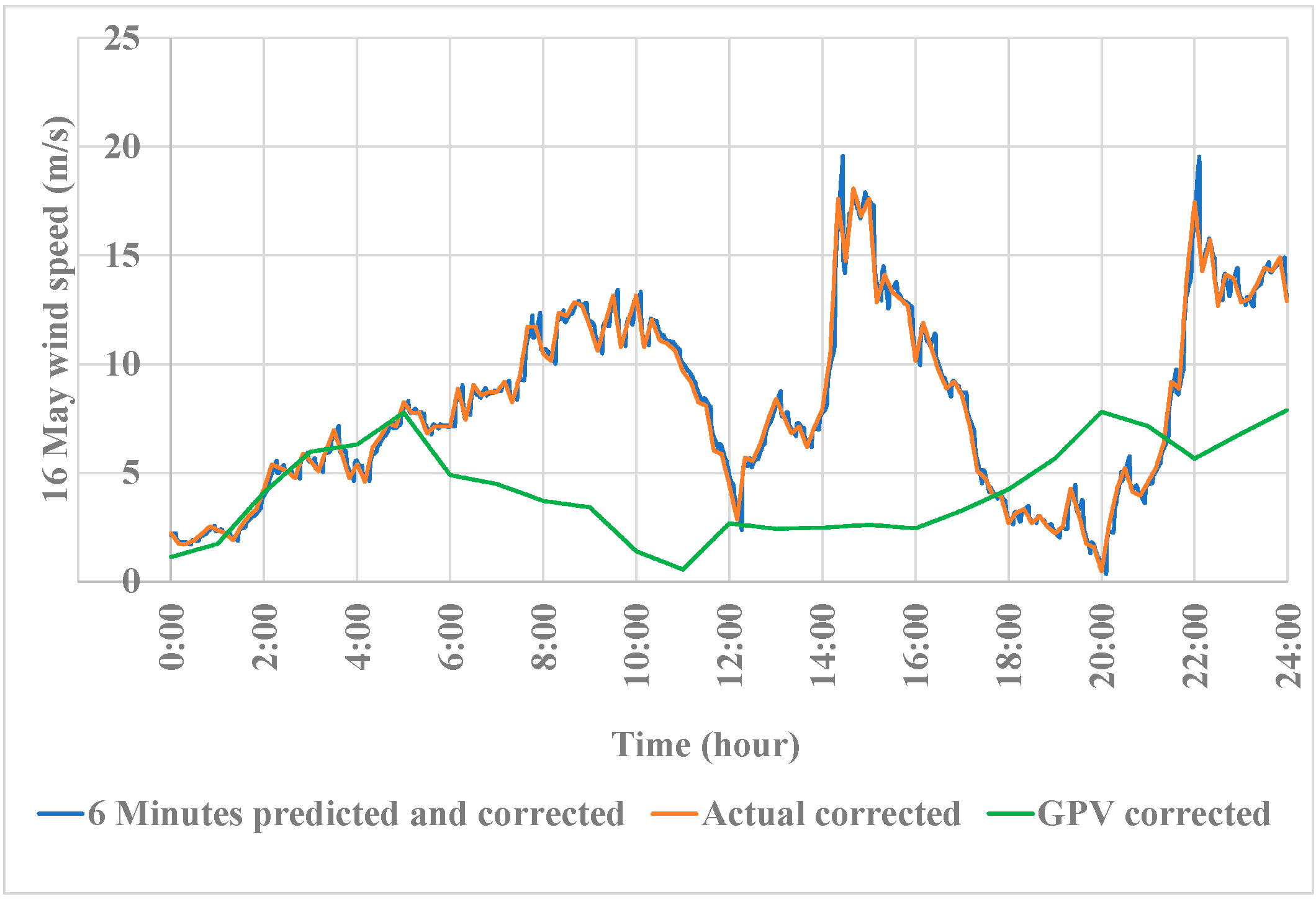
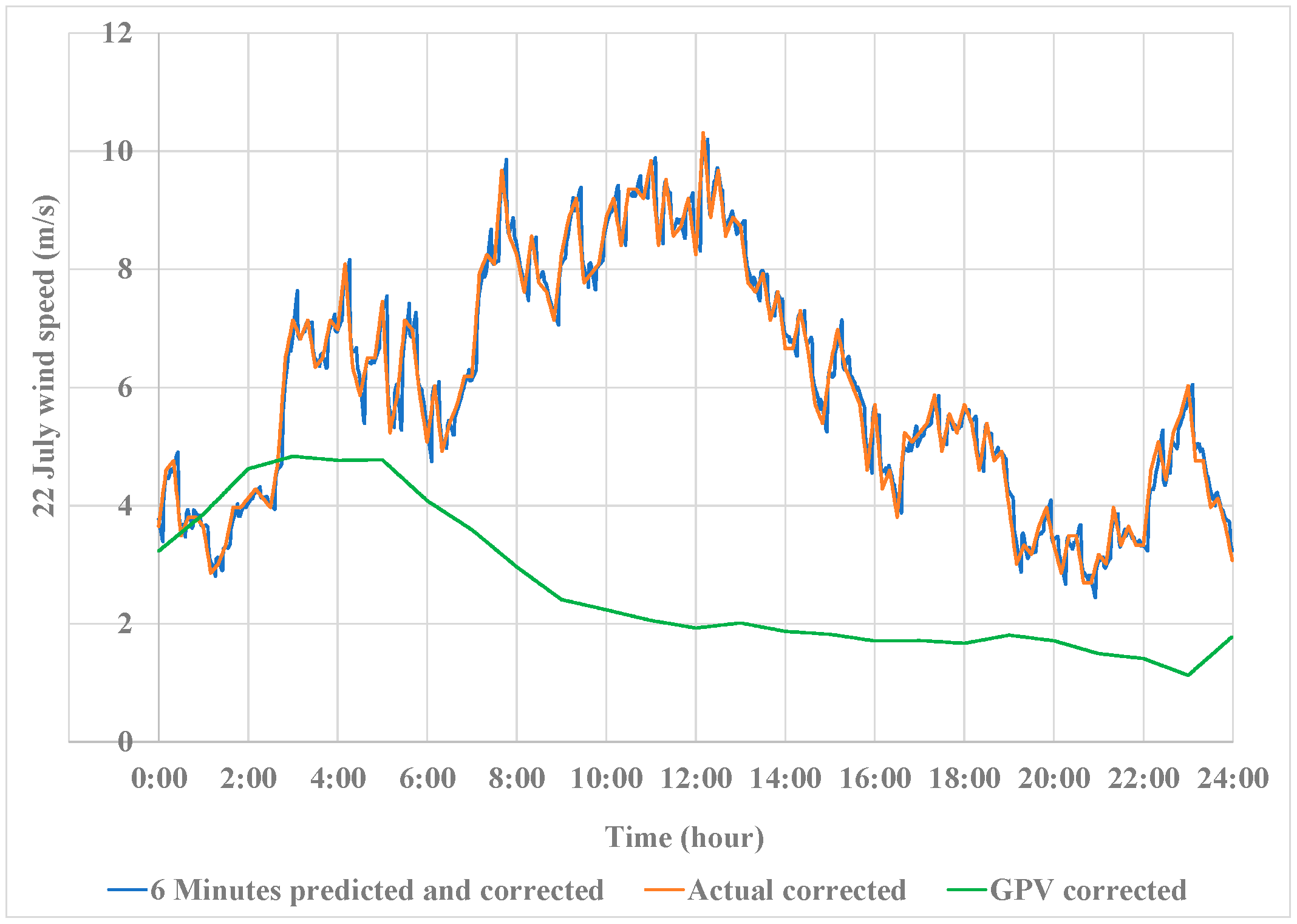
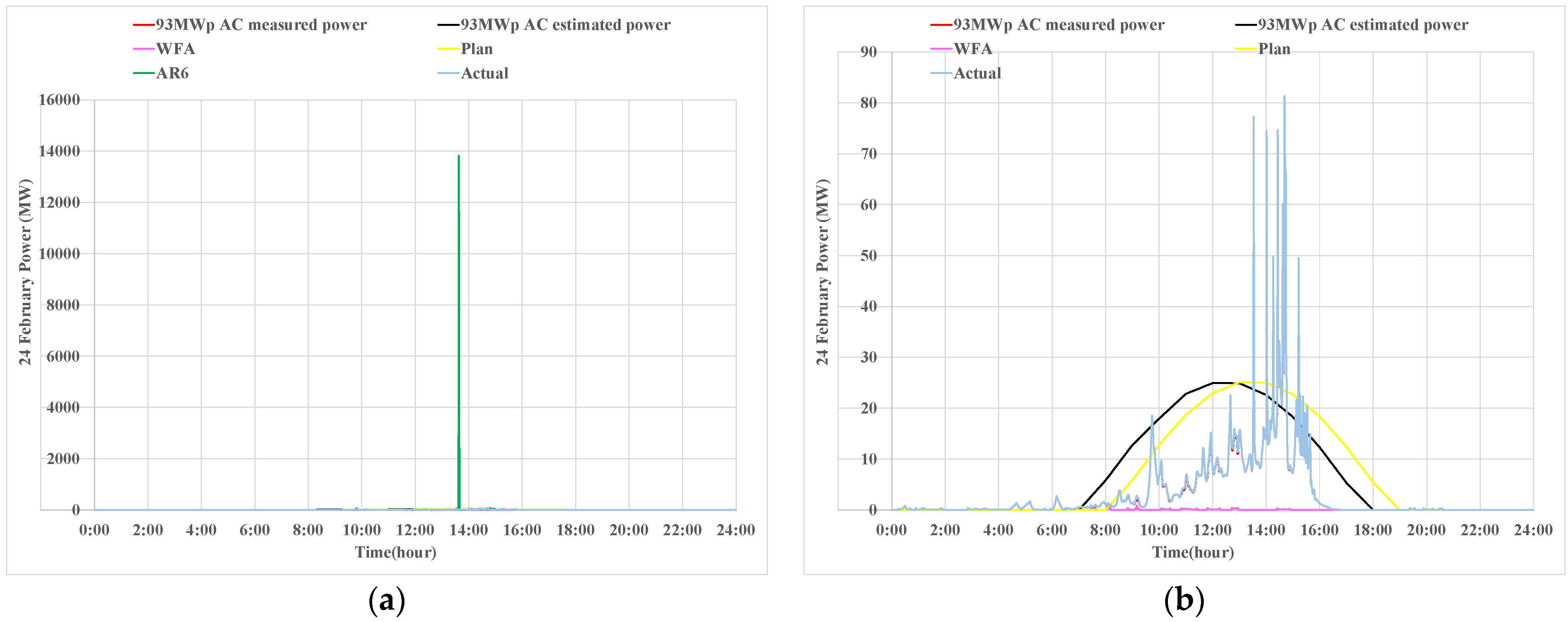
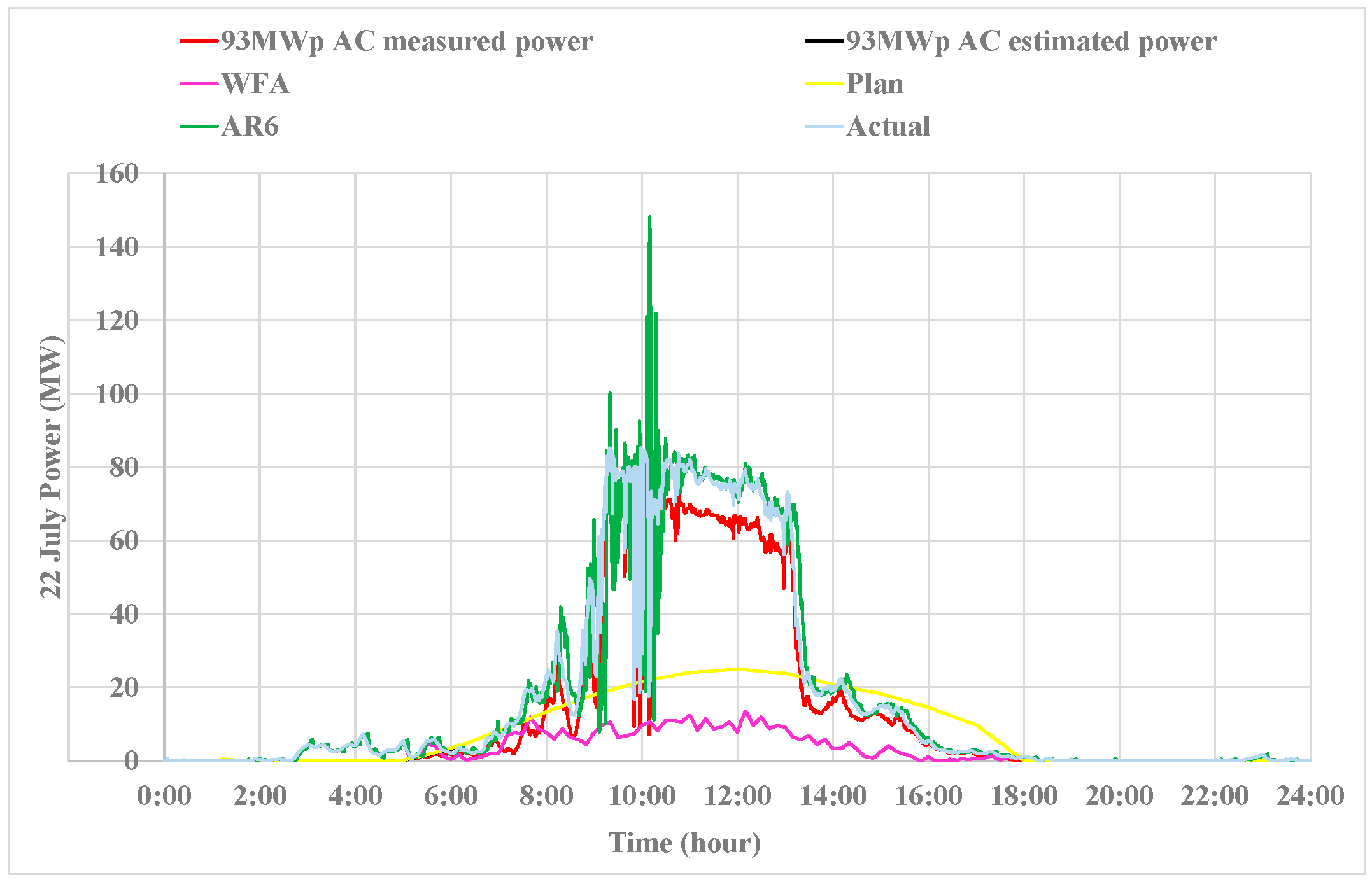
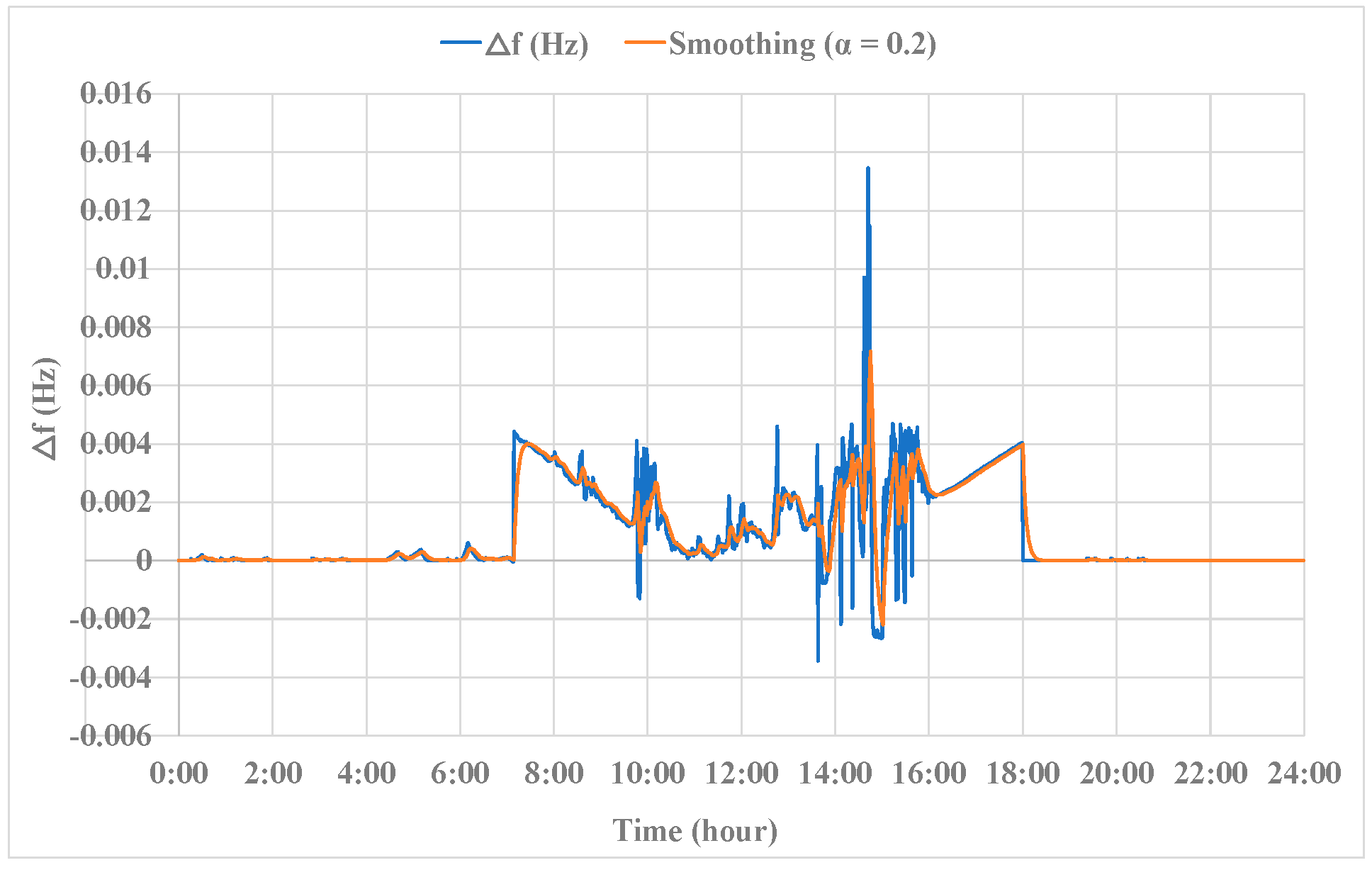
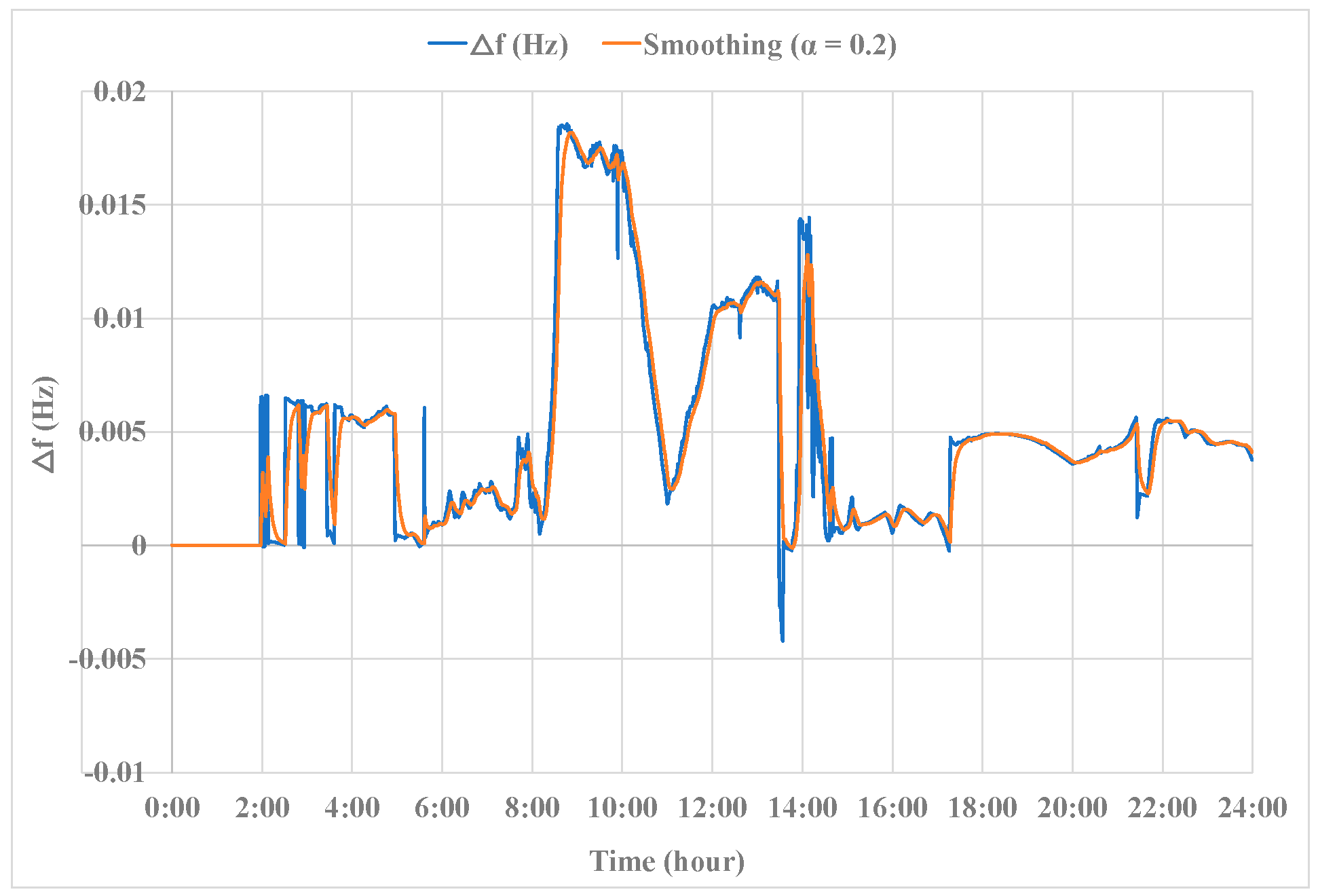
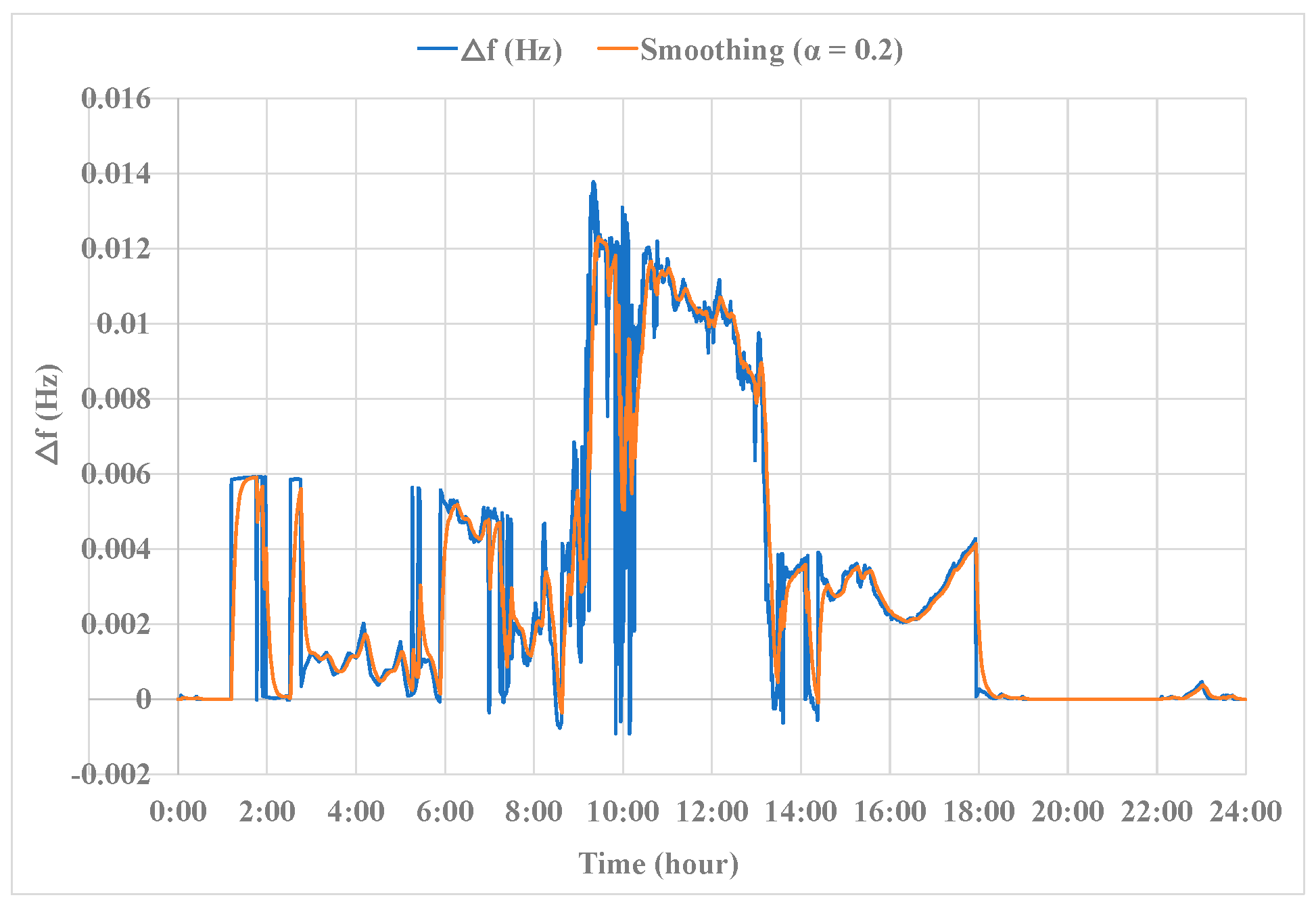
4.1. Simulation Results
4.2. Discussions
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| PV | Solar photovoltaic |
| HC | Hydropower capacity |
| 6ARW | Six-minute autoregressive wind speed prediction |
| 6ARP | Six-minute autoregressive PV power prediction |
| 1HWF | One-hour GPV wind farm |
| 1HP | One-hour NHK prediction |
| WFA | Wind farm actual power |
| PVE | Photovoltaic estimated power |
| PSS | Power system stability |
| FS | Frequency stability |
| HPP | Hybrid power plant |
| JMA | Japan Meteorological Agency |
| CDF | NHK cloud distribution forecast |
| SDG | Sustainable development goal |
| WP | Wind power |
| GPV | Grid Point Value |
| NHK | Japan Broadcasting Corporation |
| DERs | Distributed energy resources |
| COP | Conference of the parties |
| UN | United Nations |
| VRE | Variable renewable energy |
References
- Westbrook, K. The Power Grid Crisis: What It Means for Everyday Families. Climate Science. Available online: https://climatecosmos.com/climate-science/the-power-grid-crisis-what-it-means-for-everyday-families/ (accessed on 19 February 2025).
- Saleh, A.M.; István, V.; Khan, M.A.; Waseem, M.; Ahmed, A.N.A. Power system stability in the Era of energy Transition: Importance, Opportunities, Challenges, and future directions. Energy Convers. Manag. X 2024, 24, 100820. [Google Scholar] [CrossRef]
- Hassan, Q.; Algburi, S.; Sameen, A.Z.; Salman, H.M.; Jaszczur, M. A review of hybrid renewable energy systems: Solar and wind-powered solutions: Challenges, opportunities, and policy implications. Results Eng. 2023, 20, 101621. [Google Scholar] [CrossRef]
- Bhattacharyya, A.; Yoon, S.; Hastak, M. Economic Impact Assessment of Severe Weather–Induced Power Outages in the US. J. Infrastruct. Syst. 2021, 27, 04021038. [Google Scholar] [CrossRef]
- Hansen, A.D.; Adamou, P.; Giagkou, X.; Rigas, F.; Sakamuri, J.; Altin, M.; Nuno, E.; Sørensen, P. Dynamic Modeling of Wind-Solar-Storage Based Hybrid Power Plant. In Proceedings of the 18th Wind Integration Workshop, Dublin, Ireland, 16–18 October 2019; Available online: https://backend.orbit.dtu.dk/ws/portalfiles/portal/197791357/9B_1_WIW19_248_paper_Das_Kaushik.pdf (accessed on 17 March 2025).
- International Energy Agency. The Power of Transformation: Wind, Sun and the Economics of Flexible Power Systems. IEA 2014, 10, 160–179. Available online: https://iea.blob.core.windows.net/assets/b6a02e69-35c6-4367-b342-2acf14fc9b77/The_power_of_Transformation.pdf (accessed on 27 December 2024).
- Chayapathi, V.; Sharath, B.; Anitha, G.S. Voltage Collapse Mitigation By Reactive Power Compensation At the Load Side. Int. J. Res. Eng. Technol. 2013, 2, 251–257. [Google Scholar] [CrossRef]
- Sattar, F.; Ghosh, S.; Isbeih, Y.J.; El Moursi, M.S.; Al Durra, A.; El Fouly, T.H.M. A predictive tool for power system operators to ensure frequency stability for power grids with renewable energy integration. Appl. Energy 2024, 353, 122226. [Google Scholar] [CrossRef]
- Hatziargyriou, N.; Milanovic, J.; Rahmann, C.; Ajjarapu, V.; Canizares, C.; Erlich, I.; Hill, D.; Hiskens, I.; Kamwa, I.; Pal, B.; et al. Definition and Classification of Power System Stability-Revisited & Extended. IEEE Trans. Power Syst. 2021, 36, 3271–3281. [Google Scholar] [CrossRef]
- Shair, J.; Li, H.; Hu, J.; Xie, X. Power system stability issues, classifications and research prospects in the context of high-penetration of renewables and power electronics. Renew. Sustain. Energy Rev. 2021, 145, 111111. [Google Scholar] [CrossRef]
- Chandarahasan, C.; Percis, E.S. The accessible large-scale renewable energy potential and its projected influence on Tamil Nadu’s grid stability. Indones. J. Electr. Eng. Comput. Sci. 2023, 31, 609–616. [Google Scholar] [CrossRef]
- Qin, B.; Wang, M.; Zhang, G.; Zhang, Z. Impact of renewable energy penetration rate on power system frequency stability. Energy Rep. 2022, 8, 997–1003. [Google Scholar] [CrossRef]
- Rahman, A.; Murad, S.W.; Mohsin, A.K.M.; Wang, X. Does renewable energy proactively contribute to mitigating carbon emissions in major fossil fuels consuming countries? J. Clean. Prod. 2024, 452, 142113. [Google Scholar] [CrossRef]
- Yuping, S.; Shenghu, S.; Tiwari, A.K.; Khan, S.; Zhao, X. Impacts of renewable energy on climate risk: A global perspective for energy transition in a climate adaptation framework. Appl. Energy 2024, 362, 122994. [Google Scholar] [CrossRef]
- HivePower. Grid Stability Issues with Renewable Energy Sources: How They Can Be Solved. 22 March 2021. Available online: https://www.hivepower.tech/blog/grid-stability-issues-with-renewable-energy-how-they-can-be-solved (accessed on 6 December 2024).
- International Energy Agency. Net Zero by 2050 a Roadmap for the Global Energy Sector. Available online: https://iea.blob.core.windows.net/assets/deebef5d-0c34-4539-9d0c-10b13d840027/NetZeroby2050-ARoadmapfortheGlobalEnergySector_CORR.pdf (accessed on 15 November 2024).
- Arbabzadeh, M.; Sioshansi, R.; Johnson, J.X.; Keoleian, G.A. The role of energy storage in deep decarbonization of electricity production. Nat. Commun. 2019, 10, 3413. [Google Scholar] [CrossRef]
- Wei, H.; Xin, L.; Liu, P. Types of CO2 Emission Reduction Technologies and Future Development Trends. Eng. Rural Dev. 2022, 25, 50–54. [Google Scholar] [CrossRef]
- Kosugi, T.; Tokimatsu, K.; Yoshida, H. Evaluating new CO2 reduction technologies in Japan up to 2030. Technol. Forecast. Soc. Change 2005, 72, 779–797. [Google Scholar] [CrossRef]
- KIZUNA. Climate Transition Bonds Show Japan’s Commitment to Carbon Neutrality. 27 September 2024. Available online: https://www.japan.go.jp/kizuna/2024/09/climate_transition_bonds.html (accessed on 12 December 2024).
- Tohoku Electric Power Group. Tohoku Electric Power Group Sustainability Report 2023; Tohoku Electric Power Group: Sendai City, Japan, 2023; Available online: https://www.tohoku-epco.co.jp/ir/report/integrated_report/pdf/tohoku_sustainability2023en.pdf#page=15 (accessed on 29 December 2024).
- Tohoku Electric Power Network Co. Feed-in Tariff Scheme for Renewable Energy. Available online: https://nw.tohoku-epco.co.jp/consignment/renew/pdf/saisei.pdf (accessed on 26 December 2024). (In Japanese).
- Grant, E.; Clark, C.E. Hybrid power plants: An effective way ofdecreasing loss-of-load expectation. Energy 2024, 307, 132245. [Google Scholar] [CrossRef]
- Kim, J.; Millstein, J.H.; Wiser, D.; Mulvaney-Kemp, R. Renewable-battery hybrid power plants in congested electricity markets: Implications for plant configuration. Renew. Energy 2024, 232, 121070. [Google Scholar] [CrossRef]
- Denholm, P.; Nunemaker, J.; Gagnon, P.; Cole, W. The potential for battery energy storage to provide peaking capacity in the United States. Renew. Energy 2020, 151, 1269–1277. [Google Scholar]
- Denholm, P.; Mai, T. Timescales of energy storage needed for reducing renewable energy curtailment. Renew. Energy 2019, 130, 388–399. [Google Scholar] [CrossRef]
- Aziz, A.; Oo, A.T.; Stojcevski, A. Analysis of frequency sensitive wind plant penetration effect on load frequency control of hybrid power system. Electr. Power Energy Syst. 2018, 99, 603–617. [Google Scholar] [CrossRef]
- Ji, W.; Hong, F.; Zhao, Y.; Liang, L.; Du, H.; Hao, J.; Fang, F.; Liu, J. Applications of flywheel energy storage system on load frequency regulation combined with various power generations: A review. Renew. Energy 2024, 223, 119975. [Google Scholar] [CrossRef]
- Kennedy, C.; Bertram, D.; White, C.J. Reviewing the UK’s exploited hydropower resource (onshore and offshore). Renew. Sustain. Energy Rev. 2024, 189, 113966. [Google Scholar] [CrossRef]
- Sample, J.E.; Duncan, N.; Ferguson, M.; Cooksley, S. Scotland’s hydropower: Current capacity, future potential and the possible impacts of climate change. Renew. Sustain. Energy Rev. 2015, 52, 111–122. [Google Scholar] [CrossRef]
- Sarmiento-Vintimilla, J.C.; Larruskain, D.M.; Torres, E.; Abarrategi, O. Assessment of the operational flexibility of virtual power plants to facilitate the integration of distributed energy resources and decision-making under uncertainty. Int. J. Electr. Power Energy Syst. 2024, 155, 109611. [Google Scholar] [CrossRef]
- Karapici, V.; Trojer, A.; Lazarevikj, M.; Pluskal, T.; Chernobrova, A.; Nezirić, E.; Zuecco, G.; Alerci, A.L.; Seydoux, M.; Doujak, E.; et al. Opportunities of hidden hydropower technologies towards the energy transition. Energy Rep. 2024, 12, 5633–5647. [Google Scholar] [CrossRef]
- Zhou, C.; Doroodchi, E.; Moghtaderi, B. Figure of Merit Analysis of a Hybrid Solar-Geothermal Power Plant. Engineering 2013, 5, 26. [Google Scholar] [CrossRef]
- Tohoku Electric Power Group. Tohoku Electric Power Group Integrated Report 2024. 2024. Available online: https://www.tohoku-epco.co.jp/ir/report/integrated_report/pdf/tohoku_integratedreport2024en.pdf (accessed on 29 December 2024).
- Ahsan, L.; Iqbal, M. Dynamic Modeling of an Optimal Hybrid Power System for a Captive Power Plant in Pakistan. Jordan J. Electr. Eng. 2022, 8, 195. [Google Scholar] [CrossRef]
- Testbook Edu Solutions Pvt. Ltd. Power System Stability: Know Definition & Types Of Stability. Testbook. Available online: https://testbook.com/electrical-engineering/power-system-stability (accessed on 19 February 2025).
- Energiewende, A. Integrating Renewables into the Japanese Power Grid by 2030. 148/1-S-2019/EN. Available online: https://www.renewable-ei.org/pdfdownload/activities/REI_Agora_Japan_grid_study_FullReport_EN_WEB.pdf (accessed on 30 January 2025).
- Tchokomani Moukam, T.D.; Sugawara, A.; Shawapala, I.L.; Bello, Y.; Li, Y. Stabilization of Electricity by Mesh Method and Combination of Renewable Energy System. In Proceedings of the International Council on Electrical Engineering Conference 2024, Kitakyushu, Japan, 30 June–4 July 2024. [Google Scholar]
- JMA/GPV Weather Maps. 2024. Available online: https://www.basso-continuo.com/WeatherGPV/index_e.htm (accessed on 30 December 2024).
- NHK (Japan Broadcasting Corporation). NHK News Web. 2024. Available online: https://www.nhk.or.jp/kishou-saigai/city/status/15100001510700/ (accessed on 30 December 2024).
- Vocabulary.com. Mesh. 2024. Available online: https://www.vocabulary.com/dictionary/mesh (accessed on 30 December 2024).
- Population of Cities in Japan 2024. 2024. Available online: https://worldpopulationreview.com/cities/japan (accessed on 25 October 2024).
- Introduction to Clouds. Available online: https://www.ncei.noaa.gov/sites/default/files/sky-watcher-cloud-chart-noaa-nasa-english-version.pdf (accessed on 9 February 2024).
- Zhu, X.; Yan, J.; Lu, N. A Graphical Performance-Based Energy Storage Capacity Sizing Method for High Solar Penetration Residential Feeders. IEEE Trans. Smart Grid 2017, 8, 3–12. [Google Scholar] [CrossRef]
- Brownson, T.P.S.U.J.; Earth, C.O.; Sciences, M. Clear Sky Model and Measured Irradiance Data. 2023. Available online: https://www.e-education.psu.edu/eme810/node/698 (accessed on 20 March 2024).
- Sahebzadeh, S.; Rezaeiha, A.; Montazeri, H. Vertical-axis wind-turbine farm design: Impact ofrotor setting and relative arrangement on aerodynamic performance ofdouble rotor arrays. Energy Rep. 2022, 8, 5793–5819. [Google Scholar] [CrossRef]
- Vestas. VestasV80-2.0 MWFacts and Figures. 2011. Available online: https://www.ledsjovind.se/tolvmanstegen/Vestas%20V90-2MW.pdf (accessed on 19 February 2024).
- Chaudhari, J. Understanding Autoregressive (AR) Models for Time Series Forecasting. 25 July 2023. Available online: https://jaichaudhari.medium.com/understanding-autoregressive-ar-models-for-time-series-forecasting-508016498a1e (accessed on 31 December 2024).
- 2025 Statistics How To. Autoregressive Model: Definition & The AR Process. Statistics How To. 2025. Available online: https://www.statisticshowto.com/autoregressive-model/ (accessed on 19 February 2025).
- J. M. Agency. JMA Height for Niigata. 2024. Available online: https://www.jma-net.go.jp/niigata/gaikyo/geppo/kishou_ichiran.pdf (accessed on 17 March 2025). (In Japanese)
- Bañuelos-Ruedas, F.; Camacho, C.Á.; Rios-Marcuello, S. Methodologies Used in the Extrapolation of Wind Speed Data at Different Heights and Its Impact in the Wind Energy Resource Assessment in a Region. Wind. Farm-Tech. Regul. Potential Estim. Siting Assess. 2011, 97, 114. [Google Scholar] [CrossRef]
- Hiroshi, A.; Yasutsugu, K.; Meng, I. A method for estimating offshore winds using a three-dimensional wind model. Jpn. Soc. Civ. Eng. 2007, 54, 134. Available online: http://library.jsce.or.jp/jsce/open/00008/2007/54-0131.pdf (accessed on 13 October 2023). (In Japanese).
- Glattfelder, A.H.; Huser, L.; Dörfler, P.; Steinbach, J. Automatic Control for Hydroelectric Power Plants. In Control Systems, Robotics, and Automation; Encyclopedia of Life Support Systems (EOLSS): Oxford, UK, 2009; Volume XVIII, Available online: https://www.eolss.net/Sample-Chapters/C18/E6-43-33-04.pdf (accessed on 25 October 2023).








| Coverage Type | Amount | Generating Power |
|---|---|---|
| Sunny | 0 | 1 |
| Cloudy | 0.7 | 0.3 |
| Rainy | 0.9 | 0.1 |
| Rainy with snow | 1 | 0 |
| Snowy | 1 | 0 |
| Rectangles (1–49) | Related Land Ratio | Land and Cloud Impact | Temporal Clear Sky Power (Wp) |
|---|---|---|---|
| 1–3, 8, 9, 15, 28, 35, 41–49 | 0 | 0 | 0 |
| 4 | 0 | 0 | 0 |
| 5 | 0.17 | 0.04539 | 0 |
| 6 | 0.65 | 0.195 | 0 |
| 7 | 0.08 | 0.024 | 0 |
| 10 | 0.15 | 0.07875 | 0 |
| 11 | 0.7 | 0.21 | 3.139 |
| 12 | 1 | 0.3 | 9.202 |
| 13 | 1 | 0.3 | 15.327 |
| 14 | 0.4 | 0.12 | 20.884 |
| 16 | 0.4 | 0.4 | 25.402 |
| 17 | 0.95 | 0.6175 | 28.521 |
| 18 | 1 | 0.3 | 30 |
| 19 | 1 | 0.3 | 29.7254 |
| 20 | 0.8 | 0.24 | 27.72 |
| 21 | 0.2 | 0.06 | 24.132 |
| 22 | 0.4 | 0.34 | 19.25 |
| 23 | 1 | 1 | 13.46 |
| 24 | 1 | 0.65 | 7.273 |
| 25 | 1 | 0.3 | 1.463 |
| 26 | 1 | 0.3 | 0 |
| 27 | 0.27 | 0.081 | 0 |
| 29 | 0.75 | 0.75 | 0 |
| 30 | 0.99 | 0.99 | 0 |
| 31 | 1 | 0.65 | |
| 32 | 1 | 0.3 | |
| 33 | 0.8 | 0.24 | |
| 34 | 0.1 | 0.03 | |
| 36 | 0.21 | 0.21 | |
| 37 | 0.17 | 0.17 | |
| 38 | 0.56 | 0.364 | |
| 39 | 0.32 | 0.096 | |
| 40 | 0.08 | 0.024 | |
| 39.1 | |||
| Time Since Start-Up Operation (s) | |
|---|---|
| To the end of the bypass valve opening | 21 |
| Until the end of the main valve opening | 156 |
| Waterwheel start-up | 160 |
| Up to excitation | 206 |
| Until the automatic synchronization system is activated | 233 |
| Up to synchronous parallelism | 245 |
| Up to a given load | 347 |
| Location | Ratio |
| At sea | 0.60 |
| On a low-lying island | 0.55 |
| Coast on the windward side, low land in the vicinity | 0.50 |
| The downwind side of the coast, low land, or at sea in the vicinity | 0.40 |
| Open land with few obstructions | 0.40 |
| Shielded land and cities | 0.30 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tchokomani Moukam, T.D.; Sugawara, A.; Li, Y.; Bello, Y. An Evaluation of the Power System Stability for a Hybrid Power Plant Using Wind Speed and Cloud Distribution Forecasts. Energies 2025, 18, 1540. https://doi.org/10.3390/en18061540
Tchokomani Moukam TD, Sugawara A, Li Y, Bello Y. An Evaluation of the Power System Stability for a Hybrid Power Plant Using Wind Speed and Cloud Distribution Forecasts. Energies. 2025; 18(6):1540. https://doi.org/10.3390/en18061540
Chicago/Turabian StyleTchokomani Moukam, Théodore Desiré, Akira Sugawara, Yuancheng Li, and Yakubu Bello. 2025. "An Evaluation of the Power System Stability for a Hybrid Power Plant Using Wind Speed and Cloud Distribution Forecasts" Energies 18, no. 6: 1540. https://doi.org/10.3390/en18061540
APA StyleTchokomani Moukam, T. D., Sugawara, A., Li, Y., & Bello, Y. (2025). An Evaluation of the Power System Stability for a Hybrid Power Plant Using Wind Speed and Cloud Distribution Forecasts. Energies, 18(6), 1540. https://doi.org/10.3390/en18061540







