Optimal Configuration Strategy of PV and ESS for Enhancing the Regulation Capability of Electric Vehicles Under the Scenario of Orderly Power Utilization

Abstract

Orderly power consumption is an important method for maintaining the supply–demand balance in the power system. However, the large-scale integration of renewable energy significantly raises demand-side load flexibility requirements, challenging the implementation of orderly power utilization. The optimal configuration and scheduling of distributed energy resources (DER), including electric vehicles (EVs) and energy storage systems (ESS), represent promising approaches to addressing this issue. However, current research neglects the influence of DER configuration schemes on the participation rate of EV users in orderly power utilization. This work proposes an optimized configuration strategy for PV and ESS to enhance the participation rate of EV users in grid regulation. An economic configuration model of PV and ESS is constructed to obtain the optimal configuration plan. An incentive pricing strategy based on the configuration plan is proposed to improve the participation rate of EV users in orderly power scheduling. Simulation results demonstrate the effectiveness of the proposed configuration strategy.

1. Introduction

The growing integration of renewable energy and diversified load demands has significantly increased the unpredictability and volatility of both power generation and load demand [1,2,3], challenging orderly power utilization under extreme scenarios such as severe weather and equipment failures [4,5,6]. The large-scale integration of distributed energy resources (DERs), including energy storage systems (ESS) and electric vehicles (EVs), has further intensified this issue [7,8,9].

To address these challenges in orderly power utilization, current research has predominantly adopted two complementary strategies: (1) optimal scheduling of existing flexible resources [10,11,12,13,14,15], and (2) optimal configuration of newly deployed DERs [16,17,18]. In the realm of optimal scheduling of existing flexible resources, reference [19] introduces a strategy for flexibility resource optimization, leveraging the load-shifting capability of ESS to enhance the scheduling efficiency of grid-connected microgrids. Reference [20] employs demand-side resources, including EVs, ESS, and adjustable loads, to deliver flexibility services, effectively mitigating the inherent uncertainty of renewable energy generation. In the realm of optimal configuration for newly deployed distributed energy resources (DERs) [21,22], distributed energy storage systems (ESS) and photovoltaic (PV) systems have emerged as indispensable components in modern power system configurations [23,24,25]. This prominence stems from their threefold advantages of flexibility, reliability, and cost-effectiveness [26]. Reference [27] introduced a DC-DC multisource converter-based grid-interactive microgrid, which integrates PV, wind, and hybrid energy storage to achieve a 92% reduction in renewable power output fluctuations. Building on this, reference [28] developed a life-cycle economic optimization framework for PV-ESS hybrid systems, addressing the inherent challenges of PV generation intermittency while reducing levelized costs by 18%. Reference [29] proposes an equilibrium optimization algorithm for optimal PV and ESS integration in radial distribution networks, enhancing system stability and efficiency. Nevertheless, the prohibitive costs associated with the configuration and operational regulation of existing energy storage systems pose substantial barriers to their widespread adoption in orderly power management [30].

V2G enables EVs to serve as flexible and cost-effective portable ESS [31]. Orderly charge–discharge scheduling enhances load-side capacity and grid flexibility without additional infrastructure [32,33,34]. Existing research has extensively investigated EVs as dispatchable resources and their coordinated scheduling with other flexible assets. References [35,36] have optimized EV charging in parking lots integrated with ESS and PV systems. Building on this, reference [37] proposed an EV charging strategy for microgrids (MGs), incorporating wind/PV units, CHP systems, ESS, and DR-enabled loads as complementary flexible resources. However, existing research has neglected the influence of electric vehicle (EV) travel patterns on distributed energy resource (DER) configuration decisions, thereby failing to fully unlock the flexibility potential of EVs [38,39]. Furthermore, current incentive strategies often assume fixed DER parameters, resulting in insufficient adaptive coordination between infrastructure capacity and EV demand-side responsiveness [40].

However, existing studies primarily focus on either EV users’ response capabilities or the optimal configuration of PV and ESS to enhance grid supply–demand stability, neglecting the impact of other DER consumption behaviors in the distribution network on EV response [41]. To address this gap, this study proposes an optimal PV and ESS configuration strategy to enhance EV regulation capability. An EV regulation model is developed based on the origin–destination (OD) matrix, along with a joint PV-ESS configuration model and an incentive pricing strategy for EV charging and discharging, aiming to improve EV participation rates under orderly power utilization. Simulation results validate the effectiveness of the proposed strategy. The main contributions of this paper are as follows.

(1)

An EV charging and discharging load model is developed based on traffic road and distribution network topology.

(2)

An optimal configuration model of PV and ESS that accounts for EV travel characteristics is established.

(3)

Based on the PV and ESS configuration scheme, an orderly power utilization incentive strategy for EV users is proposed to promote the supply–demand balance of the power system.

2. EV, PV, and ESS Operation Model

2.1. EV Operation Model

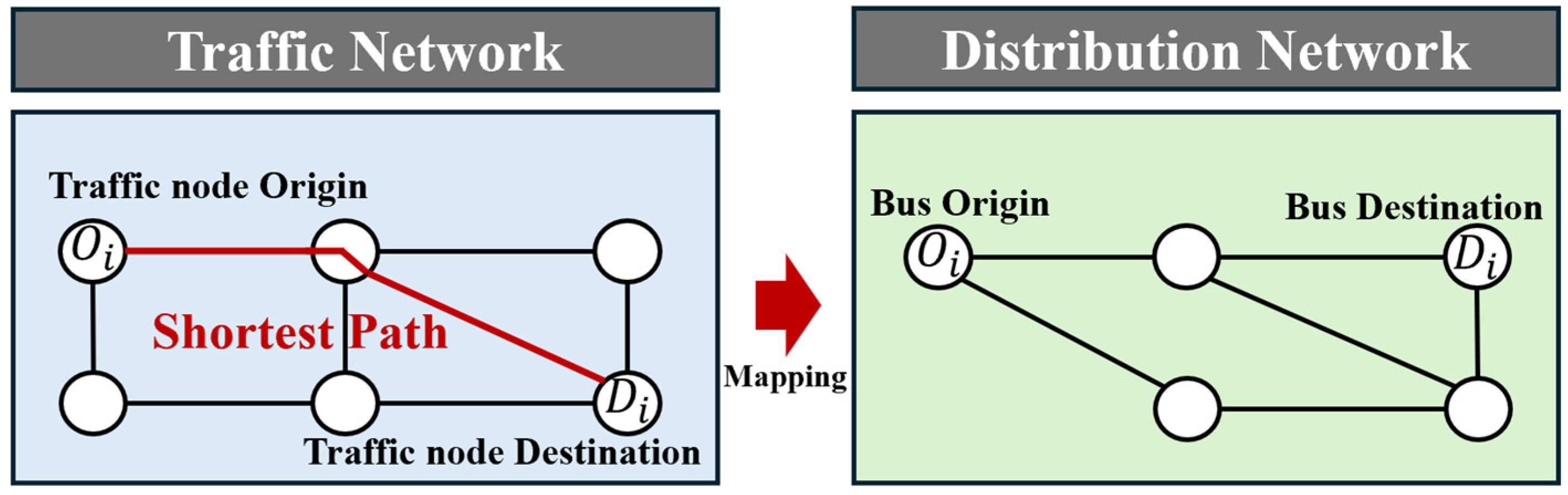
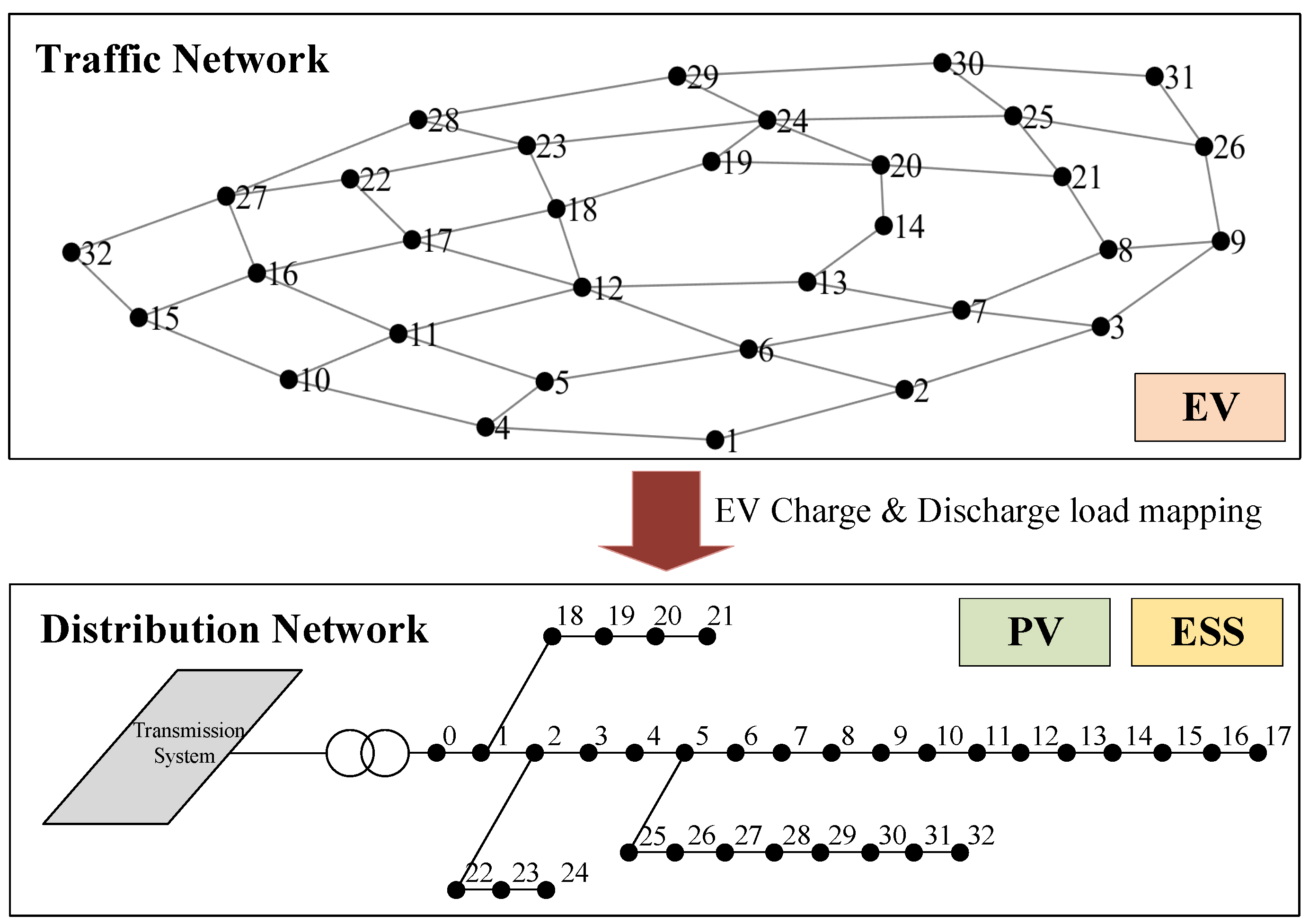
2.1.1. Traffic Network–Distribution Network Model

The traffic network serves as the foundation for EV driving and charging. The OD matrix is a tool to describe the spatial distribution of traffic demand. Its core principle is to build a matrix model to reflect the inter-regional travel demand through statistics and analysis of the traffic flow between the starting point and the end point. Therefore, we use the OD matrix to abstract the actual road network and establish a traffic network model to quantitatively describe the road network topology [42], as shown in Figure 1.

As shown in Figure 1, the OD travel matrix transforms the EV travel problem into a shortest path problem in the topology. For each EV, its origin point $O_i$ and destination $D_i$ are set respectively, and the charging and discharging loads at the initial point and destination in the traffic network can be mapped to the buses of the distribution network. The model can be established as follows [43]:

$$G^{\mathrm{T}}=\left(V,E,K,W\right)$$

(1)

$$\{\begin{array}{l}V=\left\{v_i\mid i=1,2,3,\cdots ,n\right\}\\ E=\left\{v_{ij}\mid v_i\in V,v_j\in V,i\ne j\right\}\\ K=\left\{1,2,3,\cdots ,m\right\} \\ W=\left\{w_{ij}^k\mid v_{ij}\in E,k\in K\right\} \end{array}$$

(2)

where $G^{\mathrm{T}}$ is the traffic network; $V$ represents the collection of nodes; $E$ is the set of all road sections of the network $G^{\mathrm{T}}$; $W$ is the collection of road independence weights; and K represents the set of divided time intervals, where the entire day is partitioned into m time periods.

Based on the change of traffic congestion in the traffic network, the road is divided into normal (0 < S ≤ 1.0) and severe congestion (1.0 < S ≤ 2.0) by saturation rate $S$. The road impedance of each road $j$ to the EV at time $t$ can be expressed as follows:

$$R_{j,t}=\{\begin{array}{ll}{R}_{j,t}^1: t_0\left(1+\alpha {(S)}^{\beta }\right),& 0\le S\le 1.0\\ R_{j,t}^2: t_0\left(1+\alpha {(2-S)}^{\beta }\right),& 1.0<S\le 2.0\end{array}$$

(3)

where $S=M/C$, and $M$ represents road traffic flow; $C$ is the current road capacity; $t_0$ is the travel time of the EV through the whole road when the flow is zero; and $\alpha$ and $\beta$ are impedance influence factors. The $R_{v_{ij}}\left(t\right)$ calculated by Formula (2) represents the impedance coefficient of each traffic road under different traffic impedances and represents the speed of EV driving on this road. Dijkstra algorithm is a classic shortest path search algorithm, whose core function is to find the minimum path from the starting point to the end point by iterating through the nodes in the network. Based on the road impedance analysis, the Dijkstra algorithm is used to plan the optimal path, and the optimal driving section of each EV between their $O_i$ and $D_i$ is obtained [44].

The Traffic Network–Distribution Network integration model is established as follows:

$$G^D=\left(B^D,E^D,{\psi }^D\right)$$

(4)

$$\{\begin{array}{l}{B}^D=\left\{n_i\mid i=1,2,3,\cdots ,n_G\right\}\\ E^D=\left\{\left(n_i,n_j\right)\mid n_i,n_j\in V^D\right\}\\ W=\left\{w_{ij}^k\mid v_{ij}\in E,k\in K\right\}\end{array}$$

(5)

where $B^D$ represents the buses of the distribution network; $n_i,n_j$ represent buses $i$ and $j$ in the distribution network; $E^D$ is the branch set of the distribution network; ${\psi }^D$ is the basic parameter set of the distribution network; and $n_G$ is the number of buses in the distribution network.

The load of buses is the sum of the fundamental load of the distribution network bus and the EV charging and discharging power at the bus. Formula (6) calculates the total charging power of EVs on each bus.

$$P_n=P_{n,f}+{\displaystyle \sum }_{i=1}^N{P}_{i,t}$$

(6)

where $P_n$ represents the total load of the node $n$; $P_{n,f}$ denotes the fundamental load of the $n$-th node; $N$ denotes the total number of charging vehicles in the $t$ period of the $i$-th node; and $P_{i,t}$ is the charging or discharging power of the EV $i$ in the $t$ period.

2.1.2. EV Travel Model

To plan and recommend the optimal driving route between the origin and destination for EV owners, this paper adopts the Dijkstra algorithm for route guidance. The shortest path between $O_i$ and $D_i$ is obtained by the aforementioned Dijkstra algorithm. The road network topology matrix calculates section distance $L_{OD}$. The speed of each EV is assumed to be a constant $V_i$. Travel period time $T_{a,h}^{Travel}$ in road $h$ can be expressed as follows:

$$T_{a,h}^{Travel}={\displaystyle \frac{L_h}{V_i}}$$

(7)

The total travel period shows as follows:

$$T_{a,ij}^{Travel}={\displaystyle \sum }_{h=1}^H{T}_{a,t}^{Travel}$$

(8)

From the above, the travel characteristics of EV users are sufficiently described in terms of route planning and travel time. It can be considered that EVs are not connected to charging facilities between journeys, so they do not have the ability to feed the power grid at this time. Only when EVs reach the destination or at the starting point, they will interact with the power grid.

2.1.3. EV Charging and Discharging Model

The individual EV must maintain an equilibrium between the processes of charging and discharging. However, it is crucial to note that the EV cannot perform V2G during the travel period.

$$S_{j,travel}^{EVc}=S_{j,travel}^{EVd}=0$$

(9)

where $S_{i,t}^{EVc}$ is the charging state of the EV during period $t$; $S_{i,t}^{EVd}$ is the discharging state of the $j$-th EV during period $t$; and $travel$ represents the time period when the EV is on its way—that is, the period from departure to reaching the destination and from the destination back to the starting point.

When charging and discharging the EV, it is also necessary to take into account its SOC state, which should ensure the EV can return to the starting point at a predetermined time. The remaining SOC of an EV is the superposition of the remaining charge from the previous moment, the electricity consumption during travel, and the amount of electricity charged or discharged.

$$E_{j,t}^{EV}=E_{j,t-1}^{EV}+S_{j,t-1}^{EVd}{P}_d^{EV}-S_{j,t-1}^{EVc}{P}_c^{EV}-E_{j,t-1}^{EV,Travel}$$

(10)

$$E_{min}^{EV}\le E_{j,t}^{EV}\le E_{max}^{EV}$$

(11)

where $E_{j,t}^{EV}$ is the energy storage state of the EV battery at time $t$, and $E_{j,t-1}^{EV,Travel}$ is the driving power consumption of the EV. $E_{max}^{EV}$ and $E_{min}^{EV}$ are the upper limit and lower limit of the battery capacity of the EV, respectively.

2.2. PV and ESS Operation Model

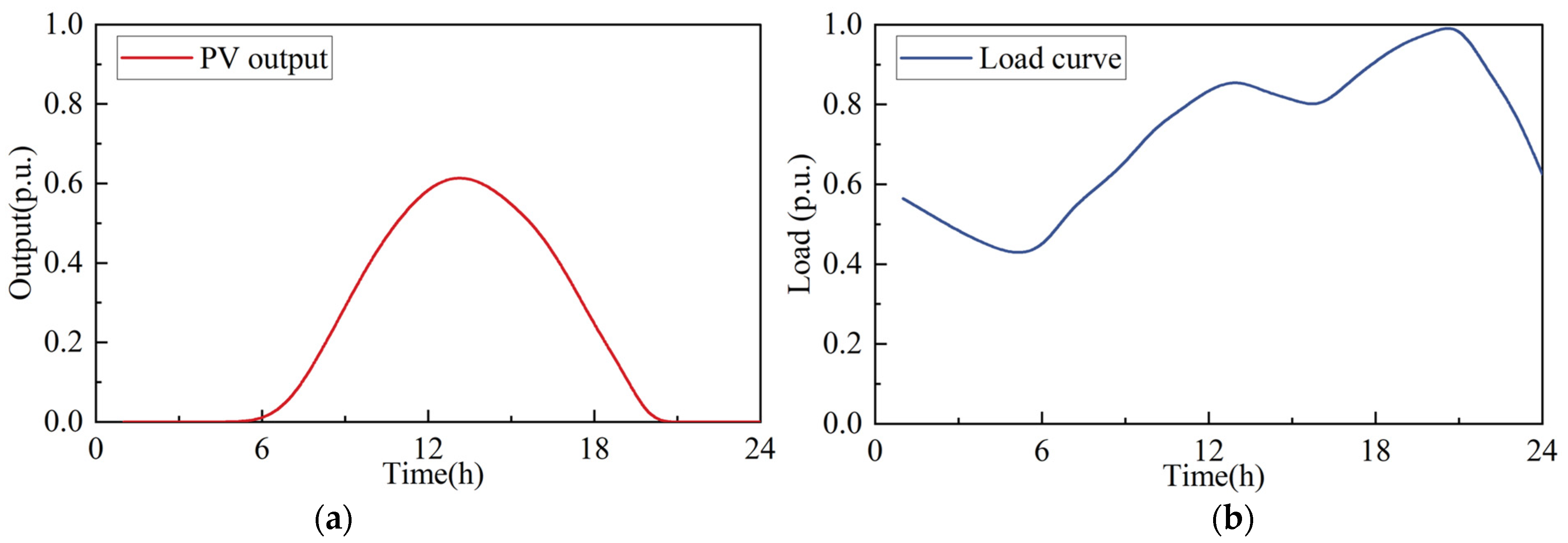
2.2.1. Distributed PV Power Plant Modeling

The relationship between the output power of a PV power plant and solar irradiance intensity is illustrated in the following section, demonstrating how energy generation varies with sunlight availability [45].

$$P_s=\{\begin{array}{l}{P}_{rated}^{PV}{\displaystyle \frac{S}{S_{rated}}}, 0\le S\le S_{rated}\\ P_{rated}^{PV} S_{rated}\le S\end{array}$$

(12)

where $P_s$ indicates the photovoltaic output power, $P_{rated}^{PV}$ indicates the rated photovoltaic power, $S_{rated}$ indicates the rated solar irradiance, and $S$ represents the actual photovoltaic irradiance.

2.2.2. Energy Storage System Modeling

Lithium-ion batteries are widely used in power grids to cut peaks, fill valleys, and stabilize new energy output due to their fast charging and discharging capabilities. The expression of its charge and discharge characteristics is as follows:

$$E_{B,t}=E_{B,0}+{{\displaystyle \int }}_0^t{P}_t^{ESS}dt$$

(13)

$$E_{B,t}-E_{B,t-1}=P_t^{CESS}{\alpha }_B\Delta t$$

(14)

$$E_{B,t}-E_{B,t-1}={\displaystyle \frac{P_t^{DESS}}{{\alpha }_B}}\Delta t$$

(15)

where $E_{B,t}$ and $E_{B,t-1}$ are the energy of the lithium-ion battery ESS at time $t$ and $t-1$, respectively; $E_{B,0}$ is the initial energy of the ESS; $P_{B,t}$ is the charging or discharging power of ESS in time $t$; $P_{B,t}^C$ and $P_{B,t}^D$ represent the charging power and discharging power of ESS at time t, respectively; ${\alpha }_B$ represents the charge-discharge efficiency of ESSs; and $\Delta t$ represents the length of the time granularity.

Lithium-ion batteries need to meet certain power limits during charging and discharging:

$$P_{min}^C\le P_t^{CESS}\le P_{max}^C$$

(16)

$$P_{min}^D\le P_t^{DESS}\le P_{max}^D$$

(17)

where $P_{min}^C$ and $P_{min}^D$ are the lower limit of charging and discharging power, respectively; $P_{max}^C$ and $P_{max}^D$ are the upper limit of charging and discharging power of ESS, respectively.

3. PV and ESS Optimal Configuration Model

3.1. Objective Function

The joint configuration model takes the minimum daily average total cost during the system planning period as the objective function. It is composed of daily investment cost $C_{inv}$ and daily operation cost $C_{ope}$.

$$\min \left\{C_{total}\right\}=C_{inv}+C_{ope}$$

(18)

where $C_{inv}$ mainly includes the daily investment cost of ESS $C_{inv}^{ESS}$ and the daily investment cost of PV power station $C_{inv}^{PV}$, which can be expressed as Formula (19)–(20).

$$C_{inv}=C_{inv}^{ESS}+C_{inv}^{PV}$$

(19)

$$\{\begin{array}{c}{C}_{inv}^{ESS}={\displaystyle \frac{1}{365}}{\displaystyle \frac{\rho {(1+\rho )}^{{\mathrm{p}}_{ESS}}}{{(1+\rho )}^{{\mathrm{r}}_{ESS}}-1}}{c}_{inv}^{ESS}{P}_{inv}^{ESS}\\ C_{inv}^{PV}={\displaystyle \frac{1}{365}}{\displaystyle \frac{\rho {(1+\rho )}^{{\mathrm{p}}_{\mathrm{pv}}}}{{(1+\rho )}^{{\mathrm{r}}_{\mathrm{pv}}}-1}}{c}_{inv}^{PV}{P}_{inv}^{PV}\end{array}$$

(20)

where $\rho$ is the discount rate; ${\mathrm{r}}_{pv}$ and ${\mathrm{r}}_{ESS}$ are the investment years of PV and ESS, respectively; $c_{inv}^{ESS}$ and $c_{inv}^{PV}$ are the investment cost coefficients, respectively; and $P_{inv}^{ESS}$ and $P_{inv}^{PV}$ are the configuration capacities, respectively.

$C_{ope}$ mainly includes the operation and maintenance cost $C_{ounit}$ of each unit, and $C_{EVcon}$ is the subsidy cost of node EV charging and discharging configuration, which is usually a negative number. Such subsidies are set for buses with a large number of EVs to reduce configuration costs.

$$C_{ope}=C_{ounit}+C_{EVcon}$$

(21)

$$\{\begin{array}{l}{C}_{\mathit{ounit}}={\displaystyle \sum _{t=1}^T}{c}_{\mathrm{E}\mathrm{S}\mathrm{S}}^{\mathrm{o}\mathrm{m}}[P_t^{CESS}+P_t^{DESS}]+{\displaystyle \sum _{t=1}^T}{c}_{\mathrm{P}\mathrm{V}}^{\mathrm{o}\mathrm{m}}{P}_t^{PV}\\ C_{EVcon}={\displaystyle \sum _{t=1}^T}{\displaystyle \sum _{i=1}^{NB}}\phi N_{i,t}^{EV}\end{array}$$

(22)

where $c_{\mathrm{ESS}}^{\mathrm{om}}$ and $c_{\mathrm{PV}}^{\mathrm{om}}$ are the operation and maintenance cost coefficients of PV and ESS, respectively; $P_t^{PV}$ is the configuration capacity of PV; $\phi$ is the EV quantity subsidy coefficient; $N_{i,t}^{EV}$ is the number of EVs connected to the grid at time $t$ in bus i.

3.2. Constraints

(1) Basic operational constraints

The optimal configuration of PV and ESS follows their basic operational constraints (12–17).

(2) Distribution network constraints

The power balance constraints of the distribution network after access to PV and ESS are as follows, which ensure that the internal electricity purchases and generation in the distribution network are equal to the electricity consumed by the load.

$${\displaystyle \sum }\left(P^{buy}+P^{PV}+P^{EV}+P^{ESS}\right)={\displaystyle \sum }\left(P^{\mathit{load}}\right)$$

(23)

where $P^{buy}$ is the purchasing power of the distribution network to the upper transmission network, $P^{PV}$ indicates the photovoltaic power, $P^{EV}$ indicates the charging and discharging power of the electric vehicle, $P^{ESS}$ indicates the battery charging and discharging power, and $P^{\mathit{load}}$ indicates load power.

The output results of this model are the configuration position and capacity of ESS and PV.

4. EV Power Utilization Incentive Strategy

The electricity price incentive strategy of EVs participating in OPU is modeled. Based on the above optimal configuration model, the optimal configuration capacity of ESS and PV is output, and the incentive price subsidy is applied to the bus with ESS and PV access to promote EV users to participate in the consumption of PV output in an orderly power consumption scenario.

4.1. EV Objective Function

$$C_{EV}={\displaystyle \sum }_t^T(P{r}_{c,t}{N}_{c,t} P_c^{EV}-P{r}_{d,t}{N}_{d,t} P_d^{EV})$$

(24)

4.2. EV Constraints

(1) Basic constraints of EV operation

The EV basic operation constraints follow Formulas (1)–(11).

(2) EV charging price subsidy constraint

$$C_{EV}={\displaystyle \sum }_t^T(P{r}_{c,t}{N}_{c,t} P_c^{EV}-P{r}_{d,t}{N}_{d,t} P_d^{EV})$$

(25)

$$P{r}_{c,t}=P{r}_{c0}+In{c}_{c,t}$$

(26)

$$0\le In{c}_{c,t}\le {\theta }^{c}P{r}_{c0}$$

(27)

where ${\vartheta }^c$ is the charging coefficient; $In{c}_{c,t}$ is the charging incentive subsidy price at time t; $P{r}_{c0}$ is the time of use (TOU) charging electricity price at time t; and ${\theta }^c$ is the charging price subsidy coefficient.

(3) EV discharging price subsidy constraint

$$In{c}_{D,t}={\displaystyle \frac{1}{{\vartheta }^D{P}_t^{PV}{P}_t^{ESS}}}$$

(28)

$$P{r}_{D,t}=P{r}_{D0}+In{c}_{D,t}$$

(29)

$$0\le In{c}_{D,t}\le {\theta }^{D}P{r}_{D0}$$

(30)

where ${\vartheta }^D$ is the discharging coefficient; $In{c}_{D,t}$ is the discharging incentive subsidy price at time t; $P{r}_{D0}$ is the time of use (TOU) discharging electricity price at time t; and ${\theta }^c$ is the discharging price subsidy coefficient.

Based on the above optimal configuration model, the optimal configuration capacity of ESS and PV is output, and the incentive price subsidy is applied to the bus with ESS and PV access to promote EV users to participate in the consumption of photovoltaic output in the orderly power consumption scenario.

5. Example Analysis

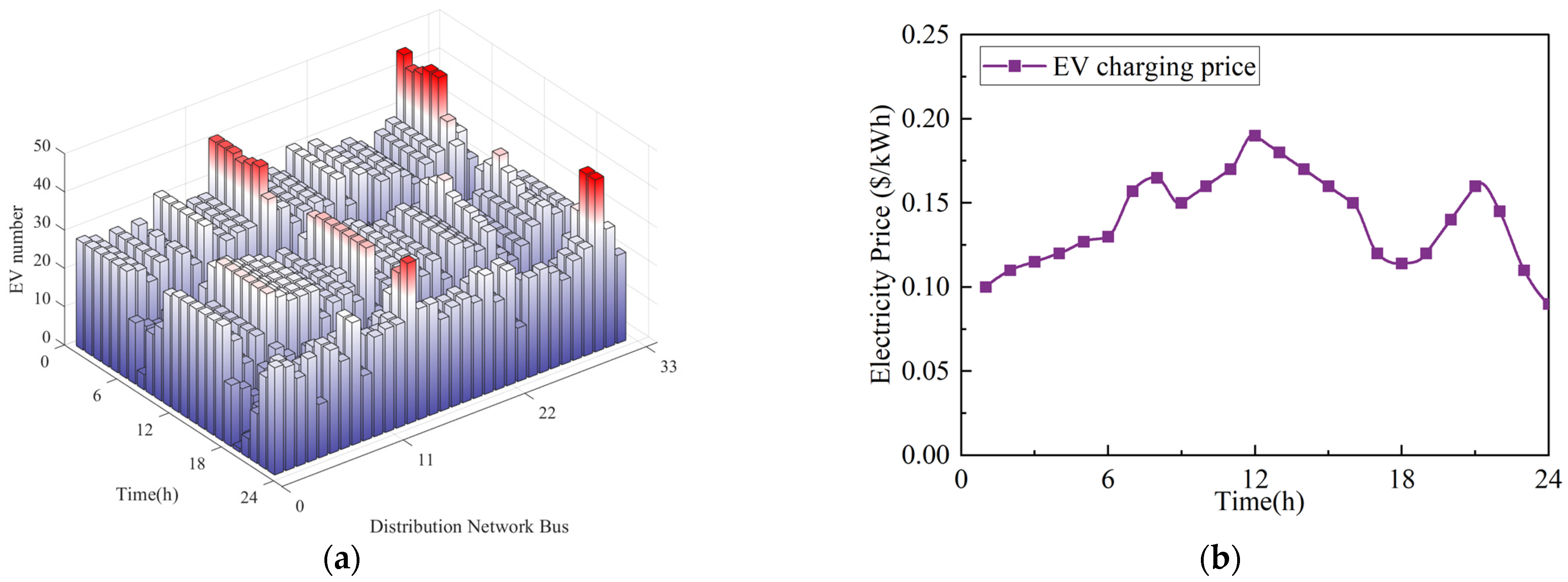
5.1. Simulation System Establishment

In this paper, a simulation system composed of a traffic network and a distribution network is constructed to verify the effectiveness of the proposed PV AND ES system optimal configuration strategy. This paper assumes that in the transmission network nodes on the high-voltage side. The simulation parameters are shown in

Table 1. PV and ESS investment and operation parameters.

PV		ESS
Investment cost	715.2 $/kW	Investment cost	1142.9 $/kWh
Operating cost	0.014 $/kW	Operating cost	0.007 $/kW
Range of capacity	0~750 kW	Range of capacity	0~200 kW/800 kWh
Abandon light cost	0.095 $/kW	Charge efficiency	90%
Discount rate		0.08
Service life		10 year

and

Table 2. EV operation parameters.

EV Parameters
EV total number	1000
EV charging power	40 kW
EV discharging power	25 kW
EV charging and discharging efficiency	90%
EV capacity	45~50 kWh

below. The IEEE 33-bus distribution network model is shown in Figure 2. Figure 3 illustrates the output curve of PV units and the load variation in the distribution network, providing a comprehensive view of the interplay between renewable energy generation and power demand. The number of EVs connected to each distribution network bus is shown in Figure 4.

In this work, we discuss the impact of the joint configuration of PV and ESS on the regulation participation rate of EV users. Considering the joint scheduling operation modes of PV and ESS, two operation scenarios are set up.

(1) Scenario 1: In this scenario, the optimal configuration of ESS and PV is not carried out. In this case, an EV follows the peak-valley charging and discharging price and is charged and discharged based on travel demand on the distribution network.

(2) Scenario 2: The optimal configuration model for ESS and PV is adopted, with EVs charging and discharging according to the structured electricity incentive price.

5.2. Results Analysis

The simulation results are shown in

Table 3. Simulation results.

Scenario	Parameters
Scenario 1	EV charging cost ($)	187.25
	EV discharging subsidy ($)	0
	EV user total cost ($)	187.25
Scenario 2	PV investment cost ($)	26,607
	PV operation cost ($)	81
	ESS investment cost ($)	28,948
	Network loss cost ($)	1353
	EV configuration subsidy ($)	−1759
	Total cost ($)	55,230
	EV charging cost ($)	179.45
	EV discharging subsidy ($)	551.71
	EV user total cost ($)	−372.26

and

Table 4. Scenario 2 PV AND ES system capacity configuration results.

PV		ESS
Location	Capacity	Location	Capacity
30	310.7 kW	13	100 kW/400 kWh

below. Table 3 presents the result parameters for Scenario 1 and Scenario 2. In Scenario 1, only the EV charging cost is considered, resulting in a positive total cost for users. In contrast, Scenario 2 introduces PV, ESS, and incentive policies, leading to a higher total system cost. However, through discharge subsidies and configuration subsidies, EV users achieve a net negative cost, indicating that the incentive policies significantly reduce the economic burden on users. Scenario 2 demonstrates that optimized configurations and incentive policies can simultaneously enhance both economic efficiency and user benefits. Table 4 presents the optimized configuration results for PV and ESS. The rated power capacity of the PV system is configured at 310.7 kW, while the ESS is configured with a power rating of 100 kW and an energy capacity of 400 kWh, ensuring sufficient energy storage and discharge capabilities to support grid stability and renewable energy integration.

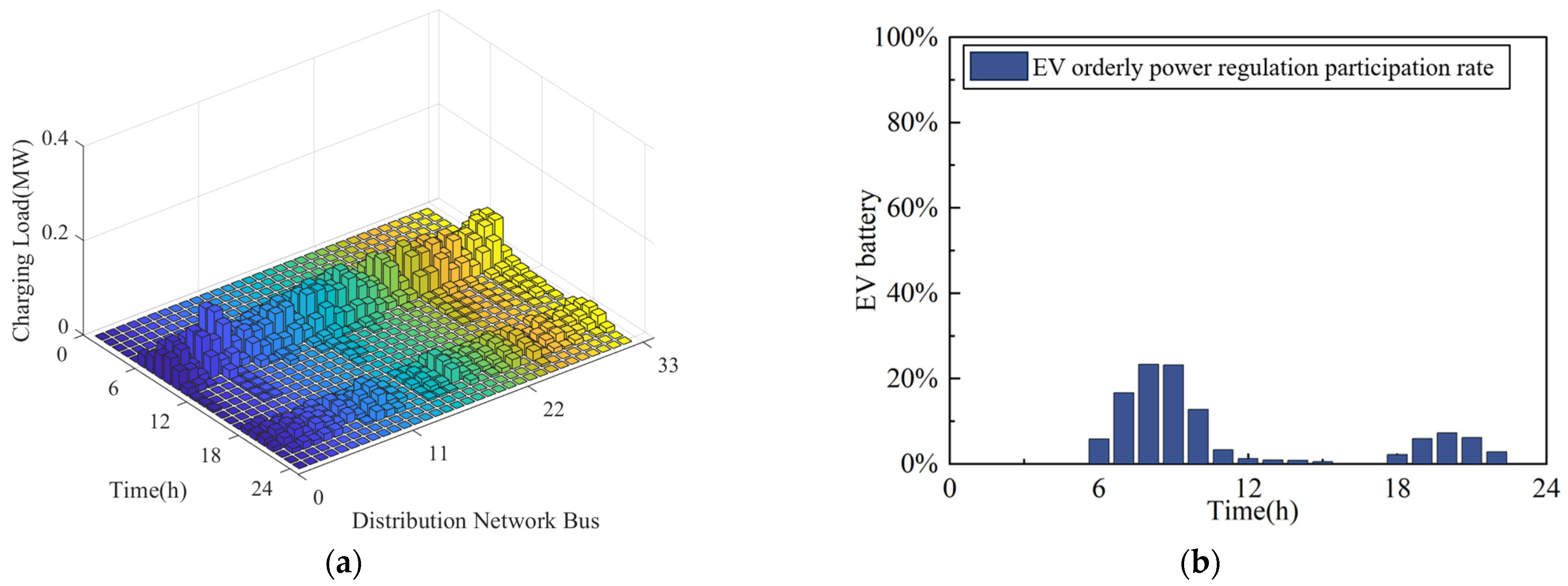
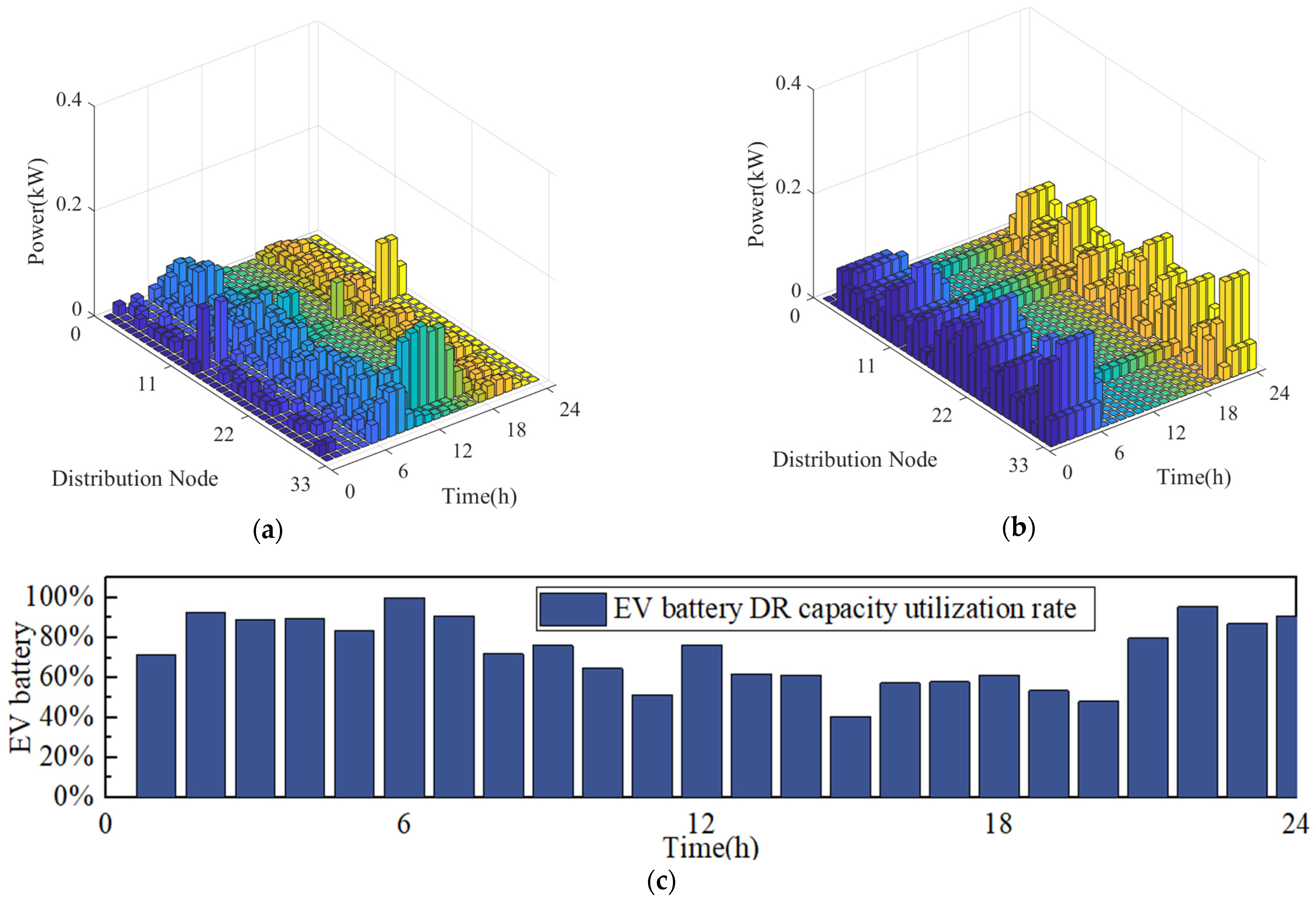
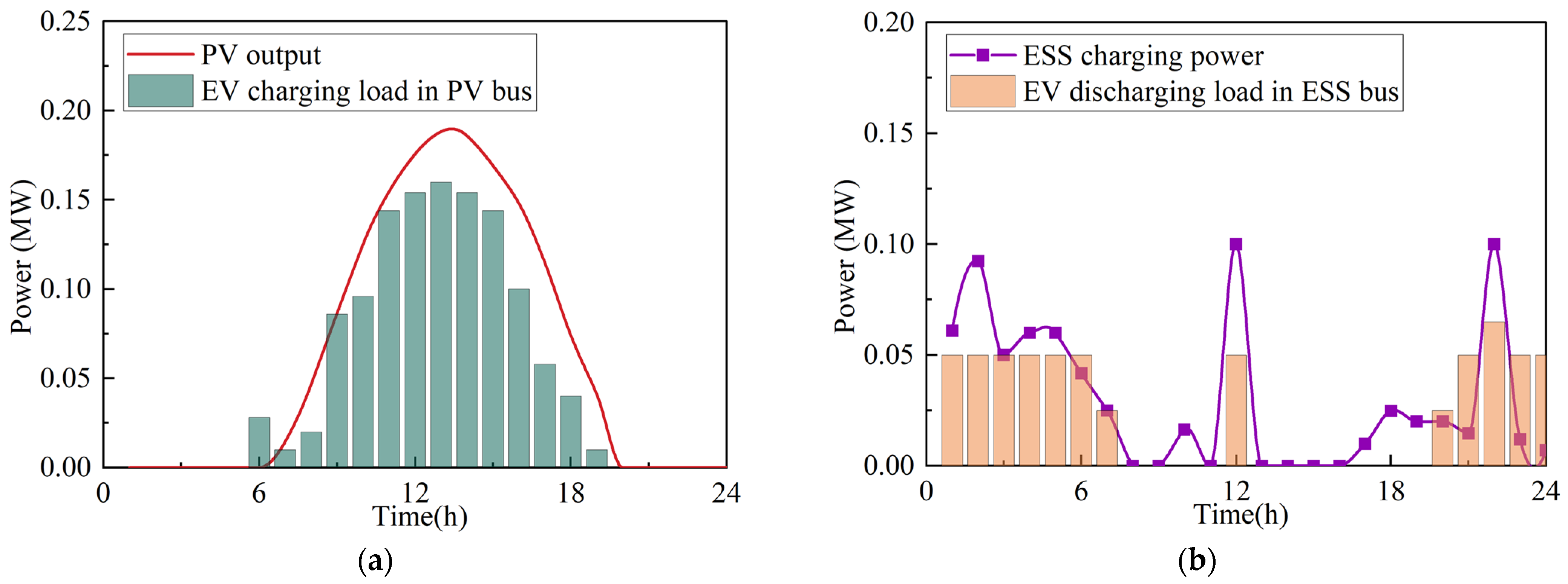
5.2.1. Scenario 1

As illustrated in Figure 5, Scenario 1 represents a baseline case where EV charging behavior is solely determined by inherent travel patterns and driving energy requirements, with no discharging activity observed. This scenario reveals a significant underutilization of the V2G regulation potential, as the maximum regulation capacity utilization rate within the SOC range reaches only 31.7%. For most of the day, EV charging and discharging remain passive, resulting in a regulation capacity utilization rate of 0% for extended periods. These findings highlight the substantial unrealized potential of V2G technology in providing grid regulation services under current operational conditions.

5.2.2. Scenario 2

As can be seen from Figure 6, the charging and discharging of electric vehicles have a spatiotemporal distribution, mainly charging during the day and discharging at night. In terms of node distribution, electric vehicles are evenly distributed at each node and make full use of battery capacity. Combined with Figure 6 and Figure 7, it can be seen that the proposed joint configuration model addresses the optimization of the capacity and geographical location of distributed resources. This work takes into account the number of EVs connected to the grid in various geographical locations to ensure an optimal arrangement of PV and ESS at the EV aggregation centers. The optimal configuration model configures PV at bus 30 and ESS at bus 13. Combined with Figure 4a and Figure 7, it can be seen that the number of EV accesses at bus 30 is relatively high, with significant fluctuations between peak and valley loads. It is a node with frequent EV user turnover, characterized by a higher demand for charging. Installing PV on buses with high EV penetration helps increase the consumption rate of renewable energy, while also reducing charging costs for EV users by providing green and low-cost electricity from renewable energy. At the same time, the number of EV accesses to bus 13 does not fluctuate significantly, the peak-valley difference in access numbers is minor, and the charging and discharging demand remains stable, making it more suitable for providing ancillary power supply services for ESS. At the same time, when charging and discharging optimization is carried out for EVs, charging and discharging subsidies are applied to the distribution network according to the operation of ESS and PV, encouraging EV users to actively respond to demand. The average regulation capacity utilization of EV users at each moment is 73.4% higher than that observed in Scenario 1. Furthermore, under the incentive of the discharge subsidy price, EVs actively discharge to participate in the charge and discharge cycles of the ESS, thereby providing additional charging capacity for the ESS. Concurrently, the incentive policy for charging and discharging has reduced the total travel charging cost for EV users from $187.25 in Scenario 1 to $372.26, enabling net negative cost travel.

As illustrated in Figure 8, the charging behavior of EV users on the PV-equipped bus exhibits a strong correlation with PV output. The total charging load closely follows the PV output curve, achieving a renewable DER consumption rate exceeding 87%. On the ESS configuration bus, the ESS charging demand is primarily offset by EV discharge capabilities. This configuration demonstrates the effective utilization of EV internal energy storage for providing grid ancillary services. The ESS operates in a manner that minimizes grid capacity constraints while offering valuable grid support during peak demand periods. Furthermore, EVs facilitate the temporal redistribution of power consumption by shifting their charging activities to off-peak periods. This mechanism enables effective power supply scheduling within the grid network, contributing to the maintenance of grid operational stability and load balancing.

It can be seen that the optimization strategy proposed in this paper determines the appropriate location and capacity of PV and ESS based on economic feasibility and EV travel characteristics. The EV power utilization incentive strategy enhances EV participation in renewable energy utilization and OPU scheduling, thereby improving grid stability.

6. Conclusions

Our approach demonstrates the potential of coordinated EV charging and discharging, combined with optimized PV and ESS configurations, to support renewable energy integration and enhance grid stability. This aligns with current policy goals aimed at reducing carbon emissions and increasing the share of renewables in the energy mix. We recommend that policymakers implement incentive pricing mechanisms and regulatory frameworks to encourage EV participation in OPU. Simulation results indicate that our proposed strategy can achieve significant cost savings. By aligning EV charging and discharging behaviors with renewable energy generation, our approach maximizes the economic benefits of DER integration. We further suggest that utilities and grid operators explore dynamic pricing models and financial incentives to promote EV user participation in OPU, thereby improving the overall economic efficiency of the power system. In this work, an optimal configuration strategy of PV and ESS for enhancing the regulation capability of EVs under the scenario of orderly power utilization is proposed. The following conclusions are drawn:

(1)

By implementing electricity price incentives, EV users can be effectively guided to participate in orderly power utilization, reducing the pressure on renewable energy consumption. As shown in the simulation results, the regulation capacity utilization rate of EVs increased from 30% to 95%, achieving negative cost travel. Additionally, the participation rate of EVs in the consumption of distributed photovoltaics reached 100%.

(2)

The charging and discharging behavior of EV users can closely match the output of renewable energy, promote the balance between supply and demand, and play a coordinating role between PV and ESS configuration to improve the economic efficiency of EV operation. In the scenarios considered in this paper, the operation of electric vehicles (EVs) is taken into account to further reduce the configuration costs of distributed resources.

(3)

The OD travel matrix model of EVs is used to simulate the daily travel demand of EV users. The modeling of EV charging and discharging characteristics is more precise, which can accurately simulate the SOC state of each EV user, so as to evaluate the surplus capacity of EV users for OPU.

(4)

By incorporating the number and capacity of EVs, the configuration location of DERs can be modified, which can effectively improve the interaction depth between EVs and DERs.

With the continuous development of EVs and the power system, the evolution from the local power balance around the bus with DER to the full configuration and utilization of DER in the overall distribution network will be the main research focus in the next step.