A Novel Prediction Model for Thermal Conductivity of Open Microporous Metal Foam Based on Resonance Enhancement Mechanisms
Abstract
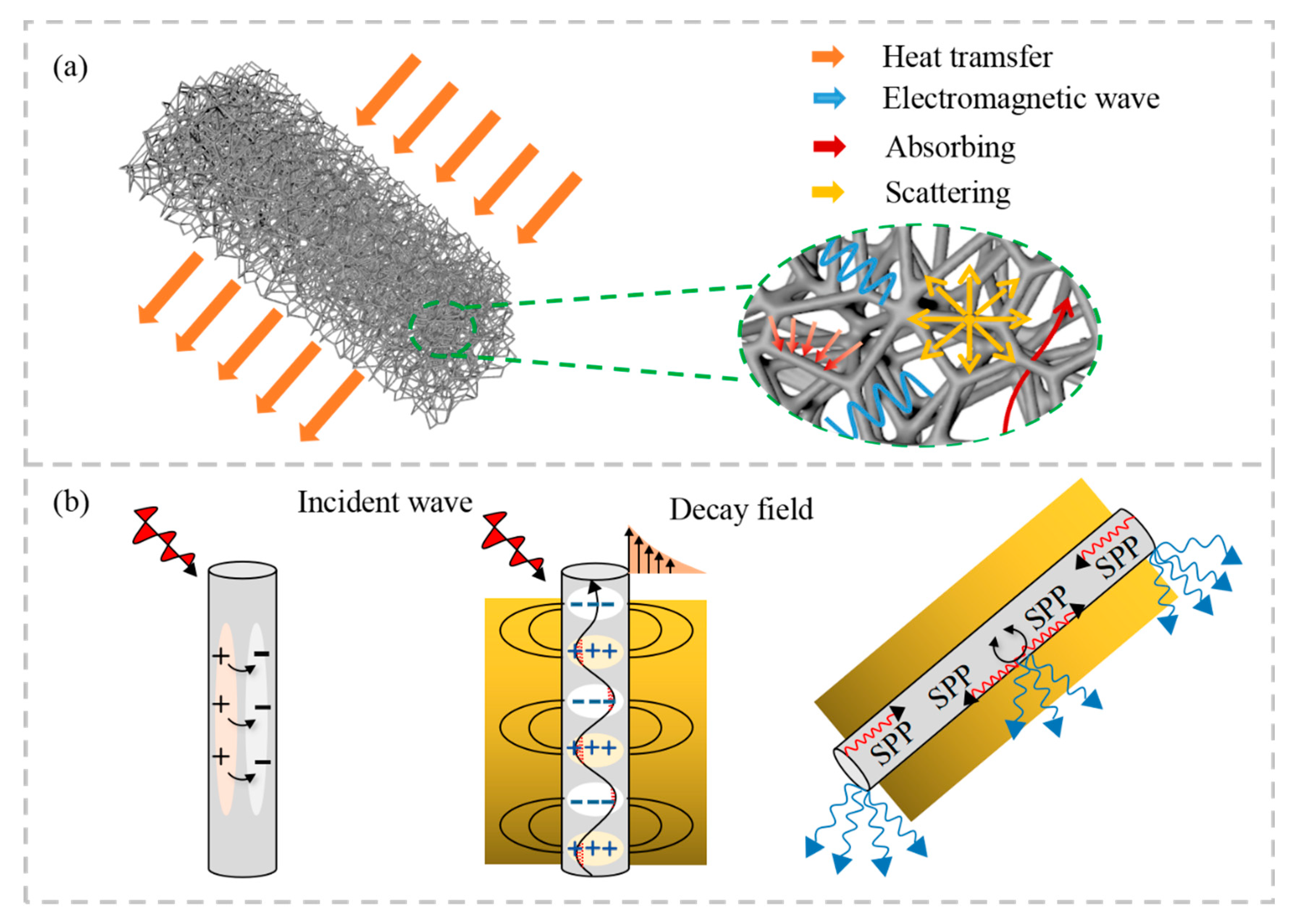
1. Introduction
2. Methods
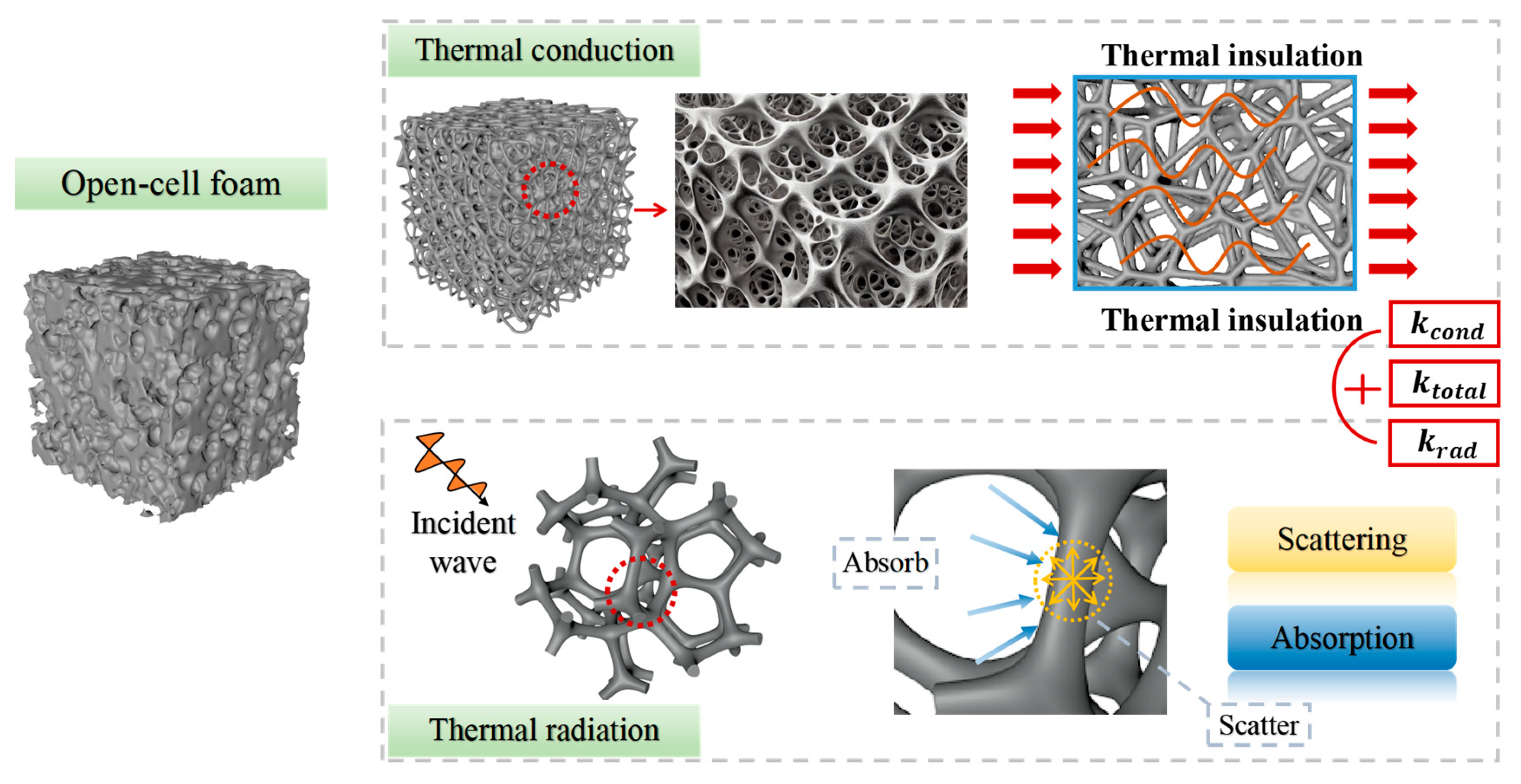
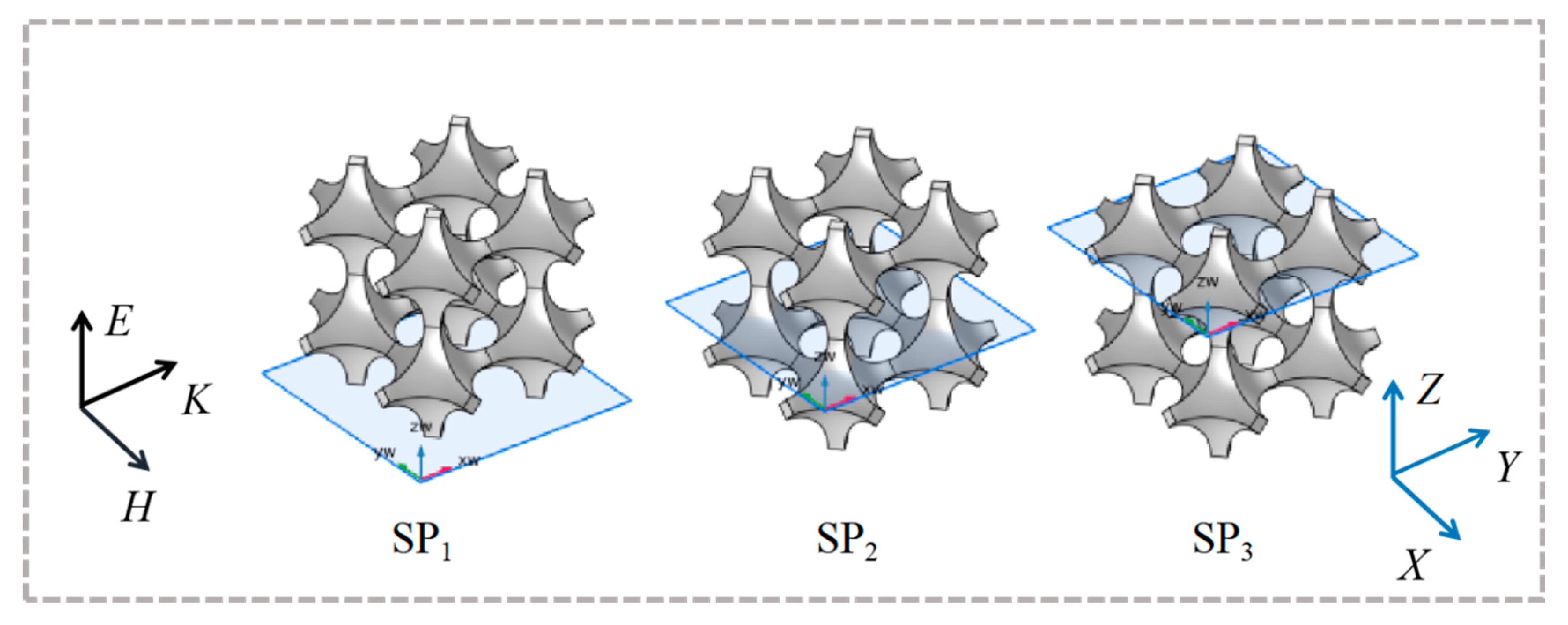
2.1. Geometric Model
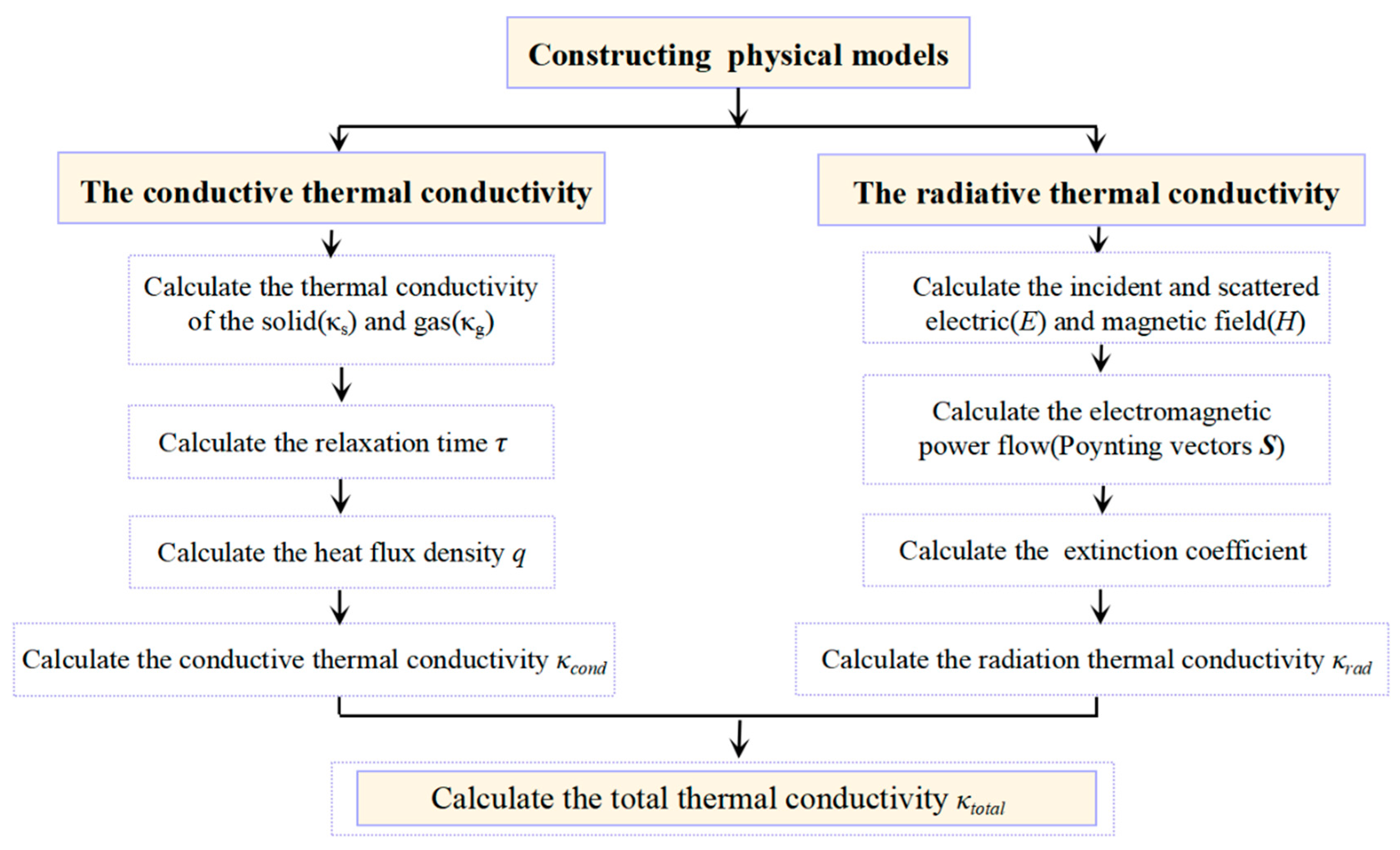
2.2. The Conductive Thermal Conductivity
2.3. The Radiative Thermal Conductivity
2.4. The Radiative Dissipation Efficiency
2.5. The Total Thermal Conductivity
3. Results and Discussion
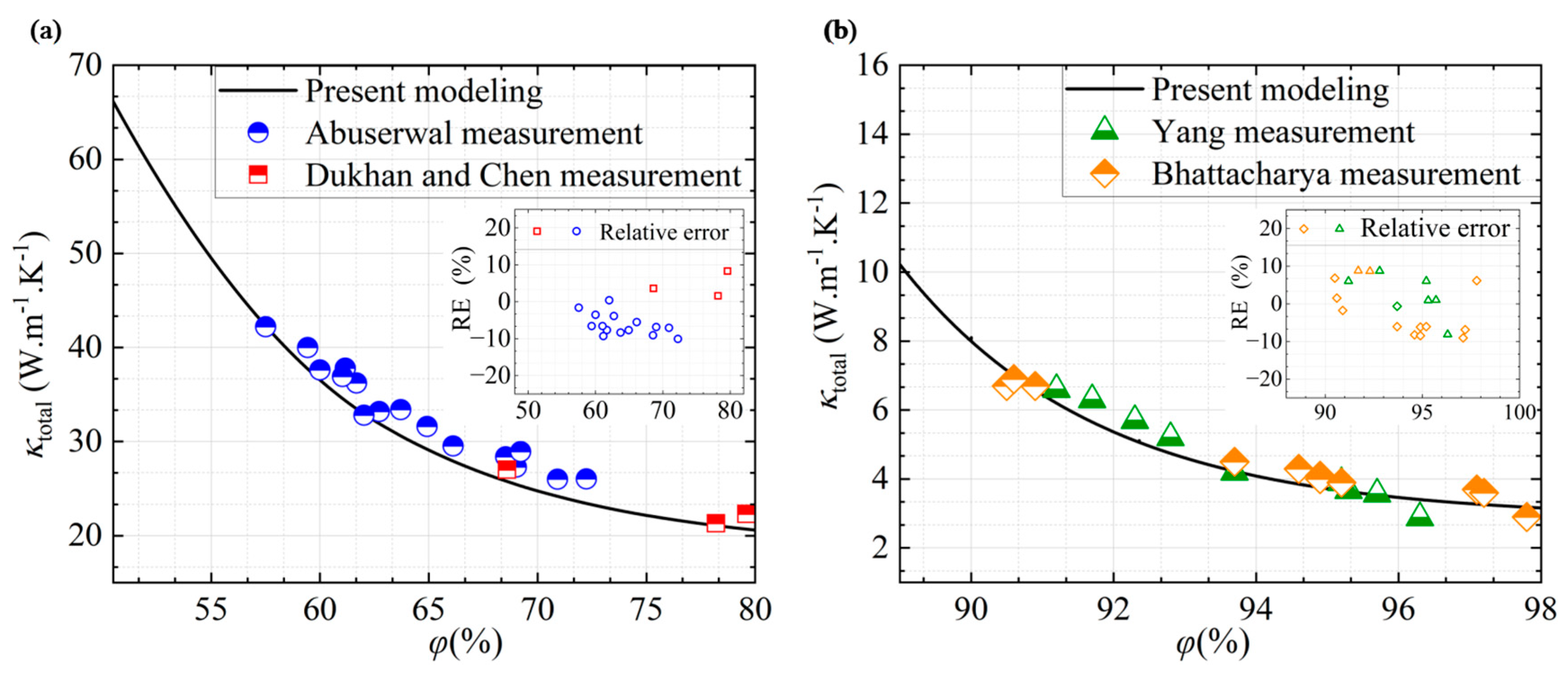
3.1. Model Verification
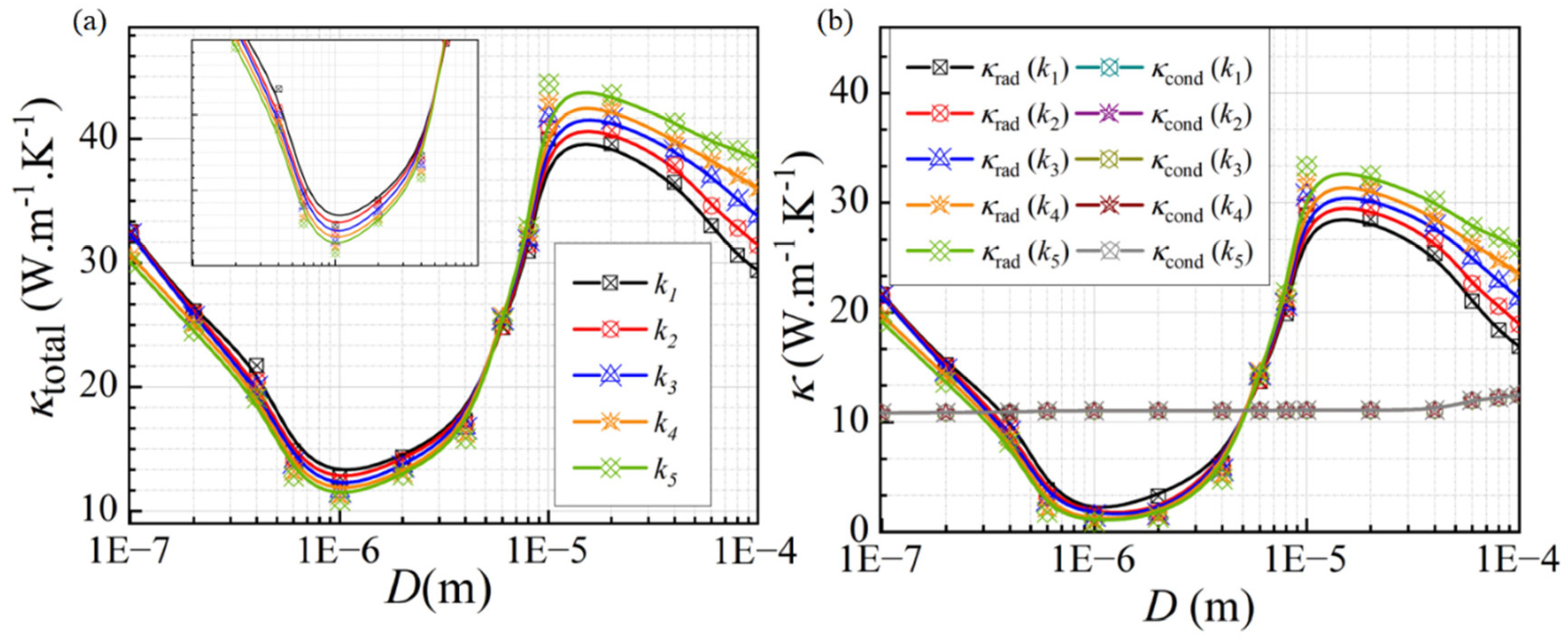
3.2. Factors Influencing the Thermal Conductivity
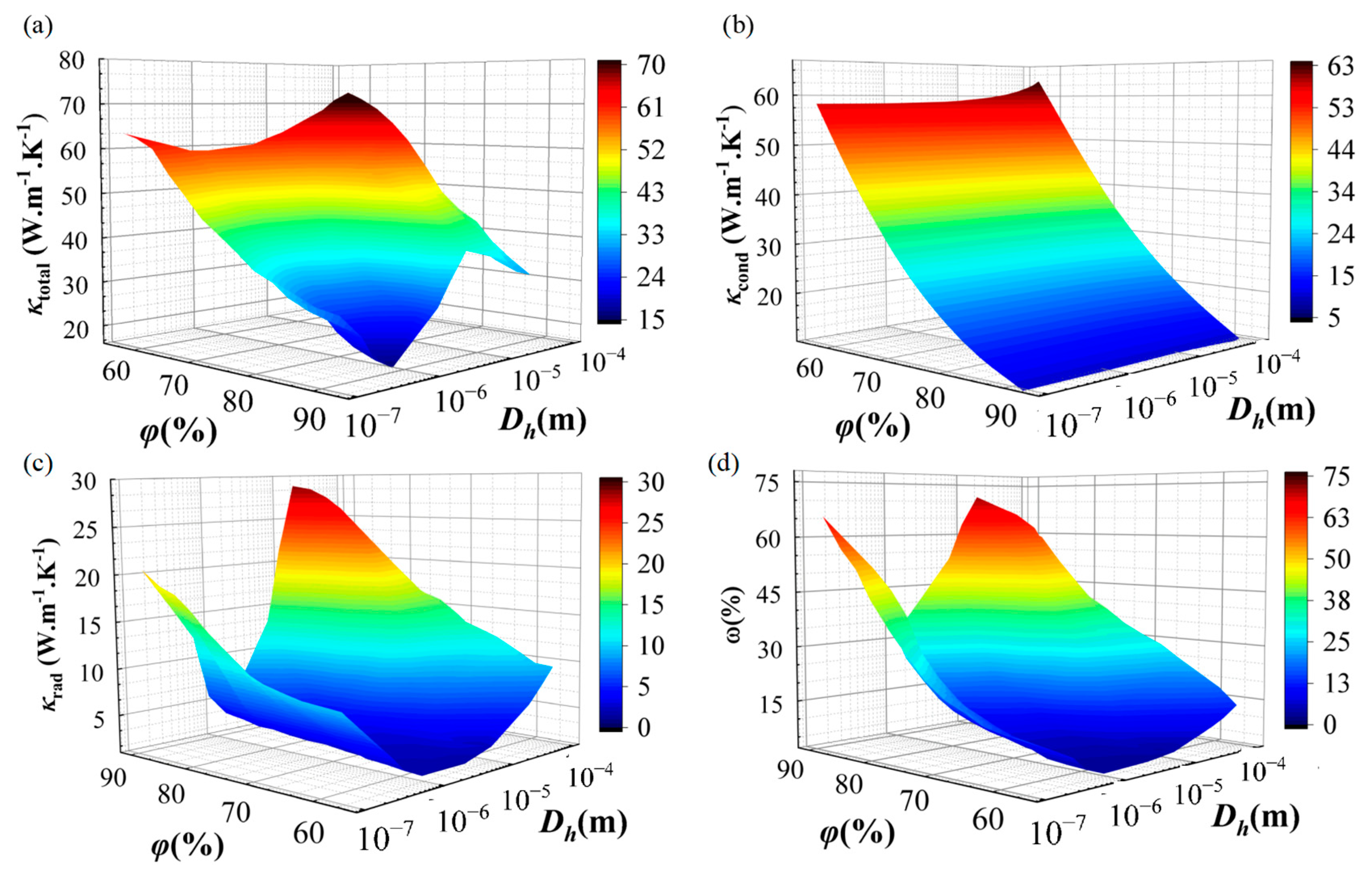
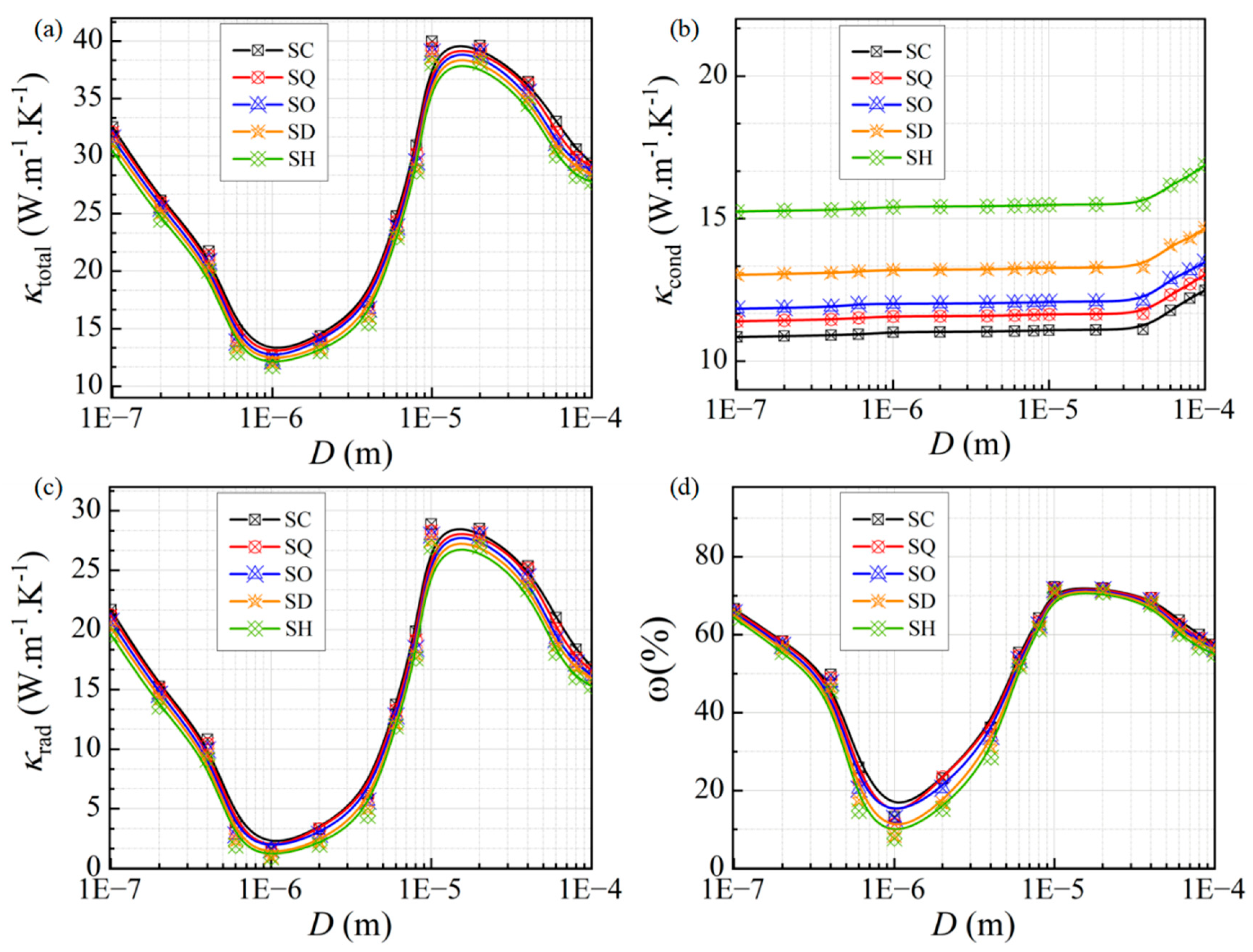
3.2.1. Effect of the Cellular Structure
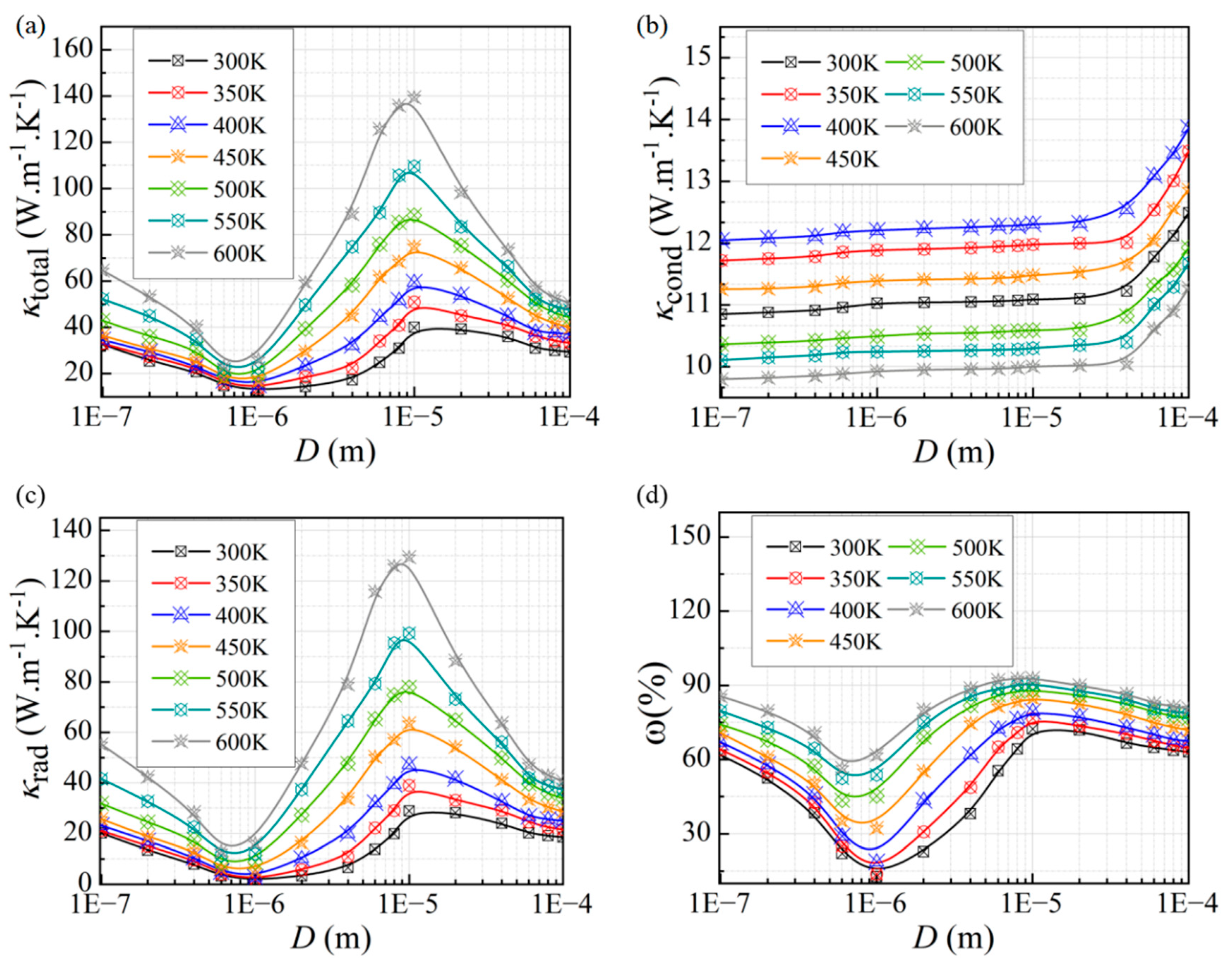
3.2.2. Effect of Temperature
3.2.3. Effect of Volume-Specific Surface Area
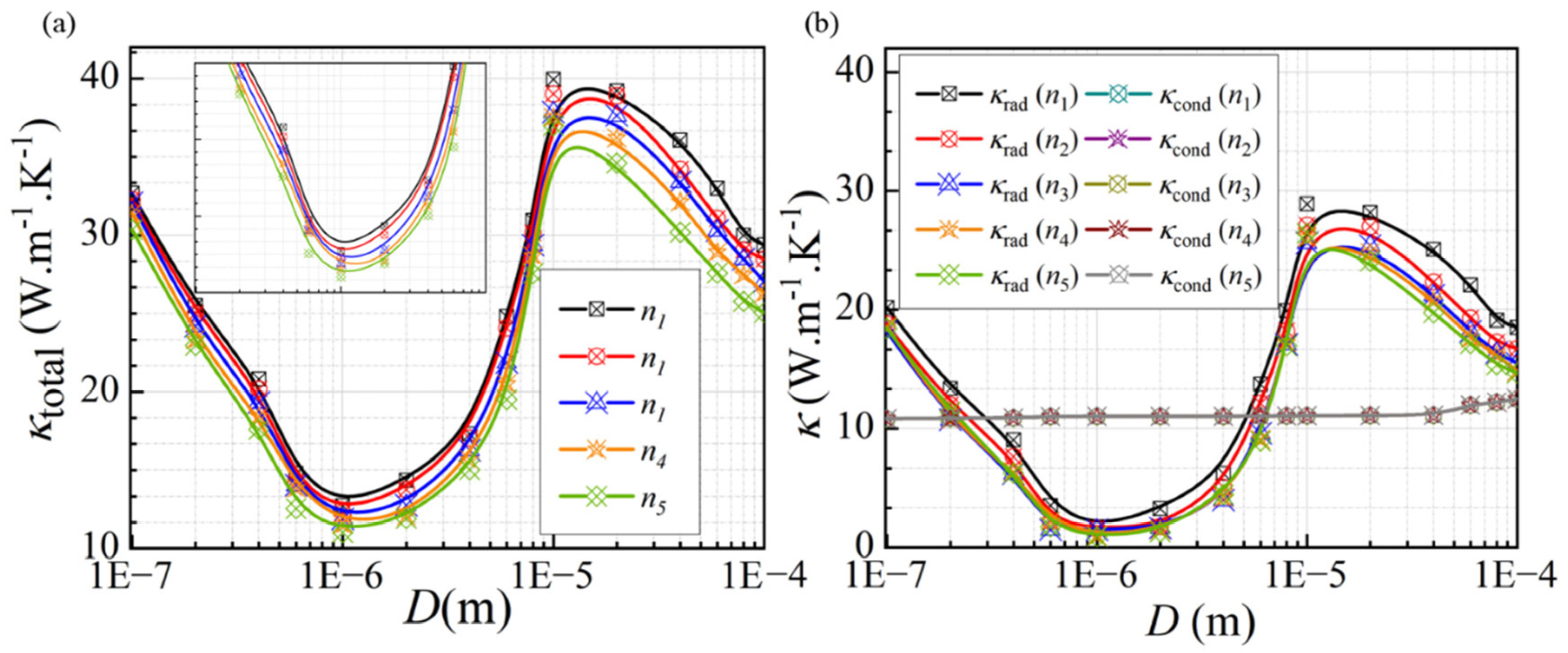
3.2.4. Effect of Refractive Index and Extinction Coefficient
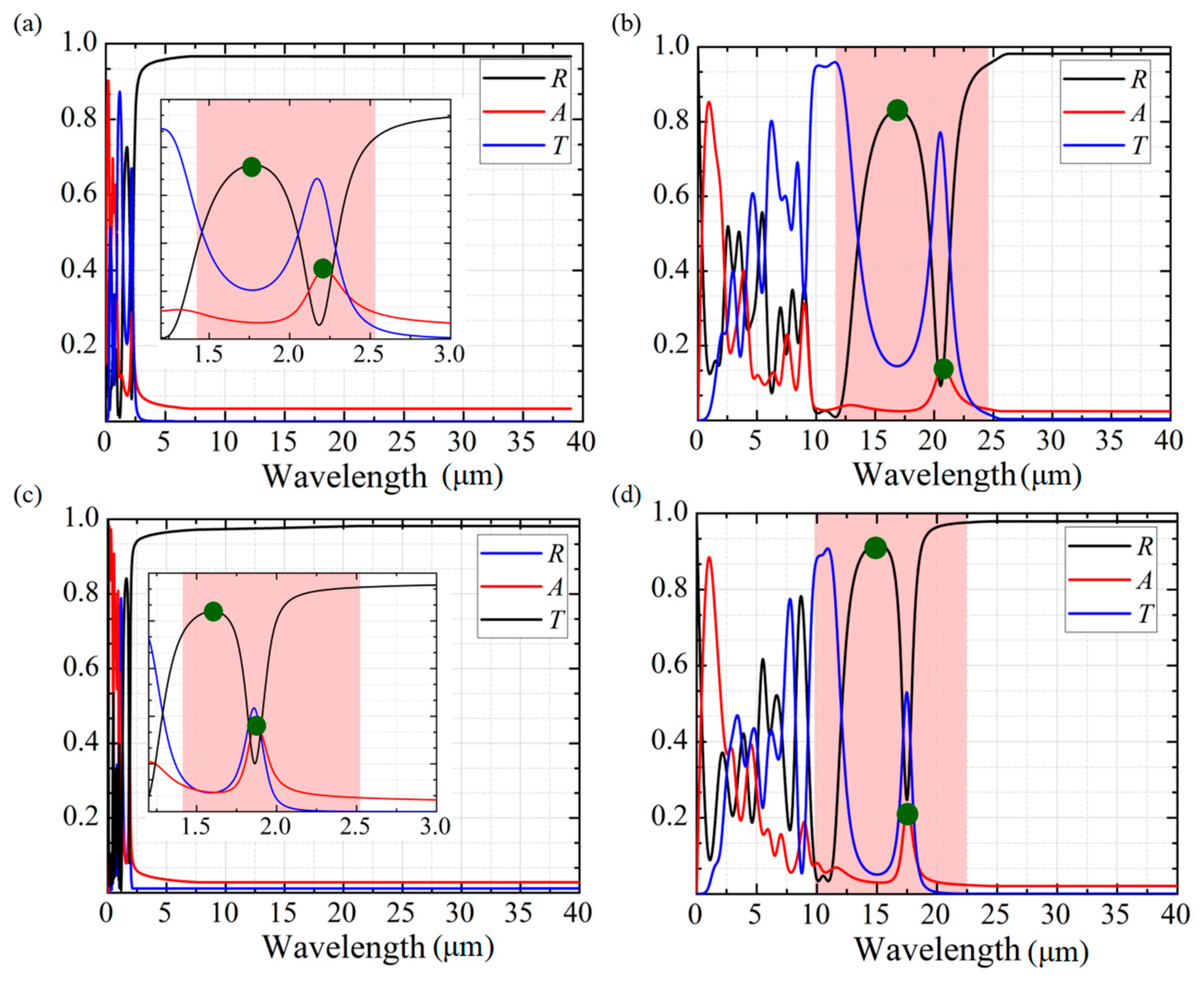
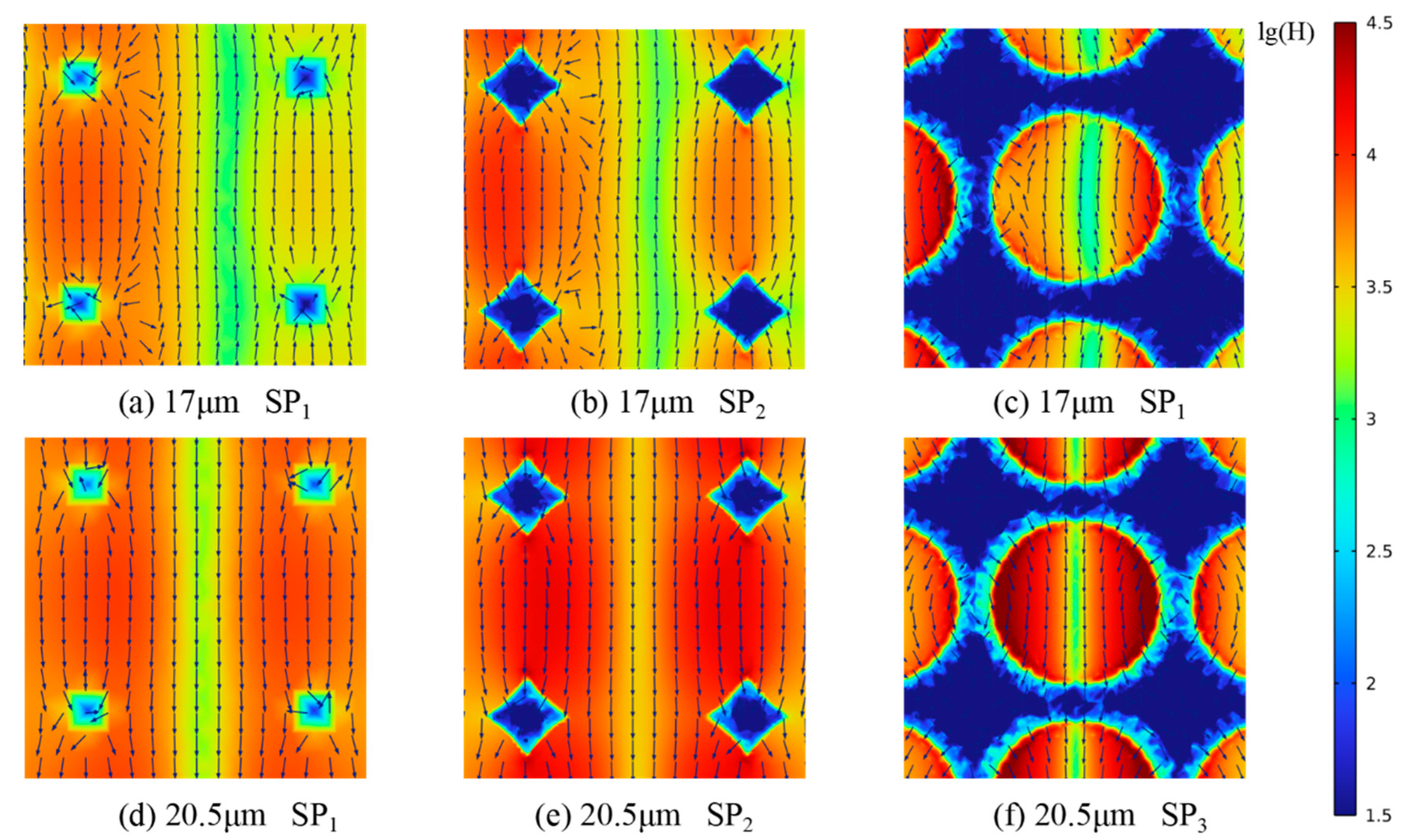
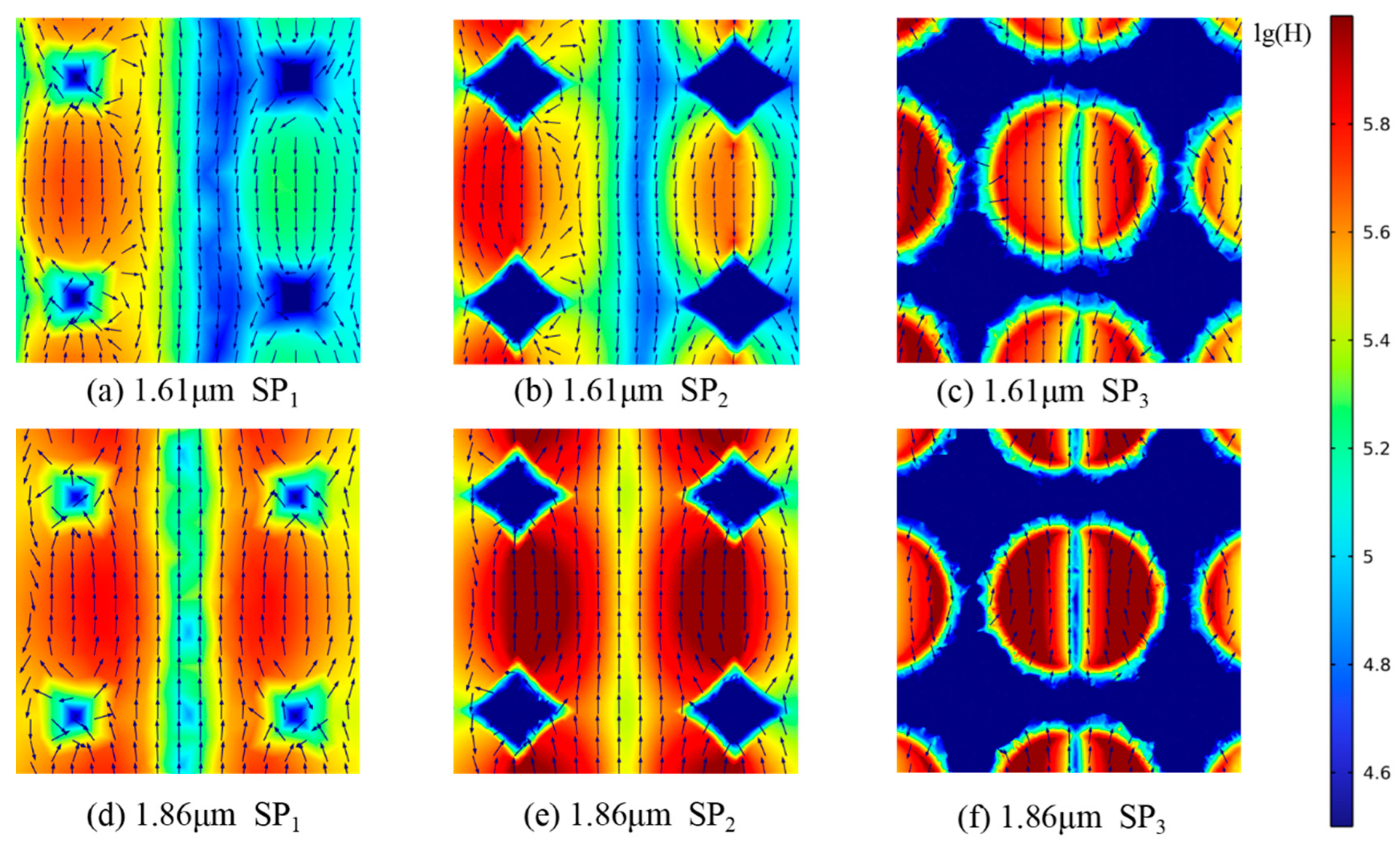
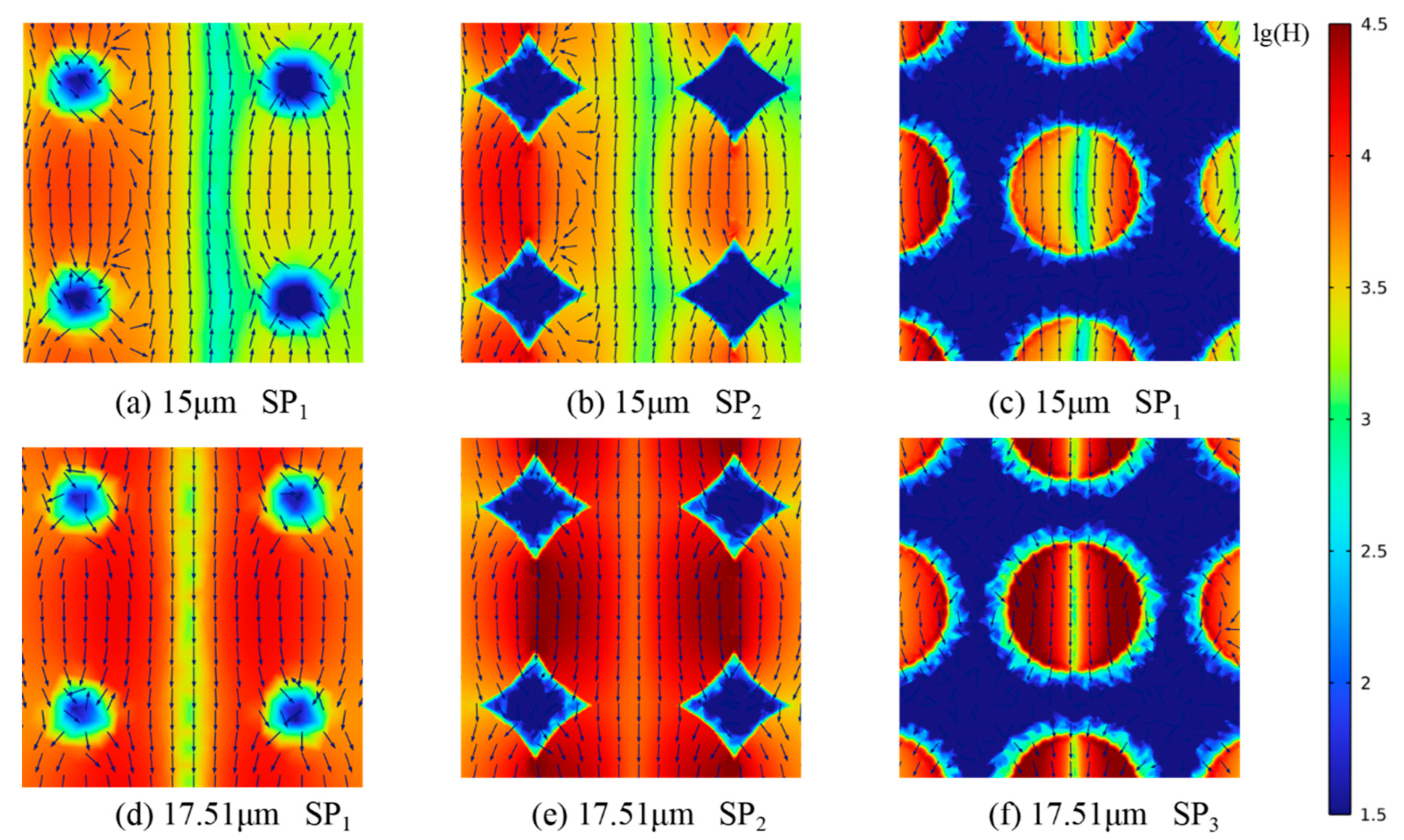
3.3. Radiative Properties Analysis
4. Conclusions
- (1)
- The equivalent thermal conductivity of micro-porous metal materials decreases with increasing porosity, with porosity having a greater impact on conductive heat transfer. The cell size structure primarily influences radiative thermal conductivity. When the cell size is comparable to the characteristic wavelength at the given temperature, radiative heat transfer significantly weakens. In most cases, conduction dominates heat transfer, but at high porosity levels, radiative thermal conductivity may exceed conductive thermal conductivity.
- (2)
- As the temperature rises, the equivalent thermal conductivity of the micro-porous structure increases. This is primarily due to the effect of temperature on the radiative energy calculation using Planck’s law, which leads to an increase in radiative thermal conductivity.
- (3)
- As the refractive index of the material increases, the equivalent thermal conductivity shows little significant change at smaller sizes (approximately less than 0.5 μm). Meanwhile, as the size increases, the equivalent thermal conductivity starts to rise significantly with the increase in refractive index. When the extinction coefficient changes, the variation in equivalent thermal conductivity follows a trend similar to that of the refractive index under large pore conditions. As the pore size decreases, the equivalent thermal conductivity decreases with an increase in extinction coefficient.
- (4)
- The spectral radiation characteristic contour map reveals that the surface plasmon polariton (SPP) resonance and the magnetic polariton (MP) resonance occur at the gas–solid interface, which significantly enhances the radiation dissipation at the gas–solid interface, improves the efficiency of radiation dissipation, and reduces the thermal conductivity of the materials.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| K | thermal conductivity | W/(m*K) |
| T | temperature | K |
| R | diameter of hole | m |
| Dh | metameric size | m |
| t | time | s |
| fi | temperature evolution function | - |
| τ | dimensional relaxation time | s |
| i | discrete direction | - |
| x | location vector | - |
| ei | discrete velocity | - |
| δt | time step | - |
| fieq | local equilibrium function | - |
| T(x,t) | local temperature | K |
| c | lattice sound speed | - |
| q | density of heat source | W/m2 |
| σa,λ | spectral absorption | m−1 |
| σs,λ | scattering coefficient | m−1 |
| σe,λ | spectral extinction coefficient | m−1 |
| B | magnetic flux density | Wb/m2 |
| D | electric displacement vector | C/m2 |
| E | electric field vector | V/m |
| H | magnetic field vector | A/m |
| J | current density | A/m2 |
| ε | permittivity | F/m |
| μ | permeability | H/m |
| σ | electrical conductivity | S/m |
| A | absorption | - |
| R | reflection | - |
| T | transmission | - |
| S | incident energy flow | W |
| n | refractive index | - |
| N | particle numbers | - |
| ∆T | temperature difference | K |
| SQ | square hole | |
| SC | circular hole | |
| SO | Octagonal hole | |
| SH | Hexagonal hole | |
| SD | Dodecagonal hole | |
| Z | cross-section | |
| VSSA | Volume-Specific Surface Area | |
| ω | κrad/κtotal | |
| Superscript | ||
| * | complex vector | - |
| a | absorption | - |
| i | incident | - |
| s | scattering | - |
| inc | incident | - |
| sca | scattering | - |
| Subscript | ||
| cond | conduction | - |
| rad | thermal radiation | - |
| total | total heat transfer | - |
References
- Yang, T.; Liu, W.; Kramer, G.J.; Sun, Q. Seasonal thermal energy storage: A techno-economic literature review. Renew. Sustain. Energy Rev. 2021, 139, 110732. [Google Scholar] [CrossRef]
- Wang, S.; Huang, Y.; Zhao, C.; Chang, E.; Ameli, A.; Naguib, H.E.; Park, C.B. Theoretical modeling and experimental verification of percolation threshold with MWCNTs’ rotation and translation around a growing bubble in conductive polymer composite foams. Compos. Sci. Technol. 2020, 199, 108345. [Google Scholar] [CrossRef]
- Khan, S.A.; Al-Ghamdi, S.G. Synthesis of graphene oxide nanofluid based micro-nano scale surfaces for high-performance nucleate boiling thermal management systems. Case Stud. Therm. Eng. 2021, 28, 101436. [Google Scholar] [CrossRef]
- Kumar, P.P.; Gireesha, B.; Venkatesh, P.; Keerthi, M. Comparative analysis of transient thermal behaviour and efficiency in longitudinal metal porous fin with combined heat and mass transfer under dehumidification conditions. Appl. Therm. Eng. 2025, 261, 125069. [Google Scholar] [CrossRef]
- Meng, J.; Yao, Z.; Du, H.; Lv, M. Thermal protection method of the solar array for stratospheric airships. Appl. Therm. Eng. 2017, 111, 802–810. [Google Scholar] [CrossRef]
- Awasthi, A.; Hwang, K.-I.; Jeon, Y. Performance improvement of novel latent thermal energy storage system with two-layer metal foam porosities. Case Stud. Therm. Eng. 2024, 60, 104668. [Google Scholar] [CrossRef]
- Khattar, M.Z.; Heyhat, M.M. Exergy, Economic and Environmental Analysis of a Direct Absorption Parabolic Trough Collector Filled with Porous Metal Foam. Energies 2022, 15, 8150. [Google Scholar] [CrossRef]
- Ke, H.; Zhou, X.; Liu, T.; Wang, Y.; Wang, H. Numerical Study of Heat and Mass Transfer in the Original Structure and Homogeneous Substitution Model for Three Dimensional Porous Metal Foam. Energies 2023, 16, 1114. [Google Scholar] [CrossRef]
- Dukhan, N. Equivalent parallel strands modeling of highly-porous media for two-dimensional heat transfer: Application to metal foam. Energies 2021, 14, 6308. [Google Scholar] [CrossRef]
- Ali, R.M.K.; Lafta Ghashim, S. Numerical analysis of the heat transfer enhancement by using metal foam. Case Stud. Therm. Eng. 2023, 49, 103336. [Google Scholar] [CrossRef]
- Liu, B.; Feng, J.; Wang, Z.-A.; Shi, G.-H. Numerical analysis of radiative transfer and prediction of spectral properties for combined material composed of nickel foam and TiO2 nanofluid. Int. J. Therm. Sci. 2024, 202, 109096. [Google Scholar] [CrossRef]
- Yu, H.; Zhang, H.; Wang, H.; Zhang, D. The equivalent thermal conductivity of the micro/nano scaled periodic cubic frame silver and its thermal radiation mechanism analysis. Energies 2021, 14, 4158. [Google Scholar] [CrossRef]
- Gong, P.; Wang, G.; Tran, M.-P.; Buahom, P.; Zhai, S.; Li, G.; Park, C.B. Advanced bimodal polystyrene/multi-walled carbon nanotube nanocomposite foams for thermal insulation. Carbon 2017, 120, 1–10. [Google Scholar] [CrossRef]
- Zhu, Y.; Yuan, J.-H.; Fang, W.-Y.; Sun, Z.-G.; Wang, J.J.A.S.S. A family of two-dimensional semiconductors with transition metal Kagome lattice, large power factor and ultralow lattice thermal conductivity. Appl. Surf. Sci. 2023, 636, 157817. [Google Scholar] [CrossRef]
- Liu, B.; Shi, J.; Liew, K.; Shen, S. Near-field radiative heat transfer for Si based metamaterials. Opt. Commun. 2014, 314, 57–65. [Google Scholar] [CrossRef]
- Kumar, V.; Raghuwanshi, S.K. Efficiency estimation and hardware implementation of solar PV module system assisted by using surface plasmon resonance sensor. Case Stud. Therm. Eng. 2023, 51, 103479. [Google Scholar] [CrossRef]
- Van Zwol, P.; Joulain, K.; Ben-Abdallah, P.; Chevrier, J. Phonon polaritons enhance near-field thermal transfer across the phase transition of VO2. Phys. Rev. B Condens. Matter Mater. Phys. 2011, 84, 161413. [Google Scholar] [CrossRef]
- Huang, J.; Xuan, Y.; Li, Q. Narrow-band spectral features of structured silver surface with rectangular resonant cavities. J. Quant. Spectrosc. Radiat. Transf. 2011, 112, 839–846. [Google Scholar] [CrossRef]
- Boomsma, K.; Poulikakos, D. On the effective thermal conductivity of a three-dimensionally structured fluid-saturated metal foam. Int. J. Heat Mass Transf. 2001, 44, 827–836. [Google Scholar] [CrossRef]
- Changqing, X.; Zhiqiang, L.; Lin, J.; Zhihua, W.; Longmao, Z. Theoretical Study and Numerical Simulation of Effective Thermal Conductivities of Open-Cell Metallic Foam. Rare Met. Mater. Eng. 2014, 43, 686–691. [Google Scholar]
- He, Y.-L.; Xie, T. Advances of thermal conductivity models of nanoscale silica aerogel insulation material. Appl. Therm. Eng. 2015, 81, 28–50. [Google Scholar] [CrossRef]
- Nie, Z.; Lin, Y.; Tong, Q. Numerical investigation of pressure drop and heat transfer through open cell foams with 3D Laguerre-Voronoi model. Int. J. Heat Mass Transf. 2017, 113, 819–839. [Google Scholar] [CrossRef]
- Xia, X.-L.; Liu, B.; Chen, X.; Sun, C. Prediction of spectral radiative property based on the microscopic ligament morphology and pore-level structure of open-cell alumina foam. Infrared Phys. Technol. 2022, 126, 104331. [Google Scholar] [CrossRef]
- Luo, M.; Wang, C.; Zhao, J.; Liu, L. Characteristics of effective thermal conductivity of porous materials considering thermal radiation: A pore-level analysis. Int. J. Heat Mass Transf. 2022, 188, 122597. [Google Scholar] [CrossRef]
- Fan, C.; Li, X.-L.; Xia, X.-L.; Sun, C. Tomography-based pore level analysis of combined conductive-radiative heat transfer in an open-cell metallic foam. Int. J. Heat Mass Transf. 2020, 159, 120122. [Google Scholar] [CrossRef]
- Lin, Y.; Yang, C.; Zhang, W.; Fukumoto, K.; Saito, Y.; Machida, H.; Norinaga, K. Estimation of effective thermal conductivity in open-cell foam with hierarchical pore structure using lattice Boltzmann method. Appl. Therm. Eng. 2023, 218, 119314. [Google Scholar] [CrossRef]
- Chen, S.; Ai, B.; Li, Y.; Huang, X.; Yang, X. The effective thermal conductivity of random isotropic porous media analysis and prediction. Eng. Anal. Bound. Elem. 2024, 167, 105895. [Google Scholar] [CrossRef]
- Yu, H.; Zhang, H.; Zhao, J.; Liu, J.; Xia, X.; Wu, X. Thermal conductivity of micro/nano-porous polymers: Prediction models and applications. Front. Phys. 2022, 17, 23202. [Google Scholar] [CrossRef]
- D’Orazio, A.; Succi, S. Boundary conditions for thermal lattice Boltzmann simulations. In Computational Science—ICCS 2003 International Conference Melbourne, Australia and St. Petersburg, Russia June 2–4, 2003 Proceedings, Part I; Springer: Berlin/Heidelberg, Germany, 2003; pp. 977–986. [Google Scholar]
- Lu, J.; Kan, A.; Zhu, W.; Yuan, Y. Numerical investigation on effective thermal conductivity of fibrous porous medium under vacuum using Lattice-Boltzmann method. Int. J. Therm. Sci. 2021, 160, 106682. [Google Scholar] [CrossRef]
- Qu, Z.; Fu, Y.; Liu, Y.; Zhou, L. Approach for predicting effective thermal conductivity of aerogel materials through a modified lattice Boltzmann method. Appl. Therm. Eng. 2018, 132, 730–739. [Google Scholar] [CrossRef]
- Wang, M.; Pan, N. Modeling and prediction of the effective thermal conductivity of random open-cell porous foams. Int. J. Heat Mass Transf. 2008, 51, 1325–1331. [Google Scholar] [CrossRef]
- Shen, S.; Narayanaswamy, A.; Chen, G. Surface phonon polaritons mediated energy transfer between nanoscale gaps. Nano Lett. 2009, 9, 2909–2913. [Google Scholar] [CrossRef] [PubMed]
- Howell, J.R.; Mengüç, M.P.; Daun, K.; Siegel, R. Thermal Radiation Heat Transfer; CRC Press: Boca Raton, FL, USA, 2020. [Google Scholar]
- Bernardo, V.; Martin-de Leon, J.; Pinto, J.; Schade, U.; Rodriguez-Perez, M.A. On the interaction of infrared radiation and nanocellular polymers: First experimental determination of the extinction coefficient. Colloids Surf. A Physicochem. Eng. Asp. 2020, 600, 124937. [Google Scholar] [CrossRef]
- Zhang, Z.M. Nano/Microscale Heat Transfer; Springer: Berlin/Heidelberg, Germany, 2007; Volume 410. [Google Scholar]
- Yu, H.; Zhang, H.; Xia, X. A fractal-skeleton model of high porosity macroporous aluminum and its heat transfer characterizes. J. Therm. Anal. Calorim. 2020, 141, 351–360. [Google Scholar] [CrossRef]
- Liu, Y.; Jin, R.; Qiu, J.; Liu, L. Spectral radiative properties of a nickel porous microstructure and magnetic polariton resonance for light trapping. Int. J. Heat Mass Transf. 2016, 98, 833–844. [Google Scholar] [CrossRef]
- Huang, Y.; Ringe, E.; Hou, M.; Ma, L.; Zhang, Z. Near-field mapping of three-dimensional surface charge poles for hybridized plasmon modes. AIP Adv. 2015, 5, 107221. [Google Scholar] [CrossRef]
- Abuserwal, A.F.; Luna, E.M.E.; Goodall, R.; Woolley, R. The effective thermal conductivity of open cell replicated aluminium metal sponges. Int. J. Heat Mass Transf. 2017, 108, 1439–1448. [Google Scholar] [CrossRef]
- Bhattacharya, A.; Calmidi, V.V.; Mahajan, R.L. Thermophysical properties of high porosity metal foams. Int. J. Heat Mass Transf. 2002, 45, 1017–1031. [Google Scholar] [CrossRef]
- Dukhan, N.; Chen, K.-C. Heat transfer measurements in metal foam subjected to constant heat flux. Exp. Therm. Fluid Sci. 2007, 32, 624–631. [Google Scholar] [CrossRef]
- Yang, X.H.; Bai, J.X.; Yan, H.B.; Kuang, J.J.; Lu, T.J.; Kim, T. An Analytical Unit Cell Model for the Effective Thermal Conductivity of High Porosity Open-Cell Metal Foams. Transp. Porous Media 2014, 102, 403–426. [Google Scholar] [CrossRef]
- Wang, J.; Wang, M.; Li, Z. A lattice Boltzmann algorithm for fluid–solid conjugate heat transfer. Int. J. Therm. Sci. 2007, 46, 228–234. [Google Scholar] [CrossRef]
- Zou, Q.; He, X. On pressure and velocity boundary conditions for the lattice Boltzmann BGK model. Phys. Fluids 1997, 9, 1591–1598. [Google Scholar] [CrossRef]
- Sacks, Z.S.; Kingsland, D.M.; Lee, R.; Lee, J.F. A perfectly matched anisotropic absorber for use as an absorbing boundary condition. IEEE Trans. Antennas Propag. 1995, 43, 1460–1463. [Google Scholar] [CrossRef]

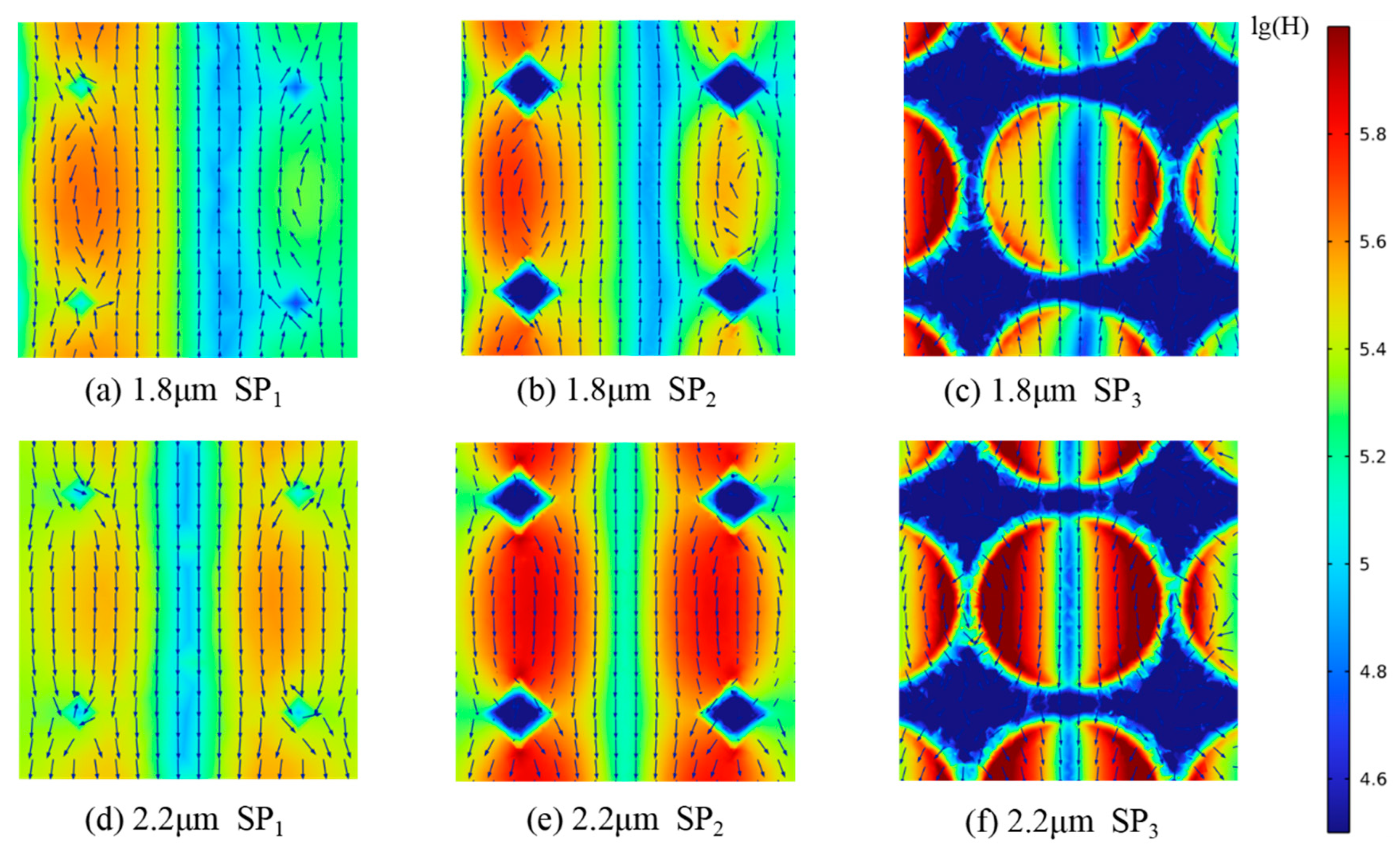
| λ = 1.8 SP1 | λ = 1.8 SP2 | λ = 1.8 SP3 | λ = 2.2 SP1 | λ = 2.2 SP2 | λ = 2.2 SP3 | |
|---|---|---|---|---|---|---|
| η (%) | 23.65 | 28.01 | 46.71 | 22.78 | 29.19 | 48.34 |
| λ = 17 SP1 | λ = 17 SP2 | λ = 17 SP3 | λ = 20.5 SP1 | λ = 20.5 SP2 | λ = 20.5 SP3 | |
|---|---|---|---|---|---|---|
| η (%) | 16.27 | 21.26 | 40.68 | 20.79 | 27.86 | 42.09 |
| λ = 1.61 SP1 | λ = 1.61 SP2 | λ = 1.61 SP3 | λ = 1.86 SP1 | λ = 1.86 SP2 | λ = 1.86 SP3 | |
|---|---|---|---|---|---|---|
| η (%) | 29.62 | 31.34 | 68.10 | 32.12 | 35.35 | 70.78 |
| λ = 15 SP1 | λ = 15 SP2 | λ = 15 SP3 | λ = 17.5 SP1 | λ = 17.5 SP2 | λ = 17.5 SP3 | |
|---|---|---|---|---|---|---|
| η (%) | 27.65 | 29.55 | 60.10 | 29.68 | 31.49 | 60.78 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, A.; Chai, J.; Ren, X.; Li, M.; Yu, H.; Wang, G. A Novel Prediction Model for Thermal Conductivity of Open Microporous Metal Foam Based on Resonance Enhancement Mechanisms. Energies 2025, 18, 1529. https://doi.org/10.3390/en18061529
Chen A, Chai J, Ren X, Li M, Yu H, Wang G. A Novel Prediction Model for Thermal Conductivity of Open Microporous Metal Foam Based on Resonance Enhancement Mechanisms. Energies. 2025; 18(6):1529. https://doi.org/10.3390/en18061529
Chicago/Turabian StyleChen, Anqi, Jialong Chai, Xiaohan Ren, Mingdong Li, Haiyan Yu, and Guilong Wang. 2025. "A Novel Prediction Model for Thermal Conductivity of Open Microporous Metal Foam Based on Resonance Enhancement Mechanisms" Energies 18, no. 6: 1529. https://doi.org/10.3390/en18061529
APA StyleChen, A., Chai, J., Ren, X., Li, M., Yu, H., & Wang, G. (2025). A Novel Prediction Model for Thermal Conductivity of Open Microporous Metal Foam Based on Resonance Enhancement Mechanisms. Energies, 18(6), 1529. https://doi.org/10.3390/en18061529






