A Fault-Severity-Assessment Model Based on Spatiotemporal Feature Fusion and Scene Generation for Optical Current Transformer

Abstract

Accurately identifying the fault type of an optical current transformer (optical CT) and evaluating the fault severity can provide strong support for the operation and maintenance of a direct current (DC) power system. In response to the problems that current research overlooks, the spatiotemporal features when making fault identification, which restrain the improvement of identification accuracy, and consider fault identification as an assessment of fault severity, which is unable to provide effective information for actual operation and maintenance work, this paper proposes an optical CT fault severity assessment model based on scene generation and spatiotemporal feature fusion. Firstly, a CNN-Transformer model is constructed to mine the fault characteristics in spatial and temporal dimensions by feature fusion, achieving accurate identification of fault types. Secondly, an improved synthetic minority oversampling method is adopted to generate virtual operating scenes, and the operating range under different operating states of the optical CT is statistically obtained. Finally, based on Shapley Additive Explanations (SHAP), the importance of the feature of optical CT is evaluated under different fault types. Reliant on the importance of features and operating range under different running states, the severity of the fault is assessed by quantifying the difference between the fault state and the normal state of the optical CT under the identified fault type. This study validated the effectiveness of the proposed method using actual operational data from an optical CT at a converter station in Hebei Province in China.

1. Introduction

In recent years, direct current (DC) transmission systems have become an important means of cross-regional power transmission due to their economic efficiency and control flexibility at high voltage levels, long distances, and large power capacities [1,2]. DC current transformers (DCCTs) are crucial primary devices in DC transmission systems, providing reliable measurement information for control protection and operational status [3]. The operational reliability of DCCTs is directly related to the safe and stable operation of DC transmission systems. Among several optional devices, optical current transformers (CT), with advantages such as strong anti-interference capability, wide bandwidth, high insulation level, compact size, and ease of installation, have been widely adopted. However, the electromagnetic environment within DC converter stations is complex [4,5], which can cause electromagnetic interference to the weak electrical systems of optical CTs, easily leading to faulty devices, thus affecting the stable operation of converter stations [6]. Moreover, given the complex physical structure and diverse types of faults in optical CTs, maintenance and inspection work pose significant challenges. There is a pressing need to develop a fault severity assessment system tailored to different types of faults, providing effective reference information for the maintenance and repair of optical CTs. By accurately identifying fault types, maintenance personnel can develop targeted repair plans, quickly locate fault locations, reduce unnecessary inspections and disassembly, and improve fault handling efficiency [7,8]. Additionally, reasonable assessments of fault severity can help optimize the allocation of maintenance resources: minor faults can be scheduled for handling during planned times, while severe faults require immediate response. This tiered management approach can more effectively utilize limited maintenance resources, reduce unnecessary emergency repairs, and lower maintenance costs.

Current methods for assessing equipment fault severity mainly fall into two categories: physics-based models and data-driven approaches. Physics-based models require analysis of the structural characteristics and fault mechanism models of the equipment; however, most equipment has complex failure mechanisms that make it difficult to establish accurate physical models. Data-driven approaches do not require physical modeling and can capture fault features well, which is mainstream in current research [9]. For instance, Ref. [10] proposes a novel hybrid method of random forest classifier for fault diagnosis of rolling bearings, which achieves high accuracy in identification. In Ref. [11], the Hilbert Huang transform (HHT) is used to transform the characteristics of the special fault from time–domain information to frequency–domain information. And a CNN-based classifier is proposed to distinguish single-phase grounding faults with high fault resistance and intermittent features. Ref. [12] has been conducted on risk assessment for Gas Insulated Switchgear (GIS) under specific defect conditions, considering factors such as the location of insulation defects, overvoltage, and defect properties. These studies normalized the GIS fault risk probability interval to [0, 1] and divided this interval into low-risk, moderate-risk, and high-risk zones. Ref. [13] has utilized machine learning methods based on features extracted from real partial discharge data to establish classifiers capable of recognizing two aging states of cable insulation. Ref. [14] proposed an identification method for insulation aging state using a backpropagation neural network optimized by particle swarm optimization, improving the precision of model fault recognition. Yet another study applied a ladder voltage method to investigate the development of four typical insulation defects, using fuzzy C-means clustering algorithms to divide different discharge stages and construct a two-level fuzzy comprehensive evaluation system for assessing the severity of partial discharge [15].

In summary, most strategies for assessing the severity of equipment faults currently rely on prior knowledge about equipment faults, dividing the severity into several levels and then using data-driven methods to mine fault features for severity identification [16]. However, due to the inconsistent internal structures and principles of different optical CTs [8], there is no unified theory regarding the fault mechanisms of optical CTs, and no relevant studies have provided qualitative descriptions of the severity of optical CT faults. There is relatively little study about fault identification concerning the faulty characteristic in both spatial and temporal dimensions, which restrains the improvement of identification accuracy. Furthermore, most existing studies view fault severity assessment as equivalent to fault severity identification, lacking detailed evaluations of fault severity under different fault types, which limits their practical engineering value.

Additionally, since optical CTs experience faults much less frequently than they operate normally, insufficient fault samples cannot adequately support comprehensive fault severity assessments. To address the issue of insufficient fault data, Ref. [17] has proposed sample generation methods based on variational autoencoders, which can effectively augment time-series sample data sequences by mining overall trends. On the other hand, Ref. [18] has introduced scene-generation methods based on autoencoders and Gaussian mixture models to construct estimated mixture models by fitting the probability distributions of existing sample data, generating short-term energy demand sample data.

Nevertheless, traditional generation models based on probability density functions often face issues such as slow convergence or sensitivity to initial conditions due to the necessity for explicit modeling of data probability distributions. Considering these issues, some researchers have utilized the Synthetic Minority Over-sampling Technique (SMOTE) combined with fuzzy logic theory to achieve good results in addressing sample imbalance problems [19]. However, SMOTE models suffer from overfitting and difficulties in effectively processing high-dimensional data or datasets with uneven sample spacing, leading to poor quality generated data [20,21].

Overall, there are two main challenges that need to be addressed: (1) overlooking the spatiotemporal features during fault identification and (2) fault identification as fault severity assessment, which is unable to provide effective information for actual operation and maintenance work. To tackle these issues, this paper aims to construct an accurate fault identification model based on spatiotemporal feature fusion. What is more, based on identification results, the fault severity assessment model is built by quantifying the differences between various fault types and normal operating conditions of optical CTs. Firstly, considering the spatial and temporal features when the fault of optical CT occurs, a CNN-Transformer model is employed to extract fault features from the optical CT state and achieve accurate identification by spatiotemporal feature fusion. Secondly, given the limited number of fault historical samples of optical CT, to accurately conclude the upper and lower bound of each state parameter under different operating states is unrealistic. Therefore, this paper uses an improved synthetic minority oversampling method together with a fault identification model to generate a large number of virtual operational scenes. Through statistical analysis in various samples, the operating ranges of each state parameter for optical CTs in different states are determined, providing data support for fault assessment. Finally, Shapley Additive Explanations (SHAP) is adopted to comprehensively evaluate the relative importance of each state parameter under different fault types, providing more precise fault information for maintenance personnel at converter stations.

The remaining parts are organized as follows: Section 2 introduces the basic ideas and proposed methods of this study. The superiority of the proposed method is verified using real optical operation data in Section 3. The summary and outlook are presented in Section 4.

2. Materials and Methods

The overall technical flowchart is shown in Figure 1. Firstly, train and validate the fault identification model using historical samples of optical CT from a converter station in Hebei province in China. On the premise of ensuring the accuracy of the identification model, a large number of virtual scenes are constructed based on sample generation algorithms, and the identification model is used to assign fault types to the virtual scenes, expanding the fault samples. Subsequently, upper and lower bounds of optical CT parameters were concluded for different types of faults, providing data support for assessing the severity of faults. Finally, fault identification was carried out for the operation samples of optical CT, and the severity of different fault types was evaluated.

2.1. Fault Identification

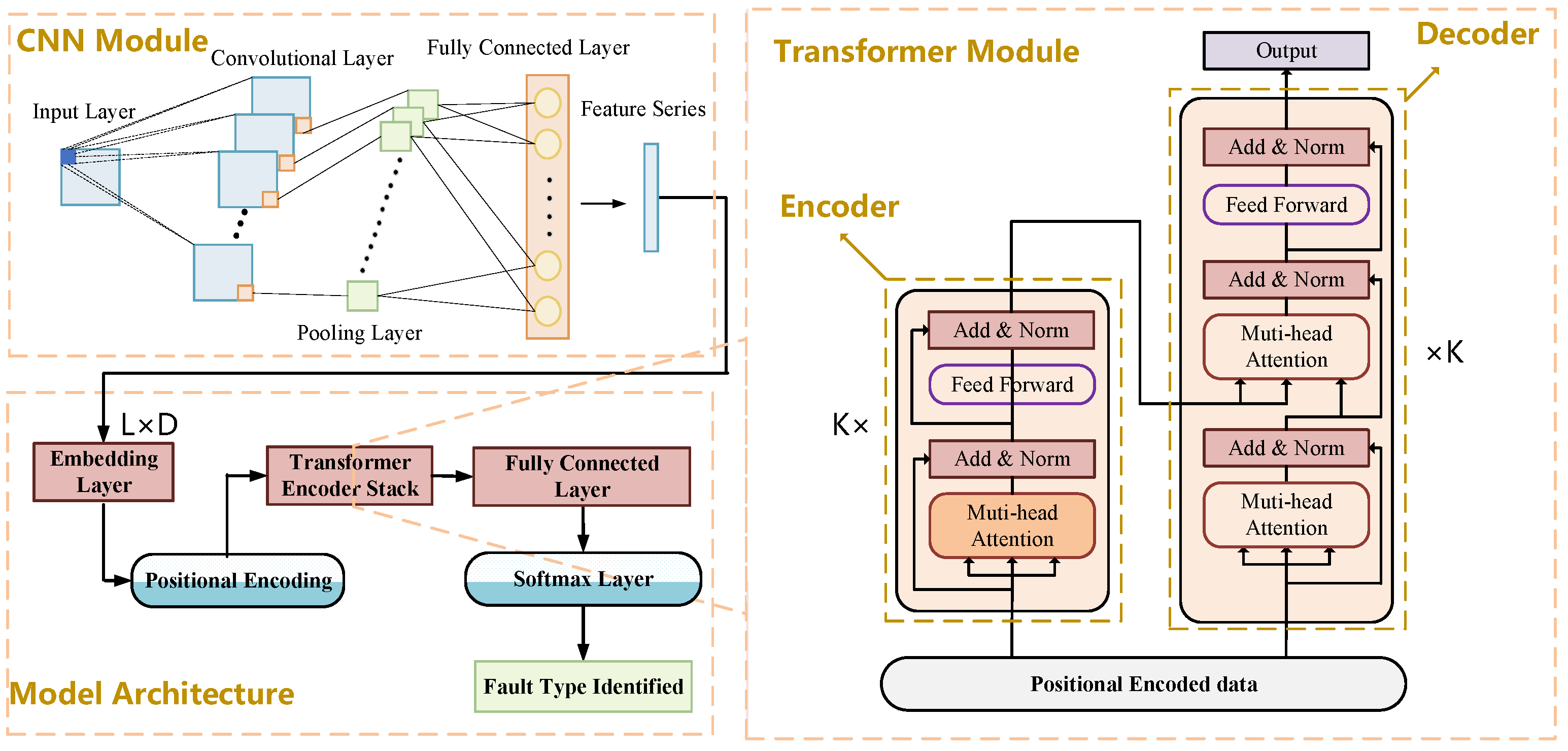
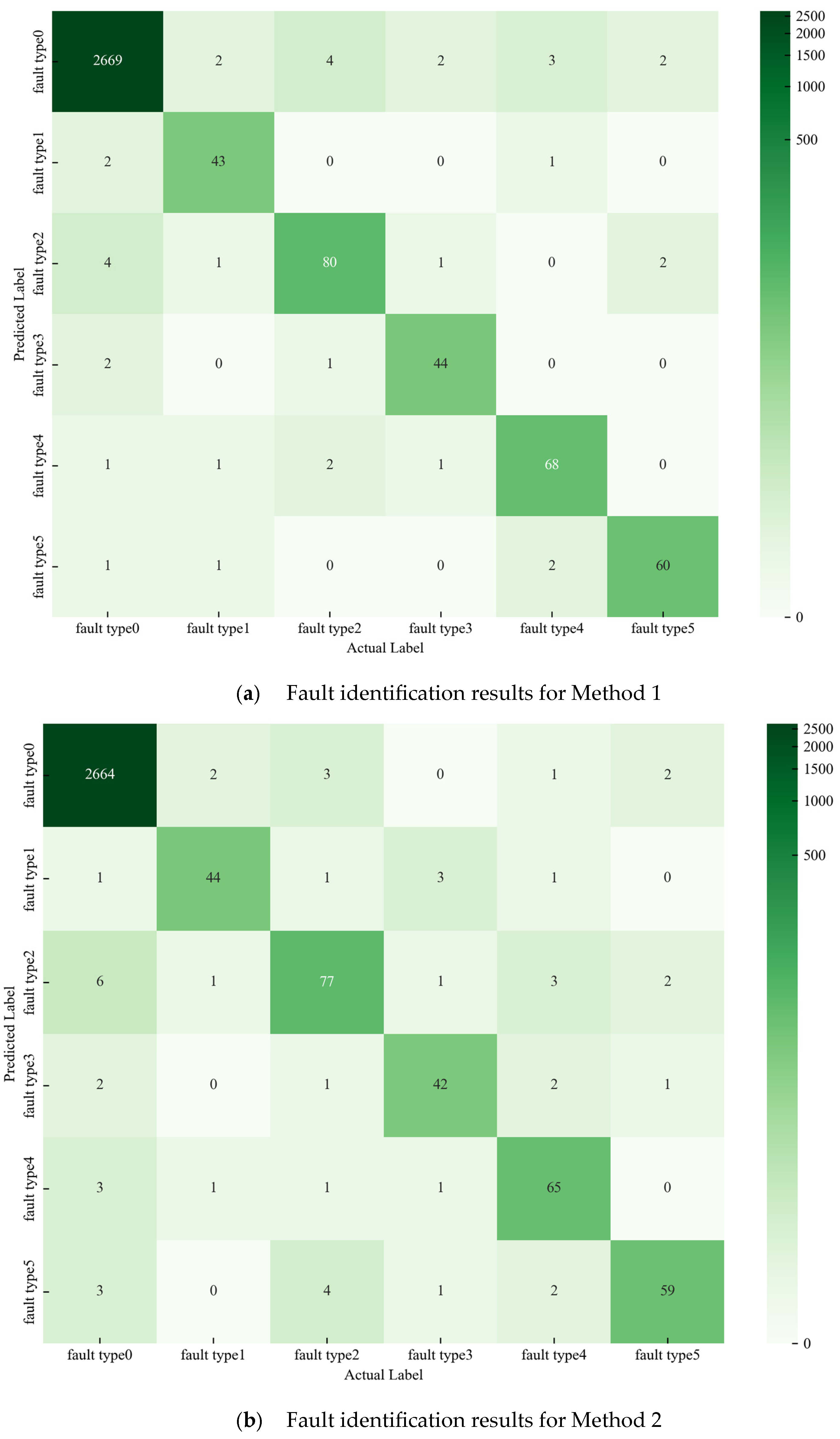
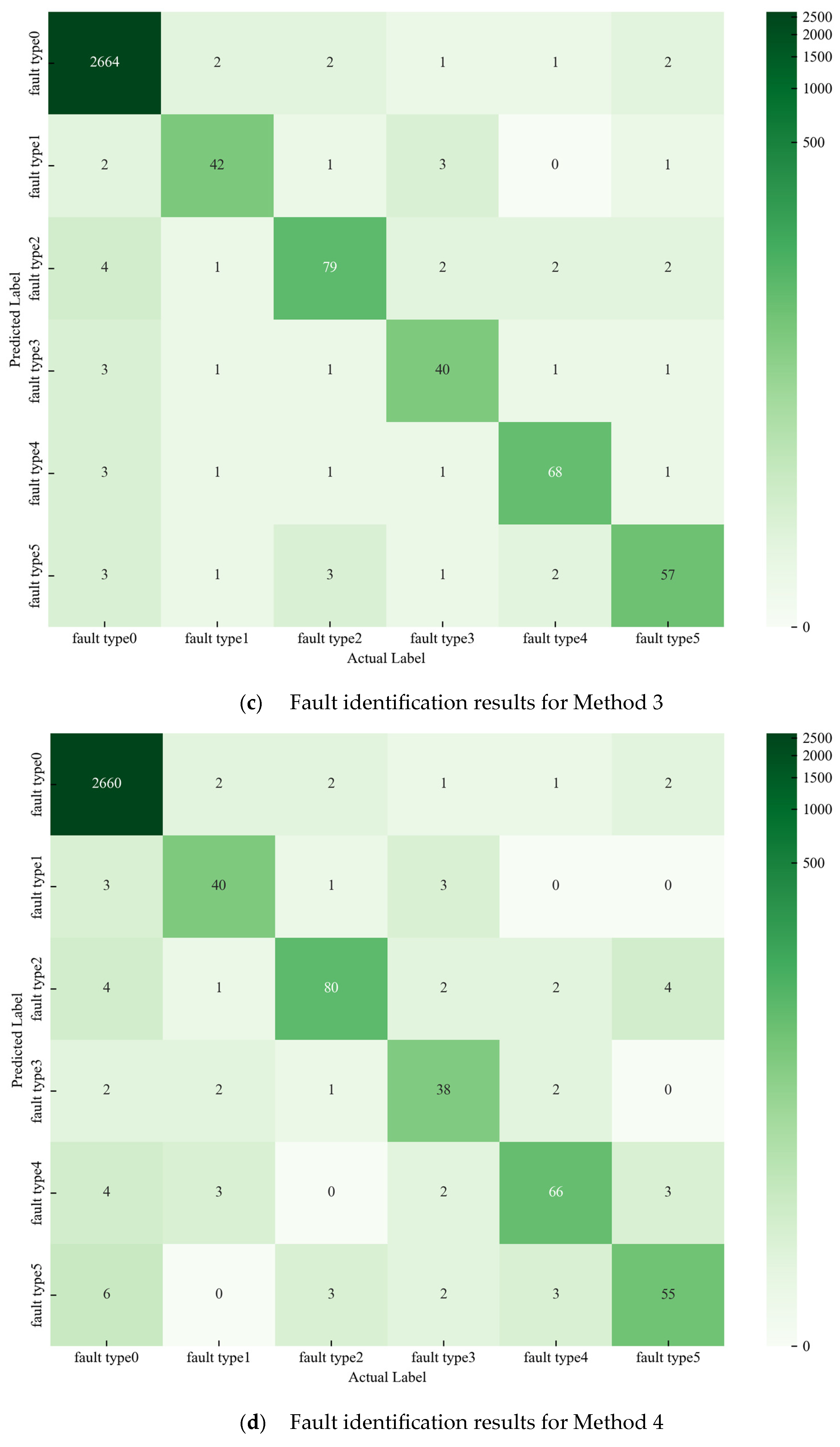
Considering both spatial and temporal dimensions to fully explore fault characteristics, this paper constructs a multi-input and single-output CNN-Transformer neural network model to learn the features under various operating conditions of optical CTs for fault identification; the details of model are shown in Figure 2. What is more, the dataset is split for training, validation, and testing with a ratio of 7:1:2. The parameters in the model are optimally selected through grid search algorithm. By traversing various combinations of optional parameters of the model, we select the set of model parameters with the best identification performance on validation dataset as the model parameters. The optional values of parameters are shown in

Table 1. Optional model parameters for grid search.

Parameters	Dimension of Convolutional Kernels	Strategy of Pooling	Embedding Output Dimension	Number of Attention Heads
Optional values	2 × 2, 3 × 3, 4 × 4, 5 × 5	Max pooling, Min pooling, Median pooling, Average pooling	4, 8, 10, 12, 16	2, 3, 4, 6, 8

.

To begin with model construction, the data processes like data cleaning and data normalization are performed, and each parameter of every sample for optical CT is in the range [0, 1]. Furthermore, due to there being six operating states of optical CT states in total, the identification results include 0~5, with 1~5 representing five fault types and 0 representing normal operating state.

Given that the occurrence of a single fault in an optical CT often accompanies changes in multiple state parameters, and changes in one parameter can potentially lead to various faults, it means that the different components of optical CT will interact with each other, indicating that there exists a complex spatial interrelationship in this device. The Convolutional Neural Networks (CNNs) [22,23,24], which mainly consist of the following structures, input layer, convolutional layer, pooling layer, activation layer, and fully connected layer, are employed in this context. The convolutional layer is primarily tasked with extracting features from input data. In this process, the convolutional kernels (or filters) slide over the data series, performing element-wise multiplications and summing the results to generate features. The resulting feature data often contain a substantial number of pixels; hence, a down-sampling operation known as pooling technique is used to make feature selections, further enhancing the efficiency and generalization ability of feature extraction and making CNNs highly effective at learning internal relationships related to optical CT faults.

The dimension of data series defined in this study is 96 × 5, meaning the time sequence concludes the operating data of 96 timesteps before and at the time of identification, and each data concludes 5 features. And the convolutional kernels with dimensions of 2 × 2 and the max pooling strategy to undergo feature extraction. After that, the dimension of features series is 94 × 1. The calculation of feature extraction is as follows:

$$H_i=\sigma (H_{i-1}\otimes W_i^k+b_i)$$

(1)

where $W_i^k$ is the weight of the k-th convolution kernel. Bias $b_i$ representing convolution operations; $\sigma$ is used to activate the function.

The Transformer model [25], proposed by Google in 2017, is famous for its ability to exact features in temporal dimension. One of its key advantages is the self-attention mechanism, which allows the model to consider all information in time series simultaneously, enabling it to capture complex relationships effectively, even over long distances. This feature significantly enhances the model’s ability to extract valuable information within data. Furthermore, positional encoding ensures that the model retains information about the order of tokens in a sequence. By adding positional encodings to the embedding layer, Transformers can understand relative positions between sequences, which is crucial for maintaining the integrity of series structures. Last but not least, the multi-head attention mechanism further boosts the model’s expressiveness by allowing it to focus on different parts of the input simultaneously. Each attention head captures distinct features from various subspaces, providing a richer representation of the input data. It is believed that this model can contribute greatly to fault identification.

In detail, this model mainly consists of two structures, encoder and decoder, as shown in Figure 2. The left and right sides correspond to the encoder and decoder structures, respectively. Both are composed of several basic Transformer blocks, which comprise a multi-head self-attention (MSA) block, a feedforward neural network (FNN), and layer normalization (represented by the light-colored boxes in the figure). Specifically, the input dimension of the first encoder in the encoder stack is L × D, where L is the length of input data dimension, set as 94 in this study, and D is a hyperparameter representing the embedding output dimension, set as 12 in this study. Due to the existence of the muti-attention head, the input is split into K which is the number of attention heads, set as 3. The dimension of input of each encoder is L × (D/K), namely 94 × 4 in this study.

Before the feature sequence $X$ after CNN module is sent to Transformer structure, the embedding layers and positional encoding layer are used to preprocess:

$$X=X\odot \mathrm{\Omega }$$

(2)

$$P{E}_{pos,2i}=\sin ({\displaystyle \frac{pos}{{1000}^{2i}/d_{\mathit{model}}}})$$

(3)

$$P{E}_{pos,2i+1}=\cos ({\displaystyle \frac{pos}{{1000}^{2i}/d_{\mathit{model}}}})$$

(4)

where $\mathrm{\Omega }$ is the multiplication parameter that needs to be trained for the embedding layers. $d_{\mathit{model}}$ is the dimension of the time series, $i$ denotes the i-th dimension of vector, $pos$ is the exact position of the current feature. Through this data preprocessing, the model can better capture the correlation between optical CT features at different time periods.

After that, the input $X$ is linearly transformed into a query matrix $Q$, a key matrix $K$, and a value matrix $V$. The attention weights are obtained by computing the dot product of $Q$ and $K$, followed by scaling and a softmax operation, as expressed by

$$\mathrm{Attention}\left(Q,K,V\right)=\mathrm{softmax}\left({\displaystyle \frac{Q{K}^T}{\sqrt{d_k}}}\right)$$

(5)

where $d_k$ is the dimension of $X$. To capture information from different subspaces, $Q$, $K$, and $V$ are usually split into multiple heads, with each head calculating attention scores in parallel. The outputs of these heads are concatenated and linearly transformed to obtain the MSA score, expressed as

$$\mathrm{MSA}\left(Q,K,V\right)=\left[{\mathrm{head}}_1,{\mathrm{head}}_2,\cdots ,{\mathrm{head}}_h\right]W$$

(6)

where $h$ is the number of heads and $W$ is the weight matrix of the linear transformation. The output of the i-th head can be calculated by the following formula:

$$hea{d}_i=Attention(Q{W}_i^Q,K{W}_i^K,V{W}_i^V)$$

(7)

where $W_i^Q$, $W_i^K$, and $W_i^V$ represent the weight matrices of the query, key, and value of the i-th head, respectively.

Then, the feature is sent to fully connected feedforward network, which consists of two dense layers, and the Relu-activated function is adopted for non-linear transformations.

$$FFN(X)=\sigma (\max (0, X{W}_1+b_1)W_2+b_2)$$

(8)

where $W_1$ and $W_2$ are the linear transformation parameters, $b_1$ and $b_2$ are the bias vector, $\sigma$ denotes the Relu activated function.

After the feature is obtained based on Transformer model, it is sent to fully connected layer, with its dimension transforming from 94 × 4 into 94 × 6, for the reason that there are 6 operating states of optical CT. Finally, based on the softmax layer, the identification result can be generated.

Overall, for the identification of state of optical CT in timestamp $t$, the CNN module is used for spatial feature extraction while the Transformer module is constructed for temporal feature extraction, depending on which the accurate identification results will be obtained.

2.2. Fault Severity Assessment

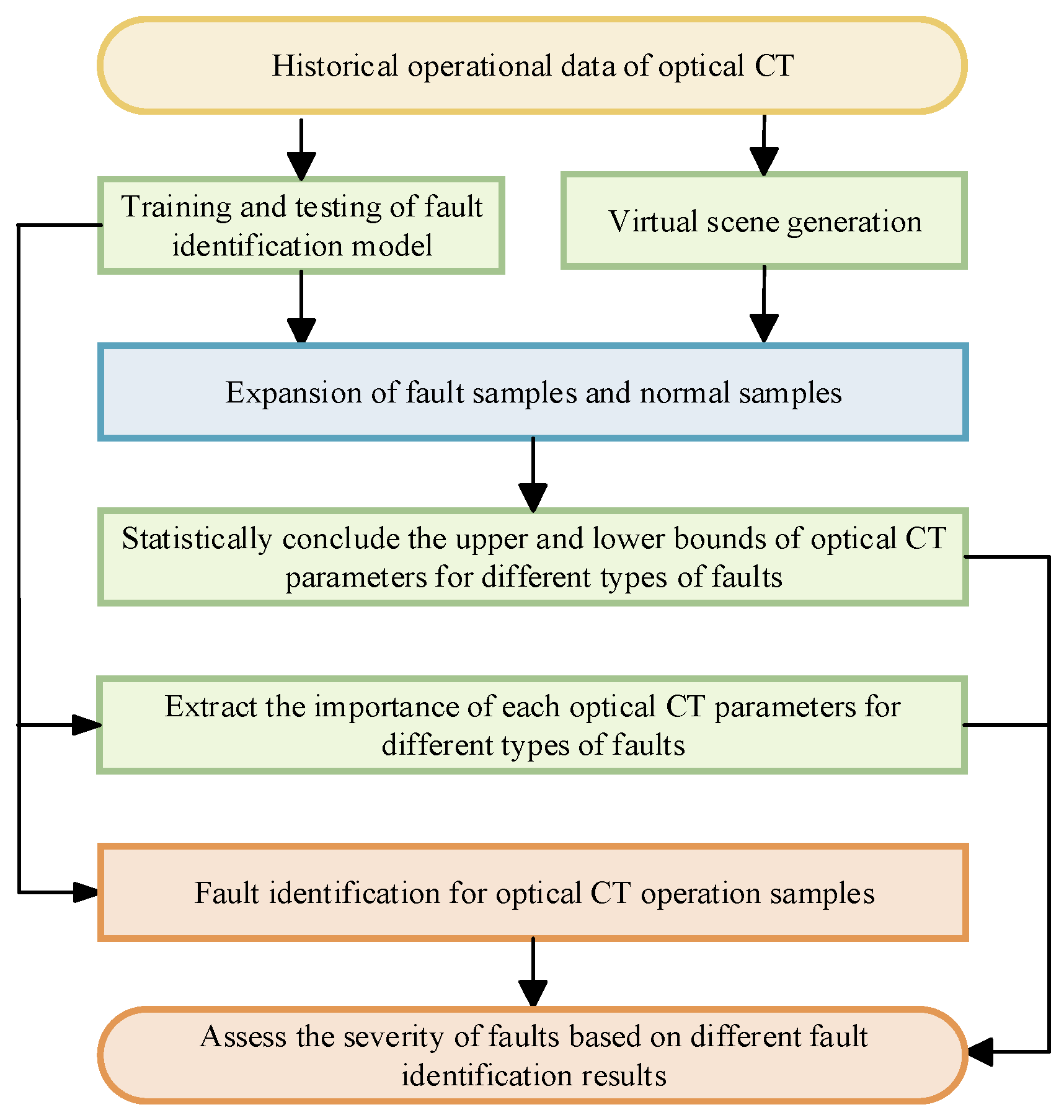
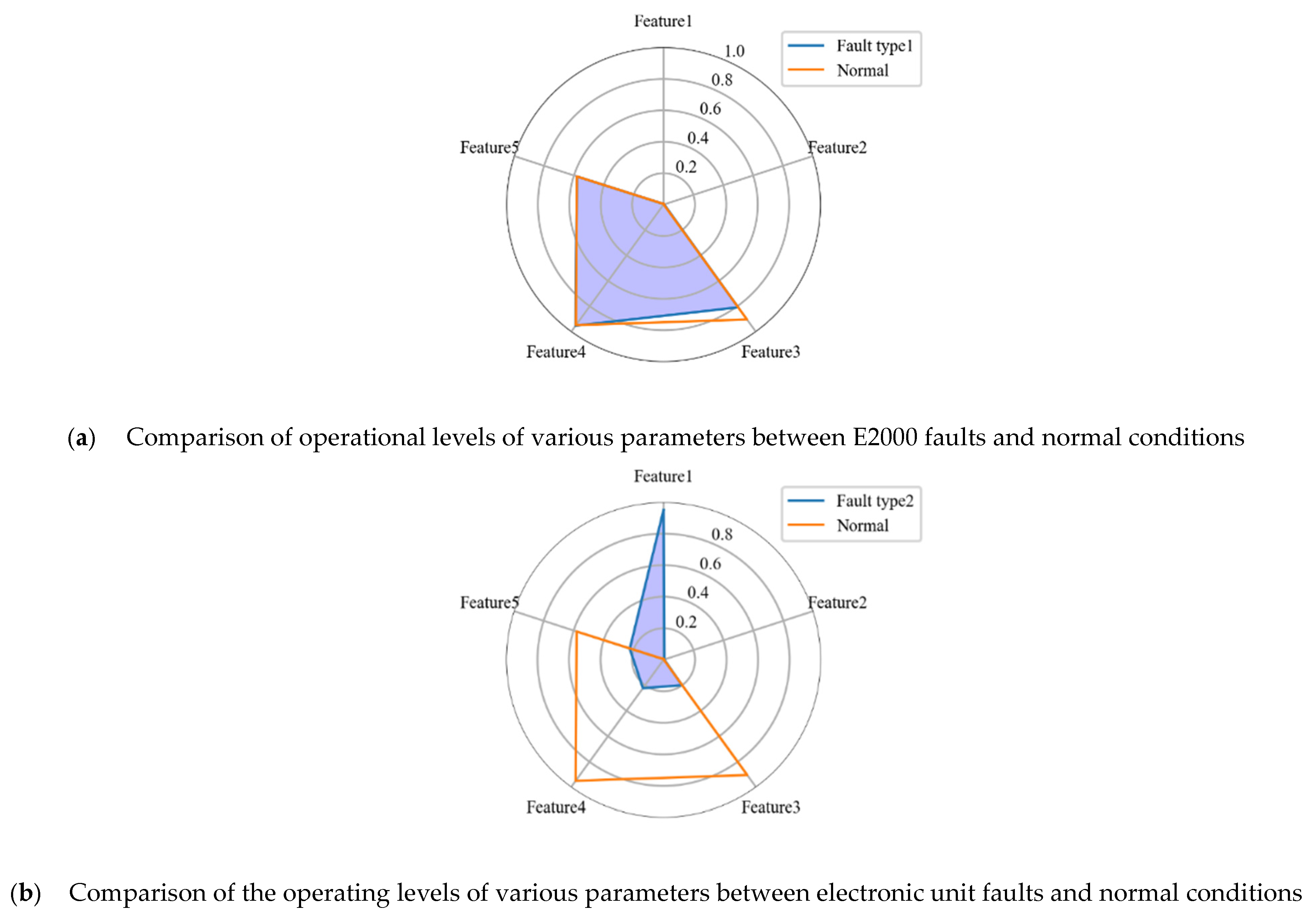
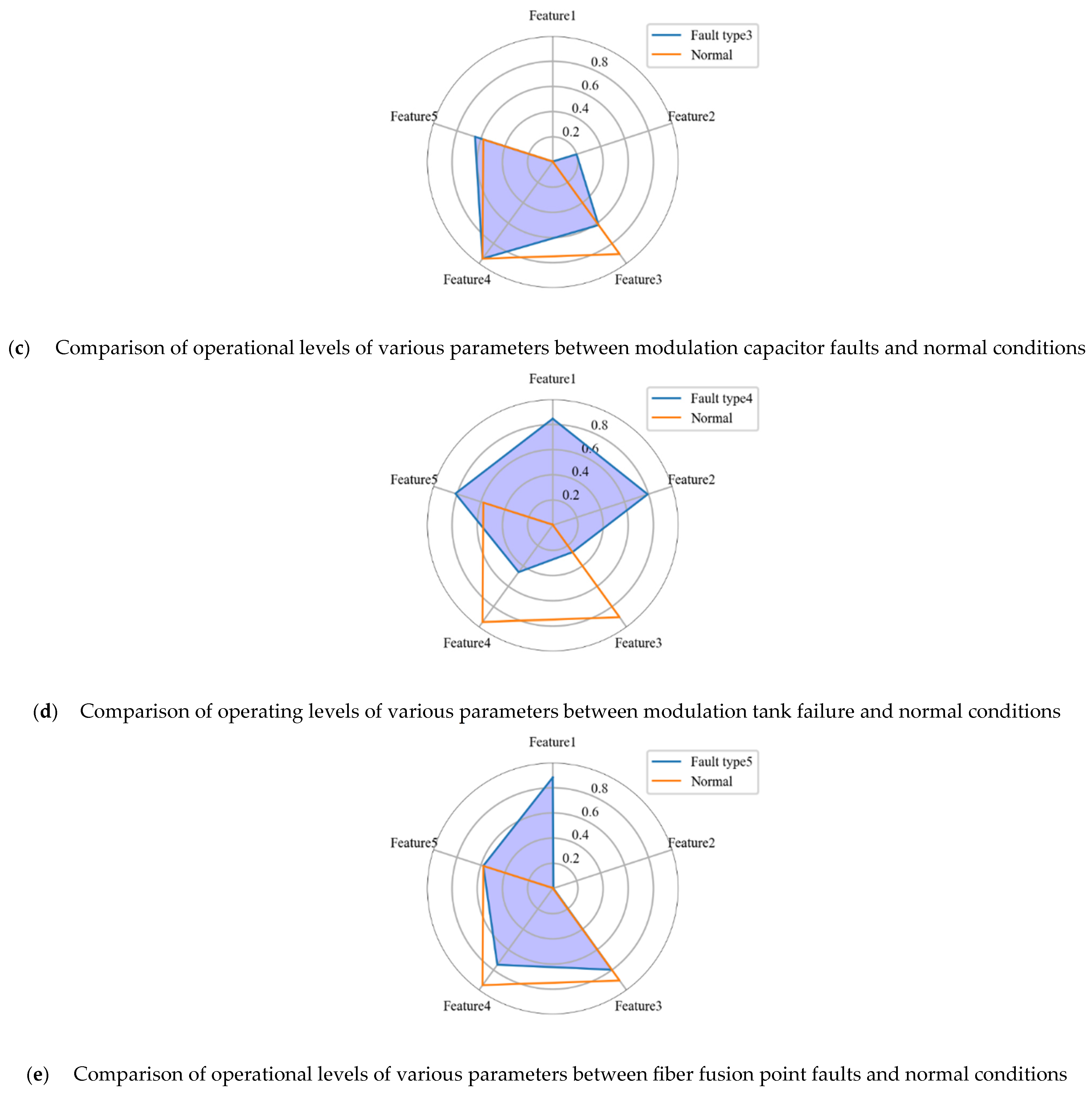
This fault severity assessment model is mainly based on the idea that the more different the state of optical CT from the normal state, the more severe the fault will be, which is testified shown in part III. In this study, the method of Shapley Additive Explanations (SHAP) is used to quantify the importance of each parameter in optical CT during different faults. Also, the range of parameters of optical CT in different operating states will be concluded according to the results of scene generation in next part, based on which the assessment of fault severity will finally be obtained.

SHAP constitutes a model interpretation framework grounded in cooperative game theory [26,27]. This approach primarily leverages the Shapley value, an element from cooperative game theory that gauges how much each team member contributes to the collective gain. In this context, the Shapley value is employed to measure both the extent and direction of influence that input features have on fault identification outcomes, as illustrated below. The absolute value of the Shapley value signifies the degree of contribution of each feature towards the identification results; the larger the absolute value, the more significant the contribution. Furthermore, the impact direction of these features on identification outcomes is denoted by whether their Shapley values are positive or negative.

$$\phi (f_n)=\sum _{S\subseteq F\setminus \left\{\begin{array}{c}{f}_n\end{array}\right\}}{\displaystyle \frac{\left|S\right|!(|F|-|S|-1)!}{\left|F\right|!}}(\nu (S\cup \{f_n\})-\nu (S))$$

(9)

where $\phi (f_n)$ is the Shapley value of feature $f_n$, which is the n-th input features. $F$ is the complete set of all the input features while $S$ is a subset of $F$. The condition $S\subseteq F\backslash \left\{f_n\right\}$ means that $S$ can only be a subset of $F$ that does not include feature $f_n$, $v\left(S\right)$ is the output when the feature subset $S$ is input, $v(S\cup \left\{f_n\right\})$ is the output when the feature subset $S$ plus feature $f_n$ as input, then $v(S\cup \left\{f_n\right\})-v\left(S\right)$ can represent the marginal contribution of feature $f_n$. From the equation, it can be concluded that SHAP creates various subsets $S$ of feature combinations, assessing the impact of including or excluding each feature $f_n$ on the model’s output.

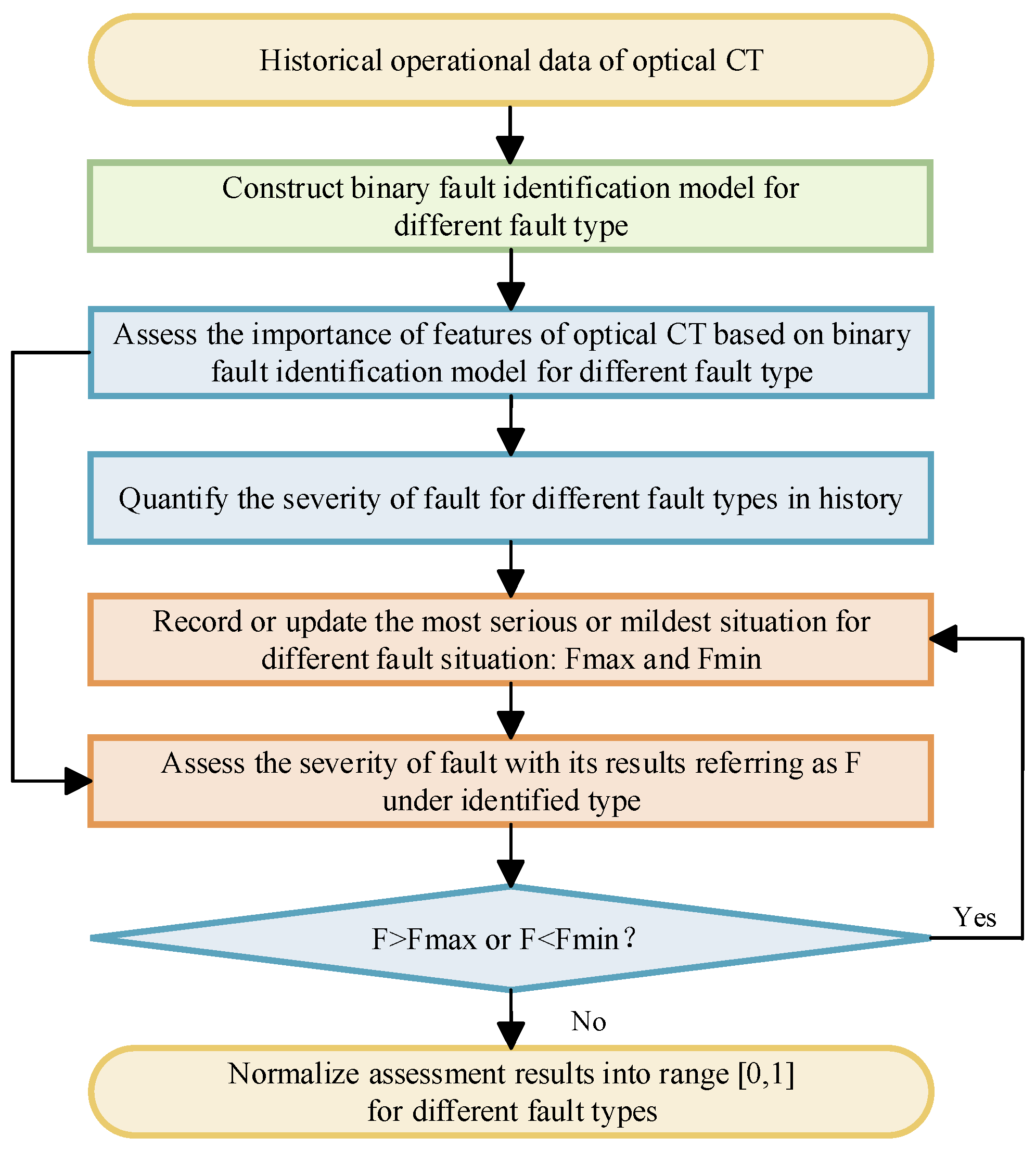
Considering the fact that under different fault states, the optical CT will show completely different operating characteristics, meaning that the importance of features of optical CT will vary with operation state. So, for every fault type, the binary identification model is constructed based on CNN-Transformer model with its results belonging to this type or not. Then, the SHAP algorithm is adopted for binary identification model to evaluate the importance of features under this operating state, referred to as $\phi (f_1)$, $\phi (f_2)$, …, $\phi (f_n)$. After that, based on the upper and lower bounds of normal operating state of optical CT, the assessment can be obtained.

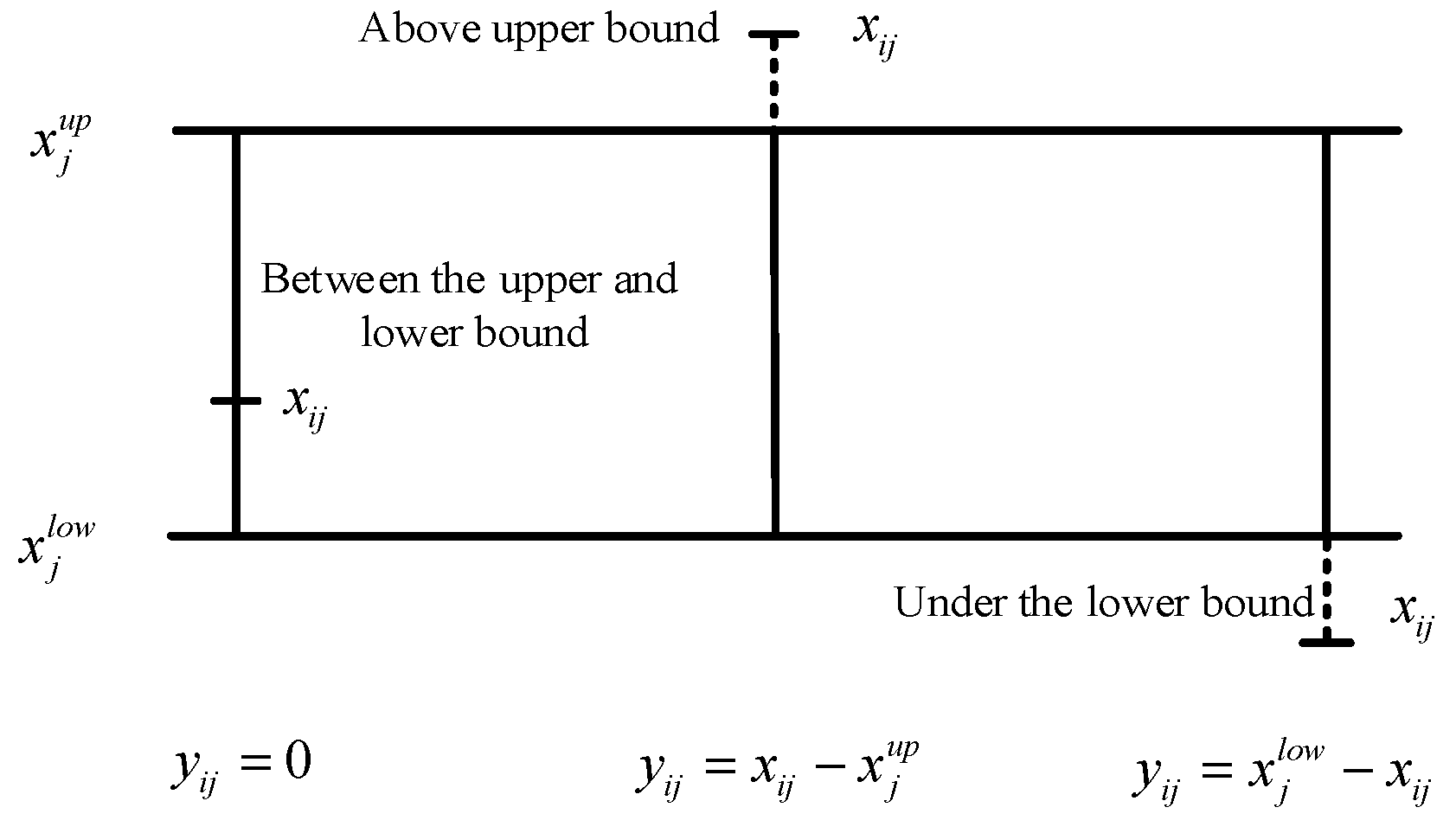
The comprehensive evaluation indicators $F_i$ is

$$y_{ij}=\max \{0,x_{ij}-x_j^{up},x_j^{low}-x_{ij}\}$$

(10)

$$F_i={\displaystyle \sum _{j=1}^n\phi (f_j)\ast y_{ij}}$$

(11)

where $x_j^{up}$ and $x_j^{low}$ are the upper and lower bounds of the j-th feature of normal operating states, respectively, which is obtained according to “SCENE GENERATION” part. $n$ is the number of total features, $y_{ij}$ is the difference between normal state and fault state for j-th feature.

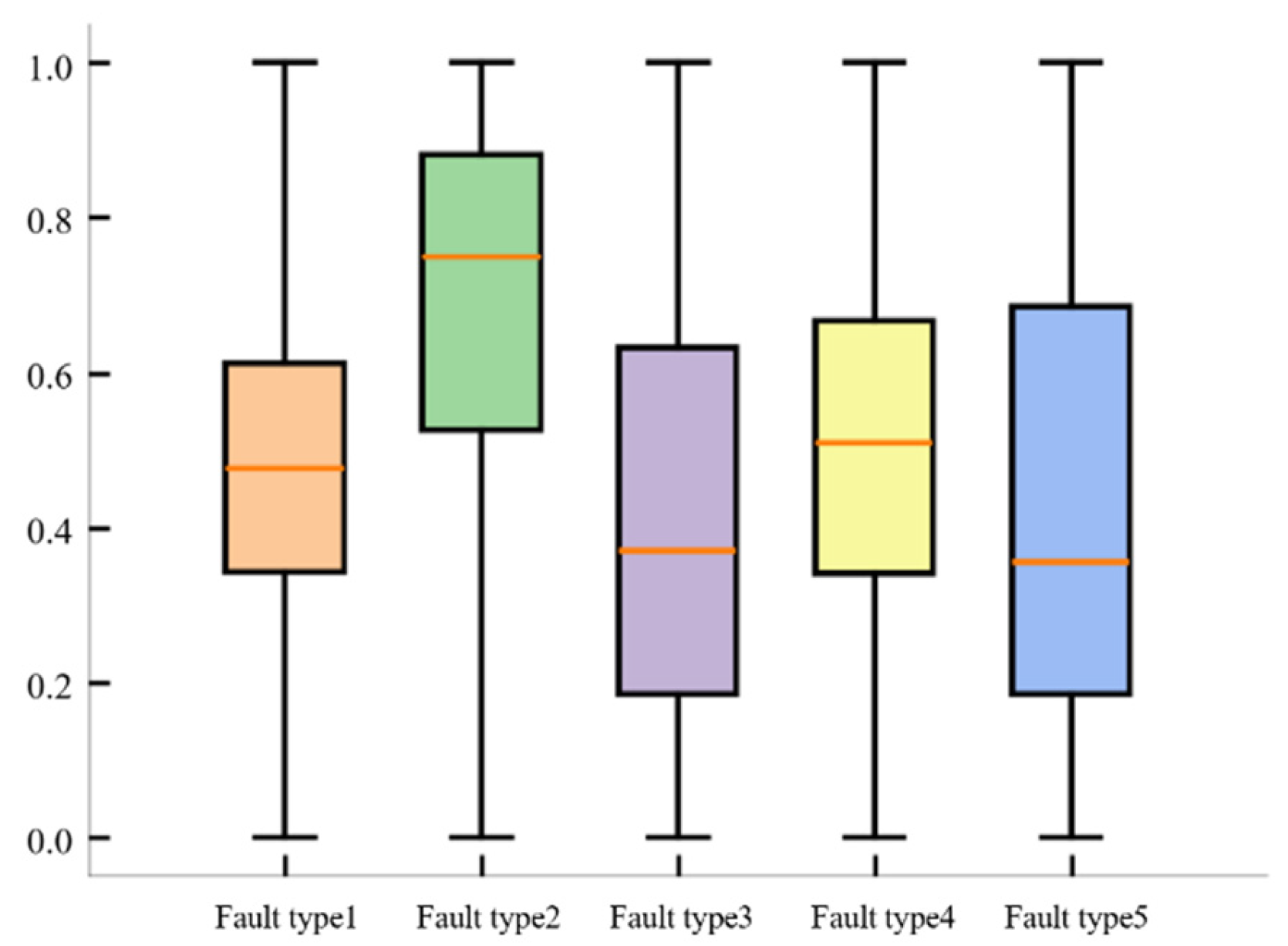
It can be seen from Figure 3 that when the optical CT is operating normally, the comprehensive evaluation index is equal to zero. The larger the fault, the more severe the fault. For each fault situation, calculate the comprehensive evaluation indicators for the most severe fault situation $F_{\max }$ and the least severe fault situation $F_{\min }$ in the history of the fault. Quantify the severity of each future sample’s corresponding fault type based on fault identification and normalization:

$$P_i={\displaystyle \frac{F_i-F_{\min }}{F_{\max }-F_{\min }}}$$

(12)

It can be seen that $P_i$ is in the range of [0, 1], and the closer it is to 1, the more severe the fault is. When a fault that is more severe or less severe than the historical situation occurs in the future, it is necessary to update $F_{\max }$ and $F_{\min }$ in real-time. The algorithm flowchart is shown in Figure 4.

2.3. Scene Generation

This study evaluates the severity of faults by analyzing the degree of difference between optical CT fault conditions and normal conditions. However, due to the limited historical samples, it is impossible to accurately conclude the exact upper and lower bounds of various parameters under different operating conditions of optical CT. Therefore, this study first used the k-means-SMOTE algorithm to simulate and generate a large number of virtual samples and analyzed them to improve the robustness of severity assessment.

Considering that the SMOTE models rely on the sample distribution characteristics, they will suffer from overfitting and difficulties in effectively processing datasets with uneven sample spacing, which will lead to poorly generated data. Due to the low occurrence frequency and sparse data sample space of fault samples, the k-means-SMOTE algorithm first uses the k-means clustering algorithm to cluster the specific operating type of sample into several clusters and then applies SMOTE within each cluster to improve the reliability of sample generation. In this way, the data will be generated from the data clusters with much tighter sample space, which will be more similar to the distribution of real data. The following contents introduce the method for a certain type of fault as an example.

At first, $k$ cluster centers ${\mu }_I$ are randomly selected from samples under the same fault type, and the historical dataset is divided into clusters according to the k-means clustering algorithm [28]:

$$C_I=\{\mathit{Feat}|I=\arg \underset{F}{\min }||\mathit{Feat}-{\mu }_F|{|}_2^2, F=1,2,\dots ,k\}$$

(13)

$$E=\sum _{I=1}^k\sum _{Feat\in C_I}||\mathit{Feat}-{\mu }_I|{|}_2^2$$

(14)

$${\mu }_I={\displaystyle \frac{1}{\left|C_I\right|}}\sum _{Feat\in C_I}\mathit{Feat}$$

(15)

where $I=1,2,\dots ,k$ means the type of cluster division, while $F=1,2,\dots ,k$ means the possible type of cluster the sample $\mathit{Feat}$ might belong to. ${\mu }_F$ denotes the possible cluster center the sample $\mathit{Feat}$ might belong to. The sample belonging to $C_I$ means the cluster is more similar to the cluster center ${\mu }_I$ than other cluster centers. This algorithm iteratively adjusts the cluster centers to minimize the Euclidean distance $E$ between all samples and their corresponding cluster centers, achieving sample clustering.

Subsequently, based on the number of samples $M$ in each cluster, the appropriate number of new synthesized samples $N$ that need to be generated is determined. Each time a sample is generated, the SMOTE algorithm randomly selects a sample $x_i=[x_{i1},x_{i2},\cdots ,x_{ij}]$, where $x_{ij}$ represents the j-th operating parameter. Then, the $k$ nearest neighbors to the sample based on the Euclidean distance are found, and one of the neighboring samples is randomly selected to generate samples using the following equation.

$${\tilde{x}}_{ij}=x_{ij}+\lambda (x_{ij\_nn}-x_{ij})$$

(16)

$${\tilde{x}}_i=[{\tilde{x}}_{i1},{\tilde{x}}_{i2,}\cdots ,{\tilde{x}}_{ij}]$$

(17)

In the formula, $\lambda$ is a randomly selected number from the interval [0, 1], which is used to control the distance between the new sample and the original sample. ${\tilde{x}}_{ij}$ represents the generation of the j-th operating parameter, ${\tilde{x}}_i$ representing the simulated generated operating sample.

Finally, the identification model is used to identify fault types in the generated sample data. In the formula, ${\tilde{y}}_i$ represents the identified fault label of generated sample ${\tilde{x}}_i$.

$${\tilde{y}}_i=CNN-Transformer({\tilde{x}}_i)$$

(18)

For each generated sample, fault identification is performed based on the CNN-Transformer model, and samples with the identified result of the same state as the generated type are selected for sample expansion. Further statistical analysis is conducted to determine the upper and lower bounds of each parameter under different operating states of optical CT in order to improve the robustness of the statistical results. For example, when it comes to normal operation state, the upper and lower bound, defined as $x_j^{up}$ and $x_j^{low}$, can be obtained according to following equations:

$$x_j^{up}=\max (\{x_{ij}\}\cup \{{\tilde{x}}_{ij}\})$$

(19)

$$x_j^{low}=\min (\{x_{ij}\}\cup \{{\tilde{x}}_{ij}\})$$

(20)

where the $\left\{{\tilde{x}}_{ij}\right\}$ represents the set of the j-th operating parameter of generation samples in normal operating state, while the $\left\{x_{ij}\right\}$ represents the set of the j-th operating parameter of historical samples in normal operating state.

3. Simulation and Discussion

3.1. Dataset Description

This study uses the historical operation dataset of optical CT from a converter station in Hebei province in China for test. The measurement sample has five parameters, LED current, modulator driving voltage, second harmonic voltage, peak input voltage, and average input voltage deviation, referred to as feature 1–5, respectively; five types of faults, E2000 fault, electronic unit fault, modulation capacitor fault, modulation tank fault, and fiber fusion point fault, referred to as fault types 1–5, respectively. The total number of samples is about 30,000, a time series with a time resolution of 15 min. The detailed description of the dataset is shown in

Table 2. Description of dataset.

Parameters	Reference for Parameters	Types of Faults	Reference for Fault Types
LED current	feature 1	E2000 fault	fault types 1
modulator driving voltage	feature 2	electronic unit fault	fault types 2
second harmonic voltage	feature 3	modulation capacitor fault	fault types 3
peak input voltage	feature 4	modulation tank fault	fault types 4
average input voltage deviation	feature 5	fiber fusion point fault	fault types 5

.

3.2. The Result of Fault Identification

In order to demonstrate the outstanding performance of the fault identification model proposed in this study, this study chose several alternative models to compare with it.

Method 1: The proposed fault identification model based on spatiotemporal feature fusion.

Method 2: The CNN fault identification model based on spatial feature extraction.

Method 3: The Transformer fault identification model based on temporal feature extraction.

Method 4: The Light Gradient Boosting Machine (LGBM) fault identification model based on feature extraction [29].

To fully test the performance of models, the dataset is split into a training dataset, validation dataset, and test dataset, with a ratio of 7:1:2. The model is trained based on the training dataset, validated on the validation dataset to obtain the best model with optimal parameters, and finally tested on the test dataset. We evaluated the identification accuracy of the model identification results on the test dataset using the following indicators:

$$e_{acc}={\displaystyle \frac{{\displaystyle \sum _{i=1}^k}{l}_i}{{\displaystyle \sum _{i=1}^k}{a}_i}} e_{pre}={\displaystyle \frac{1}{K}}{\displaystyle \sum _{i=1}^k\frac{l_i}{m_i}}$$

(21)

$$\begin{array}{c}{e}_{rec}={\displaystyle \frac{1}{K}}{\displaystyle \sum _{i=1}^k\frac{l_i}{n_i}} e_{f1}=2\ast {\displaystyle \frac{e_{pre}\ast e_{rec}}{e_{pre}+e_{rec}}}\end{array}$$

(22)

In the formula, $l_i$ is the number of correctly identified samples that belong to i-th fault type, $a_i$ is the total number of samples actually belonging to i-th fault type, $m_i$ is the added number of correctly identified samples belonging to i-th fault type and identified as i-th fault type but not actually belonging to i-th fault type. $n_i$ is the added number of correctly identified samples belonging to i-th fault type and not identified as i-th fault type but actually belonging to i-th fault type in fact.

From

Table 3. Fault identification results.

	${\mathit{e}}_{\mathit{a}\mathit{c}\mathit{c}}$	${\mathit{e}}_{\mathit{p}\mathit{r}\mathit{e}}$	${\mathit{e}}_{\mathit{r}\mathit{e}\mathit{c}}$	${\mathit{e}}_{\mathit{f}1}$
Method 1	98.80%	94.07%	93.07%	93.57%
Method 2	98.36%	89.63%	91.18%	90.40%
Method 3	98.33%	89.00%	90.33%	89.66%
Method 4	97.96%	86.59%	88.14%	87.36%

, it can be seen that the proposed model can achieve high recognition accuracy compared to other models, proving the effectiveness of fusing both spatial and temporal features. Method 2 or Method 3 only focuses on spatial features or temporal features, without organically combining both of them, demonstrating poorer model accuracy compared with Method 1. However, Method 4 overlooks feature extraction among the sequence, performing the poorest among them. The model can provide strong support for subsequent scene generation and severity assessment. The specific identification results of each model are shown in Figure 5.

3.3. The Result of Scene Generation

Subsequently, sample expansion was carried out for various types of faults, with 2000 samples for each type of fault and normal type. A fault identification model is performed on the generated data, with identification results shown in

Table 4. Fault identification results of generated samples.

	Sample Belonging to Fault Type 1	Sample Belonging to Fault Type 2	Sample Belonging to Fault Type 3	Sample Belonging to Fault Type 4	Sample Belonging to Fault Type 5	Sample Belonging to Normal Type
Identified as fault type 1	1933	25	15	12	2	6
Identified as fault type 2	11	1918	2	41	6	6
Identified as fault type 3	5	18	1927	16	26	7
Identified as fault type 4	4	7	24	1877	9	4
Identified as fault type 5	34	8	11	18	1927	5
Identified as normal type	13	24	21	36	20	1972

.

It can be seen in Table 4 that the proposed scene generation method can effectively mine the intrinsic features of the original historical samples, and the fault categories of the generated samples can be basically consistent with the types of the original samples. This study considers the generated samples with fault categories consistent with the identification results of the fault identification model as successfully generated samples under that fault category and expands them to the corresponding historical dataset.

Through statistical analysis, the upper and lower parameter operating levels under normal and various fault conditions can be obtained, as shown in

Table 5. The fluctuation range of various parameters in different situations.

	LED Current	Modulator Driving Voltage	Second Harmonic Voltage	Peak Input Voltage	Average Input Voltage Deviation
Fault type 1	58.2~58.4 mA	2.92~2.97 V	0.6153~0.69 V	1.64~1.81 V	−0.02 V
Fault type 2	85~88 mA	2.92~2.97 V	0~0.61 V	0.01~1.68 V	−0.34~0.12 V
Fault type 3	58.2~58.4 mA	3.37~4.85 V	0.14~0.86 V	1.72 V	−0.015~0.05 V
Fault type 4	83~85 mA	6~8.49 V	0~0.5 V	0.43~1.3 V	0~0.21 V
Fault type 5	84.88~85.46 mA	2.92~2.97 V	0.61~0.68 V	1.2~1.5 V	−0.02 V
Normal	58.2~58.4 mA	2.92~2.97 V	0.72~0.73 V	1.72 V	−0.02 V

. From Table 5, it can be seen that when different types of faults occur, the operating range of each parameter is not consistent. Based on the knowledge that the parameters essentially characterize the operating status of various components inside the optical CT, this study will quantitatively evaluate the targeted severity of different types of faults, providing good guidance for operation and maintenance personnel.

3.4. Assessment of Fault Severity

Firstly, by normalizing each parameter, a comparative analysis is conducted on the average operating levels of each parameter under different fault conditions and normal conditions, as shown in the figure below.

From Figure 6, it can be seen that the average operating level of different parameters under the same fault type is significantly different from that under normal conditions, and the degree of difference between the same parameter and normal conditions under different fault types is also different.

Considering the above characteristics, this study adopts a SHAP algorithm to analyze the historical operating data of various parameters when different types of faults occur and conducts a detailed analysis of the relative importance of each parameter when a certain type of fault occurs, providing data support for the refined evaluation of the severity of subsequent faults. Comparing Figure 6 with

Table 6. Importance of various features for severity under different fault conditions.

	LED Current	Modulator Driving Voltage	Second Harmonic Voltage	Peak Input Voltage	Average Input Voltage Deviation
Fault type 1	0.0003	0.002	0.9558	0.0372	0.0047
Fault type 2	0.8558	0.0011	0.0501	0.0503	0.0427
Fault type 3	0.012	0.4531	0.4432	0.05	0.0417
Fault type 4	0.4631	0.3231	0.1221	0.0812	0.0105
Fault type 5	0.7553	0.0016	0.123	0.1131	0.007

it can be seen that the proposed method can well characterize the degree of difference between parameter characteristics and normal operating conditions when faults occur. Taking the comparison of the operating levels of various parameters between electronic unit faults (fault type 2) and normal conditions as an example, as shown in Figure 6, the difference in the average operating level of LED current parameter between fault conditions and normal conditions is much greater than other parameters. As shown in Table 6, the LED current parameter has the highest relative importance in evaluating the severity of the fault, which proves the effectiveness of the proposed method. Meanwhile, as the LED current parameter reflects the intensity of light in the optical path received by the detector in the electronic unit after mirror reflection from the end of the measuring fiber, it is affected by the light source and fiber attenuation coefficient. Therefore, when the electronic unit fault occurs, this parameter will undergo significant changes, which also confirms the reliability of the conclusions obtained from this experimental method.

Based on the analysis results of the relative severity of each parameter under different fault types in Table 6, the quantitative distribution of severity for different fault types can be calculated, as shown in Figure 7. This article uses the upper and lower quartiles of the boxplot as the boundaries for severity classification, dividing severity into three levels: “extremely severe”, “moderately severe”, and “mildly severe”. This level of classification can provide a reference for subsequent operation and maintenance work. Taking electronic unit faults (fault type 2) as an example,

Table 7. Parameter operation under different severity levels of electronic unit fault types.

	LED Current	Modulator Driving Voltage	Second Harmonic Voltage	Peak Input Voltage	Average Input Voltage Deviation	Severity
Extremely serious	86.23~87.99 mA	2.92~2.97 V	0~0.31 V	0.01~0.071 V	−0.34~0.09 V	0.823~1
Moderately severe	85.43~87.77 mA	2.92~2.97 V	0.30~0.54 V	0.061~1.18 V	−0.24~0.089 V	0.511~0.823
Mild severe	85.01~85.35 mA	2.92~2.97 V	0.55~0.61 V	1.01~1.68 V	−0.02~0.12 V	0~0.511
Normal	58.2~58.4 mA	2.92~2.97 V	0.72~0.73 V	1.72 V	−0.02 V	0

provides the operating range of each parameter for each severity and normal condition sample. It can be seen that the more significant the difference between the operating level of each parameter and the normal condition, the greater the severity of the fault.

4. Conclusions and Discussion

4.1. The Superiority of the Proposed Model

This study firstly constructs a CNN-Transformer model for fault identification, based on which, the severity of faults in optical CT is evaluated depending on k-means-SMOTE and SHAP algorithms. The following conclusion is drawn:

(1)

The CNN-Transformer model can effectively fuse fault features and achieve high accuracy in fault identification by mining the spatiotemporal correlation among the time series of various features of optical CT.

(2)

The synthetic minority oversampling method based on clustering partitioning can generate high-quality fault scenarios and provide good data support for evaluating the severity of faults.

(3)

Based on the fault identification model, the SHAP algorithm can effectively quantify the importance of different features of optical CT under various operating conditions, which has good interpretability. The importance assessment results provide support for measuring the degree of difference between the operating level of various parameters of the optical CT under different fault conditions and normal conditions.

This study verifies and analyzes the practicality of the proposed method through experiments, providing a way for quantifying the severity of faults in optical CT.

4.2. Practical Contributions of the Obtained Results

Based on the accurate fault identification results and the severity assessment of fault type, we can achieve a more comprehensive perception and judgment of optical CT faults, effectively reducing the proportion of high repetition and low technical content in optical CT inspection work, enhancing the intelligence level of on-site operation and maintenance personnel.

Firstly, accurate identification results for potential fault hazards can improve the efficiency of fault handling for operation and maintenance personnel. Secondly, based on status assessment for faulty equipment, hierarchical maintenance plans can be developed to extend the full life cycle of equipment, reduce unnecessary emergency repairs, lower personnel workload, and lower operation and maintenance costs in situations where operation and maintenance resources are limited. Last but not least, since the optical CT is the crucial detection equipment for the DC system, it is closely associated with the safe operation of the power system. Accurately discovering the faults during the operation of optical CT can reduce the risk of power grid operation, effectively improving the safety and stable operation level of the power grid. From a broader perspective, we can prevent major power outages caused by cascading failures, reduce the risk of system shutdown and the huge economic losses caused by optical CT failures, and reduce the adverse social impact of major power outages.

At the same time, the lean management level of optical CT equipment can break through digital barriers, expand analysis methods and techniques, derive new production services, promote the application of emerging operation and maintenance functions, and improve the integration level of artificial intelligence technology in the power grid and even the energy industry.

At the same time, the project involves a universal fault severity assessment method system that will gradually form standards and specifications for enterprises, industries, and countries in subsequent research, guiding the daily operation and maintenance of converter station optical CT. In addition, the development, promotion, and application of the optical CT fault identification and intelligent operation and maintenance algorithm module system for converter stations will also promote the formation of the operation and maintenance supporting industry chain and drive the development of the supporting industry economy.

4.3. Limitations of Technique Dissemination

The results of this study can be widely applied to the construction of intelligent warning and monitoring platforms for optical CT in various converter stations of State Grid Corporation of China, supporting the fault analysis, diagnosis, performance evaluation, and fault disposal of operating optical CT. However, there are several points to be considered regarding the dissemination of this technology:

(1)

Compared with normal operating samples, the number of fault samples in optical CT is much smaller, which is disadvantageous for model construction for accurate fault identification and severity assessment. Although the method of sample generation in this study can be used to address this issue, the accuracy of fault sample generation depends on whether the features of fault sample can be well mined. Therefore, if there are not enough fault samples in the historical operation data of optical CT, it is impossible to obtain high fault identification accuracy and accurate fault severity assessment results.

(2)

The fault identification model designed in this study is not a universal model. Since the types of optical CT equipment used in different converter stations are not consistent, the types of equipment faults are different, which means the fault occurrence mechanism varies with the types of optical CT. Therefore, during fault identification modeling, it is necessary to model different types of optical CT equipment separately.

(3)

Considering the different operating states of optical CT in different converter stations, even the same type of optical CT will exhibit different fault operating characteristics in different environments. The parameters in the model designed for this experiment may only be applicable to a specific environment. If fault identification is to be performed on optical CT equipment in other converter stations, the model needs to be retrained for parameter adjustment.

4.4. Future Works

Although the currently proposed methods have demonstrated their reliability and superiority in this experiment, they all rely on numerical theoretical analysis, whose performance relies on the distribution characteristic of data. In addition, this experiment only focused on optical CT data from a certain converter station. There is randomness in the experimental results.

In the future, further in-depth research and analysis will be conducted from the following aspects.

(1)

To fully verify the reliability of the proposed method, fault identification and severity assessment will be conducted on historical operating data of optical CT equipment of different types and different operating environments.

(2)

A more detailed analysis comparing the proposed methodology’s performance to conventional methods considering interpretability will be included.