A Cooperative Adaptive VSG Control Strategy Based on Virtual Inertia and Damping for Photovoltaic Storage System
Abstract
1. Introduction
2. Basic Structure of the PV-Storage System
3. VSG Control Strategy
3.1. Traditional VSG Control Strategy
3.2. Dynamic Power Characteristics and Existing Problems of the Traditional VSG
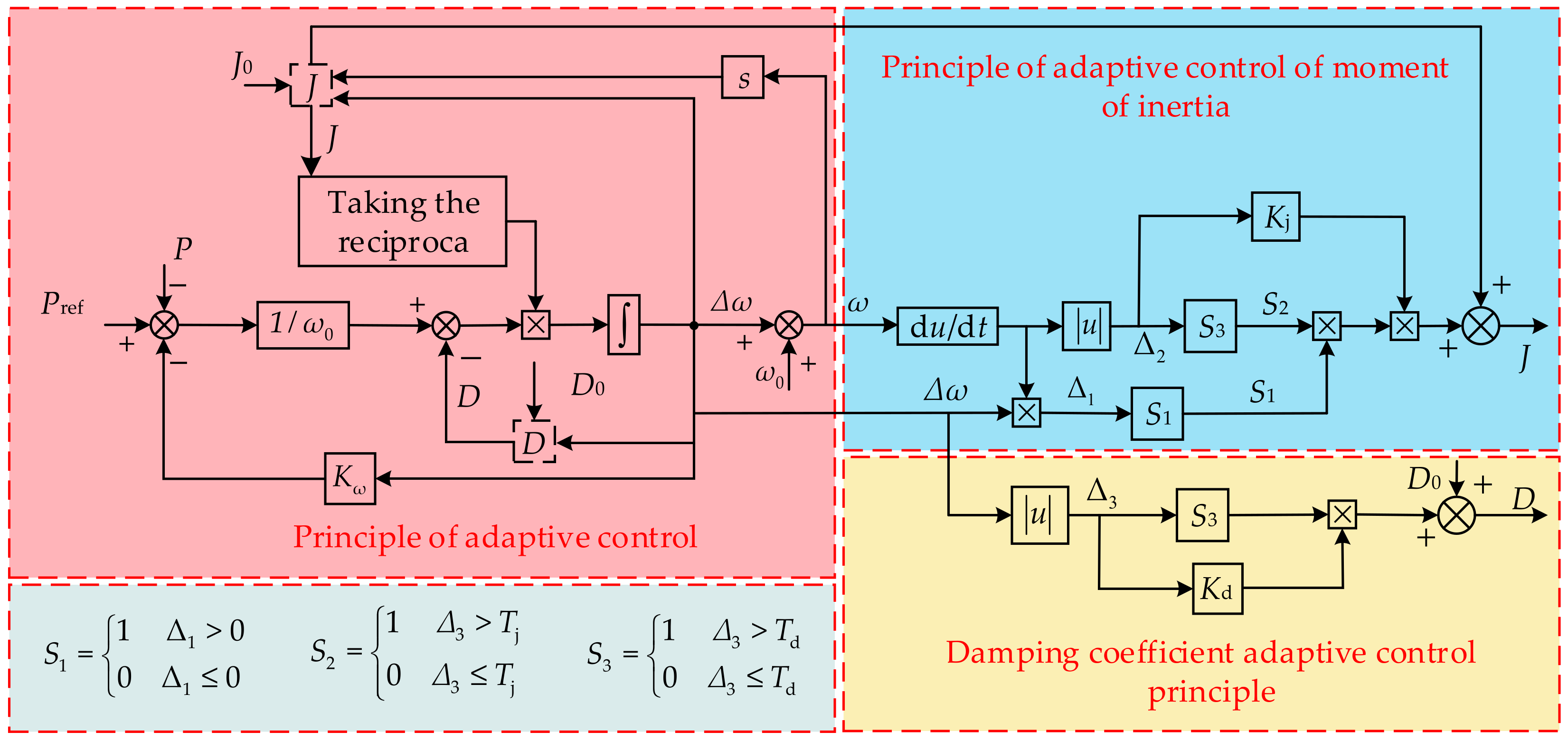
4. Virtual Inertia and Damping Adaptive Control Principle
4.1. The Influence of Virtual Inertia and Damping Coefficients on Power
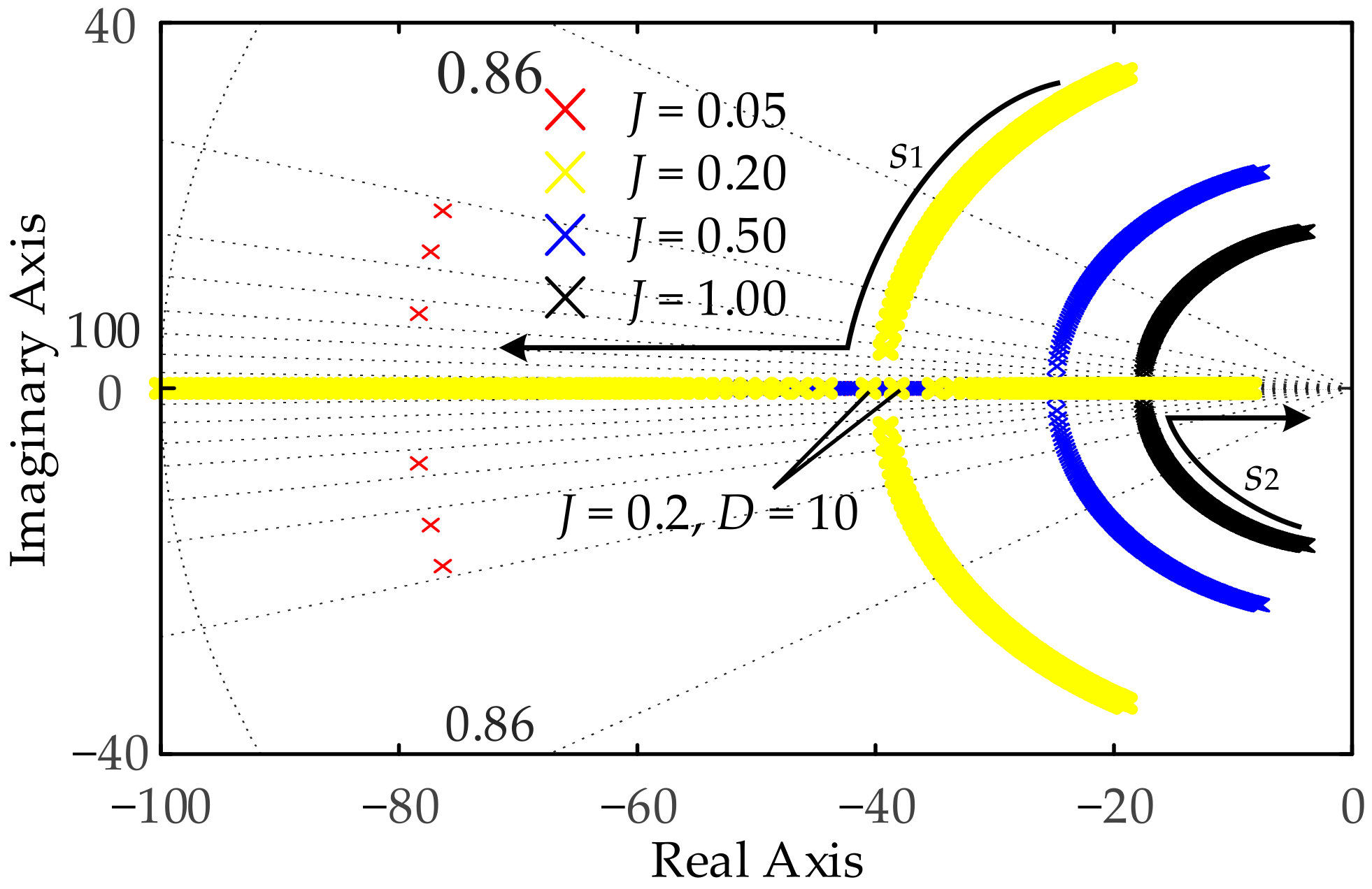
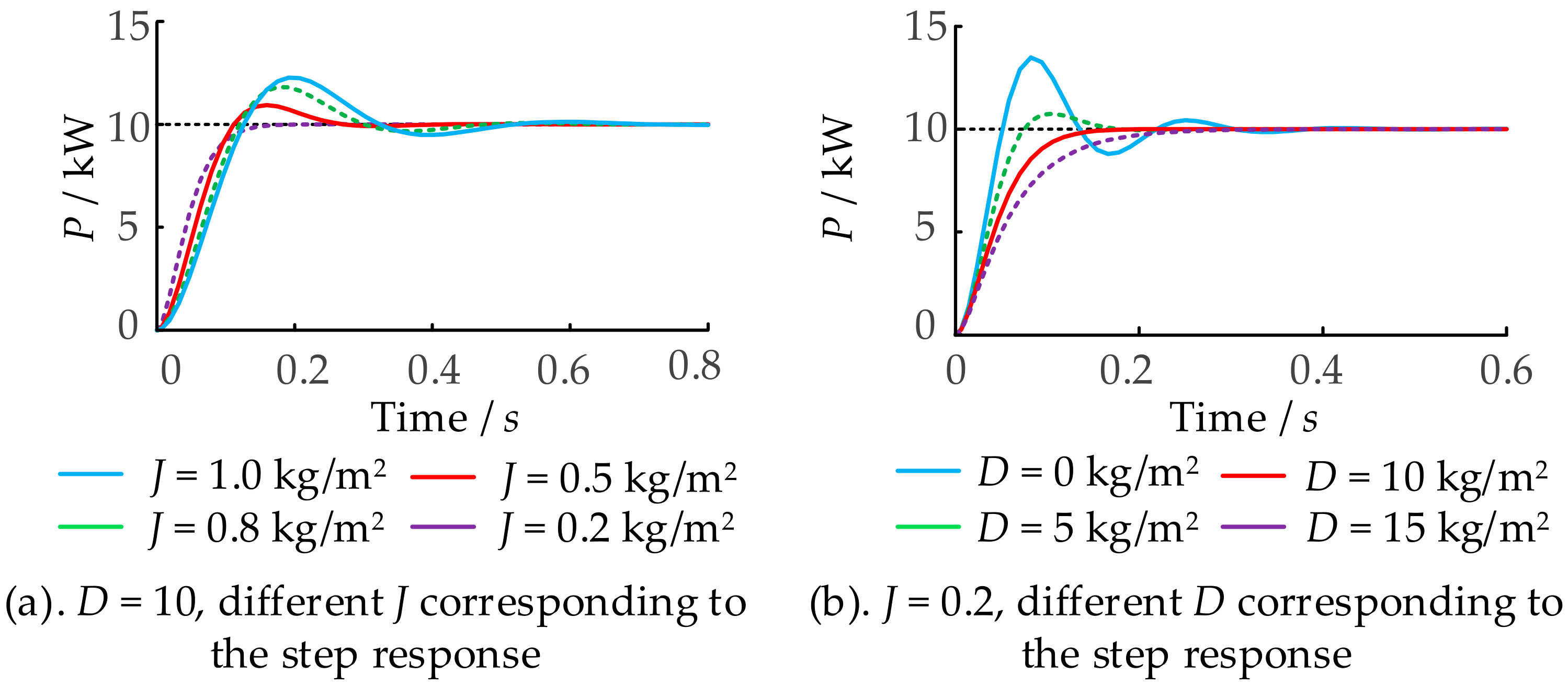
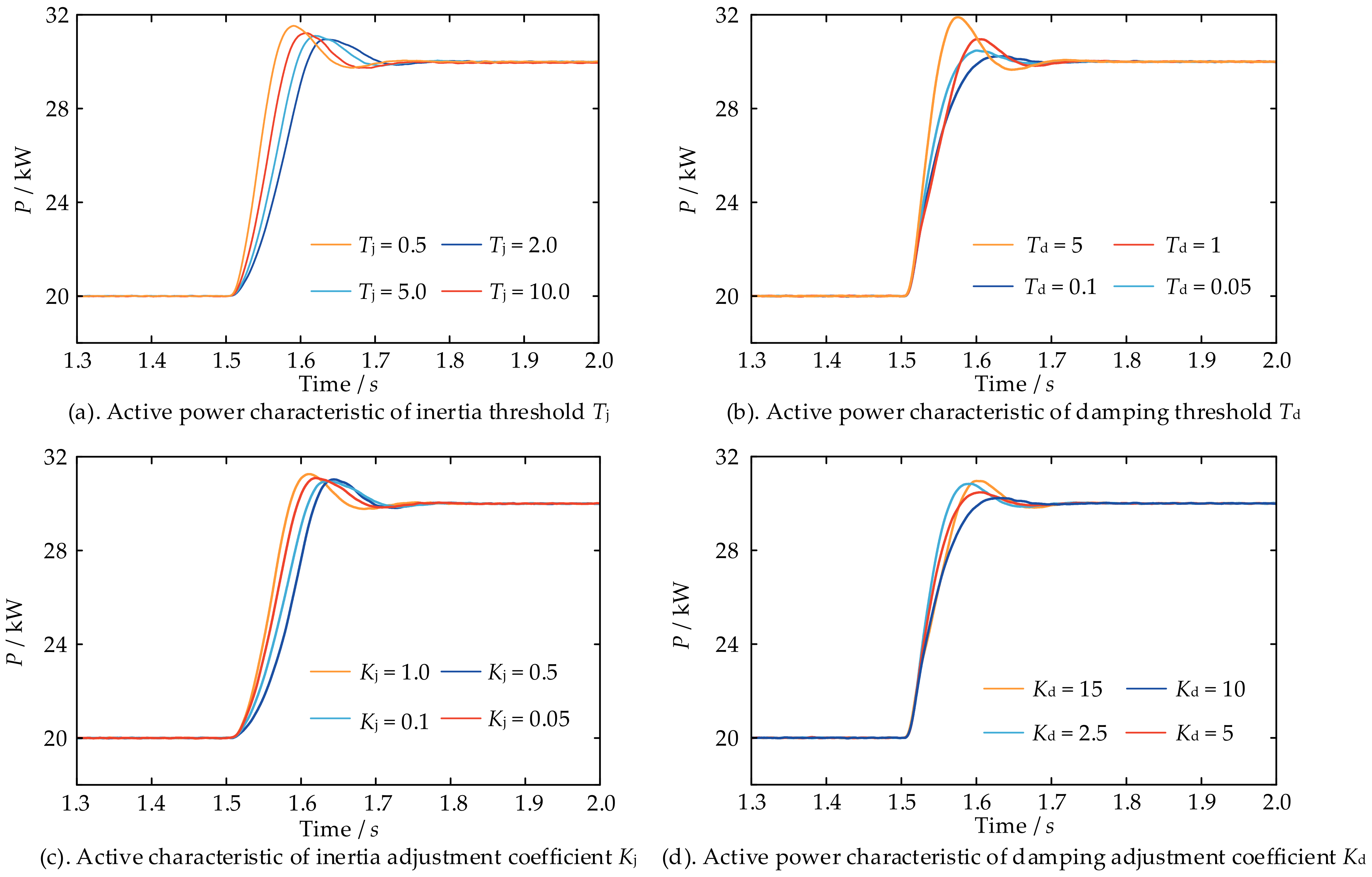
4.2. Selection of Virtual Inertia and Damping
4.3. Parameter Tuning
4.3.1. Parameter Tuning for Kω, J0, D0
4.3.2. Parameter Tuning for Tj, Td, Kj and Kd
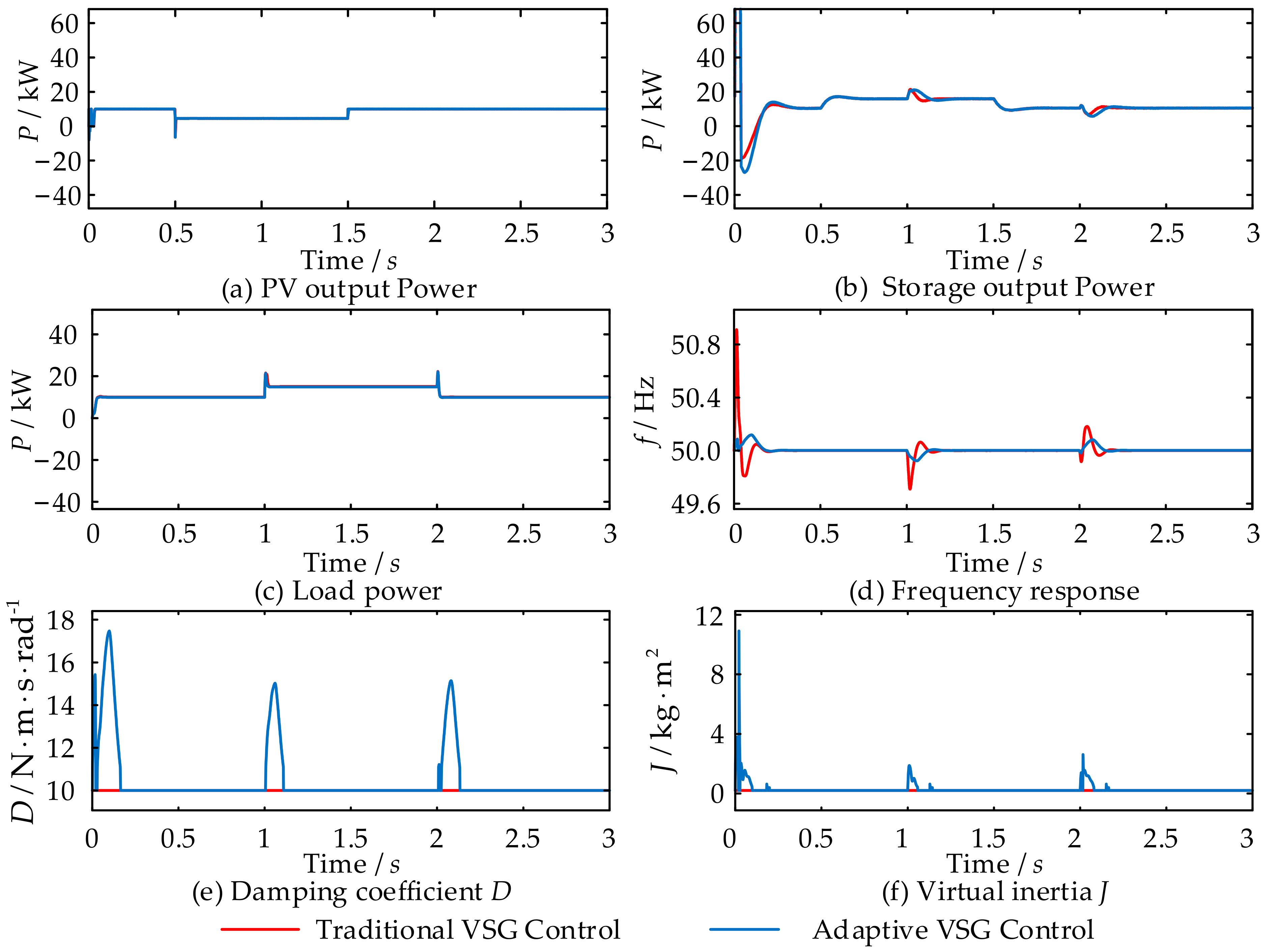
5. Simulation Analysis
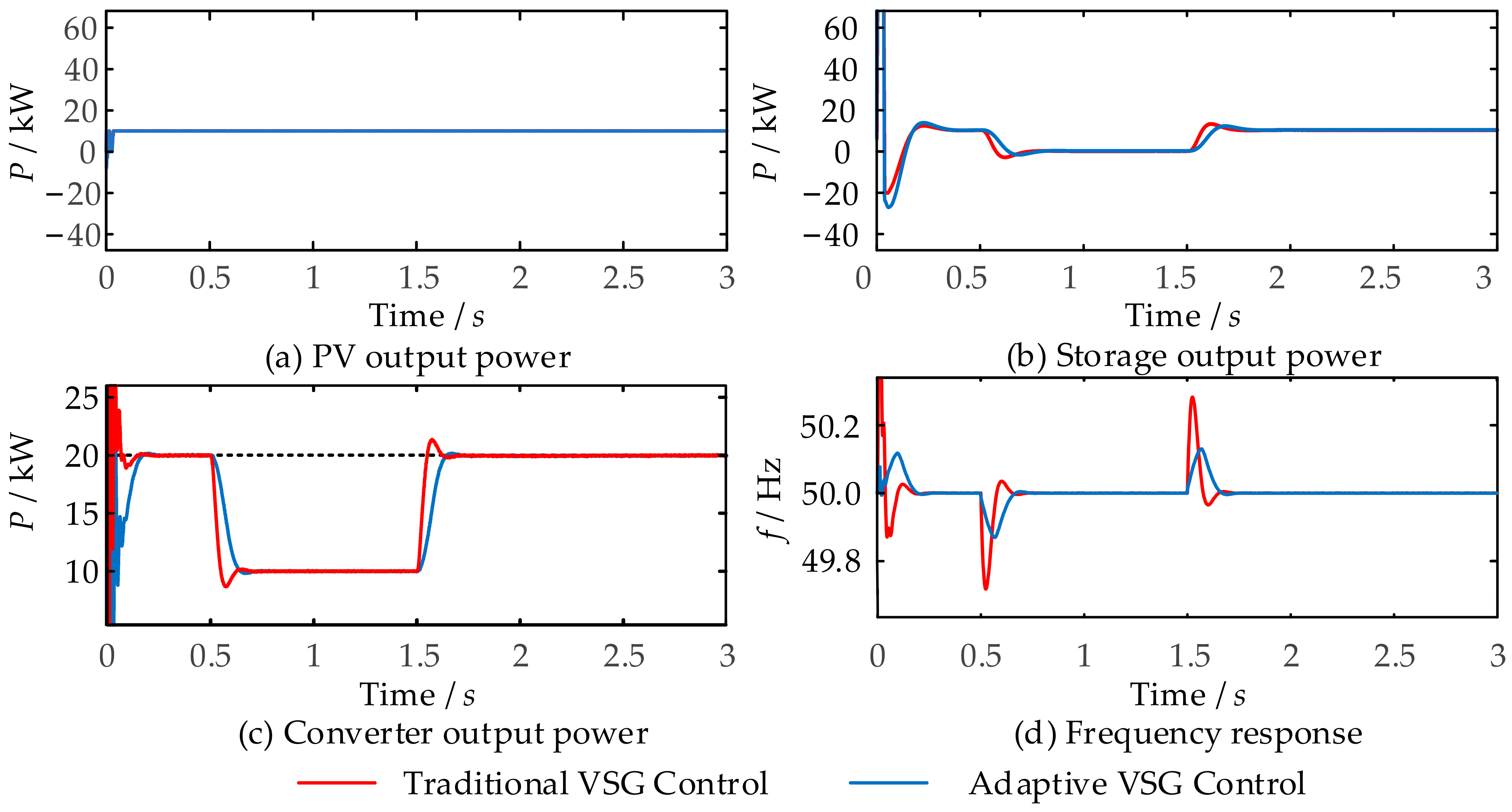
5.1. Active Power Output Variation Condition
5.2. Load Power and Light Intensity Variation Condition
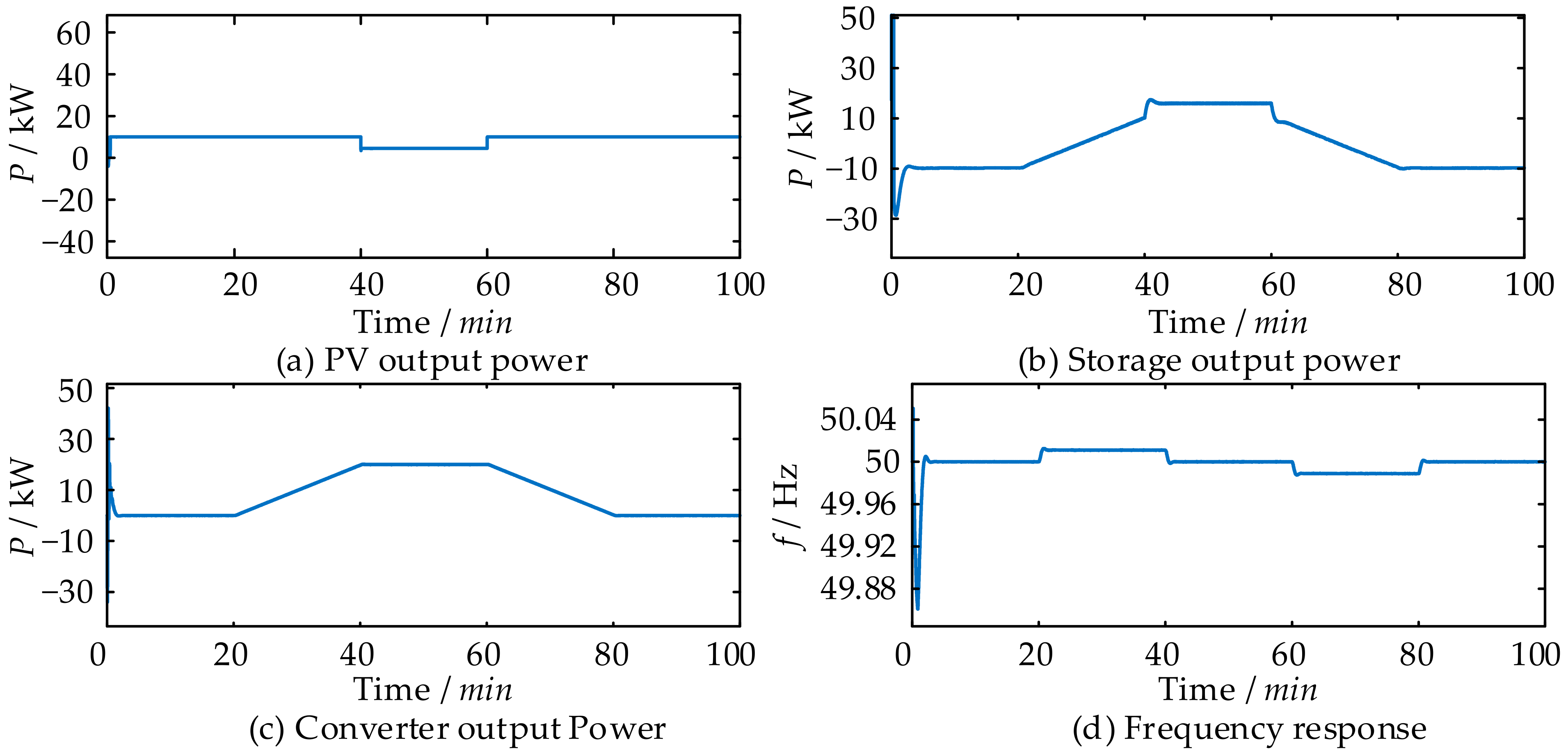
5.3. The Light Intensity Changes During Normal Grid-Connected Shutdown
6. Conclusions
- (1)
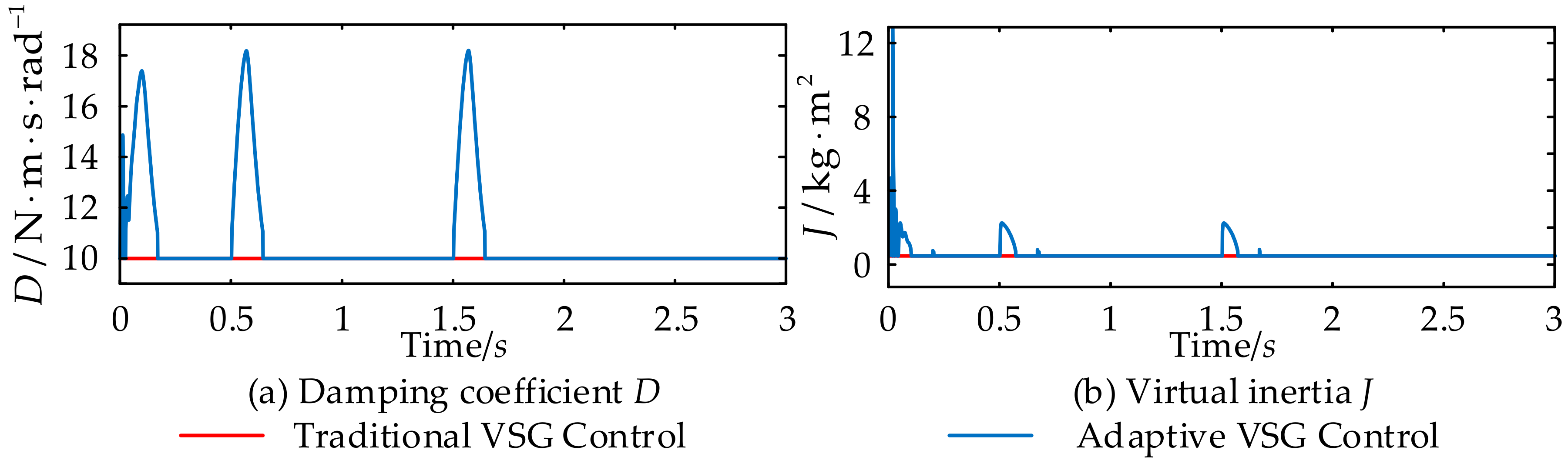
- J effectively suppresses rapid frequency fluctuations and enhances the system’s dynamic response performance. However, excessively large J may destabilize the system. Conversely, D effectively mitigates system oscillations, improves system stability, and optimizes dynamic performance. Nonetheless, increasing D can impact the rapidity of the system. The values of the two parameters influence and restrict each other, leading to a contradiction.
- (2)
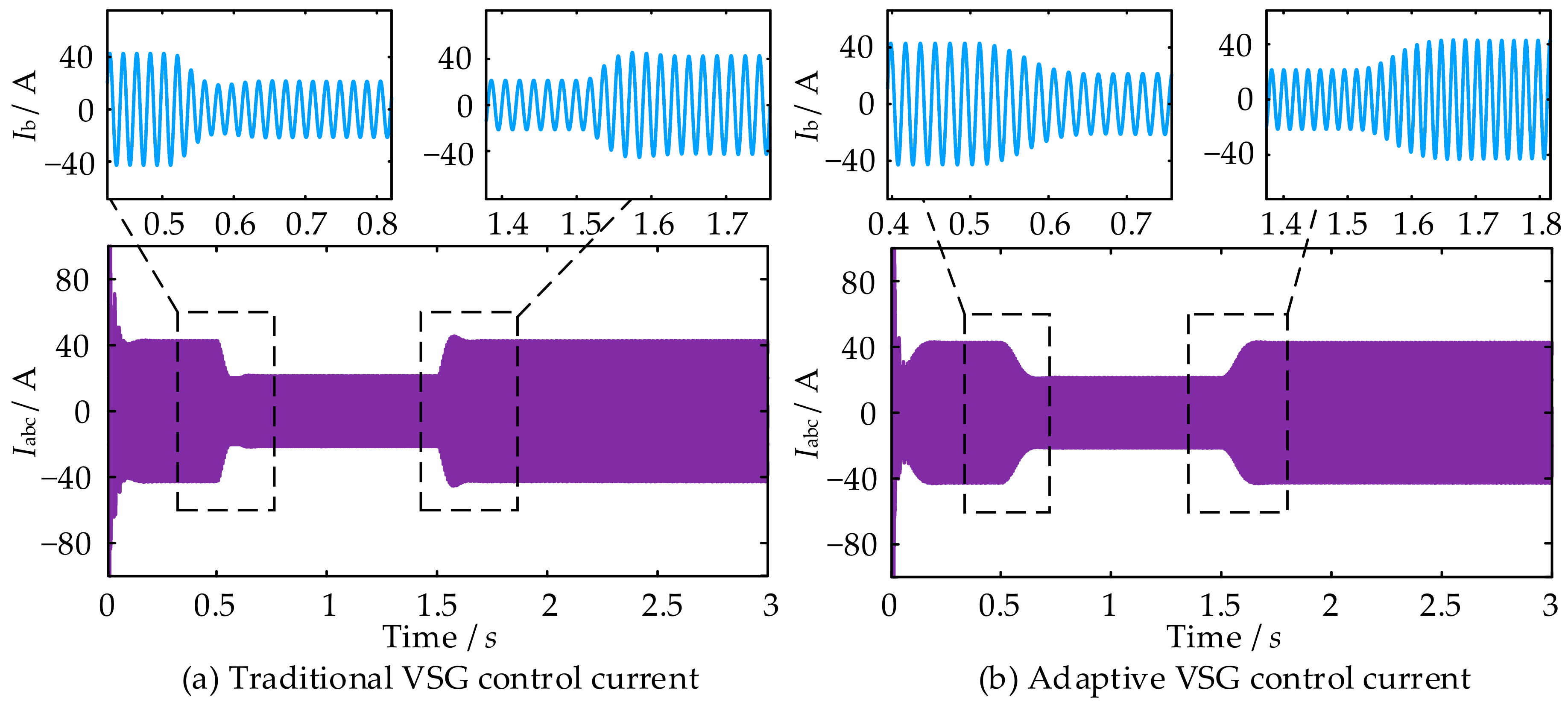
- The adaptive control strategy presented in this study outperforms traditional VSG control by effectively mitigating the instantaneous impact current from active disturbances, thus ensuring seamless electrical energy interaction. It also significantly reduces dynamic power oscillations and frequency overshoots under load disturbances, enhancing the system’s safety and reliability.
- (3)
- The introduced adaptive control strategy effectively dampens fluctuations in PV output power and regulates converter output power. It ensures that the rate of change in active power output of the PV-storage system complies with the “GB/T 19964: Regulations for Photovoltaic Power Station Access to Power System”, exceeding the standard by achieving a rate of less than 5% of installed capacity per minute, rather than the maximum allowed 10%.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, Z.; Yu, Y.; Gao, W.; Davari, M.; Deng, C. Adaptive, optimal, virtual synchronous generator control of three-phase grid-connected inverters under different grid conditions—An adaptive dynamic programming approach. IEEE Trans. Ind. Informat. 2021, 18, 7388–7399. [Google Scholar] [CrossRef]
- Shahid, A. Performance evaluation of sinusoidal and Space Vector Pulse-Width-Modulation for power quality enhancement in distributed generation systems. In Proceedings of the 2015 IEEE 6th International Symposium on Power Electronics for Distributed Generation Systems (PEDG), Aachen, Germany, 22–25 June 2015. [Google Scholar]
- Chae, W.; Kim, J.; Cho, J.; Park, J. Optimal interconnection device for distributed energy resources of customer. In Proceedings of the 2012 3rd IEEE International Symposium on Power Electronics for Distributed Generation Systems (PEDG), Aalborg, Denmark, 25–28 June 2012. [Google Scholar]
- Iqbal, S.; Xin, A.; Jan, M.U.; Salman, S.; Zaki, A.U.M.; Rehman, H.U.; Shinwari, M.F.; Abdelbaky, M.A. V2G strategy for primary frequency control of an industrial microgrid considering the charging station operator. Electronics 2020, 9, 549. [Google Scholar] [CrossRef]
- Vasudevan, K.R.; Ramachandaramurthy, V.K.; Babu, T.S.; Pouryekta, A. Synchronverter: A comprehensive review of modifications, stability assessment, applications and future perspectives. IEEE Access 2020, 8, 131565–131589. [Google Scholar] [CrossRef]
- Hirase, Y.; Sugimoto, K.; Sakimoto, K.; Ise, T. Analysis of resonance in microgrids and effects of system frequency stabilization using a virtual synchronous generator. IEEE J. Emerg. Sel. Top. Power Electron. 2016, 4, 1287–1298. [Google Scholar] [CrossRef]
- Dhingra, K.; Singh, M. Frequency support in a micro-grid using virtual synchronous generator based charging station. IET Renew. Power Gener. 2018, 12, 1034–1044. [Google Scholar] [CrossRef]
- Daili, Y.; Harrag, A. New model of multi-parallel distributed generator units based on virtual synchronous generator control strategy. Energy Ecol. 2019, 4, 222–232. [Google Scholar] [CrossRef]
- Sundaramoorthy, K.; Thomas, V.; O’Donnell, T.; Ashok, S. Virtual synchronous machine-controlled grid-connected power electronic converter as a ROCOF control device for power system applications. Electr. Eng. 2019, 101, 983–993. [Google Scholar] [CrossRef]
- Pourmohammad, M.; Toulabi, M.; Ranjbar, A.M. Application of state feedback controller to ensure robust D-stable operation of virtual synchronous generators. IEEE Trans. Energy Convers 2020, 36, 602–610. [Google Scholar] [CrossRef]
- Bevrani, H.; Ise, T.; Miura, Y. Virtual synchronous generators: A survey and new perspectives. Int. J. Electr. Power Energy Syst. 2014, 54, 244–254. [Google Scholar] [CrossRef]
- Pan, D.; Wang, X.; Liu, F.; Shi, R. Transient stability of voltage-source converters with grid-forming control: A design-oriented study. IEEE J. Emerg. Sel. Topics Power Electron. 2019, 8, 1019–1033. [Google Scholar] [CrossRef]
- Blaabjerg, F.; Teodorescu, R.; Liserre, M.; Timbus, A.V. Overview of control and grid synchronization for distributed power generation systems. IEEE Trans. Ind. Electron. 2006, 53, 1398–1409. [Google Scholar] [CrossRef]
- Sun, P.; Yao, J.; Zhao, Y.; Fang, X.; Cao, J.Y. Stability Assessment and Damping Optimization Control of Multiple Grid-Connected Virtual Synchronous Generators. IEEE Trans. Energy Convers. 2021, 36, 3555–3567. [Google Scholar] [CrossRef]
- Liu, J.; Miura, Y.; Ise, T. Comparison of dynamic characteristics between virtual synchronous generator and droop control in inverter-based distributed generators. IEEE Trans. Power Electron. 2015, 31, 3600–3611. [Google Scholar] [CrossRef]
- Shintai, T.; Miura, Y.; Ise, T. Oscillation damping of a distributed generator using a virtual synchronous generator. IEEE Trans. Power Del. 2014, 29, 668–676. [Google Scholar] [CrossRef]
- Shi, R.L.; Zhang, X.; Hu, C.; Xu, H.Z.; Gu, J.; Cao, W. Self-tuning virtual synchronous generator control for improving frequency stability in autonomous photovoltaic-diesel microgrids. J. Mod. Power Syst. 2018, 6, 482–494. [Google Scholar] [CrossRef]
- Cao, W.; Liu, K.L.; Xu, S.; Kang, H.T.; Zhao, J.F. Stabilization control strategy for shore power system with surge loads based on virtual synchronous generator. J. Electr. Eng. 2019, 14, 1045–1054. [Google Scholar] [CrossRef]
- Soni, N.; Doolla, S.; Chandorkar, M.C. Improvement of transient response in microgrids using virtual inertia. IEEE Trans. Power Delivery 2013, 28, 1830–1838. [Google Scholar] [CrossRef]
- De Brabandere, K.; Bolsens, B.; Van den Keybus, J.; Woyte, A.; Driesen, J.; Belmans, R. A voltage and frequency droop control method for parallel inverters. IEEE Trans. Power Electron. 2007, 22, 1107–1115. [Google Scholar] [CrossRef]
- Liu, J.; Liu, X.; Liu, J.; Li, X.; Wang, J. Adaptive-Droop-Coefficient VSG Control for Cost-Efficient Grid Frequency Support. IEEE Trans. Power Syst. 2024, 39, 6768–6771. [Google Scholar] [CrossRef]
- Du, Y.; Guerrero, J.M.; Chang, L.C.; Su, J.H.; Mao, M.Q. Modeling, analysis, and design of a frequency-droop-based virtual synchronous generator for microgrid applications. In 2013 IEEE ECCE Asia; IEEE: New York, NY, USA, 2013; pp. 634–649. [Google Scholar]
- Zhang, X.; Mao, F.B.; Xu, H.Z.; Liu, F.; Li, M. An optimal coordination control strategy of micro-grid inverter and energy storage based on variable virtual inertia and damping of VSG. Chin. J. Electr. Eng. 2017, 3, 25–33. [Google Scholar]
- Alipoor, J.; Miura, Y.; Ise, T. Power system stabilization using virtual synchronous generator with alternating moment of inertia. IEEE J. Emerg. Sel. Top. Power Electron. 2014, 3, 451–458. [Google Scholar] [CrossRef]
- Thomas, V.; Kumaravel, S.; Ashok, S. Fuzzy Controller-Based Self-Adaptive Virtual Synchronous Machine for Microgrid Application. IEEE Trans. Energy Convers. 2021, 36, 2427–2437. [Google Scholar] [CrossRef]
- Hou, X.C.; Sun, Y.; Zhang, X.; Lu, J.H.; Wang, P.; Guerrero, J.M. Improvement of frequency regulation in VSG-based AC microgrid via adaptive virtual inertia. IEEE Trans. Power Electron. 2019, 35, 1589–1602. [Google Scholar] [CrossRef]
- Zhang, Y.; Sun, Q.; Zhou, J.; Li, L.; Wang, P.; Guerrero, J.M. Coordinated control of networked AC/DC microgrids with adaptive virtual inertia and governor-gain for stability enhancement. IEEE Trans. Energy Convers 2020, 36, 95–110. [Google Scholar] [CrossRef]
- Zhu, Z.B.; Huang, S.P.; Li, Z.X. Research on control strategy of micro-grid adaptive damping VSG. Control Eng. China 2020, 1, 33–39. [Google Scholar]
- Ding, J.W.; Zhang, J.B.; Ma, Z.H. VSG inertia and damping coefficient adaptive control. In Proceedings of the 2020 Asia Energy and Electrical Engineering Symposium (AEEES), Chengdu, China, 28–31 May 2020; pp. 431–435. [Google Scholar]
- Lin, Y.; Zhang, J.C.; Wang, N. A management control strategy of photovoltaic-storage system based on virtual synchronous generator. Mod. Electr. Power 2017, 34, 64–73. [Google Scholar]
- Zhang, X. Coordinated control strategy for a PV-storage grid-connected system based on a virtual synchronous generator. Global Energy Interconn. 2020, 3, 51–59. [Google Scholar] [CrossRef]
- Li, J.X.; Zhao, J.B.; Qu, K.; Li, F. Boundary analysis of operation parameters of microgrid VSG considering SOC characteristics. Power Syst. Technol. 2018, 42, 1451–1457. [Google Scholar]
- Han, L.J.; Feng, X.C.; Zhao, H. Adaptive VSG control strategy considering energy storage SOC constraints. Front. Energy Res. 2023, 11, 1278648. [Google Scholar]
- Rehman, H.U.; Yan, X.W.; Abdelbaky, M.A.; Jan, M.U.; Sayed, A.R.; Zaki, S.A.; Iqbal, S. Frequency regulation and optimization of microgrid system with multi PV-VSG using advanced droop controller. In Proceedings of the 2020 IEEE 4th Conference on Energy Internet and Energy System Integration (EI2), Wuhan, China, 30 October–1 November 2020. [Google Scholar]
- Chen, X.; Qian, Y.; Xu, Y.; Shu, B.; Sheng, G. A novel pulse-source-based method for measuring transfer impedance of high frequency current sensor. Electr. Power Autom. Equip. 2019, 39, 120–124, 131. [Google Scholar]
- Rosso, R.; Wang, X.; Liserre, M.; Lu, X.; Engelken, S. Grid-forming converters: Control approaches, grid-synchronization, and future trends—A review. IEEE Open J. Ind. Appl. 2021, 2, 93–109. [Google Scholar] [CrossRef]


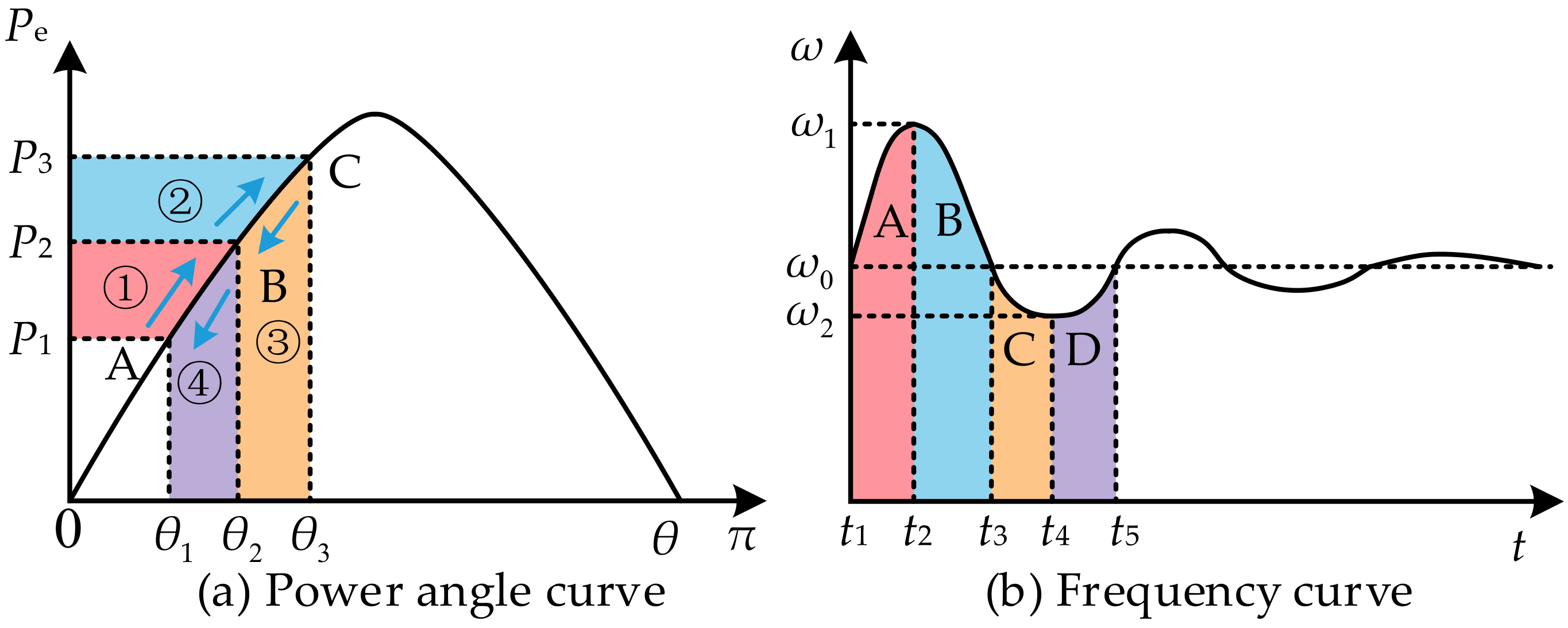

| Section | Δω | dω/dt | Δω×dω/dt | The Variation in J | The Variation in D |
|---|---|---|---|---|---|
| (1) | >0 | >0 | >0 | Increase | Increase |
| (2) | >0 | <0 | <0 | Decrease | Increase |
| (3) | <0 | <0 | >0 | Increase | Increase |
| (4) | <0 | >0 | <0 | Decrease | Increase |
| Parameter | Parameter Value |
|---|---|
| L/mH | 6 |
| C/μF | 20 |
| Udc/V | 700 |
| UN/V | 380 |
| J0/(kg∙m2) | 0.2 |
| D0/(N∙m∙s∙rad−1) | 10 |
| Kω | 5.2 |
| Kj | 0.1 |
| Tj | 2 |
| Kd | 10 |
| Td | 0.1 |
| Time (min) | Converter Output Power (kW) | Light Intensity (kW/m2) |
|---|---|---|
| 0~20 | 0 | 10 |
| 20~40 | 0→20 | 10 |
| 40~60 | 20 | 5 |
| 60~80 | 20→0 | 10 |
| 80~100 | 0 | 10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xia, Y.; Wang, Y.; Chen, Y.; Shi, J.; Yang, Y.; Li, W.; Li, K. A Cooperative Adaptive VSG Control Strategy Based on Virtual Inertia and Damping for Photovoltaic Storage System. Energies 2025, 18, 1505. https://doi.org/10.3390/en18061505
Xia Y, Wang Y, Chen Y, Shi J, Yang Y, Li W, Li K. A Cooperative Adaptive VSG Control Strategy Based on Virtual Inertia and Damping for Photovoltaic Storage System. Energies. 2025; 18(6):1505. https://doi.org/10.3390/en18061505
Chicago/Turabian StyleXia, Yan, Yao Wang, Yang Chen, Jinhui Shi, Yiqiang Yang, Wei Li, and Ke Li. 2025. "A Cooperative Adaptive VSG Control Strategy Based on Virtual Inertia and Damping for Photovoltaic Storage System" Energies 18, no. 6: 1505. https://doi.org/10.3390/en18061505
APA StyleXia, Y., Wang, Y., Chen, Y., Shi, J., Yang, Y., Li, W., & Li, K. (2025). A Cooperative Adaptive VSG Control Strategy Based on Virtual Inertia and Damping for Photovoltaic Storage System. Energies, 18(6), 1505. https://doi.org/10.3390/en18061505






