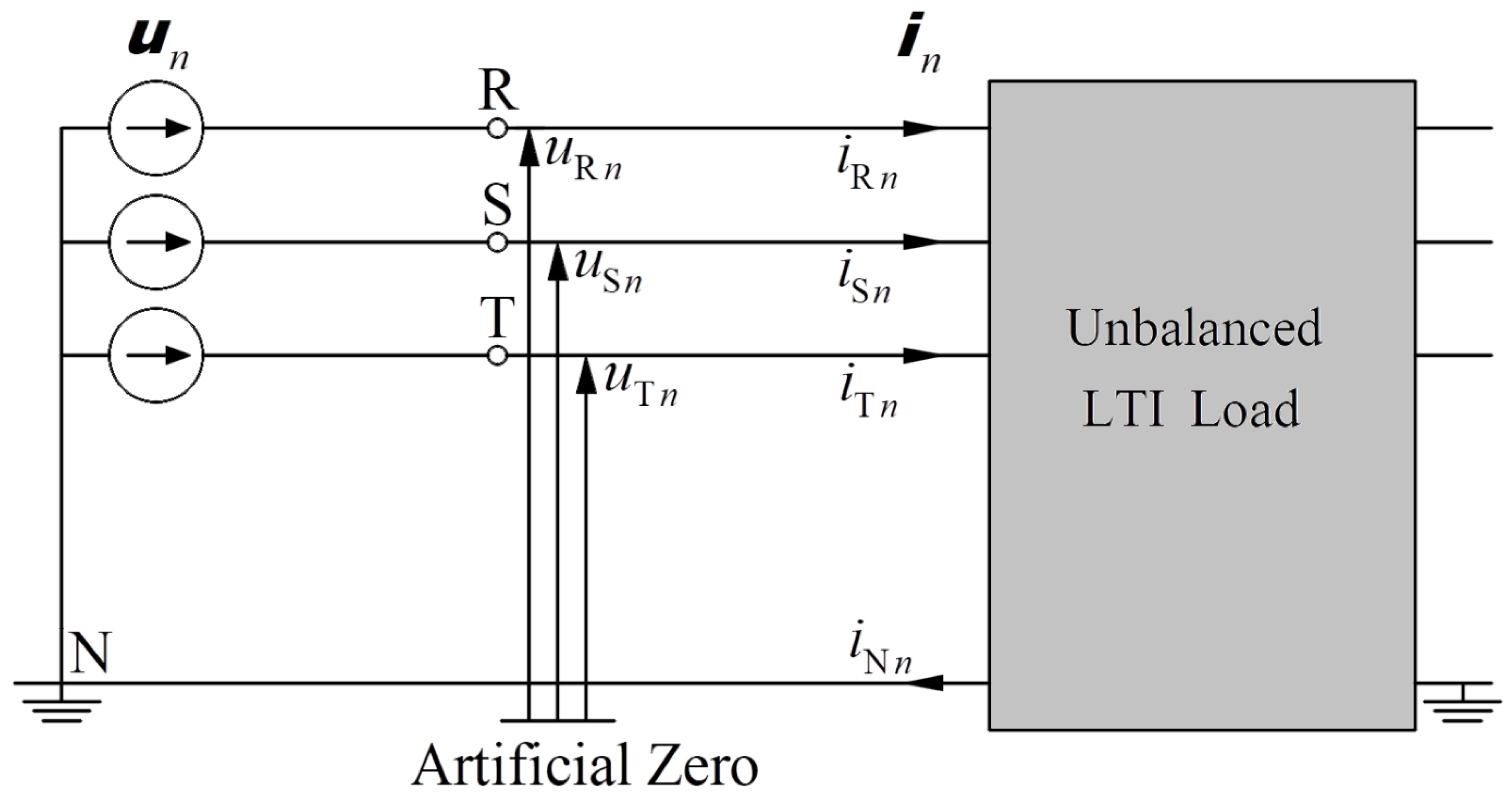
Figure 1.
Unbalanced linear receiver supplied from symmetric voltage source with higher harmonics orders.
Figure 1.
Unbalanced linear receiver supplied from symmetric voltage source with higher harmonics orders.
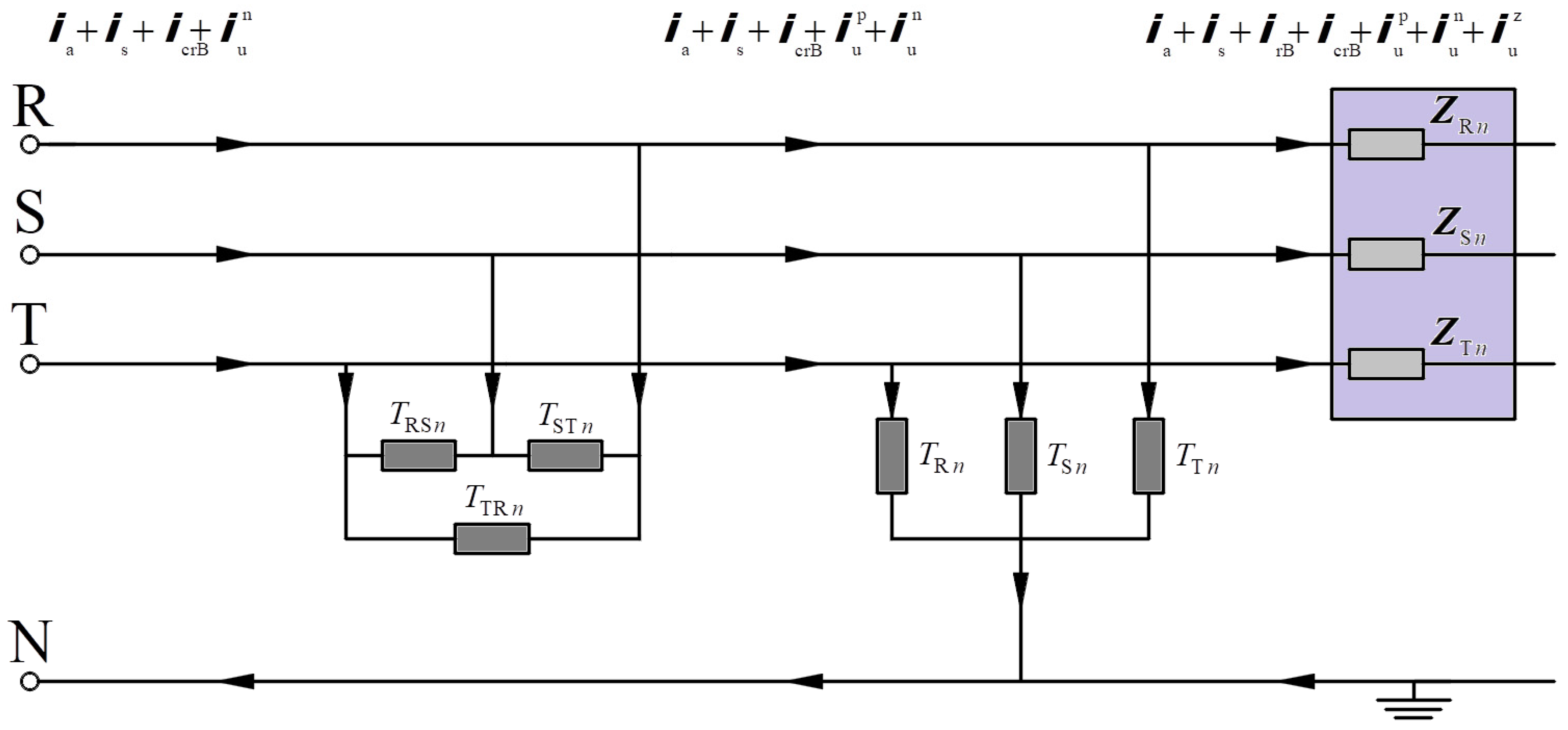
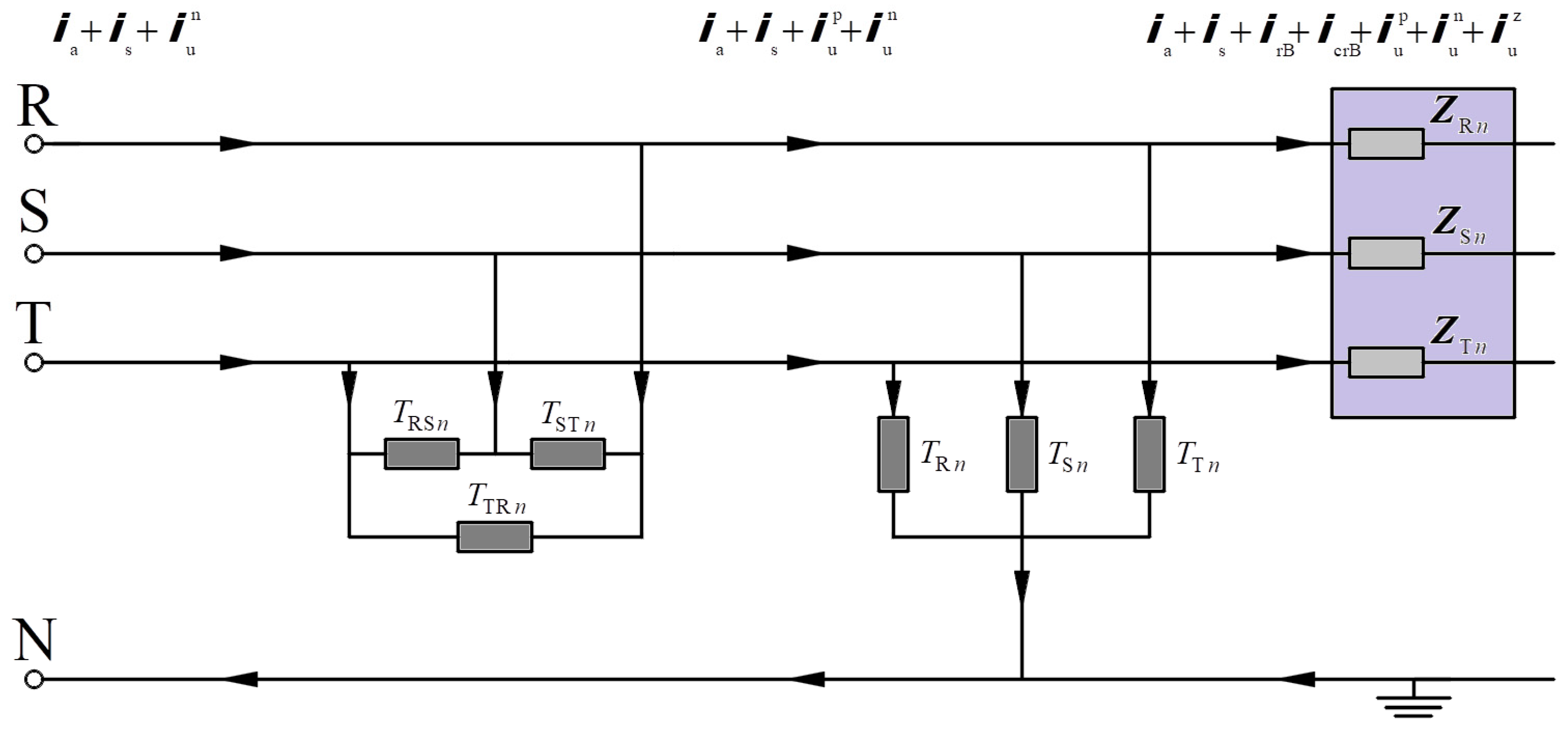
Figure 2.
Three-phase four-wire circuit scheme powered by a distorted voltage with an imbalanced linear load.
Figure 2.
Three-phase four-wire circuit scheme powered by a distorted voltage with an imbalanced linear load.
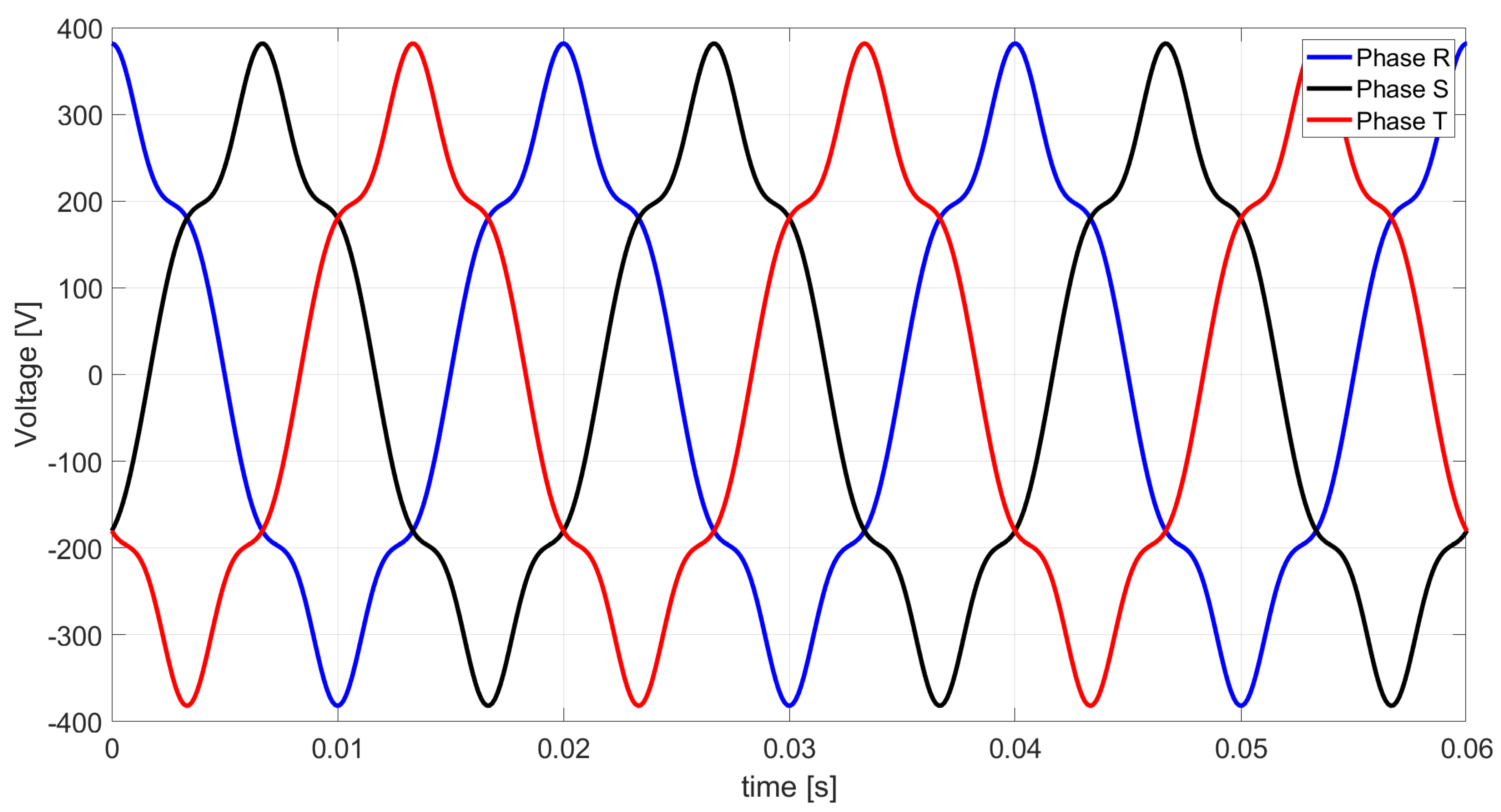
Figure 3.
Voltage waveform of a distorted voltage at the connection points of a linear asymmetric load.
Figure 3.
Voltage waveform of a distorted voltage at the connection points of a linear asymmetric load.
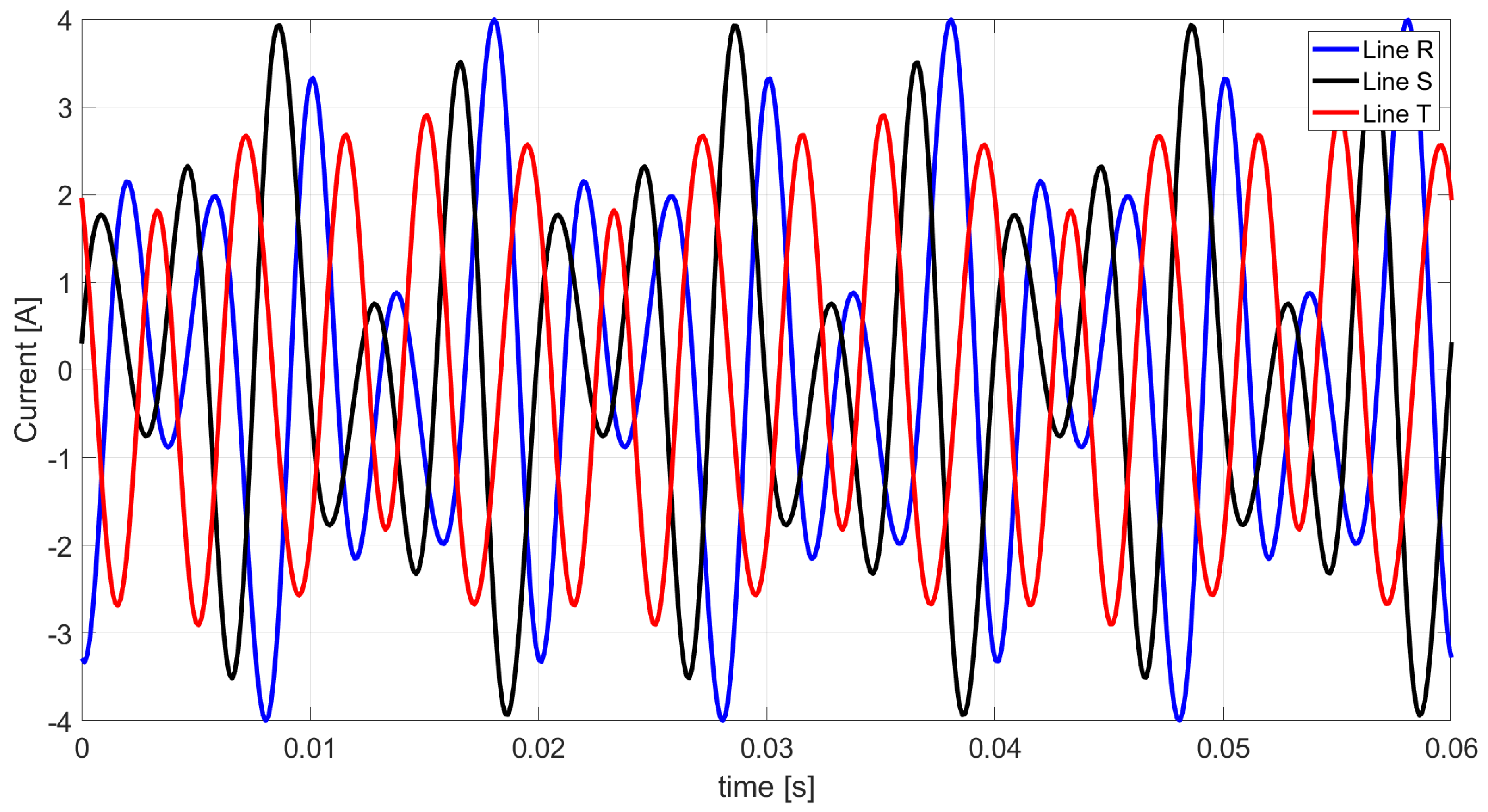
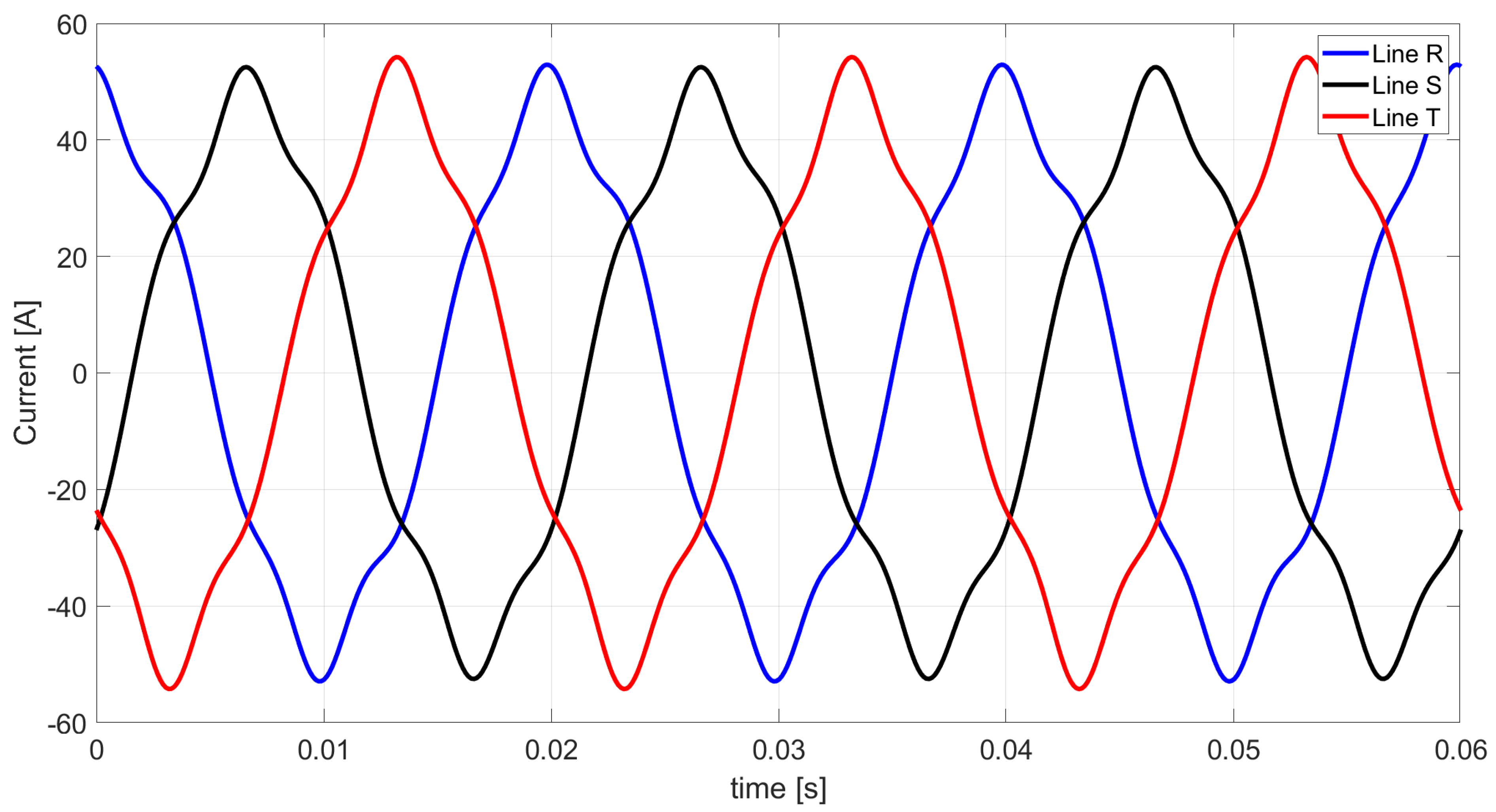
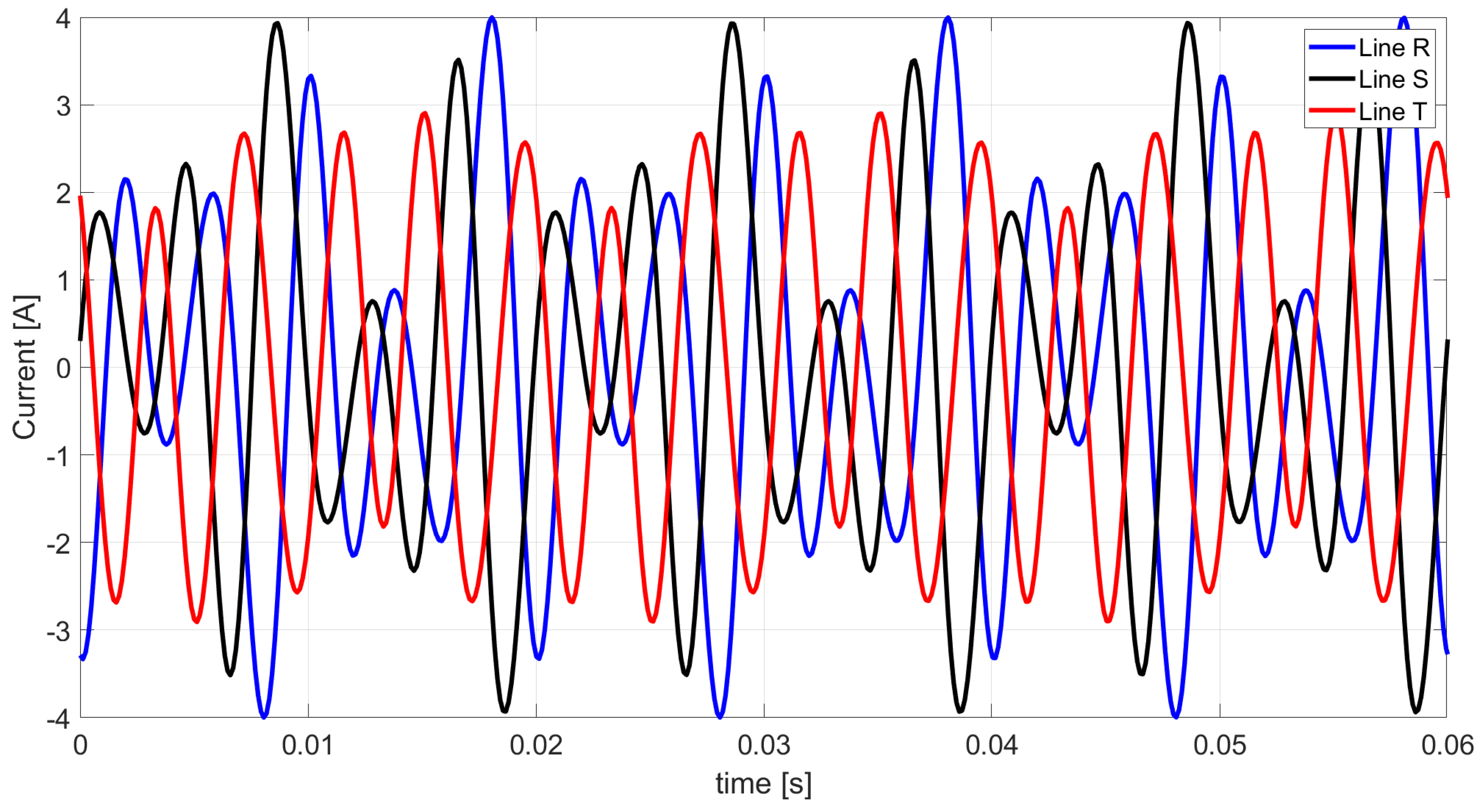
Figure 4.
Waveform of line currents obtained from Ohm’s law and Kirchhoff’s law.
Figure 4.
Waveform of line currents obtained from Ohm’s law and Kirchhoff’s law.
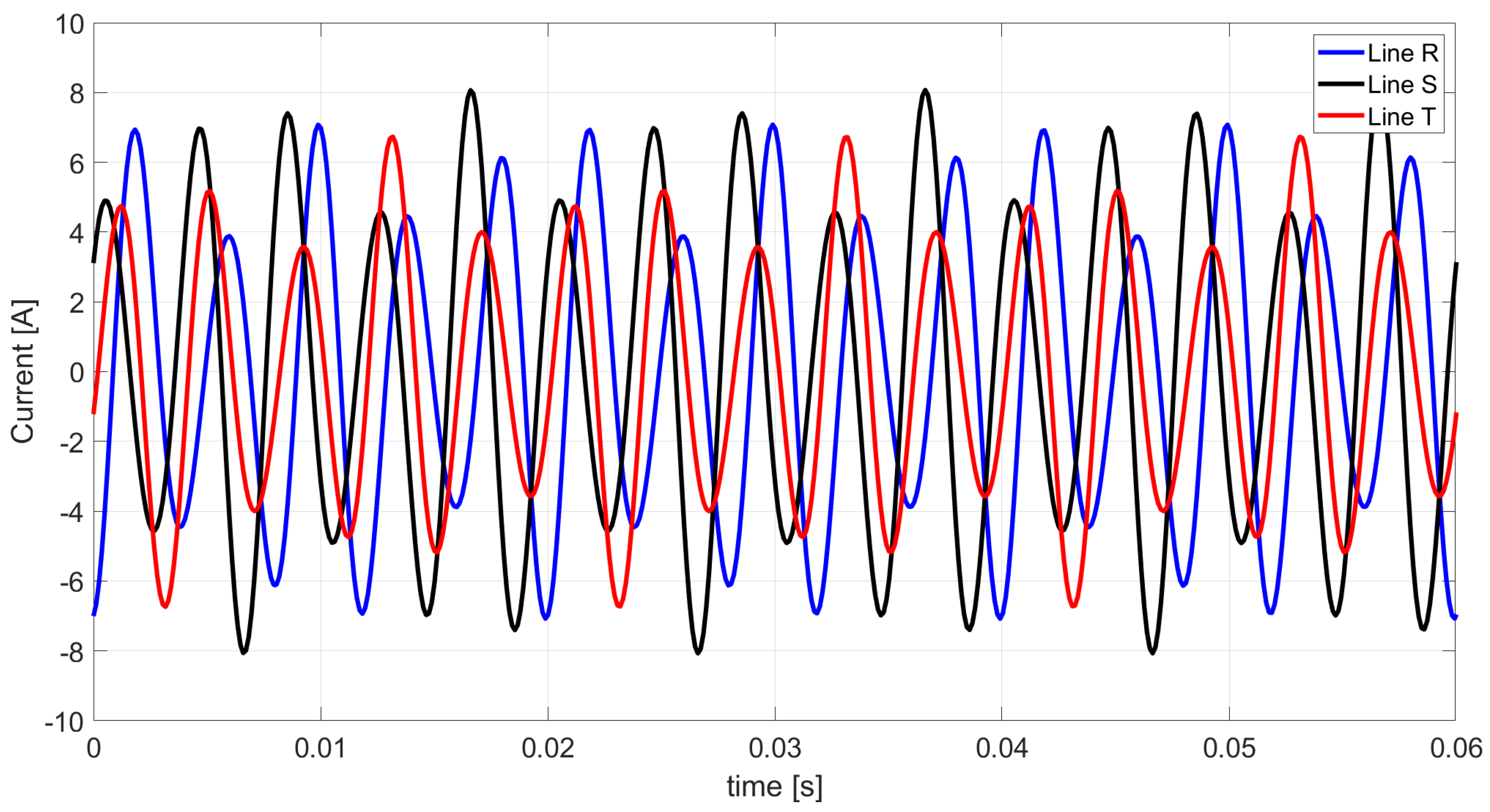
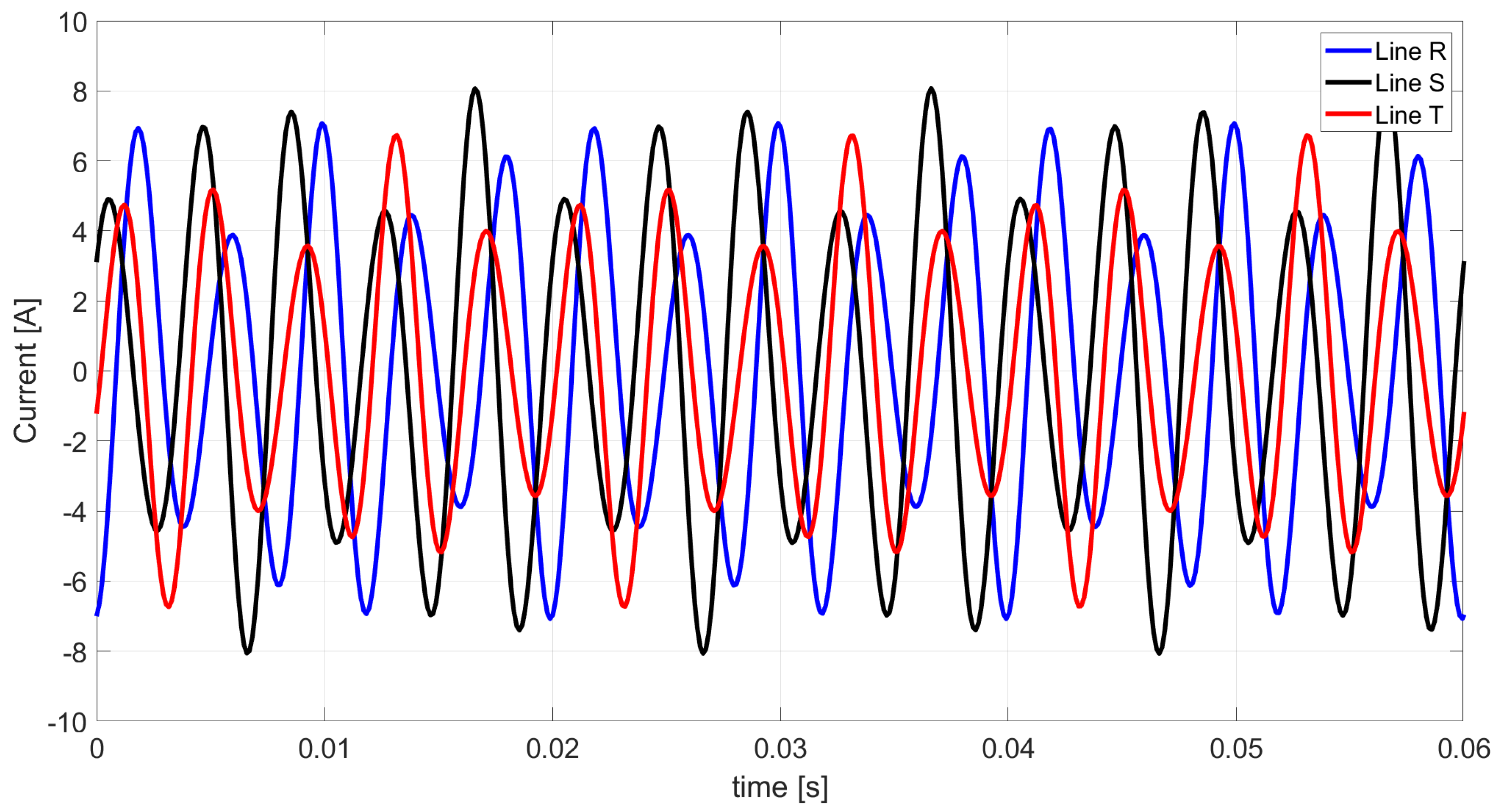
Figure 5.
Budeanu distortion current based on the extended Budeanu theory.
Figure 5.
Budeanu distortion current based on the extended Budeanu theory.
Figure 6.
View of the primary circuit with the connected compensator responsible for the perfect compensation of the Budeanu complemented reactive current and the unbalanced current.
Figure 6.
View of the primary circuit with the connected compensator responsible for the perfect compensation of the Budeanu complemented reactive current and the unbalanced current.
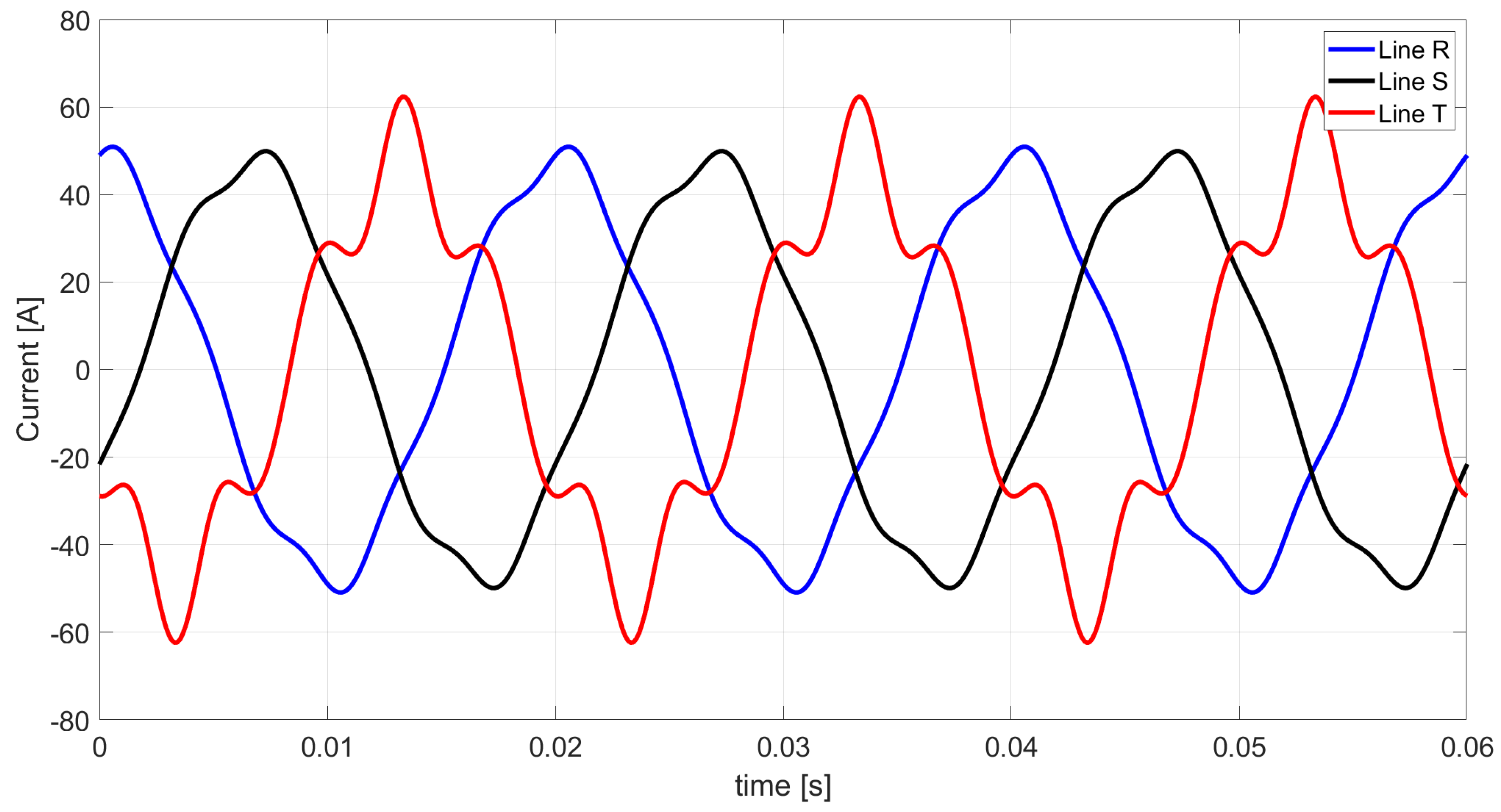
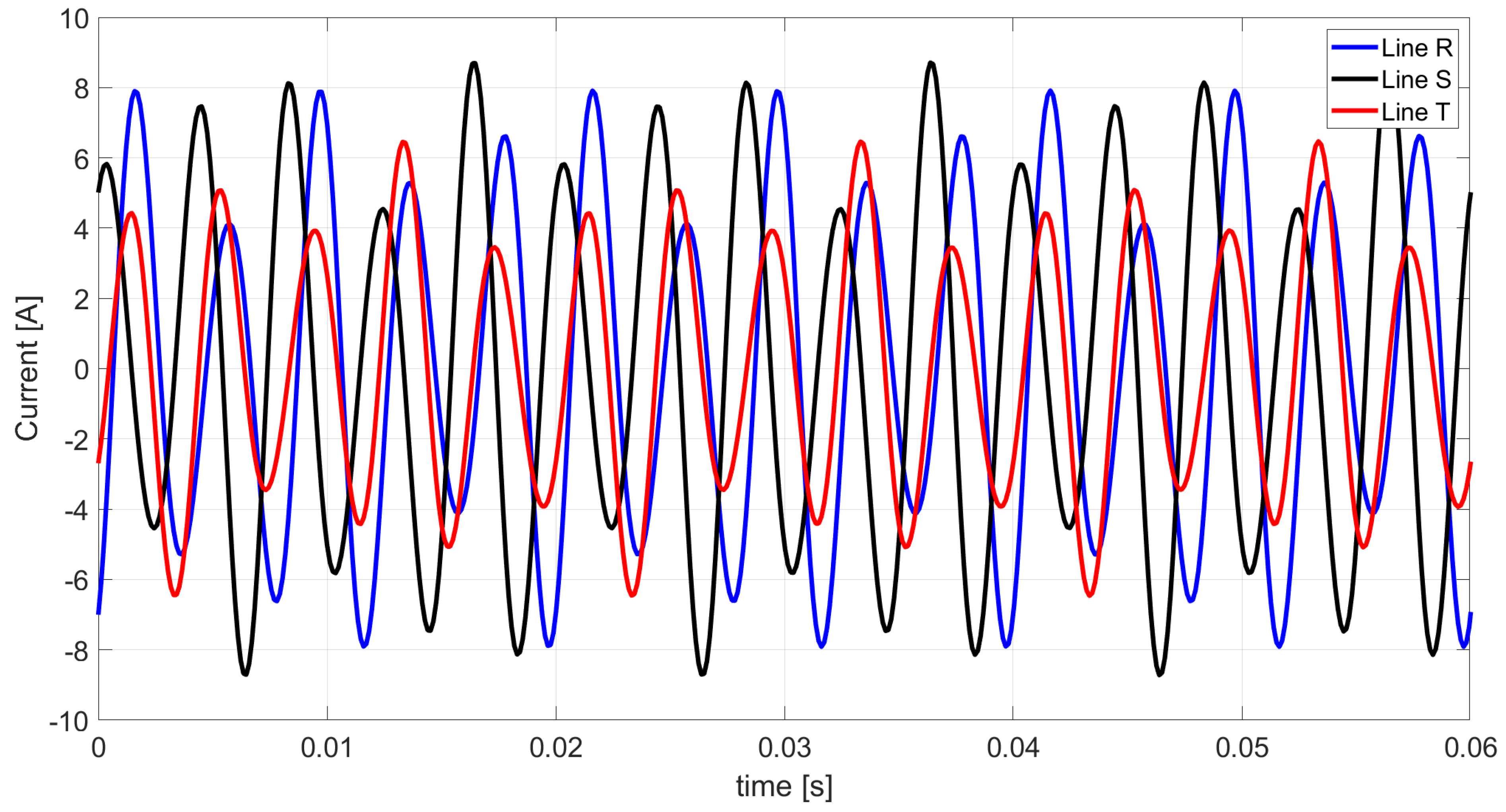
Figure 7.
Waveform of the obtained line currents after connecting the compensator of the Budeanu complemented reactive current and the unbalanced current.
Figure 7.
Waveform of the obtained line currents after connecting the compensator of the Budeanu complemented reactive current and the unbalanced current.
Figure 8.
Budeanu distortion current waveform according to extended Budeanu theory after compensation of the Budeanu complemented reactive current and the unbalanced current.
Figure 8.
Budeanu distortion current waveform according to extended Budeanu theory after compensation of the Budeanu complemented reactive current and the unbalanced current.
Figure 9.
View of the primary circuit with the compensator attached, which is responsible for minimizing the Budeanu complemented reactive current and the unbalanced current.
Figure 9.
View of the primary circuit with the compensator attached, which is responsible for minimizing the Budeanu complemented reactive current and the unbalanced current.
Figure 10.
Waveform of the obtained line currents after installing a compensator to minimize the Budeanu complemented reactive current and the unbalanced current.
Figure 10.
Waveform of the obtained line currents after installing a compensator to minimize the Budeanu complemented reactive current and the unbalanced current.
Figure 11.
Budeanu distortion current waveform according to the extended Budeanu theory after minimizing the Budeanu complemented reactive current and the unbalanced current.
Figure 11.
Budeanu distortion current waveform according to the extended Budeanu theory after minimizing the Budeanu complemented reactive current and the unbalanced current.
Figure 12.
View of the receiver with the attached compensator responsible for perfect compensation of the Budeanu reactive current and the unbalanced current.
Figure 12.
View of the receiver with the attached compensator responsible for perfect compensation of the Budeanu reactive current and the unbalanced current.
Figure 13.
Waveform of line currents obtained after connecting an ideal Budeanu reactive current and the unbalanced current compensator.
Figure 13.
Waveform of line currents obtained after connecting an ideal Budeanu reactive current and the unbalanced current compensator.
Figure 14.
Budeanu distortion current waveform according to the extended Budeanu theory after optimal compensation of the Budeanu reactive current and the unbalanced current.
Figure 14.
Budeanu distortion current waveform according to the extended Budeanu theory after optimal compensation of the Budeanu reactive current and the unbalanced current.
Figure 15.
View of the primary system with the connected compensator responsible for minimizing compensation of the Budeanu reactive current and the unbalanced current.
Figure 15.
View of the primary system with the connected compensator responsible for minimizing compensation of the Budeanu reactive current and the unbalanced current.
Figure 16.
Waveform of obtained line currents after including a compensator to minimize the Budeanu reactive current and the unbalanced current.
Figure 16.
Waveform of obtained line currents after including a compensator to minimize the Budeanu reactive current and the unbalanced current.
Figure 17.
Budeanu distortion current waveform according to the extended Budeanu theory after minimizing the Budeanu reactive current and the unbalanced current.
Figure 17.
Budeanu distortion current waveform according to the extended Budeanu theory after minimizing the Budeanu reactive current and the unbalanced current.
Figure 18.
View of the primary circuit with the attached compensator responsible for perfect compensation of the Budeanu reactive currents and the unbalanced current.
Figure 18.
View of the primary circuit with the attached compensator responsible for perfect compensation of the Budeanu reactive currents and the unbalanced current.
Figure 19.
Waveform of the obtained line currents after including an ideal compensator of the Budeanu reactive currents and the unbalanced current.
Figure 19.
Waveform of the obtained line currents after including an ideal compensator of the Budeanu reactive currents and the unbalanced current.
Figure 20.
Budeanu distortion current waveform according to the extended Budeanu theory after ideal compensation of the Budeanu reactive currents and the unbalanced current.
Figure 20.
Budeanu distortion current waveform according to the extended Budeanu theory after ideal compensation of the Budeanu reactive currents and the unbalanced current.
Figure 21.
View of the primary system with the connected compensator responsible for minimizing the Budeanu reactive currents and the unbalanced current.
Figure 21.
View of the primary system with the connected compensator responsible for minimizing the Budeanu reactive currents and the unbalanced current.
Figure 22.
Waveform of the obtained line currents after including a compensator to minimize the Budeanu reactive currents and the unbalanced current.
Figure 22.
Waveform of the obtained line currents after including a compensator to minimize the Budeanu reactive currents and the unbalanced current.
Figure 23.
Budeanu distortion current waveform according to the extended Budeanu theory after minimizing the Budeanu reactive currents and the unbalanced current.
Figure 23.
Budeanu distortion current waveform according to the extended Budeanu theory after minimizing the Budeanu reactive currents and the unbalanced current.
Table 1.
Summary of the currents and component powers based on the extended Budeanu theory.
Table 1.
Summary of the currents and component powers based on the extended Budeanu theory.
| Components | Quantity | Time Waveform | Three-Phase RMS Value |
|---|
| Active | Current | | |
| Power | - | |
| Scattered | Current | | |
| Power | - | |
| Budeanu reactive | Current | | |
| Power | - | |
| Budeanu complemented reactive | Current | | |
| Power | - | |
| Positive-sequence unbalanced | Current | | |
| Power | - | |
| Negative-sequence unbalanced | Current | | |
| Power | - | |
| Zero-sequence unbalanced | Current | | |
| Power | - | |
Table 2.
Summary of resistance, capacitive reactance, and inductive reactance values for the fundamental harmonics.
Table 2.
Summary of resistance, capacitive reactance, and inductive reactance values for the fundamental harmonics.
| Parameter in | R-Line | S-Line | T-Line |
|---|
| Resistance | 4 | 4 | 4 |
| Inductive reactance | 3.142 | 6.283 | - |
| Capacitive reactance | - | - | 1.592 |
Table 3.
Summary of three-phase active power and reactive power values of specific harmonics and the overall three-phase active power and reactive power of the entire system.
Table 3.
Summary of three-phase active power and reactive power values of specific harmonics and the overall three-phase active power and reactive power of the entire system.
| Harmonic Order | Active Power P in [W] | Reactive Power QB in [VAr] |
|---|
| n = 1 | 23,411 | 7872.5 |
| n = 3 | 7.4 | 2.7 |
| n = 5 | 240.9 | 64.2 |
| n = 7 | 6.5 | 1.3 |
| SUM | 23,665.8 | 7940.7 |
Table 4.
Summary of three-phase RMS values of component currents for individual harmonics described in the extended Budeanu theory.
Table 4.
Summary of three-phase RMS values of component currents for individual harmonics described in the extended Budeanu theory.
Harmonic
Order | | | | | | | |
|---|
| n = 1 | 58.358 | 0.409 | 19.581 | 0.180 | 0 | 39.270 | 21.599 |
| n = 3 | 1.269 | 0.418 | 0.426 | 0.114 | 0.822 | 0.587 | 0 |
| n = 5 | 7.612 | 2.976 | 2.554 | 1.318 | 3.832 | 0 | 4.745 |
| n = 7 | 1.269 | 0.520 | 0.426 | 0.274 | 0 | 0.774 | 0.663 |
| RMS | 58.880 | 3.077 | 19.756 | 1.363 | 3.920 | 39.282 | 22.124 |
Table 5.
Components of the distortion current described in extended Budeanu theory.
Table 5.
Components of the distortion current described in extended Budeanu theory.
Harmonic
Order | | | | | | |
|---|
| n = 1 | 0.409 | 0.180 | 0 | 39.270 | 21.599 | |
| n = 3 | 0.418 | 0.114 | 0.822 | 0.587 | 0 |
| n = 5 | 2.976 | 1.318 | 3.832 | 0 | 4.745 |
| n = 7 | 0.520 | 0.274 | 0 | 0.774 | 0.663 |
| RMS | 3.077 | 1.363 | 3.920 | 39.282 | 22.124 | 45.379 |
Table 6.
Summary of capacitance and inductance values required to compensate for the Budeanu complemented reactive current and the unbalanced current for a compensator with a star structure.
Table 6.
Summary of capacitance and inductance values required to compensate for the Budeanu complemented reactive current and the unbalanced current for a compensator with a star structure.
| Line | Harmonic Order |
|---|
| n = 1 | n = 3 | n = 5 | n = 7 |
|---|
| C [µF] | L [mH] | C [µF] | L [mH] | C [µF] | L [mH] | C [µF] | L [mH] |
|---|
| R | - | 297.58 | 187.1 | - | 96.61 | - | - | 3.08 |
| S | 316.53 | - | - | 8.98 | - | 4.18 | 51.22 | - |
| T | - | 36.43 | - | 10.88 | - | 8.44 | - | 7.59 |
Table 7.
Summary of capacitance and inductance values required to compensate for the Budeanu complemented reactive current and the unbalanced current for a delta-structure compensator.
Table 7.
Summary of capacitance and inductance values required to compensate for the Budeanu complemented reactive current and the unbalanced current for a delta-structure compensator.
| Line | Harmonic Order |
|---|
| n = 1 | n = 3 | n = 5 | n = 7 |
|---|
| C [µF] | L [mH] | C [µF] | L [mH] | C [µF] | L [mH] | C [µF] | L [mH] |
|---|
| RS | 101.10 | - | - | - | - | 147.2 | 1.04 | - |
| ST | - | 57.54 | - | - | 59.90 | - | - | 4.78 |
| TR | 74.99 | - | - | - | - | 7.09 | 42.21 | - |
Table 8.
Summary of three-phase active power and reactive power values of individual harmonics and total three-phase active power and reactive power of the whole system after compensation of the Budeanu complemented reactive current and the unbalanced current.
Table 8.
Summary of three-phase active power and reactive power values of individual harmonics and total three-phase active power and reactive power of the whole system after compensation of the Budeanu complemented reactive current and the unbalanced current.
| Harmonic Order | Active Power P in [W] | Reactive Power QB in [VAr] |
|---|
| n = 1 | 23,411 | 7800.6 |
| n = 3 | 7.4 | 3.7 |
| n = 5 | 240.9 | 132.7 |
| n = 7 | 6.5 | 3.7 |
| SUM | 23,665.8 | 7940.7 |
Table 9.
Summary of the three-phase RMS values of the currents’ components for the individual harmonics described in the extended Budeanu theory after compensation of the Budeanu complemented reactive current and the unbalanced current.
Table 9.
Summary of the three-phase RMS values of the currents’ components for the individual harmonics described in the extended Budeanu theory after compensation of the Budeanu complemented reactive current and the unbalanced current.
Harmonic
Order | | | | | | | |
|---|
| n = 1 | 58.358 | 0.409 | 19.581 | 0 | 0 | 0 | 0 |
| n = 3 | 1.269 | 0.418 | 0.426 | 0 | 0 | 1.285 | 0 |
| n = 5 | 7.612 | 2.976 | 2.554 | 0 | 0 | 0 | 0 |
| n = 7 | 1.269 | 0.520 | 0.426 | 0 | 0 | 0 | 0 |
| RMS | 58.880 | 3.077 | 19.756 | 0 | 0 | 1.285 | 0 |
Table 10.
Components of the distortion current defined in extended Budeanu theory.
Table 10.
Components of the distortion current defined in extended Budeanu theory.
Harmonic
Order | | | | | | |
|---|
| n = 1 | 0.409 | 0 | 0 | 0 | 0 | |
| n = 3 | 0.418 | 0 | 0 | 1.285 | 0 |
| n = 5 | 2.976 | 0 | 0 | 0 | 0 |
| n = 7 | 0.520 | 0 | 0 | 0 | 0 |
| RMS | 3.077 | 0 | 0 | 1.285 | 0 | 3.335 |
Table 11.
Summary of capacitance and inductance values necessary to minimize the Budeanu complemented reactive current and the unbalanced current for a compensator with a star structure and delta structure.
Table 11.
Summary of capacitance and inductance values necessary to minimize the Budeanu complemented reactive current and the unbalanced current for a compensator with a star structure and delta structure.
| Parameter | Configuration |
|---|
| Star | Delta |
|---|
| R | S | T | RS | ST | TR |
|---|
| L [mH] | 313.46 | 72.75 | 36.34 | 227.76 | 57.91 | 307.07 |
| C [µF] | - | 96.72 | - | 30.89 | - | 22.92 |
Table 12.
Summary of three-phase active power and reactive power values of individual harmonics and total three-phase active power and reactive power of the whole system after compensation of the Budeanu complemented reactive current and the unbalanced current.
Table 12.
Summary of three-phase active power and reactive power values of individual harmonics and total three-phase active power and reactive power of the whole system after compensation of the Budeanu complemented reactive current and the unbalanced current.
| Harmonic Order | Active Power P in [W] | Reactive Power QB in [VAr] |
|---|
| n = 1 | 23,411 | 7724.5 |
| n = 3 | 7.4 | 4 |
| n = 5 | 240.9 | 133.8 |
| n = 7 | 6.5 | 2.7 |
| SUM | 23,665.8 | 7865 |
Table 13.
Summary of the 3-phase RMS values of the currents’ components for the individual harmonics described in the extended Budeanu theory after minimizing the Budeanu complemented reactive current and the unbalanced current.
Table 13.
Summary of the 3-phase RMS values of the currents’ components for the individual harmonics described in the extended Budeanu theory after minimizing the Budeanu complemented reactive current and the unbalanced current.
Harmonic
Order | | | | | | | |
|---|
| n = 1 | 58.358 | 0.409 | 19.394 | 0.004 | 0 | 0.058 | 0.089 |
| n = 3 | 1.269 | 0.418 | 0.422 | 0.035 | 0.767 | 0.601 | 0 |
| n = 5 | 7.612 | 2.976 | 2.530 | 0.045 | 4.252 | 0 | 4.586 |
| n = 7 | 1.269 | 0.520 | 0.422 | 0.112 | 0 | 0.706 | 0.671 |
| RMS | 58.880 | 3.077 | 19.568 | 0.126 | 4.321 | 0.930 | 4.637 |
Table 14.
Components of the distortion current defined in extended Budeanu theory.
Table 14.
Components of the distortion current defined in extended Budeanu theory.
Harmonic
Order | | | | | | |
|---|
| n = 1 | 0.409 | 0.004 | 0 | 0.058 | 0.089 | |
| n = 3 | 0.418 | 0.035 | 0.767 | 0.601 | 0 |
| n = 5 | 2.976 | 0.045 | 4.252 | 0 | 4.586 |
| n = 7 | 0.520 | 0.112 | 0 | 0.706 | 0.671 |
| RMS | 3.077 | 0.126 | 4.321 | 0.930 | 4.637 | 7.108 |
Table 15.
Summary of capacitance and inductance values required to compensate for the Budeanu reactive current and the unbalanced current for a compensator with a star structure.
Table 15.
Summary of capacitance and inductance values required to compensate for the Budeanu reactive current and the unbalanced current for a compensator with a star structure.
| Line | Harmonic Order |
|---|
| n = 1 | n = 3 | n = 5 | n = 7 |
|---|
| C [µF] | L [mH] | C [µF] | L [mH] | C [µF] | L [mH] | C [µF] | L [mH] |
|---|
| R | 120.97 | - | 253.2 | - | 144.06 | - | - | 6.79 |
| S | 471.5 | - | - | 18.97 | - | 8.17 | 87.98 | - |
| T | - | 82.28 | - | 30.08 | - | 721.02 | 95.31 | - |
Table 16.
Summary of capacitance and inductance values required to compensate for the Budeanu reactive current and the unbalanced current for a delta-structure compensator.
Table 16.
Summary of capacitance and inductance values required to compensate for the Budeanu reactive current and the unbalanced current for a delta-structure compensator.
| Line | Harmonic Order |
|---|
| n = 1 | n = 3 | n = 5 | n = 7 |
|---|
| C [µF] | L [mH] | C [µF] | L [mH] | C [µF] | L [mH] | C [µF] | L [mH] |
|---|
| RS | 101.10 | - | - | - | - | 147.20 | 1.04 | - |
| ST | - | 57.54 | - | - | 59.90 | - | - | 4.78 |
| TR | 74.99 | - | - | - | - | 7.09 | 42.21 | - |
Table 17.
Summary of three-phase power values of individual harmonics and total three-phase power values of the whole system after ideal compensation of the Budeanu reactive current and the unbalanced current.
Table 17.
Summary of three-phase power values of individual harmonics and total three-phase power values of the whole system after ideal compensation of the Budeanu reactive current and the unbalanced current.
| Harmonic Order | Active Power P in [W] | Reactive Power QB in [VAr] |
|---|
| n = 1 | 23,411 | 71.9 |
| n = 3 | 7.4 | −1 |
| n = 5 | 240.9 | −68.5 |
| n = 7 | 6.5 | −2.4 |
| SUM | 23,665.8 | 0 |
Table 18.
Components of the currents for individual harmonics described in the extended Budeanu theory after ideal compensation of the Budeanu reactive current and the unbalanced current.
Table 18.
Components of the currents for individual harmonics described in the extended Budeanu theory after ideal compensation of the Budeanu reactive current and the unbalanced current.
Harmonic
Order | | | | | | | |
|---|
| n = 1 | 58.358 | 0.409 | 0 | 0.180 | 0 | 0 | 0 |
| n = 3 | 1.269 | 0.418 | 0 | 0.114 | 0 | 1.285 | 0 |
| n = 5 | 7.612 | 2.976 | 0 | 1.318 | 0 | 0 | 0 |
| n = 7 | 1.269 | 0.520 | 0 | 0.274 | 0 | 0 | 0 |
| RMS | 58.880 | 3.077 | 0 | 1.363 | 0 | 1.285 | 0 |
Table 19.
Summary of the three-phase RMS values of the components of the distortion current defined in extended Budeanu theory.
Table 19.
Summary of the three-phase RMS values of the components of the distortion current defined in extended Budeanu theory.
Harmonic
Order | | | | | | |
|---|
| n = 1 | 0.409 | 0.180 | 0 | 0 | 0 | |
| n = 3 | 0.418 | 0.114 | 0 | 1.285 | 0 |
| n = 5 | 2.976 | 1.318 | 0 | 0 | 0 |
| n = 7 | 0.520 | 0.274 | 0 | 0 | 0 |
| RMS | 3.077 | 1.363 | 0 | 1.285 | 0 | 3.602 |
Table 20.
Summary of capacitance and inductance values necessary to minimize the Budeanu reactive current and the unbalanced current for a compensator with a star structure and a delta structure.
Table 20.
Summary of capacitance and inductance values necessary to minimize the Budeanu reactive current and the unbalanced current for a compensator with a star structure and a delta structure.
| Parameter | Configuration |
|---|
| Star | Delta |
|---|
| R | S | T | RS | ST | TR |
|---|
| L [mH] | 190.36 | 48.83 | 82.33 | 227.76 | 57.91 | 307.07 |
| C [µF] | 36.95 | 144.09 | - | 30.89 | - | 22.92 |
Table 21.
Summary of three-phase power values of individual harmonics and total three-phase power values of the whole system after minimizing balancing compensation of the Budeanu reactive current and the unbalanced current.
Table 21.
Summary of three-phase power values of individual harmonics and total three-phase power values of the whole system after minimizing balancing compensation of the Budeanu reactive current and the unbalanced current.
| Harmonic Order | Active Power P in [W] | Reactive Power QB in [VAr] |
|---|
| n = 1 | 23,411 | 14.5 |
| n = 3 | 7.4 | 3.8 |
| n = 5 | 240.9 | 130.4 |
| n = 7 | 6.5 | 2.6 |
| SUM | 23,665.8 | 151.4 |
Table 22.
Summary of the three-phase RMS values of the currents’ components for each harmonic described in the extended Budeanu theory after minimizing balancing compensation of the Budeanu reactive current and the unbalanced current.
Table 22.
Summary of the three-phase RMS values of the currents’ components for each harmonic described in the extended Budeanu theory after minimizing balancing compensation of the Budeanu reactive current and the unbalanced current.
Harmonic
Order | | | | | | | |
|---|
| n = 1 | 58.358 | 0.409 | 0.373 | 0.337 | 0 | 0.144 | 0.007 |
| n = 3 | 1.269 | 0.418 | 0.008 | 0.435 | 0.784 | 0.635 | 0 |
| n = 5 | 7.612 | 2.976 | 0.049 | 2.462 | 4.332 | 0 | 4.602 |
| n = 7 | 1.269 | 0.520 | 0.008 | 0.293 | 0 | 0.705 | 0.680 |
| RMS | 58.880 | 3.077 | 0.377 | 2.539 | 4.403 | 0.960 | 4.652 |
Table 23.
Components of the distortion current defined in extended Budeanu theory.
Table 23.
Components of the distortion current defined in extended Budeanu theory.
Harmonic
Order | | | | | | |
|---|
| n = 1 | 0.409 | 0.004 | 0 | 0.058 | 0.089 | |
| n = 3 | 0.418 | 0.035 | 0.767 | 0.601 | 0 |
| n = 5 | 2.976 | 0.045 | 4.252 | 0 | 4.586 |
| n = 7 | 0.520 | 0.112 | 0 | 0.706 | 0.671 |
| RMS | 3.077 | 0.126 | 4.321 | 0.930 | 4.637 | 7.607 |
Table 24.
Summary of capacitance and inductance values required for ideal compensation of the Budeanu reactive currents and the unbalanced current for a compensator with a star structure.
Table 24.
Summary of capacitance and inductance values required for ideal compensation of the Budeanu reactive currents and the unbalanced current for a compensator with a star structure.
| Line | Harmonic Order |
|---|
| n = 1 | n = 3 | n = 5 | n = 7 |
|---|
| C [µF] | L [mH] | C [µF] | L [mH] | C [µF] | L [mH] | C [µF] | L [mH] |
|---|
| R | 122.41 | - | 239.30 | - | 127.90 | - | - | 4.61 |
| S | 472.99 | - | - | 15.37 | - | 6.16 | 73.58 | - |
| T | - | 83.26 | - | 21.92 | - | 24.25 | - | 42.39 |
Table 25.
Summary of capacitance and inductance values required for perfect compensation of the Budeanu reactive currents and the unbalanced current for a delta-structure compensator.
Table 25.
Summary of capacitance and inductance values required for perfect compensation of the Budeanu reactive currents and the unbalanced current for a delta-structure compensator.
| Line | Harmonic Order |
|---|
| n = 1 | n = 3 | n = 5 | n = 7 |
|---|
| C [µF] | L [mH] | C [µF] | L [mH] | C [µF] | L [mH] | C [µF] | L [mH] |
|---|
| RS | 101.10 | - | - | - | - | 147.20 | 1.04 | - |
| ST | - | 57.54 | - | - | 59.90 | - | - | 4.78 |
| TR | 74.99 | - | - | - | - | 7.09 | 42.21 | - |
Table 26.
Summary of three-phase power values of specific harmonics and total three-phase power values of the whole system after perfect compensation of the Budeanu reactive currents and the unbalanced current.
Table 26.
Summary of three-phase power values of specific harmonics and total three-phase power values of the whole system after perfect compensation of the Budeanu reactive currents and the unbalanced current.
| Harmonic Order | Active Power P in [W] | Reactive Power QB in [VAr] |
|---|
| n = 1 | 23,411 | 0 |
| n = 3 | 7.4 | 0 |
| n = 5 | 240.9 | 0 |
| n = 7 | 6.5 | 0 |
| SUM | 23,665.8 | 0 |
Table 27.
Values of the components for individual harmonics described in the extended Budeanu theory after ideal compensation of the Budeanu reactive currents and the unbalanced current.
Table 27.
Values of the components for individual harmonics described in the extended Budeanu theory after ideal compensation of the Budeanu reactive currents and the unbalanced current.
Harmonic
Order | | | | | | | |
|---|
| n = 1 | 58.358 | 0.409 | 0 | 0 | 0 | 0 | 0 |
| n = 3 | 1.269 | 0.418 | 0 | 0 | 0 | 1.285 | 0 |
| n = 5 | 7.612 | 2.976 | 0 | 0 | 0 | 0 | 0 |
| n = 7 | 1.269 | 0.520 | 0 | 0 | 0 | 0 | 0 |
| RMS | 58.880 | 3.077 | 0 | 0 | 0 | 1.285 | 0 |
Table 28.
Components of the distortion current defined in extended Budeanu theory.
Table 28.
Components of the distortion current defined in extended Budeanu theory.
Harmonic
Order | | | | | | |
|---|
| n = 1 | 0.409 | 0 | 0 | 0 | 0 | |
| n = 3 | 0.418 | 0 | 0 | 1.285 | 0 |
| n = 5 | 2.976 | 0 | 0 | 0 | 0 |
| n = 7 | 0.520 | 0 | 0 | 0 | 0 |
| RMS | 3.077 | 0 | 0 | 1.285 | 0 | 3.335 |
Table 29.
Summary of capacitance and inductance values necessary to minimize the Budeanu reactive currents and the unbalanced current for a compensator with a star structure and a delta structure.
Table 29.
Summary of capacitance and inductance values necessary to minimize the Budeanu reactive currents and the unbalanced current for a compensator with a star structure and a delta structure.
| Parameter | Configuration |
|---|
| Star | Delta |
|---|
| R | S | T | RS | ST | TR |
|---|
| L [mH] | 188.12 | 48.69 | 83.11 | 227.76 | 57.91 | 307.07 |
| C [µF] | 37.39 | 144.53 | - | 30.89 | - | 22.92 |
Table 30.
Summary of three-phase power values of respective harmonics and total three-phase power values of the whole system after minimization of the Budeanu reactive currents and the unbalanced current.
Table 30.
Summary of three-phase power values of respective harmonics and total three-phase power values of the whole system after minimization of the Budeanu reactive currents and the unbalanced current.
| Harmonic Order | Active Power P in [W] | Reactive Power QB in [VAr] |
|---|
| n = 1 | 23,411 | −52.9 |
| n = 3 | 7.4 | 3.8 |
| n = 5 | 240.9 | 130.5 |
| n = 7 | 6.5 | 2.6 |
| SUM | 23,665.8 | 84 |
Table 31.
Currents’ components for respective harmonics described in the extended Budeanu theory after minimization of the Budeanu reactive currents and the unbalanced current.
Table 31.
Currents’ components for respective harmonics described in the extended Budeanu theory after minimization of the Budeanu reactive currents and the unbalanced current.
Harmonic
Order | | | | | | | |
|---|
| n = 1 | 58.358 | 0.409 | 0.207 | 0.340 | 0 | 0.138 | 0.009 |
| n = 3 | 1.269 | 0.418 | 0.005 | 0.439 | 0.784 | 0.635 | 0 |
| n = 5 | 7.612 | 2.976 | 0.027 | 2.484 | 4.333 | 0 | 4.602 |
| n = 7 | 1.269 | 0.520 | 0.005 | 0.297 | 0 | 0.705 | 0.680 |
| RMS | 58.880 | 3.077 | 0.209 | 2.562 | 4.403 | 0.959 | 4.652 |
Table 32.
Components of the distortion current defined in extended Budeanu theory.
Table 32.
Components of the distortion current defined in extended Budeanu theory.
Harmonic
Order | | | | | | |
|---|
| n = 1 | 0.409 | 0.207 | 0.340 | 0 | 0.138 | |
| n = 3 | 0.418 | 0.005 | 0.439 | 0.784 | 0.635 |
| n = 5 | 2.976 | 0.027 | 2.484 | 4.333 | 0 |
| n = 7 | 0.520 | 0.005 | 0.297 | 0 | 0.705 |
| RMS | 3.077 | 0.209 | 2.562 | 4.403 | 0.959 | 7.615 |
Table 33.
Summary of the three-phase RMS values for the currents’ components for the primary circuit and the circuits after the balancing minimization and perfect compensation are performed.
Table 33.
Summary of the three-phase RMS values for the currents’ components for the primary circuit and the circuits after the balancing minimization and perfect compensation are performed.
| Component | Original System | Approach | |
|---|
| I | II | III |
|---|
| Ideal | Mini | Ideal | Mini | Ideal | Mini |
|---|
| 58.880 | 58.880 | 58.880 | 58.880 | 58.880 | 58.880 | 58.880 |
| 3.077 | 3.077 | 3.077 | 3.077 | 3.077 | 3.077 | 3.077 |
| 19.756 | 19.756 | 19.568 | 0 | 0.377 | 0 | 0.209 |
| 1.363 | 0 | 0.126 | 1.363 | 2.539 | 0 | 2.562 |
| 3.920 | 0 | 4.321 | 0 | 4.403 | 0 | 4.403 |
| 39.282 | 1.285 | 0.930 | 1.285 | 0.960 | 1.285 | 0.959 |
| 22.124 | 0 | 4.637 | 0 | 4.652 | 0 | 4.652 |
| 45.379 | 3.335 | 7.108 | 3.602 | 7.607 | 3.335 | 7.615 |
| 76.918 | 62.195 | 62.452 | 58.990 | 59.370 | 58.974 | 59.371 |
Table 34.
Summary of power factors for all considered approaches with ideal compensation and minimizing balancing compensation.
Table 34.
Summary of power factors for all considered approaches with ideal compensation and minimizing balancing compensation.
| Component | Original System | Approach | |
|---|
| I | II | III |
|---|
| Ideal | Mini | Ideal | Mini | Ideal | Mini |
|---|
| 0.766 | 0.947 | 0.943 | 0.998 | 0.992 | 0.998 | 0.992 |
Table 35.
Summary of generalized costs spent on the parts for the construction of a compensator.
Table 35.
Summary of generalized costs spent on the parts for the construction of a compensator.
| Component | Original System | Cost of Approach [u] | |
|---|
| I | II | III |
|---|
| Ideal | Mini | Ideal | Mini | Ideal | Mini |
|---|
| choke | - | 12 | 6 | 10 | 6 | 11 | 6 |
| capacitor | - | 4.5 | 1.5 | 5.5 | 2 | 5 | 2 |
| SUM | - | 16.5 | 7.5 | 15.5 | 8 | 16 | 8 |