Abstract
Heat pumps play a crucial role in decarbonizing buildings, yet conventional control strategies limit their grid-supportive potential. Model Predictive Control (MPC) offers a promising alternative to optimize energy costs and grid performance, but real-world implementations remain scarce. This study demonstrates the feasibility of MPC in a low-energy, non-residential building by integrating a controller based on electricity market prices. The system, deployed on a Raspberry Pi and integrated into the building automation system, utilizes weather forecasts and a grey-box model for load prediction. A key challenge is the lack of standardized interfaces for heat pump controls, requiring custom solutions. A 7-day performance analysis compares MPC with conventional control, focusing on economic efficiency and grid support. MPC shifts heat pump operation to periods of lower electricity prices, increasing storage temperatures and reducing the average COP from 7.6 to 6.0. Despite this, energy costs decrease by 40%, lowering the electricity procurement price from 0.36 EUR to 0.12 EUR/kWh, while the Grid Support Coefficient improves by 13%. These results confirm that MPC can enhance heat pump operation with simple component models, provided the system allows flexibility and demand is predictable.
1. Introduction
In the context of global energy transitions, achieving carbon neutrality by 2050 is a shared goal among many countries. One strategy to reduce reliance on fossil fuels is the adoption of heat pumps. Heat pumps, as a cornerstone of modern HVAC systems, play a crucial role in minimizing the carbon footprint of buildings by utilizing renewable energy sources and enhancing overall energy efficiency [1].
A 2022 study indicates that the global heat pump market has experienced significant growth, with notable increases in 2021 [2]. For instance, the European market saw a 34% rise, surpassing 2 million units sold, while China’s market grew by 7%, reaching 12.5 million units. The U.S. market also expanded, with a 15% increase in sales. Although the European Heat Pump Association found that in 2023 sales in the European marked dropped by 6.5% compared to 2022 [3], this still shows a strong overall demand for heat pump systems. This growth is driven by policy incentives, technological advancements, and increasing energy prices.
However, the increasing number of heat pumps poses challenges for the existing power grid. In Germany, the Federal Network Agency (Bundesnetzagentur), which plays a vital role in supporting the integration of renewable energy into the power grid, has recognized the need to address the grid challenges posed by the rising number of heat pumps and other controllable consumption devices. In their key issues paper, they outline measures to ensure the stability and efficiency of the power grid in the face of increasing demand [4]. This highlights the importance of sophisticated control strategies in managing the grid impact of widespread heat pump adoption.
Model Predictive Control (MPC) has emerged as a particularly promising approach for optimizing the performance of heat pumps in buildings [5]. MPC leverages predictive models to forecast future system behavior and make real-time adjustments, thus achieving significant cost reductions and load-shifting benefits [6]. Component-wise control strategies, in contrast, rely on predefined rules or setpoints without considering the overall system’s interactions or future states, therefore resulting in higher operational costs and a lack of effective load shifting [7]. By utilizing MPC, heat pump systems have the potential to more effectively balance thermal comfort, energy consumption, and cost, aligning with both economic and environmental objectives [8]. This strategy not only enhances the efficiency of the heat pumps but also contributes to grid stability by facilitating demand-side management (DSM) [9].
There is an increasing interest in this field, indicating a shift towards smarter energy consumption practices. For example, the German Heat Pump Association created the SG-Ready label, which identifies heat pumps that can be controlled via a defined interface for the purpose of DSM [10].
Thermal Energy Storage (TES) provides additional potential for load shifting, though active TES (e.g., hot water tanks, ice tanks) are not always necessary for achieving significant benefits with MPC [11]. Recent advancements in Latent Heat Thermal Energy Storage (LHTES) have demonstrated its ability to balance thermal supply with load demand [12]. Additionally, a recent case study on the integration of Ice Thermal Energy Storage (ITES) has shown its potential to avoid times of electrical peak prices [13]. Thermal Activated Building Systems (TABS) also offer additional storage capacity as passive TES [14], although their operation can be challenging due to delayed response times [15].
Table 1 summarizes relevant research in this field, clustered into the categories of technology, building type, and application.
Most existing studies on MPC have applied it in small-scale experimental setups in the lab or simulated real-world applications, with only a few studies implementing MPC in real buildings. For example, Thorsteinsson et al. (2023) conducted a long-term experimental study of MPC in a real, occupied single-family house with a heat pump, demonstrating its potential for DSM through load shifting even without a thermal energy storage [16]. Carli et al. (2019) conducted a study on the optimal regulation of an HVAC system while maintaining thermal comfort using an MPC approach, which was tested in an office building in Bari, Italy [17].
This research aims to bridge the gap between theoretical advancements and practical applications of MPC for heat pumps in low-energy buildings. By evaluating heat pump system performance, the paper seeks to contribute to the growing body of knowledge on MPC applications in building energy systems. Fischer and Madani (2017) concluded that this transfer from simulation approaches to actual applications in the field should be the topic of future research [1].
Further, the literature survey shows that most studies evaluate the performance of MPC by focusing on economic parameters. This work achieves a degree of novelty by not only evaluating and quantifying the operational cost savings but also the benefits for the electrical grid by introducing a Grid Support Coefficient (GSC) as proposed by Klein et al. (2016) [18].
Following these considerations, the primary aim of this research is to evaluate and quantify the effect of MPC on system performance, economic efficiency, and grid support compared to conventional operation.
This paper begins by introducing the demonstration building, RIZ Energie, a low-energy commercial building located in Offenburg, Germany, which is equipped with advanced heating systems, including a water-to-water heat pump, TES, and TABS. The following section describes the design and implementation of the MPC, which optimizes heat pump operation using weather forecasts, electricity market prices, and a grey-box model for load predictions. Contrary to the more complex and computationally intensive implementations employed in recent studies, this algorithm is run on a single-board computer (Raspberry Pi) using simple component models and a straightforward MPC formulation.
Next, the experimental setup is outlined, detailing the real-time integration of the MPC into the building automation system and the methods used to evaluate its performance over the period of one week compared to the conventional operation. Finally, the results are presented, showing significant reductions in energy-related costs and improvements in grid support, followed by a discussion of the challenges and broader applicability of using MPC in real-world systems.


Table 1.
Overview of recent studies regarding MPC applications in building energy systems (HP = heat pump, TES = thermal energy storage, PV = photovoltaic system, FHS = floor heating system, HVAC = heating, ventilation and air conditioning system, LV = low voltage, OF = outdoor fan, DHS = district heating system, SFH = single-family home, MFH = multi-family home).
Table 1.
Overview of recent studies regarding MPC applications in building energy systems (HP = heat pump, TES = thermal energy storage, PV = photovoltaic system, FHS = floor heating system, HVAC = heating, ventilation and air conditioning system, LV = low voltage, OF = outdoor fan, DHS = district heating system, SFH = single-family home, MFH = multi-family home).
| Paper | System | Cost Function | Application | Building Type | Performance |
|---|---|---|---|---|---|
| Patteeuw et al., 2016 [9] | HP | operational cost | simulation | MFH | 60% to 90% cost saving |
| Arabzadeh et al., 2018 [19] | HP, TES, PV and heating | energy cost | simulation | MFH | cost reduction of up to 12% |
| Viot et al., 2018 [15] | FHS in an experimental room | thermal comfort and cost estimation | experimental | experimental room | energy savings close to 40% |
| Carli et al., 2019 [17] | HVAC system | thermal comfort | real world application | non-residential | energy saving of 19.4% |
| D’Ettorre et al., 2019 [8] | HP, gas boiler, TES | energy costs | simulation | n.s. | reduction of energy cost up to 8% |
| Kuboth et al., 2019 [7] | HP, 2 TES, PV, battery | energy costs | simulation | SFH | cost reduction of 11.6% |
| Frison et al., 2019 [20] | HP, TES | energy costs, GSC | experimental | non-residential | cost saving of 5.7% and GSC improvement of 16% |
| Bechtel et al., 2020 [21] | HP, TES | energy costs | simulation | SFH | increased electricity consumption between 6.8% and 1.6% |
| Drgoňa, Picard, et al., 2020 [22] | HP, TABS, FHS, AHU, TES, gas boiler | energy usage and thermal comfort | real world application | non-residential | reduced energy usage by 53.5% and thermal comfort improvement by 36.9% |
| Kuboth et al., 2020 [23] | HP, TES, PV | energy costs | experimental | SFH | energy cost reduced by 9% |
| Löhr et al., 2021 [24] | HP, TES, PV, battery | PV self-consumption | experimental | n.s. | 11% more load shifting to times of PV generation |
| P. Sawant et al., 2021 [25] | LV grid, HP, OF, TES, Coil | energy costs | experimental | MFH | electricity cost savings of ca. 1.5% |
| Blum et al., 2022 [26] | HVAC system | energy usage | real world application | non-residential | 40% of energy usage reduction |
| Ma et al., 2022 [27] | Buildings with DHS | temperature accuracy | simulation | non-residential | ±0.5 K error of indoor temperature from set point temperature |
| Zhang et al., 2022 [28] | HVAC, PV, Battery | energy cost and/or power | real world application | non-residential | more than 10% energy cost savings |
| Baumann et al., 2023 [29] | HP, TES | energy costs | experimental | SFH | electric energy decreased by 12% and cost per unit electricity by 14% |
| Thorsteinsson et al., 2023 [16] | HP, PV | energy costs, CO2 production and thermal comfort | real world application | SFH | 2–17% cost reduction, depending on comfort level |
| Tang et al., 2024 [30] | HP, TES | flexibility assessment, flexibility exploitation | simulation | non-residential | reduced energy consumption by 2.6% and reduced energy cost by 3.2% |
2. Methodology
This chapter outlines the methodological approach adopted for implementing and evaluating MPC in a low-energy office building. The methodology involves the detailed modeling of building components, the integration of weather and electricity price predictions, and the deployment of the MPC system within the building’s existing automation system. The chapter also covers the specific experimental setup, which involves the real-time implementation of the MPC on a Raspberry Pi, enabling continuous monitoring and control of the heat pump.
2.1. Demonstration Building “RIZ Energie” and Heat Pump System
The MPC was implemented in the heating system of the low-energy building “RIZ Energie”. The building is located in Offenburg, Germany (see Figure 1) and is the newest building on the Offenburg University of Applied Sciences campus, containing offices and a technical center with different laboratories. The RIZ Energie building exemplifies a state-of-the-art commercial, non-residential low-energy building through its monovalent heat pump operation for heating and its integration into a commercial building automation system. Characterized by two heterogeneous usage zones—office and laboratory—this building presents challenges for load demand forecasting, mirroring common scenarios in similar applications, and is therefore deemed a suitable demonstration building.

Figure 1.
RIZ Energie building located in Offenburg, Germany.
The performance metrics of the RIZ Energie building (see Table 2) clearly demonstrate its low-energy standard. The final energy consumption, excluding energy generated by photovoltaic panels, amounts to 28.4 kWh/m2a, with a corresponding primary energy consumption of 50.0 kWh/m2a related to a heated surface area of 1706 m2.

Table 2.
System metrics of the RIZ Energie building.
A groundwater well provides the source for the heating and cooling system of the RIZ Energie building. In heating mode, the environmental energy from the well initially provides the heat source for the heat pump. A 75 kW heat exchanger separates the water circuits, preventing impurities from the well from entering the heat pump’s evaporator. Since the building’s heating systems require a supply temperature of 35–40 °C, the low-temperature groundwater must undergo an exergy increase, which is achieved through the heat pump.
The heating energy produced is temporarily stored in the thermal energy storage tank and then passed on to the TABS, the floor heating system (FHS), and the heating element in the air handling unit. The different TABS serve to heat and cool the three office floors and the technical center. In the offices, a distinction is made between a TABS in the middle layer of the concrete ceiling and a TABS close to the surface. The TABS in the middle layer is charged with a base heating load at night, which it then distributes to the rooms throughout the day. If there is an additional heating load requirement during daytime operation, the near-surface TABS are able to supply this additional heating load and quickly release it to the room due to its near-surface position. For this the TABS is fed with a supply temperature that is determined by the heating curve. A three-way valve after the thermal energy storage tank mixes the temperature in the tank with the returning circuit from the building to achieve the exact supply temperature needed. The TABS then charge the concrete ceilings of the office floors until the return temperature reaches a ± 0.5 K difference from the supply temperature. For the technical center, the same working principle applies for the FHS as for the TABS. A heat recovery system and heating element (which is also supplied by the storage tank) in the air handling unit heat up the supply air to a set point temperature of 20 °C.
At the same time, the environmental energy from the well is used as a source of cooling energy for process cooling in the technical center and for server cooling. Cooling is not considered further in the MPC, as it requires only electricity from the pumps and no compression stages via the heat pump.
Figure 2 shows a schematic representation of the heating concept, using a ground-water heat pump, a TES, and multiple TABS.
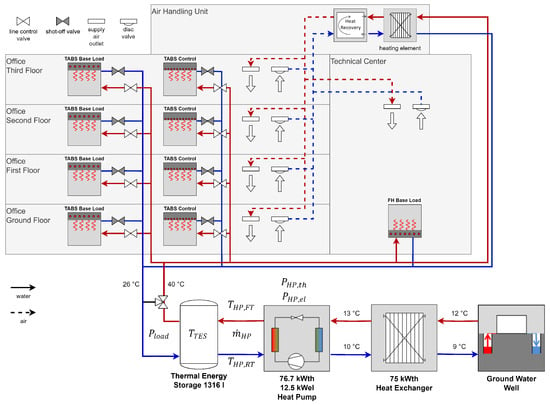
Figure 2.
Heating concept of the RIZ Energie building with temperature levels and temperature and energy variables (red = supply temperatures, blue = return temperatures).
2.2. Model Predictive Control (MPC)
2.2.1. MPC in Building Energy Systems
In building systems, MPC is typically used in closed control loops (see Figure 3). Here, represents the predicted actual states in the building, represents the predicted disturbances, such as weather conditions, and u denotes the control commands managed by the MPC. This approach ensures that the system continuously adapts to both internal states and external influences, optimizing the building operation in real-time.
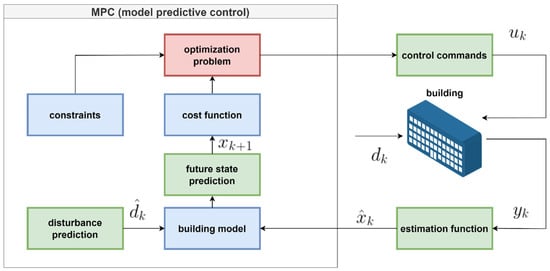
Figure 3.
General schematic representation of the control loop of an MPC control system in a building system.
The general MPC formulation for building systems according to Drgoňa et al. (2020) can be represented as shown in Equations (1)–(6) [31]:
In the mathematical formulation of the optimization problem in MPC, the objective function is initially defined as a minimization problem (see Equation (1)). Here, l represents the costs at each time step, the states, the measurements, and the input variables of the system for each time step of the prediction horizon . Equation (2) then describes the state transition from to as a function of , , and the disturbance . Equation (3) describes the prediction of the outputs , while Equation (4) shows how the building system inputs depending on the HVAC dynamics. Equation (5) describes the forecast of the disturbance signal . The initial conditions of the variables are defined in Equation (6) and correspond to the last measured state values. The states and input variables are subject to bounding constraints.
The constraints are defined in Equations (7) and (8):
The objective function is the control-independent variable to be minimized. In building applications, this typically considers thermal comfort, emissions, energy consumption or energy costs. For the latter, MPC often results in a strategy where energy is consumed during low-price periods to be used later, utilizing storage components like TES, batteries, or the thermal inertia of the building itself to shift peak loads to low-price periods. In this study the objective function is represented by Equation (9):
where is the energy consumed by the heat pump, is the day-ahead price of the electricity, is the final time of the time-dependent optimization problem, and the decision variable corresponds to the switching commands of the heat pump.
The optimization problem has a prediction horizon of 24 h and is executed every 15 min.
2.2.2. Implementation of MPC at Demonstration Building
The MPC was implemented entirely in Python 3.9.2 for this study. The advantage of the Python programming language is that it has numerous interfaces that enable communication with a wide variety of databases, libraries, and optimization algorithms with minimal programming effort. The structure of the model predictive controller is modular, i.e., the individual modules are programmed in their own scripts, which are called up in higher-level scripts. This has the advantage that individual modules are implemented gradually and can also be easily replaced in the further course of development.
The SCIP optimizer of the PySCIPOpt 4.2.0 library was selected as the optimizing algorithm [32]. Here the component models are formulated as boundary conditions and the cost function of the optimization problem is formulated from the predicted electrical power consumption of the heat pump. Since the optimization problem is a linear optimization problem, we used PySCIPOpt’s default solver SoPlex 6.0.3.
Choosing the right prediction horizon length is a balancing act. Most studies using MPC as an optimization method in a building energy system find 24 h to be an ideal trade-off between reliable predictions and optimization performance [33]. For this reason, a prediction horizon of 24 h with a control horizon of 15 min was selected for this work. The output of the MPC therefore consists of 24 h in 15-min steps, i.e., 96 control commands.
2.2.3. Heat Pump (HP)
The water-to-water heat pump is a Hoval Thermalia dual (55) with a nominal heat output of = 76.9 kW and a nominal input power of = 12.7 kW in accordance with the European norm EN 14511 [34]. Since the heat pump is operated in a quasi-static state, using the nominal power data, Equations (10) and (11) were formulated to calculate the thermal power output and the consumed electrical power of the heat pump. Equations (12) and (13) describe the condenser inlet and outlet temperature:
where is the thermal power output of the heat pump, is the electrical power consumption of the heat pump, is the decision variable of the heat pump, is the condenser inlet temperature, is the condenser outlet temperature, the nominal condenser mass flow is kg/s, and the specific heat capacity of water kJ/kgK.
2.2.4. Thermal Energy Storage (TES)
The thermal energy storage (TES) system has a capacity of VTES = 1316 L and is equipped with three temperature sensors.
There are many existing approaches for modeling TES in building systems that make it possible to model stratification behavior, such as described in Sawant et al. (2020) [35]. However, such modeling is often mathematically complex and requires the use of heuristic rule queries, such as for different charging and discharging directions. To implement a simple and fast optimizer, a simplified TES model with a single temperature for the entire storage tank was used instead, which was determined using a single energy balance of the system. For this purpose, it is assumed that the heat output of the heat pump and the consumed output of the load side at time correspond to the difference in the energy states of the storage tank at time + 1 and . Heat losses are neglected. Equation (14) was formulated for this purpose:
where the mean TES temperature is , the capacity of TES is = 1316 L, the specific heat capacity of water is kJ/kgK, the density of water is kg/m3, the thermal power output of HP is , and the thermal power consumption of the load side is .
2.2.5. System Boundaries
In addition to the two largest components of the central heating system, the surrounding temperatures and volume flows must also be modeled with sufficient accuracy. Furthermore, technical limitations of the system must also be formulated as boundary conditions of the optimization problem.
The data sheet for the heat pump shows that a maximum switch-on frequency of three times per hour must be considered. This limitation should also be adopted for the MPC control. As the control horizon is set at 15 min, no more than two switch-on processes per hour are possible anyway, which is why this limitation does not need to be explicitly modeled. Another technical limitation is the maximum flow temperature. The data sheet specifies a maximum condenser inlet temperature of 62 °C for water-to-water operation of the heat pump. This boundary condition is formulated as Equation (15):
where the maximum condenser inlet temperature is °C, is the condenser inlet temperature, and is the decision variable of the heat pump. The factor guarantees that the right-hand side of the equation is small enough to still fulfill the condition if the maximum flow temperature is exceeded.
Furthermore, a maximum storage temperature should be formulated for the heat storage tank. The flow temperatures of the TABS and heating coil consumers combined amount to a maximum of 37 °C. For this reason, the thermal store is usually charged to a maximum of 40 °C in conventional operation. However, since MPC operation is intended to be predictive, the storage tank must be able to store more thermal energy in advance than is required at that moment. For this reason, a maximum upper storage temperature of 50 °C was set. The value was not set higher because no such high temperatures were permitted in previous operation, and therefore no empirical values were available for how the system would react to the temperature increase. This boundary condition is formulated in the optimization problem as the following Equation (16):
where is the storage tank temperature at time and is the maximum storage tank temperature of 50 °C.
2.2.6. Price Prediction
Currently, there are no dynamic electricity tariffs in Germany in place for the building operator. The SMARD electricity market data portal (Bundesnetzagentur, 2024) provides dynamic predictions of electricity market prices for the next 24 h in Germany [36]. The electricity market distinguishes between term, day-ahead, and intraday prices. For the present application, day-ahead prices are considered, which are traded on the spot market for the following or current day, assuming that future dynamic tariffs will follow a similar price volatility and distribution. In general, the actual consumption and generation can be estimated more accurately as the delivery date approaches. Therefore, day-ahead prices are considered a good and reliable indicator of wholesale electricity market prices. Since the German market operates within a zonal tariff zone, the same price applies to the entire market area.
When integrated with the MPC system, the SMARD platform is utilized as a predictor for electricity prices. Web scraping is used to download the latest forecast at each iteration of the controller and feed it into the optimizer.
2.2.7. Heat Load Prediction
A simulation model of the RIZ Energie building is used for the load forecast of the MPC. This model was developed as part of the BUiLD.DIGITiZED research project and features a grey-box model that was parameterized using BIM methods and validated using measurement data [37,38]. In the model, the building is divided into five defined zones. Each floor of the office wing represents a zone, as does the technical center. For this purpose, zone-specific parameters are used, which are taken from the BIM model. The outputs of the model include the operative room temperatures for the individual zones, as well as the corresponding required heating and cooling loads.
The simulation model integrates a parameterized building model with system models of the air handling unit the TABS and the FHS. Calibration and validation were achieved by comparing simulation outputs with measured indoor climate and energy consumption data. The building model is based on a 5R1C model and is modified to replicate the behavior of the demonstration building [39]. To reflect the thermal inertia of TABS and enabling realistic modeling of heat exchange dynamics, the 5R1C model is altered by shifting the heating and cooling loads from the air node to the mass node. The model is implemented as a signal-flow-based process in Python (see Figure 4), where weather data and occupancy schedules serve as inputs. It operates linearly, with directed data flow between models, avoiding numerical iterations through simplified assumptions. The TABS control is modelled after the TABS and FHS working principles and the air handling unit is modelled after the air handling unit working principle described in Section 2.1. The output of the model is the required heat load data comprising the TABS, FHS, and air handling unit heat load, which serves as the load forecast for the MPC.
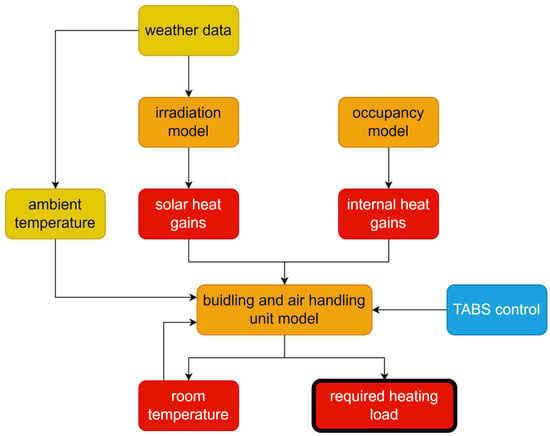
Figure 4.
Signal flow diagram of the grey-box simulation model of the building, with the predicted weather data as input and the required heating load as output (yellow = predicted data, orange = models, red = outputs, blue = control module).
2.2.8. Weather Prediction
The weather forecast represents the central disturbance variable of the control system in the context of the model predictive controller. Based on the weather forecast, the building model generates a heating load demand forecast for the observation period.
The MOSMIX weather forecasts were chosen as a suitable tool for this forecast [40]. They are a provided by the German Weather Service DWD for ca. 5400 locations. Numerous weather parameters, such as temperature and dew point at a height of 2 m, wind speed and direction, as well as radiation parameters, are predicted.
For application in the building model of the RIZ Energie building, only the temperature at a height of 2 m and global irradiance parameters were used from the MOSMIX API. The division of global radiation into direct and diffuse irradiance was carried out using Boland’s model [41]. To access the weather forecasts from MOSMIX within the MPC control loop, the corresponding DWD API wetterdienst 0.52.0 was used.
The location of the Ohlsbach weather station was chosen, as this is the geographically closest station to the RIZ Energie building at a distance of 6 km. The forecasts are available for 240 h into the future (i.e., 10 days) in hourly values. As both the building model and the MPC use a time step of 15 min, the MOSMIX forecasts are converted into 15-min steps by linear interpolation. Predictions for the next 24 h are considered, corresponding to the prediction horizon of the MPC.
2.3. Experimental Setup
The operation of the MPC is demonstrated in the heating system of the RIZ Energie building. For this purpose, the MPC controller is integrated into the existing building automation system.
2.3.1. Communication Structure
As Figure 5 shows, the building and the MPC are interconnected via the building’s monitoring system. The connection between building and monitoring system is realized via a gateway, which communicates with the building automation system (BAS) via BACnet. This is a bidirectional interface, as the monitoring system can read measurement data from the BAS as well as send switching commands corresponding to the variables and setpoints to the BAS. The setpoints are necessary because of the implementation in the BAS, which is explained in Section 2.3.3. On the other hand, the connection between the monitoring system and the MPC is entirely on the online monitoring system, where the measurement data can be downloaded and the switching commands can be uploaded. The MPC itself, which is installed on a RaspberryPi, consists of an optimizer, which obtains the load prediction from the grey-box model and the price prediction from the SMARD day-ahead prices.
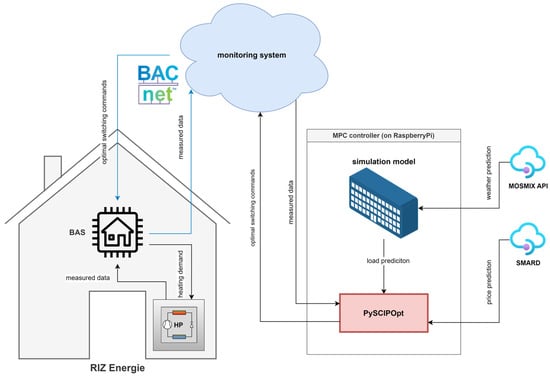
Figure 5.
Communication structure of the MPC with the RaspberryPi with the BAS of the RIZ Energie building.
2.3.2. MPC on RaspberryPi
As the MPC communicates with the building via the online monitoring platform, the algorithm must run on a computer with an internet connection. The advantage of using the PySCIPOpt interface is that no high computing power is required for the optimization itself. The entire control process, from determining the weather forecast to uploading the optimum switching commands, takes approximately 2 min.
Due to the minimum computational requirements described, a RaspberryPi was chosen as the controller (see Figure 6). It is also located within the RIZ Energie and is connected to the local network and the Internet via Ethernet. Remote access to the RaspberryPi is possible via an SSH tunnel. The MPC program is executed on the RaspberryPi, which executes the Python scripts that comprise the control loop every 15 min according to the control horizon of the MPC.

Figure 6.
RaspberryPi with remote access via an SSH tunnel.
When the Python scripts are executed, a CSV file of the optimal switching commands is created, which is then sent to the BAS via the monitoring system.
2.3.3. MPC Control of the Heat Pump
A central challenge in the real implementation of MPC is the control of the heat pump. Common solutions are, for example, artificial ambient temperatures [16], setpoint shifting [24], or SG-Ready signals [42]. In this work, the control was implemented using an artificial heat demand.
In the RIZ Energie building, the various building zones send heat requirements to the BAS, which passes these heat requirements on to the heat pump as a switch-on command and setpoint temperature. The heat requirements consist of a switching command and a setpoint temperature. They are affected by the users’ setpoint specifications and the weather conditions and thus are not influenced by the MPC.
A new data point was created in the BAS for the MPC control system, representing the additional heat requirement. This data point is overwritten solely by the MPC and then sends its heat request to the BAS, and thus to the heat pump. For this, the MPC sends the switching command as a binary variable and a setpoint temperature (0 °C when the heat pump is off and 50 °C when it is on). The MPC algorithm works predictively and can therefore send a request to the heat pump even before the real heat demand of the building arrives. This means that, in most cases, only the artificial heat demand of the MPC should take effect.
The limits and challenges of this control strategy have become clear during actual operation of the MPC. As Figure 7 shows, not all switching commands from the MPC generate a switching command from the heat pump, which ultimately leads to the heat pump actually switching on. This discrepancy between optimum switching commands and actual switch-on behavior shows that this implementation does not yet exploit the full potential of MPC control in terms of grid efficiency and cost-benefits.
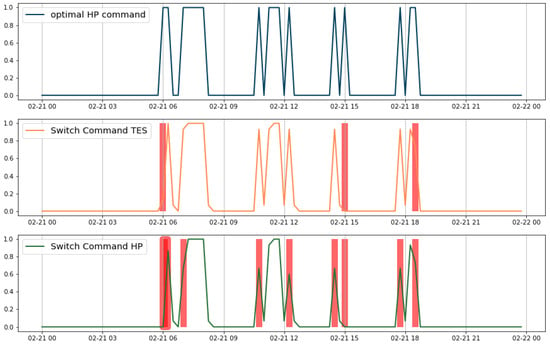
Figure 7.
Realization of the optimal switching commands in the real building system in 15-min steps. Values of less than 1 indicate a switch-on time smaller than 15 min. The red shadow highlights a deviation from the optimal command.
3. Results
The following chapter presents an analysis of the operation of MPC compared to conventional control, with a focus on load shifting potential and operational costs. Achieving comparability between the two datasets was a significant challenge, as the data reflects the real-world operation of a building. During the MPC operation tests, numerous uncontrollable external factors, such as user behavior and weather conditions, influenced the building and, consequently, the MPC. These factors cannot be replicated during the reference period for conventional control. Similar studies have also identified this issue and have employed various approaches to generate approximately comparable datasets [16]. For this study, the approach chosen was to evaluate and compare the MPC and conventional control solely based on measurement variables and assessment criteria that are independent of the aforementioned uncontrollable external factors.
Two separate one-week data sets were selected to represent the MPC and conventional operations, respectively. For the MPC operation, measurement data from 6 February 2023 to 12 February 2023 was used, while for the conventional operation, data from 5 December 2022 to 11 December 2022 was selected, with measurements taken at 15-min intervals.
3.1. Evaluation of the Heating System Performance
The initial analysis in this chapter focuses on how MPC affects the performance of the heating system. Specifically, the TES temperatures are analyzed to provide insights into the energy storage strategies of the two controllers. The distribution of these temperatures is also examined. Figure 8 presents a comparison of the time series of TES temperatures during MPC and conventional operation. Additionally, the heating power produced by the heat pump is illustrated as bars. A histogram on the y-axis shows the distribution of the mean TES temperatures, averaged over the three temperature sensors, during the two observation periods. Also, the average TES mean temperatures for the operation modes are displayed as dashed lines.
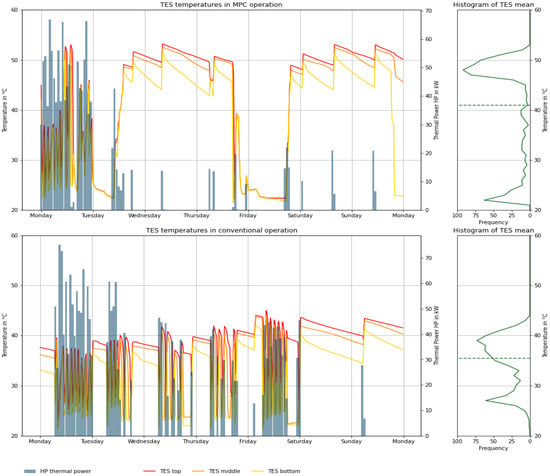
Figure 8.
Comparison of TES temperatures and thermal power of the heat pump in MPC and conventional operation with a histogram of average TES temperature.
The time series during MPC operation clearly indicates higher mean TES temperatures, reaching up to 53 °C, compared to the conventional operation, where a maximum of 45 °C was observed. A distinct difference in the charging behavior of the heat pump is also evident. During MPC operation, fewer charging cycles are observed overall; however, the storage is charged to higher final temperatures. The histogram reveals that the average TES temperature during MPC operation is predominantly between 45 °C and 50 °C or between 20 °C and 25 °C, whereas during conventional operation, temperatures between 35 °C and 40 °C or between 25 °C and 30 °C are more common. While an average TES mean temperature of 35.4 °C was measured in conventional operation, this value rose by 5.6 K to 41.0 °C in MPC operation.
During the period of conventional operation, more frequent activation of the heat pump is observed, leading to a higher amount of heating energy expended in the entire observation period (2331 kWhth in conventional operation and 1314 kWhth in MPC operation). Consequently, the heating energy produced by the heat pump is not considered in the subsequent evaluation, as it does not represent a comparable metric.
The elevated TES temperatures necessarily lead to higher supply temperatures from the heat pump. Due to the resulting greater temperature difference between the source and sink, a lower COP is expected during MPC operation. The scatter plot shown in Figure 9 compares the temperature lift with the COP for both operating modes, filtered to states when the heat pump is active.
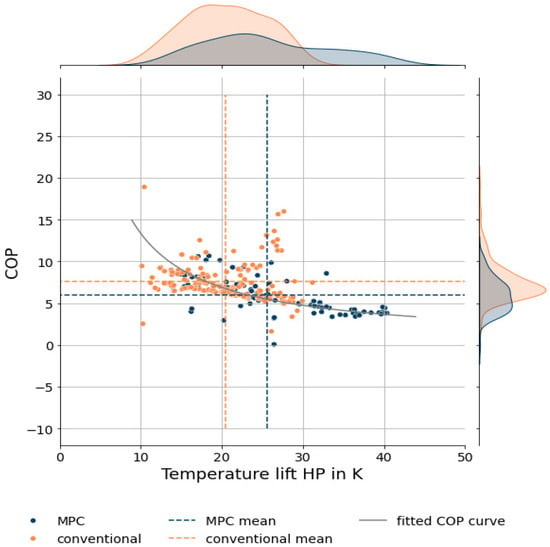
Figure 9.
COP of the heat pump over temperature lift for both MPC (blue) and conventional operation (orange) while the heat pump is in operation with the respective frequency distribution.
The second-law efficiency related to the ideal Carnot efficiency COPCarnot was determined through regression analysis. The regression yielded an efficiency of for both conventional and MPC operations. A fitted COP curve is added to the scatter plot according to Equation (17):
In conventional operation, an average COP of 7.58 was achieved, whereas during MPC operation, a lower COP of 5.96 was observed. This outcome aligns with expectations and is attributed to the higher temperature lift in MPC operation (25.6 K) compared to conventional operation (20.5 K), which can only be attributed to the optimized operation in MPC and not to an altered heating characteristic. The average source temperatures were 12.8 °C in MPC operation and 15.0 °C in conventional operation. This raises the question of whether an economic and grid-supportive operation with MPC can compensate the additional costs resulting from the lower COP.
3.2. Evaluation of the Energy Related Operational Costs
To evaluate the economic performance of the MPC operation, the electricity procurement prices at the times when electricity was consumed in both MPC and conventional operation are considered. It is important to note that electricity prices are an uncontrollable variable, and there were significant price differences between the two observation periods. Since the conventional controller operates independently of electricity prices, we apply the prices from the MPC period to the dataset of the conventional operation to compare the electricity prices on a fair basis.
The comparison of electricity procurement prices between the two operating modes is presented in Figure 10. A raincloud plot illustrates the frequency distributions, boxplots, and individual data points of the electricity prices. The comparison clearly shows that, during MPC operation, electricity is procured at significantly lower prices. The average electricity price was 0.12 EUR/kWhel in MPC operation and 0.36 EUR/kWhel in conventional operation.
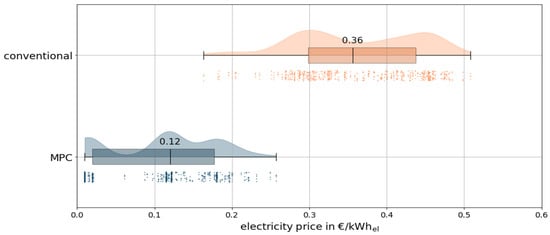
Figure 10.
Frequency distribution, boxplot, and data points of electricity prices during heat pump operation for MPC and conventional operation.
For a fair and unbiased comparison, it is important to consider the different operating conditions of the building, which is best represented by the outdoor air temperature. Figure 11 plots the electricity price against the outdoor air temperature. Naturally, the outdoor temperatures are not identical, as the operation took place in two distinct periods. Nonetheless, the operating conditions are comparable with a mean temperature of = 2.3 °C for MPC operation and = 1.9 °C for conventional operation. The effect on reducing the electricity prices can be therefore primarily attributed to the MPC operation, and not the weather conditions.
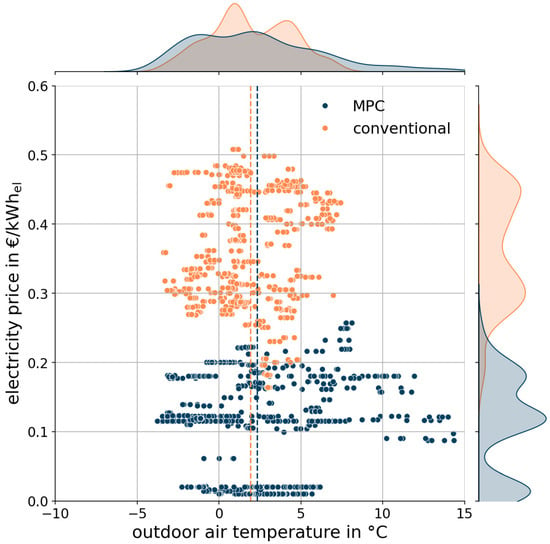
Figure 11.
Electricity price vs. the outdoor air temperature for MPC (blue) and conventional operation (orange) with the respective frequency distribution.
When interpreting these results, it is important to consider that, as mentioned in the introduction of this chapter, the amount of heating energy and thus the overall heating costs during the two observation periods are not directly comparable. Additionally, the lower COP in MPC operation must be considered, as it reflects a less favorable ratio of electrical energy consumed to thermal energy produced. Despite this effect, the MPC operation results in a lower electrical energy consumption than the conventional control, which can be attributed to differing external conditions, such as outdoor air temperature and user behavior.
To further assess the economic performance of MPC operation despite the aforementioned effects, the heating energy-specific costs are analyzed. This is done by dividing the electricity costs by the heating energy produced at that time, as shown in Equation (18):
where is the heating cost, is the consumed electrical energy of the heat pump, is the day-ahead price of electrical energy and is the produced thermal energy of the heat pump at the time .
The raincloud plot in Figure 12 illustrates the frequency distribution, boxplot, and individual data points of the heating energy costs in EUR/kWhth during the observation periods. The difference between the operating modes is smaller than in the electricity prices; on average, 1 kWh of thermal energy costs 1.8 ct in MPC operation, compared to 2.9 ct in conventional operation. This is due to the lower COP during MPC operation. Nonetheless, MPC achieves a 40% lower heating-energy specific costs in the operation period.
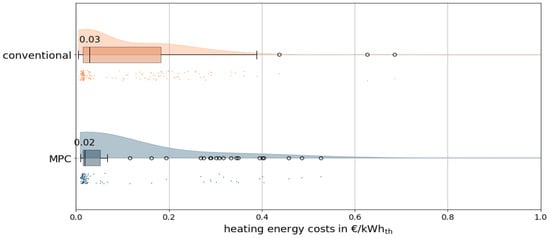
Figure 12.
Frequency distribution, boxplot, and data points of heating-specific energy costs during heat pump operation for MPC and conventional operation.
Similar to Figure 12, the plot in Figure 13 shows that the reduction in heating-energy specific costs is not influenced by differing weather conditions between the two periods, but can instead be attributed to the MPC operation.
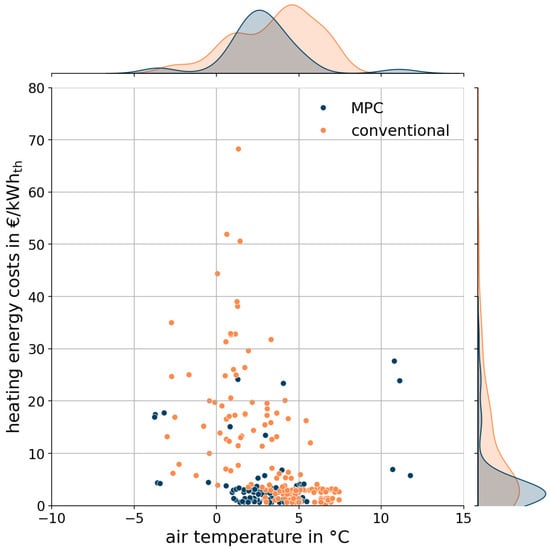
Figure 13.
Heating energy costs vs. outdoor air temperatures for MPC (blue) and conventional operation (orange) with the respective frequency distribution.
3.3. Evaluation of the Grid-Supportiveness
Furthermore, the analysis examines whether, in addition to increased economic efficiency, the load shifting benefit of MPC was also improved compared to conventional operation. Klein et al. (2016) propose the use of the Grid-Supportive Coefficient GSC for evaluating load shifting potential (see Equation (19)) [18]. The electricity costs are used as the reference value to evaluate grid-supportiveness.
The GSC is calculated by summing the products of all electricity consumption WHP,el and the corresponding electricity prices kday-ahead over a defined observation period of 24 h, with time steps for every time step . This sum is then divided by the product of the total consumed electrical energy and the average electricity price. The resulting GSC is less than 1 if the operation was grid-friendly and greater than 1 if electricity was imported from the grid in a grid-adverse manner.
The GSC is calculated for both operating modes, with the calculation performed at each time step, using the mean day ahead price for an observation period of 24 h.
Figure 14 plots the GSC against the electricity price in EUR/kWhel for each time step with electricity consumption. Additionally, the frequency distributions of the GSC and the electricity price are shown on their respective axes. The average GSC values for the entire observation period are 0.93 for MPC operation and 1.07 for conventional operation. Hence, the MPC controller operates in a grid-friendly manner with a GSC < 1 while the conventional controller operated in a grid-adverse manner with a GSC > 1 during the observation period. This indicates that the MPC achieves a 13% improvement in grid-supportiveness compared to the conventional controller.
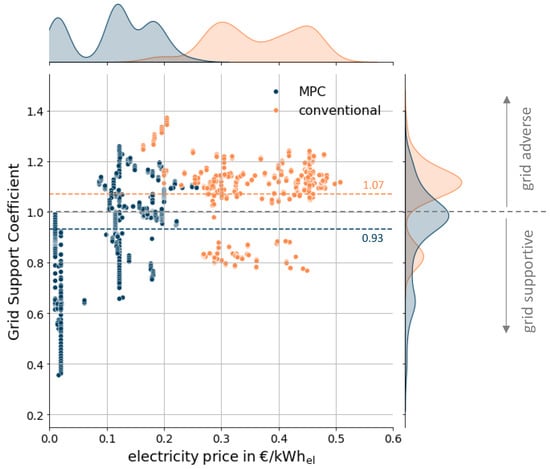
Figure 14.
GSC during heat pump operation of MPC (blue) and conventional operation (orange) (with corresponding averages as dotted lines) over electricity price.
4. Discussion
4.1. Real-World Integration into the Existing BAS and During Ongoing Operation
The integration of the MPC into the BAS system presented significant challenges due to the typically closed and proprietary nature of such systems. To overcome this, a bidirectional online API was implemented via a gateway, enabling communication between the BAS and MPC. This allowed for the reading of relevant data points and the transmission of switch-on commands to the heat pump. The process of determining heat demand posed further challenges. Generally, heat demand is based on room and outdoor temperatures, as well as the temperatures of the heating circuit’s flow and return. In the demonstration building, heat demand was determined by various consumers (such as TABS, heating registers of the ventilation system, and laboratories), but the specific calculation basis of these subsystems remained unclear due to the closed BAS system. To address this, the MPC relied on a grey-box model of the building, which modeled the different heat consumers and their respective heat demands. Although effective, this approach required considerable effort, which could potentially be reduced through the use of data-driven AI black box models in future implementations.
Another critical aspect was ensuring robust communication between the MPC and the heat pump, such as through SG-Ready signals. The implementation of these signals is manufacturer-specific and often lacks transparency [42]. The full potential of the MPC can only be realized when the signal to the heat pump is interpreted as a forced start command (SG-Ready Mode 4) rather than merely a start suggestion (SG-Ready Mode 3). This requires the MPC to be more robust in handling start commands. In practice, this was achieved by simulating an additional artificial heat demand within the MPC, which, when combined with the BAS’s recommendation, functioned as a start command in a technical sense. Thus, the heat pumps are not controlled via explicit SG-Ready signals, but by a tweaked BAS system so that all safeguards and manufacturer-specific control strategies are still in place. Despite the redundant and secure implementation in case of MPC failure, the building owner decided to return to normal operation primarily due to the lack of economic incentives, since as stated in Section 2.2.6 in the German tariff system there are currently no dynamic tariffs in place.
The potential to transfer this MPC solution to other non-residential buildings was also considered. While the parameterization of a grey-box model is time-consuming and the MPC-heat pump interface is tailored to the specific installations, the component models themselves are simple and easily parameterizable. If a robust load prediction model and an existing interface to the building are in place, the MPC approach could be adapted in other buildings. The manual and complex communication structure could be overcome by standardization or open EMS protocols, such as the openEMS initiative [43]. Data-driven, self-learning, and adaptive machine learning models may reduce the required work-load for accurate load forecasting.
4.2. Evaluation of Grid-Friendliness, Evonomic Efficiency and Thermal Comfort
The core findings of the evaluation reveal that the MPC strategy leads to an increase of average TES temperatures of 5.6 K. This results in a drop of the heat pumps COP from 7.6 in conventional operation to 6.0 in MPC operation due to the increased supply temperature from the heat pump. This issue could be mitigated by using LTES, which, due to its more stable temperatures during phase change transitions and higher specific energy storage capacity, helps maintain lower TES temperatures and, consequently, prevents an increase in the heat pump’s supply temperature. Nonetheless, the MPC strategy achieves a 40% higher economic efficiency. The grid-supportive behavior of the heat pump is also improved by the MPC, as electricity consumption from the grid on average happens during cheaper periods, as shown by the 13% decrease in GSC. This is achieved while ensuring thermal user comfort is not compromised by the altered control strategy.
As previously mentioned, the comparability of MPC with conventional operation is only partially achievable due to different weather conditions during both observation periods. This results in a higher energy demand in the period of conventional operation and slightly differing heat source temperatures of the heat pump. The results are therefore not representative for the entire year, but are only robust for the observation period. Nonetheless, the discussed effects and overall trends can be transferred to other operating conditions in other seasons. Comparability between both observation periods is achieved by using indicators which are independent from weather conditions and heat demand.
Additionally, the day-ahead electricity prices used in this study are not a factual indicator of grid conditions; residual load, share of renewables, and grid load should be also considered. The method in which electricity prices are used in the same way to other cost functions for the optimization and other benchmark variables for GSC evaluation.
The economic benefits—with cost reductions of 40%—achieved in this work exceed the results of similar real-world studies of MPC in heat pump systems, such as Thorsteinsson et al. (2023), which found a 2–17% cost reduction [16]. This can be attributed to less variability in their electricity tariffs or their longer test period of 97 days, compared to 7 days in our study. On the other hand, the improved grid-friendliness in this study is comparable with the results of Frison et al. (2019), which also used the GSC as an evaluation parameter and achieved a GSC improvement of 16% [20].
Provided there are sufficient storage capacities offering flexibility, the findings concerning grid-friendliness are transferable to comparable heating systems. Another requirement is that the demand and system dynamic can be predicted with adequate accuracy. However, a critical examination of the study suggests that a longer test period, potentially covering an entire heating period, would be advantageous. This would enhance the robustness of the results regarding both grid-supportiveness and, especially, economic efficiency.
5. Conclusions
The increasing implementation of heat pumps presents a significant challenge for the electrical power grid, driving the growing need for smart energy consumers that can adapt to grid conditions and variable electricity tariffs. This necessity underscores the importance of gathering practical experience with such implementations.
This 7-day study demonstrates that MPC, utilizing simple component models, effectively reduces energy-related costs of heat pumps by 40%. While ensuring grid-supportive operation, the GSC is improved by 13%. In MPC operation, the average TES temperature is increased by 5.6 K compared to conventional operation. The higher temperature difference between source and sink also leads to a lower thermal efficiency of the heat pump, which is observed as a COP decrease from 7.58 in conventional operation to 5.96 in MPC operation. Despite this lower efficiency of the heat pump in MPC operation, the beneficial effects of improved economic efficiency and grid-friendliness are achieved. Integrating MPC into ongoing operations poses substantial challenges, highlighting the need for standardized solutions in order to facilitate advanced control strategies.
Future research should extend the testing periods to enhance the robustness of the results and study the long-term effects of MPC operation in comparison to conventional operation. Additionally, improving the communication interface between the MPC system and the BAS is crucial to fully exploit the potential of MPC by ensuring all heat pump commands are executed, e.g., by standardized or openEMS solutions. Future research should focus on making prices, grid load, or the CO2 footprint of grid nodes transparent to enhance grid support with macroeconomic benefits, which form the basis for dynamic pricing models incentivizing MPC implementation. Moreover, the development of data-driven AI models for load forecasting could reduce the manual effort required for system modeling. Finally, standardizing interfaces for both heat pumps and opening BAS to non-proprietary MPC solutions will be essential for broader implementation.
Author Contributions
Conceptualization, L.T., J.P. and M.L.; methodology, L.T., J.P. and M.L.; software, L.T.; validation, L.T.; formal analysis, L.T. and M.L.; investigation, L.T.; resources, L.T. and J.P.; data curation, L.T.; writing—original draft preparation, L.T.; writing—review and editing, J.P. and M.L.; visualization, L.T. and M.L.; supervision, J.P. and M.L.; project administration, L.T., J.P. and M.L.; funding acquisition, J.P. and M.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the German Federal Ministry for Economic Affairs and Climate Action (BMWK), grant number 03EN1021A and 03EN3095D and badenova Energie GmbH, grant number 2023-01.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Acknowledgments
The authors are grateful to the German Federal Ministry for Economic Affairs and Climate Action (BMWK) for the support as part of the projects BUiLD.DIGITiZED and SQ-Durlach II and to the badenova Energie GmbH for the support of the project SHK.SUPPORT.
Conflicts of Interest
The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
Abbreviations
The following abbreviations are used in this manuscript:
| MPC | Model Predictive Control |
| DSM | Demand-Side Management |
| TABS | Thermal Activated Building System |
| TES | Thermal Energy Storage |
| HVAC | Heating, Ventilation and Air Conditioning |
| HP | Heat Pump |
| GSC | Grid Support Coefficient |
| MFH | Multi Family Home |
| SFH | Single Family Home |
| PV | Photovoltaic |
| OF | Outdoor Fan |
| DHS | District Heating System |
| FHS | Floor Heating System |
| BAS | Building Automation System |
| COP | Coefficient of Performance |
| CSV | Comma Separated Value |
| SG | Smart Grid |
Nomenclature
| Symbol | Description | Unit |
| a | Actuators in optimization problem | - |
| Heating costs | EUR/kWhth | |
| Heat capacity of water | kJ/kgK | |
| d | Disturbances of optimization problem | - |
| Predicted disturbances | - | |
| f | Transformation function | - |
| fHVAC | HVAC dynamics function | - |
| Grid Support Coefficient | - | |
| k | Time step of prediction horizon | - |
| Day-ahead price of electricity | EUR/kWh | |
| l | Costs at each time step | - |
| m | Additional measured variables | - |
| Condenser mass flow | kg/s | |
| N | Prediction horizon | - |
| Nominal electrical consumption of heat pump | kW | |
| Electrical power consumption of heat pump | kW | |
| Nominal power output of heat pump | kW | |
| Thermal power output of heat pump | kW | |
| Thermal power consumption of load side | kW | |
| T | Sampling time | - |
| Mean outdoor air temperature | °C | |
| Cold reservoir temperature | K | |
| Final time of optimization problem | min | |
| Hot reservoir temperature | K | |
| Condenser outlet temperature | °C | |
| Maximum condenser inlet temperature | °C | |
| Condenser inlet temperature | °C | |
| Maximum TES temperature | °C | |
| TES temperature | °C | |
| u | Control commands | - |
| Capacity of TES | Liters | |
| Electrical Energy consumed by heat pump | kWh | |
| Thermal Energy in TES | kWh | |
| Thermal Energy demand from load side | kWh | |
| x | State of optimization problem | - |
| Predicted states | - | |
| y | Measurement of optimization problem | - |
| Decision variable of heat pump | binary | |
| Heat pump efficiency | - | |
| Density of water | kg/m3 |
References
- Fischer, D.; Madani, H. On Heat Pumps in Smart Grids: A Review. Renew. Sustain. Energy Rev. 2017, 70, 342–357. [Google Scholar] [CrossRef]
- Rosenow, J.; Gibb, D.; Nowak, T.; Lowes, R. Heating up the Global Heat Pump Market. Nat. Energy 2022, 7, 901–904. [Google Scholar] [CrossRef]
- European Heat Pump Association European Heat Pump Market and Statistics Report. 2024. Available online: https://www.ehpa.org/market-data/ (accessed on 17 December 2024).
- Bundesnetzagentur Festlegungsverfahren zur Integration von steuerbaren Verbrauchseinrichtungen und Steuerbaren Netzanschlüssen nach § 14a Energiewirtschaftsgesetz. 2022. Available online: https://www.bundesnetzagentur.de/DE/Beschlusskammern/1_GZ/BK6-GZ/2022/BK6-22-300/Anlagen_Konsultation/BK6-22-300_Eckpunktepapier.pdf?__blob=publicationFile&v=1 (accessed on 27 February 2025).
- Sawant, P.A. A Contribution to Optimal Scheduling of Real-World Trigeneration Systems Using Economic Model Predictive Control; Technische Universität Dresden: Dresden, Germany, 2021. [Google Scholar]
- Killian, M.; Kozek, M. Ten Questions Concerning Model Predictive Control for Energy Efficient Buildings. Build. Environ. 2016, 105, 403–412. [Google Scholar] [CrossRef]
- Kuboth, S.; Heberle, F.; König-Haagen, A.; Brüggemann, D. Economic Model Predictive Control of Combined Thermal and Electric Residential Building Energy Systems. Appl. Energy 2019, 240, 372–385. [Google Scholar] [CrossRef]
- D’Ettorre, F.; Conti, P.; Schito, E.; Testi, D. Model Predictive Control of a Hybrid Heat Pump System and Impact of the Prediction Horizon on Cost-Saving Potential and Optimal Storage Capacity. Appl. Therm. Eng. 2019, 148, 524–535. [Google Scholar] [CrossRef]
- Patteeuw, D.; Henze, G.P.; Helsen, L. Comparison of Load Shifting Incentives for Low-Energy Buildings with Heat Pumps to Attain Grid Flexibility Benefits. Appl. Energy 2016, 167, 80–92. [Google Scholar] [CrossRef]
- SG Ready-Label. Available online: https://www.waermepumpe.de/normen-technik/sg-ready/ (accessed on 5 June 2024).
- Patel, N.R.; Rawlings, J. Applications of MPC to Building HVAC Systems. In Handbook of Model Predictive Control; Raković, S.V., Levine, W.S., Eds.; Springer International Publishing: Cham, Switzerland, 2019; pp. 607–623. ISBN 978-3-319-77489-3. [Google Scholar]
- Wan, H.; Gong, Y.; Dang, C.; Wang, S.; Huang, G. Power Control of Latent Heat Thermal Energy Storage Units Using a Model-Based Predictive Strategy. Appl. Energy 2025, 382, 125220. [Google Scholar] [CrossRef]
- Toffoletti, G.; Cortella, G.; D’Agaro, P. Thermodynamic and Economic Seasonal Analysis of a Transcritical CO2 Supermarket with HVAC Supply through Ice Thermal Energy Storage (ITES). J. Clean. Prod. 2024, 434, 139832. [Google Scholar] [CrossRef]
- Pfafferott, J.; Henze, G.P.; Lang, T. Anlagenaufwandszahlen für die Bauteilaktivierung in Abhängigkeit des Regelkonzeptes. Bauphysik 2017, 39, 279–290. [Google Scholar] [CrossRef]
- Viot, H.; Sempey, A.; Mora, L.; Batsale, J.C.; Malvestio, J. Model Predictive Control of a Thermally Activated Building System to Improve Energy Management of an Experimental Building: Part II—Potential of Predictive Strategy. Energy Build. 2018, 172, 385–396. [Google Scholar] [CrossRef]
- Thorsteinsson, S.; Kalaee, A.A.S.; Vogler-Finck, P.; Stærmose, H.L.; Katic, I.; Bendtsen, J.D. Long-Term Experimental Study of Price Responsive Predictive Control in a Real Occupied Single-Family House with Heat Pump. Appl. Energy 2023, 347, 121398. [Google Scholar] [CrossRef]
- Carli, R.; Cavone, G.; Dotoli, M.; Epicoco, N.; Scarabaggio, P. Model Predictive Control for Thermal Comfort Optimization in Building Energy Management Systems. In Proceedings of the 2019 IEEE International Conference on Systems, Man and Cybernetics (SMC), Bari, Italy, 6–9 October 2019; pp. 2608–2613. [Google Scholar]
- Klein, K.; Langner, R.; Kalz, D.; Herkel, S.; Henning, H.-M. Grid Support Coefficients for Electricity-Based Heating and Cooling and Field Data Analysis of Present-Day Installations in Germany. Appl. Energy 2016, 162, 853–867. [Google Scholar] [CrossRef]
- Arabzadeh, V.; Alimohammadisagvand, B.; Jokisalo, J.; Siren, K. A Novel Cost-Optimizing Demand Response Control for a Heat Pump Heated Residential Building. Build. Simul. 2018, 11, 533–547. [Google Scholar] [CrossRef]
- Frison, L.; Kleinstück, M.; Engelmann, P. Model-Predictive Control for Testing Energy Flexible Heat Pump Operation within a Hardware-in-the-Loop Setting. J. Phys. Conf. Ser. 2019, 1343, 012068. [Google Scholar] [CrossRef]
- Bechtel, S.; Rafii-Tabrizi, S.; Scholzen, F.; Hadji-Minaglou, J.-R.; Maas, S. Influence of Thermal Energy Storage and Heat Pump Parametrization for Demand-Side-Management in a Nearly-Zero-Energy-Building Using Model Predictive Control. Energy Build. 2020, 226, 110364. [Google Scholar] [CrossRef]
- Drgoňa, J.; Picard, D.; Helsen, L. Cloud-Based Implementation of White-Box Model Predictive Control for a GEOTABS Office Building: A Field Test Demonstration. J. Process Control 2020, 88, 63–77. [Google Scholar] [CrossRef]
- Kuboth, S.; Weith, T.; Heberle, F.; Welzl, M.; Brüggemann, D. Experimental Long-Term Investigation of Model Predictive Heat Pump Control in Residential Buildings with Photovoltaic Power Generation. Energies 2020, 13, 6016. [Google Scholar] [CrossRef]
- Löhr, Y.; Wolf, D.; Pollerberg, C.; Hörsting, A.; Mönnigmann, M. Supervisory Model Predictive Control for Combined Electrical and Thermal Supply with Multiple Sources and Storages. Appl. Energy 2021, 290, 116742. [Google Scholar] [CrossRef]
- Sawant, P.; Villegas Mier, O.; Schmidt, M.; Pfafferott, J. Demonstration of Optimal Scheduling for a Building Heat Pump System Using Economic-MPC. Energies 2021, 14, 7953. [Google Scholar] [CrossRef]
- Blum, D.; Wang, Z.; Weyandt, C.; Kim, D.; Wetter, M.; Hong, T.; Piette, M.A. Field Demonstration and Implementation Analysis of Model Predictive Control in an Office HVAC System. Appl. Energy 2022, 318, 119104. [Google Scholar] [CrossRef]
- Ma, L.; Huang, Y.; Zhang, J.; Zhao, T. A Model Predictive Control for Heat Supply at Building Thermal Inlet Based on Data-Driven Model. Buildings 2022, 12, 1879. [Google Scholar] [CrossRef]
- Zhang, K.; Prakash, A.; Paul, L.; Blum, D.; Alstone, P.; Zoellick, J.; Brown, R.; Pritoni, M. Model Predictive Control for Demand Flexibility: Real-World Operation of a Commercial Building with Photovoltaic and Battery Systems. Adv. Appl. Energy 2022, 7, 100099. [Google Scholar] [CrossRef]
- Baumann, C.; Huber, G.; Alavanja, J.; Preißinger, M.; Kepplinger, P. Experimental Validation of a State-of-the-Art Model Predictive Control Approach for Demand Side Management with a Hot Water Heat Pump. Energy Build. 2023, 285, 112923. [Google Scholar] [CrossRef]
- Tang, W.; Li, Y.; Walker, S.; Keviczky, T. Model Predictive Control Design for Unlocking the Energy Flexibility of Heat Pump and Thermal Energy Storage Systems. In Proceedings of the 2024 IEEE Conference on Control Technology and Applications (CCTA), Newcastle upon Tyne, UK, 21–23 August 2024. [Google Scholar]
- Drgoňa, J.; Arroyo, J.; Cupeiro Figueroa, I.; Blum, D.; Arendt, K.; Kim, D.; Ollé, E.P.; Oravec, J.; Wetter, M.; Vrabie, D.L.; et al. All You Need to Know about Model Predictive Control for Buildings. Annu. Rev. Control 2020, 50, 190–232. [Google Scholar] [CrossRef]
- Maher, S.; Miltenberger, M.; Pedroso, J.P.; Rehfeldt, D.; Schwarz, R.; Serrano, F. PySCIPOpt: Mathematical Programming in Python with the SCIP Optimization Suite. In Proceedings of the Mathematical Software—ICMS, Berlin, Germany, 11–14 July 2016; Springer: Cham, Switzerland, 2016; pp. 301–307. [Google Scholar]
- Simmini, F.; Caldognetto, T.; Bruschetta, M.; Mion, E.; Carli, R. Model Predictive Control for Efficient Management of Energy Resources in Smart Buildings. Energies 2021, 14, 5592. [Google Scholar] [CrossRef]
- EN 145112: 2022; Air Conditioners, Liquid Chilling Packages and Heat Pumps for Space Heating and Cooling and Process Chillers, with Electrically Driven Compressors—Part 2: Test Conditions. iTeh, Inc.: Newark, DE, USA, 2023.
- Sawant, P.; Bürger, A.; Doan, M.D.; Felsmann, C.; Pfafferott, J. Development and Experimental Evaluation of Grey-Box Models of a Microscale Polygeneration System for Application in Optimal Control. Energy Build. 2020, 215, 109725. [Google Scholar] [CrossRef]
- Bundesnetzagentur SMARD | SMARD—Strommarktdaten, Stromhandel Und Stromerzeugung in Deutschland. Available online: https://www.smard.de/home?mtm_campaign=smard&mtm_kwd=allgemein&mtm_source=google&mtm_medium=cpc&mtm_content=textad&gad_source=1&gclid=Cj0KCQjw2ou2BhCCARIsANAwM2FtLDZCG1Y-A-VX2V_TDPnHvK-bdgoJ8uVcq3XYSqFmjdL_GX1h9REaAme0EALw_wcB (accessed on 19 August 2024).
- Tomás, L. EnOB: BUiLD-DIGITiZED—IoT und BIM für die Inbetriebnahme und den Betrieb von netzdienlichen Niedrigstenergiegebäuden 2023. Available online: https://build-digitized.hs-offenburg.de/fileadmin/Sonstige_Unterseiten/build-digitized/files/Abschlussbericht_BUiLD_DIGITiZED.pdf (accessed on 27 February 2025).
- Carvajal, D. Technischer Bericht Gebäudemodellierung für das EnOB-Verbundvorhaben BUiLD.DIGITiZED 2023. Available online: https://build-digitized.hs-offenburg.de/fileadmin/Sonstige_Unterseiten/build-digitized/files/BUiLD_DIGITiZED_TechnischerBerichte_Geb%C3%A4udemodellierung.pdf (accessed on 27 February 2025).
- Horvat, I.; Dovic, D. Dynamic Method for Calculating Energy Need in HVAC Systems. Trans. FAMENA 2016. Available online: https://www.researchgate.net/publication/304490732_Dynamic_method_for_calculating_energy_need_in_HVAC_systems (accessed on 27 February 2025).
- Gutzmann, B.; Motl, A. Wetterdienst. 2024. Available online: https://zenodo.org/records/12739518 (accessed on 27 February 2025).
- Mousavi Maleki, S.A.; Hizam, H.; Gomes, C. Estimation of Hourly, Daily and Monthly Global Solar Radiation on Inclined Surfaces: Models Re-Visited. Energies 2017, 10, 134. [Google Scholar] [CrossRef]
- Baraskar, S.; Günther, D.; Wapler, J.; Lämmle, M. Analysis of the Performance and Operation of a Photovoltaic-Battery Heat Pump System Based on Field Measurement Data. Sol. Energy Adv. 2024, 4, 100047. [Google Scholar] [CrossRef]
- Feilmeier, S.; Obermeier, M.; Asen, S.; Sagar; Rieger, L.; Hannes; Ihara, H.; Grill, M.; Kaindl, L.; Fey, S.; et al. OpenEMS/Openems: 2024.9.0 2024. Available online: https://zenodo.org/records/13623309 (accessed on 27 February 2025).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).