Optimization Techniques for Low-Level Control of DC–AC Converters in Renewable-Integrated Microgrids: A Brief Review
Abstract
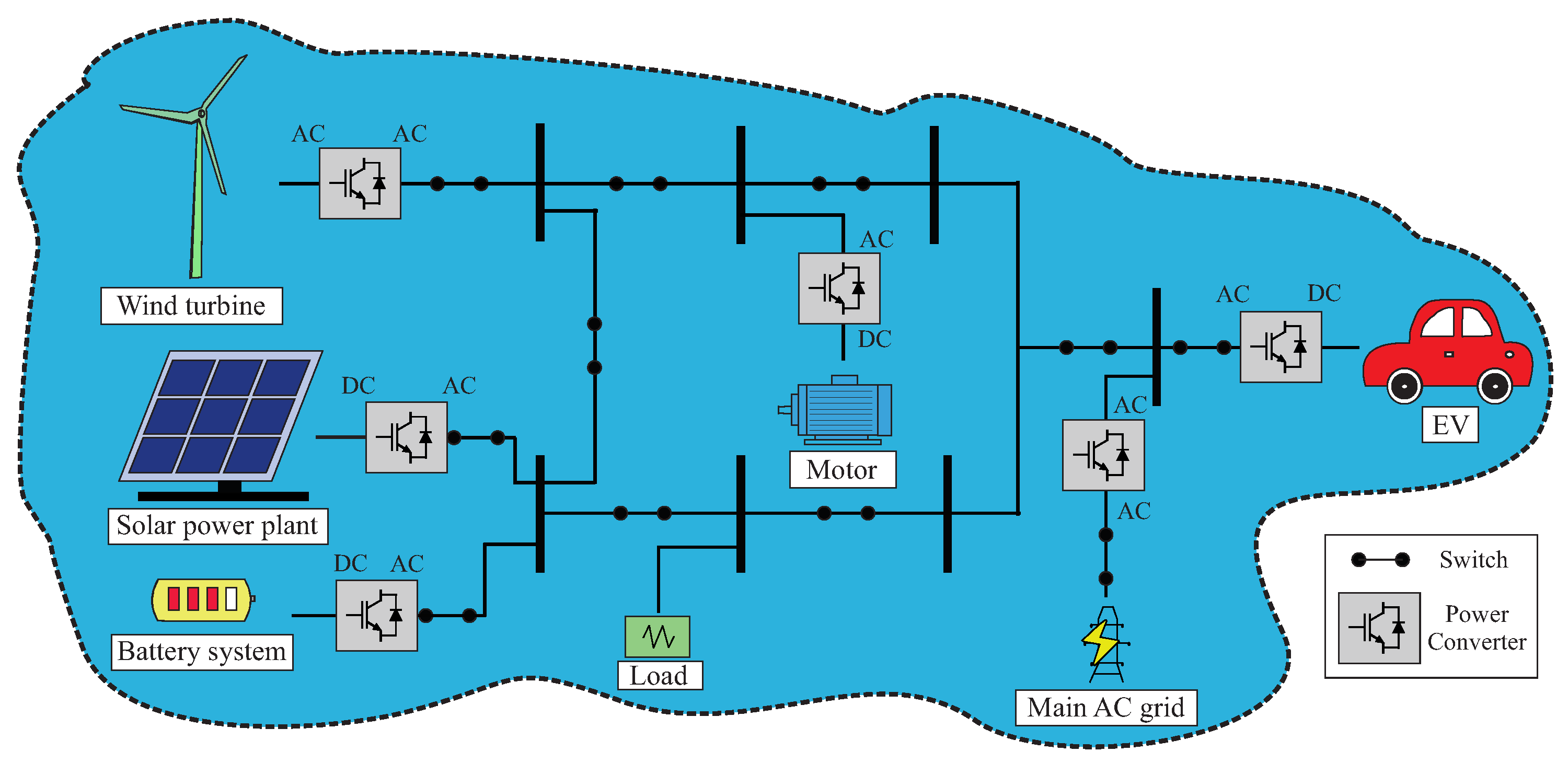
1. Introduction
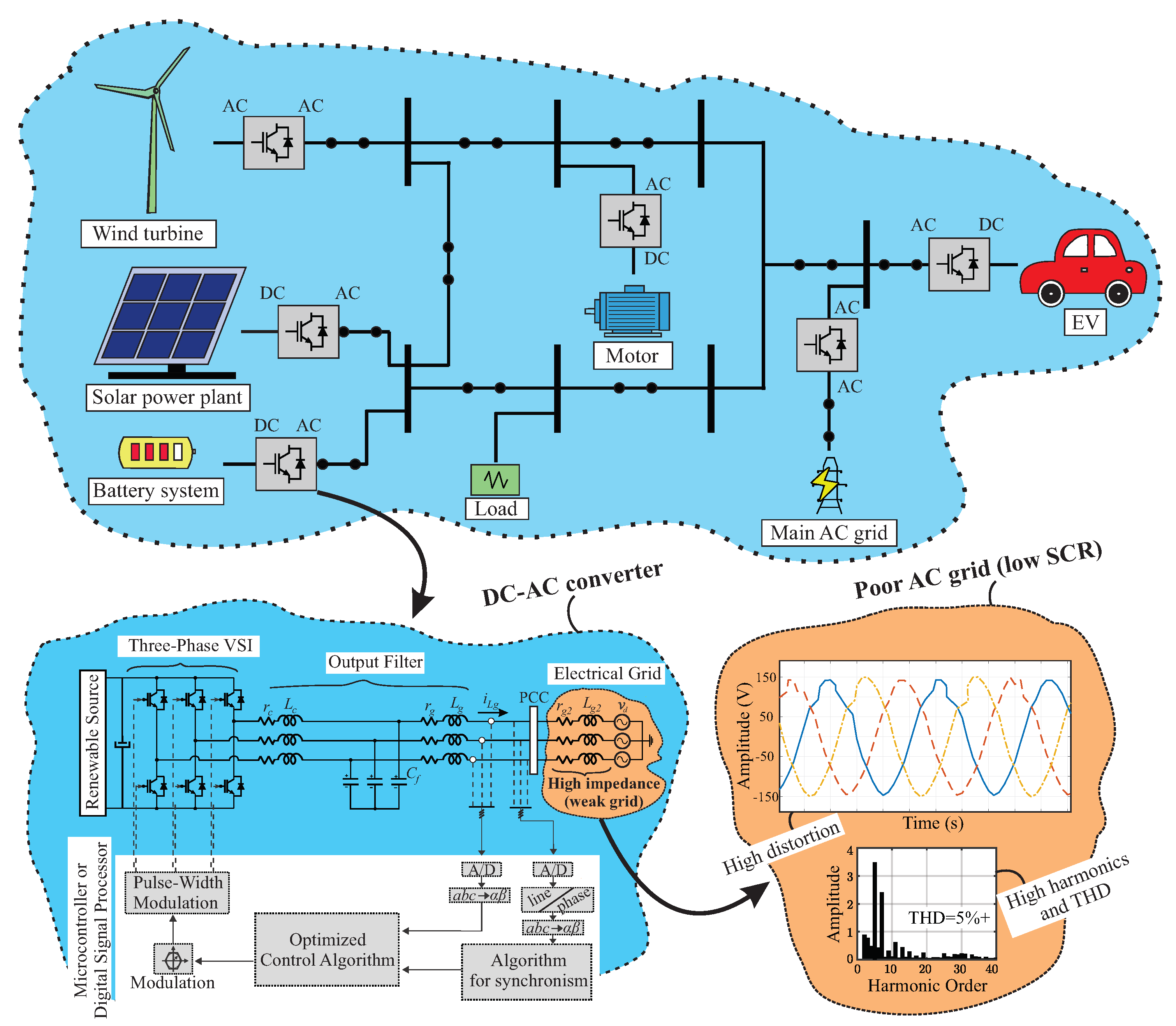
2. Key Challenges in Operation and Control of DC–AC Converters
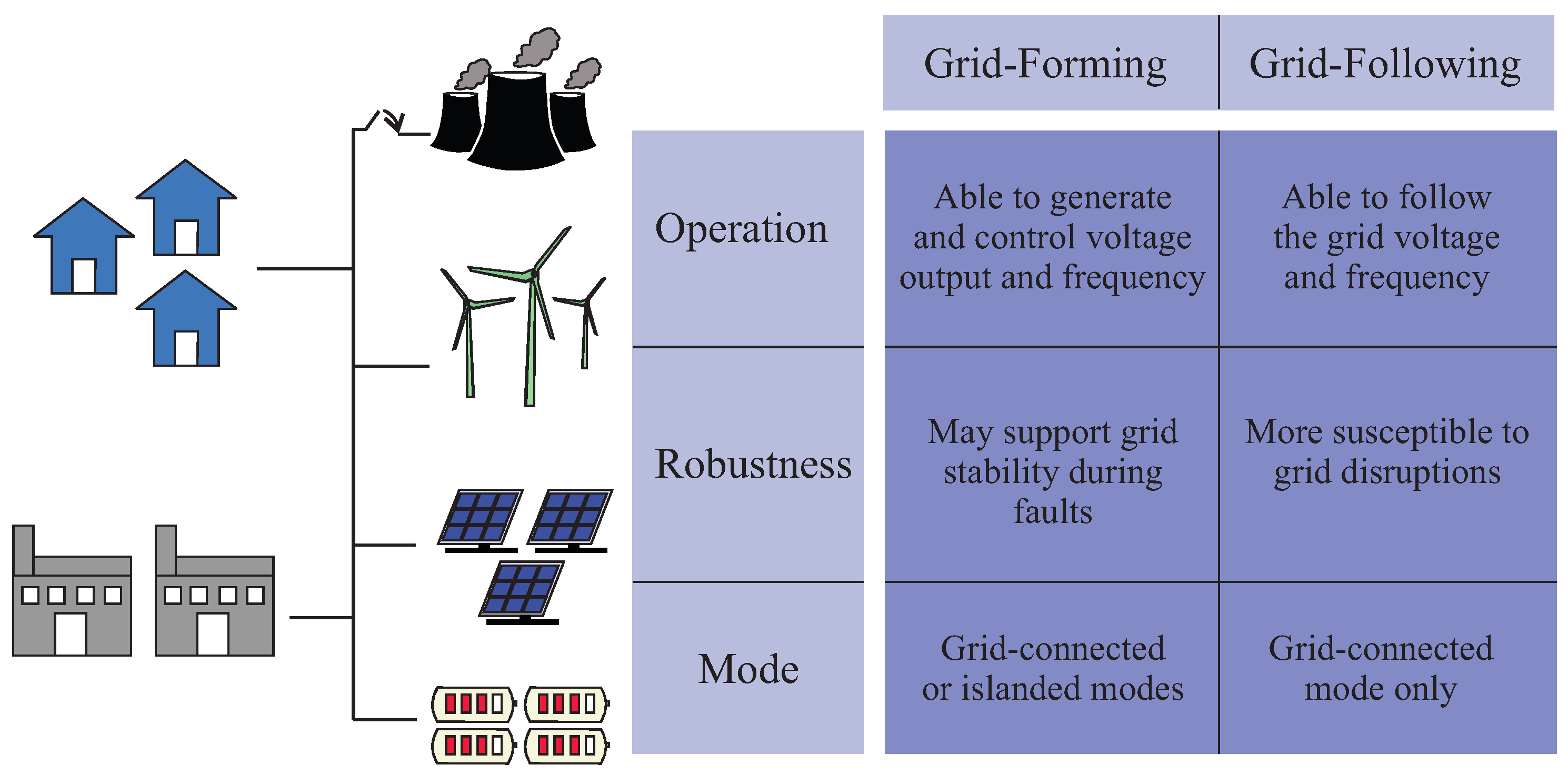
2.1. Main Challenges in Grid-Following Converters
2.2. Main Challenges in Grid-Forming Converters
3. Overview of Control Optimization
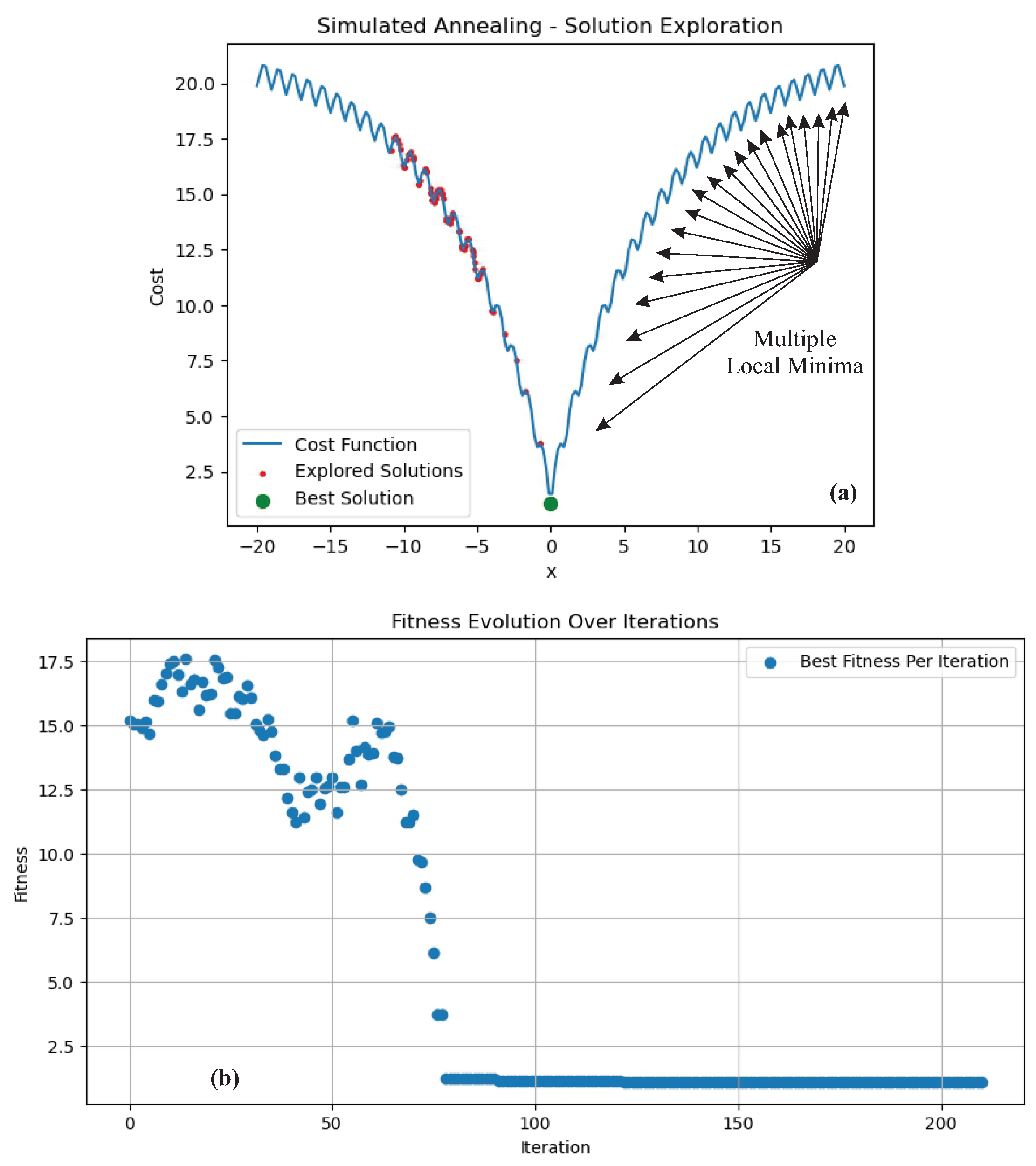
3.1. Minimizing a Function: Global Minimum and Local Minimum
3.1.1. Local Optimization
- Converges to a local minimum or maximum, depending on the problem.
- Performs well for convex functions where the local minimum is also the global minimum.
- Exhibits fast convergence but may become trapped in suboptimal solutions if multiple minima exist.
3.1.2. Global Optimization
- Broadly explore the solution space to avoid becoming trapped in local minima.
- Typically require higher computational effort.
- Suitable for nonlinear, non-convex, or highly constrained problems.
3.1.3. Key Differences Between Local and Global Optimization
3.2. Optimal Controllers
3.3. Optimized Controllers
4. Literature Review on Optimization Techniques for DC–AC Converters
4.1. Most Common Techniques for Low-Level Control of DC–AC Converters
4.1.1. Model-Based Optimization
Model Predictive Control
- is the control input and is the system output;
- is the reference signal;
- Q and R are weighting matrices;
- N is the prediction horizon;
- x is the system state, and , and define the system dynamics.
Linear Matrix Inequalities
- is the decision variable vector;
- , …, are symmetric matrices of appropriate dimensions;
- denotes negative semi-definiteness, ensuring is negative semi-definite.
- Stability analysis: using the Lyapunov function approach, system stability can be formulated as an LMI feasibility problem;
- Robust control: designing controllers that guarantee stability and performance under uncertainties, e.g., and control;
- State-feedback and observer design: finding gain matrices that satisfy performance and stability constraints.
Adaptive Control
- is the calculated parameter vector;
- is the internal signals vector;
- r is the reference signal;
- is the adaptation rate vector;
- is an auxiliary vector;
- is the reference model output;
- y is the system output.
4.1.2. Heuristics and Metaheuristics
Genetic Algorithms
Particle Swarm Optimization
- is the velocity of particle i at time step t;
- w is the inertia weight, controlling the influence of the previous velocity;
- and are acceleration coefficients that balance exploration (searching new regions of the space) and exploitation (refining known good solutions);
- and are random numbers sampled from a uniform distribution in ;
- is the personal best position of particle i, representing the best solution found by that particle;
- is the global best position found by the entire swarm.
Simulated Annealing
- If , the new solution is always accepted.
- If , the solution is accepted with probability , allowing occasional uphill moves to escape local minima.
Hybrid GA–PSO and Evolutionary Algorithms
4.1.3. Data-Driven and AI-Based Optimization
Reinforcement Learning
- is the policy that maps states to actions;
- is the reward at time step t;
- is the discount factor;
- T is the time horizon.
Deep Learning (DL)
- is the desired output;
- , represents the input data;
- is the neural network output;
- N is the number of training samples.
4.2. Stability Analysis of Optimization-Based Control Techniques
4.3. Comparison of Key Optimization Techniques and Summary
5. Future Directions and Emerging Trends
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Saeed, M.H.; Fangzong, W.; Kalwar, B.A.; Iqbal, S. A review on microgrids’ challenges & perspectives. IEEE Access 2021, 9, 166502–166517. [Google Scholar]
- International Energy Agency. Net Zero Roadmap: A Global Pathway to Keep the 1.5 °C Goal in Reach; International Energy Agency: Paris, France, 2023.
- Hu, J.; Shan, Y.; Guerrero, J.M.; Ioinovici, A.; Chan, K.W.; Rodriguez, J. Model predictive control of microgrids—An overview. Renew. Sustain. Energy Rev. 2021, 136, 110422. [Google Scholar] [CrossRef]
- Tahir, K.A.; Zamorano, M.; García, J.O. Scientific mapping of optimisation applied to microgrids integrated with renewable energy systems. Int. J. Electr. Power Energy Syst. 2023, 145, 108698. [Google Scholar] [CrossRef]
- Sulzberger, C. Pearl street in miniature: Models of the electric generating station [history]. IEEE Power Energy Mag. 2013, 11, 76–85. [Google Scholar] [CrossRef]
- Rosenberg, R.A. Academic Physics and the Origins of Electrical Engineering in America; The Johns Hopkins University: Baltimore, MD, USA, 1990. [Google Scholar]
- Kalam, A.; King, A.; Moret, E.; Weerasinghe, U. Combined heat and power systems: Economic and policy barriers to growth. Chem. Cent. J. 2012, 6, S3. [Google Scholar] [CrossRef]
- York, H.F. An outline history of nuclear proliferation. In International Terrorism and World Security; Routledge: Oxfordshire, UK, 2015; pp. 115–127. [Google Scholar]
- Stoll, B.; Andrade, J.; Cohen, S.; Brinkman, G.; Brancucci Martinez-Anido, C. Hydropower Modeling Challenges; Technical Report; National Renewable Energy Lab. (NREL): Golden, CO, USA, 2017. [Google Scholar]
- Neto, P.B.L.; Saavedra, O.R.; Oliveira, D.Q. The effect of complementarity between solar, wind and tidal energy in isolated hybrid microgrids. Renew. Energy 2020, 147, 339–355. [Google Scholar] [CrossRef]
- Kaboli, E. The Relationship Between Renewable Energy Production and Economic Growth at the Country Level. Master’s Thesis, Georgetown University, Washington, DC, USA, 2023. [Google Scholar]
- Rahman, A.; Farrok, O.; Haque, M.M. Environmental impact of renewable energy source based electrical power plants: Solar, wind, hydroelectric, biomass, geothermal, tidal, ocean, and osmotic. Renew. Sustain. Energy Rev. 2022, 161, 112279. [Google Scholar] [CrossRef]
- Yang, Y.; Xia, S.; Huang, P.; Qian, J. Energy transition: Connotations, mechanisms and effects. Energy Strategy Rev. 2024, 52, 101320. [Google Scholar] [CrossRef]
- Mohammadi, F.; Mohammadi-Ivatloo, B.; Gharehpetian, G.B.; Ali, M.H.; Wei, W.; Erdinç, O.; Shirkhani, M. Robust control strategies for microgrids: A review. IEEE Syst. J. 2021, 16, 2401–2412. [Google Scholar] [CrossRef]
- Uddin, M.; Mo, H.; Dong, D.; Elsawah, S.; Zhu, J.; Guerrero, J.M. Microgrids: A review, outstanding issues and future trends. Energy Strategy Rev. 2023, 49, 101127. [Google Scholar] [CrossRef]
- Doss-Gollin, J.; Farnham, D.J.; Lall, U.; Modi, V. How unprecedented was the February 2021 Texas cold snap? Environ. Res. Lett. 2021, 16, 064056. [Google Scholar] [CrossRef]
- Allwyn, R.G.; Al-Hinai, A.; Margaret, V. A comprehensive review on energy management strategy of microgrids. Energy Rep. 2023, 9, 5565–5591. [Google Scholar] [CrossRef]
- Yousri, D.; Farag, H.E.; Zeineldin, H.; El-Saadany, E.F. Integrated model for optimal energy management and demand response of microgrids considering hybrid hydrogen-battery storage systems. Energy Convers. Manag. 2023, 280, 116809. [Google Scholar] [CrossRef]
- Mbungu, N.T.; Siti, M.M.; Bansal, R.C.; Naidoo, R.M.; Elnady, A.; Ismail, A.A.A.; Abokhali, A.G.; Hamid, A.K. A dynamic coordination of microgrids. Appl. Energy 2025, 377, 124486. [Google Scholar] [CrossRef]
- Masrur, M.A.; Skowronska, A.G.; Hancock, J.; Kolhoff, S.W.; McGrew, D.Z.; Vandiver, J.C.; Gatherer, J. Military-based vehicle-to-grid and vehicle-to-vehicle microgrid—System architecture and implementation. IEEE Trans. Transp. Electrif. 2017, 4, 157–171. [Google Scholar] [CrossRef]
- Sarkar, R.; Saha, P.K.; Mondal, S.; Mondal, A. MAGE: Microgrids with Advanced Grid Efficiency through Battery-Aware EV management. Sustain. Cities Soc. 2024, 107, 105399. [Google Scholar] [CrossRef]
- Dahale, S.; Das, A.; Pindoriya, N.M.; Rajendran, S. An overview of DC-DC converter topologies and controls in DC microgrid. In Proceedings of the 2017 7th International Conference on Power Systems (ICPS), Pune, India, 21–23 December 2017; pp. 410–415. [Google Scholar]
- Xu, Q.; Vafamand, N.; Chen, L.; Dragičević, T.; Xie, L.; Blaabjerg, F. Review on advanced control technologies for bidirectional DC/DC converters in DC microgrids. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 9, 1205–1221. [Google Scholar] [CrossRef]
- Jadeja, R.; Ved, A.; Trivedi, T.; Khanduja, G. Control of power electronic converters in AC microgrid. In Microgrid Architectures, Control and Protection Methods; Springer: Berlin/Heidelberg, Germany, 2020; pp. 329–355. [Google Scholar]
- Hollweg, G.V.; de Oliveira Evald, P.J.D.; Tambara, R.V.; Gründling, H.A. A robust adaptive super-twisting sliding mode controller applied on grid-tied power converter with an LCL filter. Control Eng. Pract. 2022, 122, 105104. [Google Scholar] [CrossRef]
- Poolla, B.K.; Groß, D.; Dörfler, F. Placement and implementation of grid-forming and grid-following virtual inertia and fast frequency response. IEEE Trans. Power Syst. 2019, 34, 3035–3046. [Google Scholar] [CrossRef]
- Li, Y.; Gu, Y.; Green, T.C. Revisiting grid-forming and grid-following inverters: A duality theory. IEEE Trans. Power Syst. 2022, 37, 4541–4554. [Google Scholar] [CrossRef]
- Çelik, D.; Ahmed, H.; Meral, M.E. Kalman filter-based super-twisting sliding mode control of shunt active power filter for electric vehicle charging station applications. IEEE Trans. Power Deliv. 2022, 38, 1097–1107. [Google Scholar] [CrossRef]
- Wu, Y.; Wu, H.; Zhao, F.; Li, Z.; Wang, X. Influence of PLL on stability of interconnected grid-forming and grid-following converters. IEEE Trans. Power Electron. 2024, 39, 11980–11985. [Google Scholar] [CrossRef]
- Ackermann, T.; Prevost, T.; Vittal, V.; Roscoe, A.J.; Matevosyan, J.; Miller, N. Paving the way: A future without inertia is closer than you think. IEEE Power Energy Mag. 2017, 15, 61–69. [Google Scholar] [CrossRef]
- Barik, A.K.; Jaiswal, S.; Das, D.C. Recent trends and development in hybrid microgrid: A review on energy resource planning and control. Int. J. Sustain. Energy 2022, 41, 308–322. [Google Scholar] [CrossRef]
- Ibrahim, M.M.; Hasanien, H.M.; Farag, H.E.; Omran, W.A. Energy management of multi-area islanded hybrid microgrids: A stochastic approach. IEEE Access 2023, 11, 101409–101424. [Google Scholar] [CrossRef]
- Tariq, A.H.; Kazmi, S.A.A.; Hassan, M.; Ali, S.M.; Anwar, M. Analysis of fuel cell integration with hybrid microgrid systems for clean energy: A comparative review. Int. J. Hydrogen Energy 2024, 52, 1005–1034. [Google Scholar] [CrossRef]
- Fang, J.; Deng, H.; Tashakor, N.; Blaabjerg, F.; Goetz, S.M. State-space modeling and control of grid-tied power converters with capacitive/battery energy storage and grid-supportive services. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 11, 234–250. [Google Scholar] [CrossRef]
- Hollweg, G.V.; de Oliveira Evald, P.J.D.; Mattos, E.; Borin, L.C.; Tambara, R.V.; Gründling, H.A.; Su, W. A direct adaptive controller with harmonic compensation for grid-connected converters. IEEE Trans. Ind. Electron. 2023, 71, 2978–2989. [Google Scholar] [CrossRef]
- Singh Chawda, G.; Su, W.; Wang, M. A Comprehensive Review of High-Frequency AC Microgrids for Distribution Systems. IEEE Trans. Smart Grid 2024, 15, 5415–5428. [Google Scholar] [CrossRef]
- Rashidi, R.; Hatami, A.; Abedini, M. Multi-microgrid energy management through tertiary-level control: Structure and case study. Sustain. Energy Technol. Assess. 2021, 47, 101395. [Google Scholar] [CrossRef]
- Ahmad, S.; Shafiullah, M.; Ahmed, C.B.; Alowaifeer, M. A review of microgrid energy management and control strategies. IEEE Access 2023, 11, 21729–21757. [Google Scholar] [CrossRef]
- Dinkel, D.; Hillermeier, C.; Marquardt, R. Direct multivariable control for modular multilevel converters. IEEE Trans. Power Electron. 2022, 37, 7819–7833. [Google Scholar] [CrossRef]
- Hollweg, G.V.; Khan, S.A.; Chaturvedi, S.; Fan, Y.; Wang, M.; Su, W. Grid-connected converters: A brief survey of topologies, output filters, current control, and weak grids operation. Energies 2023, 16, 3611. [Google Scholar] [CrossRef]
- Sebaaly, F.; Vahedi, H.; Kanaan, H.Y.; Al-Haddad, K. Novel current controller based on MPC with fixed switching frequency operation for a grid-tied inverter. IEEE Trans. Ind. Electron. 2017, 65, 6198–6205. [Google Scholar] [CrossRef]
- Bordons, C.; Garcia-Torres, F.; Ridao, M.A. Model Predictive Control of Microgrids; Springer: Berlin/Heidelberg, Germany, 2020; Volume 358. [Google Scholar]
- Guo, B.; Su, M.; Sun, Y.; Wang, H.; Dan, H.; Tang, Z.; Cheng, B. A robust second-order sliding mode control for single-phase photovoltaic grid-connected voltage source inverter. IEEE Access 2019, 7, 53202–53212. [Google Scholar] [CrossRef]
- Teng, Q.; Xu, G.; Zheng, X.; Mai, H.; Ma, X.; Wang, Y. A novel sliding mode observer-based compound sliding mode current control with active damping for single phase grid-tied inverter system in weak grid. Int. J. Electr. Power Energy Syst. 2022, 141, 108117. [Google Scholar] [CrossRef]
- Saad, M.O.; Ulasyar, A.; Ali, W.; Zad, H.S.; Ullah, N.; Blazek, V.; Prokop, L.; Misak, S. Design and control of novel grid tied multilevel filter-less inverter using current based sliding mode control. IEEE Access 2022, 10, 115555–115570. [Google Scholar] [CrossRef]
- Tambara, R.V.; Kanieski, J.M.; Massing, J.R.; Stefanello, M.; Gründling, H.A. A discrete-time robust adaptive controller applied to grid-connected converters with LCL filter. J. Control Autom. Electr. Syst. 2017, 28, 371–379. [Google Scholar] [CrossRef]
- Li, H.; Ding, X.; Xue, R.; Li, G.; Chen, Y. Active damping adaptive controller for grid-connected inverter under weak grid. IEEE Access 2021, 9, 132442–132454. [Google Scholar] [CrossRef]
- Milbradt, D.M.C.; Hollweg, G.V.; de Oliveira Evald, P.J.D.; da Silveira, W.B.; Gründling, H.A. A robust adaptive one sample ahead preview controller for grid-injected currents of a grid-tied power converter with an LCL filter. Int. J. Electr. Power Energy Syst. 2022, 142, 108286. [Google Scholar] [CrossRef]
- Koch, G.G.; Osorio, C.R.; Pinheiro, H.; Oliveira, R.C.; Montagner, V.F. Design procedure combining linear matrix inequalities and genetic algorithm for robust control of grid-connected converters. IEEE Trans. Ind. Appl. 2019, 56, 1896–1906. [Google Scholar] [CrossRef]
- Mattos, E.; Borin, L.C.; Osório, C.R.D.; Koch, G.G.; Oliveira, R.C.; Montagner, V.F. Robust optimized current controller based on a two-step procedure for grid-connected converters. IEEE Trans. Ind. Appl. 2022, 59, 1024–1034. [Google Scholar] [CrossRef]
- Abbas, H.H.; Shafiee, Q.; Bevrani, H. Optimal passive LCL filter design for grid-connected converters in weak grids. Electr. Power Syst. Res. 2024, 235, 110896. [Google Scholar] [CrossRef]
- Speer, B.; Miller, M.; Schaffer, W.; Gueran, L.; Reuter, A.; Jang, B.; Widegren, K. Role of Smart Grids in Integrating Renewable Energy; Technical Report; National Renewable Energy Lab. (NREL): Golden, CO, USA, 2015. [Google Scholar]
- Outlook, I. Renewable Mini-Grids; International Renewable Energy Agency: Abu Dhabi, United Arab Emirates, 2016.
- Bouckaert, S.; Pales, A.F.; McGlade, C.; Remme, U.; Wanner, B.; Varro, L.; D’Ambrosio, D.; Spencer, T. Net Zero by 2050: A Roadmap for the Global Energy Sector; International Energy Agency: Paris, France, 2021.
- Chawda, G.S.; Shaik, A.G.; Mahela, O.P.; Padmanaban, S.; Holm-Nielsen, J.B. Comprehensive review of distributed FACTS control algorithms for power quality enhancement in utility grid with renewable energy penetration. IEEE Access 2020, 8, 107614–107634. [Google Scholar] [CrossRef]
- Alenius, H. Modeling and Electrical Emulation of Grid Impedance for Stability Studies of Grid-Connected Converters. Master’s Thesis, Tampere University of Technology, Tampere, Finland, 2018. [Google Scholar]
- Qin, W.; Wang, P.; Han, X.; Du, X. Reactive power aspects in reliability assessment of power systems. IEEE Trans. Power Syst. 2010, 26, 85–92. [Google Scholar] [CrossRef]
- Spring, A.; Wirth, G.; Becker, G.; Pardatscher, R.; Witzmann, R. Grid influences from reactive power flow of photovoltaic inverters with a power factor specification of one. IEEE Trans. Smart Grid 2015, 7, 1222–1229. [Google Scholar] [CrossRef]
- Alenius, H.; Luhtala, R.; Messo, T.; Roinila, T. Autonomous reactive power support for smart photovoltaic inverter based on real-time grid-impedance measurements of a weak grid. Electr. Power Syst. Res. 2020, 182, 106207. [Google Scholar] [CrossRef]
- Chawda, G.S.; Shaik, A.G. Power quality mitigation in weak AC grid with low X/R ratios using distribution static compensator controlled by LMF algorithm. In Proceedings of the 2020 IEEE Region 10 Symposium (TENSYMP), Dhaka, Bangladesh, 5–7 June 2020; pp. 44–47. [Google Scholar]
- Liu, Q.; Caldognetto, T.; Buso, S. Stability analysis and auto-tuning of interlinking converters connected to weak grids. IEEE Trans. Power Electron. 2019, 34, 9435–9446. [Google Scholar] [CrossRef]
- Chawda, G.S.; Shaik, A.G. Enhancement of wind energy penetration levels in rural grid using ADALINE-LMS controlled distribution static compensator. IEEE Trans. Sustain. Energy 2021, 13, 135–145. [Google Scholar] [CrossRef]
- Chawda, G.S.; Shaik, A.G. A reactive power-based adaptive approach for synchronization of DFIG into the weak grid to support existing WE infrastructure. Int. J. Electr. Power Energy Syst. 2024, 157, 109850. [Google Scholar] [CrossRef]
- Ochoa, D.E.; Galarza-Jimenez, F.; Wilches-Bernal, F.; Schoenwald, D.A.; Poveda, J.I. Control systems for low-inertia power grids: A survey on virtual power plants. IEEE Access 2023, 11, 20560–20581. [Google Scholar] [CrossRef]
- Badrudeen, T.U.; Nwulu, N.I.; Gbadamosi, S.L. Low-inertia control of a large-scale renewable energy penetration in power grids: A systematic review with taxonomy and bibliometric analysis. Energy Strategy Rev. 2024, 52, 101337. [Google Scholar] [CrossRef]
- Alemi, P.; Bae, C.J.; Lee, D.C. Resonance suppression based on PR control for single-phase grid-connected inverters with LLCL filters. IEEE J. Emerg. Sel. Top. Power Electron. 2015, 4, 459–467. [Google Scholar] [CrossRef]
- Wu, W.; Liu, Y.; He, Y.; Chung, H.S.H.; Liserre, M.; Blaabjerg, F. Damping methods for resonances caused by LCL-filter-based current-controlled grid-tied power inverters: An overview. IEEE Trans. Ind. Electron. 2017, 64, 7402–7413. [Google Scholar] [CrossRef]
- Giacomini, J.C.; Michels, L.; Pinheiro, H.; Rech, C. Design methodology of a passive damped modified LCL filter for leakage current reduction in grid-connected transformerless three-phase PV inverters. IET Renew. Power Gener. 2017, 11, 1769–1777. [Google Scholar] [CrossRef]
- Jiang, S.; Liu, Y.; Liang, W.; Peng, J.; Jiang, H. Active EMI filter design with a modified LCL-LC filter for single-phase grid-connected inverter in vehicle-to-grid application. IEEE Trans. Veh. Technol. 2019, 68, 10639–10650. [Google Scholar] [CrossRef]
- Wu, W.; Zhang, Y.; Blaabjerg, F.; Chung, H.S.H. A new type of three-phase asymmetric-LCL power filter for grid-tied voltage source inverter with step-up transformer. IEEE Trans. Ind. Electron. 2021, 69, 11936–11945. [Google Scholar] [CrossRef]
- Al-Barashi, M.; Meng, X.; Liu, Z.; Saeed, M.S.; Tasiu, I.A.; Wu, S. Enhancing power quality of high-speed railway traction converters by fully integrated T-LCL filter. IET Power Electron. 2023, 16, 699–714. [Google Scholar] [CrossRef]
- Basso, T.; Chakraborty, S.; Hoke, A.; Coddington, M. IEEE 1547 Standards advancing grid modernization. In Proceedings of the 2015 IEEE 42nd Photovoltaic Specialist Conference (PVSC), New Orleans, LA, USA, 14–19 June 2015; pp. 1–5. [Google Scholar]
- Cho, N.; Wendha, B.; Luthfi, M. Evaluations on the harmonic allocation methods of IEC 61000-3-6 and IEEE Standard 519 in the distribution systems. Electr. Power Syst. Res. 2024, 230, 110260. [Google Scholar] [CrossRef]
- Borin, L.C.; Hollweg, G.V.; Osório, C.R.; Carnielutti, F.M.; Oliveira, R.C.; Montagner, V.F. Automated test-driven design for robust optimized current control of GTIs operating under normal and abnormal grid conditions. Control Eng. Pract. 2024, 143, 105790. [Google Scholar] [CrossRef]
- Al-Shetwi, A.Q.; Sujod, M.Z.; Blaabjerg, F.; Yang, Y. Fault ride-through control of grid-connected photovoltaic power plants: A review. Sol. Energy 2019, 180, 340–350. [Google Scholar] [CrossRef]
- Zeb, K.; Islam, S.U.; Khan, I.; Uddin, W.; Ishfaq, M.; Busarello, T.D.C.; Muyeen, S.; Ahmad, I.; Kim, H. Faults and Fault Ride Through strategies for grid-connected photovoltaic system: A comprehensive review. Renew. Sustain. Energy Rev. 2022, 158, 112125. [Google Scholar] [CrossRef]
- Alshahrani, S.; Khan, K.; Abido, M.; Khalid, M. Grid-forming converter and stability aspects of renewable-based low-inertia power networks: Modern trends and challenges. Arab. J. Sci. Eng. 2024, 49, 6187–6216. [Google Scholar] [CrossRef]
- Rocabert, J.; Luna, A.; Blaabjerg, F.; Rodriguez, P. Control of power converters in AC microgrids. IEEE Trans. Power Electron. 2012, 27, 4734–4749. [Google Scholar] [CrossRef]
- Rosso, R.; Wang, X.; Liserre, M.; Lu, X.; Engelken, S. Grid-forming converters: Control approaches, grid-synchronization, and future trends—A review. IEEE Open J. Ind. Appl. 2021, 2, 93–109. [Google Scholar] [CrossRef]
- He, X.; Huang, L.; Subotić, I.; Häberle, V.; Dörfler, F. Quantitative stability conditions for grid-forming converters with complex droop control. IEEE Trans. Power Electron. 2024, 39, 10834–10852. [Google Scholar] [CrossRef]
- Zhang, C.; Dou, X.; Wang, L.; Dong, Y.; Ji, Y. Distributed cooperative voltage control for grid-following and grid-forming distributed generators in islanded microgrids. IEEE Trans. Power Syst. 2022, 38, 589–602. [Google Scholar] [CrossRef]
- Teng, Y.; Deng, W.; Pei, W.; Li, Y.; Dingv, L.; Ye, H. Review on grid-forming converter control methods in high-proportion renewable energy power systems. Glob. Energy Interconnect. 2022, 5, 328–342. [Google Scholar] [CrossRef]
- Bower, W.I.; Ton, D.T.; Guttromson, R.; Glover, S.F.; Stamp, J.E.; Bhatnagar, D.; Reilly, J. The Advanced Microgrid. Integration and Interoperability; Technical Report; Sandia National Lab. (SNL-NM): Albuquerque, NM, USA, 2014. [Google Scholar]
- IEEE Std 1547.2-2023; IEEE Application Guide for IEEE Std 1547™-2018, IEEE Standard for Interconnection and Interoperability of Distributed Energy Resources with Associated Electric Power Systems Interfaces. IEEE: Piscataway, NJ, USA, 2024; pp. 1–291. [CrossRef]
- IEEE Std 519-2022; IEEE Standard for Harmonic Control in Electric Power Systems. IEEE: Piscataway, NJ, USA, 2022; pp. 1–31. [CrossRef]
- Mahmud, R.; Hoke, A.; Narang, D. Validating the test procedures described in UL 1741 SA and IEEE P1547.1. In Proceedings of the 2018 IEEE 7th World Conference on Photovoltaic Energy Conversion (WCPEC) (A Joint Conference of 45th IEEE PVSC, 28th PVSEC & 34th EU PVSEC), Waikoloa, HI, USA, 1–15 June 2018; pp. 1445–1450. [Google Scholar] [CrossRef]
- IEEE Std 1815; IEEE Draft Standard for Exchanging Information Between Networks Implementing IEC 61850 and (Distributed Network Protocol-DNP3). IEEE: Piscataway, NJ, USA, 2012; pp. 1–283.
- Masetti, C. Revision of European Standard EN 50160 on power quality: Reasons and solutions. In Proceedings of the 14th International Conference on Harmonics and Quality of Power-ICHQP 2010, Bergamo, Italy, 26–29 September 2010; pp. 1–7. [Google Scholar]
- Murray, R.M. Optimization-Based Control; California Institute of Technology: Pasadena, CA, USA, 2009; pp. 111–128. [Google Scholar]
- Törn, A.; Žilinskas, A. Global Optimization; Springer: Berlin/Heidelberg, Germany, 1989; Volume 350. [Google Scholar]
- Floudas, C.A.; Pardalos, P.M. Recent Advances in Global Optimization; Princeton University Press: Princeton, NJ, USA, 2014. [Google Scholar]
- Tabibpour, S.A.; Madanizadeh, S.A. Solving High-Dimensional Dynamic Programming Using Set Transformer. SSRN 2024. [Google Scholar]
- Lü, X.; He, S.; Xu, Y.; Zhai, X.; Qian, S.; Wu, T.; WangPei, Y. Overview of improved dynamic programming algorithm for optimizing energy distribution of hybrid electric vehicles. Electr. Power Syst. Res. 2024, 232, 110372. [Google Scholar] [CrossRef]
- Liberzon, D. Calculus of Variations and Optimal Control Theory: A Concise Introduction; Princeton University Press: Princeton, NJ, USA, 2011. [Google Scholar]
- Chen, W.H. Stability analysis of classic finite horizon model predictive control. Int. J. Control Autom. Syst. 2010, 8, 187–197. [Google Scholar] [CrossRef]
- Chen, H.; Allgöwer, F. A quasi-infinite horizon nonlinear model predictive control scheme with guaranteed stability. Automatica 1998, 34, 1205–1217. [Google Scholar] [CrossRef]
- Scokaert, P.O.; Rawlings, J.B. Constrained linear quadratic regulation. IEEE Trans. Autom. Control 1998, 43, 1163–1169. [Google Scholar] [CrossRef]
- Hannan, M.; Tan, S.Y.; Al-Shetwi, A.Q.; Jern, K.P.; Begum, R. Optimized controller for renewable energy sources integration into microgrid: Functions, constraints and suggestions. J. Clean. Prod. 2020, 256, 120419. [Google Scholar] [CrossRef]
- Dmitruk, K.; Sikorski, A. A Novel Continuous Control Set Current-Based Model Predictive Control for a Three-Phase, Two-Level AC/DC Converter with the LCL filter. IEEE Trans. Power Electron. 2024. [Google Scholar] [CrossRef]
- Sivadharshini, A.; Nguyen, N.D.; Lee, Y.I. Model Predictive Current Control for Grid-connected Inverter Considering the PLL Dynamics. Int. J. Control Autom. Syst. 2024, 22, 3255–3265. [Google Scholar] [CrossRef]
- Song, Y.; Zhang, B.; Wen, C.; Wang, D.; Wei, G. Model predictive control for complicated dynamic systems: A survey. Int. J. Syst. Sci. 2025, 1–26. [Google Scholar] [CrossRef]
- Derakhshan, S.; Kanathipan, K.; Abbasi, M.; Cheema, M.A.M.; Lam, J. A Robust H∞ State Feedback Controller Enabling a Medium Voltage Five-Level Grid-Connected Inverter for Grid Code Compliance. IEEE Trans. Power Deliv. 2023, 39, 647–660. [Google Scholar] [CrossRef]
- Koch, G.G.; Osório, C.R.; Oliveira, R.C.; Montagner, V.F. Robust Control Based on Observed States Designed by Means of Linear Matrix Inequalities for Grid-Connected Converters. Energies 2023, 16, 2047. [Google Scholar] [CrossRef]
- Hollweg, G.V.; Tambara, R.V.; Massing, J.R.; Borin, L.C.; Mattos, E.; Koch, G.G.; Osório, C.R.D.; Montagner, V.F. Model reference adaptive controllers with improved performance for applications in LCL-filtered grid-connected converters. Control Eng. Pract. 2023, 138, 105591. [Google Scholar] [CrossRef]
- Hollweg, G.V.; Evald, P.J.D.d.O.; Tambara, R.V.; Su, W.; Gründling, H.A. A modified robust adaptive super-twisting sliding mode controller for grid-connected converters. Int. J. Control Autom. Syst. 2023, 21, 3151–3165. [Google Scholar] [CrossRef]
- da Silva, M.S.; Hollweg, G.V.; Leston, L.A.; de Oliveira Evald, P.J.D. Enhancing energy quality and grid stability with improved adaptive controller for renewable energy conversion systems under weak grid conditions. Electr. Power Syst. Res. 2024, 237, 111041. [Google Scholar] [CrossRef]
- Hollweg, G.V.; de Oliveira Evald, P.J.D.; Mattos, E.; Borin, L.C.; Tambara, R.V.; Montagner, V.F. Self-tuning methodology for adaptive controllers based on genetic algorithms applied for grid-tied power converters. Control Eng. Pract. 2023, 135, 105500. [Google Scholar] [CrossRef]
- Babu, V.V.; Roselyn, J.P.; Sundaravadivel, P. Multi-objective genetic algorithm based energy management system considering optimal utilization of grid and degradation of battery storage in microgrid. Energy Rep. 2023, 9, 5992–6005. [Google Scholar] [CrossRef]
- Iqbal, H.; Sarwat, A. Improved Genetic Algorithm-Based Harmonic Mitigation Control of an Asymmetrical Dual-Source 13-Level Switched-Capacitor Multilevel Inverter. Energies 2025, 18, 35. [Google Scholar] [CrossRef]
- Jasim, A.M.; Jasim, B.H.; Bureš, V.; Mikuleckỳ, P. A novel cooperative control technique for hybrid AC/DC smart microgrid converters. IEEE Access 2023, 11, 2164–2181. [Google Scholar] [CrossRef]
- Hollweg, G.V.; Evald, P.J.D.d.O.; Mattos, E.; Borin, L.C.; Tambara, R.V.; Montagner, V.F. Optimized parametrization of adaptive controllers for enhanced current regulation in grid-tied converters. Int. J. Adapt. Control Signal Process. 2024, 38, 200–220. [Google Scholar] [CrossRef]
- Nayak, P.C.; Mishra, S.; Prusty, R.C.; Panda, S. Hybrid whale optimization algorithm with simulated annealing for load frequency controller design of hybrid power system. Soft Comput. 2023, 1–24. [Google Scholar]
- Izci, D.; Ekinci, S.; Çelik, E.; Bajaj, M.; Blazek, V.; Prokop, L. Dynamic load frequency control in power systems using a hybrid simulated annealing based quadratic interpolation optimizer. Sci. Rep. 2024, 14, 26011. [Google Scholar] [CrossRef]
- de Oliveira Evald, P.J.D.; Hollweg, G.V.; Borin, L.C.; Mattos, E.; Tambara, R.V.; Montagner, V.F.; Gründling, H.A. A smart parametrisation for robust adaptive PI controller applied on renewable energy power generation systems under weak and uttermost weak grid conditions. Comput. Electr. Eng. 2024, 116, 109203. [Google Scholar] [CrossRef]
- Parada, V. Automatic Generation of Algorithms; CRC Press: Boca Raton, FL, USA, 2025. [Google Scholar]
- Singh Chawda, G.; Prakash Mahela, O.; Gupta, N.; Khosravy, M.; Senjyu, T. Incremental conductance based particle swarm optimization algorithm for global maximum power tracking of solar-PV under nonuniform operating conditions. Appl. Sci. 2020, 10, 4575. [Google Scholar] [CrossRef]
- Gao, F.; Hu, R.; Yin, L. Variable boundary reinforcement learning for maximum power point tracking of photovoltaic grid-connected systems. Energy 2023, 264, 126278. [Google Scholar] [CrossRef]
- Xu, Y.; Gao, W.; Li, Y.; Xiao, F. Operational optimization for the grid-connected residential photovoltaic-battery system using model-based reinforcement learning. J. Build. Eng. 2023, 73, 106774. [Google Scholar] [CrossRef]
- Hollweg, G.V.; Bui, V.H.; Da Silva, F.L.; Glatt, R.; Chaturvedi, S.; Su, W. An RMRAC with Deep Symbolic Optimization for DC–AC Converters Under Less-Inertia Power Grids. IEEE Open Access J. Power Energy 2023, 10, 629–642. [Google Scholar] [CrossRef]
- Rajamallaiah, A.; Karri, S.P.K.; Alghaythi, M.L.; Alshammari, M.S. Deep reinforcement learning based control of a grid connected inverter with LCL-filter for renewable solar applications. IEEE Access 2024, 12, 22278–22295. [Google Scholar] [CrossRef]
- Thajeel, S.M.; Atilla, D.Ç. Reinforcement Neural Network-Based Grid-Integrated PV Control and Battery Management System. Energies 2025, 18, 637. [Google Scholar] [CrossRef]
| Challenge | GFM Converters | GFL Converters |
|---|---|---|
| Synchronization | Self-regulated; does not rely on an external reference | Requires external grid voltage for synchronization |
| Voltage and frequency regulation | Must generate and stabilize voltage and frequency | Follows grid voltage and frequency |
| Control complexity | Higher due to frequency control, droop control, virtual inertia, and power-sharing algorithms | Lower, as the reference is externally defined |
| Transition handling | Must ensure smooth transitions between grid-connected and islanded operation | Typically remains grid-connected; islanding can cause instability |
| Inertia and stability | Requires synthetic inertia and damping techniques to compensate for low system inertia | Contributes to inertia issues in weak grids but does not directly compensate |
| Load variation response | Directly responsible for stabilizing sudden load changes | Reacts to changes but relies on the grid for stability |
| Multi-inverter coordination | Requires precise coordination to avoid circulating currents and phase mismatches | Less critical since synchronization is externally dictated |
| Standards | Description | Comments |
|---|---|---|
| IEEE 1547 | Provides criteria and requirements for the interconnection of distributed energy resources with electric power systems. | Establishes uniform standards for performance, operation, testing, safety, and maintenance of interconnections. Ensures reliable integration of DERs into the grid. |
| IEEE 519 | Defines recommended practices and requirements for harmonic control in power systems. | Specifies acceptable levels of voltage and current harmonics to maintain power quality and mitigate interference issues in microgrids. |
| UL 1741 | Standard for inverters, converters, controllers, and interconnection system equipment for distributed energy resources. | Ensures compliance with safety and performance requirements for grid-tied inverters and converters. Often used in conjunction with IEEE 1547. |
| IEC 61850 | Standard for communication networks and systems in substations. | Defines protocols and data models for substation automation, supporting seamless communication between protection and control devices in microgrids. |
| EN 50160 | Specifies voltage characteristics of electricity supplied by public distribution networks in Europe. | Ensures consistency in voltage levels, waveform quality, and power frequency across different grid conditions. |
| EN 50549-1 | Defines requirements for the connection of generating plants to distribution networks. | Focuses on grid connection of renewable energy systems up to and including Type B generation, ensuring compliance with grid stability criteria. |
| NPR 9090 | Dutch practice guideline for low-voltage DC installations. | Provides design and safety considerations for DC microgrids, emphasizing proper isolation and protection mechanisms. |
| Aspect | Local Optimization | Global Optimization |
|---|---|---|
| Search Scope | Limited to a local region | Searches the entire solution space |
| Convergence Speed | Fast for convex functions | Typically slower due to broader search |
| Risk of Becoming Stuck | High (in local minima) | Lower (designed to escape local minima) |
| Computational complexity | Lower | Higher |
| Suitable Problems | Convex and smooth functions | Nonlinear, non-convex, and complex problems |
| Example Methods | Gradient Descent, Newton’s Method | Genetic Algorithms, Particle Swarm, Reinforcement Learning |
| Optimization Technique | Key Characteristics | Advantages | Limitations | Ref. | Comments |
|---|---|---|---|---|---|
| Model Predictive Control | Utilizes system models to predict future states and optimize control actions | Ensures optimal performance | Requires highly accurate models; stability, design, and implementation are challenging | [100,101] | Effective for systems with well-defined dynamics; may perform poorly when unmodeled dynamics are significant |
| Linear Matrix Inequalities | Employs convex optimization techniques for controller design | Provides robust control solutions with low computational burden; may achieve optimal performance | Limited to linear or linearized systems; may be conservative | [102,103] | Suitable for systems where linear approximations are valid |
| Adaptive control | May require a reference model (if direct-type); operates by estimating or measuring system states; can be designed with simplified reduced-order models | Robust to matched and unmatched dynamics; delivers satisfactory performance (may not be optimal); can stabilize unstable systems | Challenging to design initial gains; stability, design, and implementation are nontrivial | [104,106] | Suitable for various systems; non-minimum phase zeros and frequency-rich references may pose challenges |
| Genetic Algorithm | Mimics natural selection to find optimal solutions | Does not require explicit models; flexible and simple to implement | May converge to local optima; computationally demanding; usually implemented offline | [107,108] | Useful for complex optimization problems with large search spaces; easily combinable with other metaheuristics |
| Particle Swarm Optimization | Simulates the social behavior of swarms to explore optimal solutions | Simple implementation; efficient search capabilities; faster convergence compared to similar metaheuristics | May suffer from premature convergence; requires parameter tuning; computationally demanding; usually implemented offline | [110,111] | Effective for optimizing microgrid operations with multiple renewable sources; easily combinable with other metaheuristics |
| Reinforcement Learning | Learns optimal control policies through interaction with the environment | Handles complex, nonlinear dynamics; adaptable and potentially highly robust to uncertainties | Requires extensive, high-quality training data; usually implemented offline | [117,118] | Promising for systems with high uncertainty and variability; computationally intensive (especially for training) |
| Neural network-based control | Utilizes neural networks to model and control system behavior | Capable of approximating complex functions; adaptable and potentially highly robust to uncertainties | Prone to overfitting with deep architectures; requires extensive high-quality data; usually implemented offline | [119,120] | Promising for systems where traditional modeling is challenging; needs substantial computational resources (especially for training) |
| Optimization Technique | Boundary Conditions | Challenges |
|---|---|---|
| Model Predictive Control | Requires an accurate system model; works best with systems that have well-defined state-space representations | Computationally intensive for high-dimensional systems; stability and feasibility depend on tuning and constraints; may struggle with harsh unmodeled dynamics |
| Linear Matrix Inequalities | Limited to convex optimization problems; most effective for linear or linearized systems | May be conservative; not suitable for highly nonlinear systems; require accurate system characterization |
| Adaptive control | Can handle system uncertainties; typically assumes system dynamics are slowly time-varying or, at least, much slower than the adaptation rate | Requires appropriate parameter initialization; stability depends on adaptation laws; non-minimum phase systems pose challenges |
| Genetic Algorithm | Effective for global optimization in high-dimensional spaces; does not require explicit system models | High computational cost; convergence is not guaranteed to be globally optimal; often requires offline implementation |
| Particle Swarm Optimization | Works well for problems with large search spaces; requires a well-defined fitness function | Susceptible to premature convergence; requires parameter tuning; typically implemented offline due to computational demands |
| Reinforcement Learning | Suitable for highly nonlinear and uncertain environments; can adapt to dynamic conditions | Requires extensive training data; computationally expensive for real-time applications; stability and safety are difficult to guarantee |
| Neural network-based control | Can approximate complex nonlinear functions; does not require explicit system equations | Prone to overfitting; requires large datasets for training; computationally expensive, limiting real-time feasibility |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hollweg, G.V.; Singh Chawda, G.; Chaturvedi, S.; Bui, V.-H.; Su, W. Optimization Techniques for Low-Level Control of DC–AC Converters in Renewable-Integrated Microgrids: A Brief Review. Energies 2025, 18, 1429. https://doi.org/10.3390/en18061429
Hollweg GV, Singh Chawda G, Chaturvedi S, Bui V-H, Su W. Optimization Techniques for Low-Level Control of DC–AC Converters in Renewable-Integrated Microgrids: A Brief Review. Energies. 2025; 18(6):1429. https://doi.org/10.3390/en18061429
Chicago/Turabian StyleHollweg, Guilherme Vieira, Gajendra Singh Chawda, Shivam Chaturvedi, Van-Hai Bui, and Wencong Su. 2025. "Optimization Techniques for Low-Level Control of DC–AC Converters in Renewable-Integrated Microgrids: A Brief Review" Energies 18, no. 6: 1429. https://doi.org/10.3390/en18061429
APA StyleHollweg, G. V., Singh Chawda, G., Chaturvedi, S., Bui, V.-H., & Su, W. (2025). Optimization Techniques for Low-Level Control of DC–AC Converters in Renewable-Integrated Microgrids: A Brief Review. Energies, 18(6), 1429. https://doi.org/10.3390/en18061429












