A Novel AVR System Utilizing Fuzzy PIDF Enriched by FOPD Controller Optimized via PSO and Sand Cat Swarm Optimization Algorithms

Abstract

Power system stability is managed through various control loops, including the Automatic Voltage Regulator (AVR), which regulates the terminal voltage of synchronous generators. This study integrated Fuzzy Logic Control (FLC) and a Proportional–Integral–Derivative controller with Filtered derivative action (PIDF) to propose a hybrid Fuzzy PIDF controller enhanced by Fractional-Order Proportional-Derivative (FOPD) for AVR applications. For the first time, the newly introduced Sand Cat Swarm Optimization (SCSO) algorithm was applied to the AVR system to tune the parameters of the proposed fuzzy controller. The SCSO algorithm has been recognized as a powerful optimization tool and has demonstrated success across various engineering applications. The well-known Particle Swarm Optimization (PSO) algorithm was also utilized in this study to optimize the gains of the proposed controller. The Fuzzy PIDF plus FOPD is a novel configuration that is designed to be a robust control technique for AVR to achieve an excellent performance. In this research, the Fuzzy PIDF + FOPD controller was optimized using the PSO and SCSO algorithms by minimizing the Integral Time Absolute Error (ITAE) objective function to enhance the overall performance of AVR systems. A comparative analysis was conducted to evaluate the superiority of the proposed approach by benchmarking the results against those of other controllers reported in the literature. Furthermore, the robustness of the controller was assessed under parametric uncertainties and varying load disturbances. Also, its robustness was examined against disturbances in the control signal. The results demonstrate that the proposed Fuzzy PIDF + FOPD controller tuned by the PSO and SCSO algorithms delivers exceptional performance as an AVR controller, outperforming other controllers. Additionally, the findings confirm the robustness of the Fuzzy PIDF + FOPD controller against parametric uncertainties, establishing its potential for a successful implementation in real-time applications.

1. Introduction

1.1. General Overview

The Automatic Voltage Regulator (AVR) is one of the two critical controllers operating within a Synchronous Generator (SG). According to power system theory, these controllers include the centrally managed Load–Frequency Controller (LFC) and the locally controlled AVR. The AVR functions as a simple closed-loop control system, adjusting the voltage output of the SG through an exciter signal [1].

Ensuring robust and consistent control is crucial for maintaining power system stability and reliability. Voltage stability in power systems relies on balancing the reactive power demanded by loads with the reactive power supplied by SGs. While modern power systems utilize advanced methods such as shunt capacitors, shunt/series reactors, and FACTS devices to maintain this equilibrium, the literature consistently identifies the AVR as the most effective technique [2]. Moreover, power-generating units constantly strive to minimize power losses, a critical challenge in control engineering, to enhance overall efficiency and performance. One of the most effective strategies to address these losses is the optimal design and implementation of AVR systems [3].

The primary function of an AVR system is to maintain the generator’s output voltage at predetermined standard levels, ensuring stability and consistency in power generation. These systems are integral to achieving a reliable and efficient operation by mitigating voltage fluctuations and optimizing overall generator performance. A crucial aspect of AVR systems is their ability to minimize power losses within the generator section through precise voltage regulation. Operating within a closed-loop configuration, AVR systems consist of five interdependent components: the regulator, amplifier, exciter, generator, and sensor. These components work in unison to maintain voltage stability and ensure effective control, highlighting the indispensable role of AVR systems in modern power generation infrastructure [4,5].

1.2. Literature Review

Voltage variation remains a critical challenge in power systems, prompting the development of various control techniques founded on diverse theoretical frameworks. Among these, the Proportional–Integral–Derivative (PID) controller has emerged as a foundational approach, extensively utilized not only for voltage regulation but also across a broad spectrum of control applications [6]. It is reported that approximately 90% of industrial control loops employ this conventional method, reflecting its reliability and widespread acceptance [7]. Over time, the PID controller has been adapted into numerous configurations based on advanced theoretical principles and has been hybridized with other control methodologies to enhance its performance. Furthermore, its integration with soft computing techniques has enabled the optimization of gain parameters, thereby achieving superior performance and improved operational efficiency.

A review of the recent literature highlights the development of a wide range of control strategies for AVR systems, including linear, optimal, and robust control approaches. However, most studies consider the traditional PID as a good and easy solution.

Table 1. Outline of the control methods and optimization tools of AVR systems in the literature.

Reference	Control Method	Optimization Tool
[8]	PID	Local Unimodal Sampling Optimization (LUSA) algorithm
[9]	PID	Improved kidney-inspired (IKA) algorithm
[10]	PID	Tree Seed Algorithm (TSA)
[11]	PID	Improved Whale Optimization Algorithm (IWOA)
[12]	PID	Artificial Bee Colony (ABC) Algorithm
[13]	PID	Stochastic Fractal Search (SFS) algorithm
[14]	PID	Water Wave Optimization (WWO)
[15]	PID	Cuckoo Search (CS)
[16]	PID	Particle Swarm Optimization (PSO)
[17]	PID	Grey Wolf Optimizer (GWO)
[18]	PID	Zebra Optimization Algorithm (ZOA)
[19]	PID	Improved Variants of Reptile Search Algorithm (RSA)
[20]	PID	Ant Colony Optimization and Nelder–Mead algorithm (ACONM)
[21]	PIDA	Whale Optimization Algorithm (WOA)
[22]	FOPID and Filtered FOPID	Hybrid simulated annealing (SA) and white shark optimization (WSO) algorithm
[23]	FOPID	Chaotic Black Widow Optimization (ChBWO)
[24]	FOPID	Modified Smoothed Function Algorithm (MSFA)
[25]	PIλDND2N2	Coyote Optimization Algorithm (COA)
[26]	FVOPID	Yellow Saddle Goatfish (YSG) algorithm
[27]	FOPID	Dumbo Octopus Algorithm (DOA)
[28]	FOPID	Automated Algorithm Design (AAD)
[29]	TIλDND2N2	Equilibrium Optimizer (EO) Algorithm
[30]	SMC	Improved Particle Swarm Optimization (IPSO) algorithm
[31]	MPC	Arithmetic Optimization Algorithm (AOA)
[32]	H infinity	Manually tuned
[33]	Adaptive Control	Genetic algorithm (GA)
[34]	LQR	Manually tuned
[35]	Adaptive Neuro-Fuzzy Inference System (ANFIS)	Self-tuned
[36]	FLC	Imperialistic Competitive Algorithm (ICA)
[37]	FLC	Manually tuned

provides a comprehensive overview of the existing AVR controllers from the literature. The conventional PID controller has been widely employed in AVR systems due to its simplicity and ease of implementation. However, achieving optimal performance requires precise tuning of the controller’s parameters (${\mathrm{K}}_{\mathrm{p}}, {\mathrm{K}}_{\mathrm{i}}, {\mathrm{K}}_{\mathrm{d}}$) to effectively manage load disturbances and address uncertainties in system parameters. Traditional tuning methods, such as Ziegler–Nichols (ZN), Trial-and-Error (TE), Cohen–Coon (CC), and root-locus techniques, often fall short in delivering accurate results, particularly in complex systems. To overcome these limitations, researchers have increasingly turned to soft computing based on heuristic and metaheuristic optimization algorithms to determine the optimal PID parameters. Optimization tools such as the Local Unimodal Sampling Optimization (LUSA) algorithm [8], improved kidney-inspired (IKA) algorithm [9], Tree Seed Algorithm (TSA) [10], Improved Whale Optimization Algorithm (IWOA) [11], Artificial Bee Colony (ABC) algorithm [12], Stochastic Fractal Search (SFS) algorithm [13], Water Wave Optimization (WWO) [14], Cuckoo Search (CS) [15], Particle Swarm Optimization (PSO) [16], Grey Wolf Optimizer (GWO) [17], Zebra Optimization Algorithm (ZOA) [18], Improved Variants of Reptile Search Algorithm (RSA) [19], and Ant Colony Optimization and Nelder–Mead algorithm (ACONM) [20] have been used to determine the optimal values of the PID controller in order to achieve the best possible performance.

While the classical PID controller is widely acknowledged for its effectiveness, numerous variants have been proposed in the literature to enhance its flexibility and improve performance in AVR systems. These advanced configurations aim to address the limitations of the traditional PID approach, offering more robust and adaptive solutions to meet the dynamic requirements of modern power systems. A PID with acceleration gain (PIDA) tuned by the Whale Optimization Algorithm (WOA) is proposed in [21]. The proposed PIDA achieved better performance than the classical PID. Fractional-Order PID (FOPID) with two more parameters, λ and μ in addition to the main three ${\mathrm{K}}_{\mathrm{p}}, {\mathrm{K}}_{\mathrm{i}}, {\mathrm{K}}_{\mathrm{d}}$, where λ is the order integration and μ is the order of differentiator is also considered for AVR applications. It has been reported that the FOPID is likely to outperform the traditional PID. In [22], the hybrid simulated annealing (SA) and white shark optimization (WSO) algorithm were used to optimally tune the parameters of PID, FOPID, and filtered FOPID, in which promising results were obtained. Chaotic Black Widow Optimization (ChBWO) was used in [23] to determine the optimal gains of FOPID for an AVR system using a new cost function. A Modified Smoothed Function Algorithm (MSFA) is proposed in [24] to tune the parameters of FOPID, and a fast and robust performance was secured. Different configurations and hybridization were introduced to further enhance the reliability and overall performance of the FOPID controller. A novel PI^λDND²N²-based Coyote Optimization Algorithm (COA) is introduced in [25] for AVR applications. This controller outperformed the classical PID, FOPID, and ${\mathrm{PIDD}}^2$. A new Fractional-Variable-Order PID (FVOPID)-based Yellow Saddle Goatfish (YSG) algorithm for AVR systems is presented in [26]. Other unique versions of FOPID based on different optimization techniques for AVR applications are presented in [27,28,29].

Notably, other modern control methodologies, including Sliding Mode Control (SMC) [30], Model Predictive Control (MPC) [31], H infinity control [32], adaptive control [33], and Linear Quadratic Regulator (LQR) [34], have been relatively underutilized in AVR applications. These strategies are known for their robust performance in handling system uncertainties and disturbances, offering potential advantages over conventional approaches.

Sliding Mode Control (SMC) is highly valued for its ability to handle matched uncertainties effectively, guaranteeing that system trajectories converge to and remain on a specified sliding surface. This feature grants SMC a degree of immunity to specific disturbances. While it has proven effective in fields such as power electronics, its real-world application is frequently hindered by issues like the chattering effect and the intricacies involved in its implementation.

Model Predictive Control (MPC) excels in managing multi-variable systems and constraints by forecasting future system behavior and optimizing control inputs accordingly. This advanced approach makes it well-suited for intricate and dynamic systems. However, its reliance on precise system models and substantial computational resources can limit its effectiveness in real-time applications.

H∞ control is tailored to manage systems with nonlinearities and uncertainties, delivering robust performance in varying conditions. By framing the control duty as a mathematical optimization task, H∞ controllers achieve stabilization with guaranteed performance bounds. However, their practical implementation can be limited by the intricate design process and the requirement for very detailed system mathematical models.

Adaptive control continuously modifies controller parameters in real time to accommodate system changes, which, in turn, enhances the performance. This method has found widespread use in areas like aerospace, where systems frequently encounter significant uncertainties. Despite its potential, the complexity involved in designing and analyzing adaptive controllers has constrained their broader adoption.

Linear Quadratic Regulator (LQR) offers an optimal control framework by minimizing a quadratic cost function that balances state error and control effort. It provides a systematic design methodology for linear systems, making it a popular choice in control applications. However, LQR does not inherently address robustness to model uncertainties, which can be a limitation in certain scenarios.

Despite the theoretical strengths of these advanced control strategies, their practical application in AVR systems remains relatively rare. This can be attributed to challenges such as implementation complexity, computational demands, and the need for accurate system modeling. Addressing these challenges could facilitate broader adoption and unlock their full potential in AVR applications.

Fuzzy Logic Control (FLC) has demonstrated successful implementations across a diverse range of applications owing to its notable advantages, including robustness, ease of design, and reduced reliance on precise system modeling. Despite these merits, FLC has received comparatively less attention in the context of AVR applications, representing a potential area for further research. Although the utilization of FLC in AVR applications has been limited [35,36,37], existing studies have yielded promising results, underscoring the potential for further investigation into its capabilities and potential enhancements in this domain.

1.3. Motivation and Contribution

In AVR systems, achieving an optimal equilibrium between rapid dynamic response and system stability constitutes a fundamental challenge. A fast transient response, albeit accompanied by overshoot, facilitates prompt voltage stabilization, which is particularly critical in dynamic operational environments characterized by frequent and abrupt load variations. This capability ensures the system can swiftly restore nominal voltage levels following disturbances, thereby minimizing operational downtime and preserving system continuity. However, such rapid responses may transiently exceed predefined voltage thresholds, posing a risk of damage to sensitive equipment, particularly electronic devices susceptible to voltage transients. Conversely, a slower response devoid of overshoot maintains voltage within stringent safety limits, thereby ensuring the protection of connected equipment. Nevertheless, this approach may result in transient undervoltage or overvoltage conditions during load transitions, potentially undermining system performance and reliability. Consequently, designing an ideal AVR controller requires balancing these competing objectives—harmonizing rapid response with minimal overshoot—based on specific application requirements and system constraints to ensure both performance and safety.

While various control strategies have been developed to address these challenges, their practical implementation in AVR systems continues to face limitations. Traditional controllers, such as PID controllers, remain the most commonly used due to their simplicity, cost-effectiveness, and ease of implementation. These controllers, however, exhibit inherent limitations in handling nonlinearities, parametric uncertainties, and high system sensitivities—conditions increasingly common in modern applications.

For instance, PID controllers are often unable to provide robust performance in scenarios where operating points vary significantly, leading to degraded voltage stability during dynamic load changes.

Advanced control strategies, including adaptive control and SMC, offer enhanced robustness and adaptability for AVR systems. Adaptive control, for example, dynamically amends controller gains in real time to compensate for changing system dynamics. This ability has been shown to significantly improve performance in environments with high uncertainty or variable loads, as evidenced by its successful application in aerospace systems. However, adaptive controllers are often characterized by high design complexity and require precise real-time tuning, which can hinder their widespread adoption in AVR systems. Similarly, SMC is well-regarded for its robustness against matched uncertainties and its ability to maintain system trajectories within a sliding manifold, rendering it insensitive to certain disturbances. Research has demonstrated its effectiveness in power electronics and voltage regulation tasks. Nevertheless, SMC’s practical implementation is often limited by the chattering phenomenon—a high-frequency oscillation that can compromise system performance and even induce mechanical or electrical wear in certain applications.

FLCs have emerged as a promising alternative for AVR applications due to their ability to handle system nonlinearities and uncertainties without requiring a precise mathematical model. FLCs employ linguistic rules and expert knowledge to make control decisions, making them particularly suitable for complex systems with dynamic behaviors. Despite their advantages, existing FLC designs often fail to address reliability considerations, which are critical for ensuring consistent performance under varying operating conditions. For example, while some fuzzy control approaches effectively improve voltage regulation, many lack mechanisms to ensure robustness against parametric uncertainties and load disturbances.

In summary, while traditional PID controllers remain widely used due to their simplicity and low cost, they often fall short in addressing the demands of modern AVR applications. Advanced methods such as adaptive control and SMC, although theoretically robust and effective, are hindered by their implementation complexity and computational overhead. Similarly, fuzzy control methods show potential for AVR systems but require further development to incorporate reliability and robustness into their design frameworks. These limitations highlight the need for innovative control strategies that not only address the challenges of voltage regulation but also provide enhanced reliability, robustness, and ease of implementation for AVR systems in dynamic and uncertain environments. This paper introduces a novel hybrid fuzzy controller that combines the adaptability of Fuzzy Logic Control with the advantages of classical control techniques while explicitly addressing performance reliability. The key contributions of this study are summarized as follows:

• Innovative Controller Design: A unique AVR configuration is proposed, integrating a Fuzzy Proportional–Integral–Derivative with Filtered derivative action (PIDF) controller with an FOPD (Fuzzy PIDF + FOPD) controller. This hybrid configuration leverages the strengths of both fuzzy and classical control methodologies to enhance system stability and performance.
• Optimization via Sand Cat Swarm Optimization (SCSO) algorithm: The algorithm is utilized for the first time in AVR applications to optimize the parameters of the proposed controller. This metaheuristic algorithm is selected for successful implementation in handling complex optimization problems, ensuring the controller achieves optimal performance. The widely and successfully implemented PSO algorithm is also employed in this study to optimize the parameters of the proposed controller.
• Comprehensive Comparative Analysis: A detailed comparative analysis is conducted between the proposed controller and other controllers reported in the literature.
• Robustness Assessment: The proposed Fuzzy PIDF + FOPD controller is rigorously tested for robustness against parametric uncertainties and various load disturbances. The results demonstrate the controller’s resilience and reliability in maintaining voltage stability under challenging operating conditions.

By integrating advanced fuzzy control with fractional-order dynamics and employing a novel optimization technique, this study offers a significant advancement in AVR controller design. The findings underscore the potential of the proposed approach to address the limitations of existing methods, ensuring reliable and robust voltage regulation in dynamic and uncertain environments.

1.4. Paper Organization

This research paper has been categorized as follows: Section 2 describes the mathematical model of the AVR system and its step response with no controller equipped. Section 3 explains the structure of the introduced controller and provides a concise description of the utilized optimization tool and objective function. Section 4 demonstrates and discusses the obtained results. Section 5 provides a robustness analysis of the AVR system with the controller. Finally, Section 6 provides a brief conclusion and proposes different directions for future work.

2. The AVR System

Figure 1 provides an overview of the mechanism of the AVR system. The AVR system is primarily composed of four key components: the amplifier, exciter, sensor, and generator. These components collectively ensure the regulation of the generator’s terminal voltage, which is critical for maintaining consistent power quality.

During power generation, the terminal voltage of an unregulated generator may fluctuate due to varying load conditions. Such fluctuations can significantly degrade the overall power quality. To address this issue, a closed-loop control system, such as the AVR, is indispensable for ensuring stable and high-quality power output.

In the AVR system, the generator’s terminal voltage is continuously monitored by a voltage feedback sensor. The amplifier processes the voltage error, defined as the difference between the feedback voltage and the reference voltage. If the voltage error is positive, the exciter increases the excitation current to boost the voltage gain, and conversely, it reduces the excitation when the voltage error is negative. This feedback mechanism ensures that the generator’s terminal voltage remains regulated, thereby maintaining optimal power quality.

As illustrated in Figure 1, the AVR system’s structure is defined by its four fundamental components: the amplifier, exciter, sensor, and generator. The block diagram of the system is presented in Figure 2, and the transfer functions of these components, which characterize their dynamic behavior, are represented in

Table 2. The range and implemented values of the AVR model.

AVR Component	Transfer Function	Implemented Value
Generator	${\displaystyle \frac{{\mathrm{K}}_{\mathrm{g}}}{1 + \mathrm{s} {\mathsf{\tau }}_{\mathrm{g}}}}$	${\mathrm{K}}_{\mathrm{g}}=1, {\mathsf{\tau }}_{\mathrm{g}}=1$
Excitor	${\displaystyle \frac{{\mathrm{K}}_{\mathrm{e}}}{1 + \mathrm{s} {\mathsf{\tau }}_{\mathrm{e}}}}$	${\mathrm{K}}_{\mathrm{e}}=1, {\mathsf{\tau }}_{\mathrm{e}}=0.4$
Sensor	${\displaystyle \frac{{\mathrm{K}}_{\mathrm{s}}}{1 + \mathrm{s} {\mathsf{\tau }}_{\mathrm{s}}}}$	${\mathrm{K}}_{\mathrm{s}}=1, {\mathsf{\tau }}_{\mathrm{s}}=0.01$
Amplifier	${\displaystyle \frac{{\mathrm{K}}_{\mathrm{a}}}{1 + \mathrm{s} {\mathsf{\tau }}_{\mathrm{a}}}}$	${\mathrm{K}}_{\mathrm{g}}=10, {\mathsf{\tau }}_{\mathrm{g}}=0.1$

[10].

The transfer function of the AVR system is modeled using Laplace transform. Each component of the model is linearized for analytical convenience. The closed-loop transfer function of the model presented in Figure 2 based on the parameters given in Table 2 is illustrated in Equation (1). The step response of the system is illustrated in Figure 3, with the corresponding characteristics detailed in

Table 3. The characteristics of the AVR model.

Characteristics	Value
Peak Overshoot	1.5066 pu
Peak Time	0.7522 s
Settling Time	6.9865 s
Rise Time	0.2607

. The system’s model features a single zero located at −100, two real poles positioned at −99.9712 + 0 i and −12.4892 + 0 i, and a pair of conjugate poles at −0.5198 + 4.6642 i and −0.5198–4.6642 i, as depicted in the root locus plot presented in Figure 4.

$${\mathrm{TF}}_{\mathrm{AVR}}={\displaystyle \frac{0.1 \mathrm{s}+10}{0.0004 {\mathrm{s}}^4+0.045 {\mathrm{s}}^3+0.555 {\mathrm{s}}^2+1.51 \mathrm{s}+11}}$$

(1)

Based on the aforementioned characteristics, it is evident that an appropriate control design is essential to enhance the system’s overall performance. The development and analysis of the controller are detailed in Section 3.

3. The Proposed Controller and Optimization Tool

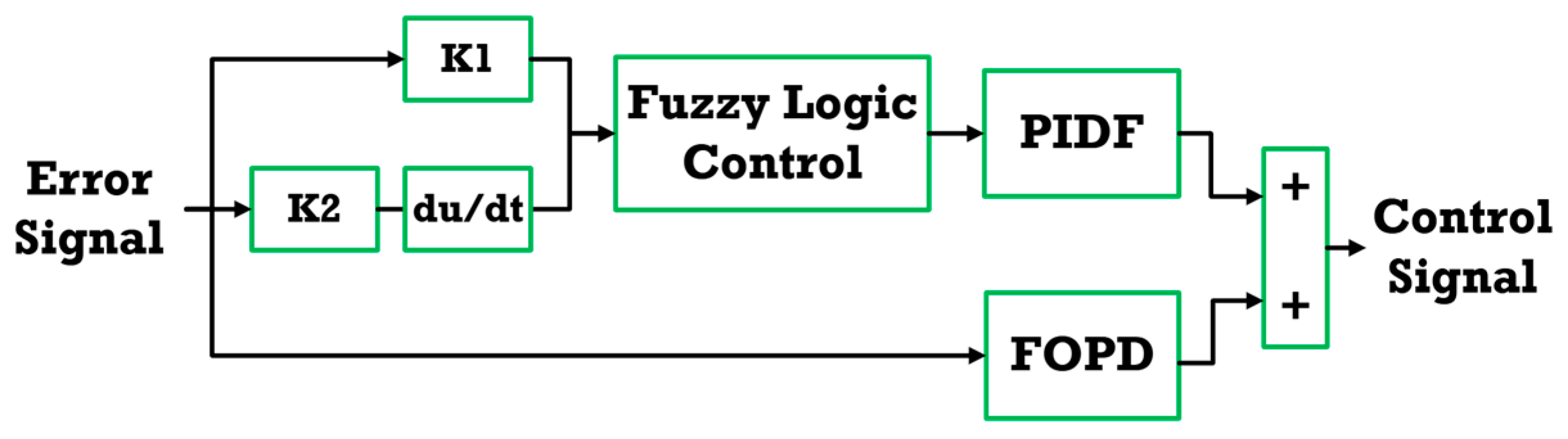
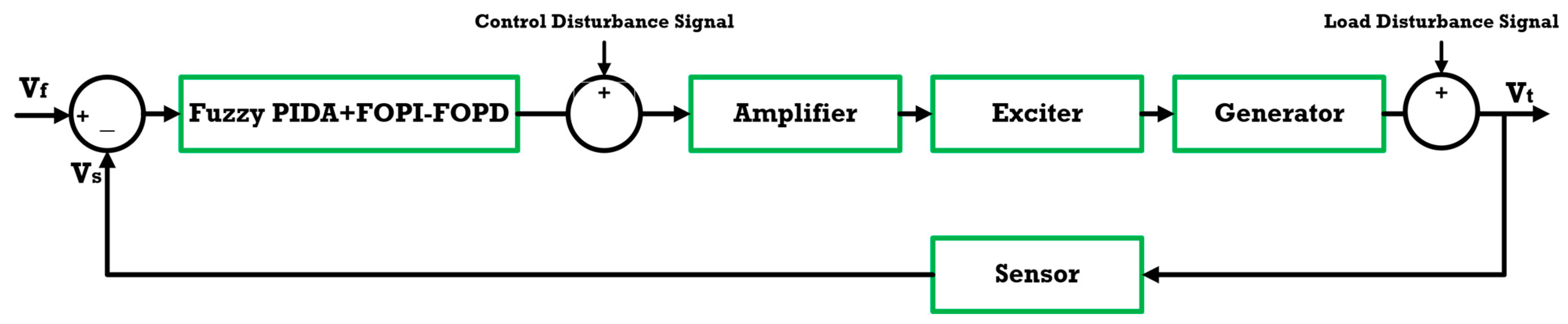
3.1. Fuzzy PIDF Plus FOPD

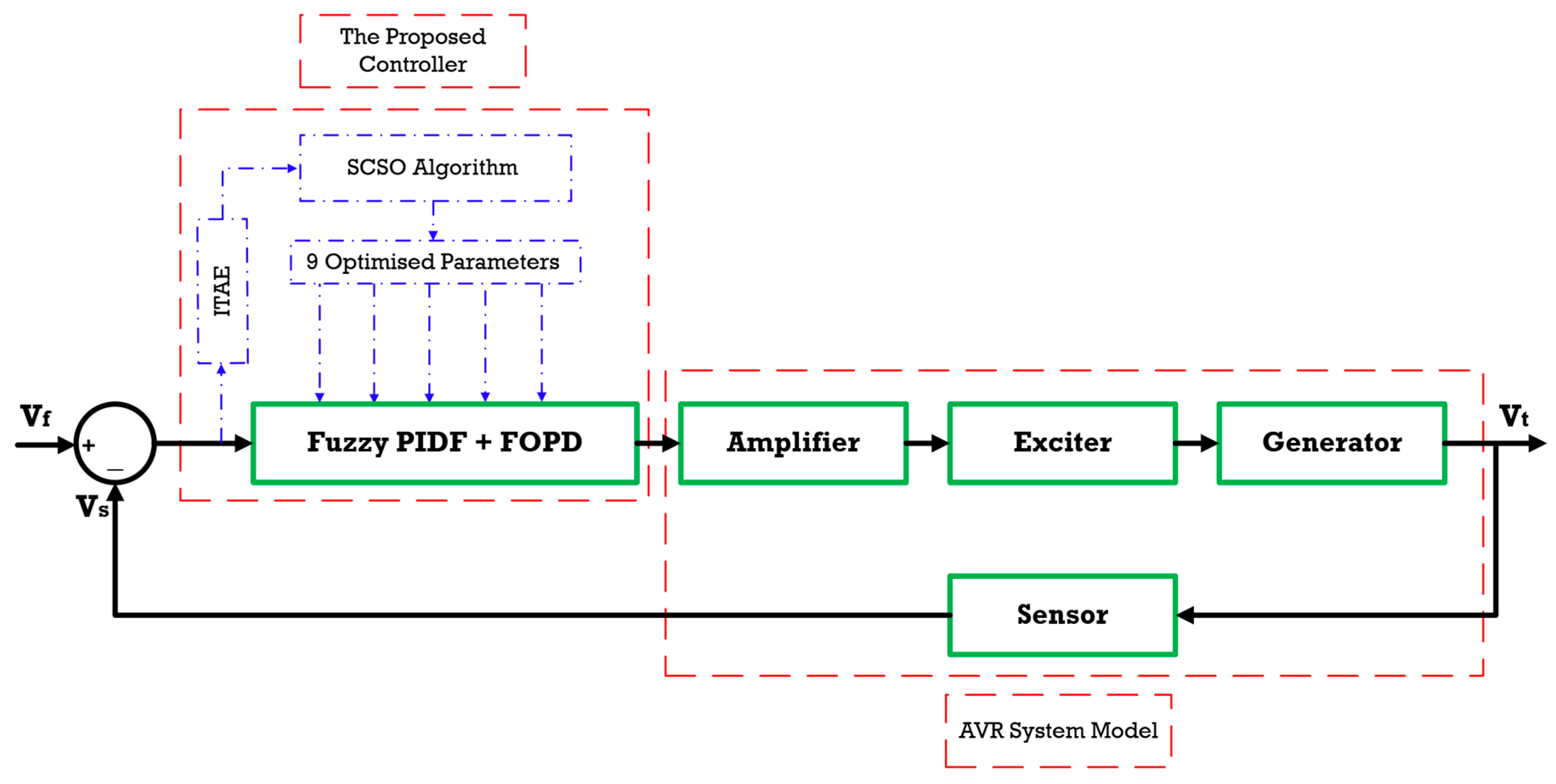
Figure 5 illustrates the structural schematic of the proposed control strategy, which integrates three core components: a fuzzy logic controller, a PIDF controller, and an FOPD controller. The fuzzy logic controller is meticulously designed with two primary input variables: the error signal and its derivative. 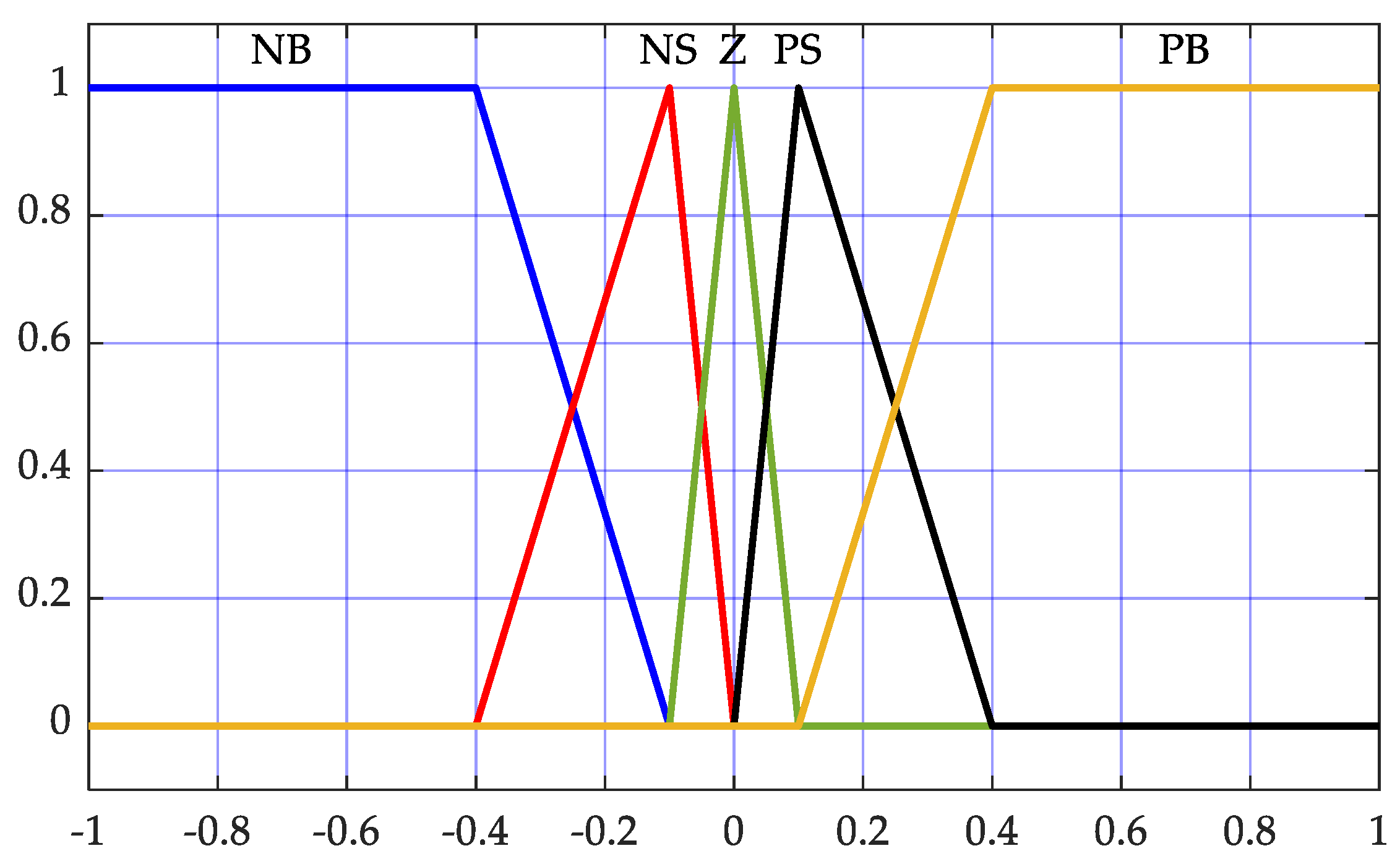These inputs are normalized using scaling factors, denoted as ${\mathrm{K}}_1 {\mathrm{and} \mathrm{K}}_2$, respectively. The controller produces a single output, which is subsequently directed as an input to the PIDF controller. To maintain the computational simplicity and efficiency of the fuzzy controller, the design incorporates five triangular membership functions for both input and output variables, as depicted in Figure 6. These membership functions are defined as Negative Big (NB), Negative Small (NS), Zero (Z), Positive Small (PS), and Positive Big (PB). The output of the fuzzy controller is determined through a rule base comprising 25 fuzzy rules, which are systematically outlined in

Table 4. The rule base of the FLC part.

Error	Change of Error
	NB	NS	Z	PS	PB
NB	NB	NB	NB	NS	Z
NS	NB	NB	NS	Z	PS
Z	NB	NS	Z	BS	PB
PS	NS	Z	PS	PB	PB
PB	Z	PS	PB	PB	PB

. These rules were formulated based on an in-depth analysis of the dynamic characteristics of the testbed model. The Mamdani inference mechanism is employed for the fuzzification process, facilitating the conversion of crisp input data into fuzzy sets. For defuzzification, the centroid method is applied, converting the fuzzy output into a precise, real-valued control signal. This methodological approach ensures both the computational efficiency and robust performance of the fuzzy logic controller. The PIDF controller is another form of the conventional PID controller, incorporating an additional gain parameter, referred to as the filter action gain with the derivative (${\mathrm{K}}_{\mathrm{f}}$). The transfer function of the PIDF controller is presented in Equation (2), where ${\mathrm{K}}_{\mathrm{p}}, {\mathrm{K}}_{\mathrm{i}}, {\mathrm{K}}_{\mathrm{d}}, \mathrm{and} {\mathrm{K}}_{\mathrm{F}}$ are the proportional, integral, derivative, and filter gains, respectively.

$${\mathrm{PIDF} \mathrm{Controller}}_{\mathrm{c}}\left(\mathrm{S}\right)={\mathrm{K}}_{\mathrm{p}}+{\displaystyle \frac{{\mathrm{K}}_{\mathrm{i}}}{\mathrm{S}}}+{\displaystyle \frac{{\mathrm{K}}_{\mathrm{d}}{\mathrm{K}}_{\mathrm{F}}}{1+ {\mathrm{K}}_{\mathrm{F}} \frac{1}{\mathrm{S}}}}$$

(2)

Concurrently, the FOPD controller processes the error signal as its input. The transfer function of the FOPD controller is presented in Equation (3); μ is the order of differentiator, ${\mathrm{K}}_{\mathrm{p}1}$ is the proportional gain for the FOPD controller, and ${\mathrm{K}}_{\mathrm{d}1}$ is the derivative gain.

$${\mathrm{FOPD} \mathrm{Controller}}_{\mathrm{c}}\left(\mathrm{S}\right)=({\mathrm{K}}_{\mathrm{p}1}+{(\mathrm{K}}_{\mathrm{d}1}{\mathrm{S}}^{\mathsf{\mu }})$$

(3)

The final control signal is synthesized by integrating the output of the fuzzy-PIDF controller with that of the FOPD controller. This unified control architecture markedly enhances the overall performance of the proposed control strategy.

3.2. Sand Cat Swarm Optimization (SCSO), PSO Algorithm, and Objective Function

The Sand Cat Swarm Optimization (SCSO) algorithm is a nature-inspired metaheuristic derived from the unique behaviors of sand cats in their natural habitat [38]. The SCSO algorithm offers several advantages, making it highly effective for complex engineering problems. It balances exploration and exploitation phases through adaptive sensitivity control, which helps avoid local optima and improves convergence rates. With reduced parameter dependency, SCSO simplifies implementation and requires less tuning. Its robust search capability ensures adaptability to dynamic environments, such as fluctuating load conditions in power systems. The algorithm is computationally efficient with low memory requirements, making it suitable for real-time applications. SCSO is versatile, being applicable to both global optimization and real-world problems, including smart grids, robotics, and bioinformatics. Its decentralized agent behavior allows for effective scalability in high-dimensional problem spaces, mitigating the curse of dimensionality. Additionally, SCSO’s flexibility enables it to handle nonlinear or discontinuous constraints, making it suitable for multi-objective optimization and energy-efficient design tasks.

The algorithm emulates the sand cat’s specialized mechanisms for searching and hunting prey. Sand cats possess distinctive characteristics compared to domestic cats, such as the ability to detect low-frequency sounds, adapt to the harsh desert environment, and employ specialized hunting strategies. While their physical appearance is similar to that of domestic cats, sand cats are distinguished by a dense layer of fur on their palms and soles, aiding in their survival in arid terrains.

A notable behavioral adaptation of sand cats is their extraordinary capacity to detect low-frequency sounds, particularly those below 2 kHz, which they use to locate prey. This unique foraging and hunting ability forms the foundation of the SCSO algorithm, which is designed to identify solutions close to the global optimum. According to the No Free Lunch (NFL) theorem [39,40], no single metaheuristic algorithm can guarantee optimal performance for every optimization problem. Nevertheless, the SCSO algorithm has demonstrated reliable performance across a wide range of optimization tasks, making it a competitive choice among existing metaheuristic approaches.

The execution of the SCSO algorithm commences with the initialization of the parameter search space, a foundational step shared among population-based metaheuristic algorithms. The search space is randomly populated within specified lower and upper bounds, which are defined by the constraints of the optimization problem. These bounds establish the limits within which the search is conducted. The dimensionality of the search space is dictated by the number of decision variables (represented as columns), while the number of search agents corresponds to the rows. This randomly generated search space comprises candidate solutions that are progressively refined through iterative processes, enabling the algorithm to converge toward an optimal solution.

To evaluate the quality of candidate solutions, a well-defined fitness (or cost) function tailored to the specific optimization problem is employed. Depending on the problem’s objective—whether maximization or minimization—the algorithm steers the search process toward the optimal solution. During each iteration, the SCSO algorithm ensures that all candidate solutions remain within the specified boundaries of the search space.

The search agents then explore the search space continuously, updating their positions and progressing toward regions where the optimal solution is likely to reside. This process mimics the sand cat’s hunting mechanism, where it methodically approaches the prey’s predicted location. The exploration and exploitation strategies employed by the SCSO algorithm are designed to balance global exploration and local refinement, ensuring robust convergence to solutions near the global optimum. The specific mechanisms governing the search and hunting strategies differ among metaheuristic algorithms, contributing to their unique strengths and applicability to various optimization challenges.

In the SCSO algorithm, the prey-searching mechanism is augmented by the unique capability of each sand cat to detect and exploit low-frequency noise emissions. The sensitivity range (R) for each search agent is predefined within the interval [2,0]. The parameter $\overrightarrow{r_G}$ denotes the general sensitivity range, which systematically decreases from 2 to 0 over the course of iterations, as regulated by Equations (4)–(6).

In Equation (4), the parameter $S_M$, which corresponds to the sand cat’s ability to perceive low-frequency signals below 2 kHz, is assigned a value of 2. The iterative process is characterized by ${iter}_c$, representing the current iteration number, and ${iter}_{max}$ denoting the maximum number of iterations. Additionally, $\overrightarrow{X_c}$ refers to the current position of the search agent,$\overrightarrow{X_b}$ indicates the best position encountered so far, and $\overrightarrow{X_{rand}}$ denotes a randomly selected position within the search space, as defined in Equations (7), (8a) and (8b).

In the SCSO algorithm, search agents exhibit a circular motion to explore the search space effectively and investigate potential global solutions. This circular movement facilitates diversification by enabling agents to explore different directions. The random angle $\mathsf{\vartheta }$, uniformly distributed between 0 and 360 degrees, is incorporated as a cosine function (cos($\mathsf{\vartheta }$)) to model this behavior [40].

The primary structural equations governing the SCSO algorithm are presented in Equation (9). These equations encapsulate the algorithm’s unique mechanisms for balancing exploration and exploitation, enabling robust convergence toward the global optimum by leveraging the sand cat’s biologically inspired hunting strategies.

$$\overrightarrow{{\mathrm{r}}_{\mathrm{G}}}= {\mathrm{S}}_{\mathrm{M}}-\left({\displaystyle \frac{{\mathrm{S}}_{\mathrm{M}} \times {\mathrm{iter}}_{\mathrm{c}}}{{\mathrm{iter}}_{\max }}}\right)$$

(4)

$$\mathrm{R}=2 \times \overrightarrow{{\mathrm{r}}_{\mathrm{G}}} \times \mathrm{rand} \left(0, 1\right)-\overrightarrow{{\mathrm{r}}_{\mathrm{G}}}$$

(5)

$$\overrightarrow{\mathrm{r}}=\overrightarrow{{\mathrm{r}}_{\mathrm{G}}} \times \mathrm{rand} \left(0, 1\right)$$

(6)

$$\overrightarrow{\mathrm{X}}\left(\mathrm{t}+1\right)=\overrightarrow{\mathrm{r}}. \left(\overrightarrow{{\mathrm{X}}_{\mathrm{b}}}\left(\mathrm{t}\right)- \mathrm{rand} \left(0, 1\right). \overrightarrow{{\mathrm{X}}_{\mathrm{c}}} (\mathrm{t})\right)$$

(7)

$$\overrightarrow{{\mathrm{X}}_{\mathrm{rnd}}}=\left|\mathrm{rand} \left(0, 1\right). \overrightarrow{{\mathrm{X}}_{\mathrm{b}}}\left(\mathrm{t}\right)-\overrightarrow{{\mathrm{X}}_{\mathrm{c}}}\left(\mathrm{t}\right)\right|$$

(8a)

$$\overrightarrow{\mathrm{X}}\left(\mathrm{t}+1\right)=\overrightarrow{{\mathrm{X}}_{\mathrm{b}}}\left(\mathrm{t}\right)-\overrightarrow{\mathrm{r}}. \overrightarrow{{\mathrm{X}}_{\mathrm{rnd}}}.\cos \left(\mathsf{\vartheta }\right)$$

(8b)

$$\overrightarrow{\mathrm{X}}\left(\mathrm{t}+1\right)=\left\{\begin{array}{cc}\overrightarrow{\mathrm{r}}. \left(\overrightarrow{{\mathrm{X}}_{\mathrm{b}}}\left(\mathrm{t}\right)- \mathrm{rand} \left(0, 1\right). \overrightarrow{{\mathrm{X}}_{\mathrm{c}}} (\mathrm{t})\right)\hfill & \left|\mathrm{R}\right| >1\\ \left(\overrightarrow{{\mathrm{X}}_{\mathrm{b}}}\left(\mathrm{t}\right)-\overrightarrow{\mathrm{r}} . \overrightarrow{{\mathrm{X}}_{\mathrm{rnd}}} .\cos \left(\mathsf{\vartheta }\right)\right)\hfill & \left|\mathrm{R}\right| \le 1\end{array}\right.$$

(9)

The fundamental operational principle of the Sand Cat Swarm Optimization (SCSO) method is to identify potential optimal solutions within a randomly initialized search space, drawing inspiration from the sand cat’s behavior of seeking and attacking prey. Depending on the problem at hand, the objective of the algorithm can be framed as either the minimization or maximization of an appropriate cost function. 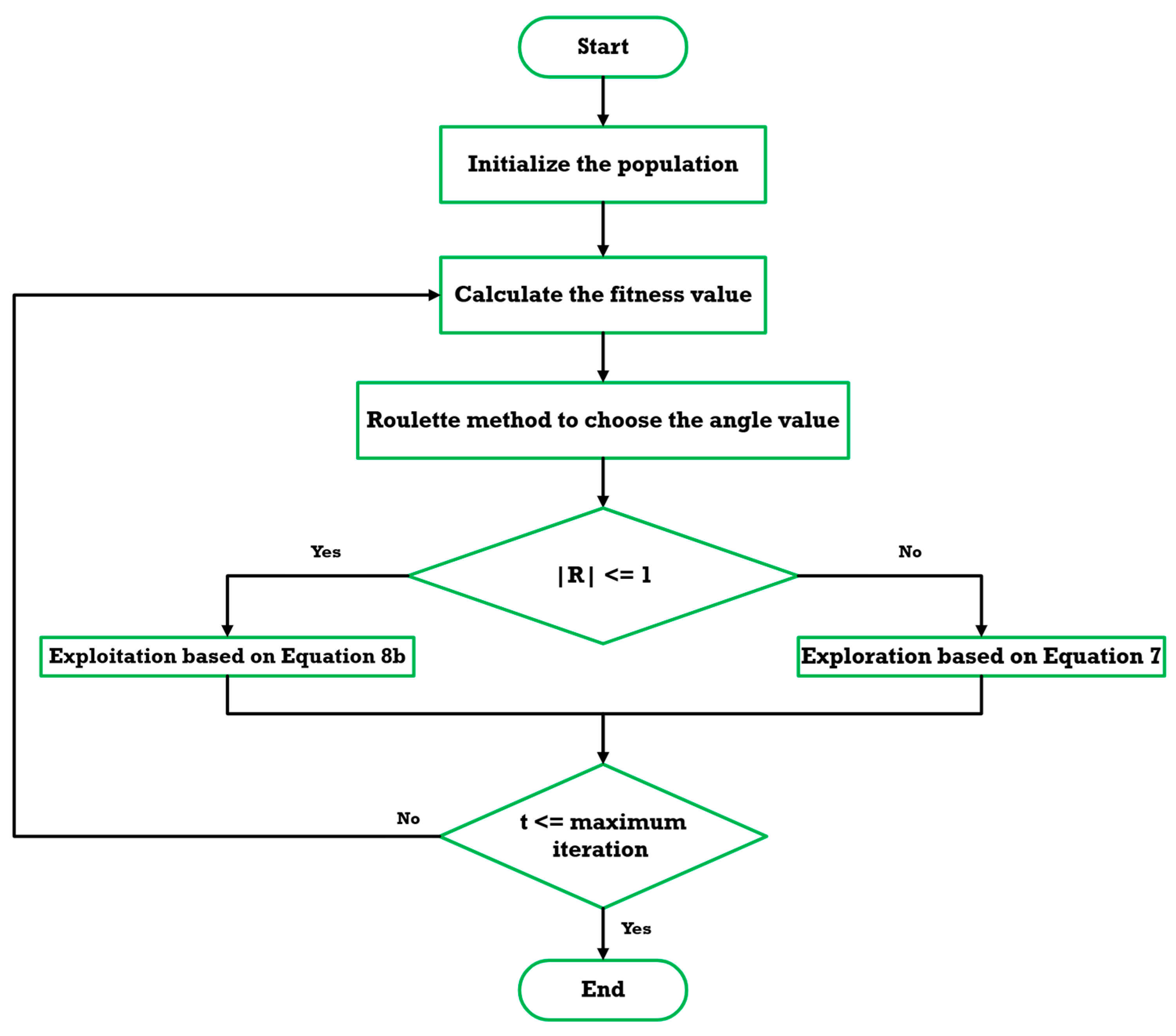Figure 7 illustrates the flowchart of the SCSO algorithm. Based on this flowchart and the following procedural steps, the optimal control parameters can be determined:

Step 1: The initial phase entails configuring the parameters for the SCSO-based control algorithm and establishing the lower and upper bounds for the unknown parameters within the designated search space. In the context of the AVR system, these parameters represent the gains of the proposed controller, encompassing a total of nine controller gains, as illustrated in Figure 8. Furthermore, it is necessary to define the number of search agents and the maximum number of iterations to guide the optimization process.

Step 2: Each search agent evaluates the fitness value of its corresponding candidate solution based on the problem’s defined cost function. This step facilitates the assessment of solution quality in the context of the optimization objective.

Step 3: The SCSO algorithm is then executed to determine the optimal solution. Based on the fitness function, the algorithm identifies the best score and the corresponding optimal position within the search space. Subsequently, the positions of the search agents are updated according to Equation (4). It is important to emphasize that selecting an appropriate performance index for the metaheuristic algorithm is critical to achieving effective optimization.

Step 4: A predefined stopping criterion is incorporated as part of the SCSO algorithm. In this case, the stopping criterion is satisfied when the maximum number of iterations is reached, signaling the algorithm to terminate.

PSO is a nature-inspired optimization algorithm that simulates the collective behavior of birds or fish. It initializes a population of particles (candidate solutions) that move within the search space, adjusting their positions based on personal experience and the best-performing neighbor. Each particle updates its velocity and position using a combination of its own best-known solution and the global best solution found by the swarm. This iterative process enables PSO to efficiently explore and exploit the search space, making it effective for solving complex optimization problems. More explanation about the mechanism of the algorithm and how it can be implemented is well explained in [16,41]. The parameters of the PSO used in this study are set as shown in

Table 5. PSO parameters.

No. Particles	Wmax	Wmin	C1	C2	Vmax	Vmin	No. Iterations
50	1.2	0.2	1.2	1.2	(ub − lb) × 0.2	−Vmax	50

.

Here are the definitions of the PSO parameters:

➢

No. Particles is the number of particles, the total number of particles (candidate solutions) in the swarm. In this case, 50 particles are used.

➢

No. Iteration is the maximum iterations, the maximum number of iterations the algorithm will run before stopping, set to 50.

➢

Wmax is the maximum inertia weight, the upper limit of the inertia weight, which controls the influence of a particle’s previous velocity on its current velocity. A larger value encourages global exploration.

➢

Wmin is the minimum inertia weight, the lower limit of the inertia weight, promoting local exploitation as the algorithm progresses.

➢

C1 is the cognitive coefficient, the acceleration coefficient that controls the influence of a particle’s personal best solution on its velocity update.

➢

C2 is the social coefficient, the acceleration coefficient that controls the influence of the global best solution (best solution found by any particle) on the particle’s velocity update.

➢

Vmax is the maximum velocity, the upper limit of the particle’s velocity, preventing excessive movement. It is calculated as 20% of the search space range (upper bounds−lower bounds).

➢

Vmin is the minimum velocity, the lower limit of the particle’s velocity, ensuring that velocity does not drop below a certain threshold. It is set as −Vmax.

These parameters govern the exploration and exploitation balance in the PSO algorithm, affecting its convergence speed and solution quality.

In this study, the gains of the proposed Fuzzy PIDF + FOPD used for AVR applications were fine-tuned using the SCSO algorithm by minimizing the Integral Time Absolute Error (ITAE) cost function, which is mathematically expressed as in Equation (10):

$$\mathrm{Objective} \mathrm{function}=\mathrm{ITAE}={\int }_0^{\mathrm{t}}\left|\mathrm{e}\right|.\mathrm{t}.\mathrm{dt}$$

(10)

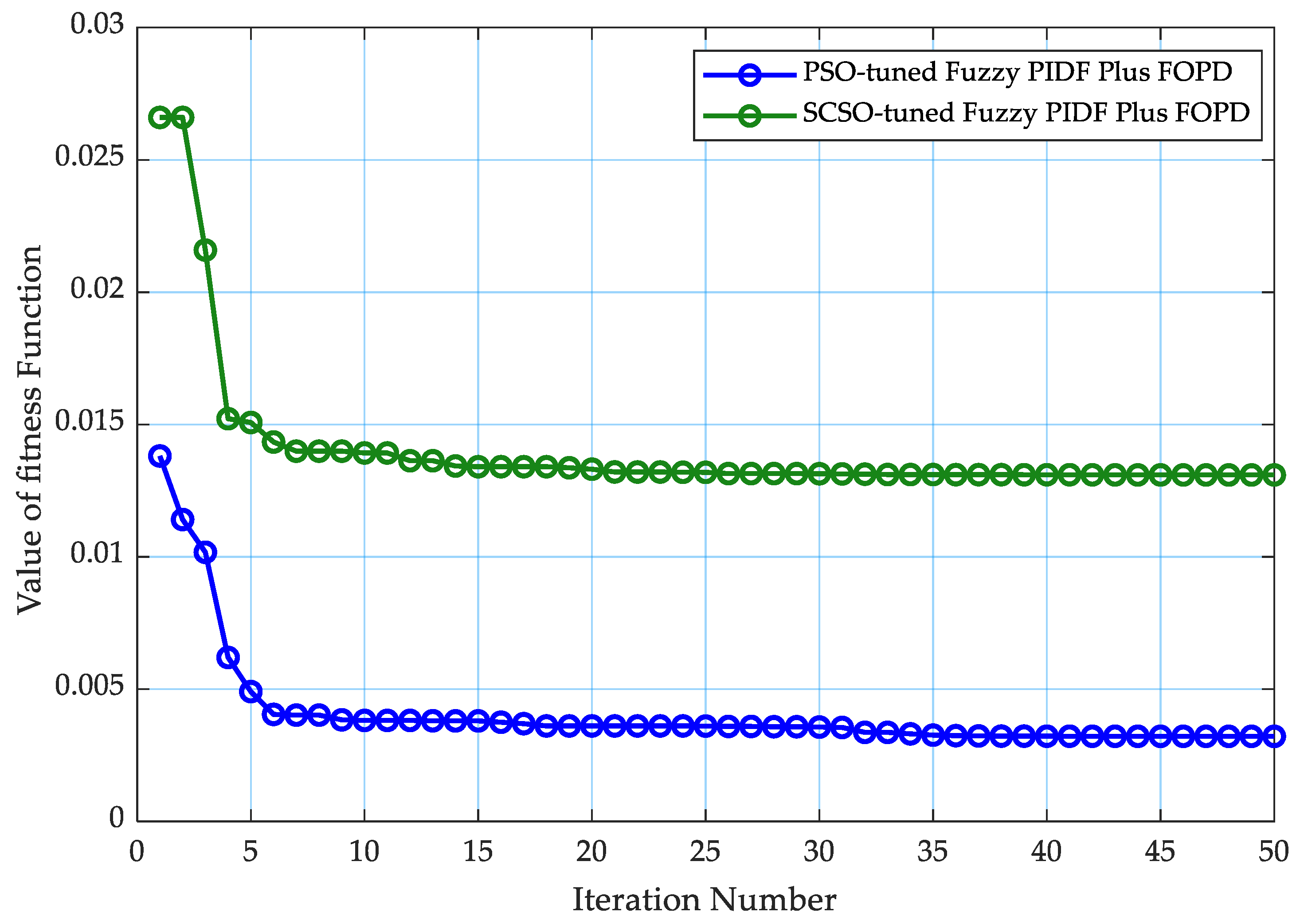
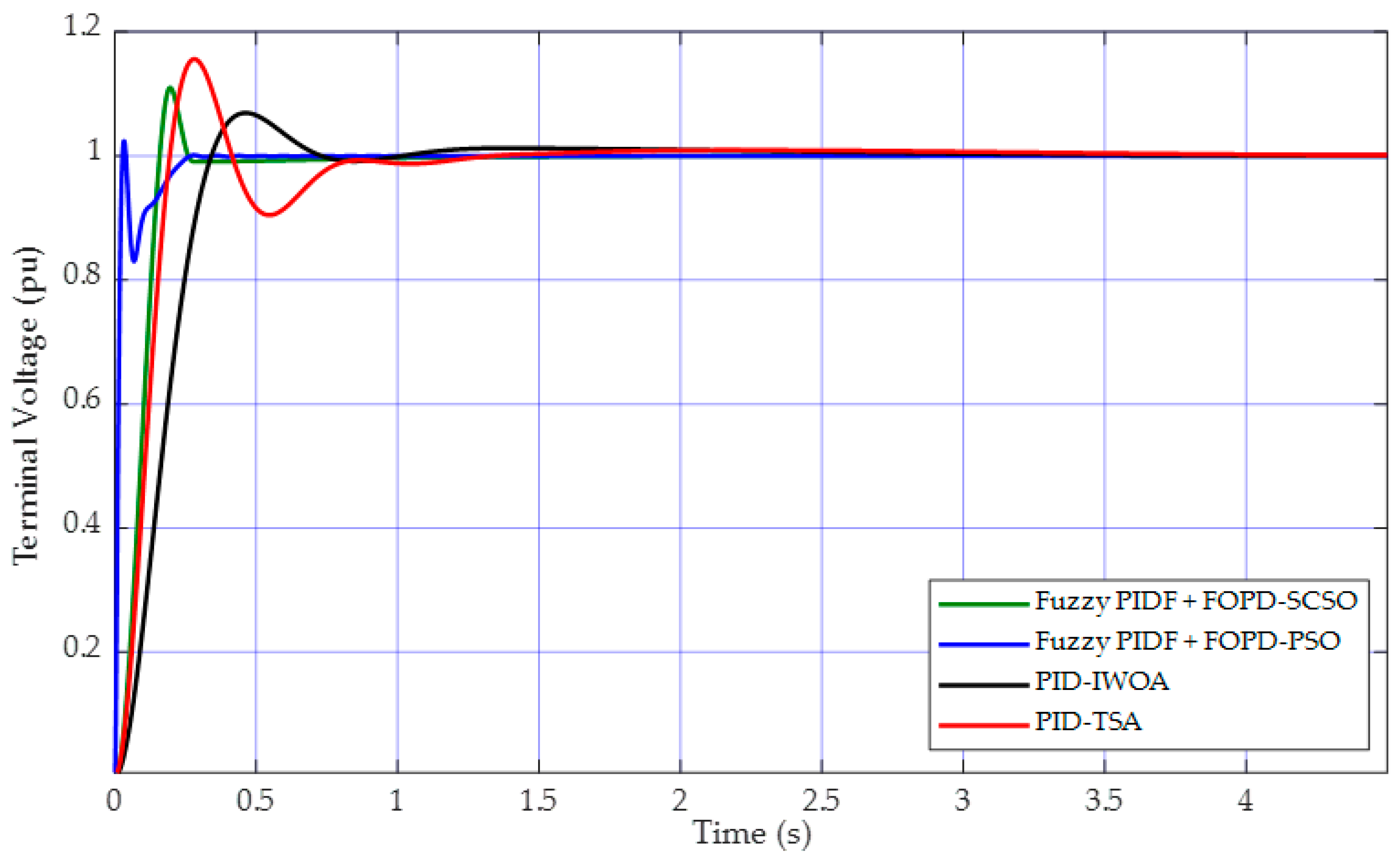
To ensure a sensible computational time for parameter tuning, the algorithm’s population size and the number of iterations were both set to 50. Additionally, the sensitivity range (${\mathrm{r}}_{\mathrm{G}}$) was defined from 0 to 2, while the phase control range (R) was set as [−2${\mathrm{r}}_{\mathrm{G}}$ to 2${\mathrm{r}}_{\mathrm{G}}$]. 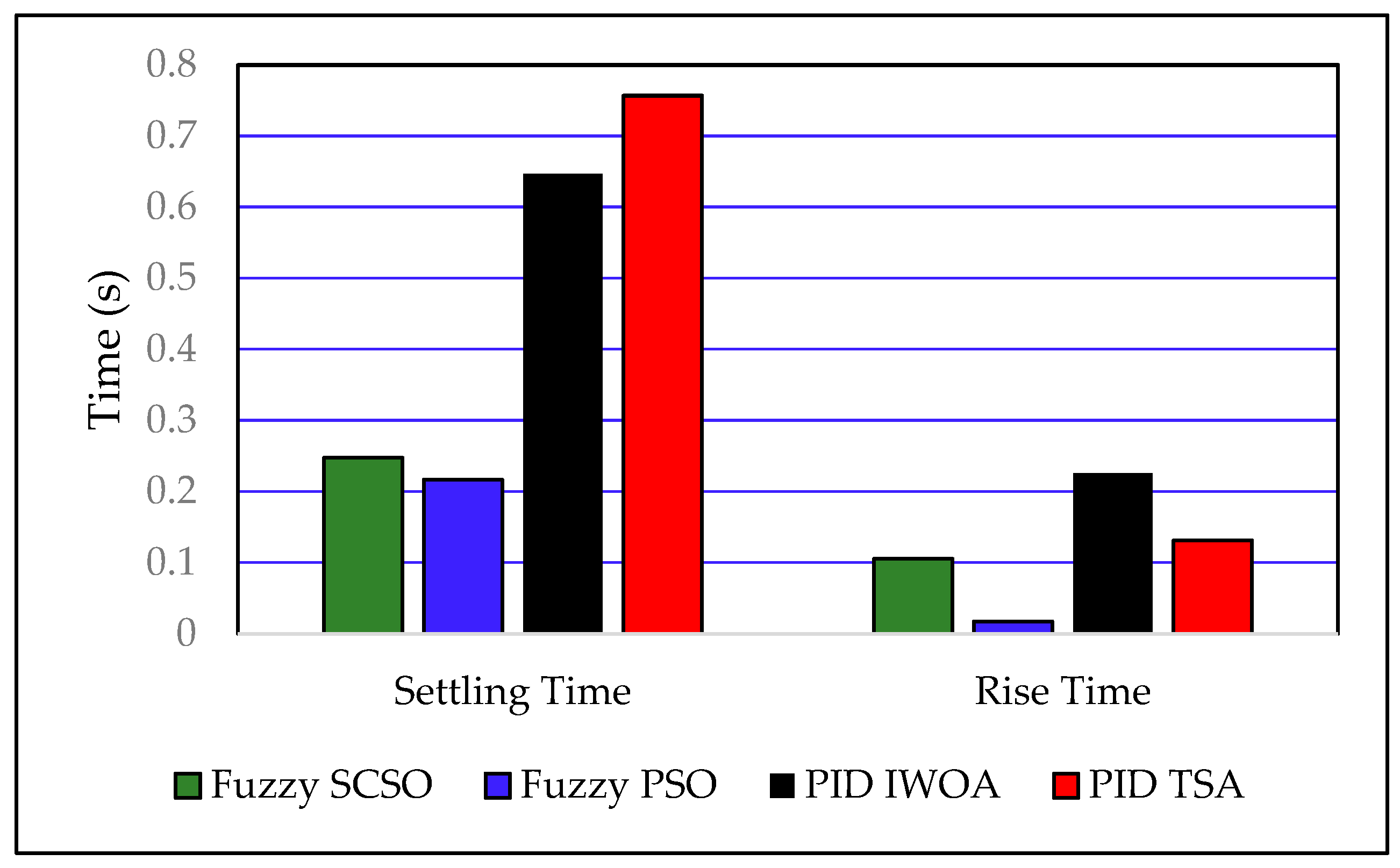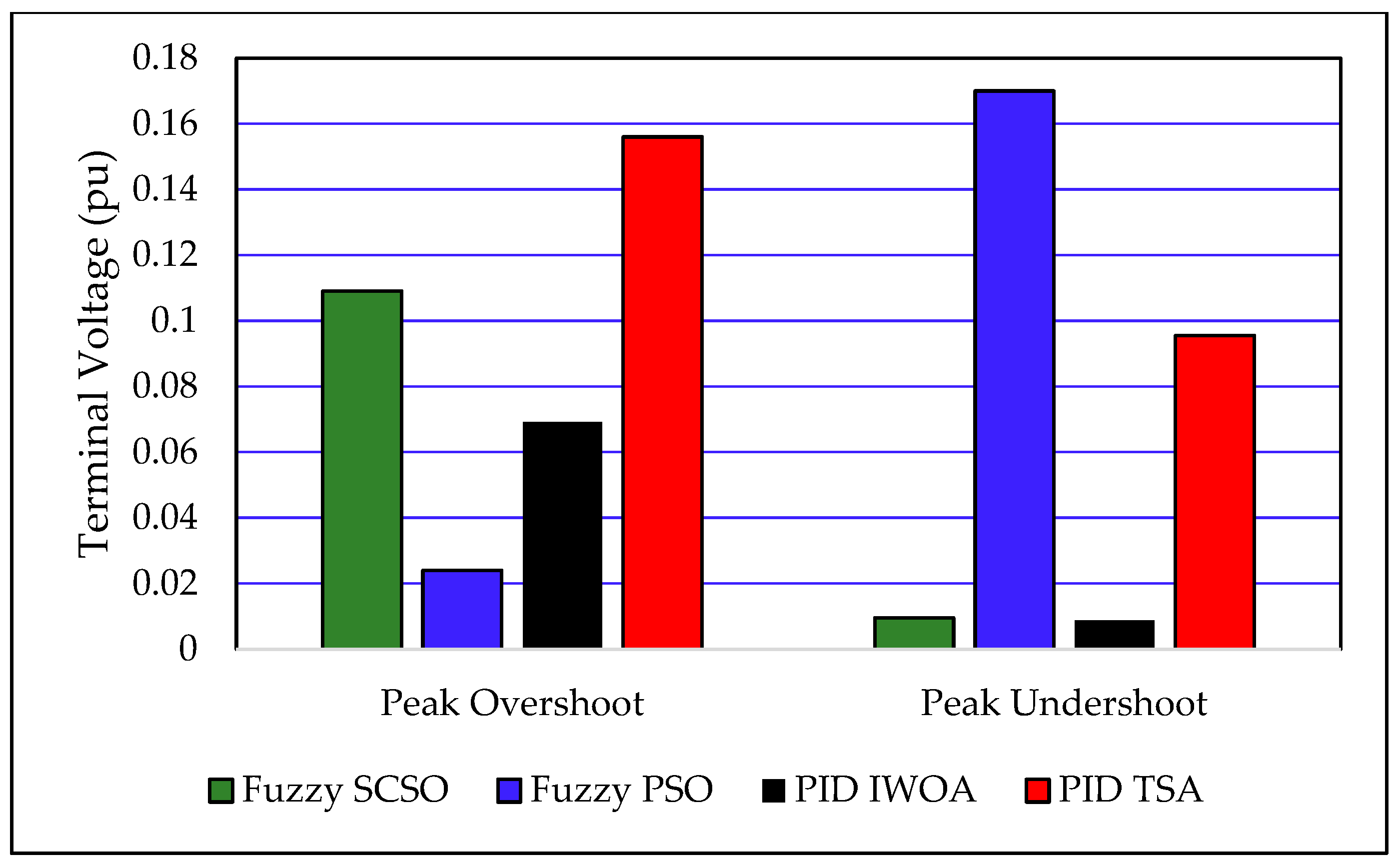The convergence curves of the PSO algorithm- and SCSO algorithm-tuned proposed controller are illustrated in Figure 9. The optimal parameters of the proposed AVR controller, obtained using the SCSO and PSO algorithms by minimizing the Integral of Time-weighted Absolute Error (ITAE), are summarized in

Table 6. The optimal values of the Fuzzy PIDF + FOPD controller tuned by the SCSO and PSO algorithms.

Controller		Parameters
Fuzzy PIDF + FOPD	Fuzzy	${\mathrm{K}}_1$			${\mathrm{K}}_2$
	SCSO	1.998677			0.1283334
	PSO	2			0.0069
	PIDF	${\mathrm{K}}_{\mathrm{p}}$	${\mathrm{K}}_{\mathrm{i}}$		${\mathrm{K}}_{\mathrm{d}}$		${\mathrm{K}}_{\mathrm{f}}$
	SCSO	1.999611	2		0.8082235		399.542
	PSO	2	2		1.6369		329.902
	FOPD	${\mathrm{K}}_{\mathrm{p}1}$		${\mathrm{K}}_{d1}$		$\mu$
	SCSO	1.253544		0.750269		0.9999161
	PSO	2		0.261		2

.

4. Results and Discussion

This study was carried out using MATLAB 2024a, where the SCSO algorithm was programmed in an .m file, while the AVR system and the proposed controller were modeled and simulated within the MATLAB Simulink environment. A step response with an amplitude of 1 pu was employed as the reference input. To evaluate the effectiveness of the proposed control strategy, the results were compared with those of other methodologies documented in the literature, specifically PID controllers tuned using IWOA [11] and TSA [10]. The PID gains utilized in these comparative studies are detailed in

Table 7. PID controller optimal gains based on different algorithms reported in the literature.

Controller	Parameters
	${\mathbf{K}}_{\mathbf{P}}$	${\mathbf{K}}_{\mathbf{I}}$	${\mathbf{K}}_{\mathbf{D}}$
PID-TSA	1.1281	0.9567	0.5671
PID-IWOA	0.8167	0.6898	0.2799

.

The performance metrics of the system response, including peak overshoot (PO) in per unit (pu), peak undershoot (PU) in pu, settling time (Ts) in seconds, rise time (Tr) in seconds, and the ITAE cost function value, are summarized in

Table 8. The features of the AVR model based on different control algorithms.

Controller	Characteristics
	OS (pu)	US (pu)	Ts	Tr	ITAE
Proposed Fuzzy-SCSO	0.109	0.0095	0.24761	0.1054	0.013095
Proposed Fuzzy-PSO	0.024	0.17	0.2166	0.0173	0.0032
PID IWOA	0.069178	0.0088	0.6465	0.2258	0.07078
PID TSA	0.15593	0.09545	0.7568	0.1311	0.08791

. Figure 10 depicts the dynamic response of the AVR system utilizing the proposed fuzzy-based control structure, alongside comparative results from PID controllers optimized using various tuning algorithms, as documented in prior studies.

As outlined in the design methodology, the proposed Fuzzy PIDF + FOPD controller is engineered to achieve an optimal balance between rapid response and robust stability. The results presented in Figure 9 and Table 8 demonstrate that the proposed AVR controller delivers superior overall performance. It achieves the best settling time (0.1621 s), rise time (0.0173 s), overshoot (0.024 pu), and objective function value (0.0032) among the evaluated methods. Additionally, it attains the second-lowest peak undershoot, further underscoring its effectiveness. It is evident that the Fuzzy PIDF + FOPD controller, when optimized using both the PSO and SCSO algorithms, exhibits comparable performance in terms of overall system response. However, a nuanced distinction arises in the transient behavior of the system: the PSO-tuned controller tends to produce a more pronounced undershoot, while the SCSO-tuned controller results in a marginally higher overshoot.

Figure 11, Figure 12 and Figure 13 provide a detailed comparative analysis of the performance metrics for AVR control systems developed using various methodologies, including the proposed Fuzzy PIDF + FOPD approach. Figure 11 specifically compares the settling time and rise time across different control strategies. Figure 12 presents a bar chart analysis of the cost function values achieved by each method, while Figure 13 illustrates the maximum overshoot and undershoot, expressed in per unit (pu), for the evaluated methodologies. These figures collectively offer a comprehensive evaluation of the dynamic performance and stability characteristics of the respective control strategies.

Figure 10, Figure 11, Figure 12 and Figure 13 and Table 8 clearly demonstrate that the suggested controller exhibits exceptional behavior as an AVR. It surpasses several techniques previously introduced in the literature, showcasing a stable and fast response. These findings strongly support the feasibility of implementing this controller in real-time applications.

5. Robustness Investigation

The system parameters, such as gains and time constants, are inherently prone to fluctuations, which can substantially degrade the performance of closed-loop control systems. Although these variations are of critical importance, their impact on AVR systems has received limited attention in the existing body of literature. This study undertook a thorough investigation into the influence of parameter variations on the overall performance of the AVR system, addressing this gap in research. To evaluate the influence of parametric uncertainties, each parameter was varied by ±40% from its nominal value as given in

Table 9. Assumed cases for parametric uncertainty analysis.

Case	Nominal Value	Variation Range	New Value
Generator Coefficient	${\mathrm{K}}_{\mathrm{g}}=1$	+40% and −40%	1.4 and 0.6
Generator Time Constant	${\mathsf{\tau }}_{\mathrm{g}}=1$	+40% and −40%	1.4 and 0.6
Excitor Constant	${\mathrm{K}}_{\mathrm{e}}=1$	+40% and −40%	1.4 and 0.6
Exciter Time Constant	${\mathsf{\tau }}_{\mathrm{e}}=0.4$	+40% and −40%	0.56 and 0.24
Sensor Constant	${\mathrm{K}}_{\mathrm{s}}=1$	+40% and −40%	1.4 and 0.6
Sensor Time Constant	${\mathsf{\tau }}_{\mathrm{s}}=0.01$	+40% and −40%	0.014 and 0.006
Amplifier Constant	${\mathrm{K}}_{\mathrm{a}}=10$	+40% and −40%	14 and 6
Amplifier Time Constant	${\mathsf{\tau }}_{\mathrm{a}}=0.1$	+40% and −40%	0.14 and 0.06
Random critical case	${\mathrm{K}}_{\mathrm{g}}=1$	−40%	0.6
	${\mathrm{K}}_{\mathrm{e}}=1$	+40%	1.4
	${\mathsf{\tau }}_{\mathrm{e}}=0.4$	+40%	0.56
	${\mathrm{K}}_{\mathrm{a}}=10$	+40%	14
	${\mathsf{\tau }}_{\mathrm{a}}=0.1$	−40%	0.06
	${\mathsf{\tau }}_{\mathrm{s}}=0.01$	−40%	0.006

. Figure 14 illustrates the impact of these parametric uncertainties on the AVR system in the absence of a controller.

The subfigures presented in Figure 14 clearly demonstrate that parameter variations result in a significant degradation of the model’s overall performance. In certain cases, the system exhibited a slight oscillatory behavior. To further examine this aspect, a rigorous scenario involving parametric uncertainty was analyzed, in which six key parameters of the AVR system were subjected to variations of ±40% from their nominal values, as outlined in Table 9. The proposed Fuzzy PIDF + FOPD controller was applied to the system to evaluate its robustness under these extreme conditions and to assess its overall response and performance. Importantly, the optimal gains identified under nominal operating conditions were retained without modification, underscoring the controller’s capacity to accommodate dynamic system variations without necessitating re-tuning. This demonstrates the controller’s robustness and effectiveness in maintaining stability and performance under significant parametric uncertainties.

Figure 15 illustrates the step response of the AVR model under parametric uncertainty. Despite significant variations in system parameters, the system consistently operated within an acceptable performance range. Notably, the response under uncertain conditions exhibited a marginally reduced overshoot for the Fuzzy PIDF + FOPD controller tuned by SCSO and an increased undershoot for the same controller tuned by PSO. This behavior can be attributed to the cumulative effects of parameter deviations, which may alter the system’s damping ratio, directly influencing the overshoot and undershoot characteristics. Such a scenario represents a realistic random case that the system might encounter during real-time operations. The robustness analysis results highlight the superior reliability and robustness of the proposed fuzzy-based control system for AVR applications.

To assess the effectiveness of the Fuzzy PIDF + FOPD controller, the system was evaluated under varying load conditions, control signal disturbances, and parametric uncertainties. Fluctuations in the connected electrical load can induce variations in the generator’s output voltage, posing a significant challenge to maintaining system stability. Similarly, control signal disturbances in an AVR system may arise from various factors, including noise, communication errors, sensor inaccuracies, faulty components, external interference, and instability in the control loop [22]. Such disturbances can significantly degrade system performance if not adequately addressed. Therefore, it is imperative to design the AVR controller with robust mechanisms to mitigate the effects of these disturbances. These testing scenarios represent some of the most demanding conditions the system may encounter during real-time operation, providing a comprehensive evaluation of the controller’s effectiveness. The block diagram of the AVR system under these two disturbances is shown in Figure 16.

An excellent aspect of the controller’s robustness is its ability to reject load disturbance effects on the model under control. As noted in [42], disturbances amounting to up to 5% of the generator’s output voltage are considered acceptable; however, controllers must be capable of managing and mitigating disturbances that surpass this limit. In alignment with previous research, this study introduced disturbances equivalent to 10% of the reference voltage, directly applied to the generator’s output, to evaluate the system’s response and control efficacy.

Figure 17 depicts the applied disturbances and the step response under both normal operating conditions and a scenario involving parametric uncertainties. The proposed controller exhibits a pronounced ability to effectively mitigate these disturbances, ensuring a stable and reliable response across diverse operating conditions. These results substantiate the controller’s robust performance and its capacity to handle demanding operational challenges with high reliability.

6. Conclusions and Future Work

This study introduced a novel AVR control design utilizing a Fuzzy PIDF + FOPD controller optimized through the SCSO and PSO algorithms. The proposed methodology demonstrated exceptional performance in achieving rapid response, stability, and robustness across diverse operational conditions, surpassing existing approaches. key metrics such as overshoot, settling time, rise time, and ITAE were improved from 0.15593 pu, 0.7568 s, 0.2258 s, and 0.08791 to 0.024 pu, 0.2166 s, 0.0173 s, and 0.0032, respectively. Comprehensive robustness evaluations further validated the system’s resilience to parametric uncertainties, load disturbances, and variations in control signals, underscoring its suitability for real-time implementation in dynamic and uncertain environments. Nevertheless, the computational time associated with the SCSO algorithm for identifying optimal controller gains remains a notable limitation, presenting a critical area for future refinements.

This study acknowledges the importance of incorporating nonlinear aspects, such as exciter limiters, generator saturation, and mechanical constraints, into the AVR model to better reflect real-world system dynamics, which have been underexplored in the literature. Additionally, the transient variations in voltage and frequency during dynamic load fluctuations, along with their potential influence on the sensor’s transfer function, represent critical considerations for accurate system modeling. Addressing these factors in future research would significantly enhance the practical applicability and fidelity of the proposed approach.

Further investigations could focus on refining the overshoot and undershoot, thereby improving overall system performance. Exploring alternative optimization algorithms may also yield enhanced controller behavior. Moreover, integrating the fuzzy controller with advanced control strategies, such as Sliding Mode Control (SMC), could create a synergistic effect, further improving dynamic response and control precision.