Residential Electricity Demand Modelling: Validation of a Behavioural Agent-Based Approach
Abstract
1. Introduction
2. Methods
2.1. Socioeconomic Variables
2.2. Behaviour, Appliances, and Lighting
2.3. Space and Water Heating
2.4. Implementation: Neighbourhoods and Validation Cases
2.4.1. Seasonal Variation
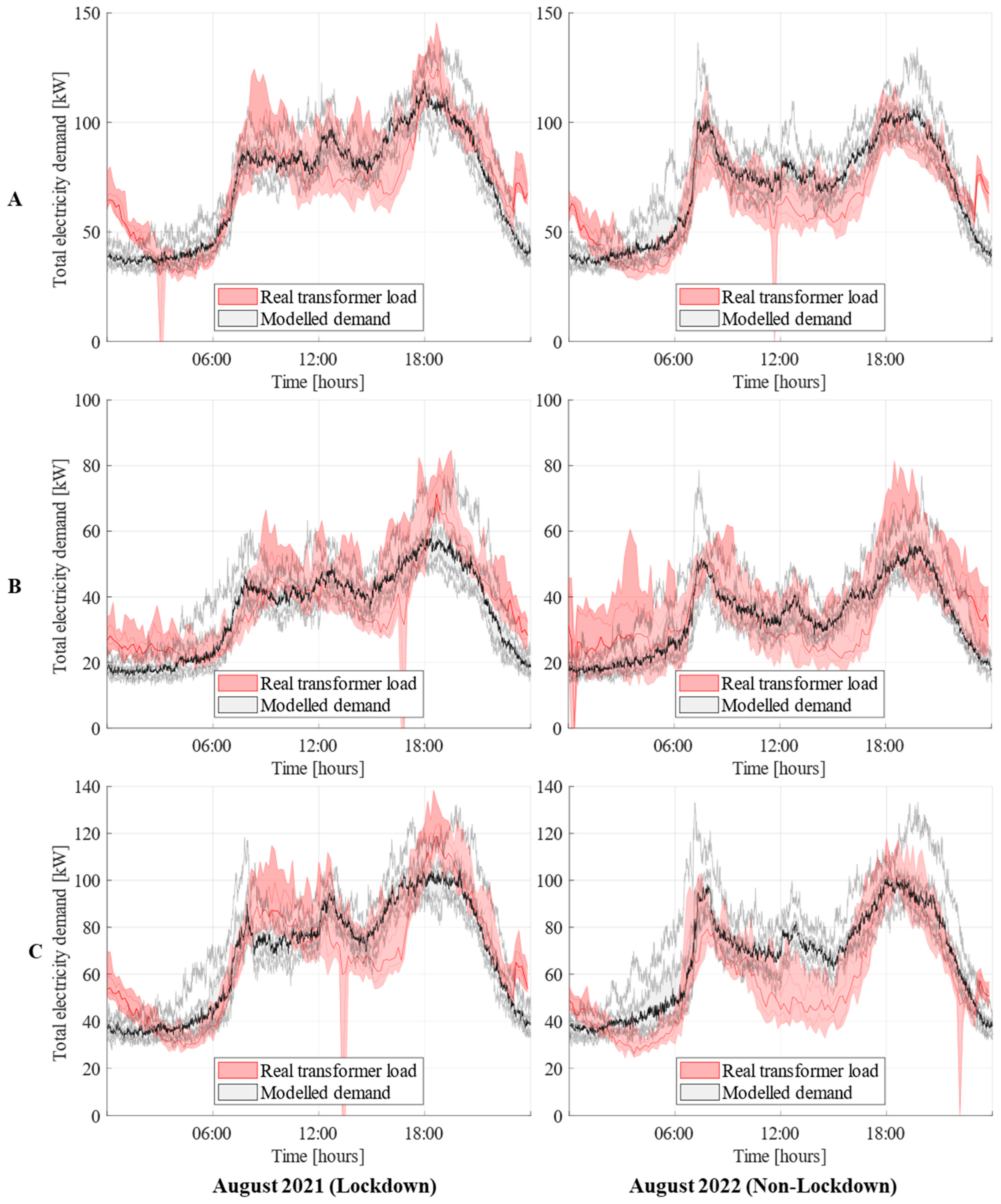
2.4.2. Lockdown Variation
| Neighbourhood A | Neighbourhood B | Neighbourhood C | |
|---|---|---|---|
| Number of houses Nhouses | 68 | 34 | 69 |
| Proportion residential ICPs | 94% | 97% | 100% |
| Proportion electric HWC | 72% | 46% | 72% |
| Location | Tauranga | Ōakura | Tauranga |
| Average gross income [NZD/person/year] | 23,200 (3rd decile) | 46,000 (7th decile) | 40,900 (7th decile) |
| NZDep | 8 | 4 | 5 |
| Median age | 39 years | 40 years | 51 years |
| Variable | Value | Source |
|---|---|---|
| Average annual income | , see Table 3 | |
| Number of houses | , see Table 3 | |
| Average occupant age | , see Table 3 | |
| Appliance use profiles | , see Figure 2 | |
| Appliance characteristics | , see Table 1 | |
| Mean heater power | , 5000 W | [106] |
| Proportion of houses with heat pumps | , 19% | [122,123] |
| Mean preferred temperature (max) | , 24 °C | Estimated from [106] |
| Mean preferred temperature (min) | , 16 °C | Estimated from [106] |
| Mean house age | , 40 years | [124] |
| Mean house size | , 150 m2 | [125,126] |
| Mean number of floors | , 1.5 | [125,126] |
| Story height | , 2.4 m | [125,126] |
| Mean window–wall ratio | , 0.22 | [58] |
| House insulation level | , see Table 2 | |
| Mean trips/person/day (Ntrips) | , 0.8 | [67] |
| Mean wake time (twake) | , 0700 h | [99,100] |
| Mean sleep time (tsleep) | , 2200 h | [99,100] |
| Departure and arrival time (tleave, tarrive) | , varies | [67,103] |
| Proportion working from home | , 10% (100% in lockdown) | |
| Proportion of electric HWCs | , see Table 3 | |
| Average HWC temperature setpoint (Tset) | , 62 °C | [106] |
| HWC inlet temperature (Tin) | , 15 °C | [117,118] |
| HWC outlet temperature (Tout) | , 40 °C | |
| Average HWC heater power (PHWC) | , 1500 W | [106] |
| Average HWC volume | , 150 L | [113] |
| Average hot water demand | , 50 L/person/day | [115,118] |
| Kloss | , 0.854 WK−1 | [106,117,118] |
| Timestep (dt) | , 60 s |
3. Results
4. Discussion
Limitations and Future Work
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Abbreviation | Description | |
| ABM | Agent-based model | |
| BLC | Building loss coefficient | |
| DR | Demand response | |
| HWC | Hot water cylinder | |
| ICP | Installation control point | |
| NZDep | New Zealand Index of Socioeconomic Deprivation | |
| WC | Wealth coefficient | |
| Variable | Unit | Description |
| A | m2 | Surface area |
| BLC | WK−1 | Rate of heat loss according to temperature difference |
| Cp | Jkg−1K−1 | Specific heat of water |
| dist | m | Distance travelled per trip |
| HC | JK−1 | Internal heat capacity of house |
| I | NZD | Income |
| Kloss | WK−1 | Thermal loss coefficient from hot water cylinder |
| Kmix | Thermostatic valve mixing factor | |
| Llight | Wm−2 | Irradiance |
| Nactive | Number of active agents | |
| Nbulbs | Number of lightbulbs | |
| Nhouses | Number of houses | |
| Noccupants | Number of occupants | |
| Ntrips | Number of trips away from home per day | |
| P | W | Power |
| QDHW | W | Heat loss from hot water use |
| Qloss | W | Heat loss from HWC standing losses |
| R | Wm−2K−1 | Insulation rating |
| Theat | K | Temperature below which agents use heating |
| Thouse | K | Temperature inside house |
| THWC | K | Hot water cylinder tank temperature |
| Tin | K | Hot water cylinder inlet temperature |
| Tmax | K | Maximum preferred comfort temperature |
| Tmin | K | Minimum preferred comfort temperature |
| Tout | K | Hot water cylinder outlet temperature |
| Toutside | K | Outside ambient temperature |
| tarrive | s | Time agent arrives home |
| tleave | s | Time agent leaves home |
| twake | s | Time agent rises from bed |
| tsleep | s | Time agent goes to sleep |
| WC | Wealth coefficient | |
| ρ | kgm−3 | Density of water |
| Subscript | Description | |
| avg | Average | |
| HWC | Hot water cylinder | |
| i | House (i = 1: Nhouses) | |
| max | Maximum | |
| min | Minimum | |
| t | Time | |
References
- Cevik, S. Climate Change and Energy Security: The Dilemma or Opportunity of the Century? Environmental Economics and Policy Studies; IMF: Washington, DC, USA, 2024; pp. 1–20. [Google Scholar]
- Tarroja, B.; Mulvaney, D.; Peer, R.A.M.; Grubert, E. Evaluating the Effectiveness of Cost-Minimal Planning of Decarbonized Electricity Systems in Reducing Life Cycle Greenhouse Gas Emissions. Environ. Res. Energy 2025, 2, 015008. [Google Scholar] [CrossRef]
- Viviescas, C.; Lima, L.; Diuana, F.A.; Vasquez, E.; Ludovique, C.; Silva, G.N.; Huback, V.; Magalar, L.; Szklo, A.; Lucena, A.F.P. Contribution of Variable Renewable Energy to Increase Energy Security in Latin America: Complementarity and Climate Change Impacts on Wind and Solar Resources. Renew. Sustain. Energy Rev. 2019, 113, 109232. [Google Scholar] [CrossRef]
- Lehmann, P.; Creutzig, F.; Ehlers, M.-H.; Friedrichsen, N.; Heuson, C.; Hirth, L.; Pietzcker, R. Carbon Lock-out: Advancing Renewable Energy Policy in Europe. Energies 2012, 5, 323–354. [Google Scholar] [CrossRef]
- Olabi, A.G.; Abdelkareem, M.A. Renewable Energy and Climate Change. Renew. Sustain. Energy Rev. 2022, 158, 112111. [Google Scholar] [CrossRef]
- Sugiyama, M. Climate Change Mitigation and Electrification. Energy Policy 2012, 44, 464–468. [Google Scholar] [CrossRef]
- Ministry of Business Innovation and Employment. Electricity Demand and Generation Scenarios (EDGS); Ministry of Business Innovation and Employment: Wellington, New Zealand, 2024. [Google Scholar]
- Ministry of Business Innovation & Employment. Electricity Statistics; Ministry of Business Innovation and Employment: Wellington, New Zealand, 2023. [Google Scholar]
- Smil, V. How the World Really Works: The Science Behind How We Got Here and Where We’re Going; Viking: New York, NY, USA, 2022; ISBN 978-0593297063. [Google Scholar]
- Pimentel Pincelli, I.; Brent, A.C.; Hinkley, J.T.; Sutherland, R. Scaling up Solar and Wind Electricity: Empirical Modelling and a Disruptive Scenario for Their Deployments in Aotearoa New Zealand. J. R. Soc. N. Z. 2024, 1–23. [Google Scholar] [CrossRef]
- Haluti, I.J.; MSM, S.I.S.; Mayasri, A. Renewable Energy: A Cornerstone in The Transition Toward a Sustainable Future. JKA 2024, 1, 2. [Google Scholar] [CrossRef]
- Egerer, J.; Oei, P.-Y.; Lorenz, C. Renewable Energy Sources as the Cornerstone of the German Energiewende. In Energiewende “Made in Germany”: Low Carbon Electricity Sector Reform in the European Context; Springer Nature: Cham, Switzerland, 2018; pp. 141–172. [Google Scholar]
- Grubert, E.; Hastings-Simon, S. Designing the Mid-transition: A Review of Medium-term Challenges for Coordinated Decarbonization in the United States. Wiley Interdiscip. Rev. Clim. Change 2022, 13, e768. [Google Scholar] [CrossRef]
- Deb, S.; Tammi, K.; Kalita, K.; Mahanta, P. Impact of Electric Vehicle Charging Station Load on Distribution Network. Energies 2018, 11, 178. [Google Scholar] [CrossRef]
- Wei, M.; McMillan, C.A.; de la Rue du Can, S. Electrification of Industry: Potential, Challenges and Outlook. Curr. Sustain./Renew. Energy Rep. 2019, 6, 140–148. [Google Scholar] [CrossRef]
- Baruah, P.J.; Eyre, N.; Qadrdan, M.; Chaudry, M.; Blainey, S.; Hall, J.W.; Jenkins, N.; Tran, M. Energy System Impacts from Heat and Transport Electrification. Proc. Inst. Civ. Eng. Energy 2014, 167, 139–151. [Google Scholar] [CrossRef]
- Kwasinski, A. Quantitative Model and Metrics of Electrical Grids’ Resilience Evaluated at a Power Distribution Level. Energies 2016, 9, 93. [Google Scholar] [CrossRef]
- Susa, D.; Lehtonen, M.; Nordman, H. Dynamic Thermal Modeling of Distribution Transformers. IEEE Trans. Power Deliv. 2005, 20, 1919–1929. [Google Scholar] [CrossRef]
- IRENA. Global Energy Transformation: A Roadmap to 2050, 2019 ed.; IRENA: Abu Dhabi, United Arab Emirates, 2019. [Google Scholar]
- Boston Consulting Group. Climate Change in New Zealand: The Future Is Electric; Boston Consulting Group: Sydney, Australia, 2022. [Google Scholar]
- Faiella, I.; Lavecchia, L.; Miniaci, R.; Valbonesi, P. Household Energy Poverty and the “Just Transition”. In Handbook of Labor, Human Resources and Population Economics; Zimmermann, K.F., Ed.; Springer International Publishing: Cham, Switzerland, 2020; pp. 1–16. ISBN 978-3-319-57365-6. [Google Scholar]
- Biswas, S.; Echevarria, A.; Irshad, N.; Rivera-Matos, Y.; Richter, J.; Chhetri, N.; Parmentier, M.J.; Miller, C.A. Ending the Energy-Poverty Nexus: An Ethical Imperative for Just Transitions. Sci. Eng. Ethics 2022, 28, 36. [Google Scholar] [CrossRef]
- Joskow, P.L. Challenges for Wholesale Electricity Markets with Intermittent Renewable Generation at Scale: The US Experience. Oxf. Rev. Econ. Policy 2019, 35, 291–331. [Google Scholar] [CrossRef]
- Mathieu, J.L.; Verbič, G.; Morstyn, T.; Almassalkhi, M.; Baker, K.; Braslavsky, J.; Bruninx, K.; Dvorkin, Y.; Ledva, G.S.; Mahdavi, N. A New Definition of Demand Response in the Distributed Energy Resource Era. arXiv 2024, arXiv:2410.18768. [Google Scholar]
- Handique, A.J.; Peer, R.A.M.; Haas, J. Understanding the Challenges for Modelling Islands’ Energy Systems and How to Solve Them. Curr. Sustain./Renew. Energy Rep. 2024, 11, 95–104. [Google Scholar] [CrossRef]
- Mohseni, S.; Brent, A.C.; Kelly, S.; Browne, W.N. Demand Response-Integrated Investment and Operational Planning of Renewable and Sustainable Energy Systems Considering Forecast Uncertainties: A Systematic Review. Renew. Sustain. Energy Rev. 2022, 158, 112095. [Google Scholar] [CrossRef]
- Kirkerud, J.G.; Nagel, N.O.; Bolkesjø, T.F. The Role of Demand Response in the Future Renewable Northern European Energy System. Energy 2021, 235, 121336. [Google Scholar] [CrossRef]
- Meschede, H. Increased Utilisation of Renewable Energies through Demand Response in the Water Supply Sector—A Case Study. Energy 2019, 175, 810–817. [Google Scholar] [CrossRef]
- Rasheed, M.; Javaid, N.; Awais, M.; Khan, Z.; Qasim, U.; Alrajeh, N.; Iqbal, Z.; Javaid, Q. Real Time Information Based Energy Management Using Customer Preferences and Dynamic Pricing in Smart Homes. Energies 2016, 9, 542. [Google Scholar] [CrossRef]
- Ahmed, M.; Mohamed, A.; Homod, R.; Shareef, H. Hybrid LSA-ANN Based Home Energy Management Scheduling Controller for Residential Demand Response Strategy. Energies 2016, 9, 716. [Google Scholar] [CrossRef]
- Oprea, S.-V.; Bâra, A.; Uță, A.I.; Pîrjan, A.; Căruțașu, G. Analyses of Distributed Generation and Storage Effect on the Electricity Consumption Curve in the Smart Grid Context. Sustainability 2018, 10, 2264. [Google Scholar] [CrossRef]
- Varne, A.R.; Blouin, S.; Williams, B.L.M.; Denkenberger, D. The Impact of Abrupt Sunlight Reduction Scenarios on Renewable Energy Production. Energies 2024, 17, 5147. [Google Scholar] [CrossRef]
- Clastres, C. Smart Grids: Another Step towards Competition, Energy Security and Climate Change Objectives. Energy Policy 2011, 39, 5399–5408. [Google Scholar] [CrossRef]
- Prehoda, E.W.; Schelly, C.; Pearce, J.M. US Strategic Solar Photovoltaic-Powered Microgrid Deployment for Enhanced National Security. Renew. Sustain. Energy Rev. 2017, 78, 167–175. [Google Scholar] [CrossRef]
- Williams, B.; Bishop, D. Flexible Futures: The Potential for Electrical Energy Demand Response in New Zealand. Energy Policy 2024, 195, 114387. [Google Scholar] [CrossRef]
- Haider, H.T.; See, O.H.; Elmenreich, W. A Review of Residential Demand Response of Smart Grid. Renew. Sustain. Energy Rev. 2016, 59, 166–178. [Google Scholar] [CrossRef]
- Stephenson, J.; Ford, R.; Nair, N.-K.; Watson, N.; Wood, A.; Miller, A. Smart Grid Research in New Zealand—A Review from the GREEN Grid Research Programme. Renew. Sustain. Energy Rev. 2018, 82, 1636–1645. [Google Scholar] [CrossRef]
- Jones, R.V.; Fuertes, A.; Lomas, K.J. The Socio-Economic, Dwelling and Appliance Related Factors Affecting Electricity Consumption in Domestic Buildings. Renew. Sustain. Energy Rev. 2015, 43, 901–917. [Google Scholar] [CrossRef]
- Williams, B.; Bishop, D.; Gallardo, P.; Chase, J.G. Demand Side Management in Industrial, Commercial, and Residential Sectors: A Review of Constraints and Considerations. Energies 2023, 16, 5155. [Google Scholar] [CrossRef]
- Gyamfi, S.; Krumdieck, S. Price, Environment and Security: Exploring Multi-Modal Motivation in Voluntary Residential Peak Demand Response. Energy Policy 2011, 39, 2993–3004. [Google Scholar] [CrossRef]
- Howden-Chapman, P.; Viggers, H.; Chapman, R.; O’Dea, D.; Free, S.; O’Sullivan, K. Warm Homes: Drivers of the Demand for Heating in the Residential Sector in New Zealand. Energy Policy 2009, 37, 3387–3399. [Google Scholar] [CrossRef]
- Ruoso, A.C.; Ribeiro, J.L.D. The Influence of Countries’ Socioeconomic Characteristics on the Adoption of Electric Vehicle. Energy Sustain. Dev. 2022, 71, 251–262. [Google Scholar] [CrossRef]
- Karatasou, S.; Santamouris, M. Socio-Economic Status and Residential Energy Consumption: A Latent Variable Approach. Energy Build. 2019, 198, 100–105. [Google Scholar] [CrossRef]
- Dogan, B.; Trabelsi, N.; Khalfaoui, R.; Ghosh, S.; Shahzad, U. Role of Ethnic Diversity, Temperature Changes, and Socio-Economic Conditions for Residential Energy Use and Energy Expenditures: Evidence from the United States. Energy Build. 2022, 276, 112529. [Google Scholar] [CrossRef]
- Losi, A.; Mancarella, P.; Vicino, A. Socioeconomic Aspects of Demand Response. In Integration of Demand Response into the Electricity Chain; Wiley: Hoboken, NJ, USA, 2015; pp. 215–239. [Google Scholar]
- Brown, M.A.; Chapman, O. The Size, Causes, and Equity Implications of the Demand-Response Gap. Energy Policy 2021, 158, 112533. [Google Scholar] [CrossRef]
- Vahabi, A.R.; Latify, M.A.; Rahimiyan, M.; Yousefi, G.R. An Equitable and Efficient Energy Management Approach for a Cluster of Interconnected Price Responsive Demands. Appl. Energy 2018, 219, 276–289. [Google Scholar] [CrossRef]
- The Economist. What Donald Trump and Bernie Sanders Get Wrong about Credit Cards. The Economist, 21 November 2024.
- Herraiz-Cañete, Á.; Ribó-Pérez, D.; Bastida-Molina, P.; Gómez-Navarro, T. Forecasting Energy Demand in Isolated Rural Communities: A Comparison between Deterministic and Stochastic Approaches. Energy Sustain. Dev. 2022, 66, 101–116. [Google Scholar] [CrossRef]
- Happle, G.; Fonseca, J.A.; Schlueter, A. A Review on Occupant Behavior in Urban Building Energy Models. Energy Build. 2018, 174, 276–292. [Google Scholar] [CrossRef]
- Williams, B.; Gallardo, P.; Bishop, D.; Chase, J.G. Impacts of Electric Vehicle Policy on the New Zealand Energy System: A Retro-Analysis. Energy Rep. 2023, 9, 3871. [Google Scholar] [CrossRef]
- de Hoog, J.; Thomas, D.A.; Muenzel, V.; Jayasuriya, D.C.; Alpcan, T.; Brazil, M.; Mareels, I. Electric Vehicle Charging and Grid Constraints: Comparing Distributed and Centralized Approaches. In Proceedings of the 2013 IEEE Power & Energy Society General Meeting, Vancouver, BC, Canada, 21–25 July 2013; pp. 1–5. [Google Scholar]
- Dupont, B.; Dietrich, K.; De Jonghe, C.; Ramos, A.; Belmans, R. Impact of Residential Demand Response on Power System Operation: A Belgian Case Study. Appl. Energy 2014, 122, 1–10. [Google Scholar] [CrossRef]
- Setlhaolo, D.; Xia, X. Optimal Scheduling of Household Appliances with a Battery Storage System and Coordination. Energy Build. 2015, 94, 61–70. [Google Scholar] [CrossRef]
- Setlhaolo, D.; Xia, X. Combined Residential Demand Side Management Strategies with Coordination and Economic Analysis. Int. J. Electr. Power Energy Syst. 2016, 79, 150–160. [Google Scholar] [CrossRef]
- Luthander, R.; Widén, J.; Munkhammar, J.; Lingfors, D. Self-Consumption Enhancement and Peak Shaving of Residential Photovoltaics Using Storage and Curtailment. Energy 2016, 112, 221–231. [Google Scholar] [CrossRef]
- Hu, M.; Xiao, F. Price-Responsive Model-Based Optimal Demand Response Control of Inverter Air Conditioners Using Genetic Algorithm. Appl. Energy 2018, 219, 151–164. [Google Scholar] [CrossRef]
- Bishop, D.; Mohkam, M.; Williams, B.L.M.; Wu, W.; Bellamy, L. The Impact of Building Level of Detail Modelling Strategies: Insights into Building and Urban Energy Modelling. Eng 2024, 5, 2280–2299. [Google Scholar] [CrossRef]
- Haldi, F.; Robinson, D. The Impact of Occupants’ Behaviour on Building Energy Demand. J. Build. Perform. Simul. 2011, 4, 323–338. [Google Scholar] [CrossRef]
- Vahedipour-Dahraie, M.; Rashidizadeh-Kermani, H.; Anvari-Moghaddam, A.; Siano, P.; Catalao, J.P.S. Short-Term Reliability and Economic Evaluation of Resilient Microgrids under Incentive-Based Demand Response Programs. Int. J. Electr. Power Energy Syst. 2022, 138, 107918. [Google Scholar] [CrossRef]
- Yu, D.; Wang, J.; Li, D.; Jermsittiparsert, K.; Nojavan, S. Risk-Averse Stochastic Operation of a Power System Integrated with Hydrogen Storage System and Wind Generation in the Presence of Demand Response Program. Int. J. Hydrogen Energy 2019, 44, 31204–31215. [Google Scholar] [CrossRef]
- Yao, E.; Samadi, P.; Wong, V.W.S.; Schober, R. Residential Demand Side Management under High Penetration of Rooftop Photovoltaic Units. IEEE Trans. Smart Grid 2015, 7, 1597–1608. [Google Scholar] [CrossRef]
- Kepplinger, P.; Huber, G.; Petrasch, J. Autonomous Optimal Control for Demand Side Management with Resistive Domestic Hot Water Heaters Using Linear Optimization. Energy Build. 2015, 100, 50–55. [Google Scholar] [CrossRef]
- Kepplinger, P.; Huber, G.; Petrasch, J. Demand Side Management via Autonomous Control-Optimization and Unidirectional Communication with Application to Resistive Hot Water Heaters; ENOVA: Eisenstadt, Austria, 2014; 8p. [Google Scholar]
- Good, N.; Karangelos, E.; Navarro-Espinosa, A.; Mancarella, P. Optimization under Uncertainty of Thermal Storage-Based Flexible Demand Response with Quantification of Residential Users’ Discomfort. IEEE Trans. Smart Grid 2015, 6, 2333–2342. [Google Scholar] [CrossRef]
- Braas, H.; Jordan, U.; Best, I.; Orozaliev, J.; Vajen, K. District Heating Load Profiles for Domestic Hot Water Preparation with Realistic Simultaneity Using DHWcalc and TRNSYS. Energy 2020, 201, 117552. [Google Scholar] [CrossRef]
- Lojowska, A.; Kurowicka, D.; Papaefthymiou, G.; Van Der Sluis, L. Stochastic Modeling of Power Demand Due to EVs Using Copula. IEEE Trans. Power Syst. 2012, 27, 1960–1968. [Google Scholar] [CrossRef]
- Guo, Z.; Afifah, F.; Qi, J.; Baghali, S. A Stochastic Multiagent Optimization Framework for Interdependent Transportation and Power System Analyses. IEEE Trans. Transp. Electrif. 2021, 7, 1088–1098. [Google Scholar] [CrossRef]
- Widén, J.; Wäckelgård, E. A High-Resolution Stochastic Model of Domestic Activity Patterns and Electricity Demand. Appl. Energy 2010, 87, 1880–1892. [Google Scholar] [CrossRef]
- Vellei, M.; Martinez, S.; Le Dréau, J. Agent-Based Stochastic Model of Thermostat Adjustments: A Demand Response Application. Energy Build. 2021, 238, 110846. [Google Scholar] [CrossRef]
- Carlucci, S.; Causone, F.; Biandrate, S.; Ferrando, M.; Moazami, A.; Erba, S. On the Impact of Stochastic Modeling of Occupant Behavior on the Energy Use of Office Buildings. Energy Build. 2021, 246, 111049. [Google Scholar] [CrossRef]
- Schweizer, V.J.; Morgan, M.G. Bounding US Electricity Demand in 2050. Technol. Forecast. Soc. Change 2016, 105, 215–223. [Google Scholar] [CrossRef]
- Inglesi, R. Aggregate Electricity Demand in South Africa: Conditional Forecasts to 2030. Appl. Energy 2010, 87, 197–204. [Google Scholar] [CrossRef]
- Mirjat, N.H.; Uqaili, M.A.; Harijan, K.; Das Walasai, G.; Mondal, M.A.H.; Sahin, H. Long-Term Electricity Demand Forecast and Supply Side Scenarios for Pakistan (2015–2050): A LEAP Model Application for Policy Analysis. Energy 2018, 165, 512–526. [Google Scholar] [CrossRef]
- Alizadeh, M.; Scaglione, A.; Davies, J.; Kurani, K.S. A Scalable Stochastic Model for the Electricity Demand of Electric and Plug-In Hybrid Vehicles. IEEE Trans. Smart Grid 2014, 5, 848–860. [Google Scholar] [CrossRef]
- Trotter, I.M.; Bolkesjø, T.F.; Féres, J.G.; Hollanda, L. Climate Change and Electricity Demand in Brazil: A Stochastic Approach. Energy 2016, 102, 596–604. [Google Scholar] [CrossRef]
- de Marchi, S.; Page, S.E. Agent-Based Models. Annu. Rev. Political Sci. 2014, 17, 1–20. [Google Scholar] [CrossRef]
- Samanidou, E.; Zschischang, E.; Stauffer, D.; Lux, T. Agent-Based Models of Financial Markets. Rep. Prog. Phys. 2007, 70, 409. [Google Scholar] [CrossRef]
- Wang, L.; Ahn, K.; Kim, C.; Ha, C. Agent-Based Models in Financial Market Studies. J. Phys. Conf. Ser. 2018, 1039, 012022. [Google Scholar] [CrossRef]
- Lye, R.; Tan, J.P.L.; Cheong, S.A. Understanding Agent-Based Models of Financial Markets: A Bottom–up Approach Based on Order Parameters and Phase Diagrams. Phys. A Stat. Mech. Its Appl. 2012, 391, 5521–5531. [Google Scholar] [CrossRef]
- Shinde, P.; Amelin, M. Agent-Based Models in Electricity Markets: A Literature Review. In Proceedings of the 2019 IEEE Innovative Smart Grid Technologies—Asia (ISGT Asia), Chengdu, China, 21–24 May 2019; pp. 3026–3031. [Google Scholar]
- Dehghanpour, K.; Nehrir, M.H.; Sheppard, J.W.; Kelly, N.C. Agent-Based Modeling of Retail Electrical Energy Markets with Demand Response. IEEE Trans. Smart Grid 2016, 9, 3465–3475. [Google Scholar] [CrossRef]
- Zhou, Z.; Zhao, F.; Wang, J. Agent-Based Electricity Market Simulation with Demand Response from Commercial Buildings. IEEE Trans. Smart Grid 2011, 2, 580–588. [Google Scholar] [CrossRef]
- Xu, S.; Chen, X.; Xie, J.; Rahman, S.; Wang, J.; Hui, H.; Chen, T. Agent-Based Modeling and Simulation for the Electricity Market with Residential Demand Response. CSEE J. Power Energy Syst. 2020, 7, 368–380. [Google Scholar]
- Latifi, M.; Rastegarnia, A.; Khalili, A.; Sanei, S. Agent-Based Decentralized Optimal Charging Strategy for Plug-in Electric Vehicles. IEEE Trans. Ind. Electron. 2018, 66, 3668–3680. [Google Scholar] [CrossRef]
- Van Der Kam, M.; Peters, A.; Van Sark, W.; Alkemade, F. Agent-Based Modelling of Charging Behaviour of Electric Vehicle Drivers. J. Artif. Soc. Soc. Simul. 2019, 22, 7. [Google Scholar] [CrossRef]
- Olivella-Rosell, P.; Villafafila-Robles, R.; Sumper, A.; Bergas-Jané, J. Probabilistic Agent-Based Model of Electric Vehicle Charging Demand to Analyse the Impact on Distribution Networks. Energies 2015, 8, 4160–4187. [Google Scholar] [CrossRef]
- Benenson, I.; Martens, K.; Birfir, S. PARKAGENT: An Agent-Based Model of Parking in the City. Comput. Environ. Urban. Syst. 2008, 32, 431–439. [Google Scholar] [CrossRef]
- Rai, V.; Henry, A.D. Agent-Based Modelling of Consumer Energy Choices. Nat. Clim. Change 2016, 6, 556–562. [Google Scholar] [CrossRef]
- Hesselink, L.X.W.; Chappin, E.J.L. Adoption of Energy Efficient Technologies by Households—Barriers, Policies and Agent-Based Modelling Studies. Renew. Sustain. Energy Rev. 2019, 99, 29–41. [Google Scholar] [CrossRef]
- Rai, V.; Robinson, S.A. Agent-Based Modeling of Energy Technology Adoption: Empirical Integration of Social, Behavioral, Economic, and Environmental Factors. Environ. Model. Softw. 2015, 70, 163–177. [Google Scholar] [CrossRef]
- Silvia, C.; Krause, R.M. Assessing the Impact of Policy Interventions on the Adoption of Plug-in Electric Vehicles: An Agent-Based Model. Energy Policy 2016, 96, 105–118. [Google Scholar] [CrossRef]
- Wang, Z.; Paranjape, R. Agent-Based Simulation of Home Energy Management System in Residential Demand Response. In Proceedings of the 2014 IEEE 27th Canadian Conference on Electrical and Computer Engineering (CCECE), Toronto, ON, Canada, 4–7 May 2014; pp. 1–6. [Google Scholar]
- Golmohamadi, H.; Keypour, R.; Bak-Jensen, B.; Pillai, J.R. A Multi-Agent Based Optimization of Residential and Industrial Demand Response Aggregators. Int. J. Electr. Power Energy Syst. 2019, 107, 472–485. [Google Scholar] [CrossRef]
- Zheng, M.; Meinrenken, C.J.; Lackner, K.S. Agent-Based Model for Electricity Consumption and Storage to Evaluate Economic Viability of Tariff Arbitrage for Residential Sector Demand Response. Appl. Energy 2014, 126, 297–306. [Google Scholar] [CrossRef]
- Zhang, Z.; Jing, R.; Lin, J.; Wang, X.; van Dam, K.H.; Wang, M.; Meng, C.; Xie, S.; Zhao, Y. Combining Agent-Based Residential Demand Modeling with Design Optimization for Integrated Energy Systems Planning and Operation. Appl. Energy 2020, 263, 114623. [Google Scholar] [CrossRef]
- Wang, Y.; Lin, H.; Liu, Y.; Wennersten, R.; Sun, Q. Agent-Based Modeling of High-Resolution Household Electricity Demand Profiles: A Novel Tool for Policy Evaluating. In Proceedings of the 2017 IEEE Conference on Energy Internet and Energy System Integration (EI2), Beijing, China, 26–28 November 2017; pp. 1–6. [Google Scholar]
- Statistics New Zealand. New Zealand Census of Population and Dwellings; Statistics New Zealand: Wellington, New Zealand, 2018. [Google Scholar]
- Dorofaeff, T.F.; Denny, S. Sleep and Adolescence. Do New Zealand Teenagers Get Enough? J. Paediatr. Child. Health 2006, 42, 515–520. [Google Scholar] [CrossRef]
- Galland, B.C.; De Wilde, T.; Taylor, R.W.; Smith, C. Sleep and Pre-Bedtime Activities in New Zealand Adolescents: Differences by Ethnicity. Sleep. Health 2020, 6, 23–31. [Google Scholar] [CrossRef]
- Williams, B.; Bishop, D.; Hooper, G.; Chase, J.G. Driving Change: Electric Vehicle Charging Behavior and Peak Loading. Renew. Sustain. Energy Rev. 2024, 189, 113953. [Google Scholar] [CrossRef]
- Ministry of Transport. Vehicle Km Travelled (VKT). Available online: https://www.transport.govt.nz/statistics-and-insights/fleet-statistics/sheet/vehicle-kms-travelled-vkt-2 (accessed on 11 July 2022).
- Anderson, B.; Parker, R.; Myall, D.; Moller, H.; Jack, M. Will Flipping the Fleet F** k the Grid? In Proceedings of the 7th IAEE Asia-Oceania Conference 2020: Energy in Transition, Auckland, New Zealand, 12–15 February 2020. [Google Scholar]
- Yilmaz, S.; Firth, S.K.; Allinson, D. Occupant Behaviour Modelling in Domestic Buildings: The Case of Household Electrical Appliances. J. Build. Perform. Simul. 2017, 10, 582–600. [Google Scholar] [CrossRef]
- Kelly, J.; Knottenbelt, W. The UK-DALE Dataset, Domestic Appliance-Level Electricity Demand and Whole-House Demand from Five UK Homes. Sci. Data 2015, 2, 150007. [Google Scholar] [CrossRef]
- Isaacs, N.; Camilleri, M.; Burrough, L.; Pollard, A.; Saville-Smith, K.; Fraser, R.; Rossouw, P.; Jowett, J. Energy Use in New Zealand Households: Final Report on the Household Energy End-Use Project (Heep); BRANZ Study Report: Porirua, New Zealand, 2010; Volume 221, pp. 15–21. [Google Scholar]
- Bizzozero, F.; Gruosso, G.; Vezzini, N. A Time-of-Use-Based Residential Electricity Demand Model for Smart Grid Applications. In Proceedings of the 2016 IEEE 16th International Conference on Environment and Electrical Engineering (EEEIC), Florence, Italy, 7–10 June 2016; pp. 1–6. [Google Scholar]
- Battini, F.; Pernigotto, G.; Gasparella, A. A Shoeboxing Algorithm for Urban Building Energy Modeling: Validation for Stand-Alone Buildings. Sustain. Cities Soc. 2023, 89, 104305. [Google Scholar] [CrossRef]
- Battini, F.; Pernigotto, G.; Gasparella, A. District-Level Validation of a Shoeboxing Simplification Algorithm to Speed-up Urban Building Energy Modeling Simulations. Appl. Energy 2023, 349, 121570. [Google Scholar] [CrossRef]
- Bishop, D.; Gallardo, P.; Williams, B.L.M. A Review of Multi-Domain Urban Energy Modelling Data. Clean. Energy Sustain. 2023, 2, 10016. [Google Scholar] [CrossRef]
- Maxim, A.; Grubert, E. Highly Energy Efficient Housing Can Reduce Peak Load and Increase Safety under Beneficial Electrification. Environ. Res. Lett. 2023, 19, 014036. [Google Scholar] [CrossRef]
- Ministry of Business Innovation and Employment. New Zealand Building Code H1 Energy Efficiency Acceptable Solution H1/AS1: Energy Efficiency for All Housing, and Buildings Up to 300 M2; Ministry of Business Innovation and Employment: Wellington, New Zealand, 2021. [Google Scholar]
- HeatingForce. What Size Hot Water Cylinder Do I Need? Available online: https://heatingforce.co.uk/blog/what-size-cylinder-do-i-need/ (accessed on 11 November 2021).
- Jordan, U.; Vajen, K. DHWcalc: Program to Generate Domestic Hot Water Profiles with Statistical Means for User Defined Conditions. In Proceedings of the ISES Solar World Congress, Orlando, FL, USA, 6–12 August 2005; pp. 8–12. [Google Scholar]
- Basson, J. The Heating of Residential Sanitary Water (in Afrikaans); National Building Research Institute: Pretoria, South Africa, 1983. [Google Scholar]
- Parker, D.S.; Fairey, P.W.; Lutz, J.D. Estimating Daily Domestic Hot-Water Use in North American Homes. ASHRAE Trans. 2015, 121, 258–270. [Google Scholar]
- Bishop, D.; Nankivell, T.; Williams, B. Peak Loads vs. Cold Showers: The Impact of Existing and Emerging Hot Water Controllers on Load Management. J. R. Soc. N. Z. 2023, 1–26. [Google Scholar] [CrossRef]
- Williams, B.; Bishop, D.; Docherty, P. Assessing the Energy Storage Potential of Electric Hot Water Cylinders with Stochastic Model-Based Control. J. R. Soc. N. Z. 2023, 1–17. [Google Scholar]
- Atkinson, J.; Salmond, C.; Crampton, P.; Viggers, H.; Lacey, K. NZDep2023 Index of Socioeconomic Deprivation: Research Report; University of Otago: Wellington, New Zealand, 2024. [Google Scholar]
- Ministry of Health. Aotearoa New Zealand’s COVID-19 Elimination Strategy: An Overview; Ministry of Health: Wellington, New Zealand, 2021. [Google Scholar]
- Statistics New Zealand. Household Economic Survey (Income) 2018; Statistics New Zealand: Wellington, New Zealand, 2018. [Google Scholar]
- French, L.J. Active Cooling and Heat Pump Use in New Zealand: Survey Results; BRANZ: Porirua, New Zealand, 2008. [Google Scholar]
- Buckett, N.R. National Impacts of the Widespread Adoption of Heat Pumps in New Zealand; BRANZ: Porirua, New Zealand, 2007. [Google Scholar]
- Stats, N.Z. Housing in Aotearoa: 2020; NZ Government: Wellington, New Zealand, 2020. [Google Scholar]
- Khajehzadeh, I.; Vale, B. How House Size Impacts Type, Combination and Size of Rooms: A Floor Plan Study of New Zealand Houses. Archit. Eng. Des. Manag. 2017, 13, 291–307. [Google Scholar] [CrossRef]
- Khajehzadeh, I.; Vale, B. Large Housing in New Zealand: Are Bedroom and Room Standards Still Good Definitions of New Zealand House Size. In Proceedings of the the 9th Australasian Housing Researchers Conference, Auckland, New Zealand, 17 February 2016; The University of Auckland: Auckland, New Zealand; 2016; pp. 17–19. [Google Scholar]
- Dortans, C.; Jack, M.W.; Anderson, B.; Stephenson, J. Lightening the Load: Quantifying the Potential for Energy-Efficient Lighting to Reduce Peaks in Electricity Demand. Energy Effic. 2020, 13, 1105–1118. [Google Scholar] [CrossRef]
- Renwick, J.; Mladenov, P.; Purdie, J.; McKerchar, A.; Jamieson, D. The Effects of Climate Variability and Change upon Renewable Electricity in New Zealand. In Climate Change Adaptation in New Zealand: Future Scenarios and Some Sectoral Perspectives; New Zealand Climate Change Centre: Wellington, New Zealand, 2010; pp. 70–81. [Google Scholar]
- Dortans, C.; Anderson, B.; Jack, M. NZ GREEN Grid Household Electricity Demand Data: EECA Data Analysis (Part B) Report v2. 1; University of Otago: Dunedin, New Zealand, 2019. [Google Scholar]
- Octopus Energy. Use Your Power Wisely—The Lowdown on Our Off-Peak and Night Rates. Available online: https://octopusenergy.nz/blog/the-lowdown-on-our-off-peak-and-night-rates (accessed on 23 December 2024).
- Electric Kiwi. Power Plans. Available online: https://www.electrickiwi.co.nz/power/plans (accessed on 23 December 2024).
- Powershop. Get Shifty (Time of Use). Available online: https://www.powershop.co.nz/help/get-shifty-time-of-use/ (accessed on 23 December 2024).
- Porteiro, R.; Hernández-Callejo, L.; Nesmachnow, S. Electricity Demand Forecasting in Industrial and Residential Facilities Using Ensemble Machine Learning. Rev. Fac. Ing. Univ. Antioq. 2022, 102, 9–25. [Google Scholar] [CrossRef]
- Cai, H.; Shen, S.; Lin, Q.; Li, X.; Xiao, H. Predicting the Energy Consumption of Residential Buildings for Regional Electricity Supply-Side and Demand-Side Management. IEEE Access 2019, 7, 30386–30397. [Google Scholar] [CrossRef]
- Dilaver, Z.; Hunt, L.C. Modelling and Forecasting Turkish Residential Electricity Demand. Energy Policy 2011, 39, 3117–3127. [Google Scholar] [CrossRef]
- Jiang, Q.; Huang, C.; Wu, Z.; Yao, J.; Wang, J.; Liu, X.; Qiao, R. Predicting Building Energy Consumption in Urban Neighborhoods Using Machine Learning Algorithms. Front. Urban Rural Plan. 2024, 2, 6. [Google Scholar] [CrossRef]
- Gao, S.; Zhang, X.; Gao, L.; Zhou, Y.; Wu, T. A Novel Residential Electricity Load Prediction Algorithm Based on Hybrid Seasonal Decomposition and Deep Learning Models. SSRN 2024. [Google Scholar] [CrossRef]
- Wijaya, T.K.; Vasirani, M.; Humeau, S.; Aberer, K. Cluster-Based Aggregate Forecasting for Residential Electricity Demand Using Smart Meter Data. In Proceedings of the 2015 IEEE International Conference on Big Data (Big Data), Santa Clara, CA, USA, 29 October–1 November 2015; pp. 879–887. [Google Scholar]
- Pipattanasomporn, M.; Kuzlu, M.; Rahman, S.; Teklu, Y. Load Profiles of Selected Major Household Appliances and Their Demand Response Opportunities. IEEE Trans. Smart Grid 2013, 5, 742–750. [Google Scholar] [CrossRef]
- Cetin, K.S.; Tabares-Velasco, P.C.; Novoselac, A. Appliance Daily Energy Use in New Residential Buildings: Use Profiles and Variation in Time-of-Use. Energy Build. 2014, 84, 716–726. [Google Scholar] [CrossRef]
- Howden-Chapman, P.; Crane, J.; Keall, M.; Pierse, N.; Baker, M.G.; Cunningham, C.; Amore, K.; Aspinall, C.; Bennett, J.; Bierre, S. He Kāinga Oranga: Reflections on 25 Years of Measuring the Improved Health, Wellbeing and Sustainability of Healthier Housing. J. R. Soc. N. Z. 2024, 54, 290–315. [Google Scholar] [CrossRef]
- Nicholls, L.; Strengers, Y. Peak Demand and the ‘Family Peak’ Period in Australia: Understanding Practice (in)Flexibility in Households with Children. Energy Res. Soc. Sci. 2015, 9, 116–124. [Google Scholar] [CrossRef]
- Jose, L.; Raxworthy, M.; Williams, B.L.M.; Denkenberger, D. Be Clever or Be Cold: Repurposed Ovens for Space Heating Following Global Catastrophic Infrastructure Loss. EarthArXiv 2024. [Google Scholar] [CrossRef]
- Williams, B.; Croft, H.; Hunt, J.; Viloria, J.; Sherman, N.; Oliver, J.; Green, B.; Turchin, A.; García Martínez, J.; Pearce, J.; et al. Wood Gasification in Catastrophes: Electricity Production from Light Duty Vehicles. EarthArXiv 2025. [Google Scholar] [CrossRef]
- Cook, L. Illuminating the Intergenerational Value of Regular Population Censuses Whilst Amidst a Population Storm; Economic Policy Centre: Auckland, New Zealand, 2024. [Google Scholar]
- Electricity Authority. Unaccounted for Electricity. Available online: https://www.emi.ea.govt.nz/All/Reports/CPMJNV (accessed on 24 January 2025).
- Energy Efficiency and Conservation Authority. Solar Energy in New Zealand. Available online: https://www.eeca.govt.nz/insights/energy-in-new-zealand/renewable-energy/solar/ (accessed on 9 February 2025).
- Wang, X.; Lo, K. Just Transition: A Conceptual Review. Energy Res. Soc. Sci. 2021, 82, 102291. [Google Scholar] [CrossRef]
- Newell, P.; Mulvaney, D. The Political Economy of the ‘Just Transition’. Geogr. J. 2013, 179, 132–140. [Google Scholar] [CrossRef]



| Appliance | Average Power [kW] | Average Runtime [min] |
|---|---|---|
| Dishwasher | 0.7 | 60 |
| Tumble drier | 1.1 | 60 |
| Washing machine | 0.7 | 45 |
| Cooker | 1.0 | 30 |
| Oven | 0.7 | 30 |
| Grill | 1.5 | 20 |
| Hob | 1.0 | 20 |
| Television | 0.1 | 120 |
| Other electronics | 0.8 | 30 |
| Baseline | 0.4 | N/A |
| Year | Zone 1 | Zone 2 | Zone 3 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Walls | Floor | Roof | Walls | Floor | Roof | Walls | Floor | Roof | |
| 1978–2000 | 0.9 | 0.9 | 1.9 | 0.9 | 0.9 | 1.9 | 0.9 | 0.9 | 1.9 |
| 2000–2007 | 1.5 | 1.3 | 1.9 | 1.5 | 1.3 | 1.9 | 1.5 | 1.3 | 1.9 |
| 2007–2021 | 1.9 | 1.3 | 2.9 | 1.9 | 1.3 | 1.9 | 2.0 | 1.3 | 3.3 |
| 2021– | 2.0 | 1.3 | 3.3 | 2.0 | 1.3 | 3.3 | 2.4 | 1.3 | 3.6 |
| Summer | Winter | |
|---|---|---|
| Neighbourhood A | 0.73 | 0.83 |
| Neighbourhood B | 0.81 | 0.82 |
| Neighbourhood C | 0.82 | 0.83 |
| Summer | Winter | |||
|---|---|---|---|---|
| Modelled Demand [kWh] | Real Load [kWh] | Modelled Demand [kWh] | Real Load [kWh] | |
| Neighbourhood A | 1301 | 1204 | 1691 | 1660 |
| Neighbourhood B | 615 | 602 | 834 | 805 |
| Neighbourhood C | 1270 | 1020 | 1675 | 1270 |
| August 2021 (Lockdown) | August 2022 (Non-Lockdown) | |
|---|---|---|
| Neighbourhood A | 0.86 | 0.83 |
| Neighbourhood B | 0.84 | 0.66 |
| Neighbourhood C | 0.87 | 0.86 |
| August 2021 (Lockdown) | August 2022 (Non-Lockdown) | |||
|---|---|---|---|---|
| Modelled Demand [kWh] | Real Load [kWh] | Modelled Demand [kWh] | Real Load [kWh] | |
| Neighbourhood A | 1657 | 1720 | 1596 | 1514 |
| Neighbourhood B | 830 | 885 | 793 | 822 |
| Neighbourhood C | 1632 | 1624 | 1590 | 1354 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Williams, B.L.M.; Hooper, R.J.; Gnoth, D.; Chase, J.G. Residential Electricity Demand Modelling: Validation of a Behavioural Agent-Based Approach. Energies 2025, 18, 1314. https://doi.org/10.3390/en18061314
Williams BLM, Hooper RJ, Gnoth D, Chase JG. Residential Electricity Demand Modelling: Validation of a Behavioural Agent-Based Approach. Energies. 2025; 18(6):1314. https://doi.org/10.3390/en18061314
Chicago/Turabian StyleWilliams, Baxter L. M., R. J. Hooper, Daniel Gnoth, and J. G. Chase. 2025. "Residential Electricity Demand Modelling: Validation of a Behavioural Agent-Based Approach" Energies 18, no. 6: 1314. https://doi.org/10.3390/en18061314
APA StyleWilliams, B. L. M., Hooper, R. J., Gnoth, D., & Chase, J. G. (2025). Residential Electricity Demand Modelling: Validation of a Behavioural Agent-Based Approach. Energies, 18(6), 1314. https://doi.org/10.3390/en18061314






