Research on the Health Evaluation of a Pump Turbine in Smoothing Output Volatility of the Hybrid System Under a High Proportion of Wind and Photovoltaic Power Connection
Abstract
1. Introduction
2. Mathematical Models and Methods
2.1. System Output Model
2.1.1. Mathematical Model of Wind Power Generation
2.1.2. Mathematical Model of PV Power Generation
2.1.3. Output Model of Pumped Storage
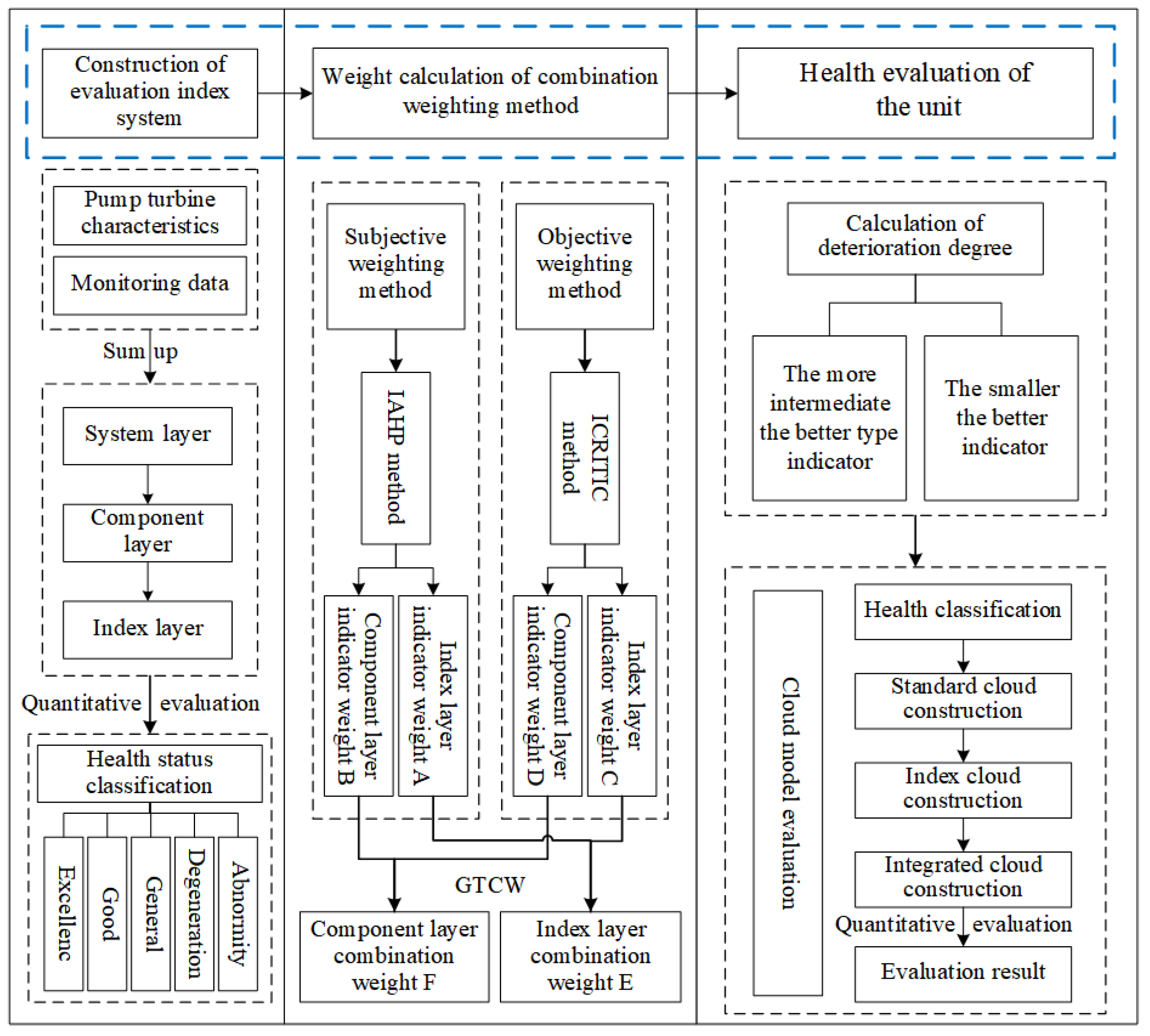
2.2. Health Evaluation Methods
2.2.1. Improved Analytic Hierarchy Process (IAHP)
2.2.2. Improved Criteria Importance Through Intercriteria Correlation Analysis Method (ICRITIC)
- (1)
- The m predictive objects and the j th indicator value aij of the i object among the n predictive indicators constitute the original predictive indicator value matrix .
- (2)
- Positive and negative indicators are standardized to the initial matrix B according to two standardizations: the larger the better and the smaller the better, respectively, to obtain matrix . The standardized formula is calculated as follows:where Equations (10) and (11) are the larger and better indicators and the smaller and better indicators, respectively, and aij is the initial value of the indicator.
- (3)
- The information entropy ej of the jth indicator is calculated according to the entropy weight method with the following formula:where , is the standardized value of the indicator.
- (4)
- The mean difference vj for each indicator of the standardized matrix B is calculated using the following formula:
- (5)
- The quantitative coefficients of the degree of independence of each evaluation indicator are calculated using the following formula:where rkj is the correlation coefficient between the indicators in matrix B.
- (6)
- The quantitative coefficients rj for calculating the combined informativeness and degree of independence of each indicator are given in the following formulas:
- (7)
- The weight ω2 of the indicator layer is calculated using the following formula:
2.2.3. Game Theory Combinatorial Weighting (GTCW)
- (1)
- Construct the set of base weight vectors ωk. Suppose Q weight calculation methods are adopted to assign weights to n evaluation indicators in the indicator evaluation system based on the combination of game theory ideas. Then, the corresponding weight vectors can be obtained, and the arbitrary linear combination of n weight vectors, the weight set is further obtained:where is the weighting factor.
- (2)
- Construct the optimal linear combination. By optimizing the weight coefficients , the deviation between ω and each is minimized by the following equation:
- (3)
- Solve for the final portfolio weights ω:
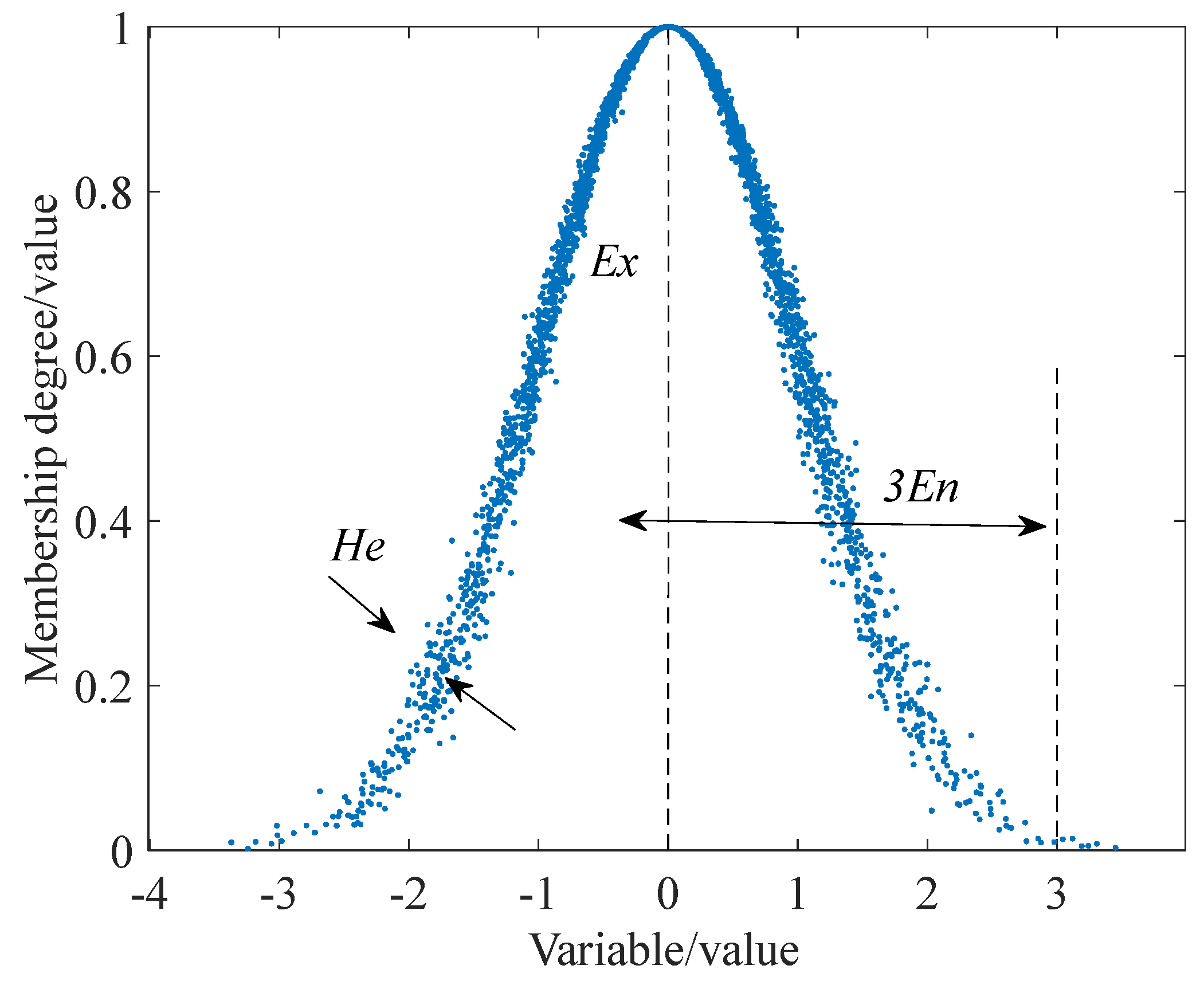
2.2.4. Cloud Model (CM)
2.3. Health Evaluation Model
2.3.1. Model Composition
2.3.2. Evaluation of the Indicator System
2.3.3. Construction of Cloud Model
- (1)
- For the smaller the better type indicator, such as the temperature parameter, the deterioration formula can be expressed as:
- (2)
- For intermediate more-optimal type indicators, such as pressure, the deterioration formula can be expressed as:where g(x) is the degradation, < γ1 < γ2 < (γ1 and γ2 are optimal); x is the measured value of the parameter, and [, ] are the parameter operating intervals.
- (3)
- Integrated cloud solving and quantization
3. Analysis of Results
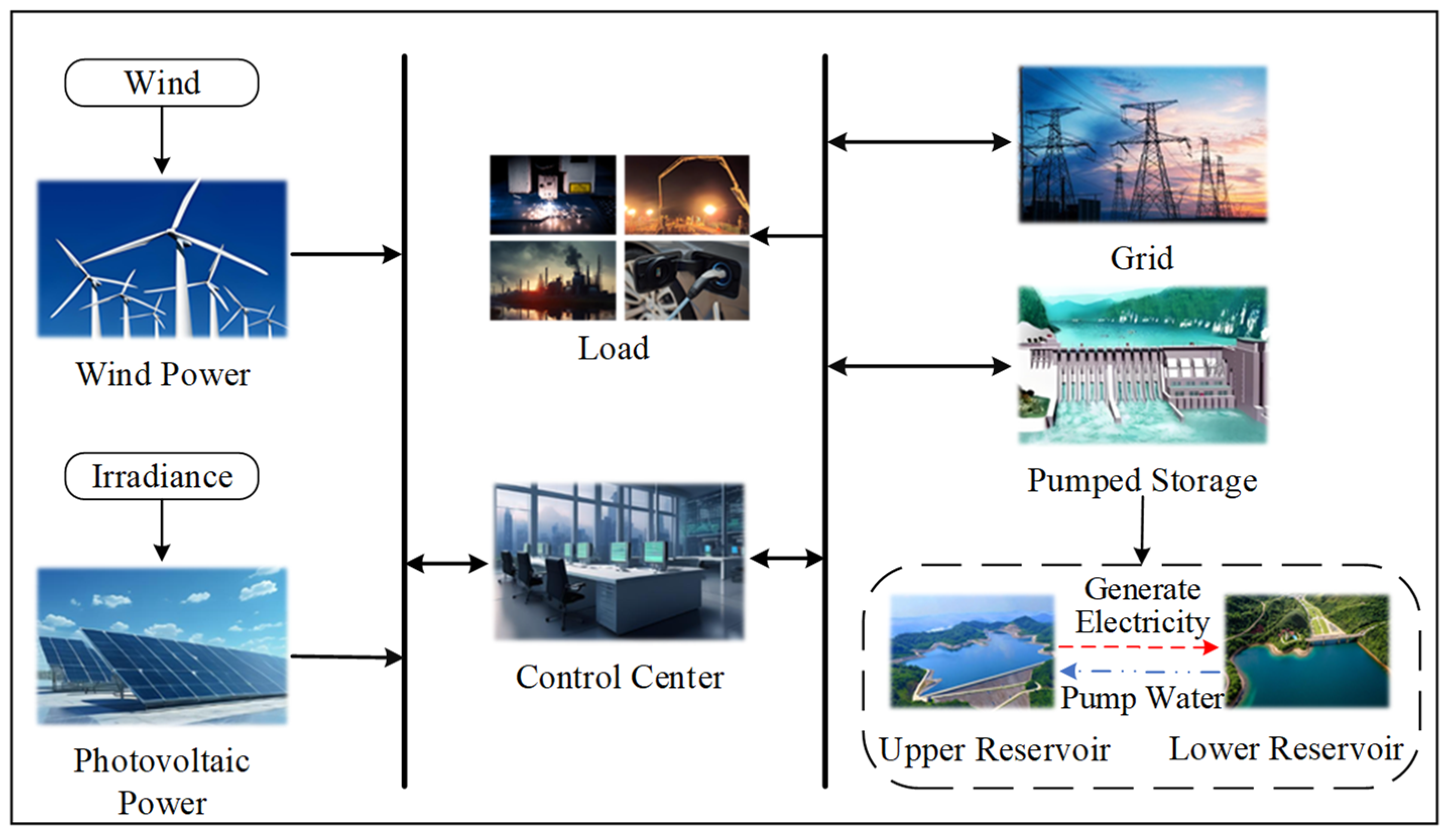
3.1. System Composition and Mode of Operation
- (1)
- When wind and PV power generation is sufficient, and the load demand is not large at that time, the excess power will be pumped through the pumped storage plant to convert the excess power into water potential energy storage to be used when the load peaks.
- (2)
- When the load demand is large but the wind and PV power generation is insufficient, for example, the wind and PV power generation has been fully generated but still cannot meet the demand of the grid load, the pumped storage power station will have stored water released to the lower reservoir, and the potential energy of the water will be converted into electricity, using pumped storage fast peak shifting frequency adjustment ability and rapid tracking of the load, to solve the demand of the power grid.
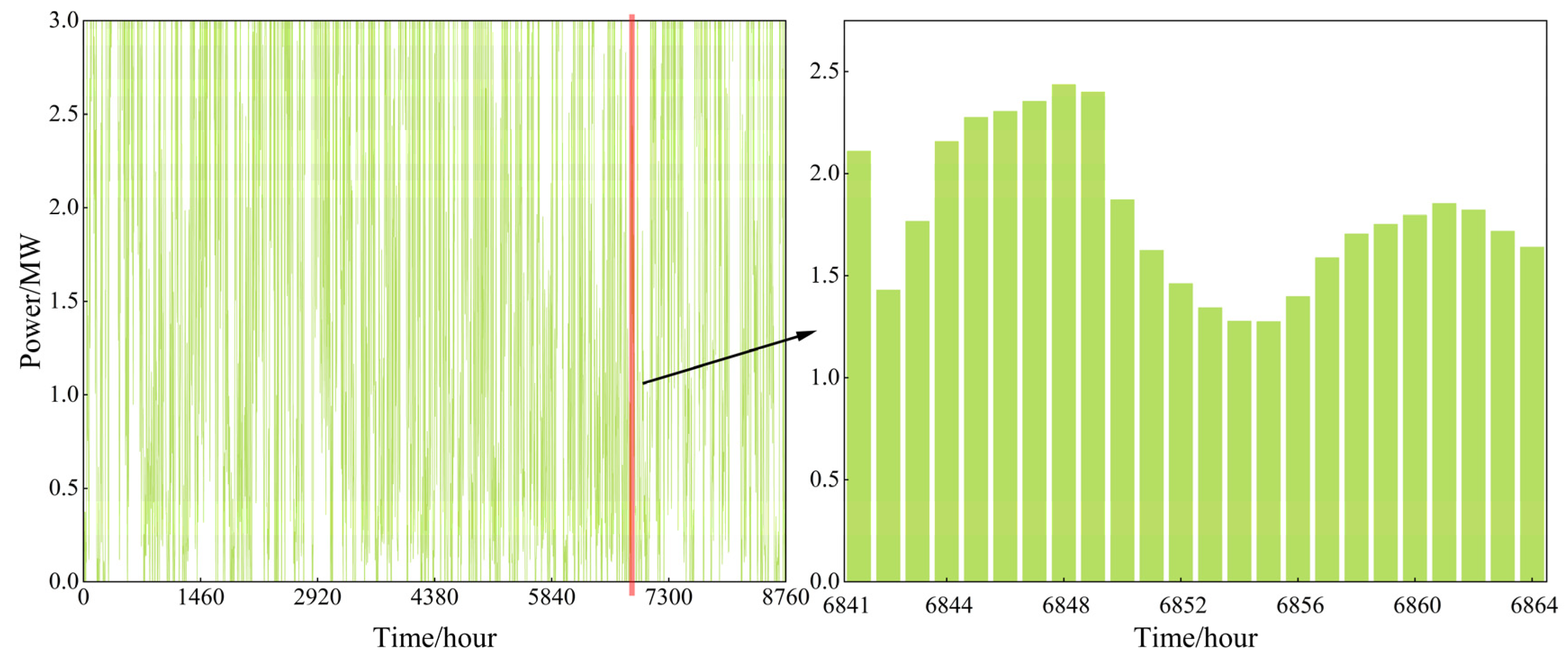
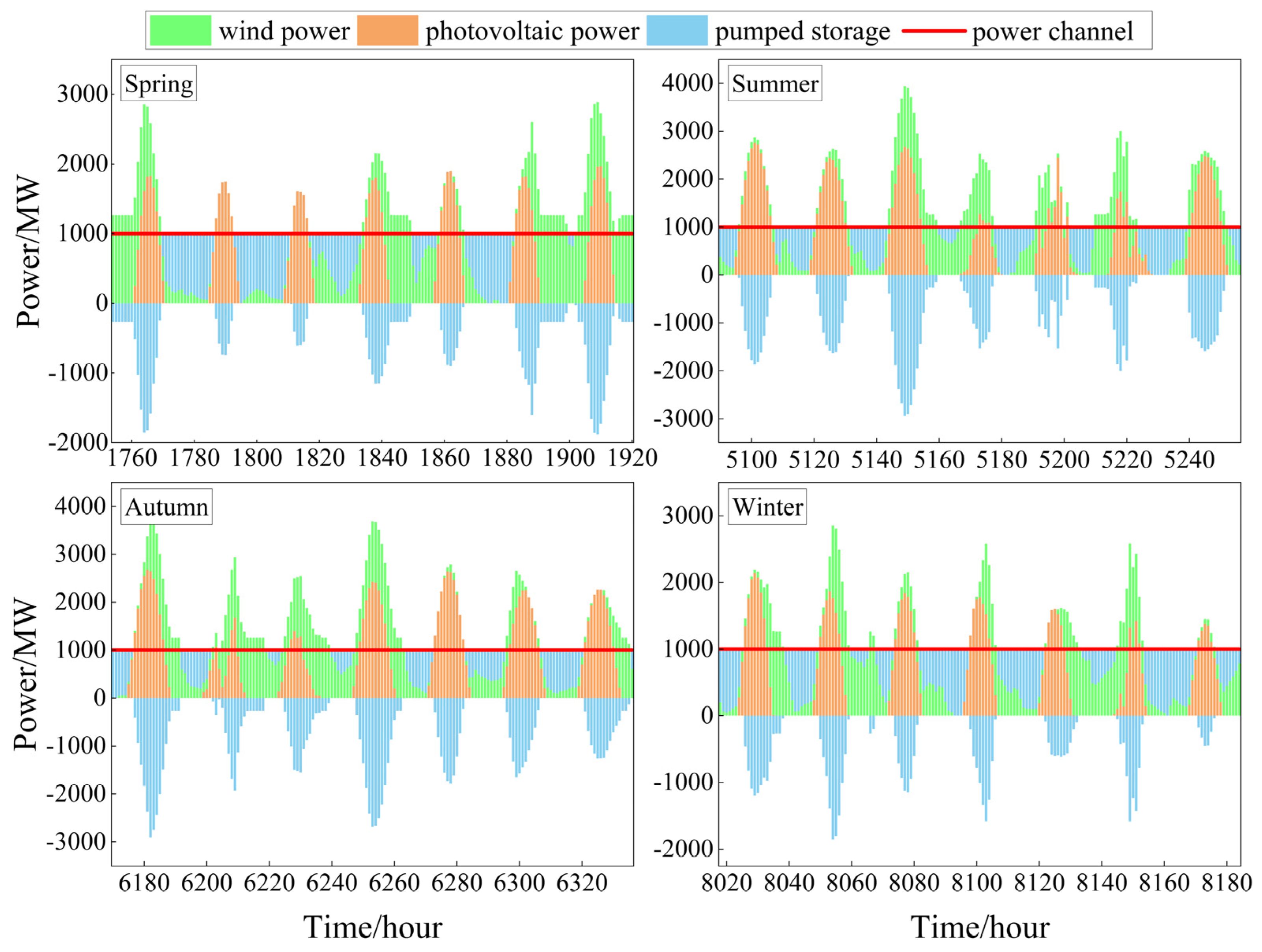
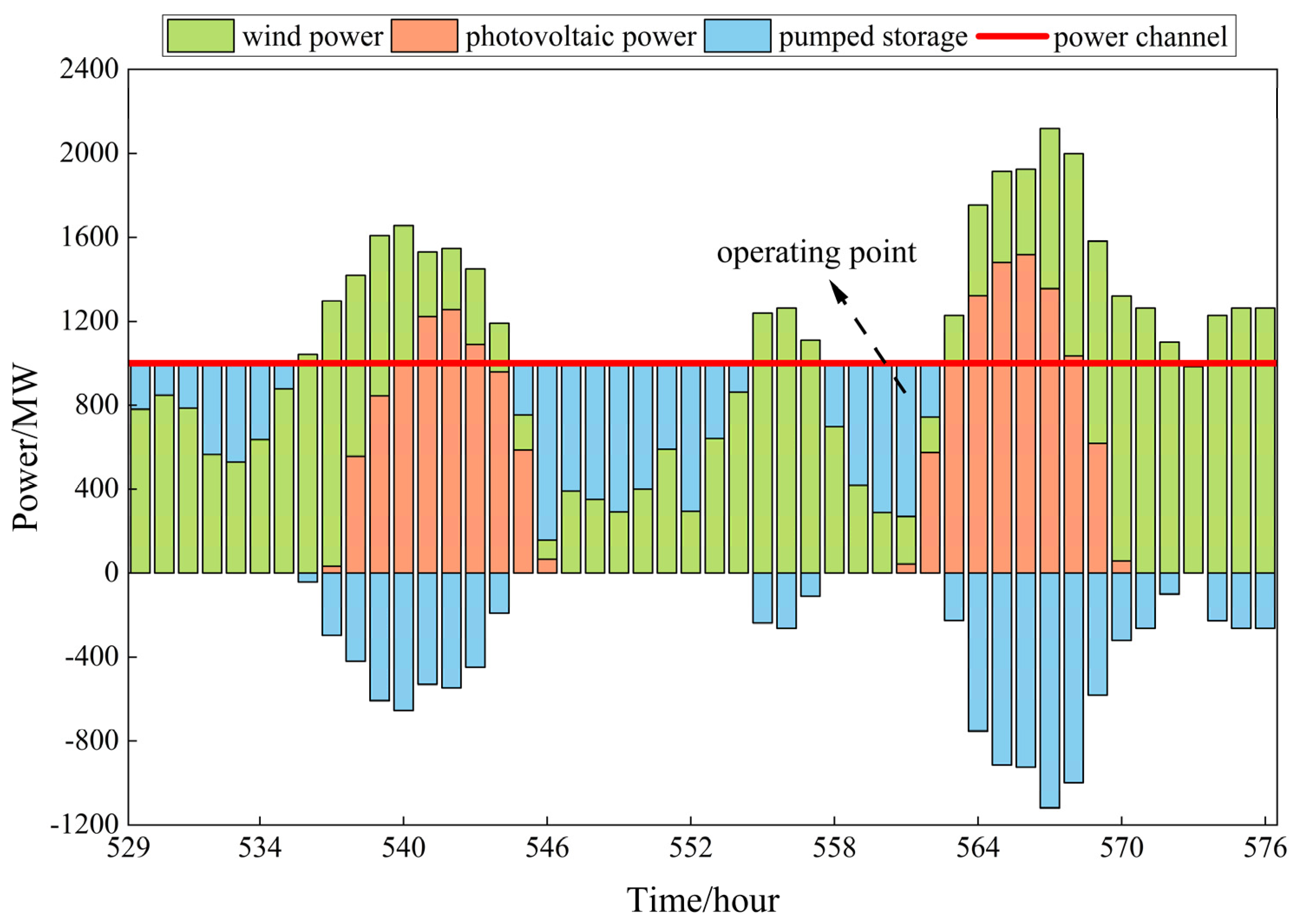
3.2. System Output Characteristics
3.3. Weights Solution
3.4. Cloud Model Health Evaluation
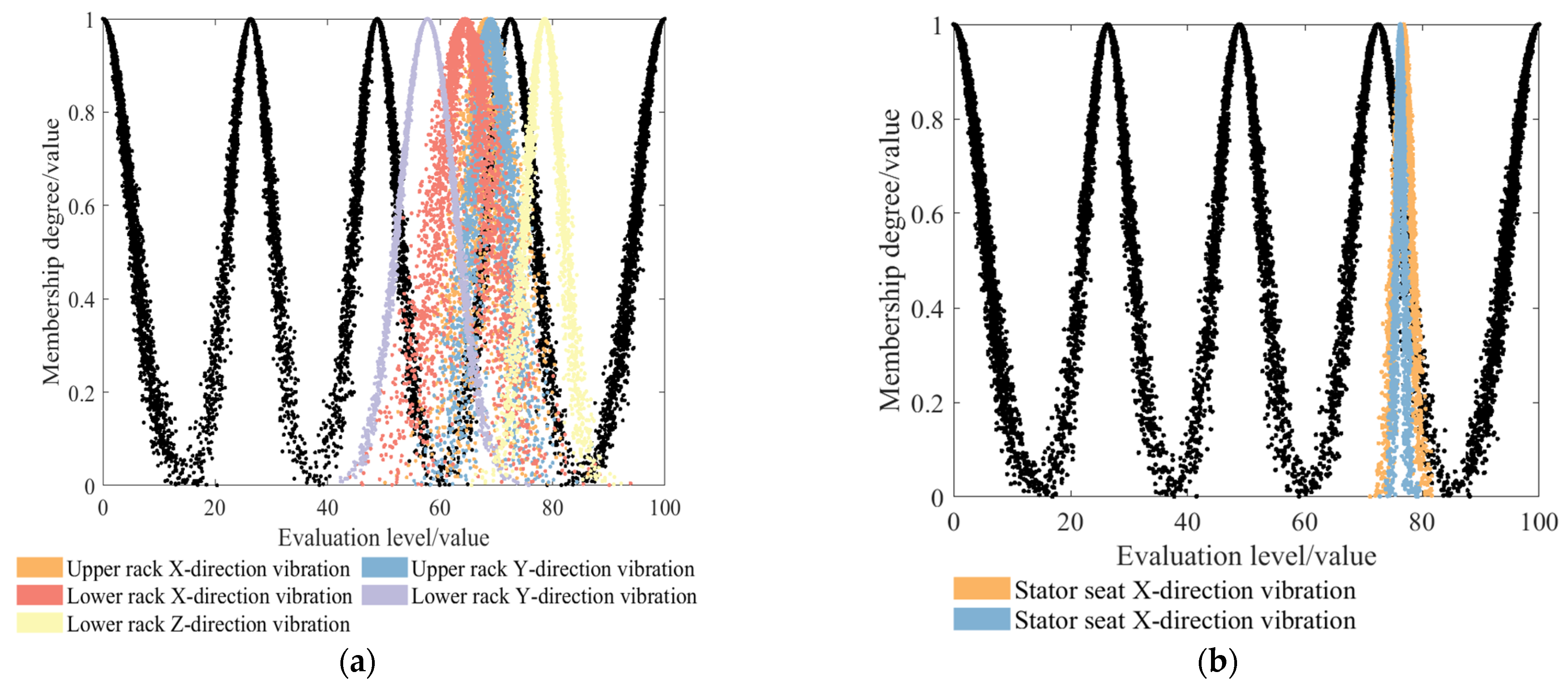
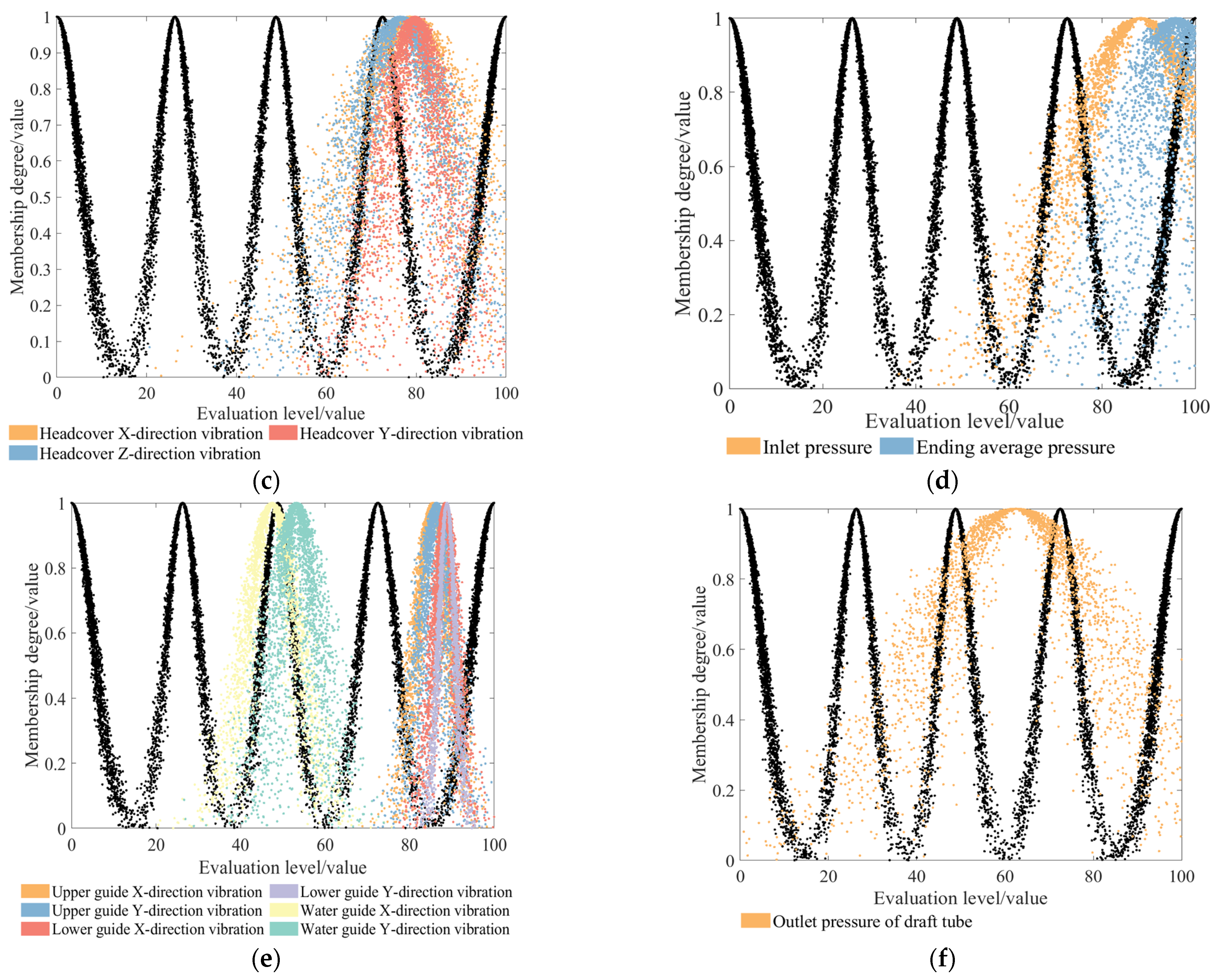
3.4.1. Index Cloud Solving
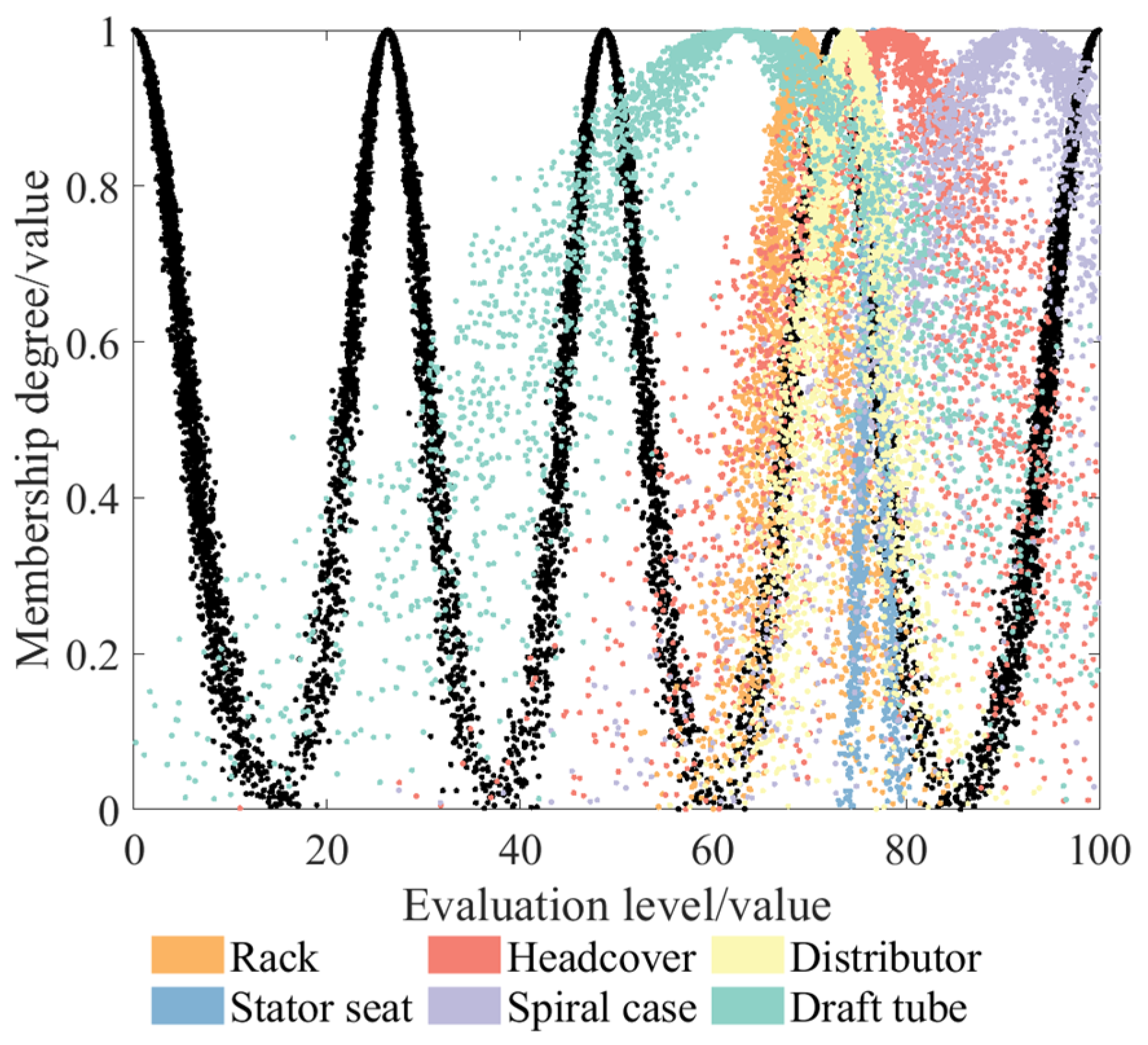
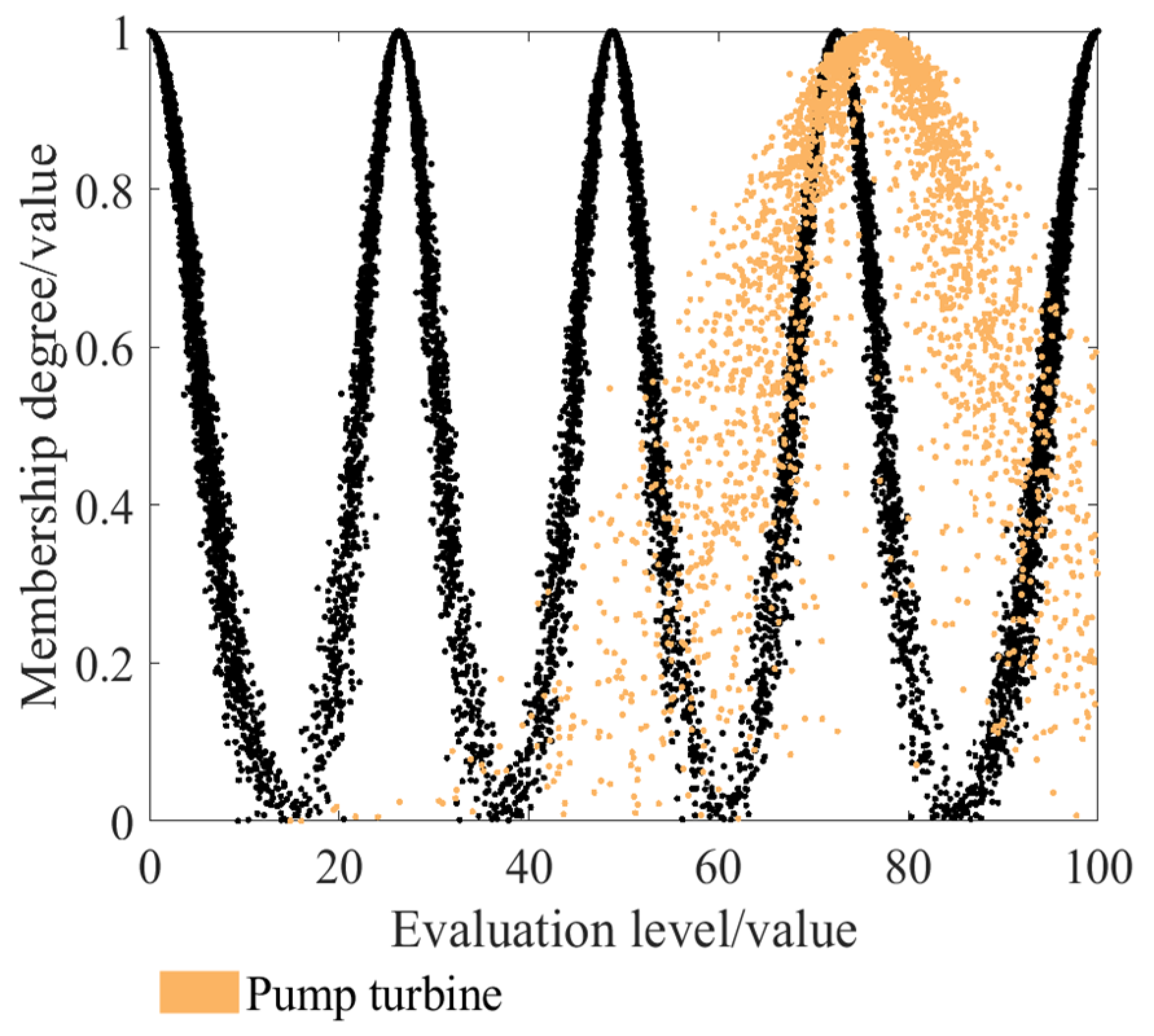
3.4.2. Integrated Cloud Solving
4. Conclusions
- (1)
- By analyzing the output characteristics of wind and PV in the hybrid system over a year (8760 h) and the output characteristics of the hybrid wind/PV/pumped storage system over a typical week (168 h) in all four seasons, the study shows that the pumped storage units switch operating conditions more frequently when smoothing out large-scale wind and PV fluctuations.
- (2)
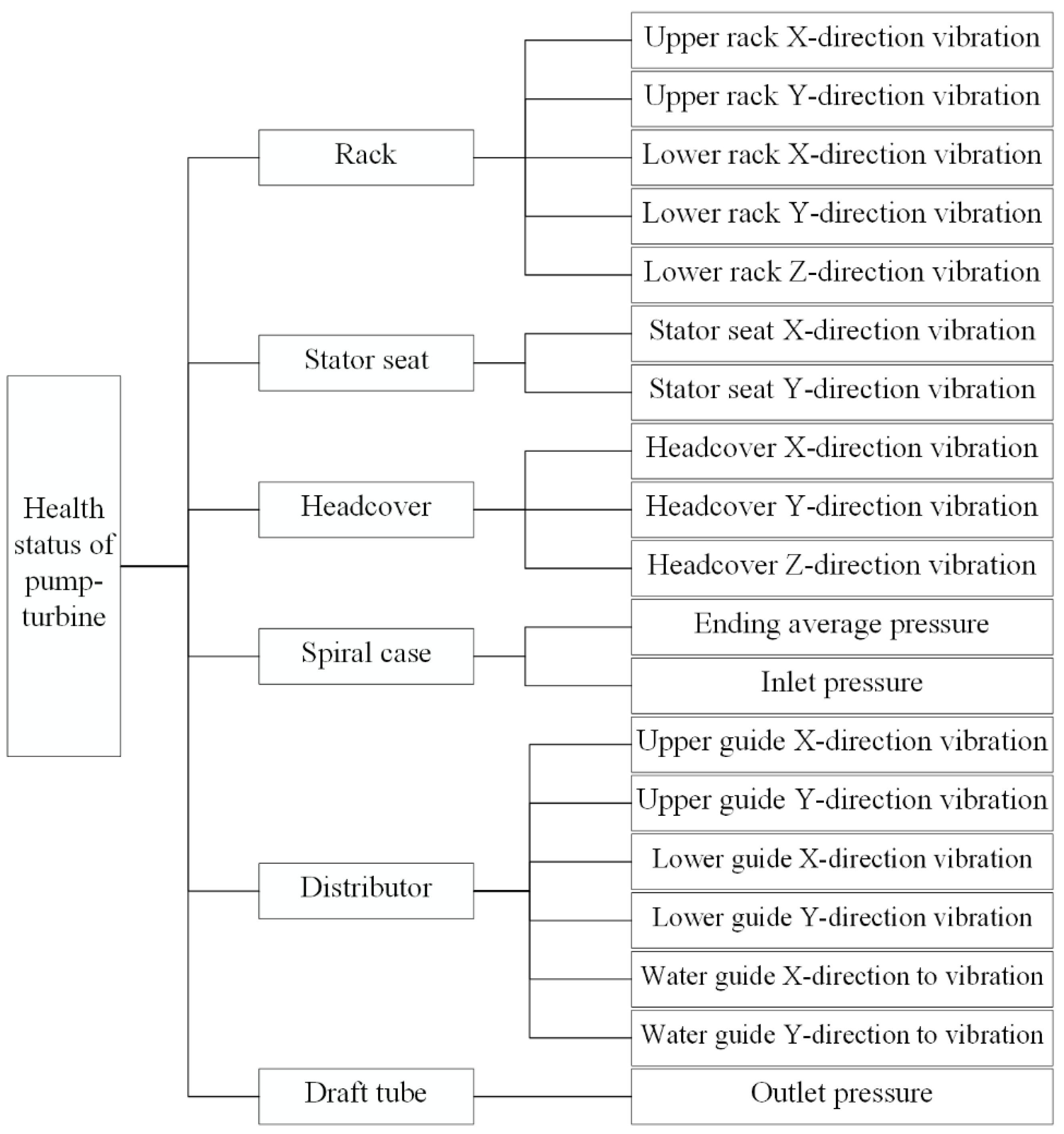
- A set of pump turbine health evaluation index systems based on high proportion of wind and PV power connection background was constructed, including one system layer index, six component layer indexes, and 19 index layer indexes, and the final weights of the indexes were determined based on the GTCW method. The results showed that the weight values of each evaluation index were in the following order: stator seat (0.233), spiral case (0.224), and draft tube (0.195); the weight of these three indicators is high, and the impact on the overall performance of the unit is large and should be paid attention to.
- (3)
- Based on the cloud model, a health state evaluation model of the pump turbine was constructed, and the health condition of the unit was quantitatively analyzed by the degree of affiliation. The results show that the draft tube (Ex = 62.476) and the water guide index in the distributor mechanism (Ex = 50.333) have different degrees of deterioration tendency, and suitable overhauling strategies need to be formulated to avoid further damages; the numerical characteristics of the cloud model of the overall health status of the pump turbine are (Ex = 76.411, En = 12.071, He = 4.014), and in the good grade, the affiliation degree reaches 0.7772, reflecting that the unit is in good condition and the overall performance is stable.
- (4)
- The methods of this research are also applicable to other energy storage solutions using pump turbine systems for smoothing the output of the hybrid wind/PV systems, such as abandoned mine pumped storage and compressed air energy storage. These systems can achieve more stable operations in smoothing output fluctuations under high proportions of wind/PV power connection by utilizing the health assessment technology of pump turbine systems, thereby enhancing the efficiency of renewable energy utilization. There are still some limitations in this study. First of all, the results of the model are highly dependent on the quality and accuracy of the input data. If there is noise or error in the data, the reliability of the evaluation results may be affected. Secondly, this study did not fully consider the influence of external factors such as dynamic changes in water quality, which may limit the adaptability of the model in different situations.
- (5)
- The research and analysis in this paper are mainly based on the external characteristics of the unit, focusing on the operation characteristics of the pump turbine and the construction of the health evaluation model under the conditions of high-proportion wind and PV access. The direction of future research work is to further analyze the internal characteristics of the unit, especially the factors related to the vortex structure. This analysis can provide important theoretical support for understanding the internal flow characteristics, energy conversion efficiency, and health state of the unit, and help provide new ideas and methods for the optimization of the unit operation and fault diagnosis.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| a | Diode quality factor |
| aij | Initial value of the indicator |
| b | Electronic charge (C) |
| bij | Standardized value of the indicator |
| B | Boltzmann’s constant (J/K) |
| d | The degree of deterioration of the index |
| ej | Information entropy |
| Hy | Head of the pumped storage unit under pumping conditions (m) |
| Hp | Head of the pumped storage unit under turbine operation (m) |
| Hmax | Upper limit of health assessment level score |
| Ip | PV generation current (A) |
| Ir | Reverse saturation current of the diode (A) |
| N1 | Number of parallel PV cells |
| N2 | Number of series PV cells |
| NW | Number of fans installed |
| Pw | Wind power output (MW) |
| Ppv | PV output (MW) |
| Pwr | Rated power of the fan (MW) |
| Py | Output of pumped storage unit under pump condition (MW) |
| Pp | Output of pumped storage unit under water turbine condition (MW) |
| Qy | Flow rate of the unit under pumping conditions (m3/s) |
| Qp | Flow rate of the unit under turbine operation (m3/s) |
| rij | An element in a judgment matrix |
| rkj | Correlation coefficient between the indicators |
| rj | Quantitative coefficients |
| Sw | Swept area of the rotor (m2) |
| T | Operating temperature of the PV cell (°C) |
| UPV | Output voltage of the PV cell (V) |
| v | Wind speed flowing through the wind turbine (m/s) |
| vi | Cut-in wind speed (m/s) |
| vo | Cut-out wind speed (m/s) |
| vr | Rated speed of the fan (r/min) |
| vj | The average difference of each indicator |
| W | Arbitrary linear combination set of weights |
| x | Parameter measurement value |
| xmax | The maximum value of the parameter run |
| xmin | The minimum value of the parameter run |
| Xmax | The maximum value of evaluation interval |
| Xmin | The minimum value of evaluation interval |
| Greek alphabet | |
| φ | Membership of the index |
| ρ | Air density (kg/m3) |
| τ | Fan’s coefficient of performance (%) |
| ηy | Unit efficiency under pump conditions (%) |
| ηp | Unit efficiency under water turbine condition (%) |
| λmax | Largest eigenvalue of the judgment matrix |
| ω2 | The weights obtained by ICRITIC method |
| ω | The final combined weight |
| αk | Weight coefficient |
| αi | Value of the weight of the i th indicator |
| γ1 | The minimum value of the parameter in the optimal interval |
| γ2 | The maximum value of the parameter in the optimal interval |
References
- Zhao, X.; Ma, X.; Chen, B.; Shang, Y.; Song, M. Challenges toward carbon neutrality in China: Strategies and countermeasures. Resour. Conserv. Recycl. 2022, 176, 105959. [Google Scholar] [CrossRef]
- Li, Z.; Li, W.; Zhang, Z.; Chang, G.; Lyu, J.; Yue, G.; Li, L.; Ni, W. Development Strategy of Flexible Resources in China’s Power System under the Carbon Peaking and Carbon Neutrality Goals. Strateg. Study CAE 2024, 26, 108–120. [Google Scholar]
- Koholé, Y.W.; Fohagui, F.C.V.; Tchuen, G. A holistic overview of Cameroon renewable energy sources: Potentials, achievements, challenges and perspectives. Int. J. Ambient. Energy 2022, 43, 7308–7320. [Google Scholar] [CrossRef]
- Arabzadeh, V.; Frank, R. Creating a renewable energy-powered energy system: Extreme scenarios and novel solutions for large-scale renewable power integration. Appl. Energy 2024, 374, 124088. [Google Scholar] [CrossRef]
- Ai, C.; Zhang, L.; Gao, W.; Yang, G.; Wu, D.; Chen, L.; Chen, W.; Plummer, A. A review of energy storage technologies in hydraulic wind turbines. Energy Convers. Manag. 2022, 264, 115584. [Google Scholar] [CrossRef]
- Arunkumar, A.P.; Kuppusamy, S.; Muthusamy, S.; Pandiyan, S.; Panchal, H.; Nagaiyan, P. An extensive review on energy management system for microgrids. Energy Sources Part A Recovery Util. Environ. Eff. 2022, 44, 4203–4228. [Google Scholar] [CrossRef]
- Lin, J.; Gu, Y.; Wang, Z.; Zhao, Z.; Zhu, P. Operational characteristics of an integrated island energy system based on multi-energy complementarity. Renew. Energy 2024, 230, 120890. [Google Scholar] [CrossRef]
- Wu, C.; Chen, Z.; Zhang, Y.; Feng, J.; Xie, Y.; Qin, C. A case study of multi-energy complementary systems for the building based on Modelica simulations. Energy Convers. Manag. 2024, 306, 118290. [Google Scholar] [CrossRef]
- Yongli, W.; Pengxu, D.; Miaomiao, X.; Yiwen, L.; Dong, Z.; Ximei, L. Research on collaborative operation optimization of multi-energy stations in regional integrated energy system considering joint demand response. Int. J. Electr. Power Energy Syst. 2024, 155, 109507. [Google Scholar]
- Liao, S.; Su, K.; Yu, Q.; Wang, D.; Zhang, Q.; Qi, M. Optimal Capacity Allocation for Wind-Solar Station Considering Power Response of Pumped Storage. In Proceedings of the 2019 IEEE 3rd Conference on Energy Internet and Energy System Integration (EI2), Changsha, China, 8–10 November 2019; pp. 2053–2058. [Google Scholar]
- Ren, Y.; Jin, K.; Gong, C.; Hu, J.; Liu, D.; Jing, X.; Zhang, K. Modelling and capacity allocation optimization of a combined pumped storage/wind/photovoltaic/hydrogen production system based on the consumption of surplus wind and photovoltaics and reduction of hydrogen production cost. Energy Convers. Manag. 2023, 296, 117662. [Google Scholar] [CrossRef]
- Menéndez, J.; Schmidt, F.; Konietzky, H.; Fernández-Oro, J.M.; Galdo, M.; Loredo, J.; Díaz-Aguado, M.B. Stability analysis of the underground infrastructure for pumped storage hydropower plants in closed coal mines. Tunn. Undergr. Space Technol. 2019, 94, 103117. [Google Scholar] [CrossRef]
- Menéndez, J.; Fernández-Oro, J.M.; Galdo, M.; Loredo, J. Efficiency analysis of underground pumped storage hydropower plants. J. Energy Storage 2020, 28, 101234. [Google Scholar] [CrossRef]
- Chen, Y.; Feng, L.; Mansir, I.B.; Taghavi, M.; Sharma, K. A new coupled energy system consisting of fuel cell, solar thermal collector, and organic Rankine cycle; Generation and storing of electrical energy. Sustain. Cities Soc. 2022, 81, 103824. [Google Scholar] [CrossRef]
- Wang, Y.-Y.; Mori, A. A review of dynamic changes in complementarities and transition pathways toward distributed energy resource–based electrical system. Renew. Energy Focus 2024, 51, 100626. [Google Scholar] [CrossRef]
- Aguilar, F.I.; Gibson, R.B. Advancing a New Generation of Sustainability-Based Assessments for Electrical Energy Systems: Ontario as an Illustrative Application—A Review. Energies 2023, 16, 6285. [Google Scholar] [CrossRef]
- Yi, Y.; Chang, L.; Wu, B.; Zhao, J.; Peng, H.; Li, L.; Wang, A. Life Cycle Assessment of Energy Storage Technologies for New Power Systems under Dual-Carbon Target: A Review. Energy Technol. 2024, 12, 2301129. [Google Scholar] [CrossRef]
- Prasasti, E.; Joseph, M.; Miao, X.; Zangeneh, M.; Terheiden, K. Design of shaft-and rim-driven contra-rotating reversible pump-turbine to optimize novel low-head pumped hydro energy storages. Energy 2024, 306, 132237. [Google Scholar] [CrossRef]
- Yu, W.; Liu, C.; Chen, W.; Zhang, H.; Yu, Y.; Wang, D.; Wei, F. Development status and technical challenges of new low-carbon technologies for power systems under the dual-carbon goal. In Proceedings of the 2024 7th International Conference on Energy, Electrical and Power Engineering (CEEPE), Yangzhou, China, 26–28 April 2024. [Google Scholar]
- Wu, M.; Shi, J.; Wen, H.; Qiu, Y.; Guo, C. Research on power and energy balance of new power system under low carbon emission path. Energy Rep. 2022, 8, 197–207. [Google Scholar] [CrossRef]
- Hu, B.; Xie, K.; Shao, C.; Pan, C.; Lin, C.; Zhao, Y. Commentary on Risk of New Power System Under Goals of Carbon Emission Peak and Carbon Neutrality: Characteristics, Indices and Assessment Methods. Autom. Electr. Power Syst. 2023, 47, 1–15. [Google Scholar]
- Wang, W.; Yu, T.; Huang, Y.; Han, Y.; Liu, D.; Shen, Y. The situation and suggestions of the new energy power system under the background of carbon reduction in China. Energy Rep. 2021, 7, 1477–1484. [Google Scholar] [CrossRef]
- Alaoui, L.C.; Drid, S.; Ouriagli, M.; Mehdi, D. Overview of Photovoltaic and Wind Electrical Power Hybrid Systems. Energies 2023, 16, 4778. [Google Scholar] [CrossRef]
- Yahya, W.; Saied, K.M.; Nassar, A.; Qader, M.R.; Al-Nehari, M.; Zarabia, J.; Jian, Z. Optimization of a hybrid renewable energy system consisting of a of PV/wind turbine/battery/fuel cell integration and component design. Int. J. Hydrogen Energy 2024, 94, 1406–1418. [Google Scholar] [CrossRef]
- Qudah, A.; Almerbati, A.; Mokheimer, E.M.A. Techno-economic analysis and optimization of standalone Hybrid Photovoltaic (PV)/Wind Turbine (WT) with water tank storage driven Reverse Osmosis (RO) desalination system. Desalination 2025, 600, 118522. [Google Scholar] [CrossRef]
- Ren, Y.; Sun, K.; Zhang, K.; Han, Y.; Zhang, H.; Wang, M.; Jing, X.; Mo, J.; Zou, W.; Xing, X. Optimization of the capacity configuration of an abandoned mine pumped storage/wind/photovoltaic integrated system. Appl. Energy 2024, 374, 124089. [Google Scholar] [CrossRef]
- Sun, K.; Li, K.-J.; Pan, J.; Liu, Y.; Liu, Y. An optimal combined operation scheme for pumped storage and hybrid wind-photovoltaic complementary power generation system. Appl. Energy 2019, 242, 1155–1163. [Google Scholar] [CrossRef]
- Jurasz, J.; Dąbek, P.B.; Kaźmierczak, B.; Kies, A.; Wdowikowski, M. Large scale complementary solar and wind energy sources coupled with pumped-storage hydroelectricity for Lower Silesia (Poland). Energy 2018, 161, 183–192. [Google Scholar] [CrossRef]
- Wang, Z.; Fang, G.; Wen, X.; Tan, Q.; Zhang, P.; Liu, Z. Coordinated operation of conventional hydropower plants as hybrid pumped storage hydropower with wind and photovoltaic plants. Energy Convers. Manag. 2023, 277, 116654. [Google Scholar] [CrossRef]
- Dhingra, T.; Sengar, A.; Sajith, S. A fuzzy analytic hierarchy process-based analysis for prioritization of barriers to offshore wind energy. J. Clean. Prod. 2022, 345, 131111. [Google Scholar] [CrossRef]
- Chuanhao, F.; Yan, C.; Yan, Z.; Long, Z.; Wenjuan, W.; Bin, L.; Sijie, T. Using Fuzzy Comprehensive Evaluation to Assess the Competency of Full-Time Water Conservancy Emergency Rescue Teams. Mathematics 2022, 10, 2111. [Google Scholar] [CrossRef]
- Meng, X.; Chang, J.; Wang, X.; Wang, Y.; Wang, Z. Flood control operation coupled with risk assessment for cascade reservoirs. J. Hydrol. 2019, 572, 543–555. [Google Scholar] [CrossRef]
- Luan, W.; Wei, Z.; Liu, B.; Yu, Y. A training-free non-intrusive air conditioning load monitoring method based on fuzzy comprehensive evaluation. Appl. Energy 2024, 376, 124058. [Google Scholar] [CrossRef]
- Hou, J.; Gao, T.; Yang, Y.; Meng, S. Battery inconsistency evaluation based on hierarchical weight fusion and fuzzy comprehensive evaluation method. J. Energy Storage 2024, 84, 110878. [Google Scholar] [CrossRef]
- Castellani, F.; Natili, F.; Astolfi, D.; Vidal, Y. Wind turbine gearbox condition monitoring through the sequential analysis of industrial SCADA and vibration data. Energy Rep. 2024, 12, 750–761. [Google Scholar] [CrossRef]
- Liu, D.; Wang, S.; Fan, Y.; Fernandez, C.; Blaabjerg, F. An optimized multi-segment long short-term memory network strategy for power lithium-ion battery state of charge estimation adaptive wide temperatures. Energy 2024, 304, 132048. [Google Scholar] [CrossRef]
- Wang, C.; Huang, Z.; He, C.; Lin, X.; Li, C.; Huang, J. Research on remaining useful life prediction method for lithium-ion battery based on improved GA-ACO-BPNN optimization algorithm. Sustain. Energy Technol. Assess. 2025, 73, 104142. [Google Scholar] [CrossRef]
- Zhang, S.; Zhou, H. Transformer Fault Diagnosis Based on Multi-Strategy Enhanced Dung Beetle Algorithm and Optimized SVM. Energies 2024, 17, 6296. [Google Scholar] [CrossRef]
- Zhao, W.; Egusquiza, M.; Valero, C.; Valentín, D.; Presas, A.; Egusquiza, E. On the use of artificial neural networks for condition monitoring of pump-turbines with extended operation. Measurement 2020, 163, 107952. [Google Scholar] [CrossRef]
- Dorber, M.; Scherer, L.; Verones, F. Midpoint characterization factors to assess impacts of turbine water use from hydropower production. Int. J. Life Cycle Assess. 2024, 29, 2151–2164. [Google Scholar] [CrossRef]
- Zhang, F.; Liu, J.; Liu, Y.; Li, Y.; Duan, R.; Chen, Z.; Jiang, X. Heterogeneous graph contrastive learning-based transductive health condition assessment of Francis turbine unit. Eng. Appl. Artif. Intell. 2025, 145, 110240. [Google Scholar] [CrossRef]
- Chen, H.; Pan, J.; Wang, S.; Ma, J.; Zhang, W. Fatigue Damage Assessment of Turbine Runner Blades Considering Sediment Wear. Appl. Sci. 2024, 14, 4660. [Google Scholar] [CrossRef]
- Zhang, F.; Liu, J.; Liu, Y.; Li, H.; Jiang, X. Data-model-interactive enhancement-based Francis turbine unit health condition assessment using graph driven health benchmark model. Expert Syst. Appl. 2024, 249, 123724. [Google Scholar]
- Su, W.; Li, Q.; Zheng, W.; Han, Y.; Yu, Z.; Bai, Z.; Han, Y. Enhancing wind-solar hybrid hydrogen production through multi-state electrolyzer management and complementary energy optimization. Energy Rep. 2024, 11, 1774–1786. [Google Scholar] [CrossRef]
- Nasrabadi, A.M.; Korpeh, M. Techno-economic analysis and optimization of a proposed solar-wind-driven multigeneration system; case study of Iran. Int. J. Hydrogen Energy 2023, 48, 13343–13361. [Google Scholar] [CrossRef]
- Wang, J.; Wen, Y.; Wu, K.; Ding, S.; Liu, Y.; Tian, H.; Zhang, J.; Wang, L.; Cao, Q.; Zhang, Y.; et al. Optimization study of wind, solar, hydro and hydrogen storage based on improved multi-objective particle swarm optimization. J. Energy Storage 2024, 93, 112298. [Google Scholar]
- Ahadi, P.; Fakhrabadi, F.; Pourshaghaghy, A.; Kowsary, F. Optimal site selection for a solar power plant in Iran via the Analytic Hierarchy Process (AHP). Renew. Energy 2023, 215, 118944. [Google Scholar]
- Zhao, S.; Tang, S. Comprehensive evaluation of transmission network planning scheme based on improved analytic hierarchy process, CRITIC method and TOPSIS. Electr. Power Autom. Equip. 2019, 39, 143–148+162. [Google Scholar]
- Šostar, M.; Ristanović, V. Assessment of influencing factors on consumer behavior using the AHP model. Sustainability 2023, 15, 10341. [Google Scholar] [CrossRef]
- Diakoulaki, D.; Mavrotas, G.; Papayannakis, L. Determining objective weights in multiple criteria problems: The CRITIC method. Comput. Oper. Res. 1995, 22, 763–770. [Google Scholar]
- Li, Y.-N.; Hu, Z.-H. A tri-system urban waterlogging risk assessment framework based on GIS- game theory combination weight: A case of Zhengzhou City. Nat. Hazards 2024, 120, 14649–14681. [Google Scholar]
- Mao, Y.; Luobin, Z.; Yang, C. Wind speedpower curve modeling method based on hybrid half-cloud model. Electr. Power Autom. Equip. 2020, 40, 106–114. [Google Scholar]
- Cheng, J.; Duan, Z. Cloud model based sine cosine algorithm for solving optimization problems. Evol. Intell. 2019, 12, 503–514. [Google Scholar]
- Zhang, B.; Yang, Y.; Liu, L.; Ma, Z. Operation status evaluation of hydraulic turbine regulation system based on improved AHP and cloud model. Yangtze River 2024, 55, 219–225. [Google Scholar]
- Liu, J.; An, B.; Zhang, W.; Gan, Q. Review of health status evaluation of large wind turbines. Power Syst. Prot. Control. 2023, 51, 176–187. [Google Scholar]
- Gong, Y.; Jiang, Y.; Liang, X. Similarity Measurement for Normal Cloud Models Based on Fuzzy Similarity Measure. Syst. Eng. 2015, 33, 133–137. [Google Scholar]




| Type of PS Unit | Installed Capacity/MW | Turbine Power/MW | Pump Power/MW | Rated Head/m |
|---|---|---|---|---|
| Mixed-flow single-stage reversible type | 4 × 300 | 306 | 324.2 | 550 |
| Scale Value | Meaning |
|---|---|
| Equally important |
| Slightly important |
| Strongly important |
| Significantly important |
| Definitely important |
| Rank | 1 | 2 | 3 | 5 | 6 |
|---|---|---|---|---|---|
| RI | 0 | 0 | 0.52 | 1.12 | 1.24 |
| Method | Advantage Description | Focus on Solving Problems |
|---|---|---|
| Traditional CRITIC method | The weight is determined by the correlation between indicators to ensure the rationality of the evaluation results. | The objectivity and impartiality of index weights, especially the mutual influence of indicators. |
| Entropy weight method | It can identify indicators with large information and give them higher weights to reflect the real situation. | Address the problem of information asymmetry and strengthen the influence of important indicators. |
| IAHP method | The combination of analytic hierarchy process and fuzzy mathematics can deal with uncertainty and subjectivity in complex decision making. | Conduct multi-level and multi-index decision analysis to optimize resource allocation and evaluation. |
| Game theory method of weighting | Combine subjective and objective empowerment to reduce subjectivity and error caused by single empowerment. | Seek the consistency between evaluation indicators and optimize the decision-making process. |
| Cloud model | It deals with the uncertain transformation of qualitative and quantitative information, and the description ability is stronger than that of fuzzy membership function. | Accurate assessment of uncertainty issues, such as health assessment of pump turbines. |
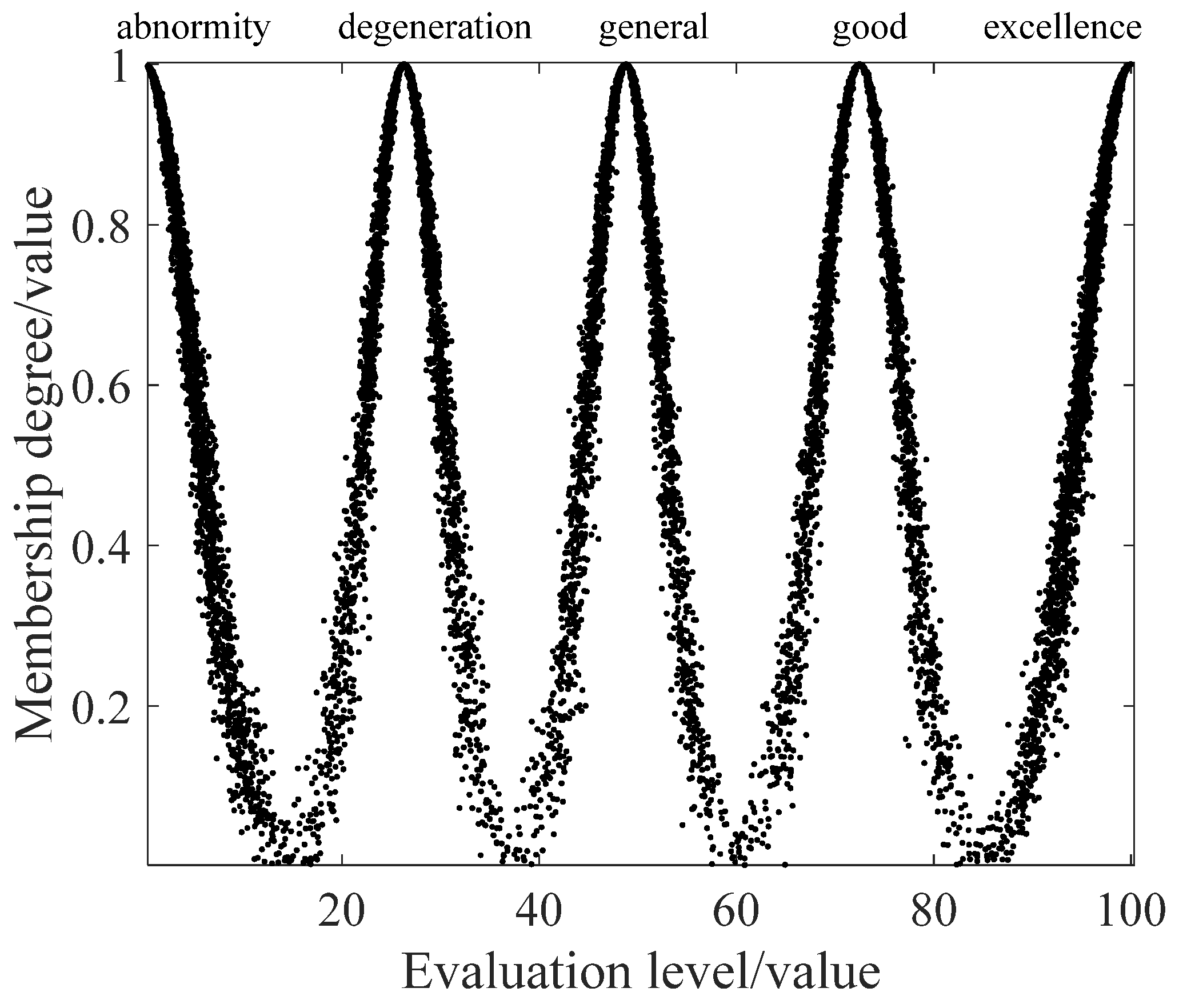
| Health Status | Interval Range | Health Status Description |
|---|---|---|
| Excellence | 85~100 | Indicator is in the normal range and close to the optimal value |
| Good | 60~85 | Indicators are generally satisfactory, with no deterioration trend |
| General | 37.5~60 | A small number of indicators are close to the warning value, but most of the indicators are generally acceptable, with a deterioration trend. |
| Degeneration | 15~37.5 | Indicators are close to the warning value, with a deterioration trend |
| Abnormality | 0~15 | The unit is operating abnormally, and the indicator data exceed the threshold value. |
| Numerical Characteristics | Abnormity | Degeneration | General | Good | Excellence |
|---|---|---|---|---|---|
| Ex | 0 | 26.3 | 48.8 | 72.5 | 100 |
| En | 5 | 3.75 | 3.75 | 4.17 | 5 |
| He | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 |
| Component Layer | Subjective Weights | Objective Weights | Combination Coefficients | Combination Weights | Index Layer | Subjective Weights | Objective Weights | Combination Coefficients | Combination Weights | Combined Weights |
|---|---|---|---|---|---|---|---|---|---|---|
| Rack A1 | 0.091 | 0.107 | ω1 = 0.4802 ω2 = 0.5198 | 0.099 | A11 | 0.226 | 0.213 | ω1 = 0.7548 ω2 = 0.2542 | 0.225 | 0.022 |
| A12 | 0.271 | 0.234 | 0.264 | 0.026 | ||||||
| A13 | 0.161 | 0.189 | 0.170 | 0.017 | ||||||
| A14 | 0.115 | 0.180 | 0.133 | 0.013 | ||||||
| A15 | 0.226 | 0.185 | 0.218 | 0.022 | ||||||
| Stator seat A2 | 0.076 | 0.378 | 0.233 | A21 | 0.417 | 0.496 | ω1 = 0.6840 ω2 = 0.3160 | 0.442 | 0.103 | |
| A22 | 0.583 | 0.504 | 0.558 | 0.130 | ||||||
| Headcover A3 | 0.152 | 0.113 | 0.132 | A31 | 0.433 | 0.307 | ω1 = 0.7625 ω2 = 0.2375 | 0.403 | 0.053 | |
| A32 | 0.309 | 0.375 | 0.325 | 0.043 | ||||||
| A33 | 0.258 | 0.319 | 0.272 | 0.036 | ||||||
| Spiral case A4 | 0.341 | 0.117 | 0.224 | A41 | 0.545 | 0.497 | ω1 = 0.9370 ω2 = 0.0630 | 0.542 | 0.121 | |
| A42 | 0.455 | 0.503 | 0.458 | 0.103 | ||||||
| Distributor A5 | 0.127 | 0.108 | 0.117 | A51 | 0.275 | 0.123 | ω1 = 0.5044 ω2 = 0.4956 | 0.200 | 0.023 | |
| A52 | 0.229 | 0.132 | 0.181 | 0.021 | ||||||
| A53 | 0.164 | 0.115 | 0.139 | 0.016 | ||||||
| A54 | 0.137 | 0.116 | 0.126 | 0.015 | ||||||
| A55 | 0.098 | 0.250 | 0.173 | 0.020 | ||||||
| A56 | 0.098 | 0.265 | 0.180 | 0.021 | ||||||
| Draft tube A6 | 0.213 | 0.178 | 0.195 | A61 | 1.000 | 1.000 | ω1 = 0.5000 ω2 = 0.5000 | 1.000 | 0.195 |
| Indicators | Parameters (Ex, En, He) | Abnormity | Degradation | General | Good | Excellence |
|---|---|---|---|---|---|---|
| Rack | (69.3459, 3.5861, 1.3229) | 0.0000 | 0.0000 | 0.0084 | 0.9910 | 0.0006 |
| Stator seat | (76.5678, 0.9935, 0.2588) | 0.0000 | 0.0000 | 0.0000 | 0.9998 | 0.0002 |
| Headcover | (78.1769, 10.1289, 4.6672) | 0.0000 | 0.0005 | 0.0461 | 0.7832 | 0.1702 |
| Spiral case | (91.7296, 12.7871, 4.9559) | 0.0000 | 0.0002 | 0.0131 | 0.2765 | 0.7102 |
| Distributor | (73.9884, 4.1202, 1.5261) | 0.0000 | 0.0000 | 0.0019 | 0.9928 | 0.0053 |
| Draft tube | (62.4756, 20.7153, 5.8250) | 0.0102 | 0.0858 | 0.3667 | 0.4487 | 0.0885 |
| Pump turbine | (76.4117, 12.0705, 4.0141) | 0.0000 | 0.0019 | 0.0741 | 0.7772 | 0.1468 |
| Part Name | Forecast Result | Actual Result |
|---|---|---|
| Upper rack | Good | Good |
| Lower rack | Good | Good |
| Upper guide | Good | Good |
| Lower guide | Good | Excellence |
| Water guide | General | General |
| Rack | Good | Good |
| Stator seat | Good | Good |
| Headcover | Good | Good |
| Spiral case | Excellence | Good |
| Distributor | Good | Good |
| Draft tube | Good | General |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ren, Y.; Zhang, H.; Wu, L.; Zhang, K.; Cheng, Z.; Sun, K.; Sun, Y.; Hu, L. Research on the Health Evaluation of a Pump Turbine in Smoothing Output Volatility of the Hybrid System Under a High Proportion of Wind and Photovoltaic Power Connection. Energies 2025, 18, 1306. https://doi.org/10.3390/en18051306
Ren Y, Zhang H, Wu L, Zhang K, Cheng Z, Sun K, Sun Y, Hu L. Research on the Health Evaluation of a Pump Turbine in Smoothing Output Volatility of the Hybrid System Under a High Proportion of Wind and Photovoltaic Power Connection. Energies. 2025; 18(5):1306. https://doi.org/10.3390/en18051306
Chicago/Turabian StyleRen, Yan, Haonan Zhang, Lile Wu, Kai Zhang, Zutian Cheng, Ketao Sun, Yuan Sun, and Leiming Hu. 2025. "Research on the Health Evaluation of a Pump Turbine in Smoothing Output Volatility of the Hybrid System Under a High Proportion of Wind and Photovoltaic Power Connection" Energies 18, no. 5: 1306. https://doi.org/10.3390/en18051306
APA StyleRen, Y., Zhang, H., Wu, L., Zhang, K., Cheng, Z., Sun, K., Sun, Y., & Hu, L. (2025). Research on the Health Evaluation of a Pump Turbine in Smoothing Output Volatility of the Hybrid System Under a High Proportion of Wind and Photovoltaic Power Connection. Energies, 18(5), 1306. https://doi.org/10.3390/en18051306







