Abstract
Power generation is an important part of air vehicle energy management when developing long-endurance and reusable hypersonic aircraft. In order to utilize an air turbine power generation system on board, fuel-based rotating cooling has been researched to cool the turbine’s rotor blades. For fuel-cooling air turbines, each blade corresponds to a separate cooling channel. All the separate cooling channels cross together and form a distributary cavity and a confluence cavity in the center of the disk. In order to determine the flow characteristics in the distributary and confluence cavities, computational fluid dynamics (CFD) simulations using the shear–stress–transport turbulence model were carried out under the conditions of different rotating speeds and different mass flow rates. The results showed great differences between non-rotating flow and rotating flow conditions in the distributary and confluence cavities. The flow in the distributary and confluence cavities has rotational velocity, with obvious layering distribution regularity. Moreover, a high-speed rotational flow surface is formed in the confluence cavity of the original structure, due to the combined functions of centrifugal force, inertia, and the Coriolis force. Great pressure loss occurs when fluid passes through the high-speed rotational flow surface. This pressure loss increases with the increase in rotating speed and mass flow rate. Finally, four structures were compared, and an optimal structure with a separated outlet channel was identified as the best structure to eliminate this great pressure loss.
1. Introduction
Power generation serves as an important part of energy management in hypersonic air vehicles. For power generation systems on board, an air turbine has obvious advantages, such as high power density and a small weight. However, the blade of the air turbine needs to be cooled since the temperature of the incoming air is very high. Internal cooling is widely used to protect turbines [1,2]. However, because the temperature of the compressed incoming air is too high, hydrocarbon fuel becomes the only coolant suitable for hypersonic aircraft.
The cooling of rotor blades using hydrocarbon fuel involves the flow and heat transfer of hydrocarbon fuel in a rotating channel. However, previous research on fuel flow and heat transfer was often conducted under nonrotating conditions. For example, Feng et al. [3] investigated the influence of turbulence and heat transfer on the performance of fuel pyrolysis inside a mini-channel. Liu et al. [4] investigated fuel steam reforming inside a mini-channel. Sun et al. [5] utilized the SST k-ω turbulence model to investigate the flow and heat transfer characteristics of turbulent hydrocarbon fuel flow in rectangular channels, with a particular focus on the conditions under which heat transfer deterioration occurs. Cong et al. [6] employed the SST k-ω model to study the advantages of helical cruciform fuel systems in terms of the heat transfer area-to-volume ratio and inter-channel mixing. Through CFD simulations, they obtained data on the velocity field and heat transfer coefficients. Studies show that fuel as a coolant for engines has good cooling capacity.
Since rotation generated additional force, including centrifugal force and Coriolis force, the flow and heat transfer characteristics in a rotating channel were greatly different from those in a nonrotating channel [7]. Under rotating conditions, due to the Coriolis force, a pair of counter-rotating vortices appeared in the rotating channel, resulting in significantly different heat transfer effects between the leading and trailing edges. The higher the rotational speed, the better the overall heat transfer effect, but the flow resistance is also greater, and local heat transfer deterioration might occur [8]. Jiang et al. [9] conducted experiments on rotational cooling using hydrocarbon fuels. Their research showed that the heat transfer efficiency of the trailing edge surface of the centrifugal channel was better than that of the leading-edge surface, and the effects of centrifugal force and buoyancy helped to reduce the deterioration in heat transfer. Ibrahim et al. [10] conducted experimental research on a rotating triangular thermosiphon and investigated the effect of rotational speed on the heat transfer coefficient. The working fluid R134a evaporated, flowed upward and flowed downward under the action of gravity and centrifugal force after condensation. During the condensation process, rotation could increase the heat transfer coefficient. Akhter et al. [11] achieved 45.62% heat transfer enhancement by using a double-diffusive mixed convective hybrid nanofluid for the rotating heat surface. Dong et al. [12] investigated the flow and heat transfer characteristics of hydrocarbon fuels under rotating conditions. They conducted numerical simulations using the SST k-ω model and found that rotation induces strong pressure gradients, causing the density and dynamic viscosity of hydrocarbon fuels to increase by up to 65.1% and 405%, respectively. Du et al. [13] studied the vortex cooling mechanism using the standard k-ω turbulence model under rotating conditions. As the rotation number increases, the cooling airflow velocity decreases, and the pressure drop increases, leading to a reduction in heat transfer intensity. Sun et al. [14] employed the SST k-ω turbulence model to study the influence of buoyancy-driven supercritical hydrocarbon fuel flow on heat transfer characteristics in rectangular channels. Buoyancy-assisted flow accelerated the formation of secondary flows and promoted the transition of the flow from an initially fully developed turbulent state to a laminar state.
Regarding research on turbine-related rotating cooling, air was the most commonly used cooling medium. The team led by Han [15,16] conducted decades of research on the air-rotating cooling of turbine blades, particularly on heat transfer enhancement structures such as ribs and fins. The ribs and fins in the channel could improve the flow field and reduce the possibility of local heat transfer deterioration. Huang and Liu et al. [17,18,19] carried out numerous experiments to investigate the influence of aspect ratio, flow direction, channel orientation, pin-fins, and ribs on the flow and heat transfer characteristics of air centrifugal flow in a rotating channel. Lorenzon et al. [20] also used thermochromic liquid crystals to measure temperature. By establishing a single function with temperature and color, temperature was obtained based on crystal color. According to the temperature distribution, the Nusselt number distribution under rotational conditions could be obtained. The experimental results of Ekkad and Singh [21] indicated that the Coriolis force and centrifugal force induced by rotation had a significant impact on the flow distribution and heat transfer performance within cooling channels. In order to increase the heat transfer coefficient, Abdelmaksoud et al. [22] injected a small amount of water mist into the air and studied the performance. The results indicated that utilizing the latent heat from the vaporization of a small amount of water mist could significantly improve the cooling capacity, reduce the consumption of mainstream air, and enhance the membrane cooling effect. In comparison, it could be seen that the comprehensive cooling capacity of rotating cooling using a liquid working fluid was higher than with air rotating cooling, but the flow resistance and uneven temperature distribution were also more pronounced. This was because liquids not only had greater heat absorption capacity and better heat transfer performance but also higher viscosity.
In addition, high-speed rotating cooling using hydrocarbon fuel also involves the problem of supergravity flow and heat transfer. Jiang et al. [23] first enhanced the turbulence intensity of a convective system by increasing the gravitational acceleration, studied the heat transfer characteristics of the system, and analyzed the influence of the Coriolis force. This study contributed to enhancing our understanding of convection within planets and flow and heat transfer issues in rotating machinery. Later, Jiang et al. [24] also proposed and developed a novel supergravity-driven turbulent heat convection system. The research team found that within a range of Rayleigh numbers exceeding one order of magnitude, results consistent with the scaling law of the ultimate range were observed, indicating that Coriolis forces under strong rotational conditions significantly affect turbulent motion. Li et al. [25] conducted experimental research on the flow of R245fa refrigerant in a horizontal tube under different gravity levels. The results indicated that fluid disturbance and the secondary flow caused by the Coriolis force could significantly enhance heat transfer efficiency.
In recent years, numerical simulation has become an important method for studying rotating cooling. Nabilah et al. [26] conducted numerical simulations using the k-ω turbulence model to investigate the heat transfer enhancement of heating tubes. Their results indicated that the maximum thermal enhancement factor could reach 1.3. Li et al. [27] proposed a multi-field coupled particle flow modeling and control method for microreactors based on computational fluid dynamics, which can effectively elucidate the evolution mechanism of multi-field coupled flow fields and is used to analyze particle distribution patterns under ultrasonic excitation. Zheng et al. [28] introduced a multiphase flow heat transfer model, based on the lattice Boltzmann method, to investigate the dynamic changes and temperature distribution patterns seen during the process of bubble rupture. Dong et al. [29] used the standard k-ε model to compare and analyze the flow characteristics and heat transfer performance of turbine cooling channels under stationary and rotating conditions. The additional forces due to rotation significantly increased turbulence intensity, flow resistance, and heat transfer levels. Khattak et al. [30] studied the heat transfer characteristics and flow field of nanofluids passing through nonlinear porous stretching sheets. A numerical solution was obtained using the projectile method, combined with RK-4 technology and Newton’s method. Shah et al. [31] found, through numerical simulations, that the entropy of the rotating cooling process decreases with increasing rotational parameters. Zhang et al. [32] employed a microscopic multiphase coupled transport dynamics model based on the volume of fluid smoothing and the Kistler dynamic contact angle model, aiming to investigate the transport evolution of droplets on the external surfaces and internal pore spaces of porous media. Tan et al. [33] presented an overview of multiphase fluid dynamics modeling, the mechanisms of material surface processing and removal, techniques for the assisted enhancement of finishing processes, and observation techniques for the impact effects of abrasive particles and bubble cavitation on surfaces. Abrar et al. [34,35] studied the effect of micro-rotation on heat transfer and entropy generation in tangent hyperbolic mixed nanofluids. The numerical results indicated that mixing nanofluids in micro-rotating tangent hyperbolic fluids could improve the thermal performance of the system. The authors of [36] also used numerical simulation methods to study the flow and heat transfer problems in high-speed rotating channels and found that the pressure in the flow field follows a quadratic distribution along the radial direction, while the rotation number is the determining parameter of the flow field characteristics.
From the literature review, it was evident that hydrocarbon fuels have gained widespread recognition as coolants for aircraft and exhibit excellent cooling performance. In past studies, cooling channels were mostly stationary, and numerical simulations predominantly utilized the k-ω SST turbulence model. Regarding rotating cooling, current research primarily employed air or fuel as the cooling medium. When air was used as the medium, there was no excessive pressure variation within the channel, and the technology for injecting air into cooling channels is relatively mature. The models used for air-based rotating cooling were diverse, including k-ω, SST, and k-ε, each applicable to different conditions. Studies using fuel as the cooling medium mainly focused on the flow and heat transfer issues within the blade’s internal regions, often overlooking the characteristics of fuel entering and exiting the cooling channels. Due to the high costs associated with hydrocarbon fuel and rotating cooling, numerical simulations were predominantly employed for research, with the SST turbulence model being the most common. By using numerical simulation methods, it was possible to simulate rotating cooling under high-speed and complex geometric conditions, thereby saving time and economic costs. This could quickly optimize the cooling structure and provide a good supplement to the research on the heat transfer mechanism of rotating cooling.
In our previous studies [37,38,39], the geometry model was simplified to a single square channel from a radial inlet to a radial outlet, which ignored the impact of the inlet section and outlet section in the axis. However, if the inlet or outlet parts were in the center of the axis, all cooling channels could cross together and shape themselves into a distributary cavity and a confluence cavity inside the turbine disk. Therefore, fuel flowed into the centrifugal channels from the distributary cavity and flowed out of the centripetal channels into the confluence cavity. The flow characteristics in distributary and confluence cavities are not clear at present, which may cause an inability to implement the fuel-based rotating cooling method. For this purpose, a computational fluid dynamics (CFD) model on rotating flow with fuel in distributary and confluence cavities was established, based on a hundred-kW-level air turbine [37]. The distributary cavity and confluence cavity were shaped to investigate the characteristics of distributary flow and confluence flow under high rotating speed conditions.
2. Physical Model
The rotor of the onboard hundred-kW class air turbine is shown in Figure 1a [37]. The whole cooling structure, designed based on the turbine, is shown in Figure 1b. The coolant fuel flows into the channel from the axis center and enters the distributary cavity, where the fuel is distributed into 36 separate cooling channels, corresponding to the 36 blades. In the separated cooling channels, cooling fuel flows along the radial outflow direction to the blade until the flow direction changes in the U-type duct in the blade. After cooling the blade, the fuel flows along the radial inflow direction to a confluence cavity and flows out of the rotor from the other side of the cooling channel in the axis center. To avoid the cooling channel crossing, the side length of the square channel was selected as 1 mm, and the diameters of the distributary and confluence cavities are both 25 mm. From Figure 1b, the cooling channel has obvious periodicity. One channel is used for research, as shown in Figure 1c, with geometry sizes. The mesh of the one-channel geometry model is drawn up as shown in Figure 1d. When generating the grid, mesh refinement is mainly carried out near the wall surface. The thickness of the first layer of the grid is 1 μm, with a growth ratio of 1.1. At the outlet of the distributary cavity and the inlet of the confluence cavity, the mesh is refined by considering the large fluctuations in the flow.
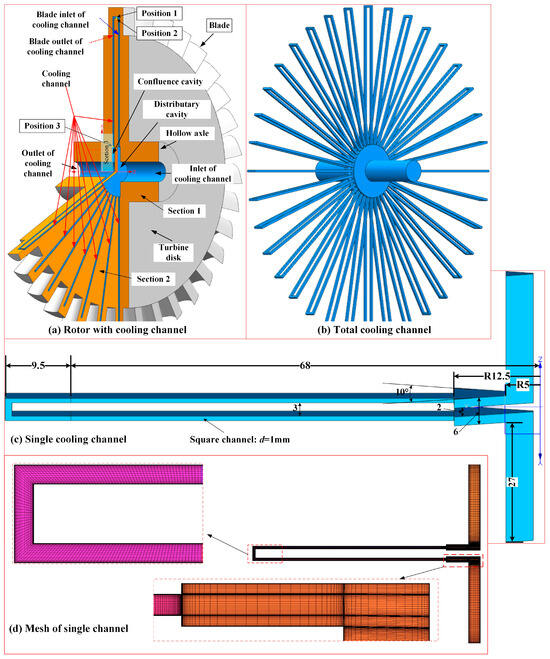
Figure 1.
Geometry model and mesh.
3. Numerical Details
3.1. Summary of the Working Conditions
In this paper, the main purpose was to investigate the flow characteristics in the distributary cavity and confluence cavity and optimize the structure of the cooling channel, based on the research results. Rotating speeds and mass flow rates were the main factors affecting flow velocity and Coriolis force. The rated rotating speed of the air turbine cooled in this study and the designed cooling mass flow rate were 57,000 RPM and 5 g/s per cooling channel [37]. The operating range of a typical turbine speed increases from 0 to around 120% of the rated speed. Therefore, the rotating speed range was 0–70,000 RPM. In order to further reduce the cooling flow rate, this study chose smaller mass flow rates of 1 g/s and 3 g/s for comparison. Therefore, the mass flow rates were 1, 3, and 5 g/s for a single channel. The working conditions in this study are shown in Figure 2.

Figure 2.
Summary of the studied channels.
3.2. Physical Properties of the Working Fluid
Decane is the usual replacement for hydrocarbon fuel. The basic parameters of decane were obtained from REFPROP 10.0 [40], including mole mass, density, specific heat capacity, thermal conductivity, and dynamic viscosity. The inlet temperature and pressure of the cooling channel were 350 K and 3 MPa. Since heat transfer did not occur in the distributary cavity and confluence cavity, and the average temperature difference between the distributary cavity and confluence cavity was only 19 K, the physical properties of the decane changed very little without a phase change. Therefore, the properties of the decane used in the CFD simulation were assumed to be constant, and the main parameters are listed in Table 1.

Table 1.
Physical properties of decane, as used in the CFD simulation.
3.3. Governing Equations
The sets of equations solved by ANSYS CFX 18.0 were the unsteady Navier–Stokes equations in their conservation form. The equations of mass, momentum, and energy conservation are presented in Equations (1)–(3) [39].
Continuity equation:
Momentum equation:
Energy equation:
The SST k-ω model accounts for the transport of turbulent shear stress and gives highly accurate predictions of flow separation under adverse pressure gradients. It solves two transport equations, namely, the first, k, for the turbulent kinetic energy, and the second, the turbulent frequency, ω.
The k equation can be expressed as in Equation (4).
The ω equation can be expressed as in Equation (5).
3.4. Boundary Conditions and CFD Configurations
Boundaries and solver controls were set as follows. The inlet boundary conditions of the cooling channel were set using the mass flow rate and static temperature, while the outlet boundary conditions were set using static pressure. A constant rotating speed was set for the fluid domain. A constant heat flux of 1.743 MW/m2, resulting from the coupled simulation results with an air turbine reported in Ref. [37], was set for the heated surfaces inside the blades. The two sides of the fluid in the axis were set as rotational periodicity interfaces. The other boundary walls were set as no-slip adiabatic smooth walls.
The total energy heat transfer model and shear–stress–transport (SST) turbulence model were used as fluid models in this study. The basic settings of solver control were an upwind advection scheme and first-order turbulence numerics. The timescale factor was set at 0.5, and the convergence criteria were set to maintain the stability of the residual curve.
3.5. CFD Model Validation
Due to the challenges associated with conducting experiments on the flow and heat transfer of hydrocarbon fuels under rotating conditions, there is currently a limited amount of published experimental data available. The CFD model was validated with the published experimental data given in Ref. [9], under the conditions of a mass flow rate of 1.11 g/s, an inlet temperature of 373.15 K, and an inlet pressure of 3.5 MPa. The comparison between the CFD results and experimental results is shown in Figure 3. It can be seen that in most cases, the temperature errors were below 10%. This error was due to the boundary in the CFD simulation being adiabatic, but there was a certain amount of heat loss in the actual conditions.
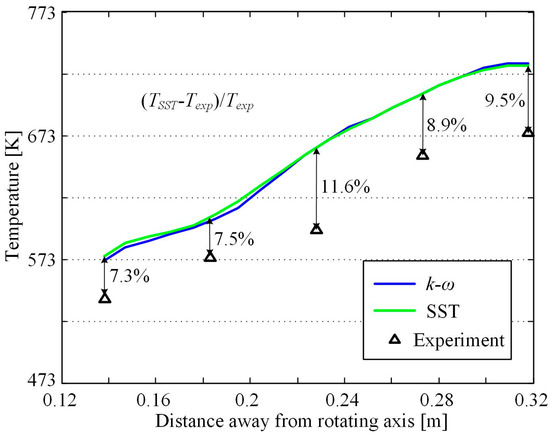
Figure 3.
CFD validation for the turbulence model.
Regarding numerical method validation, k-ε, RNG, k-ω, and SST were compared in a previous study [37]. The k-ε and RNG turbulence models had significant errors, while the k-ω and SST turbulence models had very similar results, with temperature distributions differing by less than 10% from experimental results, as shown in Figure 3. This was because the SST and k-ω turbulence models had advantages when calculating boundary layer and velocity separation. Meanwhile, in Ref. [38], regarding dimensionless temperature, the experimental results were very close to the numerical simulation results. Due to the close correlation between temperature distribution and velocity distribution, it can be inferred that the velocity distribution was also consistent with the actual situation. Meanwhile, considering that most of the current CFD research on hydrocarbon fuel flow in static channels used the SST turbulence model, the SST turbulence model was eventually adopted in this study. The Y+ of the used mesh was about 0.9 under the maximum mass flow rate conditions of 5 g/s per cooling channel.
3.6. Grid Independence Verification
A steady-state three-dimensional simulation was carried out with ANSYS CFX 18.0 software. Grid independence was performed for the cooling channel to ensure the mesh number was enough. The flow parameters, including the temperature, pressure, wall heat transfer coefficient, and velocity of the three positions, numbered 1, 2, and 3, as shown in Figure 1a, could be obtained from the CFD result. Point 1 was located at the midpoint of the U-shaped channel along the flow direction, where the pressure was highest. The temperature at this point was also influenced by heating from the blades, making both the temperature and pressure at Point 1 significant. Point 2 was situated directly below Point 1 on the inner wall surface, and its local wall heat transfer coefficient reflects the local heat transfer capability, making it highly representative. Point 3 was located at the outlet of the centripetal channel, where a high-speed rotational surface was found, making the velocity at this point particularly important. Therefore, the temperature and pressure at Point 1, the wall heat transfer coefficient at Point 2, and the velocity at Point 3 were selected as parameters for grid independence verification. The grid independence verification results under working conditions of 5 g/s and 57,000 RPM are displayed in Table 2. As can be seen, with the increase in grid number, the temperature, pressure, wall heat transfer coefficient, and velocity were all close to being stable. The error induced by the increase in the number of grids did not exceed 0.34%. The CFD simulations were carried out using a 72-thread computer. Considering both simulation speed and accuracy, a mesh with 1,000,232 nodes was used for the CFD simulation, and each scenario required approximately 3000 steps to converge.

Table 2.
Grid independence verification.
3.7. Uncertainty of the CFD Model and Sensitivity Analysis
The validation of the CFD model was crucial to ensure that the numerical simulation results aligned with reality. The uncertainties in the CFD simulations in this study primarily resulted from errors in the physical properties of the working fluid, assumptions such as the no-slip boundary condition and adiabatic wall, errors in the turbulence model, and errors in the grid accuracy. Firstly, the assumption of constant physical properties for the working fluid could lead to simulation errors. Within the pressure range of 3–90 MPa, the variations in density, specific heat capacity, thermal conductivity, and dynamic viscosity were within 5.6%, 1.7%, 15.8%, and 38.7%, respectively. Secondly, wall friction and heat dissipation could introduce simulation errors. Thirdly, grid accuracy could also cause simulation errors, but in this study, through grid independence verification, the error due to grid accuracy was kept within 0.34%. The combination of these various errors manifests as the overall error in the CFD simulations. Based on the currently available experimental data comparison for hydrocarbon fuel rotational cooling, the error in CFD simulations is approximately 10%. This essentially meets the precision requirements for numerical simulation.
A sensitivity analysis was conducted to examine the impact of the physical properties of the working fluid, using inlet and outlet pressures and velocities as metrics. The results indicated that the errors in pressure and velocity due to density were less than 2.13% and 2.71%, respectively. For specific heat, the errors in pressure and velocity were less than 0.19% and 0.96%, respectively. The errors attributable to thermal conductivity were less than 0.13% for pressure and 0.96% for velocity. Regarding viscosity, the errors in pressure and velocity were less than 3.30% and 3.38%, respectively. It was evident that density had a stronger sensitivity to pressure and velocity, whereas the influence of specific heat and thermal conductivity was weaker. Although dynamic viscosity was significantly affected by pressure changes, the resulting errors in velocity and pressure were relatively small.
4. Results and Discussion
4.1. Flow Characteristics in the Distributary Cavity
The velocity distributions and streamlines in the distributary cavity under nonrotating and rotating conditions with the same mass flow rate of 5 g/s are shown in Figure 4. As can be seen, under nonrotating conditions, the fuel encounters the inner face of the distributary cavity at the first turning region, which results in two strong vortexes. Fuel flows into the centrifugal channel from the inner face and forms a high-velocity region due to the decrease in the flow area. Meanwhile, as seen with the velocity vector shown in Figure 5c, the velocity under nonrotating conditions is almost symmetrical between the leading side and the trailing side.
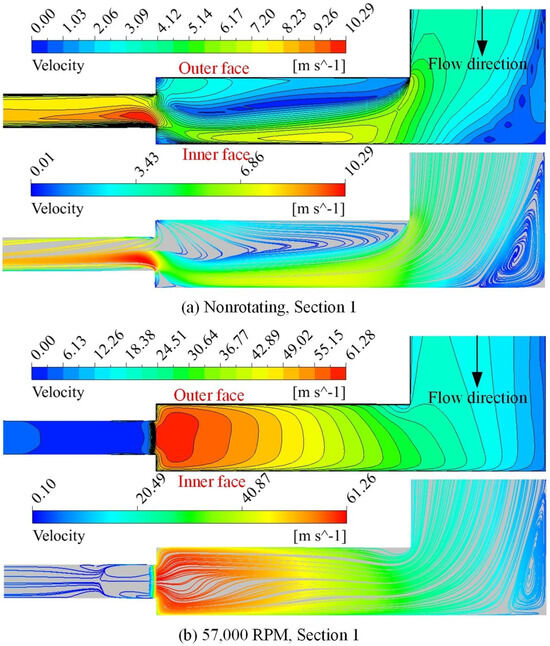
Figure 4.
Velocity distributions and streamlines in the distributary cavity under nonrotating and rotating conditions.
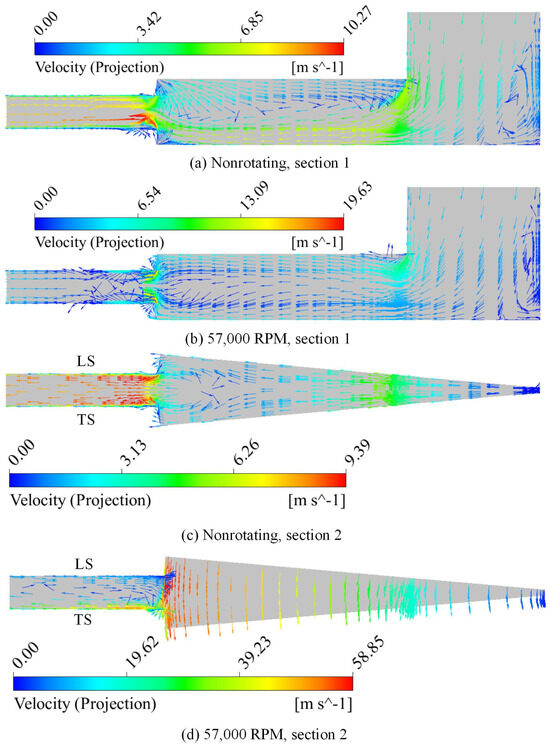
Figure 5.
Velocity vector of the distributary cavity under nonrotating and rotating conditions.
In contrast, the flow characteristics under rotating conditions are obviously different from those under nonrotating conditions. The velocity presented a layering distribution in the distributary cavity and the velocity increased along a centrifugal direction. From the streamline, the fuel does not immediately impel the inner face under rotating conditions but first turns to the outer face and then twists toward the inner face. Since the fuel has centrifugal flow velocity, which results in the Coriolis force; the fuel gains rotational velocity in the axis center rotating channel as a result. The rotational direction of flow is opposite to the rotating direction of the channel. After fuel enters the distributary cavity, the flow keeps the rotational velocity and velocity increases with the increase in radial distance, which results in the obvious layering distributary pattern of velocity shown in Figure 4b. After the fuel flows out of the distributary cavity and enters the centrifugal channel, the velocity magnitude sharply decreases by more than 10 times. In the velocity vector distribution in Figure 5b, fuel flows out of the distributary cavity under rotating conditions in a very different way compared with nonrotating conditions. The high-velocity rotational flow impels the trailing side of the centrifugal channel with the effect of centrifugal force and inertia force when fluid passes the location of the distributary cavity outlet. Consequently, a large vortex is formed in the root of the centrifugal channel between the leading side and trailing side, which results in a smaller velocity in the centrifugal channel, as shown in Figure 4b.
Overall, under nonrotating conditions, the flow of the fluid is primarily influenced by inertial forces, making its flow pattern within the distributary cavity relatively easy to predict, with relatively simple local vortex systems. Upon entering the centrifugal channel, the flow velocity significantly increases, due to the reduction in the cross-sectional area. However, under rotating conditions, the velocity of the central flow in the distributary cavity is much higher than that near the wall region, and it sharply decreases at the entrance of the centrifugal channel. The manner in which the fluid flows from the distributary cavity into the centrifugal channel can be intuitively observed in Figure 5d. The main direction of fluid movement in the distributary cavity is circumferential. At the outlet of the distributary cavity, under the action of centrifugal force, part of the fluid flows closely along the wall surface into the centrifugal channel, forming a large vortex at the entrance of the centrifugal channel. The fluid on the LS surface exhibits reverse flow. It is evident that the Coriolis force at high rotational speeds significantly alters the flow distribution pattern within the distributary cavity.
The alteration in the flow dynamics significantly impacts the pressure distribution within the channel, thereby influencing the pressure loss in the diversion cavity. As shown in Figure 6, in the nonrotating channel, the total pressure is constant before entering the distributary cavity. Pressure loss occurs when fuel flows through the distributary cavity, due to the flow turning and the vortex and flow area decreasing. The total pressure loss of the distributary cavity is about 13 kPa. It can be said that under static conditions, the loss in the diversion cavity mainly stems from local resistance. Compared with nonrotating conditions, the total pressure loss reaches 980 kPa under rotating conditions. It is evident that the Coriolis force diminishes the flow capacity of the diversion cavity. When altering its flow direction, the fluid must overcome not only the inertial forces but also the Coriolis force. Moreover, it can be seen that the pressure range under rotating conditions is about 13.1–15.4 MPa, which is much higher than the pressure range under nonrotating conditions. At the outlet of the diversion cavity, a significant pressure gradient emerges, yet the pressure within the centrifugal channel remains above 13 MPa. This will be explained in Section 4.2.
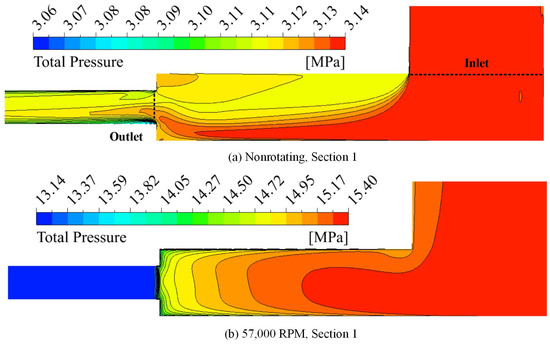
Figure 6.
Total pressure distribution of the distributary cavity under nonrotating and rotating conditions.
4.2. Flow Characteristics in the Confluence Cavity and the Phenomenon of the Flow Barrier
The velocity distribution and streamlines in the confluence cavity under rotating and nonrotating conditions, with the same mass flow rate of 5 g/s, are shown in Figure 7. As can be seen, it is easy to judge and analyze the flow characteristics according to the flow inertia for nonrotating conditions. Due to the jet effect, two low-velocity zones are formed on the inner and outer surfaces of the diversion cavity. Moreover, as the fluid flows into the confluence cavity, the velocity gradually decreases due to the increase in the flow area. In comparison, the flow characteristic in the confluence cavity under rotating conditions makes a great difference. There is obvious velocity layering inside the confluence cavity. Along the centripetal direction, the velocity increases first and then decreases. The velocity has a maximum value at the radial position of about R/d = 5, where the fuel turns from the confluence cavity to the outlet center channel in the axis. From the streamlines shown in Figure 7 and the velocity vector shown in Figure 8, after the fuel enters the confluence cavity, the fuel is squeezed against the inner and outer faces of the confluence cavity, due to the combined effect of centrifugal force and inertia force, in a reverse direction, which forms two vortexes in the corner. Then, the fuel flows into the outlet axis center channel along the inner and outer faces and flows together at the turning position, which forms two reverse vortexes at a position of about R/d = 10. From the velocity vector under rotating conditions shown in Figure 8c, it can be seen that a great deal of fuel flows from the outlet to the confluence cavity and is divided in two directions at the turning position, which results in two large vortexes in the axis center channel, as can be seen from the streamline shown in Figure 7. One vortex prevents the fuel from flowing through the turning region. Fuel can only flow from the confluence cavity to the outlet in a small area. Therefore, the fuel is squeezed together at the turning position. Meanwhile, after the fuel enters the confluence cavity, the fuel will rotate due to the effect of the Coriolis force. The rotational direction is the same as the channel rotating direction. The rotational velocity has a maximum value at the turning position. From the velocity vector shown in Figure 8d, it can be concluded that the velocity component in the rotating direction is much higher than the velocity component in the radial direction. A high rotational velocity cylindrical surface is formed at the turning position. The fuel has to pass through this high rotational surface and overcome high flow resistance, resulting in great pressure loss, which is the so-called flow barrier phenomenon seen in this study.
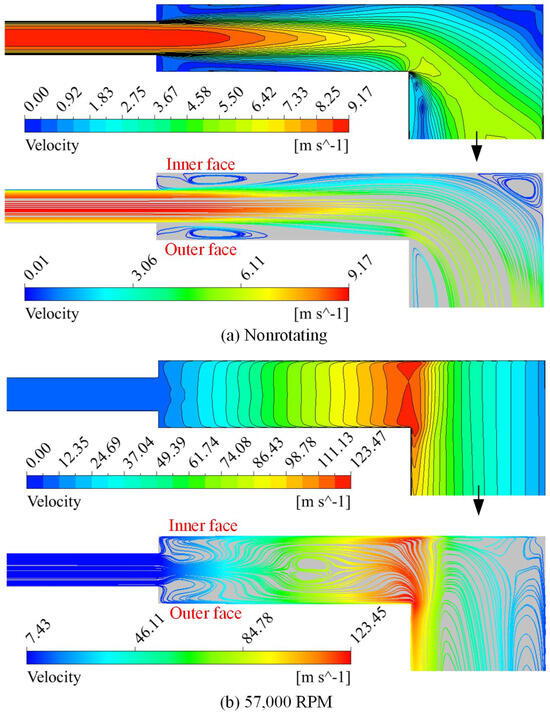
Figure 7.
Velocity distribution and streamlines of the confluence cavity under nonrotating and rotating conditions.
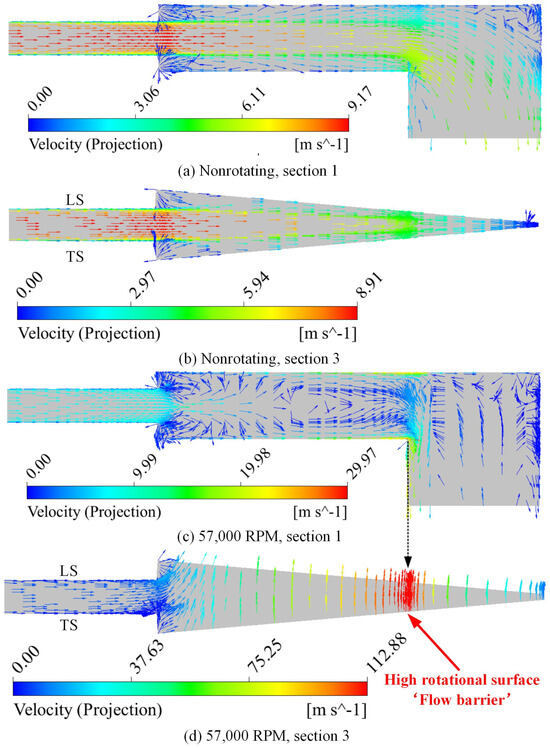
Figure 8.
Velocity vector of the confluence cavity under nonrotating and rotating conditions.
The total pressure distributions under nonrotating and rotating conditions are shown in Figure 9. As can be seen, the total pressure loss in the confluence cavity under nonrotating conditions is very small. The average total pressure loss is 10 kPa. In comparison, the total pressure under rotating conditions has a steep gradient at the turning region. The maximum total pressure is above 13 MPa. That is why the total pressure in the distributary cavity is at the level of 15 MPa. The total pressure loss of the confluence cavity under rotating conditions reaches 4.67 MPa. This high total pressure loss can reflect the impeding effect of the flow barrier on the flow. The static pressure distribution along a radial direction in the center of the centrifugal and centripetal channels is shown in Figure 10. As can be seen, when the radial distance is above R/d = 12.5, the static pressure almost overlaps. However, the pressure in the distributary cavity is obviously higher than the pressure in the confluence cavity, which is due to the effect of the flow barrier inside the confluence cavity. Therefore, the inlet pressure should be much higher than the outlet pressure. The pressure difference between the cooling channel inlet and the outlet in this condition is 10.5 MPa. With the effect of the flow barrier, the average outlet total pressure reaches 5.05 MPa.
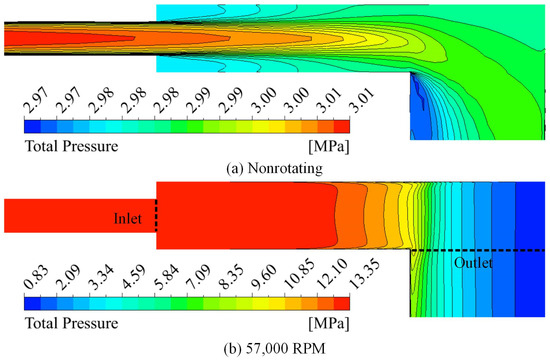
Figure 9.
Total pressure distribution of the confluence cavity under nonrotating and rotating conditions.
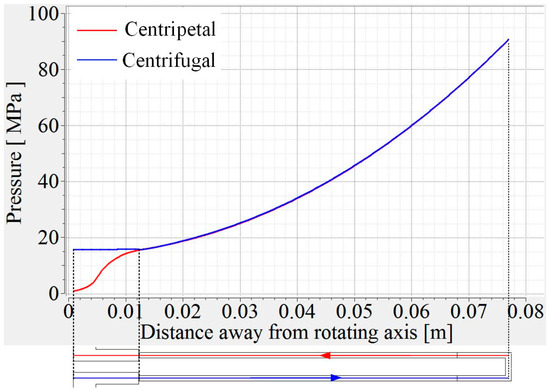
Figure 10.
Static pressure distribution along a radial direction in the centrifugal and centripetal channels under rotating conditions.
4.3. Variation of Vortexes in the Centrifugal and Centripetal Channels
This study mainly focuses on the distributary cavity and confluence cavity, and the physical properties of the working fluid in these two cavities change very little. Therefore, an assumption of fixed properties is adopted throughout this simulation. At a rotating speed of 57,000 RPM and a mass flow rate of 5 g/s, the variation pattern of the vortexes along the channel is shown in Figure 11, and the results have been compared with those in our previous study [38]. From Figure 11, it can be seen that starting from 20 mm, two opposing rotating vortexes gradually form in the centrifugal channel. In the beginning, the two opposing vortexes are symmetrically distributed on the inner and outer sides. Then, two opposing small vortices gradually form on the TS or trailing surface. When the fluid approaches the turning area, the vortex structure begins to change, the vortices on the TS surface gradually dissipate, the outer vortices begin to expand, and the inner vortices begin to shrink. When turning toward the centripetal channel, the outer vortex almost disappears, presenting a large vortex. However, with the centripetal channel, a vortex gradually forms on the outer side, and counter-rotating vortices reappear in the channel. Meanwhile, two small counter-rotating vortices gradually form near the LS surface. The entire vortex is basically symmetrical between the inner and outer sides. We compared the results with those in Ref. [38], and the vortex structures in the centrifugal and centripetal channels below 55 mm without heating were relatively similar. The vortex in the heating zone in Ref. [38] was more complex because of changes in the physical properties in the heating zone.
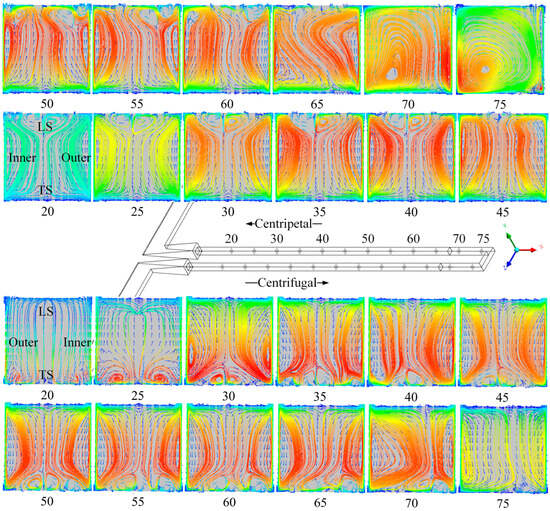
Figure 11.
Variations in vortex from the centrifugal channel to the centripetal channel.
4.4. Effects of Rotation Speeds and Mass Flow Rates
The mass flow rate and rotation speed are two important factors affecting rotating flow. In this section, all the working conditions listed in Figure 2 are analyzed to investigate the variation in the regularity of the flow barrier effect from the viewpoint of pressure loss. The average inlet and outlet pressures of all working conditions are shown in Figure 12. As can be seen, the inlet and outlet pressures both increase with the increase in rotation speed. Especially regarding the inlet pressure, the inlet pressure increases rapidly after the rotation speed rises above 10,000 RPM, which indicates that the flow barrier effect becomes more and more obvious with an increase in rotation speed. Meanwhile, a higher mass flow rate will result in a more serious flow barrier effect. In real operating conditions, the static pressure should be higher than the static inlet pressure of the rotating channel to guarantee that fuel can flow into the rotating channel. For example, under the conditions of 57,000 RPM and 5 g/s, the inlet pressure should be higher than 15.71 MPa and the outlet pressure should be reduced to 4.29 MPa. The results show that the pressure drop between the rotating channel inlet and the outlet has a two-order fitting relationship with rotation speed.
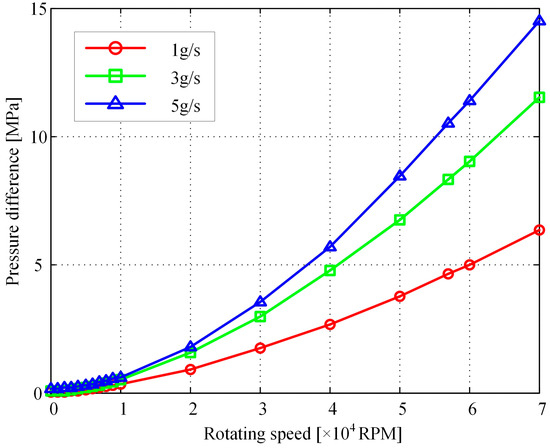
Figure 12.
Pressure difference between the inlet and outlet of the rotating channel.
4.5. Structure Optimization for Eliminating the Flow Barrier Effect
From the above study, it can be concluded that the flow barrier effect occurs under rotating conditions and results in high pressure loss in the cooling channel. Moreover, the pressure loss increases rapidly with an increase in rotating speed. Therefore, it is necessary to optimize the structure of the confluence cavity to eliminate the flow barrier effect. Because the main pressure loss appeared in the confluence cavity, the structural improvement mainly focuses on optimizing the outlet section of the confluence cavity. In this section, four structures of the outlet section, as shown in Figure 13, are investigated to compare the effect by comparing the pressure loss. The diameter of the outlet channel is enlarged in model 1. The turning degree of the confluence cavity is modified from a right angle to an oblique angle for model 2. For model 3, the outlet channel is no longer in the center of the axis and each cooling channel has a separated outlet channel, which means that there is no confluence cavity yet.
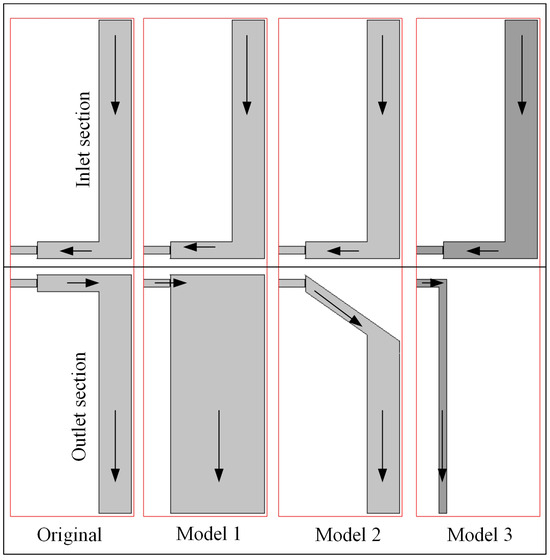
Figure 13.
Four outlet structures (The arrows indicate the flow direction).
According to Figure 10, the flow barrier effect can result in a static pressure jump in the confluence cavity. Under the conditions of 57,000 RPM and 5 g/s, the static pressure distribution along the radial distance in the centripetal channel for the four outlet structures is shown in Figure 14. The pressure resulting from the centrifugal force in a rotating channel can be calculated with Equation (6). As can be seen, when using model 1 and model 3, the pressure jump disappears, while the pressure jump still exists when using model 2, even though the pressure jump is smaller than the original model. Comparing model 1 and model 3, the pressure loss using model 3 is smaller. The total pressure and static pressure for the four models are all listed in Table 3. As can be seen in Table 3, the total pressure loss using model 3 is the smallest and the inlet static pressure is also the smallest. Since the outlet of model 3 is not in the center of the rotating axis, the outlet static pressure is about 3.056 MPa. Therefore, model 3 may be the most suitable cooling channel structure for a fuel-cooling rotating air turbine.
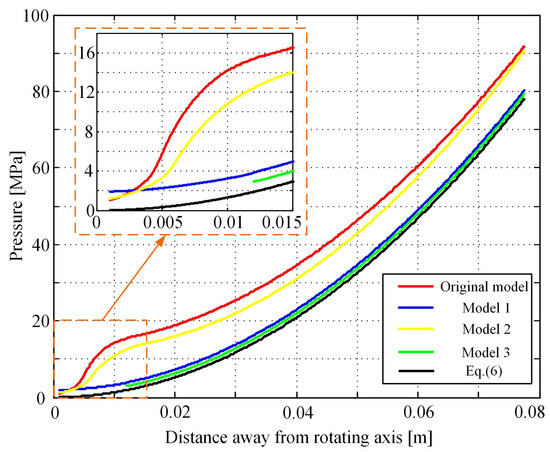
Figure 14.
Pressure distributions along the radial direction in the centripetal channel for different outlet structures.

Table 3.
Pressure parameters of the rotating channel under conditions of 57,000 RPM and 5 g/s.
Here, R indicates the radial distance away from the rotating axis.
5. Conclusions
In this paper, the flow characteristics of rotating flow in the distributary cavity and confluence cavity using hydrocarbon fuel are investigated with CFD simulations. The influence of mass flow rate and rotating speed on the fuel’s rotating flow is studied and four structures are compared. Based on the numerical results, it can be concluded that:
- (1)
- The existing distributary and confluence cavities make the fuel’s rotating flow more complex and form a high-speed rotational flow. The rotational flow in the distributary cavity has a reverse rotating direction to the rotating channel, while the rotational flow in the confluence cavity has the same rotating direction as the rotating channel.
- (2)
- Under high rotation speed conditions, when the fluid flows from the confluence cavity to the axis center channel, a rotational flow with high rotational speed is formed, due to the combined effect of centrifugal force, inertia force, and the Coriolis force at the turning position. The fluid has to pass through a high rotational flow surface and overcome great flow resistance, which results in high pressure loss.
- (3)
- The pressure loss increases with the increase in rotating speed, and a high mass flow rate can result in obvious pressure loss. Modifying the outlet section structure can effectively eliminate the flow barrier effect. In this study, the optimal structure model 3 with a separated outlet channel shows the best performance with the smallest pressure loss.
Prospectively, this study mainly supplements fuel-based rotating cooling. It is demonstrated that the original structure has significant defects, which can cause huge pressure losses during the convergence process, leading to difficulties in flow. This article explains the reasons for the high level of pressure losses and proposes a structure that can eliminate these pressure losses, providing a reference for the application of fuel-based rotating cooling. Moreover, the primary tasks for the future encompass the following aspects: (1) designing and conducting high-speed rotating cooling experiments with hydrocarbon fuels, (2) designing and developing high-speed dynamic and static joints, with a focus on addressing leakage issues in these joints, and (3) leveraging the thermal acceleration effect of rotating cooling to investigate the scheme of a closed-loop liquid cooling system.
Author Contributions
Conceptualization, K.Z. and H.S.; methodology, K.Z. and H.M.; validation, H.S.; formal analysis, H.M.; investigation, K.Z. and H.S.; data curation, K.Z. and H.S.; writing—original draft preparation, K.Z. and H.S.; writing—review and editing, H.M. and J.Q.; visualization, K.Z. and H.S.; supervision, J.Q.; funding acquisition, H.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Provincial Key Research Project of Higher Education Institutions in Henan (25B470004), and the Doctoral Foundation of the Zhengzhou University of Light Industry (13501050032).
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Acknowledgments
The authors thank the reviewers for their valuable advice on this paper.
Conflicts of Interest
The authors declare no conflicts of interest.
Nomenclature
| d | hydraulic diameter [mm] |
| n | rotating speed [RPM] |
| p | pressure [Pa] |
| R | radial distance away from the rotating axis [m] |
| T | temperature [K] |
| Greek symbols | |
| ρ | density [kg/m3] |
| π | circular constant |
| Subscript | |
| SST | SST turbulence model |
| exp | experiment |
| Abbreviations | |
| CFD | computational fluid dynamics |
| SST | shear–stress–transport |
| LS | leading side |
| TS | trailing side |
References
- Chu, H.-C.; Chen, H.-C.; Han, J.-C. Numerical simulation of flow and heat transfer in rotating cooling passage with turning vane in hub region. J. Heat Transf. 2017, 140, 021701. [Google Scholar] [CrossRef]
- Xie, G.; Sunden, B. Conjugated analysis of heat transfer enhancement of an internal blade tip-wall with pin-fin arrays. J. Enhanc. Heat Transf. 2011, 18, 149–165. [Google Scholar] [CrossRef]
- Feng, Y.; Liu, S.; Qin, J.; Cao, Y.; Jiang, Y.; Zhang, S. Numerical study on the influence of turbulence on the pyrolysis of hydrocarbon fuel in mini-channel. Int. J. Heat Mass Transf. 2018, 119, 768–776. [Google Scholar] [CrossRef]
- Liu, S.; Feng, Y.; Cao, Y.; Gong, K.; Zhou, W.; Bao, W. Numerical simulation of supercritical catalytic steam reforming of aviation kerosene coupling with coking and heat transfer in mini-channel. Int. J. Therm. Sci. 2019, 137, 199–214. [Google Scholar] [CrossRef]
- Sun, F.; Li, Y.; Sunden, B.; Xie, G. The Behavior of Turbulent Heat Transfer Deterioration in Supercritical Hydrocarbon Fuel Flow Considering Thermal Resistance Distribution. Int. J. Therm. Sci. 2019, 141, 19–32. [Google Scholar] [CrossRef]
- Cong, T.; Zhang, R.; Wang, B.; Xiao, Y.; Gu, H. Single-phase flow in helical cruciform fuel assembly with conjugate heat transfer. Prog. Nucl. Energy 2022, 147, 104199. [Google Scholar] [CrossRef]
- Zhang, Y.; Cao, Y.; Feng, Y.; Xu, S.; Wang, J.; Qin, J. A new modeling method to estimate the heat transfer characteristics of supercritical aviation kerosene RP-3 with pyrolysis. Chem. Eng. Sci. 2023, 267, 118324. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, S.; Wang, C.; Tan, X. Recent advances in film cooling enhancement: A review. Chin. J. Aeronaut. 2020, 33, 1119–1136. [Google Scholar] [CrossRef]
- Jiang, P.; Lu, Z.; Guo, Y.; Zhu, Y. Experimental investigation of convective heat transfer of hydrocarbon fuels at supercritical pressures within rotating centrifugal channel. Appl. Therm. Eng. 2019, 147, 101–112. [Google Scholar] [CrossRef]
- Ibrahim, E.; Moawed, M.; Berbish, N.S. Heat transfer characteristics of rotating triangular thermosyphon. Heat Mass Transf. 2012, 48, 1539–1548. [Google Scholar] [CrossRef]
- Akhter, R.; Ali, M.M.; Alim, A. Magnetic field impact on double diffusive mixed convective hybrid-nanofluid flow and irreversibility in porous cavity with vertical wavy walls and rotating solid cylinder. Results Eng. 2023, 19, 101292. [Google Scholar] [CrossRef]
- Dong, M.; Huang, H. Hydrocarbon Fuel Flow and Heat Transfer Investigation in Rotating Channels. Energies 2023, 16, 5020. [Google Scholar] [CrossRef]
- Du, C.; Li, L.; Fan, X. Numerical study on vortex cooling flow and heat transfer behavior under rotating conditions. Int. J. Heat Mass Transf. 2017, 105, 638–647. [Google Scholar] [CrossRef]
- Sun, F.; Li, Y.; Manca, O.; Xie, G. An evaluation on the laminar effect of buoyancy-driven supercritical hydrocarbon fuel flow and heat transfer characteristics. Int. J. Heat Mass Transf. 2019, 142, 118414. [Google Scholar] [CrossRef]
- Nuntakulamarat, M.; Shiau, C.-C.; Han, J.-C. Heat transfer and pressure drop measurements in a high aspect ratio channel with circular pins and strip fins. J. Therm. Sci. Eng. Appl. 2020, 12, 031019. [Google Scholar] [CrossRef]
- Zhang, M.; Wang, N.; Han, J.-C. Internal heat transfer of film-cooled leading edge model with normal and tangential impinging jets. Int. J. Heat Mass Transf. 2019, 139, 193–204. [Google Scholar] [CrossRef]
- Huang, S.-C.; Wang, C.-C.; Liu, Y.-H. Heat transfer measurement in a rotating cooling channel with staggered and inline pin-fin arrays using liquid crystal and stroboscopy. Int. J. Heat Mass Transf. 2017, 115, 364–376. [Google Scholar] [CrossRef]
- Chia, K.-C.; Huang, S.-C.; Liu, Y.-H. Experimental investigation of heat transfer on the internal tip wall in a rotating two-pass rectangular channel. J. Therm. Sci. Eng. Appl. 2021, 13, 011025. [Google Scholar] [CrossRef]
- Huang, S.-C.; Liu, Y.-H. High rotation number effect on heat transfer in a leading edge cooling channel of gas turbine blades with three channel orientations. J. Therm. Sci. Eng. Appl. 2013, 5, 041003. [Google Scholar] [CrossRef]
- Lorenzon, A.; Casarsa, L. Validation of the transient liquid crystal thermography technique for heat transfer measurements on a rotating cooling passage. Energies 2020, 13, 4759. [Google Scholar] [CrossRef]
- Ekkad, S.V.; Singh, P. Detailed heat transfer measurements for rotating turbulent flows in gas turbine systems. Energies 2020, 14, 39. [Google Scholar] [CrossRef]
- Abdelmaksoud, R.; Wang, T. A Numerical investigation of air/mist cooling through a conjugate, rotating 3d gas turbine blade with internal, external, and tip cooling. J. Therm. Sci. Eng. Appl. 2021, 13, 021004. [Google Scholar] [CrossRef]
- Jiang, H.; Zhu, X.; Wang, D.; Huisman, S.G.; Sun, C. Supergravitational turbulent thermal convection. Sci. Adv. 2020, 6, eabb8676. [Google Scholar] [CrossRef] [PubMed]
- Jiang, H.; Wang, D.; Liu, S.; Sun, C. Experimental evidence for the existence of the ultimate regime in rapidly rotating turbulent thermal convection. Phys. Rev. Lett. 2022, 129, 204502. [Google Scholar] [CrossRef] [PubMed]
- Li, C.; Fang, X.; Luo, Z.; Dai, Q. Flow boiling heat transfer and pressure drop of R245fa inside horizontal 1.62 mm and 2.43 mm tubes under hypergravity. Int. J. Refrig. 2023, 148, 96–107. [Google Scholar] [CrossRef]
- Syaiful; Nabilah, H.; Utomo, M.T.S.; Suprihanto, A.; Soetanto, M.F. Numerical simulation of heat transfer enhancement from tubes surface to airflow using concave delta winglet vortex generators. Results Eng. 2022, 16, 100710. [Google Scholar] [CrossRef]
- Li, L.; Xu, P.; Li, Q.; Yin, Z.; Zheng, R.; Wu, J.; Bao, J.; Bai, W.; Qi, H.; Tan, D. Multi-field coupling particle flow dynamic behaviors of the microreactor and ultrasonic control method. Powder Technol. 2025, 454, 120731. [Google Scholar] [CrossRef]
- Zheng, G.; Xu, P.; Wang, T.; Yan, Q. Study on the bubble collapse characteristics and heat transfer mechanism of the microchannel reactor. Processes 2025, 13, 281. [Google Scholar] [CrossRef]
- Dong, A.; Yan, P.; Qian, X.; Han, W.; Wang, Q. Rotation effect on flow and heat transfer for high-temperature rotor blade in a heavy gas turbine. J. Therm. Sci. 2021, 30, 707–715. [Google Scholar] [CrossRef]
- Khattak, S.; Ahmed, M.; Abrar, M.N.; Uddin, S.; Sagheer, M.; Javeed, M.F. Numerical simulation of Cattaneo–Christov heat flux model in a porous media past a stretching sheet. Waves Random Complex Media 2025, 35, 1230–1249. [Google Scholar] [CrossRef]
- Shah, S.; Abrar, M.N.; Akhtar, K.; Khan, A.; Abdeljawad, T. Entropy formation analysis for magnetized UCM fluid over an exponentially stretching surface with PST and PSHF wall conditions. AIMS Math. 2023, 8, 11666–11683. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, Z.; Li, L.; Wang, C.; Wu, J.; Xie, Y.; Yin, Z.; Tan, D. Deposition mechanism of microscopic impacting droplets on flexible porous substrates. Int. J. Mech. Sci. 2025, 288, 110050. [Google Scholar] [CrossRef]
- Tan, Y.; Ni, Y.; Xu, W.; Xie, Y.; Li, L.; Tan, D. Key technologies and development trends of the soft abrasive flow finishing method. J. Zhejiang Univ. A 2023, 24, 1043–1064. [Google Scholar] [CrossRef]
- Abrar, M.N.; Uddin, S.; Akhtar, K. Rheology of suspended hybrid nanoparticles in micro-rotating tangent hyperbolic fluid over a stretching surface. J. Central South Univ. 2023, 30, 1231–1245. [Google Scholar] [CrossRef]
- Khan, A.S.; Abrar, M.N.; Uddin, S.; Awais, M.; Usman, I. Entropy generation due to micro-rotating Casson’s nanofluid flow over a nonlinear stretching plate: Numerical treatment. Waves Random Complex Media 2022, 35, 1–16. [Google Scholar] [CrossRef]
- Sun, H.; Qin, J.; Huang, H.; Yan, P. Numerical simulation of flow and heat transfer in a square rotating u-duct using hydrocarbon fuel. J. Heat Transf. 2019, 141, 031701. [Google Scholar] [CrossRef]
- Sun, H.; Qin, J.; Li, H.; Huang, H.; Yan, P. Research of a combined power and cooling system based on fuel rotating cooling air turbine and organic Rankine cycle on hypersonic aircraft. Energy 2019, 189, 116183. [Google Scholar] [CrossRef]
- Sun, H.; Qin, J.; Huang, H.; Yan, P. Investigation of hydrocarbon fuel rotating flow considering the variation of physical properties. Int. J. Heat Mass Transf. 2019, 142, 118372. [Google Scholar] [CrossRef]
- Sun, H.; Gao, P.; Li, H.; Hou, F.; Yuan, P. Investigation of water phase change rotating cooling for high temperature turbine. Results Eng. 2024, 21, 101707. [Google Scholar] [CrossRef]
- Lemmon, E.W.; Bell, I.H.; Huber, M.L.; McLinden, M.O. NIST Standard Reference Database 23: Reference Fluid Thermodynamic and Transport Properties-REFPROP, Version 10.0; Standard Reference Data Program; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2018. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).