Abstract
Recently, as the market share of electric vehicles (EVs) has increased, how to handle the increased electricity demand for EV charging in the power grid and how to use EV batteries from a grid-operating aspect have become more important. Also, from the perspective of individual EVs, Vehicle-to-Grid (V2G) technologies that reduce the cost for each vehicle’s charging in conjunction with the power grid are significant. In this paper, the V2G control problem at the individual vehicle level is studied using a Dynamic Programming (DP) algorithm that considers EVs’ charging efficiency. The DP algorithm is developed to generate an optimized charging/discharging power profile that minimizes electricity costs, while satisfying the constraints of the initial and final battery states of charge, for given a time-of-use electricity price. To show the effectiveness of the proposed algorithm, simulation is conducted for three different charging scenarios (unidirectional charging, bidirectional charging, and unidirectional charging with cost variations based on electricity usage), and the results showed that DP can achieve significant cost savings of about 30% compared to the normal charging method. Also, the result of DP is compared with that of Linear Programming, demonstrating that DP outperforms Linear Programming in cost savings for the V2G control problem.
1. Introduction
With the recent rapid growing of the electric vehicle (EV) market, the interest in Vehicle-to-Grid (V2G) technology has been increased. V2G refers to the technology that connects EVs to the power grid, while battery in EVs can be used as energy storage to supply or sell remaining power. With V2G, EVs can reduce charging costs for electricity, and also, by providing a backup energy buffer to the power grid, the stability of the grid can be enhanced significantly [,,]. As the EV market has grown recently, the synergy between EVs and the grid could play a significant role in the management of the energy mix, including renewable energy by compensating for its intermittency []. Also, it is expected that V2G helps manage the recently increased charging load demand due to EVs [].
While various studies have been conducted on V2G technology, one of the key aspects is charge scheduling strategies for EVs []. Charge scheduling is a complicated problem to consider due to various factors such as the constraints of the grid, electricity prices, the EV’s battery state of charge (SOC), and the charging demands of the EV. This complexity makes the problem challenging from both an economic and operational perspective. One promising methodology is optimization-based approaches, which can effectively manage the complexity of V2G systems involving multiple objective functions and constraints. In contrast, heuristic strategies can offer the advantages of being simple and intuitive [], but they are limited in handling multiple constraints and in achieving optimal performance.
For V2G application, optimization methods such as Linear Programming (LP) and Quadratic Programming (QP) have been used widely [,,]. They are fast and efficient, while Nonlinear Programming or Mixed Integer Programming (MIP) are also used for more complex cases, including nonlinear characteristics of the battery, the grid, or varying charging rates involving integers [,]. Algorithms such as Genetic Algorithm (GA) and Particle Swarm Optimization (PSO) are also often used. In [], GA is utilized for plug-in hybrid electric vehicles with the objectives of minimizing both cost and battery aging. In [], the multivariant route optimization problem is solved by GA incorporating Markov decision process. In [], PSO is used for unit commitment with V2G. Here, binary PSO for generating units and the integer version of PSO for V2G vehicles are used. These algorithms can deal with multiple objectives and constraints and their conflicting relationship.
Also, Dynamic Programming (DP) can be utilized for V2G optimization. DP is a well-known optimization algorithm for solving complex problems in a recursive manner []. Many studies have used DP for V2G problems. In [], an entire EV fleet of midsize delivery trucks is modeled as a single aggregate battery, and DP is applied for control. In [], approximate DP is used for the coordination of a charging station at a V2G aggregator. The main advantage of DP is that it can obtain global optimal solutions, regardless of the system’s characteristic. However, DP has the limitation that it requires prior knowledge of the entire problem, which makes it difficult to apply as a real-time solution considering that many V2G problems are often combined with uncertainties [,,]. Therefore, when there are uncertainties, DP needs to be modified or combined with other algorithms. For example, in [], a DP–Game theory approach for scheduling a single EV is proposed for extension to multiple EVs. In [], the V2G problem is defined as an infinite-horizon Markov decision process, and adaptive DP is utilized for dealing with the uncertainty of EV availability.
However, for charge scheduling of an EV, when TOU prices are available a day in advance or beforehand, DP becomes reasonable to obtain optimal solutions. Furthermore, previous methods such as LP tend to simplify vehicle efficiency, but DP can account for the detail efficiency while ensuring global optimum, thus making it more suitable for the V2G problem of a single EV; also, it can always satisfy customers’ requirement of battery final SOC. However, from the perspective of individual EVs, there has been limited research on how to optimize the charging profile as shown in Table 1. Considering that when applying V2G to a large fleet of EVs, optimizing all vehicles at once is computationally burdensome, and also from a security perspective, there is the need for decentralized computing [], charging optimization at the vehicle level is necessary.

Table 1.
Comparison between the proposed study and the literature.
In this paper, based on our previous study in [], a study about optimal charge scheduling based on DP is conducted from the perspective of a single EV. The contributions of this paper are as follows: (1) The optimal control problem for V2G is defined to find the global optimal solution using DP. Given the information of the TOU price, the optimal charge schedule to minimize cost, while satisfying the final battery SOC constraint, is found. (2) Also, an individual vehicle system-level efficiency model is defined and included in the optimization process using DP, and the optimal solutions acquired from each scenario at the vehicle level are compared and analyzed. The remainder of this paper is organized as follows. In Section 2, a vehicle simulation model and V2G charging scenarios are explained, and in Section 3 the optimal control problem is defined and the DP algorithm for solving the V2G problem is presented. In Section 4, the simulation results and discussion are given. Finally, the conclusions with future work are given in Section 5.
2. Model for Simulation
2.1. Vehicle Efficiency Model
In this study, a vehicle model is used for V2G calculation and for testing the proposed algorithm. The vehicle model is for calculating efficiency during charging and discharging the battery in EVs. Here, the vehicle model is primarily composed of an electric battery and an on-board charger (OBC). These models are used to consider efficiency in charging/discharging processes. For the battery, a lithium-ion polymer battery model with a capacity of 110 Ah is used. Here, the battery model is presented by a simple equivalent circuit model; the battery SOC dynamics can be given as shown in Equation (1):
where is the open circuit voltage of a battery, which is the function of the battery SOC; is the battery internal resistance, which is also a function of the battery SOC; and is the battery capacity. On the other hand, power consumption in the battery, , is as below:
where is OBC efficiency, which is a function of input power, . In Figure 1, the efficiency of the OBC is given, and in Figure 2, the open circuit voltage and internal resistance of battery are given. In this study, experiments or validations for the battery model were not conducted; however, the equivalent circuit model is widely used in applications such as electric vehicle fuel efficiency performance evaluation [,], which is suitable for assessing efficiency performance. Also, it is possible to incorporate the battery’s performance degradation into the V2G control problem by using its equivalent circuit model when the battery parameters are given. For example, the battery’s State of Health (SOH) can be estimated as internal resistance and battery capacity [,], and based on this estimation, the V2G charging schedule can be optimized accordingly.
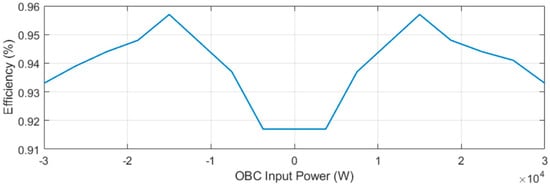
Figure 1.
Efficiency of on-board charger.
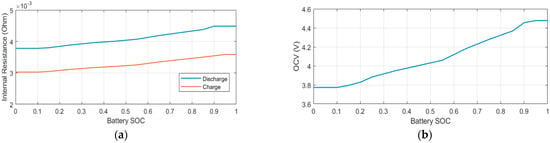
Figure 2.
Battery parameter: (a) internal resistance; (b) open circuit voltage.
2.2. Time-of-Use Pricing Scenarios
On the other hand, for the TOU price, it is assumed that electricity price varies depending on the time of day, and is defined on a 24 h basis. Here, electricity costs are higher during peak demand and lower during off-peak times; thus, the TOU price is designed to encourage consumers to charge their electricity usage when demand on the power grid is lower. Therefore, TOU price can help to balance the grid and avoid the need for power plants to generate additional power during peak periods. Also, in this paper, the optimization is conducted not only for maximizing the economic benefits based on TOU pricing but also to account for the energy losses that occur when the battery in an EV is charged and discharged. These losses, which typically occur due to factors such as efficiencies in the energy conversion process, reduce the amount of usable energy that can be exchanged with the grid. By considering this efficiency, the optimization can more accurately determine the best times and powers to charge or discharge the battery, improving the overall performance of the V2G system.
In this study, the TOU price scenarios are given as three types: the first is unidirectional charging only, where the vehicle can charge but not discharge, with the TOU price for charging shown in Figure 3a; the second is bidirectional charging, where both charging and discharging are possible, with the discharging price set lower than the charging price as shown in Figure 3b; and the third depends on the power consumption, where the pricing varies based on whether the power usage exceeds 10 or 20 kWh, as shown in Figure 3c. For simplicity, it is assumed that the TOU pricing policy is predefined, and the entire TOU price for the specific duration is given in advance, before the optimal control algorithm starts calculation. This is often the case in planned pricing by utility companies or electricity contracts, where the vehicle owner can be aware of the pricing schedule in advance.
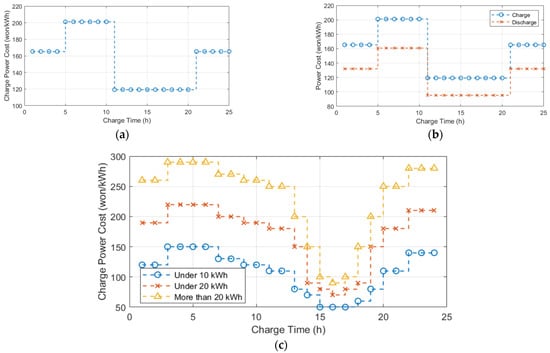
Figure 3.
Different TOU pricing scenarios: (a) case I: unidirectional charging only; (b) case II: bidirectional charging; (c) case III: pricing according to the power usage.
Based on this vehicle charging model and TOU price scenarios, a vehicle simulation was conducted to demonstrate the effectiveness of the proposed algorithm based on the vehicle efficiency model and the given TOU plan. The definition of the optimal control problem in V2G and the DP algorithm are given in the next section.
3. Control Algorithm: Dynamic Programming
3.1. Optimal Control Problem
The optimal control problem when it comes to V2G from the perspective of individual vehicles is defined to minimize objective function (also called optimal cost-to-go) for a given TOU price in discretized form as follows:
where is the total cost, starting from initial SOC condition and applying a control input of over the time horizon 0 to N, which includes both the intermediate operational cost and final cost term for the desired final SOC value. is as follows:
where is the charging/discharging power applied at time step , and is the TOU price at that time step. On the other hand, is as follows:
where is the penalty cost for not matching the desired final SOC boundary value. SOC dynamics evolve according to Equation (3b), where describes the relationship between the current SOC, the applied charging/discharging power, and how the SOC changes over time, as explained using Equations (1) and (2) in the previous chapter. Here, battery dynamics are defined as time-invariant without consideration of battery degradation or aging. However, if necessary, the reduced battery capacity and efficiency with battery model parameters can be considered in the long term in accordance with charging costs to compensate for reduced battery performance. Therefore, for optimization, the control problem is to find the charging profile by considering the given battery SOC along with efficiency and TOU price. This problem is equivalent to the problem of finding the SOC trajectory of the battery, considering the SOC at each time step, charging/discharging power, and TOU price, to minimize cost while satisfying the boundary value of the final battery SOC, which is defined by the customer.
3.2. Dynamic Programming Algorithm
DP can be used to find the solution of the given optimal control problem. Based on Bellman equation, the idea of DP can be represented generally in the form of backward induction in a recursive manner as follows.
For ,
For ,
here, at the final time step , the optimal cost at the final time step, is given by immediate cost according to the final battery SOC value, , and for , the optimal cost-to-go function is given recursively based on all such possible actions of , which is in the way of the backward induction.
In this study, to solve DP, forward induction is applied in which the problem is solved step by step from the initial state and progresses towards to the final state, which can also be represented in a recursive manner as follows.
For ,
For ,
where is as follows:
here, as shown in the above equations and in Figure 4, the “optimal cost from start value” for each node is sequentially calculated in the forward direction starting from the initial battery SOC condition, and the optimal path is derived from the path that satisfies the final SOC condition. In the meantime, since the SOC values acquired based on the control input may not align with each value in the grid, interpolation is performed to calculate the corresponding grid values.
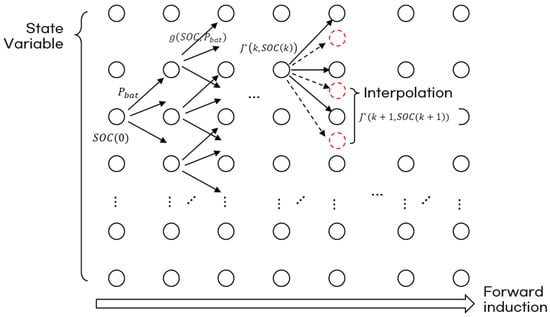
Figure 4.
Forward induction of DP.
In contrast to backward induction, which works backward from the final to the initial state, forward induction can predict future states and select the optimal control at each step.
Here, it is assumed that the TOU price is predefined. However, even if TOU prices vary over time or the desired final battery SOC changes, the forward induction approach can adjust the control to minimize costs at each specific time, considering the price fluctuations and the final boundary value. Also, forward induction leads to simpler, more intuitive problem solving. On the other hand, in this study, since the TOU prices are predefined, the DP can compute an optimal path that minimizes total costs by considering the immediate cost of the control and the state transitions. This guarantees that the system will achieve the best possible solution for the given constraints and the TOU prices, which is a significant advantage of DP. However, the causality in DP, which enables globally optimized decisions to be made sequentially, requires information about the TOU price and constraints in advance before the calculation. Here, assuming that the TOU pricing policy is predefined, as explained in Section 2, the deterministic DP algorithm explained above can be applied. However, when the TOU pricing is not known in advance, extended approaches, such as stochastic DP or reinforcement learning, can be used, which is beyond the scope of this study.
To apply DP to the control problem, it is required to set up the grids for state variables of battery SOC and control inputs of the charging/discharging power. These grids allow one to discretize the continuous problem space, enabling computationally feasible solutions while ensuring the key dynamics of the system. In this study, the unit time step is defined as 1 h and the battery SOC is divided into 50 discrete values from 1% to 99%. Battery SOC is the key variable that describes the condition of the system. Here, the goal is to balance computational efficiency and the accuracy. For example, SOC could be discretized by 1%, meaning there would be 99 grid points, which requires more computational load compared to 50 grid points. For the control input of charging/discharging power to be discretized in a similar manner, battery charging power ranges from 0 to 30 kW (−30 to 30 kW for bidirectional) are divided into 51 grid points. The discretization levels for parameters are given in Table 2. Based on the proposed DP algorithm, the vehicle charging simulation model and TOU price introduced in Section 2 are applied. The simulation result and analysis are given in the next section.

Table 2.
Parameter discretization of DP.
4. Simulation Results and Discussion
In this study, the proposed DP algorithm was tested and verified through vehicle simulation based on three different case scenarios. For the comparison, different strategies of the normal charging strategy and an LP-based strategy were tested.
4.1. Case Studies for Different TOU Prices
First of all, the normal charging/discharging strategy is used, in which, once the initial and target SOC are defined, a constant power is applied at each time step to charge (or discharge) the battery. This approach assumes a straightforward power application over time, without adjusting for variations in TOU pricing or system dynamics. The battery’s SOC is either increased or decreased at a fixed rate based on the predetermined power, ensuring that the battery reaches the target SOC by the end of the specified time.
Firstly, for case I, which is unidirectional charging where only charging is possible, the simulation results are presented in Figure 5. In this scenario, the initial and the final battery SOC are assumed to be 40% and 90%, respectively, which are arbitrary values. In the simulation results, it is observed that, using DP, the charging power varies according to TOU price. Specifically, when the TOU price is low (when time is 11 h~21 h), the battery is charged, while during high-price periods, the battery SOC is unchanged. This behavior reflects the DP’s characteristic of optimizing charging times in order to minimize costs based on the varying TOU price. Additionally, it is observed that the final SOC matches the predefined value well.
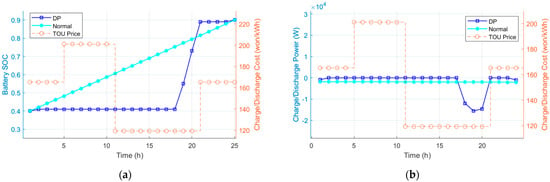
Figure 5.
Simulation result for case I (): (a) battery SOC; (b) charge power input for DP and normal.
For case II (bidirectional charging), the simulation results are presented in Figure 6. In this scenario, both charging and discharging are possible. Here, the initial battery SOC is also set to 40%, and the final SOC is assumed to be 90%. The simulation results indicate that, using the DP approach, the charging and discharging strategy is determined based on the TOU price, the same as in case I. When the TOU price is low, the battery is charged, while during high-price periods, discharging is preferred to maximize cost benefits. This bidirectional approach allows for more flexibility in optimizing the battery’s SOC by both charging and discharging according to price fluctuations.
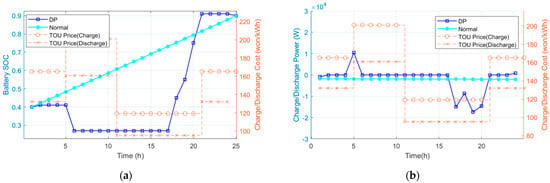
Figure 6.
Simulation result for case II (): (a) battery SOC; (b) charge power input for DP and normal.
For case III (variable charging costs based on power consumption and charging only), the simulation results follow a similar pattern, which is given in Figure 7. In this case, the charging cost is determined by the power consumption, with different pricing structures applied depending on whether the usage exceeds certain thresholds (10 or 20 kWh). Using the DP approach, it can be seen that the charging strategy is adjusted according to the power consumption and pricing. When power usage is lower, the charging cost is cheaper, and when it exceeds a threshold, higher costs apply, prompting the charging strategy to adapt accordingly. As in previous cases, the final SOC is closely aligned with the predefined target, demonstrating the effectiveness of the DP method.
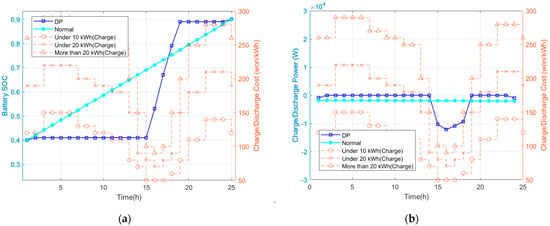
Figure 7.
Simulation result for case III (): (a) battery SOC; (b) charge power input for DP and normal.
In Table 3, the results of charging cost, total energy used, and mean price, which is the average applied electricity rate, for both the normal strategy case and the DP case are presented. An interesting observation here is that, when considering the losses that occur during the charging/discharging process, the absolute amount of battery energy consumed (total energy) tends to be almost the same. However, DP still proves beneficial, as the associated costs, due to the TOU pricing structure, result in cost savings. Therefore, even though the absolute power usage is almost same, the overall cost can be reduced by strategically managing the charging and discharging process, making this optimization approach based on DP make sense. Additionally, compared to the normal method, which simply charges battery uniformly to meet the end battery charging conditions from the initial battery level, it was confirmed that DP can achieve a cost reduction of approximately 25.2–33.7% in each case.

Table 3.
Simulation result for normal and DP method.
Additionally, scenarios with different initial and final battery SOC conditions were tested. The simulation results are presented in Table 4. When the initial and final battery SOC are 0.1 and 0.9, respectively, the cost savings of DP compared to normal methods are 25.8~31.0%, similar to the previous case. However, for case II with initial and final SOCs of 0.7 and 0.9, the cost saving in DP is significant at 80.3%. This result shows that in case II (bidirectional charging), DP maximized cost benefit by discharging and charging the battery (selling and buying the electricity) using the sufficient energy buffer from 0.1 to 0.9 of the SOC, while the normal method cannot, as shown in Figure 8. Overall, it can be confirmed that DP shows cost savings of about 30~40% in most cases, but it varies depending on TOU scenarios and battery SOC conditions.

Table 4.
Simulation result for normal and DP method for different initial and final battery SOCs.
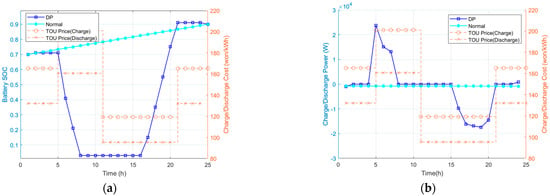
Figure 8.
Simulation result for case II (): (a) battery SOC; (b) charge power input for DP and normal.
Regarding the computational load of DP, it was observed that for case I, case II, and case III, the computation times were approximately 0.6~0.8 s on average, when performed on a desktop computer (intel Core i7-10700K CPU @3.80GHz). Although the execution environment on the vehicle’s VCU differs from that of a desktop computer, considering that V2G vehicle charging occurs usually over a period of tens of minutes to hours, the computational complexity of DP is manageable on the vehicle’s VCU.
4.2. Comparison Study with Linear Programming-Based Methods
Also, in this study, for case I, another comparison was made with the LP-based strategy. LP is one of the widely used optimization methods and has been applied to V2G problems [,,]. For the application of LP, the objective function and constraints were set identically to those in the DP problem as Equations (3a)–(3e). However, unlike DP, it is difficult to apply the efficiency when using LP. This is because the charging efficiency varies depending on the vehicle’s charging and discharging power and the battery’s SOC. As a result, LP is not able to incorporate the changes in charging efficiency along with variations in control input (charging power) or state variable of the battery SOC, as performed sequentially in DP.
Instead, the average efficiency can be calculated and applied for LP; for each current SOC, potential SOC changes with respect to the charging and discharging power are calculated and average values can be found as shown in Figure 9. However, due to the error introduced in this approximation, it is difficult for LP to satisfy the final SOC constraints set by the driver. In Figure 10, a final battery SOC target of 0.9 is estimated, but in the simulation result, there is a discrepancy of about 2% in the battery SOC. On the other hand, in the DP, the efficiency considering the battery SOC change is reflected, and the target SOC in DP calculation results matches that of the simulation results well.
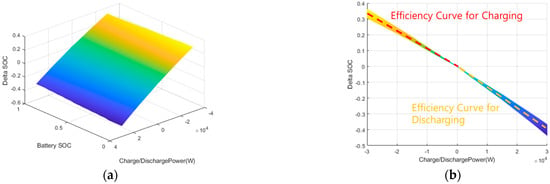
Figure 9.
Efficiency approximation for LP: (a) SOC change based on charging power and the battery’s current SOC; (b) average efficiency curve for charging and discharging.
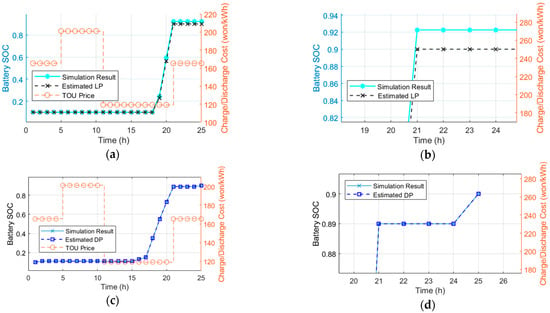
Figure 10.
Final battery SOC value error: (a) LP result with constant efficiency value; (b) LP result (enlarged); (c) DP result with efficiency model; (d) DP result (enlarged).
For LP, to solve this problem, it requires a receding horizon control approach (also called Model Predictive Control, MPC), where the current and target SOC are recalculated at each time step, and only first control input is used. The simulation results are presented in Table 5. For case I, when the initial SOC is set to 10% and the final SOC to 90%, the performance of the normal (uniform charging power), MPC, and DP methods was compared. Additionally, in the case of DP, the performance was also evaluated when the discretization level of the battery SOC grid, , was adjusted. The simulation results show that while the MPC also performs well, the DP method demonstrates superior cost performance, which represents the global optimum for the given optimization problem definition. This is due to the sequential consideration of vehicle charging efficiency along with battery SOC profile, and it was observed that even when the battery SOC grid is coarse (= 50), the performance of DP outperforms that of LP, with further improvements in performance when the grid is made finer.

Table 5.
Simulation result for normal, MPC (LP), and DP (case I, ).
4.3. Case Study for Effect of Battery Performance Degradation
On the other hand, V2G charging strategies reflecting battery performance degradation are also an important issue to consider at the vehicle system level. In this study, assuming battery degradation, scenarios of V2G charging optimization at the vehicle level were explored using DP. Based on [,], cycling aging is assumed such that battery capacity fades by 80% and internal resistance for both charging and discharging increases by 50% after 900 cycles, and battery capacity fades by 70% and internal resistance increases by 130% after 1800 cycles. Simulation results are provided in Table 6. In case I (initial and final SOC of 0.1 and 0.9), as battery performance degrades, the charging cost also decreases. This is due to the decrease in battery capacity according to degradation. Therefore, when the initial conditions of the battery and the final SOC conditions are the same, less capacity needs to be charged. However, when considering the cost relative to the capacity of the charged battery, it can be observed that the cost per capacity increases slightly due to the increased internal resistance of the battery. On the other hand, in the case II scenario for both initial and final SOCs of 0.9, as battery performance degrades, the cost benefit that EV can earn reduces significantly (79% for 900 cycles and 67% for 1800 cycles), due to the decrease in available energy buffer (battery capacity) of the EV battery. While these results highlight the need to analyze the actual charging cost variations caused by battery performance degradation under different scenarios, this study shows that, by using DP, the global optimum can be obtained for different scenarios, which also can be used for benchmarking value for other control methodologies.

Table 6.
Simulation result for DP considering battery performance degradation.
5. Conclusions and Future Work
In this paper, a DP-based V2G control algorithm to determine electricity charging costs for EVs was studied. The DP algorithm was constructed by incorporating the vehicle charging efficiency model, making it possible to implement the solution in a way that ensures the final SOC constraints are properly satisfied when applied to different EV V2G scenarios. The DP algorithm showed significant cost-saving performance compared to the normal charging strategy and outperformed Linear Programming. In relation to V2G research, the application of DP from the vehicle’s perspective in this study is important, as it can be used to calculate the best possible solution for the given V2G control problem, while satisfying constraints. It can also serve as a basis for future research on the optimization of EVs in V2G applications. As future work, experiments in real vehicle V2G systems and validation of the proposed algorithm are required. Also, control methodologies considering the impact of battery degradation could be developed using the proposed DP algorithm, which will also enable balanced V2G control at the vehicle level between charging cost saving and management of battery durability. On the other hand, the limitations of DP as an offline controller and its computational complexity are unavoidable, so for problems with high uncertainty or large-scale problems like EV fleets, it is necessary to apply methodologies such as stochastic DP or reinforcement learning, which are extensions of DP. However, even in such cases, since the global optimum performance of DP can be used as a benchmark, the proposed algorithm in this study can be used to assess the optimal performance of V2G control methodologies. As future work, the DP algorithm could be formulated for V2G systems including various, coexisting renewable energy resources, providers, and consumers, not only at the vehicle system level, but also as an EV charging station or V2G aggregator.
Author Contributions
Conceptualization, H.L., H.K. (Hyunjoong Kim) and H.K. (Hyunsup Kim); methodology, H.L. and H.K. (Hyewon Kim); software, H.L. and H.K. (Hyunjoong Kim); formal analysis, H.L. and H.K. (Hyunjoong Kim); writing, H.L.; supervision, H.K. (Hyunsup Kim); project administration, H.K. (Hyewon Kim). All authors have read and agreed to the published version of the manuscript.
Funding
The present research was supported by the research fund of Dankook University in 2022.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
Authors Hyewon Kim and Hyunsup Kim were employed by Hyundai Motors Company. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| V2G | Vehicle to Grid |
| EV | Electric Vehicle |
| DP | Dynamic Programming |
| SOC | State of Charge |
| TOU | Time-of-use |
References
- Dik, A.; Omer, S.; Boukhanouf, R. Electric Vehicles: V2G for Rapid, Safe, and Green EV Penetration. Energies 2022, 15, 803. [Google Scholar] [CrossRef]
- Yilmaz, M.; Krein, P.T. Review of the Impact of Vehicle-to-Grid Technologies on Distribution Systems and Utility Interfaces. IEEE Trans. Power Electron. 2013, 28, 5673–5689. [Google Scholar] [CrossRef]
- Morais, H.; Sousa, T.; Vale, Z.; Faria, P. Evaluation of the Electric Vehicle Impact in the Power Demand Curve in a Smart Grid Environment. Energy Convers. Manag. 2014, 82, 268–282. [Google Scholar] [CrossRef]
- Shi, R.; Li, S.; Zhang, P.; Lee, K.Y. Integration of Renewable Energy Sources and Electric Vehicles in V2G Network with Adjustable Robust Optimization. Renew. Energy 2020, 153, 1067–1080. [Google Scholar] [CrossRef]
- Qian, K.; Zhou, C.; Allan, M.; Yuan, Y. Modeling of Load Demand Due to EV Battery Charging in Distribution Systems. IEEE Trans. Power Syst. 2011, 26, 802–810. [Google Scholar] [CrossRef]
- Tan, K.M.; Ramachandaramurthy, V.K.; Yong, J.Y. Integration of Electric Vehicles in Smart Grid: A Review on Vehicle to Grid Technologies and Optimization Techniques. Renew. Sustain. Energy Rev. 2016, 53, 720–732. [Google Scholar] [CrossRef]
- Cao, Y.; Tang, S.; Li, C.; Zhang, P.; Tan, Y.; Zhang, Z.; Li, J. An Optimized EV Charging Model Considering TOU Price and SOC Curve. IEEE Trans. Smart Grid 2012, 3, 388–393. [Google Scholar] [CrossRef]
- Sortomme, E.; El-Sharkawi, M.A. Optimal Scheduling of Vehicle-to-Grid Energy and Ancillary Services. IEEE Trans. Smart Grid 2012, 3, 351–359. [Google Scholar] [CrossRef]
- Ahn, C.; Li, C.T.; Peng, H. Optimal Decentralized Charging Control Algorithm for Electrified Vehicles Connected to Smart Grid. J. Power Sources 2011, 196, 10369–10379. [Google Scholar] [CrossRef]
- Sundström, O.; Binding, C. Flexible Charging Optimization for Electric Vehicles Considering Distribution Grid Constraints. IEEE Trans. Smart Grid 2012, 3, 26–37. [Google Scholar] [CrossRef]
- Khezri, R.; Steen, D.; Wikner, E.; Tuan, L.A. Optimal V2G Scheduling of an EV with Calendar and Cycle Aging of Battery: An MILP Approach. IEEE Trans. Transp. Electrif. 2024, 10, 10497–10507. [Google Scholar] [CrossRef]
- Bai, X.; Qiao, W. Robust Optimization for Bidirectional Dispatch Coordination of Large-Scale V2G. IEEE Trans. Smart Grid 2015, 6, 1944–1954. [Google Scholar] [CrossRef]
- Lunz, B.; Walz, H.; Sauer, D.U. Optimizing Vehicle-to-Grid Charging Strategies Using Genetic Algorithms under the Consideration of Battery Aging. In Proceedings of the 2011 IEEE Vehicle Power and Propulsion Conference, Chicago, IL, USA, 6–9 September 2011; pp. 1–7. [Google Scholar]
- Abdulaal, A.; Cintuglu, M.H.; Asfour, S.; Mohammed, O.A. Solving the Multivariant EV Routing Problem Incorporating V2G and G2V Options. IEEE Trans. Transp. Electrif. 2017, 3, 238–248. [Google Scholar] [CrossRef]
- Saber, A.Y.; Venayagamoorthy, G.K. Unit Commitment with Vehicle-to-Grid Using Particle Swarm Optimization. In Proceedings of the 2009 IEEE Bucharest PowerTech, Bucharest, Romania, 28 June–2 July 2009; pp. 1–8. [Google Scholar]
- Kirk, D.E. Optimal Control Theory: An Introduction; Courier Corporation: Chelmsford, MA, USA, 2004; ISBN 0486434842. [Google Scholar]
- Škugor, B.; Deur, J. Dynamic Programming-Based Optimisation of Charging an Electric Vehicle Fleet System Represented by an Aggregate Battery Model. Energy 2015, 92, 456–465. [Google Scholar] [CrossRef]
- Xu, J.; Wong, V.W.S. An Approximate Dynamic Programming Approach for Coordinated Charging Control at Vehicle-to-Grid Aggregator. In Proceedings of the 2011 IEEE International Conference on Smart Grid Communications (SmartGridComm), Brussels, Belgium, 17–20 October 2011; pp. 279–284. [Google Scholar]
- Li, Z.; Wu, L.; Xu, Y.; Zheng, X. Stochastic-Weighted Robust Optimization Based Bilayer Operation of a Multi-Energy Building Microgrid Considering Practical Thermal Loads and Battery Degradation. IEEE Trans. Sustain. Energy 2022, 13, 668–682. [Google Scholar] [CrossRef]
- Ebrahimi, M.; Rastegar, M.; Mohammadi, M.; Palomino, A.; Parvania, M. Stochastic Charging Optimization of V2G-Capable PEVs: A Comprehensive Model for Battery Aging and Customer Service Quality. IEEE Trans. Transp. Electrif. 2020, 6, 1026–1034. [Google Scholar] [CrossRef]
- Kavousi-Fard, A.; Niknam, T.; Fotuhi-Firuzabad, M. Stochastic Reconfiguration and Optimal Coordination of V2G Plug-in Electric Vehicles Considering Correlated Wind Power Generation. IEEE Trans. Sustain. Energy 2015, 6, 822–830. [Google Scholar] [CrossRef]
- Ovalle, A.; Hably, A.; Bacha, S. Optimal Management and Integration of Electric Vehicles to the Grid: Dynamic Programming and Game Theory Approach. In Proceedings of the 2015 IEEE International Conference on Industrial Technology (ICIT), Seville, Spain, 17–19 March 2015; pp. 2673–2679. [Google Scholar]
- Xie, S.; Zhong, W.; Xie, K.; Yu, R.; Zhang, Y. Fair Energy Scheduling for Vehicle-to-Grid Networks Using Adaptive Dynamic Programming. IEEE Trans. Neural Netw. Learn. Syst. 2016, 27, 1697–1707. [Google Scholar] [CrossRef]
- Shang, Y.; Li, Z.; Shao, Z.; Jian, L. Secure and Efficient V2G Scheme through Edge Computing and Federated Learning. In Proceedings of the 2022 4th International Conference on Smart Power and Internet Energy Systems, Beijing, China, 27–30 October 2022; pp. 2250–2255. [Google Scholar]
- Kim, H.; Myeong, H.; Park, I.; Choi, J.H.; Kim, K. Vehicle-to-Grid Charging Optimization of Electric Vehicle. In Proceedings of the 2020 IEEE Conference on Control Technology and Applications (CCTA), Montreal, QC, Canada, 24–26 August 2020; pp. 1–6. [Google Scholar]
- Saldana, G.; Martin, J.I.S.; Zamora, I.; Asensio, F.J.; Onederra, O.; Gonzalez, M. Empirical Electrical and Degradation Model for Electric Vehicle Batteries. IEEE Access 2020, 8, 155576–155589. [Google Scholar] [CrossRef]
- Amir, S.; Gulzar, M.; Tarar, M.O.; Naqvi, I.H.; Zaffar, N.A.; Pecht, M.G. Dynamic Equivalent Circuit Model to Estimate State-of-Health of Lithium-Ion Batteries. IEEE Access 2022, 10, 18279–18288. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).