Abstract
This article presents the design and implementation of a DC–DC power converter for application in electric vehicle (EV) fast-charging systems. The prototype is of the resonant LLC type and consists of a high-power transformer operating at high frequency, which is an essential feature for the adequate behavior of the EV fast-charging system as a whole. As demonstrated throughout the article, by using this converter topology as well as its specific operating modes, such as for achieving zero-voltage switching (ZVS) and zero-current switching (ZCS), it is possible to enhance efficiency by reducing conduction and switching losses as well as to increase power density. The details of the high-power high-frequency transformer (HFT), considering different designs, are presented and discussed. With the implemented laboratorial prototype fully developed with silicon carbide (SiC) power semiconductor devices, it was possible to demonstrate and validate the main features of the resonant LLC converter, including high efficiency, under distinct conditions of operation.
1. Introduction
Electric mobility and the ongoing energy transition are increasingly important issues today. There is an urgent need for technological development in this direction, and people are giving more consideration to the use of public transportation and to the utilization of electric vehicles (EVs) [1]. This leads to a reduction in transportation costs and, from an environmental perspective, helps to minimize CO2 emissions and other pollutant gases [2]. As evidence of this, Figure 1 shows a notable increase in the number of EVs by the end of 2023, ranging from under 1 million sales to over 40 million sales [3]. However, there are still some factors that require further technological development for the mass adoption of EVs, namely: (i) a reduction in the EVs’ price; (ii) a shorter charging time; and (iii) an increase in the expected battery lifetime [4,5]. In addition to these factors, there are political and social limitations, such as legislation that does not favor the use of these vehicles or issues such as the lack of space for charging [6]. To harness the growth of electric mobility, it is equally important not only to increase the number of charging stations but also to develop improved technological solutions for the charging process of EVs [7]. From AC charging (on-board or off-board) to advanced DC fast-charging systems (off-board), as depicted in Figure 2, there are various topologies that meet different charging needs [8]. Concerning the AC–DC stage, where several topologies are available, the three-phase boost-type rectifier is distinguished by its high efficiency, low total harmonic distortion (THD), straightforwardness, cost-effective configuration, and the capacity to facilitate bidirectional flow [9,10].
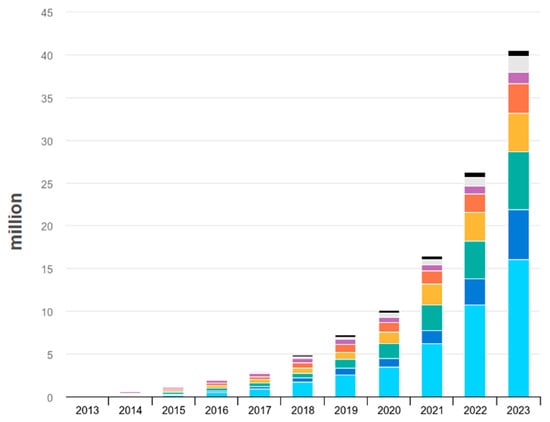
Figure 1.
Global EV stock over the last 10 years (2013–2023) [3].
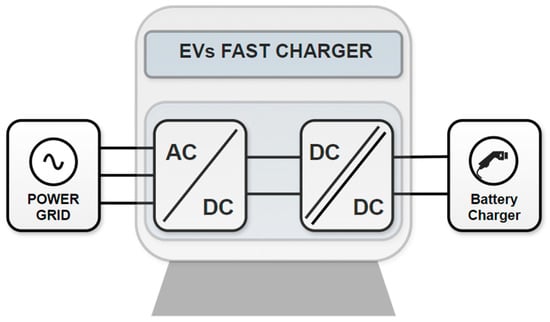
Figure 2.
Composition of an EV fast charger, based on an AC–DC three-phase and an isolated DC–DC converter.
However, the use of this technology presents a significant number of challenges, including the potential for high-voltage stress, the risk of current surges at the start, and vulnerability to overcurrent during short-circuits. Another example is the three-phase buck-type rectifier, characterized by the lower starting current and voltage stress on the components. In comparison, boost rectifiers result in greater reliability and a wider range of output voltage regulation, but like the boost type, they have some issues, such as significant conduction losses due to the use of diodes and switches in series [11].
For the isolated DC–DC converter, the literature indicates the use of multiple topologies that may be divided into two main groups, namely, the isolated and the non-isolated types [12]. The interleaved three-phase LLC resonant converter is particularly effective in achieving high efficiency under full load conditions due to the distribution of power losses across the three legs [13]. This results in a reduction in thermal strain and minimization of stress on critical components such as capacitors and power switches, which contributes to an enhanced level of reliability. Furthermore, the leg deactivation enables the converter to sustain its efficiency across a wide range of loads, although it requires an elevated level of design and control complexity due to the necessity for meticulous leg management [14]. Nevertheless, the converter’s efficiency tends to decline at lower loads, rendering it less suitable for applications where load levels are subject to frequent fluctuations [15]. Another topology is the dual active bridge (DAB) converter, which is particularly well suited to applications that necessitate bidirectional power flow, such as vehicle-to-grid (V2G) and grid-to-vehicle (G2V) functionalities [16]. The modulation technique facilitates seamless switching, which contributes to a reduction in switching losses and an enhancement in overall efficiency. Furthermore, the DAB converter is capable of efficiently managing a diverse range of output voltages, thereby offering versatility for different types of batteries [17]. However, both sides of the converter are susceptible to high conduction losses, which can be mitigated through the utilization of a semiconductor switch with low on-state drain-to-source resistance (RDS(on)) [18,19].
As a final input, the non-isolated DC–DC multilevel converter stands out for its ability to generate high-quality power with minimal total harmonic distortion, thus reducing the need for extensive filtering components [20]. The converter is highly scalable and modular, making it an optimal choice for integration into various charging infrastructures, particularly those requiring high-power applications. The converter can efficiently handle high voltage levels without the need for transformers, which allows a reduction in both the overall size and the cost of the charging system. However, incorporating an increased number of components such as capacitors and switches can result in a more complex system architecture and higher costs. In addition, the control system is subject to greater complexity due to the need to supervise various voltage levels and switching operations [21]. In Table 1, it is possible to see some advantages and disadvantages of other possibilities of DC–DC converters.

Table 1.
Advantages and disadvantages of different DC–DC power converter solutions for EV fast-charging systems.
The distinguished points of this paper are as follows: (i) Presentation of the converter design process showing, step by step, the most relevant details, including distinct designs of the HFT aiming to verify the influence of key parameters. (ii) Detailed design and implementation of a resonant LLC converter for applications in EV fast-charging systems with the main goal of proving that their use is more advantageous compared with the topologies seen before. A comparison with the main similar topologies is also presented and compared in terms of advantages and disadvantages, supporting the benefits of the resonant LLC converter. (iii) Computer validation for the most relevant operation conditions for input values of 900 V and with a 1:1 conversion ratio at a switching frequency (fsw) of 100 kHz, validating the operating principle and the key features (e.g., operation with ZVS and ZCS). (iv) A laboratory prototype designed for a power value of 50 kW, including the respective experimental validations for different scenarios of operation but for power values only up to 1 kW. (v) Experimental validation of various HFT configurations to demonstrate that the developed prototype achieves high efficiency through the improvement of the HFT design as well as the utilization of SiC power devices.
This paper is structured as follows: Section 2 presents the LLC resonant converter, while its operation principle is validated with computational simulation in Section 3. The design and development of the HFT are presented in Section 4, while the developed laboratory prototype and the respective experimental validations are presented in Section 5. The main conclusions are presented in Section 6.
2. Design of the DC–DC LLC Resonant Converter
The initial concept of a resonant converter consists of incorporating resonant tanks into power converters to create oscillatory voltage and/or current waveforms, creating conditions for ZVS or ZCS. This makes it possible to reduce switching losses due to soft switching [22]. Specifically, isolated DC–DC LLC resonant converters have become a good option for EV fast-charging applications, since the use of ZVS and ZCS soft-switching techniques helps to reduce losses and, consequently, significantly increase efficiency. This allows an increase in the value of fsw while reducing power density [23].
The resonant LLC converter under study is composed of four different stages, as shown in Figure 3: (i) the full-bridge inverter, constituting four switching elements capable of generating a square wave with the same value as the input voltage, thus supporting a higher current; (ii) the resonant LLC tank, made up of a coil and a capacitor in series and a coil in parallel with the primary side of the transformer; (iii) the full-bridge diode rectifier; (iv) an output filter capacitor used to obtain a constant voltage at the load [24]. In addition to these four different stages, the proposed solution also has an HFT (included in the resonant tank) to ensure galvanic isolation between the converter’s input and output, so that it is possible to adjust the voltage through the transformation ratio, if necessary.
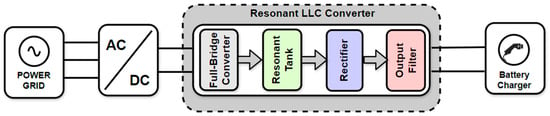
Figure 3.
Block diagram of an EV fast-charging system highlighting the internal constitution of the resonant LLC converter.
2.1. Design of the Isolated DC–DC LLC Resonant Converter
The unidirectional converter under study, as shown Figure 4, operates in three modes with different resonant frequencies. Operation of the converter at an fsw higher than the resonant frequency (fr) is used for the ZVS, which is in a delayed power factor mode. Conversely, the operation of the converter at an fsw lower than fr is used for the ZCS, which is in an advanced power factor mode. Operating at fr, the circuit does not operate in either ZVS or ZCS; therefore, for EV charging applications, it is recommended that this LLC converter operate above the to achieve optimal point of efficiency and stability [25]. In this article, a key focus is related to the design to operate above the resonance frequency, therefore optimizing the system’s performance in the widest possible frequency range, with a gain value equal to 1.
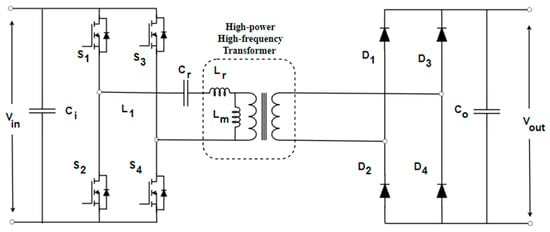
Figure 4.
Topology of the DC–DC resonant LLC converter.
The input DC voltage is converted into a square wave with a full-bridge inverter and transferred to the LLC resonant tank. The resonant tank circuit consists of a resonant inductance (Lr), a magnetizing inductance (Lm), and a resonant capacitor (Cr). Diodes D1 and D2 are used to rectify the alternating voltage at the HFT secondary side terminals. The capacitor used as the output load filter is represented as Co. As seen above, the isolated DC–DC resonant LLC converter has two distinct frequencies (fr1 and fr2). This can be calculated from [26,27] the following:
The load resistance transferred to the resonant equivalent circuit (Rac), which depends on the transformation ratio (n), is given by
The quality factor (Q) of the LLC converter is calculated using
The normalized frequency (fn) is calculated by
The relationship between the two inductances (m) is given by
Finally, in the equivalent circuit of the LLC converter with a non-ideal transformer, the ratio between the output and input voltages (Gd) corresponds to the gain of the resonant circuit and is given by
Thus, it is possible to see that the parameter m represents the relationships between the inductors of the resonant tank, influencing the maximum gain (Gdmax) of the converter. Larger values of m allow greater flexibility in the circuit, enabling higher gains, while smaller values restrict the resonant behavior. Figure 5 illustrates how different values of m affect the system’s performance in terms of efficiency, stability, and amplification capability, making it an essential parameter for optimizing the resonant converter. The same figure shows the effect of Q, which directly influences the Gd parameter of the resonant circuit. Lower values of Q result in wider, flatter gain curves, indicating a less selective response and lower peak gain. On the other hand, higher values of Q produce narrower curves with higher peaks, reflecting greater selectivity and amplification around Fr. Hence, the Q effect demonstrates how the quality factor controls the bandwidth and resonant behavior of the system, and it is essential to defining the performance and efficiency of the resonant converter.
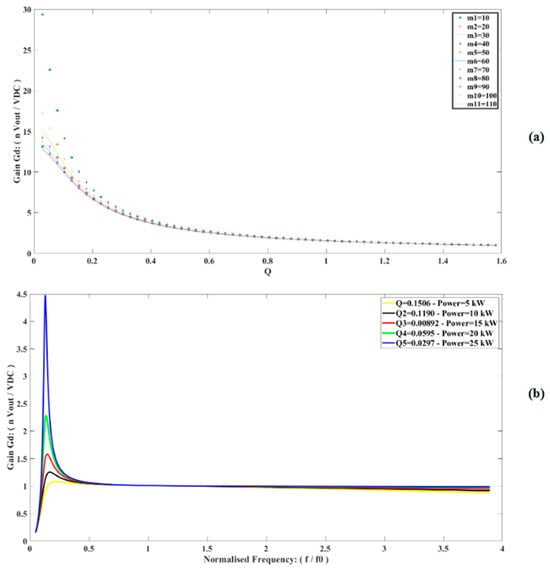
Figure 5.
Plots of different effects in the curve gain: (a) m effect; (b) Q effect.
2.2. Advantages and Disadvantages of the Isolated DC–DC Resonant LLC Converter
The LLC resonant converter is a popular choice for high-efficiency and high-power-density applications such as fast chargers for EVs. It offers several significant advantages over other DC–DC converter topologies. By increasing the fsw to values above 100 kHz, this type of converter manages to increase the power density, which in turn leads to a reduction in the size of the magnetic components. Consequently, this results in a more compact and lightweight EV charging station design. Given this, some advantages of the LLC resonant converter are as follows [28]: (i) An increased fsw translates into increased power density and reduced size and weight of the components, making the prototype lighter and smaller. (ii) A higher switching efficiency, with the use of soft-switching techniques such as ZVS and ZCS, minimizes switching losses, reducing thermal stress and consequently increasing the useful life of the components. (iii) Galvanic isolation provided by the HFT isolates the input from the output, improving operational safety and allowing flexibility in system design. (iv) Improved dynamic response through fr operation allows a quick response to load variations. In addition to these advantages, the converter also has some disadvantages that can be an obstacle to its use for other purposes [29]: (i) The complexity of the project increases as it requires a more complex design compared with other isolated DC–DC converter topologies; allied with the high difficulty of adjusting the resonant components, this can complicate development and increase project time. (ii) The cost of high-frequency and high-efficiency components can be more expensive, and the production of the HFT can also increase the cost. (iii) Controlling an LLC resonant converter is more challenging due to its highly frequency-dependent response. (iv) Ensuring system stability under all operating conditions can require advanced control techniques. (v) Small variations in the values of the resonant components can significantly affect the converter’s performance.
2.3. Soft Switching vs. Hard Switching
The switching process is extremely important in the development of power converters and other electronic devices, as it has a direct impact on the efficiency and reliability of the system. Two main approaches to switching have been identified: traditional switching and soft switching. Each of these approaches has its distinctive characteristics, advantages, and disadvantages depending on the purpose of each design [28,29].
In the traditional approach, electronic switches, such as transistors, are switched on and off abruptly [30]. Hard switching leads to rapid transitions in current and voltage, which, in turn, lead to higher switching losses. During these transitions, current and voltage are simultaneously present in the semiconductor devices, which results in significant power losses, as shown in Figure 6. In addition, these losses result in the generation of heat, which requires the use of heat sinks and additional cooling systems to keep the components within the specified temperature range. In addition, traditional switching methods have been identified as a source of electromagnetic interference (EMI) [31]. This can disrupt the operation of other electronic devices, and the rapid transitions intensify the electrical and thermal stress on the semiconductor components, thus reducing their lifespan and reliability. However, hard switching is simpler to implement and control, requiring no additional circuitry to manage the switching transitions [32].
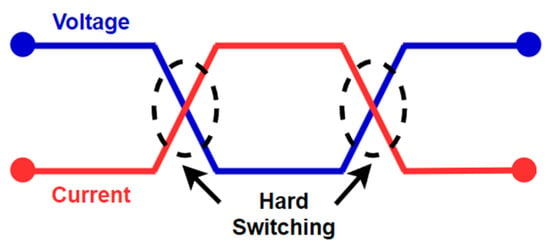
Figure 6.
Representation of the principle of operation with hard switching.
In contrast, soft switching employs modulation techniques to reduce the losses and stress associated with current and voltage transitions [33]. The two main soft-switching techniques are ZVS and ZCS. In ZVS switching, the switches are triggered when the voltage across them is at its minimum, thus minimizing the energy losses that occur during the switching process [34]. This is achieved through resonant circuits that generate a sinusoidal voltage variation, as shown in Figure 7. On the other hand, for ZCS switching, the switches are activated when the current flowing through them is zero.
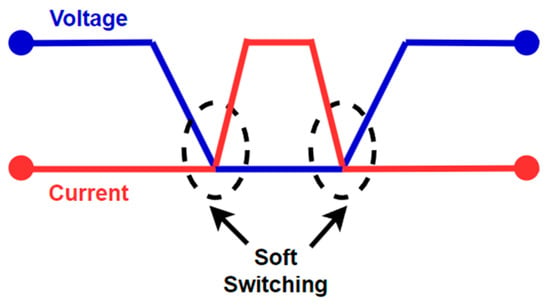
Figure 7.
Representation of the principle of operation with soft switching.
Soft switching offers several significant advantages. Firstly, the reduction in switching losses significantly improves system efficiency, resulting in lower heat production and reduced heat dissipation requirements. In addition, smooth transitions reduce the generation of electromagnetic noise [35]. Another important advantage is the increased lifetime of the components due to the reduced electrical and thermal stress. However, these benefits have a lot of challenges. Implementing soft-switching techniques requires additional circuits such as resonant networks, which increases the complexity of the project. Tuning and calibrating these circuits can be complicated and require more development time, and manufacturing costs can be higher due to the need for additional components and more complex circuits. The efficiency of soft-switching techniques can also vary with the load, requiring sophisticated control to maintain efficiency over a wide operating range, as can be seen in Figure 8 [36].
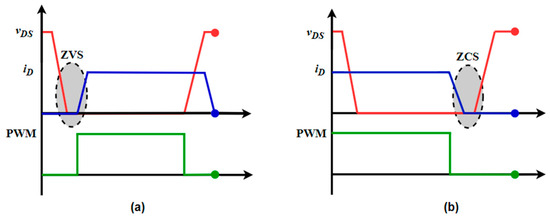
Figure 8.
Examples of switching techniques: (a) ZVS switching; (b) ZCS switching.
With that, the choice between soft switching and hard switching depends on the specific requirements of the application. Soft switching is ideal for applications that require high efficiency and low EMI. However, the additional complexity and cost can be a significant disadvantage in such scenarios. A careful assessment of the system requirements and the characteristics of each switching method is essential to making the right choice when designing power converters and other electronic devices.
2.4. High-Frequency Transformer Design
The HFT design process begins with the analysis of its equivalent circuit, as shown in Figure 9, to understand how the Lr and Lm values are obtained.
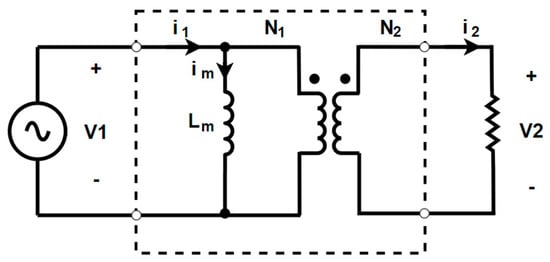
Figure 9.
Equivalent electric circuit of the HFT.
After obtaining the HFT’s equivalent circuit, some steps must be taken into consideration to calculate the additional parameters, including the number of turns and the number of copper wires in parallel in each coil. Thus, the steps are as follows [37]:
- Select the core with the “product of area” method using the following equation, where is the input power, is the maximum magnetic flux density, k is the packing factor, and J is the current density:
- 2.
- Determine the number of turns on the primary and secondary sides of the HFT (N1 and N2, respectively) using the following equations, where S represents the cross-sectional area of the magnetic core:
- 3.
- Calculate the cross-sectional area of the wire for and through the following equations, where I1 and I2 represent the current in the primary and secondary windings of the transformer, respectively. ID1 and ID2 represent the current in the diodes, and ILrms represents the rms value of the current in the resonant tank:
- 4.
- Calculate the winding losses (Pp) and the losses in the HFT core (Ps) through several steps to determine the HFT’s global efficiency.
- 4.1.
- Winding losses:
- 4.2.
- Find the HFT core losses using the datasheet for operating conditions.
- 4.3.
- Total sum of losses and calculation of HFT efficiency ():
These steps facilitate a more comprehensive understanding of the HFT design. The possibility of obtaining an efficiency close to 100% is of the utmost importance. Once the above calculations have been completed, it is essential to consider how the HFT should be wound. The choice of core material, shape, and size determines the optimum winding method, allowing variable resonance inductance values to be obtained, as shown in Figure 10. In addition, the HFT magnetizing inductance can be influenced by the space between the two cores.
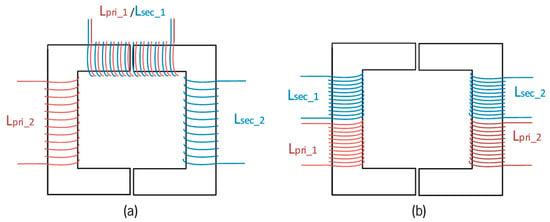
Figure 10.
Possibilities for the arrangement of the windings in the HFT: (a) Proposed design for HFT1, with one primary and one secondary winding together in one part of the transformer and one primary and one secondary winding separated. (b) Proposed design for HFT2, with the secondary winding wound on top of the primary winding on both sides.
3. Computational Validation
To facilitate comprehension of the system’s operational mechanics before its implementation in a tangible context, a series of simulations were conducted. This approach was undertaken to enhance certainty regarding the converter to be deployed. Preliminary simulations were conducted to improve the impact of resonant tank sizing on the system behavior. Subsequently, a basic control system was introduced, followed by the integration of the final circuit. This circuit will serve as a point of reference for future comparisons with the prototype. For a more comprehensive grasp of the simulation parameters, one may consult Table 2, which provides a more detailed account of the values in question. It is crucial to highlight that the objective of this simulation was to achieve an input voltage value that is identical to the output voltage value. To this end, a 1:1 HFT was employed. To calculate the predicted efficiency, the actual models of the MOSFETs and the diode were constructed to achieve the greatest possible approximation of the anticipated real values.

Table 2.
Electric parameters for the proposed simulation values.
3.1. Operating Principle Validation
To thoroughly comprehend the operation of the isolated DC–DC converter, it is imperative to grasp the behavior of several pivotal variables. One of the most significant factors is the voltage across Cr, as it directly impacts the overall system performance. It is important to highlight those variations in the converter design, including changes in the HFT winding configuration, can significantly influence the peak voltage across Cr. As illustrated in Figure 11, an increase in the value of Cr results in a reduction in the peak voltage, while a decrease has the opposite effect. Secondly, it is extremely important to comprehend the influence of the resonance current (Ilr) on the system, i.e., the effect on these values of changing the design. An analysis of Figure 12 shows that there is no change in Ilr when the design values are varied; however, it should always be borne in mind that the value should not be too high in order not to compromise the design and the cost of producing a prototype.
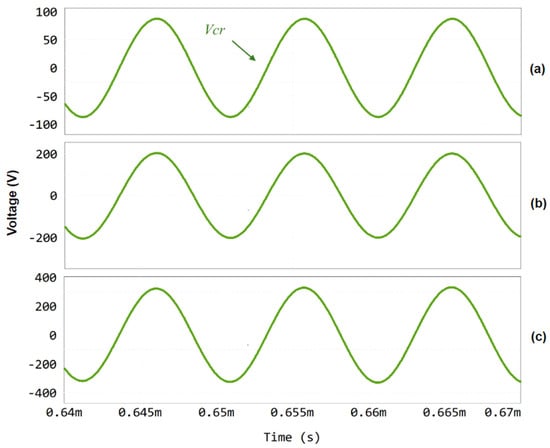
Figure 11.
Simulation results showing the voltage variation in Cr (Vcr) for different case studies: (a) Case 1, with peak voltage value equal to 87 V; (b) Case 2, with peak voltage value equal to 205 V; (c) Case 3, with peak voltage value equal to 318 V.
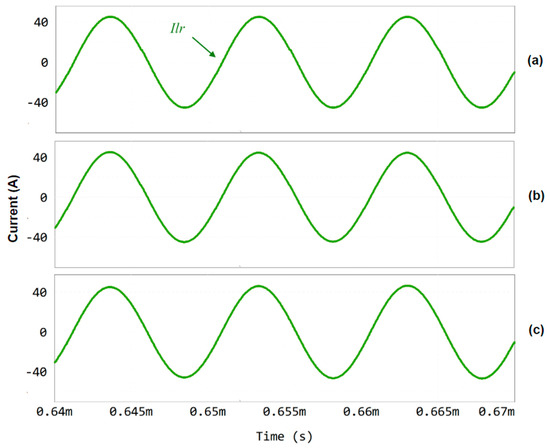
Figure 12.
Simulation results showing the current variation (Ilr) for different case studies: (a) Case 1, with peak current value equal to 44 A; (b) Case 2, with peak voltage value equal to 44.2 A; (c) Case 3, with peak voltage value equal to 44.3 A.
After the analysis of these factors, it is essential to analyze the voltage waveforms at four other crucial points: (i) the converter input side (Vin); (ii) the HFT’s primary side (Vprim); (iii) the HFT’s secondary side (Vsec); and (iv) the output of the HFT (Vout). Considering the above points, the converter is of the DC–DC type, and it is expected that both the input and the output will have continuous and equal voltage values, located in both cases around 900 V, as shown in Figure 13.
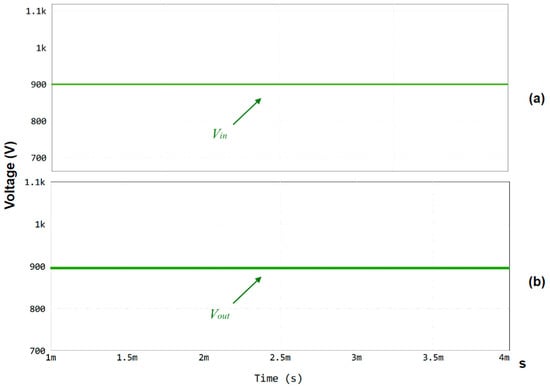
Figure 13.
Simulation results showing the voltage waveforms for the DC–DC resonant LLC converter at (a) the input side (Vin) and (b) the output side (Vout).
By observing Figure 14, it is possible to conclude that Vprim and Vsec are minimally influenced by the configuration of the resonant tank. On the secondary side, it is also possible to observe the voltage after it has been transformed by the HFT. Given the 1:1 turns ratio of the HFT, Vsec will be equal in magnitude to Vprim. This characteristic ensures that the HFT faithfully reproduces the voltage levels, giving a clear understanding of the behavior of the circuit at both stages.
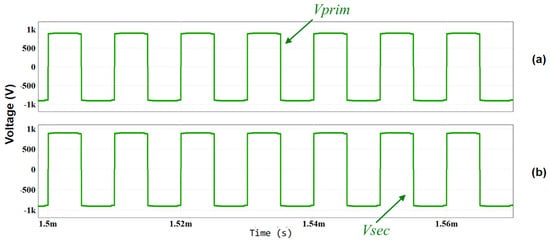
Figure 14.
Simulation results showing the voltage waveforms on the HFT: (a) Primary side (Vprim); (b) Secondary side (Vsec).
In this context, it is possible to understand how the system will behave and which components are the best option. Firstly, we see that by increasing the value of the Lr, the coil reduces the frequency range, which can make it easier to obtain a real value for the HFT design; secondly, it is known that increasing the value of the Cr is not advantageous for the system, as it means a substantial increase in the voltage value. It is also worth noting that the value of the peak current in the Lr does not change much with these variations. Finally, with a 1:1 transformation ratio for the HFT, Vin and Vout as well as Vprim and Vsec are expected to have similar peak and RMS values.
3.2. ZVS and ZCS Control Simulations
The simulations performed for the soft-switching techniques, namely ZVS and ZCS, produced compelling results that strongly confirm the effectiveness of these approaches in optimizing both the efficiency and reliability of power converters. These methods play a critical role in reducing switching losses and component stress, thereby extending the overall life of the system. Figure 15 provides a visual representation of the ZVS and ZCS techniques during the simulation process, showing their distinct operating characteristics. The observed behavior is the direct result of the careful integration and finetuning of the various parameters discussed in previous sections. These parameters include the resonant circuit design, fsw, and load conditions, all of which contribute to achieving the desired soft-switching conditions. The results emphasize the importance of a holistic approach to system design, where the interplay of electrical, mechanical, and thermal factors ensures optimum performance, highlighting the potential of ZVS and ZCS as highly effective strategies for advancing modern power electronics applications.
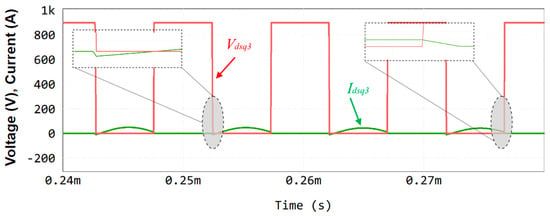
Figure 15.
Simulation results showing the voltage (VDSq3) and current (IDSq3) waveforms on the SiC power device q3, which validates the ZVS and ZCS operation.
Analyzing this result, it is possible to confirm the ZVS and ZCS operation, i.e., the voltage (vDSq3) increases when the current (iDSq3) reaches zero. On the other hand, the voltage (vDSq3) becomes zero when the current (iDSq3) increases. In this way, the ZVS and ZCS operation is reached, which is fundamental to increasing the efficiency of the converter.
3.3. Influence of Power and Frequency on Converter Operation
The complete behavior of the system was presented for a series of case studies with the same power value. However, the question remained as to how power and frequency affect the system. Firstly, the influence of power was analyzed, with all the results previously seen for two different power values (5 kW and 15 kW) being presented and compared with the values previously analyzed with a power of 25 kW. The analysis showed that a reduction in power results in a linear decrease in the current and voltage values in the Lm and Cr, respectively. In addition, the response time of the ZVS and ZCS controls remain unchanged, while there is a decrease in the negative current in the IDSq3, as shown in Figure 16.
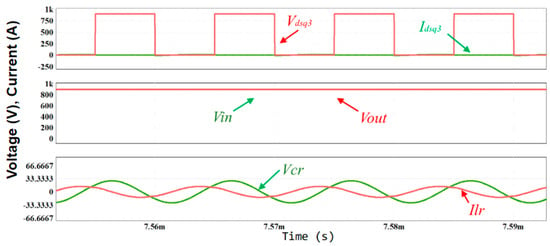
Figure 16.
Simulation results showing the influence of decreasing the operating power.
Figure 17 shows the case study for 15 kW, where it is again clear that there is a decrease in the values compared with the initial case and an increase compared with the previous case. It is also evident that the power value does not affect the converter, and it needs to be taken into consideration only when developing the prototype to size the system for the desired power value.

Figure 17.
Simulation results showing the influence of increasing the operating power.
In addition to the effect of increasing the operating power, which, as seen above, influences the system’s behavior, it is also necessary to understand the behavior in response to frequency alterations. As observed earlier, the system’s behavior is optimal within a certain frequency range where the gain is equal to one, i.e., if it operates outside of this range, the converter will not operate at the fr and will behave differently than desired. To understand this, two different cases are shown with the same power and with two frequencies other than 100 kHz, i.e., 50 kHz and 150 kHz. In Figure 18, with fsw below the ideal value, the system fails to reach the soft-switching condition. Additionally, the expected sinusoidal waveforms of Vcr and Ilr are not properly formed.
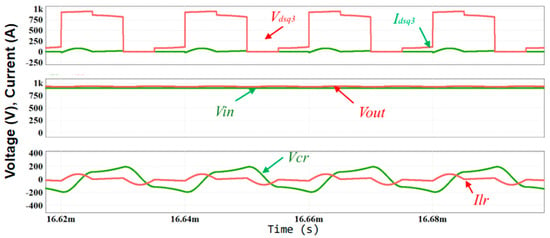
Figure 18.
Simulation results show the influence of decreasing the fsw on the system (50 kHz).
In the next case, at a value different from the ideal but closer to the fsw range, it is visible that the system’s behavior improves somewhat, although this indicates that all values outside the range will be detrimental to the system’s expected behavior, as shown in Figure 19.
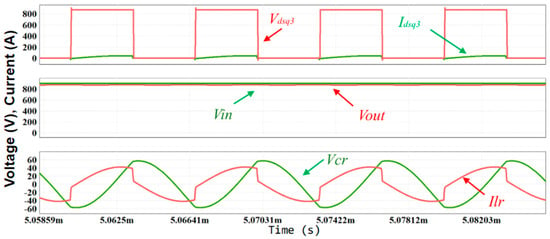
Figure 19.
Simulation results showing the influence of increasing the fsw on the system (150 kHz).
4. HFT Development and Prototype Assembly
To conduct meaningful tests on the converter, it is imperative to develop a tangible and effective prototype that can effectively execute the concept developed in the simulation environment with optimal efficiency. To achieve this, it is crucial to accurately implement the HFT, which is a pivotal component of this topology. Additionally, ensuring the appropriate interconnections between all system components is essential for the success of this prototype.
4.1. Implementation of a Real HFT
As will be seen in the following sections, the most crucial aspect of the implementation of a laboratory prototype of this topology is undoubtedly the design of the HFT. While other components are equally important, it is of the utmost importance to comprehend the way the HFT is to be wound, the cores that are to be employed, and the number of turns in both the primary and secondary circuits. It should be noted that the HFT utilized in this development was designed to accommodate power values of 25 kW and an fsw of 100 kHz. To achieve this, a core with the reference UF120/80/40 was selected from the company IF cores, from which there are three core options: PQ core, EE core, and UU core. The UU core (UF120/80/40) was selected due to its superior isolation and reduced leakage inductance compared with the other options. Its symmetric design and enclosed winding configuration ensure a more uniform magnetic path, tighter coupling between windings, and minimal flux leakage. These features contribute to improved electromagnetic interference (EMI) suppression and higher efficiency. The UU core is particularly advantageous for this type of application (EV charging stations), where optimized isolation, minimal energy losses, and reliable performance are critical [38], because of its two U-shaped cores. Once the core had been selected, the thickness of the copper to be used was determined, i.e., 0.1 mm, using 800 cables in parallel with 12 turns in the primary and 12 turns in the secondary and with a 1:1 turn ratio, due to the main objective of having Vout be equal to Vin. To facilitate the construction of the HFT, 3D parts were produced in which the HFT cores were fixed, as show Figure 20.

Figure 20.
A 3D mold was implemented to create the ‘O’-shaped core with the dimensions 17 cm long, 12 cm wide, 6 cm deep, and 3 mm material thickness.
Ten different designs were initially tested to understand how the different ways of winding the HFT affected the values of the Lr and the magnetization field, and consequently, the value of the Cr. It is possible to verify some examples in Figure 21.
- Design 1: Wrap 12 turns of the primary and 12 turns of the secondary on top on both sides.
- Design 2: Wrap 6 turns plus 6 primary turns, and then, on top, 6 turns plus 6 secondary turns, repeating on both sides.
- Design 3: Wind 12 primary turns and another 12 secondary turns.
- Design 4: Wind 12 turns plus 12 turns of the primary on one side and 12 turns plus 12 turns on the other side of the secondary.
- Design 5: Wind 12 turns of the primary plus 12 turns of the secondary on each side, using the larger side.
- Design 6: Wind 12 turns plus 12 turns in parallel of the primary plus 12 turns of the secondary on both sides.
- Design 7: Wind 12 turns of the primary on one side plus 12 turns of the secondary on the other side, and then, on the larger side, wind 12 turns of the primary plus 12 turns of the secondary in parallel.
- Design 8: Wind 12 turns of the primary plus 12 turns of the secondary in parallel on one side, and then, 12 turns of the primary plus 12 turns of the secondary on the other.
- Design 9: Wrap 12 turns of the secondary, 12 turns of the primary, 12 turns of the secondary, and 12 turns of the primary divided among the 4 sides.
- Design 10: Wind 12 turns of the primary, 12 turns of the primary, 12 turns of the secondary, and 12 turns of the secondary, changing the order of Design 9.

Figure 21.
Three different designs according to the shape of the body: (a) Design 5, (b) Design 8, (c) Design 3.
For these designs, the results presented in Table 3 were obtained.

Table 3.
Values of Lm and Lr were obtained for different HFT designs.
To obtain these values, specific tests were conducted in open and closed circuits, so that it was possible to visualize the values, as shown in Figure 22, Figure 23 and Figure 24.

Figure 22.
Values obtained through Design 1 tests: (a) Lo1 equal to 144 µH; (b) Lo2 equal to 154 µH; (c) Ls1 equal to 1.47 µH.

Figure 23.
Values obtained through Design 4 tests: (a) Lo1 equal to 196 µH; (b) Lo2 equal to 199 µH; (c) Ls1 equal to 70 µH.

Figure 24.
Values obtained through Design 8 tests: (a) Lo1 equal to 157 µH; (b) Lo2 equal to 158 µH; (c) Ls1 equal to 2.5 µH.
Consequently, it was possible to obtain two solutions (chosen due to their proximity to the values used in the simulation environment) to assess their performance on the laboratory prototype. Based on the design of two transformers, as show Figure 25 it was possible to identify the advantages and disadvantages of each.

Figure 25.
HFTs development: (a) The first HFT had Lo1 equal to 173 µH, Lo2 equal to 172 µH, and Ls1 equal to 3 µH. (b) The second HFT had equal to 147 µH, equal to 148 µH, and equal to 12.5 µH.
4.2. Prototype Assembly
Following the completion of the design process, simulations, and the implementation of an HFT, it was possible to create a laboratory prototype capable of handling power up to 25 kW. The system was subdivided into four discrete printed circuit boards (PCBs), with one PCB dedicated to the converter’s input power system (comprising the input capacitor, SiCs, and resonant capacitors) and a second PCB allocated to the output power system (encompassing the rectifier bridge and output filter). Regarding the control system and the way the power system was implemented, it was necessary to divide the PCB control system into discrete sections. The initial main PCB incorporated the DSP utilized for the prototype’s control system in addition to the power supply systems and drivers as well as the current and input voltage sensors. The second PCB, situated near the output, incorporated solely the signal processing apparatus for the voltage and current output sensors.
Furthermore, in addition to the implementation of the PCBs, protection systems, including contactors and switches, were incorporated into the prototype to facilitate a more straightforward connection between the user and the prototype. It should be noted that it is possible to visualize the prototype in Figure 26 that was implemented and subsequently tested.

Figure 26.
Implemented prototype with the different PCBs and all the connections with the user.
5. Experimental Results
Once the tests on the control hardware were completed, it was possible to move on to the tests on the power hardware, which were divided into two phases. These values were dimensioned using the equations seen in Section 2 of this article. By setting the fsw value, considering that the resonant LLC converter operates more efficiently at higher switching frequencies, the 100 kHz frequency was selected based on the transformer design process and applied within the simulation environment. In an initial phase, the first HFT, designed for an fsw of 104 kHz, was tested with a capacitor tank of around 600 µH and with voltage values between 30 V and 60 V. These values were then modified. In a second phase, the second HFT was used for an fsw between 127 kHz and 131 kHz with a capacitor tank of around 800 µH and voltage values between 30 V and 110 V. With these tests, it was possible to better understand the converter’s operation in a laboratory environment and all the adjustments needed for 1 kW power. During the tests, no additional control methods were implemented beyond the hardware-level control provided by the soft switching achieved through the circuit design. The prototype contained overcurrent and overvoltage protection only.
5.1. Test with First HFT Design
The experimental validation began by working within the initially calculated values, i.e., an fsw value of 104 kHz, a 600 µH capacitor bank, and a voltage value of 60 V, as shown in Figure 27. Notwithstanding, the results obtained were not as expected, since there was some noise in Vsec, and the input and output current waveforms (Iprim and Isec, respectively) were not completely sinusoidal as predicted, which indicates a discontinuous mode of operation, because the transformer was operating below the value of Fr.
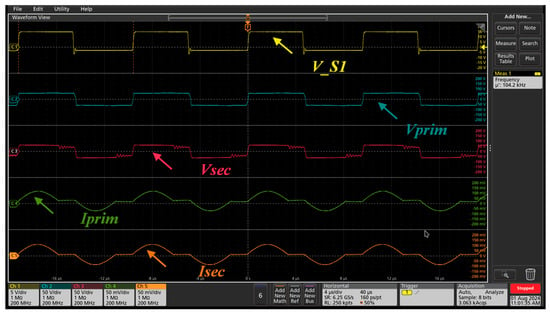
Figure 27.
Experimental test using the first transformer with 1 kW of power and 100 kHz of fsw. Yellow line: PWM signal at MOSFET 1 (V_S1); blue line: voltage signal at the HFT input side (Vprim); red line: voltage signal at the HFT output side (Vsec); green line: current signal at the HFT input side (Iprim); orange line: current signal at the HFT output side (Isec).
To address this, an attempt was made to see how the system could be altered to improve its behavior and achieve the results obtained in the simulation environment. Initially, at the same fsw value, the capacitor tank was increased to 800 µF, as shown in Figure 28. There was an improvement in the system’s performance, which was close to the predicted behavior, but it was still not in agreement, which led to the conclusion that it would be necessary to adjust the fsw value to the correct value, i.e., 127 kHz.
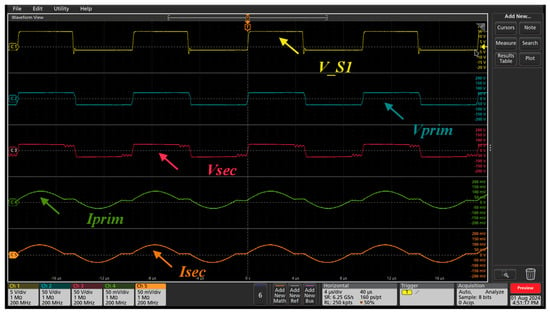
Figure 28.
Experimental test using the first transformer with 1 kW of power and 100 kHz of fsw. Channel 1 yellow line: PWM signal at MOSFET 1 (V_S1); blue line: voltage signal at the HFT input side (Vprim); red line: voltage signal at the HFT output side (Vsec); green line: current signal at the HFT input side (Iprim); orange line: current signal at the HFT output side (Isec).
As Fsw increases, it is clear, as shown in Figure 29, that the system is getting closer to the desired behavior predicted in the simulation environment. Taking into consideration the approach to the ideal behavior, it was also necessary to understand whether the converter was achieving soft-switching control.
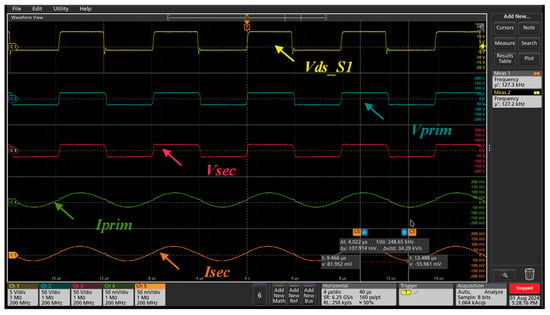
Figure 29.
Experimental test using the first transformer with 1 kW of power and 127 kHz of fsw. Yellow line: PWM signal at MOSFET 1 (V_S1); blue line: voltage signal at the HFT input side (Vprim); red line: voltage signal at the HFT output side (Vsec); green line: current signal at the HFT input side (Iprim); orange line: current signal at the HFT output side (Isec).
With the same tested values, the appearance of the ZVS control was tested, as shown in Figure 30. This situation is not yet visible, which makes it clear that there is some parameter in the converter that does not completely match what has been calculated with the values used in the simulation environment; therefore, it was necessary to readjust the values calculated for the prototype.
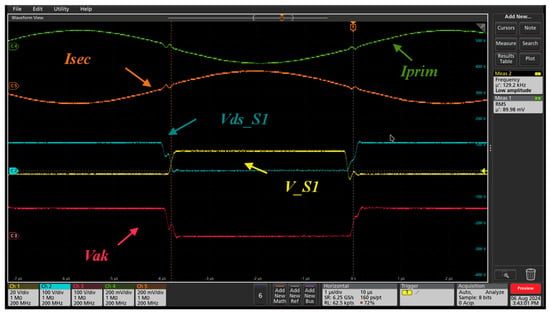
Figure 30.
Experimental test using the first transformer with 1 kW of power and 127 kHz of Fsw. Yellow line: PWM signal at MOSFET 1 (V_S1); blue line: voltage signal (Vds); red line: anode-to-cathode (Vak) voltage signal; green line: current signal at the HFT input (Iprim); orange line: current signal at the HFT output (Isec).
The first values showed that incorrect sizing of the HFT can affect the system’s behavior. So, it was necessary to change the HFT design by increasing the value of the resonance inductance and the fsw, as shown in the following section.
5.2. Test with Second HFT Design
As seen above, the results obtained using the first HFT design were not as expected; therefore, a second HFT with the same characteristics as the one designed in Figure 30 was used, changing the value of the fsw (50 kHz) and maintaining the value of the capacitor tank (800 µH). Considering and applying a voltage between 0 V and 110 V, an improvement in the system’s behavior is visible in Figure 31 where it is noticeable that both the input voltage and output voltage waves (blue and red, respectively) and the input current and output current waves (green and orange, respectively) are similar to those observed in the simulation environment.
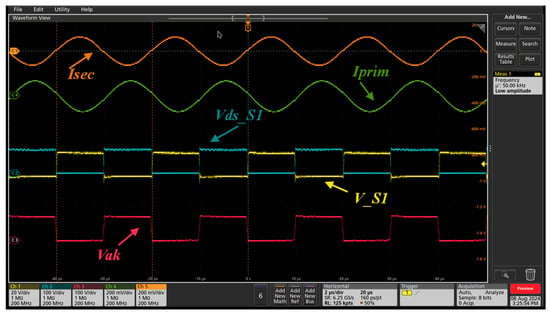
Figure 31.
Experimental test using the second transformer with 1 kW of power and 50 kHz of fsw. Yellow line: PWM signal at MOSFET 1 (V_S1); blue line: voltage signal (Vds); red line: anode-to-cathode (Vak) voltage signal; green line: current signal at the HFT input (Iprim); orange line: current signal at the HFT output (Isec).
Having concluded that the system was behaving as intended, all that remained was to confirm the existence of soft switching, which, as verified in the previous section, was the biggest problem concerning the HFT. Figure 32 shows the existence of soft switching (blue line and yellow line); i.e., it shows that the voltage passing through the diode is active only when the source voltage of the MOSFET is equal to zero, which indicates the correct operation of the ZVS control. By checking this parameter, the correct operation of the entire system can now be seen in a laboratory environment using a prototype capable of proving the correct operation of the converter despite the small changes it was subjected to during the 1 kW test phase.
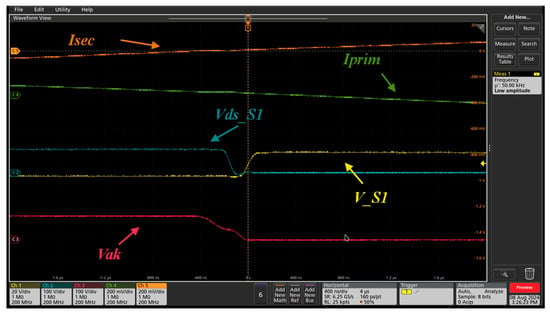
Figure 32.
Experimental test using the second transformer with 1 kW of power and 50 kHz of fsw. Yellow line: PWM signal at MOSFET 1 (V_S1); blue line: voltage signal (Vds); red line: anode-to-cathode (Vak) voltage signal; green line: current signal at the HFT input (Iprim); orange line: current signal at the HFT output (Isec).
5.3. Efficiency Results
Finally, it is possible to see in Figure 33 that the converter achieved high efficiency in a simulation environment using dynamic semiconductor models to get as close as possible to the real values. In the experimental validation, an efficiency of 96.6% was achieved with an operating power of 1 kW. This efficiency is expected to improve as the power increases, aligning with the system’s design specifications, where the soft-switching behavior will approach its optimal performance and optimal design.
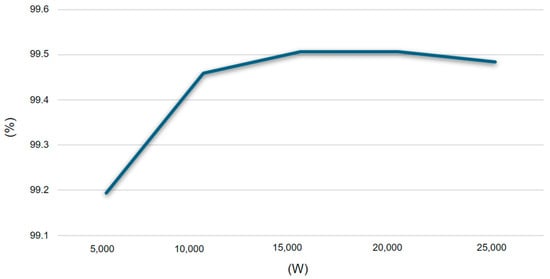
Figure 33.
Efficiency for an operating power range from 5 kW to 25 kW in the simulation environment.
6. Conclusions
The evolution of electric vehicles (EVs) and their widespread adoption presents considerable challenges related to charging times, vehicle autonomy, battery durability, and innovative fast-charging systems. Aligned with such evolution, this article presents the design and development of a laboratory prototype of a DC–DC resonant LLC converter for electric vehicle (EV) fast chargers. The various phases of the design and implementation process of a laboratorial prototype are outlined, with a special emphasis on the design of the HFT, which proves to be the most crucial part of the DC–DC resonant LLC converter. The critical significance of the high-power, high-frequency transformer (HFT) design, which exerts a profound influence on the system’s behavior, is presented in detail, considering various designs (e.g., in terms of the possibilities for the arrangement of the primary and secondary windings in the HFT), with the objective of identifying their effects on the DC–DC resonant LLC converter. In addition, the prototype was fully developed, considering the utilization of silicon carbide (SiC) power devices. A set of relevant simulation and experimental results are presented, validating the operating principle as well as the specific operating modes of the DC–DC resonant LLC converter when achieving zero-voltage switching (ZVS) and zero-current switching (ZCS). By combining these features, it is possible to reduce conduction and switching losses and, therefore, achieve a high-efficiency operation under distinct conditions of operation.
Author Contributions
Conceptualization, J.R. and S.A.; methodology, J.R.; formal analysis, V.M.; investigation, J.R. and S.A.; writing—original draft preparation, J.R.; writing—review and editing, J.R., S.A., S.C., G.R., J.L.A. and V.M. All authors have read and agreed to the published version of the manuscript.
Funding
This paper was supported by the Alliance for the Energy Transition (56) co-financed by the Recovery and Resilience Plan (PRR) through the European Union. This work has been supported by FCT—Fundação para a Ciência e Tecnologia within the R&D Unit Project of ALGORITMI Centre. This work is also part of the project that has received funding from the European Union’s Horizon Europe research and innovation program under the Marie Sklodowska-Curie Doctoral Networks grant agreement No 101072414 (E2GO). João Rocha has a scholarship with the reference ATE_BI_2023_02_CALG (2). Gonçalo Rego has a scholarship with the reference ATE_BI_2024_01_CALG (1). Sergio Coelho is supported by the doctoral scholarship 2021.08965.BD, granted by FCT—Fundação para a Ciência e Tecnologia.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Sathiyan, S.P.; Pratap, C.B.; Stonier, A.A.; Peter, G.; Sherine, A.; Praghash, K. Comprehensive Assessment of Electric Vehicle Development, Deployment, and Policy Initiatives to Reduce GHG Emissions: Opportunities and Challenges. IEEE Access 2022, 10, 53614–53639. [Google Scholar] [CrossRef]
- Van der Steen, M.; Van Deventer, P.; De Brujin, H.; van Twist, M.J.W. Governing and Innovation: The Transition to E-Mobility—A Dutch Perspective. World Electr. Veh. J. 2012, 5, 58–71. [Google Scholar] [CrossRef]
- International Energy Agency (IEA). Trends in Electric Cars—Global EV Outlook 2024—Analysis. Available online: https://www.iea.org/reports/global-ev-outlook-2024/trends-in-electric-cars (accessed on 18 November 2024).
- Amin, S.; Rocha, J.; Monteiro, V.; Costa, N. Three-Level Zero-Voltage Transition Interleaved Buck Converter with DC Transformer-based Isolation for EV Fast Charging Stations. In Technological Innovation for Human-Centric Systems, Proceedings of the 15th IFIP WG 5.5/SOCOLNET Advanced Doctoral Conference on Computing, Electrical and Industrial Systems, DoCEIS 2024, Caparica, Portugal, 3–5 July 2024; IFIP Advances in Information and Communication Technology; Camarinha-Matos, L.M., Ferrada, F., Eds.; Springer Nature: Cham, Switzerland, 2024; Volume 716, pp. 244–253. [Google Scholar] [CrossRef]
- Redondo-Iglesias, E.; Vinot, E.; Venet, P.; Pelissier, S. Electric Vehicle Range and Battery Lifetime: A Trade-Off. In Proceedings of the EVS32, Lyon, France, 19–22 May 2019; p. 9. Available online: https://hal.science/hal-02143273 (accessed on 18 November 2024).
- Omahne, V.; Knez, M.; Obrecht, M. Social Aspects of Electric Vehicles Research—Trends and Relations to Sustainable Development Goals. World Electr. Veh. J. 2021, 12, 15. [Google Scholar] [CrossRef]
- Bisoyi, S.; Terang, P.; Pathak, L.; Singh, A.; Singh, S.; Khare, R. Design of an EV Charging System with Improved Performance. In Sustainable Energy and Technological Advancements, Proceedings of the ISSETA Shillong, India, 24–25 September 2021; Springer: Singapore, 2022; pp. 541–558. [Google Scholar] [CrossRef]
- Trivedi, N.; Gujar, N.S.; Sarkar, S.; Pundir, S.P.S. Different fast charging methods and topologies for EV charging. In Proceedings of the 2018 IEEMA Engineer Infinite Conference (eTechNxT), New Delhi, India, 13–14 March 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Saadaoui, A.; Ouassaid, M.; Maaroufi, M. Overview of Integration of Power Electronic Topologies and Advanced Control Techniques of Ultra-Fast EV Charging Stations in Standalone Microgrids. Energies 2023, 16, 1031. [Google Scholar] [CrossRef]
- Safayatullah, M.; Elrais, M.T.; Ghosh, S.; Rezaii, R.; Batarseh, I. A Comprehensive Review of Power Converter Topologies and Control Methods for Electric Vehicle Fast Charging Applications. IEEE Access 2022, 10, 40753–40793. [Google Scholar] [CrossRef]
- Zhou, K.; Wu, Y.; Wu, X.; Sun, Y.; Teng, D.; Liu, Y. Research and Development Review of Power Converter Topologies and Control Technology for Electric Vehicle Fast-Charging Systems. Electronics 2023, 12, 1581. [Google Scholar] [CrossRef]
- Alhurayyis, I.; Elkhateb, A.; Morrow, J. Isolated and Nonisolated DC-to-DC Converters for Medium-Voltage DC Networks: A Review. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 7486–7500. [Google Scholar] [CrossRef]
- Wei, C.; Hu, Z.; Zhang, F.; Shao, J.; Narain, A. A SiC Based 30kW Three-Phase Interleaved LLC Resonant Converter for EV Fast Charger. In Proceedings of the PCIM Europe 2022—International Exhibition and Conference for Power Electronics, Intelligent Motion, Renewable Energy and Energy Management, Nürnberg, Germany, 10–12 May 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Sheng, B.; Zhou, X.; Liu, W.; Chen, Y.; Liu, Y.-F.; Sen, P.C. Analysis and Control of Three-Phase Interleaved SCC-LLC Resonant Converter Load Sharing Considering Component Tolerance. In Proceedings of the 2020 IEEE Energy Conversion Congress and Exposition (ECCE), Detroit, MI, USA, 11–15 October 2020; pp. 385–392. [Google Scholar] [CrossRef]
- Trung, T.H.; Linh, N.H.; Canh, H.V.; Pham, P.V. Unbalanced three-phase interleaved LLC resonant converter: Current phase angle balancing technique. Int. J. Power Electron. Drive Syst. 2022, 13, 1056. [Google Scholar] [CrossRef]
- Hasseni, S. Design and Control of Bidirectional Dual Active Bridge DC-DC Converter for Dynamic Electric Vehicle Charging and Vehicle-to-Grid Operations. Ph.D. Thesis, Glasgow Caledonian Univesiry, Glasgow, UK, 2021. [Google Scholar]
- Eyvazi, H.; Alimohammadi, Z.; Sheikhi, A.; Adelighalehtak, Y.; Poursheykh, T. Analysis of dual active bridge-based on-board battery charger for electric and hybrid vehicles. Int. J. Sci. Res. Arch. 2024, 12, 216–230. [Google Scholar] [CrossRef]
- Mathew, A.; Prasad, U.R.; Madhu, G.M.; Naik, N.; Vyjayanthi, C.; Subudhi, B. Performance Analysis of a Dual Active Bridge Converter in EV Charging Applications. In Proceedings of the 2022 International Conference for Advancement in Technology (ICONAT), Goa, India, 21–22 January 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Coelho, S.; Sousa, T.J.C.; Monteiro, V.D.F.; Machado, L.; Afonso, J.L.; Couto, C. Comparative Analysis and Validation of Different Modulation Strategies for a Dual Active Bridge Converter. Available online: https://repositorium.sdum.uminho.pt/handle/1822/80157 (accessed on 18 November 2024).
- Lim, S.-K.; Lee, H.-S.; Cha, H.-R.; Park, S.-J. Multi-Level DC-DC Converter for E-Mobility Charging Stations. IEEE Access 2020, 8, 48774–48783. [Google Scholar] [CrossRef]
- Kouro, S.; Malinowski, M.; Gopakumar, K.; Pou, J.; Franquelo, L.G.; Wu, B. Recent Advances and Industrial Applications of Multilevel Converters. IEEE Trans. Ind. Electron. 2010, 57, 2533–2580. Available online: https://ieeexplore.ieee.org/document/5482117 (accessed on 18 November 2024). [CrossRef]
- Ngo, T.; Nguyen-Quang, N. Improving Battery Charging Efficiency with Soft Switching Technique. In Proceedings of the 5th World Conference on Applied Sciences, Engineering & Technology, Ho Chi Minh City, Vietnam, 2–4 June 2016. [Google Scholar]
- Kim, D.-H.; Kim, M.-S.; Hussain Nengroo, S.; Kim, C.-H.; Kim, H.-J. LLC Resonant Converter for LEV (Light Electric Vehicle) Fast Chargers. Electronics 2019, 8, 362. [Google Scholar] [CrossRef]
- Elezab, A.; Zaied, O.; Abulnaga, A.; Narimani, M. High-Efficiency LLC Resonant Converter with Wide Output Range of 200–1000 V for DC-Connected EVs Ultra-Fast Charging Stations. IEEE Access 2023, 11, 33037–33048. [Google Scholar] [CrossRef]
- Israr, M.; Samuel, P. Study and Design of DC-DC LLC Full Bridge Converter for Electric Vehicle Charging Application. In Proceedings of the 5th International Conference on Power, Control & Embeded Systems (IPSCES), Allahabad, India, 6–8 January 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Rocha, J.; Amin, S.; Rego, G.; Monteiro, V. Step-by-Step Design of a LLC Resonant Converter for EV Fast Charging Applications. In Proceedings of the 2024 8th International Young Engineers Forum on Electrical and Computer Engineering (YEF-ECE), Caparica/Lisbon, Portugal, 5 July 2024; pp. 45–50. [Google Scholar] [CrossRef]
- Delgado, M.T.; Buja, G.; Czarkowski, D. Resonant Power Converters: An Overview with Multiple Elements in the Resonant Tank Network. IEEE Ind. Electron. Mag. 2016, 10, 21–45. [Google Scholar] [CrossRef]
- Liu, F.; Yan, J.; Ruan, X. Zero-Voltage and Zero-Current-Switching PWM Combined Three-Level DC-DC Converter. IEEE Trans. Ind. Electron. 2010, 57, 1644–1654. [Google Scholar] [CrossRef]
- Lalitha, A.S.; Chakraborty, S.; Kumar, S.S. A Zero Voltage Switching Based Soft Switching Boost DC-DC Converter for Vehicle to Grid Applications with Enhanced Energy Efficiency. In Proceedings of the 2022 3rd International Conference for Emerging Technology (INCET), Belgaum, India, 27–29 May 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Cittanti, D.; Gammeter, C.; Huber, J.; Bojoi, R. A Simplified Hard-Switching Loss Model for Fast-Switching Three-Level T-Type SiC Bridge-Legs. Electronics 2022, 11, 1686. [Google Scholar] [CrossRef]
- Abdulhakeem, M.; Sahid, M.R.; Sutikno, T. Overview of Soft-Switching DC-DC Converters. Int. J. Power Electron. Drive Syst. IJPEDS 2006, 9, 2006. [Google Scholar] [CrossRef]
- Riegler, B.; Mütze, A. Volume Comparison of Passive Components for Hard-Switching Current- and Voltage-Source-Inverters. In Proceedings of the 2021 IEEE Energy Conversion Congress and Exposition (ECCE), Vancouver, BC, Canada, 10–14 October 2021; pp. 1902–1909. [Google Scholar] [CrossRef]
- Ebli, M.; Pfost, M. An analysis of the switching behavior of GaN-HEMTs. In Proceedings of the 2017 International Symposium on Signals, Circuits, and Systems (ISSCS), Iasi, Romania, 13–14 July 2017; pp. 1–4. [Google Scholar] [CrossRef]
- Lee, I.-O.; Moon, G.-W. Soft-Switching DC-DC Converter With a Full ZVS Range and Reduced Output Filter for High-Voltage Applications. IEEE Trans. Power Electron. 2023, 28, 112–122. [Google Scholar] [CrossRef]
- Nadolny, Z. Design and Optimization of Power Transformer Diagnostics. Energies 2023, 16, 6466. [Google Scholar] [CrossRef]
- Khosrogorji, S.; Soori, S.; Torkaman, H. A new design strategy for DC-DC LLC resonant converter: Concept, modeling, and fabrication. Int. J. Circuit Theory Appl. 2019, 47, 1645–1663. [Google Scholar] [CrossRef]
- Sucameli, M.; Adragna, C. LLC Resonant Converters as Isolated Power Factor Corrector Pre-Regulators—Analysis and Performance Evaluation. Energies 2023, 16, 7114. [Google Scholar] [CrossRef]
- Liu, Y.-C.; Chen, C.; Chen, K.-D.; Syu, Y.-L.; Tsai, M.-C. High-Frequency LLC Resonant Converter with GaN Devices and Integrated Magnetics. Energies 2019, 12, 1781. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).