Abstract
Hydraulic fracturing is a key technology to build productivity in shale reservoirs; however, the evolution mechanism of fractures is extremely complex, especially in reservoirs with natural weak-planes development. There is an urgent need to conduct systematic research on the influence of natural weak planes on the vertical propagation of hydraulic fractures. This article takes the deep shale gas block of Luzhou in Southern Sichuan as the research basis and conducts different conditions of true triaxial large-scale hydraulic fracturing physical simulation experiments as well as the characteristics of natural weak-plane reservoir development and reservoir geological characteristics. This study clarifies the interaction mechanism between hydraulic fractures and natural weak planes and identifies the influence of parameters such as vertical stress difference, natural fracture strength, and approach angle on the propagation path of hydraulic fractures in reservoirs with developed natural weak planes, which help us gain a deeper insight into the interaction mechanism between fracture and weak plane. This study indicates that the widely developed natural weak planes in shale reservoirs significantly affect the initiation, propagation, and final distribution of hydraulic fractures. Based on pressure response characteristics, the fracture initiation types can be categorized into two scenarios: initiation along the direction of the maximum principal stress and initiation along natural weak planes. The propagation modes of fractures can be divided into three types: propagation perpendicular to natural weak planes, propagation parallel to natural weak planes, and multi-fracture propagation. The post-pressure fracture distribution patterns can be classified into four types: through-going fractures, T-shaped fractures, compound fractures, and complex fracture networks. The absence of developed natural weak planes, high vertical stress differences, high natural weak-plane cementation strength, and large intersection angles are favorable conditions for the vertical propagation of hydraulic fractures. The research findings enrich the fundamental theory of vertical propagation of hydraulic fractures in shale reservoirs with developed natural weak planes and provide a scientific basis for the formulation and optimization of stimulation schemes for deep shale reservoirs, contributing to better stimulation effects in the Southern Sichuan shale gas block.
1. Introduction
In recent years, with the rapid development of the economy, the contradiction in the supply structure of oil and gas resources (Table 1) has become apparent. As of 2023, China’s dependence on foreign oil and natural gas is about 72% and 42%, respectively [1,2,3]. The demand for energy and the degree of dependence on foreign energy have been increasing year by year. Improving the energy supply structure and promoting the diversified development of energy supply are of great strategic significance in relieving the contradiction between energy supply and demand [4,5,6,7]. Shale gas, as an important clean energy source, increasingly plays a key role in the structural transformation of the world’s energy. There is a world-leading amount of proven shale gas reserves in China, especially in the Sichuan Basin and its surrounding areas, which are rich in shale gas resources. Their good exploration value and development potential make them the focus of unconventional oil and gas resources exploration [8,9,10,11,12,13,14,15,16,17,18].

Table 1.
China’s energy structure in recent years.
Compared with conventional reservoir properties, shale reservoirs exhibit extremely low matrix porosity and permeability, and multi-stage hydraulic fracturing is commonly used to effectively enhance the production capacity of shale reservoirs [19,20,21,22,23]. Previous studies have shown that the fracture network formed after large-scale hydraulic fracturing is significantly different from the traditional dual-wing planar fractures, exhibiting a markedly complex reticulated structure [24,25,26,27,28]. Influenced by the widely developed natural weak planes (naturally occurring structural planes or interfaces that exist in the reservoir), shale reservoirs exhibit strong anisotropy, and the complexity of the hydraulic fracture evolution process and fracture propagation paths increases significantly [29,30,31,32,33,34,35]. During the hydraulic fracturing process, there are still challenges, such as insufficient understanding of fracture propagation patterns, limited actual reservoir modification range, and actual stimulation effects after fracturing that do not match expectations. Therefore, conducting in-depth research on the impact of rock properties and natural weak planes on the vertical propagation patterns of hydraulic fractures is essential for providing the scientific basis and technical support to predict fracture propagation behavior accurately and formulate effective fracturing design plans to improve the production efficiency of shale reservoirs in Southern Sichuan.
This study conducts true triaxial large-scale hydraulic fracturing physical simulation experiments with natural shale rock sample in Luzhou block under different conditions for reservoirs with developed natural weak planes and geological characteristics to discuss the height propagation law and fracture distribution shapes under different states of natural weak-plane development and various geological parameter conditions. This study clarifies the extent of the impact of parameters such as vertical stress differences, natural fracture strength, and approach angles on the propagation path of hydraulic fractures in reservoirs with developed natural weak planes, which provides a reference for further understanding the interaction mechanism of fracture and weak plane intersections.
2. Reservoir Characteristics and Physical Model Similarity Design
2.1. Development Characteristics of Natural Weak Planes in Shale Reservoirs
The widespread development of natural weak planes is a significant characteristic of shale reservoirs, mainly manifested as bedding planes, fracture systems, and faults, which form a complex fracture network in shale reservoirs from micro to macro scales. Based on the analysis of seismic data, outcrop observations, core samples, and experimental results, the scale of natural weak planes varies significantly, with a wide distribution range. Faults (Figure 1a) can reach scales of up to kilometers, whereas micro-fractures are typically only on the micrometer to millimeter scale. Natural fractures (Figure 1b) include sealed fractures, open fractures, and micro-fractures. Sealed fractures are filled or partially filled with minerals and have relatively high fracture strength, while open fractures are not filled and allow fluid passage, with a development scale similar to that of sealed fractures. Typically, open fractures can be connected to form fracture networks that extend over considerable distances. Bedding planes (Figure 1c) are horizontal interfaces formed during the sedimentation process, with thicknesses ranging from a few microns to a few millimeters, and are continuously distributed in the reservoir, with lengths that can reach hundreds or even thousands of meters. When intersecting with hydraulic fractures, bedding planes, natural fractures, and faults do not show significant differences in their mechanisms of action, mainly reflecting their characteristics and differences through development scale and the strength of the weak planes.

Figure 1.
Natural weak plane system in Shale Reservoir.
2.2. Physical Model Similarity Design
Similarity theory is the foundation for conducting physical simulations of hydraulic fracturing fracture propagation. According to the full three-dimensional hydraulic fracturing models by Cleary et al. and Clifton et al. [36,37,38,39], the similarity criteria to be followed when establishing indoor physical experiments are as follows:
The main parameter for the similarity criteria between physical model experiments and field hydraulic fracturing is the dimensionless fracture toughness k, which is calculated as follows:
In which , , and are combined parameters, and the calculation formula is as follows:
In the formula:
—dimensionless effective stress, dimensionless;
—effective stress, MPa;
—plane strain Young’s modulus, MPa;
—dimensionless time factor, dimensionless;
—velocity, m3/s;
—wellbore radius, m;
—dimensionless stress intensity factor, dimensionless;
—dimensionless elastic modulus factor, dimensionless;
k—dimensionless fracture toughness, dimensionless;
—flow rate, m3/s;
— fracturing fluid viscosity, mPa·s;
—plane strain Young’s modulus, MPa;
—Poisson’s ratio, dimensionless;
—fracture toughness, MPa·m1/2;
T—time, s.
The propagation of hydraulic fractures is almost entirely within the viscous propagation regime, where the corresponding dimensionless fracture toughness k needs to be significantly less than 1 [40]. The dimensionless fracture toughness calculated from experimental parameters should be close to the actual field construction conditions. In the calculation formula, the plane strain Young’s modulus, Poisson’s ratio, and rock fracture toughness are inherent properties of the rock. Increasing the viscosity of the fracturing fluid is the best way to obtain a lower dimensionless fracture toughness. Combining the rock mechanical parameters measured in the experiment and the pump injection rate of the true triaxial large-scale hydraulic fracturing experimental system, a fracturing fluid with a viscosity of 1.5 Pa·s glycerin is selected. At laboratory temperature, its density is 1.261 g/cm3, and its viscosity is 1500 mPa·s. The fracturing fluid is dyed blue with methylene blue as a tracer. The distribution range of the dyed fracturing fluid, combined with the results of acoustic emission monitoring, is used to determine the morphology of the hydraulic fractures after fracturing.
3. Experimental Plan Design
3.1. Model Design and Fabrication
Based on the development characteristics of natural weak planes in the target reservoir, the experiment designed shale samples with undeveloped natural weak planes (Figure 2), shale samples with developed orthogonal natural weak planes (Figure 3), and shale samples with developed non-orthogonal natural weak planes (Figure 4). The dimensions of the samples are 300 mm × 300 mm × 300 mm. A metal casing with a diameter of 20 mm and a length of 150 mm pre-exists in the middle of the samples. The casing end is horizontally cut to create a pre-existing fracture for the initiation of hydraulic fracturing. The annular space between the metal casing and the rock sample is consolidated with a high-strength epoxy resin to ensure that the fluid pumped during the fracturing experiment does not break through from the annulus. The stress loading during the experiment is shown in Figure 5.

Figure 2.
Experimental rock samples with undeveloped natural weak planes.

Figure 3.
Experimental rock samples with developed orthogonal natural weak planes.

Figure 4.
Experimental rock samples with developed non-orthogonal natural weak planes.
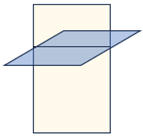
Figure 5.
Rock sample and stress loading direction diagram.
3.2. Experimental Equipment and Procedure
The experimental setup, as shown in Figure 6, consists of four parts: the rock sample triaxial gripping system, the displacement system, the pneumatic control system, and the data acquisition system. The system is capable of gripping rock samples with dimensions of 100 mm, 300 mm, and 500 mm. The pump injection rate ranges from 1 mL/min to 120 mL/min, the pump injection pressure ranges from 0 MPa to 100 MPa, the temperature control range is from room temperature to 100 °C, and the maximum loading stress is 80 MPa. Acoustic emission devices are used to monitor the fracture evolution process throughout the experiment, and the three-dimensional reconstruction of the fractures is performed in conjunction with the sectioning results of the rock samples. The experimental procedure is depicted in Figure 7.

Figure 6.
True triaxial hydraulic fracturing simulation system.

Figure 7.
Experimental procedure.
3.3. Experimental Plan
This experiment conducts vertical propagation experiments of hydraulic fractures under different rock and natural weak-plane properties to study the evolution characteristics of fractures as well as the intersection rules of fractures and weak planes under conditions such as the presence or absence of natural weak planes, different vertical stress differences, different consolidation strengths of natural weak planes, and different approaching angles. The average Young’s modulus, the average Poisson’s ratio, the average compressive strength, and the average tensile strength are 30 GPa, 0.25, 145 MPa, and 4 MPa, respectively. The Young’s modulus and Poisson’s ratio of naturally developed weak face samples have no significant difference from those of undeveloped weak face samples, the average compressive strength is significantly reduced to 69 MPa, and the average tensile strength is 1 MPa. The minimum principal stress in the experiment is set to 10 MPa, with the vertical stress difference being the difference between the vertical stress and the minimum principal stress. The experimental pump injection rate is 20 mL/min. The experimental numbers and plans are shown in Table 2.

Table 2.
Experimental scheme.
4. Experimental Results Analysis
Based on the acoustic emission monitoring results and the sectioning results of rock samples after the experiment, this study achieves a three-dimensional reconstruction of the hydraulic fractures. The fractured rock samples, acoustic emission monitoring results, three-dimensional reconstruction diagrams of the hydraulic fractures, and the hydraulic fracturing pressure curves for each rock sample are shown in Figure 8.

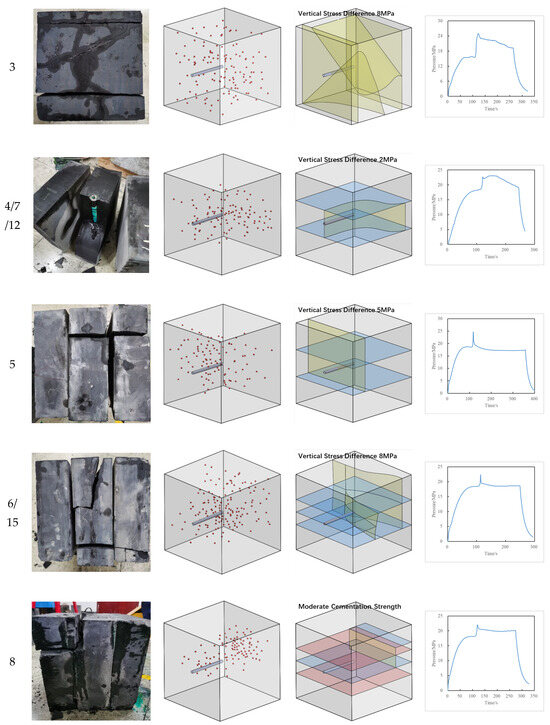
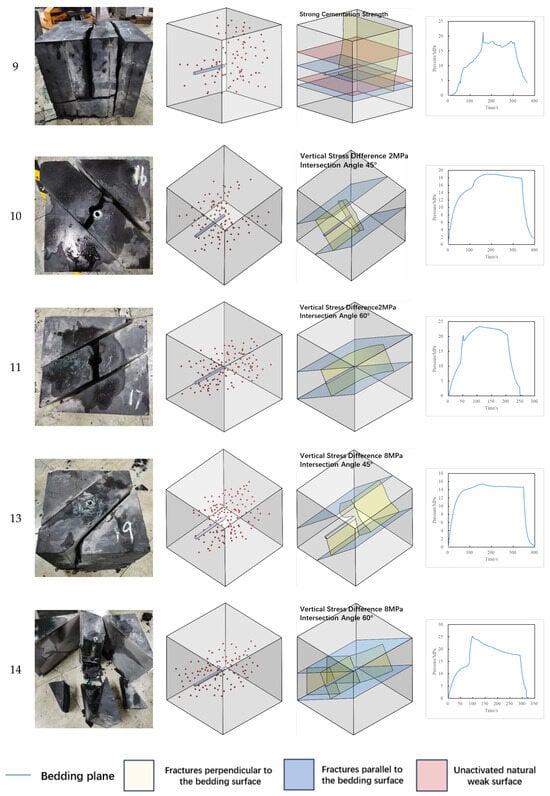
Figure 8.
Experimental results.
4.1. Analysis of Fracture Evolution Characteristics
- (1)
- Initiation Characteristics of Hydraulic Fractures
The fracture evolution process includes three stages: fracture initiation, fracture propagation, and fracture closure. There is a clear fracture indication between the first and second stages of the pressure curves for rock samples numbered 2, 3, 4, 5, 6, 8, 9, 11, and 14. The pump pressure peaks and then rapidly decreases, with significant pressure fluctuations (Figure 9a). The distribution range of the fracture initiation pressure for the rock samples is from 20.2 MPa to 26.7 MPa, with an average fracture initiation pressure of 23.25 MPa. The initiation mode is perpendicular to the bedding plane. When the cementation degree of the rock layer near the perforated casing is strong or the stress difference is large, hydraulic fractures initiate in this manner. Rock samples numbered 1, 10, and 13 do not show a clear fracture indication between the first and second stages of their pressure curves (Figure 9b). The pump pressure changes caused by the fracture initiation are not significant, and the initiation mode is along natural weak planes. After the casing pressure reaches a certain level, the micro-fractures near the casing open and continue to extend. In reservoirs with developed bedding planes, faults, and natural weak planes, hydraulic fractures may initiate in this manner during hydraulic fracturing. Generally, the number of fracture strips is positively correlated with the fracture indication. Rock sample number 2 has two fractures that correspond to the number of its fracture indications, and its initiation mode should be perpendicular to the bedding plane.

Figure 9.
Pressure characteristics of different hydraulic fracturing initiation modes.
- (2)
- Hydraulic Fracture Propagation and Distribution Characteristics
As shown in Figure 10 and Figure 11, based on the path of fracture propagation during the hydraulic fracturing process and the pattern of pressure changes, hydraulic fracture propagation types can be categorized into three types: propagation perpendicular to natural weak planes, propagation parallel to natural weak planes, and propagation along multiple fractures. As shown in Figure 11, the pressure curve exhibits characteristics of increase or relative stability. After the fracture initiates, it extends in a direction perpendicular to the natural weak planes. During the propagation process, the fracture must open the reservoir rocks, which requires overcoming significant resistance. If natural weak planes are not developed in a reservoir, a transverse fracture (Table 3a) will form after fracturing; otherwise, it will form either a transverse fracture (Table 3b) or a composite fracture (Table 3d) depending on whether the hydraulic fracture activates the natural weak planes. The direction of the maximum principal stress in the reservoir is the main controlling factor for the propagation direction of this type of hydraulic fracture.

Figure 10.
Pressure curve of hydraulic fracture along the maximum principal stress direction.

Figure 11.
Pressure curve of hydraulic fracture along natural weak planes and multiple fractures.

Table 3.
Hydraulic fracture propagation and distribution characteristics.
As shown in Figure 12, the pressure curves exhibit varying degrees of pressure drops (0.7 MPa to 7 MPa). When the direction of hydraulic fracture propagation is influenced by the developed natural weak planes (bedding planes, natural fractures) in the reservoir and becomes the main controlling factor for the direction of fracture propagation, the hydraulic fracture will activate the natural fracture and turn along the natural weak plane upon encountering it. The hydraulic fracturing ultimately forms an I-shape fracture (or T-shaped fracture) (Table 3c). When the hydraulic fracture initiates and extends along multiple fractures, the hydraulic fractures ultimately form a complex fracture network (Table 3e).
4.2. Analysis of Influencing Factors
- (1)
- Development of Natural Weaknesses
Figure 9 shows two sets of experiments simulating the hydraulic fracture propagation under conditions with developed and undeveloped natural weaknesses in the reservoir. The experimental results indicate that in the samples without pre-existing natural weaknesses (1#, 2#, and 3#), except for sample 1#, where the hydraulic fracturing activated the shale bedding plane and fracture propagated along the bedding plane (Figure 12a), samples 2# and 3# both penetrated the entire rock sample perpendicular to the natural weak planes, forming a transverse fracture (Figure 12b,c), while in the samples with pre-existing natural weaknesses (4#, 5#, and 6#), the vertical propagation distance of the fracture was limited by the pre-existing natural weaknesses, with at least one direction of vertical propagation being hindered. Among them, sample 4# had both upward and downward fracture propagations limited, and the post-fracturing fracture distribution exhibited characteristics of an I-shaped fracture (Figure 12d). Samples 5# and 6# had their upper hydraulic fractures breaking through the limitations of the natural weaknesses, while the lower fracture propagations were obstructed, resulting in a post-fracturing fracture distribution exhibiting characteristics of a T-shaped fracture (Figure 12e,f). The fracture height was generally lower than that of the corresponding samples without pre-existing weaknesses. The widespread development of natural weaknesses in the reservoir is an unfavorable factor for the interlayer propagation of hydraulic fractures, limiting the vertical propagation height of the hydraulic fractures.

Figure 12.
The fracture distribution patterns after pressure in different states of natural weak-plane development.
- (2)
- Vertical Stress Difference
The vertical stress difference refers to the difference between the vertical geostress and the minimum horizontal principal stress. In this experiment, three levels of stress differences were set: low stress differences (2 MPa), medium stress differences (5 MPa), and high stress differences (8 MPa). Samples 1#, 2#, and 3#, as well as 4#, 5#, and 6#, represent the fracturing experimental results of rock samples with undeveloped and developed natural weakness planes under different stress difference conditions, respectively. As the vertical stress difference increases from 2 MPa to 8 MPa, the final distribution patterns of fractures in samples 1#, 2#, and 3# gradually change from T-shaped fractures to transverse fractures, while those in samples 4#, 5#, and 6# gradually change from I-shaped fractures to T-shaped fractures. When the vertical stress difference is small, the geostress has less constraint on the fracture propagation direction, and hydraulic fractures are more likely to activate natural weaknesses and turn along them. At this time, the anisotropy of the rock (bedding, faults, etc.,) becomes the main controlling factor for the vertical propagation of fractures. As the vertical stress difference increases, the control of stress on the propagation of hydraulic fractures gradually strengthens, and the directionality of fracture propagation becomes more pronounced, with the vertical stress difference becoming the main controlling factor for vertical propagation.
Figure 13 shows the number of post-fracturing fracture strips under vertical stress differences of 2 MPa and 8 MPa. Under the 2 MPa stress condition, the post-fracturing fracture strips for natural weak planes of 45°, 60°, and 90°are 4, 3, and 3, respectively. Under the 8MPa stress condition, the post-fracturing fracture strips for natural weak planes of 45°, 60°, and 90° are 5, 6, and 5, respectively. There are more post-fracturing fracture strips under the 8 MPa condition, and the fracture distribution pattern is more complex. Under high-stress conditions, the internal damage in shale reservoirs is intensified. Although hydraulic fractures are constrained by the maximum principal stress and extend along the direction of the maximum principal stress, the natural weak planes produced by stress damage under high-stress conditions have a significant impact on the propagation of hydraulic fractures, resulting in a more complex final distribution pattern of post-fracturing fractures compared to low-stress conditions.

Figure 13.
The number of post-stress fractures under different stress conditions.
- (3)
- Natural Weak-Plane Cementation Strength
In this experiment, three levels of cementation strength for natural weak planes were set: weak (sample 7), moderate (sample 8), and strong (sample 9). After the experiment, their respective tensile strengths were measured to be 0.511 MPa, 0.991 MPa, and 2.1 MPa. As shown in Figure 14, natural weak planes with lower strength tend to cause hydraulic fractures to turn along the natural weak planes, limiting the vertical propagation height of the fractures and resulting in the formation of I-shaped fractures after fracturing; natural weak planes with moderate and strong cementation strengths have higher tensile and shear strengths and are less likely to be activated by hydraulic fractures after intersection, typically showing an intersection result that crosses but does not activate the natural weak planes, leading to the formation of transverse fractures after fracturing. The greater the cementation strength of natural weak planes, the more conducive it is to the vertical propagation of hydraulic fractures.

Figure 14.
Fracture distribution patterns under varying weak-plane cementation strengths.
- (4)
- Intersection Angle
Figure 15 shows the results of the interaction between hydraulic fractures and natural weak planes at intersection angles of 45°, 60°, and 90° under vertical stress differences of 2 MPa and 8 MPa. Under the 2 MPa condition, all three groups of experiments with intersection angles of 45°, 60°, and 90° demonstrated that the natural weak planes were activated upon intersection with the hydraulic fractures. The hydraulic fractures followed the natural weak planes and continued propagating, exhibiting characteristics of I-shaped fractures. Under the 8 MPa condition, the two groups of experiments with intersection angles of 45° and 60° showed consistent fracture propagation patterns, also forming I-shaped fractures after fracturing. However, in the group with an intersection angle of 90°, the hydraulic fracture activated the natural weak planes but maintained its original direction of propagation, penetrating the natural weak planes to form a composite fracture. The larger the intersection angle between the hydraulic fracture and the natural weak planes, the more conducive it is to the vertical propagation of the hydraulic fracture.

Figure 15.
Fracture distribution patterns at different intersection angles.
In summary, the statistical results of all experiments are shown in Table 4. On the one hand, experiments 2#, 3#, 5#, 6#, 8#, and 9# had hydraulic fractures that vertically extended beyond the limitations of natural weak planes. The absence of developed natural weak planes, high vertical stress differences, high cementation strength of natural weak planes, and large intersection angles are favorable conditions for the vertical propagation of hydraulic fractures. On the other hand, experiments 1#, 4#, 10#, 11#, 13#, and 14# had hydraulic fractures that were captured by the widely developed natural weak planes in the shale reservoir during their vertical propagation, with the vertical propagation of the fractures being hindered. The presence of developed natural weak planes, low vertical stress differences, low cementation strength of natural weak planes, and small intersection angles can limit the vertical propagation of hydraulic fractures.

Table 4.
Statistics of experimental results.
5. Conclusions
(1) A true triaxial large-scale hydraulic fracturing physical simulation device was utilized to investigate the impact of natural weak planes in shale reservoirs on the propagation of hydraulic fractures. This study elucidated the modes of fracture initiation, propagation characteristics, and post-fracturing fracture distribution under various influencing factors. These findings enhance our understanding of the interaction mechanisms between hydraulic fractures and natural weak planes.
(2) The types of fracture initiation can be divided into two types: initiation along the direction of maximum principal stress and initiation along natural weak planes. The modes of fracture propagation can be divided into three types: propagation perpendicular to natural weak planes, propagation parallel to natural weak planes, and propagation along multiple fractures. The post-fracturing fracture geometry can be categorized into four types: transverse fractures, I-shaped fractures, composite fractures, and complex fracture networks.
(3) The widely developed natural weak planes in shale reservoirs have a significant impact on the vertical propagation of hydraulic fractures. The fracture evolution process is complex and influenced by many factors, among which the absence of developed natural weak planes, high vertical stress differences, high cementation strength of natural weak planes, and large intersection angles are favorable conditions for the vertical propagation of hydraulic fractures. Under conditions of high vertical stress differences, the fracture distribution morphology becomes more complex.
Author Contributions
Methodology, Z.F. and X.C.; Formal analysis, Y.L.; Investigation, J.Z. and L.H.; Writing—original draft, Y.H.; Writing—review & editing, Y.L.; Visualization, L.H.; Supervision, X.C.; Funding acquisition, Y.L. and X.C. All authors have read and agreed to the published version of the manuscript.
Funding
This study was supported by the National Natural Science Foundation of China (U23B20156), National Natural Science Foundation of China (No. 52204052), the Science and Technology Cooperation Project of the CNPC-SWPU Innovation Alliance, and the Sichuan Science and Technology Program (No. 2023NSFSC0933).
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author(s).
Conflicts of Interest
Authors Yitao Huang, Juhui Zhu, Le He and Zeben Fang were employed by the company Downhole Service Company of CNPC Chuanqing Drilling Engineering Company Limited. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Qian, X.; Lu, R.; Luo, L. Global oil and gas industry in 2023 and outlook for 2024. Int. Pet. Econ. 2024, 32, 1–13. [Google Scholar]
- Chen, X.; Huang, Y.; Li, Y.; Shen, C. Numerical simulation study on evolution law of three-dimensional fracture network in unconventional reservoirs. Front. Energy Res. 2024, 11, 1337069. [Google Scholar] [CrossRef]
- Gao, Y.; Wang, B.; Hu, Y.; Gao, Y.; Hu, A. Development of China’s natural gas: Review 2023 and outlook 2024. Nat. Gas Ind. 2024, 44, 166–177. [Google Scholar]
- Lei, L.; Li, Y.; Peng, Z. Viewing China’s Oil and Gas Resource Strategy from the Development Situation of World Oil and Gas Resources. Sino-Glob. Energy 2019, 24, 1–7. [Google Scholar]
- Chen, J.; Wang, N.; Tang, H.; Li, J.; Xiong, B. Impact of sustained low oil prices on China’s oil & gas industry system and coping strategies. Nat. Gas Ind. 2016, 36, 1–6. [Google Scholar]
- Boyer, C.; Clark, B.; Jochen, V.; Lewis, R.; Miller, C.K. Shale gas: A global resource. Oilfield Rev. 2011, 23, 28–39. [Google Scholar]
- Rodriguez, N.D.; Philp, R.P. Geochemical characterization of gases from the Mississippian Barnett shale, Fort Worth basin, Texas. AAPG Bull. 2010, 94, 1641–1656. [Google Scholar] [CrossRef]
- Zhang, F.; Li, G.; Zheng, X.; Wu, Q.; Li, Z.; Qi, Z.; Wang, J.; Zhang, L. Enlightenment from the post shale revolution era in North America. China Pet. Explor. 2022, 27, 26–39. [Google Scholar]
- Dou, L.; Li, D.; Wen, Z.; Wang, Z.; Mi, S.; Zhang, Q. History and outlook of global oil and gas resources evaluation. Acta Pet. Sin. 2022, 43, 1035–1048. [Google Scholar]
- Sohail, G.M.; Radwan, A.E.; Mahmoud, M. A review of Pakistani shales for shale gas exploration and comparison to North American shale plays. Energy Rep. 2022, 8, 6423–6442. [Google Scholar] [CrossRef]
- Bellani, J.; Verma, H.K.; Khatri, D.; Makwana, D.; Shah, M. Shale gas: A step toward sustainable energy future. J. Pet. Explor. Prod. Technol. 2021, 11, 2127–2141. [Google Scholar] [CrossRef]
- Syed, F.I.; Alnaqbi, S.; Muther, T.; Dahaghi, A.K.; Negahban, S. Smart shale gas production performance analysis using machine learning applications. Pet. Res. 2022, 7, 21–31. [Google Scholar] [CrossRef]
- Zhao, J.; Ren, L.; Jiang, T.; Hu, D.; Wu, L.; Wu, J.; Yin, C.; Li, Y.; Hu, Y.; Lin, R.; et al. Ten years of gas shale fracturing in China: Review and prospect. Nat. Gas Ind. B 2022, 9, 158–175. [Google Scholar] [CrossRef]
- Omari, A.; Wang, C.; Li, Y.; Xu, X. The progress of enhanced gas recovery (EGR) in shale gas reservoirs: A review of theory, experiments, and simulations. J. Pet. Sci. Eng. 2022, 213, 110461. [Google Scholar] [CrossRef]
- Guo, X.; Borjigin, T.; Wei, X.; Yu, L.; Lu, X.; Sun, L.; Wei, F. Occurrence mechanism and exploration potential of deep marine shale gas in Sichuan Basin. Acta Pet. Sin. 2022, 43, 453–468. [Google Scholar]
- Nie, H.; He, Z.; Liu, G.; Du, W.; Wang, R.; Zhang, G. Genetic mechanism of high-quality shale gas reservoirs in the Wufeng–LongmaxiFms in the Sichuan Basin. Nat. Gas Ind. B 2021, 8, 24–34. [Google Scholar] [CrossRef]
- Zhai, G.; Wang, Y.; Zhou, Z.; Yu, S.; Chen, X.; Zhang, Y. Exploration and research progress of shale gas in China. China Geol. 2018, 1, 257–272. [Google Scholar] [CrossRef]
- Solarin, S.A.; Gil-Alana, L.A.; Lafuente, C. An investigation of long range reliance on shale oil and shale gas production in the US market. Energy 2020, 195, 116933. [Google Scholar] [CrossRef]
- Lecampion, B.; Bunger, A.; Zhang, X. Numerical methods for hydraulic fracture propagation: A review of recent trends. J. Nat. Gas Sci. Eng. 2018, 49, 66–83. [Google Scholar] [CrossRef]
- Sampath, K.; Perera, M.S.A.; Ranjith, P.G. Theoretical overview of hydraulic fracturing break-down pressure. J. Nat. Gas Sci. Eng. 2018, 58, 251–265. [Google Scholar] [CrossRef]
- Liu, X.; Rasouli, V.; Guo, T. Numerical simulation of stress shadow in multiple cluster hydraulic fracturing in horizontal wells based on lattice modelling. Eng. Fract. Mech. 2020, 238, 107278. [Google Scholar] [CrossRef]
- Li, N.; Zhang, S.; Zou, Y.; Ma, X.; Zhang, Z.; Li, S.; Chen, M.; Sun, Y. Acoustic Emission Response of Laboratory Hydraulic Fracturing in Layered Shale. Rock Mech. Rock Eng. 2018, 51, 3395–3406. [Google Scholar] [CrossRef]
- AlTammar, M.J.; Agrawal, S.; Sharma, M.M. Effect of geological layer properties on hydraulic-fracture initiation and propagation: An experimental study. SPE J. 2019, 24, 757–794. [Google Scholar] [CrossRef]
- Li, Y.; Hu, W.; Zhang, Z.; Zhang, Z.; Shang, Y.; Han, L.; Wei, S. Numerical simulation of hydraulic fracturing process in a naturally fractured reservoir based on a discrete fracture network model. J. Struct. Geol. 2021, 147, 104331. [Google Scholar] [CrossRef]
- Huang, L.; Tan, J.; Fu, H.; Liu, J.; Chen, X.; Liao, X.; Wang, X.; Wang, C. The non-plane initiation and propagation mechanism of multiple hydraulic fractures in tight reservoirs considering stress shadow effects. Eng. Fract. Mech. 2023, 292, 109570. [Google Scholar] [CrossRef]
- Chen, X.; Zhao, J.; Li, Y.; Yan, W.; Zhang, X. Numerical simulation of simultaneous hydraulic fracture growth within a rock layer. Implic. Stimul. Low-Permeability Reserv. 2019, 124, 13227–13249. [Google Scholar]
- Yaghoubi, A. Hydraulic fracturing modeling using a discrete fracture network in the Barnett Shale. Int. J. Rock Mech. Min. Sci. 2019, 119, 98–108. [Google Scholar] [CrossRef]
- Zheng, P.; Xia, Y.; Yao, T.; Jiang, X.; Xiao, P.; He, Z.; Zhou, D. Formation mechanisms of hydraulic fracture network based on fracture interaction. Energy 2022, 243, 123057. [Google Scholar] [CrossRef]
- Wang, H. Hydraulic fracture propagation in naturally fractured reservoirs: Complex fracture or fracture networks. J. Nat. Gas Sci. Eng. 2019, 68, 102911. [Google Scholar] [CrossRef]
- Rahimi-Aghdam, S.; Chau, V.-T.; Lee, H.; Nguyen, H.; Li, W.; Karra, S.; Rougier, E.; Viswanathan, H.; Srinivasan, G.; Bažant, Z.P. Branching of hydraulic cracks enabling permeability of gas or oil shale with closed natural fractures. Proc. Natl. Acad. Sci. USA 2019, 116, 1532–1537. [Google Scholar] [CrossRef] [PubMed]
- Zhang, F.; Damjanac, B.; Maxwell, S. Investigating hydraulic fracturing complexity in naturally fractured rock masses using fully coupled multiscale numerical modeling. Rock Mech. Rock Eng. 2019, 52, 5137–5160. [Google Scholar] [CrossRef]
- Kolawole, O.; Ispas, I. Interaction between hydraulic fractures and natural fractures: Current status and prospective directions. J. Pet. Explor. Prod. Technol. 2020, 10, 1613–1634. [Google Scholar] [CrossRef]
- Taleghani, A.D.; Gonzalez-Chavez, M.; Yu, H.; Asala, H.; Hao, H. Numerical simulation of hydraulic fracture propagation in naturally fractured formations using the cohesive zone model. J. Pet. Sci. Eng. 2018, 165, 42–57. [Google Scholar] [CrossRef]
- Zhou, Z.; Hou, Z.; Guo, Y.; Zhao, H.; Wang, D.; Qiu, G.; Guo, W. Experimental study of hydraulic fracturing for deep shale reservoir. Eng. Fract. Mech. 2024, 37, 110259. [Google Scholar] [CrossRef]
- Tang, J.; Wu, K.; Li, Y.; Hu, X.; Liu, Q.; Ehlig-Economides, C. Numerical investigation of the interactions between hydraulic fracture and bedding planes with non-orthogonal approach angle. Eng. Fract. Mech. 2018, 200, 1–16. [Google Scholar] [CrossRef]
- Cleary, M.P. Analysis of Mechanisms and Procedures for Producing Favourable Shapes of Hydraulic Fractures. In Proceedings of the SPE Annual Technical Conference and Exhibition, Dallas, TX, USA, 21–24 September 1980. [Google Scholar]
- Settari, A.; Cleary, M.P. Development and Testing of a Pseudo-Three-Dimensional Model of Hydraulic Fracture Geometry. SPE Prod. Eng. 1986, 1, 449–466. [Google Scholar] [CrossRef]
- Clifton, R.J.; Abou-Sayed, A.S. On the Computation of the Three-Dimensional Geometry of Hydraulic Fractures. In Proceedings of the Symposium on Low Permeability Gas Reservoirs, Denver, CO, USA, 20–22 May 1979. [Google Scholar]
- Clifton, R.J.; Abou-Sayed, A.S. A Variational Approach to the Prediction of the Three-Dimensional Geometry of Hydraulic Fractures. In Proceedings of the SPE/DOE Low Permeability Gas Reservoirs Symposium, Denver, CO, USA, 27–29 May 1981. [Google Scholar]
- Chen, X. Numerical Investigation of Non-Uniform Fracture Growth in Multi-Stage Hydraulic Fracturing. Ph.D. Thesis, Southwest Petroleum University, Chengdu, China, 2018. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).