Application of State Models in a Binary–Temporal Representation for the Prediction and Modelling of Crude Oil Prices
Abstract
1. Introduction
2. Literature Overview
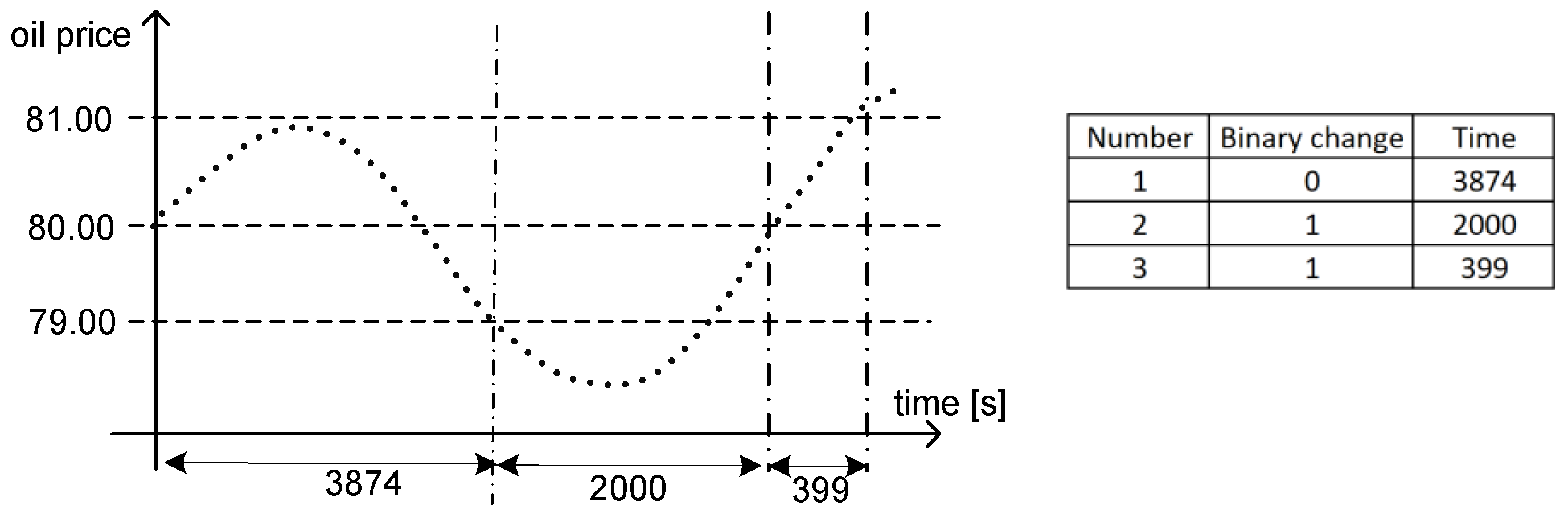
3. Representation of Crude Oil Rates
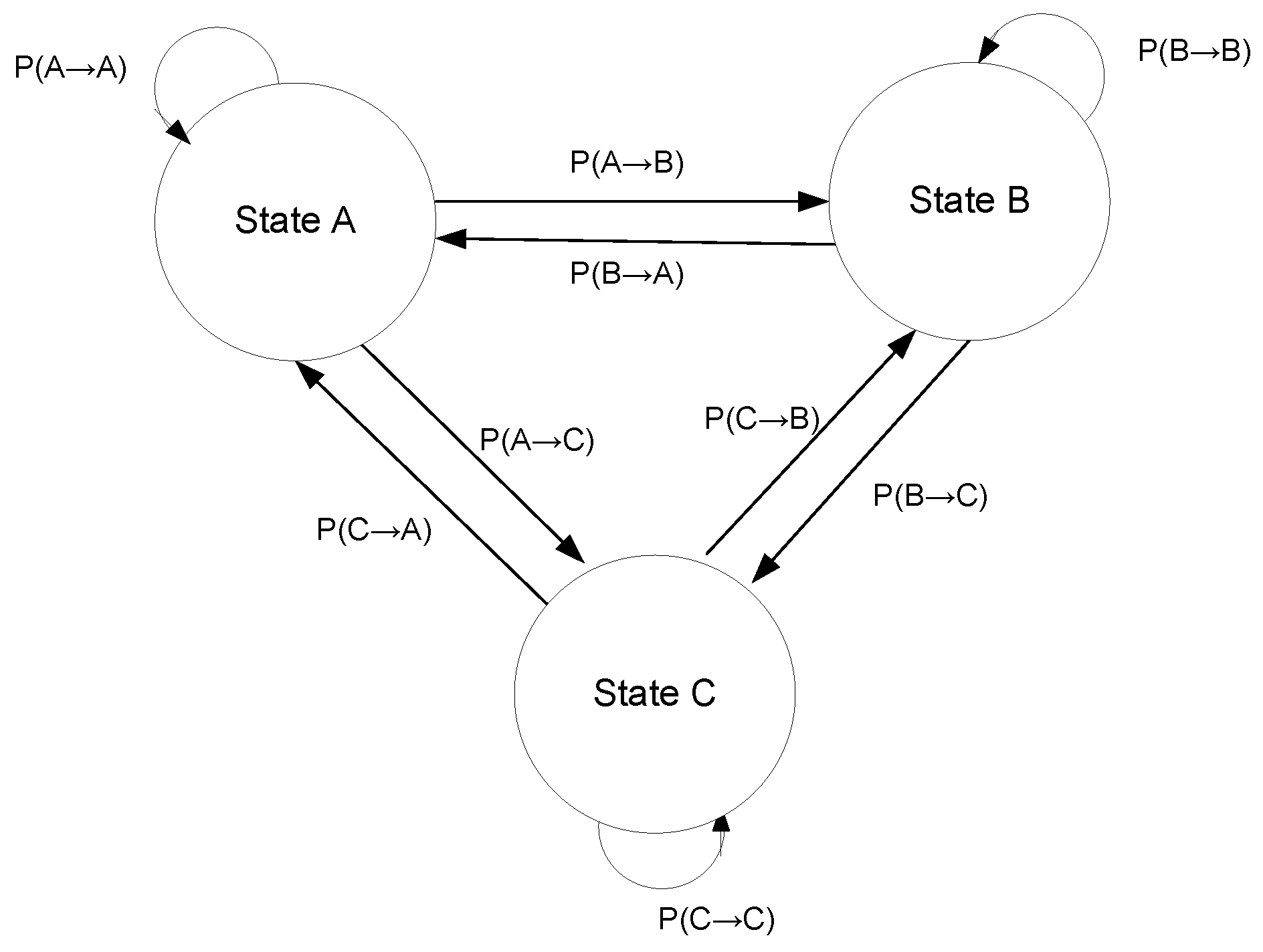
4. Modelling of Crude Oil Rates Using State Models in a Binary–Temporal Representation
Assumptions of State Modelling
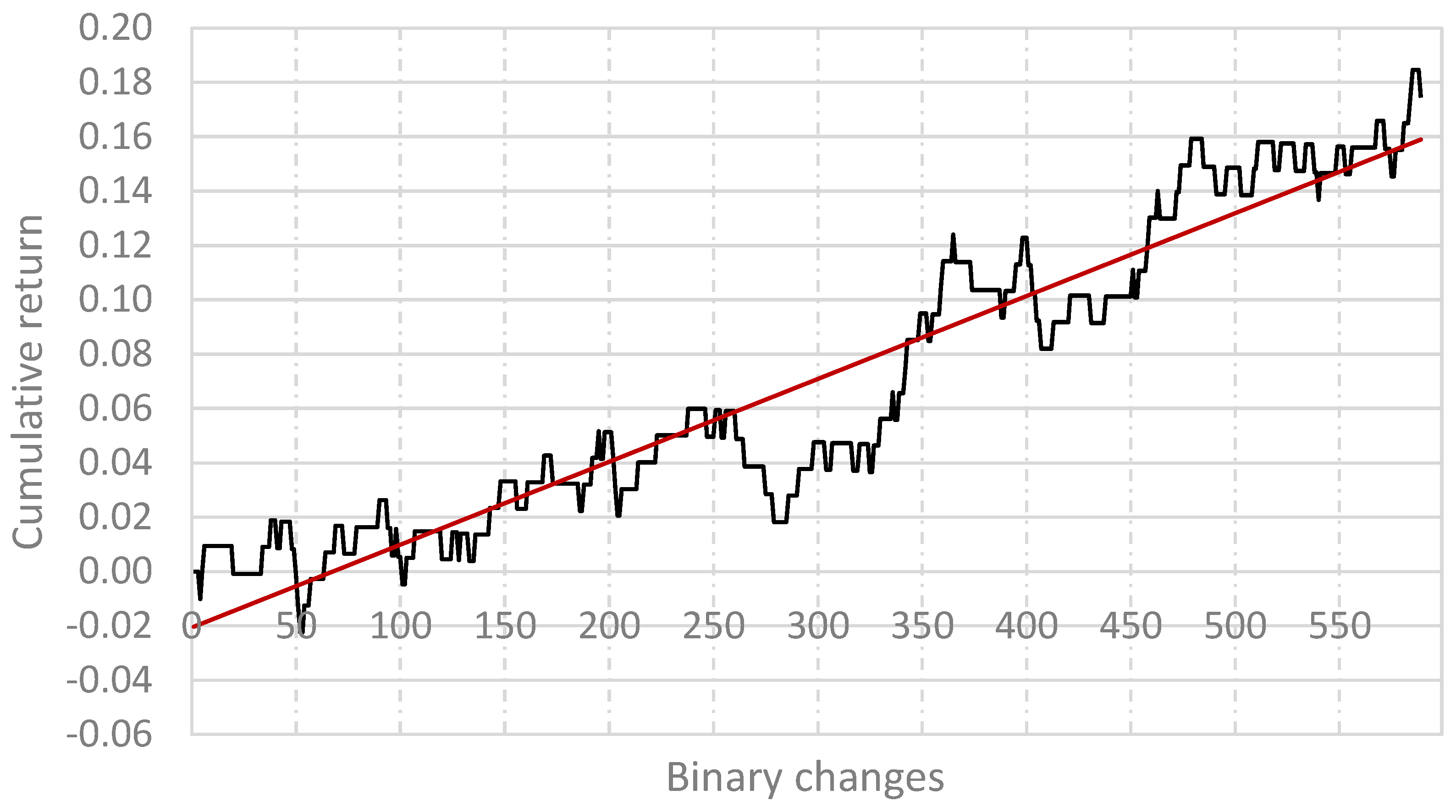
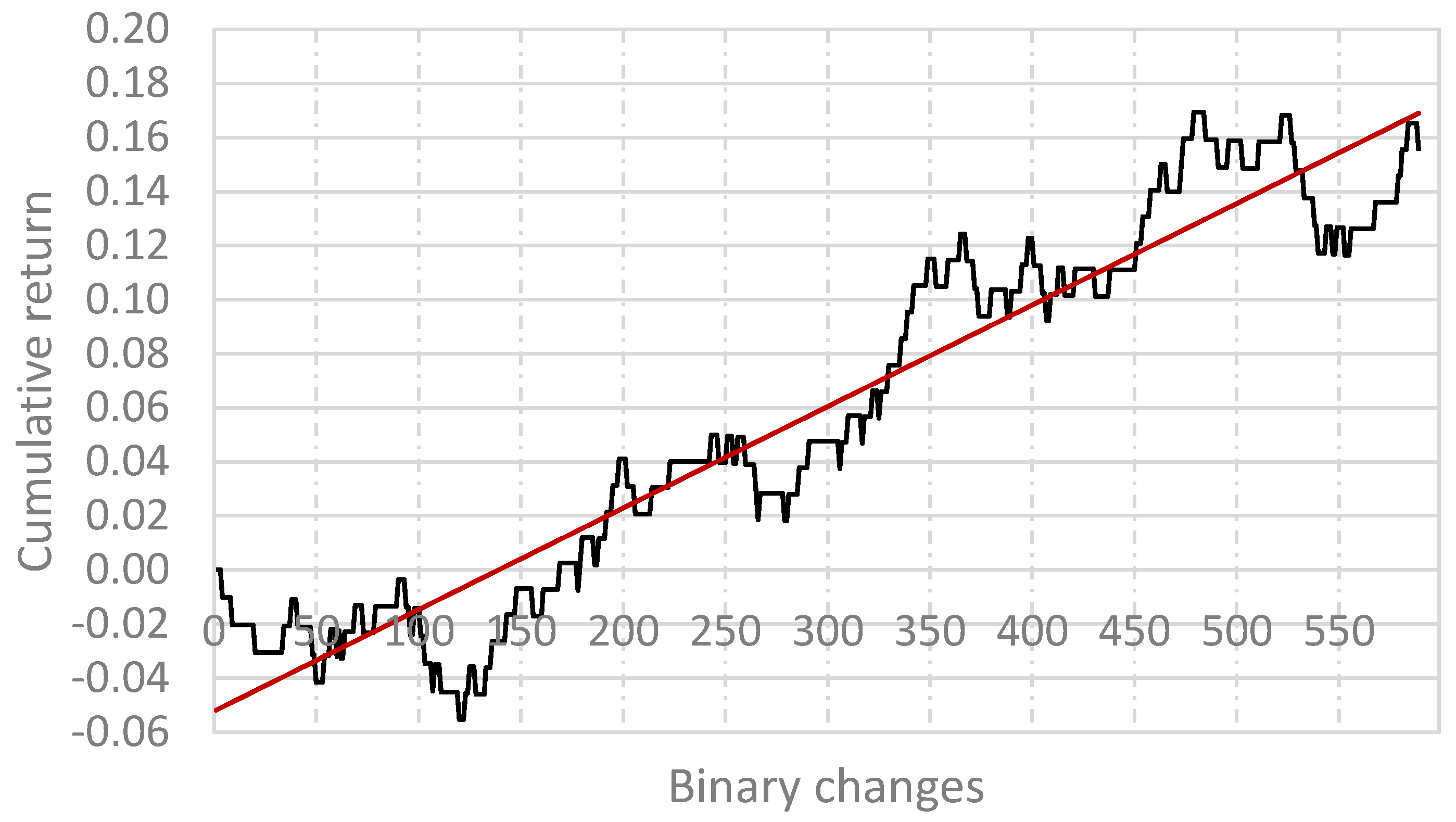
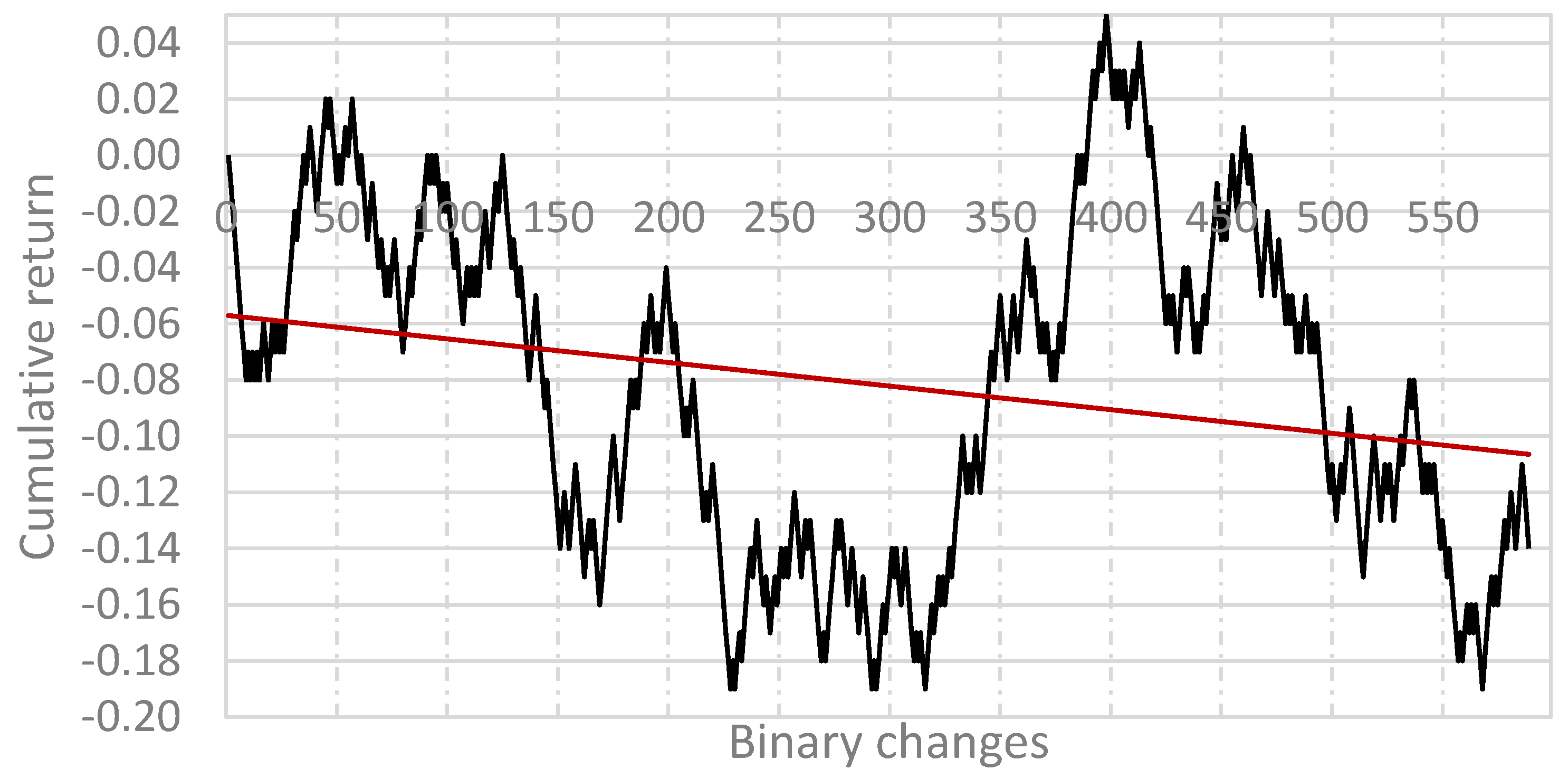
5. Construction, Verification and Optimization of Algorithmic Trading Systems Based on State Models
5.1. Construction of an Algorithmic Trading System
5.2. Data
5.3. Optimization Model Parameters
5.4. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kilian, L. The economic effects of energy price shocks. J. Econ. Lit. 2008, 46, 871–909. [Google Scholar] [CrossRef]
- van de Ven, D.J.; Fouquet, R. Historical energy price shocks and their changing effects on the economy. Energy Econ. 2017, 62, 204–216. [Google Scholar] [CrossRef]
- Barrera-Rey, F.; Seymour, A. The Brent Contract for Differences (CFD): A Study of an Oil Trading Instrument, Its Market and Its Influence on the Behaviour of Oil Prices; Oxford Institute for Energy Studies: Oxford, UK, 1996. [Google Scholar]
- Stasiak, M.D.; Staszak, Ż. Modelling and Forecasting Crude Oil Prices Using Trend Analysis in a Binary-Temporal Representation. Energies 2024, 17, 3361. [Google Scholar] [CrossRef]
- Tiwari, A.K.; Trabelsi, N.; Alqahtani, F.; Hammoudeh, S. Analysing systemic risk and time-frequency quantile dependence between crude oil prices and BRICS equity markets indices: A new look. Energy Econ. 2019, 83, 445–466. [Google Scholar] [CrossRef]
- Mensi, W.; Yousaf, I.; Vo, X.V.; Kang, S.H. Asymmetric spillover and network connectedness between gold, BRENT oil and EU subsector markets. J. Int. Financ. Mark. Inst. Money 2022, 76, 101487. [Google Scholar] [CrossRef]
- Salamai, A.A. Deep learning framework for predictive modelling of crude oil price for sustainable management in oil markets. Expert Syst. Appl. 2023, 211, 118658. [Google Scholar] [CrossRef]
- Awijen, H.; Ben Ameur, H.; Ftiti, Z.; Louhichi, W. Forecasting oil price in times of crisis: A new evidence from machine learning versus deep learning models. In Annals of Operations Research; Springer: Berlin/Heidelberg, Germany, 2023; pp. 1–24. [Google Scholar]
- Yin, L.; Yang, Q. Predicting the oil prices: Do technical indicators help? Energy Econ. 2016, 56, 338–350. [Google Scholar] [CrossRef]
- Mahdiani, M.R.; Khamehchi, E. A modified neural network model for predicting the crude oil price. Intellect. Econ. 2016, 10, 71–77. [Google Scholar] [CrossRef]
- Moreno, P.; Figuerola-Ferretti, I.; Muñoz, A. Forecasting Oil Prices with Non-Linear Dynamic Regression Modeling. Energies 2024, 17, 2182. [Google Scholar] [CrossRef]
- Weijermars, R.; Sun, Z. Regression analysis of historic oil prices: A basis for future mean reversion price scenarios. Glob. Financ. J. 2018, 35, 177–201. [Google Scholar] [CrossRef]
- Tudor, C.; Anghel, A. The financialization of crude oil markets and its impact on market efficiency: Evidence from the predictive ability and performance of technical trading strategies. Energies 2021, 14, 4485. [Google Scholar] [CrossRef]
- Degiannakis, S.; Filis, G. Forecasting oil prices: High-frequency financial data are indeed useful. Energy Econ. 2018, 76, 388–402. [Google Scholar] [CrossRef]
- Filippidis, M.; Filis, G.; Magkonis, G. Evaluating oil price forecasts: A meta-analysis. Energy J. 2024, 45, 49–67. [Google Scholar] [CrossRef]
- Kaufman, P.J. A Guide to Creating A Successful Algorithmic Trading Strategy; Wiley: Hoboken, NJ, USA, 2016. [Google Scholar]
- Tudor, C.; Sova, R. Flexible decision support system for algorithmic trading: Empirical application on crude oil markets. IEEE Access 2022, 10, 9628–9644. [Google Scholar] [CrossRef]
- Bojnourdi, E.Z.; Mansoori, A.; Jowkar, S.; Ghiasvand, M.A.; Rezaei, G.; Tabatabaei, S.A.; Keshvari, M.M. Predicting successful trading in the West Texas Intermediate crude oil cash market with machine learning nature-inspired swarm-based approaches. Front. Appl. Math. Stat. 2024, 10, 1376558. [Google Scholar] [CrossRef]
- Stasiak, M.D. Candlestick—The main mistake of economy research in high-frequency markets. Int. J. Financ. Stud. 2020, 8, 59. [Google Scholar] [CrossRef]
- Stasiak, M.D. A study on the influence of the discretisation unit on the effectiveness of modelling currency exchange rates using the binary-temporal representation. Oper. Res. Decis. 2018, 28, 57–70. [Google Scholar]
- Stasiak, M.D. Algoritmic Trading System Based on State Model for Moving Average in a Binary-Temporal Representation. Risks 2022, 10, 69. [Google Scholar] [CrossRef]
- Schwager, J.D. Getting Started in Technical Analysis; John Wiley & Sons: Hoboken, NJ, USA, 1999; Volume 19. [Google Scholar]
- Kirkpatrick, C.D.; Dahlquist, J.R. Technical Analysis: The Complete Resource for Financial Market Technicians; FT Press: Upper Saddle River, NJ, USA, 2010. [Google Scholar]
- Schlossberg, B. Technical Analysis of the Currency Market: Classic Techniques for Profiting from Market Swings and Trader Sentiment; John Wiley & Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- De Villiers, V. The Point and Figure Method of Anticipating Stock Price Movements Complete Theory & Practice; A Reprint of the 1933 Edition Including a Chart on the 1929 Crash; Windsor Books: New York, NY, USA, 1933. [Google Scholar]
- Logue, D.E.; and Sweeney, R.J. White noise in imperfect markets: The case of the franc/dollar exchange rates. J. Financ. 1977, 32, 761–768. [Google Scholar] [CrossRef]
- Sandubete, J.E.; Escot, L. Chaotic signals inside some tick-by-tick financial time series. Chaos Solitons Fractals 2020, 137, 109852. [Google Scholar] [CrossRef]
- Ghazani, M.M.; Ebrahimi, S.B. Testing the adaptive market hypothesis as an evolutionary perspective on market efficiency: Evidence from the crude oil prices. Financ. Res. Lett. 2019, 30, 60–68. [Google Scholar] [CrossRef]
- Okoroafor, U.C.; Leirvik, T. Time varying market efficiency in the Brent and WTI crude market. Financ. Res. Lett. 2022, 45, 102191. [Google Scholar] [CrossRef]
- Dimitriadou, A.; Gogas, P.; Papadimitriou, T.; Plakandaras, V. Oil market efficiency under a machine learning perspective. Forecasting 2018, 1, 157–168. [Google Scholar] [CrossRef]
- Stasiak, M.; Staszak, Ż. Are Changes in Crude Oil Prices Predictable? In Sustainable Global Economic Development within 2025 Vision: Research and Practice; Proceedings of the 43rd International Business Information Management Association Conference (IBIMA), Granada, Spain, 27–28 November 2024; Soliman, K.S., Ed.; IBIMA Publishing LLC: King of Prussia, PA, USA, 2024. [Google Scholar]
- Malkiel, B.G. Efficient market hypothesis. In Finance; Palgrave Macmillan: London, UK, 1989; pp. 127–134. [Google Scholar]
- Young, T.W. Calmar ratio: A smoother tool. Futures 1991, 20, 40. [Google Scholar]
- Psaradellis, I.; Laws, J.; Pantelous, A.A.; Sermpinis, G. Performance of technical trading rules: Evidence from the crude oil market. Eur. J. Financ. 2019, 25, 1793–1815. [Google Scholar] [CrossRef]
- Pardo, R. The Evaluation and Optimization of Trading Strategies; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Dbouk, W.; Jamali, I. Predicting daily oil prices: Linear and non-linear models. Res. Int. Bus. Financ. 2018, 46, 149–165. [Google Scholar] [CrossRef]
| State | Probab. of Inc. | Probab. of Dec. | Number of Occurrences |
|---|---|---|---|
| {0,0} | 0.4941 | 0.5059 | 937 |
| {0,1} | 0.5218 | 0.4782 | 895 |
| {1,0} | 0.4833 | 0.5167 | 896 |
| {1,1} | 0.5079 | 0.4921 | 951 |
| State | Probab. of Inc. | Probab. of Dec. | Number of Occurrences |
|---|---|---|---|
| {(0,0);0} | 0.4928 | 0.5072 | 769 |
| {(0,0);1} | 0.5000 | 0.5000 | 168 |
| {(0,1);0} | 0.5129 | 0.4871 | 698 |
| {(0,1);1} | 0.5533 | 0.4467 | 197 |
| {(1,0);0} | 0.4795 | 0.5205 | 684 |
| {(1,0);1} | 0.4953 | 0.5047 | 212 |
| {(1,1);0} | 0.5136 | 0.4864 | 699 |
| {(1,1);1} | 0.4920 | 0.5079 | 252 |
| State | Probab. of Inc. | Probab. of Dec. | Number of Occurrences |
|---|---|---|---|
| {(0,0);1} | 0.5279 | 0.4721 | 322 |
| {(0,0);0} | 0.4734 | 0.5266 | 583 |
| {(0,0);−1} | 0.5312 | 0.4688 | 32 |
| {(1,0);1} | 0.4929 | 0.5071 | 495 |
| {(1,0);0} | 0.5678 | 0.4322 | 199 |
| {(1,0);−1} | 0.5473 | 0.4527 | 201 |
| {(0,1);1} | 0.4759 | 0.5241 | 477 |
| {(0,1);0} | 0.5202 | 0.4798 | 223 |
| {(0,1);−1} | 0.4592 | 0.5408 | 196 |
| {(1,1);1} | 0.5234 | 0.4766 | 321 |
| {(1,1);0} | 0.3750 | 0.6250 | 48 |
| {(1,1);−1} | 0.5103 | 0.4897 | 582 |
| State | Probab. of Inc. | Probab. of Dec. | Number of Occurrences |
|---|---|---|---|
| {(0,0);0;0} | 0.5045 | 0.4955 | 111 |
| {(0,0);0;1} | 0.3818 | 0.6182 | 55 |
| {(0,0);−1;0} | 0.4240 | 0.5760 | 158 |
| {(0,0);−1;1} | 0.5209 | 0.4791 | 311 |
| {(0,0);1;0} | 0.5250 | 0.4750 | 40 |
| {(0,0);1;1} | 0.5191 | 0.4809 | 262 |
| {(0,1);0;0} | 0.4956 | 0.5044 | 115 |
| {(0,1);0;1} | 0.4921 | 0.5079 | 63 |
| {(0,1);−1;0} | 0.5692 | 0.4308 | 65 |
| {(0,1);−1;1} | 0.5084 | 0.4916 | 297 |
| {(0,1);1;0} | 0.6479 | 0.3521 | 71 |
| {(0,1);1;1} | 0.5106 | 0.4894 | 284 |
| {(1,0);0;0} | 0.4519 | 0.5481 | 104 |
| {(1,0);0;1} | 0.5077 | 0.4923 | 65 |
| {(1,0);−1;0} | 0.5125 | 0.4875 | 80 |
| {(1,0);−1;1} | 0.5069 | 0.4931 | 288 |
| {(1,0);1;0} | 0.3651 | 0.6349 | 63 |
| {(1,0);1;1} | 0.4831 | 0.5169 | 296 |
| {(1,1);0;0} | 0.6239 | 0.3761 | 117 |
| {(1,1);0;1} | 0.3859 | 0.6141 | 57 |
| {(1,1);−1;0} | 0.4390 | 0.5609 | 41 |
| {(1,1);−1;1} | 0.5076 | 0.4924 | 262 |
| {(1,1);1;0} | 0.4519 | 0.5481 | 135 |
| {(1,1);1;1} | 0.5191 | 0.4808 | 339 |
| State | Recommendation | Probab. of Success |
|---|---|---|
| {(0,0);1} | BUY | 0.5279 |
| {(0,0);0} | SELL | 0.5266 |
| {(0,0);−1} | BUY | 0.5312 |
| {(1,0);1} | 0.5071 | |
| {(1,0);0} | BUY | 0.5678 |
| {(1,0);−1} | BUY | 0.5473 |
| {(0,1);1} | SELL | 0.5241 |
| {(0,1);0} | BUY | 0.5202 |
| {(0,1);−1} | SELL | 0.5408 |
| {(1,1);1} | BUY | 0.5234 |
| {(1,1);0} | SELL | 0.6250 |
| {(1,1);−1} | 0.5103 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stasiak, M.D.; Staszak, Ż.; Siwek, J.; Wojcieszak, D. Application of State Models in a Binary–Temporal Representation for the Prediction and Modelling of Crude Oil Prices. Energies 2025, 18, 691. https://doi.org/10.3390/en18030691
Stasiak MD, Staszak Ż, Siwek J, Wojcieszak D. Application of State Models in a Binary–Temporal Representation for the Prediction and Modelling of Crude Oil Prices. Energies. 2025; 18(3):691. https://doi.org/10.3390/en18030691
Chicago/Turabian StyleStasiak, Michał Dominik, Żaneta Staszak, Joanna Siwek, and Dawid Wojcieszak. 2025. "Application of State Models in a Binary–Temporal Representation for the Prediction and Modelling of Crude Oil Prices" Energies 18, no. 3: 691. https://doi.org/10.3390/en18030691
APA StyleStasiak, M. D., Staszak, Ż., Siwek, J., & Wojcieszak, D. (2025). Application of State Models in a Binary–Temporal Representation for the Prediction and Modelling of Crude Oil Prices. Energies, 18(3), 691. https://doi.org/10.3390/en18030691








