Improved Multi-Objective Strategy Diversity Chaotic Particle Swarm Optimization of Ordered Charging Strategy for Electric Vehicles Considering User Behavior
Abstract
1. Introduction
- (1)
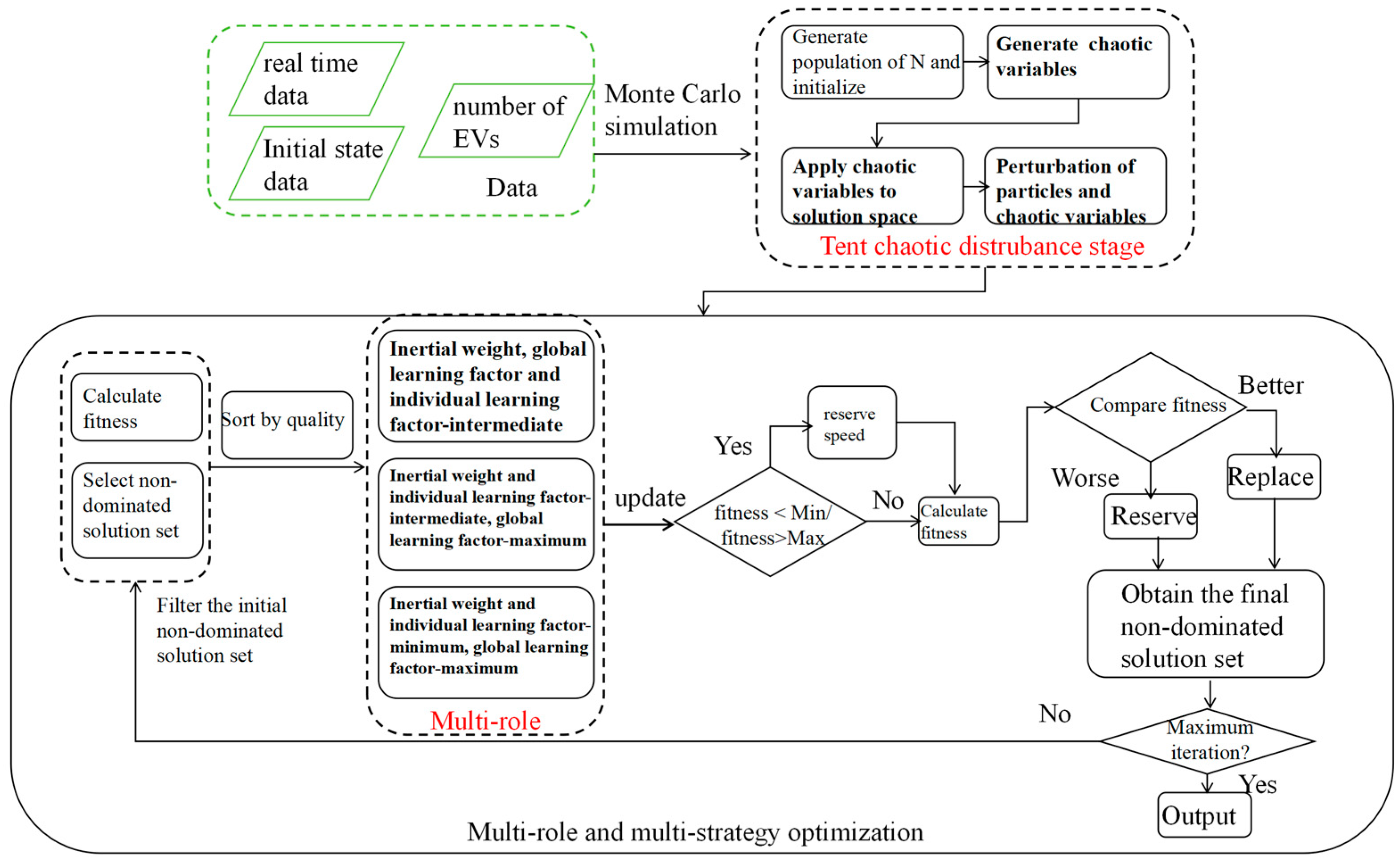
- Multi-role multi-strategy optimization mechanism: The particles are first sorted using the non-dominated sorting method to obtain their hierarchy. Then, different search strategies are applied to particles based on their hierarchy and density. Specifically, particles with great diversity and convergence are categorized as elite particles, which are closest to the global optimum. They are assigned intermediate values of the learning factor and inertia weight. General particles have slightly lower performance but still need to converge towards the global optimum at a faster rate. They are assigned larger global learning factors, while their personal learning factors and inertia weights are set to intermediate values. Poor-performing particles adopt the maximum global learning factor smaller personal learning factors and inertia weights to improve their search capability;
- (2)
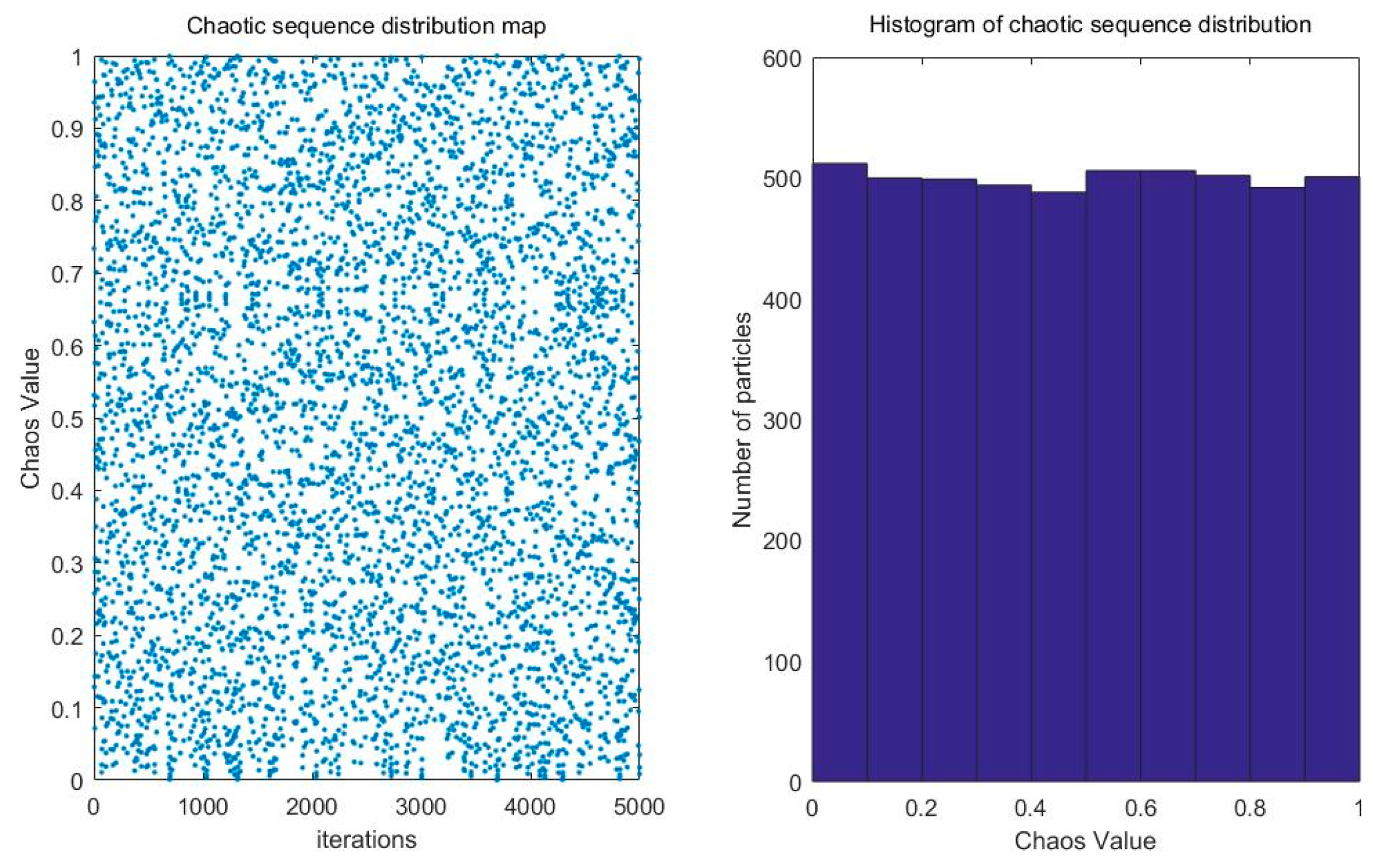
- Tent chaotic sequence perturbation: To improve the quality of the initial solutions, Tent chaotic sequence perturbation is introduced during the population initialization stage in the algorithm. In each iteration, Tent chaotic sequence perturbation is executed to update the population particles and maintain their diversity throughout the algorithm iteration process.
2. Microgrid Modeling and Control Algorithm
2.1. Microgrid Modeling
2.2. Tent Chaotic Perturbation Sequence
| Algorithm 1 Tent chaotic sequence algorithm |
| Input: particle.position Output: adjusted particle.position procedure Tent 1. Input 2. Initialize x,N 3. for i = 1:N 4. If xi < 0.5 5. xi = 2 × i 6. else 7. xi = 2 × (1 − i) 8. end if 9. end for |
2.3. Multi-Role and Multi-Strategy Optimization
| Algorithm 2 Non-dominated particles sorting algorithm |
| Input: position,N,obj1,obj2,di1,di2 Output: adjusted sorting procedure MMMO 1. Input 2. for i = 1:N 3. midu(i) = 2/(di1 + di2) 4. lfi = (midu(j1)/midu(i) + midu(j2)/midu(i)) + 2 5. Di = 1/(di2 + 2) 6. end for 7. frontvalue = non-dominated(position,obj1,obj2) 8. for i = 1:N 9. if lf(i) > 1 10. frontvalue(i) = frontvalue(i) + 1 11. end if 12. adjusted sorting = power(frontvalue(i,1)) + power(Di,1) 13. end for 14. adjustedsorting = sortrows(adjusted sorting,1); |
2.4. Control Strategy
| Algorithm 3 Multi-role Multi-strategy PSO algorithm |
| Input: number of EVs, load, average electricity price Output: adjusted electricity price and load 1. Input 2. obtain parameters using Monte Carlo simulation method procedure MOPSO 3. for each particle i 4. Initialize velocity Vi and position Xi for particle i 5. Particle.position = Tent(postion) 6. Evaluate particle i and set pBesti = Xi 7. end for 8. gBest = min{pBesti} 9. particle.sorting = MMMO(npop,position,obj1,obj2) 10. while not stop 11. for i = 1 to N 12. update the velocity and position of particle i 13. Evaluate particle i 14. if fit(Xi) better than fit(pBesti) 15. pBesti = Xi; 16. if fit(pBesti) < fit(gBest) 17. gBest = pBesti; 18. end for 19. end while 20. print gBest end procedure |
3. Simulation and Case Study Results
3.1. Analysis of the Impact of the Number of EVs on Microgrids
3.2. Load Optimization
3.3. User Satisfaction Optimization
3.4. Normalization Objective Optimization
3.5. 24 h Load Optimization
3.6. 24 h Electricity Price Optimization
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kou, P.; Liang, D.; Gao, L.; Gao, F. Stochastic coordination of plug-in electric vehicles and wind turbines in microgrid: A model predictive control approach. IEEE Trans. Smart Grid 2016, 7, 1537–1551. [Google Scholar] [CrossRef]
- Pure Power—Wind Energy Targets for 2020 and 2030. European Wind Energy Association. Available online: https://www.osti.gov/etdeweb/biblio/21514309 (accessed on 1 January 2025).
- Economics of Wind Energy. European Wind Energy Association. Available online: https://www.ewea.org/fileadmin/files/library/publications/reports/Economics_of_Wind_Energy.pdf (accessed on 1 January 2025).
- Shared Solar: Current Landscape, Market Potential, and the Impact of Federal Securities Regulation. U.S. Department of Energy. Available online: http://www.nrel.gov/docs/fy15osti/63892.pdf (accessed on 1 January 2025).
- Lund, H.; Kempton, W. Integration of renewable energy into the transport and electricity sectors through V2G. Energ Policy 2008, 36, 3578–3587. [Google Scholar] [CrossRef]
- Nguyen, H.K.; Song, J.B. Optimal charging and discharging for multiple PHEVs with demand side management in vehicle-to-building. J. Commun. Netw. 2012, 14, 662–671. [Google Scholar] [CrossRef]
- Cardoso, G.; Stadler, M.; Chehreghani Bozchalui, M.; Sharma, R.; Marnay, C.; Barbosa-Povoa, A.; Ferrao, P. Stochastic programming of vehicle to building interactions with uncertainty in PEVs driving for a medium office building. In Proceedings of the 39th Annual Conference of the IEEE Industrial Electronics Society (IECON), Vienna, Austria, 10–13 November 2013; pp. 7648–7653. [Google Scholar]
- Harding, J.; Powell, G.; Yoon, R.; Fikentscher, J.; Doyle, C.; Sade, D.; Wang, J. Vehicle-to-Vehicle Communications: Readiness of V2V Technology for Application; Report No. DOT HS 812 014; National Highway Traffic Safety Administration: Washington, DC, USA, 2014. [Google Scholar]
- Vadi, S.; Bayindir, R.; Colak, A.M.; Hossain, E. A review on communication standards and charging topologies of V2G and V2H operation strategies. Energies 2019, 12, 3748. [Google Scholar] [CrossRef]
- Sun, F.; Hou, W.; Yin, B.; Xi, H. Preliminary studies on the linking of building hybrid energy system and distributed power generation system. In Proceedings of the International Conference on Sustainable Power Generation and Supply, Nanjing, China, 6–7 April 2009; pp. 1–6. [Google Scholar]
- Huang, H.; Cai, Y.; Xu, H.; Yu, H. A multiagent minority-game based demand-response management of smart buildings toward peak load reduction. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 2017, 36, 573–585. [Google Scholar] [CrossRef]
- Van Heuveln, K.; Ghotge, R.; Annema, J.A.; van Bergen, E.; van Wee, B.; Pesch, U. Factors influencing consumer acceptance of vehicle-to-grid by electric vehicle drivers in the Netherlands. Travel Behav. Soc. 2021, 24, 34–45. [Google Scholar] [CrossRef]
- Kester, J.; de Rubens, G.Z.; Sovacool, B.K.; Noel, L. Public perceptions of electric vehicles and vehicle-to-grid (V2G): Insights from a Nordic focus group study. Transp. Res. D Transp. Environ. 2019, 74, 277–293. [Google Scholar] [CrossRef]
- Kwon, Y.; Son, S.; Jang, K. User satisfaction with battery electric vehicles in South Korea. Transp. Res. D Transp. Environ. 2020, 82, 102306. [Google Scholar] [CrossRef]
- Ghotge, R.; Nijssen, K.P.; Annema, J.A.; and Lukszo, Z. Use before you choose: What do EV drivers think about V2G after experiencing it? Energies 2022, 15, 4907. [Google Scholar] [CrossRef]
- Chai, Y.T.; Che, H.S.; Tan, C.; Tan, W.N.; Yip, S.C.; Gan, M.T. A two-stage optimization method for Vehicle to Grid coordination considering building and Electric Vehicle user expectations. Int. J. Electr. Power Energy Syst. 2023, 148, 108984. [Google Scholar] [CrossRef]
- Saber, A.Y.; Venayagamoorthy, G.K. Unit commitment with vehicle-to-grid using particle swarm optimization. In Proceedings of the 2009 IEEE Bucharest PowerTech, Bucharest, Romania, 28 June–2 July 2009; pp. 1–8. [Google Scholar]
- Borges, N.; Soares, J.; Vale, Z. Multi-objective particle swarm optimization to solve energy scheduling with vehicle-to-grid in office buildings considering uncertainties. IFAC Pap. 2017, 50, 3356–3361. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, S.; Ji, G. A comprehensive survey on particle swarm optimization algorithm and its applications. Math. Probl. 2015, 2015, 1–38. [Google Scholar] [CrossRef]
- Alegre, S.; Míguez, J.V.; Carpio, J. Modelling of electric and parallel-hybrid electric vehicle using Matlab/Simulink environment and planning of charging stations through a geographic information system and genetic algorithms. Renew. Sustain. Energy Rev. 2017, 74, 1020–1027. [Google Scholar] [CrossRef]
- Korotunov, S.; Tabunshchyk, G.; Okhmak, V. Genetic algorithms as an optimization approach for managing electric vehicles charging in the smart grid. In Proceedings of the Third International Workshop on Computer Modeling and Intelligent Systems, CEUR, Zaporizhzhia, Ukraine, 27 April–1 May 2020; pp. 184–198. [Google Scholar]
- Abdullah-Al-Nahid, S.; Khan, T.A.; Taseen, M.A.; Jamal, T.; Aziz, T. A novel consumer-friendly electric vehicle charging scheme with vehicle to grid provision supported by genetic algorithm based optimization. J. Energy Storage 2022, 50, 104655. [Google Scholar] [CrossRef]
- Habib, H.U.R.; Subramaniam, U.; Waqar, A.; Farhan, B.S.; Kotb, K.M.; Wang, S. Energy cost optimization of hybrid renewables based V2G microgrid considering multi objective function by using artificial bee colony optimization. IEEE Access. 2020, 8, 62076–62093. [Google Scholar] [CrossRef]
- Chandrasekaran, K.; Hemamalini, S.; Simon, S.P.; Padhy, N.P. Thermal unit commitment using binary/real coded artificial bee colony algorithm. Electr. Power Syst. Res. 2012, 84, 109–119. [Google Scholar] [CrossRef]
- Zhang, S.; Luo, Y.; Li, K. Multi-objective route search for electric vehicles using ant colony optimization. In Proceedings of the 2016 American Control Conference (ACC), Boston, MA, USA, 6–8 July 2016. [Google Scholar]
- Tangrand, K.; Bremdal, B.A. Using Ant Colony Optimization to determine influx of EVs and charging station capacities. In Proceedings of the 2016 IEEE International Energy Conference (ENERGYCON), Leuven, Belgium, 4–8 April 2016; pp. 1–6. [Google Scholar]
- Van Laarhoven, P.J.; Aarts, E.H. Simulated Annealing; Springer Netherlands: Dordrecht, The Netherlands, 1987; pp. 7–15. [Google Scholar]
- Sousa, T.; Soares, T.; Morals, H.; Castro, R.; Vale, Z. Simulated annealing to handle energy and ancillary services joint management considering electric vehicles. Electr. Power Syst. Res. 2016, 136, 383–397. [Google Scholar] [CrossRef]
- Wang, B.; Xu, J.; Cao, B.; Xu, D.; Zou, Z. Optimization of energy management system for hybrid power sources of electric vehicles using simulated annealing algorithm. J. Xi’an Jiaotong Univ. 2015, 49, 90–96. [Google Scholar]
- Salman, S.S.; Islam, M.M. Optimal Dispatch for A Microgrid with Distributed Generations and EV Charging Load. In Proceedings of the 2023 IEEE Power & Energy Society Innovative Smart Grid Technologies Conference (ISGT), Washington, DC, USA, 16–19 January 2023. [Google Scholar]
- Wang, C.; Qin, F.; Xiang, X.S.; Jiang, H.; Zhang, X.Y. A Dual-Population-Based Co-Evolutionary Algorithm for Capacitated Electric Vehicle Routing Problems. IEEE Trans. Transp. Electrification 2024, 10, 2663–2676. [Google Scholar] [CrossRef]
- Luo, T.Y.; Heng, Y.; Xing, L.N.; Ren, T.; Li, Q.; Qin, H. A Two-Stage Approach for Electric Vehicle Routing Problem with Time Windows and Heterogeneous Recharging Stations. Tsinghua Sci. Technol. 2024, 29, 1300–1322. [Google Scholar] [CrossRef]
- Eltamaly, A.M. A Novel Strategy for Optimal PSO Control Parameters Determination for PV Energy Systems. Sustainability 2021, 13, 1008. [Google Scholar] [CrossRef]
- Deb, K.; Agrawal, S.; Pratap, A.; Meyarivan, T. A fast elitist non-dominated sorting genetic algorithm for multi-objective optimization: NSGA-II. In Parallel Problem Solving from Nature PPSN VI, Proceedings of the 6th International Conference, Paris, France, 18–20 September 2000; Springer: Berlin/Heidelberg, Germany, 2000; Volume 6, pp. 849–858. [Google Scholar]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T.A.M.T. A Fast and Elitist Multiobjective Genetic Algorithm: NSGA-II. IEEE Trans. Evol. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Zhang, T.; Chen, X.; Yu, Z.; Zhu, X.; Shi, D. A Monte Carlo Simulation Approach to Evaluate Service Capacities of EV Charging and Battery Swapping Stations. IEEE Trans Ind. Inform. 2018, 14, 3914–3923. [Google Scholar] [CrossRef]
- Alatas, B.; Akin, E.; Ozer, A.B. Chaos Embedded Particle Swarm Optimization Algorithms. Chaos Solitons Fractals 2009, 40, 1715–1734. [Google Scholar] [CrossRef]
- Wei, Y.Q.; Dai, Y.S.; Zhang, Y.N.; Chen, J.; Ding, J.J. Adaptive Chaotic Embedded Particle Swarm Optimization Based on Tent Mapping. J. Comput. Eng. Appl. 2013, 49, 45–49. [Google Scholar]
- Moradi, M.H.; Abedini, M.; Tousi, S.R.; Hosseinian, S.M. Optimal siting and sizing of renewable energy sources and charging stations simultaneously based on differential evolution algorithm. Int. J. Electr. Power Energy Syst. 2015, 73, 1015–1024. [Google Scholar] [CrossRef]
- Qiao, B.; Liu, J. Multi-objective dynamic economic emission dispatch based on electric vehicles and wind power integrated system using differential evolution algorithm. Renew Energ. 2020, 154, 316–336. [Google Scholar] [CrossRef]
- Shang, X.; Li, Y.; Huang, R. A charging and discharging model for electric vehicles based on consortium blockchain using multi-objective gray wolf algorithm. Recent Adv. Electr. Electron. Eng. 2022, 15, 640–652. [Google Scholar]
- Liu, B.; Pan, Z.; Tan, Z.; Wang, D.; Yu, T. A real-time schedule optimization of massive electric vehicles and energy storage system based on grey wolf optimizer. In Proceedings of the 2018 IEEE 8th Annual International Conference on CYBER Technology in Automation, Control, and Intelligent Systems (CYBER), Tianjin, China, 19–23 July 2018; pp. 1160–1165. [Google Scholar]
- Zhuang, Z.; Jin, T. Capacity configuration and control strategy of EV charging station with integrated wind power and energy storage based on SSA. In Proceedings of the 2021 IEEE 5th Conference on Energy Internet and Energy System Integration (EI2), Taiyuan, China, 22–24 October 2021; pp. 4316–4322. [Google Scholar]
- Xu, H.Q.; Gu, S.; Fan, Y.C.; Li, X.S.; Zhao, Y.F.; Zhao, J.; Wang, J.J. A strategy learning framework for particle swarm optimization algorithm. Inf. Sci. 2023, 619, 126–152. [Google Scholar] [CrossRef]
- Li, X.; Wang, L.; Jiang, Q.; Li, N. Differential evolution algorithm with multi-population cooperation and multi-strategy integration. Neurocomputing 2021, 421, 285–302. [Google Scholar] [CrossRef]
- Hashemi, A.B.; Meybodi, M.R. A multi-role cellular PSO for dynamic environments. In Proceedings of the 2009 14th International CSI Computer Conference, Tehran, Iran, 20–21 October 2009; pp. 412–417. [Google Scholar]
- Marini, F.; Walczak, B. Particle swarm optimization (PSO). A tutorial. Chemom. Intell Lab Syst. 2015, 149, 153–165. [Google Scholar] [CrossRef]
- Coello, C.A.C.; Lechuga, M.S. MOPSO: A proposal for multiple objective particle swarm optimization. In Proceedings of the 2002 Congress on Evolutionary Computation CEC’02 (Cat. No. 02TH8600), Honolulu, HI, USA, 12–17 May 2002; Volume 2, pp. 1051–1056. [Google Scholar]
- Breunig, M.M.; Kriegel, H.P.; Ng, R.T.; Sander, J. LOF: Identifying density-based local outliers. In Proceedings of the 2000 ACM SIGMOD International Conference on Management of Data, Dallas, TX, USA, 15–18 May 2000; pp. 93–104. [Google Scholar]
- Zhang, Q.; Hu, Y.; Tan, W.; Li, C.; Ding, Z. Dynamic time-of-use pricing strategy for electric vehicle charging considering user satisfaction degree. Appl. Sci. 2020, 10, 3247. [Google Scholar] [CrossRef]
- Ahmadi, S.; Arabani, H.P.; Haghighi, D.A.; Beheshtaein, M.H. Optimal use of vehicle-to-grid technology to modify the load profile of the distribution system. J. Energy Storage 2020, 31, 101627. [Google Scholar] [CrossRef]
- Yu, X.L.; Xiaodong, M.; Jun, Z.A.H.N.G.; Zhen, W. Chaos sparrow search optimization algorithm. J. Beijing Univ. Aeronaut. Astronautics 2021, 47, 1712–1720. [Google Scholar]
- Couceiro, M.; Ghamisi, P.; Couceiro, M.; Ghamisi, P. Particle swarm optimization. In Proceedings of the 2016 International Conference on Swarm Intelligence; Springer International Publishing: Berlin/Heidelberg, Germany, 2016; pp. 1–10. [Google Scholar]
- Liang, W.W.; Jin, Y.W.; Chen, J.C.; Li, G.Q.; Hu, M.Z.; Dong, J.H. Multi-objective particle swarm optimization algorithm with multi-role and multi-strategy. J. Zhejiang Univ. (Eng. Sci.) 2022, 56, 531–541. [Google Scholar]
- Long, Q.; Wu, X.; Wu, C. Non-dominated sorting methods for multi-objective optimization: Review and numerical comparison. J. Ind. Manag. Optim. 2021, 17, 1001–1023. [Google Scholar] [CrossRef]
- Seada, H.; Deb, K. Non-dominated sorting based multi/many-objective optimization: Two decades of research and application. In Multi-Objective Optimization: Evolutionary to Hybrid Framework; Springer: Berlin/Heidelberg, Germany, 2018; pp. 1–24. [Google Scholar]
- Becker, T.A.; Sidhu, I.; Tenderich, B. Electric Vehicles in the United States: A New Model with Forecasts to 2030; Center for Entrepreneurship and Technology, University of California: Berkeley, CA, USA, 2009; pp. 1–24. [Google Scholar]
- Soltani-Sobh, A.; Heaslip, K.; Stevanovic, A.; Bosworth, R.; Radivojevic, D. Analysis of the electric vehicles adoption over the United States. Transp. Res. Procedia 2017, 22, 203–212. [Google Scholar] [CrossRef]
- Li, G.; Liu, C.C.; Mattson, C.; Lawarrée, J. Day-ahead electricity price forecasting in a grid environment. IEEE Trans. Power Syst. 2007, 22, 266–274. [Google Scholar] [CrossRef]
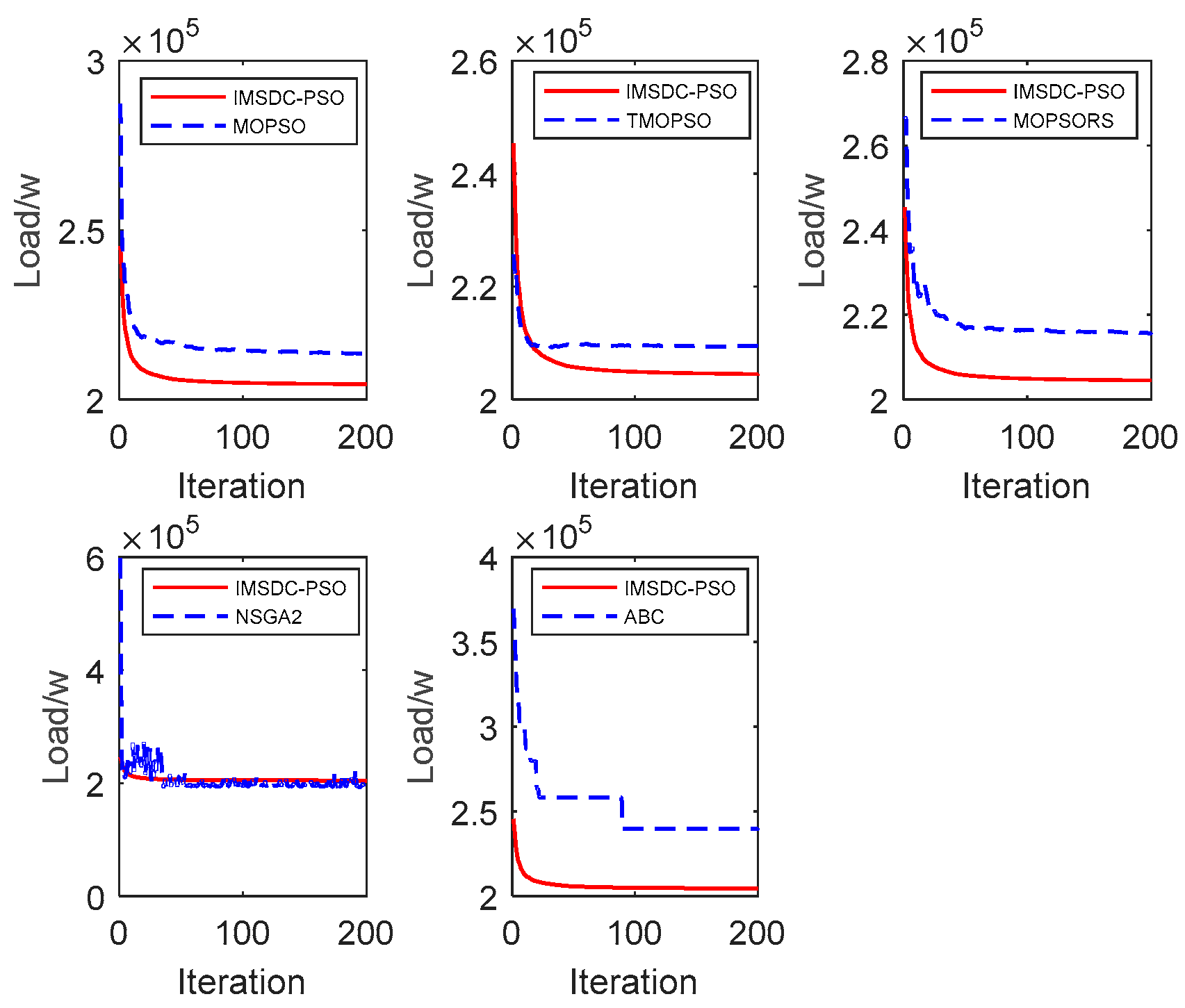
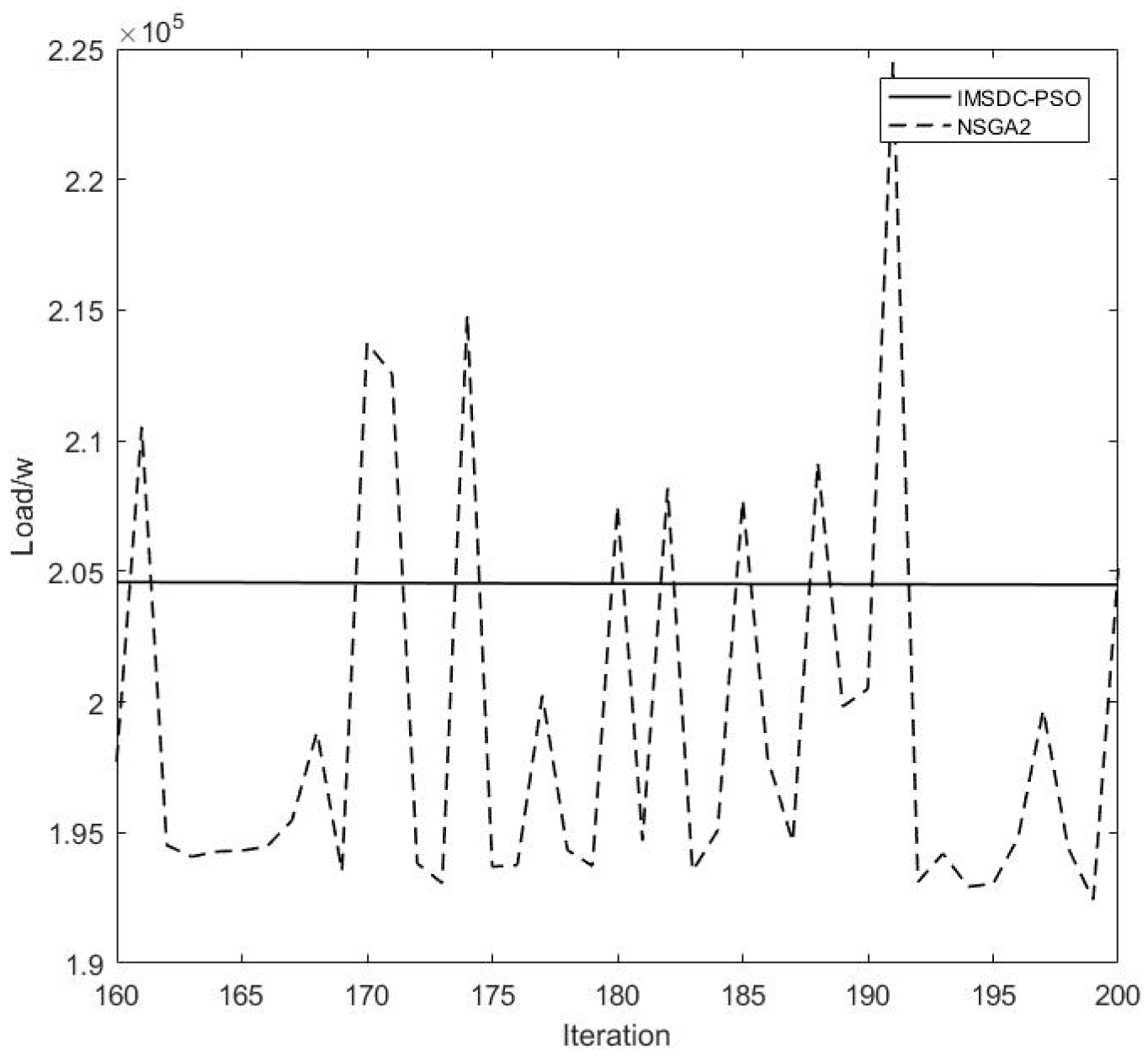
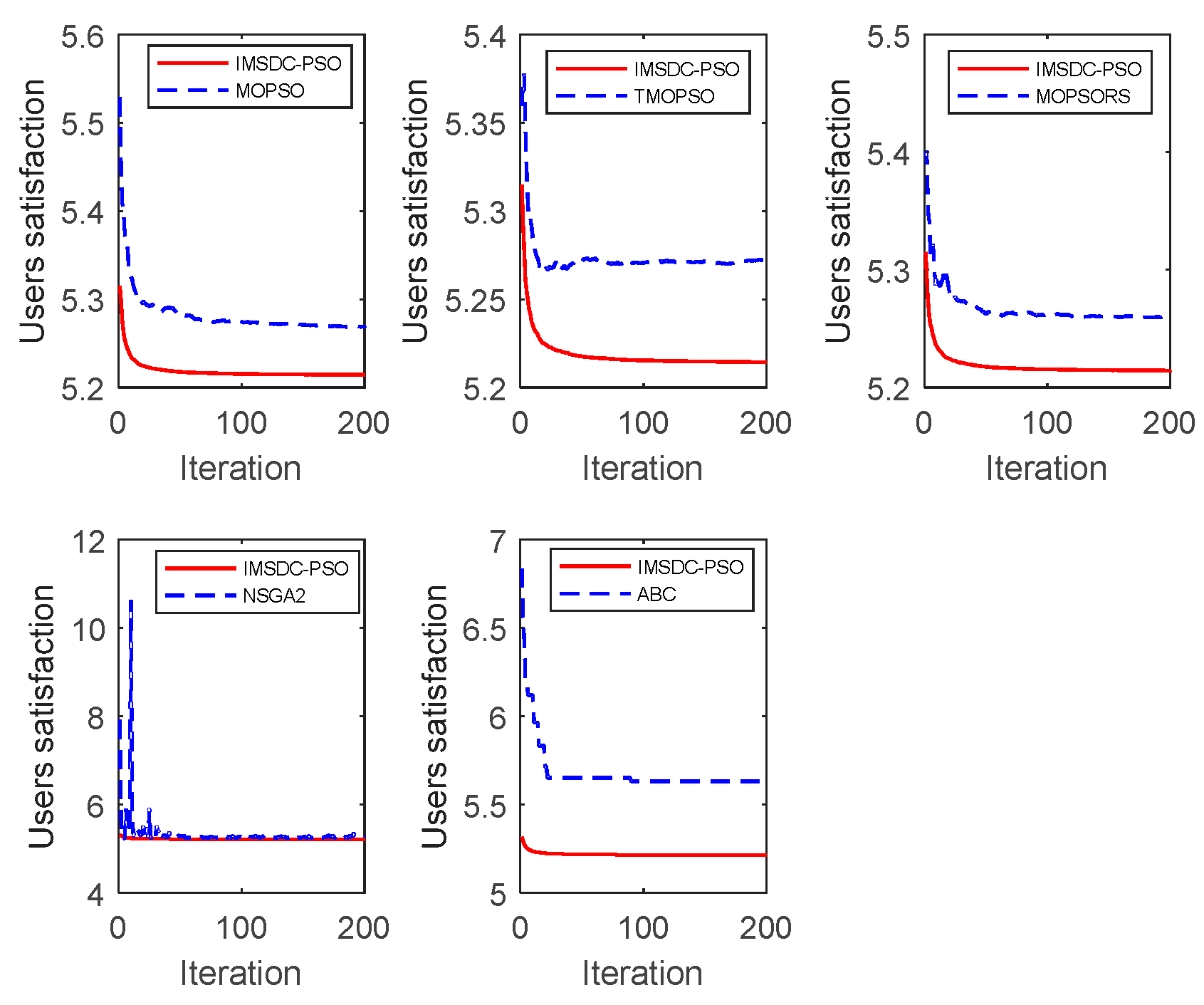
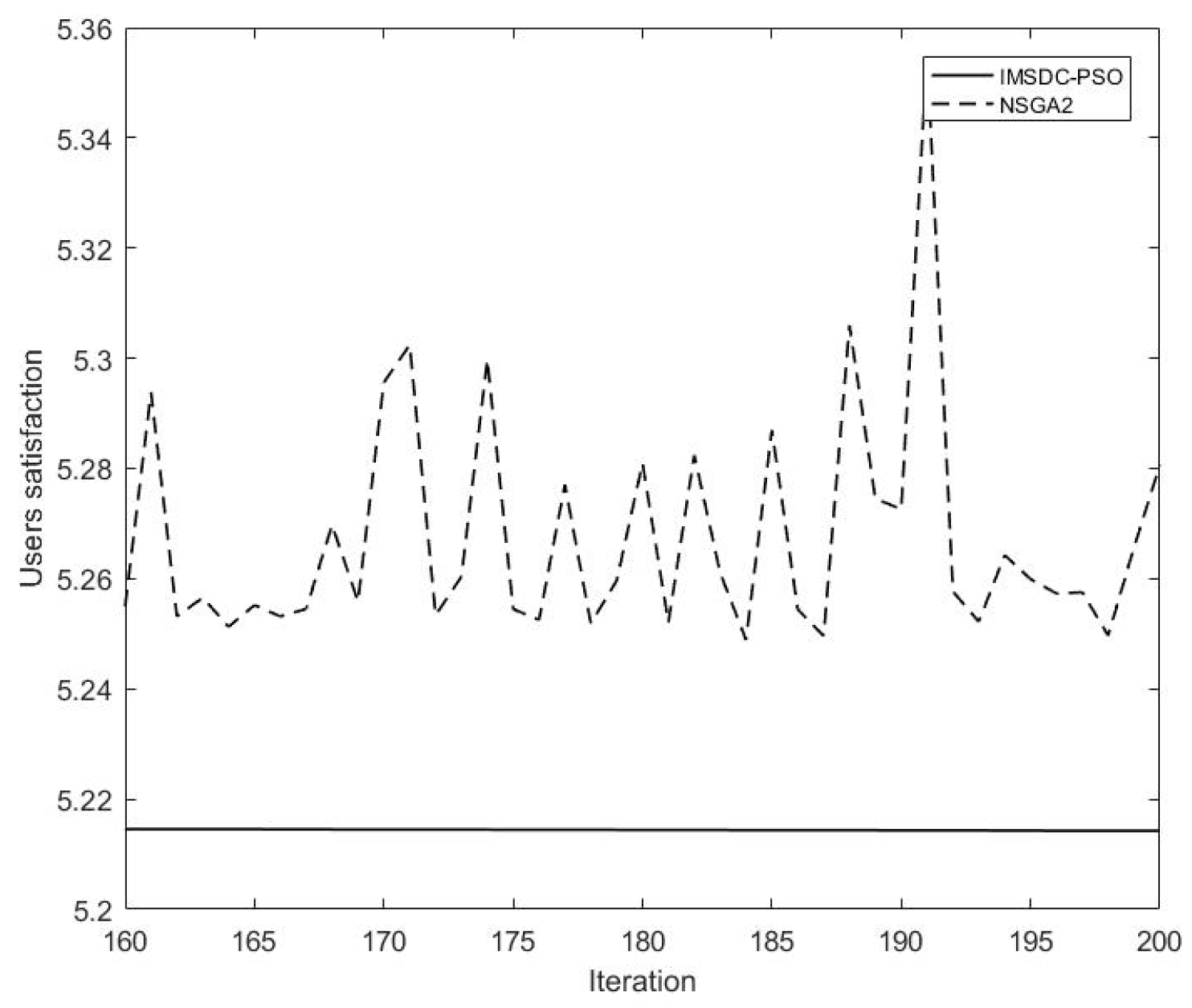
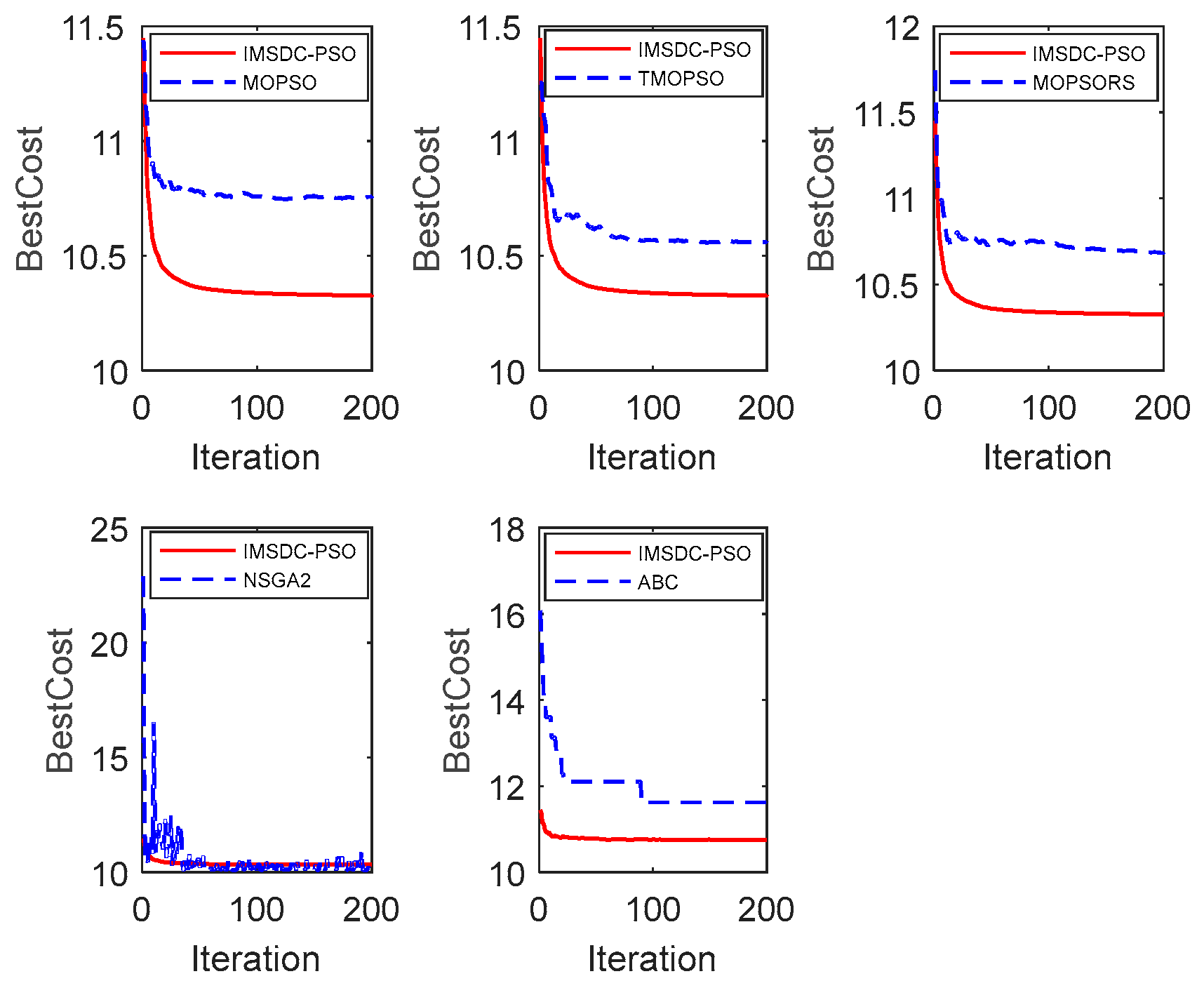
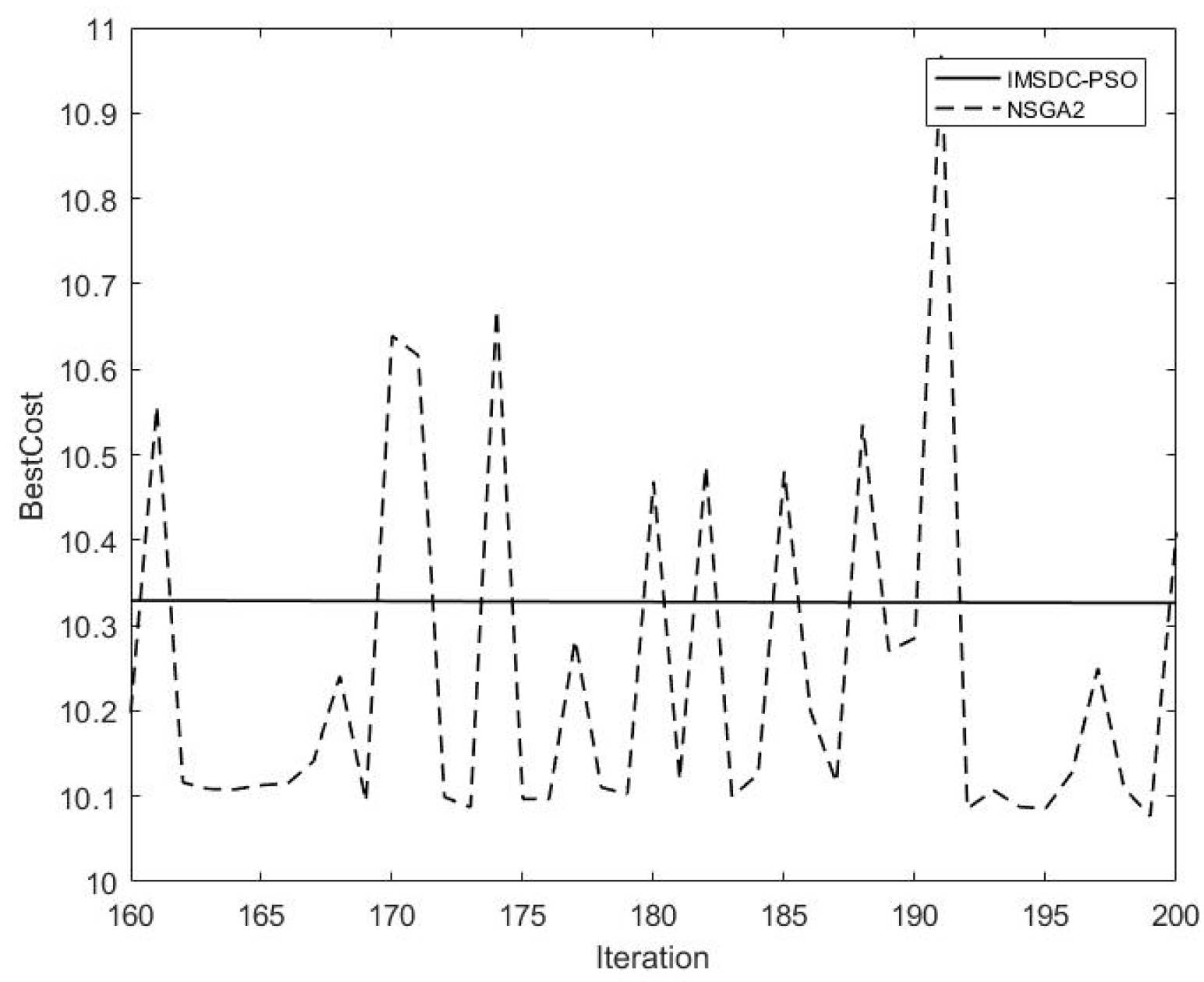
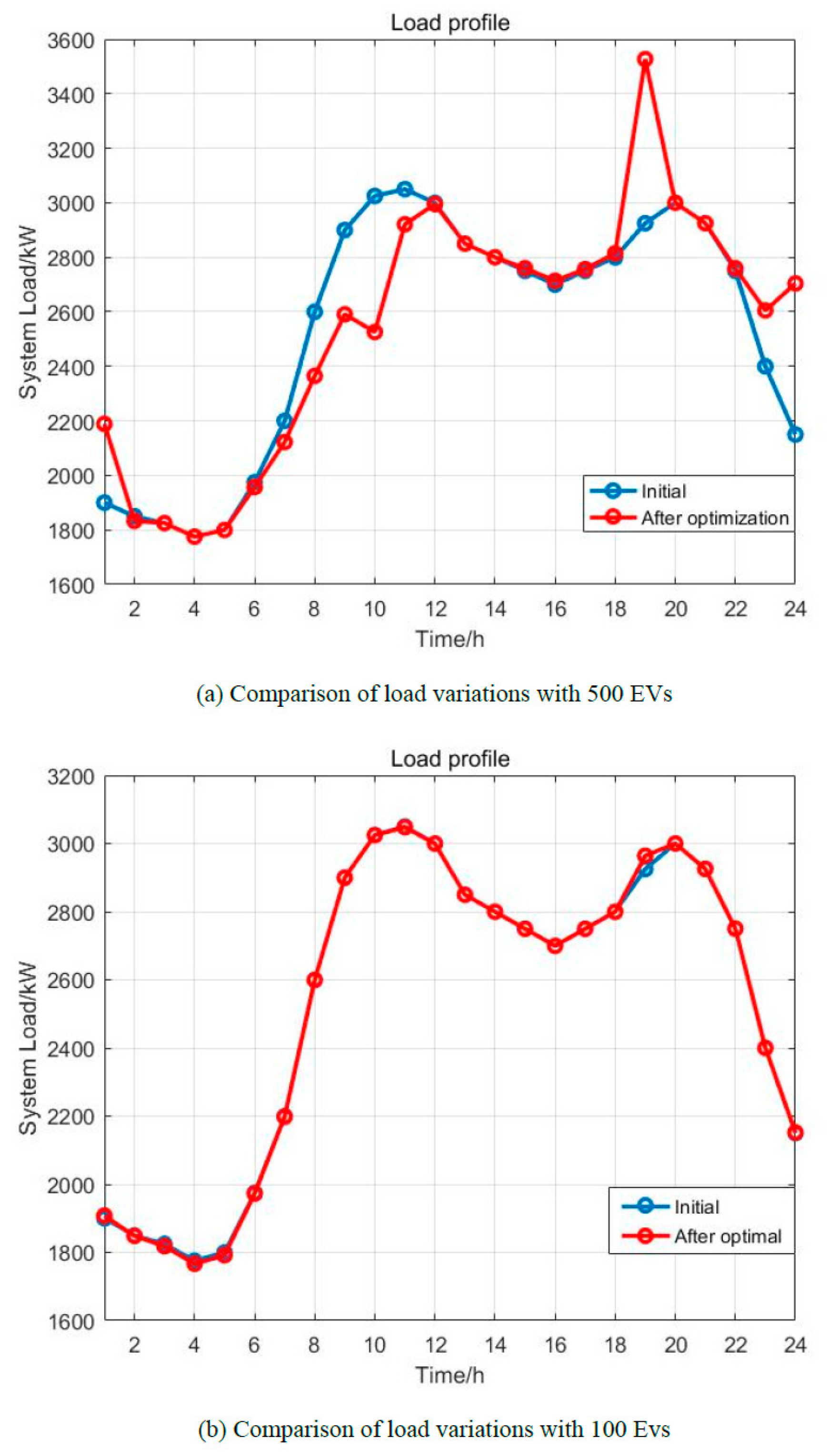
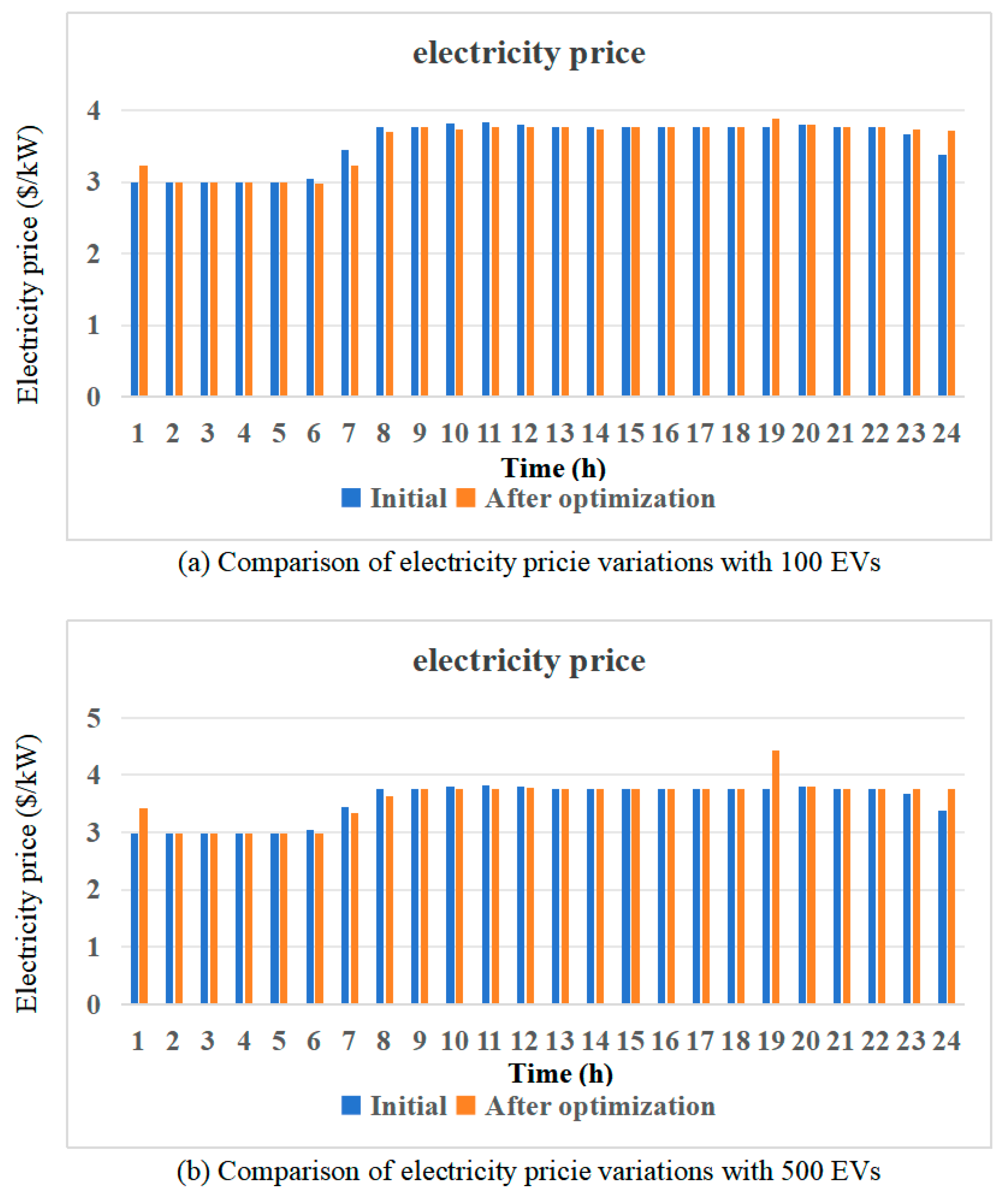
| Method | Load (kW) | Users’ Satisfaction | Convergence Speed |
|---|---|---|---|
| IMSDC-PSO | 204.555 | 5.21 | 12.3 min |
| MOPSO | 210.970 | 5.26 | 11.6 min |
| TMOPSO | 204.457 | 5.24 | 13.5 min |
| MOPSO_RS | 209.820 | 5.23 | 17.4 min |
| NSGA2 | 204.621 | 5.25 | 22.3 min |
| C-NSGA2 | 204.535 | 5.24 | 24.1 min |
| ABC | 225.191 | 5.39 | 27.4 min |
| C-ABC | 221.573 | 5.28 | 30.7 min |
| Method | Load (kW) | Users’ Satisfaction | Convergence Speed |
|---|---|---|---|
| IMSDC-PSO | 210.787 | 5.24 | 25.3 min |
| MOPSO | 218.884 | 5.30 | 24.1 min |
| TMOPSO | 210.926 | 5.28 | 26.4 min |
| MOPSO_RS | 218.991 | 5.26 | 28.2 min |
| NSGA2 | 215.014 | 5.29 | 28.7 min |
| C-NSGA2 | 214.891 | 5.28 | 30.4 min |
| ABC | 243.635 | 5.61 | 31.4 min |
| C-ABC | 244.832 | 5.58 | 32.1 min |
| Method | Load (kW) | Users’ Satisfaction | Convergence Speed |
|---|---|---|---|
| IMSDC-PSO | 214.377 | 5.29 | 35.4 min |
| MOPSO | 222.046 | 5.35 | 33.7 min |
| TMOPSO | 217.492 | 5.34 | 36.8 min |
| MOPSO_RS | 227.259 | 5.29 | 38.6 min |
| NSGA2 | 228.700 | 5.30 | 39.2 min |
| C-NSGA2 | 228.943 | 5.31 | 40.1 min |
| ABC | 263.882 | 5.73 | 41.1 min |
| C-ABC | 262.783 | 5.68 | 42.5 min |
| Method | Initial Value (kW) | Mean Value (kW) | Final Value (kW) |
|---|---|---|---|
| IMSDC-PSO | 245.327 | 206.294 | 204.485 |
| MOPSO | 281.317 | 216.228 | 213.650 |
| TMOPSO | 225.686 | 209.916 | 209.461 |
| MOPSO_RS | 266.238 | 218.387 | 215.618 |
| NSGA2 | 597.771 | 206.875 | 205.119 |
| C-NSGA2 | 596.624 | 207.248 | 206.754 |
| ABC | 369.592 | 252.034 | 239.652 |
| C-ABC | 370.237 | 253.849 | 241.873 |
| Method | Initial Value (kW) | Mean Value (kW) | Final Value (kW) |
|---|---|---|---|
| IMSDC-PSO | 5.31 | 5.22 | 5.21 |
| MOPSO | 5.53 | 5.28 | 5.27 |
| TMOPSO | 5.36 | 5.27 | 5.27 |
| MOPSO_RS | 5.40 | 5.27 | 5.26 |
| NSGA2 | 7.92 | 5.33 | 5.28 |
| C-NSGA2 | 8.01 | 5.47 | 5.34 |
| ABC | 6.84 | 5.68 | 5.63 |
| C-ABC | 6.88 | 5.62 | 5.57 |
| Method | Initial Value (kW) | Mean Value (kW) | Final Value (kW) |
|---|---|---|---|
| IMSDC-PSO | 11.45 | 10.38 | 10.33 |
| MOPSO | 11.44 | 10.78 | 10.76 |
| TMOPSO | 11.25 | 10.61 | 10.56 |
| MOPSO_RS | 11.74 | 10.75 | 10.68 |
| NSGA2 | 22.86 | 10.50 | 10.41 |
| C-NSGA2 | 23.72 | 11.72 | 11.27 |
| ABC | 16.08 | 11.98 | 11.62 |
| C-ABC | 17.17 | 12.71 | 11.25 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, S.; Ma, C.; Cao, Z. Improved Multi-Objective Strategy Diversity Chaotic Particle Swarm Optimization of Ordered Charging Strategy for Electric Vehicles Considering User Behavior. Energies 2025, 18, 690. https://doi.org/10.3390/en18030690
Zhao S, Ma C, Cao Z. Improved Multi-Objective Strategy Diversity Chaotic Particle Swarm Optimization of Ordered Charging Strategy for Electric Vehicles Considering User Behavior. Energies. 2025; 18(3):690. https://doi.org/10.3390/en18030690
Chicago/Turabian StyleZhao, Shuyi, Chenshuo Ma, and Zhiao Cao. 2025. "Improved Multi-Objective Strategy Diversity Chaotic Particle Swarm Optimization of Ordered Charging Strategy for Electric Vehicles Considering User Behavior" Energies 18, no. 3: 690. https://doi.org/10.3390/en18030690
APA StyleZhao, S., Ma, C., & Cao, Z. (2025). Improved Multi-Objective Strategy Diversity Chaotic Particle Swarm Optimization of Ordered Charging Strategy for Electric Vehicles Considering User Behavior. Energies, 18(3), 690. https://doi.org/10.3390/en18030690






