Short-Term Building Electrical Load Prediction by Peak Data Clustering and Transfer Learning Strategy
Abstract
1. Introduction
1.1. Related Work
1.2. Main Contribution of This Work
1.3. Paper Organization
2. Principles and Methods
2.1. Instance-Based Transfer Learning
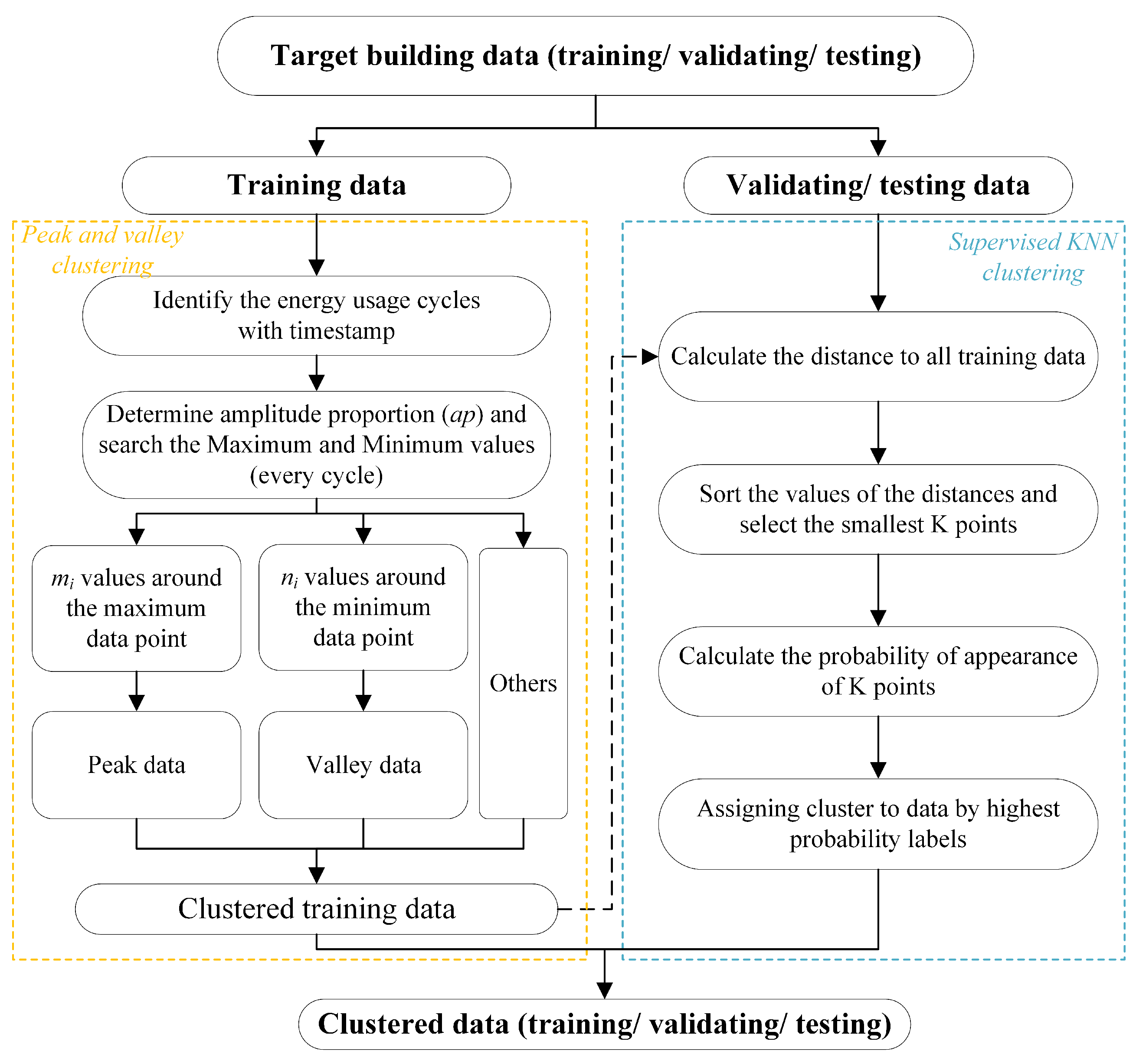
2.2. Data Clustering Method
2.3. Two-Stage Selection of Similarity Data
2.3.1. Similar Buildings Recognition
2.3.2. Similar Data Selection
2.4. The Proposed Predictive Model Framework
3. Case Studies
3.1. Benchmark Case
3.1.1. Description of Target and Source Domain Buildings
3.1.2. Data Clustering of Target Domain
3.1.3. Data Selection from Similar Buildings
3.1.4. Prediction Results
3.1.5. Discussion and Analysis
- (1)
- The combination effect of data clustering and transfer learning
- (2)
- The influence of KNN classification on the overall prediction accuracy
- (3)
- The influence of LSH data selection on the overall prediction accuracy
- (4)
- Performance comparison with other reported models
3.2. Campus Building Case A
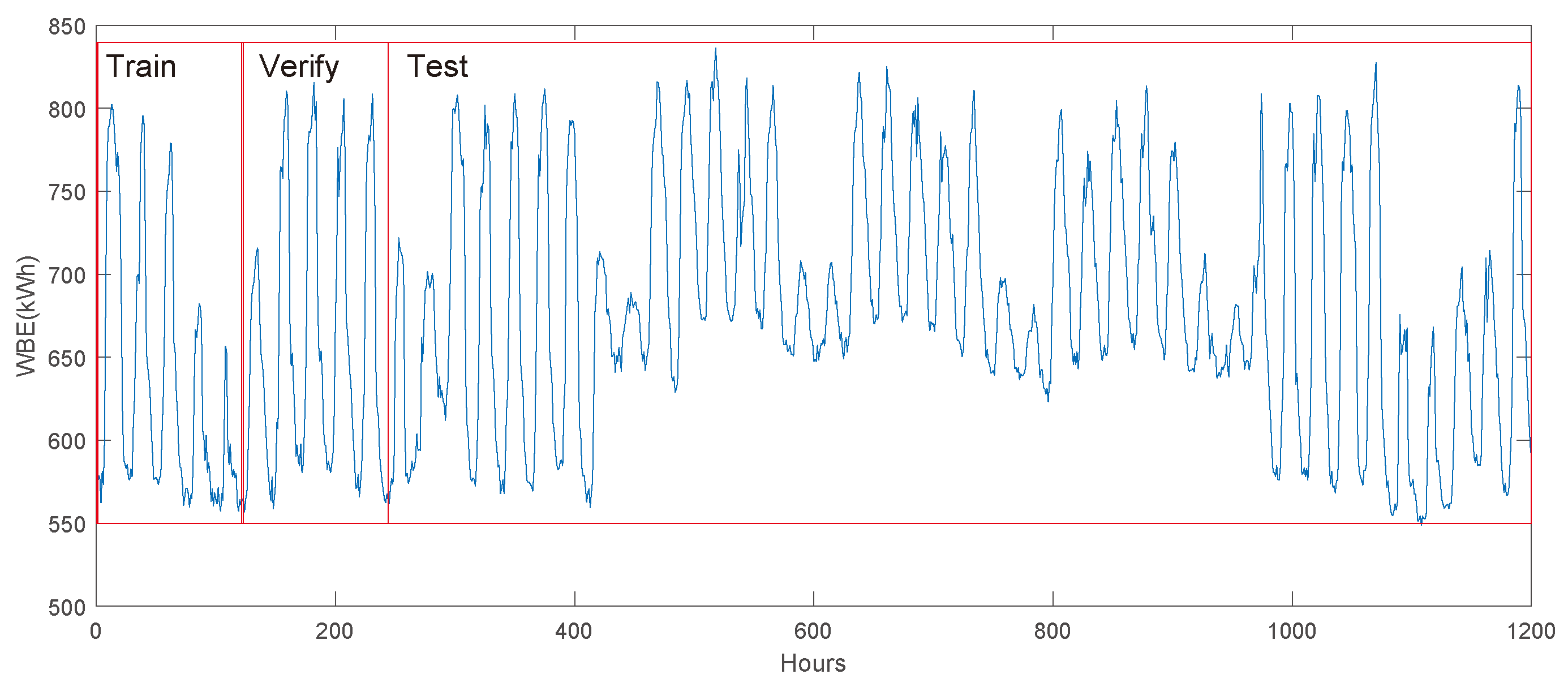
3.2.1. Description of Target Building Data
3.2.2. Two-Stage Selection of Source Domain Data
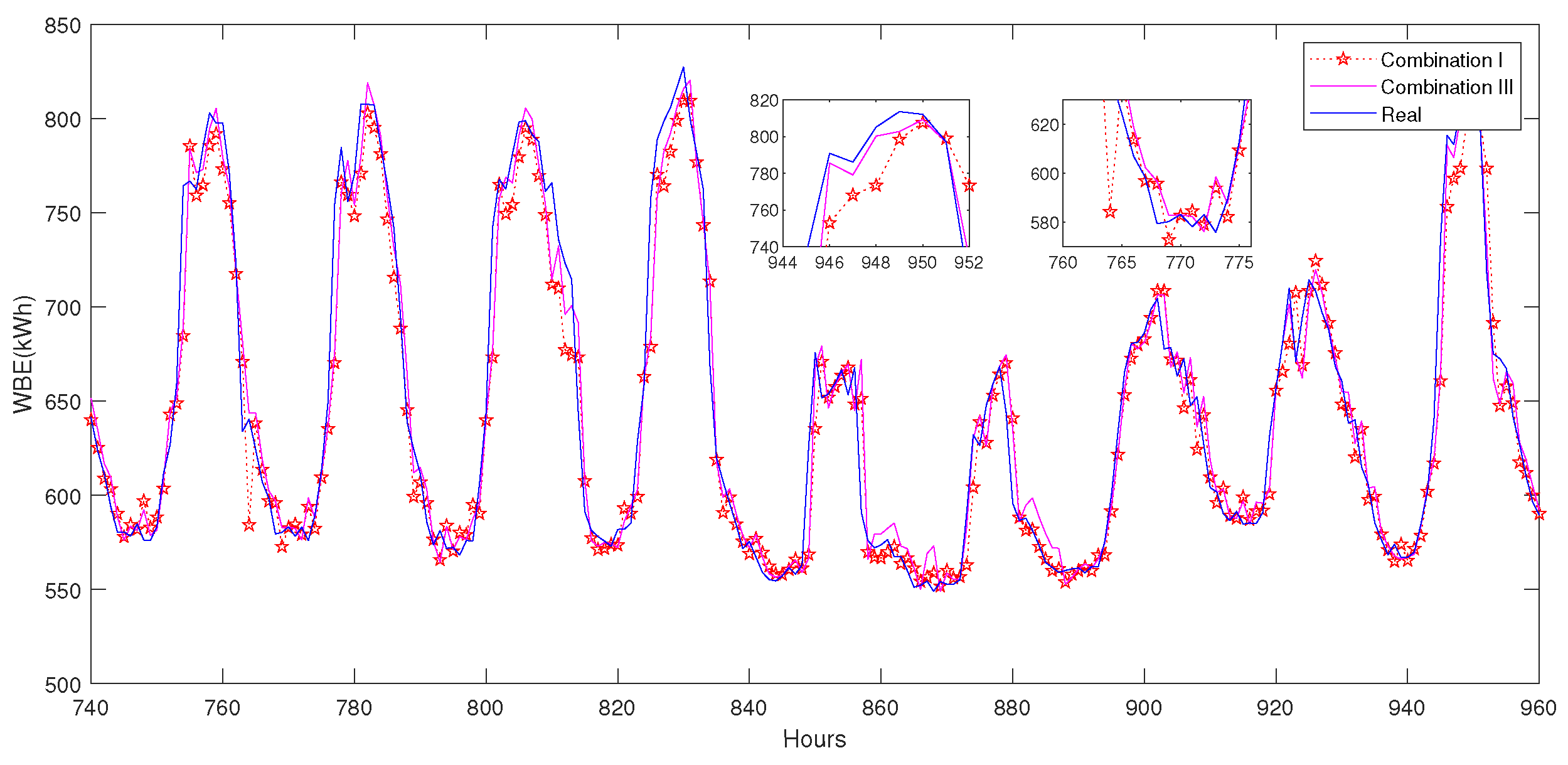
3.2.3. Results
3.3. Campus Building Case B
3.3.1. Description of Target and Source Buildings
3.3.2. Data Clustering for Target Domain and Data Selection from Similar Building
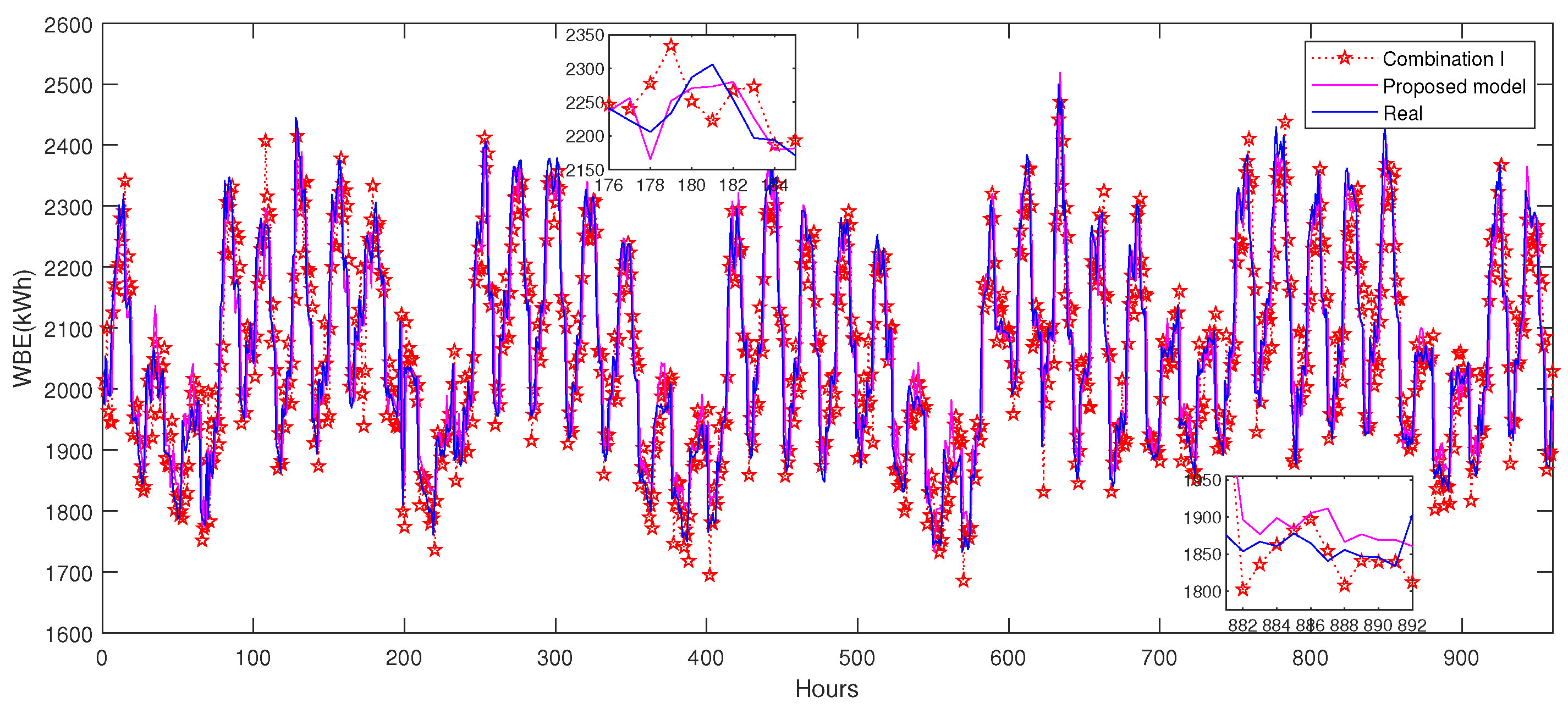
3.3.3. Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AdaBoost | adaptive boosting |
| ap | amplitude proportion |
| ASHRAE | American Society of Heating Refrigerating and Air-conditioning Engineers |
| BP | back propagation neural network |
| DTW | dynamic time warping |
| ELM | extreme learning machine |
| FCM | fuzzy C-mean |
| Elman | Elman recurrent neural network |
| iTrAdaBoost | improved transfer adaptive boosting algorithm |
| IBTL | instance-based transfer learning |
| KNN | K-nearest neighbors |
| LSH | locality sensitive hashing |
| LSTM | long short-term memory |
| MBTL | model-based transfer learning |
| MMD | maximum mean discrepancy |
| MIC | maximum information coefficient |
| MAE | mean absolute error |
| MAPE | mean absolute percentage error |
| MK-MMD | multi-core maximum mean discrepancy |
| NNS | nearest neighbor search |
| RBF | radial basis function |
| RF | random forest |
| RMSE | root mean square error |
| T-SNE | t-distributed stochastic neighbor embedding |
| WD | Wasserstein distance |
| label space | |
| M | the set number of building data |
| N | the feature number of each set |
| p-Wasserstein distance | |
| weighting update factor | |
| threshold | |
| domain feature space |
References
- Dechamps, P. The IEA World Energy Outlook 2022—A brief analysis and implications. Eur. Energy Clim. J. 2023, 11, 100–103. [Google Scholar] [CrossRef]
- Al-Rakhami, M.; Gumaei, A.; Alsanad, A.; Alamri, A.; Hassan, M.M. An ensemble learning approach for accurate energy load prediction in residential buildings. IEEE Access 2019, 7, 48328–48338. [Google Scholar] [CrossRef]
- Chen, Z.; Chen, Y.; Xiao, T.; Wang, H.; Hou, P. A novel short-term load forecasting framework based on time-series clustering and early classification algorithm. Energy Build. 2021, 251, 111375. [Google Scholar] [CrossRef]
- Li, K.; Tian, J.; Xue, W.; Tan, G. Short-term electricity consumption prediction for buildings using data-driven swarm intelligence based ensemble model. Energy Build. 2021, 231, 110558. [Google Scholar] [CrossRef]
- Filgueiras, D.B.; Coelho da Silva, F.L. A study on the prediction of electricity consumption considering the energy efficiency measures—Applied in case of the Brazilian public sector. Energy Effic. 2023, 16, 94. [Google Scholar] [CrossRef]
- Zhou, X.; Sun, J.; Tian, Y.; Lu, B.; Hang, Y.; Chen, Q. Hyperspectral technique combined with deep learning algorithm for detection of compound heavy metals in lettuce—ScienceDirect. Food Chem. 2020, 321, 126503. [Google Scholar] [CrossRef]
- Pavlatos, C.; Makris, E.; Fotis, G.; Vita, V.; Mladenov, V. Enhancing Electrical Load Prediction Using a Bidirectional LSTM Neural Network. Electronics 2023, 12, 4652. [Google Scholar] [CrossRef]
- Chen, C.; Zhu, W.; Steibel, J.; Siegford, J.; Norton, T.J. Classification of drinking and drinker-playing in pigs by a video-based deep learning method. Biosyst. Eng. 2020, 196, 1. [Google Scholar] [CrossRef]
- Liu, J.; Abbas, I.; Noor, R.S. Development of Deep Learning-Based Variable Rate Agrochemical Spraying System for Targeted Weeds Control in Strawberry Crop. Agronomy 2021, 11, 1480. [Google Scholar] [CrossRef]
- Smola, A.J.; Gretton, A.; Borgwardt, K. Maximum mean discrepancy. In Proceedings of the 13th International Conference, ICONIP, Hong Kong, China, 3–6 October 2006; pp. 3–6. [Google Scholar]
- Panaretos, V.M.; Zemel, Y. Statistical aspects of Wasserstein distances. Annu. Rev. Stat. Appl. 2019, 6, 405–431. [Google Scholar] [CrossRef]
- Kinney, J.B.; Atwal, G.S. Equitability, mutual information, and the maximal information coefficient. Proc. Natl. Acad. Sci. USA 2014, 111, 3354–3359. [Google Scholar] [CrossRef] [PubMed]
- Borgwardt, K.M.; Gretton, A.; Rasch, M.J.; Kriegel, H.P.; Schölkopf, B.; Smola, A.J. Integrating structured biological data by kernel maximum mean discrepancy. Bioinformatics 2006, 22, e49–e57. [Google Scholar] [CrossRef] [PubMed]
- Li, K.; Wei, B.; Tang, Q.; Liu, Y. A data-efficient building electricity load forecasting method based on maximum mean discrepancy and improved TrAdaBoost algorithm. Energies 2022, 15, 8780. [Google Scholar] [CrossRef]
- Lu, Y.; Wang, G.; Huang, S. A short-term load forecasting model based on mixup and transfer learning. Electr. Power Syst. Res. 2022, 207, 107837. [Google Scholar] [CrossRef]
- Wei, N.; Yin, C.; Yin, L.; Tan, J.; Liu, J.; Wang, S.; Qiao, W.; Zeng, F. Short-term load forecasting based on WM algorithm and transfer learning model. Appl. Energy 2024, 353, 122087. [Google Scholar] [CrossRef]
- Yuan, Y.; Chen, Z.; Wang, Z.; Sun, Y.; Chen, Y. Attention mechanism-based transfer learning model for day-ahead energy demand forecasting of shopping mall buildings. Energy 2023, 270, 126878. [Google Scholar] [CrossRef]
- Tian, Y.; Sehovac, L.; Grolinger, K. Similarity-based chained transfer learning for energy forecasting with big data. IEEE Access 2019, 7, 139895–139908. [Google Scholar] [CrossRef]
- Li, Y.; Bao, T.; Chen, H.; Zhang, K.; Shu, X.; Chen, Z.; Hu, Y. A large-scale sensor missing data imputation framework for dams using deep learning and transfer learning strategy. Measurement 2021, 178, 109377. [Google Scholar] [CrossRef]
- Gao, N.; Shao, W.; Rahaman, M.S.; Zhai, J.; David, K.; Salim, F.D. Transfer learning for thermal comfort prediction in multiple cities. Build. Environ. 2021, 195, 107725. [Google Scholar] [CrossRef]
- Li, A.; Xiao, F.; Fan, C.; Hu, M. Development of an ANN-based building energy model for information-poor buildings using transfer learning. Build. Simul. 2020, 14, 1–13. [Google Scholar] [CrossRef]
- Pardamean, B.; Muljo, H.H.; Cenggoro, T.W.; Chandra, B.J.; Rahutomo, R. Using transfer learning for smart building management system. J. Big Data 2019, 6, 1–12. [Google Scholar] [CrossRef]
- Gao, Y.; Ruan, Y.; Fang, C.; Yin, S. Deep learning and transfer learning models of energy consumption forecasting for a building with poor information data. Energy Build. 2020, 223, 110156. [Google Scholar] [CrossRef]
- Pinto, G.; Wang, Z.; Roy, A.; Hong, T.; Capozzoli, A. Transfer learning for smart buildings: A critical review of algorithms, applications, and future perspectives. Adv. Appl. Energy 2022, 5, 100084. [Google Scholar] [CrossRef]
- Zeng, P.; Sheng, C.; Jin, M. A learning framework based on weighted knowledge transfer for holiday load forecasting. J. Mod. Power Syst. Clean Energy 2019, 7, 329–339. [Google Scholar] [CrossRef]
- Li, G.; Wu, Y.; Liu, J.; Fang, X.; Wang, Z. Performance evaluation of short-term cross-building energy predictions using deep transfer learning strategies. Energy Build. 2022, 275, 112461. [Google Scholar] [CrossRef]
- Li, Z.; Liu, B.; Xiao, Y. Cluster and dynamic-TrAdaBoost-based transfer learning for text classification. In Proceedings of the 13th International Conference on Natural Computation, Fuzzy Systems and Knowledge Discovery (ICNC-FSKD), Guilin, China, 29–31 July 2017; IEEE: New York, NY, USA, 2017; pp. 2291–2295. [Google Scholar]
- Tong, X.; Xu, X.; Huang, S.L.; Zheng, L. A mathematical framework for quantifying transferability in multi-source transfer learning. Adv. Neural Inf. Process. Syst. 2021, 34, 26103–26116. [Google Scholar]
- Lu, H.; Wu, J.; Ruan, Y.; Qian, F.; Meng, H.; Gao, Y.; Xu, T. A multi-source transfer learning model based on LSTM and domain adaptation for building energy prediction. Int. J. Electr. Power Energy Syst. 2023, 149, 109024. [Google Scholar] [CrossRef]
- Wei, B.; Li, K.; Zhou, S.; Xue, W.; Tan, G. An instance based multi-source transfer learning strategy for building’s short-term electricity loads prediction under sparse data scenarios. J. Build. Eng. 2024, 85, 108713. [Google Scholar] [CrossRef]
- Qian, F.; Ruan, Y.; Lu, H.; Meng, H.; Xu, T. Enhancing source domain availability through data and feature transfer learning for building power load forecasting. In Building Simulation; Springer: Berlin/Heidelberg, Germany, 2024; pp. 1–14. [Google Scholar]
- Li, K.; Zhang, J.; Chen, X.; Xue, W. Building’s hourly electrical load prediction based on data clustering and ensemble learning strategy. Energy Build. 2022, 261, 111943. [Google Scholar] [CrossRef]
- Wu, X.; Zhou, J.; Wu, B.; Sun, J.; Dai, C. Identification of tea varieties by mid-infrared diffuse reflectance spectroscopy coupled with a possibilistic fuzzy c-means clustering with a fuzzy covariance matrix. J. Food Process. Eng. 2019, 42, e13298. [Google Scholar] [CrossRef]
- Li, L. Combining Transfer Learning and Ensemble Algorithms for Improved Citrus Leaf Disease Classification. Agriculture 2024, 14, 1549. [Google Scholar] [CrossRef]
- Dai, W.; Yang, Q.; Xue, G.R.; Yu, Y. Boosting for transfer learning. In Proceedings of the 24th International Conference on Machine Learning, Corvallis, OR, USA, 20–24 June 2007; pp. 193–200. [Google Scholar]
- Elman, J.L. Finding structure in time. Cogn. Sci. 1990, 14, 179–211. [Google Scholar] [CrossRef]
- Shen, T.; Zou, X.; Shi, J.; Li, Z.; Huang, X.; Yiwei, X.; Wu, C. Determination geographical origin and flavonoids content of goji berry using near-infrared spectroscopy and chemometrics. Food Anal. Methods 2016, 9, 68–79. [Google Scholar]
- Che, J.; Wang, J.; Tang, Y. Optimal training subset in a support vector regression electric load forecasting model. Appl. Soft Comput. 2012, 12, 1523–1531. [Google Scholar] [CrossRef]
- Andoni, A.; Indyk, P.; Nguyen, H.L.; Razenshteyn, I. Beyond locality-sensitive hashing. In Proceedings of the Twenty-Fifth Annual ACM-SIAM Symposium on Discrete Algorithms, SIAM, Portland, OR, USA, 5–7 January 2014; pp. 1018–1028. [Google Scholar]
- Kalantari, I.; McDonald, G. A data structure and an algorithm for the nearest point problem. IEEE Trans. Softw. Eng. 1983, 5, 631–634. [Google Scholar] [CrossRef]
- Ohlsson, M.B.; Peterson, C.O.; Pi, H.; Rognvaldsson, T.S.; Soderberg, B.P. Predicting System Loads with Artificial Neural Networks—Methods and Results from The Great Energy Predictor Shootout. Ashrae-Trans. Am. Soc. Heat. Refrig. Airconditioning Engin. 1994, 100, 1063–1074. [Google Scholar]
- Huang, D.; He, S.; He, X.; Zhu, X. Prediction of wind loads on high-rise building using a BP neural network combined with POD. J. Wind. Eng. Ind. Aerodyn. 2017, 170, 1–17. [Google Scholar]
- Liu, C.; Sun, B.; Zhang, C.; Li, F. A hybrid prediction model for residential electricity consumption using holt-winters and extreme learning machine. Appl. Energy 2020, 275, 115383. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, Y.; Zeng, R.; Srinivasan, R.S.; Ahrentzen, S. Random Forest based hourly building energy prediction. Energy Build. 2018, 171, 11–25. [Google Scholar] [CrossRef]
- Zhang, A.; Zhang, L. RBF neural networks for the prediction of building interference effects. Comput. Struct. 2004, 82, 2333–2339. [Google Scholar] [CrossRef]
- Zhou, X.; Lin, W.; Kumar, R.; Cui, P.; Ma, Z. A data-driven strategy using long short term memory models and reinforcement learning to predict building electricity consumption. Appl. Energy 2022, 306, 118078. [Google Scholar] [CrossRef]












| Literature | Source Domain | Similarity Judgment Method | Predictive Model | Building Type |
|---|---|---|---|---|
| Li et al. (2022) [26] | Single source | MMD | DANN-LSTM | Office/Education |
| Li et al. (2022) [14] | Single source | MMD | iTrAdaboost-BP | Education |
| Lu et al. (2022) [15] | Single source | MIC | LSTM | Residence |
| Yuan et al. (2023) [17] | Single source | MMD | Attention-CNN-LSTM | Commerce |
| Lu et al. (2023) [29] | Multi-source | DTW | MK-MMD-LSTM | Railway building |
| Qian et al. (2024) [31] | Multi-source | DTW | iTrAdaboost-LSTM | Office/Education |
| Li et al. (2024) [30] | Multi-source | WD | NNS-iTrAdaboost-LSTM | Education |
| Building No. | WD | Building Type | Square Feet | Air Temperature (°C) | Sea Level Pressure |
|---|---|---|---|---|---|
| Target | - | Education | 182,943 | 0–38.3 | 987.3 –1035.9 |
| S1(#1092) | 1006.48 | Office | 105,167 | −26.1–37.8 | 987.2–1046.5 |
| S2(#1289) | 1009.99 | Education | 194,441 | −17.2–35.6 | 982.6–1043.4 |
| S3(#780) | 1011.23 | Education | 120,836 | −16.1–36.7 | 986.8–1042.7 |
| S4(#192) | 1011.57 | Education | 151,637 | 2.2–48.3 | 996.1–1032.2 |
| S5(#1328) | 1014.73 | Education | 279,840 | −28.8–11.8 | 983.6–1036.6 |
| S1447(#803) | 5093.44 | Education | 182,986 | −28.8–33.9 | 983.6–1043.8 |
| S1448(#794) | 5151.56 | Education | 731,945 | −28.8–33.9 | 983.6–1043.8 |
| S1449(#801) | 5326.67 | Education | 484,376 | −28.8–33.9 | 983.6–1043.8 |
| Model | Transfer Learning | Data Clustering | MAE (kWh) | MAPE (%) | RMSE (kWh) |
|---|---|---|---|---|---|
| Elman | No | No | 26.94 | 3.80 | 35.17 |
| iTrAdaboost-Elman | Yes | No | 18.39 | 2.63 | 24.31 |
| Proposed model | Yes | Yes | 13.68 | 1.96 | 19.31 |
| Transfer Learning | Data Clustering | LSH | “Peak” Data | “Valley” Data | “Others” Data | Integrated |
|---|---|---|---|---|---|---|
| I. All data | No | No | 2.22 | 1.59 | 3.40 | 2.63 |
| II. All clusters | Yes | No | 2.10 | 1.43 | 3.26 | 2.50 |
| III. Clusters of Peak/Valley | Yes | No | 2.10 | 1.43 | 2.29 | 2.05 |
| Proposed model | Yes | Yes | 1.91 | 1.30 | 2.29 | 1.96 |
| Classification | Classification | Amounts of | Prediction Accuracy (MAPE, %) | |||
|---|---|---|---|---|---|---|
| Method | Accuracy (%) | Clustered Data | “Peak” | “Valley” | “Others” | Overall |
| Timestamp | 100.0 | 226/243/491 | 1.63 | 1.13 | 2.50 | 1.95 |
| KNN (K = 4) | 71.9 | 349/172/439 | 2.02 | 1.40 | 2.34 | 2.06 |
| KNN (K = 5) | 74.2 | 317/198/445 | 1.96 | 1.30 | 2.29 | 1.96 |
| KNN (K = 6) | 72.8 | 347/181/432 | 2.02 | 1.37 | 2.32 | 2.03 |
| LSH Usage | Value of Threshold () | Amount of Selected Data | MAE (kWh) | MAPE (%) | RMSE (kWh) | Time (s) |
|---|---|---|---|---|---|---|
| No | − | − | 18.39 | 2.63 | 24.31 | 79.5 |
| Yes | 0.30 | 2024 | 14.00 | 2.01 | 19.48 | 120.9 |
| Yes | 0.35 | 1701 | 14.10 | 2.02 | 19.50 | 110.5 |
| Yes | 0.40 | 523 | 13.68 | 1.96 | 19.31 | 87.0 |
| Yes | 0.45 | 183 | 14.30 | 2.06 | 19.65 | 82.7 |
| Model | MAE (kWh) | MAPE (%) | RMSE (kWh) | Time (s) |
|---|---|---|---|---|
| Elman | 26.94 | 3.80 | 35.17 | 1.72 |
| BP [42] | 32.11 | 4.71 | 40.70 | 1.25 |
| ELM [43] | 34.30 | 5.01 | 45.07 | 1.13 |
| RF [44] | 27.64 | 4.03 | 35.13 | 1.17 |
| RBF [45] | 27.39 | 3.97 | 37.51 | 19.12 |
| LSTM [46] | 32.13 | 4.68 | 40.43 | 16.78 |
| MMD-iTrAdaboost-BP [14] | 18.83 | 2.71 | 25.05 | 79.5 |
| NNS-iTrAdaboost-LSTM [30] | 17.81 | 2.56 | 23.00 | 436.7 |
| Proposed model | 13.68 | 1.96 | 19.31 | 87.0 |
| Building No. | WD | Building Type | Square Feet | Air Temperature (°C) | Sea Level Pressure |
|---|---|---|---|---|---|
| S1 (#375) | 1040.18 | Office | 850,354 | −10.6–37.8 | 991.5–1040.9 |
| S2 (#223) | 1121.81 | Education | 261,188 | 2.2–47.2 | 999.3–1028.2 |
| S3 (#365) | 1181.60 | Healthcare | 819,577 | −10.6–37.8 | 991.5–1040.9 |
| S4 (#645) | 1220.96 | Education | 304,333 | 1.1–35.0 | 999.8–1031.7 |
| Transfer Learning | Data Clustering | LSH | MAE (kWh) | MAPE (%) | RMSE (kWh) |
|---|---|---|---|---|---|
| I. All data | No | No | 56.60 | 2.73 | 77.02 |
| II. All clusters | Yes | No | 49.29 | 2.39 | 67.70 |
| III. Clusters of Peak/Valley | Yes | No | 44.32 | 2.14 | 62.22 |
| Proposed model | Yes | Yes | 42.95 | 2.09 | 60.79 |
| Model | Clustering | MAE (kWh) | MAPE (%) | RMSE (kWh) |
|---|---|---|---|---|
| Elman | No | 489.16 | 21.94 | 646.66 |
| iTrAdaboost-Elman | No | 343.12 | 15.85 | 433.51 |
| Proposed model | Yes | 254.60 | 12.23 | 326.04 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, K.; Zhou, S.; Zhao, M.; Wei, B. Short-Term Building Electrical Load Prediction by Peak Data Clustering and Transfer Learning Strategy. Energies 2025, 18, 686. https://doi.org/10.3390/en18030686
Li K, Zhou S, Zhao M, Wei B. Short-Term Building Electrical Load Prediction by Peak Data Clustering and Transfer Learning Strategy. Energies. 2025; 18(3):686. https://doi.org/10.3390/en18030686
Chicago/Turabian StyleLi, Kangji, Shiyi Zhou, Mengtao Zhao, and Borui Wei. 2025. "Short-Term Building Electrical Load Prediction by Peak Data Clustering and Transfer Learning Strategy" Energies 18, no. 3: 686. https://doi.org/10.3390/en18030686
APA StyleLi, K., Zhou, S., Zhao, M., & Wei, B. (2025). Short-Term Building Electrical Load Prediction by Peak Data Clustering and Transfer Learning Strategy. Energies, 18(3), 686. https://doi.org/10.3390/en18030686







