Modelling and Transient Simulation of District Heating Networks Based on a Control Theory Approach †
Abstract
1. Introduction
2. Materials and Methods
2.1. Hydraulic Model
2.2. Thermodynamic Model
2.3. Comprehensive Model
3. Results
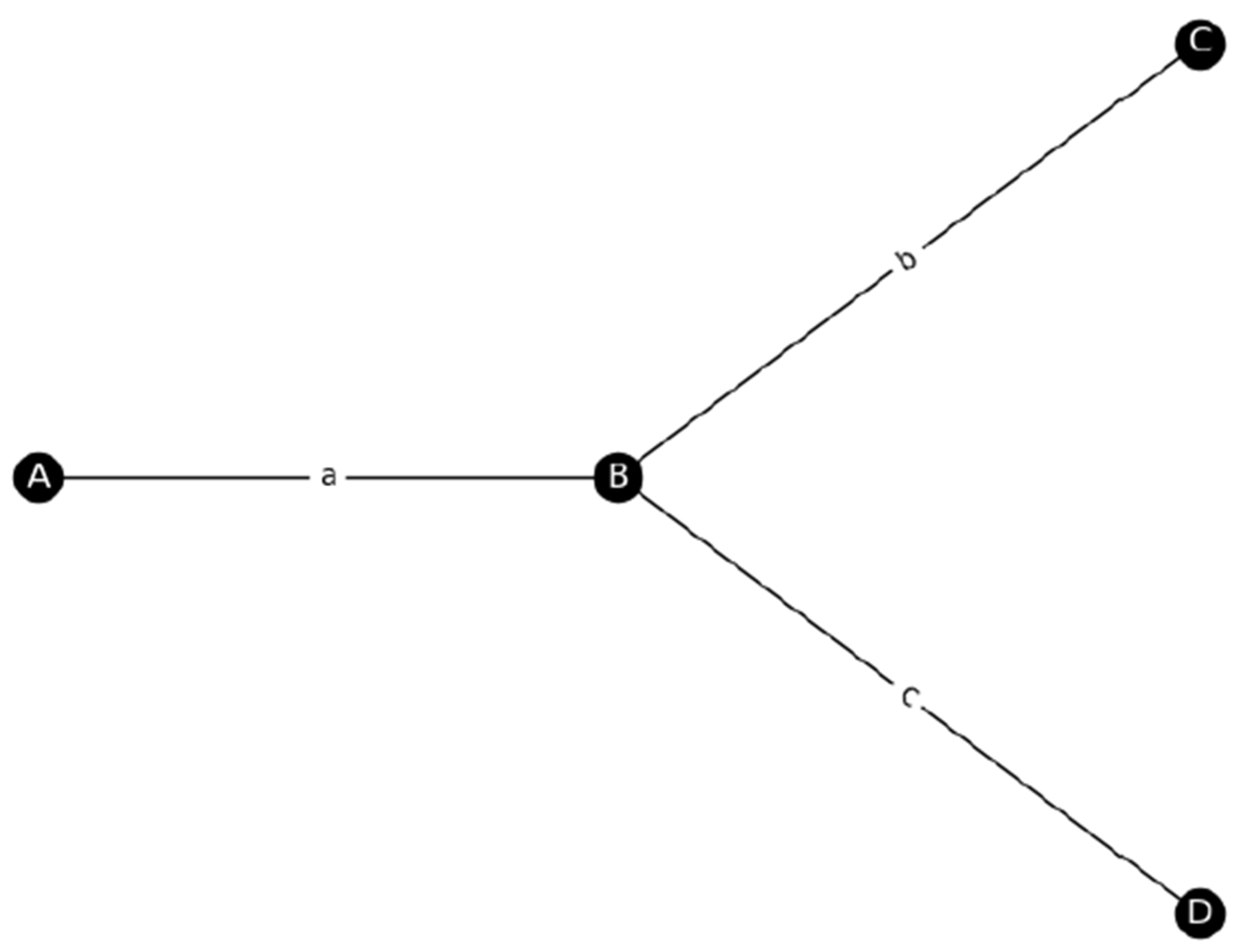
3.1. Simulations of Single-Looped Networks
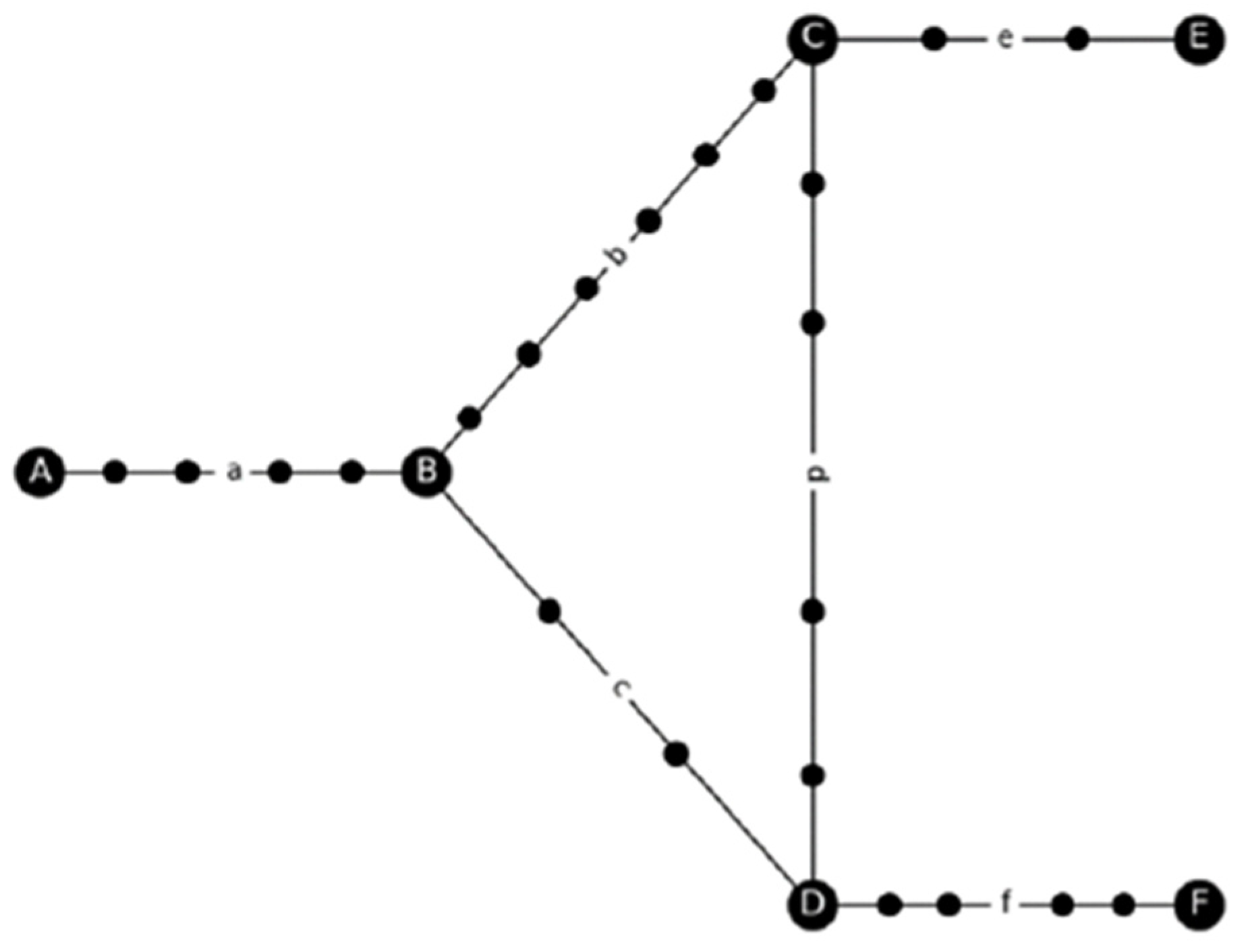
3.2. Simulations of Multiple-Looped Networks
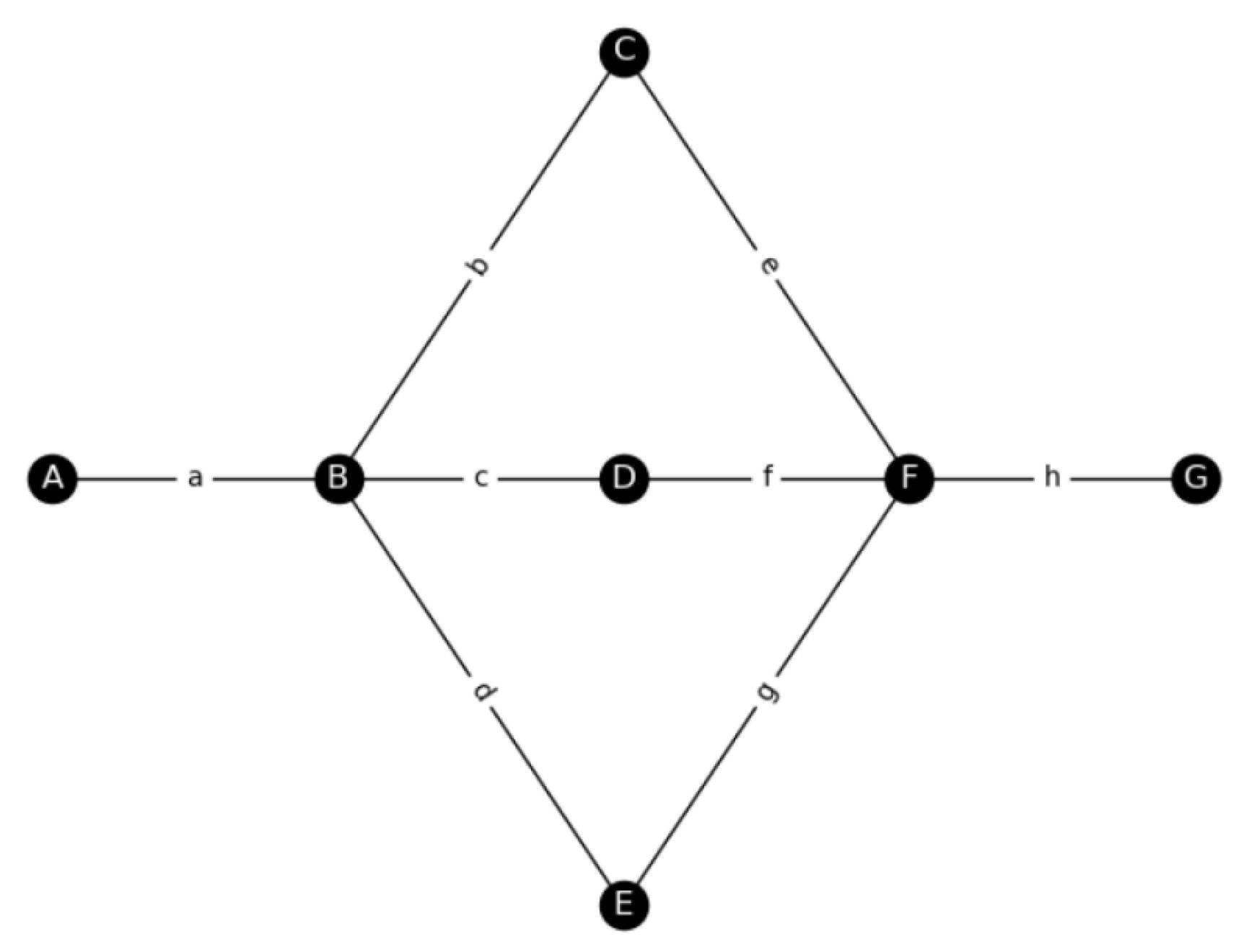
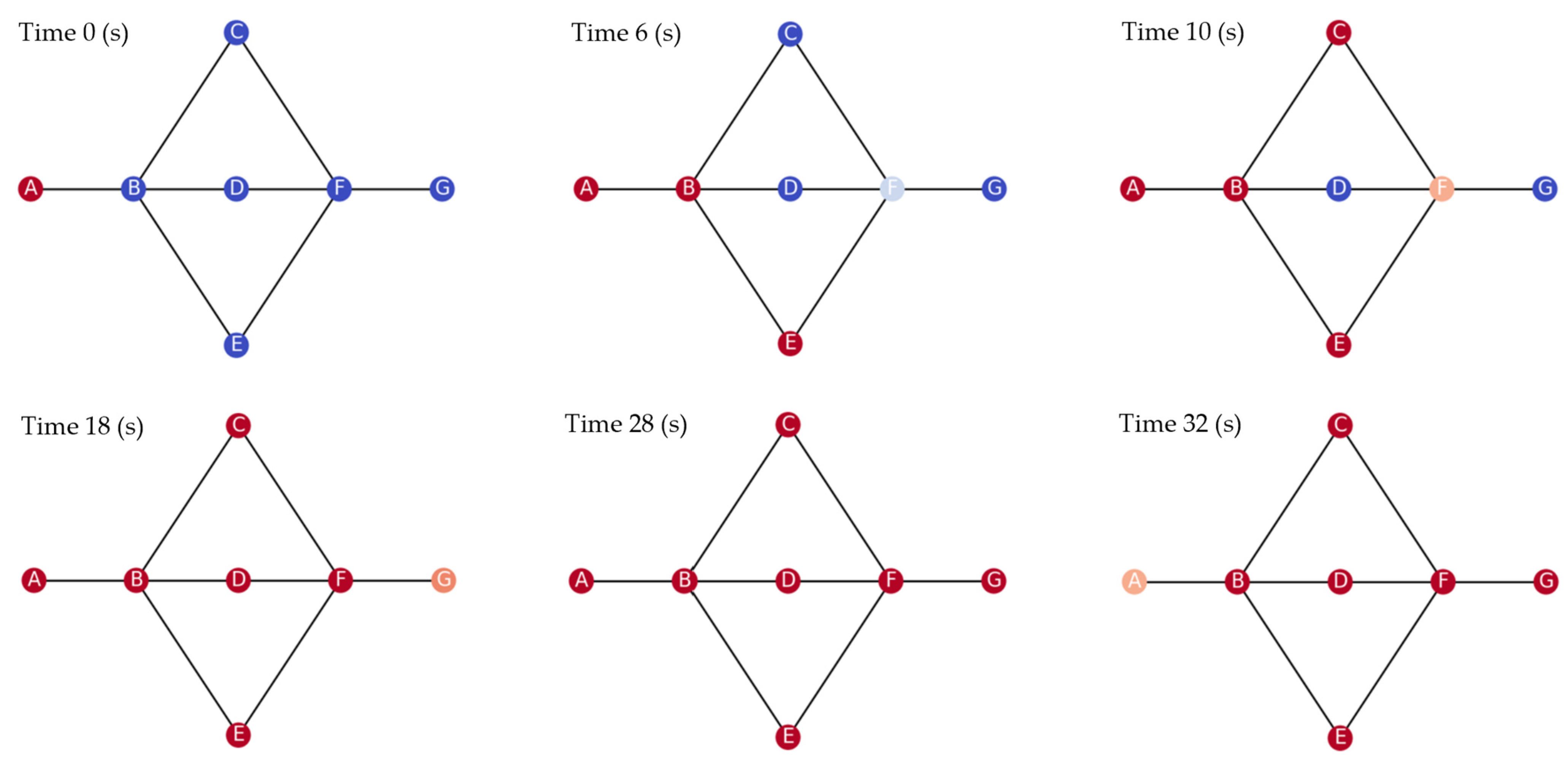
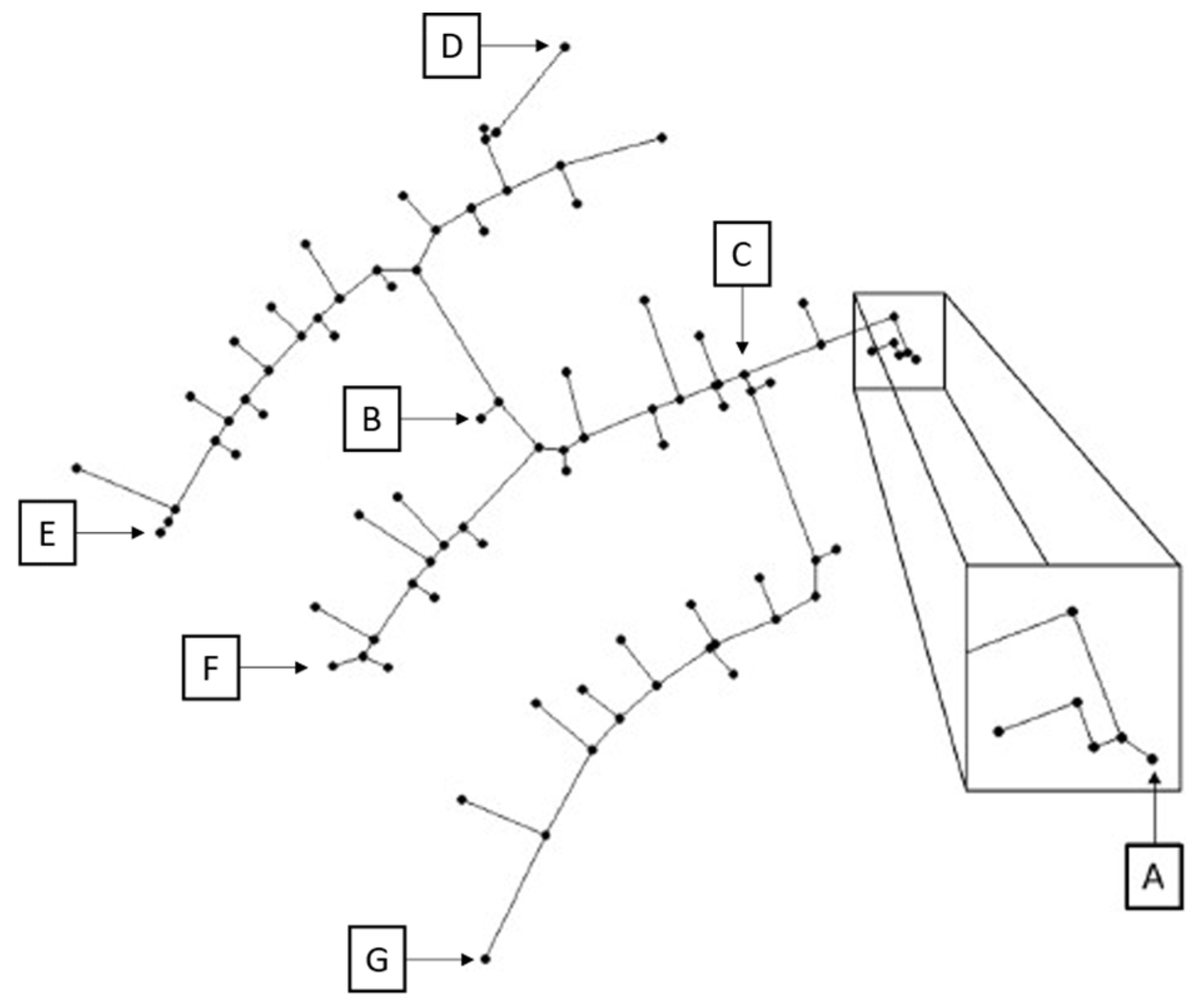
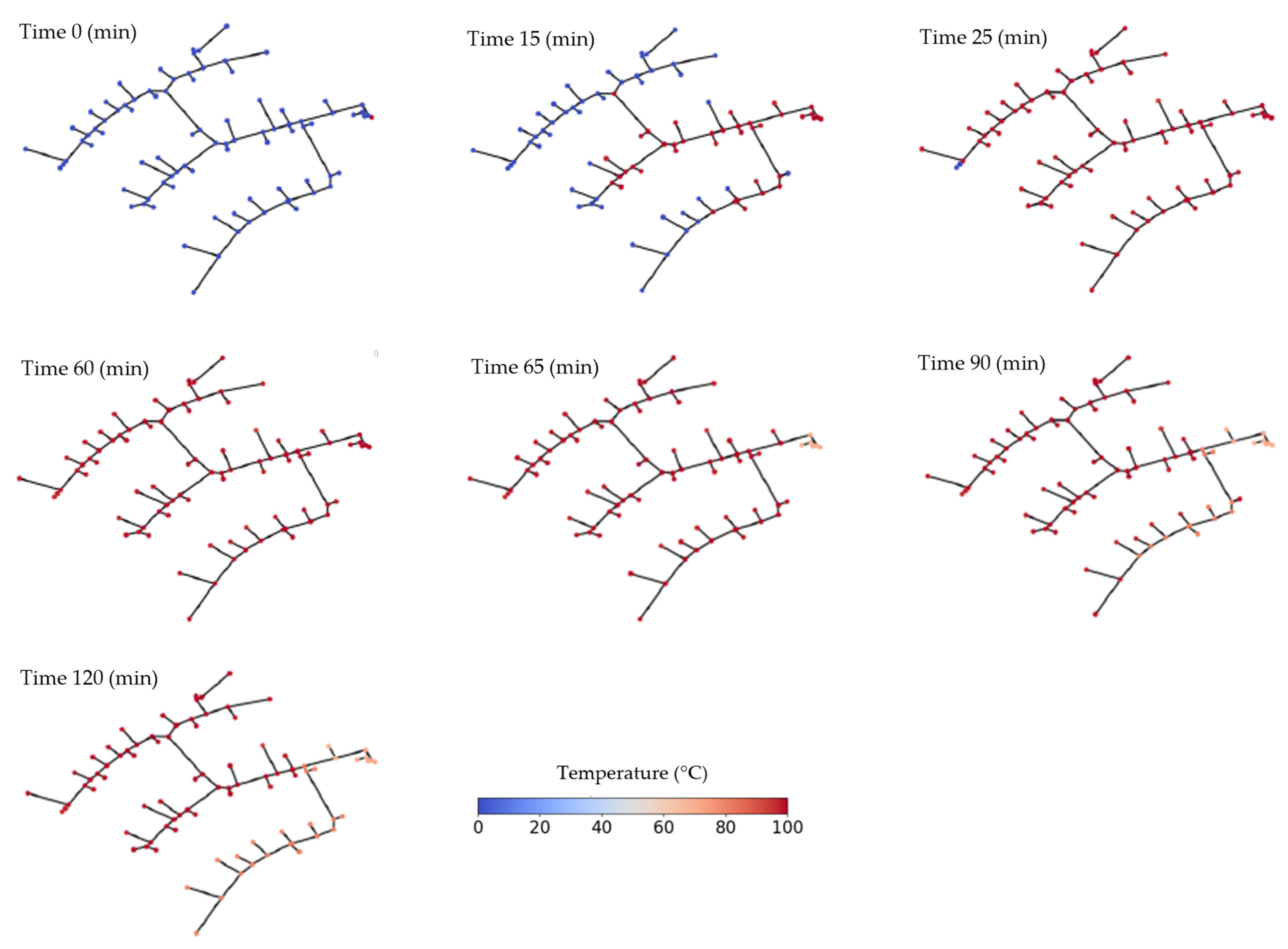
3.3. Simulations of a Non-Looped Networks
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| A | / | State-space matrix |
| x(t) | / | State-space variable |
| B | / | Input matrix |
| u(t) | / | Input variable |
| / | Change in state-space variable | |
| / | Hydraulic model matrix | |
| (kg/s) | Unknown massflow | |
| (kg/s) | Massflow sources | |
| / | Incidence matrix | |
| / | Arbitrary shortened incidence matrix | |
| / | Adjusted loop matrix | |
| / | Loop matrix | |
| K | (-) | Pipe resistance coefficient |
| L | (m) | Pipe length |
| (-) | Friction factor | |
| D | (m) | Inner pipe diameter |
| (kg/m3) | Density | |
| (m/s2) | Gravitational acceleration | |
| J | / | Jacobi matrix |
| / | System of equations | |
| (J/s) | Change in internal energy | |
| h | (J/kg) | Enthalpy |
| c | (J/kg) | Kinetic energy |
| z | (J/kg) | Potential energy |
| (J/s) | Heat loss | |
| m | (kg) | Mass |
| T | (°C) | Temperature |
| cp | (J/(KgK)) | Heat capacity |
| U | (W/(m2K)) | Heatloss coefficient |
| / | Thermodynamical model matrix | |
| dt | (s) | Timestep |
| t | (s) | Time |
| num | / | Number of sub-nodes |
| Indices | ||
| / | Incoming values | |
| / | Outgoing values | |
| / | Node values | |
| / | Pipe values | |
| / | Values of the current timestep | |
| i | / | Pipe identification number |
Appendix A

| Pipe | Massflow Simulation (kg/s) | Massflow Epanet (kg/s) |
|---|---|---|
| A | 2 | 2 |
| B | 2 | 2 |
| Simulation | Theoretical Values | ||||||
|---|---|---|---|---|---|---|---|
| Time (s) | A (°C) | B (°C) | C (°C) | Time (s) | A (°C) | B (°C) | C (°C) |
| 0 | 100 | 0 | 0 | 0 | 100 | 0 | 0 |
| 5 | 100 | 99.99 | 0 | 3.76 | 100 | 99.99 | 0 |
| 10 | 100 | 99.99 | 0 | - | 100 | 99.99 | 0 |
| 15 | 100 | 99.99 | 99.76 | 11.27 | 100 | 99.99 | 99.76 |
| 20 | 100 | 99.99 | 99.76 | - | 100 | 99.99 | 99.76 |
| 25 | 100 | 99.99 | 99.76 | - | 100 | 99.99 | 99.76 |
| 30 | 100 | 99.99 | 99.76 | - | 100 | 99.99 | 99.76 |
| 0–30 s | 30–60 s | |||
|---|---|---|---|---|
| Pipe | Massflow Simulation (kg/s) | Massflow Epanet (kg/s) | Massflow Simulation (kg/s) | Massflow Epanet (kg/s) |
| a | 4 | 4 | 4 | 4 |
| b | 1 | 1 | 3 | 3 |
| c | 3 | 3 | 1 | 1 |
| Simulation | Theoretical Values | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Time (s) | A (°C) | B (°C) | C (°C) | D (°C) | Time (s) | A (°C) | B (°C) | C (°C) | D (°C) | |
| 0–30 s | 0 | 100 | 0 | 0 | 0 | 0 | 100 | 0 | 0 | 0 |
| 2 | 100 | 95.03 | 0 | 0 | 1.88 | 100 | 99.999 | 0 | 0 | |
| 4 | 100 | 99.99 | 0 | 0 | - | 100 | 99.999 | 0 | 0 | |
| 6 | 100 | 99.99 | 0 | 99.998 | 4.38 | 100 | 99.999 | 0 | 99.998 | |
| 10 | 100 | 99.99 | 99.997 | 99.998 | 9.4 | 100 | 99.999 | 99.997 | 99.998 | |
| 12 | 100 | 99.99 | 99.997 | 99.998 | - | 100 | 99.999 | 99.997 | 99.998 | |
| 30–60 s | 14 | 100 | 99.99 | 99.996 | 99.998 | 14 | 100 | - | - | - |
| 16 | 100 | 99.99 | 99.998 | 99.998 | 15.88 | 100 | 99.99 | - | - | |
| 18 | 100 | 99.99 | 99.998 | 99.997 | 16.51 | 100 | 99.99 | 99.998 | - | |
| 20 | 100 | 99.99 | 99.998 | 99.997 | - | 100 | 99.99 | 99.998 | - | |
| 22 | 100 | 99.99 | 99.998 | 99.996 | 21.52 | 100 | 99.99 | 99.998 | 99.996 | |
| 28 | 100 | 99.99 | 99.998 | 99.996 | - | 100 | 99.99 | 99.998 | 99.996 | |
| 30 | 100 | 99.9992 | 99.9982 | 99.9962 | - | 100 | 99.9992 | 99.9982 | 99.9962 | |
References
- Schojda, D.; Scheipers, J.; Roes, J.; Hoster, H. Modelling and Simulation of Transient District Heating Networks Based on a Control Theory Approach. In Proceedings of the 19th Conference on Sustainable Development of Energy Water and Environment Systems (SDEWES 2024), Rome, Italy, 9–13 September 2024. [Google Scholar]
- Jie, P.; Tian, Z.; Yuan, S.; Zhu, N. Modeling the dynamic characteristics of a district heating network. Energy 2012, 39, 126–134. [Google Scholar] [CrossRef]
- Stevanovic, V.D.; Zivkovic, B.; Prica, S.; Maslovaric, B.; Karamarkovic, V.; Trkulja, V. Prediction of thermal transients in district heating systems. Energy Convers. Manag. 2009, 50, 2167–2173. [Google Scholar] [CrossRef]
- Gabrielaitiene, I.; Bøhm, B.; Sunden, B. Modelling temperature dynamics of a district heating system in Naestved, Denmark—A case study. Energy Convers. Manag. 2007, 48, 78–86. [Google Scholar] [CrossRef]
- Del Hoyo Arce, I.; López, S.H.; Perez, S.L.; Rämä, M.; Klobut, K.; Febres, J.A. Models for fast modelling of district heating and cooling networks. Renew. Sustain. Energy Rev. 2018, 82, 1863–1873. [Google Scholar] [CrossRef]
- Oppelt, T.; Urbaneck, T.; Gross, U.; Platzer, B. Dynamic thermo-hydraulic model of district cooling networks. Appl. Therm. Eng. 2016, 102, 336–345. [Google Scholar] [CrossRef]
- Licklederer, T.; Hamacher, T.; Kramer, M.; Perić, V.S. Thermohydraulic model of Smart Thermal Grids with bidirectional power flow between prosumers. Energy 2021, 230, 120825. [Google Scholar] [CrossRef]
- van der Heijde, B.; Fuchs, M.; Ribas Tugores, C.; Schweiger, G.; Sartor, K.; Basciotti, D.; Helsen, L. Dynamic equation-based thermo-hydraulic pipe model for district heating and cooling systems. Energy Convers. Manag. 2017, 151, 158–169. [Google Scholar] [CrossRef]
- Guelpa, E. Impact of network modelling in the analysis of district heating systems. Energy 2020, 213, 118393. [Google Scholar] [CrossRef]
- Menapace, A.; Avesani, D. Global Gradient Algorithm Extension to Distributed Pressure Driven Pipe Demand Model. Water Resour Manag. 2019, 33, 1717–1736. [Google Scholar] [CrossRef]
- Vesterlund, M.; Toffolo, A.; Dahl, J. Simulation and analysis of a meshed district heating network. Energy Convers. Manag. 2016, 122, 63–73. [Google Scholar] [CrossRef]
- Becker, G.; Klemm, C.; Vennemann, P. Open Source District Heating Modeling Tools—A Comparative Study. Energies 2022, 15, 8277. [Google Scholar] [CrossRef]
- Sartor, K.; Thomas, D.; Dewallef, P. A comparative study for simulating heat transport in large district heating networks. Int. J. Heat Technol. 2018, 36, 301–308. [Google Scholar] [CrossRef]
- Blommaert, M.; Wack, Y.; Baelmans, M. An adjoint optimization approach for the topological design of large-scale district heating networks based on nonlinear models. Appl. Energy 2020, 280, 116025. [Google Scholar] [CrossRef]
- Larsen, H.V.; Pálsson, H.; Bøhm, B.; Ravn, H.F. Aggregated dynamic simulation model of district heating networks. Energy Convers. Manag. 2002, 43, 995–1019. [Google Scholar] [CrossRef]
- Zheng, W.; Hou, Y.; Li, Z. A Dynamic Equivalent Model for District Heating Networks: Formulation, Existence and Application in Distributed Electricity-Heat Operation. IEEE Trans. Smart Grid 2021, 12, 2685–2695. [Google Scholar] [CrossRef]
- Ancona, M.A.; Melino, F.; Peretto, A. An Optimization Procedure for District Heating Networks. Energy Procedia 2014, 61, 278–281. [Google Scholar] [CrossRef]
- Çengel, Y.A. Heat Transfer: A Practical Approach, 2nd ed.; McGraw-Hill Series in Mechanical Engineering; McGraw-Hill: Boston, MA, USA, 2003. [Google Scholar]
- Zhang, S.; Pan, G.; Li, B.; Gu, W.; Fu, J.; Sun, Y. Multi-Timescale Security Evaluation and Regulation of Integrated Electricity and Heating System. IEEE Trans. Smart Grid 2024, 1. [Google Scholar] [CrossRef]
- Jiang, M.; Speetjens, M.; Rindt, C.; Smeulders, D. A data-based reduced-order model for dynamic simulation and control of district-heating networks. Appl. Energy 2023, 340, 121038. [Google Scholar] [CrossRef]
- Bastida, H.; Ugalde-Loo, C.E.; Abeysekera, M.; Qadrdan, M.; Wu, J. Thermal Dynamic Modelling and Temperature Controller Design for a House. Energy Procedia 2019, 158, 2800–2805. [Google Scholar] [CrossRef]
- Chua, L.O.; Lin, P.-M. Computer-Aided Analysis of Electronic Circuits: Algorithms and Computational Techniques; Prentice-Hall Series in Electrical and Computer Engineering; Prentice-Hall: Englewood Cliffs, NJ, USA, 1975. [Google Scholar]
- Liu, X.; Jenkins, N.; Wu, J.; Bagdanavicius, A. Combined Analysis of Electricity and Heat Networks. Energy Procedia 2014, 61, 155–159. [Google Scholar] [CrossRef]
- Liu, X. Combined Analysis of Electricity and Heat Networks. Ph.D. Thesis, Cardiff University, Cardiff, Wales, 2013. [Google Scholar]




| 0–30 s | 30–60 s | |||
|---|---|---|---|---|
| Pipe | Massflow Simulation (kg/s) | Massflow Epanet (kg/s) | Massflow Simulation (kg/s) | Massflow Epanet (kg/s) |
| a | 4 | 4 | 4 | 4 |
| b | 1 | 1 | 3 | 3 |
| c | 3 | 3 | 1 | 1 |
| 0–30 s | 30–60 s | |||
|---|---|---|---|---|
| Pipe | Massflow Simulation (kg/s) | Massflow Epanet (kg/s) | Massflow Simulation (kg/s) | Massflow Epanet (kg/s) |
| a | 4 | 4 | 2 | 2 |
| b | 2.01 | 1.95 | 0.77 | 0.77 |
| c | 1 | 1 | −2 | −2 |
| d | 1.99 | 2.05 | 1.23 | 1.23 |
| e | 1 | 1 | 2 | 2 |
| f | 1.01 | 0.95 | 1.77 | 1.77 |
| Hour 1 | Hour 2 | |||
|---|---|---|---|---|
| Node | Massflow Simulation (kg/s) | Massflow Epanet (kg/s) | Massflow Simulation (kg/s) | Massflow Epanet (kg/s) |
| A | −2.53 | −2.53 | −0.53 | −0.53 |
| B | 0.03 | 0.03 | −1.97 | −1.97 |
| C | 0.73 | 0.73 | 0.73 | 0.73 |
| D | 0.20 | 0.20 | 0.20 | 0.20 |
| E | 0.02 | 0.02 | 0.02 | 0.02 |
| F | 0.24 | 0.24 | 0.24 | 0.24 |
| G | 0.20 | 0.20 | 0.20 | 0.20 |
| Simulation | Theoretical Values | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Time (s) | A (°C) | B (°C) | C (°C) | D (°C) | F (°C) | E (°C) | Time(s) | A (°C) | B (°C) | C (°C) | D (°C) | F (°C) | E (°C) | |
| 0–30 s | 0 | 100 | 0 | 0 | 0 | 0 | 0 | 0 | 100 | 0 | 0 | 0 | 0 | 0 |
| 2 | 100 | 0 | 0 | 0 | 0 | 0 | - | 100 | 0 | 0 | 0 | 0 | 0 | |
| 4 | 100 | 99.67 | 0 | 0 | 0 | 0 | 3.76 | 100 | 99.99 | 0 | 0 | 0 | 0 | |
| 6 | 100 | 99.99 | 0 | 0 | 0 | 0 | - | 100 | 99.99 | 0 | 0 | 0 | 0 | |
| 8 | 100 | 99.99 | 99.99 | 66.26 | 0 | 0 | 7.5/7.54 | 100 | 99.99 | 99.99 | 66.31 | 0 | 0 | |
| 10 | 100 | 99.99 | 99.99 | 66.31 | 0 | 0 | - | 100 | 99.99 | 99.99 | - | 0 | 0 | |
| 12 | 100 | 99.99 | 99.99 | 66.31 | 66.30 | 99.99 | 11.30/11.26 | 100 | 99.99 | 99.99 | - | 66.30 | 99.99 | |
| 14 | 100 | 99.99 | 99.99 | 66.31 | 66.30 | 99.99 | - | 100 | 99.99 | 99.99 | - | - | 99.99 | |
| 16 | 100 | 99.99 | 99.99 | 99.99 | 66.30 | 99.99 | 14.93 | 100 | 99.99 | 99.99 | 99.996 | - | 99.99 | |
| 18 | 100 | 99.99 | 99.99 | 99.99 | 66.30 | 99.99 | - | 100 | 99.99 | 99.99 | 99.996 | - | 99.99 | |
| 20 | 100 | 99.99 | 99.99 | 99.99 | 99.99 | 99.99 | 18.69 | 100 | 99.99 | 99.99 | 99.996 | 99.99 | 99.99 | |
| 30 | 100 | 99.99 | 99.99 | 99.99 | 99.99 | 99.99 | - | 100 | 99.99 | 99.99 | 99.996 | 99.99 | 99.99 | |
| 30–60 s | 32 | 70 | 99.99 | 99.99 | 99.99 | 99.99 | 100 | 32 | 70 | - | - | - | - | 100 |
| 38 | 70 | 69.99 | 99.99 | 99.99 | 99.99 | 100 | 37.52 | 70 | 69.99 | - | - | - | 100 | |
| 40 | 70 | 69.99 | 99.99 | 99.99 | 99.99 | 100 | - | 70 | 69.99 | - | - | - | 100 | |
| 44 | 70 | 69.99 | 99.99 | 87.90 | 99.99 | 100 | 43.63 | 70 | 69.99 | - | 87.70 | - | 100 | |
| 46 | 70 | 69.99 | 91.66 | 87.70 | 87.81 | 100 | - | 70 | 69.99 | - | - | - | 100 | |
| 48 | 70 | 69.99 | 91.66 | 87.70 | 87.70 | 100 | 47.27 | 70 | 69.99 | 91.66 | - | - | 100 | |
| 50 | 70 | 69.99 | 91.66 | 87.70 | 87.70 | 100 | - | 70 | 69.99 | 91.66 | - | - | 100 | |
| 52 | 70 | 69.99 | 91.66 | 82.81 | 87.70 | 100 | 51.52 | 70 | 69.99 | 91.66 | 82.78 | - | 100 | |
| 54 | 70 | 69.99 | 91.66 | 82.78 | 82.80 | 100 | 53.40 | 70 | 69.99 | 91.66 | 82.78 | 82.78 | 100 | |
| 56 | 70 | 69.99 | 91.66 | 82.78 | 82.78 | 100 | - | 70 | 69.99 | 91.66 | 82.78 | 82.78 | 100 | |
| 60 | 70 | 69.99 | 91.66 | 82.78 | 82.78 | 100 | - | 70 | 69.99 | 91.66 | 82.78 | 82.78 | 100 | |
| Simulation | Theoretical Values | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Time (min) | A (°C) | B (°C) | C (°C) | D (°C) | E (°C) | F (°C) | G (°C) | Time (min) | A (°C) | B (°C) | C (°C) | D (°C) | E (°C) | F (°C) | G (°C) | |
| 0–30 s | 0 | 100 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 100 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 100 | 57.46 | 0 | 0 | 0 | 0 | 0 | 2.1 | 100 | 99.99 | 0 | 0 | 0 | 0 | 0 | |
| 4 | 100 | 99.99 | 0 | 0 | 0 | 0 | 0 | - | 100 | 99.99 | 0 | 0 | 0 | 0 | 0 | |
| 6 | 100 | 99.99 | 0 | 0 | 99.99 | 43.5 | 0 | 4.6/5.1 | 100 | 99.99 | 0 | 0 | 99.99 | 43.5 | 0 | |
| 8 | 100 | 99.99 | 99.99 | 0 | 99.99 | 43.5 | 0 | 6.7 | 100 | 99.99 | 99.99 | 0 | 99.99 | - | 0 | |
| 10 | 100 | 99.99 | 99.99 | 0 | 99.99 | 69.8 | 0 | 10 | 100 | 99.99 | 99.99 | 0 | 99.99 | 79.31 | 0 | |
| 12 | 100 | 99.99 | 99.99 | 0 | 99.99 | 79.31 | 0 | - | 100 | 99.99 | 99.99 | 0 | 99.99 | - | 0 | |
| 14 | 100 | 99.99 | 99.99 | 99.76 | 99.99 | 79.31 | 43.5 | 13.7/12.3 | 100 | 99.99 | 99.99 | 99.99 | 99.99 | - | 43.5 | |
| 16 | 100 | 99.99 | 99.99 | 99.99 | 99.99 | 79.31 | 43.5 | - | 100 | 99.99 | 99.99 | 99.99 | 99.99 | - | - | |
| 18 | 100 | 99.99 | 99.99 | 99.99 | 99.99 | 99.99 | 79.31 | 17.3/17.2 | 100 | 99.99 | 99.99 | 99.99 | 99.99 | 99.99 | 79.31 | |
| 20 | 100 | 99.99 | 99.99 | 99.99 | 99.99 | 99.99 | 79.31 | - | 100 | 99.99 | 99.99 | 99.99 | 99.99 | 99.99 | 99.99 | |
| 28 | 100 | 99.99 | 99.99 | 99.99 | 99.99 | 99.99 | 99.99 | - | 100 | 99.99 | 99.99 | 99.99 | 99.99 | 99.99 | 99.99 | |
| 30–60 s | 30 | 70 | 99.99 | 99.99 | 100 | 99.99 | 99.99 | 99.99 | 30 | 70 | - | - | 100 | - | - | - |
| 32 | 70 | 99.99 | 99.99 | 100 | 99.99 | 99.99 | 99.99 | - | 70 | - | - | 100 | - | - | - | |
| 38 | 70 | 99.99 | 99.99 | 100 | 99.99 | 99.99 | 99.99 | - | 70 | - | - | 100 | - | - | - | |
| 40 | 70 | 90.36 | 99.99 | 100 | 99.99 | 99.99 | 99.99 | 38.2 | 70 | 90.36 | - | 100 | - | - | - | |
| 42 | 70 | 90.36 | 99.99 | 100 | 90.36 | 95.9 | 99.99 | 40.8 | 70 | 90.36 | - | 100 | 90.36 | - | - | |
| 44 | 70 | 90.36 | 90.36 | 100 | 90.36 | 95.9 | 99.99 | 43 | 70 | 90.36 | 90.36 | 100 | 90.36 | - | - | |
| 46 | 70 | 90.36 | 90.36 | 100 | 90.36 | 95.9 | 99.99 | - | 70 | 90.36 | 90.36 | 100 | 90.36 | - | - | |
| 48 | 70 | 90.36 | 90.36 | 100 | 90.36 | 92.5 | 99.99 | 46.3 | 70 | 90.36 | 90.36 | 100 | 90.36 | 92.5 | - | |
| 50 | 70 | 90.36 | 90.36 | 100 | 90.36 | 92.5 | 95.87 | - | 70 | 90.36 | 90.36 | 100 | 90.36 | 92.5 | - | |
| 52 | 70 | 90.36 | 90.36 | 100 | 90.36 | 92.5 | 95.87 | - | 70 | 90.36 | 90.36 | 100 | 90.36 | 92.5 | - | |
| 54 | 70 | 90.36 | 90.36 | 100 | 90.36 | 92.5 | 92.56 | 53.5 | 70 | 90.36 | 90.36 | 100 | 90.36 | 92.5 | 92.49 | |
| 60 | 70 | 90.36 | 90.36 | 100 | 90.36 | 92.5 | 92.49 | - | 70 | 90.36 | 90.36 | 100 | 90.36 | 92.5 | 92.49 | |
| Simulation | Theoretical Values | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Time (min) | A (°C) | B (°C) | C (°C) | D (°C) | E (°C) | F (°C) | G (°C) | Time (min) | A (°C) | B (°C) | C (°C) | D (°C) | E (°C) | F (°C) | G (°C) | |
| Hour 1 | 0 | 100 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 100 | 0 | 0 | 0 | 0 | 0 | 0 |
| 4 | 100 | 0 | 99.85 | 0 | 0 | 0 | 0 | 3.16 | 100 | 0 | 99.85 | 0 | 0 | 0 | 0 | |
| - | 100 | 0 | 99.85 | 0 | 0 | 0 | 0 | - | 100 | 0 | 99.85 | 0 | 0 | 0 | 0 | |
| 13 | 100 | 0.46 | 99.85 | 0 | 0 | 0 | 0 | 13.11 | 100 | 98.50 | 99.85 | 0 | 0 | 0 | 0 | |
| 14 | 100 | 98.50 | 99.85 | 0 | 0 | 0 | 0 | - | 100 | 98.50 | 99.85 | 0 | 0 | 0 | 0 | |
| - | 100 | 98.50 | 99.85 | 0 | 0 | 0 | 0 | - | 100 | 98.50 | 99.85 | 0 | 0 | 0 | 0 | |
| 20 | 100 | 98.50 | 99.85 | 0 | 0 | 98.27 | 0 | 19.77 | 100 | 98.50 | 99.85 | 0 | 0 | 98.27 | 0 | |
| 21 | 100 | 98.50 | 99.85 | 98.22 | 0 | 98.27 | 97.51 | 20.44/20.29 | 100 | 98.50 | 99.85 | 98.22 | 0 | 98.27 | 97.51 | |
| - | 100 | 98.50 | 99.85 | 98.22 | 0 | 98.27 | 97.51 | - | 100 | 98.50 | 99.85 | 98.22 | 0 | 98.27 | 97.51 | |
| 28 | 100 | 98.50 | 99.85 | 98.22 | 94.04 | 98.27 | 97.51 | 27.85 | 100 | 98.50 | 99.85 | 98.22 | 95.47 | 98.27 | 97.51 | |
| 29 | 100 | 98.50 | 99.85 | 98.22 | 95.47 | 98.27 | 97.51 | - | 100 | 98.50 | 99.85 | 98.22 | 95.47 | 98.27 | 97.51 | |
| Hour 2 | 61 | 70 | 100 | 99.85 | 98.22 | 95.47 | 98.27 | 97.51 | 61 | 70 | 100 | 99.85 | 98.22 | 95.47 | 98.27 | 97.51 |
| 70 | 70 | 100 | 99.40 | 98.71 | 95.47 | 98.27 | 97.51 | 69.91 | 70 | 100 | - | 98.70 | - | - | - | |
| 71 | 70 | 100 | 99.36 | 98.71 | 95.47 | 98.26 | 97.51 | - | 70 | 100 | - | 98.70 | - | - | - | |
| - | 70 | 100 | - | 98.71 | - | - | - | - | 70 | 100 | - | 98.70 | - | - | - | |
| 73 | 70 | 100 | 99.27 | 98.71 | 95.47 | 98.54 | 97.51 | 72.94 | 70 | 100 | - | 98.70 | - | 98.55 | - | |
| 74 | 70 | 100 | 99.22 | 98.71 | 95.47 | 98.56 | 97.51 | - | 70 | 100 | - | 98.70 | - | 98.55 | - | |
| - | 70 | 100 | - | 98.71 | - | 98.56 | - | - | 70 | 100 | - | 98.70 | - | 98.55 | - | |
| 78 | 70 | 100 | 80.76 | 98.71 | 95.94 | 98.56 | 97.47 | 77.32 | 70 | 100 | - | 98.70 | 95.94 | 98.55 | - | |
| - | 70 | 100 | - | 98.71 | 95.94 | 98.56 | - | - | 70 | 100 | - | 98.70 | 95.94 | 98.55 | - | |
| 87 | 70 | 100 | 80.72 | 98.71 | 95.94 | 98.56 | 97.08 | 86.64 | 70 | 100 | 80.72 | 98.70 | 95.94 | 98.55 | - | |
| - | 70 | 100 | 80.72 | 98.71 | 95.94 | 98.56 | - | - | 70 | 100 | 80.72 | 98.70 | 95.94 | 98.55 | - | |
| 104 | 70 | 100 | 80.72 | 98.71 | 95.94 | 98.56 | 78.83 | 103.76 | 70 | 100 | 80.72 | 98.70 | 95.94 | 98.55 | 78.83 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schojda, D.; Scheipers, J.; Roes, J.; Hoster, H. Modelling and Transient Simulation of District Heating Networks Based on a Control Theory Approach. Energies 2025, 18, 658. https://doi.org/10.3390/en18030658
Schojda D, Scheipers J, Roes J, Hoster H. Modelling and Transient Simulation of District Heating Networks Based on a Control Theory Approach. Energies. 2025; 18(3):658. https://doi.org/10.3390/en18030658
Chicago/Turabian StyleSchojda, Dominik, Jan Scheipers, Jürgen Roes, and Harry Hoster. 2025. "Modelling and Transient Simulation of District Heating Networks Based on a Control Theory Approach" Energies 18, no. 3: 658. https://doi.org/10.3390/en18030658
APA StyleSchojda, D., Scheipers, J., Roes, J., & Hoster, H. (2025). Modelling and Transient Simulation of District Heating Networks Based on a Control Theory Approach. Energies, 18(3), 658. https://doi.org/10.3390/en18030658










