Characteristics and Optimization of Transient Process of Pump-Turbine Units in Power Generation Mode
Abstract
1. Introduction
2. Model of Pump–Turbine Regulation System
2.1. Model of Diversion Pipeline
2.1.1. Elastic Water Hammer Model
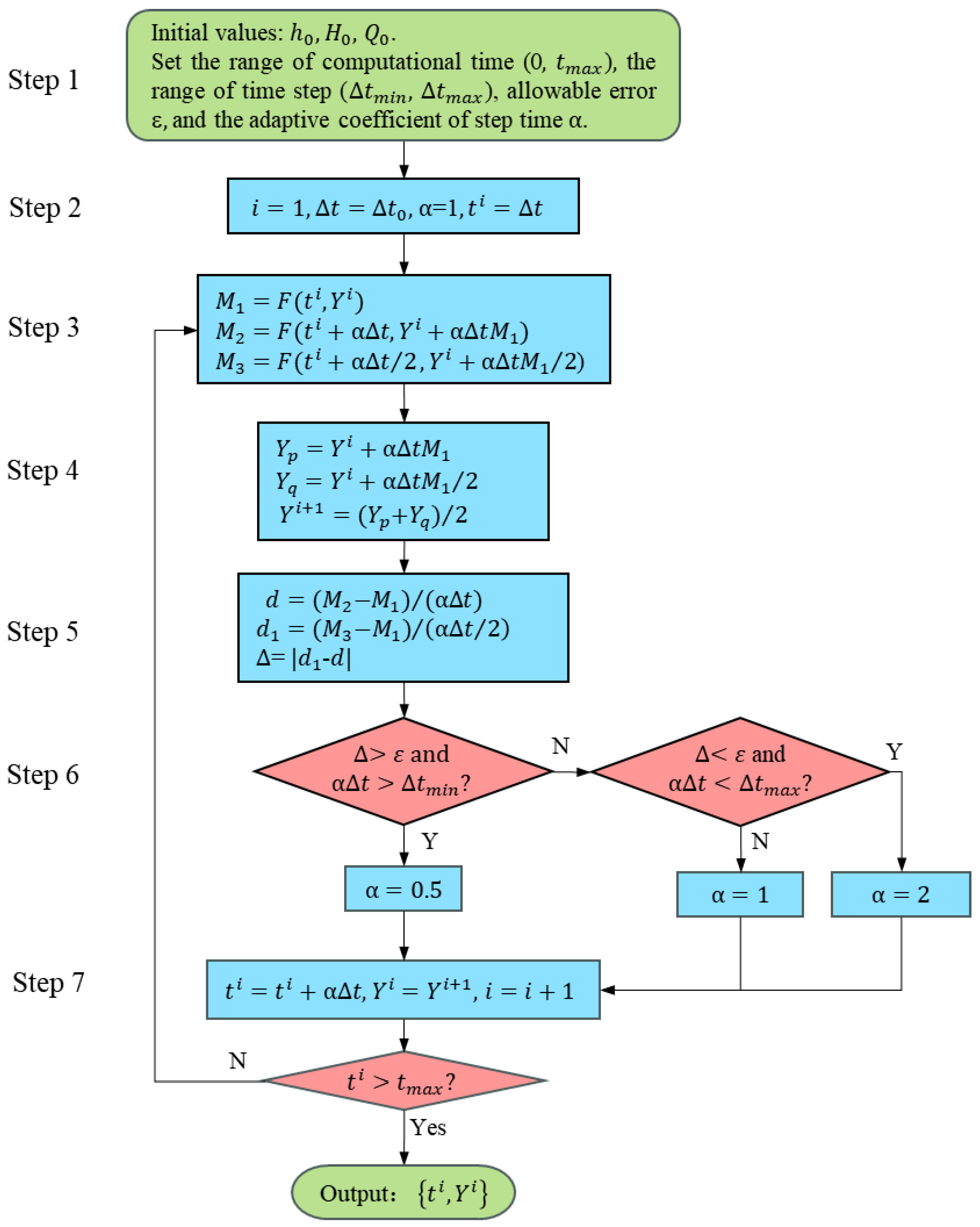
2.1.2. Algorithm of Hydraulic Transient Process
2.2. Hydraulic Boundary Treatment
2.2.1. Upstream and Downstream Reservoirs
2.2.2. Surge Chamber
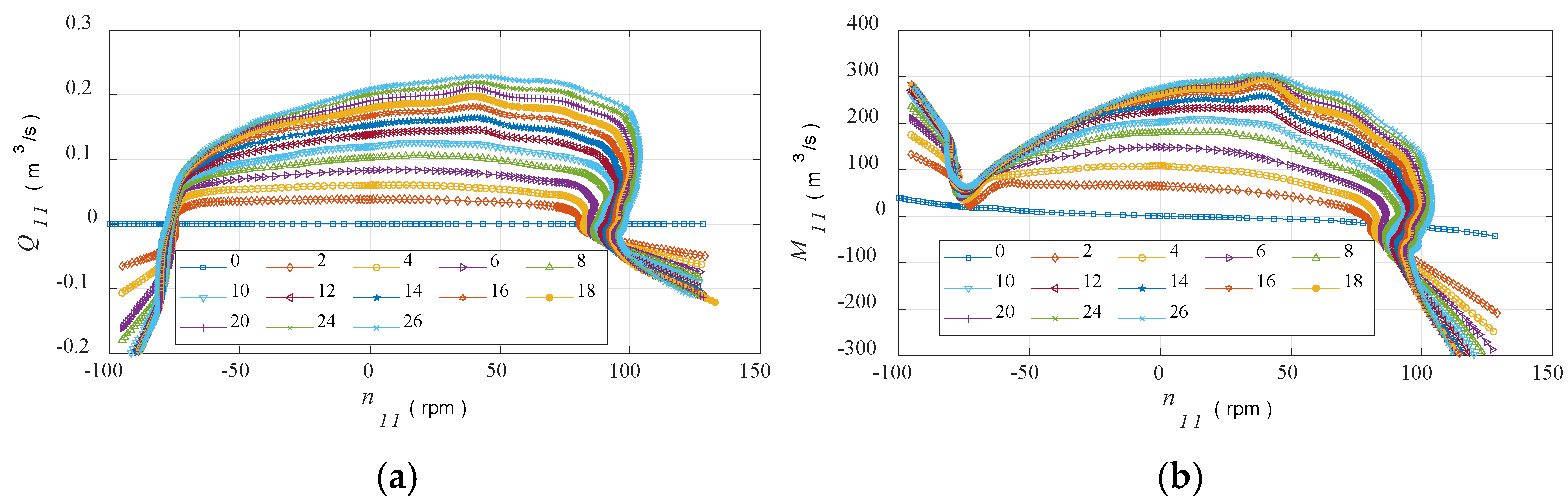
2.2.3. Pump–Turbine
2.3. Synchronous Generator
2.4. Governor
3. Project Overview and Parameters
4. Results and Discussion
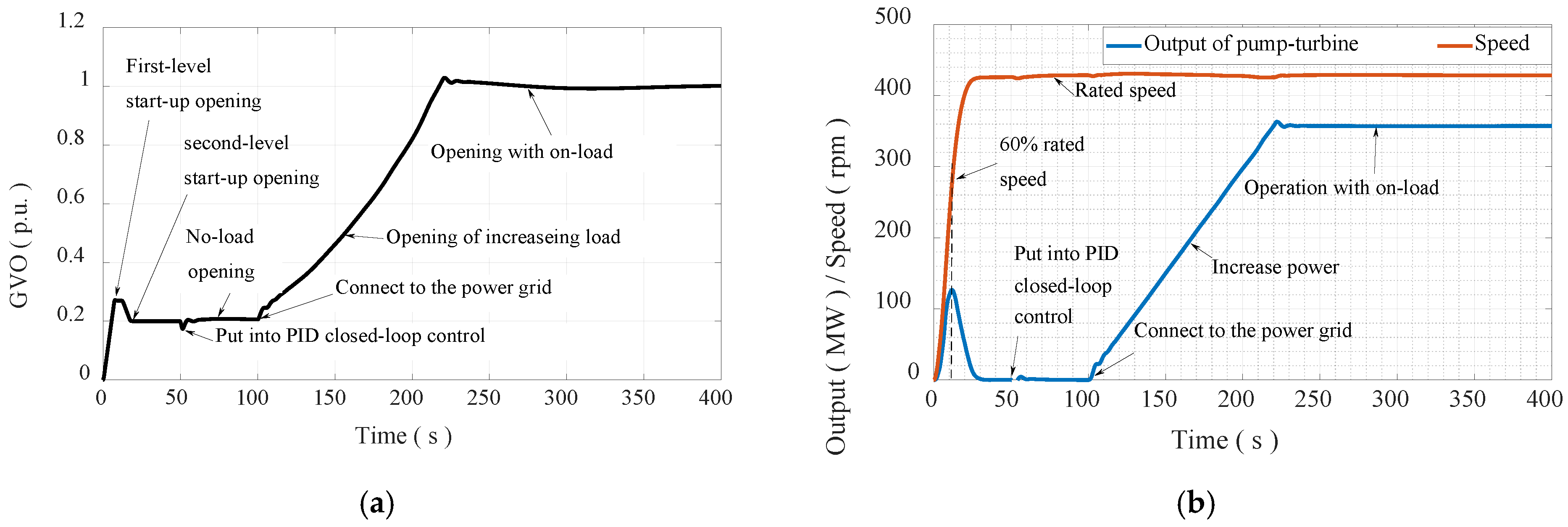
4.1. Transient Process of Start-Up and On-Load
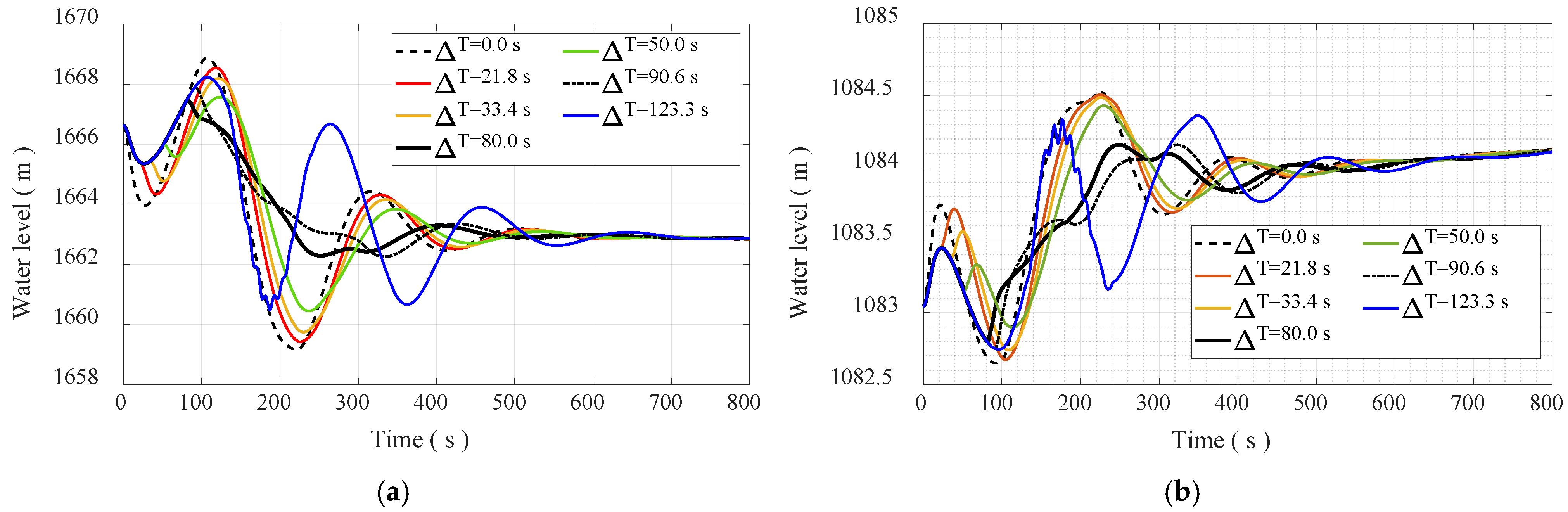
4.2. The Transient Process of Load Regulation Under Power Generation Mode
4.3. Transient Process of Load Rejection
5. Conclusions
- (1)
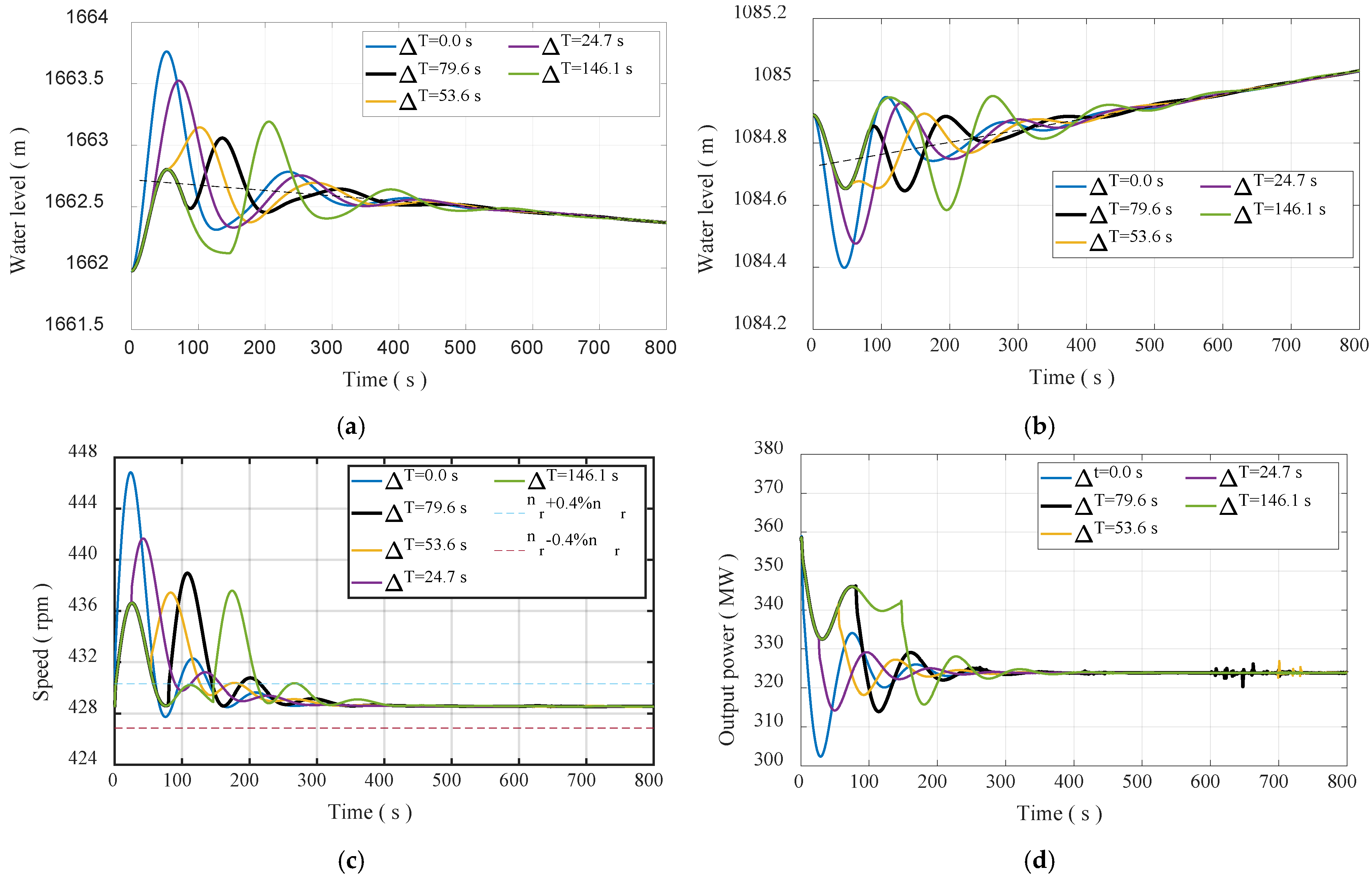
- The appropriate start-up interval time is very important for suppressing the water level fluctuation of the surge chambers and improve the transient characteristics of the PTUs. The results show that after one PTU is started up, when the discharge flowing into the upstream surge chamber is the largest, then another PTU is started up, the transient characteristics of the PTUs are the best.
- (2)
- Using the peak staggered valley filling method makes it difficult to minimize the water level fluctuation amplitude of the surge chamber and the rotational speed fluctuation amplitude of the PTU simultaneously, because their fluctuation periods are not consistent. Therefore, during the load regulation process, frequency fluctuation should be controlled as a priority to improve the transient characteristics of the PTU.
- (3)
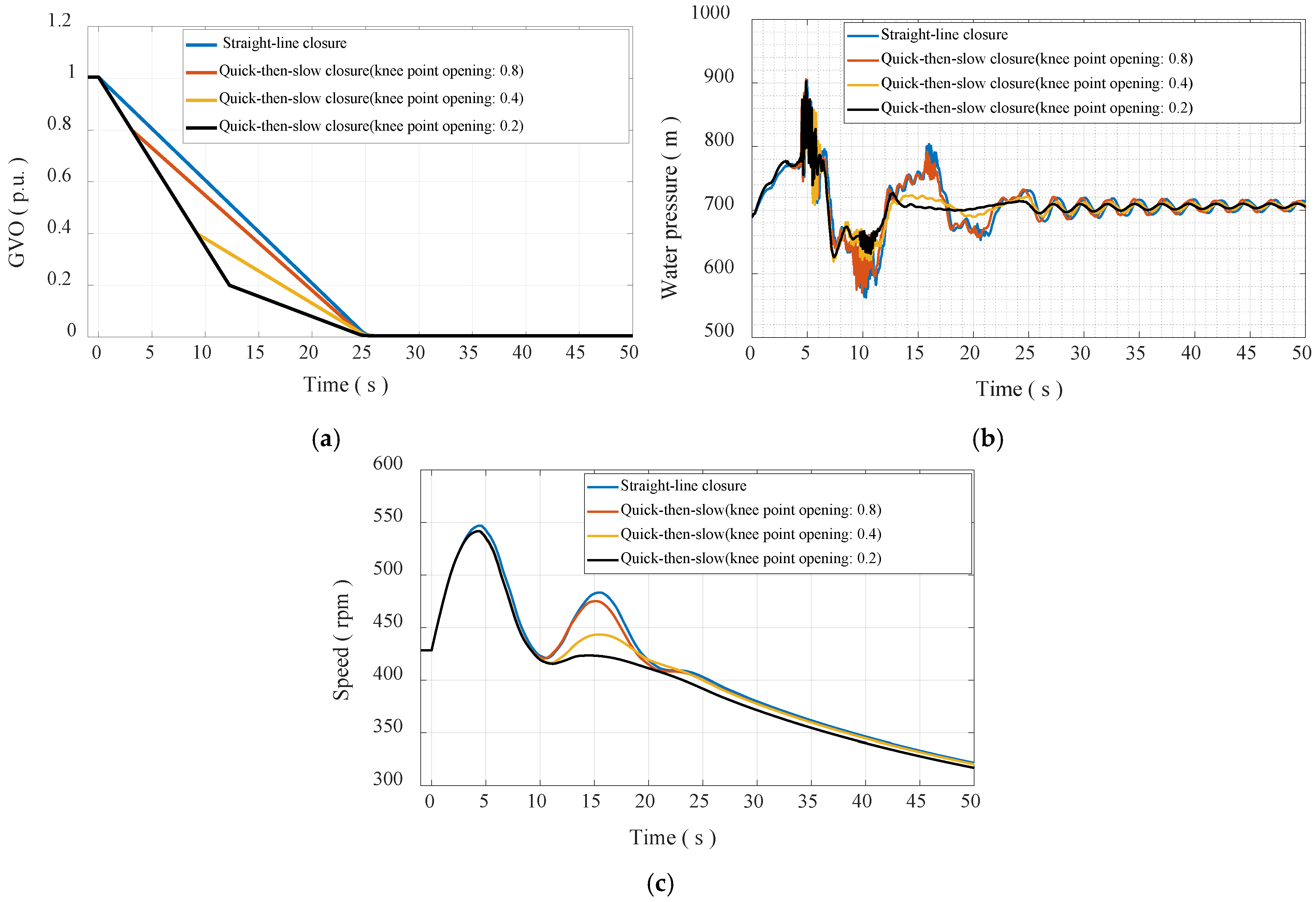
- Compared with the traditional characteristic line method, the presented method captures the pulsating pressure well. The quick-then-slow closure law, especially the knee point opening of the guide vanes is within 40% during load rejection, can significantly improve the characteristics of the transient process and shorten the duration of the pulsating pressure.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Available online: https://www.nea.gov.cn/2024-01/26/c_1310762246.htm (accessed on 15 August 2024).
- Zhang, Y.M.; Wang, L.; Wang, N.; Duan, L.; Zong, Y.; You, S.; Maréchal, F.; Van Herle, J.; Yang, Y. Balancing wind-power fluctuation via onsite storage under uncertainty: Power-to-hydrogen-to-power versus lithium battery. Renew. Sustain. Energy Rev. 2019, 116, 109465. [Google Scholar] [CrossRef]
- Zhang, Y.; Xu, Y.; Zhou, X.; Guo, H.; Zhang, X.; Chen, H. Compressed air energy storage system with variable configuration for accommodating large-amplitude wind power fluctuation. Appl. Energy 2019, 239, 957–968. [Google Scholar] [CrossRef]
- Zhang, Y.; Xu, Y.; Guo, H.; Zhang, X.; Guo, C.; Chen, H. A hybrid energy storage system with optimized operating strategy for mitigating wind power fluctuations. Renew. Energy 2018, 125, 121–132. [Google Scholar] [CrossRef]
- Xu, B.; Zhu, F.; Zhong, P.A.; Chen, J.; Liu, W.; Ma, Y.; Guo, L.; Deng, X. Identifying long-term effects of using hydropower to complement wind power uncertainty through stochastic programming. Appl. Energy 2019, 253, 113535. [Google Scholar] [CrossRef]
- Rahmati, I.; Foroud, A.A. Pumped-storage units to address spinning reserve concerns in the grids with high wind penetration. J. Energy Storage 2020, 31, 101612. [Google Scholar] [CrossRef]
- Li, Y.; Yang, W.; Zhao, Z.; Huang, Y.; Liao, Y.; Yang, J. Ancillary service quantitative evaluation for primary frequency regulation of pumped storage units considering refined hydraulic characteristics. J. Energy Storage 2022, 45, 103414. [Google Scholar] [CrossRef]
- Medium and Long-Term Development Plan for Pumped Storage (2021~2035) Was Issued and Implemented. Available online: https://www.gov.cn/xinwen/2021-09/09/content_5636487.htm (accessed on 20 August 2024). (In Chinese)
- Cavazzini, G.; Covi, A.; Pavesi, G.; Ardizzon, G. Analysis of the Unstable Behavior of a Pump-Turbine in Turbine Mode: Fluid-Dynamic and Spectral Characterization of the S-Shape Characteristic. ASME J. Fluids Eng. 2016, 138, 021105. [Google Scholar] [CrossRef]
- Chazarra, M.; Pérez-Díaz, J.I.; García-González, J.; Praus, R. Economic viability of pumped-storage power plants participating in the secondary regulation service. Appl. Energy 2018, 216, 224–233. [Google Scholar] [CrossRef]
- Zhao, Z.W.; Zhang, H.; Chen, D.Y.; Gao, X. No-Load Stability Analysis of Pump Turbine at Startup-Grid Integration Process. J. Fluids Eng. 2019, 141, 081113. [Google Scholar] [CrossRef]
- Sun, H.; Xiao, R.; Liu, W.; Wang, F. Analysis of S Characteristics and Pressure Pulsations in a Pump-Turbine with Misaligned Guide Vanes. ASME J. Fluids Eng. 2013, 135, 051101. [Google Scholar] [CrossRef]
- Yang, M.Q.; Zhao, W.Q.; Bi, H.L.; Yang, H.; He, Q.; Huang, X.; Wang, Z. Flow-Induced Vibration of Non-Rotating Structures of a High-Head Pump-Turbine during Start-Up in Turbine Mode. Energies 2022, 15, 8743. [Google Scholar] [CrossRef]
- Zeng, W.; Yang, J.D.; Hu, J.H.; Yang, J. Guide-Vane Closing Schemes for Pump-Turbines Based on Transient Characteristics in S-shaped Region. J. Fluids Eng. 2016, 138, 051302. [Google Scholar] [CrossRef]
- Zhao, Z.; Yang, J.; Yang, W.; Hu, J.; Chen, M. A coordinated optimization framework for flexible operation of pumped storage hydropower system: Nonlinear modeling, strategy optimization and decision making. Energy Convers. Manag. 2019, 194, 75–93. [Google Scholar] [CrossRef]
- Ye, J.W.; Zeng, W.; Zhao, Z.G.; Yang, J.; Yang, J. Optimization of Pump Turbine Closing Operation to Minimize Water Hammer and Pulsating Pressures During Load Rejection. Energies 2020, 13, 1000. [Google Scholar] [CrossRef]
- Zhang, H.; Su, D.; Guo, P.C.; Zhang, B.; Mao, Z. Stochastic dynamic modeling and simulation of a pump-turbine in load-rejection process. J. Energy Storage 2021, 35, 102196. [Google Scholar] [CrossRef]
- Xu, L.C.; Peng, Y.J.; Tang, W.; Liu, D.M.; Liu, X.B. Flow characteristics and pressure pulsation in the S characteristic area of model pump turbine. Chin. J. Hydrodyn. 2022, 37, 213–225. (In Chinese) [Google Scholar] [CrossRef]
- Chen, L.; Yu, X.D.; Li, G.H.; Zhang, M.; Chen, S.; Zhang, J. Influence of reverse S characteristics of pump-turbines on transient pressure during load rejection. Chin. J. Hydrodyn. 2022, 41, 112–119. (In Chinese) [Google Scholar] [CrossRef]
- Liu, C.P.; Zhao, Z.G.; Yang, J.B.; Yan, S.; Yang, J.; Yin, X. Hydraulic-mechanical-electrical coupled model framework of variable-speed pumped storage system: Measurement verification and accuracy analysis. J. Energy Storage 2024, 89, 111714. [Google Scholar] [CrossRef]
- Zhang, C.B.; Yang, M.J.; Li, J.Y. Detailed modelling and parameters optimisation analysis on governing system of hydro-turbine generator unit. IET Gener. Transm. Distrib. 2018, 12, 1045–1051. [Google Scholar] [CrossRef]
- Zhang, L.; Jiang, H.Z. Variable Step Euler Method for Real-time Simulation. In Proceedings of the 2012 2nd International Conference on Computer Science and Network Technology, Changchun, China, 29–31 December 2012. [Google Scholar]
- Zhang, C.B.; Cao, W.Z.; Xie, T.T.; Wang, C.; Shen, C.; Wen, X.; Mao, C. Operational Characteristics and Optimization of Hydro-PV Power Hybrid Electricity System. Renew. Energy 2022, 200, 601–613. [Google Scholar] [CrossRef]
- Pan, X.H.; Cheng, Y.C.; Wang, J.F. Research Progress of the Processing of Pump Turbine Characteristic Curve. J. Yangtze River Sci. Res. Inst. 2014, 31, 117–123. (In Chinese) [Google Scholar] [CrossRef]
- Xiao, W.; Han, C.Z.; Chen, L.; Ren, S.; Xu, L.; Cao, W. Study on the Vibration Law of Pump Turbine Unit and Powerhouse in Pumped-storage Power Station. Hydropower Pumped Storage 2023, 9, 10–19. (In Chinese) [Google Scholar] [CrossRef]


| Parameter | Symbol | Value | Unit | Parameter | Symbol | Value | Unit |
|---|---|---|---|---|---|---|---|
| Proportional gain | 4.0 | / | Permanent droop | 1.0 | % | ||
| Integrational gain | 0.1 | 1/s | Power droop | 1.0 | % | ||
| Differential gain | 3.0 | s | Servomotor response time constant | 0.65 | s |
| Name | Parameter | Symbol | Value | Unit | Name | Parameter | Symbol | Value | Unit |
|---|---|---|---|---|---|---|---|---|---|
| Turbine | Max. water head | 608.9 | m | Generator | Rated speed | 428.6 | rpm | ||
| Rated water head | 567.0 | m | Rated capacity | 350 | MW | ||||
| Min. water head | 537.3 | m | Rated speed | 428.6 | rpm | ||||
| Rated output | 357 | MW | Power factor | 0.9 | / | ||||
| Rated discharge | 71.3 | m3/s | Rated voltage | 15.75 | kV | ||||
| Rated efficiency | 90.0 | % |
| Scheme | Description |
|---|---|
| Scheme 1 | Two PTUs are started up at the same time. |
| Scheme 2 | After PTU No.1 is started up, when the discharge flowing out the upstream surge chamber is the largest, then PTU No.2 is started up. |
| Scheme 3 | After PTU No.1 is started up, when the discharge flowing into/out the upstream surge chamber is zero, then PTU No.2 is started up. |
| Scheme 4 | After PTU No.1 is started up, when the discharge flowing into the upstream surge chamber is the largest, then PTU No.2 is started up. |
| Scheme 5 | After PTU No.1 is started up, when the water level in the upstream surge chamber is the lowest, then PTU No.2 is started up. |
| Scheme 6 | After PTU No.1 is started up, when the water level in the upstream surge chamber returns to the initial water level, then PTU No.2 is started up. |
| Scheme 7 | After PTU No.1 is started up, when the water level in the upstream surge chamber is the highest, then PTU No.2 is started up. |
| Scheme | Interval Time ∆T (s) | Water Level in Upstream Surge Chamber (m) | Water Level in Downstream Surge Chamber (m) | ||||
|---|---|---|---|---|---|---|---|
| Highest | Lowest | Difference | Highest | Lowest | Difference | ||
| Scheme 1 | 0.0 | 1668.86 | 1659.15 | 9.71 | 1084.53 | 1082.65 | 1.88 |
| Scheme 2 | 21.8 s | 1668.54 | 1659.42 | 9.12 | 1084.51 | 1082.68 | 1.83 |
| Scheme 3 | 33.4 | 1668.18 | 1659.74 | 8.44 | 1084.49 | 1082.74 | 1.75 |
| Scheme 4 | 80.0 | 1667.46 | 1662.29 | 5.17 | 1084.16 | 1082.79 | 1.37 |
| Scheme 5 | 50.0 | 1667.56 | 1660.44 | 7.12 | 1084.43 | 1082.90 | 1.53 |
| Scheme 6 | 90.6 | 1667.92 | 1662.26 | 5.66 | 1084.16 | 1082.75 | 1.41 |
| Scheme 7 | 123.3 | 1668.23 | 1660.47 | 7.76 | 1084.36 | 1082.75 | 1.61 |
| Scheme | Interval Time ∆T (s) | Rotational Speed (rpm) | Regulation Time (s) | ||
|---|---|---|---|---|---|
| Maximum | Minimum | Amplitude | |||
| Scheme 1 | 0.0 | 446.84 | 427.75 | 18.24 | 140.20 |
| Scheme 2 | 79.6 | 438.96 | 428.61 | 10.36 | 215.50 |
| Scheme 3 | 53.6 | 437.44 | 428.68 | 8.84 | 126.40 |
| Scheme 4 | 24.7 | 441.61 | 428.68 | 13.01 | 155.73 |
| Scheme 5 | 146.1 | 437.58 | 428.63 | 8.98 | 210.90 |
| Scheme | Opening of Knee Point (p.u.) | Time of Occurrence (s) | Scheme | Opening of Knee Point (p.u.) | Time of Occurrence (s) |
|---|---|---|---|---|---|
| Scheme 1 | / | / | Scheme 3 | 0.4 | 9.20 |
| Scheme 2 | 0.8 | 3.11 | Scheme 4 | 0.2 | 12.26 |
| Scheme | Max. Water Pressure (m) | Max. Speed (rpm) | Scheme | Max. Water Pressure (m) | Max. Speed (rpm) |
|---|---|---|---|---|---|
| Scheme 1 | 904.78 | 547.04 | Scheme 3 | 891.71 | 541.69 |
| Scheme 2 | 905.67 | 541.69 | Scheme 4 | 902.35 | 541.69 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, M.; Liu, J.; Yu, J.; Nie, C. Characteristics and Optimization of Transient Process of Pump-Turbine Units in Power Generation Mode. Energies 2025, 18, 602. https://doi.org/10.3390/en18030602
Zhang M, Liu J, Yu J, Nie C. Characteristics and Optimization of Transient Process of Pump-Turbine Units in Power Generation Mode. Energies. 2025; 18(3):602. https://doi.org/10.3390/en18030602
Chicago/Turabian StyleZhang, Minglu, Jie Liu, Junqin Yu, and Changhua Nie. 2025. "Characteristics and Optimization of Transient Process of Pump-Turbine Units in Power Generation Mode" Energies 18, no. 3: 602. https://doi.org/10.3390/en18030602
APA StyleZhang, M., Liu, J., Yu, J., & Nie, C. (2025). Characteristics and Optimization of Transient Process of Pump-Turbine Units in Power Generation Mode. Energies, 18(3), 602. https://doi.org/10.3390/en18030602





