Deep-Learning Techniques Applied for State-Variables Estimation of Two-Mass System
Abstract
1. Introduction
- Presentation of the design, application, and tests of the state-variables estimators based on the Convolutional Neural Networks and the long short-term memory models. It should be noticed that the considered estimators contain typical operations from the CNN and the LSTM neural networks. However, the hybrid topology, which leads to promising results, is original.
- Implementation of the shaft torque and the motor speed deep neural estimators for the two-mass system. The simulation results present high precision of sample calculation and robustness against object parameter disturbances.
- The first part of the paper deals with theoretical considerations. The following step is dedicated to hardware implementation and experimental verification. For this purpose, the low-cost device was selected, and the algorithms were implemented using rapid prototyping tools.
2. State Controller Applied for the Two-Mass System—A Mathematical Description
3. Deep Neural State Variables Estimators
3.1. The Structure of the Neural Models
3.2. The Design Procedure of Neural Estimators
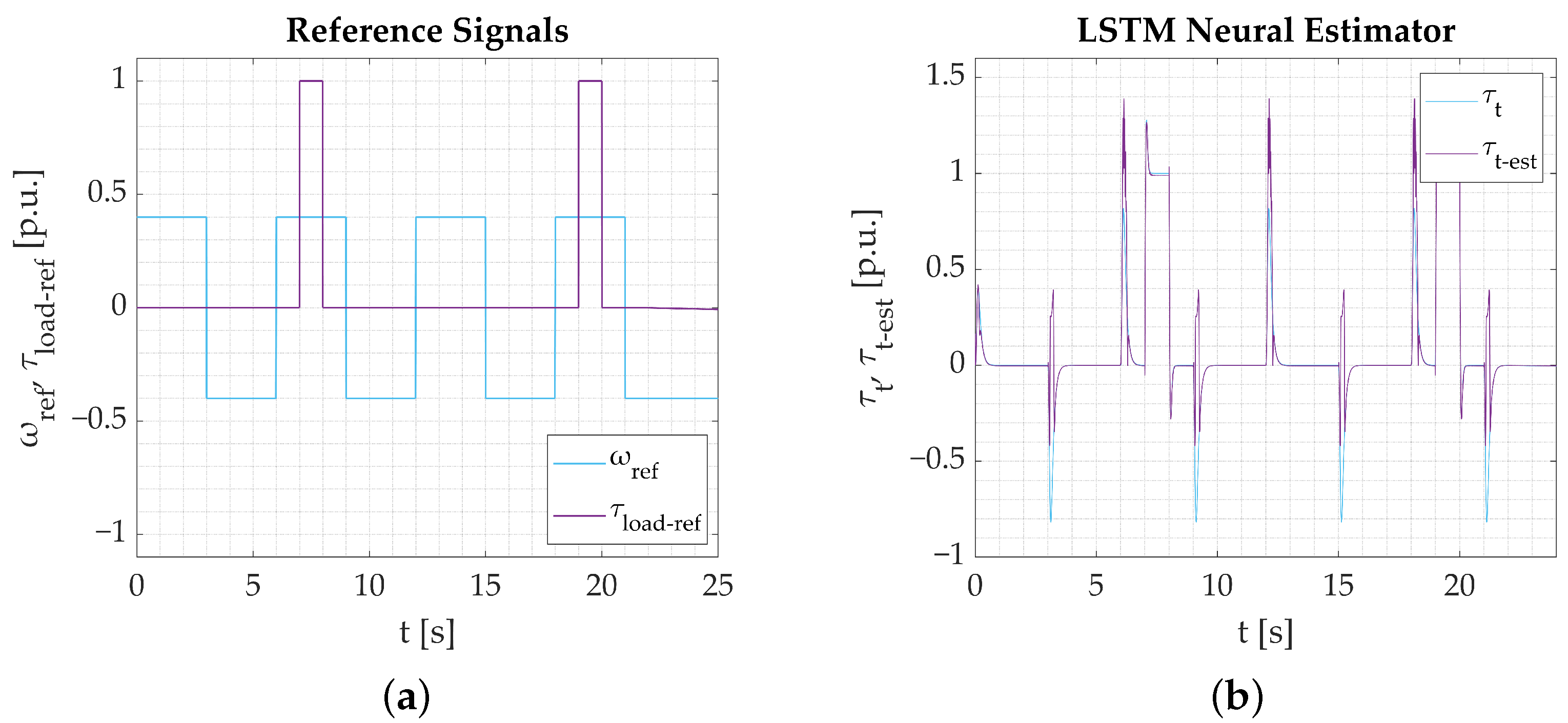
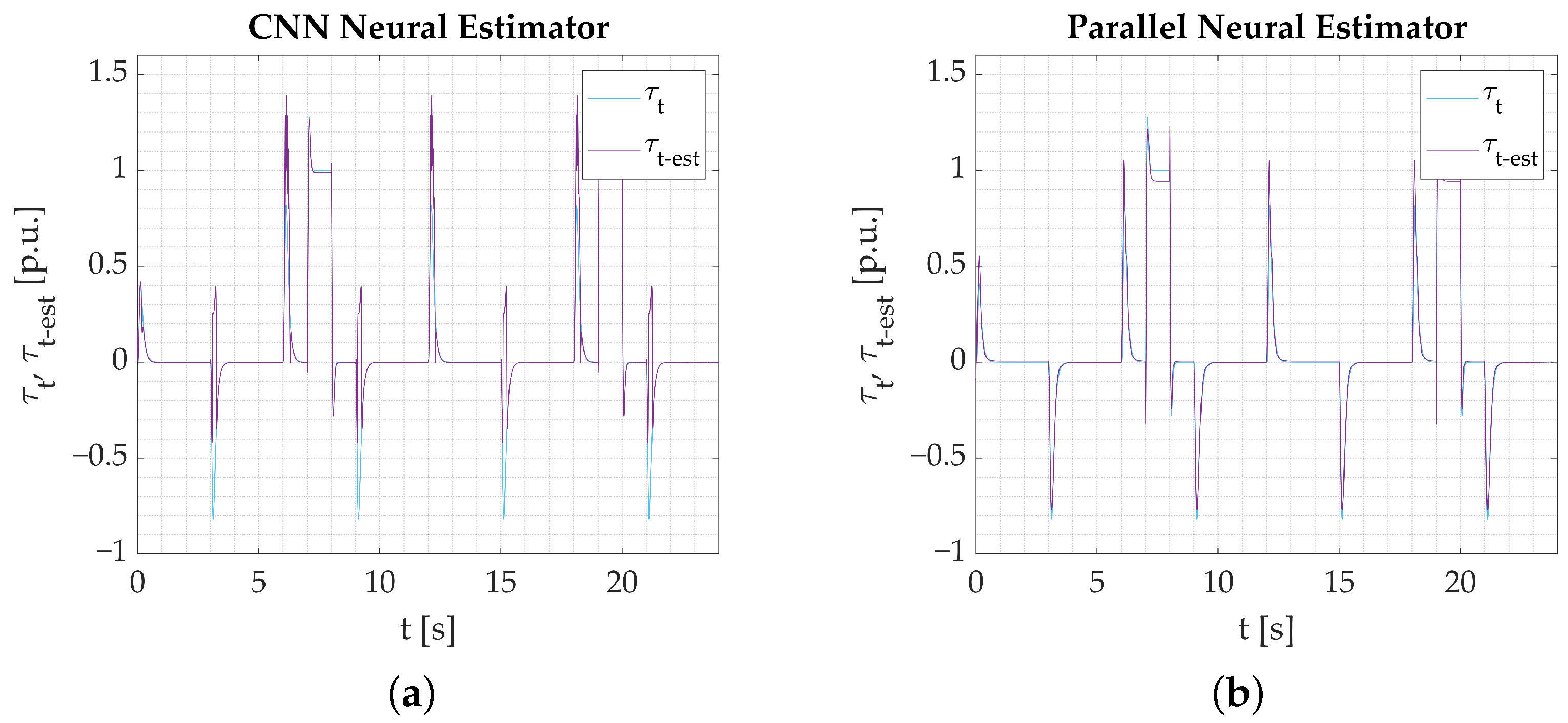
4. Simulation Tests of the State Variables Estimators Based on Deep Neural Networks
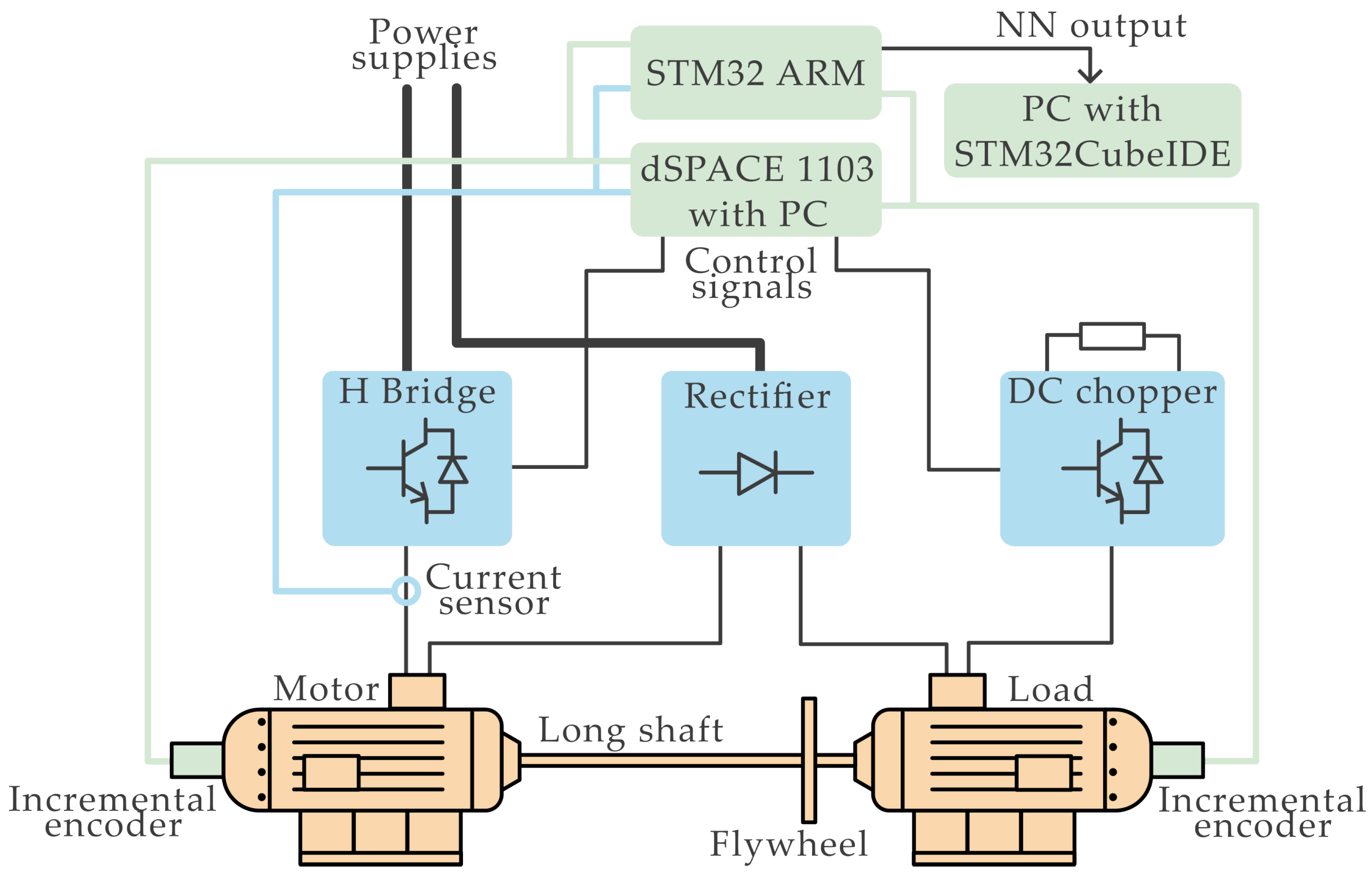
5. Hardware Implementation of the Neural Models Applied for Signals of Two-Mass System Estimation
5.1. The Laboratory Equipment
5.2. Low-Cost Implementation of the Deep Neural Network
5.3. Calculations Based on the Real Data
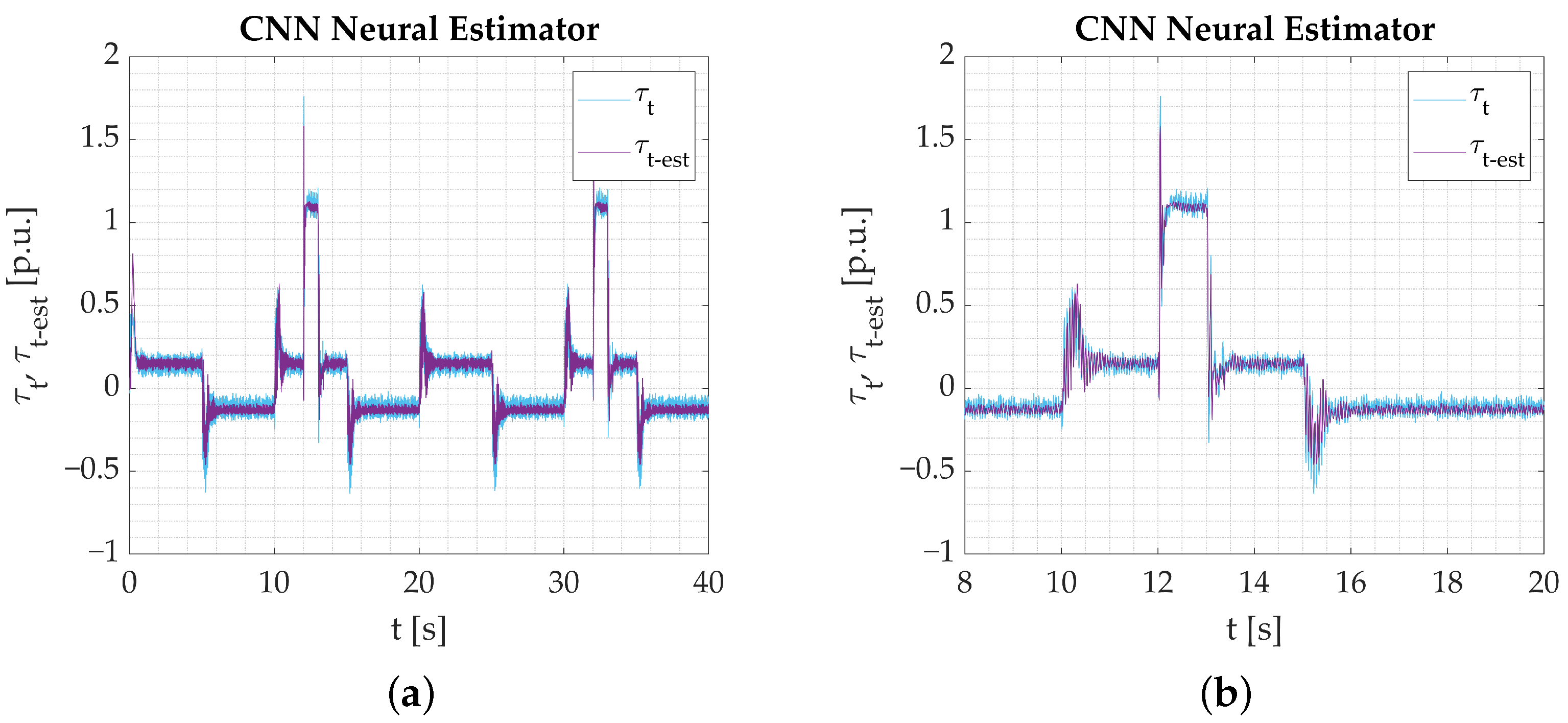
5.4. Experimental Tests
6. Concluding Remarks
- The main concept of the article is to verify whether deep-learning tools can enhance the versatility of neural estimators. The main points of concern include the reaction of the created networks to varying plant parameters and different operating points, quickness of response to dynamic states, and simultaneous additional benefits, e.g., filtering out white noise from the sensor signals.
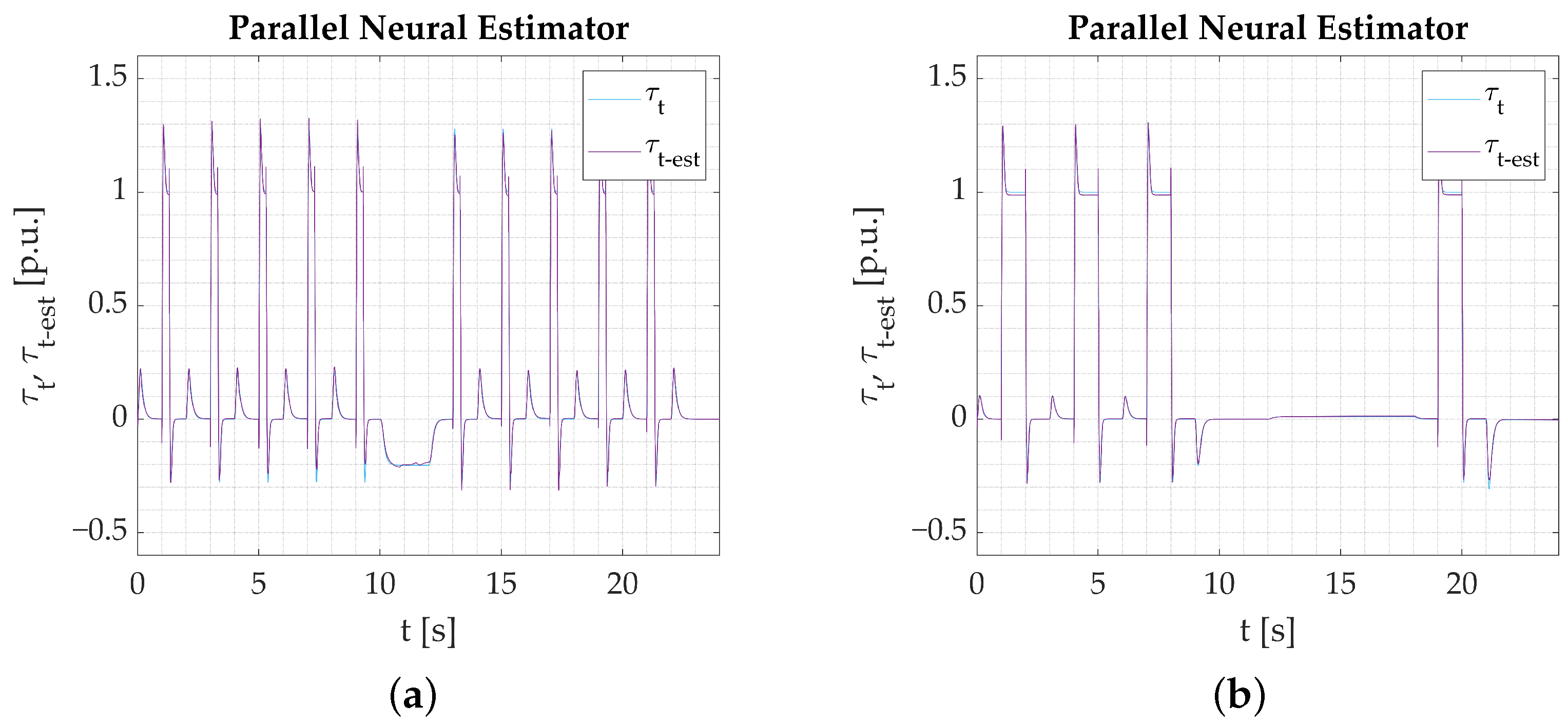
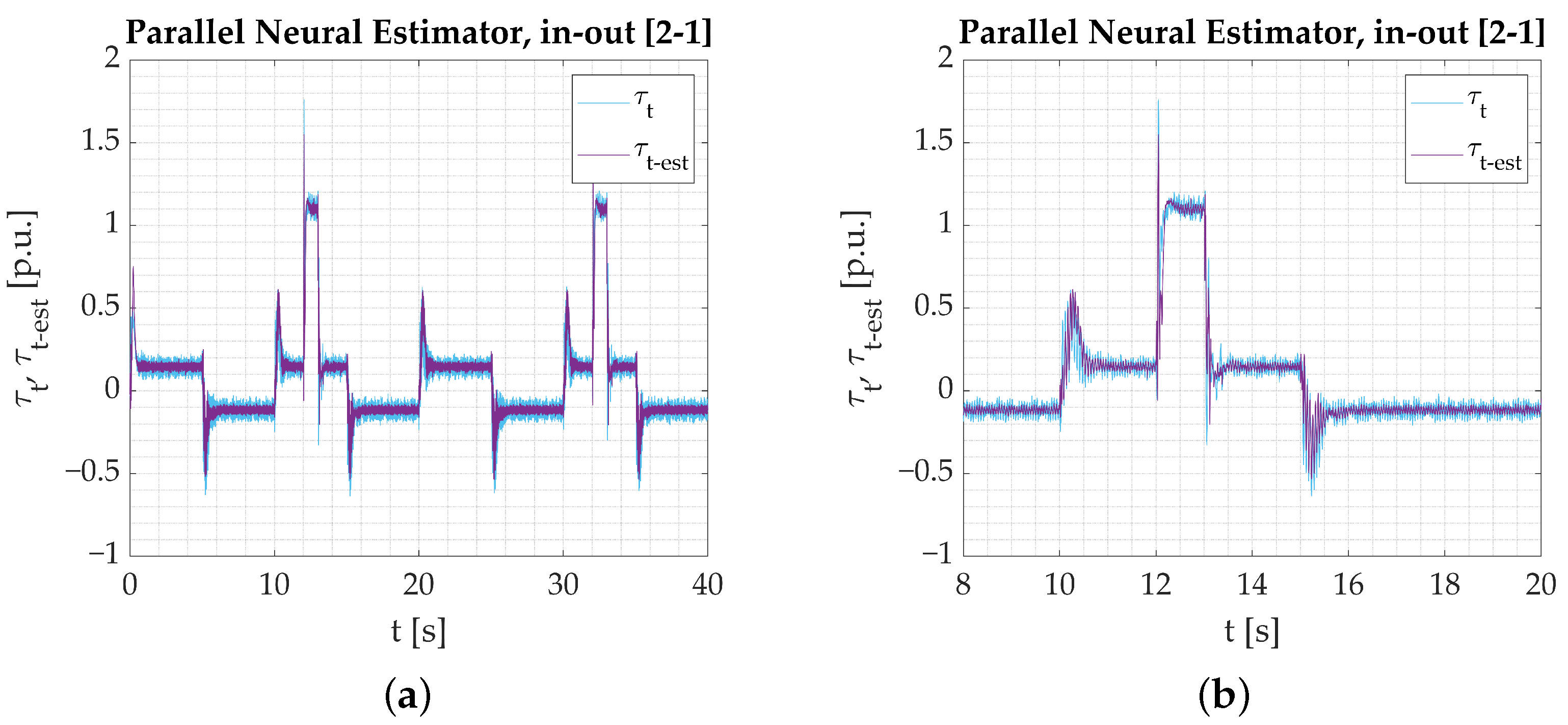
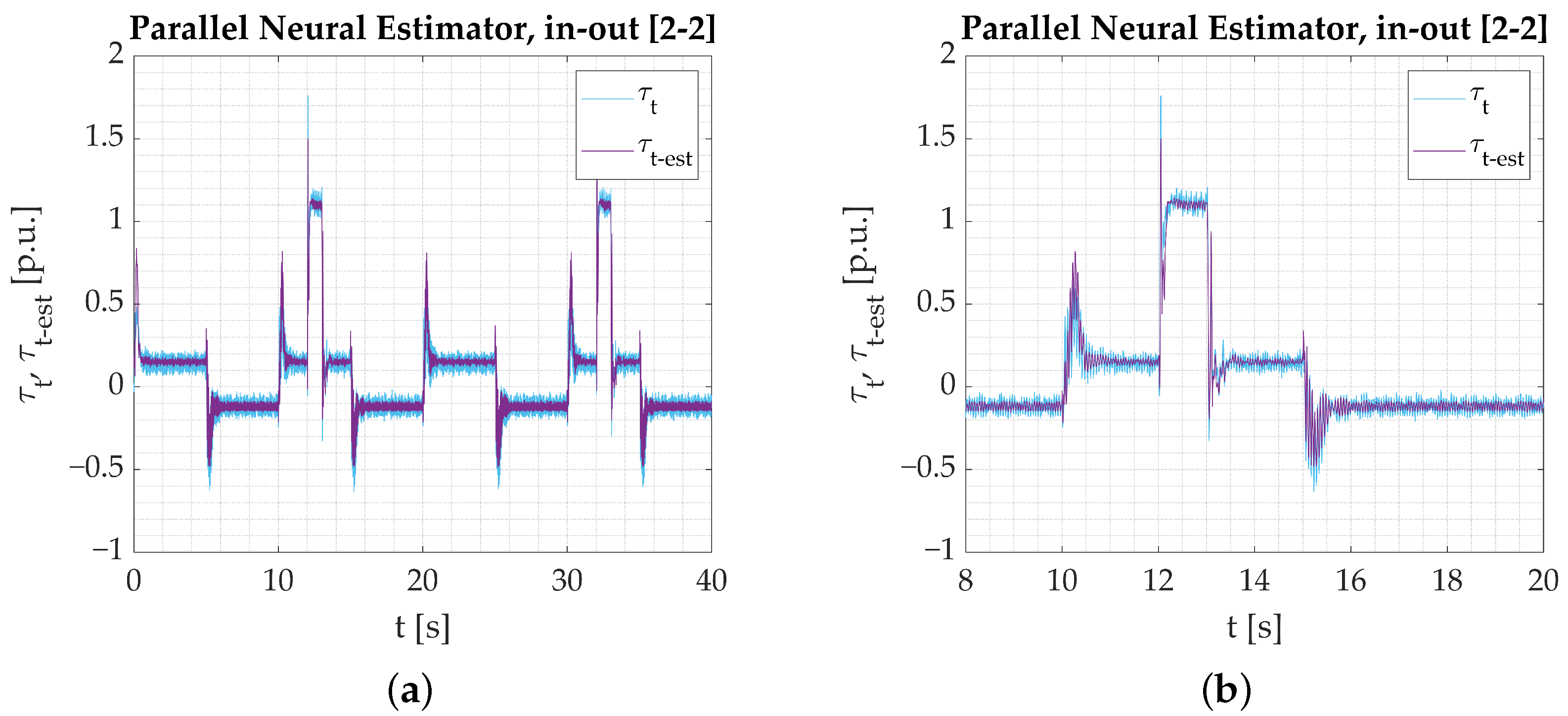
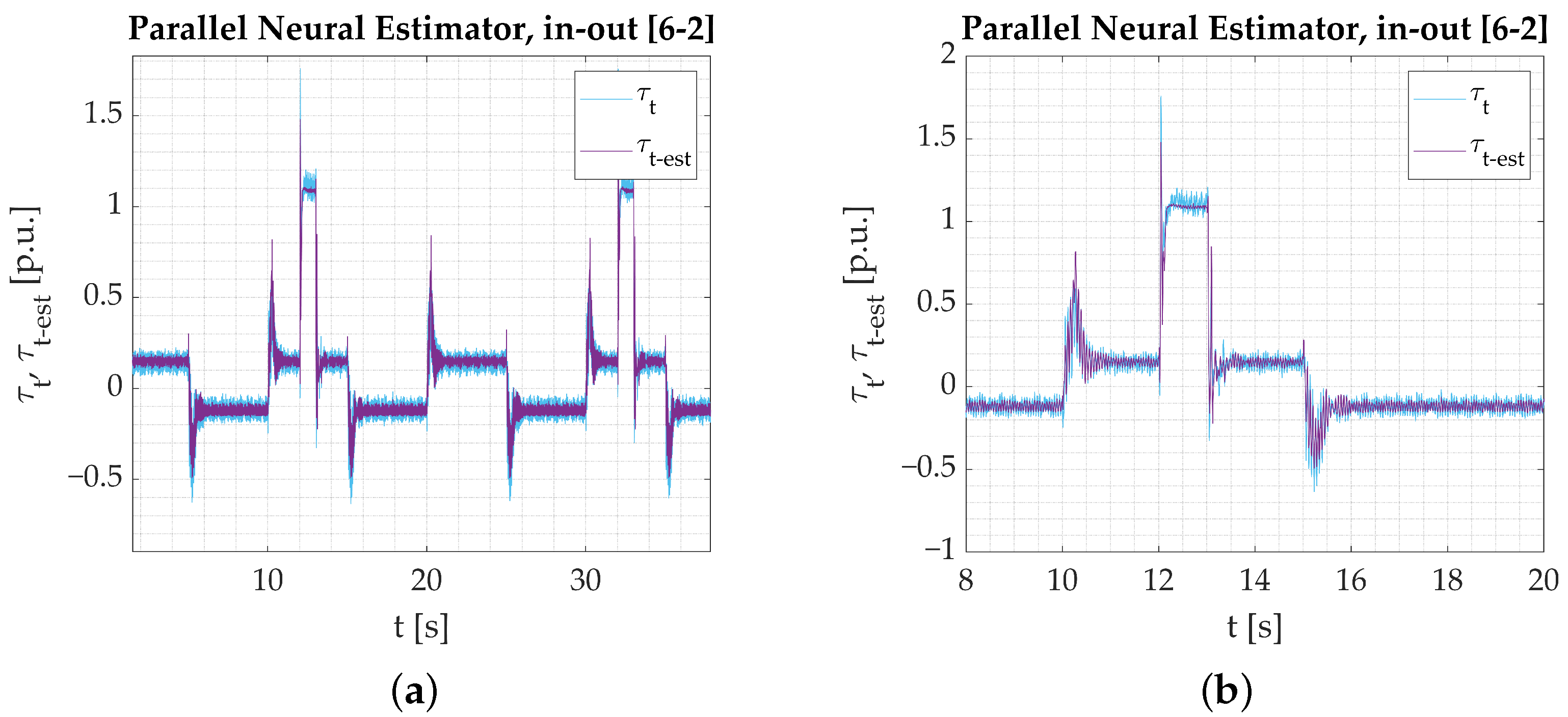
- Numerical studies serve as an initial stage of verification. The results help distinguish the networks’ tendencies and capabilities, but the main focus is put on the possibility of their application in programmable devices. Simulations show that the proposed Parallel neural model is eligible based on its estimation performance. The results are not substantially better than what could be expected from shallow neural networks. However, as stated earlier, at this stage, the most important information is that the model is eligible for application.
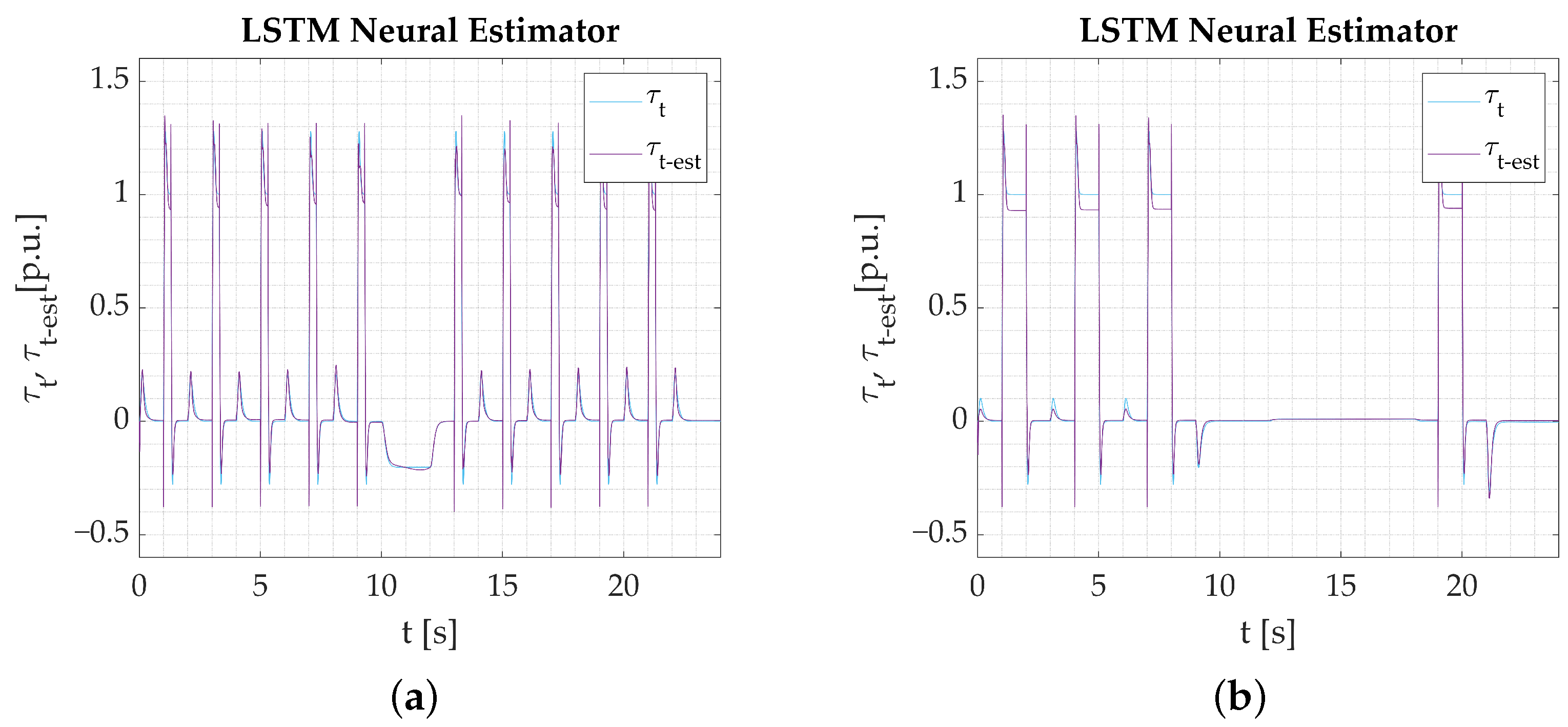
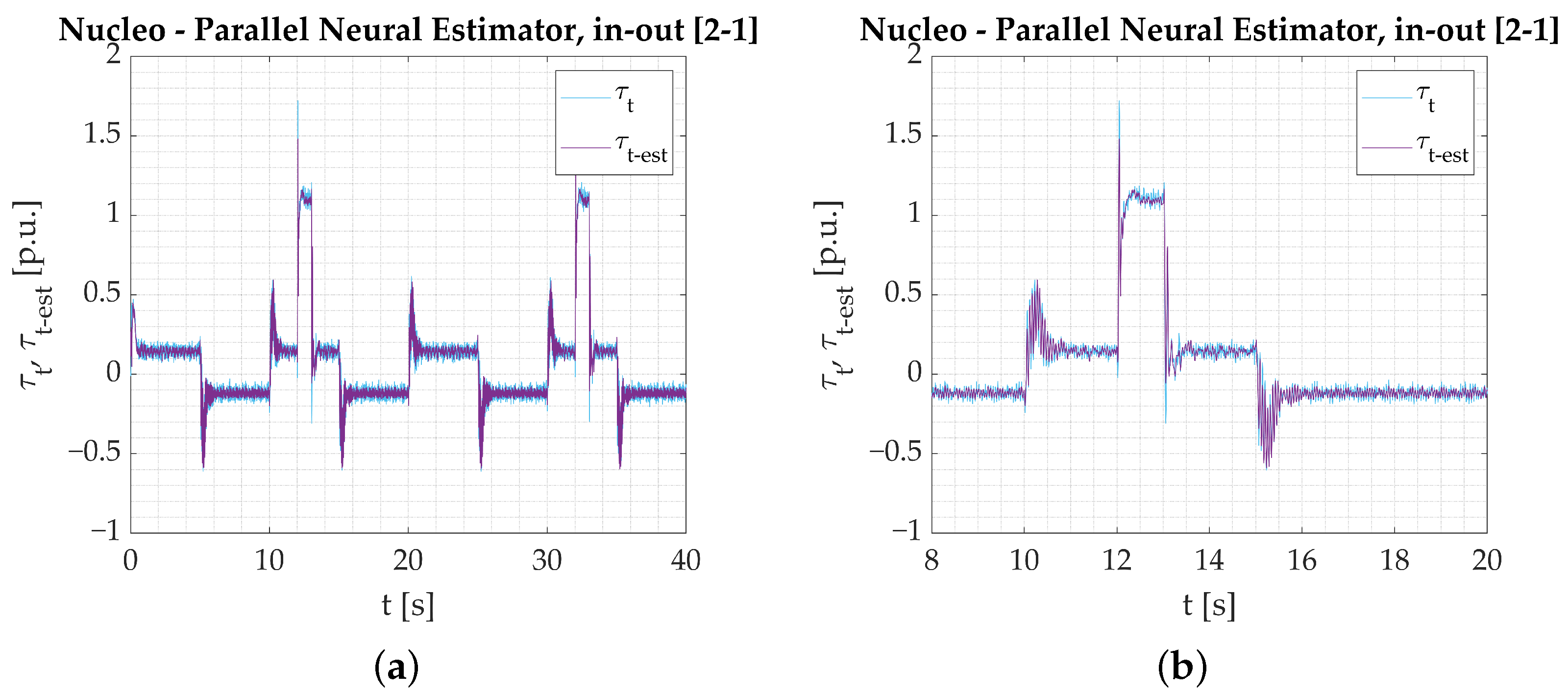
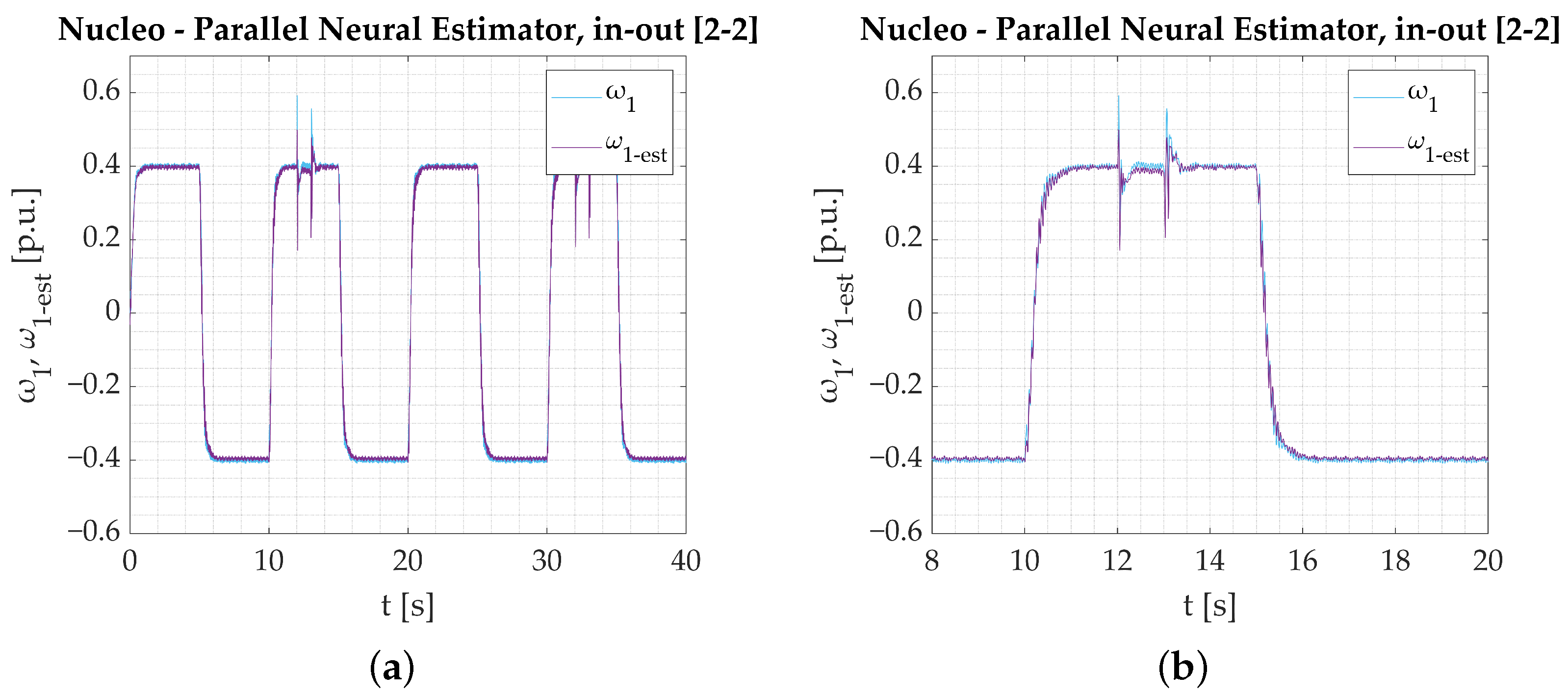
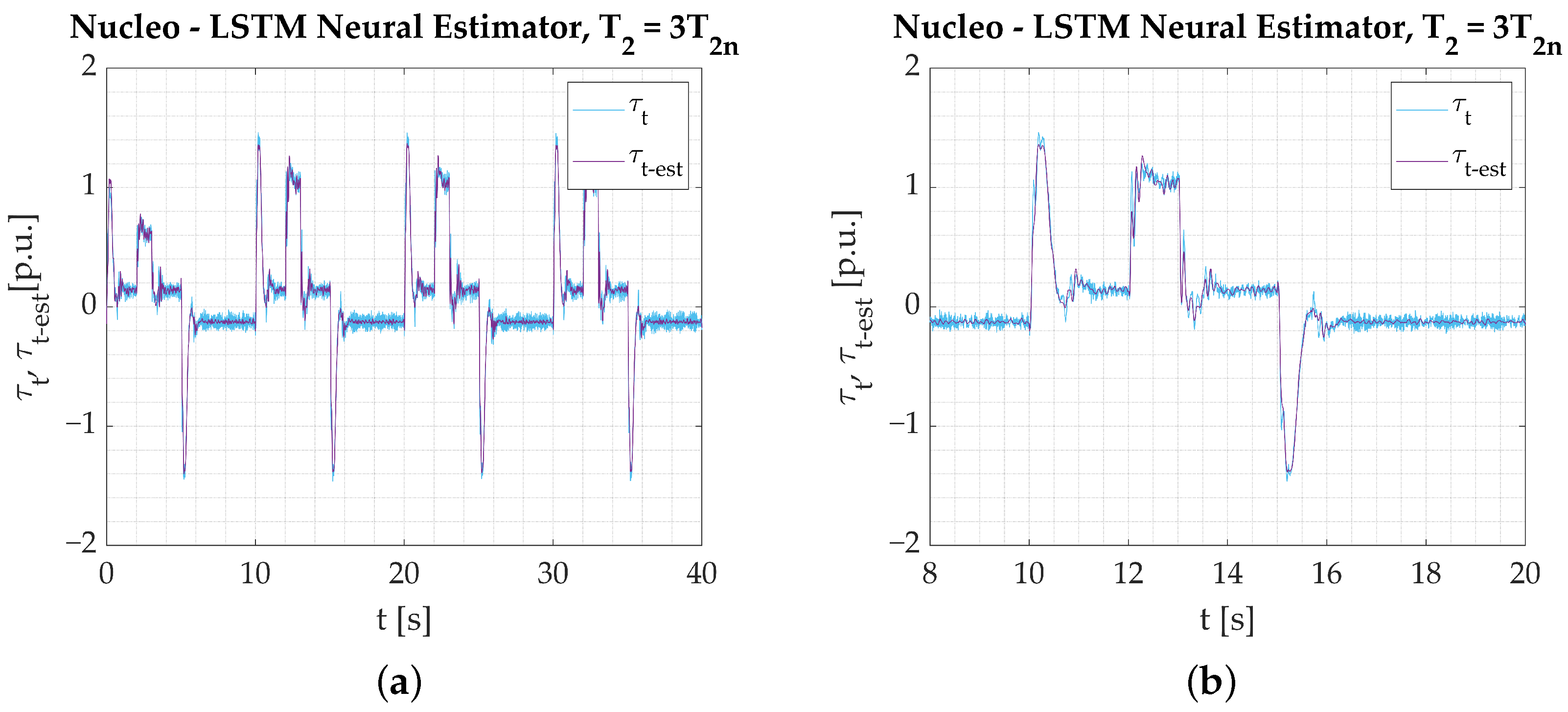
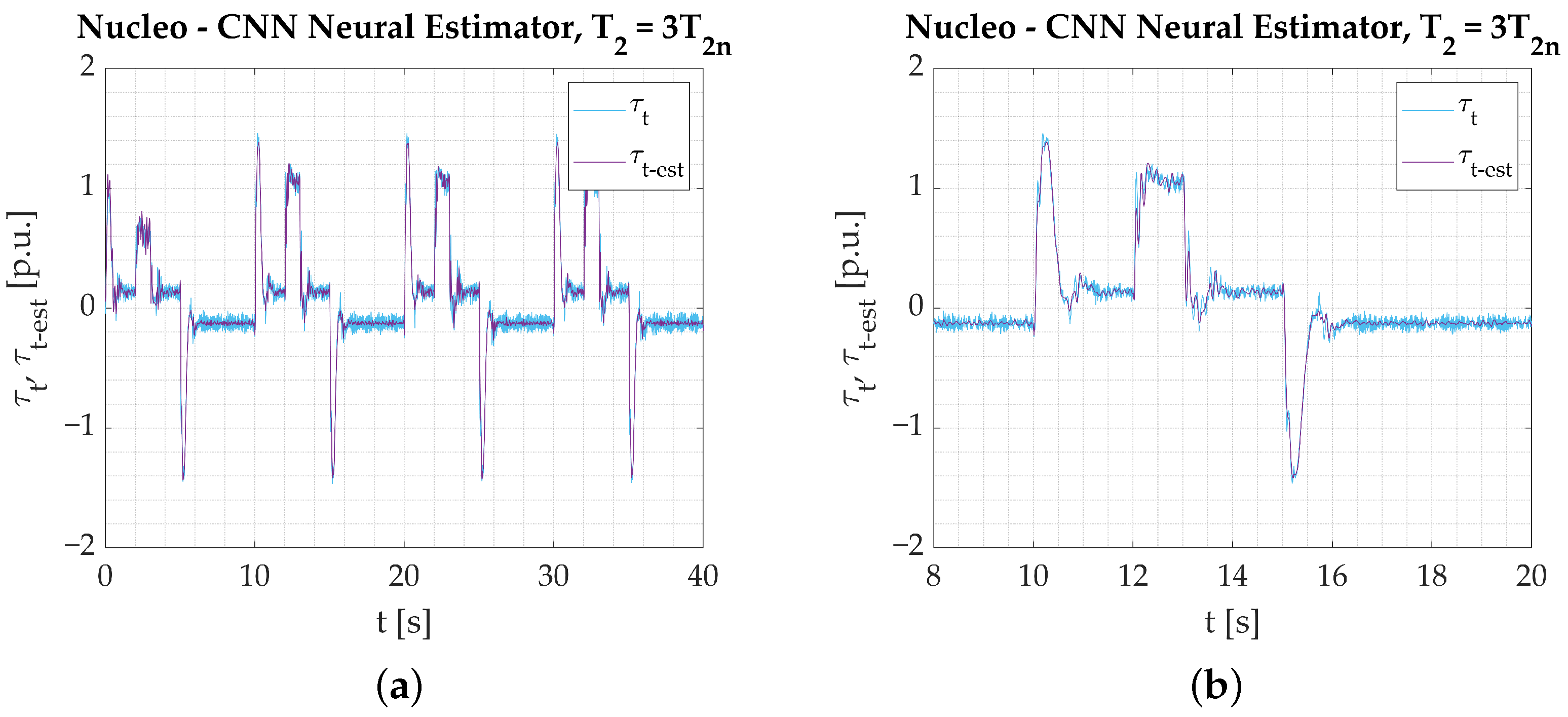
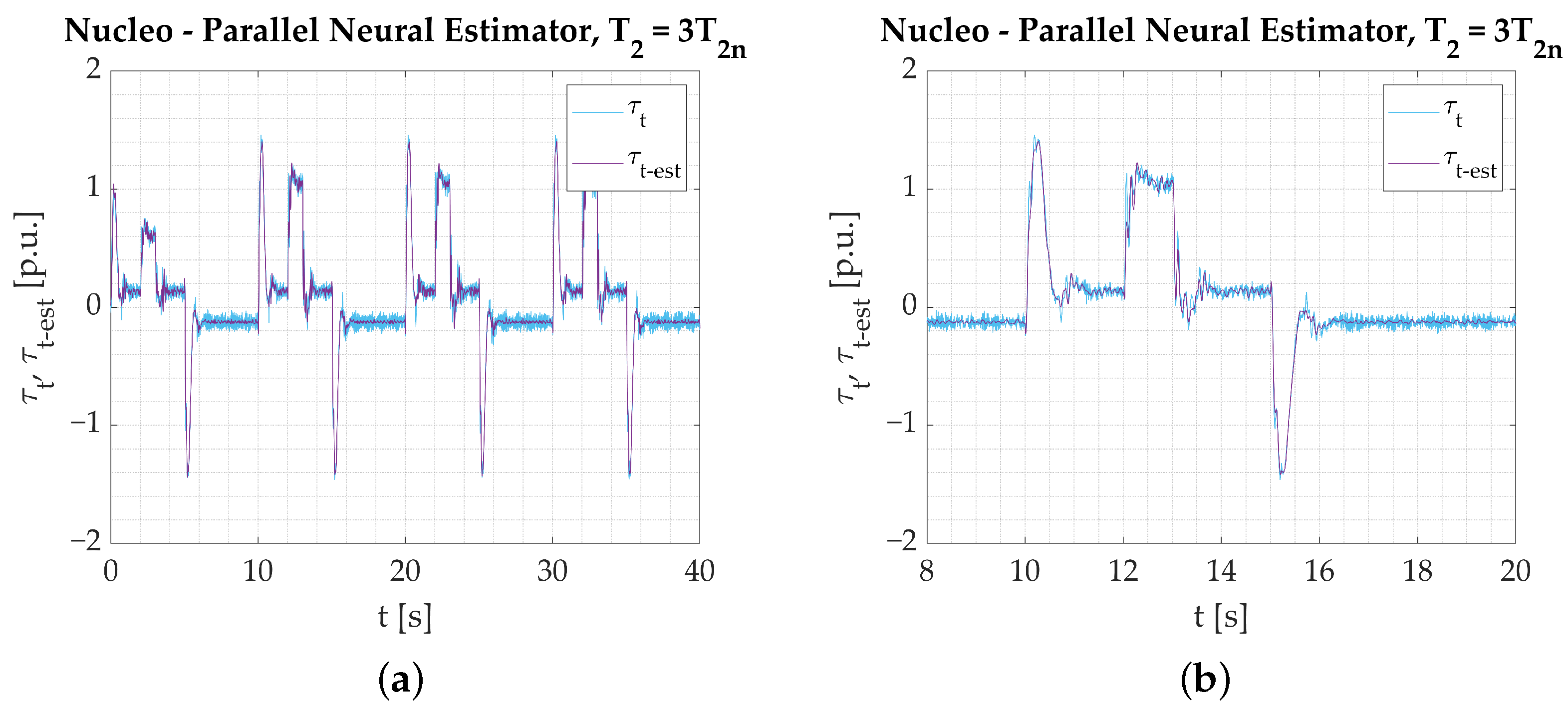
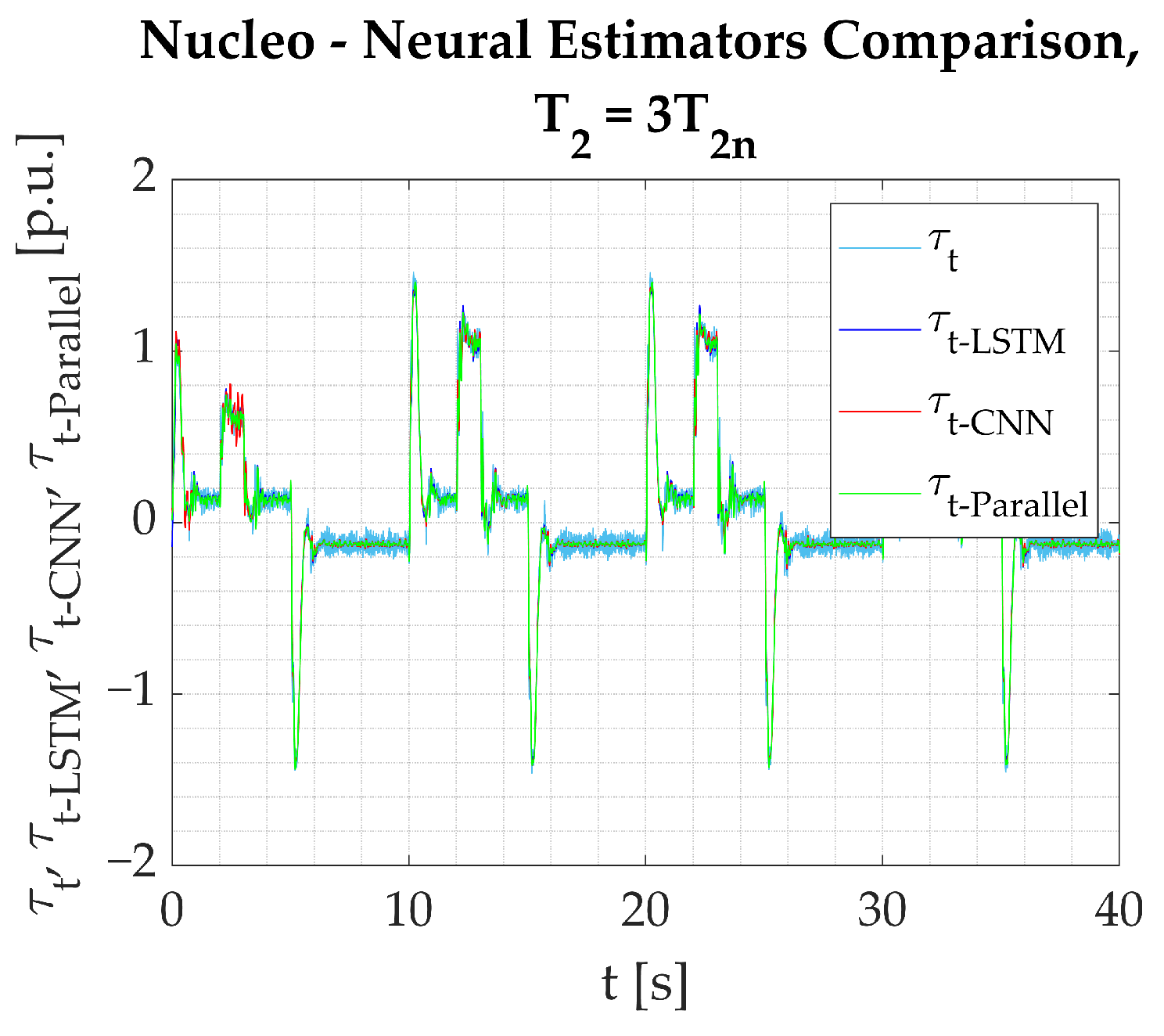
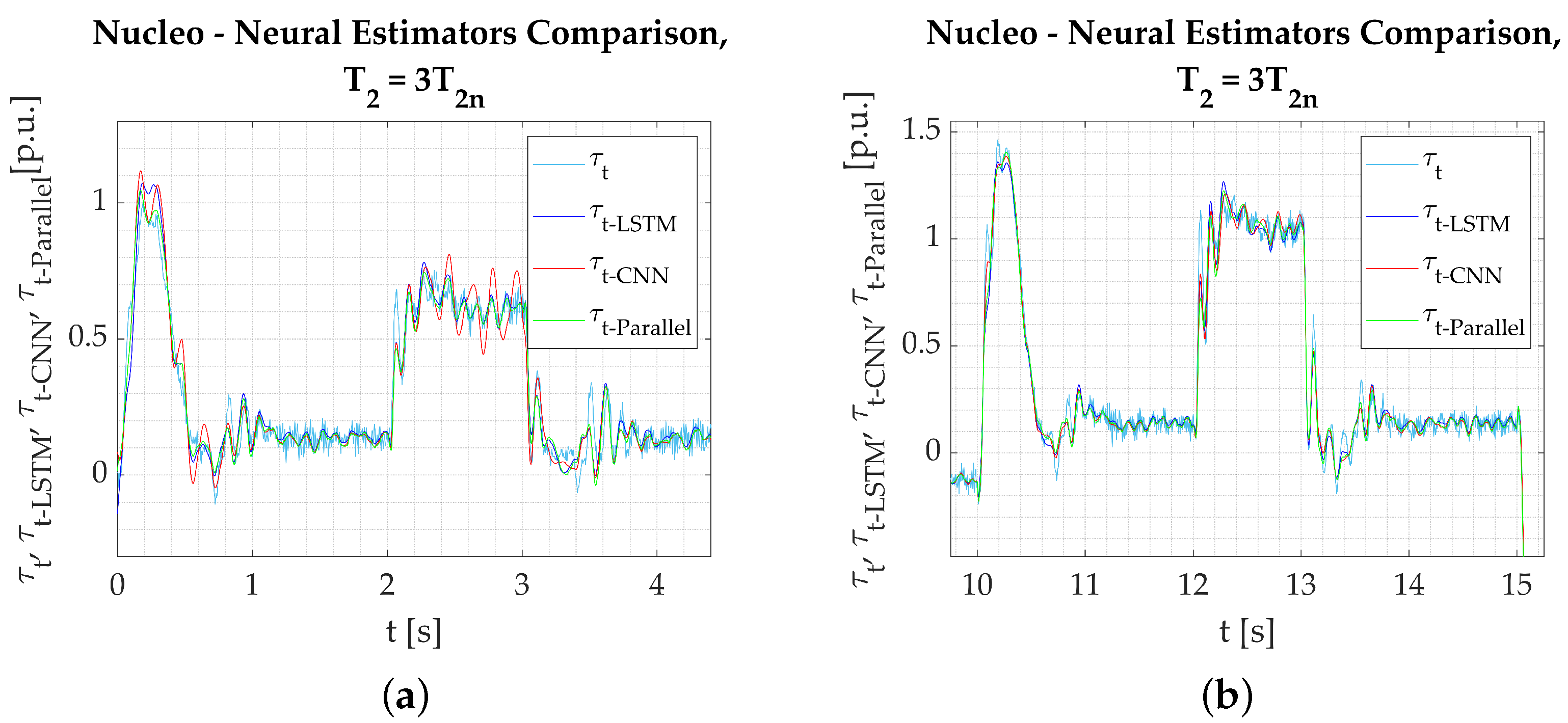
- The calculations performed on the experimental data obtained from the test bench confirm the assumptions from simulation studies. All the networks provide a good reaction to dynamic states and show their applicability to real-time verification. Among the three tested models, the Parallel Neural Network provides the most accurate coverage of all dynamic states (rapid change in direction, reaction to load torque). The worst-performing network for the nominal plant parameters is the LSTM. The output signal is not well amplified during reversions. There is an error in the steady state when load torque is activated, and the peaks are not projected well when the signal is in negative values. CNN results are better; however, it is also unable to precisely estimate the torsional torque when the load is applied.
- Establishing a performance factor may not serve as a basis for fair comparison in this study because convolution affects the network output in the steady states. The applied filtering adds to the estimation error, but it is not necessarily a negative outcome that needs to be penalized. That is why it is preferred that the performance of the networks is assessed solely on the graphical interpretation of the obtained results.
- The Parallel Neural Network enables the estimation of more than one state variable without significant structure modification. Only the output vector must be extended. To obtain comparable results, longer and more precise training needs to be conducted. It is believed that the estimation error could be related to the number of estimated signals. This could be verified in future research.
- Extending the input vector with additional signals greatly improves the performance of shallow networks. In the presented research, however, the proposed deep parallel neural model was not positively affected by such an addition. Only additional noise was inserted into the output. No beneficial effects are observed in this case. It is speculated that further training might bring positive results, but the results shown in the article do not endorse the need for further research in this direction.
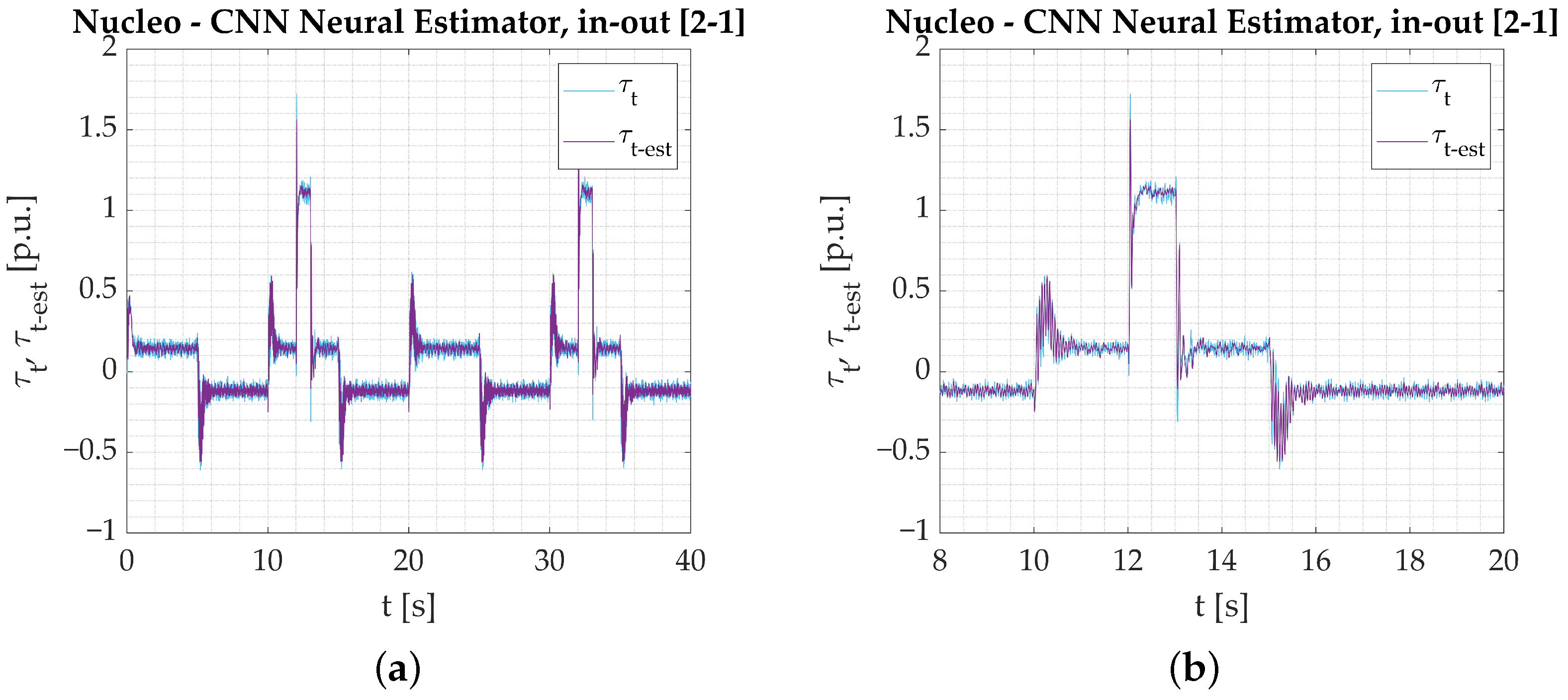
- Deep neural models prepared to operate in the ARM processor were trained on a dedicated dataset. The original data needed to be downsampled to adhere to the device calculation capabilities. Thanks to that, the training time was also reduced, the networks became more robust against measurement noise (better data generalization), and the characteristic features were easier to distinguish, which helped balance the gathered dataset and improve model performance.
- The ARM neural network execution results in visually similar outcomes. That is the reason the estimation error is used to objectively compare the acquired estimator outputs. It proves that estimated torsional torque data sets differ negligibly.
- The use of deep-learning techniques allows the accomplishment of multivariable estimation tasks without having to modify the neural network structure. Even though in this work, estimation of motor speed was performed, similar steps could be taken to obtain the estimation of the load machine speed .
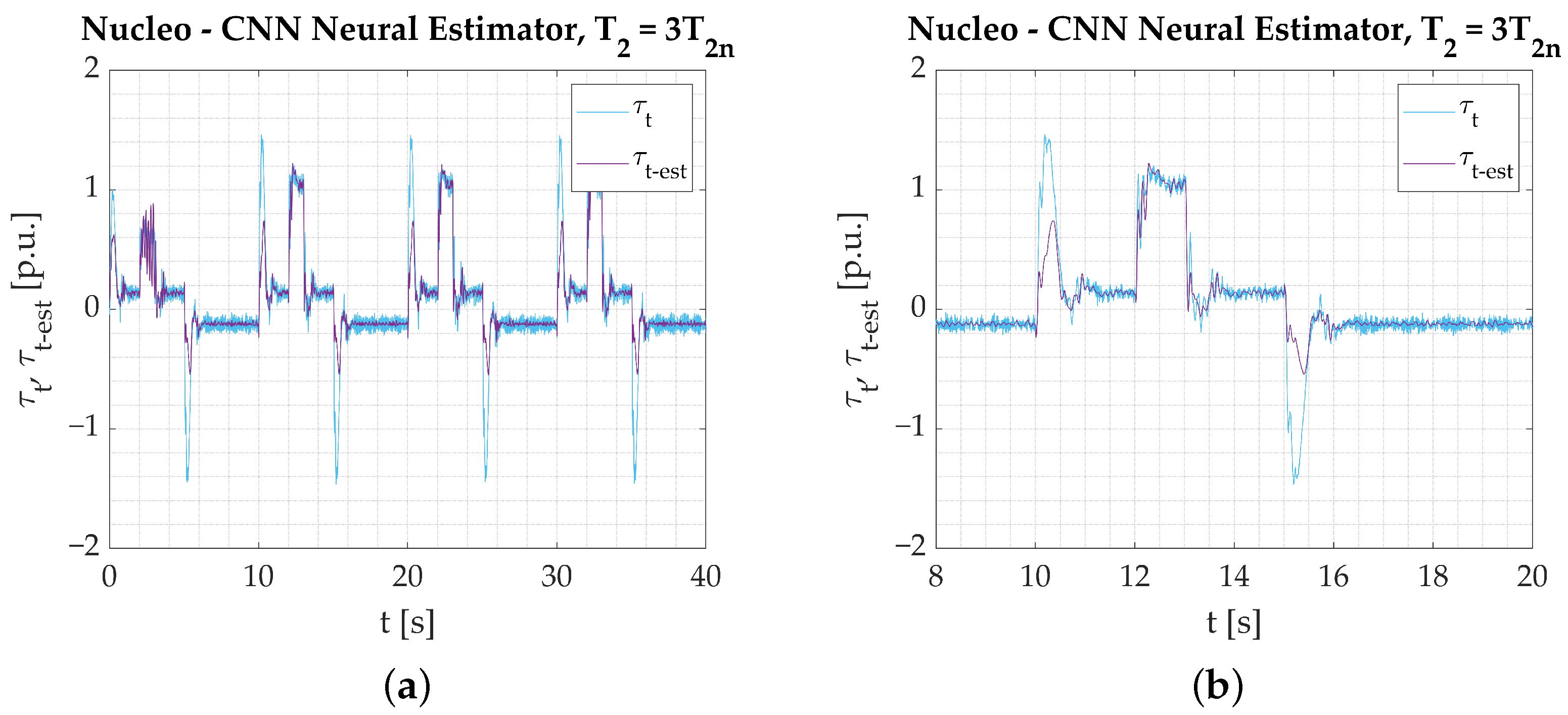
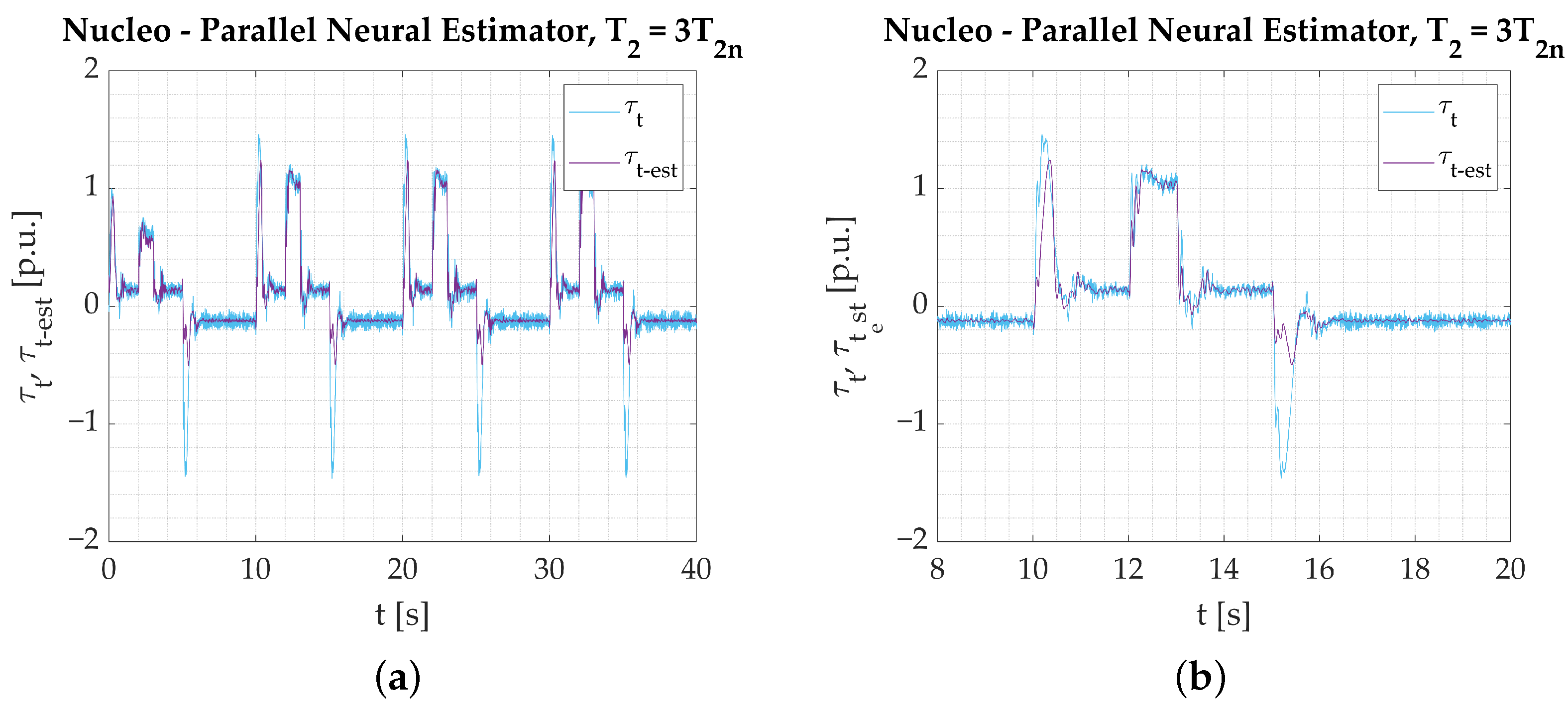
- Changing the plant parameters in the next part of experimental tests clearly emphasizes the differences between tested structures (in case those changes are not included in the training process).
- Applied modification of the training dataset involves one speed return inclusion (for the changed plant parameters) only. That leads to the conclusion that even a gentle modification of the training dataset may remarkably extend a variety of circumstances for which a network is prepared. It may also prepare the neural structure to work at different operational points without the necessity of adjusting the estimator parameters after being deployed.
- The differences noticed between particular network responses are negligible. Thus, the estimation error is calculated again. After conducting the final estimation error analysis, it turns out that (Table 5) the Parallel [2-1] neural estimator features the best response.
- It is worth noting that conducting the estimation error analytically does not always provide an objective, unambiguous review. The estimation error value obtained for the CNN Neural Network (with plant parameters change included in the training process) differs from the one calculated for the Parallel [2-1] network marginally. However, transients of the predicted variables (during the early stage of the drive work, Figure 39a—t = 2–3 s) accentuate unwanted fluctuations, which may be dangerous in real-life scenarios. It would raise a serious concern if the estimated torsional torque variable were part of a closed-loop control system.
- To conclude all research results objectively, the obtained increase factors are compared with the results acquired for nominal plant parameters. Final factor values are calculated according to the same criteria. The final estimation error increase comparison is applied for real-time network execution only, as the presented approach (in the authors’ opinion) constitutes the most vulnerable case, which is also mandatory from the real-life application point of view.
- The smallest increase of the estimation error for significant change in the plant parameters (not included in the training data) is noticed in the case of the Parallel [2-1] neural estimator. It leads to the conclusion that the Parallel Neural Network features the highest robustness to unpredictable circumstances that may occur in real-life scenarios.
- The proposed deep neural estimators have been proven to feature satisfying responses combined with high robustness to the changed plant parameters and the capability of being prepared for different operational points at once. However, the issue of practical, industrial deployment often forces the need for conducting additional adjustments of existing machines/factory lines. The complexity of modern industry involves a variety of different communication protocols, analog and digital sensors, resolution of the transferred data or different sample time steps. Thus, it turns out that the hypothetical implementation of the new solution may often lead to different difficulties, which may dishearten engineers and workers. The choice of an STM-based platform not only provides the versatility of the established tool but also makes the whole implementation process feasible. The Cortex M7 offers a variety of different communication protocols (including CAN bus), a wide range of different clock frequencies it can work with, and a broad range of different internal peripherals. All the mentioned advantages make the Nucleo a perfect base, which makes the deployment process easy and affordable.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, W.; Xue, J.; Fan, X.; Zhu, L. Loss Analysis of Permanent Magnet Synchronous Motor System Based on Strategy-Circuit-Field Co-Simulation and an Accurate Iron Loss Calculation Method. IEEE Access 2024, 12, 168339–168348. [Google Scholar] [CrossRef]
- Wang, X.; Shen, J.; Sun, S.; Xiao, D.; Liu, Y.; Wang, Z. General Modeling and Control of Multiple Three-Phase PMSM Drives. IEEE Trans. Power Electron. 2025, 40, 1900–1909. [Google Scholar] [CrossRef]
- Giesbrecht, M.; Torllone de Carvalho Ferreira, G.; Raimundo da Silva, R.; Milfont, L.D. Electric Machine Design and Fault Diagnosis for Electric Aircraft Propulsion in the Context of the Engineering Research Center for the Aerial Mobility of the Future. In Proceedings of the 2023 IEEE Workshop on Power Electronics for Aerospace Applications (PEASA), Nottingham, UK, 18–19 July 2023; pp. 1–5. [Google Scholar] [CrossRef]
- Rivas-Martínez, G.I.; Rodas, J.; Herrera, E.; Doval-Gandoy, J. A Novel Approach to Performance Evaluation of Current Controllers in Power Converters and Electric Drives Using Non-Parametric Analysis. IEEE Lat. Am. Trans. 2025, 23, 68–77. [Google Scholar] [CrossRef]
- Orlowska-Kowalska, T.; Wolkiewicz, M.; Pietrzak, P.; Skowron, M.; Ewert, P.; Tarchala, G.; Krzysztofiak, M.; Kowalski, C.T. Fault Diagnosis and Fault-Tolerant Control of PMSM Drives—State of the Art and Future Challenges. IEEE Access 2022, 10, 59979–60024. [Google Scholar] [CrossRef]
- Pajchrowski, T.; Siwek, P.; Wójcik, A. Adaptive Neural Controller for Speed Control of PMSM with Torque Ripples. In Proceedings of the 2022 IEEE 20th International Power Electronics and Motion Control Conference (PEMC), Brasov, Romania, 25–28 September 2022; pp. 564–570. [Google Scholar] [CrossRef]
- Niewiara, L.J.; Tarczewski, T.; Gierczynski, M.; Grzesiak, L.M. Designing a Hybrid State Feedback Control Structure for a Drive With a Reluctance Synchronous Motor. IEEE Trans. Ind. Electron. 2024, 71, 8351–8361. [Google Scholar] [CrossRef]
- Kaminski, M.; Tarczewski, T. Neural Network Applications in Electrical Drives—Trends in Control, Estimation, Diagnostics, and Construction. Energies 2023, 16, 4441. [Google Scholar] [CrossRef]
- Wang, F.; Wei, Y.; Young, H.; Ke, D.; Yu, X.; Rodríguez, J. Low-Stagnation Model-Free Predictive Current Control of PMSM Drives. IEEE Trans. Ind. Electron. 2024, 1–12. [Google Scholar] [CrossRef]
- Wang, Y.; Li, P.; Shen, J.X.; Jiang, C.; Huang, X.; Long, T. Adaptive Periodic Disturbance Observer Based on Fuzzy Logic Compensation for Speed Fluctuation Suppression of PMSM Under Periodic Loads. IEEE Trans. Ind. Appl. 2024, 60, 5751–5762. [Google Scholar] [CrossRef]
- Miyahara, K.; Katsura, S. Energy Localization in Spring-Motor Coupling System by Switching Mass Control. In Proceedings of the 2023 IEEE International Conference on Mechatronics (ICM), Loughborough, UK, 15–17 March 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Takeuchi, I.; Kaneda, T.; Katsura, S. Modeling and Control of Two-mass Resonant System Based on Element Description Method. In Proceedings of the 2021 IEEE 30th International Symposium on Industrial Electronics (ISIE), Kyoto, Japan, 20–23 June 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Szabat, K.; Orlowska-Kowalska, T. Vibration Suppression in a Two-Mass Drive System Using PI Speed Controller and Additional Feedbacks—Comparative Study. IEEE Trans. Ind. Electron. 2007, 54, 1193–1206. [Google Scholar] [CrossRef]
- Wang, C.; Yang, M.; Zheng, W.; Long, J.; Xu, D. Vibration Suppression With Shaft Torque Limitation Using Explicit MPC-PI Switching Control in Elastic Drive Systems. IEEE Trans. Ind. Electron. 2015, 62, 6855–6867. [Google Scholar] [CrossRef]
- Brock, S.; Łuczak, D.; Nowopolski, K.; Pajchrowski, T.; Zawirski, K. Two Approaches to Speed Control for Multi-Mass System With Variable Mechanical Parameters. IEEE Trans. Ind. Electron. 2017, 64, 3338–3347. [Google Scholar] [CrossRef]
- Zoubek, H.; Pacas, M. Encoderless Identification of Two-Mass-Systems Utilizing an Extended Speed Adaptive Observer Structure. IEEE Trans. Ind. Electron. 2017, 64, 595–604. [Google Scholar] [CrossRef]
- Yang, Q.; Mao, K.; Zheng, S.; Le, Y. Rotor Position Estimation Based on Fast Terminal Sliding Mode for Magnetic Suspension Centrifugal Compressor Drives. IEEE Trans. Instrum. Meas. 2024, 73, 1–11. [Google Scholar] [CrossRef]
- Wang, T.; Yu, Y.; Zhang, Z.; Jin, S.; Wang, B.; Xu, D. An Auxiliary Variable-Based MRAS Speed Observer for Stable Wide-Speed Operation in Sensorless Induction Motor Drives. IEEE J. Emerg. Sel. Top. Power Electron. 2024, 12, 4926–4940. [Google Scholar] [CrossRef]
- Liu, Y.; Li, H.; He, W. Rotor Position Estimation Method for Permanent Magnet Synchronous Motor Based on High-Order Extended Kalman Filter. Electronics 2024, 13, 4978. [Google Scholar] [CrossRef]
- Liu, J.; Li, M.; Xie, E. Noncascade Structure Equivalent SMC for PMSM Driving Based on Improved ESO. IEEE Trans. Power Electron. 2025, 40, 611–624. [Google Scholar] [CrossRef]
- Li, H.; Zhang, R.; Shi, P.; Xiao, P.; Zheng, K.; Qiu, T. State Parameters Estimation for Distributed Drive Electric Vehicle Based on PMSMs’ Sensorless Control. IEEE Sens. J. 2024, 24, 24054–24069. [Google Scholar] [CrossRef]
- Djellouli, Y.; El Mehdi ARDJOUN, S.A.; Zerdali, E.; Denai, M.; Chafouk, H. Real Time Implementation of a Speed/Torque Sensorless Observer for Induction Motor Utilizing Extended Kalman Filtering Technique. In Proceedings of the 2024 3rd International Conference on Advanced Electrical Engineering (ICAEE), Sidi-Bel-Abbes, Algeria, 5–7 November 2024; pp. 1–5. [Google Scholar] [CrossRef]
- Chen, Z.; Chen, F.; Huang, X.; Li, Z.; Wu, M. DEA-tuning of Reduced-order Extended Luenberger Sliding Mode Observers(ELSMO) for Sensorless Control of High-speed SPMSM. In Proceedings of the 2021 IEEE International Electric Machines & Drives Conference (IEMDC), Hartford, CT, USA, 17–20 May 2021; pp. 1–7. [Google Scholar] [CrossRef]
- Reddy, S.V.B.S.; Kumar, B.; Swaroop, D. Investigations on Training Algorithms for Neural Networks Based Flux Estimator Used in Speed Estimation of Induction Motor. In Proceedings of the 2019 6th International Conference on Signal Processing and Integrated Networks (SPIN), Noida, India, 7–8 March 2019; pp. 1090–1094. [Google Scholar] [CrossRef]
- Zhang, X.; Jiang, Q. Research on Sensorless Control of PMSM Based on Fuzzy Sliding Mode Observer. In Proceedings of the 2021 IEEE 16th Conference on Industrial Electronics and Applications (ICIEA), Chengdu, China, 1–4 August 2021; pp. 213–218. [Google Scholar] [CrossRef]
- Lin, X.; Xu, R.; Yao, W.; Gao, Y.; Sun, G.; Liu, J.; Peretti, L.; Wu, L. Observer-Based Prescribed Performance Speed Control for PMSMs: A Data-Driven RBF Neural Network Approach. IEEE Trans. Ind. Inform. 2024, 20, 7502–7512. [Google Scholar] [CrossRef]
- Soufyane, B.; Abdelhamid, R.; Smail, Z. Signed-Distance Fuzzy Logic Controller Adaptation Mechanism based MRAS Observer for Direct-Drive PMSG Wind Turbines Sensorless Control. In Proceedings of the 2020 American Control Conference (ACC), Denver, CO, USA, 1–3 July 2020; pp. 4083–4089. [Google Scholar] [CrossRef]
- Erenturk, K. Gray-fuzzy control of a nonlinear two-mass system. J. Frankl. Inst. 2010, 347, 1171–1185. [Google Scholar] [CrossRef]
- Deponti, M.; Pejovski, D.; Gerlando, A.D.; Perini, R. A Nonlinear Extended State Observer Design for Torsional Vibrations Estimation in PMSM Drive. In Proceedings of the 2024 International Conference on Electrical Machines (ICEM), Torino, Italy, 1–4 September 2024; pp. 1–7. [Google Scholar] [CrossRef]
- Kaminski, M. Adaptive Gradient-Based Luenberger Observer Implemented for Electric Drive with Elastic Joint. In Proceedings of the 2018 23rd International Conference on Methods & Models in Automation & Robotics (MMAR), Miedzyzdroje, Poland, 27–30 August 2018; pp. 53–58. [Google Scholar] [CrossRef]
- Liu, Y.; Song, B.; Zhou, X.; Gao, Y.; Chen, T. An Adaptive Torque Observer Based on Fuzzy Inference for Flexible Joint Application. Machines 2023, 11, 794. [Google Scholar] [CrossRef]
- Szabat, K.; Tran-Van, T.; Kaminski, M. A Modified Fuzzy Luenberger Observer for a Two-Mass Drive System. IEEE Trans. Ind. Inform. 2015, 11, 531–539. [Google Scholar] [CrossRef]
- Auger, F.; Hilairet, M.; Guerrero, J.M.; Monmasson, E.; Orlowska-Kowalska, T.; Katsura, S. Industrial Applications of the Kalman Filter: A Review. IEEE Trans. Ind. Electron. 2013, 60, 5458–5471. [Google Scholar] [CrossRef]
- Szabat, K.; Orlowska-Kowalska, T. Application of the Kalman Filters to the High-Performance Drive System With Elastic Coupling. IEEE Trans. Ind. Electron. 2012, 59, 4226–4235. [Google Scholar] [CrossRef]
- Szabat, K.; Orlowska-Kowalska, T. Performance Improvement of Industrial Drives With Mechanical Elasticity Using Nonlinear Adaptive Kalman Filter. IEEE Trans. Ind. Electron. 2008, 55, 1075–1084. [Google Scholar] [CrossRef]
- Szabat, K.; Wróbel, K.; Dróżdż, K.; Janiszewski, D.; Pajchrowski, T.; Wójcik, A. A Fuzzy Unscented Kalman Filter in the Adaptive Control System of a Drive System with a Flexible Joint. Energies 2020, 13, 2056. [Google Scholar] [CrossRef]
- Szabat, K.; Wróbel, K.; Śleszycki, K.; Katsura, S. States Estimation of the Two-Mass Drive System Using Multilayer Observer. In Proceedings of the 2021 IEEE 19th International Power Electronics and Motion Control Conference (PEMC), Gliwice, Poland, 25–29 April 2021; pp. 743–748. [Google Scholar] [CrossRef]
- Szabat, K.; Tokarczyk, A.; Wróbel, K.; Katsura, S. Application of the Multi-Layer Observer for a Two-Mass Drive System. In Proceedings of the 2020 IEEE 29th International Symposium on Industrial Electronics (ISIE), Delft, The Netherlands, 17–19 June 2020; pp. 265–270. [Google Scholar] [CrossRef]
- Abiodun, O.I.; Jantan, A.; Omolara, A.E.; Dada, K.V.; Mohamed, N.A.; Arshad, H. State-of-the-art in artificial neural network applications: A survey. Heliyon 2018, 4, e00938. [Google Scholar] [CrossRef]
- Widrow, B.; Lehr, M. 30 years of adaptive neural networks: Perceptron, Madaline, and backpropagation. Proc. IEEE 1990, 78, 1415–1442. [Google Scholar] [CrossRef]
- Orlowska-Kowalska, T.; Szabat, K. Neural-Network Application for Mechanical Variables Estimation of a Two-Mass Drive System. IEEE Trans. Ind. Electron. 2007, 54, 1352–1364. [Google Scholar] [CrossRef]
- Belov, M.P.; Van Lanh, N.; Khoa, T.D. State Observer based Elman Recurrent Neural Network for Electric Drive of Optical-Mechanical Complexes. In Proceedings of the 2021 IEEE Conference of Russian Young Researchers in Electrical and Electronic Engineering (ElConRus), St. Petersburg, Moscow, Russia, 26–29 January 2021; pp. 802–805. [Google Scholar] [CrossRef]
- Nicola, M.; Nicola, C.I.; Duţă, M. Sensorless Control of PMSM using FOC Strategy Based on Multiple ANN and Load Torque Observer. In Proceedings of the 2020 International Conference on Development and Application Systems (DAS), Suceava, Romania, 21–23 May 2020; pp. 32–37. [Google Scholar] [CrossRef]
- Zhang, S.; Wallscheid, O.; Porrmann, M. Machine Learning for the Control and Monitoring of Electric Machine Drives: Advances and Trends. IEEE Open J. Ind. Appl. 2023, 4, 188–214. [Google Scholar] [CrossRef]
- Orlowska-Kowalska, T.; Kaminski, M. Effectiveness of Saliency-Based Methods in Optimization of Neural State Estimators of the Drive System With Elastic Couplings. IEEE Trans. Ind. Electron. 2009, 56, 4043–4051. [Google Scholar] [CrossRef]
- Łuczak, D.; Wójcik, A. The study of neural estimator structure influence on the estimation quality of selected state variables of the complex mechanical part of electrical drive. In Proceedings of the 2017 19th European Conference on Power Electronics and Applications (EPE’17 ECCE Europe), Warsaw, Poland, 11–14 September 2017; pp. P.1–P.10. [Google Scholar] [CrossRef]
- Orlowska-Kowalska, T.; Kaminski, M. FPGA Implementation of the Multilayer Neural Network for the Speed Estimation of the Two-Mass Drive System. IEEE Trans. Ind. Inform. 2011, 7, 436–445. [Google Scholar] [CrossRef]
- Mathesh, G.; Saravanakumar, R.; Salgotra, R. Novel Machine Learning Control for Power Management Using an Instantaneous Reference Current in Multiple-Source-Fed Electric Vehicles. Energies 2024, 17, 2677. [Google Scholar] [CrossRef]
- Lin, F.J.; Huang, M.S.; Chen, S.G.; Hsu, C.W.; Liang, C.H. Adaptive Backstepping Control for Synchronous Reluctance Motor Based on Intelligent Current Angle Control. IEEE Trans. Power Electron. 2020, 35, 7465–7479. [Google Scholar] [CrossRef]
- Malarczyk, M.; Zychlewicz, M.; Stanislawski, R.; Kaminski, M. Electric Drive with an Adaptive Controller and Wireless Communication System. Future Internet 2023, 15, 49. [Google Scholar] [CrossRef]
- Liu, W.; Wang, Z.; Liu, X.; Zeng, N.; Liu, Y.; Alsaadi, F.E. A survey of deep neural network architectures and their applications. Neurocomputing 2017, 234, 11–26. [Google Scholar] [CrossRef]
- Li, Z.; Liu, F.; Yang, W.; Peng, S.; Zhou, J. A Survey of Convolutional Neural Networks: Analysis, Applications, and Prospects. IEEE Trans. Neural Netw. Learn. Syst. 2022, 33, 6999–7019. [Google Scholar] [CrossRef]
- Mustafa, A.; Sasamura, T.; Morita, T. Sensorless Speed Control of Ultrasonic Motors Using Deep Reinforcement Learning. IEEE Sens. J. 2024, 24, 4023–4035. [Google Scholar] [CrossRef]
- Li, Y.; Sun, T.; Zhang, W.; Li, S.; Liang, J.; Wang, Z. A Torque Observer for IPMSM Drives Based on Deep Neural Network. In Proceedings of the 2019 14th IEEE Conference on Industrial Electronics and Applications (ICIEA), Xi’an, China, 19–21 June 2019; pp. 1530–1535. [Google Scholar] [CrossRef]
- Derugo, P.; Kahsay, A.H.; Szabat, K.; Shikata, K.; Katsura, S. A Novel PI-Based Control Structure with Additional Feedback from Torsional Torque and Its Derivative for Damping Torsional Vibrations. Energies 2024, 17, 4786. [Google Scholar] [CrossRef]
- Ogata, K. Modern Control Engineering; Prentice Hall: Hoboken, NJ, USA, 2002. [Google Scholar]
- Åström, K.; Murray, R. Feedback Systems: An Introduction for Scientists and Engineers, Second Edition; Princeton University Press: Princeton, NJ, USA, 2021. [Google Scholar]
- Ackermann, J. Der Entwurf linearer Regelungssysteme im Zustandsraum. Automatisierungstechnik 1972, 20, 297–300. [Google Scholar] [CrossRef]
- Frobenius, G. Ueber lineare Substitutionen und bilineare Formen. J. Reine Angew. Math. 1877, 84, 1–63. [Google Scholar]

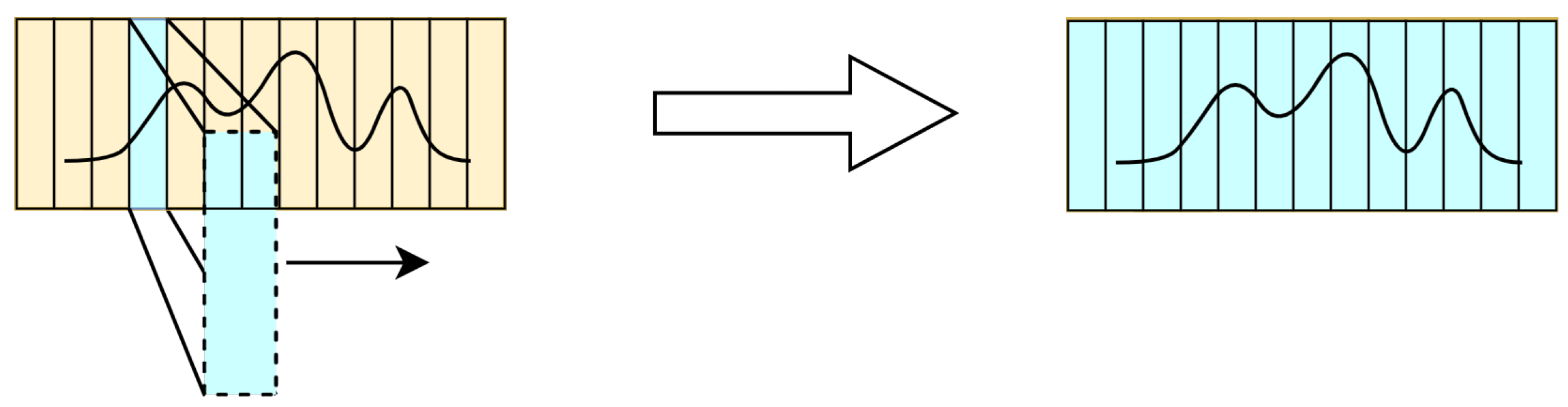

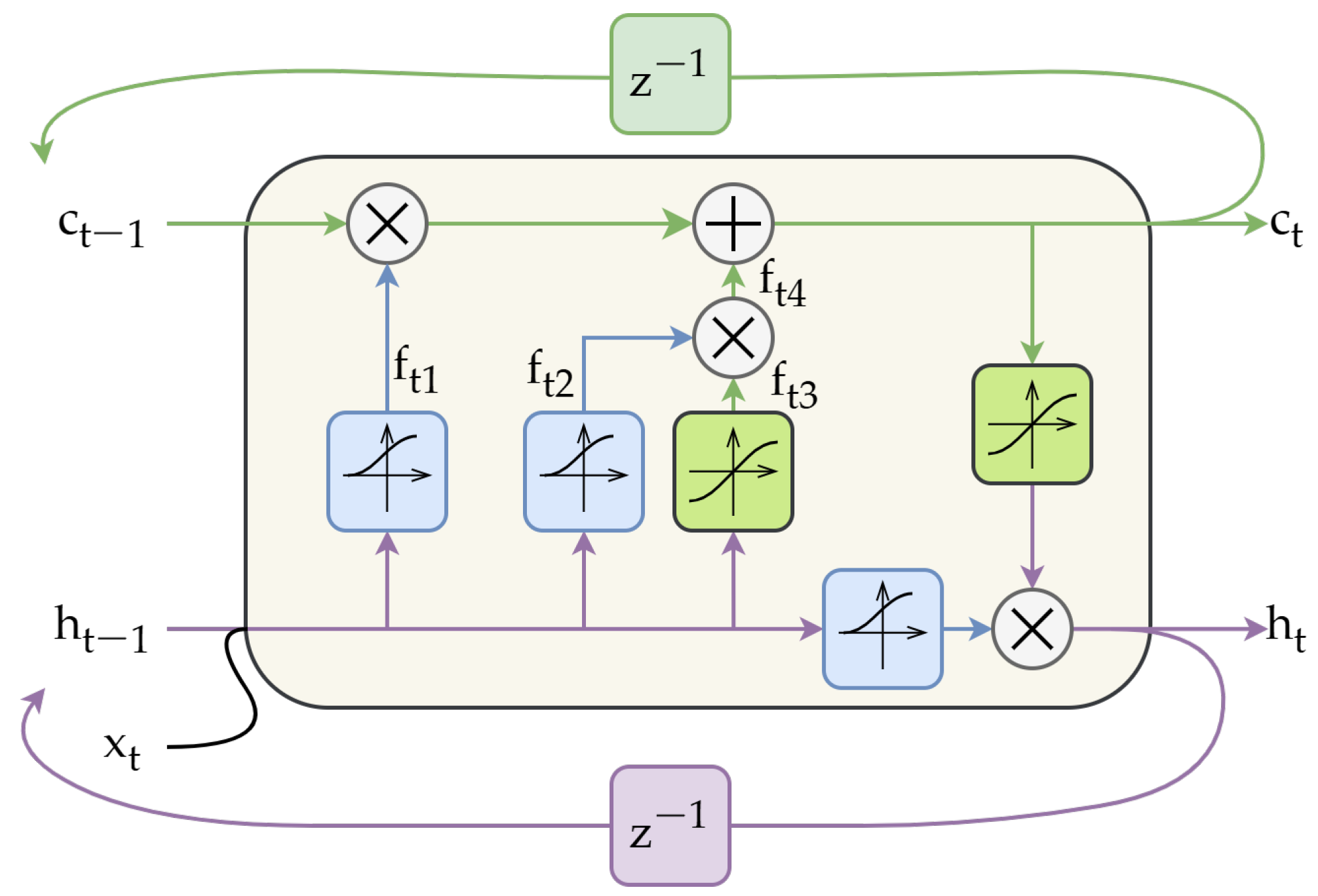
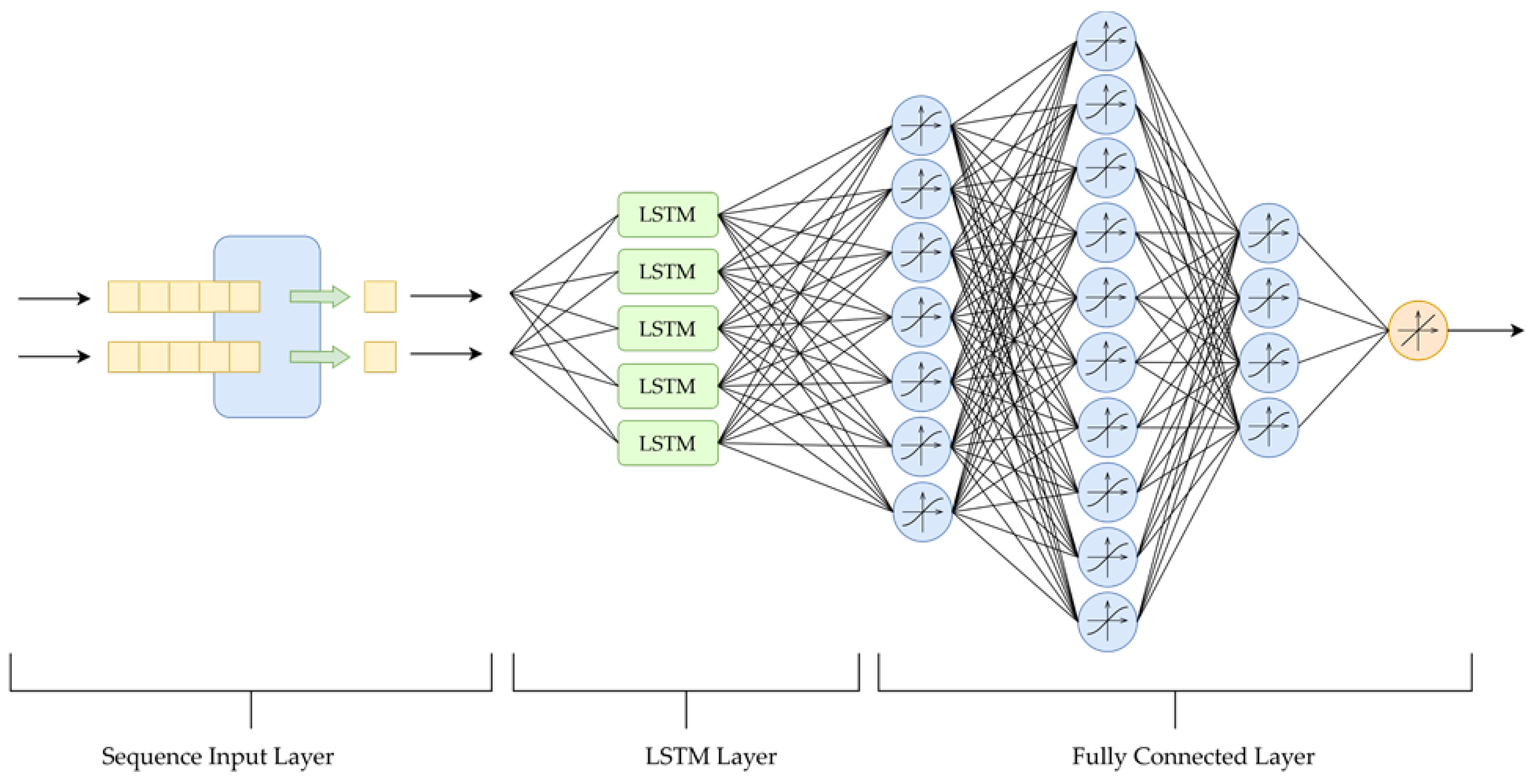

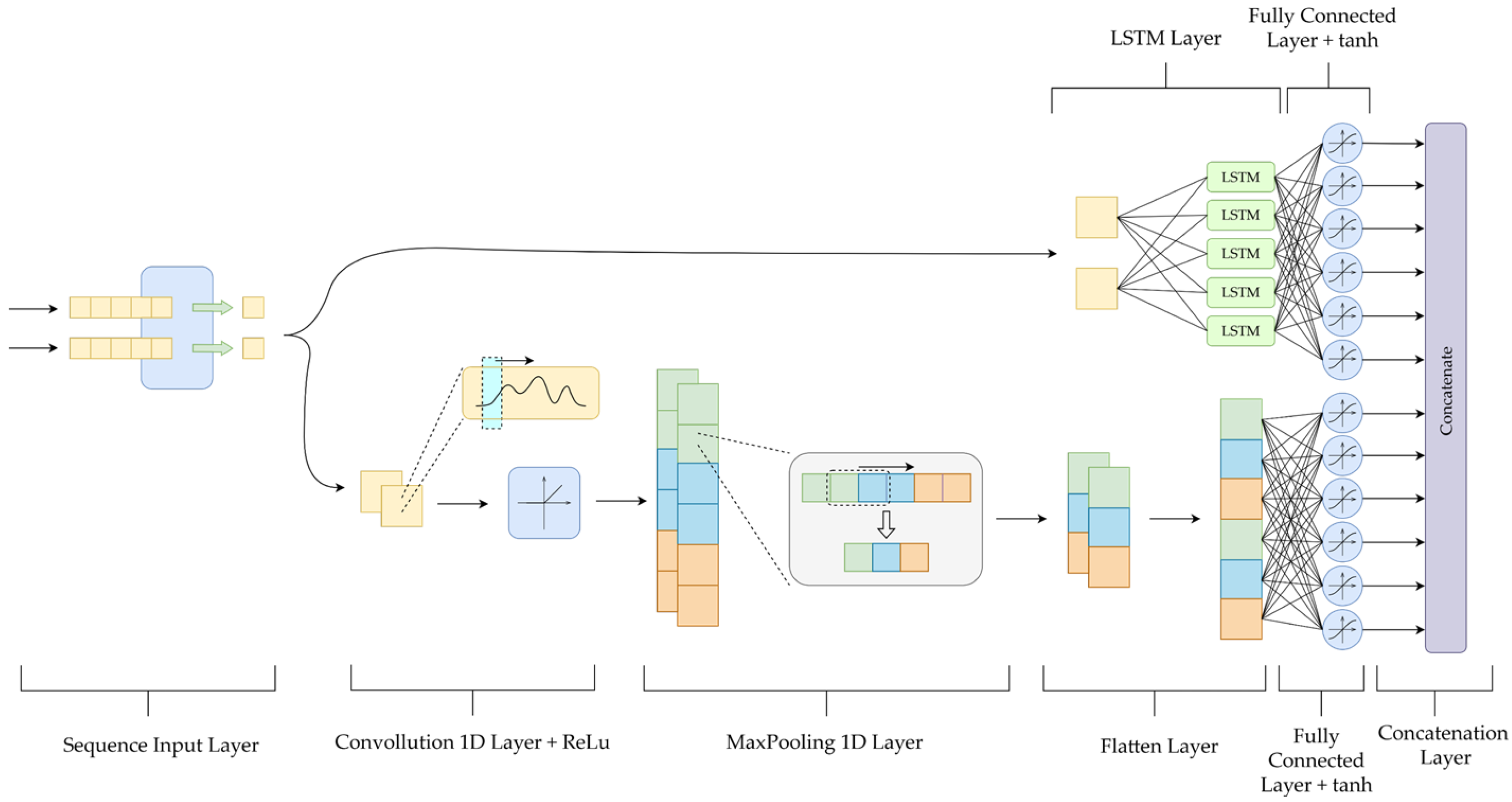


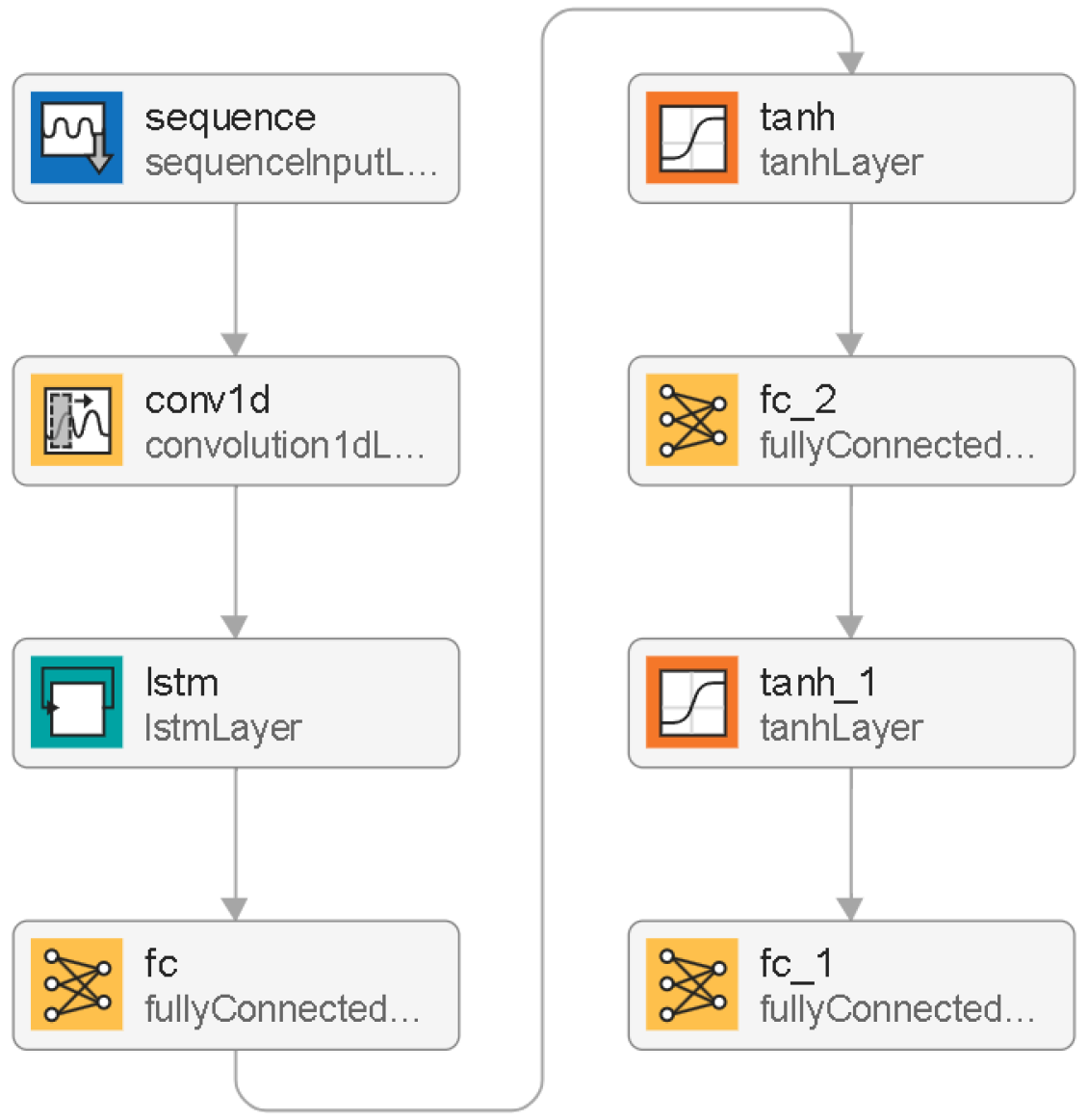
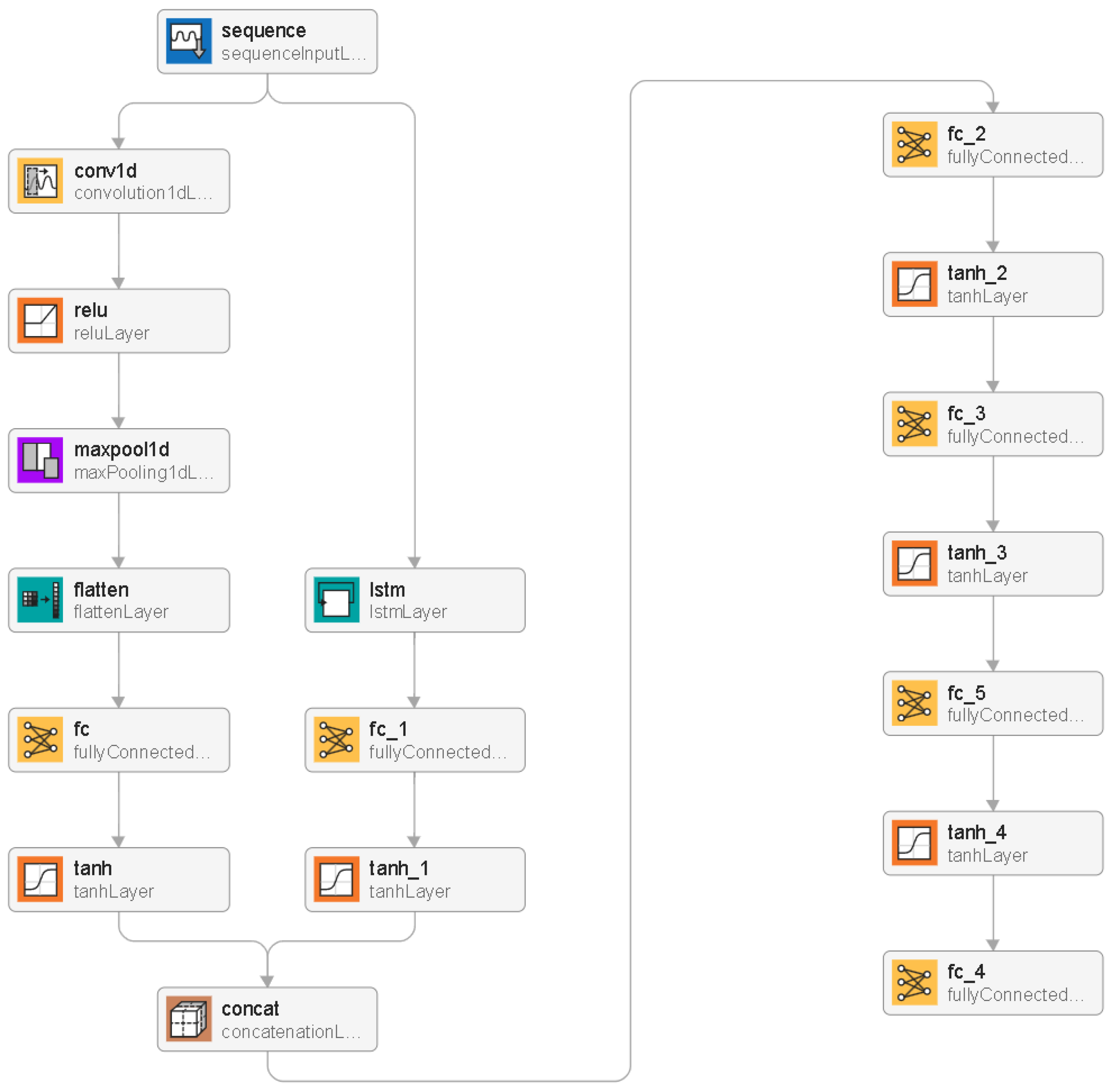









| Name of the Layer | Input Size | Number of Hidden Neurons | Activation Function |
|---|---|---|---|
| Sequence Input Layer | 2 | — | — |
| LSTM Layer | 2 | 12 | sigmoid & tanh |
| Fully Connected Layer | 12 | 24 | tanh |
| Fully Connected Layer | 24 | 32 | tanh |
| Fully Connected Layer | 32 | 16 | tanh |
| Output Neuron | 16 | 1 | linear |
| Name of the Layer | Input Size | Number of Filters | Number of Hidden Neurons | Activation Function |
|---|---|---|---|---|
| Sequence Input Layer | 2 | — | — | — |
| 1-D Convolution Layer | 2 | 16 | — | — |
| LSTM Layer | 16 | — | 32 | sigmoid & tanh |
| Fully Connected Layer | 32 | — | 48 | tanh |
| Fully Connected Layer | 48 | — | 16 | tanh |
| Output Neuron | 16 | — | 1 | linear |
| Name of the Layer | Input Size | Number of Filters/Pool Size * | Number of Hidden Neurons | Activation Function |
|---|---|---|---|---|
| Sequence Input Layer | 2 | — | — | — |
| 1-D Convolution Layer | 2 | 16 | — | ReLU |
| 1-D MaxPooling Layer | 16 | 2 * | — | — |
| Flatten Layer | — | — | — | — |
| Fully Connected Layer | 16 | — | 24 | tanh |
| LSTM Layer | 2 | — | 12 | sigmoid & tanh |
| Fully Connected Layer | 12 | — | 24 | tanh |
| Concatenation Layer | — | — | — | — |
| Fully Connected Layer | 48 | — | 32 | tanh |
| Fully Connected Layer | 32 | — | 16 | tanh |
| Fully Connected Layer | 16 | — | 8 | tanh |
| Output Neuron | 8 | — | 1 | linear |
| Parameter | Value | Symbol |
|---|---|---|
| Nominal Motor Power | 500 W | |
| Nominal Angular Speed | 1450 RPM | |
| Nominal Encoder Resolution | 36,000 p./rev. | — |
| D.C. Motor Mechanical Time Constant | 0.203 s | |
| D.C. Load Machine Mechanical Time Constant | 0.285 s | |
| Elastic Shaft Mechanical Time Constant | 0.0026 s | |
| dSPACE DSP sample time | 0.0005 s |
| Neural Network Type | for Not Included in the Training Process | for Included in the Training Process |
|---|---|---|
| LSTM Neural Estimator | 9.09% | 4.04% |
| CNN Neural Estimator | 9.10% | 4.00% |
| Parallel [2-1] Neural Estimator | 8.36% | 3.92% |
| Neural Network Type | for Not Included in the Training Process | Increase Factor |
|---|---|---|
| LSTM Neural Estimator | 2.05% | 7.04% |
| CNN Neural Estimator | 2.02% | 7.08% |
| Parallel [2-1] Neural Estimator | 2.07% | 6.29% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kaczmarczyk, G.; Stanislawski, R.; Kaminski, M. Deep-Learning Techniques Applied for State-Variables Estimation of Two-Mass System. Energies 2025, 18, 568. https://doi.org/10.3390/en18030568
Kaczmarczyk G, Stanislawski R, Kaminski M. Deep-Learning Techniques Applied for State-Variables Estimation of Two-Mass System. Energies. 2025; 18(3):568. https://doi.org/10.3390/en18030568
Chicago/Turabian StyleKaczmarczyk, Grzegorz, Radoslaw Stanislawski, and Marcin Kaminski. 2025. "Deep-Learning Techniques Applied for State-Variables Estimation of Two-Mass System" Energies 18, no. 3: 568. https://doi.org/10.3390/en18030568
APA StyleKaczmarczyk, G., Stanislawski, R., & Kaminski, M. (2025). Deep-Learning Techniques Applied for State-Variables Estimation of Two-Mass System. Energies, 18(3), 568. https://doi.org/10.3390/en18030568







