Multi-Parameter Assessment and Validation of Cable Insulation Using Game Theory and Fuzzy Comprehensive Evaluation

Abstract

Accurate assessment of high-voltage cable insulation condition is essential for safe operation in complex tunnel environments. Traditional methods relying on single diagnostic indicators and fixed weighting schemes often suffer from limited accuracy and adaptability. This paper proposes a multi-parameter assessment method integrating game theory with fuzzy comprehensive evaluation. Five types of online monitoring data, namely cable surface temperature, sheath grounding current, partial discharge, tunnel humidity, and ambient temperature, are selected as diagnostic parameters. Subjective and objective weights are first derived using the analytic hierarchy process and the entropy weight method, and then optimally integrated through a game-theoretic framework. Fuzzy membership functions are applied to construct an evaluation matrix, enabling quantitative and graded assessment of insulation condition. A case study on 110 kV tunnel high-voltage land cables in Zhejiang, China, verifies the effectiveness of the approach. Results show that the proposed method more accurately reflects actual operating conditions and provides higher diagnostic precision and robustness compared with single-feature and traditional weighting methods. By combining expert knowledge with real monitoring data, this study develops a scientific and practical framework for insulation condition assessment, offering reliable support to real-time insulation monitoring and predictive maintenance applications of high-voltage power transmission systems.

1. Introduction

High-voltage cables are essential components of modern power systems, and cross-linked polyethylene (XLPE) insulated cables are widely applied due to their superior electrical and mechanical properties [1]. Over time, insulation degradation occurs, making accurate assessment of cable condition critical for reliable grid operation [2]. Traditional diagnostic methods, including preventive testing and offline measurements, are time-consuming, inefficient, and may risk cable damage. The development of smart sensing technologies and the power of the Internet of Things has enabled online monitoring, providing real-time data on cable surface temperature, partial discharge, sheath current, and environmental conditions. This facilitates timely evaluation of insulation health and supports data-driven management of cable systems [3,4].

Condition-based maintenance (CBM) technology has been widely applied in advanced countries such as those in Europe, the United States, and Japan [5]. The United States was the first to conduct research on CBM, while Japan began exploring condition-based maintenance for power equipment in the early 1980s [6]. Around the same period, many European countries also reformed their maintenance systems and started to implement CBM. In China, research on condition-based maintenance began around 2000, and related studies and projects are now being actively promoted [6]. For both the State Grid Corporation of China and China Southern Power Grid, CBM of power supply equipment mainly consists of four key stages: equipment condition monitoring, equipment risk assessment, equipment condition evaluation, and maintenance decision-making [7]. These components together form a complex decision-making system. To optimize the entire process, more accurate monitoring data and more efficient and reliable evaluation methods are required [8].

Current research on fault diagnosis technologies can generally be divided into three categories: knowledge-based, model-based, and signal processing–based methods [9]. The knowledge-based approach relies on experts to analyze multiple sources of information and develop corresponding diagnostic schemes, making it suitable for various applications [10]. However, it requires extensive expert prior knowledge and lacks strong objectivity, so it is often combined with other techniques for optimization [11]. For example, Ref. [12] integrated fault tree analysis with an expert system to diagnose transformer faults and identify optical fiber current transformer failures, with its effectiveness verified through practical cases. The model-based method designs mathematical models and obtains fault information by comparing the difference between measured data and model outputs [13]. As shown in Ref. [14], a cable system model was built in MATLAB/Simulink consisting of three cable sections and two unaged joints. Time-domain reflectometry (TDR) was used to simulate the reflection characteristics under different insulation conditions, and experimental validation confirmed the model’s accuracy. However, model accuracy may be limited due to the need for detailed physical information and inevitable discrepancies with real equipment [15]. The signal processing–based method analyzes measurement data directly by constructing models from the signal itself to extract fault information [16]. For instance, Ref. [17] proposed a method based on electromagnetic field scanning probe measurements combined with the Superlet transform to detect weak abnormal signals caused by structural or material defects, while Ref. [18] visualized the harmonic characteristics of cable sheath grounding currents and applied the YOLOv5 algorithm for defect identification, improving the efficiency of online insulation fault recognition. This method does not require mathematical modeling, making it easier to implement and promote, though sufficient data for accurate modeling can usually be obtained only when severe faults occur [16].

A large amount of measured data accumulated from insulation monitoring has been used to establish insulation aging criteria. Ref. [19] developed a thermal single-factor aging model based on the Arrhenius equation and experimental data. Ref. [20] introduced the concept of an aging factor through dielectric spectroscopy experiments and established a standard model for water tree aging assessment. Ref. [21] applied principal component analysis to evaluate voltage and dielectric loss parameters. Ref. [22] investigated the variation in trap parameters during the aging process using the polarization–depolarization current (PDC) method and isothermal relaxation trap theory. Ref. [23] utilized neural networks for power equipment evaluation, which exhibit strong adaptability but rely heavily on large datasets.

However, traditional single evaluation methods often suffer from strong subjectivity and insufficient objectivity, making it difficult to accurately reflect the relative importance of monitoring indicators under complex operating conditions [24]. To address this issue, scholars have proposed various multi-criteria decision-making (MCDM) methods [25,26]. The Analytic Hierarchy Process (AHP) constructs a judgment matrix and incorporates expert knowledge, effectively capturing the decision-maker’s subjective assessment of indicator importance [27]. The Entropy Weight Method (EWM), based on information theory, objectively determines indicator weights according to data dispersion, thus reducing human interference and better reflecting the intrinsic variability of sample data [28]. Both methods have been widely applied in condition assessment of power equipment in China [29]. The Game Theory (GT) approach, which selects optimal strategies to maximize benefits, can optimize multiple types of weights [30]. Since the 2000s, it has frequently appeared in Chinese studies, especially in power equipment condition evaluation and energy management, though similar concepts are less common in international literature on power systems [31]. Ref. [32] applied fuzzy clustering to analyze cable operation data. Ref. [33] proposed a multi-state comprehensive evaluation method based on expert scoring. Ref. [34] combined longitudinal and transverse cable information using fuzzy theory and the AHP for condition assessment. Ref. [35] selected breakdown strength, thermal decomposition temperature, and carbonyl index as aging factors to construct a fuzzy clustering model. Refs. [36,37] applied improved AHP methods but relied heavily on expert experience. Ref. [38] evaluated cable joints using parameters such as joint temperature and tunnel humidity but lacked multi-source data fusion. Refs. [39,40] proposed an optimized model based on game theory that combines indicator importance with data characteristics, resulting in more reasonable and reliable weight distribution. Although these cable condition assessment methods assign subjective weights to cable parameters, the weighting process remains relatively rigid and cannot fully reflect the actual condition of the equipment.

In summary, in cable insulation assessment, weight determination mainly relies on subjective or objective methods. Subjective methods are often rigid and overly influenced by expert opinion, while objective methods may overlook valuable expert knowledge. Current Chinese guidelines mostly use subjective weighting, highlighting the role of experience. Combining game theory allows integration of both approaches, making weight allocation more balanced. Additionally, cable health cannot be reflected by a single parameter, so integrating multiple monitoring indicators is crucial for accurate insulation assessment and health management [41].

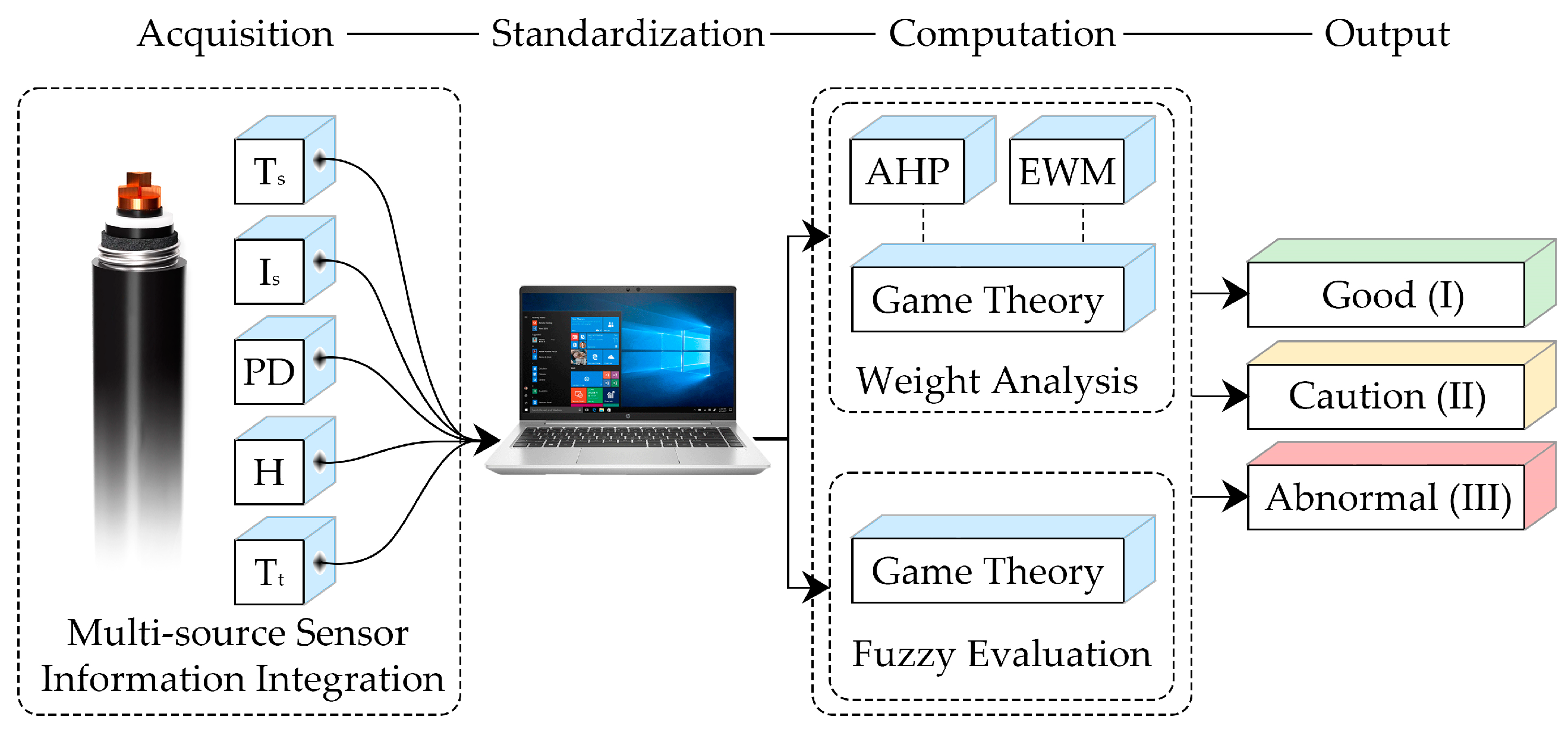
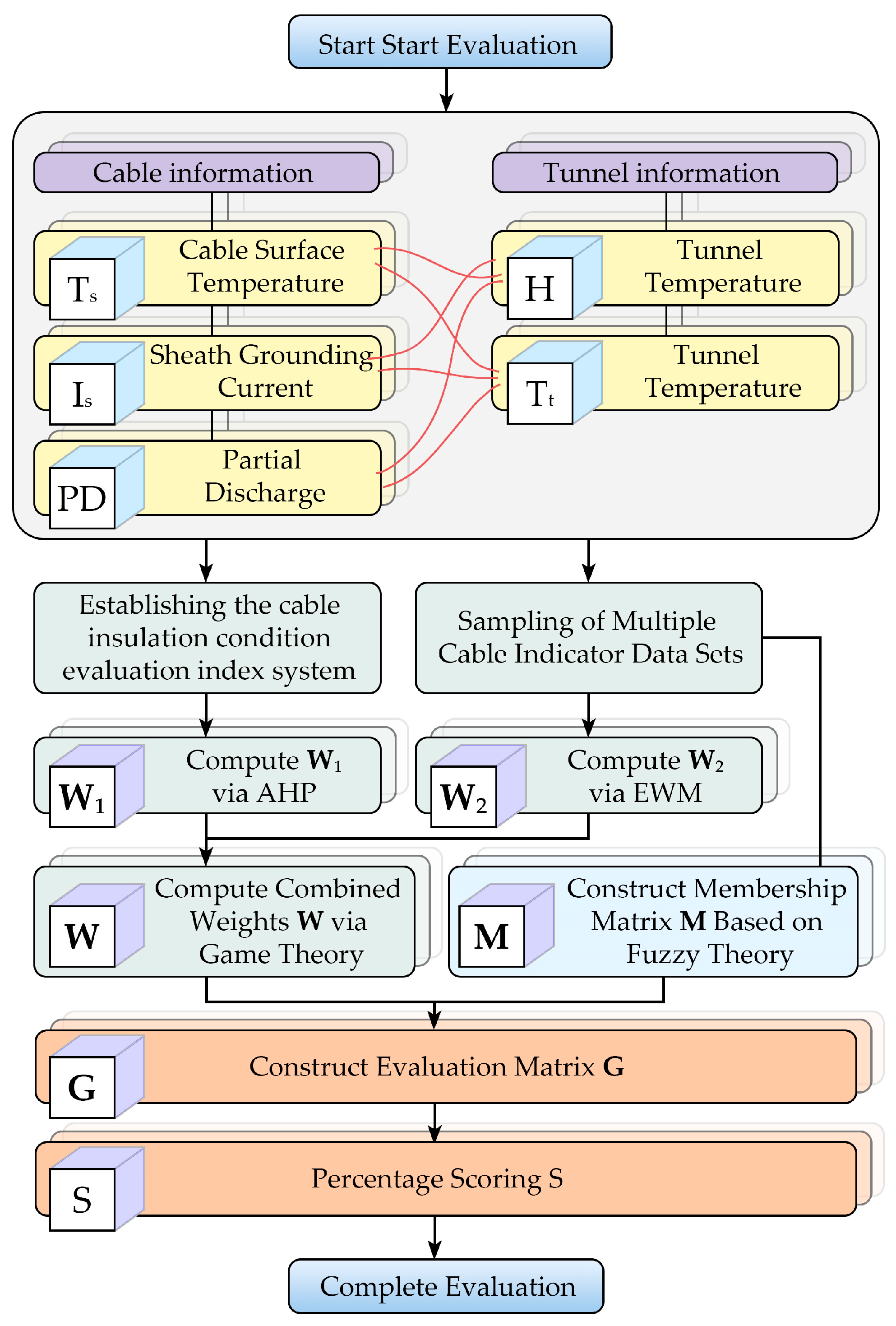
To address the limitations of single-feature diagnostics and rigid weight assignments, this study proposes a multi-parameter insulation assessment method combining game theory and fuzzy comprehensive evaluation. Five online monitoring indicators including cable surface temperature, sheath grounding current, partial discharge, tunnel humidity, and ambient temperature are used. Subjective and objective weights are first determined using analytic hierarchy process and entropy weight methods, then integrated through game theory. A fuzzy membership function constructs the evaluation matrix, enabling quantitative classification of insulation condition. Case studies on 110 kV tunnel-installed high-voltage cables demonstrate improved diagnostic accuracy and robustness compared with single-parameter or traditional weight assignment methods, providing a systematic and reliable tool for insulation condition assessment and health management in complex operating environments.

2. Cable Insulation Evaluation Framework

Based on relevant Chinese standards, including Technical Specification for State Detection for High Voltage Cable Lines [42] and State Grid Corporation Cable Tunnel Management Specification, five key parameters are defined for the online evaluation of XLPE cable insulation. In this study, only real-time online monitoring parameters were selected as evaluation indicators. Although certain parameters such as cable surface temperature and tunnel temperature may exhibit some degree of correlation, they reflect different thermal sources, with cable surface temperature representing the thermal stress of the cable itself and tunnel temperature representing the influence of the surrounding environment. Therefore, both parameters are retained as independent indicators. Aging-related factors such as service age, Tan δ, and PDC measurements are not included because they rely on offline testing or historical records that are not continuously available in the tunnel monitoring system. The objective of this study is to develop an evaluation framework that relies exclusively on continuously available online monitoring data. The five selected diagnostic parameters, as illustrated in Figure 1, are as follows:

• Cable Surface Temperature: The heat generated in the insulation arises from electromagnetic losses within the field. As the insulation deteriorates, electromagnetic losses increase, leading to a corresponding rise in cable surface temperature [43,44].
• Sheath Grounding Current: Abnormal sheath grounding current is often caused by damage to the cable’s outer sheath. Mechanical impact or termite intrusion can compromise the insulation, creating multi-point grounding loops. The resulting potential difference between the ground and sheath drives circulating currents, significantly increasing the grounding current [45,46].
• Partial Discharge (PD): When the uniformity of the insulation medium is disrupted, local electric field concentrations occur at weak points, triggering partial discharges. Monitoring PD magnitudes provides a direct indication of insulation degradation [47,48].
• Tunnel Humidity: Water tree defects are a major factor leading to the deterioration of XLPE cable insulation and reduced service life. Previous studies indicate that water tree formation is strongly influenced by environmental humidity. Under sufficient humidity conditions, XLPE cables energized in operation are prone to develop water trees [49].
• Tunnel Temperature: With rising ambient temperature, the extreme values of axial deformation and radial expansion of the main insulation layer increase approximately linearly, which further contributes to the deterioration of the cable’s insulation performance [50].

By integrating these five parameters, a multi-sensor state evaluation model for cable insulation can be established, as shown in Figure 2. Furthermore, when assessing the insulation condition of high-voltage cables using this model, it is necessary to classify the insulation state. Referring to standard classification methods in the power industry, the insulation condition is divided into three levels: Good (Level I), Caution (Level II), and Abnormal (Level III).

2.1. Construction of Indicator Weight Vector

In fuzzy evaluation, it is essential to determine the weight distribution of individual indicators. The rational assignment of weights plays a critical role in assessing the insulation performance of terrestrial cables. In this section, weight optimization is carried out using two conventional approaches: the Analytic Hierarchy Process (AHP) and the Entropy Weight Method (EWM). The former relies heavily on expert judgment, which provides a degree of credibility but is subject to strong subjectivity. The latter is based on the distribution and intrinsic patterns of real-time data, offering greater objectivity and accuracy. To address the limitations of applying either method alone, this study introduces a modified weighting model by integrating game theory, which balances subjective and objective weights and enhances the robustness of the evaluation system.

2.1.1. Subjective Weighting Using AHP

The Analytic Hierarchy Process (AHP) [51,52] is an experience-based method grounded in expert judgment. By applying Saaty’s nine-point scale, a pairwise comparison matrix of characteristic indicators can be constructed, which serves as the basis for deriving subjective weights. Suppose there are n indicators of cable insulation performance. According to expert knowledge and Saaty’s nine-point scale, the comparison values c_ij between indicator pairs are determined, leading to the construction of the comparison matrix of the research object, expressed as C = [c_ij]_n×n. Subsequently, the following formula is used to construct new geometric components:

$${\widehat{p}}_i=\sqrt[n]{{\displaystyle \prod _{j=1}^n{c}_{ij}}}$$

(1)

The weight matrix is then constructed, and the aggregated comparison matrix is normalized to determine the weight of each indicator:

$$p_i={\displaystyle \frac{{\widehat{p}}_i}{{\displaystyle \sum _{i=1}^n{\widehat{p}}_i}}}$$

(2)

Here, p_i denotes the subjective weight of each indicator, and the vector of these weights is denoted as W₁. Subsequently, a consistency check matrix is constructed, and the consistency verification formula is established:

$$CR={\displaystyle \frac{l-n}{RI(n-1)}}$$

(3)

$$\lambda ={\displaystyle \frac{1}{n}}{\displaystyle \sum _{i=1}^n\frac{{\displaystyle \sum _{j=1}^n{c}_{ij}{p}_j}}{p_i}}$$

(4)

Here, λ denotes the maximum eigenvalue of the matrix, RI is the average random consistency index, and CR is the consistency ratio. To avoid conflicts arising from expert judgments and to ensure the rationality of the evaluation matrix, the CR value is calculated according to

Table 1. Average random consistency index standard value.

n	1	2	3	4	5	6	7	8	9	10
RI	0	0	0.52	0.89	1.12	1.26	1.36	1.41	1.46	1.49

for consistency verification.

2.1.2. Objective Weighting Using Entropy Method

The entropy weight method [53,54] is an objective weighting approach, where the magnitude of the entropy reflects the information-carrying value of each indicator. Suppose there are n cable insulation performance indicators and m evaluation samples, forming the matrix R as follows:

$$R=\left[\begin{array}{llll}{r}_{11}\hfill & r_{12}\hfill & \dots \hfill & r_{1n}\hfill \\ r_{21}\hfill & r_{22}\hfill & \dots \hfill & r_{2n}\hfill \\ \dots \hfill & \dots \hfill & \dots \hfill & \dots \hfill \\ r_{m1}\hfill & r_{m2}\hfill & \dots \hfill & r_{mn}\hfill \end{array}\right]$$

(5)

Here, r_ij denotes the value of the j-th indicator for the i-th sample, where i = 1, 2, …, m and j = 1, 2, …, n. To ensure comparability across indicators with different units and directions, the data are standardized to a common dimension. In this process, positive indicators are treated as larger-is-better attributes, while negative indicators are treated as smaller-is-better attributes. The standardized values are expressed as r’_ij, and the normalization procedure is formulated as follows:

$${r^{\prime }}_{ij}={\displaystyle \frac{r_{ij}-\min (r_{1j},\dots ,r_{mj})}{\max (r_{1j},\dots ,r_{mj})-\min (r_{1j},\dots ,r_{mj})}}$$

(6)

$${r^{\prime }}_{ij}={\displaystyle \frac{\max (r_{1j},\dots ,r_{mj})-r_{ij}}{\max (r_{1j},\dots ,r_{mj})-\min (r_{1j},\dots ,r_{mj})}}$$

(7)

Furthermore, the entropy value of each indicator is calculated. The entropy is determined by the following expression:

$$e_j={\displaystyle \frac{{\displaystyle \sum _{i=1}^m{p}_{ij}\ln p_{ij}}}{\ln m}}$$

(8)

$$p_{ij}={\displaystyle \frac{{r^{\prime }}_{ij}}{{\displaystyle \sum _{i=1}^m{r^{\prime }}_{ij}}}}$$

(9)

Here, e_j denotes the entropy value of the j-th indicator. The entropy weight of each evaluation indicator is determined based on its entropy value, and the calculation is defined as follows:

$$w_j={\displaystyle \frac{1-e_j}{{\displaystyle \sum _{j=1}^n(1-e_j)}}}$$

(10)

Here, w_j denotes the objective weight of each indicator, and the vector composed of all w_j is denoted as W₂.

2.1.3. Optimal Weighting via Game Theory

Game theory [55] provides a mechanism for maximizing collective benefit through cooperation and competition. By allowing multiple decision schemes to interact strategically, it reconciles conflicting interests among decision-makers and achieves an optimal equilibrium. Leveraging the advantages of both subjective and objective weighting methods, game theory can yield a more scientifically robust and comprehensive set of indicator weights. The simplified game-theoretic formulation used in this study follows the commonly adopted practice in the power system research, where the objective is to obtain an optimal compromise between subjective and objective weights rather than to model a full strategic interaction [31]. This approach ensures computational efficiency and compatibility with real-time online monitoring requirements. Based on the results from AHP and entropy weighting, the updated weight vector is expressed as:

$$W^T={\displaystyle \sum _{i=1}^2{k}_i{W}_i^T}$$

(11)

Here, k_i controls the contribution of each weighting scheme to the final result, and W_i denotes the weight vectors obtained, respectively, from the subjective AHP method and the objective entropy method. To achieve a comprehensive weight that balances and coordinates both subjective and objective approaches, a function is constructed with the objective of minimizing the deviation, expressed as follows:

$$error=\min {‖{\displaystyle \sum _{i=1}^2{k}_i{W}_i^T-W_j^T}‖}_2\hspace{0.33em}\hspace{0.33em}j=1,2$$

(12)

Based on the differential properties of the matrix, the first-order optimality condition of Equation (12) can be expressed as follows:

$$\left[\begin{array}{l}{\mathbf{W}}_1\cdot {\mathbf{W}}_1^T\hspace{0.33em}\hspace{0.33em}{\mathbf{W}}_1\cdot {\mathbf{W}}_2^T\\ {\mathbf{W}}_2\cdot {\mathbf{W}}_1^T\hspace{0.33em}\hspace{0.33em}{\mathbf{W}}_2\cdot {\mathbf{W}}_2^T\end{array}\right]\left[\begin{array}{l}{\mathbf{k}}_1\\ {\mathbf{k}}_2\end{array}\right]=\left[\begin{array}{l}{\mathbf{W}}_1\cdot {\mathbf{W}}_1^T\\ {\mathbf{W}}_2\cdot {\mathbf{W}}_2^T\end{array}\right]$$

(13)

Here, Equation (13) is solved using MATLAB 2020A to determine the optimal weight vector W.

$$k_i^{*}={\displaystyle \frac{\left|k_i\right|}{{\displaystyle \sum _{i=1}^2\left|k_i\right|}}}$$

(14)

$$W^T={\displaystyle \sum _{i=1}^2{k}_i^{*}{W}_i^T}$$

(15)

Here, $k_i^{*}$ represents the normalized combination coefficient obtained from the preliminary coefficient k_i, ensuring that all coefficients are non-negative and sum to one. Thus, $k_i^{*}$ reflects the relative contribution of each weighting scheme in the final fusion process. The resulting vector W denotes the optimized weight vector produced by the game-theoretic approach after coordinating the subjective and objective weights through these normalized coefficients.

2.2. Construction of Evaluation Matrix

Fuzzy theory provides a modeling framework based on fuzzy sets and membership functions. In this context, fuzzy sets describe the categorical state of each indicator for a given sample, while membership functions quantify the degree of belonging of each indicator to a particular category. For evaluating the insulation condition of high-voltage tunnel cables, three states are defined: good, caution, and abnormal. A smooth ridge-shaped membership function based on piecewise sinusoidal transitions, is employed to characterize the degree of membership, which is mathematically expressed as follows:

$$f_1(u_i)=\left\{\begin{array}{cc}1& u_i\le b_0\\ {\displaystyle \frac{1}{2}}-{\displaystyle \frac{1}{2}}\sin [{\displaystyle \frac{\pi }{b_1-b_0}}(u_i-{\displaystyle \frac{b_0+b_1}{2}})]& b_0<u_i\le b_1\\ 0& u_i>b_1\end{array}\right.$$

(16)

$$f_2(u_i)=\left\{\begin{array}{cc}0& u_i\le b_0\\ {\displaystyle \frac{1}{2}}+{\displaystyle \frac{1}{2}}\sin [{\displaystyle \frac{\pi }{b_1-b_0}}(u_i-{\displaystyle \frac{b_0+b_1}{2}})]& b_0<u_i\le b_1\\ 1& b_1<u_i\le b_2\\ {\displaystyle \frac{1}{2}}-{\displaystyle \frac{1}{2}}\sin [{\displaystyle \frac{\pi }{b_3-b_2}}(u_i-{\displaystyle \frac{b_2+b_3}{2}})]& b_2<u_i\le b_3\\ 0& u_i>b_3\end{array}\right.$$

(17)

$$f_3(u_i)=\left\{\begin{array}{cc}0& u_i\le b_2\\ {\displaystyle \frac{1}{2}}+{\displaystyle \frac{1}{2}}\sin [{\displaystyle \frac{\pi }{b_3-b_2}}(u_i-{\displaystyle \frac{b_2+b_3}{2}})]& b_2<u_i\le b_3\\ 1& u_i>b_3\end{array}\right.$$

(18)

Here, u_i represents the state value of each insulation parameter, and f_i(u_i) denotes the membership function of each parameter element within the domain U for the three insulation conditions: good, caution, and abnormal. b_i define the transition intervals between these states and are determined according to the reference thresholds provided by the online monitoring manufacturer together with long-term engineering experience. Figure 3 presents an example of the ridge-shaped membership functions for the partial discharge parameter, illustrating how different membership degrees are assigned as the indicator value moves across the defined state ranges.

Based on the reference values provided by a certain online monitoring manufacturer, the evaluation indices b_i corresponding to the insulation conditions of each parameter are listed in

Table 2. Index evaluation standard reference value.

Feature Parameter	Good/b0	Caution/b1	Caution/b2	Abnormal/b3
Cable Temperature/°C	35	40	45	58
Grounding Circulating Current/A	5	10	15	20
Partial Discharge/pC	5	50	150	300
Tunnel Temperature/°C	30	35	40	45
Tunnel Humidity/%	50	75	83	95

.

The actual cable parameter data are input into the membership functions to obtain the comprehensive fuzzy matrix for each indicator. Subsequently, based on the integrated weights determined using game theory and the fuzzy comprehensive evaluation method, the overall cable insulation performance evaluation matrix G is calculated as follows:

$$G=W\times M=[g_1,g_2,g_3]$$

(19)

Here, G denotes the comprehensive evaluation matrix of the high-voltage cable insulation state, and g_i represents the membership values corresponding to the insulation state of each cable. To meet practical engineering requirements, a more precise classification can be obtained through quantitative processing. Based on the 100-point scoring method reported in [56], the score values corresponding to each insulation state level are listed in

Table 3. Scoring values for each status level.

Score S	Insulation Condition	Recommended Action
80 ≤ S ≤ 100	Good (Level I)	Normal operation, continue use.
40 ≤ S < 80	Caution (Level II)	Use with caution, perform regular monitoring.
0 ≤ S < 40	Abnormal (Level III)	Shut down for maintenance, consider decommissioning.

.

The quantitative comprehensive evaluation score S for the insulation condition of high-voltage terrestrial cables is calculated as:

$$S=90g_1+60g_2+20g_3$$

(20)

2.3. Evaluation Model Development Procedure

In summary, based on the above discussion, the workflow for establishing the high-voltage cable insulation evaluation model can be summarized as follows, as illustrated in Figure 4:

• Indicator system and data preparation: Construct the cable insulation evaluation framework and identify cable parameters (partial discharge, cable temperature, grounding current) and tunnel parameters (tunnel temperature, tunnel humidity) as evaluation indicators. Collect multiple sets of cable indicator data and establish the insulation condition evaluation system.
• Weight determination: Determine subjective weights W₁ using the Analytic Hierarchy Process (AHP) and objective weights W₂ using the entropy method. Then, integrate them via game theory to obtain the combined weight vector W. Construct the membership matrix M based on fuzzy theory.
• Matrix construction: Combine the integrated weights W with the membership matrix M to determine the comprehensive evaluation matrix G.
• Result conversion: Convert the evaluation matrix G into a score on a 100-point scale to obtain the quantitative result S.
• Evaluation completion: Based on the 100-point score S, complete the assessment of the cable insulation condition.

3. Case Study of High-Voltage Terrestrial Cable Insulation Assessment

3.1. Data Collection

To validate the proposed method, six 110 kV high-voltage terrestrial cables in service in different tunnels across Zhejiang Province, China, were selected as case studies. The monitoring data were obtained from the utility’s online monitoring platform, which is operated under the manufacturer’s built-in data acquisition and control procedures, ensuring the authenticity and reliability of the recorded measurements. The insulation condition of each cable was evaluated based on operational data collected at a specific time during the summer of 2023. Notably, none of the six cables had a history of significant faults.

The insulation condition assessment of high-voltage terrestrial cables is primarily based on online monitoring of operational parameters. These data are processed and analyzed using scientific methods to determine the insulation level of the target cable, enabling timely implementation of appropriate preventive measures. As shown in Figure 5, the experimental data were collected via the intelligent integrated monitoring system of Zhejiang Electric Power Company, which employs underlying sensors to achieve comprehensive monitoring of underground high-voltage cable operation.

Table 4. Circuit test results of Hexiu 2438 Line.

Line Name	Parameter	Measured Value
Hexiu 2438 Line	Partial Discharge/pC	7.0
	Grounding Circulating Current/A	2.1
	Cable Temperature/°C	21.5
	Tunnel Temperature/°C	20.6
	Tunnel Humidity/%	56.0
	Water Level/m	0.5
	Service Age/years	2.5

presents the actual operational data of a high-voltage terrestrial cable in service in Zhejiang Province.

3.2. Determination of Indicator Weights

The subjective weights of each indicator were first calculated using the Analytic Hierarchy Process (AHP). Based on Table 1 and expert judgment, the relative importance of the five indicators was considered as follows: Partial Discharge > Grounding Circulating Current > Cable Temperature > Tunnel Temperature > Tunnel Humidity. Accordingly, the resulting pairwise comparison matrix of the evaluation indicators is presented in

Table 5. Discriminant matrix.

Indicator	Partial Discharge	Grounding Circulating Current	Cable Temperature	Tunnel Temperature	Tunnel Humidity
Partial Discharge	1	2	3	5	6
Grounding Circulating Current	1/2	1	3	4	5
Cable Temperature	1/3	1/3	1	2	3
Tunnel Temperature	1/5	1/4	1/2	1	2
Tunnel Humidity	1/6	1/5	1/3	1/2	1

.

Based on Equations (3) and (4), the maximum eigenvalue of the judgment matrix is calculated as 5.09, and its consistency ratio is

CR = 0.0201 < 0.1000

(21)

indicating that the matrix meets the consistency requirement. The resulting subjective weights of the evaluation indicators are thus given by W₁:

W₁ = [0.4265, 0.2980, 0.1392, 0.0829, 0.0534]

(22)

Next, the objective weights of the indicators were calculated using the entropy method. Before deriving the weights, the sample data were preprocessed according to the entropy-based normalization procedure. All selected parameters were treated as negative indicators, as higher numerical values generally correspond to greater insulation stress or less favorable operating conditions. Accordingly, lower values represent better performance. After standardization, the processed results are presented in

Table 6. Negative indicator preprocessing.

Cable Line	Partial Discharge	Grounding Circulating Current	Cable Temperature	Tunnel Temperature	Tunnel Humidity
1#	0.8824	0.9218	0.7476	1.0000	1.0000
2#	1.0000	0.9492	0.7864	1.0000	1.0000
3#	0.7647	0.7160	0.5825	0.4493	0.3000
4#	0.6471	1.0000	0.0000	0.0000	0.2972
5#	0.0000	0.3320	1.0000	0.0000	0.1778
6#	0.2941	0.0000	0.4951	0.9420	0.0000

.

Based on Table 6 and using Equations (8)–(10), the entropy values and corresponding objective weights for each evaluation indicator are calculated, as summarized in

Table 7. Entropy and objective weight value.

Indicator	Partial Discharge	Grounding Circulating Current	Cable Temperature	Tunnel Temperature	Tunnel Humidity
Entropy	0.8620	0.8662	0.8819	0.7500	0.7766
Objective Weight	0.1599	0.1550	0.1367	0.2896	0.2588

.

Based on multiple sets of terrestrial cable sample data, the final objective weight vector for the evaluation indicators is determined as:

W₂ = [0.1599, 0.1550, 0.1367, 0.2896, 0.2588]

(23)

Finally, the comprehensive weights of the evaluation indicators are calculated using game theory. Denote the combined subjective and objective weight scheme as W₃ = [W₁, W₂]^T. Based on the principles of game theory, the weights in this scheme are optimized and integrated. According to Equations (13)–(15), the resulting values of the linear combination coefficients k are:

K = [0.6624, 0.3376]

(24)

Ultimately, the comprehensive weight vector of all evaluation indicators is obtained as W:

W = k × W₃ = [0.3365, 0.2497, 0.1384, 0.1527, 0.1227]

(25)

The resulting weight vector W = [0.3365, 0.2497, 0.1384, 0.1527, 0.1227] reflects the relative importance of the five diagnostic parameters in the insulation condition assessment. The highest weight (0.3365) assigned to partial discharge indicates that PD is the most sensitive and direct indicator of insulation degradation, as the onset or intensification of local discharge activity is closely associated with defect initiation, moisture ingress, and dielectric aging in XLPE cables. The tunnel humidity and cable surface temperature receive the next highest weights (0.2497 and 0.1527), consistent with the fact that thermal environmental stress strongly influences insulation aging and accelerates deterioration under high-moisture or poor-ventilation conditions. The grounding circulating current (0.1384) is weighted moderately, reflecting its role in indicating sheath integrity and grounding path stability. The lowest weight (0.1227) corresponds to tunnel temperature, which primarily captures background environmental variation and therefore provides less direct information about insulation defects compared with the other parameters. Overall, the obtained weights align well with established engineering understanding of the degradation mechanisms of high-voltage XLPE cables.

3.3. Fuzzy Comprehensive Evaluation

As a case study, the Hexiu-2438 110 kV terrestrial cable in Zhejiang (see Table 4) is evaluated using the fuzzy comprehensive method. The membership values of its insulation parameters, derived from Equations (16)–(18), are summarized in

Table 8. Evaluation results of land cable insulation parameters.

Insulation Parameter	Evaluation Matrix (Good, Attention, Abnormal)
Partial Discharge	(0.9951, 0.0049, 0.0000)
Grounding Circulating Current	(1.0000, 0.0000, 0.0000)
Cable Temperature	(1.0000, 0.0000, 0.0000)
Tunnel Temperature	(1.0000, 0.0000, 0.0000)
Tunnel Humidity	(0.8645, 0.1355, 0.0000)

.

By applying Equation (19), the fuzzy evaluation results of the insulation parameters were synthesized to obtain the overall assessment of the high-voltage land cable. The calculated comprehensive evaluation outcome is given as follows:

G = W × M = [0.9817, 0.0183, 0.0000]

(26)

By applying Equation (20), the synthesized comprehensive evaluation result yields an insulation score of:

S = 89.4520

(27)

Based on the classification criteria in Table 3, the insulation state of the cable is determined to be Good (Grade I). Following the same procedure, the insulation states of the remaining tunnel-installed HV cables were evaluated, and the results are summarized in

Table 9. Evaluation result.

Cable Line	Evaluation Matrix	State Score	Assessment Result
1#	[0.9817, 0.0183, 0.0000]	89.4520	Good (Grade I)
2#	[0.9834, 0.0166, 0.0000]	89.5012	Good (Grade I)
3#	[0.8708, 0.1292, 0.0000]	86.1235	Good (Grade I)
4#	[0.8628,0.1372, 0.0000]	85.8826	Good (Grade I)
5#	[0.7268, 0.2595, 0.0137]	81.2574	Good (Grade I)
6#	[0.6047, 0.2906, 0.1047]	73.9518	Caution (Grade II)

.

As shown in Table 9, Cable 2# achieved the highest comprehensive score (89.5012), corresponding to an insulation state classified as Good. In contrast, Cable 6# obtained the lowest score (73.9518), which falls into the Caution category. Both Cable 1# and Cable 2# were assessed as Good, and although their scores are relatively close, the quantitative evaluation still allows for a clear distinction between their insulation performances. Overall, the ranking of the six tunnel-installed HV cables, from best to worst, is: 2# > 1# > 3# > 4# > 5# > 6#.

3.4. Results Validation and Comparison

3.4.1. Comparison Across Samples

To verify the validity of the proposed algorithm, a comparative analysis was conducted using actual cable condition samples. These samples were determined based on online monitoring records, historical operation data, routine inspections, and expert assessment provided by Zhejiang Electric Power Company. The decision-making evaluation results are summarized in

Table 10. Sample comparative analysis.

Cable Line	Proposed Method (Score)	Evaluation Result	Actual Condition
1#	89.4520	Good (Grade I)	Good (Grade I)
2#	89.5012	Good (Grade I)	Good (Grade I)
3#	86.1235	Good (Grade I)	Good (Grade I)
4#	85.8826	Good (Grade I)	Good (Grade I)
5#	81.2574	Good (Grade I)	Good (Grade I)
6#	73.9518	Caution (Grade II)	Good (Grade I)

.

Analysis of Table 10 reveals that, compared with the actual operational records of the six cable samples provided by Zhejiang Power Company, the proposed method shows a deviation in the evaluation of Cable 6#. To further investigate this discrepancy, the specific monitoring data of Tunnel Cable 6# are presented for detailed analysis, as summarized in

Table 11. Circuit test results.

Parameter	Measured Value for Cable 6#
Partial Discharge/pC	17
Grounding Circulating Current/A	8.82(A)/9.4(B)/9.4(C)
Cable Temperature/°C	24.1
Tunnel Temperature/°C	21
Tunnel Humidity/%	92
Service Age/years	3
Historical Load/A	100~200

.

Based on the measured values listed in Table 11, it can be observed that all parameters remain within the normal range according to the evaluation criteria provided by the online monitoring manufacturer, except that the grounding circulating current and tunnel humidity exhibit noticeable abnormal variations. Consequently, a historical analysis was conducted using the tunnel humidity, water level, and grounding current data collected on that day for the cable route. The historical trends of tunnel humidity and water level are presented in Figure 6, while the temporal variation in grounding current is shown in Figure 7.

Analysis of Figure 6 indicates that the tunnel humidity remains persistently above 90%, together with a continuous rise in water level throughout the day. Such long-lasting high-moisture conditions are widely recognized to accelerate surface discharge activity and increase insulation stress. For the grounding circulating current, Figure 7 illustrates that although the values in early September still fall within the manufacturer’s limits, the increase relative to earlier records (e.g., August 31) is substantial and exhibits a clear upward trend, indicating a non-negligible change in the grounding system.

Moreover, such deviations may also be influenced by environmental fluctuations or minor sensor drift inherent to long-term online monitoring, which further highlights the need for multi-parameter evaluation rather than relying solely on single-threshold judgments. If evaluated by a single parameter alone, the grounding current of Cable 6# would still be classified as normal, since the measured value is below 50 A, the phase unbalance index is less than 3, and the ratio of historical grounding current to load current remains below 10%. However, when considering the concurrent increase in tunnel humidity, rising water level, and the abnormal trend of grounding current, the combined behavior suggests an early-stage deviation from stable operating conditions. This multi-parameter deviation cannot be reflected by single-parameter diagnostics.

Therefore, the sample analysis demonstrates that the proposed model is capable of identifying early-warning characteristics that are not captured by traditional threshold-based methods, supporting its objectivity and practical robustness in assessing in-service HV cables.

3.4.2. Comparison with Conventional Methods

Based on the determined weights, the insulation condition of the sample cables was further evaluated using two conventional approaches: the AHP–fuzzy method and the entropy weight–fuzzy method. The corresponding evaluation results are summarized in

Table 12. Evaluation results based on hierarchical method.

Cable Line	Evaluation Matrix	Assessment Result
1#	[0.9907, 0.0093, 0.0000]	Good (Grade I)
2#	[0.9928, 0.0072, 0.0000]	Good (Grade I)
3#	[0.9383, 0.0617, 0.0000]	Good (Grade I)
4#	[0.9282, 0.0718, 0.0000]	Good (Grade I)
5#	[0.7592, 0.2348, 0.0060]	Good (Grade I)
6#	[0.6172, 0.3373, 0.0455]	Good (Grade I)

and

Table 13. Evaluation results based on entropy weight method.

Cable Line	Evaluation Matrix	Assessment Result
1#	[0.9642, 0.0358, 0.0000]	Good (Grade I)
2#	[0.9649, 0.0351, 0.0000]	Good (Grade I)
3#	[0.7381, 0.2619, 0.0000]	Good (Grade I)
4#	[0.7343, 0.2657, 0.0000]	Good (Grade I)
5#	[0.6631, 0.3081, 0.0288]	Good (Grade I)
6#	[0.5801, 0.1990, 0.2209]	Good (Grade I)

, respectively.

Analysis of the evaluation matrices in Table 12 and Table 13 indicates that, compared with the entropy weight method, which reflects objective weighting, the AHP-based results exhibit noticeable deviations, largely due to their stronger subjectivity. Moreover, under the traditional single-weight fuzzy evaluation framework, the results for Cable 6# differ not only from those obtained by the proposed method but also fail to provide finer discrimination among cables assigned to the same insulation grade. Such approaches can only distinguish cables at the categorical level without enabling a more nuanced comparison of insulation performance.

Therefore, the engineering case study demonstrates that the proposed method can effectively evaluate the insulation condition of tunnel HV cables. By integrating multisource sensing data such as partial discharge, temperature, and grounding current, the method overcomes the limitations of single-feature diagnosis and single-weighting approaches. It thus provides a novel and practical strategy for insulation condition assessment of 110 kV tunnel HV cables under multi-source sensing environments.

4. Conclusions

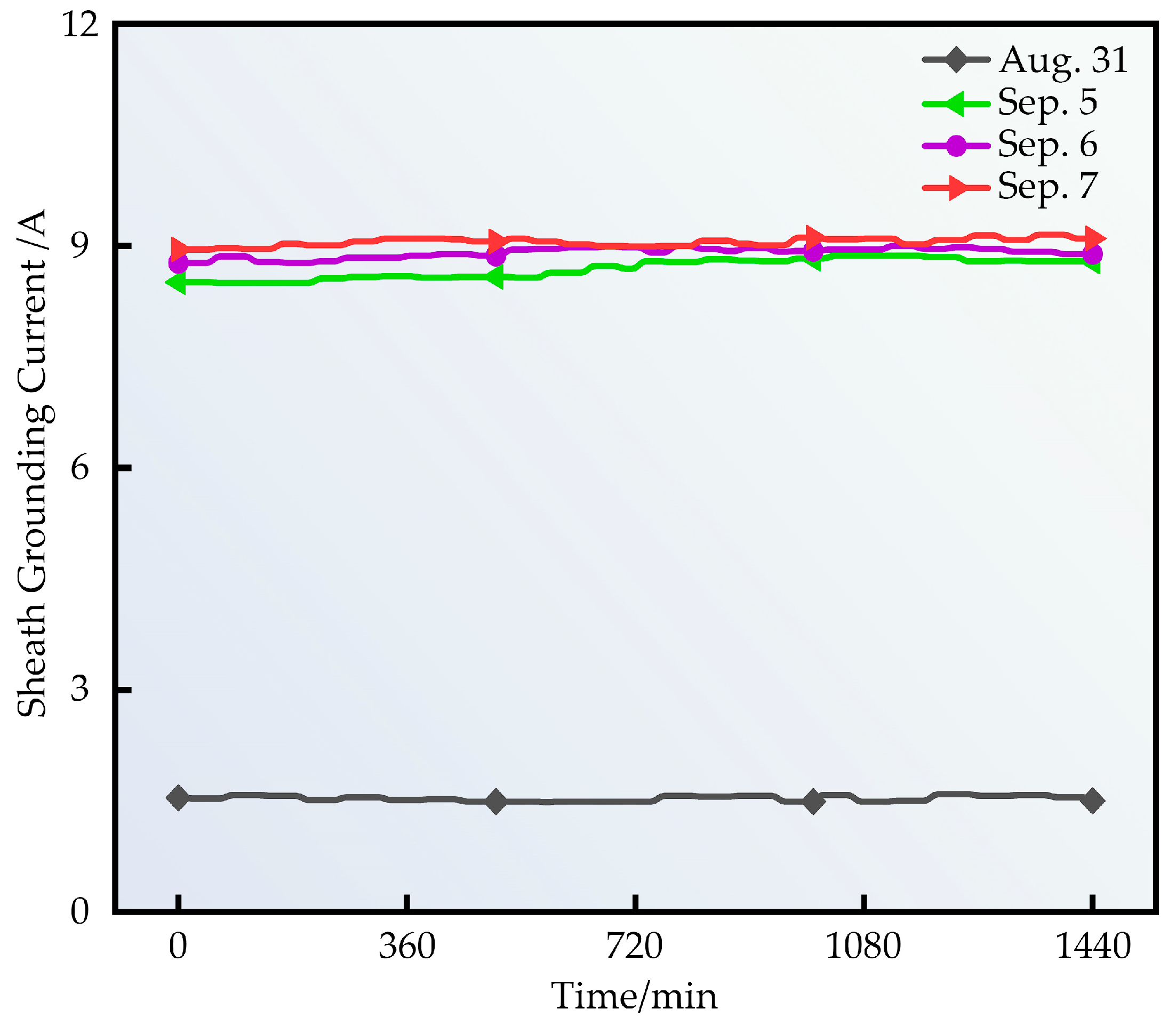
In this study, a novel insulation condition assessment method for 110 kV tunnel high-voltage cables was developed by integrating game-theory-based weighting with a fuzzy comprehensive evaluation framework. By constructing a multi-index system that incorporates partial discharge, grounding circulating current, temperature, and environmental parameters, the method provides a more comprehensive representation of insulation performance under real operating conditions. The game-theoretic weighting strategy effectively reconciles subjective expert judgment with objective data-driven variation, enabling a more balanced and scientifically grounded determination of indicator weights than relying solely on traditional AHP or entropy weighting. Meanwhile, the fuzzy evaluation framework addresses uncertainty and threshold ambiguity inherent in insulation diagnostics, providing a smoother and more realistic mapping from monitoring parameters to insulation states. Case studies on in-service tunnel cables further demonstrate that the proposed model not only produces reliable insulation grading but also distinguishes subtle differences between cables that may be overlooked by single-parameter or single-threshold methods, thereby enhancing diagnostic precision and engineering applicability.

Looking ahead, the methodology presented in this work offers promising potential for broader generalization. Owing to its reliance on routinely available online monitoring data and its computationally lightweight structure, the framework may be extended to real-time condition monitoring scenarios or incorporated into intelligent diagnostic platforms. Although this study focuses on 110 kV tunnel cables, the underlying principles are adaptable to other voltage levels and different cable configurations. Future research may further explore the integration of aging-related degradation indicators, the use of alternative or adaptive membership functions, and the incorporation of data-driven or machine-learning-based weighting schemes as more extensive datasets become available. Such developments are expected to enhance the robustness, adaptability, and long-term engineering value of multi-parameter insulation assessment methods.