Optimal Location and Sizing of BESS Systems with Inertia Emulation to Improve Frequency Stability in Low-Inertia Electrical Systems

Abstract

Traditionally, the dynamics of power systems have been governed by synchronous generators and their associated rotating masses. However, with the increasing penetration of renewable generation and power electronic interfaces, the inertia contributed by rotating machines has been gradually displaced. This makes it imperative to study alternative elements capable of mitigating the reduction in inertia in modern power systems. This article addresses the problem of optimal sizing and placement of Battery Energy Storage Systems to enhance frequency response in power grids through the application of optimization techniques such as Genetic Algorithms (GA) and Particle Swarm Optimization (PSO). Several inertia scenarios are analyzed, where the algorithms determine the optimal locations for Battery Energy Storage Systems units while minimizing the total installed Battery Energy Storage Systems capacity. As key contributions, this study models Battery Energy Storage Systems units, which emulate inertial responses based on the system’s Rate of Change of Frequency, and evaluates the impact of Battery Energy Storage Systems on frequency stability by analyzing parameters such as the frequency nadir, zenith, and steady-state frequency according to the installed Battery Energy Storage System’s size and location. A comparative analysis of the optimization scenarios shows that the Particle Swarm Optimization algorithm with 50% rotational inertia is the most efficient, requiring the lowest total installed power (277.11 MW). It is followed by the Particle Swarm Optimization algorithm with 100% rotational inertia (285.79 MW) and Genetic Algorithms with 50% rotational inertia (285.57 MW). In contrast, Genetic Algorithms with 25% rotational inertia demand the highest total installed Battery Energy Storage Systems power (307.44 MW), a result directly associated with a significant reduction in system inertia. Overall, an inverse relationship is observed between the available inertia level and the required Battery Energy Storage Systems capacity: the lower the inertia, the greater the power that the Battery Energy Storage Systems must supply to keep the system frequency within acceptable operational limits.

1. Introduction

The increasing penetration of renewable energy sources in electric power systems has posed significant operational challenges, particularly with respect to frequency stability. Technologies such as wind and photovoltaic generation do not provide synchronous inertia to the system, leading to a reduction in effective inertia and, consequently, an increase in the rate of change of frequency (RoCoF) during disturbances. This decline in the system’s ability to withstand frequency variations compromises the security and reliability of power supply, especially in systems with a high share of renewable generation and low inertia.

In this context, battery energy storage systems (BESS) employing inertia emulation strategies have emerged as a viable solution to mitigate the adverse effects of reduced inertia. Through appropriate control of their frequency response, BESS can provide immediate dynamic support, stabilizing frequency in the initial moments following a disturbance and reducing the RoCoF. However, to maximize their technical and economic effectiveness, it is essential to determine their optimal placement and sizing within the power system.

This article addresses the issue of optimal placement and sizing of BESS with inertia emulation to enhance frequency stability in low-inertia power systems. A methodology is proposed based on (specify the specific method, e.g., metaheuristic algorithms, mathematical programming, modal analysis, etc.), which enables the determination of the optimal location and capacity of BESS, considering both technical and economic criteria. Through simulations on a representative test system, the impact of the placement and sizing strategy on frequency stability is evaluated, providing guidelines for the efficient integration of BESS into grids with high penetration of renewable generation.

1.1. Related Works

The integration of BESS into modern power grids has been the focus of numerous studies proposing innovative control strategies and optimization methods to enhance system performance and stability. In ref. [1], a control strategy combining adaptive droop control with an adaptive state of charge (SoC) recovery mechanism for primary frequency regulation (PFR) was presented, improving frequency stability and reducing mechanical stress on conventional generating units. In ref. [2], a hierarchical control scheme was introduced, integrating BESS SoC into frequency regulation through a multilevel strategy, with its effectiveness validated using Hardware-in-the-Loop testing. In ref. [3], a secondary frequency control strategy based on the degree of participation of BESS was proposed, utilizing a fuzzy logic inference system and a quadratic programming algorithm to optimize task allocation. In ref. [4], a load frequency control (LFC) strategy was presented, incorporating detailed dynamic models of wind turbines, HVDC systems, BESS, and synchronous generators, demonstrating significant improvements in frequency stability. In ref. [5], a control strategy for hybrid energy storage systems was developed, integrating BESS and pumped hydro energy storage to enhance PFR in grids with high renewable penetration. Finally, in ref. [6], the role of BESS in providing additional inertial support in grids with high renewable energy penetration was investigated, emphasizing the importance of optimal BESS sizing to balance costs and stability benefits. These studies underscore the fundamental role of BESS in improving frequency regulation and the stability of modern power grids, especially in contexts of high renewable energy penetration.

The integration of BESS in microgrids and isolated systems has been extensively studied, with various control strategies proposed to enhance frequency regulation and system stability. In ref. [7], a control strategy was presented that integrates SoC management with load frequency control in isolated microgrids, using a shifted droop control mechanism that dynamically adjusts BESS operation based on five distinct SoC scenarios, thereby improving system stability and SoC management. In ref. [8], a frequency control strategy for isolated greenhouses was proposed, integrating BESS and Light-Emitting Diode lighting loads, using a two-stage control that combines the fast response of BESS and Light-Emitting Diode lighting loads with frequency restoration via diesel generators. In ref. [9], a multifunctional adaptive control strategy was introduced for energy management and voltage-frequency regulation in isolated microgrids composed of photovoltaic (PV) units, BESS, and hybrid PV/BESS units, integrating decentralized and distributed control for optimal performance. In ref. [10], an integrated multifunctional control scheme was presented for stand-alone BESS in synchronous generator-based microgrids, highlighting the use of a state of charge-based adaptive high-pass filter for frequency regulation and unbalanced load compensation. In ref. [11], a reserve-based frequency support strategy for BESS in isolated residential microgrids was proposed, introducing a reserve control layer within the conventional LFC architecture to improve frequency stability during emergency conditions. Finally, in ref. [12], a control framework for voltage and frequency regulation in weak grids with wind turbines, PV, and BESS was presented, utilizing a fixed-time containment control strategy that enables BESS to simultaneously regulate voltage and frequency while maintaining SoC balance. These studies highlight the importance of advanced and adaptive control strategies for the effective integration of BESS in microgrids and isolated systems, enhancing system stability and efficiency.

The integration of BESS with renewable energy sources has been extensively studied to enhance frequency stability in low-inertia systems. In ref. [13], a methodology was proposed to mitigate over-frequency events through optimal BESS allocation in wind-dominated systems, using a Particle Swarm Optimization-based model. In ref. [14], the role of BESS in improving frequency response in low-inertia, solar-dominated systems was investigated, integrating inertia response and PFR strategies within the traditional LFC framework. In ref. [15], a virtual inertia control approach was presented, incorporating a coordinated SoC recovery mechanism with secondary frequency control of generators, optimizing battery utilization and reducing BESS energy consumption by 36%. In ref. [16], the use of energy storage systems, including superconducting magnetic energy storage and BESS, was explored to improve frequency response in wind-dominated grids, demonstrating that the combination of superconducting magnetic energy storage and BESS reduced system costs by 76.9% compared to BESS-only solutions. In ref. [17], a strategy for optimal BESS sizing and placement in high wind penetration systems was proposed, integrating model predictive control (MPC) for coordinated frequency and voltage regulation. In ref. [18], a coordinated control strategy between variable-speed wind turbines and BESS was investigated to enhance fast frequency response, using a SoC-based adaptive droop control. In ref. [19], a control strategy was presented to mitigate torsional vibrations in doubly-fed induction generators using a BESS-based damper, improving torsional damping and maintaining frequency stability. In ref. [20], a model predictive control MPC-based strategy was developed to enable a hybrid wind farm and BESS unit to provide fast frequency regulation, validated through Hardware-in-the-Loop simulations. Finally, ref. [21] presents a coordinated control strategy for a voltage-source-converter-based high-voltage direct current-connected wind farms with a BESS for providing frequency support.

The optimization of BESS for participation in energy markets and grid stability has been widely explored in various studies. In ref. [22], the economic viability of residential PV-BESS installations was evaluated, highlighting the importance of storage sizing and self-consumption for profitability, particularly in systems with a capacity factor ≥ 18%. In ref. [23], a revenue stacking model was proposed that combines fast frequency regulation with participation in the Italian balancing market, enhancing efficiency and investment returns by 13%. In ref. [24], the financial viability of BESS in households with dynamic electricity contracts in the Netherlands was analyzed, concluding that the gradual phase-out of net metering negatively affects BESS profitability. In ref. [25], a reinforcement learning framework was presented for adaptive BESS scheduling in dynamic markets, demonstrating greater profitability and resilience to price fluctuations compared to traditional methods. In ref. [26], a probabilistic forecasting framework for BESS SoC under primary frequency control was developed, employing multi-attention recurrent neural networks to enhance prediction accuracy and reliability. In ref. [27], a setpoint frequency control method was introduced to integrate renewable energy sources, optimizing BESS operation and reducing grid balancing costs. These studies underscore the crucial role of BESS in improving profitability, grid stability, and the efficient integration of renewable energy into energy markets.

Control strategies for BESS have been essential in improving the stability of power systems. In ref. [28], a real-time optimal control method was presented that enables the simultaneous provision of primary frequency control and local voltage regulation by dynamically adjusting active and reactive power setpoints, with its effectiveness validated on a utility-scale BESS at EPFL, Lausanne. In ref. [29], a self-adaptive control strategy was proposed that classifies disturbances into step and small continuous types, introducing two models to prevent frequency degradation and ensure SoC recovery, demonstrating improvements in frequency stability and long-term economic operation. Meanwhile, ref. [30] developed a contingency reserve assessment framework for fast frequency response across multiple large-scale BESS, using genetic algorithms to optimize reserves and enhance grid resilience under high renewable penetration. As for ref. [31], a methodology was presented to determine the required BESS capacity in the Korean power system to compensate for reduced inertia under high renewable penetration scenarios, highlighting the effectiveness of BESS in frequency control. In ref. [32], a rule-based programming algorithm was introduced for BESS management in prosumers, optimizing energy flows with lower computational costs and demonstrating scalability for renewable energy communities.

The integration of BESS into grid infrastructures and industrial energy systems has proven essential for enhancing stability and energy efficiency. In ref. [33], the use of BESS to mitigate transmission congestion in the Brazilian Interconnected System was analyzed, highlighting its potential to improve grid flexibility, albeit with challenges related to high comparative costs. Meanwhile, ref. [34] explored the application of BESS in the Puducherry Smart Grid to reduce demand peaks through a Model Predictive Control strategy, achieving a 20% reduction in peak demand and improvements in voltage stability. In ref. [35], an integrated industrial power supply system was developed, combining renewable sources, carbon capture and storage, and BESS, resulting in a 59.78% reduction in carbon emissions and emphasizing the need for policy incentives to ensure economic feasibility. Finally, ref. [36] proposed an optimization model for BESS sizing in microgrids, employing mixed-integer linear programming and Benders decomposition, ensuring frequency stability by integrating transient dynamics into the model. These studies underscore the importance of BESS in improving energy infrastructure, integrating renewable energy, and supporting industrial sustainability.

Other control and optimization strategies for BESS have been proposed to improve frequency stability and economic viability in modern power systems. In ref. [37], a shared-use leasing strategy for distributed BESS in joint energy and frequency control ancillary services markets was proposed, demonstrating economic benefits for both owners and users. In ref. [38], an optimal configuration method with opportunity constraints for BESS in networks with high integration of variable renewable energy was developed, enhancing both frequency stability and economic feasibility. In ref. [39], a Controller Hardware-in-the-Loop simulation approach was introduced to evaluate the fast frequency response of BESS, employing an advanced frequency detection algorithm that improves accuracy and robustness. In ref. [40], the effectiveness of BESS in improving frequency stability in islanded networks with high renewable penetration was investigated using Particle Swarm Optimization to tune control parameters. In ref. [41], a risk-preference-based optimization model for user-side BESS configuration was presented, balancing economic viability and operational stability. In ref. [42], a methodology for optimal placement of frequency regulation energy storage systems was introduced, enhancing frequency recovery in modern networks. In ref. [43], an optimization approach for BESS placement and sizing was developed using metaheuristic algorithms such as PSO, Firefly Algorithm, and Bat Algorithm, showing improvements in frequency stability. In ref. [44], a control strategy for grid-following and grid-forming inverters in microgrids integrated with solar energy and BESS was presented, improving grid stability and frequency response. Lastly, ref. [45] proposed a mixed-integer linear programming model to optimize the sizing of renewable energy communities, enhancing energy self-management and sustainability. These studies underscore the importance of BESS integration for frequency stability, economic viability, and sustainable energy management in modern power grids.

The article ref. [46] proposes a novel optimization algorithm called the Binary Random Dynamic Arithmetic Optimization Algorithm to determine the optimal location and sizing of Electric Vehicle Charging Stations in power distribution networks. The study’s main contribution lies in enhancing the existing Arithmetic Optimization Algorithm by integrating a Binary Search Algorithm and a Random High-Speed Jumping strategy to improve both exploration and exploitation capabilities. This hybridization allows for faster convergence and avoidance of local optima. The method was tested on the IEEE 33-bus network, minimizing a multi-objective function that includes active power losses, total harmonic distortion, and voltage deviation. Results demonstrated that Binary Random Dynamic Arithmetic Optimization Algorithm achieves 2–4% lower line losses and shorter computation time compared to traditional metaheuristics like PSO, HHO, and standard Arithmetic Optimization Algorithm, showing its superior efficiency, robustness, and accuracy for EVCS placement and planning.

Energy Storage Systems are presented as a key solution to mitigate the intermittency of renewable energies and strengthen grid resilience. Among their technologies, batteries stand out by providing emergency backup, black-start capability, and regulation services. Various studies show that ESS balance supply and demand, enable response to extreme events (heat waves, floods, typhoons), and ensure continuity of critical demand, albeit at additional costs. Despite their high initial investment, ESS provide multiple benefits: energy backup, load leveling, improvement of supply quality and reliability, reduced vulnerabilities, and support for the transition toward more efficient and productive decentralized grids [47].

The article [48] analyzes the operation of the Chinese electricity market under a dual scheme, where regulated and deregulated transactions coexist under high wind energy penetration. Its main contribution lies in defining and classifying the so-called “unbalanced funds,” proposing detailed calculation formulas that cover cases of congestion, mismatches between generation and consumption, low-voltage users, purchasing agents, and, in particular, those arising from the coexistence of regulated and deregulated markets. To this end, it develops a market clearing model based on DC power flow with security, ramping, and contract constraints, validated through simulations on the IEEE-39 bus system using real data from a Chinese province. The results show that high wind participation amplifies unbalanced funds due to renewable dispatch priority and its mismatch with demand curves, leading to financial and equity distortions in the market. In this context, although this study does not directly address storage systems, its conclusions are highly relevant to BESS, as these can mitigate imbalances caused by wind intermittency by storing surpluses and releasing them during deficit periods, thereby helping to reduce unbalanced funds, improve the match between generation and demand, and strengthen the stability and reliability of the electricity market.

1.2. Main Contributions

Previous studies have extensively examined BESS technologies, their interaction with power systems, and their role in providing ancillary services. However, a significant knowledge gap remains: no prior work has assessed, in an integrated manner, how the location and sizing of RoCoF-based inertia-emulating BESS influence the overall frequency dynamics of the system, particularly when jointly considering critical metrics such as Nadir, Zenith, RoCoF, and steady-state frequency. Existing contributions typically address synthetic inertia control, BESS optimization, or frequency performance indicators in isolation; yet, there is no methodological framework that simultaneously incorporates inertia emulation, multi-metric frequency assessment, and the optimal spatial and capacity allocation of BESS within the grid. Accordingly, the contributions of this work are as follows:

• A BESS model that emulates inertia based on the system’s RoCoF is implemented, with the aim of evaluating its impact on key frequency metrics.
• The impact of BESS placement and sizing on the dynamic behavior of frequency is assessed, jointly considering the metrics of Nadir, Zenith, steady-state frequency, and RoCoF.
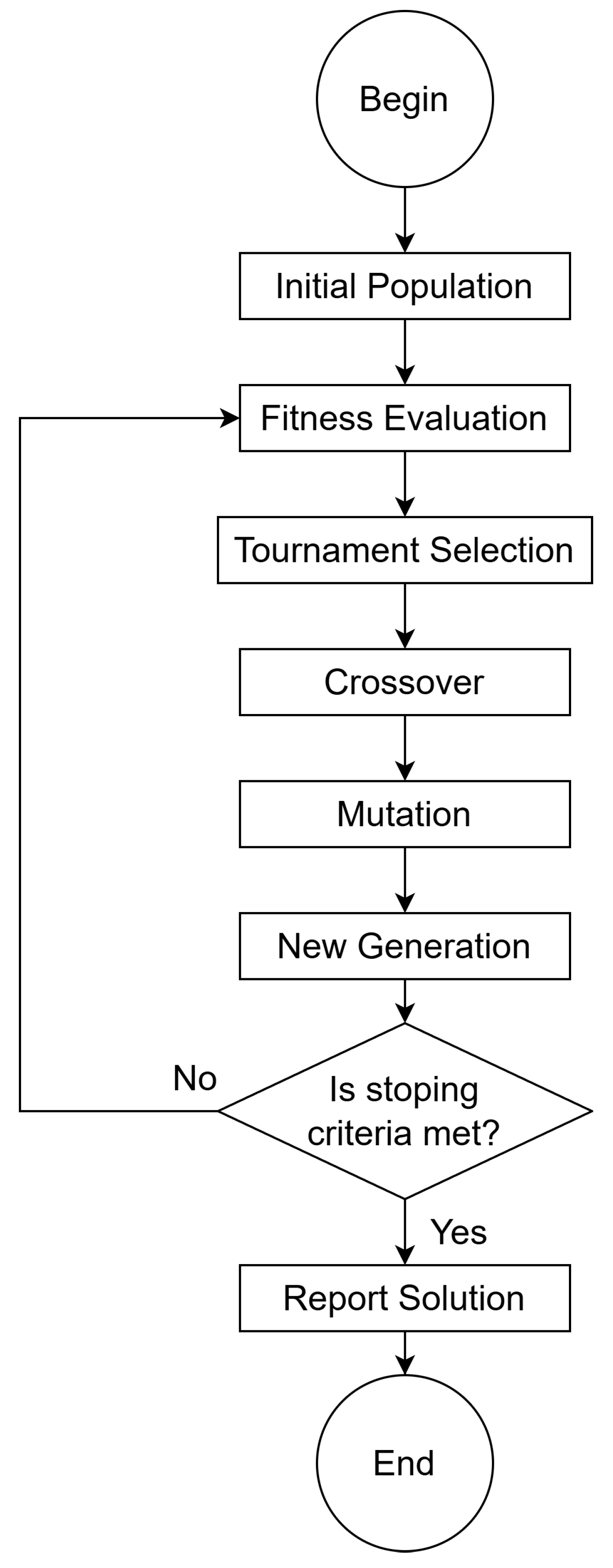
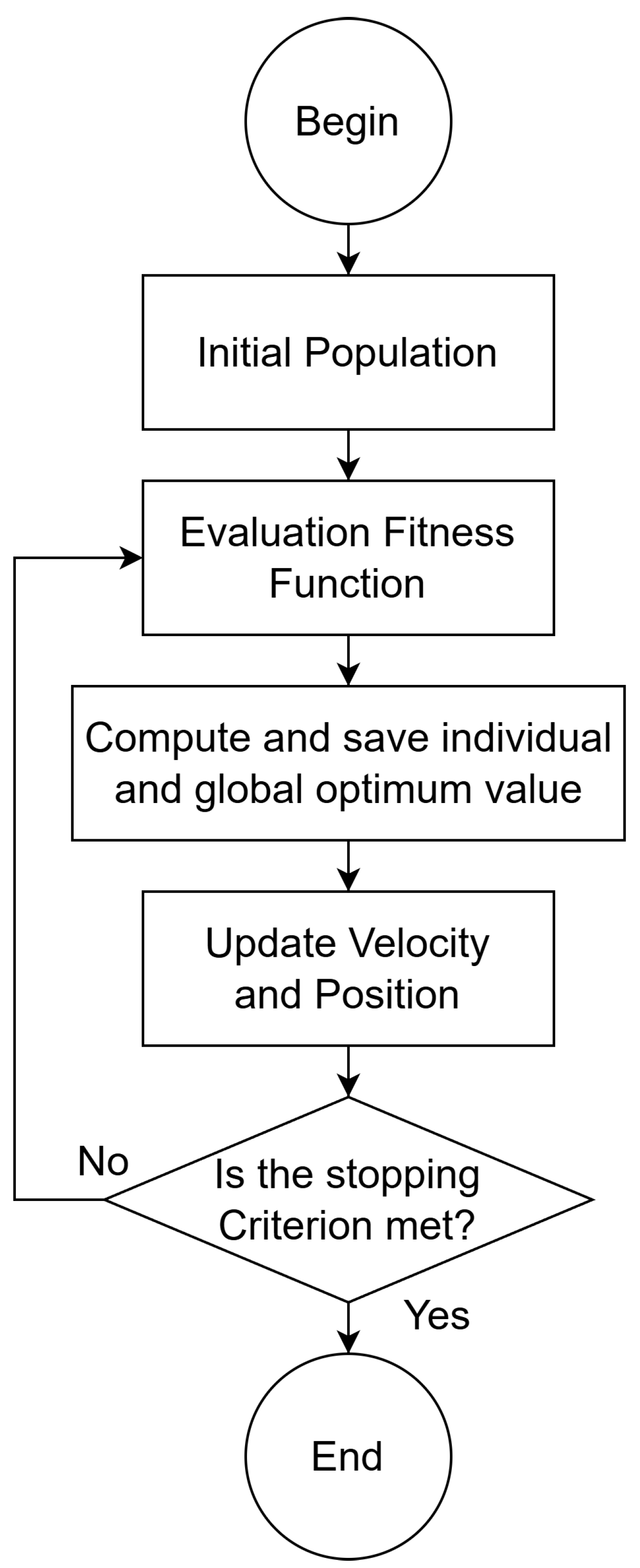
• Two heuristic optimization techniques—Particle Swarm Optimization (PSO) and Genetic Algorithm (GA)—are implemented and compared to determine the optimal placement and sizing of RoCoF-based inertia-emulating BESS within the power grid.

This article presents an original approach that differs from comparable methods through the simultaneous integration of inertia modeling based on the RoCoF and the joint optimization of BESS placement and sizing using PSO and GA.

Traditional BESS sizing methods, such as those based on mixed-integer linear programming [36], MPC [34], or hierarchical predictive control strategies [17], primarily address frequency regulation from a control or energy management perspective, without explicitly considering synthetic inertia response derived from the frequency derivative. Other metaheuristic approaches, such as PSO, the Firefly Algorithm [43], or the Bat Algorithm [43], have focused mainly on optimizing power or location parameters, without incorporating combined dynamic metrics such as Nadir, Zenith, RoCoF, and steady-state frequency.

Table 1. Comparative contributions on BESS siting and sizing for frequency stability enhancement.

Reference	Strategy/Contribution	Application	Key Benefit
This Article	BESS model emulating inertia from RoCoF + Optimization (PSO, GA)	Low-inertia power systems	Joint optimization of BESS siting and sizing considering Nadir, Zenith, RoCoF, and steady-state frequency
[13]	PSO-based optimal siting	High wind penetration systems	Mitigation of over-frequency events
[17]	MPC for coordinated control	High wind penetration systems	Optimization of frequency and voltage regulation
[43]	Metaheuristic optimization (PSO, FA, BA)	Frequency support	Optimal siting and sizing of BESS
[6]	Inertial support with BESS	High renewable energy networks	Importance of optimal BESS sizing
[31]	Required BESS capacity estimation	South Korean power system	Frequency control under high renewable penetration
[36]	mixed-integer linear programming + Benders decomposition	Microgrids	Transient dynamics integration for stability improvement
[40]	PSO-based control parameter optimization	Islanded networks	Enhancement of frequency stability
[5]	Hybrid control of BESS and pumped hydro energy storage (BESS + PHES)	Primary Frequency Regulation (PFR)	Improvement of frequency support in high-renewable grids

presents a comparative overview of selected studies that address optimal siting and sizing of BESS for frequency stability enhancement. It highlights the strategies used (e.g., metaheuristics, predictive control, mixed-integer linear programming, their application contexts (such as low-inertia systems, high renewable penetration, and microgrids), and the main contributions regarding frequency metrics like RoCoF, Nadir, and steady-state frequency. The proposed article is included for reference, emphasizing its novel approach to jointly optimizing BESS placement and capacity while emulating synthetic inertia based on RoCoF.

This work is organized as follows: Section 1.3 presents fundamental concepts related to the need for virtual inertia in power systems and analyzes the impact of decreasing system inertia. Section 1.4 reviews different approaches to inertia in power systems, including strategies for virtual inertia implementation. In Section 1.5, the implemented model for the BESS system is described, along with the control loop designed for inertia emulation. Section 2 details the methodology employed in the study. 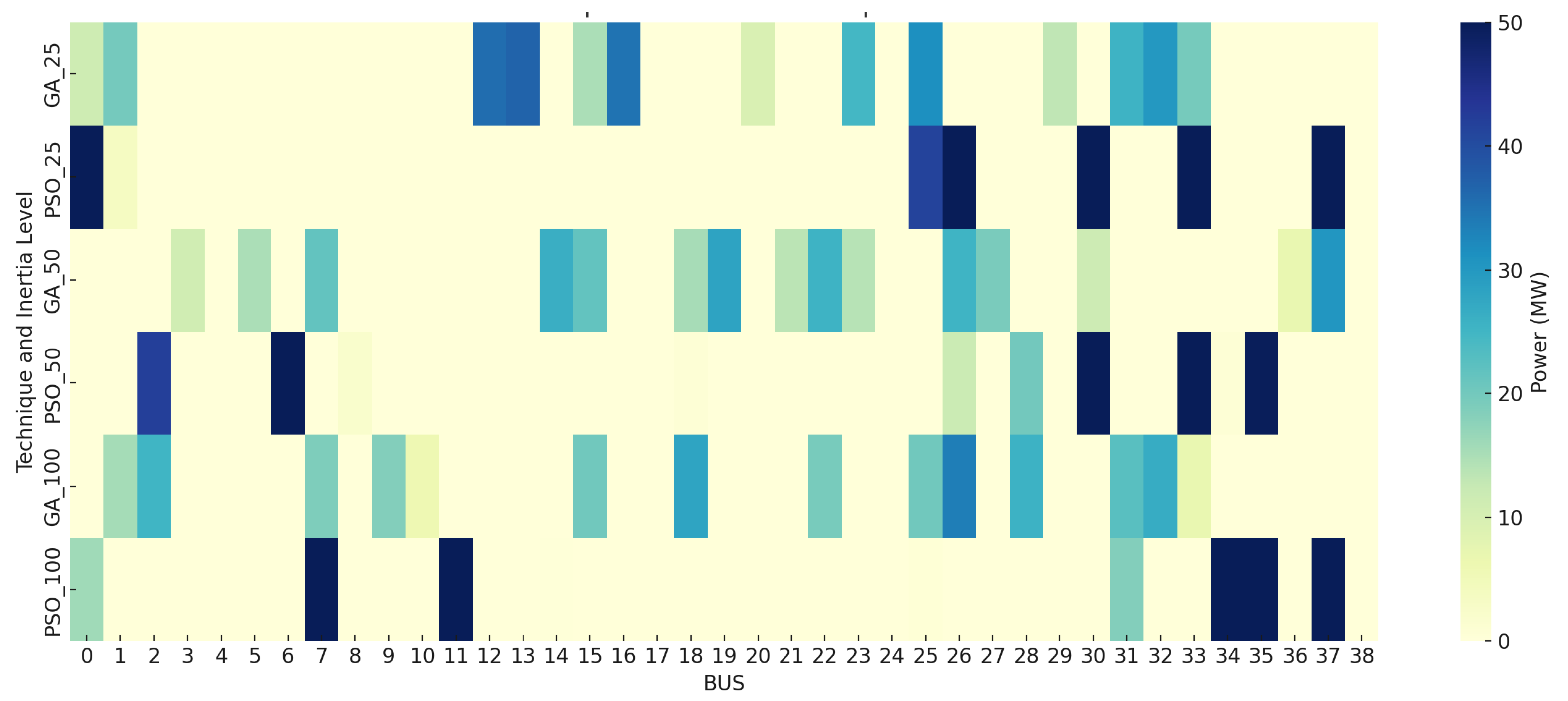Section 3 explains the optimal placement and sizing of the BESS within the power system, highlighting the implementation of GA and PSO techniques. 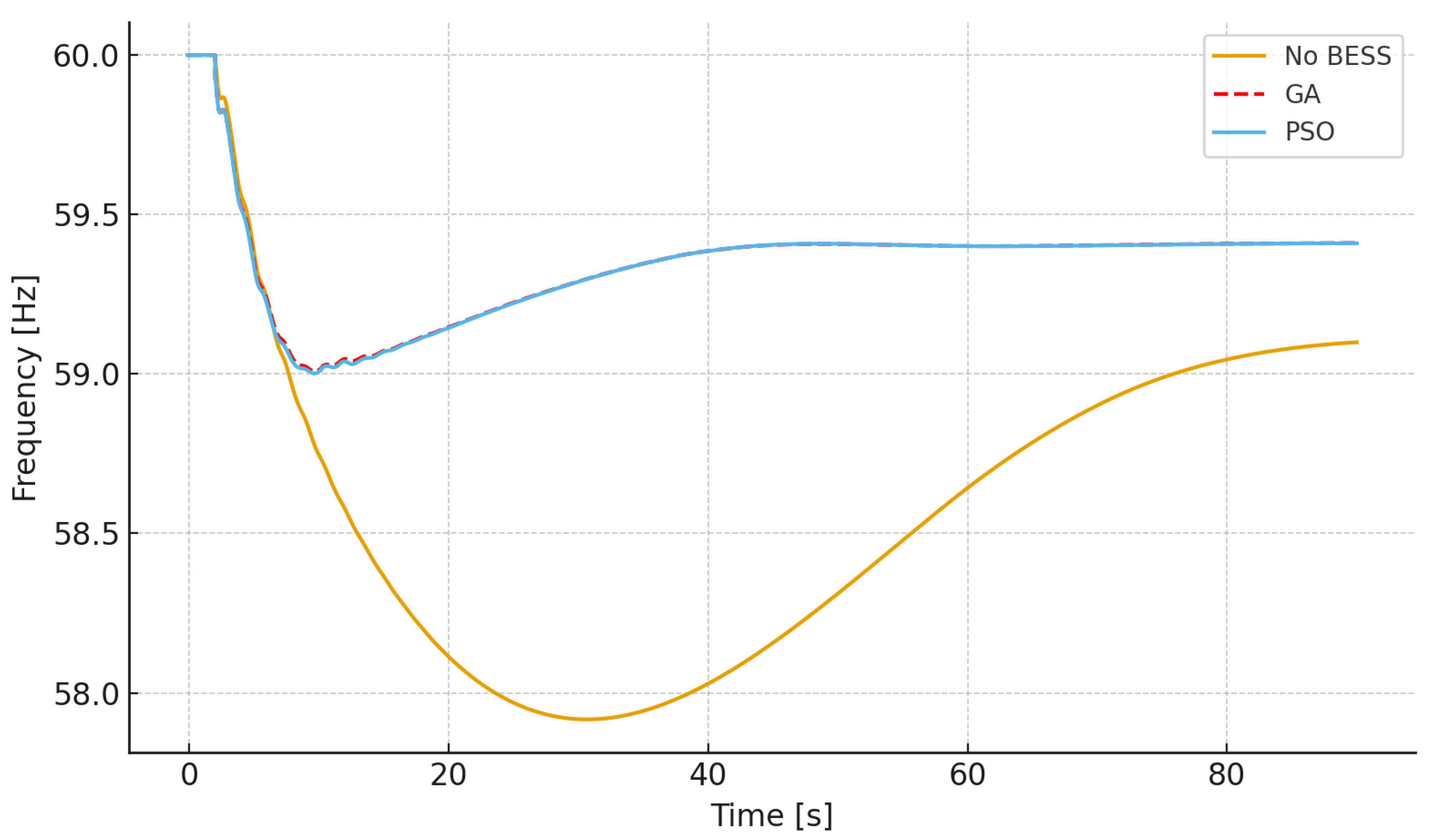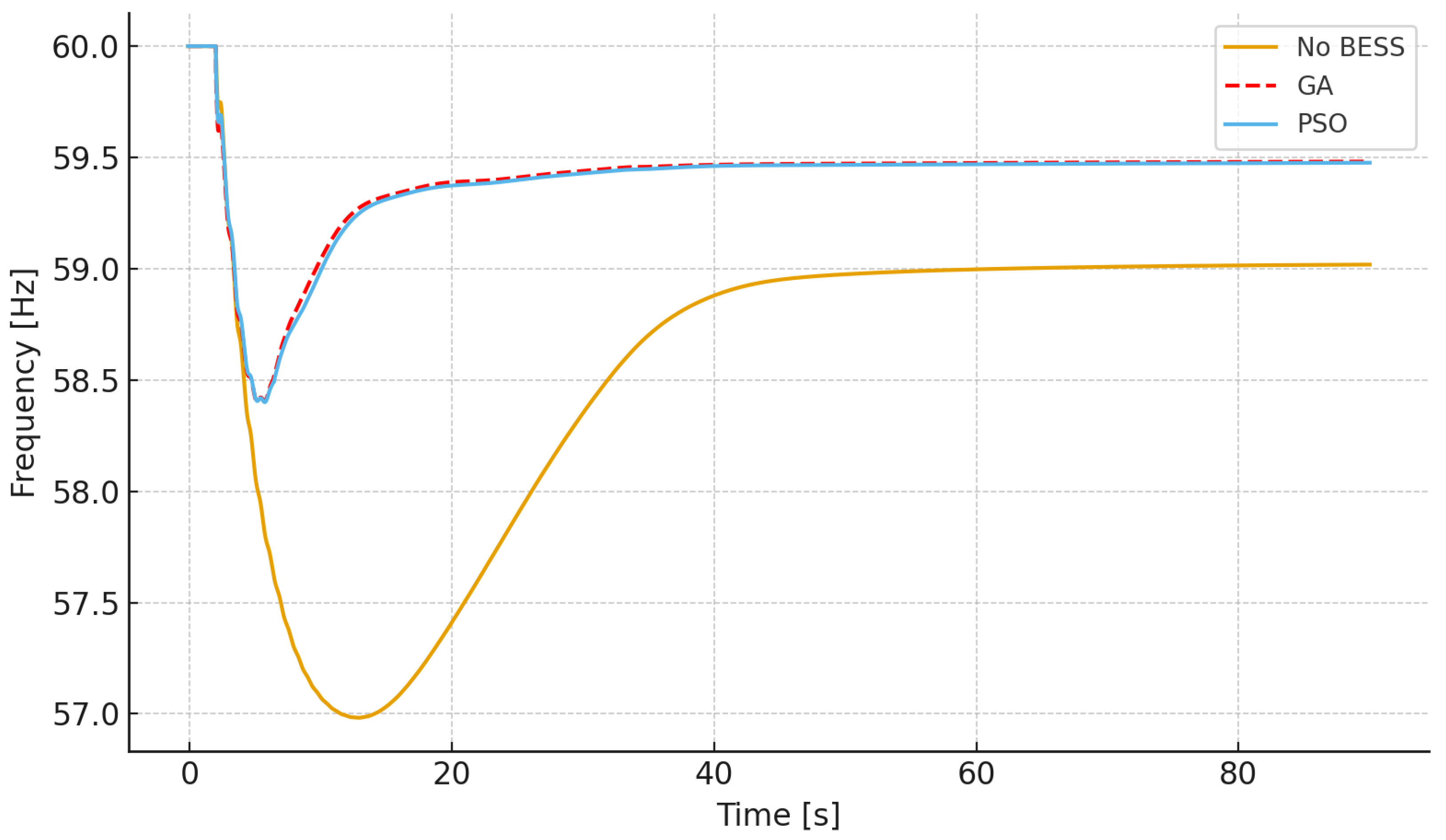Section 4 presents the results obtained from applying GA and PSO to the optimization problem under various inertia scenarios. Section 5 presents the discussion. Section 5.5 presents limitations and implementation challenges. Section 5.6 explains the practical implementation. Section 5.7 explains the theoretical-practical integration. Finally, Section 6 presents the conclusions of the study.

1.3. Need for Virtual Inertia in Power Systems

Traditionally, inertia in electric power systems has been directly dependent on rotating machines and on the electromagnetic coupling between their rotating masses and the electrical grid [49]. With the integration of power electronic interfaces, a decoupling occurs between generators, rotating loads, and the grid, which prevents the kinetic energy stored in their rotating masses from mitigating transients in the system [50]. As a result, it becomes necessary to define methodologies that enable the grid to maintain inertia levels H such that the magnitude of frequency deviation is minimized during generation-load imbalances.

In this way, the system dynamics would exhibit a slower and more damped response, increasing the critical clearing times for fault removal and allowing sufficient margins to perform switching actions to counteract active power imbalances caused by faults or events such as the loss of transmission lines, generation units, loads, etc. [50].

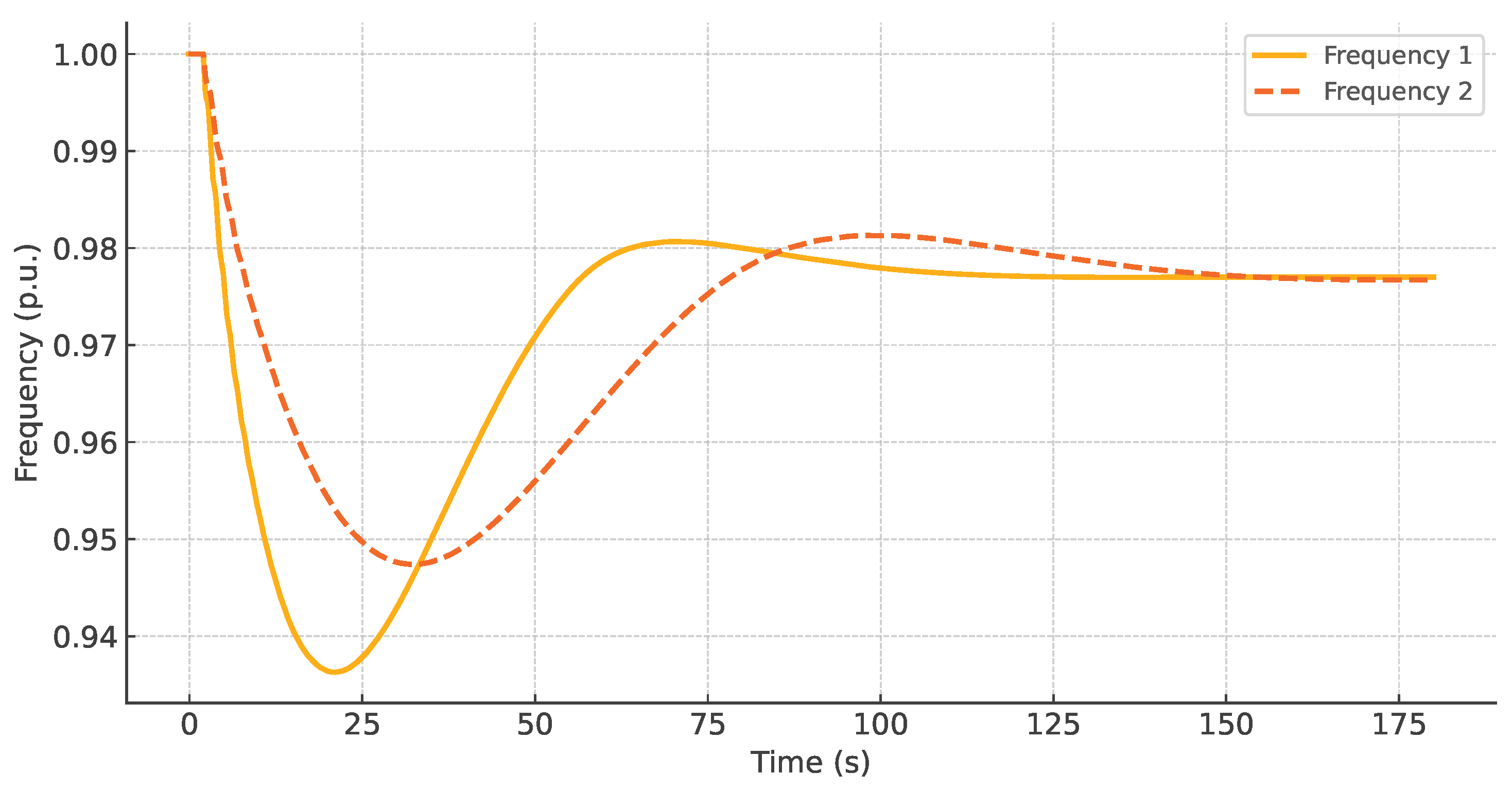
Figure 1 illustrates how frequency is affected by changes in system inertia levels. The curve labeled Frequency 1 corresponds to the IEEE 39-bus system with a 50% loss of inertia, while the curve labeled Frequency 2 represents the same system operating with 100% of its original inertia. A generation-load imbalance results in frequency excursions, and this imbalance is initially counteracted by the system’s inertia $H_s$, as expressed in Equation (1), where the inertia $H_g$ of each generator is defined in Equation (2) [50].

$$\begin{array}{c}\hfill H_s=\sum _i{\displaystyle \frac{H_{g,i}{S}_{g,i}}{S_s}}\end{array}$$

(1)

$$\begin{array}{c}\hfill H_{g,i}={\displaystyle \frac{E_{kin,i}}{S_{g,i}}}={\displaystyle \frac{J{\left(2\pi f_n\right)}^2}{2S_{g,i}}}\end{array}$$

(2)

where $E_{kin,i}$ is the kinetic energy of the generator, J the moment of inertia, $S_s$ the total system power, $f_n$ the nominal system frequency, and $S_{g,i}$ the power of each generator.

The RoCoF is the instantaneous rate of change of frequency following an imbalance in the system caused by a disturbance. Generation loss, sudden load disconnection, and islanding operation are examples of such disturbances.

The initial $RoCoF$, assuming zero load damping [50], is expressed as follows in Equation (3):

$$\begin{array}{c}\hfill RoCoF={\displaystyle \frac{df}{dt}}={\displaystyle \frac{\Delta P}{2H}}{f}_0\end{array}$$

(3)

where $\Delta P$ is the size of the contingency (lost MW), H is the system inertia (MW-seconds), $f_0$ is the frequency at the time of the disturbance (Hz), and $df/dt$ is the rate of change of frequency (Hz/s).

A slow-response scenario for RoCoF, within the range of seconds to minutes, is associated with the inertia provided by synchronous generators along with their governors, which help to reduce the RoCoF. Enhancing grid inertia control within this physical time frame could be naturally achieved through the use of synchronous condensers. On the other hand, a fast-response scenario for RoCoF control could involve the rapid injection of energy, either by increasing generation or reducing load.

Inverter-Based Power Sources (IBPS), such as wind, solar, batteries, supercapacitors, and flywheels, can provide a fast frequency response. However, these devices inherently lack an inertial response, making a control loop that enables energy delivery proportional to changes in system speed or frequency necessary.

These limitations in the system’s inertial response motivate the review of inertia emulation techniques, which are presented in the following section.

1.4. Inertia in Power Systems

In power systems, frequency reflects the state of balance between generation and demand, serving as an indicator of system speed. This balance is affected by variations in generation or load. For instance, in the event of a generator unit outage, the system enters an overload condition where demand exceeds generation, resulting in a frequency drop as the system slows down. Thus, inertia plays a fundamental role in the behavior of AC power grids, as the magnitude and rate of frequency deviations are directly related to the system’s inertia levels. In other words, the more synchronous machines are directly connected to the system, the more stable it becomes. In this way, by releasing or absorbing energy through the rotating masses of electrical machines, the system instantaneously compensates for imbalances. Subsequently, generator control systems provide additional energy from reserves, activating the Automatic Generation Control (AGC), and in later stages, tertiary control mechanisms [51].

The integration of energy sources that do not provide inertial response alters the system’s ability to effectively respond to frequency disturbances, especially in the initial stages. This highlights the need to implement controlled inertial responses through power electronic interfaces, with the aim of ensuring the safe and reliable operation of the power system.

1.4.1. Inertia Constant and Swing Equation

The inertia constant of a power system, denoted as H, or that of a specific generator, $H_i$, represents the kinetic energy stored in the system’s rotating masses, expressed as $E_{c0}$. This value indicates the time, in seconds, required to replenish that energy under nominal operating conditions, considering the nominal mechanical speed ${\omega }_{sm}={\left(2\pi f_n\right)}^2$ and the nominal apparent power $S_{base}$. The mathematical relationship that defines the total system inertia can be represented by Equation (2) [49].

The relationship between the frequency measured at the generator $f_i$ and the power imbalance $\Delta P_i$ at its terminals is expressed by Equation (4):

$$\begin{array}{c}\hfill {\displaystyle \frac{2H_i}{f_n}}·{\displaystyle \frac{d{f}_i}{dt}}=p_{m,i}-p_{e,i}=\Delta p_{i}i=1,2,\dots ,N\end{array}$$

(4)

where $p_{m,i}$ is the mechanical power of the turbine in p.u., $p_{e,i}$ is the electrical power in p.u., $\Delta p_i$ is the power imbalance between generation and load in p.u., $H_i$ is the inertia constant in seconds, $f_n$ is the frequency at point i in Hz, $f_n$ is the nominal system frequency in Hz, and $d{f}_i/dt$ is the rate of change of frequency in Hz/s.

If the instant at which a disturbance occurs, $t=t_0$, is known, along with the power imbalance $\Delta p_i\left(t_0\right)$ and the rate of change of frequency $d{f}_i/dt$, the inertia delivered by the generator can be calculated using Equation (5):

$$\begin{array}{c}\hfill {\widehat{H}}_i={\displaystyle \frac{\Delta p_i\left(t_0\right)f_n}{2·\frac{d{f}_i}{dt}{|}_{t=t_0}}}\end{array}$$

(5)

This calculation is valid for a limited period following the disturbance, before other factors alter the system dynamics. The frequency change, known as RoCoF, can be estimated through consecutive frequency measurements and calculating the slope using:

$$\begin{array}{c}\hfill {\displaystyle \frac{d{f}_i}{dt}}{|}_{t=t_0}\cong {\displaystyle \frac{f_i\left(t_0^{+}\right)-f_i\left(t_0^{-}\right)}{t_0^{+}-t_0^{-}}}\end{array}$$

(6)

where $f_i\left(t_0^{+}\right)$ and $f_i\left(t_0^{-}\right)$ are the frequency values measured immediately after and before the instant $t_0$, respectively.

1.4.2. Synthetic Inertia

BESS systems do not inherently provide inertial response. To address this limitation, control loops are implemented that link grid frequency to the active power delivered by the device, thereby enabling a response to disturbances. According to [52], there are two main strategies for implementing inertia: continuous RoCoF control and single-action RoCoF control. Continuous control uses instantaneous RoCoF measurements, allowing for greater adaptability, although it requires advanced filters to avoid amplifying noise introduced by differentiating the frequency. On the other hand, single-action control is simpler and more predictable, but less adaptable to dynamic changes [53]. After determining the frequency, its time derivative should be filtered before being multiplied by a gain constant known as the synthetic inertia constant Equation (7):

$$\Delta p=2H_{syn}·{\displaystyle \frac{d{f}_{sys}}{dt}}$$

(7)

where $\Delta p$ is the active power injected by the BESS, $H_{syn}$ is the synthetic inertia constant, and $f_{sys}$ is the system frequency.

Inertial energy can come from different sources, including the DC-link capacitor [54], BESS, or the kinetic energy stored in rotating components of wind turbines [55]. Figure 2 illustrates a simplified diagram showing how inertial control can be implemented in BESS devices. P* represents the power setpoint corresponding to the value delivered by the BESS when operating in steady-state conditions. In turn, P denotes the total power supplied, which includes both the power used for inertia emulation and the power specified by the setpoint.

Once the strategies for implementing synthetic inertia have been identified, the following section describes the proposed BESS model with inertia emulation capability.

1.5. Battery Energy Storage Systems

Figure 3 presents the BESS system architecture used in this analysis. It comprises a battery, a charge controller that ensures charging and discharging remain within defined boundaries, and measurement units tasked with tracking key electrical variables such as voltage, real and reactive power, and frequency. At the core of the control scheme is a PQ controller, which governs the flow of real and reactive power to and from the BESS [43].

The regulation of active power is managed via the $I_{dref}$ signal, while $I_{qref}$ determines the reactive power. These references are transmitted to a PWM-based power converter through the charge controller, which facilitates the power exchange in accordance with the PQ controller’s commands.

The control system also incorporates a frequency control loop, designed to modify the active power reference delivered to the PQ controller in response to frequency deviations in the grid and a preset droop characteristic. This frequency regulation mechanism is depicted in Figure 2. For the purposes of this work, the battery model assumes that its output voltage is a function of its SoC, internal resistance, and nominal capacity (Cbat). With battery capacity treated as a constant, the model follows a standard equation relating terminal voltage to SoC and battery current [43].

$$V_t=[SoC{V}_{Max}+(1-SoC)V_{Min}]-I{R}_i$$

(8)

where $V_t$ represents the terminal voltage of the battery, while $SoC$ denotes the State of Charge. The variable I corresponds to the battery current, and $R_i$ is the internal resistance. The maximum voltage, $V_{Max}$, indicates the voltage level when the battery is fully charged, whereas $V_{Min}$ refers to the voltage when the battery is fully discharged.

Figure 3 illustrates the control architecture of a BESS, designed to regulate the injection of active and reactive power, as well as to participate in frequency control of an electrical grid. The system begins with the measurement of key electrical variables such as AC voltage (AC Voltage Measurement), active and reactive power (PQ Measurement), and system frequency (Frequency Measurement). The measured frequency feeds the frequency control block, which compares the measured frequency with a reference and generates an active power adjustment signal ($d{P}_{ref}$). This signal, along with the voltage and power measurements, is processed by the power controller (PQ Control), which calculates the required active ($I_{dref}$) and reactive ($I_{qref}$) current references for the operation of the BESS.

Simultaneously, the battery model provides internal information about the storage system, including cell voltage ($V_{cell}$), cell current ($I_{cell}$), and state of charge (SOC). These parameters are used by the charge controller (Charge Controller), which integrates the current references and the battery conditions to generate efficient operating commands. Finally, these references are sent to the PWM converter, which regulates the BESS energy output to the electrical grid.

The diagram in Figure 4 presents the control scheme designed to emulate inertia in a BESS, contributing to frequency support in the electrical grid. The system receives the measured frequency signal $Frq$ as input, from which the time derivative $dF/dt$ is calculated using a differentiator block weighted by a gain K. This signal represents the RoCoF, a critical variable under contingency conditions. To mitigate the effect of potential high-frequency noise, the derivative signal is processed through a first-order filter with gain $K_1$ and time constant T, thereby obtaining the signal $dfilter$, which provides a smoothed estimate of the RoCoF.

The output of the filter is subsequently amplified by a gain $K_g$, generating a proportional signal that represents the synthetic inertial response power to be delivered by the BESS. In parallel, the measured frequency signal is also used to calculate the deviation from its nominal value, scaled by a gain $K_m$, enabling a control action proportional to the frequency error. Both signals—the one corresponding to the RoCoF and the one for frequency error—are combined along with a compensation constant $K_c$, ultimately generating the active power reference signal $P_{ref}$. This reference is used to control the power that the BESS must inject or absorb, thereby emulating the effect of inertia. The gains have been set manually, and their values are presented in

Table 2. Gains of the inertial control module.

Gain	Name	Parameter
$K_s$	Derivative gain	1
$K_f$	Filter gain	12
$T_f$	Filter time constant (seconds)	20
$K_m$	Frequency gain	1
$K_c$	External gain	1
$K_g$	Overall gain	−1

.

As the battery supplies energy to the grid, the SoC value decreases. The SoC under discharge conditions can be estimated using Equation (9):

$$So{C}_t=So{C}_{t-1}-{\int }_0^t{\displaystyle \frac{I}{C_{bat}}}dt$$

(9)

where $So{C}_t$ is the state of charge of the battery at time t, $So{C}_{t-1}$ is the initial state of charge expressed as a percentage, I is the measured charge/discharge current in amperes (A), t is the time measured in seconds (s), and $C_{bat}$ is the battery capacity in ampere-hours (Ah).

With the BESS model defined, the next step is to structure the optimization methodology that will enable the assessment of its optimal placement and sizing within the power system.

2. Methodology

The process begins with modeling the key components of the electric power system, including the excitation system, speed governor, generator dynamics, BESS units, and the characteristics of transmission lines and loads.

Following this, an optimization problem is defined with the main goal of minimizing the total installed power of the BESS units ($P_{BES{S}_i}$), while also identifying their optimal locations within the network. The problem formulation incorporates essential operational constraints such as frequency Nadir and Zenith, RoCoF, and steady-state frequency requirements. Given its nonlinear and non-convex characteristics, the problem is tackled using heuristic optimization techniques.

This study employs two optimization algorithms: the Particle Swarm Optimization (PSO) algorithm and the Genetic Algorithm (GA). The methodology proposed for this study is structured into four stages:

Stage 1: Power System Modeling

In the first stage, the main components of the electric power system are modeled, including:

• Generator models and their dynamics.
• Excitation systems (AVR) and speed governors (governor models).
• Load and transmission line models.
• BESS.

Stage 2: Formulation of the Optimization Problem

In this stage, an optimization problem is formulated with the objective of minimizing the installed BESS power in the network while complying with the following frequency constraints:

• Nadir: Minimum frequency value reached after an event.
• Zenith: Maximum frequency value reached after an event.
• Steady-State Frequency: Ensures that the frequency reaches a non-critical operating level, from which secondary and tertiary control actions can restore the nominal operating value.

Stage 3: Solution of the Optimization Problem

To solve the problem, two heuristic algorithms are employed:

• Particle Swarm Optimization (PSO) algorithm.
• Genetic Algorithm (GA).

Both algorithms were selected for their ability to address complex and nonlinear problems. In addition, specific modifications were made to handle continuous variables (BESS sizes) and discrete variables (BESS locations).

Stage 4: Results and Analysis

In this stage, the obtained results are analyzed to identify the algorithm with the best performance. Based on this analysis, the optimal locations and sizes of the BESS units that maximize system frequency stability following disturbances are determined. These results enable the proposal of practical configurations for implementing BESS in the power system.

Stage 5: Implementation

The GA and PSO algorithms were programmed and executed in Python 3.9, enabling efficient and reproducible simulations, while the power system modeling and electrical simulations were carried out in PowerFactory DigSILENT.

2.1. Iterative Optimization Scheme

2.1.1. Python–PowerFactory Data Exchange

The interaction is established through the PowerFactory API, which enables direct invocation of network model objects from a Python script.

• Python generates the decision variables.
• These variables are transmitted to PowerFactory via COM/DIgSILENT-Python API calls, where the parameters of the system elements are updated.
• PowerFactory executes the power flow or dynamic simulation and returns metrics (minimum frequency, RoCoF, losses, etc.), which are received by Python to feed the objective function and update the solution population of the optimization algorithm.

2.1.2. Synchronization in Iterative Optimization

The cycle follows a master–slave logic:

• Python (master): selects the candidate parameter set.
• PowerFactory (slave): runs the simulation with the specified parameters.
• Python: waits for the execution to complete before proceeding to the next iteration.

Synchronization is managed by blocking execution in Python until PowerFactory returns results, ensuring that there is no overlap of simulations or inconsistent readings of intermediate data. This is critical for evolutionary algorithms, where each individual requires a complete evaluation before proceeding to the next generation.

2.1.3. Error Handling

Since co-simulation processes may fail (due to numerical ill-conditioning, model instability, or API errors), exception handling routines are integrated into Python:

• If PowerFactory does not converge or returns an error, Python logs the failure and assigns a penalized value to the objective function (penalty technique).

The proposed methodology is implemented within the framework of an optimization problem, whose development is detailed in the following section.

3. Optimal Placement and Sizing of BESS

The mathematical modeling for the optimal placement and sizing of BESS aims to minimize the total power supplied by the BESS units while determining the most strategic locations within the power system. This process is carried out under a set of fundamental technical and operational constraints, including compliance with the frequency Nadir, minimum and maximum size limits of the BESS and steady-state frequency. These constraints ensure that the system operates in a stable and efficient manner while optimizing BESS integration into the grid to enhance the reliability and stability of the power system.

3.1. Mathematical Model

The objective of the model is to minimize the total power supplied by the BESS units while identifying the optimal locations and fulfilling the necessary operational constraints to ensure the stability and reliability of the power system.

In the model, the size of the BESS to be installed at each bus in the power system is denoted as $BES{S}_i$ and is expressed in megawatts (MW). Each bus considered for BESS installation is identified within the range of possible locations, from $Bu{s}_1$ to $Bu{s}_N$. The size of the BESS at each bus is determined according to technical constraints, including the minimum and maximum power limits for each system and the total sum of the installed BESS units, which must not exceed the allowed penetration limit, $BES{S}_{limit}$.

The RoCoF and the steady-state frequency are considered to ensure the dynamic stability of the system, meeting established limits such as the allowable RoCoF range (±1.5 Hz/s in a 60 Hz system, equivalent to 0.0025 p.u./s). Likewise, the state of charge (SoC) of the batteries must be maintained within defined limits, between $So{C}_{Min}$ and $So{C}_{Max}$, to extend their lifespan and ensure efficient operation.

3.1.1. Objective Function

The objective function is defined as follows:

$$min\sum _{i=1}^N{P}_{BES{S}_i}$$

(10)

where $P_{BES{S}_i}$ denotes the power supplied by the BESS unit installed at bus i, and N is the total number of buses in the system.

3.1.2. Constraints

• Frequency Nadir Constraint:

  $$f_{nadir}\ge f_{min}$$

  (11)

  in which $f_{nadir}$ represents the minimum frequency value reached after a disturbance, and $f_{min}$ is the acceptable lower limit.
• Frequency Zenith Constraint:

  $$f_{max}\ge f_{Zenith}$$

  (12)

  where $f_{Zenith}$ is the maximum frequency value allowed after a disturbance, and $f_{max}$ is the acceptable upper limit.
• Minimum and maximum size constraint of the BESS:

  $$P_{BES{S}_{min}}\le P_{BES{S}_i}\le P_{BES{S}_{max}}$$

  (13)

  where $P_{BES{S}_{min}}$ and $P_{BES{S}_{max}}$ represent the minimum and maximum size limits of the BESS system.
• Steady-state frequency constraint:

  $$f_{ss}=f_{nominal}$$

  (14)

  where $f_{ss}$ is the steady-state frequency and $f_{nominal}$ is the nominal system frequency.

The objective function in Equation (10) was formulated under the assumption that the BESS power injection is linearly proportional to the synthetic inertia control action, neglecting converter and storage losses. The optimization considers only the total installed power as a proxy for investment cost, assuming uniform cost per MW. Moreover, the system is modeled as balanced and lossless in steady state, and the dynamic response is evaluated solely through frequency indicators (Nadir, Zenith, RoCoF, and steady-state frequency), disregarding higher-order electromagnetic effects. These simplifications allow the problem to be tractable using heuristic algorithms while preserving the essential dynamics of frequency stability

3.2. Optimization Algorithms

The optimal placement and sizing of Battery Energy Storage Systems (BESS) in power networks constitutes a mixed-integer nonlinear problem. It combines discrete decisions (location of candidate nodes, number of units) with continuous variables (storage capacity), subject to non-convex constraints associated with frequency stability and power limits. In this context, exact methods such as Branch-and-Bound or mixed-integer programming become impractical, as complexity grows exponentially and convergence may become trapped in infeasible solutions for large-scale systems.

Evolutionary algorithms such as Genetic Algorithm (GA) and Particle Swarm Optimization (PSO) offer specific advantages:

• GA is robust for handling discrete and binary variables (e.g., selecting installation nodes), thanks to its chromosomal encoding and crossover/mutation operators, which enable the exploration of spatial combinations without requiring gradients or continuity in the objective functions.
• PSO is more efficient in exploring continuous spaces (e.g., energy and power sizing), with fast convergence toward promising regions, making it suitable for tuning capacity magnitudes under the system’s dynamic constraints.
• Both algorithms tolerate nonlinearities, non-differentiable functions, and multimodal search spaces—features inherent to the BESS problem when aspects such as frequency control, investment costs, and dynamic performance are considered.

Compared to alternatives such as simulated annealing or ant colony optimization, GA and PSO exhibit a better balance between global diversification and local exploitation, and their implementation is more straightforward in co-simulation environments (Python–PowerFactory). Furthermore, numerous reports in the literature validate their effectiveness in electrical planning problems, supporting their selection over more recent hybrid methods which, although promising, still lack maturity and robustness in large-scale applications.

Nature-inspired optimization algorithms, such as the GA and PSO, are techniques inspired by biological processes that aim to solve complex optimization problems [56] through approximations and/or suboptimal solutions. In this work, GA and PSO are employed to address the problem of BESS placement and sizing to improve frequency stability in power systems, as described by Equations (1)–(7).

The selection of the Particle Swarm Optimization (PSO) and Genetic Algorithm (GA) methods is aligned with the specific characteristics of the optimization problem under study, which combines discrete variables (BESS unit locations) and continuous variables (power sizing), and exhibits highly nonlinear and non-convex behavior due to the dynamic constraints associated with system frequency stability. Classical deterministic approaches—such as linear or quadratic programming or gradient-based algorithms—are unsuitable in this context, as they require continuous, differentiable, or convex objective functions, conditions that are not met in the Python–PowerFactory co-simulation used in this work.

In this regard, PSO and GA provide complementary advantages. GA is particularly well suited for handling search spaces with discrete components, owing to its chromosomal encoding and crossover and mutation operators, which enable efficient exploration of spatial combinations of candidate buses without relying on gradient-based information. This makes GA a robust tool for identifying BESS placement configurations in large-scale systems. Conversely, PSO exhibits strong convergence properties in problems involving continuous variables and relatively bounded optimal regions, allowing precise tuning of installed power capacities while satisfying the system’s dynamic constraints. Its update mechanism, based on the individual and collective experience of the particles, supports efficient exploration of high-dimensional search spaces.

Both algorithms also demonstrate tolerance to noisy or discontinuous objective functions, a particularly relevant aspect in this study since each fitness evaluation depends on a full dynamic simulation in PowerFactory, where numerical failures, measurement discontinuities, and variability associated with time integration may occur. Their ability to operate effectively under these conditions, together with their proven applicability in numerous studies on power system planning and stability, supports their selection as the main optimization techniques for this work.

3.2.1. Genetic Algorithm (GA)

Genetic algorithms (GAs) are a class of metaheuristic optimizers inspired by Darwinian evolution. They reproduce the principle of natural selection, whereby the most “fit” members of a population are more likely to pass their traits to subsequent generations. The search begins with an initial population of potential solutions (each encoded as a chromosome (i.e., a solution vector)) and iteratively evolves this population to determine the optimal sizing and placement of M-SSSC devices.

Figure 5 displays the flowchart of the GA implemented in this study. The algorithm begins by randomly generating an initial population, ensuring that the values of the decision variables fall within predefined limits. Each individual in this population is then assessed through a fitness evaluation, where the objective function is computed. Following this, a tournament selection method is applied: a small group of individuals is randomly chosen, and the one with the highest fitness score is selected. These selection rounds are performed in pairs, with the selected individuals advancing to the crossover phase of the algorithm.

During this phase, the selected individuals undergo crossover, where genetic material is exchanged at randomly chosen points to generate a new set of candidate solutions, or offspring. These offspring are then subject to mutation, which involves introducing random alterations with a predefined probability. This step is essential to enhance diversity in the population and avoid premature convergence to local optima. Each mutation respects the predefined limits of the variables to ensure the resulting solutions remain valid. After crossover and mutation, a selection process retains the most fit individuals from both the parent and offspring pools, preserving a fixed population size across generations. The algorithm continues iterating until the predefined number of generations is reached.

Genetic Algorithms have demonstrated strong performance across a wide range of electrical engineering applications. These include vulnerability analysis [57], protection system coordination [58], system expansion planning [59], and the design of Under-Frequency Load Shedding (UFLS) strategies [60]. In addition, numerous studies, such as [61,62], have highlighted the efficacy of GAs in determining the optimal placement and sizing of FACTS devices.

3.2.2. Particle Swarm Optimization (PSO)

PSO is a stochastic, population-based optimization technique introduced in [63], drawing inspiration from the coordinated movement patterns observed in bird flocks and fish schools. In contrast to GAs, PSO does not utilize crossover or mutation operations. Instead, it relies on the motion of particles—each symbolizing a potential solution—within an n-dimensional search space, where their behavior is governed by rules that dictate changes in position and velocity. The operational flow of the PSO algorithm applied in this study is illustrated in Figure 6.

The algorithm initializes a swarm of particles randomly scattered across the search domain, each with associated vectors for position and velocity. As the algorithm iterates, particles update their trajectories by considering two key references: the best solution each particle has encountered individually (personal best) and the best-known solution achieved by the entire swarm (global best).

The mathematical formulations for updating particle velocities and positions are provided in Equations (15) and (16), as detailed in [64]. PSO has demonstrated its versatility and effectiveness across a broad range of electrical engineering challenges, including control systems [65], demand-side management [66], and the optimal siting and sizing of FACTS devices [67], among others.

$$\overrightarrow{v_i}(t+1)=\omega \left(t\right)\overrightarrow{v_i}\left(t\right)+c_1{r}_1[{\overrightarrow{x}}_{pBes{t}_i}-x_i\left(t\right)]+c_2{r}_2[{\overrightarrow{x}}_{gBest}-{\overrightarrow{x}}_i\left(t\right)]$$

(15)

$$x_i(t+1)=x_i\left(t\right)+v_i(t+1)$$

(16)

In this case, t denotes the iteration; $w\left(t\right)$ is the inertia weight; $\overrightarrow{v_i}$ is the velocity vector of the i-th particle; $\overrightarrow{x}i$ is the position vector of the i-th particle; $\overrightarrow{x}gBest$ is the global best historical position of the entire swarm; $\overrightarrow{x}pBesti$ is the personal best historical position of particle i; $c_1$ and $c_2$ are the personal and global learning coefficients, respectively, while $r_1$ and $r_2$ are random numbers uniformly distributed in the range [0, 1] [63].

3.3. Co-Simulation Framework

The following are the steps of the flowcharts representing the optimization process in Python using GA and PSO, along with the electrical simulations in PowerFactory, to evaluate the optimal placement and sizing of BESS systems in electric power systems.

3.3.1. GA Co-Simulation

The Figure 7 presents the flowchart of the optimization process for the location and sizing of BESS systems, integrating a genetic algorithm implemented in Python with electrical simulations performed in PowerFactory.

• Step 1: The vector $X[Ni,P_{BESS}]$ is defined to establish the decision variables, where $Ni$ represents the location of the BESS and $P_{BESS}$ represents the power assigned to the BESS.
• Step 2: The vectors $X_{min}\left[\right]$ and $X_{max}\left[\right]$ are defined, which determine the lower and upper bounds for each variable in the decision vector.
• Step 3: An initial population of solutions (X vectors) is generated that complies with the established limits.
• Step 4: Each generated solution ($X[Ni,P_{BESS}]$) is sent to PowerFactory for evaluation through electrical simulations.
• Step 5: A steady-state simulation is run to establish the initial conditions of the system.
• Step 6: The BESS units are inserted into the system with their respective power ratings and locations according to the X vector.
• Step 7: A dynamic simulation of the system is performed to observe the frequency behavior after a disturbance.
• Step 8: Frequency parameter review is carried out, extracting the values of: Nadir (minimum frequency), Zenith (maximum frequency), and steady-state value.
• Step 9: It is verified whether the parameters comply with technical and regulatory limits.
• Step 10: Are the constraints satisfied?
  Yes → the solution is returned without penalty.
  No → the objective function is penalized.
• Step 11: Objective Function Evaluation (Fitness), Each individual in the population is evaluated based on its performance, considering frequency metrics and any applied penalties.
• Step 12: Individuals are selected for reproduction based on their fitness (best-performing solutions).
• Step 13: The vectors of selected parents are combined to generate offspring (new solutions).
• Step 14: Some variables in the offspring are randomly altered to promote diversity.
• Step 15: A new population is formed with the generated individuals.
• Step 16: It is checked whether a termination condition has been met.
  Yes → proceed to step 17
  No → return to step 4
• Step 17: End, if the stopping criterion is met, the process concludes and the best solution found is selected.

3.3.2. Cosimulacion PSO

The Figure 8 shows the flowchart of the optimization process for the location and sizing of BESS systems, based on a PSO optimization algorithm implemented in Python and coupled via co-simulation with PowerFactory for electrical evaluation.

• Step 1: The vector $X[Ni,P_{BESS}]$ is defined to establish the decision variables, where $Ni$ represents the location of the BESS and $P_{BESS}$ represents the power assigned to the BESS.
• Step 2: The vectors $X_{min}\left[\right]$ and $X_{max}\left[\right]$ are defined, which determine the lower and upper bounds for each variable in the decision vector.
• Step 3: An initial population of solutions (X vectors) is generated that complies with the established limits.
• Step 4: Each generated solution ($X[Ni,P_{BESS}]$) is sent to PowerFactory for evaluation through electrical simulations.
• Step 5: A steady-state simulation is run to establish the initial conditions of the system.
• Step 6: The BESS units are inserted into the system with their respective power ratings and locations according to the X vector.
• Step 7: A dynamic simulation of the system is performed to observe the frequency behavior after a disturbance.
• Step 8: Frequency parameters are reviewed, extracting the values of: Nadir (minimum frequency), Zenith (maximum frequency), and steady-state value.
• Step 9: It is verified whether the parameters meet technical and regulatory limits.
• Step 10: Are the constraints satisfied?
  Yes → the solution is returned without penalty.
  No → the objective function is penalized.
• Step 11: Objective Function Evaluation (Fitness). Each individual in the population is evaluated based on its performance, considering frequency metrics and any applied penalties.
• Step 12: The velocity and position of each particle are updated according to the rules of the algorithm used.
• Step 13: A new population is built with the updated solutions for the next iteration.
• Step 14: It is verified whether the stopping criterion has been met.
  Yes → the process ends and the best solution is obtained.
  No → the cycle repeats from step 4.
• Step 15: The process ends.

4. Results

4.1. Case Studies

For the study, three scenarios are proposed in which the system inertia corresponds to 100%, 50%, and 25%, respectively. The event to which the network is subjected corresponds to the disconnection of the largest generator (generator 06 with 650 MW), assuming that under this fault, the frequency experiences the worst operational case. In addition, the frequency behavior is evaluated under three conditions: without the connection or contribution of BESS systems, with the BESS system configured by the GA, and finally, when the BESS system operates with the configuration optimized by the PSO.

4.2. Analysis of the IEEE 39-Bus System

Table 3. IEEE 39-Bus System lines.

Name	Terminal i	Terminal j	R1 ($\Omega$)	X1 ($\Omega$)	Length (km)
Line 01–02	Bus 01	Bus 02	4.165876	48.91928	163.0643
Line 01–39	Bus 01	Bus 39	1.19025	29.75625	99.1875
Line 02–03	Bus 02	Bus 03	1.547325	17.97277	59.90925
Line 02–25	Bus 02	Bus 25	8.33175	10.23615	34.1205
Line 03–04	Bus 03	Bus 04	1.547325	25.35233	84.50775
Line 03–18	Bus 03	Bus 18	1.309275	15.83033	52.76775
Line 04–05	Bus 04	Bus 05	0.9522001	15.2352	50.784
Line 04–14	Bus 04	Bus 14	0.9521999	15.35423	51.18075
Line 05–06	Bus 05	Bus 06	0.23805	3.09465	10.3155
Line 05–08	Bus 05	Bus 08	0.9521999	13.3308	44.436
Line 06–07	Bus 06	Bus 07	0.7141501	10.9503	36.501
Line 06–11	Bus 06	Bus 11	0.8331751	9.760051	32.5335
Line 07–08	Bus 07	Bus 08	0.4761001	5.47515	18.2505
Line 08–09	Bus 08	Bus 09	2.737574	43.20608	144.0202
Line 09–39	Bus 09	Bus 39	1.19025	29.75625	99.1875
Line 10–11	Bus 10	Bus 11	0.4761001	5.118075	17.06025
Line 10–13	Bus 10	Bus 13	0.4761001	5.118075	17.06025
Line 13–14	Bus 13	Bus 14	1.071225	12.02153	40.07175
Line 14–15	Bus 14	Bus 15	2.14245	25.82843	86.09475
Line 15–16	Bus 15	Bus 16	1.071225	11.18835	37.2945
Line 16–17	Bus 16	Bus 17	0.8331751	10.59323	35.31075
Line 16–19	Bus 16	Bus 19	1.9044	23.20988	77.36625
Line 16–21	Bus 16	Bus 21	0.9522001	16.06837	53.56125
Line 16–24	Bus 16	Bus 24	0.3570751	7.022476	23.40825
Line 17–18	Bus 17	Bus 18	0.8331751	9.760051	32.5335
Line 17–27	Bus 17	Bus 27	1.547325	20.59133	68.63775
Line 21–22	Bus 21	Bus 22	0.9522001	16.6635	55.545
Line 22–23	Bus 22	Bus 23	0.7141501	11.4264	38.088
Line 23–24	Bus 23	Bus 24	2.61855	41.65875	138.8625
Line 25–26	Bus 25	Bus 26	3.8088	38.44508	128.1503
Line 26–27	Bus 26	Bus 27	1.66635	17.49668	58.32225
Line 26–28	Bus 26	Bus 28	5.118075	56.41785	188.0595
Line 26–29	Bus 26	Bus 29	6.784425	74.39063	247.9688
Line 28–29	Bus 28	Bus 29	1.66635	17.97277	59.90925

summarizes the electrical properties of the lines in the IEEE 39-Bus system, a more complex test system than the previous one. Key data such as resistance and reactance in ohms, as well as the length of each line, are included. This information is essential for detailed modeling and for simulating load flow and stability.

Table 4. IEEE 39-Bus System Transformers.

Name	Rated Power (MVA)	HV	Vnom AT (kV)	/	Vnom BT (kV)	LV	Short-Circuit Voltage (%)
Trf 02–30 YNy0	1000	YN	345	/	16.5	Y	18.1
Trf 06–31 YNy0	700	YN	345	/	16.5	Y	17.5
Trf 10–32 YNy0	800	YN	345	/	16.5	Y	16.0
Trf 11–12 YNy0	300	YN	345	/	138	Y	13.06
Trf 13–12 YNy0	300	YN	345	/	138	Y	13.06
Trf 19–20 YNy0	1000	YN	345	/	230	Y	13.82
Trf 19–33 YNy0	800	YN	345	/	16.5	Y	11.37
Trf 20–34 YNy0	300	YN	230	/	16.5	Y	10.81
Trf 22–35 YNy0	800	YN	345	/	16.5	Y	11.44
Trf 23–36 YNy0	700	YN	345	/	16.5	Y	19.04
Trf 25–37 YNy0	700	YN	345	/	16.5	Y	16.25
Trf 29–38 YNy0	1000	YN	345	/	16.5	Y	15.62

lists the transformers in the IEEE 39-Bus system, indicating their voltage levels (HV/LV), vector group configuration, and short-circuit impedance. These data are relevant for assessing power transfer between voltage levels and the system’s response to disturbances.

Table 5. Results for different inertia levels and BESS configurations.

Case	Inertia (%)	${\mathit{P}}_{\mathbf{BESS}}$-GA	${\mathit{P}}_{\mathbf{BESS}}$-PSO	Nadir-PSO	Nadir-GA	Zenith-PSO	Zenith-GA	Fss-PSO	Fss-GA
1	100	287.4498	285.7925	59.0013	59.0071	59.4077	59.4076	59.4015	59.4041
		No	No	57.9169	-	59.0997	-	59.0997	-
2	50	285.5669	277.1074	58.7020	58.6790	59.4142	59.4122	59.4130	59.4120
		No	No	57.4833	-	59.0631	-	59.0503	-
3	25	307.4428	296.0724	58.4001	58.4049	59.4752	59.4807	59.4741	59.4768
		No	No	56.9821	-	59.0169	-	59.0112	-

presents the total installed BESS power, nadir, zenith, and steady-state frequency (Fss) values for each of the studied cases. As system inertia is reduced (from 100% to 25%), frequency stability indicators deteriorate, particularly the nadir and Fss in the absence of BESS. However, the integration of BESS using GA and PSO significantly enhances the system’s dynamic response. In all scenarios, PSO achieves performance that is comparable to or better than GA, while requiring less installed power, positioning it as a more efficient alternative. When comparing inertia levels with the corresponding BESS power requirements, it is observed that Case 3, which corresponds to 25% inertia, demands a higher BESS capacity to compensate for the 75% inertia reduction and maintain acceptable frequency parameters. As inertia is lost, the system loses its natural ability to resist frequency variations.

There is an inverse relationship between the system’s inertia level and the BESS power requirement: the lower the inertia, the greater the power that must be supplied by the BESS to keep the frequency within acceptable operating limits. However, in Case 2, the BESS power requirement is slightly lower than in the case with 100% inertia. This is because, although the system with 100% inertia offers greater resistance to frequency deviations, recovering from the nadir requires more power from the BESS.

The PSO algorithm exhibits the best performance, as shown in Table 5, providing a solution with lower power while satisfying all the constraints.

Table 6. Results of meta-heuristic techniques.

BUS	GA_25		PSO_25		GA_50		PSO_50		GA_100		PSO_100
	State	Power	State	Power	State	Power	State	Power	State	Power	State	Power
1	1	11.3818	1	50	0	0	0	0	0	0	1	15.9185
2	1	19.9126	1	3.6463	0	0	0	0	1	15.6194	0	0
3	0	0	0	0	0	0	1	42.0124	1	25.1281	0	0
4	0	0	1	0.1	1	11.0413	0	0	0	0	0	0
5	0	0	0	0	0	0	0	0	0	0	1	0.1
6	0	0	0	0	1	14.9399	0	0	0	0	0	0
7	0	0	1	0.1	0	0	1	50	0	0	0	0
8	0	0	0	0	1	21.6358	0	0	1	18.8687	1	50
9	0	0	0	0	0	0	1	2.0320	0	0	0	0
10	0	0	1	0.1	0	0	0	0	1	18.5199	1	0.1
11	0	0	1	0.1	0	0	0	0	1	5.9770	0	0
12	0	0	0	0	0	0	0	0	0	0	1	50
13	1	35.6697	0	0	0	0	0	0	0	0	0	0
14	1	36.7489	1	0.1	0	0	0	0	0	0	0	0
15	0	0	0	0	1	26.2278	0	0	0	0	1	0.3021
16	1	14.8526	0	0	1	21.5287	1	0.1	1	20.2508	1	0.1
17	1	34.9167	1	0.1	0	0	0	0	0	0	0	0
18	0	0	0	0	0	0	1	0.1	0	0	0	0
19	0	0	0	0	1	15.3355	1	0.5995	1	27.9435	1	0.1
20	0	0	0	0	1	28.1772	0	0	0	0	0	0
21	1	9.6743	0	0	0	0	0	0	0	0	0	0
22	0	0	0	0	1	13.5072	0	0	0	0	0	0
23	0	0	1	0.1	1	25.5809	0	0	1	19.3424	0	0
24	1	24.7332	0	0	1	14.0077	0	0	0	0	0	0
25	0	0	0	0	0	0	0	0	0	0	0	0
26	1	31.3633	1	41.4261	0	0	0	0	1	20.2934	1	0.4824
27	0	0	1	50	1	25.3828	1	11.7561	1	33.5153	0	0
28	0	0	1	0.1	1	19.2563	1	0.1	0	0	1	0.1
29	0	0	0	0	0	0	1	20.0354	1	25.7742	0	0
30	1	13.1060	1	0.1	0	0	0	0	0	0	0	0
31	0	0	1	50	1	11.6083	1	50	0	0	0	0
32	1	25.5333	0	0	0	0	0	0	1	22.6197	1	18.4893
33	1	29.9492	0	0	0	0	0	0	1	26.7232	0	0
34	1	19.6007	1	50	0	0	1	50	1	6.8735	1	0.1
35	0	0	0	0	0	0	0	0	0	0	1	50
36	0	0	1	0.1	0	0	1	0.6551	0	0	1	50
37	0	0	0	0	1	6.9716	1	49.7167	0	0	0	0
38	0	0	1	50	1	30.3653	0	0	0	0	1	50

presents the results of the BESS sizing and placement across the buses of the IEEE 39-Bus system. These results are also graphically illustrated in Figure 9. A comparative analysis of the optimization scenarios reveals that the PSO algorithm with 50% rotational inertia (PSO_50) is the most efficient, achieving the lowest total installed power (277.11 MW). It is followed by PSO_100 (285.79 MW) and GA_50 (285.57 MW). However, GA_25 shows the highest total BESS installation (307.44 MW), mainly due to the loss of system inertia. Although PSO_25 slightly improves performance compared to GA_25, it results in high power concentrations in certain buses (e.g., 50 MW at Bus 1). As the level of rotational inertia increases, the total installed power tends to decrease and the distribution becomes more balanced. Nevertheless, some areas still exhibit high concentration levels, such as Buses 35 and 38 in PSO_100.

With the reduction in inertia, the system exhibits a faster and less damped response to disturbances, resulting in a higher RoCoF and more pronounced nadir values. As shown in Figure 10, the frequency response for Case 1, which corresponds to 100% of the original rotational inertia, presents a lower nadir and a gentler rate of decline compared to Cases 2 and 3. Additionally, the solution provided by the PSO algorithm results in a lower nadir with 1.65 MW less BESS power. On the other hand, the case with the lowest BESS power requirement is Case 2, corresponding to 50% rotational inertia, as illustrated in Figure 11. In this case, the PSO-based solution achieves a difference of 8.46 MW and yields a better frequency response.

Case 2, shown in Figure 11, requires less BESS power because the level of inertia allows the BESS to provide virtual inertia without opposing the frequency change, as it does in Case 1. At the same time, it retains sufficient rotational inertia to avoid the high RoCoF observed in Case 3. On the other hand, Figure 12 shows the system behavior when only 25% of the original rotational inertia is available, resulting in a faster frequency response characterized by a higher RoCoF and a more pronounced nadir.

Figure 13 compares the evolution of the objective function for the PSO and GA algorithms. PSO exhibits a rapid decrease during the initial iterations, indicating an effective early exploration of the search space and quickly reaching lower values, although it later stabilizes and stops improving. GA, in contrast, reduces the objective function more slowly: it maintains higher values for a larger number of iterations and decreases gradually, reflecting a broader and more sustained exploration process. Ultimately, PSO reaches the lowest final value, while GA converges to a slightly higher one. Overall, PSO is faster but more prone to premature convergence, whereas GA is slower but more robust in global search.

5. Discussion

The validation of the proposed methodology was carried out through a systematic process combining model verification, consistency checks, and cross-validation of optimization results. Although the study primarily focuses on frequency stability enhancement, it was essential to ensure that the simulation framework and optimization routines produced reliable and reproducible outcomes.

5.1. Model Verification and Numerical Consistency

The dynamic model implemented in PowerFactory was verified by comparing the frequency response of the IEEE 39-bus system against reference studies available in the literature under equivalent inertia conditions. The base case (100% inertia without BESS) was used as a benchmark to confirm that the simulated frequency nadir and steady-state values matched those reported in the literatury within a tolerance of ±0.05 Hz. Furthermore, the co-simulation interface between Python and PowerFactory was validated by repeating identical runs to ensure deterministic results, revealing a maximum deviation below 0.2% between iterations.

5.2. Optimization Algorithm Validation

To assess the robustness of the optimization process, both GA and PSO were executed for multiple independent trials (20 runs per case) using distinct random seeds. The convergence curves demonstrated stable behavior and convergence within 50–60 generations for GA and 35–40 iterations for PSO, with standard deviations below 3% in total installed BESS power. This confirms the repeatability and numerical stability of both algorithms. Additionally, PSO consistently reached near-global optima with faster convergence, whereas GA exhibited higher exploration capacity, particularly for discrete placement variables.

5.3. Cross-Comparison and Sensitivity Analysis

A sensitivity analysis was conducted by varying the inertia constants and controller gains (Ks, Kf, Tf) by ±10% to evaluate the impact on frequency metrics. The results showed that frequency nadir and steady-state deviations remained within acceptable bounds, confirming the resilience of the optimization under parametric uncertainty. Likewise, the relative difference between GA and PSO solutions in total installed BESS power was consistently below 5%, validating the coherence of the results across distinct metaheuristic approaches.

5.4. Future Work

The present study does not explicitly consider voltage magnitude constraints, converter losses, or degradation effects associated with BESS cycling, which simplifies the formulation but may introduce small deviations in absolute performance metrics. Future work will integrate voltage regulation and reactive power control into the optimization framework, enabling a comprehensive multiobjective analysis that jointly addresses frequency and voltage stability.

5.5. Limitations and Implementation Challenges

Although the proposed methodology demonstrates promising results in terms of frequency stability enhancement through optimal BESS allocation and inertia emulation, several limitations should be considered when moving towards real-world applications. First, the study relies on the IEEE-39 bus test system, which provides valuable insights but cannot fully represent the operational complexity of large-scale or hybrid transmission networks. Second, the practical deployment of BESS is subject to regulatory frameworks, market incentives, and cost constraints that were not modeled in this work. Third, the optimization procedure requires detailed dynamic data and high computational resources, which may be challenging to obtain in real-time or in systems with incomplete datasets. Finally, the integration of BESS with existing control and protection schemes may face interoperability and cybersecurity challenges. Addressing these issues in future work will be key to ensuring the scalability and applicability of the proposed approach.

5.6. Practical Implementation

The proposed methodology can be practically implemented in real-world power systems by integrating the optimization and co-simulation framework into existing utility planning and operation tools. The practical deployment involves both the offline planning phase, where the optimal placement and sizing of BESS units are determined, and the online operational phase, where control strategies are applied in real time to emulate synthetic inertia.

5.6.1. Offline Planning Stage

In the planning stage, utilities or system operators can use historical frequency disturbance data and grid topology models (e.g., IEEE 39-bus or equivalent regional networks) to perform the optimization routine. The Python–PowerFactory co-simulation framework can be directly adapted to actual grid databases, allowing iterative evaluations under different inertia and contingency scenarios. The resulting optimal BESS locations and capacities provide a strategic guideline for investment planning, enabling a reduction in total installed storage power while maintaining adequate frequency stability margins.

5.6.2. Real-Time Operation and Control

In practice, once the BESS units are installed at the optimized buses, their control systems can be configured to execute the synthetic inertia emulation loop described in Figure 4. The control algorithm measures the instantaneous frequency and its rate of change (RoCoF), filters the signal, and dynamically adjusts the active power injection through a PQ converter. These actions can be embedded within existing energy management systems (EMS) or grid-forming inverter control software, ensuring seamless coordination with automatic generation control (AGC) and primary frequency response mechanisms.

5.6.3. Hardware and Communication Requirements

For implementation in a transmission or subtransmission network, BESS units must be equipped with:

A high-speed measurement interface capable of sampling frequency and RoCoF with a resolution of at least 50–100 ms;

A low-latency communication link between local controllers and the supervisory EMS to synchronize frequency response actions;

A standardized communication protocol (e.g., IEC 61850 or DNP3) to ensure interoperability with other protection and control systems.

5.6.4. Scalability and Integration Prospects

The methodology is scalable to large interconnected networks or microgrids by segmenting the system into operational zones and running the optimization independently for each zone. Moreover, the optimization framework can be extended to include investment cost functions, voltage regulation objectives, and degradation models to enhance techno-economic feasibility. Future integration with digital twins of the grid could enable continuous re-optimization in response to changes in renewable generation patterns or grid topology, enhancing adaptive grid resilience.

5.7. Theoretical–Practical Integration

While the theoretical formulation presented in Section 2, Section 3, Section 4, Section 5 and Section 6 establishes the mathematical foundation of the problem, its ultimate purpose is to provide a practical framework that engineers and system operators can apply to real networks. Therefore, it is essential to bridge the theoretical derivations with their engineering implications.

5.7.1. Physical Interpretation of the Mathematical Model

The equations describing inertia, frequency deviation, and synthetic inertia control (Equations (1)–(9)) are not intended as abstract mathematical constructs but as tools for quantifying the physical response of the grid to disturbances. Equation (3), for instance, expresses the RoCoF as a function of system inertia and contingency size, directly linking the mathematical derivative $df/dt$ to the observable rate at which generators decelerate after a loss of generation. Similarly, Equation (7) formalizes the synthetic inertia emulation mechanism, where the BESS injects power proportional to RoCoF—an engineering control action realizable through converter-based systems.

5.7.2. Engineering Meaning of the Optimization Problem

The optimization problem (Equations (10)–(13)) may appear as a pure mathematical minimization task; however, each component has direct operational meaning. Minimizing $\sum P_{BESSi}$ corresponds to reducing total installed power and cost, while the constraints on Nadir, Zenith, and steady-state frequency reflect compliance with reliability criteria defined by grid codes. Thus, the optimization framework provides a quantitative method for deciding where and how much storage to install to meet system-level frequency performance standards.

5.7.3. Bridging Theory and Practice

The theoretical development was intentionally complemented by simulation-based validation in PowerFactory, enabling engineers to observe how changes in model parameters translate into measurable system behavior. For example, varying the synthetic inertia gain $\left(Kg\right)$ produces a proportional change in frequency Nadir, illustrating how theoretical constants govern physical responses. This combined analytical–simulation approach ensures that the model remains both mathematically rigorous and operationally interpretable.

5.7.4. Engineering Relevance and Applicability

The methodology ultimately supports decision-making in grid operation and planning. Practitioners can use the derived equations to calibrate BESS controllers, estimate required synthetic inertia under reduced-inertia scenarios, and define capacity margins for frequency stability. In this way, the theoretical analysis forms the backbone of a practical engineering tool that bridges academic modeling and real-world implementation.

6. Conclusions

In this article, the impact on system frequency of the IEEE 39-Bus power network was evaluated, considering a multi-unit BESS scheme whose sizes and locations were selected using two optimization algorithms: Genetic Algorithm (GA) and Particle Swarm Optimization (PSO). The objective was to deliver synthetic inertia based on the system’s RoCoF. The test system was developed using the electrical system analysis tool DIgSILENT PowerFactory.

Three simulation scenarios were considered based on the system’s available rotational inertia. Case 1 corresponds to 100% of the original rotational inertia, Case 2 to 50%, and Case 3 to 25%. For all scenarios, the frequency behavior was analyzed by assessing the frequency nadir, zenith, and steady-state frequency.

With the integration of the optimization algorithms, a total of nine scenarios were evaluated, as shown in Figure 10, Figure 11 and Figure 12, including the cases where BESS units were not deployed. The general conclusions of this study are as follows:

The operation of the BESS scheme enables frequency to remain within acceptable limits during frequency events. The frequency curves exhibit improved nadirs compared to cases without BESS deployment. The inclusion of BESS is crucial in systems where rotational inertia decreases due to the integration of renewable energy sources that do not contribute inertia.

Regarding the performance of the GA and PSO algorithms, PSO achieved better nadir values with less installed BESS power, making it a more energy-efficient tool from the perspective of the power system. In all scenarios where the BESS size and location were optimized, a better frequency response was observed.