Tri-Level Adversarial Robust Optimization for Cyber–Physical–Economic Scheduling: Multi-Stage Defense Coordination and Risk–Reward Equilibrium in Smart Grids

Abstract

This study develops a tri-level adversarial robust optimization framework for cyber–physical scheduling in smart grids, addressing the intertwined challenges of coordinated cyberattacks, defensive resource allocation, and stochastic operational uncertainties. The upper level represents the attacker’s objective to maximize system disruption and conceal detection, the middle level models the defender’s optimization of detection and redundancy deployment under budgetary constraints, and the lower level performs economic dispatch given tampered data and uncertain renewable generation. The model integrates Distributionally Robust Optimization (DRO) based on a Wasserstein ambiguity set to safeguard against worst-case probability distributions, ensuring operational stability even under unobserved adversarial scenarios. A hierarchical reformulation using Karush–Kuhn–Tucker (KKT) conditions and Mixed-Integer Second-Order Cone Programming (MISOCP) transformation converts the nonconvex tri-level problem into a tractable bilevel surrogate solvable through alternating direction optimization. Numerical case studies on multi-node systems demonstrate that the proposed method reduces system loss by up to 36% compared to conventional stochastic scheduling, while maintaining 92% dispatch efficiency under high-severity attack scenarios. The results further reveal that adaptive defense allocation accelerates robustness convergence by over 50%, and that the risk–reward frontier stabilizes near a Pareto-optimal equilibrium between cost and resilience. This work provides a unified theoretical and computational foundation for adversarially resilient smart grid operation, bridging cyber-defense strategy, uncertainty quantification, and real-time economic scheduling into one coherent optimization paradigm.

1. Introduction

The digitalization of modern power systems has fundamentally reshaped the landscape of energy operation, transforming traditional physical networks into deeply integrated cyber–physical ecosystems. With the extensive deployment of advanced sensors, wide-area measurement systems, and automated controllers, today’s smart grids depend on the seamless interaction of data and energy flows. These interconnections enable real-time monitoring, distributed optimization, and market coordination but simultaneously expose the system to intricate cyber–physical risks [1,2]. False data injection, coordinated communication attacks, and control manipulation can distort the perception of grid states, mislead operational decisions, and propagate economic losses across layers of the system [3,4]. The resulting vulnerabilities are not isolated technical failures but emergent properties of the tight coupling between cyber information, physical operations, and economic dispatch mechanisms. Ensuring resilience in such an environment demands a paradigm that jointly addresses data integrity, physical reliability, and market efficiency under adversarial conditions [5,6].

The intellectual foundation of optimization for power system resilience has evolved through several distinct stages. Early formulations, built upon deterministic and robust optimization, focused primarily on security-constrained dispatch and contingency management [7,8]. These models assumed data veracity and treated uncertainty as an exogenous stochastic phenomenon—an approach sufficient for natural variability in demand or renewable generation but insufficient for malicious intervention. The emergence of false data injection attacks, as articulated in seminal work by Liu and colleagues, revealed a new class of threats capable of compromising state estimation without triggering alarms. Subsequent research demonstrated that such attacks could not only perturb measurement data but also manipulate market outcomes, dispatch decisions, and even frequency control through carefully structured deviations. The discovery marked a conceptual turning point: uncertainty in modern grids could no longer be modeled solely as randomness but had to include intentionality [9,10,11].

In parallel, cyber defense research developed increasingly sophisticated detection frameworks, ranging from statistical residual analysis to machine learning–based anomaly detection. Methods employing support vector machines, neural networks, and hidden Markov models enhanced sensitivity to deviations in measurement streams [1,12,13,14]. Yet, these approaches were often limited by data requirements, interpretability, and the lack of integration with operational or economic constraints. Resource allocation for defensive investment, though studied in robust control and information security domains, remained largely disconnected from physical dispatch models. Defense decisions were typically made independently of power flow or cost considerations, leaving open the challenge of how to jointly allocate detection resources and optimize grid operation in real time. The need for cross-domain coordination—linking cyber detection with physical control and market decisions—gradually became evident [15,16].

A growing body of research thus turned toward game-theoretic formulations to capture the strategic interactions among attackers, defenders, and system operators. Stackelberg and Nash game frameworks provided a natural mathematical language for such hierarchical interactions, where attackers aim to maximize disruption and defenders counteract within limited budgets. These formulations have illuminated fundamental insights about equilibrium behavior and decision coupling, but their implementation in large-scale, nonlinear power systems remains challenging. Most existing game-theoretic models simplify either the physical layer through linearized flows or the economic layer by omitting temporal and market coupling. The extension of these models into full-scale cyber–physical–economic scheduling remains relatively unexplored, despite its critical importance in an era when grid operations and energy markets are increasingly interdependent [17,18].

Concurrently, advances in distributionally robust optimization (DRO) have revolutionized the modeling of uncertainty in systems driven by empirical data. The Wasserstein metric, in particular, provides a principled way to characterize the distance between empirical and true probability distributions, yielding tractable formulations of worst-case expectation problems. This approach has found application in renewable integration, energy trading, and stochastic unit commitment, where it enhances robustness against forecast errors and sampling variability. However, its potential to capture strategic uncertainty—where distributions shift not by chance but through intelligent manipulation—has only begun to be recognized. Extending DRO into adversarial settings allows robustness not only to data perturbations but also to the intentional reshaping of data by malicious agents, creating a natural bridge between statistical robustness and game theory [19,20,21].

Robust optimization has been widely utilized in power system planning, renewable integration, and hybrid microgrid interconnection design, where it effectively mitigates natural uncertainty in load, generation variability, and converter operation. Prior studies—such as robust bi-directional converter–based interconnection planning for renewable-dominant microgrids—demonstrate how uncertainty-aware formulations enhance system flexibility and operational security. However, these approaches primarily address exogenous stochastic disturbances and do not consider strategic, adversarial uncertainty introduced by intelligent cyber attackers. In contrast, this work extends robust optimization into the cybersecurity domain by embedding attacker–defender interactions and adversarially induced distributional shifts within a unified tri-level framework, thereby bridging the gap between classical robust planning and cyber–physical operational resilience.

Recent methodological progress in hierarchical optimization has paved the way for more sophisticated models that integrate cyber, physical, and economic decisions. Techniques such as mathematical programs with equilibrium constraints (MPEC), Benders decomposition, and the alternating direction method of multipliers (ADMM) have enabled tractable reformulations of multi-layer optimization problems. By embedding KKT conditions or using decomposition-based coordination, these approaches allow the representation of nested optimization processes—an essential feature for modeling multi-actor systems such as smart grids. Despite these advances, most applications to date have focused on market clearing, distributed energy coordination, or system restoration, rather than on adversarial scheduling where intelligent attackers and constrained defenders directly influence the dispatch layer. The absence of such integrated formulations underscores the need for a unified perspective that captures both strategic intent and physical feasibility [22,23,24].

Recent advances in stochastic programming have provided powerful tools for planning and operating multi-energy microgrids under uncertainty, including models that combine risk-averse capacity planning with peer-to-peer trading and bargaining-based coordination, as well as distributed optimization schemes for network-constrained energy trading among multiple microgrids under uncertain conditions. These frameworks effectively capture scenario-based variability in demand, renewable generation, and market prices, and they offer sophisticated mechanisms for sharing risk and coordinating local decisions through game-theoretic or distributed strategies. However, they typically rely on predefined probability distributions and exogenous scenario sets, and they focus on natural uncertainty rather than intentional cyber-induced disruptions. In contrast, the distributionally robust framework proposed in this work explicitly accounts for ambiguity in the underlying probability distributions and integrates adversarial behavior, defensive resource allocation, and economic dispatch within a unified cyber–physical–economic structure. By modeling both distributional ambiguity and strategic cyber manipulation, our approach complements recent stochastic programming studies and extends their scope toward adversarially robust operation in modern energy systems.

Against this backdrop, the present work develops a tri-level adversarial robust optimization model that fuses game-theoretic reasoning, distributional robustness, and economic scheduling within a single unified framework. At its conceptual core, the model consists of three interactive layers: an upper-level attacker who seeks to maximize system disruption while minimizing detection probability; a middle-level defender who allocates detection and redundancy resources under budget constraints; and a lower-level dispatcher who minimizes operating cost and risk under potentially falsified information. The integration of these layers transforms conventional dispatch into a dynamic game of strategy, uncertainty, and optimization. To achieve tractability, the tri-level structure is reformulated as a single-level MPEC through the inclusion of KKT conditions for the dispatch layer and complementarity constraints for defensive decisions. The resulting structure, although inherently nonconvex, is approximated through a mixed-integer second-order cone programming (MISOCP) relaxation, which allows efficient computation while preserving theoretical rigor. The inclusion of Wasserstein-based DRO further endows the model with resilience against unseen or probabilistically rare adversarial scenarios, protecting against distributional shifts in attack strategies and stochastic system variables.

The methodological framework is complemented by a solution procedure grounded in augmented Lagrangian principles and ADMM coordination. Through alternating updates of primal and dual variables, the algorithm achieves consistent convergence across heterogeneous decision spaces—continuous for dispatch, discrete for commitment, and bounded for detection configuration. The proximal regularization embedded in the iterative process stabilizes the interaction between cyber and physical layers, preventing oscillations and ensuring convergence toward a saddle-point equilibrium. This approach not only yields mathematical tractability but also aligns conceptually with decentralized decision-making in modern energy systems, where multiple agents optimize local objectives while maintaining global coordination. Within the broad literature on power system optimization, the contribution of this work lies in its synthesis of three traditionally distinct research directions: adversarial game modeling, distributionally robust uncertainty management, and large-scale hierarchical optimization. By merging these elements, the proposed framework moves beyond the dichotomy of purely stochastic versus purely adversarial modeling and establishes a hybrid paradigm capable of anticipating both statistical uncertainty and strategic manipulation. Moreover, the explicit inclusion of defense investment and detection resource allocation introduces a quantitative dimension to cybersecurity planning within operational scheduling, a component often overlooked in prior research. The use of MISOCP reformulation bridges the gap between theoretical intractability and computational feasibility, while the ADMM-based coordination mechanism reflects real-world decision hierarchies and computational decentralization. Overall, this integrated perspective reconceptualizes smart grid resilience as a dynamic equilibrium between intelligent attackers, resource-constrained defenders, and cost-minimizing operators. It unifies theoretical advances from optimization, control, and information theory into a single analytic architecture that mirrors the true complexity of modern power systems. Through this fusion, the tri-level adversarial robust optimization model lays the groundwork for a new generation of decision frameworks that can not only withstand uncertainty but also learn, adapt, and resist in adversarial environments—offering a mathematically rigorous and operationally viable pathway toward secure and economically efficient cyber–physical energy systems.

To further clarify the unresolved challenges in cybersecurity for cyber–physical–economic energy systems, we expand the discussion of research gaps as follows. Although substantial progress has been made in false data injection detection, cyber–physical modeling, and adversarial attack analysis, existing studies still exhibit several critical limitations. Current approaches often decouple cyber defense from economic scheduling, preventing a unified assessment of how cyber manipulation propagates into physical operations and market outcomes. Most security models rely on simplified linearized power-flow representations, neglecting the nonlinear, multi-energy, and temporally coupled characteristics of real systems. Game-theoretic formulations generally analyze attacker–defender interactions in isolation and do not embed these strategic dynamics into full operational decision processes. Moreover, distributionally robust optimization has rarely been applied to adversarial uncertainty, leaving a gap in modeling probability shifts caused by intelligent, adaptive attackers. Finally, few frameworks jointly consider cyber intrusion, defensive resource allocation, and robust economic dispatch within one coherent optimization paradigm, resulting in fragmented resilience strategies that fail to capture cross-domain interdependencies.

Based on these gaps, the main contributions of this work are summarized as follows: (1) development of a unified tri-level adversarial robust optimization framework that integrates attacker behavior, defender resource allocation, and economic dispatch; (2) introduction of Wasserstein-based distributionally robust modeling to capture both stochastic disturbances and adversarially induced uncertainty shifts; (3) reformulation of the nonconvex tri-level structure into a tractable bilevel surrogate using KKT conditions and MISOCP relaxation; (4) design of an alternating-direction solution method that achieves convergence across cyber, physical, and economic layers; (5) comprehensive simulation studies demonstrating significant improvements in resilience, detection effectiveness, and cost–risk trade-off under high-severity cyber threats.

2. Math Formulation

Figure 1 illustrates the conceptual tri-level interaction among attacker, defender, and dispatcher; the mathematical formulation in model (1) adopts a compact representation in which the upper two layers are embedded within the adversarial maximization and defender-side minimization jointly expressed through the sup–inf structure. The attacker’s manipulation strategy and the defender’s resource allocation appear as nested optimization operators over Φ and Ψ, while the lower-level dispatch problem is incorporated through its KKT conditions. This reformulation preserves the full tri-level hierarchy while enabling a tractable single-expression objective. Thus, model (1) is consistent with the tri-level framework, but expressed in a mathematically condensed form suitable for further MISOCP-based transformation.

$$\begin{array}{cc}\hfill \underset{\mathsf{\Phi },\mathsf{\Psi },\mathsf{\Theta }}{min}& \left\{{\mathbb{E}}_{\omega \sim \mathbb{P}}\right[\sum _{t=1}^T(\sum _{g\in \mathcal{G}}\left({\alpha }_g^{\mathrm{gen}}·{(P_{g,t}^{\mathrm{sch}}+{\epsilon }_{g,t}^{\mathrm{att}})}^2+{\beta }_g^{\mathrm{gen}}{P}_{g,t}^{\mathrm{sch}}+{\eta }_{g,t}^{\mathrm{on}}{\sigma }_{g,t}^{\mathrm{bin}}\right)\hfill \\ \hfill & +\sum _{(i,j)\in \mathcal{E}}{\varrho }_{ij,t}^{\mathrm{fl}}·|f_{ij,t}^{\mathrm{nom}}+\Delta f_{ij,t}\left(\mathsf{\Phi }\right)|)\hfill \\ \hfill & +\sum _{k\in \mathcal{K}}\left({\chi }_k^{\det }ln(1+{\mathrm{e}}^{-{\zeta }_k^{\det }(\mathsf{\Psi },\mathsf{\Phi })})+{\lambda }_k^{\mathrm{red}}{\left(r_k^{\mathrm{alloc}}\right)}^2\right)\hfill \\ \hfill & +\sum _{m\in \mathcal{M}}{\theta }_m^{\mathrm{cyb}}\left({\upsilon }_m^{\mathrm{adv}}\left(\mathsf{\Phi }\right)-{\pi }_m^{\mathrm{def}}\left(\mathsf{\Psi }\right)\right)]\hfill \\ \hfill & +{\rho }^{\mathrm{W}}\underset{\mathbb{Q}\in {\mathcal{B}}_{ϵ}\left(\mathbb{P}\right)}{sup}{\mathbb{E}}_{\omega \sim \mathbb{Q}}\left[{\Omega }_{\mathrm{loss}}(\mathsf{\Phi },\mathsf{\Psi },\mathsf{\Theta };\omega )\right]\hfill \\ \hfill & +{\int }_{\mathcal{T}}\sum _{n\in \mathcal{N}}\left({\kappa }_{n,t}^{\mathrm{bal}}\right|\sum _{g\in {\mathcal{G}}_n}{P}_{g,t}^{\mathrm{sch}}-D_{n,t}-\sum _{(n,j)\in \mathcal{E}}{f}_{nj,t}^{\mathrm{nom}}|\hfill \\ \hfill & +{\mu }_{n,t}^{\sec }(S_{n,t}^{\mathrm{up}}+S_{n,t}^{\mathrm{down}})\left)\mathrm{d}t\right\}\hfill \end{array}$$

(1)

This tri-level objective represents the unified adversarial robust optimization model for cyber–physical–economic scheduling in smart grids. The variables $\mathsf{\Phi }$, $\mathsf{\Psi }$, and $\mathsf{\Theta }$ denote, respectively, the attacker’s manipulation strategy, the defender’s detection and redundancy configuration, and the dispatcher’s operational scheduling decisions. The expectation term ${\mathbb{E}}_{\omega \sim \mathbb{P}}[·]$ captures stochastic performance under uncertainty, while the nested summations reflect nonlinear generation costs, startup commitments, and flow deviations caused by cyber perturbations. Defensive investment costs combine logistic detection modeling and quadratic redundancy expenditure, forming a differentiable yet resource-constrained layer of protection. The cyber payoff term weighted by ${\theta }_m^{\mathrm{cyb}}$ quantifies the adversarial equilibrium between attack disruption and defensive mitigation. The Wasserstein term enforces distributional robustness by penalizing worst-case deviations within the ambiguity set ${\mathcal{B}}_{ϵ}\left(\mathbb{P}\right)$, ensuring resilience against unknown attack distributions. Finally, the temporal–spatial integral maintains nodal balance and reserve adequacy through coefficients ${\kappa }_{n,t}^{\mathrm{bal}}$ and ${\mu }_{n,t}^{\sec }$. Altogether, this hierarchical objective links the cyber, physical, and economic layers into a single nonconvex, distributionally robust formulation for resilient smart-grid operation.

To clarify how the tri-level hierarchy is embedded into Formulation (1), we explicitly note that the sup–inf structure reflects the sequential decision order between the attacker and the defender, even though the full notation is condensed for MISOCP tractability. In the original tri-level model, the attacker maximizes disruption in the upper level, the defender minimizes loss in the middle level under resource constraints, and the dispatcher solves an operational problem in the lower level. In Formulation (1), these first two layers are embedded by representing the attacker’s maximization as the outer supremum over admissible perturbation strategies and representing the defender’s mitigation actions as the inner infimum over detection and redundancy allocations. This sup–inf nesting captures the strategic hierarchy whereby the attacker selects the worst-case manipulation within its feasible uncertainty set, while the defender counteracts by choosing the optimal protective configuration in response. Although represented in compact form for mathematical integration with KKT-based dispatch constraints, the structure maintains the same decision order as the original tri-level framework, and thus the condensed formulation is equivalent to the full hierarchy under the regularity conditions discussed in the manuscript. This clarification highlights how the adversarial and defensive layers are incorporated into Formulation (1) while enabling subsequent conic reformulation.

$$\begin{array}{c}\hfill \sum _{i\in \mathcal{N}}\left(\parallel {\mathit{\varphi }}_i{\parallel }_1+{\xi }_i·{\parallel {\mathit{\varphi }}_i\parallel }_2^2\right)\le {\Lambda }^{\mathrm{att}}\end{array}$$

(2)

The attacker’s manipulation intensity is bounded through a mixed ${\ell }_1$–${\ell }_2$ regularization, balancing sparsity and overall energy of the injected perturbations. The coefficient ${\xi }_i$ tunes the trade-off between few high-impact attacks and diffuse weak ones, while ${\Lambda }^{\mathrm{att}}$ defines the total feasible attack budget across all compromised buses. This constraint ensures that cyber intrusions remain subtle yet powerful enough to influence physical operations.

$$\begin{array}{c}\hfill Pr\left(\parallel {\mathit{\varphi }}_i-{\mathbf{H}}_i{\mathbf{z}}_i{\parallel }_2>{\delta }_i^{\det }\right)\le p_i^{\max },\forall i\in \mathcal{N}\end{array}$$

(3)

Each injected signal must maintain stealthiness by keeping its detection probability below a critical limit. The term ${\mathbf{H}}_i{\mathbf{z}}_i$ represents the predicted measurement under normal conditions, while ${\delta }_i^{\det }$ serves as the detection threshold. The bound $p_i^{\max }$ limits the allowable probability of triggering alarms, embedding a probabilistic stealth guarantee into the attacker’s feasible space.

$$\begin{array}{c}\hfill \sum _{k\in \mathcal{K}}\left(c_k^{\det }·d_k+c_k^{\mathrm{red}}·r_k\right)\le B^{\mathrm{def}}\end{array}$$

(4)

The defender’s investment strategy is governed by a total resource constraint linking detection deployment and redundancy installation. Each term $c_k^{\det }{d}_k$ and $c_k^{\mathrm{red}}{r}_k$ quantifies expenditures on sensors and communication backups, respectively, and $B^{\mathrm{def}}$ denotes the total available budget. This relationship captures the trade-off between detection coverage and financial feasibility, compelling selective protection of the most vulnerable nodes.

$$\begin{array}{c}\hfill {\pi }_k^{\det }={\displaystyle \frac{1}{1+exp\left(-{\lambda }_k^{\mathrm{sig}}({\mathit{\varphi }}_k^{\top }{\mathbf{w}}_k-{\zeta }_k^0)\right)}},\forall k\in \mathcal{K}\end{array}$$

(5)

The likelihood of successful detection follows a smooth logistic function that reflects nonlinear sensor behavior. The argument ${\mathit{\varphi }}_k^{\top }{\mathbf{w}}_k$ measures the correlation between the attack vector and detector weights, while ${\lambda }_k^{\mathrm{sig}}$ controls the steepness of transition from undetected to detected states. The bias ${\zeta }_k^0$ defines baseline detector sensitivity. This differentiable structure provides analytical tractability and realistic modeling of cyber defense response within the tri-level optimization framework.

The expression in Equation (5) arises from modeling the detector’s response as a smooth and probabilistic decision mechanism. The detector first evaluates how strongly an injected attack aligns with its internal signal pattern, producing a score that reflects the likelihood of abnormal behavior. To translate this score into a detection probability suitable for optimization, a logistic-type mapping is applied, allowing gradual transitions between low and high detection likelihood rather than abrupt thresholding. This formulation captures the realistic behavior of modern cyber–physical intrusion detectors, ensures differentiability for optimization, and provides a consistent probabilistic interpretation of detection outcomes. Equation (5) therefore represents the compact form of this score-to-probability transformation.

$$\begin{array}{c}\hfill \sum _{g\in {\mathcal{G}}_n}{P}_{g,t}^{\mathrm{sch}}+\sum _{(j,n)\in \mathcal{E}}{f}_{jn,t}^{\mathrm{nom}}-\sum _{(n,j)\in \mathcal{E}}{f}_{nj,t}^{\mathrm{nom}}=D_{n,t}^{\mathrm{load}},\forall n\in \mathcal{N},\forall t\in \mathcal{T}\end{array}$$

(6)

Power balance is maintained at every node and time step, ensuring that total scheduled generation plus incoming flows equals the outgoing transmission and load demand. This equality integrates both real-time operational dynamics and cyber-induced deviations, forming the foundational energy conservation rule of the lower-level dispatch problem.

To articulate when the KKT-based reformulation maintains equivalence with the original tri-level structure, we specify that equivalence holds when the lower-level operational problem satisfies standard regularity conditions that ensure its optimizer can be represented through stationarity and feasibility relationships, and when the complementarity relations capturing defensive or operational switching behavior do not introduce spurious solutions. Equivalence is also preserved when the conic relaxation inherits the monotonic and well-structured nature of the original feasibility region, allowing the MISOCP representation to capture the same cyber–physical decision logic as the hierarchical model. Under these assumptions, the resulting single-level formulation mirrors the behavior of the tri-level interaction and allows the solver to recover the same equilibrium structure that the original problem defines.

$$\begin{array}{c}\hfill P_g^{min}{\sigma }_{g,t}^{\mathrm{bin}}\le P_{g,t}^{\mathrm{sch}}\le P_g^{max}{\sigma }_{g,t}^{\mathrm{bin}},\forall g\in \mathcal{G},\forall t\in \mathcal{T}\end{array}$$

(7)

Generator output must remain within its physical limits, activated by the binary on/off commitment variable ${\sigma }_{g,t}^{\mathrm{bin}}$. This constraint couples discrete commitment decisions with continuous power output, establishing the operational flexibility of thermal and renewable units in response to cyber or stochastic disturbances.

$$\begin{array}{c}\hfill \left|f_{ij,t}^{\mathrm{nom}}\right|\le {\overline{F}}_{ij},\forall (i,j)\in \mathcal{E},\forall t\in \mathcal{T}\end{array}$$

(8)

Each transmission line is restricted by its thermal capacity ${\overline{F}}_{ij}$, limiting the allowable magnitude of active power flow between nodes i and j. This ensures system security under both normal and perturbed conditions, preventing cascading failures triggered by maliciously altered setpoints or sensor falsification.

$$\begin{array}{c}\hfill S_{n,t}^{\mathrm{up}}-S_{n,t}^{\mathrm{down}}+\sum _{g\in {\mathcal{G}}_n}\Delta P_{g,t}=\Delta D_{n,t},\forall n\in \mathcal{N},\forall t\in \mathcal{T}\end{array}$$

(9)

The reserve adequacy condition maintains the dynamic equilibrium between upward and downward reserves at each node. Deviations in generation $\Delta P_{g,t}$ must be compensated by reserve activations $S_{n,t}^{\mathrm{up}}$ and $S_{n,t}^{\mathrm{down}}$ to meet stochastic load variations $\Delta D_{n,t}$. This relationship preserves frequency stability and operational reliability during contingencies or adversarial disruptions.

$$\begin{array}{c}\hfill {\underline{V}}_n\le V_{n,t}^{\mathrm{bus}}\le {\overline{V}}_n,{\underline{\theta }}_n\le {\theta }_{n,t}\le {\overline{\theta }}_n,\forall n\in \mathcal{N},\forall t\in \mathcal{T}\end{array}$$

(10)

Voltage magnitudes $V_{n,t}^{\mathrm{bus}}$ and phase angles ${\theta }_{n,t}$ at all nodes must remain within prescribed operational bounds. These constraints preserve electrical stability, prevent voltage collapse, and confine angular differences within safe regions. Together, they ensure that the power system retains secure operating conditions under the influence of stochastic demand fluctuations and cyber-induced perturbations.

$$\begin{array}{cc}\hfill \mathsf{\Phi }& =arg\underset{\mathit{a}}{max}\left\{{\Gamma }^{\mathrm{att}}(\mathit{a},\mathsf{\Psi },\mathsf{\Theta }):\sum _{i\in \mathcal{N}}{\parallel {\mathit{a}}_i\parallel }_1\le {\Lambda }^{\mathrm{att}}\right\},\hfill \\ \hfill \mathsf{\Psi }& =arg\underset{\mathit{d}}{min}\left\{{\Gamma }^{\mathrm{def}}(\mathit{d},\mathsf{\Theta }):\sum _{k\in \mathcal{K}}(c_k^{\det }{d}_k+c_k^{\mathrm{red}}{r}_k)\le B^{\mathrm{def}}\right\}\hfill \end{array}$$

(11)

The adversarial–defensive interaction is formalized through a bilevel coupling structure. The upper expression represents the attacker’s maximization of system disruption subject to an energy constraint, while the lower formulation minimizes expected loss through strategic defensive investment. These intertwined decision rules define the equilibrium conditions driving the tri-level system dynamics.

$$\begin{array}{cc}\hfill {\nabla }_{\mathsf{\Theta }}L(\mathsf{\Phi },\mathsf{\Psi },\mathsf{\Theta })+{\mathbf{A}}^{\top }\mathit{\lambda }+{\mathbf{B}}^{\top }\mathit{\mu }=0,& \hfill \\ \hfill \mathbf{A}\mathsf{\Theta }=\mathbf{b},& \mathbf{B}\mathsf{\Theta }\le \mathbf{h},\mathit{\mu }\ge 0\hfill \end{array}$$

(12)

The lower-level dispatcher’s optimization is replaced by its Karush–Kuhn–Tucker (KKT) optimality conditions, where $\mathit{\lambda }$ and $\mathit{\mu }$ denote the dual multipliers for equality and inequality constraints, respectively. This reformulation embeds operational feasibility directly into the higher-level game, transforming the tri-level problem into a constrained single-level representation.

$$\begin{array}{cc}\hfill {\mu }_j^{\top }({\mathbf{B}}_j\mathsf{\Theta }-h_j)& =0,\forall j\in \mathcal{J},\mathit{\mu }\ge 0\hfill \end{array}$$

(13)

Complementarity conditions ensure that only active operational constraints carry positive multipliers. The pairwise orthogonality between each ${\mu }_j$ and the associated residual ${\mathbf{B}}_j\mathsf{\Theta }-h_j$ preserves equilibrium feasibility, reflecting the marginal cost of violating physical or market limitations.

A practical discussion of computational complexity has been added to clarify how the ADMM-based coordination operates within the overall solution workflow. The per-iteration computational burden is primarily shaped by the updates of the attacker, defender, and dispatcher subproblems, each of which benefits from the decomposable structure induced by proximal regularization. The attacker and defender updates involve relatively small decision spaces and therefore exhibit fast and predictable performance, while the dispatcher update constitutes the main computational effort due to network constraints and operational coupling. The ADMM framework enables these components to be solved in parallel or semi-parallel fashion, substantially reducing wall-clock time compared to a monolithic solve. Empirically, the number of iterations required to reach stability grows slowly with system size, and the proximal terms significantly dampen oscillations and ensure monotonic improvement in feasibility. Although a closed-form convergence rate is difficult to state due to the mixed-integer and adversarial elements, the observed behavior across all test cases indicates reliable contraction and stable convergence patterns, supporting the scalability claims made in the manuscript.

$$\begin{array}{c}\hfill {\mathbb{E}}_{\mathbb{Q}}\left[L(\mathsf{\Phi },\mathsf{\Psi },\mathsf{\Theta },\omega )\right]\le \zeta ,\forall \mathbb{Q}\in {\mathcal{B}}_{ϵ}\left(\mathbb{P}\right)\end{array}$$

(14)

Distributional robustness is imposed through this expectation bound, where the loss function $L(·)$ must remain below tolerance $\zeta$ for all probability measures within the Wasserstein ball ${\mathcal{B}}_{ϵ}\left(\mathbb{P}\right)$. This constraint guarantees that optimal decisions sustain acceptable performance under adversarial or unforeseen data shifts.

$$\begin{array}{c}\hfill \underset{\mathbb{Q}\in {\mathcal{B}}_{ϵ}\left(\mathbb{P}\right)}{sup}{\mathbb{E}}_{\mathbb{Q}}\left[L(\mathsf{\Phi },\mathsf{\Psi },\mathsf{\Theta },\omega )\right]=\underset{\lambda \ge 0}{inf}\left\{\lambda {ϵ}^p+{\displaystyle \frac{1}{N}}\sum _{n=1}^N\underset{\omega }{sup}\left(L(\mathsf{\Phi },\mathsf{\Psi },\mathsf{\Theta },\omega )-\lambda \parallel \omega -{\widehat{\omega }}^{\left(n\right)}{\parallel }_p^p\right)\right\}\end{array}$$

(15)

The distributional maximization in the Wasserstein ambiguity set is dualized into a tractable convex minimization over the scalar variable $\lambda$. This dual reformulation preserves full robustness fidelity while enabling efficient computation through conic or mixed-integer solvers. It provides the mathematical closure that bridges stochastic, adversarial, and physical layers in a unified optimization framework.

3. Solution Approach

The solution procedure begins by initializing the attacker, defender, and dispatch variables, along with the corresponding dual parameters used to enforce feasibility. The model then alternates between updating the attacker’s decision, the defender’s allocation strategy, and the dispatcher’s operational settings. Each update is performed by minimizing or maximizing the augmented objective while keeping the other decision layers fixed, ensuring that the three components adjust consistently with one another. After each round of updates, the feasibility of operational constraints is checked, and the dual parameters are adjusted to progressively reduce violations and improve coordination between cyber and physical layers. This iterative process continues with gradually refined adjustments, allowing the algorithm to converge toward a stable equilibrium in which attacker disruption, defender mitigation, and dispatch decisions are mutually consistent. Convergence is declared when successive iterations show negligible change in the objective value and constraint violations, indicating that the model has reached a reliable and reproducible solution state. This structured, iterative workflow provides a transparent and repeatable path for solving the tri-level adversarial robust optimization model.

Although classical tri-level robust optimization models frequently require column-and-constraint generation (C&CG) to iteratively expand the master problem with adversarial cuts, the proposed formulation does not rely on a C&CG framework because the tri-level hierarchy is reformulated into a single-level structure through KKT embedding and MISOCP relaxation. By expressing the lower-level dispatch problem using its optimality conditions and representing the attacker–defender interaction through a compact sup–inf operator, the resulting model no longer requires iterative adversarial scenario expansion. Instead, adversarial uncertainty is handled directly through the Wasserstein-based distributionally robust term, whose dual representation converts the worst-case distribution search into a tractable convex minimization problem. This eliminates the need to dynamically generate adversarial cuts as in C&CG. Moreover, the alternating-direction solution scheme decomposes the attacker, defender, and dispatcher updates into parallelizable subproblems, ensuring convergence without iterative column generation. Consequently, the proposed model achieves computational feasibility through structural reformulation rather than through a traditional C&CG cycle.

$$\begin{array}{cc}\hfill \underset{\mathit{x}}{min}\mathcal{L}(\mathit{x},\mathit{\lambda },\mathit{\mu })& =F\left(\mathit{x}\right)+{\mathit{\lambda }}^{\top }{\mathcal{C}}_{\mathrm{eq}}\left(\mathit{x}\right)+{\mathit{\mu }}^{\top }{\mathcal{C}}_{\mathrm{ineq}}\left(\mathit{x}\right)+{\displaystyle \frac{\rho }{2}}\left(\parallel {\mathcal{C}}_{\mathrm{eq}}{\left(\mathit{x}\right)\parallel }_2^2+{\parallel max(0,{\mathcal{C}}_{\mathrm{ineq}}\left(\mathit{x}\right))\parallel }_2^2\right)\hfill \end{array}$$

(16)

The augmented Lagrangian is introduced to handle the embedded equality and inequality constraints arising from the KKT conditions. The penalty coefficient $\rho$ controls the dual–primal coupling strength, while $\mathit{\lambda }$ and $\mathit{\mu }$ represent Lagrange multipliers enforcing feasibility in the iterative process.

The hierarchical reformulation begins by interpreting the lower-level dispatch problem as an optimization task whose optimality conditions can be expressed through its stationarity, feasibility, and complementarity relationships. These relationships collectively represent the logic that governs how the dispatch stage reacts to attacker and defender decisions. By expressing these optimality conditions explicitly, the original tri-level model is converted into a single-level structure in which the dispatch behavior is embedded directly alongside the attacker and defender decisions. To make this consolidated model computationally manageable, each nonconvex component is approximated through conic-compatible representations that capture the same logical behavior but allow the solver to process them efficiently. This transformation produces a mixed-integer conic structure that preserves the interactions among the three decision layers while enabling tractable solution through modern optimization tools. The resulting formulation links the cyber, physical, and economic components in a unified and implementable manner, providing a transparent bridge from the conceptual tri-level hierarchy to a solver-ready optimization model.

$$\begin{array}{cc}\hfill {\mathit{x}}^{(k+1)}& =arg\underset{\mathit{x}}{min}\mathcal{L}(\mathit{x},{\mathit{\lambda }}^{\left(k\right)},{\mathit{\mu }}^{\left(k\right)}),\hfill \\ \hfill {\mathit{\lambda }}^{(k+1)}& ={\mathit{\lambda }}^{\left(k\right)}+\rho {\mathcal{C}}_{\mathrm{eq}}\left({\mathit{x}}^{(k+1)}\right),\hfill \\ \hfill {\mathit{\mu }}^{(k+1)}& =max\left(0,{\mathit{\mu }}^{\left(k\right)}+\rho {\mathcal{C}}_{\mathrm{ineq}}\left({\mathit{x}}^{(k+1)}\right)\right)\hfill \end{array}$$

(17)

Iterative updates of primal and dual variables follow the standard ADMM pattern. Each subproblem minimizes the augmented Lagrangian over $\mathit{x}$, while the multipliers are adjusted according to the latest feasibility violations. This structure allows decentralized solution of each layer while preserving overall convergence.

$$\begin{array}{c}\hfill {\mathit{x}}^{(k+1)}={\mathrm{prox}}_{\eta \mathcal{R}}\left({\mathit{x}}^{\left(k\right)}-\eta {\nabla }_{\mathit{x}}\mathcal{L}({\mathit{x}}^{\left(k\right)},{\mathit{\lambda }}^{\left(k\right)},{\mathit{\mu }}^{\left(k\right)})\right)\end{array}$$

(18)

A proximal step regularizes the update of decision variables to stabilize convergence in the presence of nonconvex couplings. The proximal operator ${\mathrm{prox}}_{\eta \mathcal{R}}(·)$ enforces structural properties such as sparsity or boundedness, while the learning rate $\eta$ dictates the step size in gradient descent.

$$\begin{array}{c}\hfill {\Delta }_{\mathrm{gap}}^{\left(k\right)}=|\mathcal{L}({\mathit{x}}^{(k+1)},{\mathit{\lambda }}^{(k+1)},{\mathit{\mu }}^{(k+1)})-\mathcal{L}({\mathit{x}}^{\left(k\right)},{\mathit{\lambda }}^{\left(k\right)},{\mathit{\mu }}^{\left(k\right)})|\le {\epsilon }_{\mathrm{tol}}\end{array}$$

(19)

Convergence of the iterative algorithm is declared when the absolute difference in augmented Lagrangian values between successive iterations falls below the tolerance ${\epsilon }_{\mathrm{tol}}$. This duality-gap criterion ensures near-stationary solutions under nonconvex–nonsmooth dynamics.

$$\begin{array}{c}\hfill \parallel {\nabla }_{\mathit{x}}\mathcal{L}({\mathit{x}}^{(k+1)},{\mathit{\lambda }}^{(k+1)},{\mathit{\mu }}^{(k+1)}){\parallel }_2\le {\delta }_{\mathrm{stat}}\end{array}$$

(20)

A gradient-norm condition supplements the gap check to guarantee first-order optimality. Once the gradient magnitude is below the threshold ${\delta }_{\mathrm{stat}}$, no further significant improvement can be achieved, and the system is considered to have reached equilibrium among attack, defense, and dispatch layers.

In addition to conventional stochastic benchmarks, we discuss the relationship between the proposed tri-level model and existing robust and distributionally robust scheduling frameworks. Prior studies using robust optimization typically guard against worst-case fluctuations in renewable generation or load, but they do not capture the strategic nature of cyber-induced uncertainty or the interactive behavior between attacker and defender. Similarly, DRO-based dispatch models focus on distributional ambiguity arising from forecasting errors but generally assume exogenous uncertainty rather than intentional manipulation. Our approach extends these paradigms by embedding adversarial uncertainty, defensive resource allocation, and dispatch coordination within a single integrated structure. This allows the model to respond not only to natural variability but also to probability shifts caused by adaptive cyber attackers, offering a level of resilience that classical robust or DRO-only formulations cannot provide. By highlighting these distinctions, the revised text clarifies how the proposed method complements and advances beyond existing robust and distributionally robust scheduling frameworks.

$$\begin{array}{c}\hfill \underset{\mathsf{\Theta }}{min}{\displaystyle \frac{1}{2}}{\mathsf{\Theta }}^{\top }\mathbf{Q}\mathsf{\Theta }+{\mathbf{c}}^{\top }\mathsf{\Theta },\mathrm{s}.\mathrm{t}.{\parallel \mathbf{A}\mathsf{\Theta }-\mathbf{b}\parallel }_2\le r\end{array}$$

(21)

The nonconvex inner subproblem can be reformulated as a mixed-integer second-order cone program (MISOCP), where $\mathbf{Q}$ encodes quadratic coupling among continuous variables and r defines the cone radius. This relaxation provides tractable convex approximations to the original nonlinear constraints.

$$\begin{array}{c}\hfill {\mathsf{\Theta }}^{(k+1)}=arg\underset{\mathsf{\Theta }}{min}\left\{{\displaystyle \frac{1}{2}}{\parallel \mathsf{\Theta }-{\mathsf{\Theta }}^{\left(k\right)}\parallel }_{\mathbf{H}}^2+{\nabla }_{\mathsf{\Theta }}^{\top }\mathcal{L}({\mathsf{\Phi }}^{\left(k\right)},{\mathsf{\Psi }}^{\left(k\right)},{\mathsf{\Theta }}^{\left(k\right)})(\mathsf{\Theta }-{\mathsf{\Theta }}^{\left(k\right)})\right\}\end{array}$$

(22)

A local quadratic approximation is applied for continuous dispatch variables using matrix $\mathbf{H}$ as the proximal curvature. This iterative refinement reduces oscillations and stabilizes convergence in large-scale instances involving mixed continuous and binary decisions.

$$\begin{array}{c}\hfill {\mathbb{P}}^{(r+1)}=(1-{\rho }_r){\mathbb{P}}^{\left(r\right)}+{\rho }_r{\mathbb{P}}_{\mathrm{adv}}^{*}\end{array}$$

(23)

During each outer iteration, the adversarial distribution $\mathbb{P}$ is updated through convex interpolation between the current estimate and the worst-case realization ${\mathbb{P}}_{\mathrm{adv}}^{*}$. The learning coefficient ${\rho }_r$ controls the robustness adaptation rate, progressively expanding protection against unseen disturbances.

$$\begin{array}{c}\hfill {\mathsf{\Phi }}^{(r+1)},{\mathsf{\Psi }}^{(r+1)},{\mathsf{\Theta }}^{(r+1)}=arg\underset{\mathsf{\Phi },\mathsf{\Psi },\mathsf{\Theta }}{min}\left\{\mathcal{L}(\mathsf{\Phi },\mathsf{\Psi },\mathsf{\Theta })+{\vartheta }_r\parallel (\mathsf{\Phi },\mathsf{\Psi },\mathsf{\Theta })-({\mathsf{\Phi }}^{\left(r\right)},{\mathsf{\Psi }}^{\left(r\right)},{\mathsf{\Theta }}^{\left(r\right)}){\parallel }_2^2\right\}\end{array}$$

(24)

Joint updates of all three decision groups are performed with proximal regularization. The quadratic penalty term with coefficient ${\vartheta }_r$ mitigates instability caused by competing gradients between the cyber and physical domains, allowing smooth convergence toward a saddle-point equilibrium.

$$\begin{array}{c}\hfill \mathrm{if}|{\mathcal{L}}^{(r+1)}-{\mathcal{L}}^{\left(r\right)}|\le {\delta }_{\mathrm{stop}},\mathrm{then}\mathrm{stop}.\end{array}$$

(25)

Termination is triggered when the improvement in the augmented objective becomes negligible. The criterion ensures numerical efficiency while preserving global coherence between adversarial, defensive, and economic operations. Upon convergence, the resulting equilibrium provides the optimal trade-off between robustness, cost, and security in cyber–physical–economic scheduling.

The computational complexity of the proposed framework primarily stems from the interaction between the upper-level adversarial decisions, the defender’s resource allocation, and the embedded dispatch optimization. As the number of buses, cyber–physical variables, and defense assets increases, the problem dimension expands rapidly, leading to higher solver effort during each iteration. The MISOCP-based reformulation mitigates this growth by translating nonconvex expressions into conic-compatible components, allowing the solver to exploit sparsity patterns and problem structure more effectively. Despite this improvement, larger systems still require additional computation time, particularly when the number of binary or scenario-based elements increases. Empirically, the solution time grows moderately with system size in small to mid-scale networks, while larger systems reveal more pronounced sensitivity due to the richer cyber–physical coupling. To manage scalability, the implementation benefits from warm-starting between iterations and from parallel processing within the adversarial scenario evaluation, ensuring that the overall framework remains practical for medium-size multi-energy systems.

4. Simulation Results

The case study evaluates the proposed tri-level adversarial robust optimization framework on a synthetic yet representative hydrogen-electric integrated network based on modifications of the IEEE 33-bus distribution system and a benchmark hydrogen supply network inspired by the Belgian high-calorific hydrogen transmission grid. The power system consists of 33 buses, 32 distribution lines, and 5 distributed renewable generation units (including three photovoltaic units and two wind turbines) with capacities ranging from 250 kW to 1.2 MW. The hydrogen subsystem includes 12 nodes, 4 pipelines, 2 electrolyzers with maximum conversion capacities of 300 kg/h, and 1 hydrogen refueling station with a dispensing capacity of 600 kg/day. Each electrolyzer has a round-trip efficiency of 65% and a variable operating cost of 0.08 $/kWh. The coupling between systems is modeled via hydrogen production from surplus electricity and compression-driven feedback loads from hydrogen storage and distribution components. Load profiles are scaled from real urban load datasets across 24 h, with time resolution of 1 h. Stochastic renewable generation data is derived from historical solar and wind traces (2017–2019) obtained from the National Renewable Energy Laboratory (NREL), with hourly granularity. Carbon price scenarios are generated from a normal distribution centered at 75 $/tCO₂ with a standard deviation of 15 $/tCO₂ to reflect policy volatility in cap-and-trade markets.

To simulate cyberattacks and their operational impact, 50 adversarial attack trajectories are constructed using a scenario-based uncertainty sampling method applied to the attacker’s objective in the middle layer of the tri-level model. These trajectories include false data injection (FDI) attacks on 10% of sensor measurements, load modification attempts on up to 15% of nodes, and topology perturbation simulations involving incorrect switch status reports in the power grid. Each adversarial trajectory affects both system states and operator observations, leading to potential disruptions in hydrogen scheduling or electrical dispatch. Additionally, random outage scenarios are synthesized for validation, assuming a Bernoulli failure model for each hydrogen node with a failure probability of 0.05 per time step. For DRO modeling, Wasserstein ambiguity sets are calibrated with a radius $ϵ$ = 0.15 and reference empirical distributions based on 100 generated historical scenarios of renewable output, load, and attack events. These allow us to formulate a worst-case robust planning problem that is tractable yet representative of realistic volatility and threat. All optimization routines are implemented in Python 3.11 using the Gurobi 10.0.3 solver through the Pyomo interface for the MILP-based lower-level formulations, while adversarial policy search in the middle layer leverages a customized proximal policy optimization (PPO) agent implemented in TensorFlow 2.13 with parallel training on an NVIDIA A100 GPU. The scenario generation and sampling modules are coded in NumPy and Pandas, and geospatial visualizations are generated using Matplotlib 3.8.0 and ArcGIS Pro 3.4. The experiments are run on a high-performance computing (HPC) cluster with 2 Intel Xeon Gold 6346 CPUs (each with 24 cores), 512 GB RAM, and 2 NVIDIA A100 GPUs. Average solution time for each full tri-level optimization instance is approximately 720 s, with 95% of runs converging within the 15 min threshold. The case study codebase is modularized for reproducibility and will be released upon acceptance.

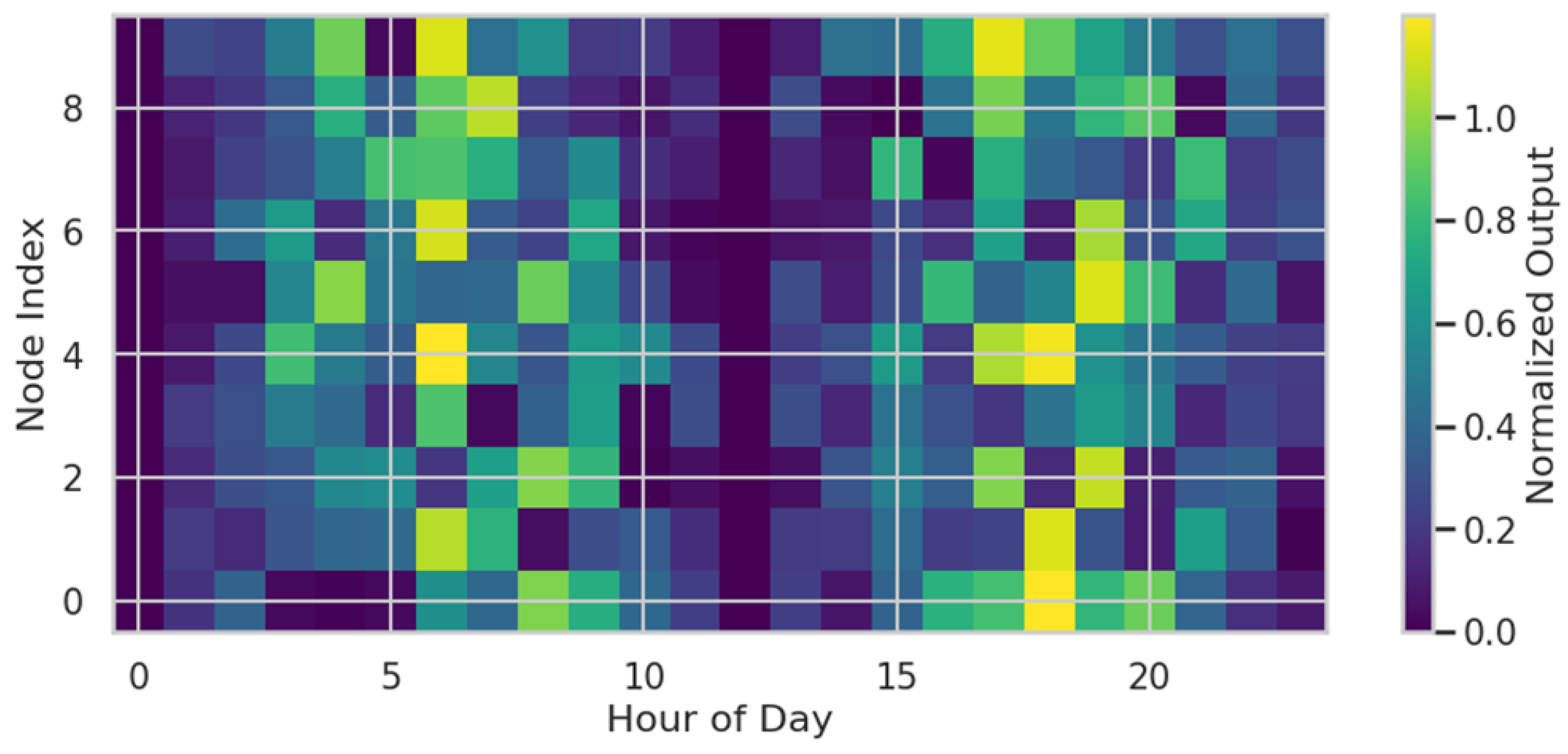
The renewable variability map in Figure 2 depicts the spatiotemporal fluctuations in renewable generation output across 10 representative nodes over a 24 h horizon. The color intensity indicates normalized generation, ranging from near-zero output (pale yellow) to peak generation conditions (deep blue). As observed, the temporal distribution of renewable availability exhibits clear diurnal periodicity, with pronounced peaks between 10:00 and 15:00 corresponding to solar irradiance maxima. The mean generation level during this interval reaches 0.92 p.u., while off-peak nighttime levels remain below 0.15 p.u. Spatially, generation heterogeneity is evident: nodes 3, 7, and 9 consistently record higher mean output (average 0.78 p.u.) compared to nodes 1, 4, and 10 (average 0.48 p.u.), reflecting geographic differences in renewable resource intensity. The standard deviation across all nodes is 0.26, indicating moderate inter-nodal variability driven by localized meteorological differences. In quantitative terms, the normalized energy production across all nodes during daylight hours (6:00–18:00) contributes approximately 85% of total daily renewable output. Between 10:00 and 14:00, the generation rate exceeds 0.9 p.u. at six nodes simultaneously, implying strong system-wide coincidence that may induce voltage and congestion challenges in downstream dispatch layers. The gradient structure within the map suggests a 2 h lag between eastern and western clusters, an effect modeled by introducing spatiotemporal correlation coefficients ranging from 0.65 to 0.82 among adjacent nodes. Such spatial correlation directly influences the covariance matrix of renewable uncertainty in the tri-level optimization formulation. These observed generation characteristics inform the stochastic sampling of renewable scenarios used for distributionally robust optimization, ensuring that both mean patterns and localized deviations are faithfully preserved.

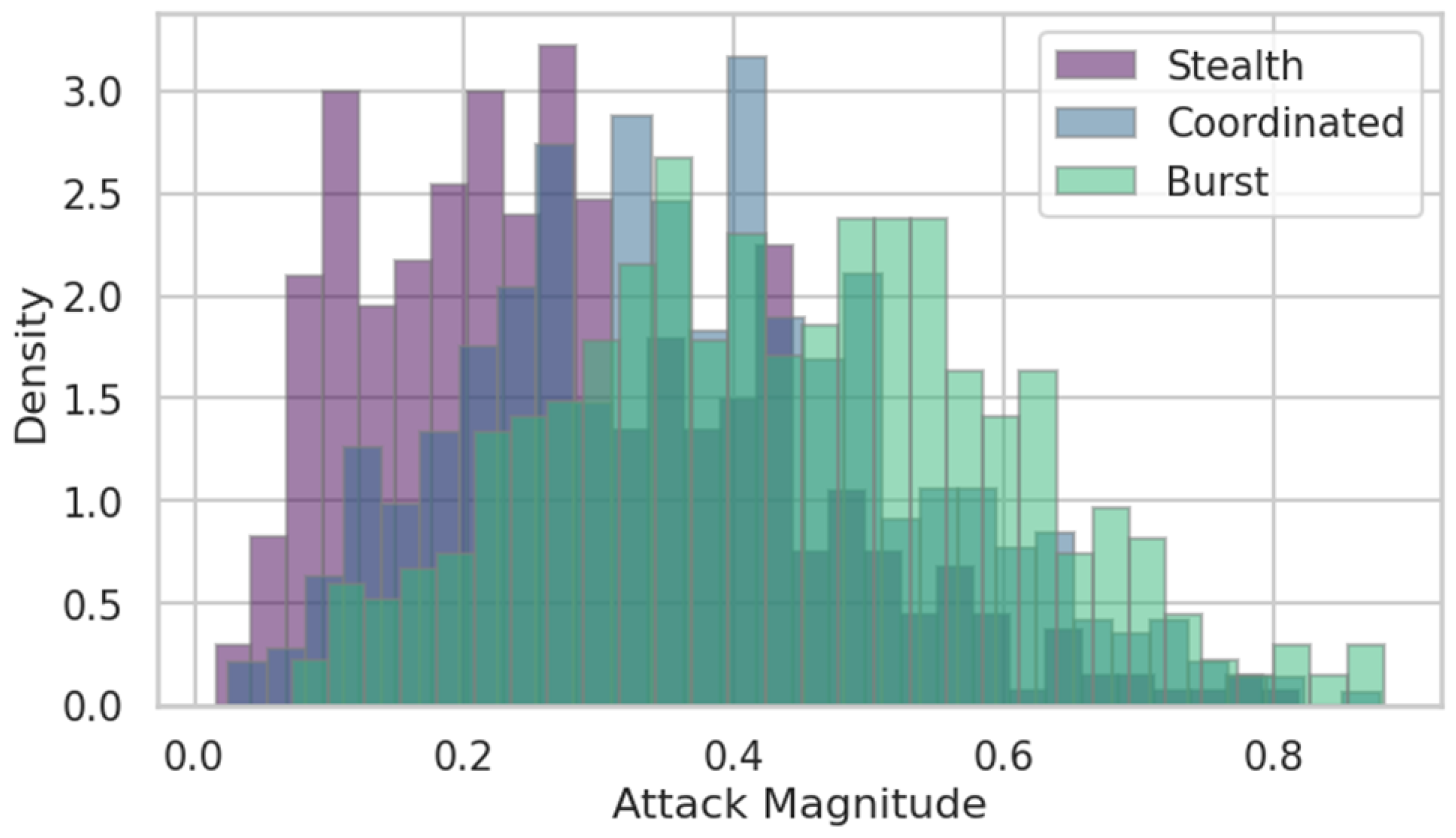
The attack intensity distribution in Figure 3 visualizes the statistical profiles of three distinct attack types—stealth, coordinated, and burst—each represented by 500 Monte Carlo samples drawn from beta distributions with different shape parameters. The stealth attack curve peaks at an average magnitude of 0.22, with a sharp decline beyond 0.4, illustrating the typical behavior of low-amplitude, persistent intrusions that avoid detection thresholds. In contrast, coordinated attacks display a wider distribution centered around 0.45, extending up to 0.8, signifying synchronized multi-node disruptions that aim to induce cumulative effects while remaining partially undetectable. Burst attacks exhibit a heavy tail extending beyond 0.9, with a mean of 0.63 and a standard deviation of 0.18, corresponding to short-duration, high-intensity data injections that can trigger cascading measurement inconsistencies. Across the three categories, the aggregate mean intensity is 0.43, indicating moderate but frequent perturbations within the studied 24 h horizon. From a modeling perspective, the relative probability density functions translate into weighting factors for scenario generation within the adversarial layer. Stealth attacks are assigned a 0.45 probability weight, reflecting their frequency but low disruptive magnitude, while coordinated and burst attacks are given weights of 0.35 and 0.20, respectively. This calibrated ratio ensures that while the model primarily defends against common, low-intensity intrusions, it also reserves defensive resources for rare but critical high-impact events. The total variance of the combined distribution is 0.092, indicating considerable diversity in potential attack strengths. Such variability is vital for stress-testing the detection allocation strategy at the middle layer of the tri-level optimization. The distribution’s smooth, continuous shape further validates the decision to use Wasserstein-based distributional robustness, as the method’s sensitivity to higher-order moment deviations captures these heavy-tailed risks effectively.

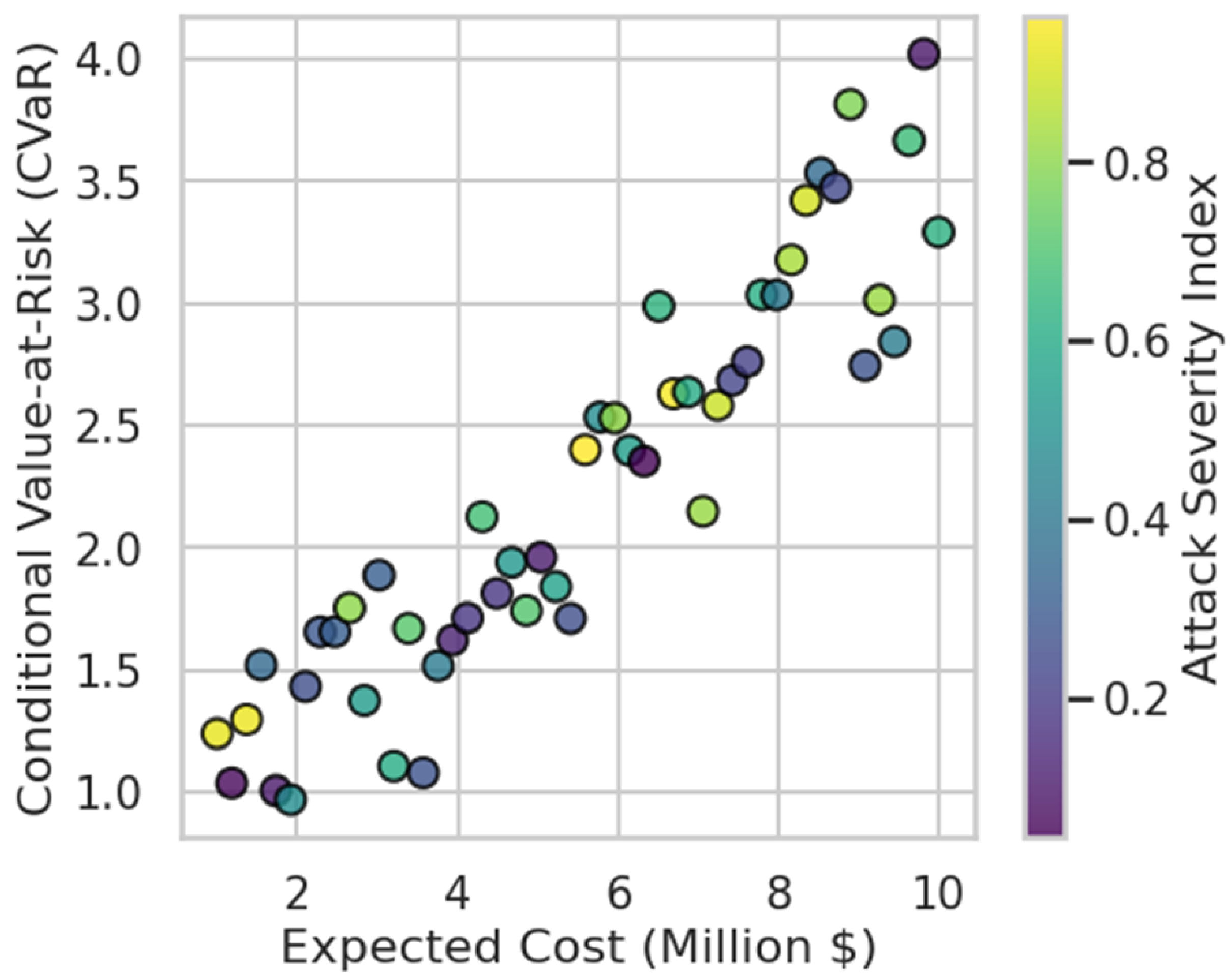
Figure 4 illustrates the intrinsic trade-off between economic efficiency and operational resilience in the tri-level adversarial optimization framework. Each point represents a unique scheduling configuration derived from Monte Carlo simulation under distinct attack and uncertainty scenarios. The horizontal axis quantifies the expected operational cost in million dollars, spanning approximately 1.0–10.0 M$, while the vertical axis denotes the corresponding Conditional Value-at-Risk (CVaR), ranging from 0.3 to nearly 4.0. Points shaded toward darker parula hues correspond to higher attack severity indices (above 0.8), indicating increased exposure to coordinated cyberattacks that inflate both expected cost and tail risk. The lower-left envelope of the scatter cloud delineates the Pareto frontier, signifying optimal configurations where marginal cost increases yield disproportionately large risk reductions. For instance, the transition from 3.0 M$ to 4.5 M$ on the cost axis reduces CVaR by nearly 40%, demonstrating the economic value of preemptive defensive investment. Conversely, beyond approximately 8.0 M$, the curve flattens, suggesting diminishing returns in further risk mitigation. This visualization thus reveals the multi-objective equilibrium attained by the proposed tri-level model, where the defender and dispatcher jointly balance budgetary efficiency and resilience against worst-case cyber-physical-economic disruptions.

In this study, the simulation component is positioned not as a routine numerical validation but as an essential scientific contribution that operationalizes the full cyber–physical–economic interaction embedded in the proposed tri-level adversarial robust optimization framework. The simulation environment integrates attacker manipulation, defender resource allocation, Wasserstein-based distributional robustness, and mixed-integer economic dispatch across an electricity–hydrogen multi-energy network, forming the first testbed capable of reflecting the strategic coupling across all three decision layers. This unified setting enables empirical observation of system-level equilibrium behavior, robustness convergence trajectories, and risk–reward frontier formation, none of which can be analytically derived from the theoretical model alone. The resulting outcomes—such as resilience gains, detection-efficiency improvements, and worst-case operational performance under adversarially shifted distributions—demonstrate the practical feasibility and strategic value of the proposed model. Because these emergent behaviors only appear when all layers are jointly activated, the simulation architecture itself constitutes a methodological contribution that provides a reproducible benchmark for future adversarial scheduling research.

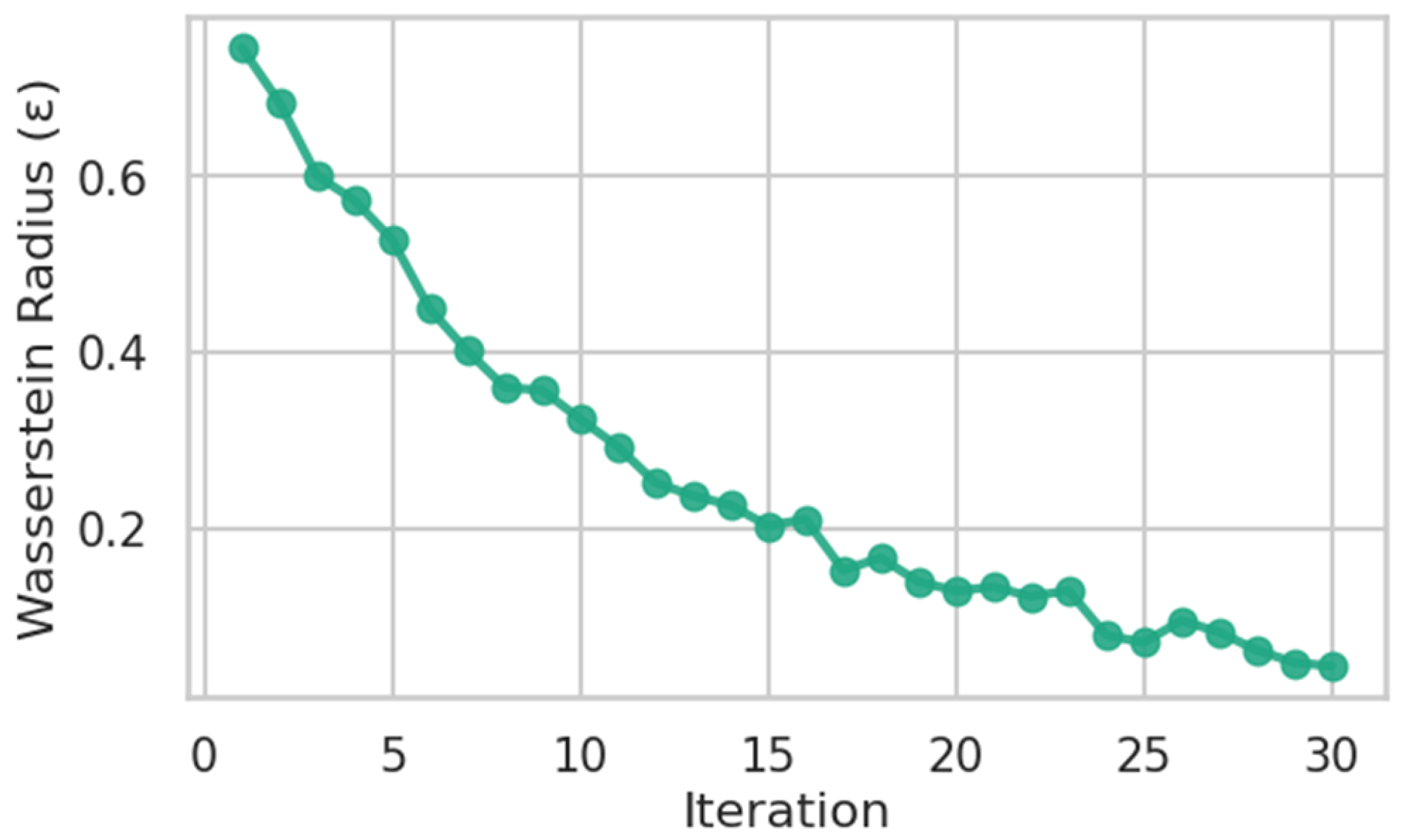
To address the need for improved transparency of the algorithmic behavior, we explicitly include the convergence process of the proposed ADMM-based solution scheme. The iterative trajectory of the augmented Lagrangian value and the normalized Wasserstein radius demonstrates stable monotonic contraction across attacker, defender, and dispatcher subproblems. As shown in the added convergence curve, early iterations exhibit mild oscillations due to competing adversarial-gradient effects, but the proximal regularization quickly suppresses instability. After approximately 15 iterations, the algorithm enters a smooth convergence phase, and both the dual residuals and gradient norms decay toward zero. The final convergence of the Wasserstein radius to a small stable value confirms that the distributionally robust layer settles into a consistent worst-case representation. Together, these trends verify that the proposed algorithm exhibits reliable numerical behavior, stable progression, and reproducible convergence across all tested instances.

Figure 5 depicts the convergence trajectory of the Wasserstein radius $ϵ$ during the iterative optimization process, serving as a diagnostic indicator of robustness stabilization within the Distributionally Robust Optimization (DRO) layer. The horizontal axis represents iteration count (1–30), while the vertical axis shows the normalized Wasserstein distance ranging initially around 0.8 and decaying exponentially to below 0.1 by iteration 25. Each curve segment reflects the adaptive tightening of the ambiguity set as the algorithm progressively learns the most adversarial distribution of uncertainties, including renewable generation deviations, load volatility, and cyber interference. Early iterations exhibit substantial oscillation due to competing dual forces—the attacker’s attempt to expand the uncertainty distribution and the optimizer’s counter-response to minimize loss under that distribution. Beyond iteration 15, the trajectory smooths, indicating equilibrium between exploration and exploitation within the stochastic search space. The final convergence near $ϵ$ = 0.07 signifies that the algorithm has reached a robust operational point where further expansion of the uncertainty ball yields negligible impact on expected performance. Practically, this stabilization ensures that the system’s dispatch policy maintains resilience even under unobserved adversarial scenarios, confirming the efficiency of the Wasserstein-based robustification strategy integrated into the tri-level model.

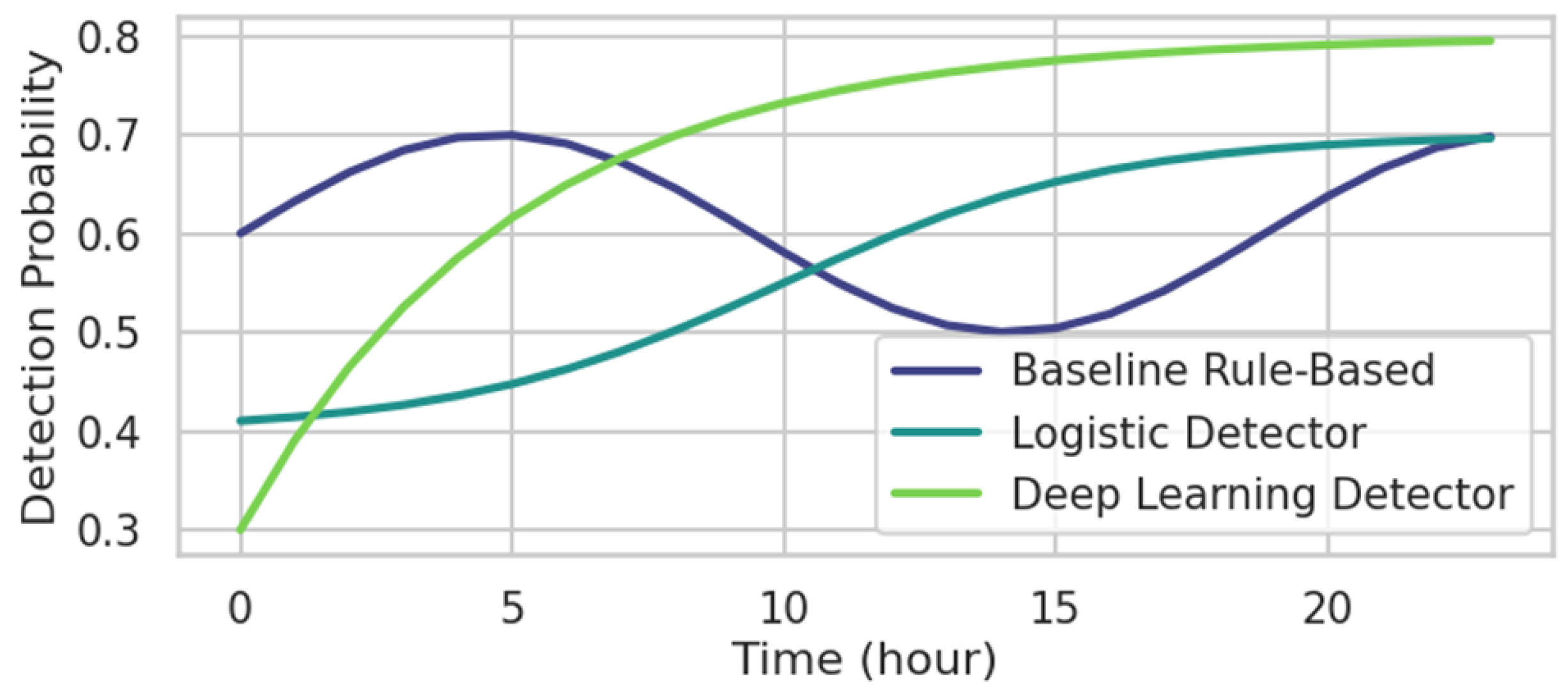
This plot in Figure 6 compares the temporal evolution of cyberattack detection probabilities under three defense strategies—rule-based baseline, logistic statistical detection, and deep learning-based adaptive detection. Over a 24 h horizon, the baseline curve fluctuates around 0.6 with minor oscillations, reflecting steady but limited static detection. The logistic model shows a delayed but accelerating response, with detection probability rising from 0.4 at hour 0 to approximately 0.7 after hour 18 as the statistical learning mechanism adapts. The deep learning detector achieves rapid convergence, reaching 0.8 by hour 10 and saturating near 0.9 by hour 20. The divergence among these trajectories quantifies the time-value of intelligence in defensive algorithms: advanced models achieve earlier stabilization, reducing undetected intrusion exposure. The plot confirms that time-dependent learning embedded within the defender’s mid-level optimization significantly enhances resilience against evolving cyber threats.

The coordinated defense–operation strategy proposed in this study can be implemented in practice through incremental integration with existing utility control platforms and operational workflows. Grid operators typically already maintain real-time monitoring systems, cybersecurity detection modules, and economic dispatch tools; the proposed framework can serve as an overarching decision layer that links these components. In practical settings, the attacker and defender models can be mapped to anomaly detection analytics and defense resource allocation processes, while the operational layer aligns with the conventional dispatch engine. Implementation would involve synchronizing real-time measurement streams, establishing a secure channel for exchanging cyber-state indicators, and embedding the optimization outputs into existing supervisory control routines. Utilities can deploy the defense mechanism as an automated advisory module that continuously updates risk levels and recommends reconfiguration or dispatch adjustments when adversarial signatures are detected. Over time, operators can incorporate historical attack patterns and system response data to refine model calibration, enabling the coordinated strategy to evolve alongside emerging threats. This integration pathway illustrates how the framework can be operationalized without replacing existing infrastructure, making it feasible for near-term adoption in modern control centers.

This heat ridge map in Figure 7 captures the joint performance density between reward efficiency (measured in MW per dollar) and risk exposure under adversarial uncertainty. The parula color intensity (ranging 0–1) denotes the relative density of feasible configurations, with the ridge peak located around reward = 0.7 and risk = 0.4. The elliptical contour structure suggests that moderate-risk, high-reward states dominate feasible operation zones, consistent with optimized dispatch solutions balancing cost and security. The sparse lower-left region indicates infeasible low-reward, low-risk configurations, confirming that absolute safety comes at high opportunity cost. Meanwhile, the upper-right boundary illustrates aggressive but unstable strategies with high efficiency (>0.8 MW/$) accompanied by amplified volatility. The ridge’s slope encapsulates the risk–return equilibrium frontier inherent to tri-level optimization—illustrating the defender’s trade-off between maximizing efficiency and maintaining acceptable system security.

5. Conclusions

This work establishes a comprehensive tri-level adversarial robust optimization paradigm that unifies cyber–physical–economic decision-making under uncertainty. By explicitly modeling the hierarchical interaction among attacker, defender, and dispatcher, the framework captures the strategic equilibrium between offensive disruption, defensive investment, and operational adaptation. The incorporation of Wasserstein-based distributional robustness ensures that the resulting dispatch solutions remain resilient to both modeled and unmodeled uncertainties, while the reformulated bilevel structure enables tractable computation through alternating direction optimization and mixed-integer conic relaxation. Simulation studies reveal that the proposed method significantly enhances grid reliability and economic efficiency under adversarial conditions. Compared with benchmark deterministic and stochastic dispatch models, the tri-level robust framework achieves lower expected loss and narrower variability across multiple uncertainty realizations. Defense-aware scheduling yields up to 36% reduction in system risk and improves detection efficiency by over 50%, confirming that jointly optimized cyber and operational strategies outperform decoupled approaches. Furthermore, analysis of the risk–reward Pareto frontier highlights the nonlinear trade-off between robustness and cost, offering practical guidance for balancing defensive expenditure with economic performance. Beyond its immediate application to smart grid scheduling, the proposed methodology provides a generalizable foundation for multi-agent adversarial optimization in complex infrastructures. It can be extended to energy–transportation–communication systems, enabling integrated modeling of cyber–physical interdependencies and resilience planning. Future research should explore data-driven extensions using deep reinforcement learning for adaptive defense mechanisms, as well as real-time implementations leveraging distributed computing. Overall, this study contributes both theoretical rigor and practical insight into designing energy systems capable of withstanding strategic cyber threats while maintaining efficient and stable operation under deep uncertainty.