Probabilistic Assessment Method of Available Inertia for Wind Turbines Considering Rotational Speed Randomness

Abstract

The large-scale integration of wind power into the grid has led to a reduction in system inertia, threatening frequency stability. There is an urgent need to accurately assess the inertia support capability of wind turbines, providing a theoretical basis for grid inertia dispatch and supporting grid frequency stability. However, due to factors such as wake effects, time-delay effects, and wind shear effects, the rotational speeds of different wind turbines within a wind farm under certain wind speed conditions exhibit probabilistic distribution characteristics. Existing research on wind turbine inertia assessment rarely accounts for the rotational speed randomness. To address this, this paper proposes a probabilistic assessment method for the available inertia of wind turbines that considers rotational speed randomness, establishes a joint probability model for wind speed and rotational speed, deriving the conditional probability density function of rotational speed. By substituting this into the frequency-domain inertia model, we achieve probabilistic inertia assessment. Using operational data from a wind farm in China, a practical case study is constructed, verifying the accuracy of the proposed probabilistic assessment method. At a wind speed of 6 m/s, the proposed method accurately captures the actual system inertia within its 90% confidence interval, in contrast to a conventional approach which yielded a significant 6.5% error.

1. Introduction

The global acceleration of renewable energy deployment, led by wind and solar power, is a critical strategy for decarbonization worldwide. This transition, however, universally challenges power system stability by displacing conventional synchronous generators and reducing the crucial system inertia that regulates grid frequency. The global decline in power system inertia, starkly evidenced by blackouts in the UK (August 2019) and Spain (April 2025), underscores the universal urgency to address stability challenges in renewable-heavy grids worldwide. Since the introduction of the “carbon peak and carbon neutrality” goals, China has been actively promoting the development of clean energy industries such as wind power, photovoltaic, and nuclear energy. By December 2024, the country’s cumulative grid-connected wind power capacity had reached 521 gigawatts, with wind power generation amounting to 991.6 terawatt-hours [1,2,3]. However, as wind power integration reaches high proportions, the grid’s inertia level continues to decline. This leads to a sharp increase in the rate of change in frequency (RoCoF) during power disturbances, a significant drop in the frequency nadir, and a substantial reduction in the system stability margin, seriously jeopardizing grid security and posing severe challenges to maintaining system frequency stability [4,5,6]. To ensure the secure and stable operation of the power grid, it is imperative to accurately assess the equivalent inertia of wind turbines and precisely predict their inertia support capabilities. This will provide critical information for grid dispatch and ultimately support grid frequency stability.

The inertia of a wind turbine is closely related to its rotational speed [7,8,9]. Typically, wind turbines operate under maximum power point tracking (MPPT) control, where a unique, predetermined rotational speed corresponds to each wind speed under specific conditions. Existing methods can accurately assess the equivalent inertia of a wind turbine based on a specific rotational speed. However, due to factors such as wake effects, wind shear effects, and time-delay effects, wind turbines at different locations within a wind farm experience significantly varying captured wind speeds. This results in the absence of a one-to-one correspondence between the average wind speed of the wind farm and the rotational speeds of individual turbines, with the rotational speeds of different turbines exhibiting distinct probabilistic distribution characteristics. If these probabilistic characteristics are ignored and the available inertia is assessed solely based on the MPPT rotational speed corresponding to the average wind speed, the evaluation results will deviate significantly from the actual support capability. If grid dispatch operators rely on such assessment results for inertia scheduling, the wind farm may either fail to meet the inertia dispatch requirements or retain an excessive margin of available inertia. Therefore, it is crucial to account for rotational speed randomness and adopt a probabilistic assessment method for wind turbine inertia to accurately estimate the available inertia level of wind turbines.

Existing research has conducted extensive work on the assessment of wind power inertia. Li et al. [10] established a Swing Equation-based Model (SFR) for wind turbines and proposed a method for assessing the minimum inertia of wind turbines. Li et al. [11] utilized frequency response indicators, such as the average rate of change in frequency, to calculate the inertia effectiveness factor, thereby determining the wind turbine’s inertia. Li et al. [12] employed a Controlled AutoRegressive (CAR) model and Recursive Least Squares identification to evaluate the aggregated equivalent inertia of wind farms. Jiang et al. [13] conducted a detailed analysis of the impact of various components of a wind turbine on inertia and established a reduced-order model for wind turbine inertia under multiple time scales based on singular perturbation theory. While the aforementioned inertia assessment methods can achieve accurate evaluation under deterministic wind speed conditions, none of them consider the impact of wind speed randomness on wind turbine inertia. In the realm of wind turbine inertia assessment considering uncertainties, Wang et al. [14] used vine Copula to establish a joint distribution model for wind speed, wind direction, and air temperature, but did not provide a detailed analysis of wind turbine inertia. Wang et al. [15] applied a two-scale spectral clustering algorithm for zoning and considered the correlation of wind speeds among turbine clusters within a wind farm for zonal inertia estimation. Gong et al. [16] clustered turbine units based on the distribution of wind speeds within the farm and used Extreme Learning Machine (ELM) to estimate the available inertia distribution of each cluster. However, Refs. [15,16] did not investigate the effects of wake effects, time-delay effects, and wind shear effects within the wind farm on rotational speed randomness, resulting in an insufficiently accurate characterization of wind turbine inertia.

In summary, while existing research can accurately assess wind turbine equivalent inertia under a determined rotational speed, this deterministic MPPT-based approach fails to capture the operational randomness in actual wind farms. Most probabilistic studies have focused solely on the inertia distribution induced by wind speed variations, largely neglecting the critical fluctuations caused by wake and shear effects under determined wind speed conditions. This oversight leads to significant inaccuracies in grid operational planning, where overestimation of inertia creates frequency stability risks while underestimation forces costly conservative scheduling.

This paper focuses on the probabilistic assessment of wind turbine inertia considering rotational speed randomness. The primary challenges lie in: (1) the correlation between the average wind speed of the wind farm and the rotational speeds of individual turbines remains inadequately characterized when accounting for wake effects, wind shear effects, and time-delay effects; (2) it is difficult to establish a probabilistic representation of the available inertia of wind turbines while incorporating rotational speed randomness.

To address the aforementioned challenges, this paper proposes a probabilistic assessment method for the available inertia of wind turbines that accounts for rotational speed randomness. The main contributions are as follows:

(1)

Probabilistic Modeling of Rotational Speed: Develops a Copula-based joint probability model that captures the dependence between wind speed and turbine rotational speed, specifically accounting for uncertainties introduced by wake and wind shear effects under determined wind speed conditions.

(2)

Confidence-Aware Inertia Assessment: A probabilistic assessment method for the available inertia of wind turbines incorporating rotational speed randomness is proposed. It incorporates rotational speed randomness to generate confidence intervals for available inertia, enabling risk-informed power system planning.

(3)

Experimental Validation with Real Data: Utilizing actual operational data from a wind farm in China for case validation, showing a 6.5% improvement in estimation accuracy compared to deterministic methods and verifying that actual inertia values fall within the predicted 90% confidence bounds.

2. Joint Probability Distribution Modeling for Wind Farm Speed and Turbine Rotational Speeds

Accurately establishing the joint probability distribution between wind farm speed and turbine rotational speed is a crucial prerequisite for capturing the inertia capability of wind turbines. The modeling process for the joint probability distribution of wind farm speed and turbine rotational speed proposed in this paper is illustrated in Figure 1. To derive a continuous joint probability distribution from discrete sample data that accurately reflects the correlation between wind farm speed and turbine rotational speed, it is necessary to first perform kernel density estimation on the discrete wind farm speed and turbine rotational speed data to obtain their continuous marginal probability distributions. Subsequently, a joint probability model for wind farm speed and turbine rotational speed is constructed by fitting a Copula function, ultimately yielding the conditional probability distribution of rotational speed.

2.1. Modeling of Marginal Probability Distributions for Wind Farm Speed and Turbine Rotational Speed

The sample data is first collected, assuming the wind farm records the station-average wind speed and the corresponding rotor speed of each turbine at one-minute intervals. The sample data is denoted as (v_w1, ω_r1), (v_w2, ω_r2)…, (v_wn, ω_rn).

The geographical location distribution of an offshore wind farm in Zhejiang is shown in Figure 2, which comprises 56 wind turbines. The key parameters of the offshore wind farm used in this case study are summarized in

Table A2. Main Parameters of the Wind Farm.

Name	Parameter	Value
Rated Capacity per Turbine	SN/MW	9
Total Installed Capacity	SN_WF/MW	504
Distance to Shore	d/km	25
Water Depth Range	h/m	18–25

of Appendix A. All 56 wind turbine generators in the Phase II wind farm are identical units, with a rated capacity of 9 MW per turbine. Taking the actual operational data from February 2025 provided by this wind farm as an example, the distribution histograms of the average wind speed and turbine rotational speeds are shown in Figure 3.

According to kernel density estimation theory, continuous probability density functions can be estimated from discrete data points. The probability density functions $\widehat{f}(v_w)$ and $\widehat{f}({\omega }_r)$ can be calculated using the following formulas:

$$\widehat{f}(v_w)={\displaystyle \frac{1}{n{h}_1}}\sum _{i=1}^{n}K\left({\displaystyle \frac{v_w-v_{wi}}{h_1}}\right)$$

(1)

$$\widehat{f}({\omega }_r)={\displaystyle \frac{1}{k{h}_2}}\sum _{i=1}^{k}K\left({\displaystyle \frac{{\omega }_r-{\omega }_{ri}}{h_2}}\right)$$

(2)

where n represent the collected sample sizes, K(u) denotes the kernel function, and h indicates the bandwidth.

To enhance computational efficiency while accounting for local smoothness of the samples, the Gaussian kernel function is selected, and the bandwidth is determined using Silverman’s rule [17].

$$K(u)={\displaystyle \frac{1}{\sqrt{2\pi }}}\exp \left[-{\displaystyle \frac{u^2}{2}}\right]$$

(3)

Applying kernel density estimation to assess the probabilities of wind farm average speed and turbine rotational speed yields the probability density functions (PDFs) for wind farm speed and turbine rotational speed. As shown in Figure 4, the PDFs derived via kernel density estimation demonstrate a good fit with the samples, accurately characterizing the random probability distributions of wind speed and turbine rotational speed. It is noteworthy that approximately one-third of the rotational speed data cluster near 0 rpm, which occurs because the turbines remain in a non-operational state for about one-third of the time, exhibiting only slight rotational angular velocity due to wind disturbances.

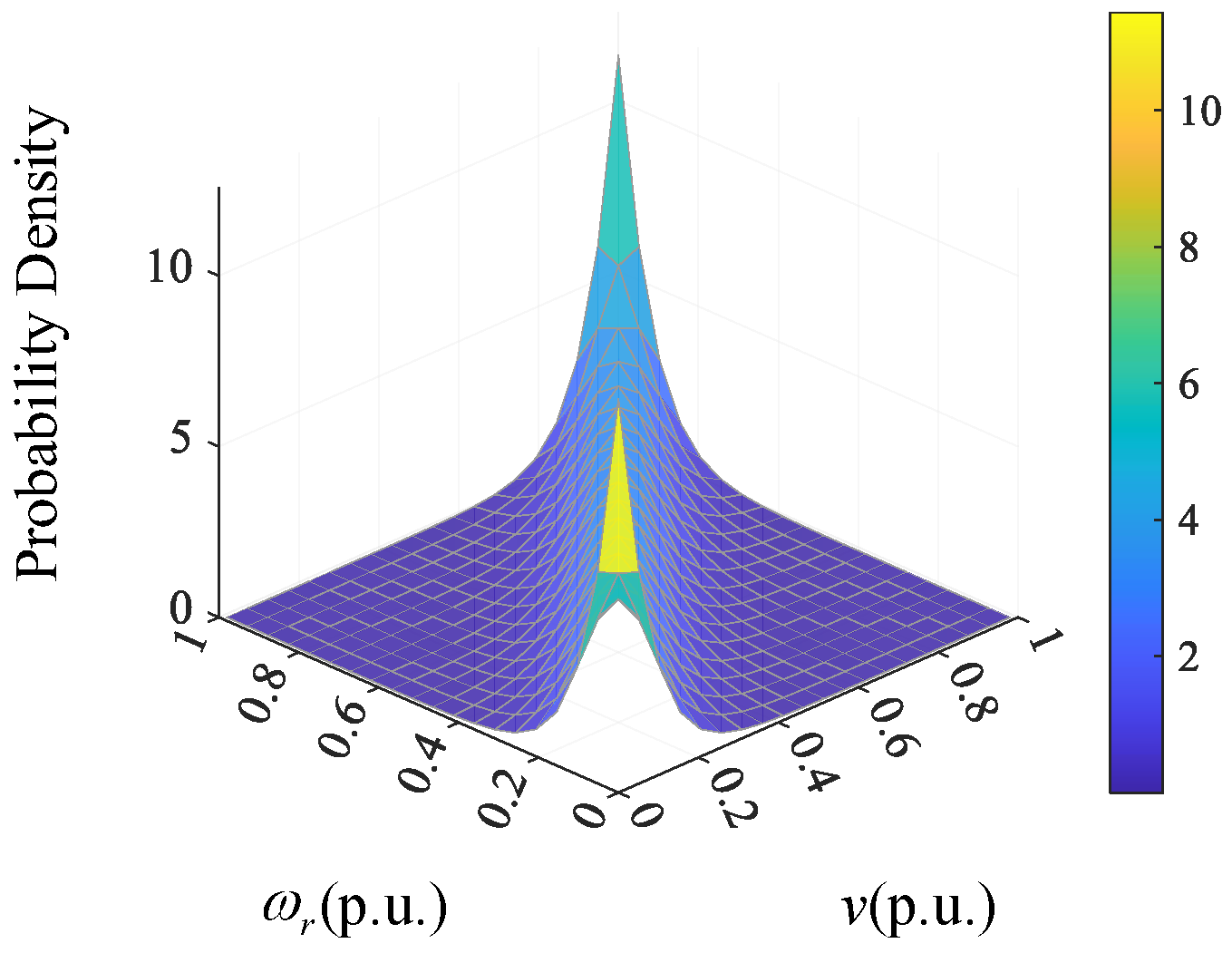
2.2. Copula-Based Modeling of Joint Probability Distribution for Wind Speed and Rotational Speed

Although the rotational speed of wind turbines exhibits probabilistic characteristics due to factors such as wake effects, time-delay effects, and wind shear effects, a certain correlation still exists between the wind farm speed and the turbine rotational speed. This section employs a Copula function to construct a joint probability distribution model for the wind farm speed and turbine rotational speed.

According to Sklar’s Theorem [18], the joint probability density function of wind farm speed and turbine rotational speed, denoted as f(v_w, ω_r) can be expressed as the product of their respective marginal density functions and a Copula function.

$$f\left(v_w,{\omega }_r\right)=c\left(F_1\left(v_w\right),F_2\left({\omega }_r\right)\right)\cdot f\left(v_w\right)\cdot f\left({\omega }_r\right)$$

(4)

Based on the marginal distributions of wind speed and rotational speed obtained in Section 2.1, a joint probability model can be constructed by selecting an appropriate Copula function.

This section employs elliptical Copulas—specifically, the Normal Copula and t-Copula—as well as Archimedean Copulas, including the Gumbel, Clayton, and Frank Copulas [19], for fitting. The probability distributions of each Copula function and their applicable data types are provided in Appendix A.

To evaluate the fitting accuracy of different Copula functions, Spearman’s and Kendall’s correlation coefficients are used for correlation analysis of the fitting results. Additionally, the squared Euclidean distance is applied to compare the fitted probability model with the original data. The formulas for calculating these coefficients are detailed in Appendix B. By integrating the above parameters, an evaluation function is constructed to uniformly assess various Copula function types and compare them with the original data. The optimal Copula function is ultimately selected for data fitting, and the computed value is denoted as Elv. A smaller Elv value indicates that the fitted joint probability model is closer to the original data, reflecting a higher degree of fitting accuracy.

$$Elv\_x={\displaystyle \frac{{(S\_x-S)}^2}{sum\_S}}+{\displaystyle \frac{{(K\_x-K)}^2}{sum\_K}}+2\cdot {\displaystyle \frac{d\_x}{sum\_\mathrm{d}}}$$

(5)

Here, S_x, K_x, d_x represent the correlation coefficients and squared Euclidean distance calculated from the selected Copula function, respectively. S and K denote the rank correlation coefficients computed from the original sample data. The terms sum_S, sum_K, sum_d are computed as follows:

$$\left\{\begin{array}{c} sum\_S={(S-S\_n)}^2+{(S-S\_t)}^2+{(S-S\_G)}^2+{(S-S\_C)}^2\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+{(S-S\_F)}^2\hfill \\ sum\_K={(K-K\_n)}^2+{(K-K\_t)}^2+{(K-K\_G)}^2+{(K-K\_C)}^2\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+{(K-K\_F)}^2\hfill \\ sum\_\mathrm{d}=d\_n+d\_t+d\_G+d\_C\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+d\_F\hfill \end{array}\right.$$

(6)

The correlation coefficients and squared Euclidean distance for each Copula function are calculated, and the evaluation function values Elv are computed as shown in

Table 1. Squared Euclidean Distance and Correlation Coefficients for Multiple Copulas.

Copula Type	Spearman Correlation Coefficient	Kendall Correlation Coefficient	Squared Euclidean Distance	Elv Value
Norm Copula	0.8335	0.7021	13.5298	0.5177
t-Copula	0.8954	0.7229	11.0272	0.3402
Gumbel Copula	0.8672	0.6889	21.2174	0.8821
Clayton Copula	0.8137	0.6289	24.7135	2.0960
Frank Copula	0.9276	0.7597	5.0905	0.1640
Original Data	0.9162	0.7409	/	/

.

Comparison with the correlation parameters of the original data reveals that, with the exception of the Clayton Copula, the rank correlation coefficients and squared Euclidean distances of the other types of Copula functions demonstrate close alignment with the original data. Among them, the Elv value computed using the Frank Copula is only 0.1640. Consequently, the Frank Copula is selected as the Copula function for fitting the wind turbine sample data. The fitted joint distribution probability density plot and distribution plot are shown in Figure 5. The figure presents the joint probability density function of wind speed v and turbine rotational speed ω_r. Through the morphology and height distribution of the density surface, it characterizes the variation and concentration of their joint probability density. The prominent probability peaks indicate the most frequent operational states. The peak near the rated rotational speed corresponds to the turbine’s primary power-generating mode, while the concentration near zero speed represents prolonged idling periods under below-cut-in wind conditions.

2.3. Conditional Probability Distribution of Rotational Speed Under Given Wind Speed

Based on the Copula function theory presented in Section 2.2, the bivariate joint probability density function of wind farm speed and turbine rotational speed can be derived as:

$$f\left(v_w,{\omega }_r\right)=c\left(u_{v_w},v_{{\omega }_r}\right)f\left(v_w\right)f({\omega }_r)$$

(7)

Based on Equation (7), the conditional probability distribution function of the turbine rotational speed under a given wind speed can be derived as:

$$F({\omega }_r|v_w)={\displaystyle \frac{{\int }_{-\infty }^{{\omega }_r}f\left({\omega }_{r1},v_w\right)\mathrm{d}{\omega }_{r1}}{f(v_w)}}$$

(8)

Differentiating the probability distribution function yields the conditional probability density function of the turbine rotational speed under given wind speed conditions as:

$$f\left({\omega }_r|v_w\right)={\displaystyle \frac{dF\left({\omega }_r|v_w\right)}{d{\omega }_r}}$$

(9)

Based on the joint probability distribution model of wind farm speed and rotor speed already fitted using the Frank Copula function, five typical wind speed values—v = 2 m/s, 4 m/s, 6 m/s, 8 m/s, and 10 m/s—were selected. These specific wind speeds were selected to represent critical operational regimes of the wind turbine: cut-in speed (2 m/s), the partial-load region (4, 6, 8 m/s), and the vicinity of the rated power (10 m/s). The corresponding conditional probability distributions of the turbine rotational speed are shown in Figure 6.

Based on the established conditional probability density functions of rotational speed under given wind speeds, the probabilistic representation of the wind turbine’s operational state is now fully characterized. This foundational model serves as the direct input for the probabilistic assessment framework developed in Section 3.

3. Probabilistic Assessment Method of Available Inertia for Wind Turbines

Wind turbines typically employ virtual inertia control to enhance their grid support capabilities [20,21]. Virtual inertia control is an enabling technique that allows inverter-based wind turbines to support grid stability. It synthesizes a response that mimics the inherent inertia of synchronous generators by temporarily regulating power output in proportion to the rate of grid frequency change. This section first assesses the equivalent inertia of the wind turbine under determined rotational speed conditions. Then, by integrating the conditional probability density function of rotational speed obtained in Section 1, a probabilistic assessment method for the available inertia of the wind turbine is proposed.

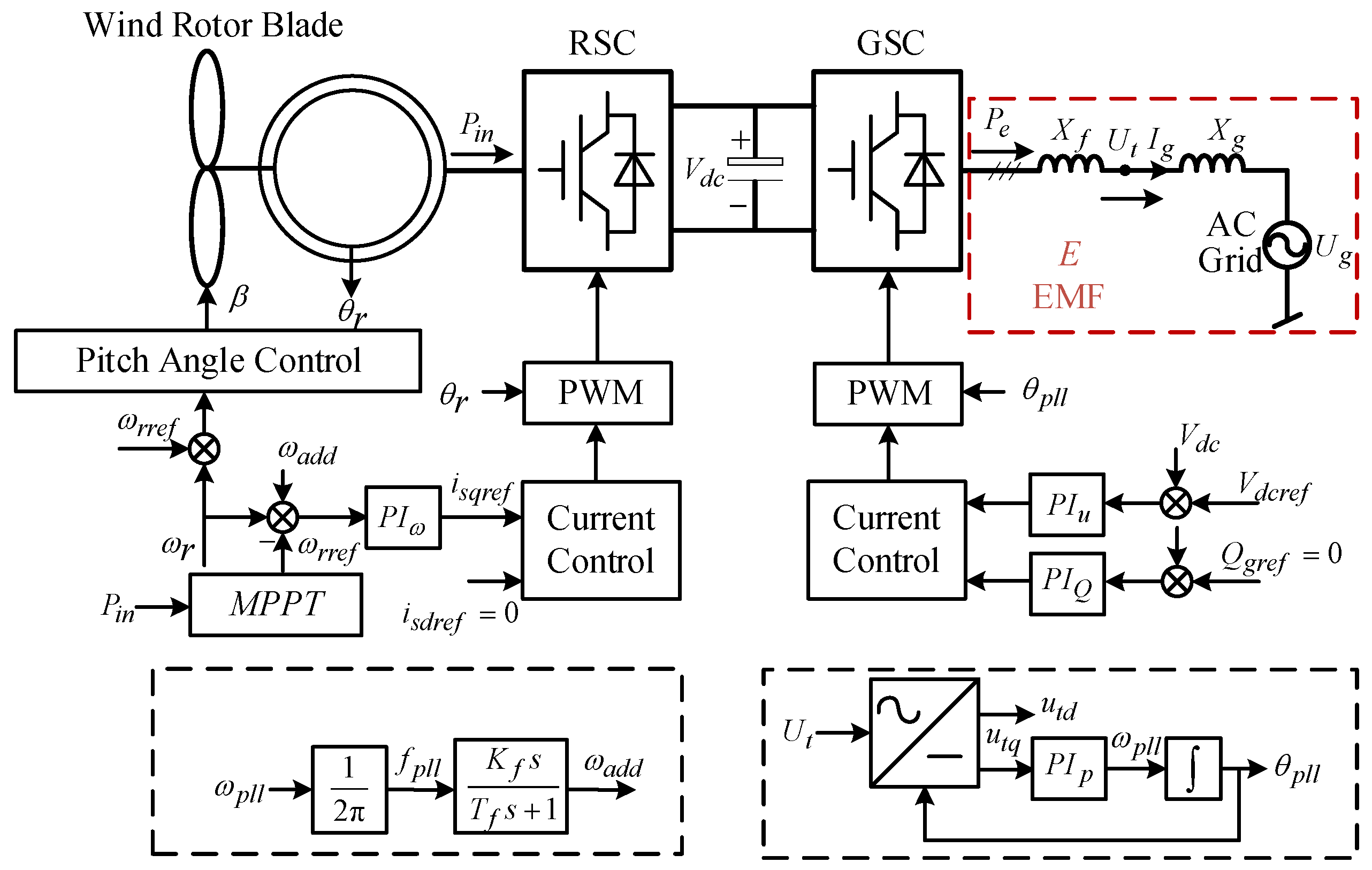
3.1. Characterization of Equivalent Inertia in Wind Turbines Under Determined Rotational Speed

This paper takes the Permanent Magnet Synchronous Generator (PMSG) as an example. Its physical and control structure is shown in Figure 7, which includes the wind rotor, the permanent magnet synchronous machine, the machine-side converter (MSC) and grid-side converter (GSC), along with their corresponding control loops.

Current research has conducted in-depth analysis of the available inertia model of wind turbines, enabling a relatively accurate characterization of the active power-frequency response process of wind turbines during inertia response. According to Zhu et al. [22], the simplified amplitude-phase motion model of the internal electromotive force (EMF) of the wind turbine is shown in Figure 8.

By analogy with the inertia of synchronous generators, the inertia transfer function of a wind turbine unit can be expressed as:

$$H(s)={\displaystyle \frac{-\frac{1}{s^2}G\frac{1}{100\pi }(M(s)+N(s))G_p}{N(s)(G_p+\frac{U_{t0}}{E_0}(1-G_p))+M(s)(K(s)N(s)G_p+1)}}$$

(10)

where

$$\left\{\begin{array}{l}G(s)={\displaystyle \frac{K(s)\cdot M(s)+\frac{U_{t0}-E_0}{E_0\cdot (1-G_p)/G_p}}{M(s)+N(s)}}\\ M(s)={\displaystyle \frac{1}{sC{V}_{dc0}}}\cdot {\displaystyle \frac{X_f}{E_0}}\cdot {\displaystyle \frac{k_{pu}s+k_{iu}}{s}}\\ N(s)={\displaystyle \frac{X_f}{E_0{U}_{t0}}}\\ G_p={\displaystyle \frac{k_{pp}s+k_{ip}}{s^2+k_{pp}s+k_{ip}}}\\ K(s)={\displaystyle \frac{\mathrm{\Delta }{P}_{in}}{\mathrm{\Delta }{\theta }_{pll}}}\end{array}\right.$$

(11)

k_pu and k_iu are PI parameters for the voltage control loop. The specific formula for K(s) is provided in Appendix B.

During the inertia response process, the virtual inertia of a wind turbine is a time-varying quantity [23]. Analyzing Equations (10) and (11), it is evident that due to the high order of the frequency-domain expression of inertia, it is difficult to directly obtain the corresponding time-domain expression through the inverse Laplace transform. To address this, a ramp-type frequency disturbance with a slope of f_r is assumed to exist in the system. Under this condition, the rate of change in the internal electromotive force angular velocity remains constant, i.e., dω/dt = constant. Based on the rotor motion equation: Jdω/dt = (P_m − P_e)/ω₀, the product term between the steady-state angular velocity and the rate of change in angular velocity under this frequency disturbance is calculated. By applying a step input of corresponding magnitude to the inertia transfer function in the MATLAB R2023a environment, the step response result represents the unbalanced active power of the system. On this basis, the computational expression for the equivalent inertia is derived as:

$$J(t)=(P_{in}-P_e)/({\omega }_0{\displaystyle \frac{\mathrm{d}\omega }{\mathrm{d}t}})$$

(12)

Furthermore, the relationship between the equivalent inertia and the virtual inertia time constant of the wind turbine is given by Equation (13). Consequently, the time-domain variation curve of the inertia time constant corresponding to the inertia response can be derived, as shown in Figure 9.

$$H={\displaystyle \frac{J{\omega }_n^2}{2S_n}}$$

(13)

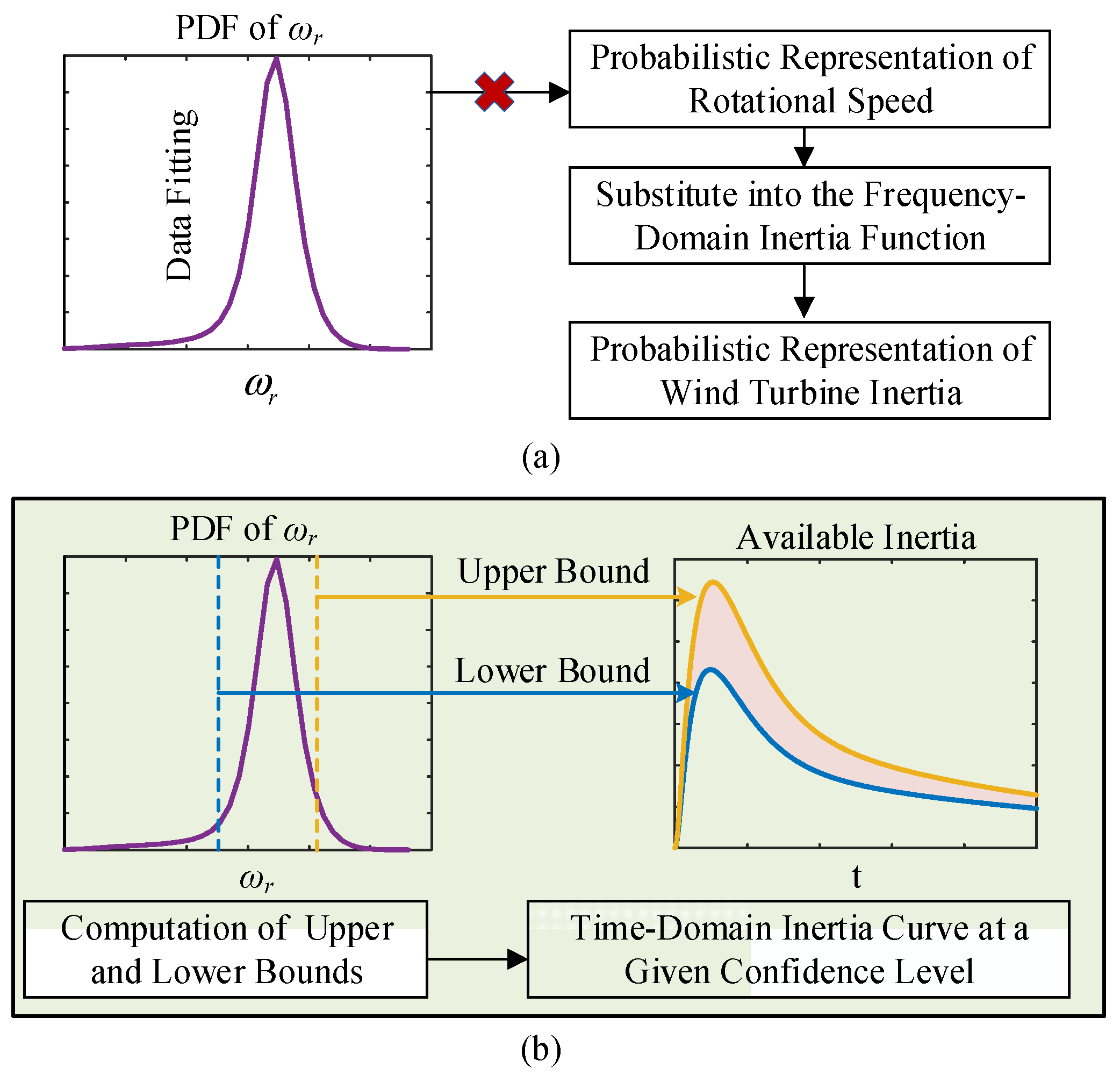
3.2. Probabilistic Assessment Framework for Wind Turbine Inertia Accounting for Rotational Speed Randomness

During wind farm operation, the combined effects of wake effects, wind shear effects, and time-delay effects cause the captured wind speed of individual turbine units to exhibit stochastic fluctuations, resulting in significant probabilistic characteristics in rotor rotational speeds. As described in Section 1, the conditional probability density function of rotational speed under given wind speed conditions has been determined using the joint and marginal probability models established in Equations (7)–(9). However, since this density function is empirically fitted from measured data and lacks an explicit analytical expression, it cannot be directly substituted into the inertia expression Equation (10) to derive the probability density function of inertia, as shown in Figure 10a.

As shown in Figure 10b, to probabilistically characterize wind turbine inertia, the confidence interval of rotational speed can be calculated through interval assessment of the rotational speed probability density function [24]. Existing literature predominantly employs the central confidence interval to represent probabilistic assessment results [25,26]. The calculation method is as follows: set the rotational speed confidence level α, and then apply the bisection search-numerical integration method to determine the lower and upper quantiles of the confidence interval, (1 − α)/2 and (1 + α)/2:

$$P(a\le X\le b)={\displaystyle {\int }_a^{b}f(x)\mathrm{d}x}=\alpha$$

(14)

$$P(X<a)={\displaystyle \frac{1-\alpha }{2}},P(X>b)={\displaystyle \frac{1-\alpha }{2}}$$

(15)

where α represents the confidence level, a denotes the lower quantile of the confidence interval, b denotes the upper quantile of the confidence interval.

Taking the calculation of the lower quantile (1 − α)/2 as an example, the detailed procedure of the bisection search-numerical integration method is illustrated in Figure 11.

Numerical integration is primarily approximated using the following formula:

$$F(\omega )\approx {\displaystyle \sum _{i=1}^n\frac{f(t_{i-1})+f(t_i)}{2}\cdot \mathrm{\Delta }t}$$

(16)

where t₀ = ω_min, t_n = ω, Δt = (ω − ω_min)/n.

After obtaining the rotational speed confidence interval for a given confidence level, the upper and lower bounds of the rotational speed are subsequently substituted into the inertia expression (11) to derive the upper and lower bounds of the wind turbine’s available inertia response curve under that confidence level.

The overall workflow of the probabilistic assessment model for available inertia is illustrated in Figure 12. The specific steps are as follows:

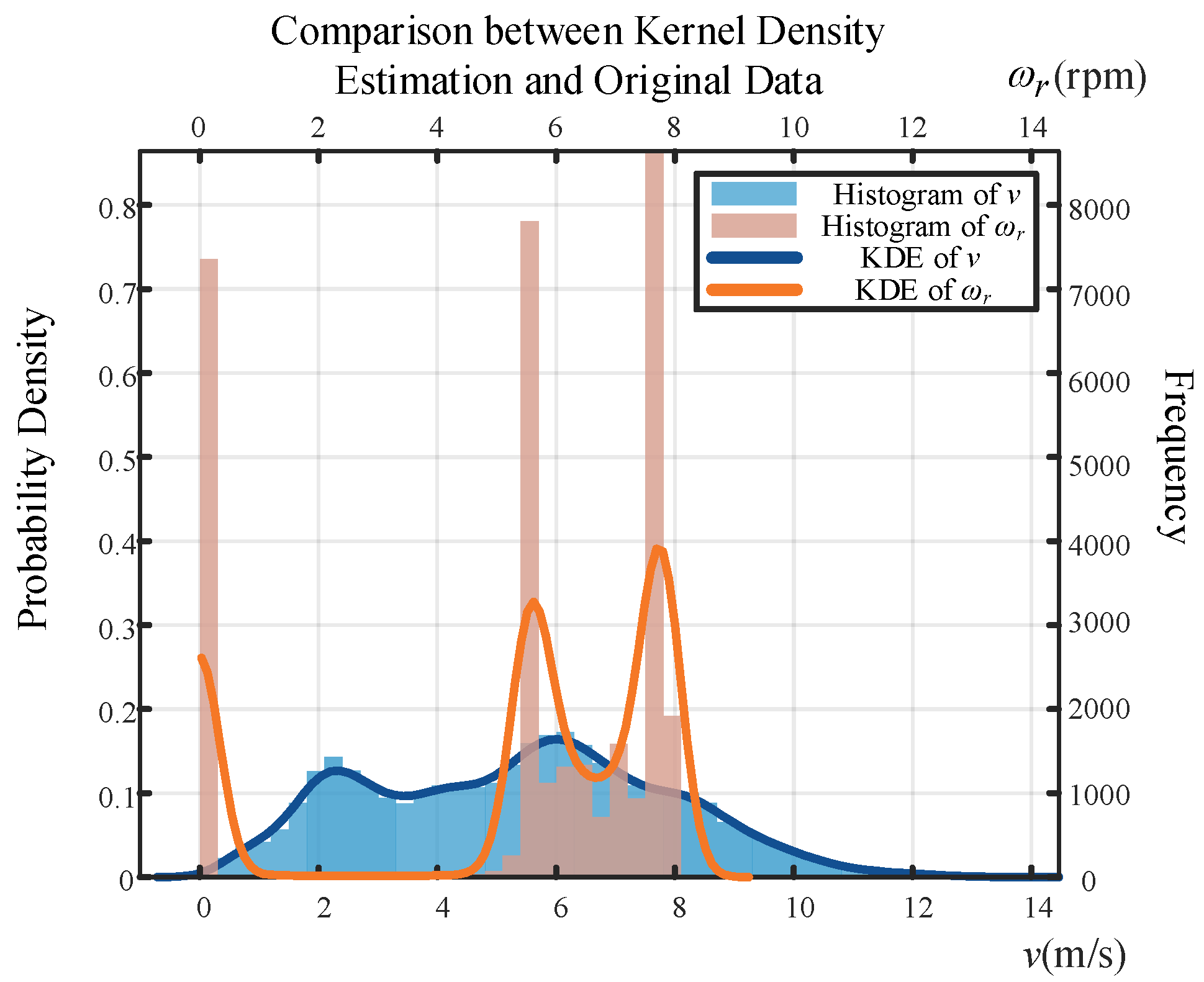
• Collect sample data and utilize kernel density estimation to approximate the discrete samples, determining the marginal probability density functions of wind farm speed and wind turbine rotational speed.
• Employ a Copula function to model the correlation between the marginal distributions, selecting the optimal Copula via an evaluation function to establish the joint probability distribution.
• Apply the bisection search-numerical integration method to compute the confidence interval of the rotational speed.
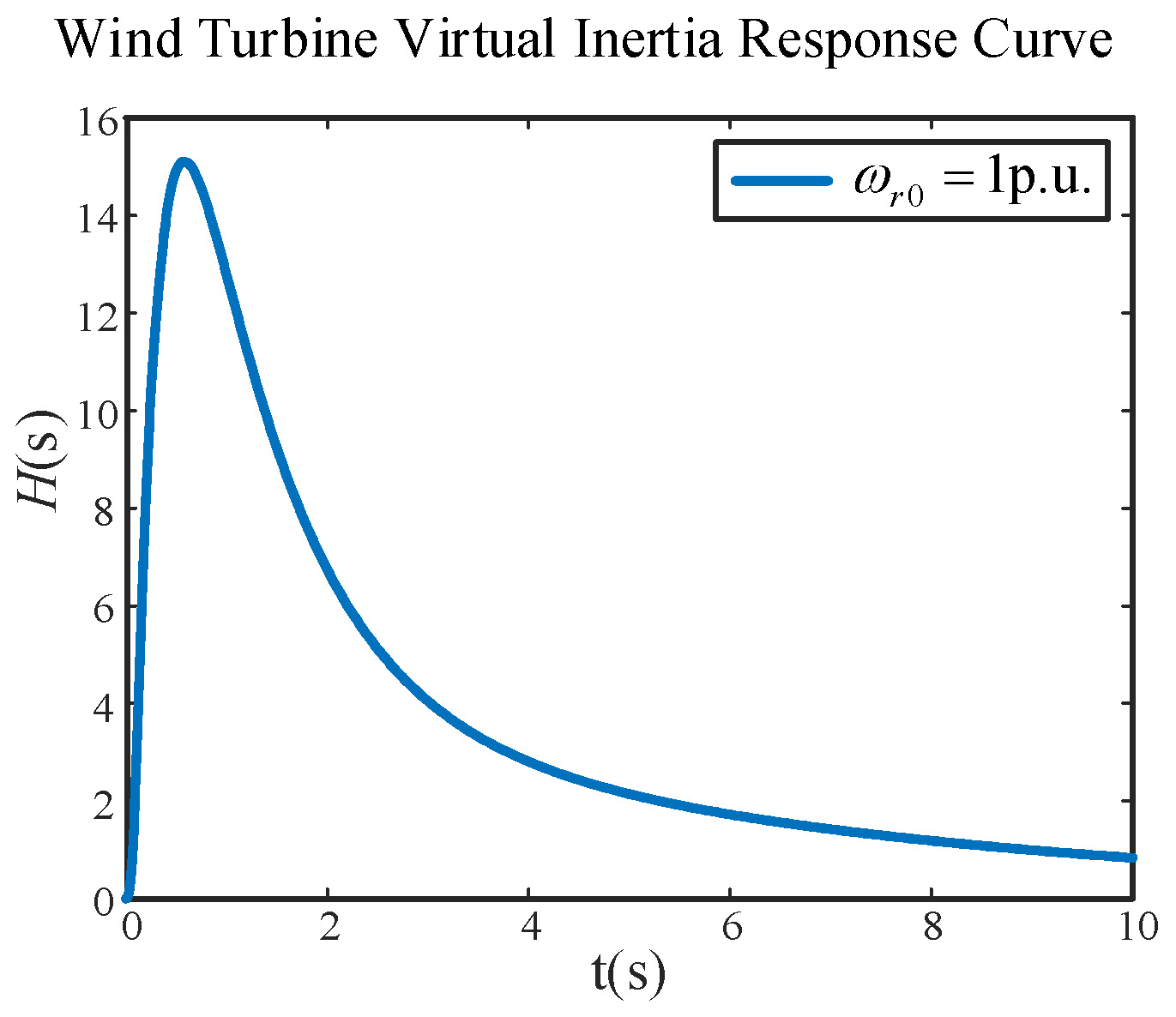
• Substitute the results into the inertia expression to obtain the upper and lower bounds of the wind turbine’s available inertia response curve for a specific confidence level α, ultimately achieving a probabilistic characterization of the wind turbine’s available inertia.

4. Case Study

The data source, sampling frequency, and duration of the operational data used in this case study are detailed in Section 2.1. To validate the accuracy of the proposed probabilistic assessment method for wind turbine inertia during operational conditions, a turbine simulation model was built in MATLAB/Simulink to probabilistically evaluate the unit’s inertia. Key parameters of the simulation model are provided in Appendix B.

Based on the probability density function of rotational speed under given wind speed conditions shown in Figure 5, the conditional probability distribution of rotational speed was obtained. Numerical integration was then applied to fixed rotational speed intervals, yielding the probabilities of different rotational speed ranges under various wind speeds, as presented in

Table 2. Probability Distribution over Rotational Speed Bins.

v (m/s)	ωr (p.u.)
	[0.5, 0.625]	[0.625, 0.75]	[0.75, 0.875]	[0.875, 1]	[1, 1.125]
2	0.0263	0.0960	0.0026	0.0004	2.14 × 10−6
4	0.0396	0.6402	0.0606	0.0090	5.46 × 10−5
6	0.0014	0.1610	0.4358	0.2891	0.0025
8	3.0 × 10−5	0.0042	0.0338	0.7692	0.1031
10	4.4 × 10−6	0.0006	0.0051	0.3945	0.4362

.

Based on the interval probability data in Table 2, a probabilistic model of wind turbine inertia is developed. Taking the condition of 8 m/s wind speed as an example, the results are shown in Figure 13.

Employing the bisection search-numerical integration method with a confidence level set at 90%, the lower and upper bounds of rotational speed under different wind speed conditions are computed. Figure 14 incorporates these rotational speed bounds into the conditional probability density function of rotational speed.

After obtaining the confidence interval and substituting it into the inertia transfer function, the time-domain inertia curve shown in Figure 15 is derived. There exists a 90% probability that the actual inertia of the wind turbine during inertia response falls within the shaded pink region in the figure.

Finally, validation of the probabilistic assessment results for the wind turbine’s available inertia—derived from February data—was conducted using March operational data from the same wind farm. The specific validation procedure involves selecting data corresponding to typical wind speed values from March, substituting them into the inertia assessment model constructed with February data, and comparing the actual inertia values against the assessment results. This comparison is illustrated in Figure 16.

It can be observed that the actual values of inertia response all fall within the 90% confidence interval. Taking wind speed v = 6 m/s as an example, there is a 90% probability that the maximum available system inertia lies between 10.7 s and 14.5 s. The actual available system inertia calculated based on March operational data is 12.3 s, which lies within the predicted interval for the system’s available inertia, thereby validating the correctness of the proposed inertia assessment method. However, if the assessment were based on the MPPT rotational speed corresponding to the average wind speed, the calculated available inertia of the wind turbine at this wind speed would be 11.5 s, deviating from the actual value by 6.5%. A quantitative comparison at other wind speeds follows the same procedure, demonstrating consistent superiority of the probabilistic method, but is omitted here for brevity. Consequently, if the assessment results of the wind turbine’s available inertia that do not account for rotational speed randomness were directly used as a basis for grid dispatch, issues such as failure to meet support requirements or excessive margin would arise. In summary, these findings demonstrate that the probabilistic assessment results for wind turbine inertia proposed in this paper exhibit high accuracy and can provide grid dispatch operators with more precise frequency support assessment data.

5. Conclusions

This paper addresses the ambiguous correlation between wind farm speed and turbine rotational speed caused by wake effects, time-delay effects, and wind shear effects, as well as the inertia uncertainty arising from rotational speed randomness. A probabilistic assessment method for the available inertia of wind turbines is proposed and validated using actual operational data from a wind farm. The main conclusions are as follows:

• A joint probability distribution model for wind farm speed and turbine rotational speed was developed using kernel density estimation and Copula function fitting, accurately characterizing the probabilistic distribution characteristics of turbine rotational speed under given wind speed conditions.
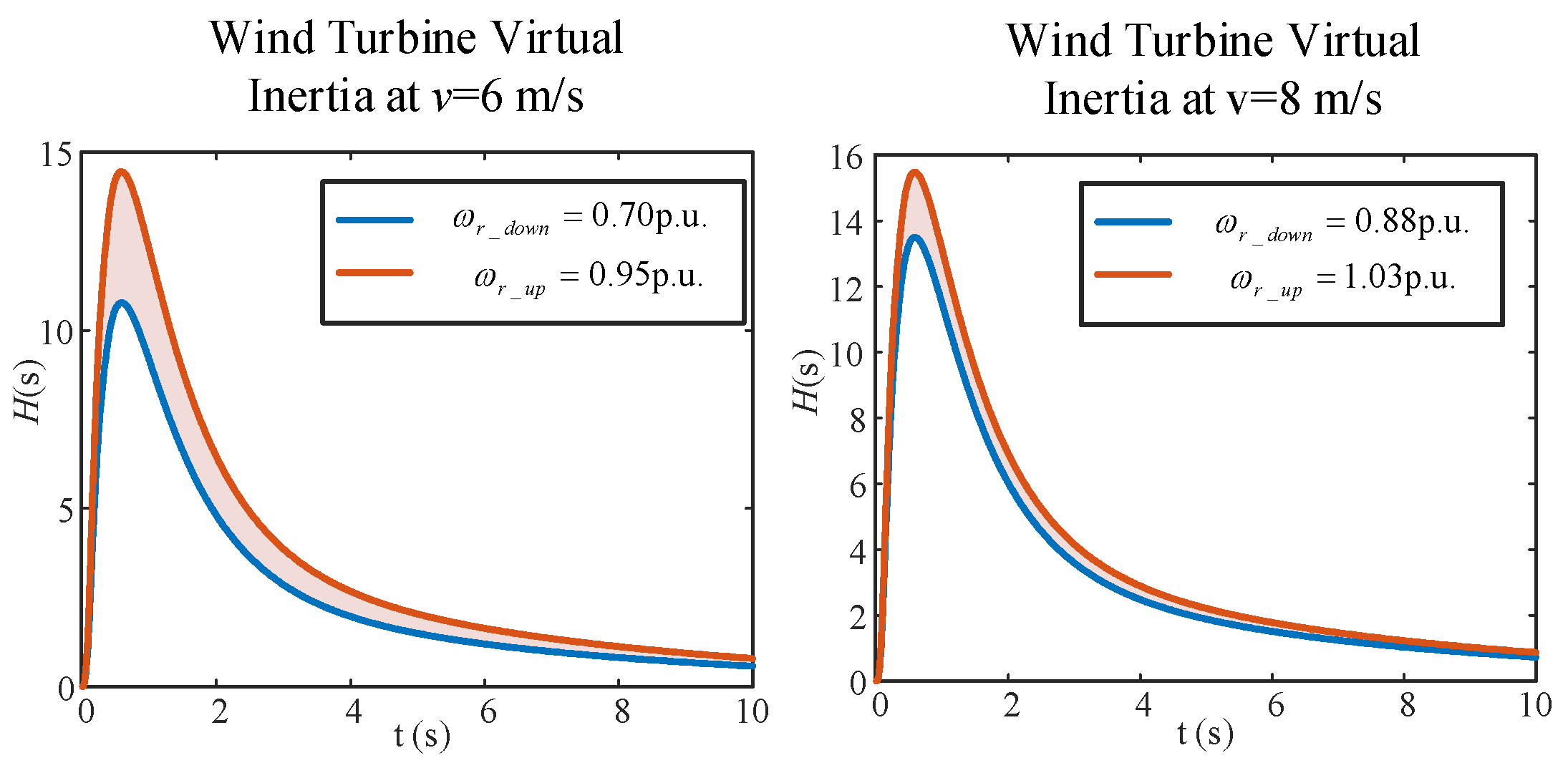
• A probabilistic assessment method for the available inertia of wind turbines was proposed by integrating the conditional probability density function of rotational speed. The actual operational data from a wind farm in Zhejiang Province of China fully validated the correctness of the proposed probabilistic assessment method. Case study results demonstrate the method’s superior reliability, successfully enclosing the actual inertia (12.3 s) within the 90% confidence band, whereas a conventional MPPT-speed-based assessment yields a 6.5% error under a 6 m/s wind speed condition.

Still, this work has certain limitations that suggest valuable future research. Potential extensions include applying the probabilistic framework to Doubly Fed Induction Generator (DFIG) systems, incorporating spatial correlation effects across multiple wind farms, and enhancing computational efficiency for real-time applications.