Algorithmic Design of Modular Two-Layer Multiphase Windings Based on Number Theory
Abstract
1. Introduction
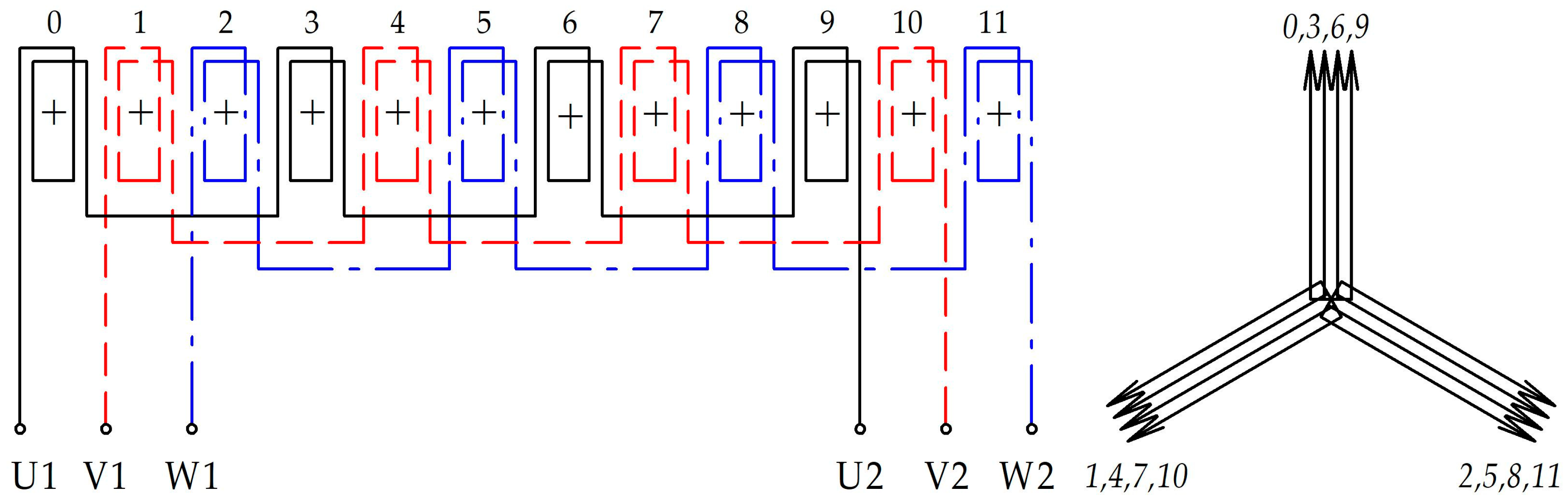
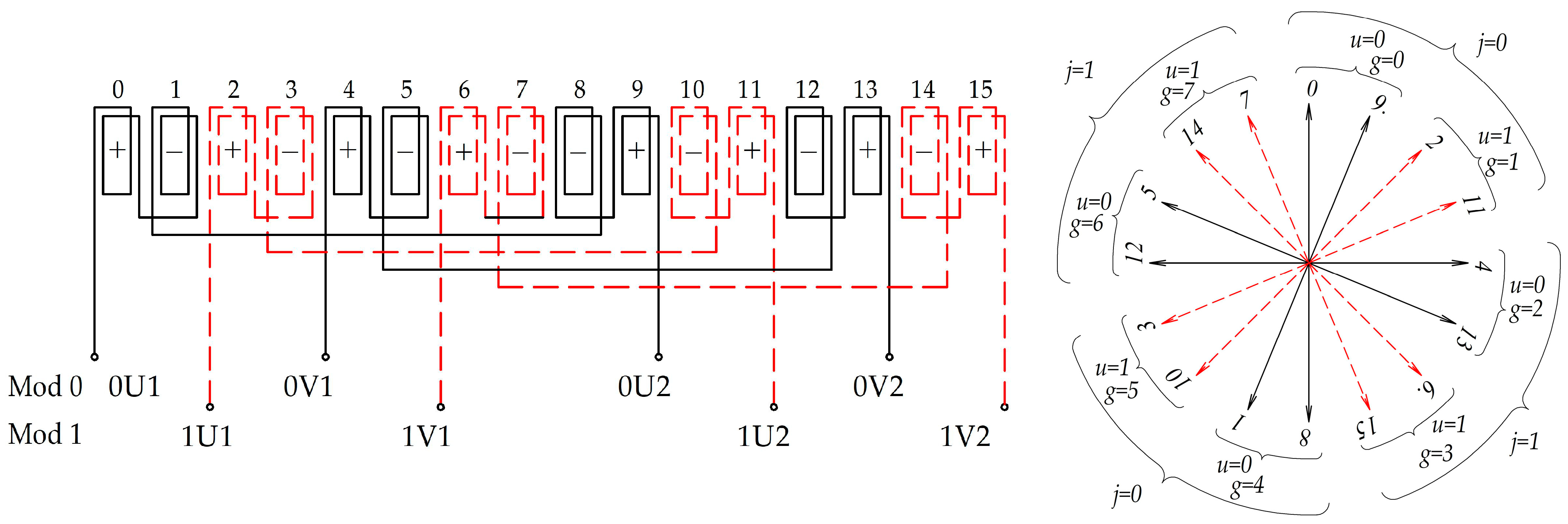
2. Algorithm for the Synthesis of Symmetrical Windings
2.1. Case d = p
2.2. Case d = 1
2.3. Case 1 < d < p
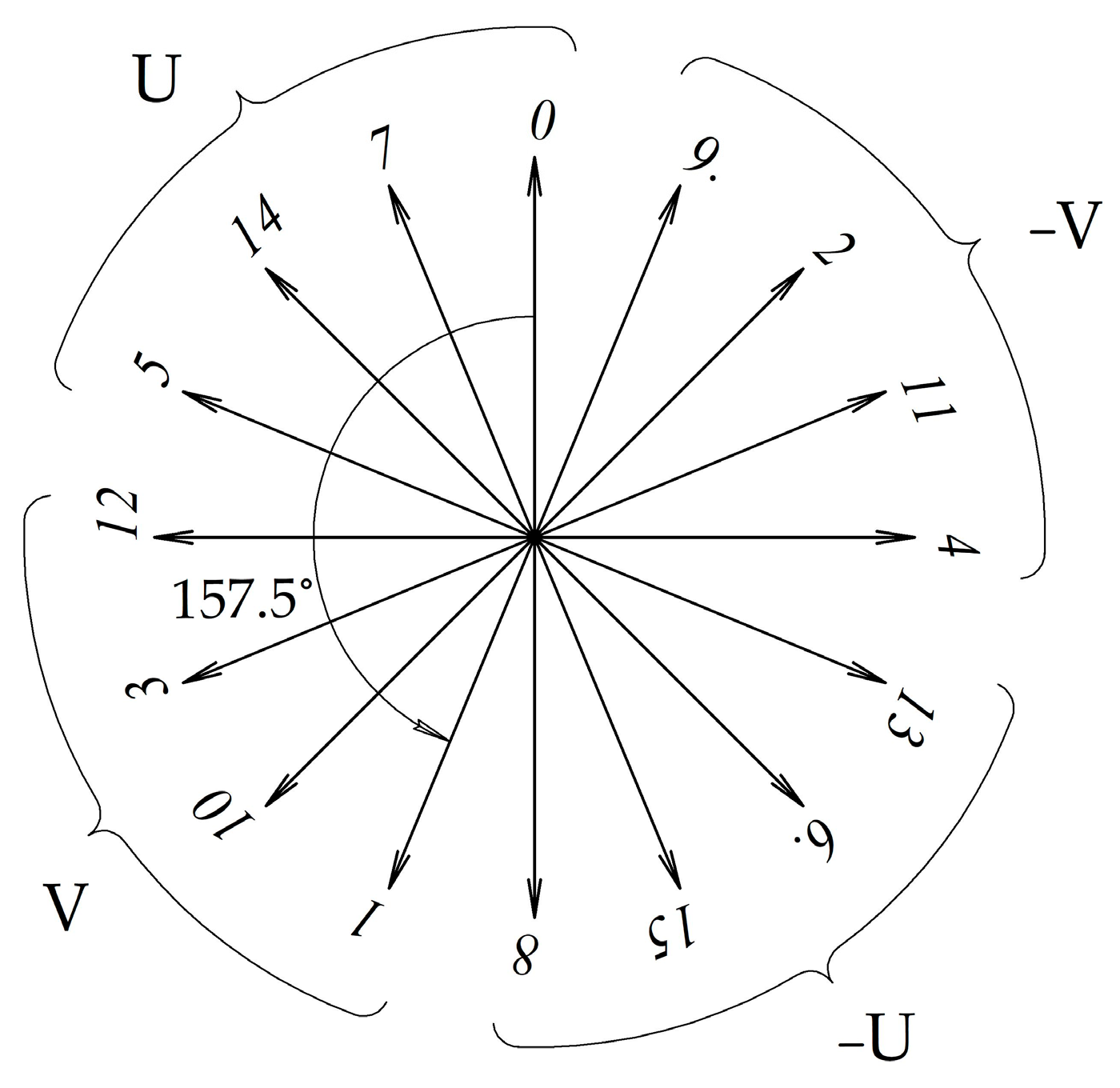
3. Distribution Factors of Modular Windings
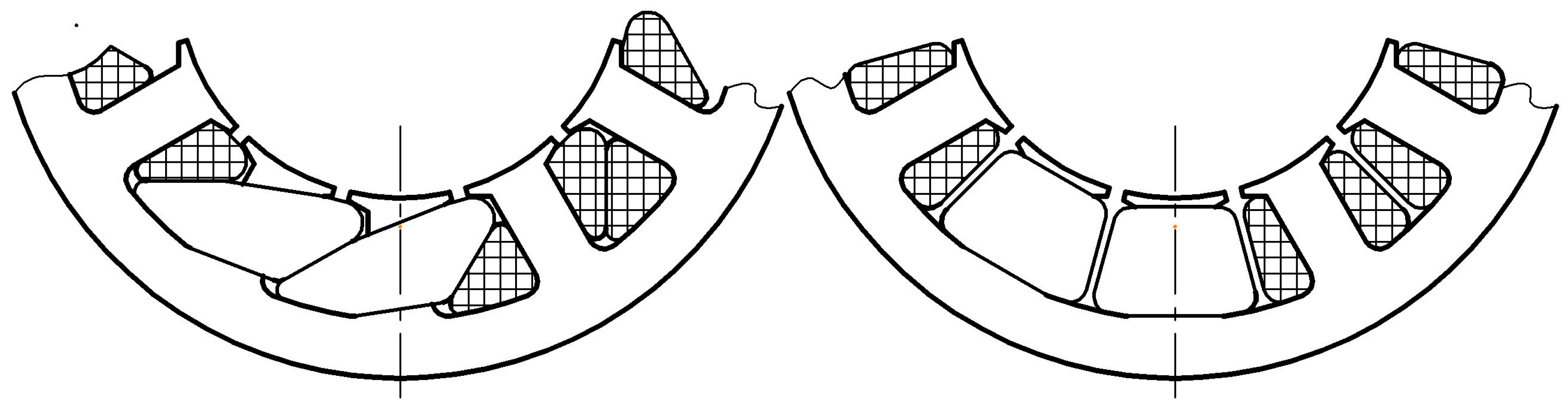
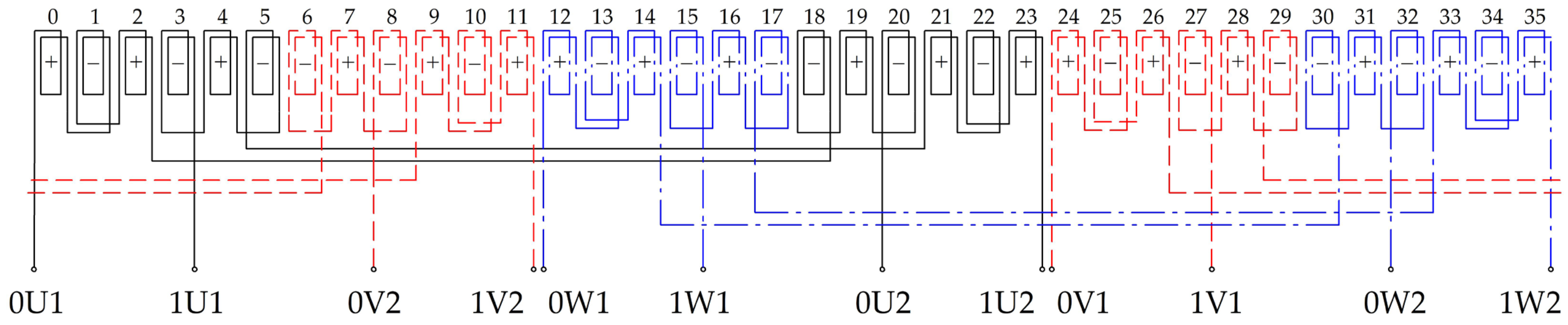
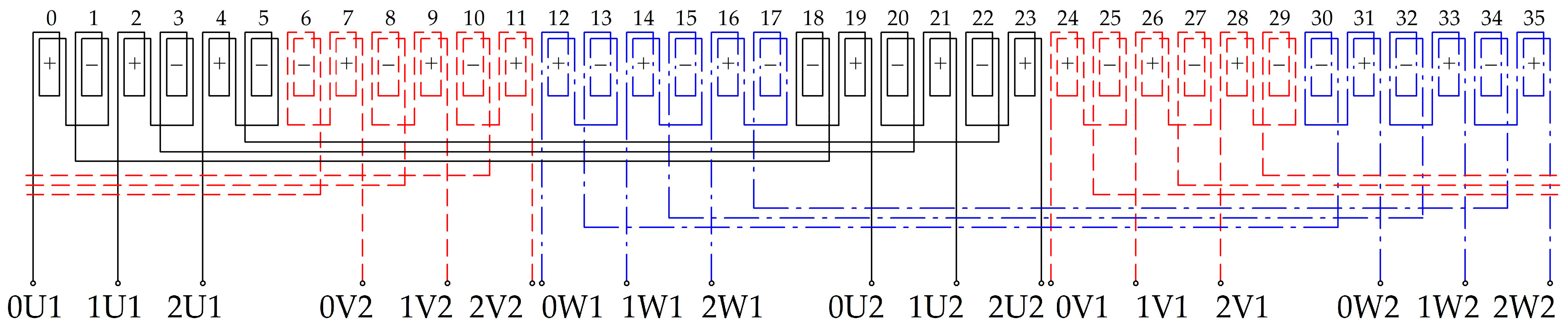
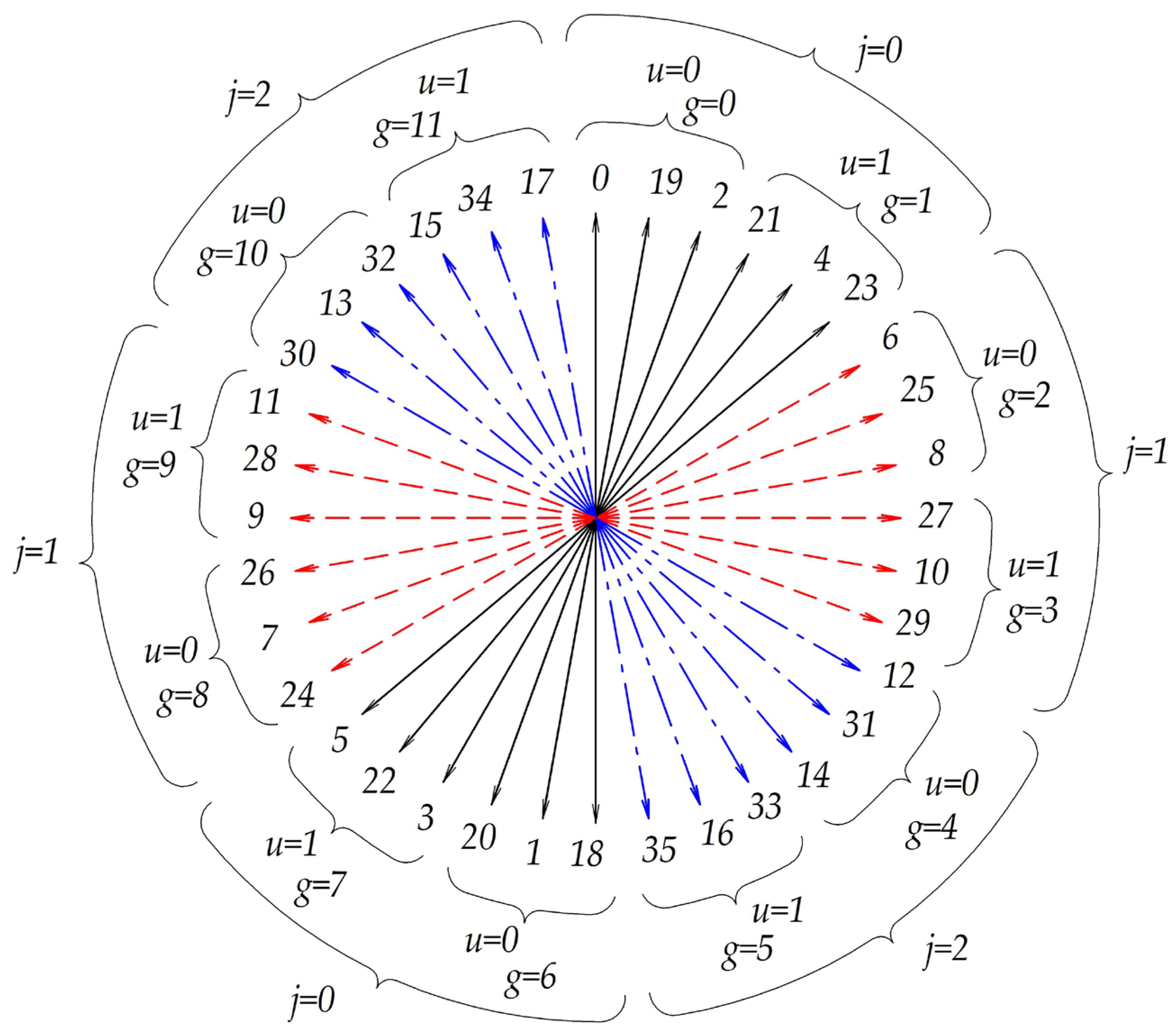
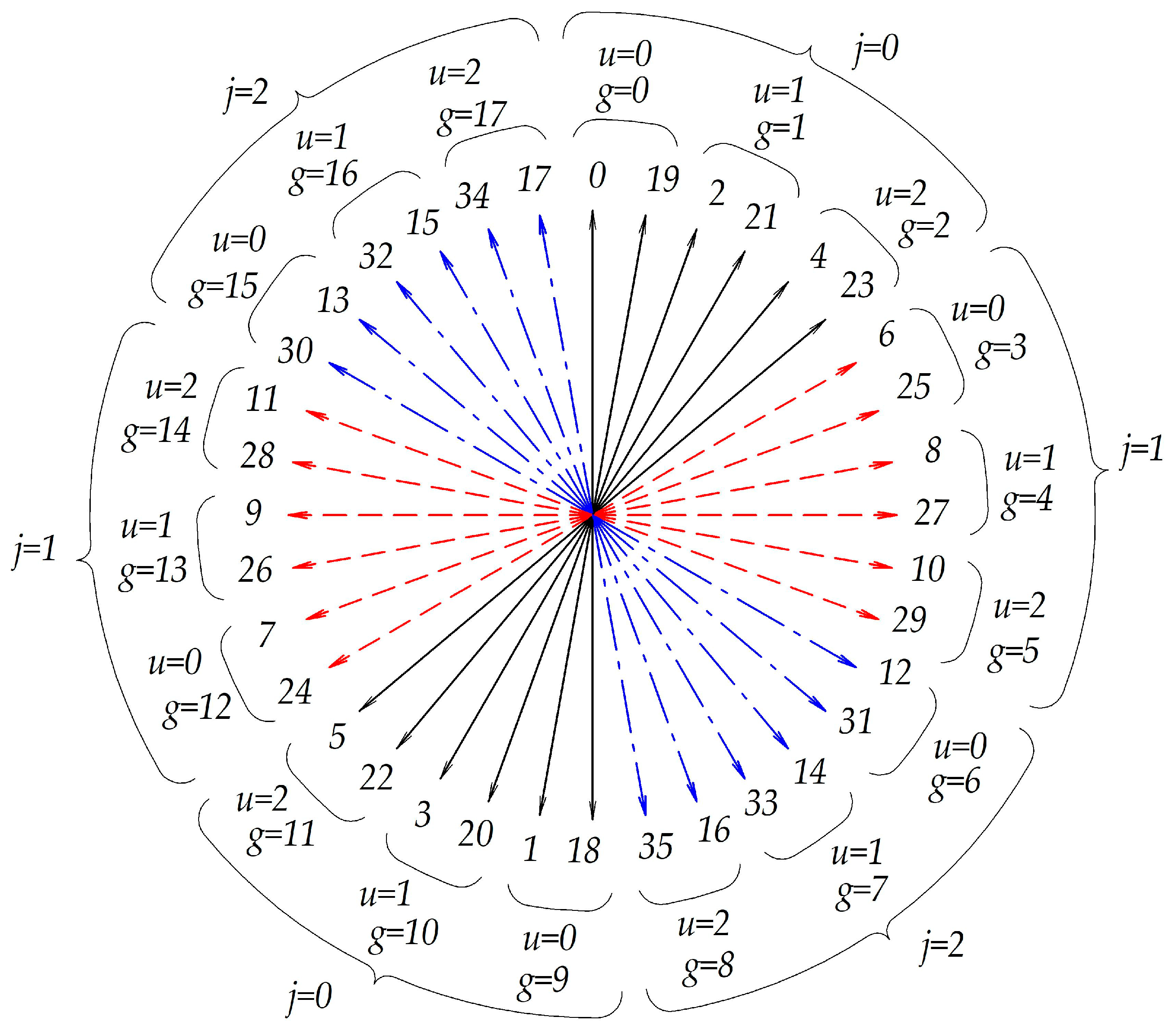
4. Examples of Applying the Winding Synthesis Algorithm
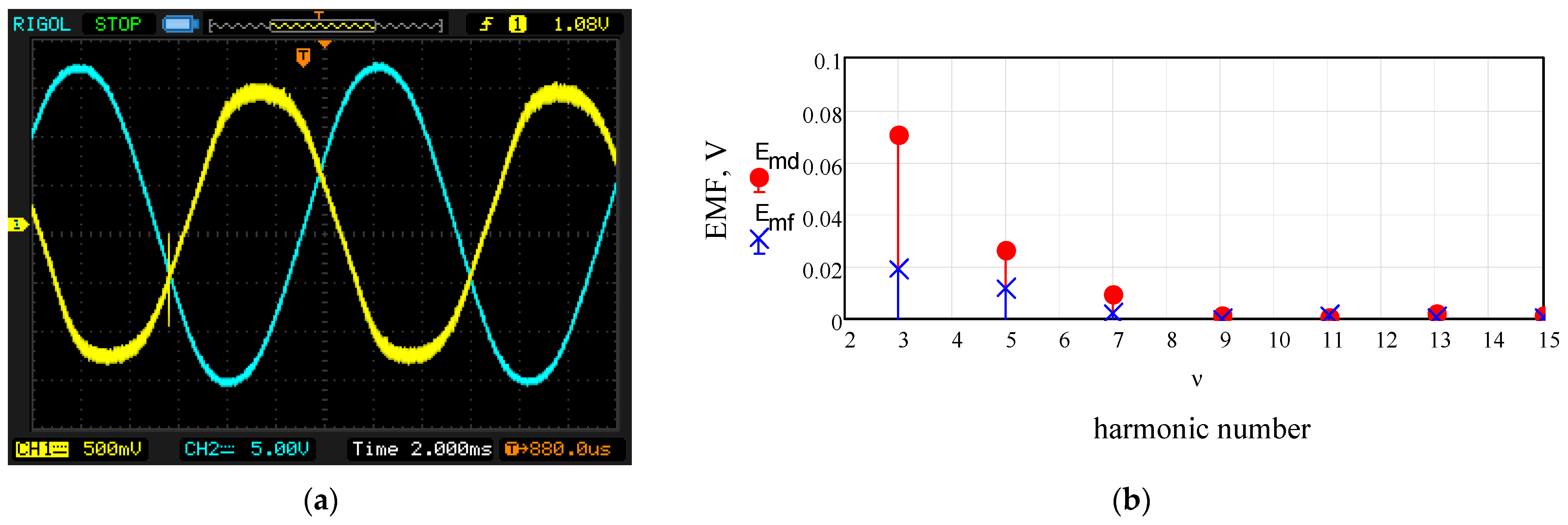
5. Experimental Studies
6. Conclusions
- The algorithmic method based on number theory is simple to apply and suitable for formalizing and automating the synthesis of the structure of multi-phase, multi-module, two-layer windings, as well as for preliminary engineering analysis.
- The star of coil EMFs should be used only for illustrative theoretical generalizations, teaching, explanations, and comparisons.
- The use of coil EMFs, rather than slot EMFs, is universal. The star of coil EMFs has S/d vectors evenly distributed, which are repeated d-fold, allowing the winding to be divided into d separate modules without angular displacement.
- A necessary condition for constructing a symmetrical AC winding is that the number of slots S be a multiple of the product of the number of phases m, the number of modules χ, and the divisor d.
- Using windings with S and p ratios that have a common divisor d > 1 is undesirable, as it increases EMF and electromagnetic torque ripples and deteriorates the filtering properties of the winding for higher harmonics if d is not a prime number.
- A two-zone winding allows doubling the number of modules without angular displacement, regardless of the S/d ratio.
- Using modular windings with angularly shifted modules increases the winding factor.
- Future research will focus on generalizing the algorithmic design method to single-layer, mixed single–double-layer, and multilayer windings.
7. Patents
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sun, Y.; Lin, Y.; Wang, Y.; Nilssen, R.; Shen, J.-X. Theory of symmetric winding distributions and a general method for winding MMF harmonic analysis. IET Electr. Power Appl. 2020, 14, 2587–2597. [Google Scholar] [CrossRef]
- Pyrhonen, J.; Jokinen, T.; Hrabovcova, V. Design of Rotating Electrical Machines; John Wiley & Sons: Chichester, UK, 2008; p. 531. ISBN 978-0-470-69516-6. [Google Scholar]
- Caruso, M.; Di Tommaso, A.O.; Marignetti, F.; Miceli, R. A general investigation on the differential leakage factor for symmetrical and asymmetrical multiphase winding design. Energies 2020, 13, 5414. [Google Scholar] [CrossRef]
- Rudden, G.-J.; Li, Z.-Q.; Zhu, Z.; Duke, A.; Clark, R. Fractional-slot concentrated windings for offshore wind turbine generators: Opportunities and challenges. IEEE Access 2024, 12, 158766–158787. [Google Scholar] [CrossRef]
- Raziee, S.M.; Steinbrink, J.; Ponick, B. Winding factor equation for main pattern of single-layer fractional-slot distributed windings. IEEE Trans. Energy Convers. 2024, 39, 988–998. [Google Scholar] [CrossRef]
- Germishuizen, J.; Kremser, A. Algebraic design of symmetrical windings for AC machines. IEEE Trans. Ind. Appl. 2021, 57, 1928–1934. [Google Scholar] [CrossRef]
- Petrov, I.; Di, C.; Lindh, P.; Niemelä, M.; Repo, A.K.; Pyrhönen, J. Fault-tolerant modular stator concentrated winding permanent magnet machine. IEEE Access 2020, 8, 7806–7816. [Google Scholar] [CrossRef]
- Caruso, M.; Di Tommaso, A.O.; Marignetti, F.; Miceli, R.; Galluzzo, G.R. A general mathematical formulation for winding layout arrangement of electrical machines. Energies 2018, 11, 446. [Google Scholar] [CrossRef]
- Xia, Y.; Wen, Z.; Zhu, Z.; Zhong, S.; Chen, Y.; Zhang, J. Research on a hybrid excitation PM synchronous generator with stator third harmonic winding excitation. IET Electr. Power Appl. 2020, 14, 418–425. [Google Scholar] [CrossRef]
- Nishanth, F.; Khamitov, A.; Severson, E.L. Design of electric machine windings to independently control multiple airgap harmonics. IEEE Trans. Ind. Appl. 2023, 60, 3039–3050. [Google Scholar] [CrossRef]
- Tang, N.; Brown, I.P. Family phenomenon in electric machine winding MMF space harmonics: Attribution and applications. IEEE Trans. Magn. 2019, 55, 1–10. [Google Scholar] [CrossRef]
- Scuiller, F. General, compact and easy-to-compute winding factor formulation. IET Electr. Power Appl. 2020, 14, 1430–1437. [Google Scholar] [CrossRef]
- Campagna, N.; Caruso, M.; Di Tommaso, A.O.; Miceli, R. A comprehensive generalized theory and classification of multiphase systems for rotating and linear electric machines. IEEE Trans. Energy Convers. 2024, 39, 2769–2780. [Google Scholar] [CrossRef]
- Babei, O.B.; Kharchyshyn, B.M.; Khai, M.V. Winding construction algorithms multipole electric machines. Electr. Power Electromech. Syst. 2024, 6, 1–10. [Google Scholar] [CrossRef]
- Wach, P. Algorithmic method of design and analysis of fractional-slot windings of AC machines. Electr. Eng. 1998, 81, 163–170. [Google Scholar] [CrossRef]
- Vann, J.D.; Ge, B. Tensor representation of electric machine windings and its connection with winding functions. In Proceedings of the 2024 IEEE Energy Conversion Congress and Exposition (ECCE), Phoenix, AZ, USA, 20–24 October 2024; pp. 5675–5681. [Google Scholar]
- Makarchuk, O.; Kharchyshyn, B.; Kasha, L. Analysis of the magneto-mechanical characteristic of double three-phase PMSM. In Proceedings of the 2021 IEEE 3rd Ukraine Conference on Electrical and Computer Engineering (UKRCON), Lviv, Ukraine, 26–28 August 2021; pp. 333–338. [Google Scholar] [CrossRef]
- Yu, J.; Yang, J.; Li, Q.; Zhao, X.; Huang, S. Influence of phase shift angle on performance of permanent-magnet machine with multiple star-delta windings for electric vehicle drive. IEEE Trans. Transp. Electr. 2025, 11, 9949–9962. [Google Scholar] [CrossRef]
- Shchur, I.; Kharchyshyn, B.; Turkovskyi, V. Simulation and experimental investigation of dual three-phase BLDC motor operation at imbalanced modular loading. Tekh. Elektrodyn. 2023, 3, 22–31. [Google Scholar] [CrossRef]
- Rao, Z.; Zhang, W.; Wu, G.; Zheng, J.; Huang, S. Characteristic analysis and predictive torque control of the modular three-phase PMSM for low-voltage high power application. Energies 2020, 13, 5606. [Google Scholar] [CrossRef]
- Kutsyk, A.; Korkosz, M.; Bogusz, P.; Semeniuk, M.; Lozynskyy, A. An Analysis of Asymmetrical and Open-Phase Modes in a Symmetrical Two-Channel Induction Machine with Consideration of Spatial Harmonics. Energies 2024, 17, 870. [Google Scholar] [CrossRef]
- Shchur, I.; Mazur, D.; Makarchuk, O.; Bilyakovskyy, I.; Turkovskyi, V.; Kwiatkowski, B.; Kalandyk, D. Improved Matlab/Simulink model of dual three-phase fractional slot and concentrated winding PM motor for EV applied brushless DC drive. Arch. Control Sci. 2022, 32, 677–707. [Google Scholar]
- Wang, Y.; Yin, D.; Zhou, Y. Magnetomotive force decomposition and harmonic analysis of fractional-slot concentrated winding. In Proceedings of the IEEE 8th Asia Conference on Power and Electrical Engineering (ACPEE), Tianjin, China, 14–16 April 2023; pp. 2212–2216. [Google Scholar] [CrossRef]
- Rudden, A.; Li, G.J.; Zhu, Z.Q.; Duke, A.; Clark, R.; Thomas, A. General design rules for space harmonic cancellation in multiphase machines with multiple converters and star-polygonal windings. IEEE Trans. Energy Convers. 2025, 40, 544–556. [Google Scholar] [CrossRef]
- Caruso, M.; Di Tommaso, A.O.; Miceli, R.; Rizzo, R. The use of slightly asymmetrical windings for rotating electrical machines. Int. Trans. Electr. Energy Syst. 2018, 28, 1–19. [Google Scholar] [CrossRef]
- Islam, M.S.; Kabir, M.A.; Mikail, R.; Husain, I. A systematic approach for stator MMF harmonic elimination using three-layer fractional slot winding. IEEE Trans. Ind. Appl. 2020, 56, 3516–3525. [Google Scholar] [CrossRef]
- Tessarolo, A.; Ciriani, C.; Bortolozzi, M.; Mezzarobba, M.; Barbini, N. Investigation into multi-layer fractional-slot concentrated windings with unconventional slot-pole combinations. IEEE Trans. Energy Convers. 2019, 34, 1985–1996. [Google Scholar] [CrossRef]
- Jung, Y.-H.; Kim, D.-M.; Cha, K.-S.; Park, S.-H.; Park, M.-R. Vibration reduction of permanent magnet synchronous motors by four-layer winding: Mathematical modeling and experimental validation. Mathematics 2025, 13, 1603. [Google Scholar] [CrossRef]
- Silva, A.M.; Ferreira, F.J.T.E.; Cistelecan, M.V.; Antunes, C.H. Multiobjective design optimization of generalized multilayer multiphase AC winding. IEEE Trans. Energy Convers. 2019, 34, 2158–2167. [Google Scholar] [CrossRef]
- Kharchyshyn, B.M.; Shchur, I.Z.; Makarchuk, O.V.; Khai, M.V. Method of Constructing Non-Cross Windings of Multipole Electrical Machines of Alternating Current. Ukrainian Patent No. 129784, 30 July 2025. Bulletin No. 31/2025. [Google Scholar]
- Sivaramakrishnan, R. Certain Number-Theoretic Episodes in Algebra, 2nd ed.; Chapman and Hall/CRC: Boca Raton, FL, USA, 2019. [Google Scholar] [CrossRef]


| i | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| n | 0 | 5 | 1 | 6 | 2 | 7 | 3 | 8 | 4 | 0 | 5 | 1 | 6 | 2 | 7 | 3 |
| l(i) | 0 | 9 | 2 | 11 | 4 | 13 | 6 | 15 | 8 | 1 | 10 | 3 | 12 | 5 | 14 | 7 |
| g(i) | 0 | 4 | 1 | 5 | 2 | 6 | 3 | 7 | 4 | 0 | 5 | 1 | 6 | 2 | 7 | 3 |
| j(i) | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| u(i) | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| sign | 1 | −1 | 1 | −1 | 1 | −1 | 1 | −1 | −1 | 1 | −1 | 1 | −1 | 1 | −1 | 1 |
| S | p | d | S/d | Kdν=1 | ys | Kpν=1 | Kwν=1 | Kdν=3 | Kpν=3 | Kwν=3 | Kdν=5 | Kpν=5 | Kwν=5 | Kdν=7 | Kpν=7 | Kwν=7 | Kdν=9 | Kpν=9 | Kwν=9 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 36 | 20 | 4 | 9 | 0.960 | 1 | 0.985 | 0.945 | 0.667 | 0.866 | 0.577 | 0.218 | 0.643 | 0.140 | −0.177 | 0.342 | 0.061 | −0.333 | 0 | 0 |
| 36 | 19 | 1 | 36 | 0.956 | 1 | 0.996 | 0.953 | 0.644 | 0.966 | 0.622 | 0.197 | 0.906 | 0.179 | −0.145 | 0.819 | 0.119 | −0.236 | 0.707 | 0.167 |
| 36 | 18 | 18 | 2 | The winding is not implemented due to violation of symmetry conditions | |||||||||||||||
| 36 | 17 | 1 | 36 | 0.956 | 1 | 0.996 | 0.953 | 0.644 | 0.966 | 0.622 | 0.197 | 0.906 | 0.179 | −0.145 | 0.819 | 0.119 | −0.236 | 0.707 | 0.167 |
| 36 | 16 | 4 | 9 | 0.960 | 1 | 0.985 | 0.945 | 0.667 | 0.866 | 0.577 | 0.218 | 0.643 | 0.140 | −0.177 | 0.342 | 0.061 | −0.333 | 0 | 0 |
| 36 | 15 | 3 | 12 | 0.966 | 1 | 0.966 | 0.933 | 0.707 | 0.707 | 0.500 | 0.259 | 0.259 | 0.067 | −0.259 | 0.259 | 0.067 | −0.707 | 0.707 | 0.5 |
| 36 | 14 | 2 | 18 | 0.960 | 1 | 0.940 | 0.902 | 0.667 | 0.500 | 0.333 | 0.218 | 0.174 | 0.038 | −0.177 | 0.766 | 0.136 | −0.333 | 1 | 0.333 |
| 36 | 13 | 1 | 36 | 0.956 | 1 | 0.906 | 0.867 | 0.644 | 0.259 | 0.167 | 0.197 | 0.574 | 0.113 | −0.145 | 0.996 | 0.145 | −0.236 | 0.707 | 0.167 |
| 36 | 12 | 12 | 3 | 1 | 1 | 0.866 | 0.866 | 1 | 0 | 0 | 1 | 0.866 | 0.866 | 1 | 0.866 | 0.866 | 1 | 0 | 0 |
| 36 | 11 | 1 | 36 | 0.956 | 1 | 0.819 | 0.783 | 0.644 | 0.259 | 0.167 | 0.197 | 0.996 | 0.196 | −0.145 | 0.423 | 0.061 | −0.236 | 0.707 | 0.167 |
| 36 | 10 | 2 | 18 | 0.960 | 1 | 0.766 | 0.735 | 0.667 | 0.500 | 0.333 | 0.218 | 0.940 | 0.204 | −0.177 | 0.174 | 0.031 | −0.333 | 1 | 0.333 |
| 36 | 9 | 9 | 4 | The winding is not implemented due to violation of symmetry conditions | |||||||||||||||
| 36 | 8 | 4 | 9 | 0.960 | 2 | 0.985 | 0.945 | 0.667 | 0.866 | 0.577 | 0.218 | 0.643 | 0.140 | −0.177 | 0.342 | 0.061 | −0.333 | 0 | 0 |
| 36 | 7 | 1 | 36 | 0.956 | 2 | 0.940 | 0.898 | 0.644 | 0.500 | 0.322 | 0.197 | 0.174 | 0.034 | −0.145 | 0.766 | 0.111 | −0.236 | 1 | 0.236 |
| 36 | 6 | 6 | 6 | 1 | 3 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 36 | 5 | 1 | 36 | 0.956 | 3 | 0.966 | 0.924 | 0.644 | 0.707 | 0.455 | 0.197 | 0.259 | 0.051 | −0.145 | 0.259 | 0.038 | −0.236 | 0.707 | 0.167 |
| 36 | 4 | 4 | 9 | 0.960 | 4 | 0.985 | 0.945 | 0.667 | 0.866 | 0.577 | 0.218 | 0.643 | 0.140 | −0.177 | 0.342 | 0.061 | −0.333 | 0 | 0 |
| 36 | 3 | 3 | 12 | 0.966 | 6 | 1 | 0.966 | 0.707 | 1 | 0.707 | 0.259 | 1 | 0.259 | −0.259 | 1 | 0.259 | −0.707 | 1 | 0.707 |
| 36 | 2 | 2 | 18 | 0.960 | 9 | 1 | 0.960 | 0.667 | 1 | 0.667 | 0.218 | 1 | 0.218 | −0.177 | 1 | 0.177 | −0.333 | 1 | 0.333 |
| 36 | 1 | 1 | 36 | 0.956 | 12 | 1 | 0.956 | 0.644 | 1 | 0.644 | 0.197 | 1 | 0.197 | −0.145 | 1 | 0.145 | −0.236 | 1 | 0.236 |
| i | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 |
| n | 0 | 10 | 1 | 11 | 2 | 12 | 3 | 13 | 4 | 14 | 5 | 15 | 6 | 16 | 7 | 17 | 8 | 18 | 9 | 0 | 10 | 1 | 11 | 2 | 12 | 3 | 13 | 4 | 14 | 5 | 15 | 6 | 16 | 7 | 17 | 8 |
| l(i) | 0 | 19 | 2 | 21 | 4 | 23 | 6 | 25 | 8 | 27 | 10 | 29 | 12 | 31 | 14 | 33 | 16 | 35 | 18 | 1 | 20 | 3 | 22 | 5 | 24 | 7 | 26 | 9 | 28 | 11 | 30 | 13 | 32 | 15 | 34 | 17 |
| g(i) | 0 | 6 | 0 | 7 | 1 | 7 | 2 | 8 | 2 | 9 | 3 | 9 | 4 | 10 | 4 | 11 | 5 | 11 | 6 | 0 | 6 | 1 | 7 | 1 | 8 | 2 | 8 | 3 | 9 | 3 | 10 | 4 | 10 | 5 | 11 | 5 |
| +/− | 1 | −1 | 1 | −1 | 1 | −1 | −1 | 1 | −1 | 1 | −1 | 1 | 1 | −1 | 1 | −1 | 1 | −1 | −1 | 1 | −1 | 1 | −1 | 1 | 1 | −1 | 1 | −1 | 1 | −1 | −1 | 1 | −1 | 1 | −1 | 1 |
| u(i) | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 |
| j(i) | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 2 | 2 | 2 | 2 | 2 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 2 | 2 | 2 | 2 | 2 | 2 |
| i | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 |
| n | 0 | 10 | 1 | 11 | 2 | 12 | 3 | 13 | 4 | 14 | 5 | 15 | 6 | 16 | 7 | 17 | 8 | 18 | 9 | 0 | 10 | 1 | 11 | 2 | 12 | 3 | 13 | 4 | 14 | 5 | 15 | 6 | 16 | 7 | 17 | 8 |
| l(i) | 0 | 19 | 2 | 21 | 4 | 23 | 6 | 25 | 8 | 27 | 10 | 29 | 12 | 31 | 14 | 33 | 16 | 35 | 18 | 1 | 20 | 3 | 22 | 5 | 24 | 7 | 26 | 9 | 28 | 11 | 30 | 13 | 32 | 15 | 34 | 17 |
| g(i) | 0 | 9 | 1 | 10 | 2 | 11 | 3 | 12 | 4 | 13 | 5 | 14 | 6 | 15 | 7 | 16 | 8 | 17 | 9 | 0 | 10 | 1 | 11 | 2 | 12 | 3 | 13 | 4 | 14 | 5 | 15 | 6 | 16 | 7 | 17 | 8 |
| +/− | 1 | −1 | 1 | −1 | 1 | −1 | −1 | 1 | −1 | 1 | −1 | 1 | 1 | −1 | 1 | −1 | 1 | −1 | −1 | 1 | −1 | 1 | −1 | 1 | 1 | −1 | 1 | −1 | 1 | −1 | −1 | 1 | −1 | 1 | −1 | 1 |
| u(i) | 0 | 0 | 1 | 1 | 2 | 2 | 0 | 0 | 1 | 1 | 2 | 2 | 0 | 0 | 1 | 1 | 2 | 2 | 0 | 0 | 1 | 1 | 2 | 2 | 0 | 0 | 1 | 1 | 2 | 2 | 0 | 0 | 1 | 1 | 2 | 2 |
| j(i) | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 2 | 2 | 2 | 2 | 2 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 2 | 2 | 2 | 2 | 2 | 2 |
| Parameter | Value |
|---|---|
| Active part dimensions: | |
| length of stator and rotor cores, mm | 140 |
| stator bore diameter, mm | 92 |
| outer diameter of stator core, mm | 138 |
| air gap, mm | 1 |
| rotor pole height, mm | 3.5 |
| Materials: | |
| stator core steel grade | M270-50A |
| permanent magnet material grade | N38SH |
| remanent flux density, T | 1.2 |
| coercivity force, kA/m | 900 |
| Winding data: | |
| number of phases | 3 × 2 |
| number of stator core slots | 36 |
| number of poles | 34 |
| coil pitch (tooth pitches) | 1 |
| number of series turns per phase | 62 × 2 |
| Parameter | Harmonic Order | |||
|---|---|---|---|---|
| 1 | 3 | 5 | 7 | |
| , V | 1.4213 | 0.0195 | 0.0119 | 2.0463 × 10−3 |
| , V | 1.4413 | 0.0704 | 0.0268 | 9.7331 × 10−3 |
| (experiment) | 0.9859 | 0.2765 | 0.4438 | 0.2102 |
| (calculation) | 0.9525 | 0.6220 | 0.1787 | 0.1190 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kharchyshyn, B.; Makarchuk, O.; Całus, D.; Khai, M.; Babei, O. Algorithmic Design of Modular Two-Layer Multiphase Windings Based on Number Theory. Energies 2025, 18, 6320. https://doi.org/10.3390/en18236320
Kharchyshyn B, Makarchuk O, Całus D, Khai M, Babei O. Algorithmic Design of Modular Two-Layer Multiphase Windings Based on Number Theory. Energies. 2025; 18(23):6320. https://doi.org/10.3390/en18236320
Chicago/Turabian StyleKharchyshyn, Bohdan, Oleksandr Makarchuk, Dariusz Całus, Mykhailo Khai, and Oleh Babei. 2025. "Algorithmic Design of Modular Two-Layer Multiphase Windings Based on Number Theory" Energies 18, no. 23: 6320. https://doi.org/10.3390/en18236320
APA StyleKharchyshyn, B., Makarchuk, O., Całus, D., Khai, M., & Babei, O. (2025). Algorithmic Design of Modular Two-Layer Multiphase Windings Based on Number Theory. Energies, 18(23), 6320. https://doi.org/10.3390/en18236320








