A Family of Fundamental Positive Sequence Detectors Based on Repetitive Schemes

Abstract

In electrical power systems, the extraction of the fundamental positive sequence (FPS) is paramount for synchronization, power calculation, and a wide variety of metering and control tasks. This work shows that a moving average filter (MAF) used in the synchronous reference frame to extract the FPS from electrical systems is equivalent to the cascade connection of a comb filter (CF) with a second-order harmonic oscillator (SOHO), with all its variables expressed in fixed reference frame coordinates. On the one hand, the CF introduces an infinite number of notches tuned at all integer harmonics of the fundamental frequency ${\omega }_0$, thus suppressing harmonic distortion in the incoming signal and acting as a repetitive-based pre-filter (RPF). On the other hand, the SOHO is responsible for delivering the fundamental component of the input signal with a unitary gain, while additionally reducing the effect of harmonic distortion. Then, it is shown that other RPFs built from previously reported repetitive schemes (all-harmonics, odd-harmonics, and the $6\ell \pm 1$ harmonics) can be placed instead of the CF, giving rise to a family of FPS detectors. In particular, this work also shows that the CF-SOHO is a special case of the FPS detector based on the all-harmonics RPF. This work provides the mathematical derivation of the FPS detector structure, tuning rules for the SOHO gain associated with each FPS detector, as well as experimental results under a reference signal subject to perturbations such as unbalance, harmonic distortion, phase, and amplitude jumps, exhibiting convergence in only half the fundamental period in most carried out tests.

1. Introduction

Grid synchronization and/or fundamental positive sequence detection methods are important tasks in the connection of distributed generation systems, where the reference signal (usually, the grid voltage) is subject to disturbances such as sags, swells, harmonic distortion, and unbalance [1]. The alternatives commonly used for synchronization under such conditions include the so-called moving average filter (MAF) operating in the synchronous reference frame [2] (often referred to as a Park filter), band-pass filters [3], delayed-signal cancellation methods, cascaded [4] or parallel [5], and, more recently, a comb filter (CF) followed by a second-order harmonic oscillator (SOHO) [6]. The latter can provide the fundamental positive sequence (FPS) (and negative sequence, if necessary) of the grid voltage, within a relatively short execution time. Recent approaches for grid synchronization include intelligent or data-driven based methods like neural networks [7,8], chaotic grey wolf optimization combined with the random forest algorithm [9], and particle swarm optimization with the gradient descent algorithm [10]. Yet, another interesting technique for grid synchronization includes repetitive controllers, with very few reported works [11,12].

Repetitive control (RC) schemes include time-lag elements in feedback/feedforward configurations to produce an infinite number of poles/zeros (peaks/notches) located in particular harmonic multiples of the fundamental frequency ${\omega }_0$. Although RC schemes date back to 1981 [13], they were referred to as RC until 1985 [14]. The purpose of an RC is to track or reject periodic signals [15], depending on where the RC is placed in the closed-loop system. If the RC is located in the direct path, then it is intended for tracking. If the RC is attached to the feedback path, then its aim is disturbance rejection, i.e., it operates as a filter.

RC found its first applications in a proton synchrotron [13] and a three-link robot manipulator [14]. Over time, RC has been applied in robotics [16,17], vibration suppression [18,19], and control of power electronics devices such as rectifiers [20], active power filters [21], boost converters [15], and inverters [22,23].

The RC in [11] assisted a phase-locked loop (PLL) developed for three-phase systems, where the grid voltage was subject to harmonic distortion, frequency, and phase variations. The RC filtered out the harmonic distortion, which facilitated the PLL, operating in the synchronous reference frame, to achieve better tracking of the frequency and phase of the incoming signal. According to the authors, very small percentages of DC offsets and unbalance in the three-phase signal were due to sensors and ADC limitations, i.e., not by signal generation.

In [12], the RC was combined with a second-order generalized integrator (SOGI) to provide an estimated frequency of the grid voltage in a single-phase system. The RC structures considered were the all-harmonics and odd-harmonics schemes. These RC schemes were modified to also cope with DC disturbances and even grid frequency variations, by including an additional integrator (in parallel to the RC) and an FIR filter to approximate the fractional part of the time-lag element, respectively.

The CF-SOHO, proposed in [6], represents an alternative to the Park filter and is directly implemented in the fixed reference frame, which leads to a faster execution than using the Park filter for positive (or negative) sequence detection. However, no such derivation has been presented so far. Therefore, one of the aims of this work is to provide a detailed derivation process to obtain such a structure. For this, the modulation/demodulation property (related to the Laplace frequency-shifting property), first introduced in [24] and fully exploited in [25], is applied to the MAF transfer function (a type of repetitive scheme used as a pre-filter), and then is also used to study other RC-based schemes, such as the 6$6\ell \pm 1$.

It should be noted that, as the CF inserts zeros (notches) at every integer harmonic multiple of a fundamental frequency ${\omega }_0$; then, other repetitive structures (producing an infinite number of resonant peaks) can be placed in a negative feedback loop to mimic the behavior of the comb filter, i.e., producing an infinite number of notches tuned at specific harmonics of ${\omega }_0$. This gives rise to a family of structures referred to as repetitive-based pre-filters (RPFs) that combined with the SOHO estimator to form a family of FPS detectors. In particular, the RPFs used in this work come from the manipulation of three different RC schemes, namely the all-harmonics [15], the odd-harmonics [26], and the $6\ell \pm 1$ [25] RC schemes. Therefore, every RPF cancels specific harmonics of the input signal. Moreover, the all and odd RPF cases become quite simplified structures after manipulation, which are mainly composed by feedforward paths, saving memory allocations during their digital implementation.

The aim of the RPFs-SOHO is to provide the FPS with unitary gain and zero phase-shift despite unbalance and harmonic distortion. Like the CF-SOHO, the RPFs-SOHO FPS detectors also operate in the fixed reference frame. These schemes have a slightly different goal compared to the work of [11], which is concerned only with obtaining (after transforming the signal into the synchronous reference frame) the frequency and phase shift of a three-phase signal. They can also be seen as an extension to the scheme in [12] intended for a single-phase system. To assess the performance of the FPS detectors, i.e., the cascade connection of RPFs and the SOHO scheme, experimental results under unbalance, harmonic distortion, phase, and amplitude jumps in the grid voltage are presented. All FPS detectors were implemented in the dSPACE DS1007 board. Moreover, simulation results are also included, to provide a comparison with the MAF-based Park filter and with SOGI-based schemes.

The main contributions of this work can be summarized as follows:

• A formal mathematical derivation of the CF-SOHO structure proposed in [6], through the application of the modulation/demodulation principle of [24] to the MAF transfer function.
• Derivation of RPF structures for the all-, odd-, and the $6\ell \pm 1$ harmonics, where the all- and odd- harmonics RPF structures become simple feedforward paths.
• Tuning rules for every RPF used in the FPS detectors.

The rest of this paper is organized as follows: Section 2 shows the mathematical derivation of the CF-SOHO for FPS detection. Section 3 presents the structure of the FPS detector based on the all-harmonics RPF, as well as the downward compatibility of this FPS detector with the CF-SOHO proposed in [6]. This section also includes the FPS detectors based on the odd- and the $6\ell \pm 1$ harmonic RPFs. Section 4 presents the experimental results of the FPS detectors based on the all-, odd- and the $6\ell \pm 1$ harmonic RPFs. Section 5 shows the simulation results of the proposed SOHO-based FPS detectors compared with the SOGI-based detectors and the MAF-based Park filter. Finally, Section 6 provides concluding remarks.

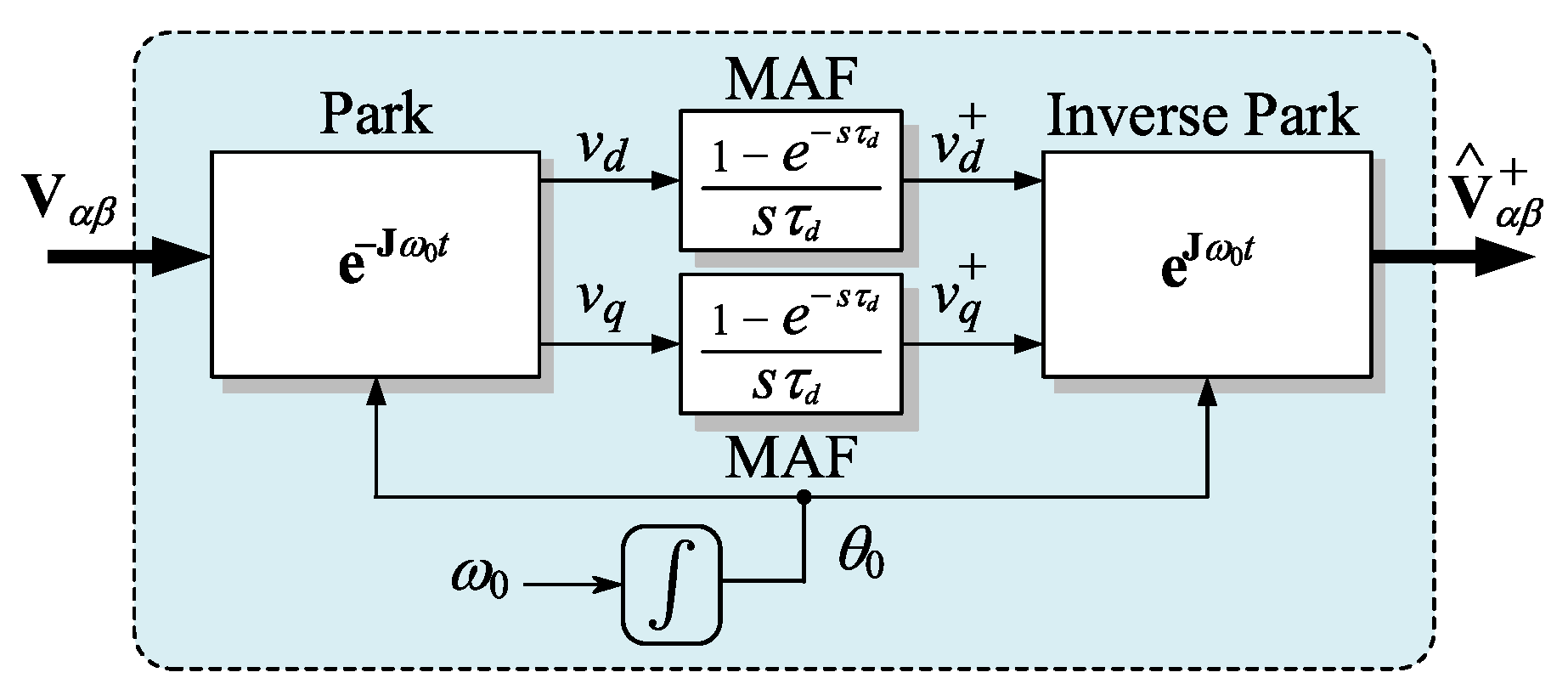
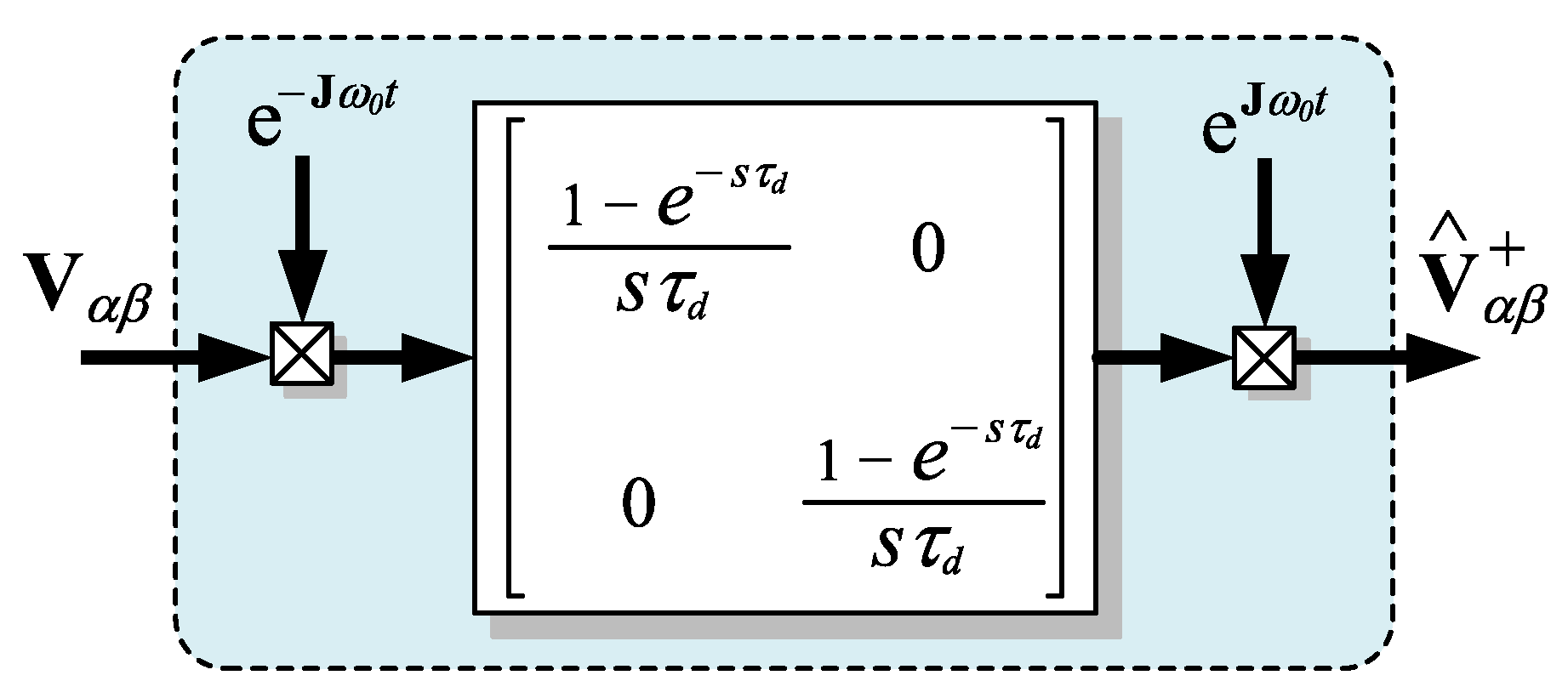
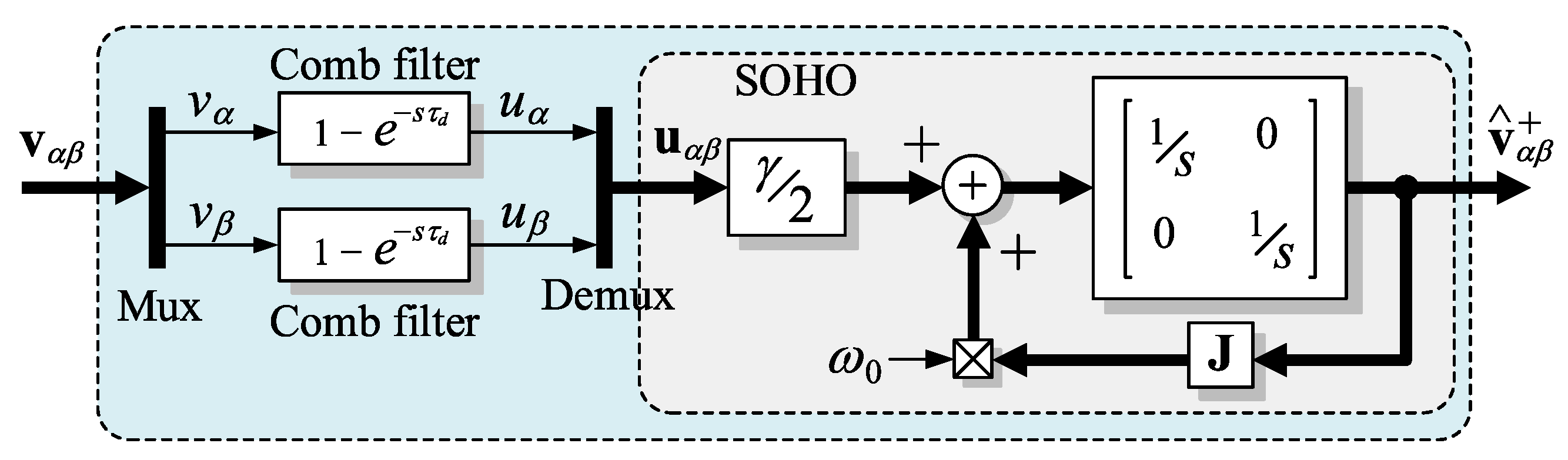
2. Origins of the CF-SOHO

The application of the modulation/demodulation property (related to the Laplace frequency-shifting property) to the MAF transfer function gives rise to a transfer function conformed by the cascade connection of a CF followed by an SOHO (for a constant frequency). In the three-phase case, the CF-SOHO is directly applied to variables expressed in fixed reference frame coordinates. This has the benefit of avoiding the rotations involved in the MAF application that operates on variables expressed in synchronous reference frame coordinates.

The MAF transfer function in continuous-time domain is given by [27]

$$G\left(s\right)={\displaystyle \frac{1-e^{-s{\tau }_d}}{s{\tau }_d}}$$

(1)

where ${\tau }_d=2\pi /{\omega }_0$ represents the MAF time-delay.

The process of obtaining the FPS of the grid voltage [2] using the MAF filter is shown in Figure 1. It consists of applying the MAF filter $G\left(s\right)$ (1) to each voltage component expressed in synchronous reference frame coordinates and then transforming back the MAF outputs to their representation in terms of fixed reference frame coordinates, i.e., in terms of $\alpha \beta$-coordinates. This structure is commonly known as a Park filter since both the direct and inverse Park transformations are involved in the calculation of the FPS.

To perform the same task, but now keeping both the input and output variables expressed in terms of $\alpha \beta$ coordinates, the MAF transfer function has to be modified by appealing to the modulation/demodulation property (related to the Laplace frequency-shifting property) presented in [24]. Basically, if the input and output signal vectors of a linear system, in this case $\mathrm{diag}\left\{G\right(s),G(s\left)\right\}$, are pre- and post-multiplied by Park and inverse Park rotation matrices, respectively, rotating at a frequency ${\omega }_0$, as shown in Figure 2, which is an equivalent representation of the Park filter in Figure 1, where

$${\mathbf{e}}^{-\mathbf{J}{\omega }_{0}t}=\left[\begin{array}{cc}cos\left({\omega }_{0}t\right)& sin\left({\omega }_{0}t\right)\\ -sin\left({\omega }_{0}t\right)& cos\left({\omega }_{0}t\right)\end{array}\right],\mathbf{J}\triangleq \left[\begin{array}{cc}0& -1\\ 1& 0\end{array}\right]$$

(2)

is the Park transform, and ${\mathbf{e}}^{\mathbf{J}{\omega }_{0}t}={\left({\mathbf{e}}^{-\mathbf{J}{\omega }_{0}t}\right)}^{\top }$ is the inverse Park transform, then both rotations can be absorbed by the MAF transfer function matrix $\mathrm{diag}\left\{G\right(s),G(s\left)\right\}$, creating a new equivalent transfer matrix description with the benefit of maintaining input and output signals vectors expressed in fixed reference frame coordinates, which considerably simplifies the implementation, i.e.,

$${\widehat{\mathbf{V}}}_{\alpha \beta }^{+}\left(s\right)=\mathbf{M}\left(s\right){\mathbf{V}}_{\alpha \beta }\left(s\right)$$

(3)

where transfer matrix $\mathbf{M}\left(s\right)$ has the following structure:

$$\mathbf{M}\left(s\right)=\left[\begin{array}{cc}{M}_{11}\left(s\right)& -M_{12}\left(s\right)\\ M_{21}\left(s\right)& M_{22}\left(s\right)\end{array}\right]$$

(4)

with each $M_{ik}\left(s\right)$ ($i\in \{1,2\}$, $k\in \{1,2\}$) being the equivalent transfer function of the MAF expressed in terms of fixed reference frame coordinates. In what follows, the derivation of transfer matrix (4) is described in detail.

From now on, the argument s is omitted in the $M_{ik}$ expressions to simplify the notation. Firstly, consider the calculation of the output time response of the system shown in Figure 2, which is an equivalent representation of the Park filter in Figure 1. This output time response can be obtained through a convolution integral expressed in matrix form as

$${\widehat{\mathbf{v}}}_{\alpha \beta }^{+}\left(t\right)={\mathbf{e}}^{-\mathbf{J}{\omega }_{0}t}{\int }_0^t\left[\begin{array}{cc}g\left(\tau \right)& 0\\ 0& g\left(\tau \right)\end{array}\right]{\mathbf{e}}^{\mathbf{J}{\omega }_0(t-\tau )}{\mathbf{v}}_{\alpha \beta }(t-\tau )d\tau$$

(5)

where $g\left(t\right)$ is the impulse response of $G\left(s\right)$ described in (1). After multiplication and reduction, the following equation is obtained:

$$\begin{array}{cc}\hfill {\widehat{\mathbf{v}}}_{\alpha \beta }^{+}\left(t\right)& ={\int }_0^{t}g\left(\tau \right)\left[\begin{array}{cc}{m}_{11}& -m_{12}\\ m_{21}& m_{22}\end{array}\right]{\mathbf{v}}_{\alpha \beta }(t-\tau )d\tau ,\hfill \\ \hfill m_{11}& =m_{22}=cos\left({\omega }_{0}t\right)cos\left({\omega }_0(t-\tau )\right)+sin\left({\omega }_{0}t\right)sin\left({\omega }_0(t-\tau )\right),\hfill \\ \hfill m_{12}& =-m_{21}=cos\left({\omega }_{0}t\right)sin\left({\omega }_0(t-\tau )\right)-sin\left({\omega }_{0}t\right)cos\left({\omega }_0(t-\tau )\right).\hfill \end{array}$$

(6)

The terms $m_{ik}$ ($i\in \{1,2\}$, $k\in \{1,2\}$) in (6) can be further reduced using trigonometric identities, yielding

$${\widehat{\mathbf{v}}}_{\alpha \beta }^{+}\left(t\right)={\int }_0^{t}g\left(\tau \right)\left[\begin{array}{cc}cos\left({\omega }_0\tau \right)& -sin\left({\omega }_0\tau \right)\\ sin\left({\omega }_0\tau \right)& cos\left({\omega }_0\tau \right)\end{array}\right]{\mathbf{v}}_{\alpha \beta }(t-\tau )d\tau .$$

(7)

The expression (7) shows that the MAF impulse response $g\left(t\right)$ is modulated by four sinusoidal terms contained in the 2 × 2 matrix. These sinusoidal terms can also be expressed as $cos\left({\omega }_{0}t\right)=\left(e^{j{\omega }_{0}t}+e^{-j{\omega }_{0}t}\right)/2$ and $sin\left({\omega }_{0}t\right)=\left(e^{j{\omega }_{0}t}-e^{-j{\omega }_{0}t}\right)/2j$, where j represents the imaginary unit. The use of these equivalences allows the application of the frequency shift operation as described in [24]. Therefore, now, in the Laplace domain, the $M_{ik}$ terms ($i\in \{1,2\}$, $k\in \{1,2\}$) can be expressed as

$$\begin{array}{cc}\hfill M_{11}=M_{22}& ={\displaystyle \frac{1}{2}}\left(\mathcal{L}\left\{e^{j{\omega }_{0}t}g\left(t\right)\right\}+\mathcal{L}\left\{e^{-j{\omega }_{0}t}g\left(t\right)\right\}\right)\hfill \\ \hfill & ={\displaystyle \frac{1}{2}}\left(G(s-j{\omega }_0)+G(s+j{\omega }_0)\right),\hfill \end{array}$$

(8)

$$\begin{array}{cc}\hfill M_{12}=-M_{21}& =-{\displaystyle \frac{1}{2j}}\left(\mathcal{L}\left\{e^{j{\omega }_{0}t}g\left(t\right)\right\}\right.-\left.\mathcal{L}\left\{e^{-j{\omega }_{0}t}g\left(t\right)\right\}\right)\hfill \\ \hfill & =-{\displaystyle \frac{1}{2j}}\left(G(s-j{\omega }_0)-G(s+j{\omega }_0)\right).\hfill \end{array}$$

(9)

To obtain (8) and (9), both linearity and frequency-shifting (modulation) properties of the Laplace transform have been used [24]. Application of (8) and (9) to $G\left(s\right)$, as described in (1), yields

$$\begin{array}{cc}\hfill M_{11}=M_{22}& =(1-e^{-s{\tau }_d})·{\displaystyle \frac{s/{\tau }_d}{s^2+{\omega }_0^2}},\hfill \end{array}$$

(10)

$$\begin{array}{cc}\hfill M_{12}=-M_{21}& =-(1-e^{-s{\tau }_d})·{\displaystyle \frac{{\omega }_0/{\tau }_d}{s^2+{\omega }_0^2}}\hfill \end{array}$$

(11)

where

$$\begin{array}{cc}\hfill G(s-j{\omega }_0)& ={\displaystyle \frac{1-e^{-(s-j{\omega }_0){\tau }_d}}{(s-j{\omega }_0){\tau }_d}},\hfill \\ \hfill G(s+j{\omega }_0)& ={\displaystyle \frac{1-e^{-(s+j{\omega }_0){\tau }_d}}{(s+j{\omega }_0){\tau }_d}}\hfill \end{array}$$

(12)

have been used.

Summarizing, the transfer matrix $\mathbf{M}\left(s\right)$ describing the FPS detection with variables expressed in terms of fixed reference frame coordinates, as presented in (3), i.e., ${\widehat{\mathbf{V}}}_{\alpha \beta }^{+}\left(s\right)=\mathbf{M}\left(s\right){\mathbf{V}}_{\alpha \beta }\left(s\right)$, is given by

$$\mathbf{M}\left(s\right)={\displaystyle \frac{(1-e^{-s{\tau }_d})}{{\tau }_d}}\left[\begin{array}{cc}{\displaystyle \frac{s}{s^2+{\omega }_0^2}}& {\displaystyle \frac{-{\omega }_0}{s^2+{\omega }_0^2}}\\ {\displaystyle \frac{{\omega }_0}{s^2+{\omega }_0^2}}& {\displaystyle \frac{s}{s^2+{\omega }_0^2}}\end{array}\right].$$

(13)

A block diagram showing the FPS detection using transfer matrix (13) is depicted in Figure 3.

In what follows, it is shown that the two MAFs in Figure 1 (with variables expressed in terms of synchronous reference frame coordinates) become a combination of a CF in cascade with an SOHO (with variables now expressed in terms of $\alpha \beta$-coordinates). In other words, $\mathbf{M}\left(s\right)$ is equivalent to the cascade connection of a CF and an SOHO scheme. For this, (13) has to be further processed using the diffeomorphic mapping established between a complex number and a particular $2\times 2$ matrix, i.e., $x+jy\to \left[\begin{array}{cc}x& -y\\ y& x\end{array}\right]$. Consequently, matrix $\mathbf{M}\left(s\right)$, given by (13), can be rewritten as follows:

$$\mathbf{M}\left(s\right)={\displaystyle \frac{(1-e^{-s{\tau }_d})}{{\tau }_d(s^2+{\omega }_0^2)}}(s+j{\omega }_0)={\displaystyle \frac{(1-e^{-s{\tau }_d})}{{\tau }_d}}{\displaystyle \frac{1}{s-j{\omega }_0}}.$$

(14)

Provided that $1/{\tau }_d=\gamma /2$, then (14) becomes

$$\mathbf{M}\left(s\right)=\underset{\mathrm{CF}}{\underbrace{(1-e^{-s{\tau }_d})}}·\underset{\mathrm{SOHO}}{\underbrace{{\displaystyle \frac{\gamma }{2(s-j{\omega }_0)}}}}$$

(15)

which coincides with the CF-SOHO scheme for FPS extraction reported in [6] (Equation (9)). That is, (13) becomes a combination of a CF in cascade connection with an SOHO tuned at the fundamental frequency ${\omega }_0$, as described in (15). Consequently, the MAF transfer function in Figure 1, with input and output variables in the synchronous reference frame coordinates, has an equivalent representation described by (15), whose input and output variables are now expressed in terms of fixed reference frame ($\alpha \beta$-) coordinates.

According to (15), first, the CF inserts zeros (notches) at every integer harmonic of the fundamental frequency ${\omega }_0$, thus attenuating all integer harmonics of ${\omega }_0$. Second, the SOHO, tuned at ${\omega }_0$, is responsible for extracting and delivering the fundamental component by processing transients from the CF output and affecting them with a local gain $\gamma =2f_0$, resulting in a unitary gain at the fundamental component for the overall process.

A state-space representation of the SOHO component in (15) (in fixed frame coordinates) for its implementation is given by [6]

$${\dot{\widehat{\mathbf{v}}}}_{\alpha \beta }^{+}={\omega }_0\mathbf{J}{\widehat{\mathbf{v}}}_{\alpha \beta }^{+}+{\displaystyle \frac{\gamma }{2}}{\mathbf{u}}_{\alpha \beta },\mathbf{J}\triangleq \left[\begin{array}{cc}0& -1\\ 1& 0\end{array}\right]$$

(16)

where ${\mathbf{u}}_{\alpha \beta }$ is the SOHO input signal. The block diagram of the combination of CF and SOHO (16) for FPS extraction, with variables expressed in terms of fixed reference frame ($\alpha \beta$-) coordinates, is shown in Figure 4.

Remark 1.

Although the CF-SOHO structure was proposed in [6], its mathematical derivation starting from the MAF transfer function is presented here for the first time, which represents one of the contributions of the present work.

3. Other RPF-SOHO Structures for FPS Detection

Notice that the CF performs an RPF operation as all existing harmonics in the input signal are canceled out. This is due to the fact that its frequency response includes an infinite number of notches, or equivalently, its transfer function involves an infinite number of zeros. The latter is due to the delay line involved in the CF implementation.

Recall that repetitive schemes are also implemented with delay lines producing an infinite number of poles at a given location, which can be translated to an infinite number of zeros after placing such a repetitive scheme in the feedback path of a feedback structure. In other words, RPFs can be built based on traditional repetitive schemes by means of a feedback structure where the repetitive scheme is placed in the negative feedback path, giving rise to the following RPF transfer function:

$$RPF\left(s\right)={\displaystyle \frac{1}{1+RC\left(s\right)}}$$

(17)

where $RC\left(s\right)$ is the transfer function of the traditional repetitive scheme. In this way, the infinite number of poles of the aforementioned repetitive controllers becomes an infinite number of zeros, producing a behavior similar to that of the CF. Moreover, in some cases, simplified schemes can be observed after performing the negative feedback loop algebra.

The design of RPFs based on a specific repetitive scheme is of great interest in case the harmonic content in a particular application is known a priori (for instance, six-pulse converters produce $6\ell \pm 1$ harmonic components [25]) because it has been observed that the use of certain specific RPFs may have the benefit of reducing the memory required to implement the FPS detection scheme, i.e., the buffer size of the digital device containing the FPS may be reduced.

In this sense, it is proposed here to replace each CF in Figure 4 with other RPFs whose design is based on different repetitive schemes, as shown in Figure 5. The latter includes, for instance, repetitive schemes for all-harmonics [15], odd-harmonics [26], and the $6\ell \pm 1$ harmonics [25], and thus, the resulting RPFs are referred to as the all-harmonics, odd-harmonics, and the $6\ell \pm 1$ harmonics RPFs, respectively. For the sake of clarity, their design as RPFs is presented as part of the derivation of each FPS detector case.

Moreover, this section also shows that the FPS detector based on the cascade connection of the all-harmonics RPF and the SOHO scheme is downward compatible with the CF-SOHO scheme under certain conditions (to be stated later).

Remark 2.

The derivation of the RPFs to be placed instead of the CFs will be performed considering single-input, single-output systems, as this is the way the CFs are used in Figure 4.

3.1. FPS Detector Based on the All-Harmonics RPF

The transfer function of the all-harmonics RC scheme is given by [15]

$$R{C}_{\mathrm{all}}\left(s\right)={\displaystyle \frac{1+e^{-2s\pi /{\omega }_0}}{1-e^{-2s\pi /{\omega }_0}}}.$$

(18)

Placing (18) in (17), leads to the following expression, referred to as the all-harmonics RPF:

$$RP{F}_{\mathrm{all}}\left(s\right)={\displaystyle \frac{1}{2}}\left(1-e^{-2s\pi /{\omega }_0}\right)$$

(19)

whose block diagram is shown in Figure 6. Notice that this RPF only comprises feedforward paths. It should be noted that this scheme is applied to the $\alpha$ and $\beta$ components of the signal vector.

In fact, the all-hamonics RPF has zeros located at every $\omega =\ell {\omega }_0$, $\ell \in \mathbb{Z}$. The magnitude plot of the frequency response of (19), shown in Figure 7a, comprises notches with an arbitrarily small gain, while the gain at the crests, between each notch, reaches a maximum of 0 dB.

The FPS detector based on the all-harmonics RPF is obtained by cascading such an RPF with an SOHO scheme (16). The resulting scheme is referred to as the all-harmonics FPS detector, whose frequency response (only the magnitude plot) is shown in Figure 7b. Notice that the unitary gain is achieved only at $\omega ={\omega }_0$ (${\omega }_0=2\pi f_0$, $f_0$ = 50 Hz in this example), and only for a given $\gamma$ gain. The tuning of this gain follows a similar procedure as the one reported in [6] for the CF-SOHO tuning. For this, the vectors in SOHO (16) are represented as complex numbers in the s domain as follows:

$$\begin{array}{c}s\left({\widehat{v}}_{\alpha }^{+}+j{\widehat{v}}_{\beta }^{+}\right)=j{\omega }_0\left({\widehat{v}}_{\alpha }^{+}+j{\widehat{v}}_{\beta }^{+}\right)+{\displaystyle \frac{\gamma }{2}}\left(u_{\alpha }+j{u}_{\beta }\right),\\ {\displaystyle \frac{{\widehat{\mathbf{V}}}_{\alpha \beta }^{+}\left(s\right)}{{\mathbf{U}}_{\alpha \beta }\left(s\right)}}={\displaystyle \frac{{\widehat{v}}_{\alpha }^{+}\left(s\right)+j{\widehat{v}}_{\beta }^{+}\left(s\right)}{u_{\alpha }\left(s\right)+j{u}_{\beta }\left(s\right)}}={\displaystyle \frac{\gamma }{2(s-j{\omega }_0)}}.\end{array}$$

(20)

Cascading (20) to the all-harmonics RPF (19) gives rise to the following transfer function that describes the FPS extraction of signals expressed in $\alpha \beta$-coordinates:

$${\displaystyle \frac{{\widehat{\mathbf{V}}}_{\alpha \beta }^{+}\left(s\right)}{{\mathbf{V}}_{\alpha \beta }\left(s\right)}}={\displaystyle \frac{\gamma \left(1-e^{-2s\pi /{\omega }_0}\right)}{4\left(s-j{\omega }_0\right)}}.$$

(21)

After evaluating (21) at $s=j\omega$; obtaining its squared magnitude; and, finally, making this latter value equal to one, the following expression is obtained:

$${\left|{\displaystyle \frac{{\widehat{\mathbf{V}}}_{\alpha \beta }^{+}\left(s\right)}{{\mathbf{V}}_{\alpha \beta }\left(s\right)}}\right|}^2={\displaystyle \frac{{\gamma }^2-{\gamma }^{2}cos\left(2\pi \omega /{\omega }_0\right)}{8\left({\omega }^2-2\omega {\omega }_0+{\omega }_0^2\right)}}=1.$$

(22)

Now, solving (22) for $\gamma$ at $\omega ={\omega }_0$ yields an indeterminate form that can be solved by applying twice the L’Hôpital’s rule, which results in

$$\gamma =4f_0.$$

(23)

The frequency response (only the magnitude plot) of the all-harmonics FPS detector, for ${\omega }_0=100\pi$ rad/s ($f_0=$50 Hz) and $\gamma =4f_0=200$, is shown in Figure 7b.

Remark 3.

The same procedure for the tuning of the gain γ can be extrapolated to other FPS detectors as it will become clear later.

Consequently, the CF-SOHO in [6] and the all-harmonics FPS detector (introduced in the present work) have the same FPS detection capabilities, as they exhibit a similar frequency response. In fact, the CF-SOHO represents a particular case of the all-harmonics FPS detector if the following conditions are met: (i) the constant at the output of the summing point in Figure 6 is set to 1, and (ii) the gain $\gamma$ of the SOHO (20) is equal to $2f_0$.

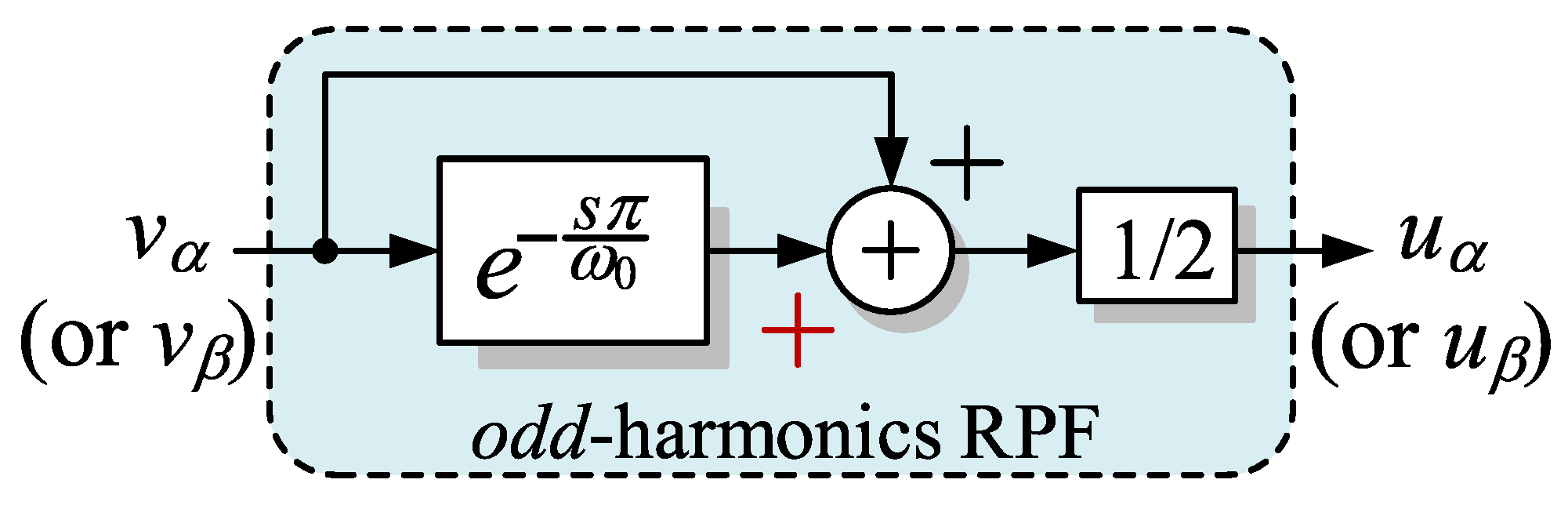
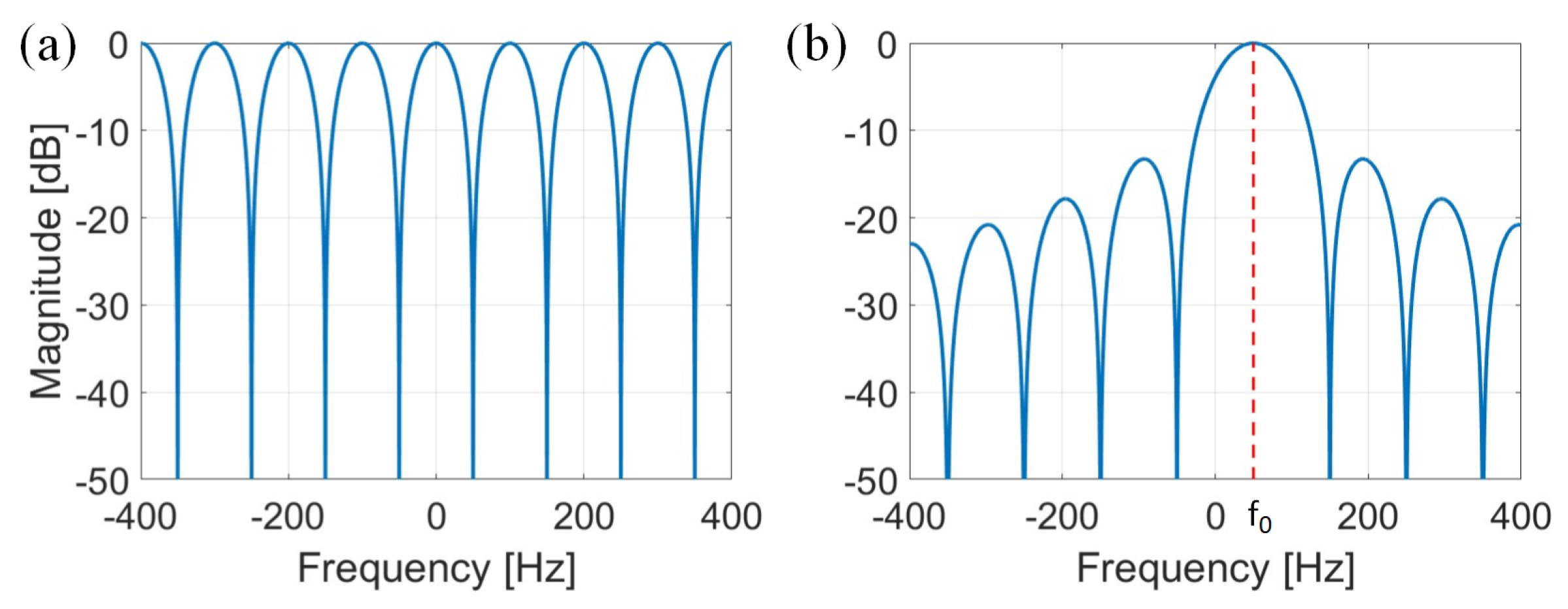
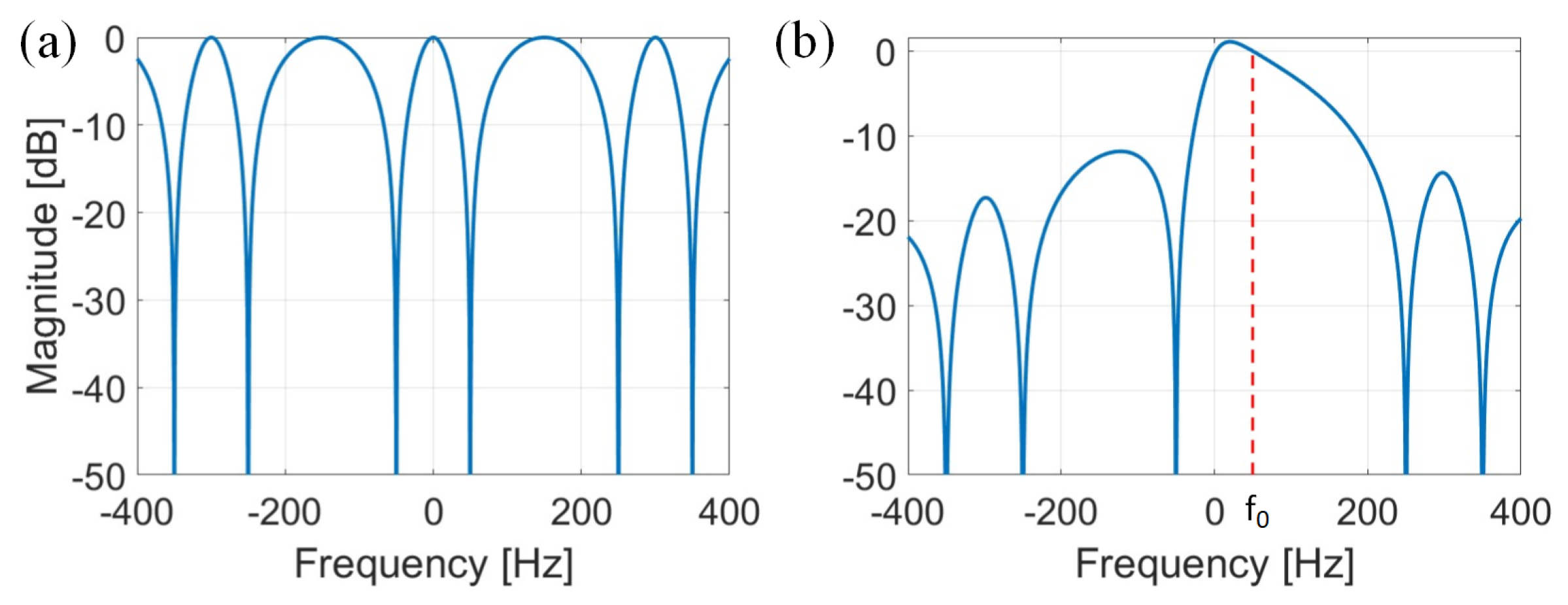
3.2. FPS Detector Based on the Odd-Harmonics RPF

Consider now the transfer function of the odd-harmonics RC scheme given by [26]

$$R{C}_{\mathrm{odd}}\left(s\right)={\displaystyle \frac{1-e^{-s\pi /{\omega }_0}}{1+e^{-s\pi /{\omega }_0}}}.$$

(24)

The simplified expression of the odd-harmonics RPF (to be used on each component of the fixed reference frame variables vector) is obtained by direct substitution of (24) in (17), yielding

$${\mathit{RPF}}_{\mathit{o}dd}\left(s\right)={\displaystyle \frac{1}{2}}\left(1+e^{-s\pi /{\omega }_0}\right)$$

(25)

which has zeros at every $\omega =\left(2\ell \pm 1\right){\omega }_0$, $\ell \in \mathbb{Z}$. The continuous-time block diagram of the odd-harmonics RPF is shown in Figure 8. The frequency response (only the magnitude plot) of (25), shown in Figure 9a, exhibits notches of an arbitrarily small gain and a gain of 0 dB in the crests between every two consecutive notches, just as in the case of all-harmonics RPF. The cascade connection of an odd-harmonics RPF (25) with an SOHO scheme (16) produces the so-called odd-harmonics FPS detector, which has a frequency response showing a unitary gain only at $\omega ={\omega }_0$. However, this is only valid for a specific gain $\gamma$, which can be obtained following a similar procedure as in the previously presented all-harmonics FPS detector. For this, the cascade connection between the odd-harmonics RPF (25) and the SOHO expressed in complex notation (20) is

$${\displaystyle \frac{{\widehat{\mathbf{V}}}_{\alpha \beta }^{+}\left(s\right)}{{\mathbf{V}}_{\alpha \beta }\left(s\right)}}={\displaystyle \frac{\gamma \left(1+e^{-s\pi /{\omega }_0}\right)}{4\left(s-j{\omega }_0\right)}}.$$

(26)

Similarly, the square of the magnitude of (26) evaluated at $s=j\omega$ is set equal to one, that is,

$${\left|{\displaystyle \frac{{\widehat{\mathbf{V}}}_{\alpha \beta }^{+}\left(s\right)}{{\mathbf{V}}_{\alpha \beta }\left(s\right)}}\right|}^2={\displaystyle \frac{{\gamma }^2+{\gamma }^{2}cos\left(\pi \omega /{\omega }_0\right)}{8\left({\omega }^2-2\omega {\omega }_0+{\omega }_0^2\right)}}=1.$$

(27)

Solving for $\gamma$ at $\omega ={\omega }_0$ in (27) and applying twice the L’Hôpital’s rule yield the following solution:

$$\gamma =8f_0.$$

(28)

The frequency response (only the magnitude plot) of the odd-harmonics FPS detector, for ${\omega }_0=100\pi$ rad/s and $\gamma =8f_0=400$, is shown in Figure 9b.

3.3. FPS Detector Based on the $6\ell \pm 1$ Harmonics RPF

Consider now the transfer function of the $6\ell \pm 1$ harmonics RC scheme given by [25]

$$R{C}_{6\ell \pm 1}\left(s\right)={\displaystyle \frac{1-e^{-\frac{2s\pi }{3{\omega }_0}}}{1+e^{-\frac{2s\pi }{3{\omega }_0}}-e^{-\frac{s\pi }{3{\omega }_0}}}}.$$

(29)

Substitution of (29) in (17) yields the following expression referred to as the $6\ell \pm 1$ harmonics RPF:

$$RP{F}_{6\ell \pm 1}\left(s\right)={\displaystyle \frac{1+e^{-\frac{2s\pi }{3{\omega }_0}}-e^{-\frac{s\pi }{3{\omega }_0}}}{2-e^{-\frac{s\pi }{3{\omega }_0}}}}$$

(30)

which is aimed at filtering out the $6\ell \pm 1$ harmonic components of signals expressed in the $\alpha \beta$-coordinates. Figure 10 shows the block diagram of the $6\ell \pm 1$ harmonics RPF. Notice that, in contrast to the all- and odd-harmonic RPFs, the $6\ell \pm 1$ harmonics RPF incorporates an additional feedback path. The transfer function (30) has zeros at every $\omega =\left(6\ell \pm 1\right){\omega }_0$, $\ell \in \mathbb{Z}$. Therefore, the frequency response of (30) (only the magnitude plot), shown in Figure 11a, shows notches with an arbitrarily small gain and crests with a 0 dB gain in between every two consecutive notches, just as in the RPFs presented above.

The $6\ell \pm 1$ harmonics RPF (30) is now combined with an SOHO (16) to form the so-called $6\ell \pm 1$ harmonics FPS detector. Similarly, this scheme must achieve a unitary gain at $\omega ={\omega }_0$ for a specific gain $\gamma$, which is tuned following the same procedure as in previous FPS detectors. For this, the $6\ell \pm 1$ harmonics FPS detector, i.e., the cascade connection between the $6\ell \pm 1$ harmonics RPF (30) and the SOHO expressed in complex notation (20), is

$${\displaystyle \frac{{\widehat{\mathbf{V}}}_{\alpha \beta }^{+}\left(s\right)}{{\mathbf{V}}_{\alpha \beta }\left(s\right)}}={\displaystyle \frac{\gamma \left(1+e^{-\frac{2s\pi }{3{\omega }_0}}-e^{-\frac{s\pi }{3{\omega }_0}}\right)}{2\left(s-j{\omega }_0\right)\left(2-e^{-\frac{s\pi }{3{\omega }_0}}\right)}}.$$

(31)

Evaluating (31) at $s=j\omega$, obtaining its squared magnitude, and setting this later equal to one yields

$${\left|{\displaystyle \frac{{\widehat{\mathbf{V}}}_{\alpha \beta }^{+}\left(s\right)}{{\mathbf{V}}_{\alpha \beta }\left(s\right)}}\right|}^2={\displaystyle \frac{{\gamma }^2\left(3+2cos\left(\frac{\omega 2\pi }{3{\omega }_0}\right)-4cos\left(\frac{\omega \pi }{3{\omega }_0}\right)\right)}{20{\omega }^2-40\omega {\omega }_0+\theta +20{\omega }_0^2}}=1$$

(32)

where $\theta \triangleq \left(32\omega {\omega }_0-16{\omega }^2-16{\omega }_0^2\right)cos\left({\displaystyle \frac{\omega \pi }{3{\omega }_0}}\right)$. Solving (32) for $\gamma$ at $\omega ={\omega }_0$ yields an indeterminate form that can be solved by applying twice the L’Hôpital’s rule. This results in the following solution:

$$\gamma =12f_0.$$

(33)

The frequency response (only the magnitude plot) of the $6\ell \pm 1$ harmonics FPS detector is shown in Figure 11b, for ${\omega }_0=100\pi$ rad/s ($f_0$ = 50 Hz) and $\gamma =600$.

3.4. A Note About Implementation Feasibility

The FPS alternatives presented thus far consist of essential components such as time-delays and integrators, which are directly implementable in the discrete-time domain via embedded devices. The convergence time generally correlates with the cumulative duration of sequential delays [28]; however, the ultimate implementation of these algorithms is often analyzed not only for precision but also for potential numerical drift.

Two primary causes of numerical divergence are instability and numerical errors associated with factors such as machine precision or round-off errors. It can be seen that the shown FPS structures lack feedback; therefore, they will be BIBO (bounded-input, bounded-output) stable if their impulse response is absolutely summable: a sequence $\left\{y\right[n\left]\right\}$ is said to be absolutely summable if the sum of the absolute values of the sequence elements is finite:

$$\sum _{n=-\infty }^{\infty }\left|y\left[n\right]\right|<\infty .$$

Consider the CF structure from (15) as a pertinent example, as it forms a crucial element of various RPF structures. Its discrete implementation comprises a buffer of d positions and a subtraction; therefore, an impulse input would generate an immediate impulse output and, after d samples, a negative impulse. That is, the output of the CF after an impulse response is absolutely summable and the CF is BIBO stable. This straightforward analysis can be extended to the other RPF structures presented (for visual clarity, see Figure 6, Figure 8 and Figure 10).

Quite more concerning is the application of a structure considering positive feedback: the MAF in (1) has an integrator and the SOHO is an autonomous oscillator. Nevertheless, both structures should always receive the RPF output; this is a crucial condition for discrete implementation [6], which is not immediately evident from their cascaded representation and seemingly inconsequential position exchange. A structure like the CF permits only transitory states or strictly symmetrical signals through, so the accompanying accumulator or oscillator remains stable from an analytical perspective. Other non-systematic numerical errors are symmetric and thus cancel out. Even noise and bit-level anomalies adhere to this stochastic behavior.

In addition, it is also known that implementing discrete oscillators is challenging. As will be shown later, a specific discretization process is used to implement the SOHO. By adhering to the discussed practices, the implementation is feasible and effective.

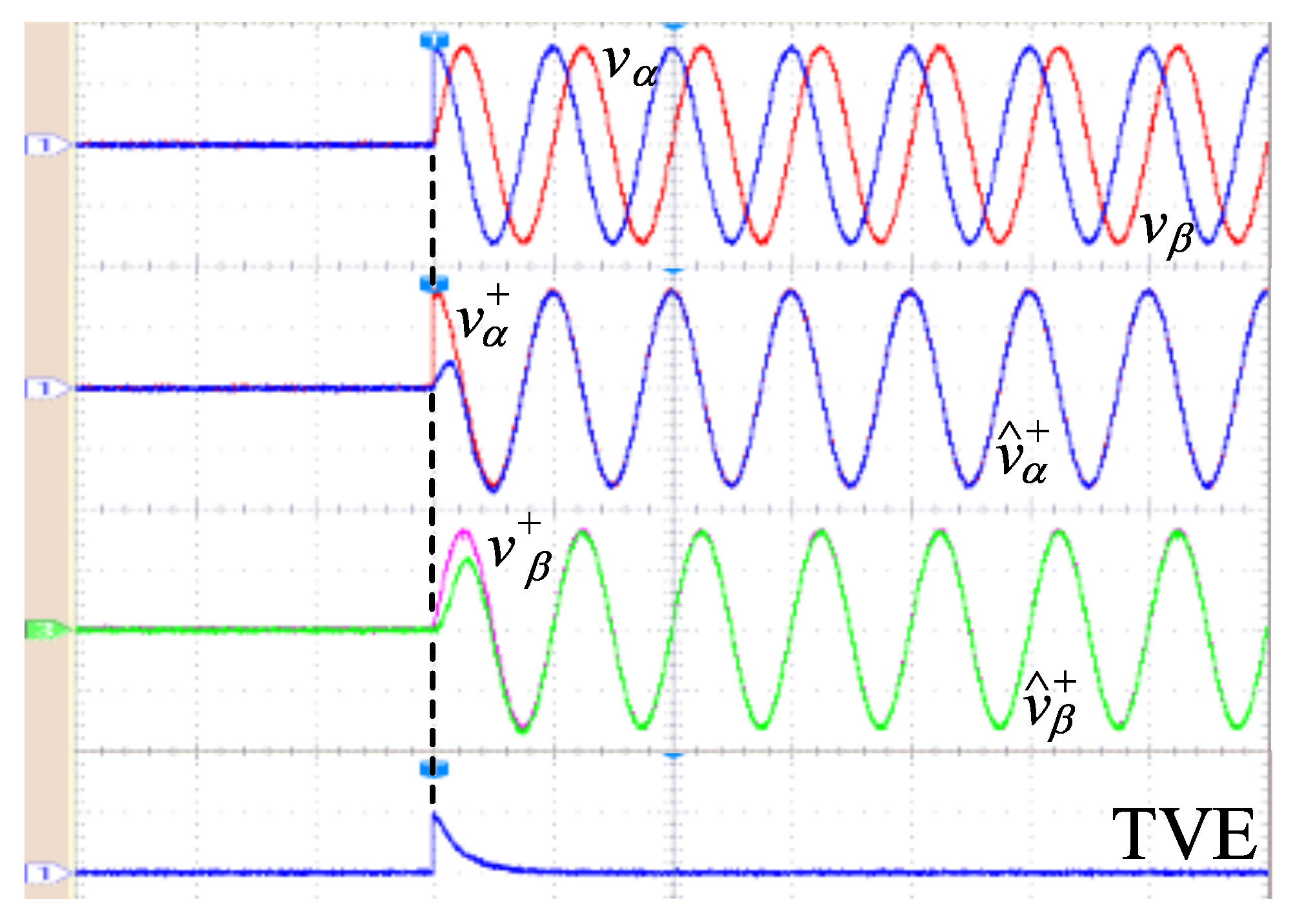
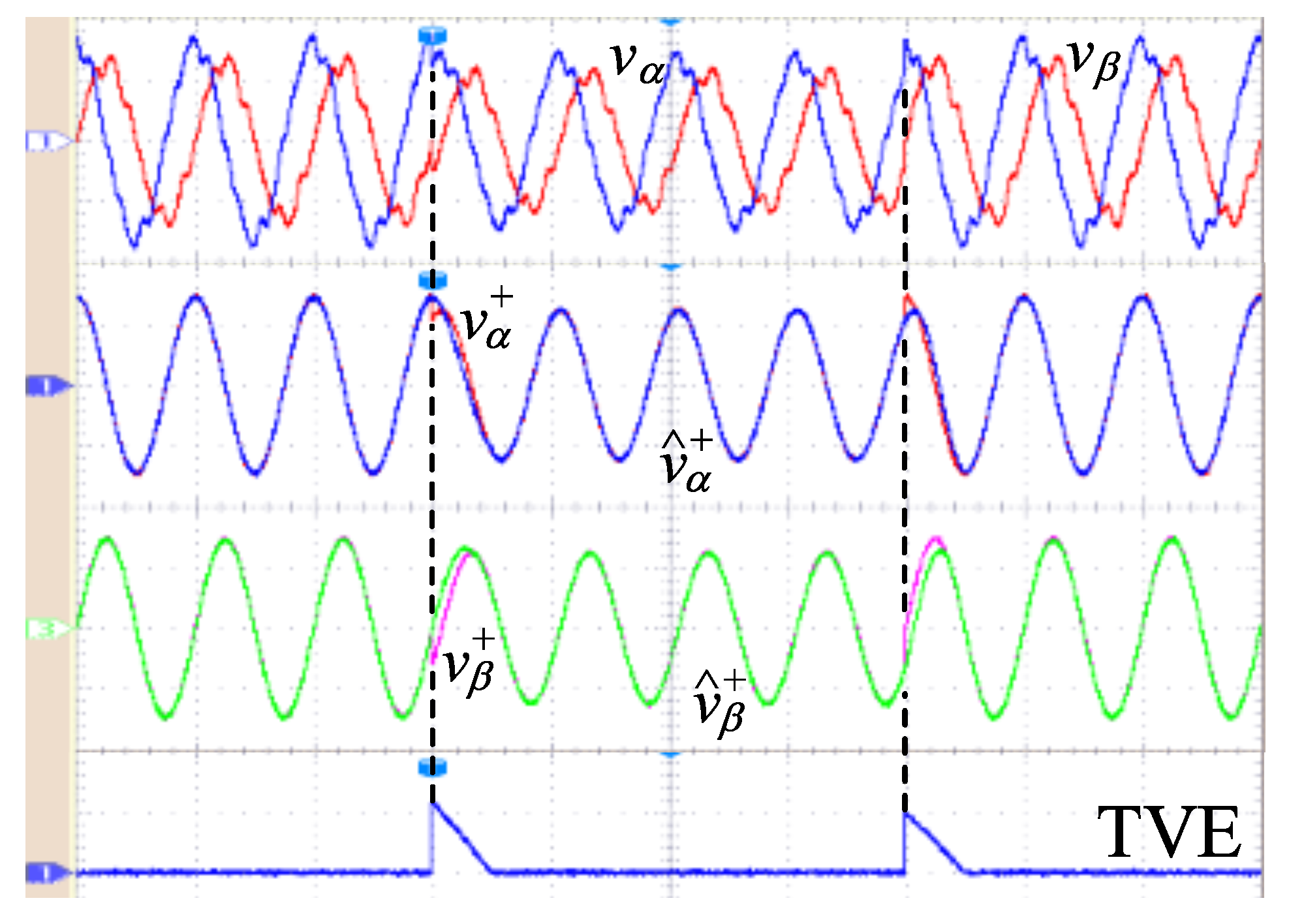
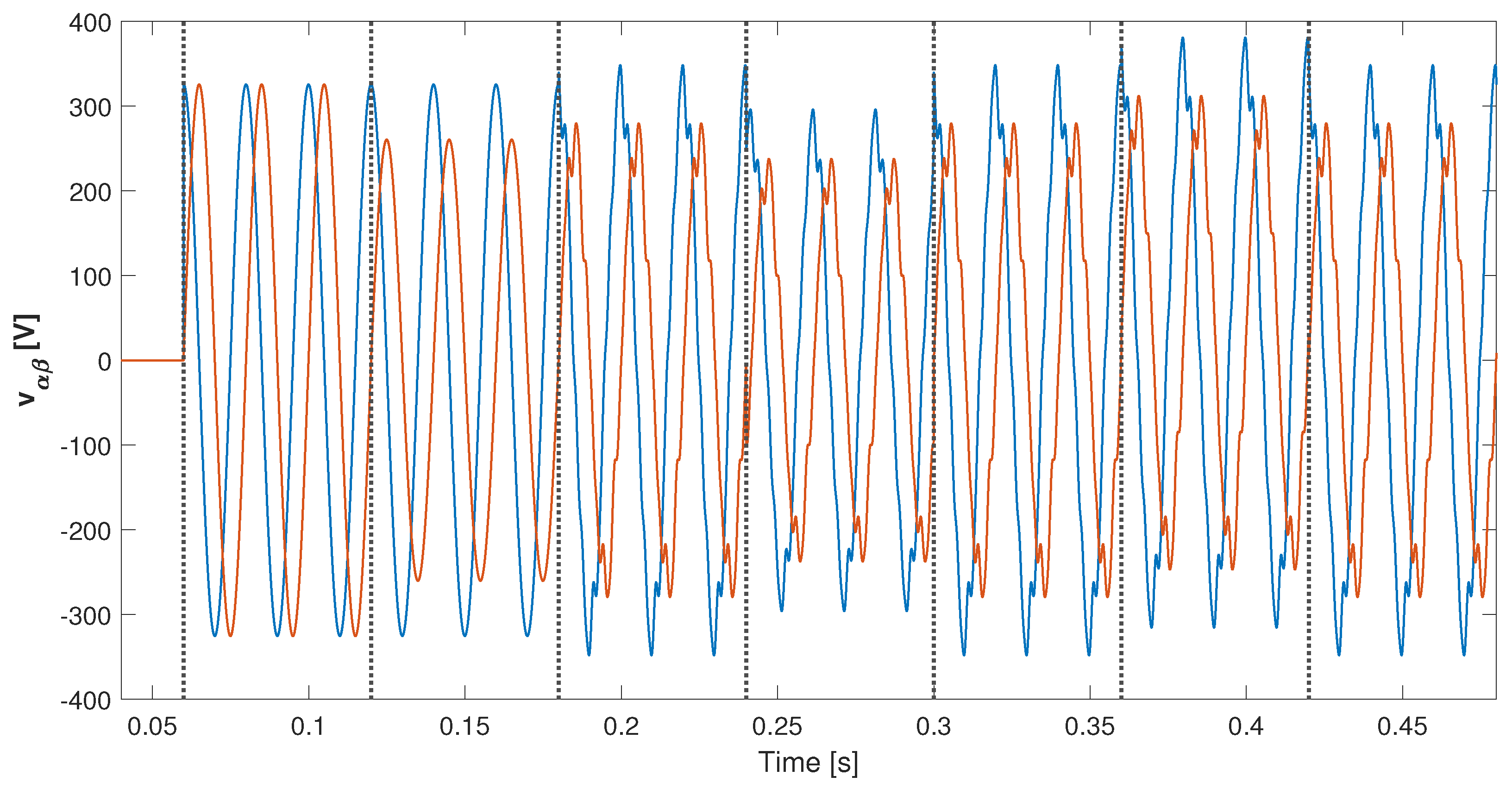
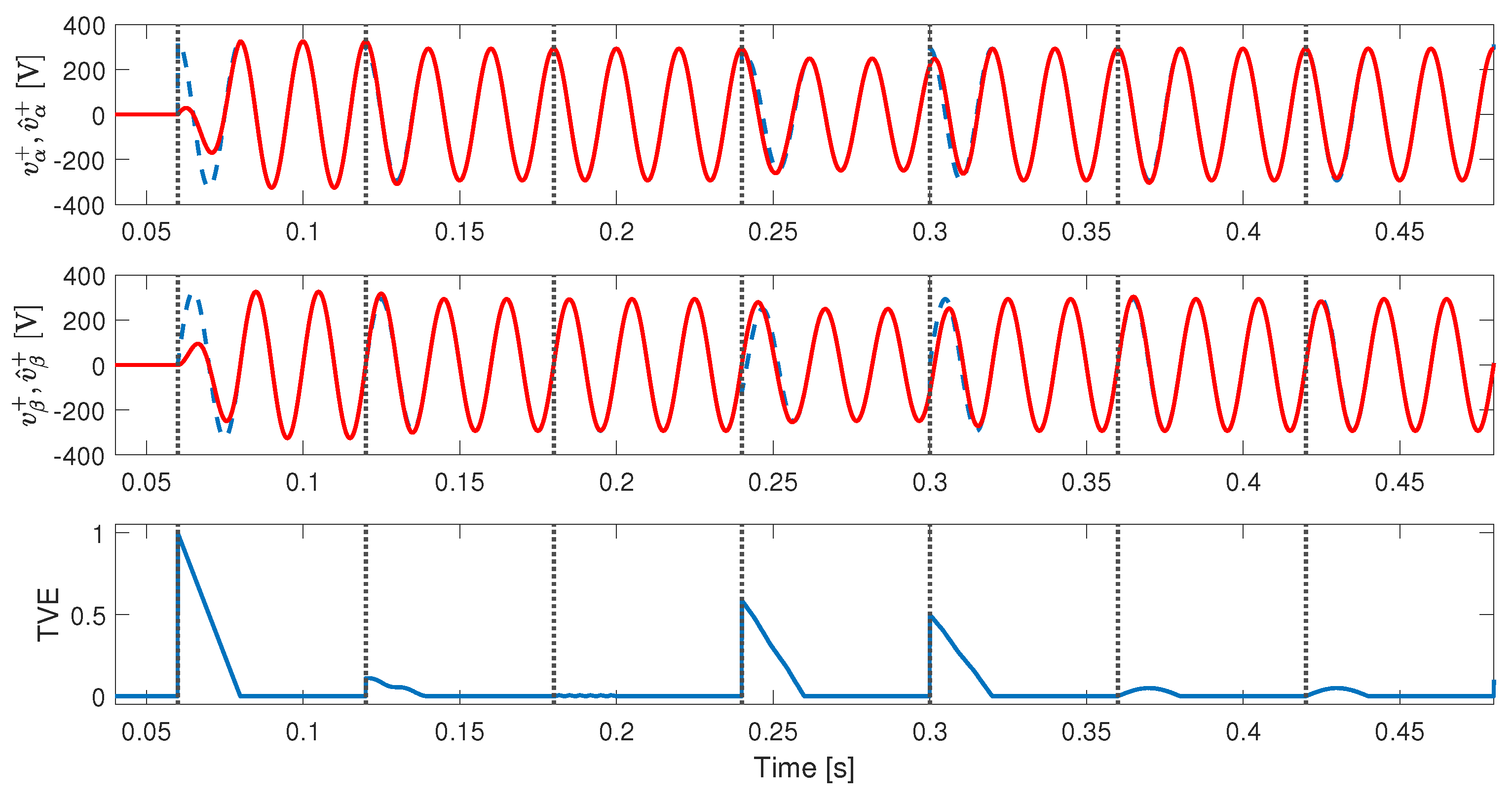
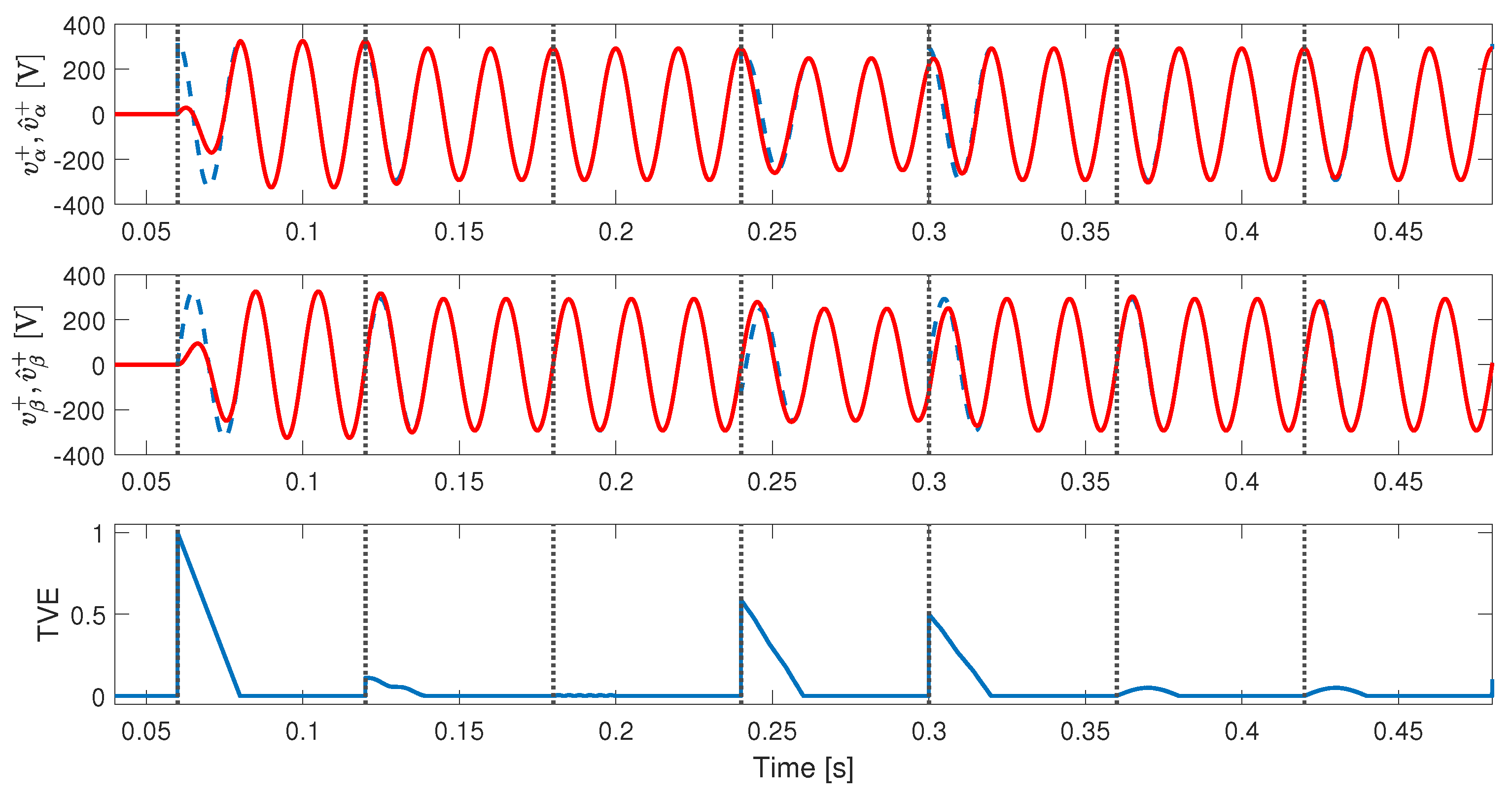
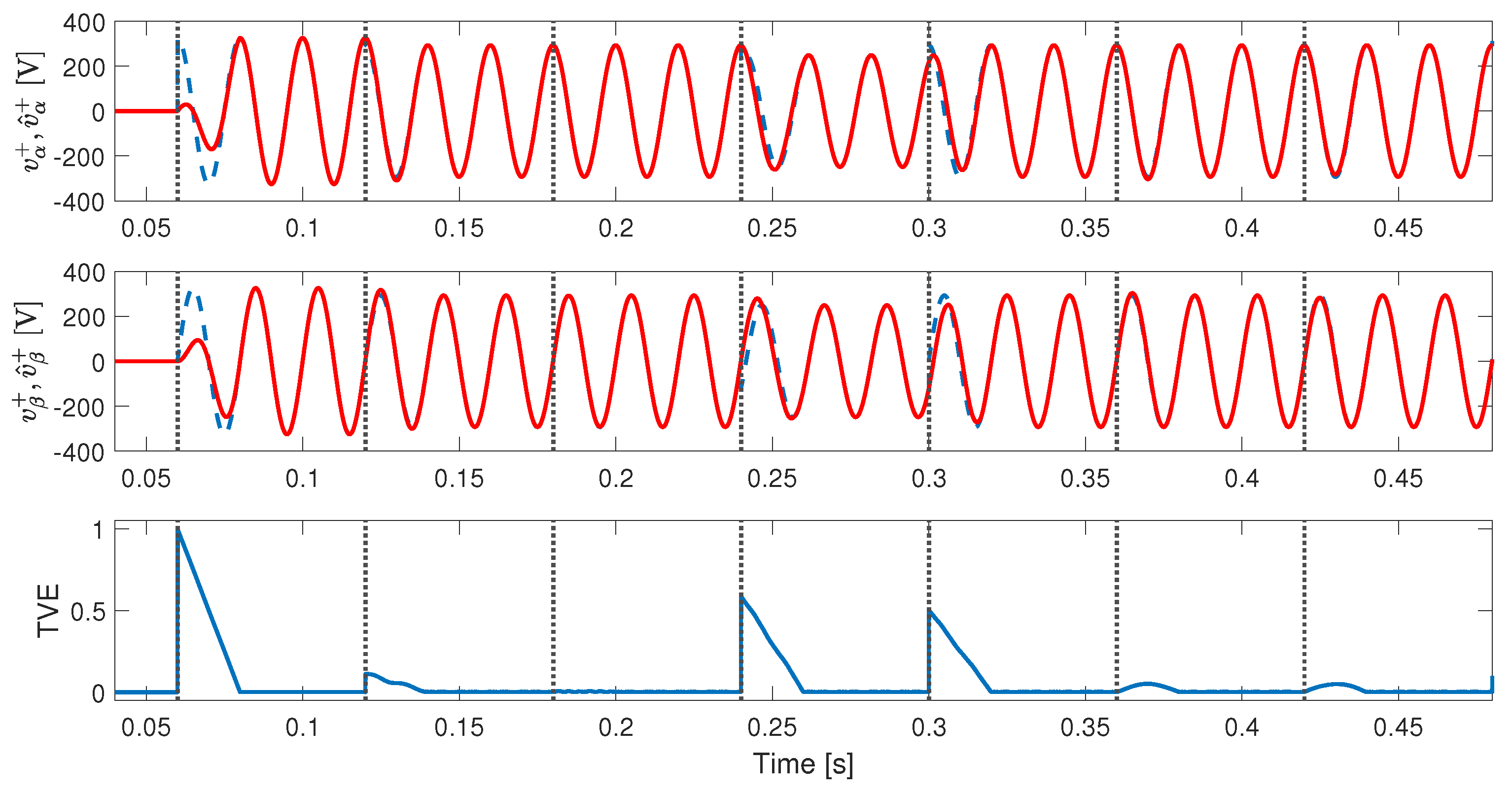
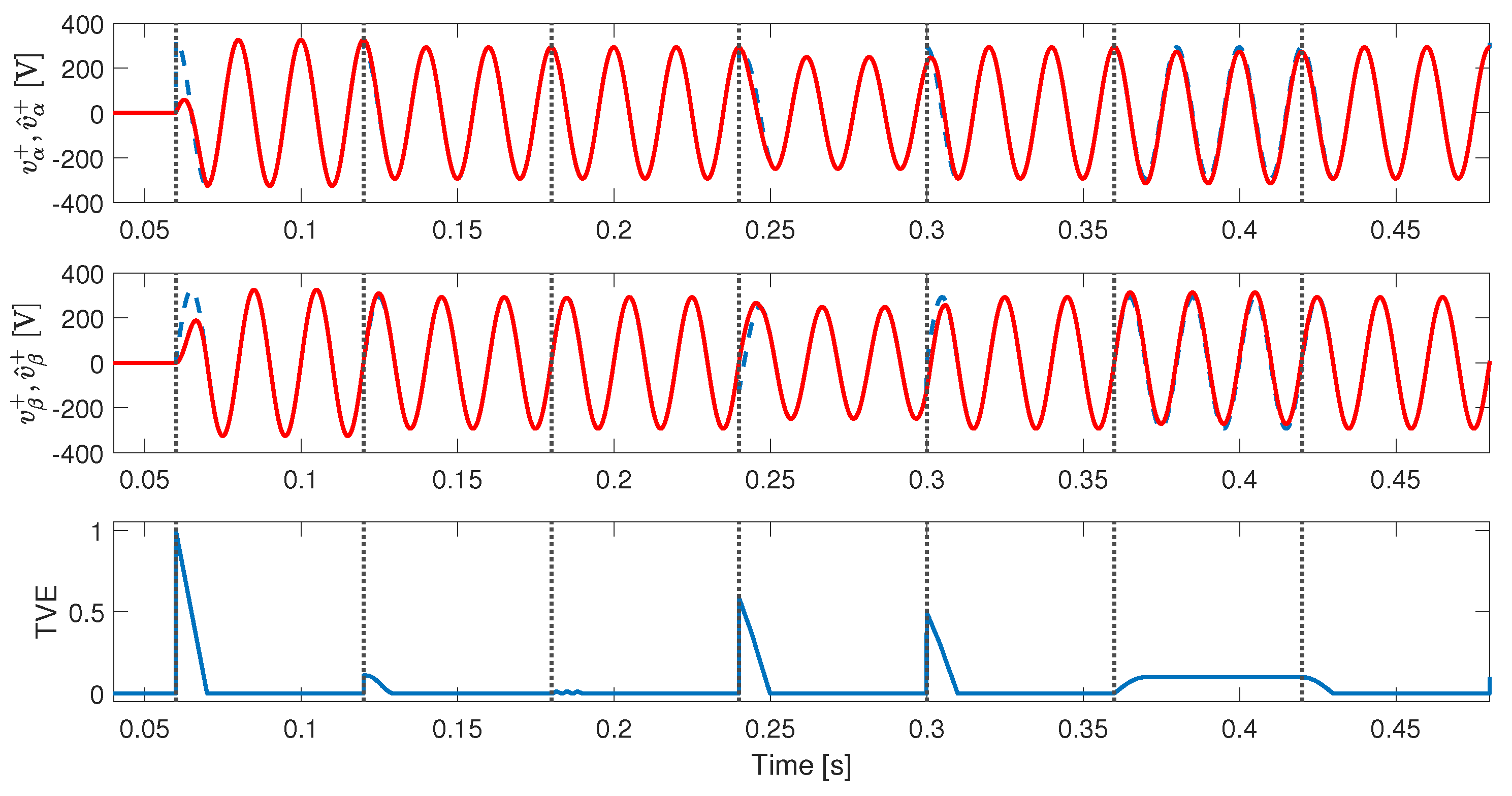
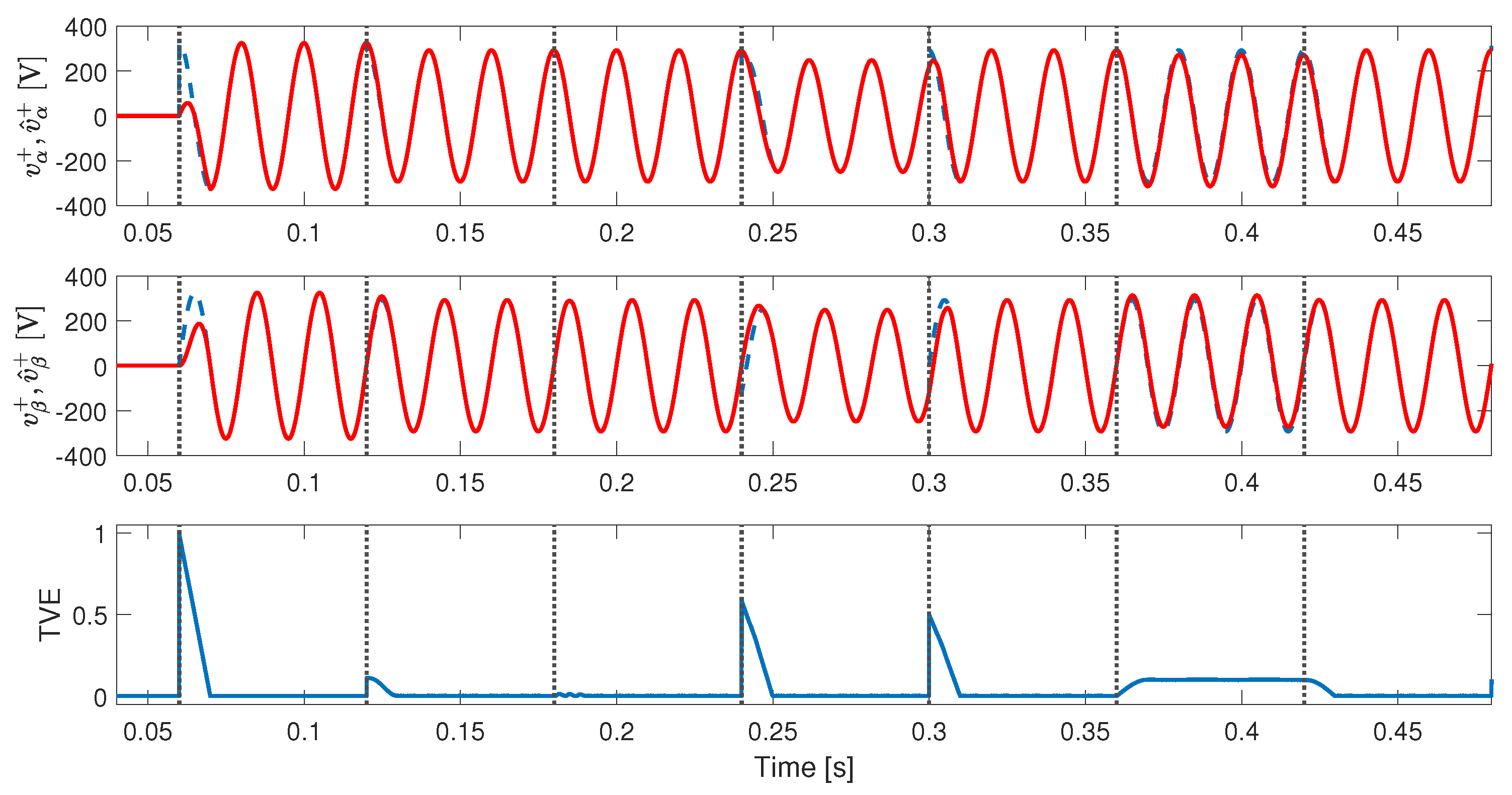
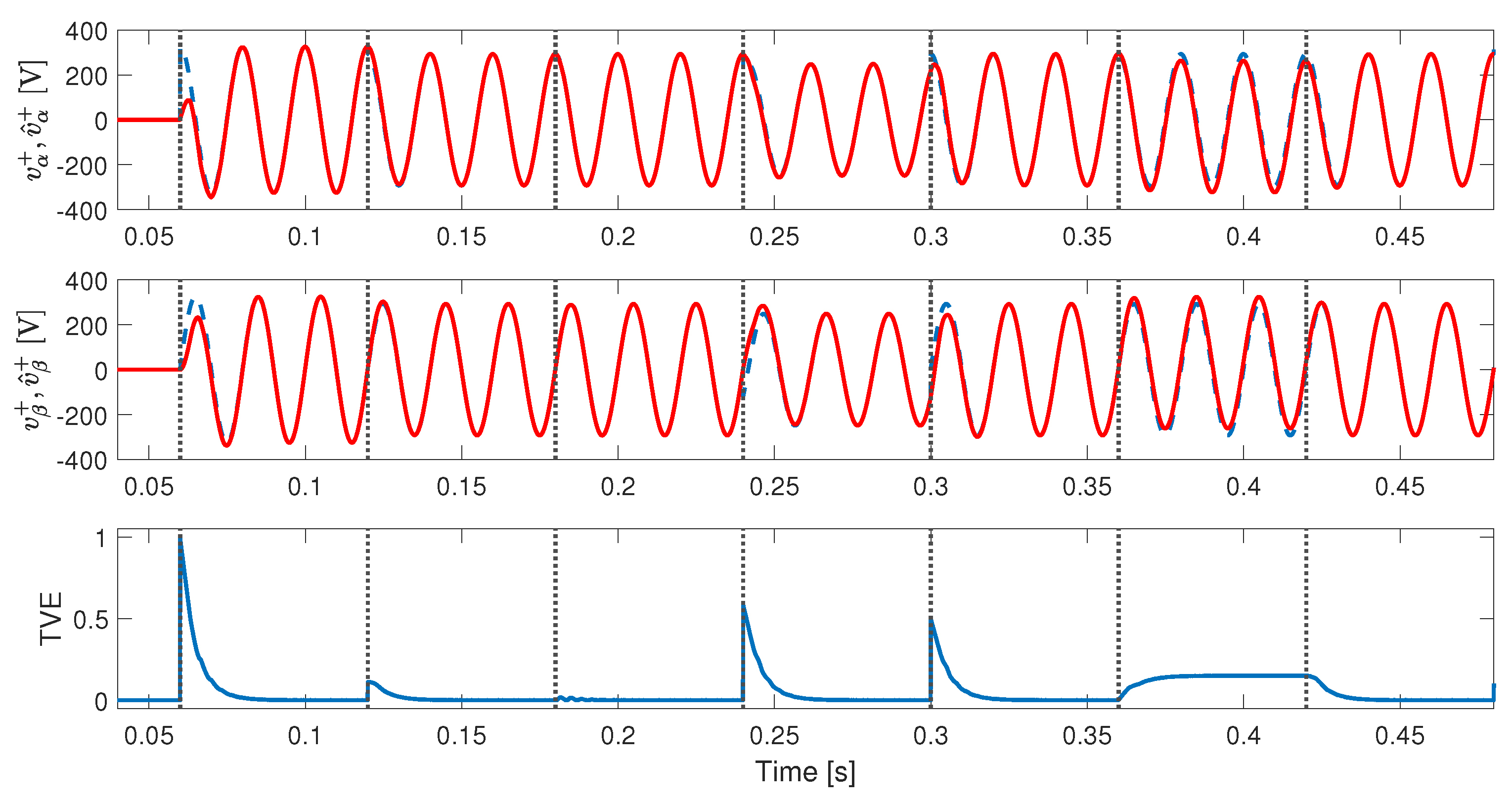
4. Real-Time Simulation Results

The FPS detectors presented above based on the different RPFs were implemented in the DS1007 board of dSPACE running at a sampling frequency of $f_s=12$ kHz. This platform includes a DS2103 board, which has 32 available DACs to access all internally generated signals to be displayed in a scope. In this same platform, the disturbed input signal has been implemented, considering a fixed fundamental frequency of 50 Hz.

On the one hand, discrete counterparts of the RPFs can be obtained by applying the z-transformation over the time-lag elements, yielding the following expressions for each of them:

$$\begin{array}{cc}\hfill & \mathit{all}-\mathrm{harmonics}:\hfill \\ \hfill & \mathcal{Z}\left\{e^{-{\displaystyle \frac{2s\pi }{{\omega }_0}}}\right\}=z^{-d_1},d_1={\displaystyle \frac{f_s}{f_0}}=240,\hfill \\ \hfill & \mathit{odd}-\mathrm{harmonics}:\hfill \\ \hfill & \mathcal{Z}\left\{e^{-{\displaystyle \frac{s\pi }{{\omega }_0}}}\right\}=z^{-d_2},d_2={\displaystyle \frac{f_s}{2f_0}}=120,\hfill \\ \hfill & 6\ell \pm 1\mathrm{harmonics}:\hfill \\ \hfill & \mathcal{Z}\left\{e^{-{\displaystyle \frac{s\pi }{3{\omega }_0}}}\right\}=z^{-d_3},d_3={\displaystyle \frac{f_s}{6f_0}}=40.\hfill \end{array}$$

It should be noted that the all-harmonics-based RPF has the larger number of memory allocations, while this number decreases to half in the odd-harmonics RPF, and the smallest value is achieved in the $6\ell \pm 1$ harmonics RPF, which may represent a benefit for RPFs dealing with these specific harmonics. Moreover, it is very important that the buffer size be an integer number; otherwise, the harmonic distortion elimination in the incoming signal will no longer take place. A buffer size containing integer and fractional parts may arise if the fundamental frequency $f_0$ changes.

The discrete version of the SOHO (16) was obtained by the exact discretization method [29], which produces

$${\widehat{\mathbf{v}}}_{\alpha \beta }^{+}\left((n+1)T\right)=\mathbf{A}{\widehat{\mathbf{v}}}_{\alpha \beta }^{+}\left(nT\right)+\mathbf{B}{\mathbf{u}}_{\alpha \beta }\left(nT\right)$$

(34)

where $n\in \mathbb{Z}$, $n\ge 0$, $T=1/f_s$ represents the sampling time and

$$\begin{array}{cc}\hfill & \mathbf{A}=\left[\begin{array}{cc}cos\left({\omega }_{0}T\right)& -sin\left({\omega }_{0}T\right)\\ sin\left({\omega }_{0}T\right)& cos\left({\omega }_{0}T\right)\end{array}\right],\hfill \end{array}$$

(35)

$$\begin{array}{cc}\hfill & \mathbf{B}={\displaystyle \frac{\gamma }{2{\omega }_0}}\left[\begin{array}{cc}sin\left({\omega }_{0}T\right)& cos\left({\omega }_{0}T\right)-1\\ 1-cos\left({\omega }_{0}T\right)& sin\left({\omega }_{0}T\right)\end{array}\right].\hfill \end{array}$$

(36)

It is important to note that (34) is valid only for a constant ${\omega }_0$. This is a disadvantage for the presented repetitive-based schemes, as they will produce signals with non-unitary amplitude and with a small phase from the real signals, if the frequency changes. A solution to this issue is under study, and it will be reported in the near future.

Moreover, to compensate for the delay introduced by the discrete implementation in any presented FPS detector, the following rotation matrix is aggregated at the output as shown in Figure 12:

$$\mathbf{R}({\omega }_{0}T/2)=\left[\begin{array}{cc}cos({\omega }_{0}T/2)& sin({\omega }_{0}T/2)\\ -sin({\omega }_{0}T/2)& cos({\omega }_{0}T/2)\end{array}\right].$$

(37)

The performance of every FPS detector (implemented as the cascade connection between the different RPFs and the SOHO) was evaluated following similar scenarios to those presented in [6], which were mainly based on the EN50160 standard [30] and typical values of phase jumps reported in [31]. The following tests were carried out:

• Startup considering a pure sinusoidal input signal.
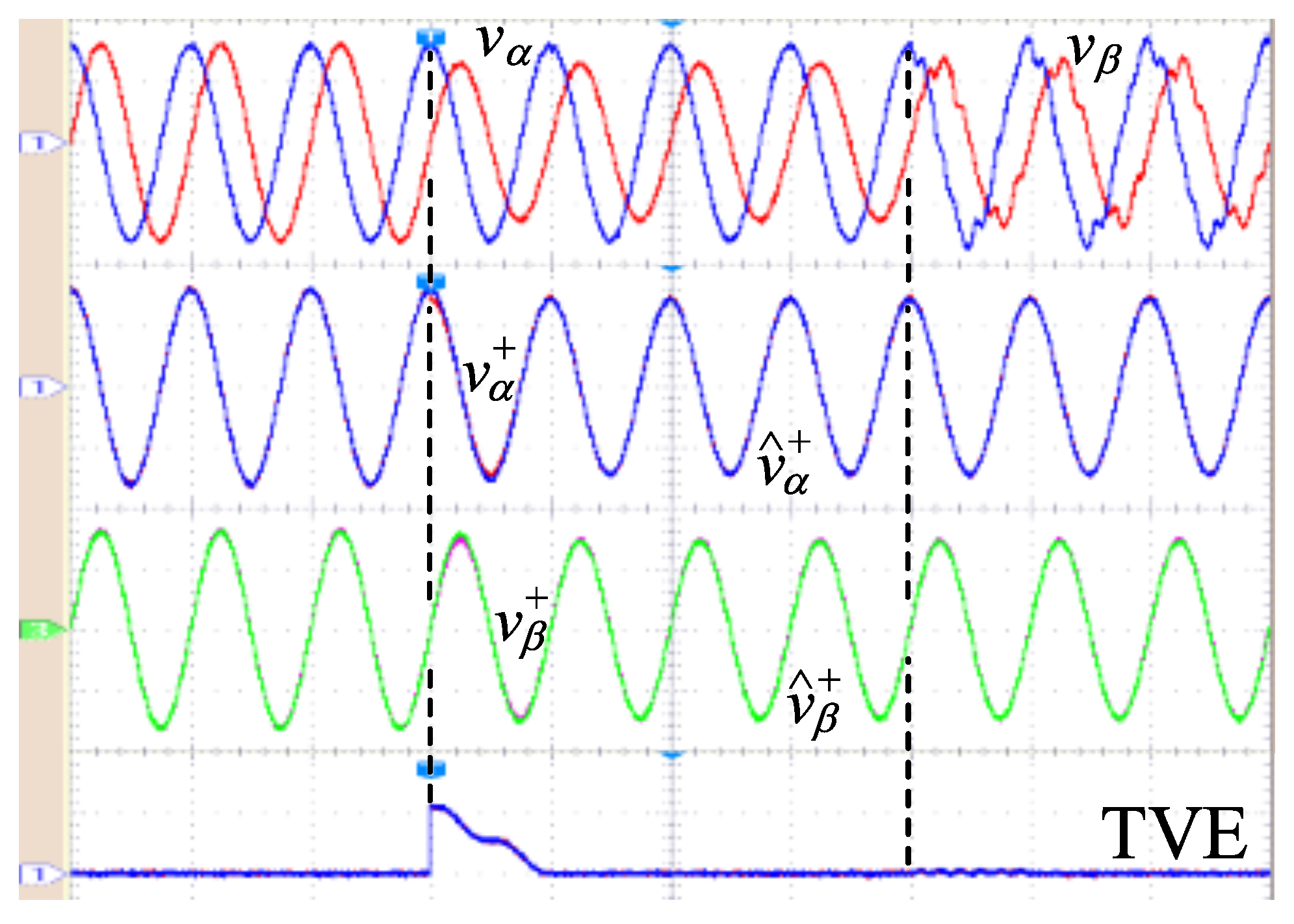
• Inserting unbalance and harmonic distortion in the input signal.
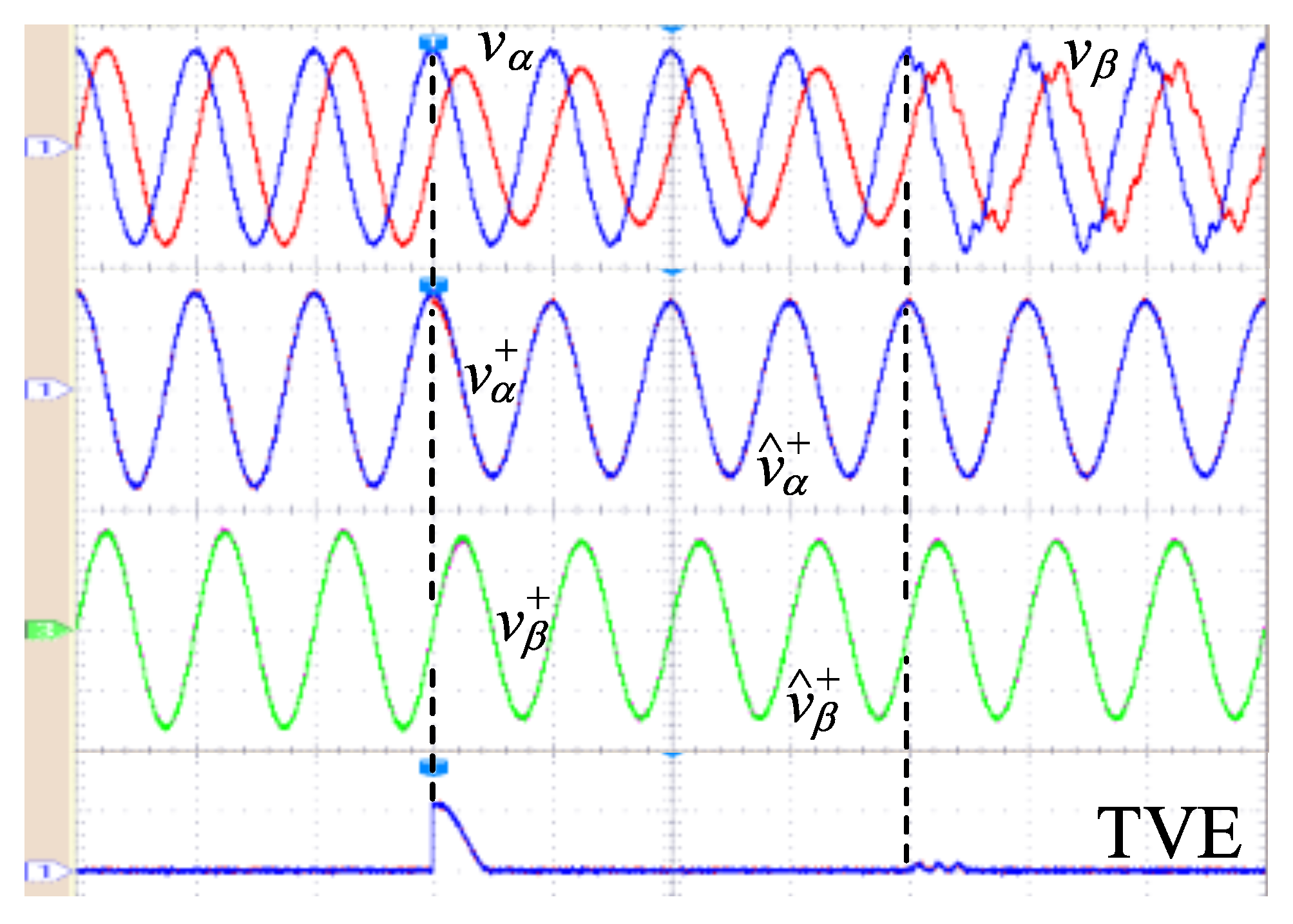
• Inserting simultaneous phase and amplitude jumps into the already unbalanced and distorted input signal.

As in [6], the total vector error (TVE) index was used to assess the performance of the proposed FPS detectors, which is defined as

$$\mathrm{TVE}\triangleq \sqrt{{\displaystyle \frac{{(v_{\alpha }^{+}-{\widehat{v}}_{\alpha }^{+})}^2+{(v_{\beta }^{+}-{\widehat{v}}_{\beta }^{+})}^2}{{v_{\alpha }^{+}}^2+{v_{\beta }^{+}}^2}}}.$$

(38)

This index was computed inside the DS1007 board and was available through one of the DACs in the board.

Each test considered a different input signal, which is described (in $\alpha \beta$-coordinates) in their corresponding subsection below.

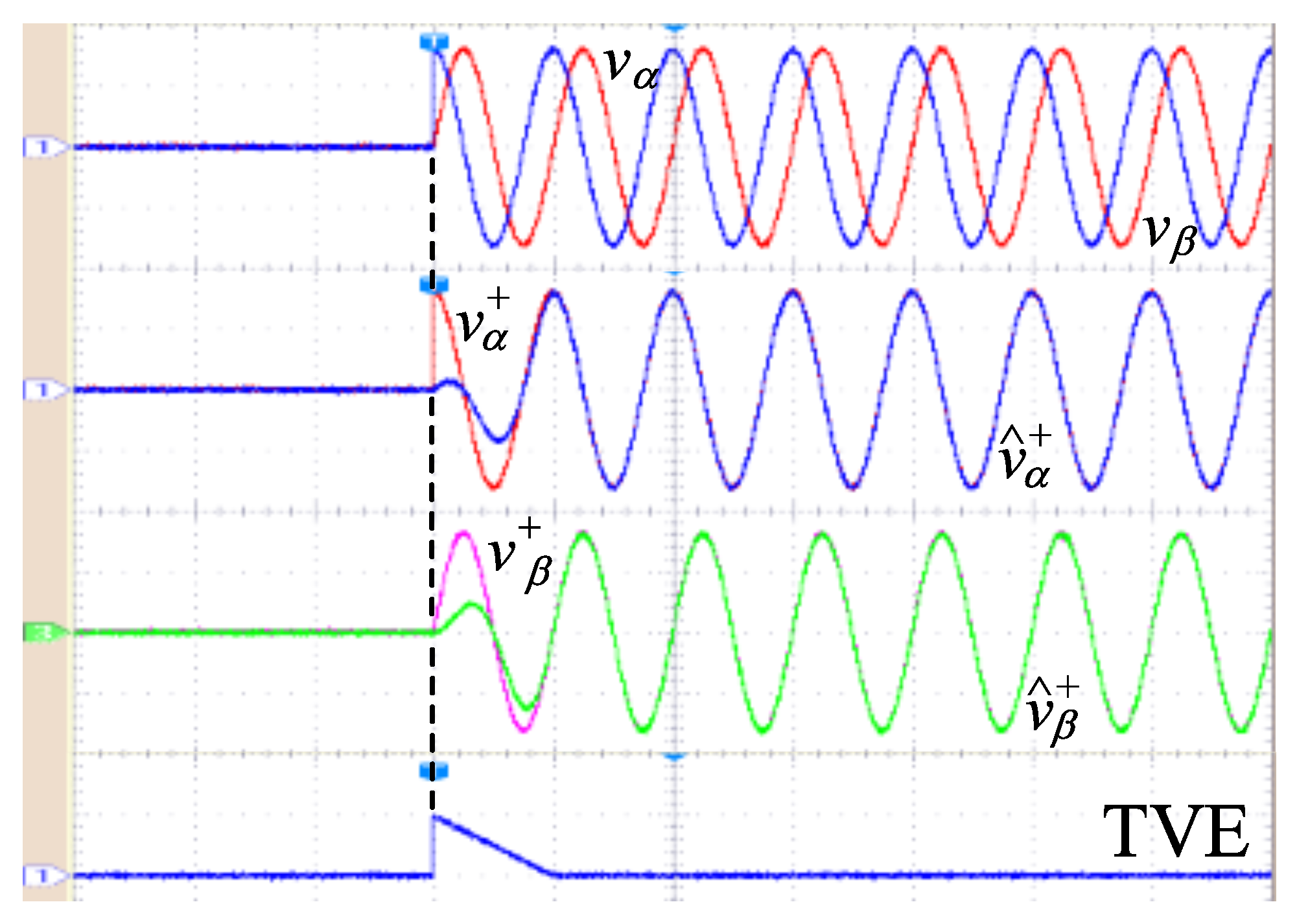
4.1. Startup Test

This test considered the response of each algorithm during the startup after being fed a pure sinusoidal input with ${\mathbf{v}}_{\alpha \beta }^{+}=230{\left[cos\left({\omega }_{0}t\right),sin\left({\omega }_{0}t\right)\right]}^{\top }$ V_RMS.

The results of this test for each FPS detector are shown in Figure 13, Figure 14 and Figure 15. These figures show, from top to bottom, the original signals $v_{\alpha }$ and $v_{\beta }$; the detected FPS signals ${\widehat{v}}_{\alpha }^{+}$ and ${\widehat{v}}_{\beta }^{+}$ overlapping the ideal positive sequence signals $v_{\alpha }^{+}$ and $v_{\beta }^{+}$; and the TVE index.

From Figure 13, Figure 14 and Figure 15, it is observed that the all-harmonics FPS detector reconstructs the positive sequence of the grid voltage in approximately one cycle (20 ms). Regarding the behavior of the odd-harmonics FPS detector and the $6\ell \pm 1$ harmonics FPS detector, both structures seem to reach the FPS in about half a cycle (10 ms). TVE responses are in agreement with the times observed from the sinusoidal responses in Figure 13, Figure 14 and Figure 15, showing that the RPFs with fewer memory allocations (the odd- and the $6\ell \pm 1$ harmonics RPFs) help to quickly detect the FPS of the grid voltage. Moreover, the TVE amplitudes in this test almost reach unity, but only at the beginning of the test.

4.2. Unbalance and Harmonic Distortion Test

This experiment introduces two disturbances to the pure sinusoidal input ${\mathbf{v}}_{\alpha \beta }^{+}={\left[230cos\left({\omega }_{0}t\right),230sin\left({\omega }_{0}t\right)\right]}^{\top }$ V_RMS. The first disturbance is a 10% unbalance, while the second one incorporates harmonic distortion (in addition to the unbalance) representing an 8% of total harmonic distortion (THD). For this, the harmonic components considered are the −5th, 7th, and −11th, with amplitudes of $0.06$, $0.047$, and $0.025$ pu, respectively, and phases of ${90}^{°}$, ${45}^{°}$, and ${30}^{°}$, respectively.

The results obtained from each FPS detector are shown in Figure 16, Figure 17 and Figure 18. All these figures show (from top to bottom) the input signals $v_{\alpha }$ and $v_{\beta }$; the detected FPS signals ${\widehat{v}}_{\alpha }^{+}$ and ${\widehat{v}}_{\beta }^{+}$ overlapping the ideal positive sequence signals $v_{\alpha }^{+}$ and $v_{\beta }^{+}$; and the TVE. In Figure 16, Figure 17 and Figure 18, the first three cycles correspond to the pure sinusoidal waveform; the next four cycles include the $10\%$ unbalance; and the last three cycles incorporate harmonic distortion to the already unbalanced signal.

Figure 16, Figure 17 and Figure 18 show that, when unbalance is introduced to the input signal, the all-harmonics FPS detector reconstructs the positive sequence of the grid voltage in approximately one cycle (20 ms), while the odd-harmonics and the $6\ell \pm 1$ harmonics FPS detectors seem to reach the FPS in about half a cycle (10 ms). However, when the input signal incorporates harmonic distortion, all algorithms seem to detect the FPS of the grid voltage almost instantaneously. The TVE amplitude reaches 0.1 after the unbalance is added to the input signal, whereas for the harmonic distortion test, only an almost imperceptible ripple was observed.

4.3. Test with Unbalance, Harmonic Distortion, Phase, and Amplitude Jumps in the Input Signal

The last test consists of adding an amplitude jump of $-0.15$ pu and a phase jump of $-{30}^{°}$ to the unbalanced and distorted signal of the second test; then, this signal is affected by an amplitude jump of $+0.15$ pu and a phase jump of ${30}^{°}$. The first selected value of the amplitude jump is in agreement with the IEEE 1159 standard [32], which establishes that the range for voltage magnitude reductions must be between 0.1 and 0.9 pu of the nominal voltage. Regarding the $-{30}^{°}$ phase jump considered in the test, it is known that typical values associated with distribution system faults are in the range of $-{30}^{°}$ to $+{30}^{°}$ [33] and, in most cases, accompanied by a lag phase angle [34]. The results of this test obtained from each FPS detector are shown in Figure 19, Figure 20 and Figure 21. All these figures show (from top to bottom) the perturbed signals $v_{\alpha }$ and $v_{\beta }$; the detected FPS signals ${\widehat{v}}_{\alpha }^{+}$ and ${\widehat{v}}_{\beta }^{+}$ overlapping the ideal positive sequence signals $v_{\alpha }^{+}$ and $v_{\beta }^{+}$; and the TVE index. In these figures, the first three cycles correspond to the unbalanced and distorted signal; the next four cycles incorporate an amplitude jump of $-0.15$ pu and a phase jump of $-{30}^{°}$; and the last three cycles include an amplitude jump of $+0.15$ pu and a phase jump of ${30}^{°}$.

Figure 19, Figure 20 and Figure 21 show that the all-harmonics FPS detector reconstructs the positive sequence of the grid voltage in approximately one cycle (20 ms), while both the odd-harmonics and the $6\ell \pm 1$ harmonics FPS detectors seem to reach the FPS in about half a cycle (10 ms). TVE amplitudes of all the algorithms in this test were around 0.5 once the amplitude and phase jumps were introduced into the input signal.

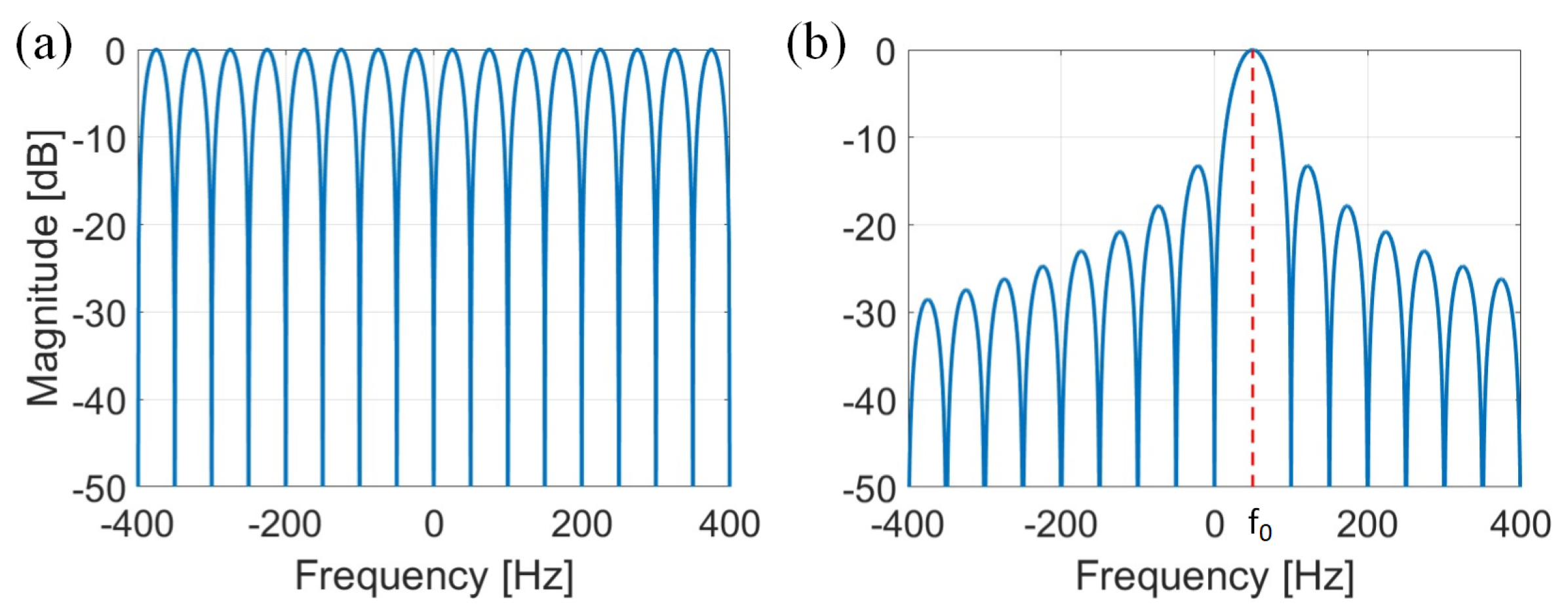
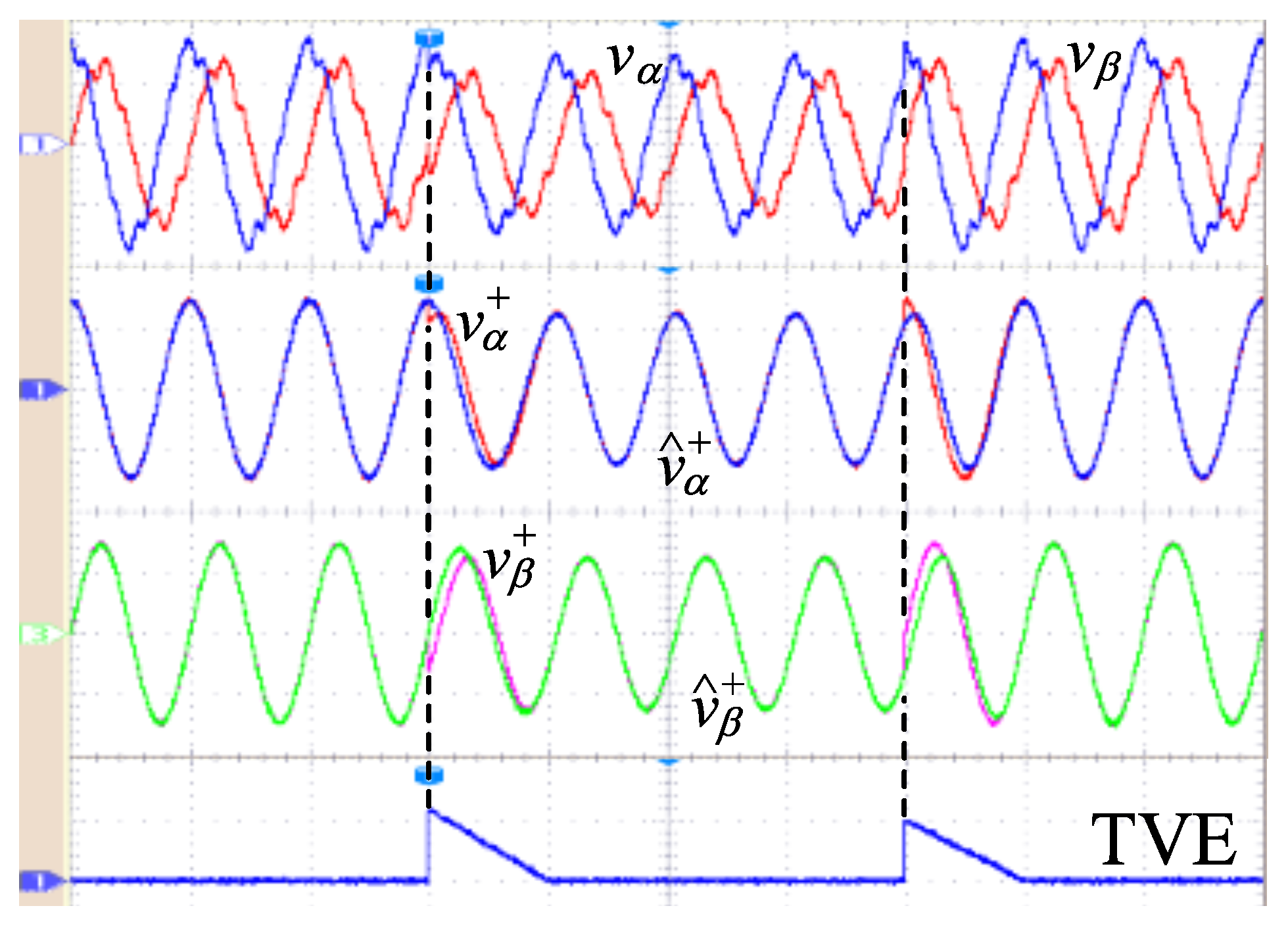
5. Comparison Results

The FPS detectors in this work were compared to the well-adopted MAF-based Park filter [2], and also, a comparison with similar schemes proposed in [12] was carried out. Recall that the proposal in [12] only considered single-phase systems, so the calculation of the FPS based on SOGI was performed as shown in [35]. The attached repetitive-based controllers to the dual SOGI were the all- and the odd-harmonics, as in [12]. Gains $k_{rc}$ and $k_f$ for the all-harmonics SOGI were fixed as 1 and $1/\pi$, while $k_{rc}=1$ and $k_f=2/\pi$ for the odd-harmonics SOGI.

All FPS detectors were simulated in the Simulink environment, using a sampling frequency of 12 kHz. This sampling frequency preserves the number of memory allocations shown at the beginning of Section 4 for all FPSs based on SOHO, while gives a buffer size of 240 units for the MAF-Park filter and the all-harmonics SOGI, and 120 units for the odd-harmonics SOGI. The tests carried out in the simulation environment were performed every 0.06 s, and they are described next:

• Test 1: Startup considering a pure sinusoidal input signal, at 0.06 s.
• Test 2: Inserting $10\%$ unbalance, at 0.12 s.
• Test 3: Including $8\%$ of THD (same harmonic components described in Section 4), at 0.18 s.
• Test 4: Adding an amplitude jump of $-0.15$ pu and a phase jump of $-{30}^{°}$, at 0.24 s.
• Test 5: Introducing an amplitude jump of $+0.15$ pu, and a phase jump of ${30}^{°}$, at 0.30 s.
• Test 6: Inserting a DC offset of $+0.1$ pu, at 0.36 s.
• Test 7: Including a DC offset of $-0.1$ pu, at 0.42 s.

All disturbances are applied to the preceding signal in the enumeration list above, i.e., unbalance is introduced in the signal described in test 1, THD is applied to the unbalanced signal in test 2, and so on. The resulting input signal ${\mathbf{v}}_{\alpha \beta }$, containing all disturbances described above, is shown in Figure 22. Dashed vertical lines mark the starting point of every test.

Figure 23, Figure 24, Figure 25, Figure 26, Figure 27, Figure 28 and Figure 29 show (from top to bottom) the detected FPS signals ${\widehat{v}}_{\alpha }^{+}$ and ${\widehat{v}}_{\beta }^{+}$ overlapping the ideal positive sequence signals $v_{\alpha }^{+}$ and $v_{\beta }^{+}$, and the TVE index, for all evaluated FPS detectors: CF-SOHO, all-harmonics SOHO, all-harmonics SOGI, MAF-based Park filter, odd-harmonics SOHO, odd-harmonics SOGI, and $6\ell \pm 1$ harmonics SOHO. Again, dashed vertical lines mark the beginning of all performed tests. From Figure 23, Figure 24, Figure 25, Figure 26, Figure 27, Figure 28 and Figure 29, it can be stated that the greater TVE value occurs at the startup test, while the smallest (or nearly imperceptible) value occurs when THD is added to the signal. Moreover, all evaluated FPS detectors achieve a zero steady-state error in the performed tests, except when a DC offset is introduced (odd-harmonics SOHO, odd-harmonics SOGI, and $6\ell \pm 1$ harmonics SOHO fail to do so).

The settling times of all FPS detectors were obtained from TVE measures and be applying the criterion stated in [6]: the time when the TVE crosses and remains below $0.01$ is taken as the settling time. Having a TVE value below $0.01$ also means that the evaluated detector converged to the true signal [6].

Table 1. Settling times (in seconds) of all simulated FPS detectors (N.A.: not available).

Test Number	CF- SOHO	All- SOHO	All- SOGI	MAF- Park	Odd- SOHO	Odd- SOGI	$6\mathit{\ell }\pm 1$ SOHO
1	0.0197	0.0197	0.0197	0.0198	0.0098	0.0098	0.0218
2	0.0173	0.0173	0.0175	0.0173	0.0080	0.0083	0.0139
3	0.0000	0.0000	0.0000	0.0000	0.0088	0.0086	0.0056
4	0.0196	0.0196	0.0195	0.0195	0.0098	0.0098	0.0200
5	0.0195	0.0195	0.0195	0.0195	0.0097	0.0097	0.0190
6	0.0186	0.0186	0.0187	0.0188	N.A.	N.A.	N.A.
7	0.0185	0.0185	0.0185	0.0186	0.0093	0.0093	0.0159

shows the settling time values for all evaluated FPS detectors, in all performed tests, while

Table 2. Maximum TVE of all simulated FPS detectors. The lowest TVE values achieved on each test are highlighted in bold-faced type.

Test Number	CF- SOHO	All- SOHO	All- SOGI	MAF- Park	Odd- SOHO	Odd- SOGI	$6\mathit{\ell }\pm 1$ SOHO
1	0.9958	0.9958	0.9958	0.9958	0.9916	0.9916	0.9875
2	0.1110	0.1110	0.1109	0.1090	0.1110	0.1109	0.1110
3	0.0062	0.0060	0.0071	0.0079	0.0127	0.0130	0.0181
4	0.5868	0.5868	0.5852	0.5856	0.5845	0.5830	0.5823
5	0.4978	0.4978	0.4984	0.4978	0.4959	0.4965	0.4940
6	0.0504	0.0495	0.0514	0.0492	0.1000	0.1016	0.1506
7	0.0504	0.0505	0.0492	0.0518	0.1004	0.0991	0.1504

shows the maximum TVE value of each FPS detector per carried out test. From Table 1, it is shown that the quickest FPS detectors are those incorporating the odd-harmonics RC, at the expenses of not removing DC offset disturbances. Table 2 highlights, in bold-faced type, the lower TVE values achieved on each test.

Finally,

Table 3. Execution times (in seconds), DC offset removal capability, and steady-state error of each FPS detector. The FPS detector that took less execution time was the CF-SOHO (typeset in boldface to enhance visual clarity).

FPS Detector	Execution Time	DC Offset Removal	Steady-State Error
CF-SOHO	0.008	Yes	No
All-SOHO	0.018	Yes	No
All-SOGI	0.019	Yes	No
MAF-Park	0.033	Yes	No
Odd-SOHO	0.010	No	Only in DC offset test
Odd-SOGI	0.017	No	Only in DC offset test
$6\ell \pm 1$-SOHO	0.012	No	Only in DC offset test

, summarizes other important characteristics for each FPS detector: the execution times (obtained via the Simulink profiler), if the detector is able to remove the DC-offset disturbance or not, and if the detector exhibits steady-state error. The FPS detector that takes less execution time is the CF-SOHO, while the method that takes more executing time is the MAF-based Park filter. Although both the CF-SOHO and the MAF-based Park filter show similar dynamic response (both have the same delay buffer), the MAF-based Park filter takes more execution time due to the rotations involved in the computation process. Out of all FPS detectors, only the CF-SOHO, the all-harmonics-based methods, and the MAF-based Park filter removed the DC offset and showed a zero steady-state error in all tests. The odd-harmonics-based methods and the $6\ell \pm 1$-harmonics SOHO failed to remove the DC offset disturbance, given a constant steady-state error in the DC offset test.

All compared FPS detectors can easily be programmed in a DSP for real-time implementation. In fact, the CF-SOHO and the MAF-based Park filter have been implemented in the TMS320F28379D from Texas Instruments in [6], where both detectors showed convergent and stable output signals. The main reason why all SOHO-based FPS detectors were programmed in the dSPACE board instead of the Texas Instrument DSP was the reduced number of DAC ports in the DSP (only two). Detailed guidelines for implementing all SOHO-based FPS detectors in the Texas Instruments DSP can be found in [28].

6. Conclusions

This work presented a family of FPS detectors based on repetitive prefilters cascaded to the SOHO. The underlying grounds of this proposal was born when the frequency-shifting property of the Laplace transform was applied to the MAF transfer function, which gave rise to a CF-SOHO (for constant frequency) structure able to operate directly in the fixed reference frame coordinates. Depending on the desired harmonics to be filtered, other RC schemes (the all-, odd-, and the $6\ell \pm 1$ harmonics) were used in a negative feedback loop that gave rise to RPFs referred to as all-, odd-, and $6\ell \pm 1$ harmonics RPFs. When these RPFs were coupled to the SOHO, FPS detectors emerged. The tuning rules for the SOHO gain were explicitly provided for each FPS detector to fit the expected frequency response, i.e., a unitary gain at the fundamental frequency. When compared to original RC schemes, the all- and odd-harmonics RPF structures reduced the number of memory locations of the digital device where the FPS detector was implemented. In addition, it was shown that the CF-SOHO is a particular case of the all-harmonics FPS detector.

Tests performed on a dSPACE board showed that the time to reconstruct the FPS signals was reduced to half of the cycle (10 ms) for the odd- and the $6\ell \pm 1$ harmonics FPS detectors, even in the presence of simultaneous disturbances (unbalance, harmonic distortion, amplitude, and phase jumps), which is an advantage over the all-harmonics FPS detector that took a full cycle (20 ms) in producing the positive-sequence signals under these simultaneous disturbances.