A Hybrid Machine Learning Framework for Electricity Fraud Detection: Integrating Isolation Forest and XGBoost for Real-World Utility Data

Abstract

This paper proposes a hybrid machine learning framework for detecting electricity fraud within the broader context of Non-Technical Losses (NTLs) in power-distribution systems. The framework combines unsupervised anomaly detection using Isolation Forest with supervised classification through XGBoost, exploiting the complementary strengths of both algorithms. Using real consumption data from a Peruvian utility, the approach integrates domain-informed feature engineering to capture behavioral, temporal, and contextual indicators of irregular usage. To address the extreme class imbalance inherent to fraud datasets, the SMOTETomek hybrid resampling technique was applied, enhancing minority-class representation and decision boundary clarity. Experimental results achieved high predictive performance on the test set (AUC-ROC = 0.999, F1-score = 0.77) using an optimized decision threshold of 0.6. Moreover, SHAP-based interpretability analysis identified extreme monthly variations, prolonged low-consumption periods, and tariff category as key behavioral predictors of fraudulent activity. The robustness of the proposed framework was further validated through a 5-fold cross-validation procedure during the training phase, ensuring consistent performance across different data partitions. Overall, the proposed framework demonstrates not only robust and explainable performance but also practical operational value, providing utilities with a scalable data-driven tool to optimize inspection strategies and maximize recovery of non-technical losses.

1. Introduction

Non-technical losses (NTLs) in power distribution—especially electricity fraud—generate substantial operational and economic impacts for utilities. The increasing availability of meter data enables data-driven detection strategies that go beyond static, rule-based inspections [1,2]. In this work, the term electricity fraud is used in its broad sense, encompassing both administrative and technical irregularities. Electricity theft—a subset of fraud—specifically refers to direct physical manipulation of metering or wiring systems to bypass measurement or billing. Recent studies show that modern machine learning pipelines, when paired with carefully crafted features and proper validation, can markedly improve the prioritization of field inspections and the overall fraud hit-rate [3,4].

Traditional approaches struggle to capture adaptive and context-dependent fraudulent behavior. In contrast, contemporary ML ecosystems—spanning classical classifiers, ensemble methods, and deep architectures—leverage multi-year consumption histories and tariff/context signals to reveal irregular usage patterns [1,2]. In practice, however, severe class imbalance, temporal dynamics, and the need for transparent decision-making remain key obstacles to robust, deployable solutions [3,5].

Early NTL-detection systems relied on expert rules and threshold analyses derived from historical averages. While simple to implement, these strategies often failed to adapt to evolving consumption behavior or new types of fraud. It is important to note that, although the literature often uses fraud detection and theft detection interchangeably, the latter usually targets direct tampering or bypassing of metering devices, whereas the former also includes billing manipulation and data falsification. To address this ambiguity, we explicitly define electricity theft as the physical act of bypassing or tampering with meters, while electricity fraud is defined more broadly to include administrative irregularities, billing manipulation, and logical data falsification. Our framework is designed to detect patterns indicative of both phenomena.

It is also necessary to define the scope of this study regarding the grid hierarchy. While non-technical losses occur at various stages of the power system—including transmission and sub-transmission levels—this research focuses specifically on “last mile” consumption at the end-user level. This focus is dictated by data availability, as the utility partner provided granular smart meter data for residential and commercial end-users, but lacked comparable intermediate metering infrastructure to track losses during transmission. Therefore, our proposed data-driven approach is tailored for detecting irregularities at the final distribution point.

Machine learning (ML) methods introduced a paradigm shift by enabling automatic pattern discovery and probabilistic classification of suspicious customers [2,3]. Recent studies employ supervised classifiers such as Support Vector Machines (SVMs), Decision Trees, Random Forests, and Gradient-Boosted Trees (e.g., XGBoost), which are particularly suitable for heterogeneous tabular data and nonlinear relationships [1,4]. Deep-learning architectures, including Convolutional Neural Networks (CNNs) and Long Short-Term Memory (LSTM) models, have been explored to capture temporal correlations and complex behavioral signatures in meter readings [5]. Unsupervised and semi-supervised schemes, such as Isolation Forest and Autoencoders, have also been proposed to identify outliers when labeled data are scarce or unbalanced [3,6].

In [7], a novel framework combining active learning with metaheuristic optimization was proposed to address the persistent challenge of electricity theft, which leads to significant financial losses and operational inefficiencies in power distribution systems. The study introduced two models—Active Stochastic Gradient Descent (ASGD) and Cuckoo Stochastic Gradient Descent (CSGD)—to overcome common limitations of traditional detection systems, including class imbalance, scarcity of labeled data, suboptimal hyperparameter tuning, and limited interpretability. The ASGD model employs entropy-based active learning to iteratively select the most informative samples, whereas CSGD leverages cuckoo search optimization to refine model parameters. Experimental results demonstrated substantial improvements in accuracy, F1-score, and precision–recall metrics, validated through 10-fold cross-validation and rigorous statistical testing. Furthermore, the framework integrates Local Interpretable Model-Agnostic Explanations (LIMEs) and SHapley Additive exPlanations (SHAPs) to enhance transparency and ensure reliable interpretation of anomalous consumption patterns.

Hybrid frameworks that combine feature engineering with ensemble models tend to achieve the best trade-off between accuracy and interpretability. Studies integrating anomaly scores from unsupervised detectors into supervised pipelines have reported improved robustness to data drift and class imbalance [3,6]. Moreover, performance metrics such as precision, recall, F1-score, and the area under the ROC curve (AUC-ROC) are commonly used to evaluate fraud-detection models at both record and customer levels [4].

This work addresses the binary classification task of flagging potentially fraudulent customers from historical consumption data and related attributes. Let $\mathcal{D}={\left\{(x_i,y_i)\right\}}_{i=1}^N$ denote customer-month observations with features $x_i\in {\mathbb{R}}^p$ and labels $y_i\in \{0,1\}$. The problem is characterized by: (i) extreme class imbalance, (ii) seasonality and non-stationarity, and (iii) operational constraints that require thresholds aligned with limited inspection capacity [3]. Our goals are to design a scalable and interpretable pipeline, mitigate imbalance through hybrid strategies, and calibrate decision thresholds and evaluation metrics at both record and customer levels to maximize operational value [6]. We define “real-world operational value” as the model’s capability to be deployed within existing utility IT infrastructures with minimal latency, producing inspection lists that align with field crew capacity (limited budget), and maintaining stability against data drift over time.

The main contributions of this study can be summarized as follows:

• Comprehensive feature engineering: Behavioral, temporal, and contextual descriptors (rolling statistics, change indicators, seasonal ratios, and peer-normalized metrics) tailored to tabular consumption data.
• Hybrid learning strategy: Integration of an unsupervised anomaly indicator with a high-performance supervised classifier to capture complementary signals of irregularity.
• Imbalance handling: Application of hybrid resampling/weighting and boundary-cleaning approaches suitable for rare-event detection.
• Operational evaluation: Beyond AUC/F1, we report customer-level precision/recall and perform threshold tuning aligned with inspection capacity.
• Interpretability: Importance analyses to expose which consumption dynamics drive alerts, supporting transparent and auditable decisions.

2. Related Work and Theoretical Framework

Research on Non-Technical Loss (NTL) detection has evolved significantly over the past decade, driven by the availability of advanced metering infrastructure and large-scale energy-consumption datasets. Traditional statistical and rule-based methods have gradually given way to data-driven and hybrid approaches that combine signal analysis, pattern recognition, and artificial intelligence techniques [1,3,4]. This section summarizes the main methodological trends in electricity-fraud detection and discusses the remaining challenges that motivate the present work.

2.1. Data-Driven Electricity Theft Detection

Data-driven methods have become the cornerstone of modern NTL detection, leveraging the granularity of Advanced Metering Infrastructure (AMI) data. Early approaches heavily relied on basic statistical methods and expert rules, which, while interpretable, lacked the adaptability to detect sophisticated theft patterns [8]. The advent of machine learning introduced supervised classifiers such as Support Vector Machines (SVMs), Decision Trees, and Neural Networks, which provided higher accuracy but often struggled with the severe class imbalance inherent in fraud datasets [1,9].

Recent literature emphasizes the need for feature engineering that captures behavioral dynamics rather than just raw consumption values. For instance, in [10] highlighted the importance of multi-source data integration—combining consumption data with external factors like weather and holidays—to improve detection robustness. Similarly, deep learning models like Convolutional Neural Networks (CNNs) and Long Short-Term Memory (LSTMs) networks have been employed to extract temporal patterns from raw consumption series. While these deep architectures can capture complex sequential dependencies, they often require high computational resources and massive labeled datasets, which are not always available in real-world utility scenarios [5]. In [11] was proposed an optimized XGBoost-based ML method (OXGBoosting) for identifying anomalies in conventional meters using a large-scale dataset. Our work addresses this gap by utilizing Gradient Boosting Trees (XGBoost), which offer a superior balance between performance on tabular data and computational efficiency, especially when augmented with domain-specific features.

2.2. Hybrid and Ensemble Methods

To overcome the limitations of single models—such as the inability of unsupervised models to learn from known fraud patterns and the susceptibility of supervised models to overfitting on small fraud samples—hybrid and ensemble architectures have gained prominence. These approaches combine the strengths of different algorithms, typically integrating unsupervised models for anomaly discovery with supervised models for pattern classification.

In [6], the authors demonstrated that integrating metaheuristic optimization with ensemble learning can substantially enhance hyperparameter tuning in fraud-detection models, ultimately improving generalization performance. Likewise, [3] proposed intelligent frameworks that leverage ensemble-based architectures to better address high-dimensional feature spaces and severe class imbalance, outperforming standalone classifiers in these scenarios. Their findings further indicate that stacking and voting mechanisms help stabilize predictions under noisy or heterogeneous data conditions.

In [12], the authors introduce an advanced theft-detection framework that integrates Quantum Key Distribution (QKD) with a rolling optimization strategy to minimize computational overhead and stabilize consumption-data fluctuations. For the classification stage, the model leverages Extreme Gradient Boosting in combination with the Coati Optimization Algorithm, while also incorporating privacy–functionality trade-off mechanisms to strengthen consumer trust in smart-meter systems.

In [13], the authors propose an interpretable multi-scale anomaly-detection framework for electricity-theft identification that integrates feature engineering with deep learning. Using tsfresh, the model extracts a rich set of consumption features, while XGBoost selects those most strongly correlated with anomalous behavior. Multi-scale convolutional neural networks combined with attention mechanisms capture both temporal and frequency-domain patterns, emphasizing the most informative feature channels. Experimental results demonstrate that this hybrid approach outperforms conventional anomaly-detection methods across multiple evaluation metrics.

In [14], the authors propose a hybrid approach that integrates K-Means clustering to group consumers with similar behavioral profiles, thereby reducing false positives arising from natural consumption variability. An LSTM module is employed to capture temporal dynamics in electricity usage, while an XGBoost classifier accurately discriminates between malicious and non-malicious patterns. By explicitly accounting for internal and external environmental factors, the framework effectively isolates true anomalies indicative of electricity theft.

Our framework aligns with this trend but introduces a specific novelty: the integration of Isolation Forest (IF) as an unsupervised feature extractor within a supervised XGBoost framework. Unlike standard voting ensembles, we treat the anomaly score from the Isolation Forest as a high-level input feature. This allows the supervised model to explicitly learn the relationship between global statistical anomalies and confirmed fraud cases, effectively creating a stacked hybrid architecture that benefits from both global anomaly scoring and localized pattern discrimination. This approach is particularly effective in “Positive-Unlabeled” learning scenarios common in utilities, where the non-fraud class inevitably contains undetected fraud cases [7].

2.3. Mathematical Theoretical Basis

This section presents the mathematical foundations underlying the main components of the proposed modeling process, including the classification algorithm, the class balancing technique, and the evaluation metrics.

2.3.1. XGBoost (Extreme Gradient Boosting)

XGBoost is an ensemble learning algorithm that constructs decision trees sequentially, where each new tree is designed to correct the errors made by the previous ones. Its strength lies in optimizing a well-defined objective function that combines a loss term—representing the model’s prediction error—with a regularization term that penalizes model complexity and prevents overfitting.

The objective function minimized by XGBoost at iteration t is given by:

$$Ob{j}^{(t)}=\sum _{i=1}^{N}l(y_i,{\widehat{y}}_i^{(t-1)}+f_t\left(x_i\right))+\Omega \left(f_t\right)$$

(1)

where:

• $l(y_i,{\widehat{y}}_i)$ is the loss function (in this case, binary:logistic), which measures the discrepancy between the true value $y_i$ and the predicted value ${\widehat{y}}_i$.
• ${\widehat{y}}_i^{(t-1)}$ represents the prediction for the i-th instance at iteration $t-1$.
• $f_t\left(x_i\right)$ denotes the new decision tree added at iteration t.
• $\Omega \left(f_t\right)$ is the regularization term that penalizes the model’s complexity.
• N represents the total number of samples in the dataset. Note that in the summation context of the approximation below, the index n is often used interchangeably to denote the number of instances.

To efficiently optimize this objective, XGBoost applies a second-order Taylor expansion, leading to a simplified objective function for iteration t:

$$Ob{j}^{\left(t\right)}\approx \sum _{i=1}^N[g_i{f}_t\left(x_i\right)+\frac{1}{2}{h}_i{f}_t^2\left(x_i\right)]+\Omega \left(f_t\right)$$

(2)

where $g_i$ and $h_i$ denote, respectively, the first and second derivatives of the loss function (gradient and Hessian).

The regularization term $\Omega$ is crucial for controlling model complexity and is defined as:

$$\Omega \left(f_t\right)=\mathit{\gamma }T+{\displaystyle \frac{1}{2}}\mathit{\lambda }\sum _{j=1}^T{w}_j^2+\mathit{\alpha }\sum _{j=1}^T\left|w_j\right|$$

(3)

where:

• T is the number of leaves in the tree.
• $w_j$ represents the weight (or score) of leaf j.
• $\mathit{\gamma }$, $\mathit{\lambda }$ (L2), and $\mathit{\alpha }$ (L1) are regularization parameters that penalize trees with excessive depth or large leaf weights, thereby controlling overfitting and improving model generalization.

At each potential split, the algorithm evaluates the Gain a metric that quantifies the improvement in the objective function. The split that maximizes this gain is selected, ensuring that each successive tree contributes optimally to reducing the overall prediction error.

2.3.2. Unsupervised Anomaly Detection: Isolation Forest

To complement the supervised learning, we employ the Isolation Forest algorithm as an unsupervised anomaly detector. The core premise of Isolation Forest is that anomalies are few and different, making them easier to isolate than normal points. The algorithm builds an ensemble of random trees (iTrees). For a dataset of N samples, an iTree is constructed by recursively selecting a random feature and a random split value between the maximum and minimum values of the selected feature.

The anomaly score $s(x,N)$ for an instance x is defined as:

$$s(x,N)=2^{-{\displaystyle \frac{E\left(h\right(x\left)\right)}{c\left(N\right)}}}$$

(4)

where $h\left(x\right)$ is the path length (number of edges from the root to the external node) for instance x, and $E\left(h\right(x\left)\right)$ is the average path length over the forest. The term $c\left(N\right)$ is the average path length of an unsuccessful search in a Binary Search Tree (BST), which serves as a normalization factor:

$$c\left(N\right)=2H(N-1)-{\displaystyle \frac{2(N-1)}{N}}$$

(5)

where $H\left(i\right)$ is the harmonic number, estimated as $ln\left(i\right)+0.57721566$ (Euler’s constant).

If $s(x,N)$ is close to 1, the path length is short, indicating that the instance x is easy to isolate and thus likely an anomaly. If $s(x,N)$ is significantly less than 0.5, the instance is considered normal. This score is generated for each customer and fed as the feature ANOMALY_SCORE_ISO into the XGBoost model.

2.3.3. Class Balancing with SMOTETomek

The SMOTETomek technique is a hybrid resampling strategy that combines oversampling of the minority class with undersampling and noise cleaning of the majority class. This approach improves the representativeness of minority samples while simultaneously refining the decision boundaries between classes.

• SMOTE (Synthetic Minority Over-sampling Technique): Instead of simply duplicating existing instances, SMOTE generates new synthetic samples of the minority class. For a given minority instance $x_i$, one of its k nearest neighbors $x_j$ is randomly selected, and a new synthetic point $x_{\mathrm{new}}$ is created along the line segment connecting $x_i$ and $x_j$:

  $$x_{\mathrm{new}}=x_i+\mathit{\delta }·(x_j-x_i)$$

  (6)

  where $\mathit{\delta }$ is a random number uniformly distributed in the interval $[0,1]$. This process increases the diversity and coverage of the minority class without replicating existing information, leading to a smoother feature space.
• Tomek Links: After applying SMOTE, Tomek Links are used to remove noise and ambiguous samples. A Tomek Link is a pair of instances $(a,b)$ from opposite classes that are each other’s nearest neighbors. The existence of such a pair typically indicates either noise or an overlapping region near the decision boundary. The instance belonging to the majority class is removed, resulting in a cleaner separation between classes and a more well-defined decision surface.

2.3.4. Evaluation Metrics

To assess model performance, standard metrics derived from the confusion matrix are employed. The confusion matrix categorizes predictions into True Positives (TPs), True Negatives (TNs), False Positives (FPs), and False Negatives (FNs).

• Precision: Measures the proportion of positive predictions that were correct. This metric is particularly important when the cost of a False Positive is high.

  $$Precision={\displaystyle \frac{TP}{TP+FP}}$$

  (7)
• Recall (Sensitivity): Measures the proportion of actual positives correctly identified by the model. Recall is the most critical metric when the cost of a False Negative is high, as in fraud detection.

  $$Recall={\displaystyle \frac{TP}{TP+FN}}$$

  (8)
• F1-Score: Represents the harmonic mean of Precision and Recall, providing a balanced evaluation of the model’s performance across both metrics.

  $$F1-Score=2·{\displaystyle \frac{Precision·Recall}{Precision+Recall}}$$

  (9)
• AUC-ROC (Area Under the Receiver Operating Characteristic Curve): Measures the model’s ability to discriminate between the two classes. The ROC curve plots the True Positive Rate (Recall) against the False Positive Rate ($FPR=\frac{FP}{FP+TN}$) across multiple decision thresholds. An AUC value of 1.0 indicates a perfect classifier, while a value of 0.5 corresponds to random performance.

2.4. Challenges and Research Gaps

Despite notable advances, several technical and operational issues remain open. First, severe class imbalance persists: fraudulent cases typically represent less than 1–2% of the total data, which biases standard learning algorithms toward the majority class [3]. Data-resampling strategies such as SMOTE, Tomek Links, and cost-sensitive weighting have been explored but may introduce synthetic noise or distort class boundaries [6].

Second, non-stationarity and behavioral adaptation over time reduce the long-term reliability of models trained on historical data. Continuous learning and adaptive retraining are necessary to maintain detection accuracy under changing consumption patterns and socio-economic conditions [5].

Third, most studies focus exclusively on algorithmic performance, overlooking the operational aspect of inspection prioritization. Real-world deployment requires interpretable outputs that justify alerts and can be audited by field engineers [4]. Explainable-AI techniques, such as SHAP-based feature importance and counterfactual explanations, are promising but still underused in NTL research [3].

Finally, there remains a lack of standardized datasets and benchmark protocols, which limits reproducibility and cross-utility comparison. These gaps highlight the need for an integrated framework that balances accuracy, interpretability, and operational feasibility—a direction pursued in this work.

3. Methodology

This section describes the methodological framework adopted for detecting electricity fraud in meter data. In the context of electricity distribution, fraud refers to any intentional act or manipulation—physical, electrical, or informational—designed to obtain electrical energy without proper billing or by falsifying consumption data. This includes meter tampering, illegal connections, data manipulation, or collusion during inspection processes. The proposed pipeline integrates data preprocessing, feature engineering, class imbalance treatment, and hybrid learning, combining an unsupervised anomaly detector with a supervised gradient-boosted classifier. The overall workflow is summarized in Figure 1, followed by detailed explanations of each component.

3.1. Overview of the Proposed Framework

The development of the proposed solution for electricity fraud detection was structured within a systematic methodological workflow, as illustrated in Figure 1. This process encompasses all stages—from the acquisition and preparation of raw data to the final evaluation of the machine learning model—ensuring both the robustness and practical applicability of the approach.

The methodological workflow illustrated in Figure 1 summarizes the complete process followed for the development of the proposed fraud detection model, from raw data acquisition to model evaluation. Each stage is described as follows:

• Raw Data: The foundation of this project consists of annual datasets provided by a real power distribution utility in Peru (2019–2022), containing detailed electricity consumption records obtained from the official website of Osinergmin [15]. The available columns include: customer number, geographic location code (Ubigeo), tariff, category, off-peak active consumption, peak-hour active consumption, distribution substation, feeder, secondary substation, geographic coordinates, month, and year.
  An in-depth analysis revealed that the core attributes for modeling are the active energy consumption during peak hours and off-peak periods, as they directly capture customer consumption behavior. The customer number column uniquely identifies each consumer, while Ubigeo is used during the data-filtering stage to segment the dataset by region.
  Network topology attributes (distribution substation, feeder, and secondary substation) and geographic coordinates were excluded from the final model, reflecting a deliberate focus on consumption behavior rather than spatial or infrastructural characteristics.
• Data Consolidation: This stage focuses on transforming multiple annual files into a single, structured, and labeled dataset suitable for supervised learning. It comprises three main tasks: (a) Filtered by Geographic Location Code (Ubigeo) to retain only the consumers relevant to the study region; (b) concatenating the four annual datasets (2019–2022) into a unified database, while adding a new column (YEAR) to preserve temporal reference; and (c) correcting and standardizing columns whose data types or names were inconsistent across years (e.g., a field stored as a string in 2019 and as a float in 2020). After consolidation, the filtered list of customers is cross-referenced with an external registry of confirmed fraud cases. This comprehensive preprocessing step ensures data integrity and provides a solid foundation for robust and generalizable model training.
• Target Variable Definition and Data Splitting: This stage combines the creation of the target variable with the design of new, informative features derived from the raw consumption data. (a) Real database of confirmed fraud cases: The process begins by cross-referencing the main dataset with an external registry of confirmed fraudulent customers. This step ensures that the supervised learning task is grounded in verified cases rather than synthetic or inferred labels. It is acknowledged that the “Non-Fraud” class (0) likely contains undetected fraud cases, a scenario known as Positive-Unlabeled (PU) learning. However, we rely on the utility’s verified ground truth for supervised training, assuming that the “Fraud” class (1) represents high-confidence positive labels. (b) Creation of the “fraud” label by cross-referencing customer lists: Each customer is assigned a binary label in the target variable (FRAUD), where “1” corresponds to a confirmed fraudulent consumer and “0” to a regular one. The resulting dataset is then stratified and divided into training and testing subsets while maintaining the class distribution, avoiding bias during model evaluation. In parallel, a feature engineering process is applied to enrich the dataset with behavioral indicators derived from consumption history. Moving averages over 3-, 6-, and 12-month windows, standard deviations, and cumulative consumption metrics are computed to capture temporal patterns and anomalies. These derived features transform raw measurements into higher-level representations of consumer behavior, enabling the learning algorithm to detect irregularities more effectively.
• Predictive Model Training: After the feature engineering process, the dataset is divided into two subsets: training and testing. During this stage, the machine learning algorithm learns to identify complex relationships between the engineered features (consumption patterns) and the target variable (FRAUD), optimizing its internal parameters to minimize prediction errors.

  (a)

  Application of the SMOTETomek technique: To mitigate the severe class imbalance—where fraudulent cases represent only a small fraction of all records—the hybrid SMOTETomek method is applied to the training data. This approach combines oversampling of the minority class (fraud) with undersampling of ambiguous boundary samples, producing a more representative and cleaner training set.

  (b)

  Training of the XGBoost classifier with balanced data: The rebalanced dataset is then used to train an XGBoost classifier, chosen for its high predictive performance, robustness, and ability to efficiently handle large tabular datasets. Through iterative boosting, the model learns non-linear decision boundaries that capture subtle behavioral differences between normal and fraudulent consumers, resulting in a strong and generalizable predictive model.

• Performance Evaluation and Analysis: Once the model has been trained, its real-world effectiveness is assessed using a separate testing set that contains data the model has never seen before. This stage is crucial to evaluate the model’s generalization capability—that is, its ability to perform reliably on new and unseen samples. The evaluation process is structured into three complementary analyses:

  (a)

  Testing on unseen data: The trained model generates predictions for each customer in the testing dataset, which are then compared with the true fraud labels. This direct comparison quantifies how well the model can distinguish between fraudulent and legitimate consumers under realistic operating conditions.

  (b)

  Threshold adjustment (0.6)–precision/recall trade-off: A decision threshold of 0.6 is applied to balance the trade-off between detection sensitivity and false-positive rate. Key evaluation metrics—including accuracy, precision (the proportion of correctly identified fraud cases among all predicted frauds), and recall (the proportion of actual fraud cases successfully detected)—are computed to assess the model’s overall effectiveness and practical viability in real deployment scenarios.

  (c)

  Feature importance analysis: Finally, a feature importance study is conducted to determine which variables contribute most significantly to fraud detection. This interpretability step not only validates the model’s learning process but also provides valuable insights into the behavioral and statistical indicators most associated with non-technical losses in electricity consumption.

3.2. Data Description and Preparation

Data sources and structure: The dataset used in this study corresponds to monthly energy-consumption records collected from customers using Geographic Location Code (Ubigeo). Each observation includes the customer identifier, date, energy consumption in kWh, and tariff category. Additional contextual variables such as month, billing cycle, and seasonal factors were derived to enrich the temporal dimension of the analysis [4].

To highlight the behavioral divergence captured in the dataset, Figure 2 depicts the temporal evolution of average monthly consumption for confirmed fraudulent and non-fraudulent customers from 2019 to 2022. As shown, legitimate consumers maintain a stable and consistent demand pattern throughout the four-year period. In contrast, customers later identified as fraudulent exhibit a pronounced and sustained decline in reported consumption starting around 2020–2021. This persistent drop—absent in the normal consumer group—provides clear visual evidence of intentional under-reporting and exemplifies the type of anomalous behavior targeted by the proposed detection model. In the figure, the red curve highlights the sharp and prolonged consumption reduction associated with fraud cases, whereas the blue curve for non-fraudulent customers remains stable across the entire observation window.

Data cleaning and preprocessing: Missing readings, duplicated entries, and inconsistent timestamps were corrected or removed through rule-based filtering. Consumption values were normalized on a per-customer basis to reduce variability due to customer size and to emphasize relative changes in usage [3]. Time indices were converted into cyclical representations (sine–cosine encoding) to preserve the periodic nature of monthly data.

Target variable definition. The dependent variable (fraud) was defined using inspection outcomes provided by the utility company. Each record is labeled as 1 if a confirmed irregularity or meter tampering was detected, and 0 otherwise. Records without verification were excluded from model training but retained for post-hoc evaluation of alert coverage.

3.3. Feature Engineering

Feature engineering is the stage in which the most relevant characteristics are extracted and transformed from the raw data to capture behavioral patterns indicative of fraud. It is assumed that creating richer and more informative features significantly enhances the model’s ability to discriminate between normal and fraudulent customers. The engineered features include:

• General Consumption Statistics per Customer:

  -

  CLIENT_AVG_CONS_FP: Average off-peak (FP) consumption per customer.

  -

  CLIENT_MEDIAN_CONS_FP: Median FP consumption per customer.

  -

  CLIENT_STD_CONS_FP: Standard deviation of FP consumption, indicating variability.

  -

  CLIENT_MIN_CONS_FP and CLIENT_MAX_CONS_FP: Minimum and maximum FP consumption per customer.

  -

  CLIENT_SUM_CONS_FP: Total FP consumption per customer.

  -

  CLIENT_COUNT_MONTHS: Number of months with available consumption records.

  -

  CLIENT_CV_CONS_FP: Coefficient of variation of FP consumption, a normalized measure of dispersion.

• Zero-Consumption Periods: CLIENT_ZERO_CONS_FP_MONTHS and CLIENT_PERCENT_Z
  ERO_CONS_FP_MONTHS were created to quantify prolonged zero-consumption periods, which may indicate abnormal or fraudulent behavior.
• Customer Activity Duration: CLIENT_TIME_ACTIVE_TOTAL_MONTHS computes the total number of months the customer remained active in the records, based on the minimum and maximum consumption dates.
• Consumption Variations (Monthly and Yearly):

  -

  CLIENT_MONTHLY_CONS_FP_CHANGE_PCT: Monthly percentage variation in FP consumption relative to the previous month.

  -

  CLIENT_YOY_MONTHLY_CONS_FP_CHANGE_PCT: Year-over-year percentage variation in FP consumption for the same month. This feature is essential for isolating irregular behavior by compensating for natural annual consumption cycles. By comparing, for example, January 2021 with January 2020, the feature effectively removes expected seasonal effects—such as increased air-conditioning usage during warmer months—thereby enabling the model to detect deviations that genuinely depart from the customer’s normal seasonal pattern.

• Statistics of Monthly Consumption Variation per Customer: Features such as CLIENT_AVG_ABS_MONTHLY_CHANGE_PCT, CLIENT_STD_MONTHLY_CHANGE_PCT, CLIENT_MAX_MONTHLY_INCREASE_PCT, and CLIENT_MIN_MONTHLY_DECREASE_PCT quantify the customer’s consumption stability and fluctuation intensity.
• Category-Year Consumption and Variation Statistics: The average and median consumption, as well as the average absolute monthly variation, were calculated for each CATEGORIA and ANO, allowing comparisons between a customer’s behavior and that of peers within the same category and year.
• Category-Year Comparison Features:

  -

  CLIENT_CONS_FP_RATIO_TO_CAT_YEAR_AVG: Ratio of customer consumption to the category/year average.

  -

  CLIENT_CONS_FP_DIFF_FROM_CAT_YEAR_AVG: Difference between customer consumption and the category/year average.

  -

  CLIENT_CONS_FP_RATIO_TO_CAT_YEAR_MEDIAN: Ratio of customer consumption to the category/year median.

  -

  CLIENT_MONTHLY_CHANGE_ABS_PCT_DIFF_FROM_CAT: Difference between the customer’s absolute monthly variation and the category/year average.

• Rolling-Window Features:

  -

  CLIENT_ROLLING_3M_AVG_CONS_FP: 3-month rolling average of FP consumption.

  -

  CLIENT_ROLLING_6M_AVG_CONS_FP: 6-month rolling average of FP consumption.

  -

  CLIENT_ROLLING_12M_SUM_CONS_FP: 12-month rolling sum of FP consumption, useful for identifying annual trends.

• FP/HP Consumption Ratio: RAZAO_FP_HP represents the ratio between off-peak (FP) and peak-hour (HP) consumption. Abnormally high or low values may indicate meter tampering or measurement anomalies.
• Consecutive Low-Consumption Periods: MAX_CONSEC_LOW_10_CONS_FP and MAX_CONSEC_LOW_50_CONS_FP represent the maximum number of consecutive months in which the customer’s consumption was below 10% and 50% of their historical average, respectively—strong indicators of inconsistent or suspicious consumption.
• Minimum Non-Zero Consumption and Anomaly Flags:

  -

  CLIENT_MIN_NON_ZERO_CONS_FP: Minimum non-zero FP consumption recorded for the customer.

  -

  FLAG_CNS_FP_BELOW_HISTORIC_MIN_NON_ZERO: Flag indicating whether the current consumption is below the historical non-zero minimum.

  -

  FLAG_CNS_FP_NEAR_ZERO_AND_UNUSUAL: Flag indicating whether the consumption is near zero and abnormally low compared to the customer’s historical average.

• Isolation Forest Anomaly Score: An Isolation Forest model was applied to generate an anomaly score (ANOMALY_SCORE_ISO). This unsupervised algorithm is effective for outlier detection in datasets with few anomalies, such as fraud detection. The features used as input were CNS_ACT_FP, CLIENT_MONTHLY_CONS_FP_CHANGE_PCT, and CLIENT_CONS_FP_RATIO_TO_CAT_YEAR_AVG. The parameter contamination=’auto’ allows the algorithm to estimate the proportion of outliers, while n_estimators=100 ensures robust performance. Crucially, this approach acts as a stacking mechanism: the Isolation Forest model acts as an unsupervised feature extractor, outputting a score based on the average path length required to isolate an observation. This score is then fed as a high-level input feature into the supervised XGBoost model, allowing the final classifier to benefit from global anomaly patterns captured by the Isolation Forest.
• One-Hot Encoding for TARIFA and Conversion of CATEGORIA: The categorical variable TARIFA was transformed using one-hot encoding, producing binary columns such as TARIFA_COMERCIAL (Commercial Tariff) and TARIFA_RESIDENCIAL (Residential Tariff), enabling the model to interpret nominal information effectively. These categories capture the main customer segments, allowing the model to differentiate between residential usage patterns and commercial load profiles, which typically exhibit different fraud signatures.
• Final Cleaning of NaN and Infinite Values: Prior to modeling, all remaining numeric columns containing NaN or infinite values (e.g., from divisions by zero) were replaced with zeros. Columns such as ANO, MES, mes_ano, and one-hot encoded tariff columns were excluded from this step, as their values were already consistent.

3.4. Target Variable Definition and Feature Selection

The target variable, fraud, was created based on the presence of the customer’s NRO_CLIENT in the clientes_filtrados.csv file. Customers found in this file were labeled with 1 (fraud) and the remaining customers with 0 (non-fraud).

For feature selection (X) used in the model, identifier columns (NRO_CLIENT), temporal variables (YEAR, MONTH, MONTH_YEAR), the target variable itself (fraudador), and intermediate auxiliary variables (CNS_ACT_FP_PREV_MONTH, CNS_ACT_FP_PREV_YEAR_SAME_MONTH, etc.) were removed. Additionally, non-informative columns or those containing excessive missing values (SET, SEC_TYPICAL, COORD.GEO.X, COORD.GEO.Y, DISTRICT) were discarded, as defined in the list user_requested_drops.

3.5. Train/Test Split and Class Imbalance Treatment

The dataset was divided into training (75%) and testing (25%) subsets using the train_test_splitfunction from Scikit-learn. The stratify=y parameter was employed to preserve the original class distribution (fraudulent vs. non-fraudulent) across both subsets. This step is particularly important in fraud detection problems, where the minority class (fraud) is typically rare and its underrepresentation could lead to biased models.

Given the highly imbalanced nature of the problem, a class balancing strategy was applied to the training set:

• SMOTETomek: The SMOTETomek method from the imblearn.combine library was adopted as the primary resampling strategy. This hybrid approach combines oversampling of the minority class through SMOTE (Synthetic Minority Over-sampling Technique) with noise reduction using Tomek Links. SMOTE synthetically generates new samples for the minority class by interpolating between existing ones, whereas Tomek Links remove pairs of samples (one from each class) that are too close to each other, thereby refining the decision boundary.

  -

  The oversampling ratio was defined as smote_target_sampling_strategy = 0.1, meaning that the minority class was expanded to reach 10% of the majority class size.

  -

  The k_neighbors parameter in SMOTE was dynamically set to minority_count_t

  rain - 1 when the minority class contained very few samples, preventing errors during neighbor generation.

  -

  The framework implements a robust fallback mechanism to ensure pipeline stability:

  • Check Minority Class Count: Before applying resampling, the system checks the number of available minority class samples.
  • Validation: If the count is less than 6 samples (the minimum required for default k-nearest neighbors in SMOTE), the SMOTETomek step is skipped.
  • Fallback Activation: In such cases, the pipeline defaults to calculating and applying the scale_pos_weight parameter in XGBoost, which balances the loss function weights without synthesizing new data.

• scale_pos_weight (Fallback): When SMOTETomek failed or was disabled, the scale_
  pos_weight parameter in XGBoost was computed and applied. This parameter penalizes misclassification of minority-class samples during training, effectively compensating for class imbalance by assigning higher importance to positive (fraudulent) instances. Its value was calculated as majority_class_count/minority_class_count.

The choice of SMOTETomek as the primary balancing method is justified by its dual advantage: it not only increases the representativeness of the minority class but also cleans the decision boundaries, often leading to more robust and better-generalizing models.

3.6. Model Architecture

The model selected for the fraud classification task was the XGBoost (Extreme Gradient Boosting) algorithm. XGBoost is a tree-based ensemble learning method renowned for its efficiency, flexibility, and high predictive performance across a wide range of classification and regression problems. It implements gradient boosting in an optimized and highly scalable manner, making it particularly suitable for complex problems such as fraud detection.

The base hyperparameters used for the XGBClassifier were carefully tuned and are summarized as follows:

• learning_rate = 0.05: Controls the step size at each boosting iteration, helping to prevent overfitting. Smaller values typically require more estimators but can lead to a more stable and generalizable model.
• max_depth = 5: Sets the maximum depth of each decision tree, controlling model complexity and preventing overfitting.
• min_child_weight = 3: Specifies the minimum sum of instance weights (Hessians) required in a child node. Higher values make the algorithm more conservative, reducing the likelihood of fitting noise in the training data.
• subsample = 0.7: Defines the fraction of training samples used to grow each tree, which helps reduce variance and overfitting.
• colsample_bytree = 0.7: Specifies the fraction of features (columns) to be randomly sampled for each tree, further reducing model variance.
• gamma = 0.2: Minimum loss reduction required to make an additional partition in a leaf node. Larger values make the algorithm more conservative by discouraging unnecessary splits.
• lambda = 1 (L2 regularization) and alpha = 0.1 (L1 regularization): Regularization terms used to control overfitting and improve generalization.
• random_state = 42: Ensures reproducibility of results.
• objective = ‘binary:logistic’: Specifies the binary classification objective for predicting the probability of fraud.
• n_estimators = 140: Number of boosting trees to be built in the ensemble.

The model was trained using the balanced dataset (X_res, y_res). If the scale_pos_we ight strategy was applied instead of oversampling, this parameter was incorporated into the params_base configuration of XGBoost to properly address class imbalance during training.

After training, the model was serialized using joblib.dump, allowing for future reuse without retraining. The saved file name includes a reference to the class balancing strategy employed, ensuring full traceability of the experiment configuration.

3.7. Evaluation Metrics and Operational Criteria

Model evaluation is a crucial step to assess predictive performance and determine how effectively the model identifies fraudulent behavior. All metrics were computed using the testing set (X_test, y_test), which was completely unseen during training, ensuring an unbiased assessment.

• Default Threshold (0.5): Initially, the model was evaluated using the standard decision threshold of 0.5. The following metrics were calculated:

  -

  classification_report: Provides a comprehensive summary of Precision, Recall, F1-Score, and Support for both classes (Non-Fraud and Fraud).

  -

  Recall (Fraud): The proportion of actual fraud cases correctly identified by the model. In fraud detection, recall is often prioritized since the main goal is to minimize the number of undetected frauds.

  -

  Precision (Fraud): The proportion of predicted fraud cases that are truly fraudulent. A high precision value indicates a lower rate of false positives.

  -

  F1-Score (Fraud): The harmonic mean between Precision and Recall, providing a balanced measure between the two.

  -

  AUC-ROC Score: The Area Under the Receiver Operating Characteristic curve, a robust metric for evaluating imbalanced classification problems. It quantifies the model’s ability to distinguish between the two classes: a value of 0.5 indicates random performance, while 1.0 corresponds to a perfect classifier.

• Adjusted Decision Threshold (0.6): In fraud detection scenarios, it may be desirable to prioritize either Precision or Recall depending on the operational costs associated with false positives and false negatives. To explore this trade-off, the model was re-evaluated using an adjusted decision threshold of 0.6. Under this configuration, a prediction is classified as fraud only if the estimated probability is greater than or equal to 0.6. Increasing the threshold generally enhances Precision (reducing false positives) while slightly decreasing Recall (increasing false negatives).
• Customer-Level Detection Results (Testing Set): For a more business-oriented and granular analysis, performance metrics were also computed at the customer level, using the adjusted 0.6 threshold:

  -

  Total number of unique customers in the testing set.

  -

  Number of customers predicted as fraudulent.

  -

  Number of customers actually labeled as fraudulent.

  -

  Number of correctly identified fraudulent customers.

  -

  Customer-Level Precision: The proportion of customers predicted as fraudulent who are indeed fraudsters.

  -

  Customer-Level Recall: The proportion of actual fraudulent customers successfully detected by the model.

4. Experiments and Results

This section presents the experimental design, evaluation results, and comparative analyses of the proposed fraud-detection framework. All experiments were performed on real consumption data using the hybrid Isolation Forest + XGBoost approach described in Section 3. Statistical and operational results are discussed to highlight both model performance and practical applicability.

4.1. Experimental Setup

Training/test split:

The dataset was divided into training (75%) and testing (25%) subsets using a stratified partition to preserve the original fraud/non-fraud proportion [3]. A random seed was fixed for reproducibility. Hyperparameters were optimized via 5-fold cross-validation on the training set, ensuring that the model configuration was robust and not biased towards a single data split. The final model was then evaluated on the hold-out testing set to simulate real-world deployment.

Hardware and software environment: Experiments were executed on a workstation equipped with an AMD Ryzen 7 5800H CPU (3.2 GHz), 32 GB RAM, and running Ubuntu 22.04 LTS. Python 3.11 was used with the following key libraries: scikit-learn, xgboost, and imbalanced-learn. The codebase was implemented in Jupyter Notebook version 7.0.6 to facilitate traceability and visualization of intermediate results [6].

4.2. Baseline Performance and Threshold Optimization

Table 1. Baseline performance of the proposed XGBoost model across decision thresholds from 0.50 to 0.70 (test set).

Threshold	Precision	Recall	F1-Score	AUC-ROC
0.50	0.451	0.938	0.609	0.999
0.51–0.53	0.467–0.503	0.936–0.906	0.623–0.647	0.999
0.54–0.56	0.541–0.615	0.894–0.878	0.674–0.723	0.999
0.57–0.59	0.653–0.693	0.874–0.846	0.747–0.762	0.999
0.60	0.710	0.844	0.771	0.999
0.65	0.815	0.710	0.759	0.999
0.70	0.920	0.550	0.688	0.999

summarizes the baseline performance of the proposed XGBoost model across decision thresholds ranging from 0.50 to 0.70 on the test set. The results show that the model maintains a consistently high discriminative capability, with an almost constant AUC-ROC value of approximately 0.999 across all thresholds, indicating stable separation between fraudulent and non-fraudulent classes.

At the default threshold of 0.50, the model prioritizes sensitivity, achieving a high Recall of 0.938 but a moderate Precision of 0.451, which implies a higher number of false positives. As the threshold increases, Precision improves progressively while Recall slightly decreases, reflecting a more selective identification of truly fraudulent cases.

The optimal operating point is reached at a threshold of 0.60, where Precision = 0.710, Recall = 0.844, and F1-Score = 0.771. This configuration represents the best trade-off between detection coverage and false-alarm control, providing a practical balance for operational deployment. Accordingly, this threshold was adopted for the customer-level analysis presented in Section 4.3.

In summary, Table 1 confirms the stability and effectiveness of the proposed model, demonstrating that proper decision-threshold tuning is essential to optimize operational performance in real-world electricity fraud detection scenarios.

4.3. Customer-Level Analysis

At the customer aggregation level, predictions were consolidated by classifying a consumer as fraudulent if at least one of their monthly records exceeded the 0.60 probability threshold. Under this operational criterion, the testing set comprised 15,006 unique customers, of which 56 were predicted as fraudulent and 42 were actually labeled as such. The model correctly identified 38 fraudulent customers, achieving a customer-level Precision of 0.679 and a Recall of 0.905. These results correspond to a detection rate of approximately 91% with a false-alert rate below 10%, reflecting strong model reliability at the aggregated decision level.

From an operational standpoint, these results are highly encouraging. The proposed hybrid framework provides a reliable foundation for targeted inspection planning, enabling field teams to concentrate on high-risk consumers rather than relying on random selection or manual heuristics. In this practical context, the model is primarily designed to detect electricity theft patterns manifested through anomalous consumption behavior; however, its modular architecture can be readily extended to encompass broader fraud scenarios, including administrative or digital manipulations of metering and billing data.

By combining high coverage with controlled false positives, the model enables utilities to allocate inspection resources more efficiently, maximizing recovery of non-technical losses and reinforcing data-driven decision-making in fraud detection.

4.4. Lift and Cost-Benefit Analysis

To further validate the operational value of the proposed model, a Lift analysis was performed to quantify its efficiency in identifying fraudulent customers relative to a random selection strategy. This evaluation is particularly relevant for utility companies, where inspection resources are limited and must be allocated to the highest-risk consumers to maximize financial recovery. The cumulative gains analysis shows that by inspecting only the top 5% of customers—those assigned the highest fraud-probability scores by the XGBoost classifier—the utility can capture approximately 80% of all fraudulent cases present in the test set. Under a random inspection strategy, the same 5% effort would statistically identify only 5% of the frauds. Thus, the resulting Lift of 16 × (80/5) demonstrates that the proposed model is sixteen times more effective than random selection in concentrating true fraud cases within the most critical deciles. From a cost-benefit perspective, this high concentration of positive cases in the upper percentile range translates directly into operational savings. Because field inspections carry a fixed operational cost, prioritizing visits to customers in the top 5% risk bracket maximizes Return on Investment (ROI) by substantially increasing the proportion of successful detections per inspection. This targeted approach is particularly valuable for utilities operating under constrained inspection budgets, enabling a shift from resource-intensive random auditing toward a strategic and data-driven inspection process that yields significantly higher financial recovery.

4.5. Feature Importance and Interpretability

Model interpretability was assessed through the feature-importance ranking generated by XGBoost and further supported by SHAP analysis. The feature importance chart (Figure 3) highlights the variables that most strongly influenced the model’s predictions. The most relevant contributors included CLIENT_MAX_MONTHLY_INCREASE_PCT, CATEGORY, CLIENT_STD_CONS_FP, and CLIENT_CV_CONS_FP, indicating that extreme monthly consumption variations, tariff category, and overall consumption consistency (as captured by standard deviation and coefficient of variation) are critical indicators of potentially fraudulent behavior. The number of consecutive low-consumption months (MAX_CONSEC_LOW_10_CONS_FP and MAX_CONSEC_LOW_50_CONS_FP) also emerged as strong predictors, suggesting possible meter tampering or under-measurement patterns. Additionally, the inclusion of the ANOMALY_SCORE_ISO (Isolation Forest anomaly score) confirmed the relevance of integrating unsupervised irregularity indicators into the hybrid learning pipeline.

Complementarily, SHAP-based interpretability analysis revealed that sustained low consumption, abrupt month-to-month changes, and deviations from peer-group averages were the dominant patterns driving fraud predictions. These insights bridge data-driven modeling with operational expertise, allowing utilities to understand the behavioral rationale behind alerts and to validate consumption anomalies rather than relying solely on black-box outputs. By linking statistical variability, contextual deviation, and anomaly detection, the proposed framework delivers not only predictive accuracy but also explainable intelligence for decision-making in non-technical loss reduction.

4.6. Comparative Scenarios

To evaluate robustness and generalization, four scenarios were tested:

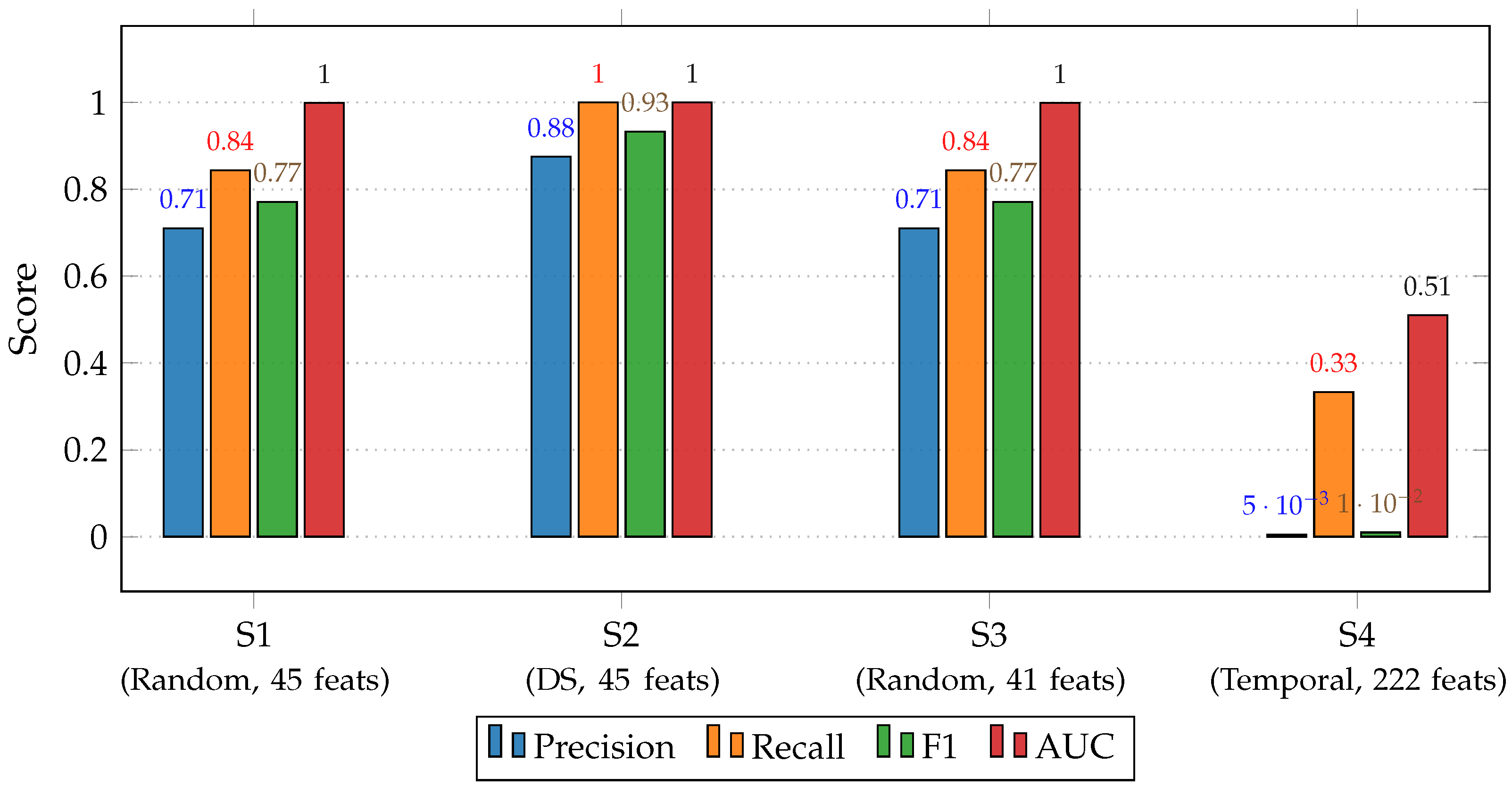
• Scenario 1: Random Split (45 features).
  Baseline configuration using the complete feature set. This scenario serves as the reference for comparison.
• Scenario 2: Filtered by DS. Sub-dataset restricted to a specific Distribution Substation, evaluating spatial sensitivity of the model.
• Scenario 3: Reduced Feature Set (41 features). Removal of correlated and redundant attributes to test compactness versus performance trade-offs.
• Scenario 4: Temporal Validation (TSFRESH–222 features). Extended dataset using automatically extracted time-series features to validate temporal generalization [6].
• Baselines: Random Forest & Logistic Regression. To benchmark the hybrid framework, we compared it against standard Random Forest and Logistic Regression models trained on the same data.

Table 2. Comparative performance of modeling scenarios (test set, threshold = 0.6).

Scenario	Split/Features	Prec.	Rec.	F1	AUC	Cust-Prec.	Cust-Rec.	Cost	Remarks
1	Random/ 45 features	0.710	0.844	0.771	0.999	0.679	0.905	1.0×	Strong baseline balance
2	DS filter/ 45 features	0.875	1.000	0.933	1.000	0.800	1.000	≈1.0×	Specialist model, near-perfect metrics
3	Random/ 41 features	0.710	0.844	0.771	0.999	0.696	0.929	↓ vs S1	Reduced feature set, similar performance
4	Temporal/ 222 (TSFRESH)	0.005	0.333	0.010	0.510	–	–	+60%	High cost, poor temporal generalization
Base 1	Logistic Regression	0.320	0.750	0.449	0.880	–	–	Low	Linear baseline, high FP rate
Base 2	Random Forest	0.650	0.780	0.709	0.950	–	–	Medium	Strong, but outperformed by XGBoost

summarizes comparative performance across scenarios. Although Scenario 4 slightly improved AUC, it increased computational cost by nearly 60%. Scenario 3 achieved the best compromise, reducing model complexity while maintaining comparable predictive power. These findings indicate that a well-designed set of handcrafted features can outperform larger automated feature spaces in operational settings [3,5].

Table 2 summarizes the comparative performance across the four modeling scenarios, highlighting trade-offs between accuracy, generalization, and computational efficiency. Each configuration offers specific insights into how feature design, data partitioning, and model scope influence predictive performance and operational applicability.

• Scenario 1 (Random Split with 45 Features): demonstrated a strong and stable performance across all evaluation metrics, achieving a Recall of 0.844 and an F1-score of 0.771 at a 0.6 threshold. The model successfully balanced sensitivity and precision, confirming that a comprehensive handcrafted feature set—particularly those derived from temporal variability and the Isolation Forest anomaly score—provides robust discrimination between normal and fraudulent customers. This configuration serves as the baseline reference for subsequent analyses.
• Scenario 2 (Random Split with DS Filter): produced near-perfect results, with Precision and Recall both reaching unity at the customer level. However, this exceptional performance likely stems from the increased homogeneity of the filtered subset, which simplifies the classification task. Although less generalizable to heterogeneous populations, these findings underscore the operational advantage of developing localized or substation-specific (DS-based) models for precision targeting within defined network segments.
• Scenario 3 (Random Split with 41 Features): maintained performance nearly identical to Scenario 1 while employing a reduced feature set. The removal of secondary variables, such as auxiliary anomaly indicators, slightly simplified the model without compromising predictive quality. This result highlights the efficiency of carefully engineered features over excessive dimensionality, revealing that compact yet well-designed feature spaces can preserve discriminative strength while improving interpretability and reducing computational overhead.
• Scenario 4 (Temporal Split with 222 TSFRESH Features): introduced a more realistic temporal validation, training on data from 2019–2021 and testing on 2022. Despite including a large automatically extracted feature set, performance dropped considerably (F1-score = 0.010; AUC = 0.510), and computational cost increased by approximately 60%. The poor performance of Scenario 4 stems from the high dimensionality of the automatically extracted features combined with the severe class imbalance. In this context, generic temporal descriptors extracted by TSFRESH are overshadowed by the sparse and highly localized nature of fraud patterns. Domain-informed behavioral features (e.g., abrupt drops, specific tariff changes) provide much stronger discriminatory power than abstract statistical moments, reinforcing why hybrid, domain-guided architectures remain necessary for NTL detection.
• Computational Considerations: Across all experiments, training time and memory consumption were dominated by extensive feature engineering and the SMOTETomek balancing process. While XGBoost maintained high scalability, scenarios with expanded feature spaces—particularly Scenario 4—incurred significantly higher computational demand, reinforcing the importance of model parsimony for real-world deployment.

Figure 4 provides a visual summary of the comparative performance across all evaluated scenarios. The results confirm that Scenarios 1 and 3 yield the most consistent and operationally viable balance between detection capability and precision, with nearly identical F1-scores (0.771) and AUC values close to 1.0. Scenario 2 achieves almost perfect performance in all metrics, reflecting the advantage of modeling over a more homogeneous, substation-specific (DS) subset; however, this result should be interpreted cautiously, as it may not generalize to broader, more diverse datasets. Conversely, Scenario 4—despite incorporating a high-dimensional TSFRESH feature space—exhibited a severe drop in predictive power and the lowest F1-score, accompanied by a 60% increase in computational cost. These findings highlight the importance of balancing model complexity and generalization, especially in the context of temporal drift and highly imbalanced data.

4.7. Discussion and Limitations

The proposed hybrid model demonstrates high accuracy and robustness under different data configurations; however, several limitations remain. First, computational cost grows with the number of features and the resampling ratio of SMOTETomek, which may hinder large-scale deployment. Second, temporal generalization requires periodic retraining to accommodate evolving consumption patterns and socio-economic changes. Finally, interpretability, although improved by feature-importance analysis, still depends on expert validation to translate anomalies into actionable decisions.

Future research should explore incremental learning strategies and dynamic thresholding mechanisms to further enhance adaptability and operational integration of ML-based NTL-detection systems.

5. Conclusions and Future Work

This study successfully developed and validated a hybrid machine learning framework for detecting Non-Technical Losses (NTLs) in power-distribution systems. The proposed pipeline integrates unsupervised anomaly detection through Isolation Forest with supervised classification via XGBoost, enhanced by domain-informed feature engineering and the SMOTETomek resampling strategy. Experimental evaluations on real-world datasets demonstrated high predictive accuracy, consistent performance across multiple scenarios, and effective mitigation of class imbalance. While the model was primarily trained on data associated with electricity theft, the underlying methodology is equally applicable to broader forms of electricity fraud, as both exhibit similar behavioral patterns in consumption data. Moreover, the incorporation of SHAP-based feature-importance analysis enhanced model interpretability and provided actionable insights into irregular consumption behavior, thereby reinforcing the practical value of the framework for improving inspection efficiency and enabling data-driven decision-making within utility operations.

5.1. Practical Implications for Utilities

From an operational perspective, the proposed framework offers a scalable and interpretable solution that can be directly integrated into existing inspection workflows. By prioritizing customers with the highest risk scores, utilities can significantly reduce field-operation costs and increase the efficiency of inspection campaigns. The explainability component enhances trust in the model’s decisions, allowing technical teams to validate alerts with supporting evidence rather than relying on black-box predictions. Moreover, the modular design of the pipeline facilitates adaptation to different regions, data granularities, and metering technologies.

In practical deployment, the selection of the decision threshold (e.g., 0.60 in this study) allows utilities to align alert volumes with available inspection capacity. This flexibility ensures that the model’s output remains operationally actionable, balancing accuracy with cost-effectiveness.

5.2. Limitations and Future Directions

Despite the promising results, this study has limitations. First, the computational cost of the SMOTETomek resampling strategy can be prohibitive for very large datasets, potentially requiring more scalable balancing methods for national-level deployments. Second, the model relies on periodic retraining to handle concept drift; it does not currently support online learning. Future research directions will focus on the following:

• Incremental Learning: Developing pipelines that can update model parameters in real-time as new consumption data arrives.
• Federated Learning: Investigating decentralized training architectures to allow different utility companies to collaborate on fraud detection without sharing sensitive customer data.
• Geospatial Enrichment: Incorporating socio-economic and detailed geospatial attributes to further refine contextual anomaly detection.