Self-Consistent Multi-Energy Flow Coordination Optimization for Hydrogen Energy Railway with Tank Car in Hydrogen Energy Parks

Abstract

The multi-energy flow coordination optimization of the self-sufficient hydrogen energy park is becoming a research focus. However, without explicit consideration of tank car, the optimization remains incomplete, thereby undermining practical applicability. In this paper, a Dynamic Adaptive Grey Wolf Optimization (DA-GWO) algorithm is proposed for self-consistent multi-energy flow coordination optimization, considering hydrogen energy-based tank cars in hydrogen railway energy parks. First, a foundational model of the hydrogen-based railway energy system was constructed that integrates green non-dispatchable units such as wind power and photovoltaics, as well as dispatchable units such as fuel cells, gas boilers, and cogeneration units. Given the diversity and complexity of in-service hydrogen railway tank cars, a probabilistic model of daily charging behaviour was constructed using a Monte Carlo method to simulate real-world operating conditions of tank cars, thereby enhancing the reliability of the hydrogen-powered railway model. Considering the diverse and complex units in the self-consistent hydrogen energy park for hydrogen-powered railways, a DA-GWO algorithm was constructed for the multi-energy flow optimization. Through a self-adaptive parameter adjustment, the algorithm’s global optimization performance is improved. Finally, the model parameters were further adjusted with data from a coastal Chinese city, and the optimization experimental tests were conducted to validate the proposed method. From the results, the proposed method can save at least 6.7% cost compared with the grey wolf optimization method and the PSO (Particle Swarm Optimization) optimization method.

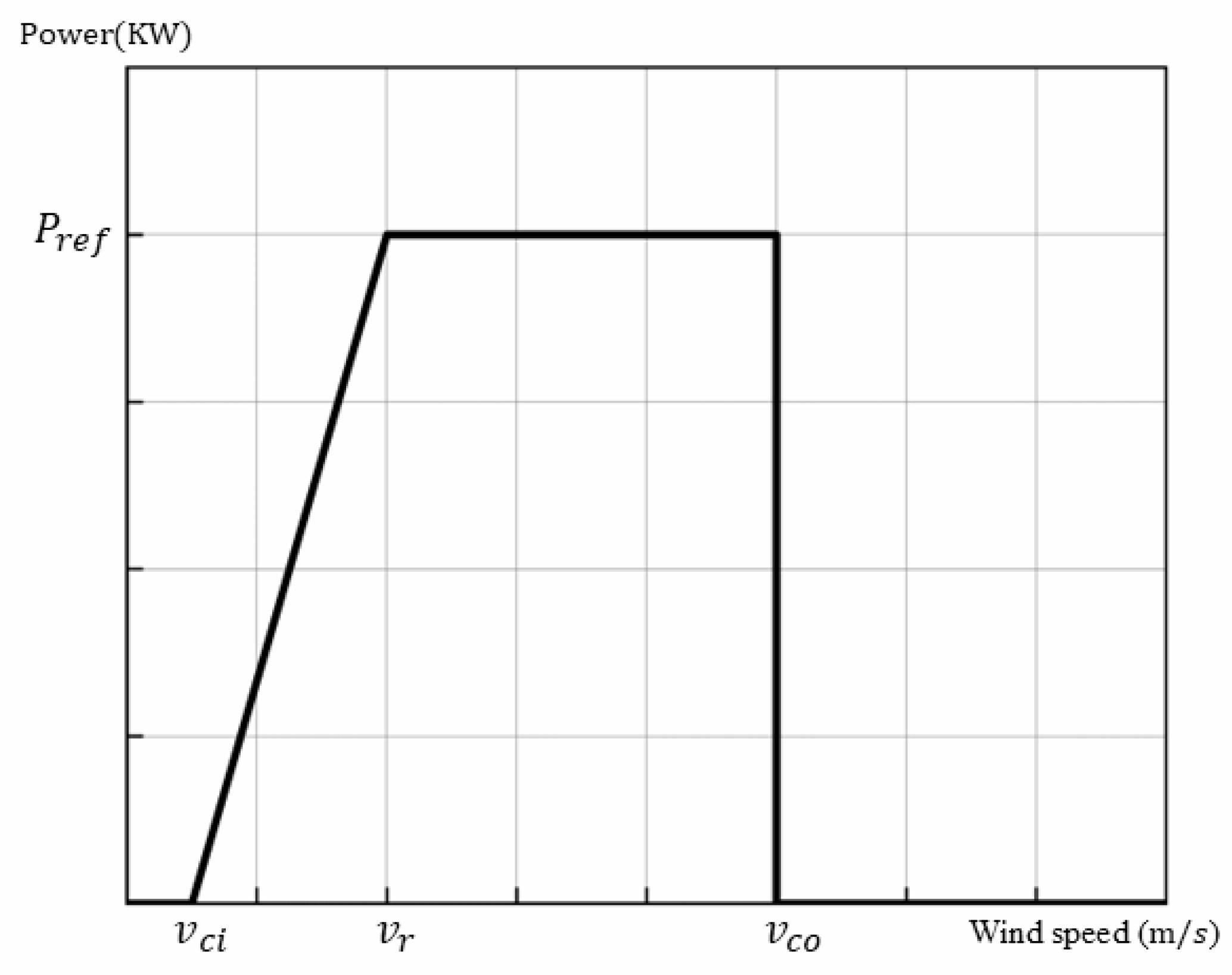
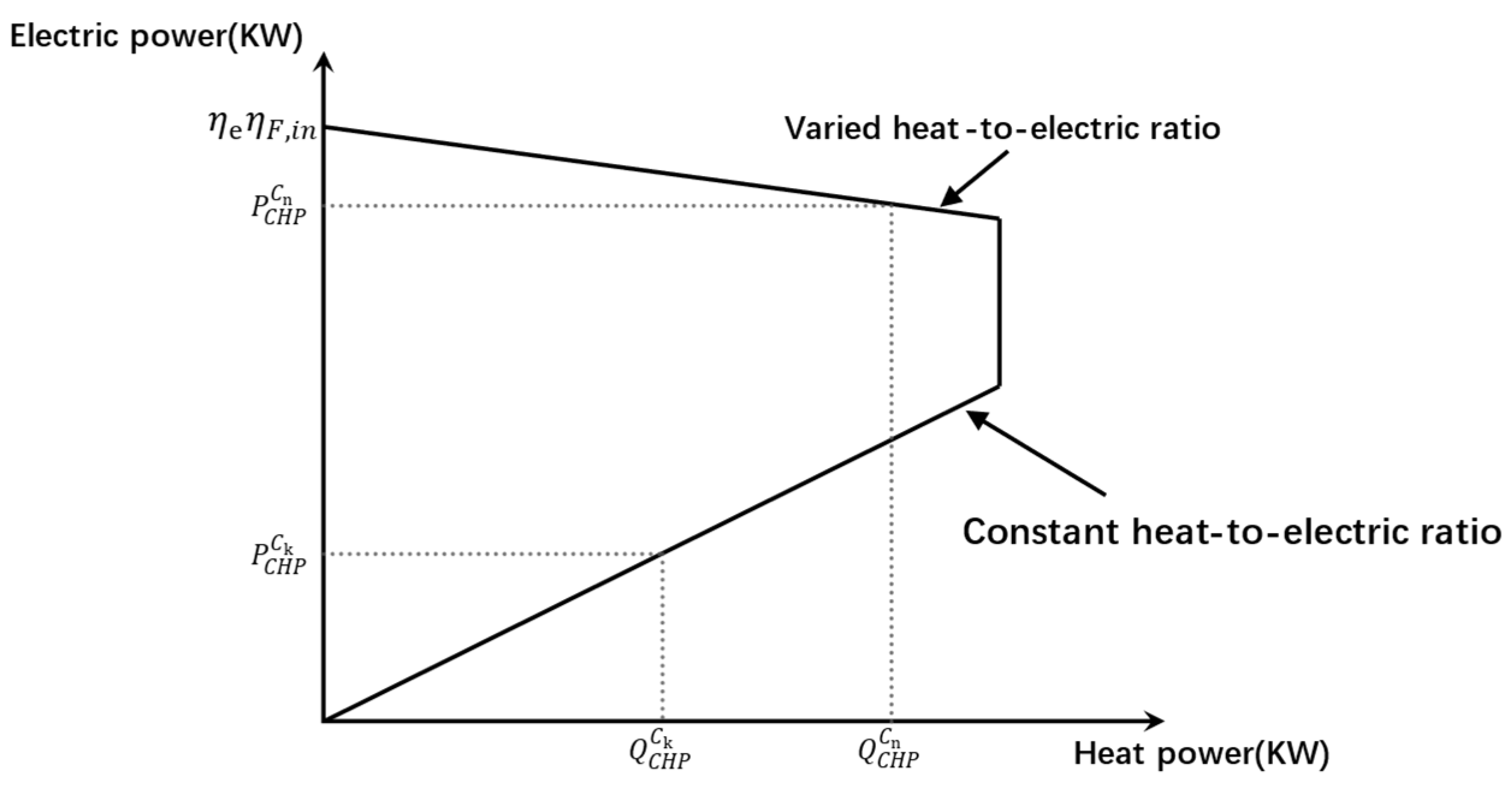
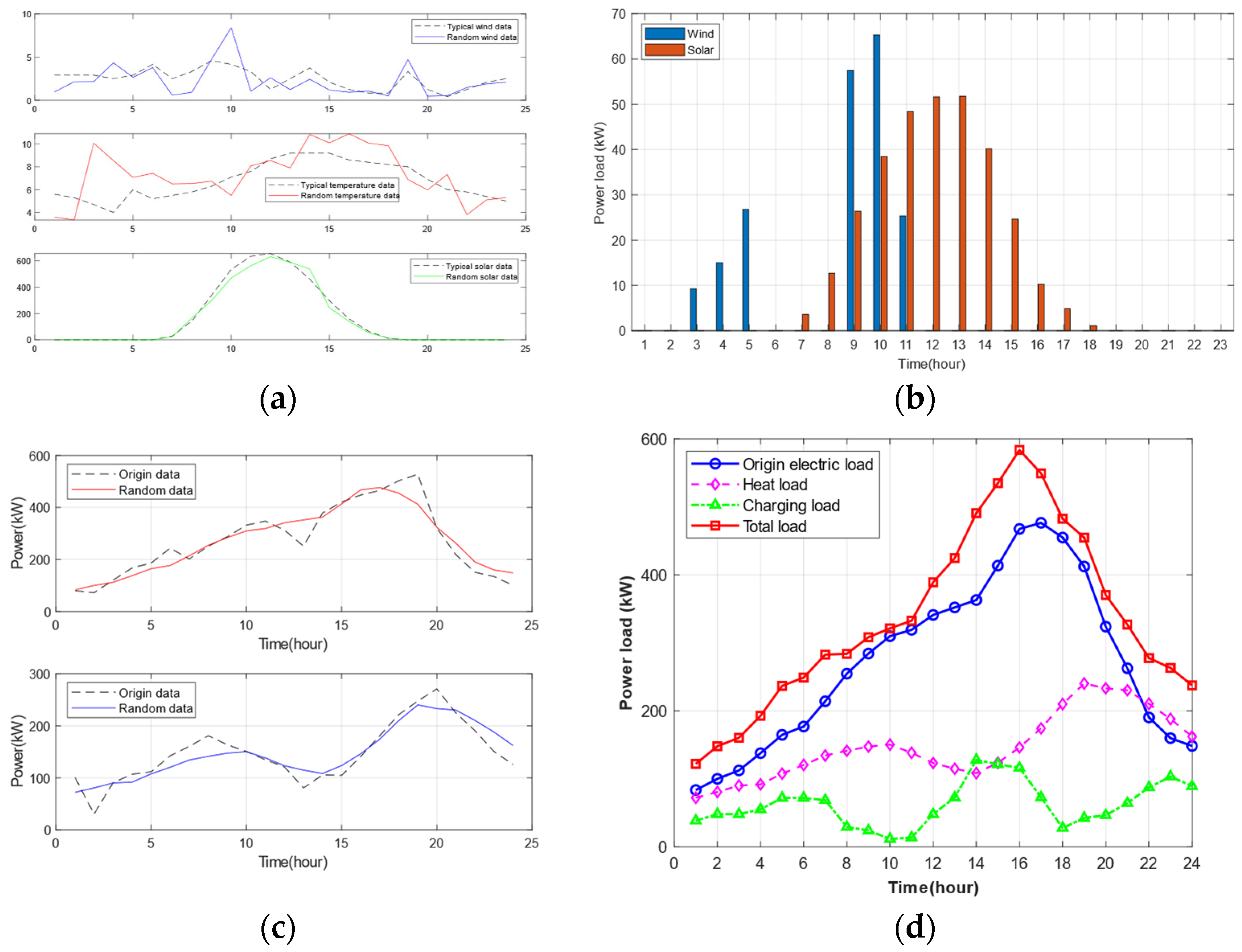
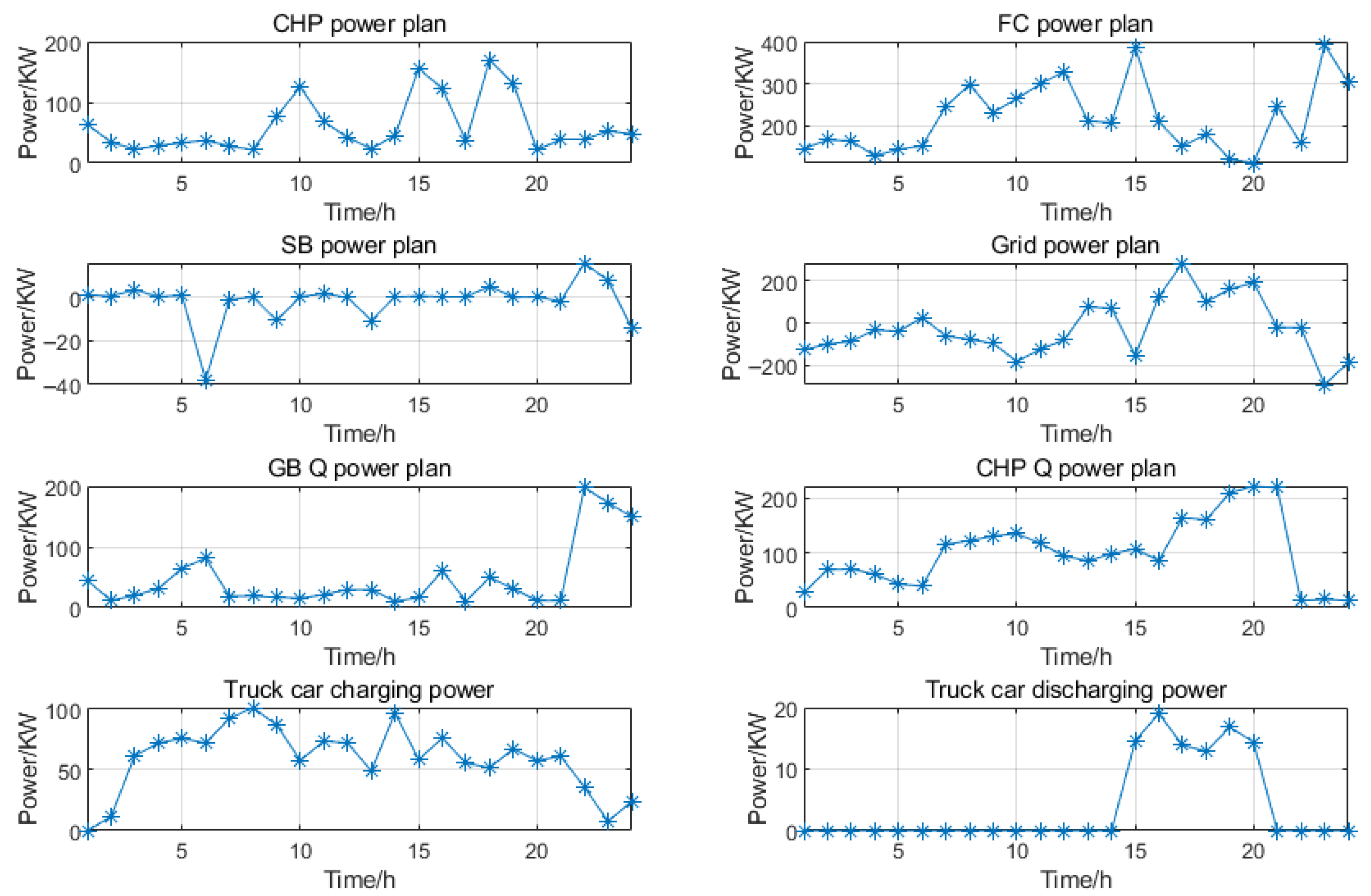
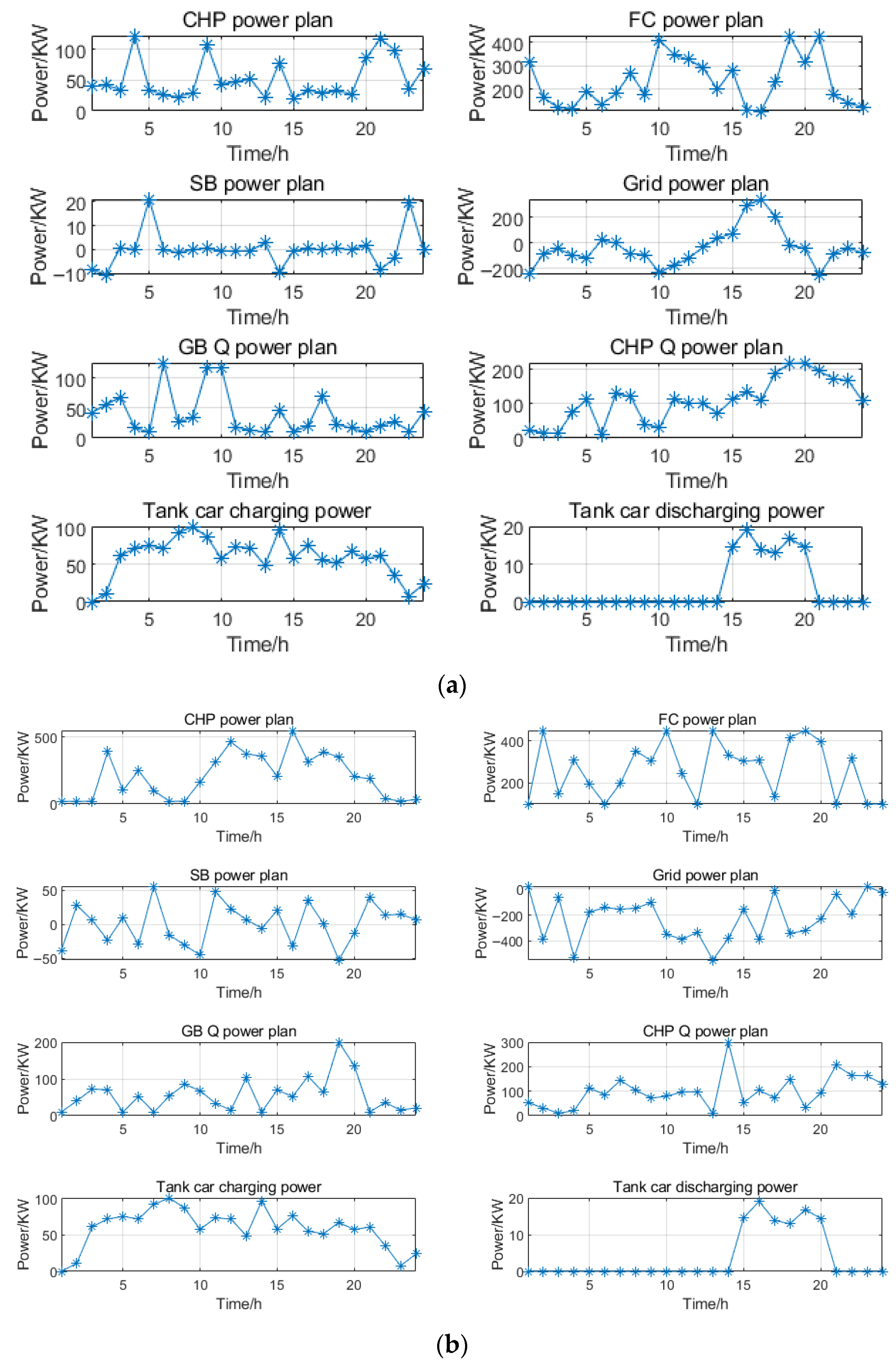
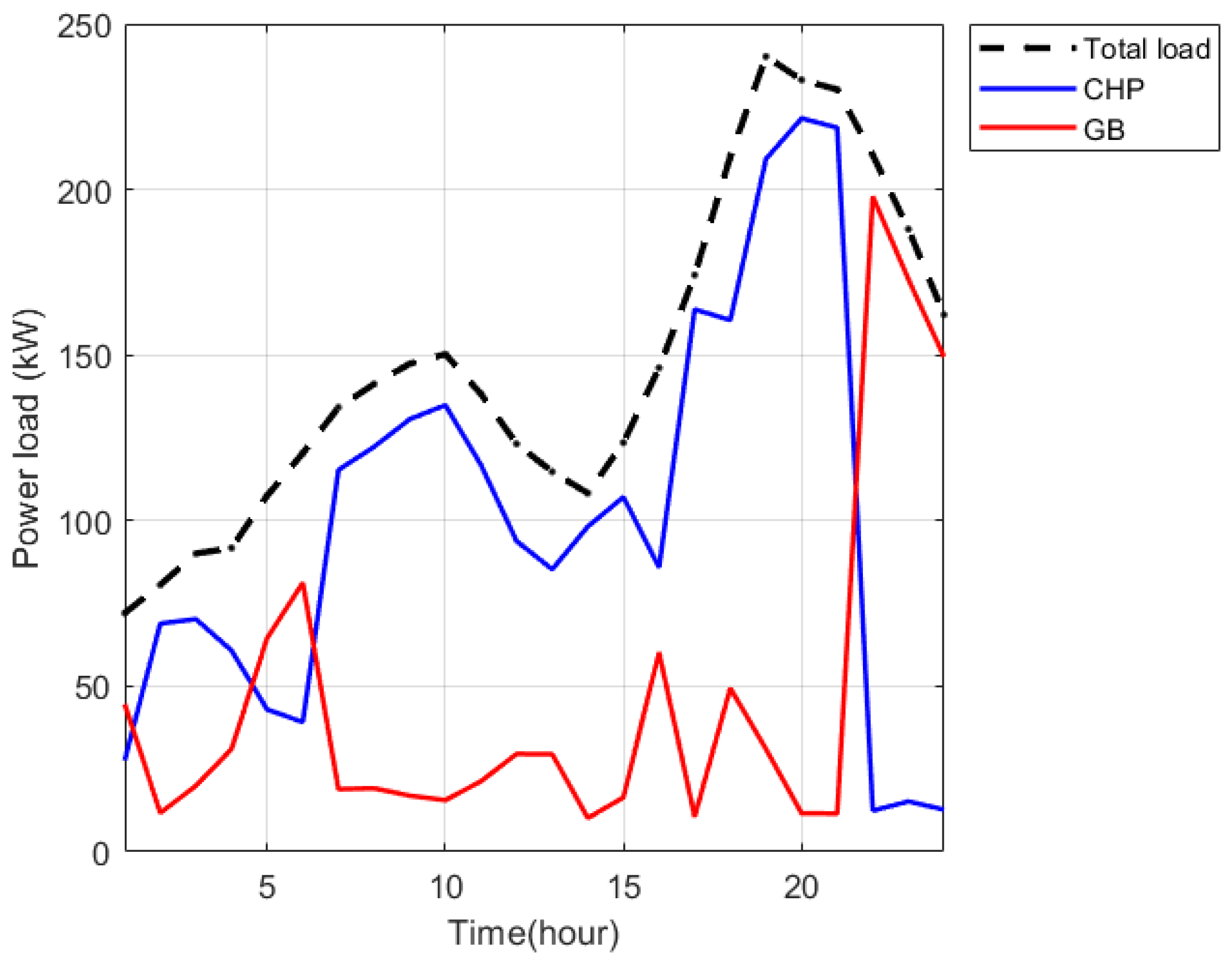
1. Introduction

With the rapid development of technology, energy consumption has grown dramatically, and carbon emissions from traditional fossil fuels have caused numerous environmental problems [1]. As a major energy consumer in the transportation industry, the rail transit system is required to consume green energy. In recent years, the decarbonization of railway systems has also become a hot topic of research [2]. Hydrogen energy has obvious advantages, such as low carbon emissions and high calorific value, and has become the ideal solution for decarbonization in many fields [3]. Therefore, in rail transportation, hydrogen energy-based locomotives have become the preferred choice for the energy transition away from traditional diesel locomotives [4].

The railway hydrogen energy self-sufficient supply is an important component in the large-scale application of hydrogen energy in the railway system [5]. Currently, more than 1600 hydrogen refuelling stations have been deployed worldwide, and green hydrogen stations are increasing rapidly. Germany has combined wind power, electrolysis, and liquefaction processes to reduce the production cost of green hydrogen to 3.5 euros per kg. Its 200 MW-scale green hydrogen plant has achieved continuous and stable operation, validating the feasibility of large-scale production of green liquefied hydrogen. Meanwhile, Toyota Motor Corporation has established a hydrogen energy supply to demonstrate the commercial application level [6,7]. Meanwhile, the Sixth Academy of China Aerospace Science and Technology Corporation, Zhongke Hydrogen Technology Co., Ltd., and the Chinese Academy of Sciences have developed renewable energy hydrogen production, hydrogen energy conversion, and system integration [8]. Yet, the real hydrogen energy-based self-consistent hydrogen energy system faces numerous challenges [9]. On the renewable energy side, wind and solar power output are subject to significant fluctuations due to environmental conditions. On the energy consumption side, the complexity of system coupling is amplified by the time-varying industrial energy consumption and environmental conditions. With the introduction of hydrogen-powered rail systems, the energy consumption requirements of large-scale hydrogen-powered rail systems will further increase dynamic coupling characteristics [10,11,12]. To achieve cost-effective hydrogen-powered railways, integrating the energy generation, storage, and utilization within a self-consistent hydrogen energy system to achieve multi-energy flow coordination optimization, has become a focus of transportation-energy integration research [13,14,15].

Therefore, a multi-energy flow coordination optimization system for industrial parks has been constructed. The comprehensive multi-energy flow system utilizes fluctuating power sources, such as wind and solar energy, along with the flexible adjustment capabilities of gas turbines and energy storage, to enhance energy utilization efficiency and increase renewable energy penetration rates [16]. However, the energy system fails to consider the hydrogen-powered railway systems. For hydrogen-powered railway systems, it is necessary to combine the characteristics of hydrogen-powered locomotives [17]. Hence, a hydrogen energy-based locomotive system was designed with economic considerations to improve the efficiency of the system [18]. From the analysis, incorporating a multi-energy flow system in hydrogen-based locomotives would enhance their efficiency and environmental performance. The PEM fuel cell with ammonia–water cooling cycle system is integrated into the multi-energy system [19]. However, as the energy demand for hydrogen energy-based locomotives gradually increases, large-scale hydrogen use will require the introduction of tank cars and pipelines [20]. Tank cars have become the solution for self-consistent hydrogen energy parks for hydrogen energy-based railways due to their flexibility, adaptability, and cost-effectiveness [21]. Nevertheless, the tank car, as an important mobile energy storage device, faces increased system uncertainty and complexity due to differences in hydrogen locomotive scheduling tasks and mileage, as well as vehicle type and charging time. To address uncertainties in arrival times and charging demands, Ren et al. considered an adaptive data-driven set to describe the randomness [22]. In addition, the artificial intelligence-based control was also introduced for the vehicle-to-grid system [23]. This effectively captured the multimodal characteristics of the data and optimized charging strategies, thereby achieving optimization for industrial parks at the electric vehicle charging level. A comprehensive energy system model was established that incorporates tank cars, treating them as part of a multi-energy flow system, thereby further optimizing the energy demand within the park [24]. Nevertheless, the introduction of tank car coupling of complex hydrogen park units would result in the curse of dimensionality, uncertainty, and high nonlinearity.

A flexible optimization method is proposed for electric vehicles based on a charge–discharge model and conducted simulation analyses in conjunction with a power system day-ahead optimization model [25]. The results indicate that accurate modelling with rule-based optimization can achieve optimization results. Given that the operation of tank cars is highly correlated with the scheduling of hydrogen-powered locomotives and is also influenced by the tank car, the complexity and uncertainty are even more diverse [26]. Hence, the metaheuristic optimization is introduced to operate the schedule of a multi-energy system [27]. However, the metaheuristic optimization is complex, which results in a lack of adaptability for the reliability and economic efficiency of the system. With the development of artificial intelligence in recent years, intelligent optimization algorithms have been introduced for complex and uncertain multi-energy flow systems in industrial parks. The genetic algorithms, particle swarm algorithms, and simulated annealing algorithms are introduced for the optimization [28,29]. However, the above methods are affected by parameters and are prone to local optima. Therefore, the Grey Wolf algorithm is introduced into system optimization due to its stronger global search capabilities and fewer parameters, which is desirable for the uncertain and nonlinear hydrogen-powered railway energy park system [30]. Given that the self-consistent hydrogen energy park system for hydrogen energy-based rail tank car is more complex and dynamic, designing a hydrogen energy park-based grey wolf algorithm that integrates adaptive adjustment mechanisms has become an effective way to improve reliability and efficiency.

In this paper, we present a self-consistent multi-energy flow coordination optimization method for hydrogen-powered railway tank car transportation in hydrogen energy parks. First, a multi-energy flow system integration model was established for the hydrogen-powered railway system, encompassing green non-dispatchable units such as wind power and photovoltaic systems, as well as dispatchable units such as fuel cells, gas boilers, and combined heat and power (CHP) units. An optimization scheduling model was developed to minimize the daily operating costs, incorporating hydrogen-powered railway tank car transportation. The model parameters were then optimized based on actual operational data. Given the diversity and complexity of actual tank car operations, a probabilistic model of daily charging behaviour was constructed using a Monte Carlo simulation to simulate actual tank car operations. For the multi-energy flow system of self-consistent hydrogen energy parks for hydrogen energy-based railways, we developed a Dynamic Adaptive Grey Wolf Optimization (DA-GWO) algorithm. Through a parameter self-adaptive adjustment mechanism, the algorithm’s global optimization capabilities have optimized the whole system. The innovations of this paper are as follows:

(1)

The tank car loads were first introduced into a self-consistent hydrogen energy park, multi-energy flow coordinated optimization, and an innovative multi-energy flow coordinated optimization for hydrogen railways.

(2)

A multi-energy flow optimization model for hydrogen energy-based railways was constructed, and parameters were optimized for actual scenarios.

(3)

A dynamic adaptive grey wolf algorithm was proposed for hydrogen energy-based railways, optimizing system costs and improving the reliability of system optimization.

The remainder of this paper is organized as follows:

Section 2 establishes an optimization scheduling model with the consideration of hydrogen energy-based railways. Section 3 introduces the proposed DA-GWO algorithm. Section 4 verifies the effectiveness of the optimization method for optimization scheduling. Section 5 presents the conclusions.

2. Multi-Energy Flow System Modelling with Tank Car for Hydrogen-Powered Railways in Industrial Parks

2.1. A Multi-Energy Flow System for Integrated Energy in Industrial Parks with the Tank Car

The multi-energy flow system architecture of the integrated power-heat energy system for hydrogen-powered railways combines the coupling network of power grids, heating networks, and natural gas pipelines, forming a microgrid. The microgrid interfaces with the external power grid through transformers and is equipped with dual-mode switching functions for grid connection and island mode, as illustrated in Figure 1 [31].

The system topology includes five power nodes, two thermal nodes, and three natural gas nodes. Among these, only node EB5, the secondary battery (SB) node, has dual energy supply and consumption functions, while the others are energy supply nodes. Distributed power generation equipment is categorized into dispatchable units (fuel cells (FC), gas turbines (GT), waste heat boilers (WHB), combined heat and power units, secondary batteries (SB), and gas boilers (GB)) and non-dispatchable units (wind turbines (WT) and photovoltaic (PV)). Centralized electricity/heat load nodes are provided for convenient dispatch management. The system encompasses four core components: generation, transmission, load, and storage. On the generation side, fossil fuels and renewable energy are converted using equipment such as gas turbines. On the transmission side, energy is transferred through a coupled network of power grids, heat grids, and gas grids. On the load side, electricity and heat demand are aggregated, and hydrogen energy-based locomotives are supplied with energy via tank cars. On the storage side, batteries are used to transfer energy over time. The production includes the utilization of waste heat from gas turbine power generation and the conversion of renewable energy. The storage phase uses batteries to smooth out supply–demand fluctuations, and the transportation phase transmits energy through the thermoelectric network, with pipeline losses often overlooked during configuration optimization. However, the architecture achieves comprehensive energy utilization by multi-energy coupling and coordinated scheduling.

2.2. Non-Dispatchable Units

2.2.1. Wind Turbines

Wind power generation is the most common green energy technology within the park. The output power is primarily affected by wind speed. Therefore, a model can be established for the wind turbine based on changes in wind speed.

Low wind speed model: when the wind speed v is too low and does not reach the cut-in wind speed $v_{vi}$, the wind turbine does not rotate, resulting in the output power being 0.

High wind speed model: when the wind speed v reaches the cut-in wind speed $v_{vi}$, the wind turbine begins to rotate, and the torque of the wind turbine increases with the wind speed. Therefore, the wind speed and the output power of the wind turbine are linearly related until the rated wind speed $v_r$ is reached.

Rated output model: when wind speed v is high, the pitch angle increases, while the wind energy utilization coefficient decreases, reducing the wind turbine’s ability to capture wind energy. This, in turn, reduces the stress on the blades and tower caused by wind energy, protecting the wind turbine while maintaining its operation at rated power $P_{ref}$.

Cut-off protection model: when the wind speed $v$ exceeds the cut-off wind speed of the wind turbine $v_{co}$, the pitch angle is adjusted to 90°, and wind energy is no longer utilized, protecting the wind turbine from being damaged by strong winds. Thus, the wind turbine’s external output power is 0.

The relationship between output power and wind speed is shown in Figure 2.

According to the model of wind speed and wind turbine output power, the following approximate relationship can be obtained:

$$P_{WT}=\left\{\begin{array}{cc}{\displaystyle \frac{(v-v_{ci})P_{ref}}{v_r-v_{ci}}}& v_{ci}<v<v_r\\ P_{ref}& v_r<v<v_{co}\\ 0& other\end{array}\right.$$

(1)

2.2.2. Photovoltaic Power Generation Unit

Photovoltaic power generation is another common green energy technology within the park. The output power can be approximately expressed:

$$P_{PV}=P_s\cdot G_{AC}/G_S\cdot (1+\alpha (T_c-T_i))$$

(2)

where $P_{PV}$ represents the output power of the photovoltaic cell, $P_s$ represents the maximum output power under standard conditions, which is related to the cell conversion efficiency and inverter efficiency, $G_{AC}$ represents the ambient light intensity (kW/m²), $G_S$ represents the light intensity under standard test conditions (kW/m²), $\alpha$ represents the power temperature coefficient, taken as 0.3%/°C, $T_c$ represents the actual operating temperature (increasing with irradiation), and $T_i$ represents the reference temperature, taken as 25 °C.

2.3. Dispatchable Units

2.3.1. Fuel Cell

Fuel cells play a crucial role as the primary power system for hydrogen-powered railways. Although the fuel cells in hydrogen-powered locomotives are installed inside the carriages and cannot be removed, they can still serve as a backup power source. Additionally, fuel cells are dispatchable power generation devices, enabling a continuous electricity supply by injecting fuel gas. By controlling the injection rate, flexible dispatch is achieved. In this section, the output power is:

$$\left\{\begin{array}{l}{P}_{FC,t}=V_{FC}^{C{H}_4}{\eta }_{FC}\\ \underset{¯}{P_{FC,t}}\le P_{FC,t}\le \overline{P_{FC,t}}\\ R_{FC,t}^{down}\cdot \mathsf{\Delta }t\le P_{FC,t}-P_{FC,t-\mathsf{\Delta }t}\le R_{FC,t}^{up}\cdot \mathsf{\Delta }t\end{array}\right.$$

(3)

where $P_{FC,t}$ represents the output power of the fuel cell, which is related to the input of natural gas per time, and natural gas per time is $V_{FC}^{C{H}_4}$, ${\eta }_{FC}$ denotes the electrical energy conversion efficiency of the natural gas fuel cell, which is affected by factors such as battery type and operating temperature. To protect the fuel cell and conserve energy, the output power of the fuel cell $P_{FC}$ is constrained by its upper and lower limits $\overline{P_{FC,t}}$ and $\underset{¯}{P_{FC,t}}$. At the same time, the response time of the output power should be considered, and the output power per time is constrained by the upper and lower limits $R_{FC,t}^{up}$ and $R_{FC,t}^{down}$ (kW/h).

2.3.2. Gas Boiler

Gas boilers (GB) are a type of heating equipment that generates thermal energy through the combustion of natural gas. They offer superior operational efficiency compared to electric boilers and oil-fired boilers and have gradually become the core component for heat flow and steam supply in self-sustaining hydrogen energy system parks.

$$\left\{\begin{array}{l}{P}_{GB,t}=V_{GB}^{C{H}_4}{\eta }_{GB}\\ \underset{¯}{P_{GB,t}}\le P_{GB,t}\le \overline{P_{GB,t}}\\ R_{GB,t}^{down}\cdot \mathsf{\Delta }t\le P_{GB,t}-P_{GB,t-\mathsf{\Delta }t}\le R_{GB,t}^{up}\cdot \mathsf{\Delta }t\end{array}\right.$$

(4)

where $P_{GB}$ represents the thermal power output of the gas boiler, whose conversion equation is related to the input of natural gas per time $V_{GB}^{C{H}_4}$, and the heating efficiency of the gas boiler ${\eta }_{GB}$. At the same time, the thermal power of the gas boiler $P_{GB}$ is subject to upper and lower limits, $\overline{P_{GB,t}}$ and $\underset{¯}{P_{GB,t}}$ represent the upper and lower limits of the thermal power output of the gas boiler, respectively. At the same time, the upper and lower limits of the ramping capacity of the output power of the gas boiler (kW/h) $R_{GB,t}^{up}$ and $R_{GB,t}^{down}$ should be considered.

2.3.3. Industrial Battery

As a dispatchable unit in a comprehensive energy system, secondary batteries (SB) store and release electrical energy in a comprehensive energy system in a reasonable manner. The secondary battery charging and discharging model i:

$$E_e(t)=(1-{\alpha }_e)E_e(t-1)+({\eta }_e^c{P}_e^c(t-1)-{\displaystyle \frac{P_e^d(t-1)}{{\eta }_e^d}})\mathsf{\Delta }t$$

(5)

where $E_e(t)$ represents the stored energy of the shared energy storage device during time period t, which can be expressed as the remaining energy from the previous time period after natural discharge, plus the energy charged and discharged during a certain period of time. ${\eta }_e^c$ and ${\eta }_e^d$ represent the charging and discharging efficiency of the battery, ${\alpha }_e$ represents the self-discharge rate of the battery, $P_e^c(t)$ and $P_e^d(t)$ represent the charging and discharging power during the time period t. The model also satisfies the following constraints:

$$\left\{\begin{array}{l}0\le P_t^c{\eta }_{FC}\le {\delta }_c\overline{P_t^c}\\ 0\le P_t^d\le {\delta }_d\overline{P_t^d}\\ {\delta }_c+{\delta }_d\le 1\\ {\delta }_c\in \left\{0,1\right\},{\delta }_d\in \left\{0,1\right\}\\ E_{\min }\le E\le E_{\max }\end{array}\right.$$

(6)

where ${\delta }_c$ and ${\delta }_d$ are a pair of binary variables used to represent the charge–discharge state of a battery, 1 indicates that the battery is in the corresponding operational state, 0 indicates that the battery is not in the corresponding operational state. $P_t^c$ and $P_t^d$ represent the charging and discharging power at time t, respectively. Due to limitations imposed by their own parameters, constraints must be placed on the upper and lower limits of the battery’s charging and discharging power $\overline{P_t^c}$ and $\overline{P_t^d}$, respectively. To protect the battery and ensure that its stored energy capacity E remains within a certain range, the upper and lower limits of stored energy $E_{\min }$ and $E_{\max }$ are set based on the charging and discharging model.

2.4. Cogeneration Unit

Combined heat and power (CHP) units are devices that simultaneously produce thermal and electrical energy, including gas turbines (GT) and waste heat boilers (WHB). The schematic diagram is shown in Figure 3.

Combined heat and power (CHP) units use gas turbines as their core equipment, with two operational modes: “heat-driven power generation” and “power-driven heat generation.” This mode is suitable for industrial parks with a hydrogen energy system transformation with a significant difference between peak and off-peak electricity prices. The thermoelectric characteristics corresponding to the two operating modes are shown in Figure 4.

The units cannot independently regulate electrical or thermal output, and their thermoelectric ratio HPR is constant due to physical structural limitations, specifically satisfying the following equation:

$$\left\{\begin{array}{l}{P}_{CHP,t}=V_{CHP,t}{H}_{C{H}_4}{\eta }_{GT}\\ Q_{CHP,t}=V_{CHP,t}{H}_{C{H}_4}{\eta }_{WHB}-Q_{loss}\\ HPR={\displaystyle \frac{{\eta }_{GT}}{{\eta }_{WHB}-(Q_{loss}/V_{CHP,t}{H}_{C{H}_4})}}\approx Const\end{array}\right.$$

(7)

where $P_{CHP,t}$ and $Q_{CHP,t}$ represent the thermal power output and electrical power output of the unit, respectively, $V_{CHP,t}$ denotes the natural gas consumed by the combined heat and power (CHP) unit per time t, $H_{C{H}_4}$ is the calorific value of natural gas. The electrical–thermal ratio HPR is primarily influenced by the structural characteristics of the CHP unit itself, ${\eta }_{GT}$ is the efficiency of the gas turbine, typically set at 40%, ${\eta }_{WHB}$ is the efficiency of the waste heat boiler, which is taken as 60% in this paper, $Q_{loss}$ is the energy loss of the gas turbine, typically assumed to be 20%. Thus, the power–heat ratio of a fixed power–heat ratio unit is approximately 1.67.

The variable thermal power ratio specifically satisfies the following equation:

$$\left\{\begin{array}{l}{P}_{CHP,t}={\displaystyle \sum _{k=1}^N{\alpha }_t^k{P}^k}\\ Q_{CHP,t}={\displaystyle \sum _{k=1}^N{\alpha }_t^k{Q}^k}\\ {\displaystyle \sum _{k=1}^N{\alpha }_t^k=1, 0\le {\alpha }_t^k\le 1}\end{array}\right.$$

(8)

where ${\alpha }_t^k$ is a coefficient that limits the power output of the CHP unit. It is related to factors such as the exhaust volume limit and the dead zone of electrical power regulation and prevents excessive pressure or blockage in the pressure cylinder.

2.5. Tank Car Load Demand Response Model

2.5.1. Energy Consumption Analysis of Tank Cars in Self-Sufficient Hydrogen Energy Parks

A self-sufficient hydrogen energy park for hydrogen-powered railways uses electric tank cars to transport energy and materials within the park. In this paper, the pressure of hydrogen-carrying tanks is 35 MPa, and the total hydrogen-carrying capacity is 10 kg. In the energy park, the daily mileage and external energy requirements are the key factors determining the daily charging needs of tank cars. Due to the influence of different tasks and working hours, this paper uses a log-normal distribution probability density function to describe the daily mileage of vehicles [32]. The specific analysis is shown:

$$f_d(x)={\displaystyle \frac{1}{x\sigma \sqrt{2\pi }}}{e}^{-{\displaystyle \frac{{(\ln x-\mu )}^2}{2{\sigma }^2}}}$$

(9)

where $f_d(x)$ is the probability density function of the daily mileage required for external energy demand for tank cars, µ and σ are the expected value and standard deviation of this normal distribution. In this article, µ = 3.2, σ = 0.88.

The SOC of the tank car at the time of grid connection is influenced by its previous driving conditions, supply to other systems, and charging strategy. Therefore, a log-normal distribution is used to describe the initial SOC of the vehicle when it connects to the grid, with the probability density function shown:

$$f_{soc}(x)={\displaystyle \frac{1}{{\sigma }_1\sqrt{2\pi }}}{e}^{-{\displaystyle \frac{{(x-\mu )}^2}{2{\sigma }_1^2}}}$$

(10)

where $f_{soc}(x)$ is the probability density function of the initial SOC of the tank car, µ₁ and σ₁ are the expected value and standard deviation of the normal distribution, respectively. Excerpt from the article, µ₁ = 0.3, σ₁ = 0.1.

The duration of energy supply for tank cars is highly correlated with their consumption levels and remaining battery capacity. The formula for calculating charging duration is:

$$t_c={\displaystyle \frac{E_{TK}}{P_{TK}\eta }}$$

(11)

where $\eta$ is the battery charging efficiency, taken as 0.9 in this paper, $E_{TK}$ is the charging power, and $P_{TK}$ is the charge/discharge power. In this paper, charging methods are categorized into slow charging, standard charging, and fast charging. The corresponding power ranges for each charging method are shown in

Table 1. Power values corresponding to charging methods.

Charging Method	Charging Power
Slow charging	[1.5, 2.0]
Regular charging	[6.3, 24.8]
Fast charging	[40, 90]

.

2.5.2. Tank Car Charging Load Based on Monte Carlo Simulation

Monte Carlo simulation is a method that approximates the solution to complex problems through extensive random sampling. By randomly sampling the daily driving distance and charging start time of each vehicle, the daily charging load of the vehicle is calculated. The specific steps for modelling based on the Monte Carlo simulation method are as follows:

Parameter definition: Generate samples of N tank cars, specify parameters such as battery capacity and battery charging efficiency for each car. This paper selects 20 tank cars with a battery capacity of 100 kW and a charging efficiency of 0.9.

Random variable sampling: Independently generate random parameters for each vehicle, including daily mileage, charging start time, required power consumption, and other parameters.

Calculate charging time: Calculate the end time based on the start time of charging, the required power, and the charging power.

Use a Monte Carlo simulation to calculate the charging load after all tank cars are stacked.

2.5.3. Tank Car Charging and Discharging Model

Considering the practical use of tank cars as flexible distributed energy storage units, the charging and discharging costs of tank cars are analyzed. The charging and discharging costs of tank cars $C_t^{TK}$ are:

$$C_{TK,t}=(\gamma P_{TK,t}^c{c}_t^{ebuy}-(1-\gamma )P_{TK,t}^d{c}_t^{esell})\mathsf{\Delta }t$$

(12)

where $P_{TK,t}^c$ and $P_{TK,t}^d$ are the charging and discharging power of the tank car during time period t, $\gamma$ is a set of 0–1 variables used to represent the charging and discharging status of the tank car during time period t.

2.6. Multi-Energy Flow System Scheduling Optimization Model with Tank Car

2.6.1. Objective Function

The objective function is constructed with the goal of minimizing the total operating cost per day, and hourly scheduling is set: the time interval is 1 h, meaning there are 24 scheduling time points in a day. The minimum cost calculation for the multi-energy flow system is performed, and the system operating cost calculation formula at time t is:

$$C_t=C_{r,t}+C_{tr,t}+C_{pu,t}+C_{TK,t}$$

(13)

where $C_t$ is the operating cost of the multi-energy flow system at time t, $C_{r,t}$ is the fuel unit and unit operating cost at time t, $C_{tr,t}$ is the transaction cost with the external power grid at time t, $C_{pu,t}$ is the penalty cost incurred from reducing the thermal load at time t, and $C_{TK,t}$ is the charging and discharging cost of the tank car.

For dispatchable units, operational costs must be prioritized. This paper proposes two CHP units, so calculations must be performed separately for models with fixed and separated heat–power ratios. During calculations, it is assumed that fuel costs and production capacity are approximately linearly related. By setting certain operational cost parameters, the following equations can be derived for fuel unit and unit operational costs:

$$C_{r,t}=\left\{\begin{array}{l}(K_{FC}\cdot P_{FC,t}+K_{CHP}\cdot g_{CHP,t}+K_{GB}\cdot Q_{GB,t})\cdot \mathsf{\Delta }t\mathrm{CHP}\mathrm{fix}\\ (k_{FC}\cdot P_{FC,t}+k_{CHP,t}^P\cdot P_{CHP,t}+k_{CHP,t}^Q\cdot Q_{CHP,t}+k_{GB}\cdot Q_{GB,t})\cdot \mathsf{\Delta }t\mathrm{CHP}\mathrm{split}\end{array}\right.$$

(14)

where $k_{FC}$ and $k_{GB}$ are the fuel and operating cost coefficients for fuel cells and gas boilers, when the CHP unit is a fixed heat–power ratio unit, $k_{CHP}$ is the unit operating cost coefficient, when the CHP unit is a heat–power ratio separation unit, $k_{CHP,t}^P$ and $k_{CHP,t}^Q$ are the unit’s electricity and heat operating cost coefficients, respectively.

Due to the existence of peak and off-peak periods for electricity consumption within the industrial park, there is a certain discrepancy between the system’s power generation capacity and the timing of electricity consumption. Therefore, the system engages in two-way electricity transactions with the external grid. Additionally, batteries can regulate electricity usage. The remaining electricity stored in the batteries can be sold to the external grid at any given time, or electricity can be purchased from the external grid to replenish stored energy or meet load demands. Therefore, penalty costs are also not considered. Thus, the transaction costs between the multi-energy flow system and the external grid are:

$$C_{tr,t}=p_t{P}_{buy,t}\mathsf{\Delta }t$$

(15)

where $p_t$ is the market electricity price at time t, which is related to the time period of electricity consumption, $P_{buy,t}$ represents the electricity traded between the system and the outside world at time t. A positive value indicates that electricity is purchased from the external grid, while a negative value indicates that electricity is sold to the external grid.

For CHP units’ heat supply, when excess heat cannot be reasonably utilized, constraints are imposed by introducing penalty costs. The penalty costs for heat rejection or heat load reduction are shown:

$$C_{pu,t}=(c^w\cdot Q_{waste,t}+c^r{Q}_{reduce,t})\cdot \mathsf{\Delta }t$$

(16)

where $c^w$ and $c^r$ are the penalty cost coefficients for heat rejection and heat load reduction, $Q_{waste,t}$ and $Q_{reduce,t}$ are the waste heat power and heat reduction power at time t.

2.6.2. Constraints

The objective function based on the lowest cost is subject to constraints imposed by the overall system capacity and the capacity of the power generation units. Specifically, these constraints can be divided into equality constraints and inequality constraints. Equality constraints include power and heat balance constraints, which are core constraint conditions. Inequality constraints include self-imposed constraints established when each power generation unit model is created. The power and heat balance constraints of the system are shown:

$$\left\{\begin{array}{l}{P}_{WT,t}+P_{PV,t}+P_{FC,t}+({\delta }_d{P}_t^d-{\delta }_c{P}_t^c)+P_{CHP,t}+P_{buy,t}=D_t^E\\ Q_{GB,t}+Q_{CHP,t}+Q_{reduce,t}-Q_{waste,t}=D_t^Q\end{array}\right.$$

(17)

where $D_t^E$ and $D_t^Q$ represent the electrical and thermal load demands at time t. Different models have constraints, such as the power capacity constraints and ramping capabilities of their units. Wind turbines and photovoltaic cells are constrained by environmental factors, while fuel cells, gas boilers, and batteries have constraints as shown in Equations (3), (4) and (6). The operation of cogeneration units satisfies the following inequality constraints:

$$\left\{\begin{array}{l}\underset{¯}{P_{CHP,t}}\le P_{CHP,t}\le \overline{P_{CHP,t}}\\ \underset{¯}{Q_{CHP,t}}\le Q_{CHP,t}\le \overline{Q_{CHP,t}}\\ R_{E,t}^{down}\cdot \mathsf{\Delta }t\le \underset{¯}{P_{CHP,t}}-\underset{¯}{P_{CHP,t-\mathsf{\Delta }t}}\le R_{E,t}^{up}\cdot \mathsf{\Delta }t\\ R_{Q,t}^{down}\cdot \mathsf{\Delta }t\le \underset{¯}{P_{CHP,t}}-\underset{¯}{P_{CHP,t-\mathsf{\Delta }t}}\le R_{Q,t}^{up}\cdot \mathsf{\Delta }t\end{array}\right.$$

(18)

The above equation includes the electrical and thermal capacity limits and ramping constraints of the cogeneration unit. In addition, waste heat power and heat reduction power should also be constrained:

$$\left\{\begin{array}{l}0\le Q_{waste,t}\le D_t^Q\\ 0\le Q_{reduce,t}\le D_t^Q\end{array}\right.$$

(19)

The load of a tank car is influenced by multiple factors, including the vehicle’s own capacity, charging power, and charging time. To avoid the safety problem, an upper limit is set to not be fully charged, which is commonly used in real applications. In this paper, the maximum capacity of the tank is set to carry 80% hydrogen. Therefore, the following constraints for tank cars are established:

$$\left\{\begin{array}{l}\underset{¯}{P_{TK}}\le P_{TK}\le \overline{P_{TK}}\\ \underset{¯}{SO{C}_{TK}}\le E\le \overline{SO{C}_{TK}}\end{array}\right.$$

(20)

where $P_{TK}$ denotes the power of the tank car and E denotes the energy stored in the tank car. $\underset{¯}{P_{TK}},\overline{P_{TK}}$ denote the upper and lower power limit of the tank car, $\underset{¯}{SO{C}_{TK}},\overline{SO{C}_{TK}}$ denote the upper and lower energy limit of the tank car. In this paper, $SO{C}_{TK}$ is 0 and $\overline{SO{C}_{TK}}$ is 0.95. During the energy limit, the battery is safe.

2.6.3. Scheduling Optimization Model

In summary, based on the objective function of minimizing operating costs, considering the operating constraints of dispatchable and non-dispatchable units, fluctuations in real-time electricity prices, and the operating modes of cogeneration units, a multi-energy flow system hourly dispatch optimization model can be established:

$$\begin{array}{l}\min {\displaystyle \sum _{t=0}^{24}{C}_t}\\ s.t.\left\{\begin{array}{l}{D}_t^E=P_{WT,t}+P_{PV,t}+P_{FC,t}+({\delta }_d{P}_t^d+{\delta }_c{P}_t^d)+P_{CHP,t}+P_{buy,t},t\in \left(0,24\right)\\ D_t^Q=Q_{GB,t}+Q_{CHP,t}+Q_{reduce,t}-Q_{waste,t},t\in \left(0,24\right)\\ P_{FC,t}=V_{FC}^{C{H}_4}{\eta }_{FC},t\in \left(0,24\right)\\ \underset{¯}{P_{FC,t}}\le P_{FC,t}\le \overline{P_{FC,t}},t\in \left(0,24\right)\\ R_{FC,t}^{down}\cdot \mathsf{\Delta }t\le P_{FC,t}-P_{FC,t-\mathsf{\Delta }t}\le R_{FC,t}^{up}\cdot \mathsf{\Delta }t,t\in \left(0,23\right)\\ P_{GB,t}=V_{GB}^{C{H}_4}{\eta }_{GB},t\in \left(0,24\right)\\ \underset{¯}{P_{GB,t}}\le P_{GB,t}\le \overline{P_{GB,t}},t\in \left(0,24\right)\\ R_{GB,t}^{down}\cdot \mathsf{\Delta }t\le P_{GB,t}-P_{GB,t-\mathsf{\Delta }t}\le R_{GB,t}^{up}\cdot \mathsf{\Delta }t,t\in \left(0,23\right)\\ 0\le P_t^c\le {\delta }_c\overline{P_t^c},t\in \left(0,24\right)\\ 0\le P_t^d\le {\delta }_d\overline{P_t^d},t\in \left(0,24\right)\\ {\delta }_c+{\delta }_d\le 1\\ {\delta }_c\in \left\{0,1\right\},{\delta }_d\in \left\{0,1\right\}\\ E_{\min }\le E_t\le E_{\max },t\in \left(0,24\right)\\ \underset{¯}{P_{CHP,t}}\le P_{CHP,t}\le \overline{P_{CHP,t}},t\in \left(0,24\right)\\ \underset{¯}{Q_{CHP,t}}\le Q_{CHP,t}\le \overline{Q_{CHP,t}},t\in \left(0,24\right)\\ R_{E,t}^{down}\cdot \mathsf{\Delta }t\le P_{CHP,t}-P_{CHP,t-\mathsf{\Delta }t}\le R_{E,t}^{up}\cdot \mathsf{\Delta }t,t\in \left(0,23\right)\\ R_{Q,t}^{down}\cdot \mathsf{\Delta }t\le Q_{CHP,t}-Q_{CHP,t-\mathsf{\Delta }t}\le R_{Q,t}^{up}\cdot \mathsf{\Delta }t,t\in \left(0,23\right)\\ 0\le Q_{waste,t}\le D_t^Q,t\in \left(0,24\right)\\ 0\le Q_{reduce,t}\le D_t^Q,t\in \left(0,24\right)\\ \underset{¯}{P_{TK,t}}\le P_{TK,t}\le \overline{P_{TK,t}},t\in \left(0,24\right)\\ \underset{¯}{SO{C}_{TK,t}}\le SO{C}_{TK,t}\le \overline{SO{C}_{TK,t}},t\in \left(0,24\right)\end{array}\right.\end{array}$$

(21)

3. Multi-Energy Flow Park Dynamic Adaptive Grey Wolf Optimization Algorithm for Hydrogen-Powered Rail Tank Car Transportation

3.1. Grey Wolf Algorithm

The Grey Wolf Optimizer (GWO) is a swarm intelligence optimization algorithm inspired by the hunting behaviour of grey wolf packs in nature [33]. The hunting behaviour, the strict hierarchical structure (α, β, δ wolf), and collaborative hunting mechanisms (encirclement, pursuit, and attack) within a grey wolf society inspired the efficient search for the optimal solution of a function. Compared to the Particle Swarm Optimization (PSO) and genetic algorithm (GA), the grey wolf algorithm has the advantages of fewer parameters, faster convergence speed, and a strong balance between global exploration and local exploitation. It can better balance local optimization and global search, and has performed excellently in power system economic dispatch, wind–solar storage optimization configuration, and power plant combination problems.

3.1.1. Hierarchy

Grey wolves are social animals in the wild, with a strict social hierarchy. The wolf pack is divided into four ranks: alpha wolf (α), beta wolf (β), delta wolf (δ), and omega wolf (ω). The alpha wolf is responsible for leading the pack in hunting and decision-making activities and holds the highest status within the pack, representing the current optimal solution. The beta wolf assists the alpha wolf and can replace the alpha wolf when necessary, representing the second-best solution. The base wolves follow the commands of the alpha and beta wolves, representing the third-best solution, while the ordinary wolves occupy the lowest rank in the pack hierarchy. They follow the leadership of other ranks during hunting and execute corresponding tasks.

3.1.2. Surround the Prey

During the pursuit, the grey wolf pack typically surrounds the prey first. The mathematical model of this behaviour can be expressed as:

$$\begin{array}{l}\overrightarrow{D}=\left|C\cdot \overrightarrow{X_p}(t)-\overrightarrow{X}(t)\right|\\ \overrightarrow{X}(t+1)=\overrightarrow{X_p}(t)-\overrightarrow{A}\cdot \overrightarrow{D}\end{array}$$

(22)

where t indicates the number of iterations in the current iteration. A and C are the cooperation coefficient vectors, and D is the distance between the grey wolf and the prey. $\overrightarrow{X_p}(t)$ represents the position of the prey in the t iteration, and $\overrightarrow{X}(t)$ represents the position vector of the grey wolf in the t iteration. The formulas for calculating the coefficient vectors A and C are as follows:

$$\begin{array}{l}A=2a{r}_1-ar\\ C=2r_2\end{array}$$

(23)

where $a$ decreases linearly from 2 to 0 with the number of iterations, $r_1$ and $r_2$ are random vectors, $r$ is a vector with each dimension equal to 1, and each dimension follows a uniform distribution U (0,1).

3.1.3. Pursuit

Grey wolves are capable of identifying the location of prey and surrounding them. Hunting is typically led by the alpha wolf, with beta and delta wolves occasionally participating as well. In each iteration, the three optimal solutions obtained so far are saved, forcing other wolves (including gamma) to update their positions according to the optimal search location using the following formula:

$$\left\{\begin{array}{l}\stackrel{\rightharpoonup }{D_{\alpha }}=\left|\stackrel{\rightharpoonup }{C_1}\cdot \stackrel{\rightharpoonup }{X_{\alpha }}-\stackrel{\rightharpoonup }{X}(t)\right|\\ \stackrel{\rightharpoonup }{D_{\beta }}=\left|\stackrel{\rightharpoonup }{C_2}\cdot \stackrel{\rightharpoonup }{X_{\beta }}-\stackrel{\rightharpoonup }{X}(t)\right|\\ \stackrel{\rightharpoonup }{D_{\delta }}=\left|\stackrel{\rightharpoonup }{C_3}\cdot \stackrel{\rightharpoonup }{X_{\delta }}-\stackrel{\rightharpoonup }{X}(t)\right|\\ \stackrel{\rightharpoonup }{X_1}=\stackrel{\rightharpoonup }{X_{\alpha }}-\stackrel{\rightharpoonup }{A_1}\cdot \stackrel{\rightharpoonup }{D_{\alpha }}\\ \stackrel{\rightharpoonup }{X_2}=\stackrel{\rightharpoonup }{X_{\beta }}-\stackrel{\rightharpoonup }{A_2}\cdot \stackrel{\rightharpoonup }{D_{\beta }}\\ \stackrel{\rightharpoonup }{X_3}=\stackrel{\rightharpoonup }{X_{\delta }}-\stackrel{\rightharpoonup }{A_3}\cdot \stackrel{\rightharpoonup }{D_{\delta }}\\ \stackrel{\rightharpoonup }{X}(t+1)={\displaystyle \frac{\stackrel{\rightharpoonup }{X_1}+\stackrel{\rightharpoonup }{X_2}+\stackrel{\rightharpoonup }{X_3}}{3}}\end{array}\right.$$

(24)

where $\stackrel{\rightharpoonup }{X_{\alpha }}$, $\stackrel{\rightharpoonup }{X_{\beta }}$, and $\stackrel{\rightharpoonup }{X_{\delta }}$ represent the position vectors of α, β, and δ in the current iteration, respectively, $\stackrel{\rightharpoonup }{X}(t)$ is the position vector of the individual in the t iteration, $\stackrel{\rightharpoonup }{C_1}$, $\stackrel{\rightharpoonup }{C_2}$, and $\stackrel{\rightharpoonup }{C_3}$ are random vectors, $\stackrel{\rightharpoonup }{D_{\alpha }}$, $\stackrel{\rightharpoonup }{D_{\beta }}$, and $\stackrel{\rightharpoonup }{D_{\delta }}$ represent the distances between other individuals in the population and α, β, and δ, respectively, $\stackrel{\rightharpoonup }{X}(t+1)$ is the updated position vector of the individual.

The figure below shows how ω wolf or other wolves (candidate wolves) update their positions based on the positions of α, β, and δ wolves in the two-dimensional search space. As shown in Figure 5, the final position will be a random position within the circle defined by the positions of the α, β, and δ wolves in the search space. In other words, the α, β, and δ wolves estimate the prey’s position, and the other wolves randomly update their positions around the prey.

3.1.4. Attack the Prey

Grey wolves complete their hunt by attacking their prey when it stops moving. Attacking the prey determines its location. This process is mainly achieved through the iterative process of decreasing the convergence factor a from 2 to 0. Thus, after the iteration is complete, the group obtains the optimal solution.

3.2. Dynamic Adaptive Grey Wolf Algorithm and Optimized Scheduling

To address the shortcomings of traditional GWO in scheduling problems, where convergence tends to occur prematurely, the GWO algorithm can be improved by increasing control parameters or changing the way control parameters are updated. On this basis, this paper combines the advantages of other algorithms to further improve the optimization and solution process of the GWO algorithm, proposing the Dynamic Adaptive GWO (DA-GWO) algorithm, which introduces the following strategies.

Nonlinear adjustment of the convergence factor α: In traditional GWO algorithms, the linear decrease in the convergence factor makes the transition from global search to local development insufficiently flexible, easily leading to early convergence to a local optimum or incomplete search in the later stages. Therefore, a Sigmoid function is used for nonlinear adjustment:

$$\alpha (t)={\alpha }_{\max }-{\displaystyle \frac{{\alpha }_{\max }-{\alpha }_{\min }}{1+e^{(10t/T_{\max }-5)}}}$$

(25)

By adjusting the parameter, the initial α value can be rapidly reduced to maintain the exploratory nature of the wolf pack and avoid prematurely settling into a local optimum. In the later stages, as the α value changes more gradually, this ensures a more thorough local optimization process, thereby improving convergence accuracy. By introducing nonlinear adjustments to balance global search with local exploration, the algorithm avoids stagnating in suboptimal solutions in complex scheduling scenarios.

Implement dynamic leader weight allocation for position updates: In traditional GWO, the position update weights of α, β, and δ wolves are equal, which does not fully utilize the superiority and inferiority information of leaders. Through fitness dynamic weight allocation:

$$\left\{\begin{array}{l}{w}_{\alpha }={\displaystyle \frac{f_{\alpha }}{f_{\alpha }+f_{\beta }+f_{\delta }}}\\ w_{\beta }={\displaystyle \frac{f_{\beta }}{f_{\alpha }+f_{\beta }+f_{\delta }}}\\ w_{\delta }=1-w_{\alpha }-w_{\beta }\\ \stackrel{\rightharpoonup }{X}(t+1)=w_{\alpha }\stackrel{\rightharpoonup }{X_1}+w_{\beta }\stackrel{\rightharpoonup }{X_2}+w_{\delta }\stackrel{\rightharpoonup }{X_3}\end{array}\right.$$

(26)

By assigning a higher weight to the alpha wolf, i.e., the optimal solution, the development of high-potential areas can be accelerated. This helps to highlight the dominant role of the alpha wolf when there are large differences in fitness, while preserving diversity when differences are small.

For the optimization scheduling of multi-energy flow systems in industrial parks targeting hydrogen-powered railway tank cars, it is first necessary to define a fitness function to calculate the fitness value of each candidate solution (wolf position) in the grey wolf algorithm. The calculated fitness value corresponds to the minimized total cost of the optimization scheduling model, which includes direct costs and penalty terms. Direct costs include CHP power generation and heating costs, fuel cell costs, grid power purchase and sale costs, and gas boiler costs. Penalty costs include penalty terms for ramping constraints of each equipment unit and penalty terms composed of thermal decay and thermal waste.

The fitness value in the DA-GWO algorithm is determined by the position vector of the grey wolf algorithm. The 96 dimensions of the position vector are defined as the power scheduling plan for four types of equipment over a 24 h period. By solving the position vector of the grey wolf using the DA-GWO algorithm, the power scheduling plan corresponding to the minimum cost can be determined. As shown in the operational cost calculations, as the aforementioned, an optimized scheduling scheme must not only meet electricity and heat power demands but also be constrained by unit operational constraints. Therefore, during the solution process, it is necessary to set position boundaries for the DA-GWO algorithm and impose constraints on the units via penalty terms. First, the 96-dimensional position boundaries are set to directly constrain the range of the solution vector, corresponding to the upper and lower limits for each unit. After each position update of the DA-GWO algorithm, a position check is performed, and any values exceeding the boundaries are forcibly truncated to ensure that the units operate within a reasonable range.

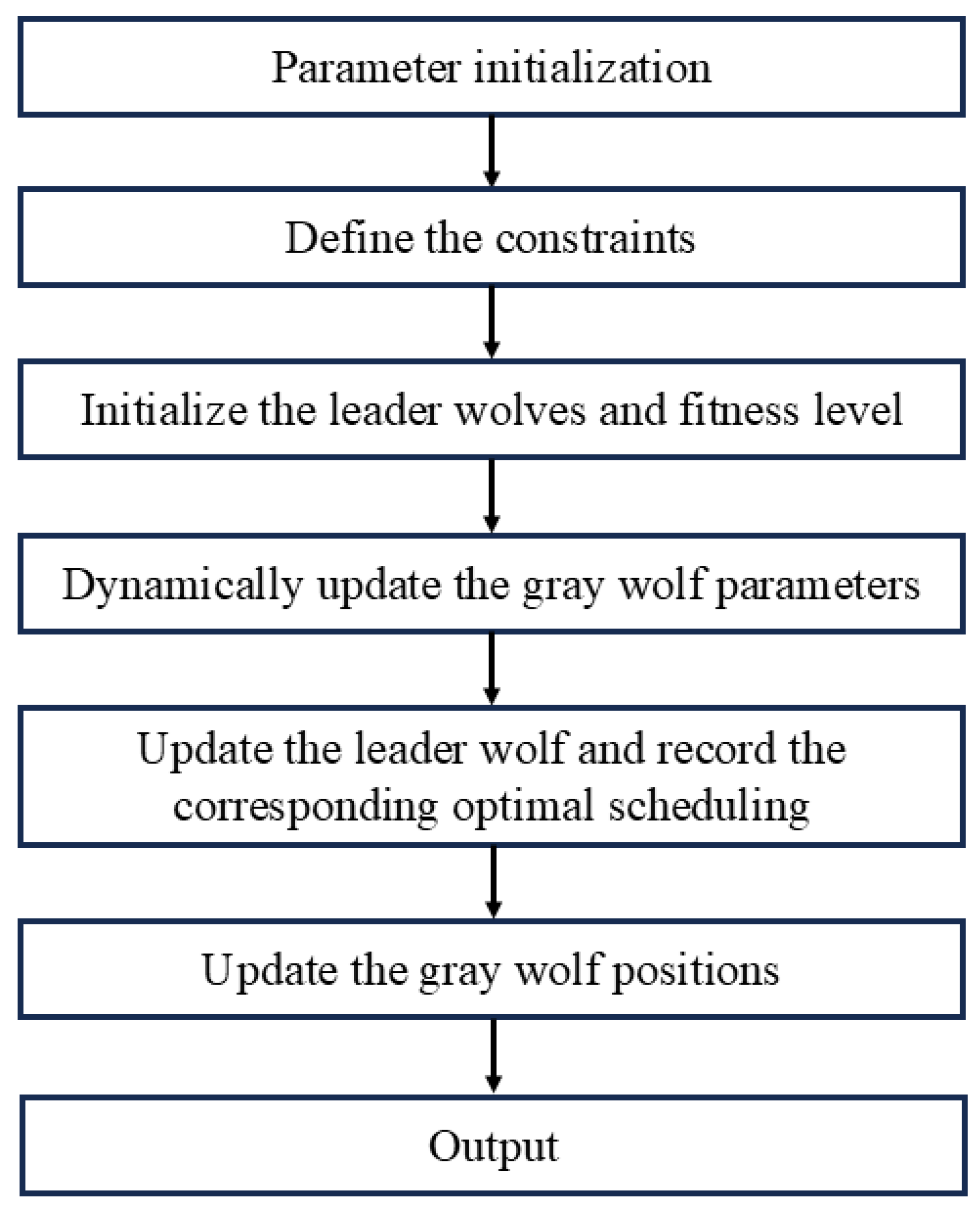
In summary, the steps for solving a multi-energy flow system using the DA-GWO algorithm are as follows.

• Perform parameter initialization: Define the scheduling cycle, define the number and type of devices, define cost parameters, grid electricity purchase and sale price tables, and penalty costs; define constraints: device power upper and lower limits, ramp rate limits, and energy storage limits.
• Grey wolf algorithm initialization: initialize grey wolf parameters, including maximum iteration count, wolf pack size, solution vector dimension dim = 96 (4 devices × 24 h), and define upper and lower bounds; generate initial population satisfying upper and lower bound constraints; initialize leader wolves (α, β, and δ) and their fitness values (set to infinity).
• Iterative optimization: When the number of iterations is less than a given value, dynamically update the grey wolf parameters. By calculating the fitness (total cost) of each wolf, force the solution vector Positions [i] to be truncated within the range [l_b, u_b]. Call the fitness function fitness1 (Positions [i]) to calculate the total cost, including the costs of each unit, GB, and waste heat, as well as the penalty term. Update the leader wolf and record the corresponding optimal scheduling results. Simultaneously update the grey wolf positions (moving toward α, β, and δ) and record the current optimal cost for plotting the convergence curve.
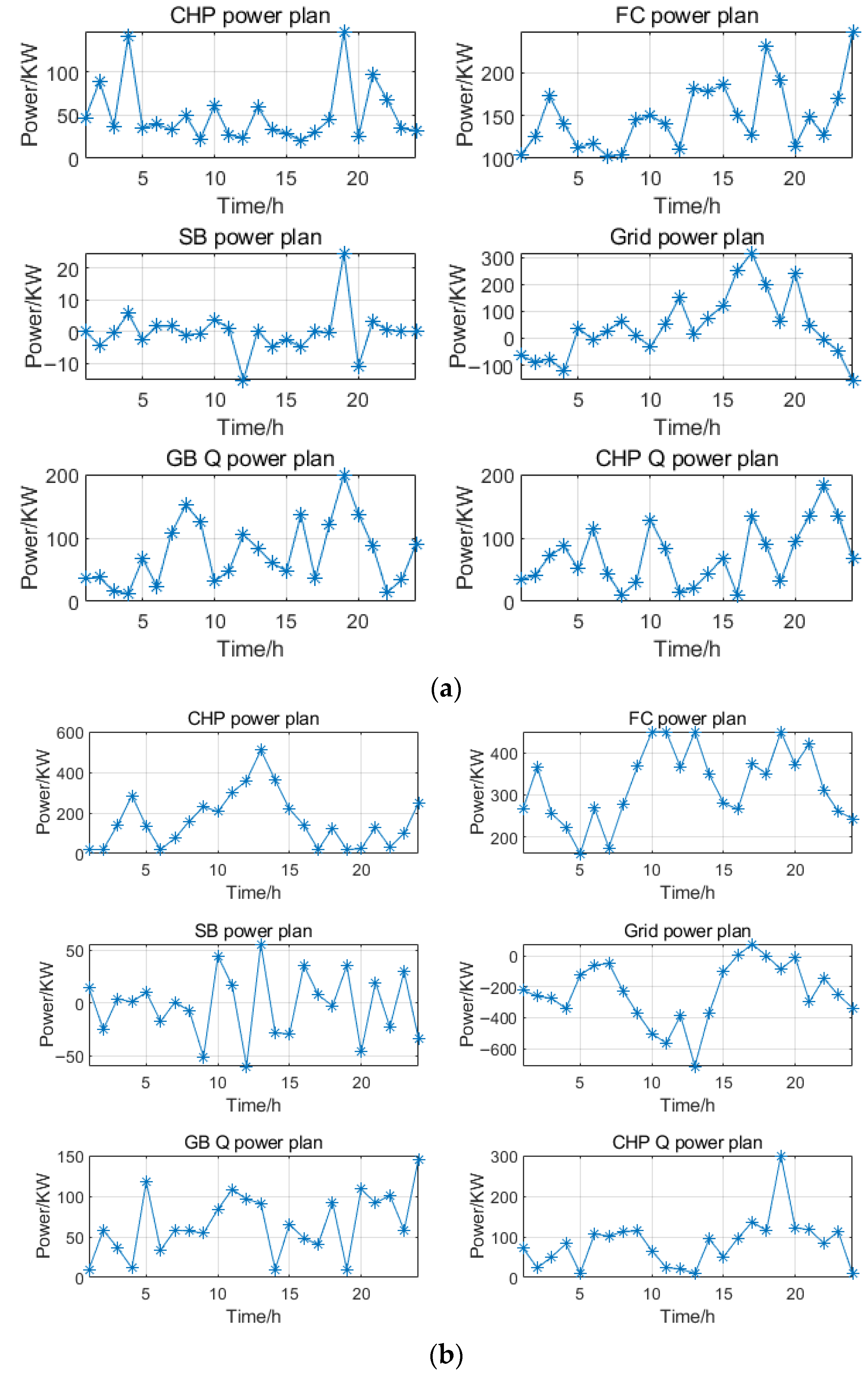
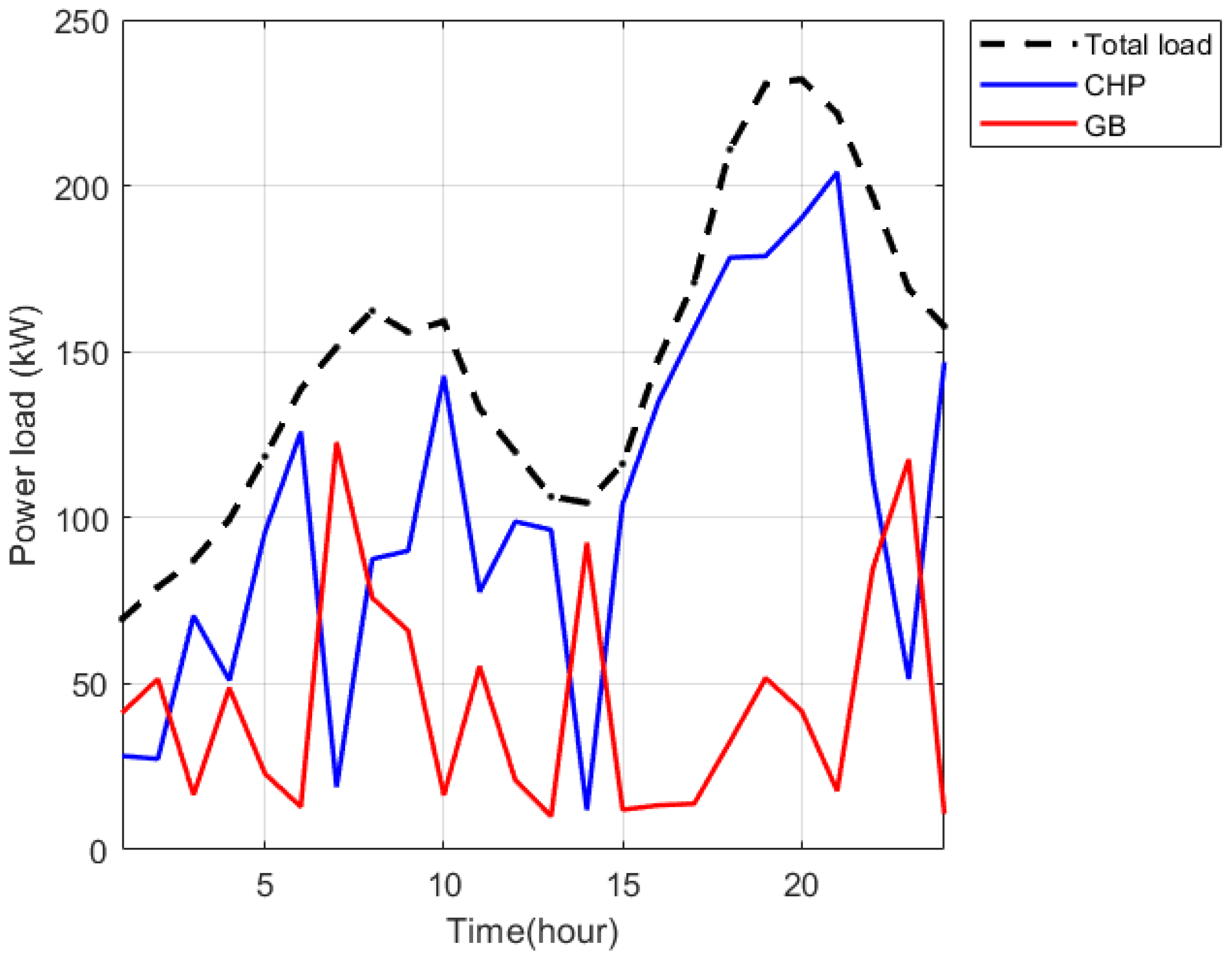
• Output results: Output the minimum cost α_score; output the optimized scheduling results for each unit, including CHP electrical power, FC power, SB charging/discharging power, and GB thermal power.

The algorithmic flowchart is shown in Figure 6.

4. Optimization and Scheduling of Multi-Energy Flow Systems in Industrial Parks for Hydrogen-Powered Railways

4.1. Data Processing

To validate the effectiveness of the proposed optimization method for multi-energy flow system optimization scheduling in hydrogen-powered railway parks, this paper selects the operational parameters of multi-energy flow coupling systems in coastal regions of China, as well as typical daily load curves for electricity, gas, and heat. The system is connected via power transmission lines and natural gas pipelines, and takes into account the characteristics of tank cars, resulting in the multi-energy flow coupling system architecture shown in Figure 1 of this paper. The scheduling cycle is 24 h, with scheduling intervals at the hourly level.

4.1.1. Source Data Selection

First, consider the data for two non-dispatchable units: wind turbines (WT) and photovoltaic cells (PV). Due to the significant impact of environmental factors, typical spring weather conditions in a coastal city in China were selected, including temperature, wind speed, and light intensity data, as shown in

Table 2. Typical spring weather data for a coastal city in China.

Moment	Temperature (°C)	Wind Speed (m/s)	Light Intensity (W/m2)
1:00	5.6	2.92	0
2:00	5.3	2.92	0
3:00	4.7	2.92	0
4:00	4	2.50	0
5:00	6	2.92	0
6:00	5.2	4.17	0
7:00	5.5	2.50	29
8:00	5.8	3.33	143
9:00	6.3	4.58	338
10:00	7.1	4.17	535
11:00	7.6	3.33	643
12:00	8.7	1.25	655
13:00	9.2	2.50	591
14:00	9.2	3.75	461
15:00	9.2	2.08	297
16:00	8.6	1.25	159
17:00	8.4	0.83	64
18:00	8.2	0.83	11
19:00	8	3.33	0
20:00	6.9	1.25	0
21:00	6	0.42	0
22:00	5.8	1.25	0
23:00	5.4	2.08	0

.

Given that the industrial park involved in this project needs to meet heating requirements, a certain range must be set, and the self-sufficiency rate cannot reach 100% under heating conditions. Power demand is supplied by fuel cells, batteries, and combined heat and power (CHP) units, while heating is provided by CHP units and gas-fired boilers. The price is inclusive of the tariff. The specific parameters of the heating units and power generation units are shown in

Table 3. Heating unit parameters.

Distributed Generation Unit	Qmin	Qmax	Ramp Rate (kW/h)	CC (yuan/kWh)
GB	10	200	70	0.56
CHP	10	300	110	0.32

and

Table 4. Power unit parameters.

Distributed Generation Unit	Pmin	Pmax	Ramp Rate (kW/h)	CC (yuan/kWh)
WT	0	150	-	-
PV	0	80	-	-
FC	100	450	150	0.4
CHP	20	550	300	0.28
SB	−150	150	-	-

.

Using the recent forecast for wind power generation, photovoltaic power generation, heat, and electricity load in a multi-energy system with combined heat and power supply in a certain industrial park as an example, a simulation was conducted. A day is divided into 24 dispatch time slots, and the electricity prices are shown in

Table 5. Industrial time-of-use electricity price table.

Phase	Corresponding Period	Electricity Purchase Price/(yuan (kWh))	Electricity Sales Price/(yuan (kWh))
peak	10:00–14:00 18:00–20:00	0.82	0.65
off-peak	23:00–6:00	0.49	0.27
shoulder	7:00–9:00 15:00–17:00, 21:00–22:00	0.60	0.38

.

4.1.2. Data Selection for Load Demand

The text selects the heat and electricity load demand conditions of a certain coastal industrial park on weekdays. The specific conditions are shown in Figure 7.

As shown in Figure 7, the industrial park’s electric heating load operates at low levels during the night. After 5:00 a.m., equipment enters a pre-startup state. After 7:00 a.m., workers gradually arrive on site, and full-scale production begins, reaching peak electricity demand. This continues until the midday break from 11:00 a.m. to 1:00 p.m., after which the load gradually decreases. Production peaks again in the afternoon and continues until evening, when production shifts to low-intensity operations and the heating load enters an energy-saving state.

The introduction of tank cars is critical to the hydrogen energy system. By simulating the energy supply characteristics of tank cars using a Monte Carlo simulation, the specific vehicle charging requirements can be determined, resulting in the daily load demand shown in Figure 8.

4.2. Calculation Example

Based on the various loads, as the aforementioned, this paper fully considers the tank car scenario to complete hourly scheduling optimization. This paper mainly focuses on DA-GWO-based ordered vehicle charging park multi-energy flow optimization scheduling that considers tank car loads, as well as DA-GWO-based ordered vehicle charging and discharging park multi-energy flow optimization scheduling that considers tanker car loads.

4.2.1. Dynamic Adaptive GWO Ordered Vehicle Charging Solution Considering Tank Car Load

In this case study, environmental factors (lighting, wind speed, and temperature) are randomly considered, along with the total power load of the tank cars. Additionally, charging must be scheduled to avoid peak electricity usage periods in industrial zones or utilize time slots with higher power generation capacity. The charging process is influenced by power and capacity, and Monte Carlo simulations are conducted based on vehicle characteristics. The study sets up 20 tank cars with a battery capacity of 100 kW, a charging/discharging power of 24 kW, with a charging efficiency of 0.9. The environmental factors considered in this case are shown in Figure 9.

As shown in Figure 9, the load of the tank car is staggered with the charging load of the industrial park, with charging concentrated after production activities have gradually concluded. Additionally, charging during the day is relatively uniform, causing minimal disruption to normal production activities. Using the above data, optimization scheduling is performed by adjusting four control variables: CHP power generation plan, FC power generation plan, SB power generation plan, and GB heating plan. The system is also configured to engage in power transactions with the external grid, selling excess power when production exceeds demand and purchasing power from the external grid when production falls short. Due to the constraint of providing an orderly energy supply to tank cars, tank car constraints are added to the constraint conditions to simulate real-world scenarios, along with corresponding penalty terms. Additionally, in the DA-GWO algorithm settings, to achieve better solution results, the wolf pack size is set to 80, and the iteration count is set to 800. The final output of each unit obtained through the DA-GWO is shown in Figure 10.

Based on the proposed DA-GWO method, the optimization scheduling can be quickly achieved, resulting in a total cost of 4689.3 yuan for the park over 24 h.

To demonstrate the performance of the proposed method, the GWO (grey wolf algorithm) method and PSO (Particle Swarm Optimization) are introduced for comparison. The comparison indicators include the price and the ratio of savings. In this paper, the ratio of savings is defined as follows:

$$Ratio={\displaystyle \frac{\left|pric{e}_{DA-GWO}-pric{e}_{compare}\right|}{pric{e}_{DA-GWO}}}$$

(27)

where Ratio denotes the ratio of savings of the proposed method compared with the comparison methods, $pric{e}_{DA-GWO}$ denotes the price cost of the proposed method, and $pric{e}_{compare}$ denotes the price cost of the comparison method.

The results of the comparison methods are provided in Figure 11 and

Table 6. The price and ratio of savings for the proposed method and the comparison methods.

Indicators	DA-GWO Method	GWO Method	PSO Method
Price (yuan)	4689.3	5002.9	7377.2
Ratio of savings	-	6.7%	57.3%
Computation time	21.4 s	19.7 s	21.5 s

.

From Figure 10 and Figure 11 and Table 6, the proposed method is among the best methods in the comparison because of the powerful optimization ability in dealing with diverse and complex units and the parameter adaptability under operational conditions.

To further compare the proposed method and comparison methods, the iteration value figure is shown in Figure 12.

Although the proposed method has achieved superior results, the inclusion of charging rate constraints has increased costs due to practical considerations regarding charging power limitations. As shown in Figure 9, the CHP unit primarily handles the heating plan, while the FC unit primarily handles the power generation plan. During peak periods, both the CHP and FC units operate at high power levels, and the power generation during this time far exceeds the system’s requirements, resulting in a significant amount of excess power being sold back to the grid. When there is a high demand for heat supply, the GB unit plays a role in diverting and regulating the heat load, while the SB unit also performs a moderate regulatory function. In most cases, due to high power generation, electricity is sold to generate profits. During power plant ramp-up, some energy is purchased from the external grid. The specific power and heat dispatch diagrams are shown in Figure 13.

As shown in Figure 13 and Figure 14, CHP and GB operate alternately to jointly bear the heat load, thereby ensuring the heating demand in spring, while FC mainly bears the power load and generates a large amount of electricity to sell to the grid, thereby improving economic efficiency. With the addition of tank car constraints, energy planning becomes more reasonable, adding a hydrogen-powered locomotive energy load, which is closer to the actual situation.

4.2.2. Consideration of Dynamic Adaptive GWO Ordered Vehicle Charging and Discharging for Tank Cars

In traditional multi-energy flow systems, tank cars are only used as energy loads. However, in practice, tank cars themselves can also serve as energy suppliers for the entire multi-energy flow system. Specifically, when electricity demand is high, tank cars can function as batteries, discharging energy to alleviate electricity pressure. To better describe the actual operating conditions, the original model is obtained from the simulation operation. Additionally, considering the coupling of CHP power generation and heating capabilities, which can cause significant fluctuations in CHP heat output during heating, a non-fixed CHP power–heat ratio model is adopted to modify the original model. To avoid the control instability and low efficiency caused by sudden changes, the autoregressive moving average (ARMA) method is introduced to smooth the original power, which is defined as:

$$y_t=c+{\displaystyle \sum _{i=1}^p{\mathsf{\Phi }}_i{y}_{t-i}+{\displaystyle \sum _{j=1}^q{\theta }_j{\epsilon }_{t-j}}}$$

(28)

where p and q denote the order, ${\mathsf{\Phi }}_i$ and ${\theta }_j$ denote the coefficient, and ${\epsilon }_{t-j}$ denotes the white noise.

Considering the complex operation of actual systems and the phenomenon of time delay in power, the fluctuation following a normal distribution with a standard deviation of 15% power is introduced in this paper. The schematic diagram is shown in Figure 13.

As shown in Figure 15, the load of the tank car is staggered with the charging load of the industrial park, and the industrial park experiences a brief but significant load peak. Therefore, the tank car is used for power dispatch during periods of high electrical load. Based on the above data, optimization scheduling is performed by adjusting four control variables: CHP power generation plan, FC power generation plan, SB power generation plan, and GB heating plan. Similarly, electricity transactions with the external grid are set up, with excess electricity sold and insufficient electricity purchased from the external grid. Since the mechanism of using tank cars for discharging during high-load periods in the industrial park has been introduced, it is necessary to consider tank cars as energy storage modules, taking into account charging and discharging tasks, to dynamically adjust the total load and enhance the regulation capability of the energy storage system. Due to the significant fluctuations in the electric and thermal load changes in the previous section, considering the limitations of the fixed electric-to-thermal ratio of the CHP units, the CHP units are modified to a separate electric–thermal ratio model, the load equations are adjusted, and additional constraints are added for the CHP units. The electric and thermal ratios are made freely adjustable, and the variable dimension of the DA-GWO algorithm is increased to 120 to store the optimization solution information for the separated CHP thermal units. The final output of each unit obtained through the DA-GWO algorithm is shown in Figure 16.

Similarly to the prior study, the GWO (grey wolf algorithm) method and PSO (Particle Swarm Optimization) are introduced for comparison. The optimization results of the comparison methods are provided in Figure 17 and

Table 7. The price and ratio of savings for the proposed method and the comparison methods with consideration of charging and discharging.

Indicators	DA-GWO Method	GWO Method	PSO Method
Price (yuan)	4421.4	4783.3	8639.3
Ratio of savings	-	8.2%	95.4%
Computation time	17.3 s	15.7 s	17.6 s

.

From Figure 16 and Figure 17 and Table 7, the proposed method is among the best methods in the comparison because of its optimization ability in dealing with diverse and complex units and the desirable adaptability to different complex operation conditions.

Based on the DA-GWO method proposed in this paper, the scheduling optimization was achieved, and the total scheduling cost for the park over 24 h was calculated to be 4421.4 yuan, representing a cost reduction compared to the results from the previous section. This was due to the use of CHP with electric-thermal separation, which allowed vehicles to discharge during high-load periods to alleviate grid pressure, reduce the need for high-cost electricity purchases, and prioritize power supply by discharging vehicles. As shown in Figure 14, the CHP system primarily handles the heating plan, while the FC system primarily handles the power generation plan. During peak periods, both the CHP and FC systems operate at high power levels. When thermal supply demand is high, the GB system performs load balancing for thermal loads, and the SB system provides appropriate regulation. During generator ramp-up and high electrical load periods, electricity is purchased from the external grid, and vehicle discharging is reduced to mitigate the impact of load peaks. The specific power and heat dispatch diagrams are shown in Figure 18 and Figure 19.

As shown in Figure 18 and Figure 19, unlike the previous section, which only considered energy consumption, the CHP and GB systems alternate operation due to the influence of power consumption, jointly bearing the thermal load, while the FC primarily bears the electrical load. Through the separation of electricity and heat in the CHP system, thermal scheduling becomes more uniform, and energy planning becomes more rational.

4.3. Sensitivity Analysis

To further compare the proposed method, the sensitivity analysis is applied. In this section, the 20% increase in peak price is introduced, which is shown in

Table 8. Industrial time-of-use electricity price table with sensitivity.

Phase	Corresponding Period	Electricity Purchase Price/(yuan (kWh))	Electricity Sales Price/(yuan (kWh))
peak	10:00–14:00 18:00–20:00	0.98	0.78
off-peak	23:00–6:00	0.49	0.27
shoulder	7:00–9:00 15:00–17:00, 21:00–22:00	0.60	0.38

.

Based on the price in Table 8, the proposed method and the comparison methods are applied, and the results are provided in Figure 20 and

Table 9. The price and ratio of savings for the proposed method and the comparison methods with sensitivity analysis.

Indicators	DA-GWO Method	GWO Method	PSO Method
Price (yuan)	4860.3	5389.1	7153.0
Ratio of savings	-	10.9%	47.2%

.

From Figure 20 and Table 9, the proposed method is among the best in the comparison methods due to its powerful optimization ability in dealing with diverse and complex units under operational conditions.

5. Conclusions

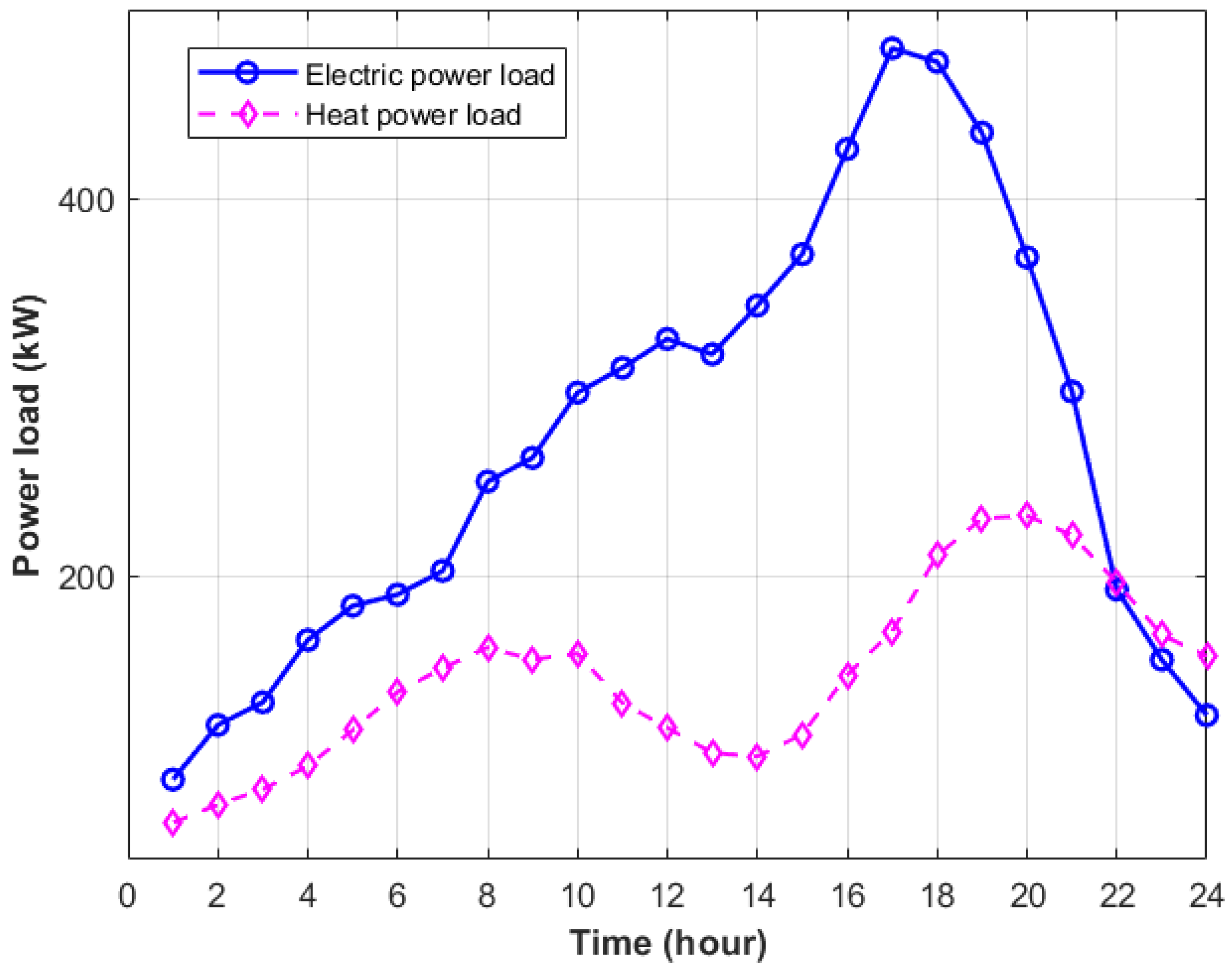
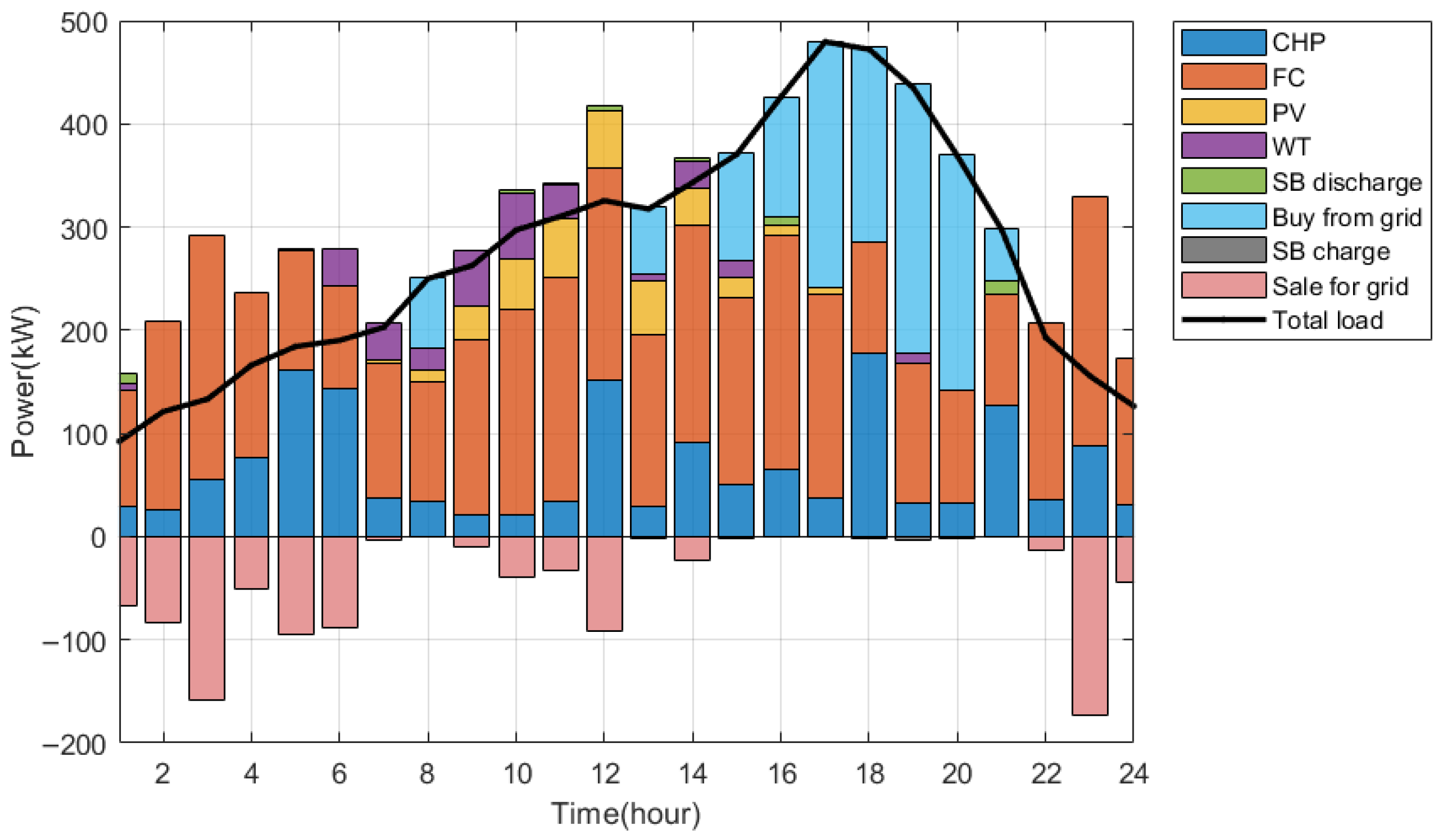
This paper investigates the problem of self-consistent multi-energy flow coordination and optimization scheduling for hydrogen-powered railway tank car transportation in hydrogen energy parks. It constructs a modelling framework based on multi-energy flow coordination optimization and an optimization scheduling method based on the DA-GWO approach. By establishing an energy flow model, the study develops basic models for non-dispatchable units such as wind power and photovoltaic systems, as well as dispatchable equipment including fuel cells, gas boilers, CHP units, and energy storage systems. Additionally, considering the characteristics of tank cars, a charging load model is proposed using the Monte Carlo simulation method, incorporating charging and discharging mechanisms, to establish an optimization scheduling model aimed at minimizing the total operating cost over a single day. Based on the constructed model, the DA-GWO method was designed to achieve optimal scheduling by comprehensively considering environmental characteristics, operating modes, and energy transfer constraints. To validate the effectiveness of the proposed method, this paper selected the load characteristics of electricity and heat in a coastal industrial park in China to optimize the model parameters. Based on the constructed model, this paper considered two scenarios: tank cars as load terminals and tank cars as both energy storage and load terminals. The results show that the proposed method can achieve multi-energy flow coordinated optimization scheduling in the industrial park.

In the future, we will further focus on the limitations of our study. 1. We will improve our methods to deal with the non-deterministic problem. 2. We will focus on longer periods of the park system for hydrogen-powered railways instead of single-day optimization. 3. We will improve the Monte Carlo method to adapt to more difficult operation conditions. 4. We will study energy unit modelling in detail, combining with health status, tank safety, and hydrogen constraints with the renewable energy availability (such as cloudy or less windy days) to further model the whole system. 5. We will also study the CO₂ emissions for the whole system.