Research on Transmission Line Vibration Based on the Dynamic Response of Strain in Straight Tower Cross Arm Structure Under Wind–Ice Loads

Abstract

Under ice and wind loads, transmission conductors undergo varying degrees of displacement, with larger displacements potentially causing direct damage to the transmission tower–line system and posing serious safety hazards. In a transmission tower–line system, the conductor’s vibration directly influences the crossarm strain response. Therefore, based on the connection characteristics between transmission conductors and tower crossarms, the crossarm strain response under ice and wind loads can be used to characterize the motion state of transmission conductors. However, the current research on the vibration of conductors based on crossarm strain dynamic responses still has gaps. In this study, we employ a finite element model of a transmission tower–line system and conduct numerical simulations of ice and wind loads under different working conditions using the controlled variable method, obtaining the variation patterns of the conductor’s displacement and crossarm strain. A functional relationship between the crossarm strain and conductor displacement response is established, and its applicability is further validated through numerical simulation analysis of the galloping of transmission conductors under icy conditions. This research provides technical support for monitoring the galloping state of transmission tower–line systems based on crossarm strain responses.

1. Introduction

Electric power has become an indispensable and vital component of industrial and agricultural production, as well as daily life, across nations around the world. Currently, the demand for electricity in different countries is exhibiting a rapid growth trend, which inevitably leads to increasingly severe power supply shortages, mismatches between the power resource distribution and regional electricity demand, and related issues. To address these challenges, countries around the world have established extensive systems of long-distance, high-capacity transmission lines. In a transmission tower–line system, transmission towers are characterized by their considerable height, light weight, and low overall stiffness; transmission conductors feature large spans and strong geometric nonlinearity. Therefore, transmission tower–line systems possess both tall and large-span structural characteristics, both of which lead to wind-sensitive structures that are prone to wind-induced damage [1]. In addition, when icing occurs on the transmission tower–line system, the icing of conductors not only increases the internal forces of the conductors but also amplifies the wind load effects on the system, potentially leading to galloping of iced conductors, which poses serious safety hazards to the transmission tower–line system. Although there are relatively mature de- and anti-icing technologies, such as the heating–melting method [2], the high number of engineering accidents indicates that timely control of the icing and vibration status of transmission lines is a prerequisite and key to effectively utilizing de-icing and ice-breaking technologies. Therefore, how to perform real-time assessment of the dynamic response of a transmission tower–line system under the combined action of icing and wind loads is crucial for ensuring the safe operation of transmission lines.

To analyze the dynamic response of a transmission tower–line system under the combined action of ice coating and wind loads, scholars have conducted systematic research. In terms of modeling transmission tower–line systems, Kempner et al. [3] simplified the transmission tower–line system into a space truss and frame structure, concentrated the wire mass at the crossarm suspension point, and selected the spring unit for connection, thus establishing a multi-point-equivalent simplified beam model. Li and Bai et al. [4] further simplified the tower–line system into a multiple-degrees-of-freedom model with multiple masses connected in series; through wind-induced dynamic response analysis and combined wind–rain excitation dynamic response analysis of their simplified model, they demonstrated that the model can accurately reflect the dynamic response of the line system. Wu et al. [5] proposed a simplified simulation method for transmission towers based on the three-dimensional isoeffect stiffness of tower–conductor connection points and compared the dynamic responses of transmission towers when modeled using the refined beam–column hybrid method and the fixed-constraint isoeffect modeling method, showing that the isoeffect stiffness method can accurately reflect the dynamic characteristics of transmission tower–line systems under general wind-induced conditions and conductor galloping.

Regarding the simulation of combined ice and wind loads on transmission tower–line systems, Jones and Peabody [6] proposed a mathematical model for uniform icing on angle steel towers, deriving isoeffect calculation formulas for the stiffness and density of tower–conductor systems and conducting analysis and verification on angle steels with consistent uniform icing thickness across different cross-sectional shapes. Shen et al. [7] conducted analyses using the additional ice element method and the density modification method based on the uniform icing model, finding that, under reasonable values of icing parameters, both the density modification and additional ice element method can provide equivalent results to the effects of icing. Merci et al. [8] conducted extensive wind tunnel experiments and theoretical research on the dynamic characteristics and wind-induced vibration responses of transmission tower–line systems, obtaining insights into their dynamic properties and wind-induced vibration characteristics under fluctuating wind loads. Chen [9] utilized the time-varying AR method to simulate fluctuating wind loads following the Davenport spectrum as a stationary Gaussian random process, concluding that, for transmission tower–line systems with relatively low tower heights and small conductor spans, a simplified single-tower model is suitable for analyzing wind-induced dynamic responses.

In the study of the dynamic response characteristics of transmission tower–line systems, Bartoli et al. [10] took the geometric nonlinearity of the overhead transmission line structure into account, established a numerical model of the conductor using the finite element method, performed time domain analysis through the direct integration method, and obtained the main dynamic characteristics of the conductor under wind load. Yu [11] established a finite element analysis model of a transmission tower–line system considering the influence of conductors and ground wires, with two towers and three lines. The along-wind fluctuating wind-induced vibration responses were analyzed for both a single tower and the two-tower three-conductor system. The study showed that when the wind attack angle was 90 degrees, the peak displacement at the top of the tower–line system increased by 37.3% compared with that of a single tower, and the maximum displacement of the tower–line system occurred at the mid-span conductors. Yasui et al. [12] developed a coupled finite element–structural analysis model of a transmission tower–line system and performed time history analysis of wind-induced vibration responses under specific wind fields. Their results indicated that the connection method between the transmission tower and conductors does not have a significant impact on the response. Additionally, the peak factor obtained from a time domain analysis was greater than that obtained from their frequency domain analysis. Battista et al. [13] established a finite element-based numerical analysis model for a transmission tower–line system and analyzed its dynamic characteristics and stability in both the time and frequency domains under simulated wind fields. They proposed a simplified two-degrees-of-freedom analysis model for evaluating the fundamental frequency in the early design stage.

In summary, scholars from various countries have conducted systematic research on the dynamic response of transmission tower–line systems under the combined action of ice coating and wind loads and identified the characteristics of these responses. However, gaps remain in the existing research: (1) Current studies mainly focus on displacement response analysis of transmission towers and conductor nodes, while monitoring the displacement response data of transmission towers and conductors under combined ice–wind loads is challenging, making it difficult to efficiently determine the dynamic response of the conductors. (2) Under the action of combined ice–wind loads, the vibration of the conductors will stimulate a change in the strain response of the crossbar, with a strong correlation existing between them. However, the current research does not involve this functional relationship. (3) Numerical simulations of wind-induced responses in existing tower–conductor systems do not yet infer the strength of the conductor vibrations based on the crossarm strain, which would aid in determining whether the transmission line is operating in a safe condition. (4) The combined load case design for icing and wind loads does not adequately reflect the characteristics of their impacts. This paper focuses on a straight tower–line system and conducts a time domain analysis of its dynamic response under ice coating and wind loads based on the strain of the crossarm. The aim is to explore the general rule of the strain response of the transmission tower’s crossarm and the displacement response of the midpoint of the transmission conductor under the combined effects of ice thickness, wind speed, and span. Based on our physical and mechanical model of the transmission tower–line system and numerical simulation results, a functional relationship between the crossarm’s strain response and conductor displacement is constructed. Combined with the numerical simulation results for ice-coating-induced conductor galloping of the transmission lines, the applicability of this functional relationship under conductor galloping conditions is discussed. According to the obtained functional relationship, the time history of the conductor displacement can be inversely inferred from the crossarm strain’s time history, thereby solving the problem of real-time monitoring of transmission line displacement and providing clear ideas and key technical support for research on and development of new monitoring devices for wind-induced disasters and ice-coating-induced galloping disasters involving transmission lines.

2. Materials and Methods

2.1. Modeling of Transmission Tower–Line System

This study, based on the load characteristics of transmission tower structures, uses ABAQUS software (2024 GA/2024.2 version) to establish a finite element analysis model for a tangent tower–line system with the type number 2G-SZC2. Due to the relatively large cross-sections of the main and diagonal members of the transmission tower, the members in this area are subjected to not only axial forces but also bending moments and shear forces. Therefore, B32 elements are used to model the main and diagonal members. Since the auxiliary members of the transmission tower have smaller cross-sections and are subjected to minimal bending and shear actions, B31 elements are used to model the auxiliary members. The specific parameters of the transmission tower are listed in

Table 1. Transmission tower model parameters.

Parameter	Numerical Value	Parameter	Numerical Value
Tower height/m	46.5	Poisson’s ratio	0.3
Nominial/m	30	EM/MPa	206,000
Leg spacing/m	7.864	YS of Q235/MPa	235
Density/$\mathrm{kg}·{\mathrm{m}}^{-3}$	7850	YS of Q355/MPa	355

. The main and diagonal members, serving as the primary load-bearing components, are made of Q355 steel, while the secondary members, which bear only a minor portion of the external loads, are constructed from Q235 steel. The constitutive model of the angle steel of the transmission tower is set as an ideal elastoplastic model, and the four nodes at the bottom of the transmission tower legs are fixed constraints.

In the finite element simulation, the T3D2 truss element was selected to model the conductors and ground wire, with their material properties being set as incompressible. The conductor type used in this study is JL/G1A-400/50 (Dazheng Wire Co., Ltd., Cangzhou, China), and the ground wire type is JLB20A-150 [14], with a horizontal span of 380 m. The length of the conductor suspension insulator string is 2.2 m, and that of the ground wire suspension insulator string is 0.4 m. Various parameters of the conductors and ground wire are shown in

Table 2. Transmission conductors and ground wire parameters.

Conductors		Ground Wire
EM/MPa	65,000	EM/MPa	69,000
Density/$\mathrm{kg}·{\mathrm{m}}^{-3}$	2388	Density/$\mathrm{kg}·{\mathrm{m}}^{-3}$	2427.5
Diameter/mm	26.82	Diameter/mm	26.6
CSA/mm2	425.24	CSA/mm2	400
AS/MPa	92.8	AS/MPa	117.5
Sag/m	16.5	Sag/m	16.5

.

In practical engineering applications, overhead conductors and ground wires can be treated as ideal flexible materials, where the horizontal tension imposed on them can only act along the tangential direction of their shape. This study employs the direct iteration method to model the conductors and ground wire [15], using the calculated horizontal tension at the conductor’s end as the equilibrium condition. The conductor model is simplified, with one end simply being supported and the other end releasing the horizontal degree of freedom while applying horizontal tension. Under the combined effects of self-weight and horizontal tension, the length and deformation parameters of the conductor model are continuously updated until static equilibrium is achieved, and the target mid-span sag is obtained. Subsequently, the free end is connected with a hinge to the adjacent tower’s insulator string end [16]. This study further establishes a finite element analysis model of the three-tower two-line transmission conductor system, as shown in Figure 1, where the X-direction is perpendicular to the line direction, the Y-direction is along the line orientation, and the Z-direction is the height direction of the transmission tower.

Regarding the mesh division of the finite element model, both simulation accuracy and computational efficiency need to be considered. In this study, all members of the straight tower crossarm, main materials, and diagonal members of the transmission tower are divided into 3 elements each, while auxiliary members of the transmission tower are divided into 1 element each; the total number of elements in the transmission tower model is 1543. The transmission conductors and ground wires are divided into one element every 10 m, and the transmission conductor and ground wire model consists of a total of 38 elements.

2.2. Simulation of Ice-Coating and Wind Load Effects

2.2.1. Isoeffect Simulation of Ice Load

(1)

Considerations for Ice Coating Simulation

During a cold winter, when certain meteorological conditions are met, conductors will ice, and the ice will continue to grow. If the icing is uniform across the entire span, when the overall icing thickness of the line exceeds the designed ice resistance capacity, the vertical and horizontal mechanical loads on the conductors and towers will increase significantly, leading to a significant increase in sag, insufficient ground clearance, and even regional and continuous tower collapses and line break accidents. If the conductor icing is uneven, unbalanced tension will be generated, causing the tower to have to withstand huge torques and bending moments, resulting in electrical faults such as inter-phase short-circuiting and insulator flashovers. In extreme cases, large-scale uniform span icing may lead to catastrophic grid collapse, which has more serious consequences [17]. Therefore, effective and targeted simulation analysis of icing on transmission towers and conductors is required. Through the results of such simulation analysis, the relationship between icing conditions and the dynamic response of the tower–conductor system can be explored.

(2)

Icing simulation based on finite element model

In our finite element analysis of the transmission tower–line system, we consider the conductors and ground wires as elastic bodies made of a single homogeneous material. The simulation of ice load is achieved by altering the density of the conductors and ground wires, while making the following two assumptions [18]:

①

The entire span of the conductors and ground wires is covered with ice, and the ice thickness is uniformly distributed along the conductor;

②

Only the influence of ice on the conductor’s weight is considered, while the effect of ice on its stiffness is neglected.

Based on the equivalent density method, the equivalent density calculation for iced conductors and transmission tower angle steels can be performed according to the following Formulas (1) and (2):

$${\rho }_{\mathit{DX}}={\displaystyle \frac{m_{\mathit{DX}}+\pi \left(dt+t^2\right){\rho }_B}{0.25d^2}}$$

(1)

$${\rho }_{JG}={\displaystyle \frac{m_{\mathit{JG}}+{\rho }_B\left(7t^2+4\mathit{at}\right)}{2\mathit{ab}-b^2}}$$

(2)

Here, ${\rho }_{DX}$ represents the isoeffect density of the conductors; ${\rho }_{JG}$ denotes the equivalent density of the angle steel; ${\rho }_B$ is the density of the ice; d is the diameter of the conductors in mm; t is the thickness of the ice coating in mm; a is the leg length of the equal-leg angle steel; b is the wall thickness of the angle steel in mm; and $m_{DX}$ and $m_{JG}$ are the masses per unit length of the conductors and angle steel, respectively, in kg.

2.2.2. Simulation of Pulsating Wind Loads

(1)

Type and Selection of Wind Load Simulation

A transmission tower–line system possesses two structural characteristics, high towers and large spans, both of which make them wind-sensitive structures. Therefore, research on the wind-induced vibration response of a transmission tower–line system is of great significance for ensuring the safe operation of lines. Under conditions of an equivalent mean wind speed, sustained and stable wind loads and unstable pulsating wind loads are the most common types. Their mechanisms of influence and degrees of damage to the transmission tower–line system are entirely different. Generally speaking, the dynamic effects caused by unstable pulsating wind loads have a much greater impact than those from sustained and stable wind loads. This is because unstable wind loads change randomly and rapidly, exhibiting significant dynamic effects that induce structural vibrations, generating dynamic accelerations and additional dynamic stresses; when the pulsation frequency of the wind approaches the natural frequency of the structure, resonance is triggered, drastically amplifying the response. Therefore, in the study of wind-induced vibration responses of transmission towers and lines, attention should be focused on the type of unstable wind load, namely, pulsating wind load.

(2)

Wind load simulation based on finite element model

This study obtains the wind speed time history through the autoregressive model of the linear filtering method. By combining the projected area of the windward surface of the transmission tower–line system and the coefficients under different working conditions, the time history data of the wind load are derived. The wind load is applied to the transmission tower–line system in the form of nodal concentrated forces [19]. The wind load acting on the transmission tower–line system is the superposition of the mean and fluctuating wind [20,21], where the mean wind describes the variation in wind speed over a long period, characterized by a long period, stable load magnitude, and constant direction, which can be treated as a static load in terms of isoeffect. The fluctuating wind, on the other hand, features a short period, random wind directions, and drastic load variations, and thus, it is considered a dynamic load. This study involves a dynamic response time history analysis of a transmission tower–line system under fluctuating wind loads based on the Davenport wind spectrum.

This study assumes that the wind load direction is perpendicular to the line direction (X-direction). The horizontal component of the wind speed, perpendicular to the conductors along the line direction, can be expressed as follows:

$$V_t=\overline{v}\left(z\right)+v\left(z,t\right)$$

(3)

In the above equation, $\overline{v}\left(z\right)$ represents the average wind speed in the X-direction at height z; $v\left(\mathrm{z},\mathrm{t}\right)$ is the fluctuating wind speed in the X-direction; and t is the time variable. Substituting the above results into Bernoulli’s equation yields the wind pressure value at height z at time t:

$$\begin{array}{cc}\hfill W\left(z,t\right)& =\hspace{0.17em}0.5\rho V^2\left(z,t\right)\hfill \\ & =0.5\rho {\overline{v}}^2\left(z,t\right)+0.5\rho \left[2\overline{v}\left(z\right)v\left(z,t\right)+v^2\left(z,t\right)\right]\hfill \\ & =\overline{W}\left(z\right)+W_d\left(z,t\right)\hfill \end{array}$$

(4)

Here, $\overline{W}\left(z\right)$ and $W_d\left(z,t\right)$ represent the mean wind pressure and fluctuating wind pressure at height z, respectively.

Since the higher-order terms of $W_d\left(z,t\right)$ are negligible in practical engineering calculations, a simplified fluctuating wind pressure calculation formula can be obtained:

$$W_d\left(z,t\right)=\rho \overline{v}\left(z\right)·v\left(z,t\right)$$

(5)

Based on the wind pressure’s area of impact and the relevant load correction coefficients [22], the final wind load is defined as shown in Equation (6):

$$W_s=W\left(z,t\right)·{\mu }_Z{·\mu }_S·{\beta }_Z·B_2{·A}_s$$

(6)

In the above formula, $W_s$ represents the standard value of the wind load on the transmission tower at time t and height Z in kN; ${\mu }_z$ is the wind pressure height variation coefficient at the reference height of 10 m; ${\mu }_{S·}$ is the shape coefficient of the construction component; ${\beta }_Z$ is the wind vibration coefficient of the tower at height z; $B_2$ is the icing increase coefficient of tower components; and $A_s$ is the projected windward area of the transmission tower in m².

The wind load acting on the conductors and ground wire is shown in Equation (7):

$$W_x=W\left(z,t\right){·\beta }_c{·\alpha }_L{·\mu }_Z{·\mu }_{\mathrm{SC}}·L_p{·D·B}_2·{\mathit{sin}}^2\theta$$

(7)

Here, ${\beta }_C$ is the wind vibration coefficient of the conductors or ground wire; ${\alpha }_L$ is the span reduction coefficient of the conductors; ${\mu }_{\mathrm{SC}}$ is the shape coefficient of the conductors or ground wire; $L_p$ is the horizontal span of the conductors or ground wire; D is the outer diameter of the conductors or the calculated outer diameter under ice coating (for bundled conductors, it is the sum of the outer diameters of all sub-conductors) in meters; and θ is the angle between the wind load and the direction of the conductors or ground wire along the route. The meanings of the remaining coefficients are the same as in Equation (7) [23].

2.3. Working Condition Design

2.3.1. Wind-Induced Response Condition Design for Iced Tower–Line Systems

(1)

Basis for Working Condition Design

The accumulation of ice on tower–line systems in natural environments is subject to relatively strict meteorological conditions. A large number of research results indicate that, when the temperature ranges from −5 °C to 0 °C and the relative humidity of the air is typically higher than 85%, the content of supercooled water droplets in the air is high, which is the most common meteorological condition for ice formation (e.g., rime ice and mixed rime ice) [24]. Based on this meteorological condition, temperature variations are not the main factor influencing the initial strain of the tower’s crossarm members. Rather, the ice thickness and wind load magnitude are the most critical factors determining the strain response of the tower crossarm. Therefore, in this study, an analysis of the influence of temperature and humidity changes on the initial strain of the crossarm is not conducted. Drawing fully on previous research results on ice state assessment under different meteorological conditions [25], this study focuses on investigating the characteristics and patterns of the strain response of the tower crossarm and the displacement response of the conductors under icing and wind speeds within a certain range, as well as establishing the relationship between the two in the form of a function.

(2)

Method for Working Condition Design

To investigate the responses of crossarm strain and conductor displacement in transmission tower–line systems under the combined action of ice and wind, this study takes the ice load, wind load, and conductor span as control variables and designs a range of working conditions for wind-induced vibration response analysis based on different ice thicknesses, basic wind speeds, and spans, as shown in Figure 2.

As shown in Figure 2, a total of 14 operating conditions are established in the numerical simulation for this study. Operating Condition 4 is taken as the standard operating condition, while the other operating conditions are divided into three categories: (1) Operating Conditions 1, 2, 3, 5, and 6 are classified as the first category, which changes the ice thickness compared with the standard operating condition. (2) Operating Conditions 7, 8, 9, and 10 are classified as the second category, which changes the wind speed compared with the standard operating condition. (3) Operating Conditions 11, 12, 13, and 14 are set as the third category, which changes the horizontal span of the conductor compared with the standard operating condition.

2.3.2. Design of Transmission Conductors and Galloping Conditions Under Icing Conditions

Under the combined action of ice coating and wind loads, ice-coated conductors (non-circular cross-section) are subjected to aerodynamic loads, including conductor drag (F_D), conductor lift (F_L), and conductor torque (F_M), which excite self-excited vibrations in the conductor, eventually evolving into ice-induced galloping. To verify the applicability of the functional relationship between the mid-span displacement of the conductor and the crossarm of the transmission tower during ice-induced conductor galloping, this section conducts an analysis of ice-induced galloping of transmission lines. Since the conductors in the transmission tower–line system used in this study are single-bundle conductors, during the ice-induced galloping process, the torque, aerodynamic lift, and aerodynamic drag are relatively small compared with their effects and can basically be neglected [26]. Therefore, in this study’s verification of ice-induced galloping of transmission lines, the conductors are subjected to the actions of aerodynamic lift (F_L) and aerodynamic drag (F_D). The calculation formulas are as follows:

$$\begin{gathered} F_L=\rho U^{2}LD{C}_L/2 \\ {F}_D=\rho U^{2}LD{C}_D/2 \end{gathered}$$

(8)

Here, ρ denotes the air density (1.29 kg/m³), U represents the horizontal wind speed (m/s), and L is the span of the conductor unit, taken as 10 m. D is the equivalent diameter of the iced conductor, with the unit being m. For the JL/G1A-400/50 conductor under study, the bare conductor diameter is 26.82 × 10⁻³·m, with corresponding adjustments based on varying ice thickness. Lift coefficients (C_L) and drag coefficients (C_D), which are related to the wind attack angle, are specified in reference [27].

This subsection describes the design of four working conditions for ice-induced galloping of transmission conductors, as shown in

Table 3. Design of Galloping Verification Conditions.

WCC	Icing (mm)	BWS (m/s)	CS (m)
A	10	15	380
B	15	15	380
C	15	10	380
D	15	15	460

.

2.4. Analysis of Numerical Simulation Results

2.4.1. Selection of Analysis Components for Transmission Tower–Line Systems

This study investigates the strain response of the crossarm section in a transmission tower–line system under different wind loads at a wind direction angle of 90 degrees, selecting four monitoring points on both the windward and leeward sides of the crossarm. Monitoring points Y-1, B-1, Y-4, and B-4 are located at the root of the crossarm, while monitoring points Y-2, B-2, Y-3, and B-3 are positioned at the loading end of the crossarm, as shown in Figure 3.

Taking the analysis results of Operating Condition 4 in Figure 2 as an example, the time history data for the strain at four analysis locations on both the windward and leeward sides were extracted, as shown in Figure 4. Under the combined action of ice and wind, the compressive stress effect at the loading end of the windward crossarm and the tensile stress effect at the loading end of the leeward crossarm were significant. Moreover, the peak strain on the windward side (Y-3) was slightly greater than that on the leeward side (B-3). Therefore, this study selects monitoring point Y-3 as the object for the strain response analysis of the transmission tower crossarm under the combined action of ice and wind loads.

2.4.2. Simulation Result Analysis

To study the wind-induced response patterns of ice-covered transmission tower–line systems based on the crossarm strain, it is necessary to analyze numerical simulation data under different working conditions. This study sets the peak value, amplitude, and mean as characteristic values based on the time history data for the midpoint displacement of the conductors and crossarm strain, as shown in Formulas (9)–(11). The peak and amplitude can preliminarily determine the intensity of the dynamic response of the tower–line system. The mean can basically determine the equilibrium position of the conductor displacement and the corresponding magnitude of the crossarm strain. Due to different ice thicknesses and spans in the first and third types of working conditions, which result in differences in the initial displacement of conductors and strain of crossarms, this study includes a comparison of the initial strain for such working conditions:

$$\mathrm{X}=\mathit{max}\left\{\left|x_1-x_0\right|,\right.\left|x_2-x_0\right|,\dots \left.\left|x_n-x_0\right|\right\}$$

(9)

$$\mathsf{∆}\mathrm{X}=\left|x_{\mathit{max}} - x_{\mathit{min}}\right|$$

(10)

$$\overline{\mathrm{X}}={\displaystyle \frac{{\sum }_{i=1}^n{x}_i}{n}}$$

(11)

In the above equations, X, $∆X$, and $\overline{X}$ represent the peak value, amplitude, and mean value of the analysis object (midpoint displacement of the conductors or strain on the crossarm), respectively; x₀, x_max, and x_min denote the initial, maximum, and minimum value of the analysis object in the time domain; and n is the number of sampling points for the analysis object in the time domain.

3. Results

3.1. Modal Analysis of Transmission Tower–Line System

(1)

Dynamic characteristics of single transmission tower

The natural frequency was obtained through modal analysis, and the Rayleigh damping coefficient of the model was calculated (the damping ratio was taken as 0.02). The Lanczos method was used to analyze the structure and extract the first five modes of the structure, as shown in Figure 5.

As shown in Figure 5, the natural frequency of a single transmission tower is significantly higher than the main frequency of 0.13 Hz that was observed in wind turbulence simulations. Therefore, under wind loads, transmission towers typically do not experience resonance phenomena. In actual power transmission systems, transmission towers are integrated with conductors and insulator strings to form a transmission tower–line system. Compared with single-tower structures, these integrated systems exhibit substantially altered modal characteristics [28], necessitating specialized modal analysis.

(2)

Modal analysis of transmission tower–line systems under different ice coating thicknesses

According to the first type of working condition settings, the span of conductors in the transmission tower–line system model is set to 380 m, with the ice thickness being sequentially set at 0 mm, 5 mm, 10 mm, 15 mm, 20 mm, and 25 mm. We used this to investigate the influence of ice thickness on the dynamic characteristics of a transmission tower–line system through modal analysis.

As shown in

Table 4. Natural vibration frequencies of partial modes in tower–line systems with different ice coating thicknesses/Hz.

Mode Order	TIC/mm
	0	5	10	15	20	25
1	0.1350	0.1339	0.1331	0.1308	0.1293	0.1276
2	0.1351	0.1340	0.1332	0.1311	0.1295	0.1278
3	0.1352	0.1343	0.1336	0.1312	0.1297	0.1280
4	0.1357	0.1348	0.1340	0.1315	0.1302	0.1300
10	0.1376	0.1363	0.1358	0.1338	0.1319	0.1314
20	0.2696	0.2674	0.2664	0.2615	0.2585	0.2551
50	0.4038	0.4010	0.3991	0.3917	0.3872	0.3821
100	0.6702	0.6647	0.6621	0.6502	0.6429	0.6344
200	1.2010	1.1936	1.1822	1.1728	1.1600	1.1454
300	3.8627	3.8503	3.8376	3.8125	3.8044	3.7865

, due to the relatively low stiffness of the conductors, the first 200 modes of the tower–line system are predominantly characterized by conductor vibrations. The thicker the ice on the conductors is, the lower the natural vibration frequencies of both the transmission tower and conductors are. This is because the ice load not only increases the conductors’ mass but also enlarges their sag, thereby enhancing the catenary effect of the conductors and reducing the natural vibration frequency of the tower–line system. An increase in ice thickness not only leads to a rise in external loads on the transmission tower–line system but also causes an overlap between the fundamental frequency of conductors and the dominant frequency of the fluctuating wind. This results in conductor resonance under fluctuating wind loads, adversely affecting the safe operation of the transmission tower–line system.

(3)

Modal analysis of transmission tower–line system under different conductor spans

According to the settings of the third working condition, the ice thickness on the transmission conductors is set to 15 mm, while the conductor span is sequentially set to 300 m, 340 m, 380 m, 420 m, and 460 m. The dynamic characteristics of the transmission tower–line system under different conductor spans are studied through modal analysis, and the analysis results are shown in

Table 5. Natural vibration frequencies of selected modes for tower–line system with different conductors spans/Hz.

Mode Order	CS/m
	300	340	380	420	460
1	0.1348	0.1327	0.1308	0.1284	0.1262
2	0.1350	0.1328	0.1311	0.1286	0.1264
3	0.1353	0.1332	0.1312	0.1291	0.1268
4	0.1344	0.1336	0.1315	0.1297	0.1272
10	0.1361	0.1354	0.1338	0.1310	0.1292
20	0.2658	0.2654	0.2615	0.2575	0.2511
50	0.3978	0.3962	0.3917	0.3758	0.3621
100	0.6602	0.6567	0.6502	0.6412	0.6225
200	1.1902	1.1801	1.1782	1.1614	1.1427
300	3.7458	3.6215	3.5324	3.4108	3.4076

.

As shown in Table 5, when the ice thickness and sag of the tower–line system remain unchanged, as the span of the conductors increases, the load of the conductors on the transmission tower increases, and the natural vibration frequency of the tower–line system decreases. When the modal of the tower–line system reaches the 200th order, the vibration begins to be dominated by the transmission tower. When the conductor span increases from 300 m to 460 m, the first-order natural vibration frequency of the conductors decreases by 6.38%, while the vibration frequency of the transmission tower decreases by 9.03%.

3.2. Time History Analysis of Dynamic Response in Tower–Line System

3.2.1. Dynamic Response Analysis of Tower–Line System Under Different Ice Thicknesses

(1)

Analysis of the influence of ice thickness on the displacement of transmission conductors

The basic wind speed for the transmission tower–line system used in this section is 15 m/s. This study investigates the vibration characteristics of the transmission conductors under different ice thicknesses. Under the first type of working conditions, the time history and characteristic values of the midpoint displacement of the transmission conductors vary with the ice thickness, as shown in Figure 6.

As shown in Figure 6, under the wind load of a basic wind speed of 15 m/s, the maximum differences in the displacement characteristics at the midpoint of the conductor due to different ice thicknesses from 0 mm to 25 mm are as follows: peak value: 2.76 m; amplitude: 2.87 m; mean value: 1.745 m; and initial value: 1.4561 m. Compared with the case without ice, the changes in peak value, amplitude, and mean value are 36.87%, 37.84%, and 34.7%, respectively. Except for the initial displacement, which increases with the increase in ice thickness, all characteristic values first increase and then decrease with increasingly thick ice coatings on the tower and conductor.

The wind-induced displacement of iced conductors is closely related to the magnitude of the wind load and their own gravity. The ratio of the external wind load to the self-weight of the conductor can be calculated using Formulas (1) and (7), as shown in Formula (12):

$${\displaystyle \frac{W}{G}}={\displaystyle \frac{4W\left(z,t\right){\beta }_c{\alpha }_L{\mu }_z{\mu }_{SC}D{B}_2}{{\rho }_{DX}{d}^{2}g}}$$

(12)

where d is the diameter of the conductor itself, and D is the outer diameter of the conductor after icing, defined as d plus twice the ice thickness t, i.e., D = d + 2t. When the ice thickness on the conductor increases from 0 mm to 25 mm, with the basic wind speed remaining unchanged, the ratio of the conductor’s wind load to its self-weight is, in order, as follows: 0.513, 0.574, 0.628, 0.593, 0.558, and 0.512. Therefore, when the ice thickness is 15 mm, the peak, amplitude, and mean value of the displacement at the midpoint of the conductor reach their maximum values.

The reasons for this phenomenon are as follows: (1) The ice on the conductor increases the unit mass of the conductor, which not only reduces the inherent frequency of the tower–conductor system, thus making it closer to the dominant frequency interval of the pulsating wind and causing resonance, but also increases the windward area of the conductor, leading to an increase in the wind load per unit length of the conductor and thereby resulting in increased conductor displacement. (2) When the thickness of the ice on the conductor exceeds 15 mm, the conductor gravity increases significantly, and the inertial suppression caused by the mass effect plays a major role, thereby reducing the conductor displacement response. (3) Due to the significant increase in conductor gravity caused by ice, the distribution of the conductor tension and line length change, resulting in the continuous growth of the initial displacement at the conductor midpoint.

Based on the Pearson correlation coefficient method [29], under the 0.05 significance level setting, the correlation coefficient between the conductor displacement feature value and ice thickness is calculated, as shown in

Table 6. Correlation between conductors displacement and ice thickness.

DCV	PV (X)	$\mathbf{AV} (∆\mathbf{X}$)	$\mathbf{MV} (\overline{\mathit{X}}$)	IV (X0)
CC	0.3842	0.4312	0.3724	0.8823
(P-V)	0.8036	0.7582	0.4705	0.00012

.

(2)

Analysis of the influence of ice thickness on crossarm strain

In the vibration analysis of conductors under different ice thicknesses, the strain on the crossarm of the transmission tower also exhibits different characteristics. Under the fluctuating wind load with a basic wind speed of 15 m/s, the time history curves of the crossarm strain response and the variation trend of the characteristic crossarm strain values with increasing ice thickness are shown in Figure 7.

As shown in Figure 7, under a pulsating wind load with a basic wind speed of 15 m/s, the crossarm strain is significantly affected by different ice thicknesses. Within an ice thickness range of 0 mm to 25 mm, both the peak and amplitude of the crossarm strain increase with the thickness of the ice on the tower and conductors, rising by 164.28% and 170.72%, respectively. Figure 6 indicates that this increase in ice thickness leads to a rise in the gravitational load of the transmission conductors, resulting in higher initial strain and mean values at the crossarm connection points, which increase by 255.6% and 215.43%, respectively. Under such working conditions, there are strong correlations between the initial strain value, mean strain value, and strain amplitude at the crossarm end with the ice thickness. The correlation coefficients between the ice thickness and characteristic strain values of the crossarm are presented in

Table 7. Correlation coefficients between ice thickness and strain characteristic values.

CSCV	PV (X)	$\mathbf{AV} (∆\mathbf{X}$)	$\mathbf{MV} (\overline{\mathit{X}}$)	IV (X0)
CC	−0.9044	0.8897	−0.9476	−0.9857
(P-V)	0.0014	0.0021	0.0003	0.0035

.

3.2.2. Dynamic Response Analysis of Tower–Line System Under Different Wind Speeds

(1)

Analysis of the influence of the basic wind speed on conductor displacement

The time history curves of displacements at the midpoint of the transmission conductors under different wind speeds, as well as the variation trend of characteristic displacement values with increasing basic wind speeds, are shown in Figure 8.

As shown in Figure 8, the characteristic values of conductor displacement increase sharply with gradual rises in the fundamental wind speed. When the fundamental wind speed increases from 5 m/s to 25 m/s, the corresponding increases are as follows: peak value: 1313.86%; amplitude: 1381.86%; and mean value: 1540.47%. The midpoint displacement of conductors shows a strong positive correlation with the fundamental wind speed values, as evidenced by the correlation coefficients in

Table 8. Correlation coefficients between basic wind speed and characteristic values of conductors displacement.

DCV	PV (X)	$\mathbf{AV} (∆\mathbf{X}$)	$\mathbf{MV} (\overline{\mathit{X}}$)
CC	0.9875	0.9753	0.9975
(P-V)	0.0024	0.0015	0.0017

.

(2)

Analysis of the influence of the basic wind speed on crossarm strain

Under fluctuating wind loads with different basic wind speeds, the conductor experiences varying degrees of vibration, leading to intense strain responses within the crossarm members. The time history curves of this strain and the variation in characteristic strain values of the crossarm are shown in Figure 9.

As shown in Figure 9 and

Table 9. Correlation coefficients between basic wind speed and strain characteristic values.

CSCV	PV (X)	$\mathbf{AV} (\mathit{\Delta }\mathit{X}$)	$\mathbf{MV} (\overline{\mathit{X}}$)
CC	−0.9823	−0.9814	−0.9442
(P-V)	0.0015	0.0022	0.0036

, under the same ice thickness, the characteristic values of the conductors increase simultaneously with the increase in basic wind speed. When the basic wind speed increases from 5 m/s to 25 m/s, the growth rates are as follows: peak value: 1624.85%; amplitude: 1910.63%; and mean value: 1362.46%. There is a strong correlation between each characteristic value and the basic wind speed.

3.2.3. Dynamic Response Analysis of Tower–Line System Under Different Span Levels

(1)

The influence of different span levels on conductor displacement

This section analyzes the dynamic response of the transmission tower–line system under the condition of 15 mm ice thickness and 15 m/s basic wind speed at different horizontal spans. The results are shown in Figure 10.

From Figure 10, it can be seen that with the increase in the conductor span, except for the initial displacement value, all characteristic displacement values first decrease and then increase. When the horizontal span of the conductors increases from 300 m to 380 m, the characteristic displacement values at the midpoint of the conductors decrease as follows: the peak decreases by 40.73%, the amplitude by 43.58%, and the mean by 14.58%. When the horizontal span of the conductors increases from 380 m to 460 m, the characteristic displacement values at the midpoint of the conductors increase as follows: the peak increases by 20.81%, the amplitude by 18.91%, and the mean by 20.36%.

This phenomenon occurs because, under the third type of working condition, the conductors exhibit the same sag. The smaller the conductor span is, the more relaxed its stress becomes, resulting in a greater displacement response under the same wind load. On the other hand, when the conductor span becomes excessively large, the conductor’s tension increases, leading to greater elongation. Additionally, an increase in span has a cumulative effect on the displacement magnitude [30]. The correlation coefficients between the conductor span and characteristic displacement values at the midpoint of the conductors are shown in

Table 10. Correlation coefficients between conductors displacement characteristic values and span length.

DCV	PV (X)	$\mathbf{AV} (\mathit{\Delta }\mathit{X}$)	$\mathbf{MV} (\overline{\mathit{X}}$)	IV (X0)
CC	0.3319	0.3251	0.5482	0.9467
(P-V)	0.5714	0.5826	0.5048	0.0007

.

(2)

The influence of different span levels on crossarm strain

Under the same wind speed and ice accumulation conditions, the span of the conductors affects the strain values at the crossarm location. Transmission tower–line systems with different horizontal spans exhibit different dynamic responses under ice and wind load effects, as shown in Figure 11.

As shown in Figure 11, under different horizontal spans, the initial strain value increases slowly with the increase in horizontal span under the same icing and wind speed conditions, with an increase of 53.28%, which is less than the 255.6% under the first type of working condition. This phenomenon indicates that conductor icing has a significantly greater impact on the crossarm strain than the change in conductor span does. As the conductor span increases, other characteristic values of the crossarm strain first decrease and then increase. Under this type of working conditions, the differences in characteristic strain values are as follows: peak value: 13.56%; amplitude: 13.51%; and mean value: 22.78%. Compared with the characteristic strain values of the first type of working conditions (described earlier), the changes are minimal.

Based on this type of working conditions, it can be concluded that in a tower–line system based on tangent towers, the impact caused by different conductor spans is mainly reflected by the conductors, while the strain response at the crossarm is less affected. Regarding the correlation coefficient between the span and strain eigenvalues, we refer to

Table 11. Correlation coefficients between conductors span and crossarm strain characteristic values.

CSSV	PV (X)	$\mathbf{AV} (\mathit{\Delta }\mathit{X}$)	$\mathbf{MV} (\overline{\mathit{X}}$)	IV (X0)
CC	−0.6118	0.6503	−0.6675	−0.9867
(P-V)	0.0528	0.0722	0.0616	0.0009

.

3.3. Model Parameter Sensitivity Analysis

As can be seen from the previous sections, the wind-induced response of a transmission tower–line system is influenced by the ice thickness, basic wind speed, and conductor span, with significant differences in the degree of influence of different parameters. To further clarify the impact of changes in different parameters of the iced transmission tower–line system, a model parameter sensitivity analysis is conducted. The amplitude of the conductor mid-span displacement and crossarm strain are taken as references to analyze and compare the impacts of different parameter variations, as shown in Figure 12.

As shown in Figure 12, among the wind-induced responses of ice-covered transmission line systems, the wind speed demonstrates the greatest influence, followed by ice thickness, and with the span showing the least impact. This occurs because the relationship between the wind speed and wind load exhibits a nonlinear quadratic pattern. When the wind speed increases uniformly, the wind load surges dramatically, causing significant displacement of conductors and strain responses in crossarms. Although the accumulation of ice on conductors causes their outer diameter to become more than twice the bare conductor diameter, the resulting ice load increase remains smaller than that caused by wind load. Given that conductor spans range from 300 to 460 m, the gravitational load increase due to span variations is less pronounced than that caused by accumulation of ice. The finite element model used in this study is based on a 2G-SZC2 straight-line transmission line system, with the lowest suspension point of the transmission tower being set at 27.8 m. According to industry standards [16], conductor spans are constrained within the specified operational range. Therefore, in this study, the wind speed is the most sensitive parameter affecting the dynamic response of transmission line systems, followed by ice thickness, while the span shows the lowest sensitivity.

In order to reflect the law of change in the dynamic response of tower–line systems more intuitively and clearly, and according to the above, two parameters (wind speed and ice coverage) with decisive influence are selected to construct three-dimensional surface maps of the peak displacement of the conductor and amplitude of the crossbeam strain, respectively, as shown in Figure 13.

4. Discussion

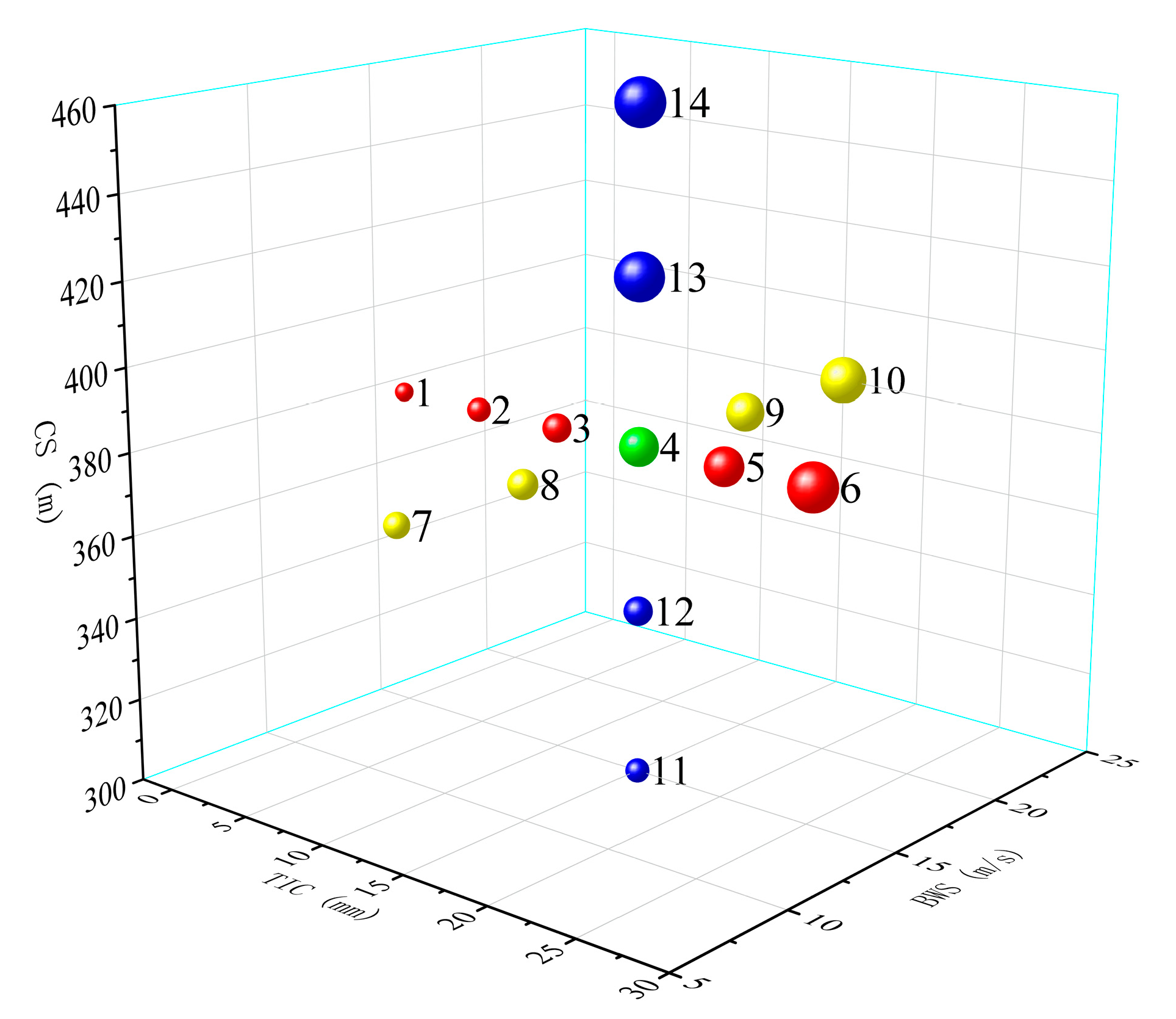
4.1. Determination of the Functional Relationship Between Crossarm Strain and Conductor Displacement

Through the previous analyses, it can be found that, under different working conditions, there is a strong correlation between conductor displacement and crossarm strain in a transmission tower–line system with external loads. The correlation coefficients between the crossarm strain and conductor displacement under various working conditions are shown in

Table 12. Correlation coefficients between crossarm strain and conductor displacement under various working conditions.

	WCN
	1	2	3	4	5	6	7
CC	−0.8193	−0.8434	−0.8453	−0.8632	−0.8477	−0.7942	−0.8154
(P-V)	0.0032	0.0024	0.0021	0.0018	0.0022	0.0036	0.0021
	WCN
	8	9	10	11	12	13	14
CC	−0.8818	−0.7982	−0.7354	−0.8869	−0.8581	−0.8725	−0.8584
(P-V)	0.0015	0.0037	0.0042	0.0019	0.0025	0.0031	0.0028

. Based on this, it can also be concluded that a functional relationship exists between these two variables.

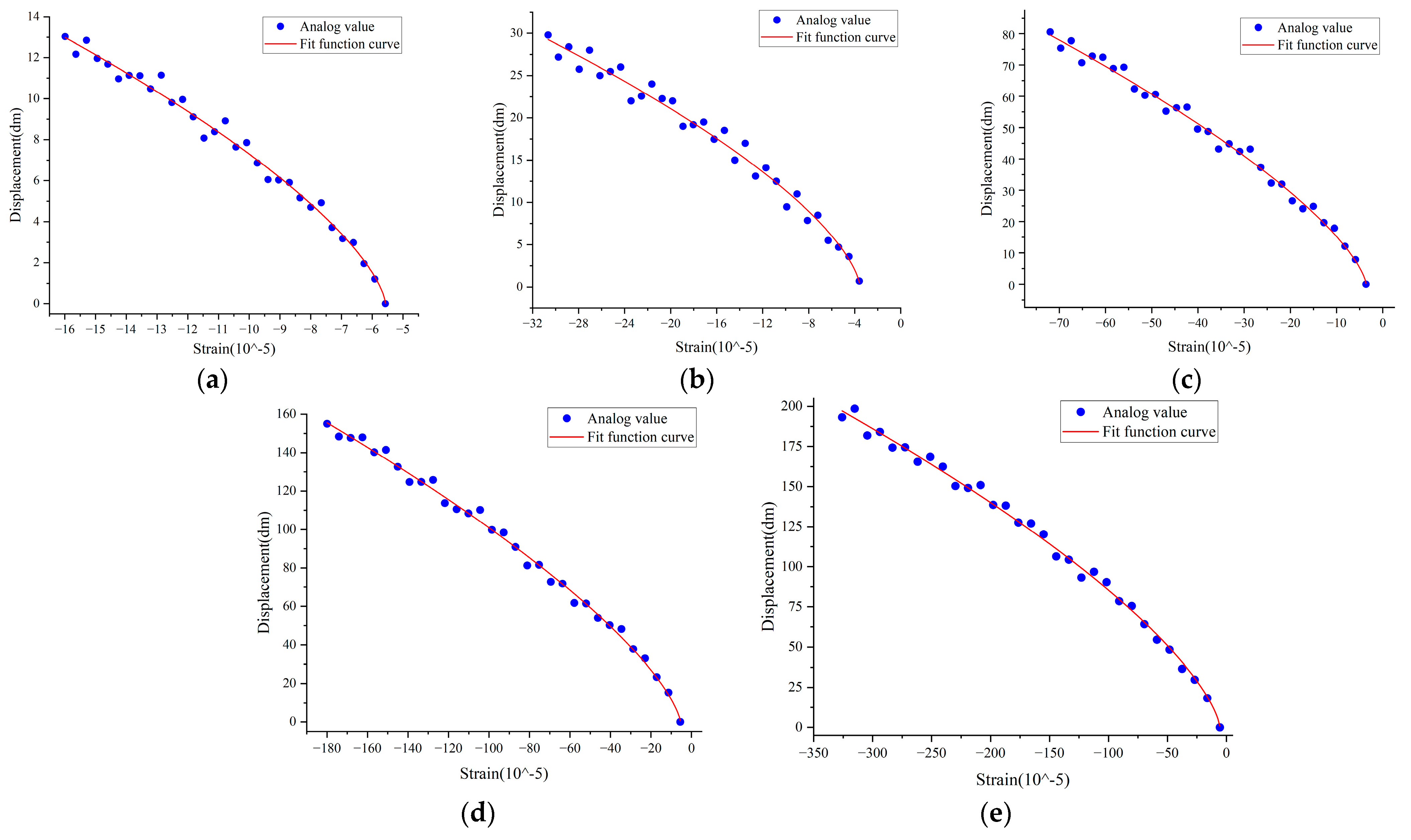
When constructing the functional relationship, the crossarm strain is selected as the independent variable, and the resultant displacement at the midpoint of the conductor is chosen as the dependent variable. First, a dataset of crossarm strain-conductor midpoint displacement is established. Based on the strain amplitude, the data is uniformly divided into 30 numerical intervals. Since this study focuses on time-domain analysis of crossarm strain and conductor displacement, each crossarm strain value has a corresponding conductor midpoint displacement value at the same moment. Therefore, the median of the strain values in each interval and the average of the corresponding conductor midpoint displacements at those moments are calculated to establish strain-displacement ordinal pairs. These ordinal pairs are then plotted as scatter points. Finally, function relationships are fitted for the displacement-strain scatter plots of each working condition, thereby establishing the functional relationships between conductor displacement and crossarm strain under various working conditions. The fitted functional relationships between conductor resultant displacement and crossarm strain under each working condition are shown in Figure 14, Figure 15 and Figure 16.

In Figure 14, Figure 15 and Figure 16, the functional relationships between the crossarm strain and midpoint displacement of the conductor under three types of operating conditions (i.e., based on different ice thicknesses, wind speeds, and conductor spans) are presented. In these figures, blue dots represent simulated values, with the horizontal coordinate indicating the median value of each strain interval, and the vertical coordinate representing the average midpoint displacement of the conductor at the corresponding crossarm strain interval. The numerous simulated value points form a scatter plot, and the red curve is the fitting function generated based on this.

(1)

The first type of working conditions

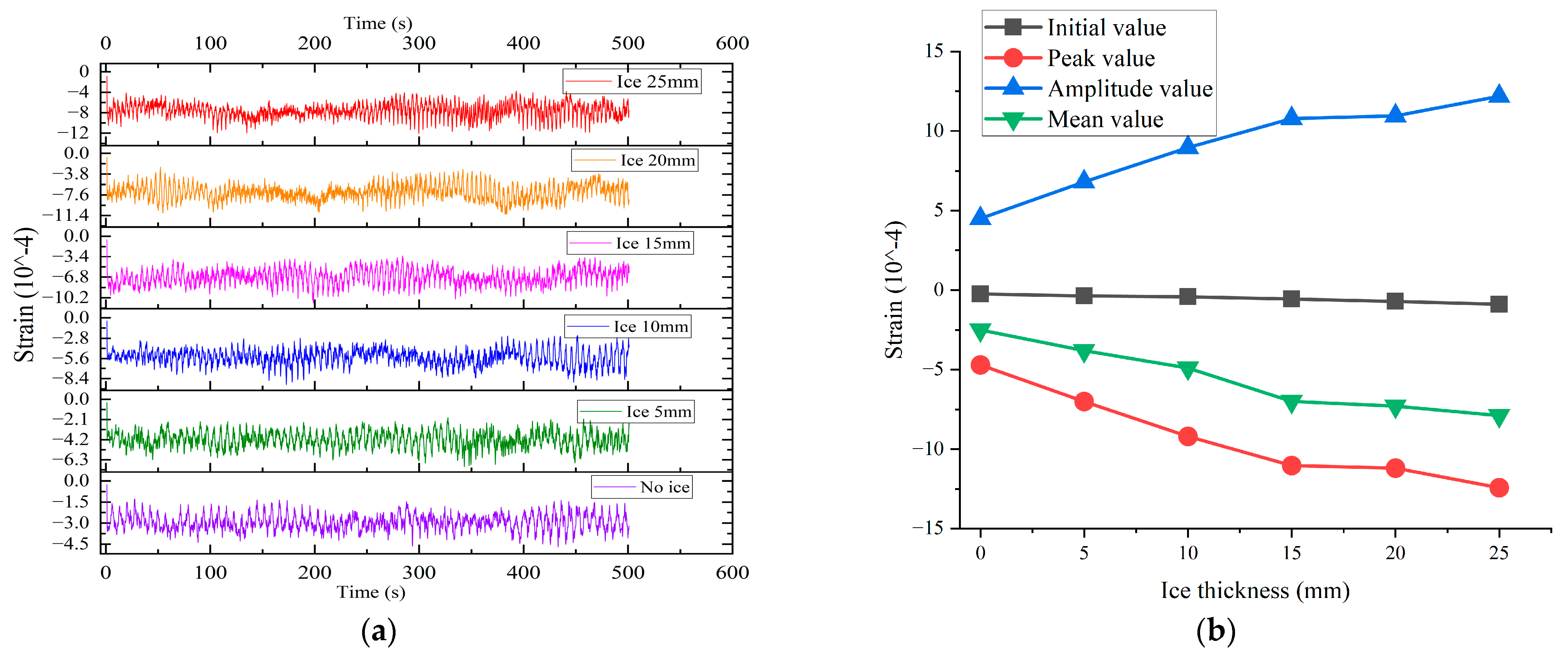
In the first type of operating conditions, the span of the conductor and the wind speed of the tower–line system remain unchanged, while the ice thickness gradually increases. When the ice thickness is small, the displacement of the conductor under wind load based on the same wind speed increases significantly. In this scenario, the gravitational effect of the ice directly increases the vertical load (dead load) of the conductor, leading to an increase in sag. The ice thickness and load increase linearly. However, within the elastic range of the material, the increase in sag is nonlinear, usually accelerating with the increase in load. When the ice thickness exceeds a certain level (15 mm in the simulation results of this study), inertial effects become dominant, and the mass of the conductor system increases sharply. Under the same external force (wind load), objects with greater mass exhibit smaller acceleration, and the huge inertial force suppresses the movement of the conductor.

According to Figure 14, Figure 15 and Figure 16, the basic formula for the functional relationship between conductor displacement and crossarm strain is as follows:

$$y=A·{\left(x-b\right)}^p$$

(13)

In the above formula, x represents the crossarm strain, with units of 10⁻⁵; y denotes the resultant displacement at the midpoint of the conductors, with units of dm; A is the comprehensive coefficient of the fitting function; b signifies the initial strain of the crossarm; and p is the fitting parameter, set as 0.7.

Under the first working condition, since the magnitude of the wind speed and the horizontal span of the conductors are specified, only the influence of the ice’s thickness on the crossarm strain is analyzed. The comprehensive coefficient A is solely related to the thickness of the ice. The impact function is defined as $f_1\left(t\right)$, where t represents the ice thickness in mm. Based on the fitting function relationships for the first type of working conditions (described earlier), $f_1\left(t\right)$ can be expressed as follows:

$$f_1\left(t\right)=0.08414·t-5.3298$$

(14)

The thickness of the ice coating on the conductors directly affects the initial strain of the crossarm, which is set as $b\left(t\right)$:

$$b\left(t\right)=-0.2524·t - 2.1889$$

(15)

From the above fitting function, the final expression of the fitting function based on the first type of working conditions can be obtained as follows:

$$y=f_1\left(t\right)·{\left[x - b_1\left(t\right)\right]}^{0.7}$$

(16)

(2)

The second type of working condition

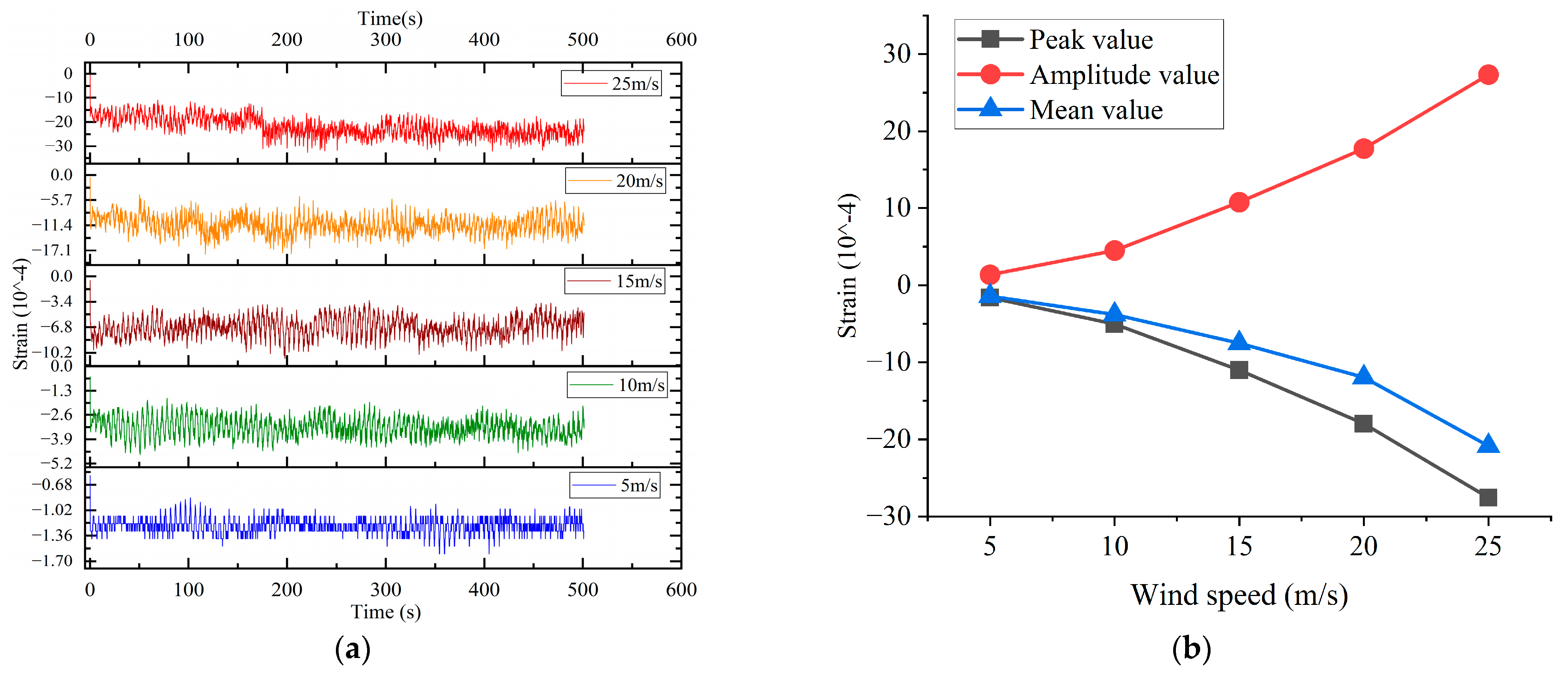
Under the second type of operating conditions, the ice thickness on the conductor and the conductor’s own span remain unchanged, while the simulated wind speed increases uniformly. When the wind speed is in a relatively low range, the displacement response of the conductor begins to appear and increases relatively gently. This is because at low wind speeds, the energy that is provided by the wind load is limited, mainly exciting low-order motion of the line, and the displacement response is primarily quasi-static. When the wind speed reaches a higher level, the displacement response increases sharply or even reaches a peak. This is because when the wind speed reaches a certain critical value, the excitation frequency of the wind load approaches a certain natural frequency of the tower–conductor system (especially the fundamental frequency), causing resonance to occur and leading to the response being sharply amplified.

Under this working condition, the comprehensive coefficient A takes the influence of the basic wind speed into account, and the basic fitting functions for conductor displacement and crossarm strain are as follows:

$$y=A{·\left[x - b_1\left(15\right)\right]}^{0.7}$$

(17)

among which ${\mathrm{A}=\mathrm{f}}_1\left(15\right){\mathrm{f}}_2\left(\mathrm{v}\right)$

$$f_2\left(v\right)=\left\{\begin{array}{c}0.0316v+0.4724 5 \mathrm{m}/\mathrm{s}\le \mathrm{v}\le 20 \mathrm{m}/\mathrm{s}\\ -0.0429v+1.9231 20 \mathrm{m}/\mathrm{s}<\mathrm{v}\le 25 \mathrm{m}/\mathrm{s}\end{array}\right.$$

(18)

In the above formula, $f_2\left(v\right)$ varies, since when the wind speed exceeds 20 m/s, the coefficients in the function between the crossarm strain and conductor displacement under this type of operating condition are lower than those under the 5~20 m/s operating condition, which leads to a decrease in the overall fitting accuracy. To more accurately reflect the change in coefficients, a piecewise function is set for this expression.

(3)

The third type of working conditions

Under the third type of operating conditions, the comprehensive coefficient takes the influence of the conductor span into account. For conductors with the same sag, the smaller the conductor span is, the more relaxed the stress of the conductor is, and under the same wind load, the displacement response of the conductor is larger; in contrast, when the conductor span is too large, the tension of the conductor is greater, leading to an increase in the elongation of the conductor. In addition, an increase in conductor span has a cumulative effect on the displacement value. At the same time, due to the increase in span causing an increase in the gravitational load of the conductor, the initial strain value of the crossarm changes. Therefore, in the initial strain term, the influence of the span is added, and the coefficient of the span’s impact on the initial strain value is set as $\mathrm{d}\left(L\right)$.

The basic expression of the fitting function for conductor displacement and crossarm strain under the third type of operating conditions is as follows:

$$y=A{·\left[x - b_1\left(15\right)d_1\left(\mathrm{L}\right)\right]}^{0.7}$$

(19)

where A = $f_1\left(15\right)f_2\left(15\right)f_3\left(L\right)$. Based on the fitted function expressions under various working conditions (shown in Figure 16), combined with the already known $f_1\left(15\right)f_2\left(15\right)$ under the first two types of working conditions, the expression for $f_3\left(L\right)$ is as follows:

$$f_3\left(L\right)=\left\{\begin{array}{c}\left(3.98\times {10}^{-3}\right)L-2.54596 300 \mathrm{m}\le \mathrm{L}\le 380 \mathrm{m}\\ -\left(6.124\times {10}^{-4}\right)L-0.801 380 \mathrm{m}<\mathrm{L}\le 460 \mathrm{m}\end{array}\right.$$

(20)

Regarding the influence of the conductor span on the initial strain value of the crossarms, the coefficient setting for this type of working conditions is ${\mathrm{b}}_1\left(15\right){\mathrm{d}}_1\left(\mathrm{L}\right)$. The fitting function between the initial strain value and the span is obtained as follows:

$$b\left(15\right)·d\left(L\right)=-0.14686L-0.05036$$

(21)

$$d_1\left(L\right)=-0.02458L-0.00843\text{\#}\left(21\right)$$

Based on the integration of fitting functions between the conductor displacement and crossarm strain under various working conditions, the following fitting relationship was obtained for the 2G-SZC2 tangent tower–line system with ice coating thicknesses of 0–25 mm: basic wind speed of 5–25 m/s and span of 300–460 m. Under combined ice–wind loading conditions, the fitting function between the mid-span conductor displacement and crossarm strain is established as follows:

$$y=f_1\left(t\right){·f}_2\left(v\right)·f_3\left(L\right)·{\left[x - b_1\left(t\right){·d}_1\left(L\right)\right]}^{0.7}$$

(22)

Here, $f_1\left(t\right)$ is the influence coefficient based on the ice thickness; $f_2\left(v\right)$ is the influence coefficient based on the wind speed; $f_3\left(L\right)$ is the influence coefficient based on different spans; $b_1\left(t\right)$ is the functional relationship between the ice thickness and initial strain of the crossarm; $d_1\left(L\right)$ is the functional relationship between the conductor span and initial strain of the crossarm; y is the conductor displacement value; x is the crossarm strain value; t is the average thickness of the ice on the tower and conductor, in mm, with the ice thickness range in this study being 0~25 mm; v is the basic wind speed of the pulsating wind, in m/s, with the basic wind speed range in this study being 5~25 m/s; and L is the span of the conductor, in m, with the conductor span range in this study being 300~460 m.

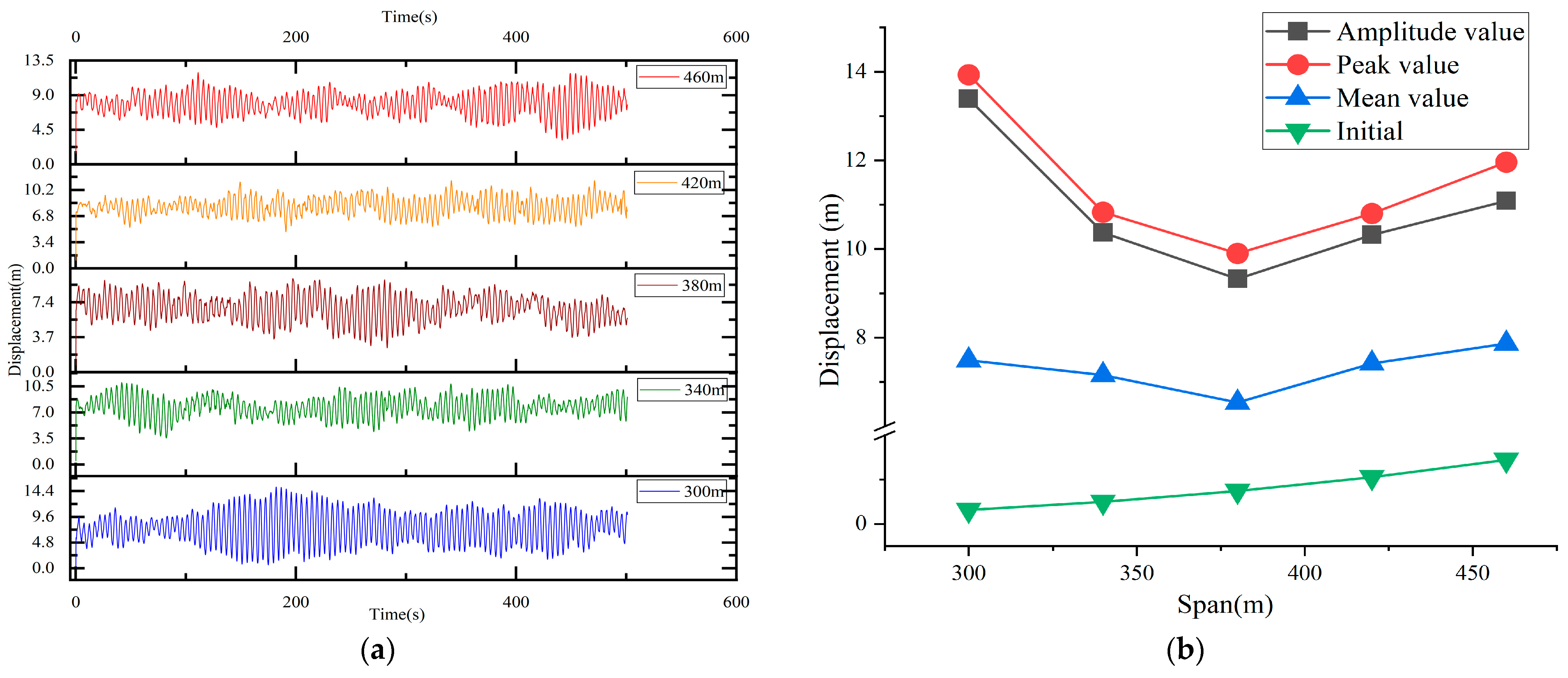
4.2. Analysis of Galloping of Iced Conductors Under Reference Working Conditions

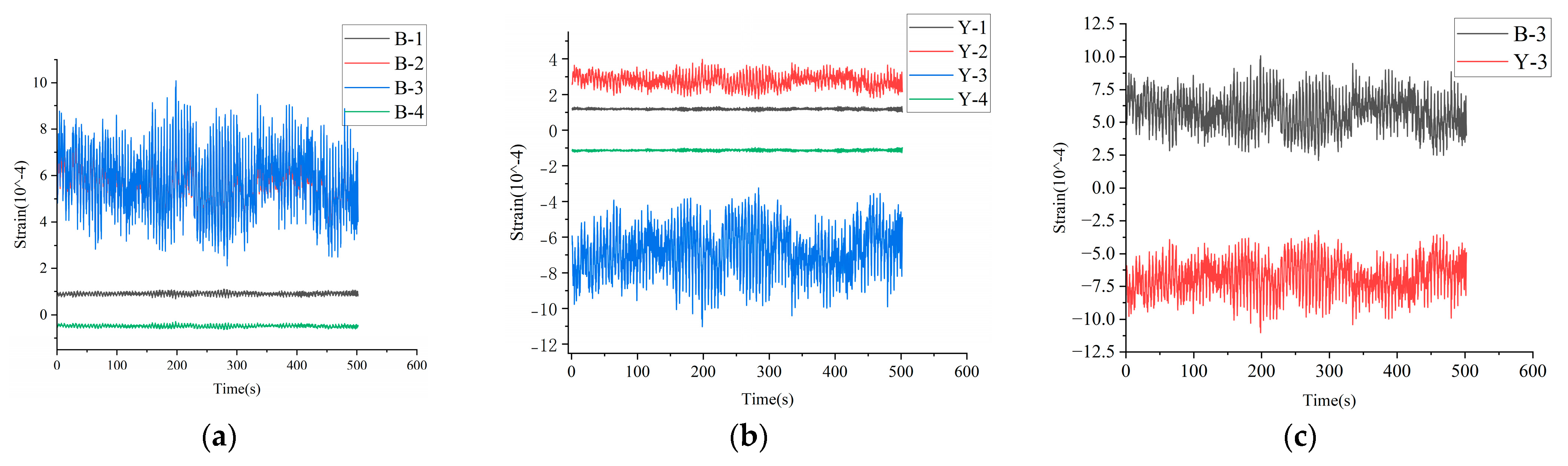
By applying the aerodynamic load on the conductors, we can simulate and analyze the ice-induced galloping of the transmission conductors. Based on the operating conditions set in this paper, the coupled effect of the aerodynamic lift and aerodynamic drag of the conductor determines the vibration mode of the conductor. The time history data for the midpoint displacement of the conductors are shown in Figure 17. Under the action of a constant external wind load, the galloping amplitude of iced transmission conductors develops gradually and finally reaches a stable state after more than 350 s. During the process of iced conductor galloping, the development trend and amplitude of the mid-span displacement of the conductor are basically consistent with those described in references [27,31]. Therefore, the numerical simulation results regarding conductor galloping are relatively accurate.

The time history data for the strain at the end of the crossarm under conductor galloping with ice coating are shown in Figure 18. The time history data for the strain of the crossarm are similar to those for the displacement at the midpoint of the conductors. The crossarm strain undergoes a gradual development process and ultimately reaches a stable state after 350 s.

During the ice-induced galloping of transmission conductors, the conductors undergo large-amplitude swinging on both sides in the along-wind direction, resulting in alternating positive and negative phenomena of the crossarm strain. In the previous analysis of the wind-induced response of the transmission tower–conductor system, the conductor always undergoes displacement on one side in the along-wind direction, causing the crossarm strain to remain negative. Therefore, the negative strain interval is selected for verification under conditions of conductor galloping. Strain–displacement data points are constructed, plotted as a scatter diagram, and compared with the calculation results of Formula (21), as shown in Figure 19.

By comparing the strain–displacement simulation values with the curve calculated using Equation (22), it can be observed that the strain–displacement data points based on conductor galloping fluctuate around the calculated values of Equation (22). Under the four working conditions—A, B, C, and D—the maximum errors are 4.75%, 6.43%, 10.58%, and 5.62%, respectively, with the overall error being controlled within 11%. This indicates that the fitting formula exhibits good applicability to the galloping of ice-covered transmission conductors.

4.3. Explanation of the Applicability of Functional Relationships

The functional relationship between the crossarm strain and conductor displacement that is obtained in this section is derived from the simulation analysis of 14 working conditions across three categories that was conducted in this study. Based on a tower–line system placed on Class B or C terrain (plain terrain) and comprising 220 kV straight-line towers, and under the premise of not considering extreme wind and weather conditions, it is concluded that a functional relationship can be established between the crossarm strain of the transmission tower and the conductor displacement within a certain range. In relatively mild natural environments, the strain of the crossarm mainly originates from the axial tension that is transmitted to the suspension point by the conductor. When the conductor undergoes displacement due to uniform icing or wind load, its catenary shape will change, thereby causing a change in tension. This change in tension directly acts at the end of the crossarm, resulting in a strong correlation between strain and displacement. Research shows that for tower–line systems with medium and short spans, the coupling effect is particularly significant. However, the applicability of this functional relationship has important limitations: First, it depends on the balance between the linear tower body response and the geometric nonlinear behavior of the transmission line. Second, the established maximum wind speed is 25 m/s, and the influence of pulsating wind may lead this relationship to exhibit a certain degree of randomness. Third, if methods considering spatial correlation, such as the Davenport wind speed spectrum, are used for simulation, the statistical ruler can be largely revealed; the functional relationship established in this study is not capable of describing the transient dynamic response relationship between the conductor and crossarm strain caused by de-icing of the conductor.

5. Conclusions

To efficiently monitor the movement of transmission conductors under combined ice and wind loads, this study performed a dynamic response analysis of a transmission tower–line system based on crossarm strain under such conditions, obtaining the response laws of the crossarm strain and conductor displacement. A functional relationship between the crossarm strain response and mid-span conductor displacement under combined ice–wind loads was established and validated. The following conclusions are drawn:

(1)

Under the combined action of ice coating and wind load, the basic wind speed, ice thickness, and conductor span all exert varying degrees of influence on the dynamic response of a tower–line system. Among these factors, the basic wind speed has the greatest impact, followed by ice thickness, while the horizontal conductor span has a relatively minor effect.

(2)

In our dynamic response analysis of transmission tower–line systems under varying ice thicknesses, the peak, amplitude, and mean values of the conductor’s mid-point displacement show initial increases, followed by subsequent decreases with increasing ice thicknesses. The characteristic values of the initial conductor displacement and crossarm strain also increase with the accumulation of ice. In terms of transmission tower–line system dynamics under different wind speeds, the characteristic values of both the conductor displacement and crossarm strain demonstrate upward trends with increasing fundamental wind speeds. Under identical sag configurations across different horizontal spans, while the values of the crossarm strain and conductor displacement exhibit initial increases with span extension, all other characteristic values follow a pattern of first rising and then decreasing with increasing spans.

(3)

The thickness of the ice coating has a dual effect on the displacement response of conductors. On the one hand, ice accretion reduces the natural vibration frequency of the tower–line system, bringing it closer to the dominant frequency of the pulsating wind spectrum and thereby increasing the likelihood of resonance under pulsating wind loads. On the other hand, when the ice thickness exceeds the critical thickness (for example, the critical ice thickness for the straight transmission tower type 2G-SZC2 used in this study is 15 mm), the gravitational effect that is induced by ice accretion becomes dominant and suppresses conductor vibration.

(4)

Based on the wind-induced response analysis of the iced transmission tower–line system, this study establishes a functional relationship between the mid-span displacement of the transmission conductor and the strain of the crossarm. Combined with our analysis of the ice-induced galloping of the transmission tower–line system, the applicability of this functional relationship is explored. The results indicate that for B- or C-type landforms in plain terrain, a tower–line system that is constructed with commonly adopted medium-to-short spans (300 m to 500 m) and 220 kV straight-line towers is applicable under the conditions of uniform ice coverage on conductors across the entire span and exclusion of extreme wind and weather, both under the ice-induced dynamic response working conditions of the tower–line system and under conductor galloping working conditions.

(5)

Engineering Significance: The established functional relationship between the crossarm strain and transmission line displacement under different operating conditions that is presented in this paper can provide technical support for the development of online monitoring devices for ice-induced galloping of transmission lines based on the crossarm microstrain. Utilizing the functional relationship studied here, such devices could be capable of effectively detecting and accurately identifying ice-induced galloping or abnormal strain and vibration of the line, thereby ensuring the safe operation of transmission lines.