The Mathematical Modelling of Nonlinear String Oscillations in an Isotropic Viscoelastic Medium Using the Example of a Long Power Line
Abstract
1. Introduction
2. Methods
2.1. Non-Conservative Lagrangian
2.2. The Mathematical Model of Nonlinear String Vibrations
2.2.1. The Linear Dissipation of Mechanical Energy Across the String
- (1)
- When the internal expression in the ordinary brackets is equal to zero.
- (2)
- The variation in the generalised coordinate function is equal to zero.
- (3)
- Both the numerators are equal to zero.
2.2.2. Nonlinear Dissipation
2.3. The Mathematical Aspects of the Existence and Uniqueness of the Solution: The Galerkin and Monotonicity Methods
2.3.1. Linear Dissipation
2.3.2. Nonlinear Dissipation
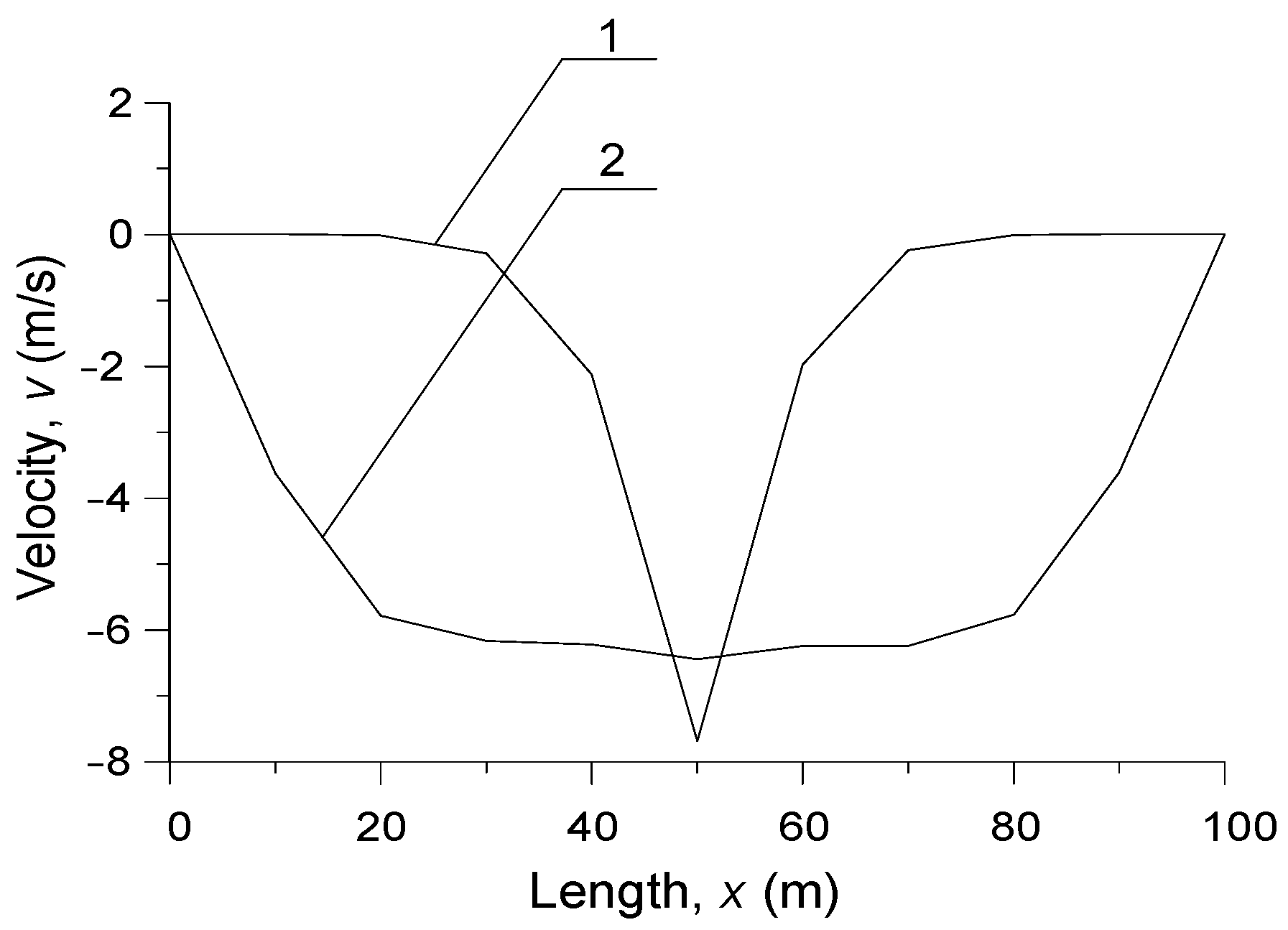
3. Computer Simulation Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chaban, A. Hamilton-Ostrogradski Principle in Electromechanical Systems; Soroki: Lviv, Ukraine, 2015; p. 488. [Google Scholar]
- Chaban, A.; Lis, M.; Lozynskyy, A.; Pukach, P.Y.; Szafraniec, A.; Vovk, M. Mathematical modelling of membrane oscillatory processes in a nonlinear viscoelastic medium via the Caputo-Fabrizio fractional operator. Sci. Rep. 2025, 15, 14555. [Google Scholar] [CrossRef]
- Jiao, J.L.; Zhao, M.M.; Jia, G.Y.; Ding, S. SPH simulation of two side-by-side LNG ships’ motions coupled with tank sloshing in regular waves. Ocean Eng. 2024, 297, 117022. [Google Scholar] [CrossRef]
- Park, J.-S.; Kim, J.-H.; Jeong, Y.-C.; Kim, H.-T.; Kim, S.-K.; Lee, J.-M. Effect of Corrugated Sheet Diameter on Structural Behavior under Cryogenic Temperature and Hydrodynamic Load. Metals 2022, 12, 521. [Google Scholar] [CrossRef]
- Liu, J.; Feng, G.; Wang, J.; Ren, H.; Song, W.; Lin, P. Fatigue Life Assessment in the Typical Structure of Large Container Vessels Based on Fracture Mechanics. J. Mar. Sci. Eng. 2023, 11, 2075. [Google Scholar] [CrossRef]
- Park, Y.I.; Kim, J.H. Artificial neural network based prediction of ultimate buckling strength of liquid natural gas cargo containment system under sloshing loads considering onboard boundary conditions. Ocean Eng. 2022, 249, 110981. [Google Scholar] [CrossRef]
- Woolley, T.; Bianca, C.; Alam, M.J.; Ramady, A.; Abbas, M.S.; El-Rashidy, K.; Azam, M.T.; Miah, M.M. Numerical Investigation of the Wave Equation for the Convergence and Stability Analysis of Vibrating Strings. AppliedMath 2025, 5, 18. [Google Scholar] [CrossRef]
- Cumber, P.S. Application of the method of lines to the wave equation for simulating vibrating strings. Int. J. Math. Educ. Sci. Technol. 2024, 56, 2298–2317. [Google Scholar] [CrossRef]
- Attaev, A. On Some Non-local Boundary Value and Internal Boundary Value Problems for the String Oscillation Equation. Bull. Karaganda Univ. Math. Ser. 2023, 110, 35–44. [Google Scholar] [CrossRef]
- Miškinis, P.; Krylovas, A.; Lavcel-Budko, O. Uniformly Valid Asymptotics for Carrier’s Mathematical Model of String Oscillations. Math. Model. Anal. 2017, 22, 337–351. [Google Scholar] [CrossRef]
- Bonfanti, A.; Kaplan, J.L.; Charras, G.T.; Kabla, A.J. Fractional viscoelastic models for power-law materials. Soft Matter 2020, 16, 6002–6020. [Google Scholar] [CrossRef]
- Sadoun, M.B.; Cherif, A.B.; Bentifour, R.; Bouhali, K.; Biomy, M.; Zennir, K. Loss of Exponential Stability for a Delayed Timoshenko System Symmetrically in Both Viscoelasticity and Fractional Boundary Controls. Symmetry 2025, 17, 423. [Google Scholar] [CrossRef]
- Kirianova, L. Modeling of Strength Characteristics of Polymer Concrete via the Wave Equation with a Fractional Derivative. Mathematics 2020, 8, 1843. [Google Scholar] [CrossRef]
- Aleroev, T.S.; Mahmoud, E.I.; Elsayed, A.M. Mathematical model of the polymer concrete by fractional calculus with respect to a spatial variable. In Proceedings of the International Conference of Young Scientists and Students “Topical Problems of Mechanical Engineering” (ToPME 2020), Moscow, Russia, 2–4 December 2020. [Google Scholar] [CrossRef]
- Tan, M.; Xu, Q.; Yuan, H.; Xu, M.; Liu, K.; Qu, A.; Xu, X. Mathematical Analysis and Numerical Computation of String Vibration Equations with Elastic Supports for Bridge Cable Force Evaluation. arXiv 2024, arXiv:2410.06439. [Google Scholar] [CrossRef]
- Valiullin, A.I.; Danilin, A.; Feldshteyn, V. Normal vibrations of sagging conductors of overhead power lines. Int. J. Comput. Civ. Struct. Eng. 2022, 18, 147–158. [Google Scholar] [CrossRef]
- Wang, J.; Liu, J. A Time-Varying String Length Method for a Suppression String Vibration. In Proceedings of the 2022 Workshop on Electronics Communication Engineering, Xi’an, China, 28–31 October 2022; Huang, L., Ed.; SPIE: Xi’an, China, 2023; p. 39. [Google Scholar] [CrossRef]
- Guo, M.; Tang, L.; Wang, H.; Liu, H.; Gao, S. A Comparative Study on Transient Vibration Suppression of Magnetic Nonlinear Vibration Absorbers with Different Arrangements. Nonlinear Dyn. 2023, 111, 16729–16776. [Google Scholar] [CrossRef]
- White, D.C.; Woodson, H.H. Electromagnetic Energy Conversion; Wiley: New York, NY, USA, 1958. [Google Scholar]
- Pukach, P.Y. On the unboundedness of a solution of the mixed problem for a nonlinear evolution equation at a finite time. Nonlinear Oscil. 2012, 14, 369–378. [Google Scholar] [CrossRef]
- Pukach, P.Y.; Il’kiv, V.; Nytrebych, Z.; Vovk, M. Investigation of the mathematical model of bending oscillations of the oil tanks’ walls in the transformers considering nonlinear dissipative forces. In Proceedings of the 14th International Conference The Experience of Designing and Application of CAD Systems in Microelectronics (CADSM), Lviv, Ukraine, 21–25 February 2017. [Google Scholar] [CrossRef]
- Carvalho, A.N.; Cholewa, J.W.; Dlotko, T. Strongly damped wave problems: Bootstrapping and regularity of solutions. J. Differ. Equ. 2008, 244, 2310–2333. [Google Scholar] [CrossRef]
- Pereira, D.C.; Raposo, C.A.; Maranhão, C.H.M. Global solution and asymptotic behavior for a wave equation type p-Laplacian with p-Laplacian damping. MathLAB J. 2020, 5, 35–45. [Google Scholar]
- Benaissa, A.; Mokeddem, S. Decay estimates for the wave equation of p-Laplacian type with dissipation of m-Laplacian type. Math. Methods Appl. Sci. 2007, 30, 237–247. [Google Scholar] [CrossRef]
- Bociu, L.; Lasiecka, I. Uniqueness of weak solutions for the semilinear wave equations with supercritical boundary/interior sources and damping. Discret. Contin. Dyn. Syst. 2008, 22, 835–860. [Google Scholar] [CrossRef]
- Chueshov, I.; Lasiecka, I. Existence, uniqueness of weak solutions and global attractors for a class of nonlinear 2D Kirchhoff-Boussinesq models. Discret. Contin. Dyn. Syst. 2006, 15, 777–809. [Google Scholar] [CrossRef]
- Rammaha, M.; Toundykov, D.; Wilstein, Z. Global existence and decay of energy for a nonlinear wave equation with p-Laplacian damping. Discret. Contin. Dyn. Syst. 2012, 32, 4361–4390. [Google Scholar] [CrossRef]
- Zhijian, Y. Global existence, asymptotic behavior and blowup of solutions for a class of nonlinear wave equations with dissipative term. J. Differ. Equ. 2003, 187, 520–540. [Google Scholar] [CrossRef]
- Mokeddem, S.; Mansour, K.B.W. The Rate at Which the Energy of Solutions for a Class of p-Laplacian Wave Equation Decays. Int. J. Differ. Equ. 2015, 3, 721503. [Google Scholar] [CrossRef]
- Yaojun, Y.; Qianqian, Z. Existence and nonexistence of global solutions for logarithmic hyperbolic equation. Electron. Res. Arch. 2022, 30, 1035–1051. [Google Scholar] [CrossRef]
- Messaoudi, S.A.; Houari, B.S. Global non-existence of solutions of a class of wave equations with non-linear damping and source terms. Math. Methods Appl. Sci. 2004, 27, 1687–1696. [Google Scholar] [CrossRef]
- Dvornyk, A.V.; Tkachenko, V.I. Almost Periodic Solutions of the Wave Equation with Damping and Impulsive Action. Ukr. Math. J. 2023, 75, 68–79. [Google Scholar] [CrossRef]
- Protsakh, N. Inverse problem for semilinear wave equation with strong damping. Front. Appl. Math. Stat. 2024, 102, 1467441. [Google Scholar] [CrossRef]
- Carvalho, A.N.; Cholewa, J.W. Attractors for strongly damped wave equations with critical nonlinearities. Pac. J. Math. 2002, 207, 287–310. [Google Scholar] [CrossRef]
- Lions, J.-L. Quelques Méthodes de Résolution des Problèmes aux Limites non Linéaires; Dunod: Paris, France, 2002; 554p, ISBN 978-210-006-847-0. [Google Scholar]
- Gajewski, H.; Gröger, K.; Zacharias, K. Nichtlineare Operatorgleichungen und Operatordifferentialgleichungen; De Gruyter: Berlin, Germany; Boston, MA, USA, 1974; 296p, ISBN 978-311-271-788-2. [Google Scholar]
- Coddington, E.A.; Levinson, N. Theory of Ordinary Differential Equations; McGraw-Hill Inc.: New York, NY, USA, 1955; 429p, ISBN 978-007-099-256-6. [Google Scholar]
- Zeidler, E. Nonlinear Functional Analysis and its Applications: II/B: Nonlinear Monotone Operators; Springer: New York, NY, USA, 1990; 756p, ISBN 978-038-797-167-4. [Google Scholar]
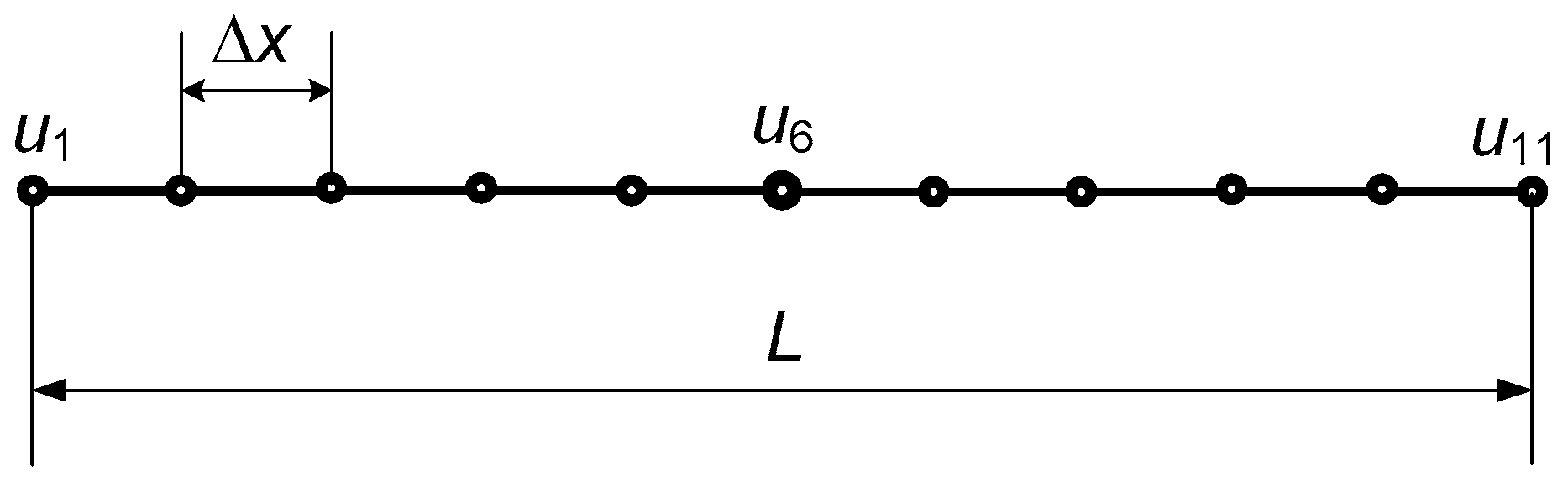

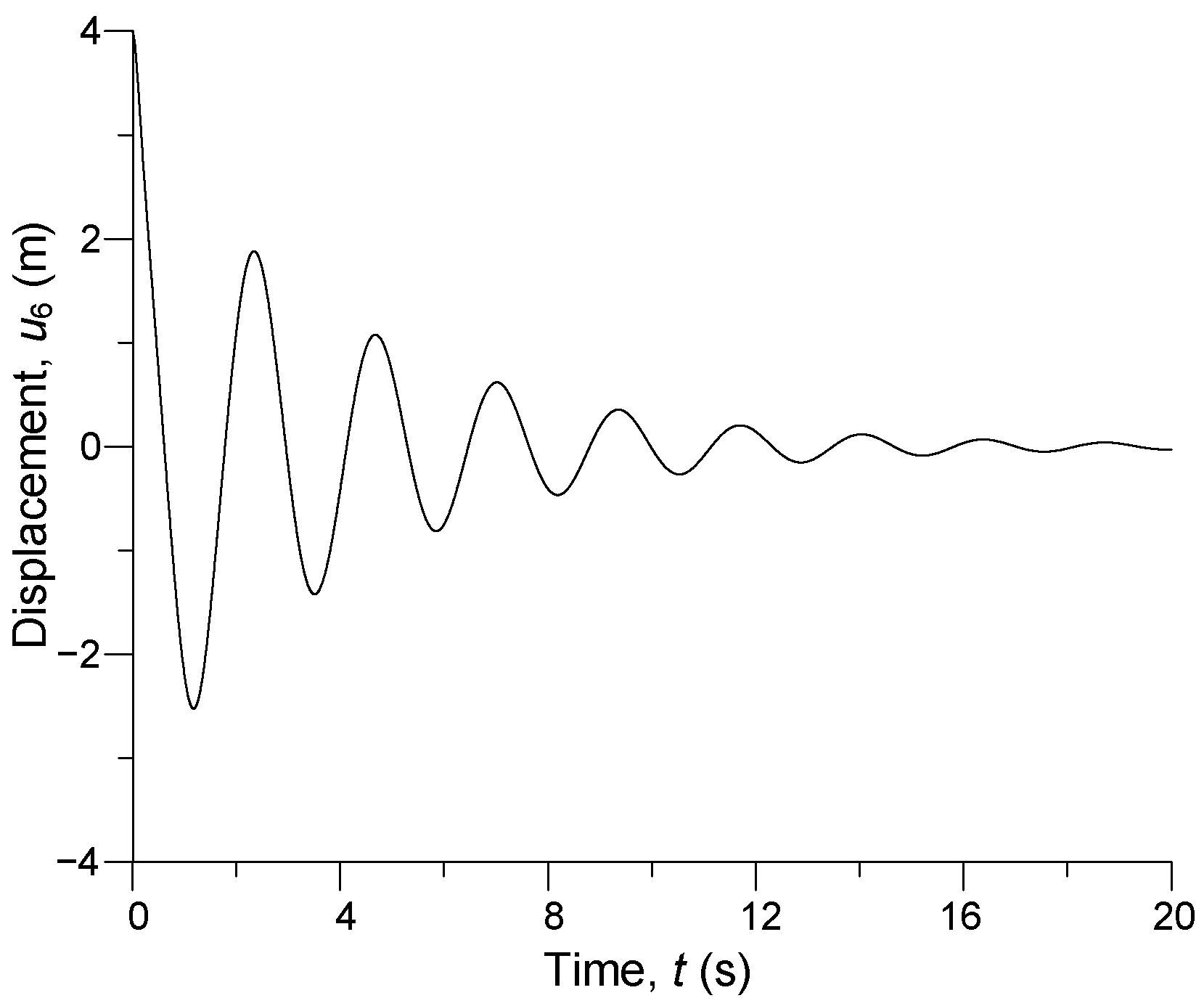
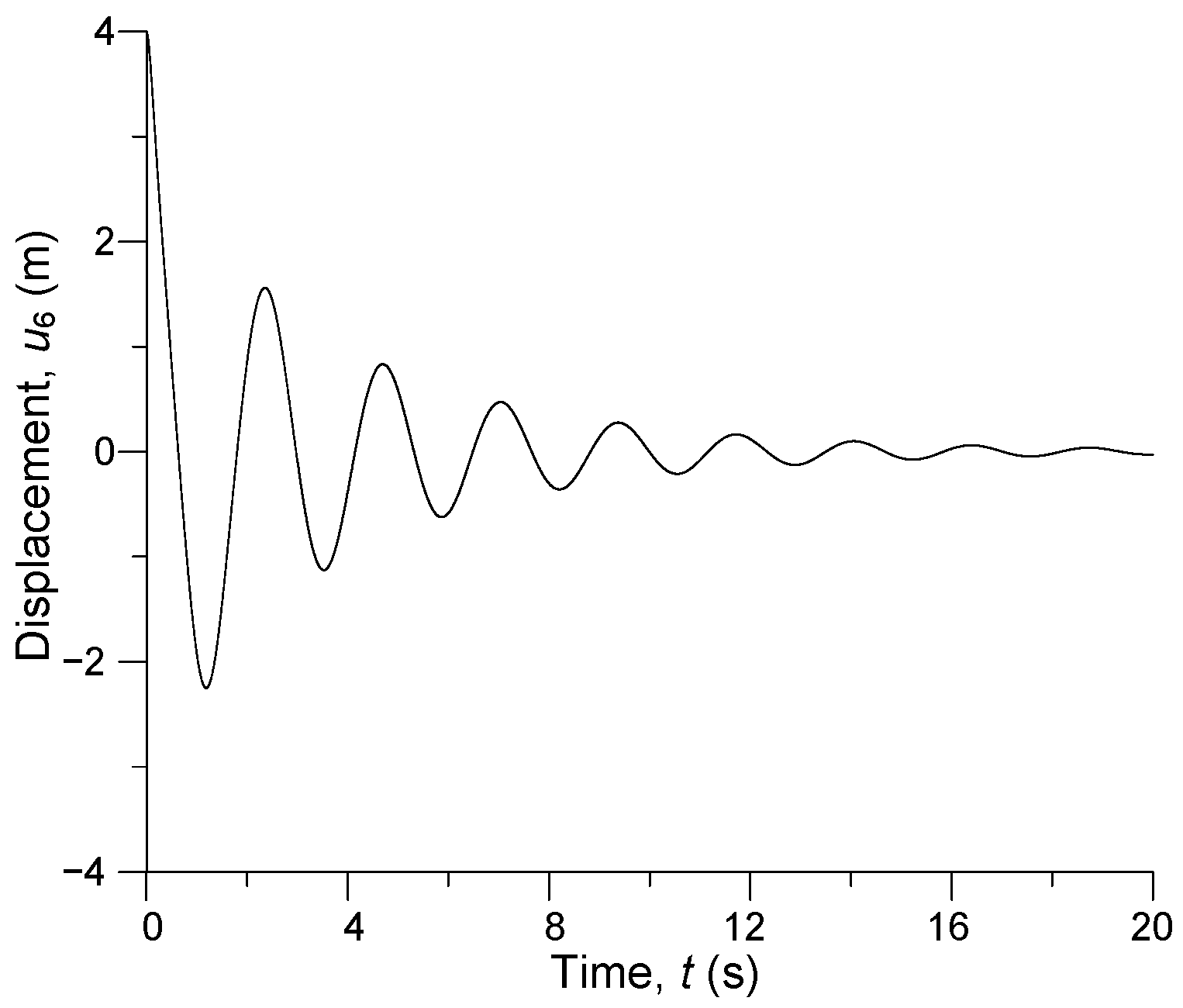
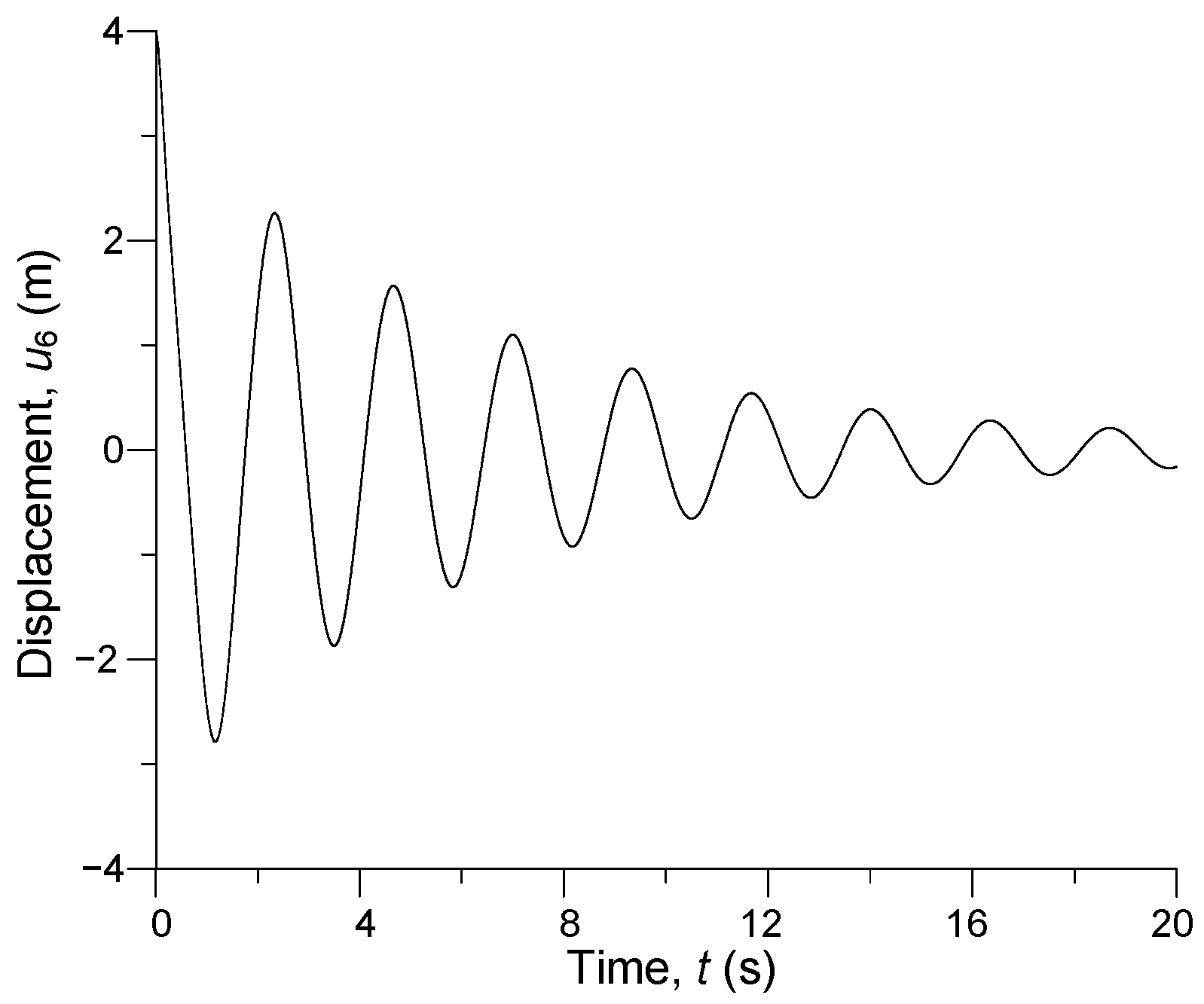

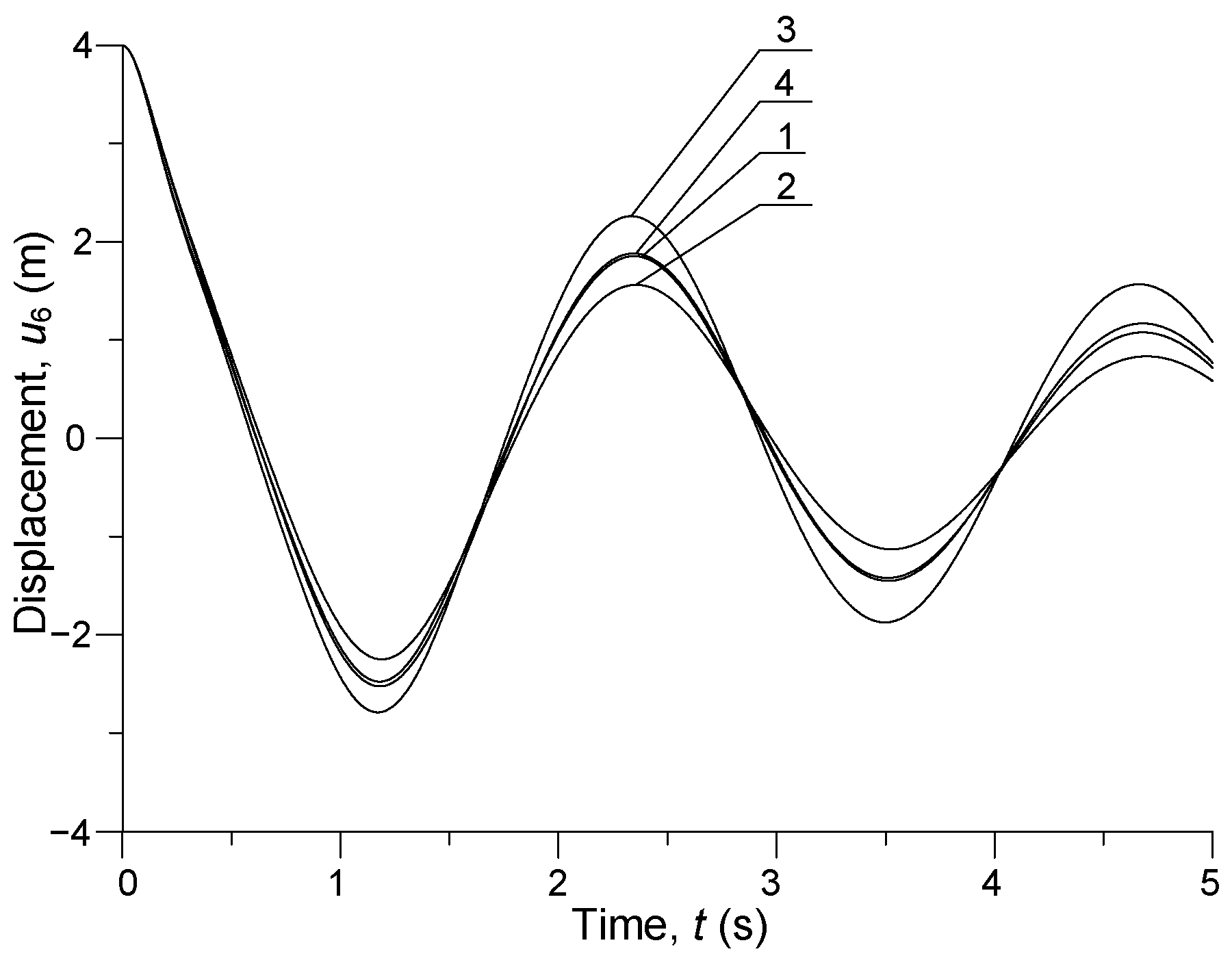
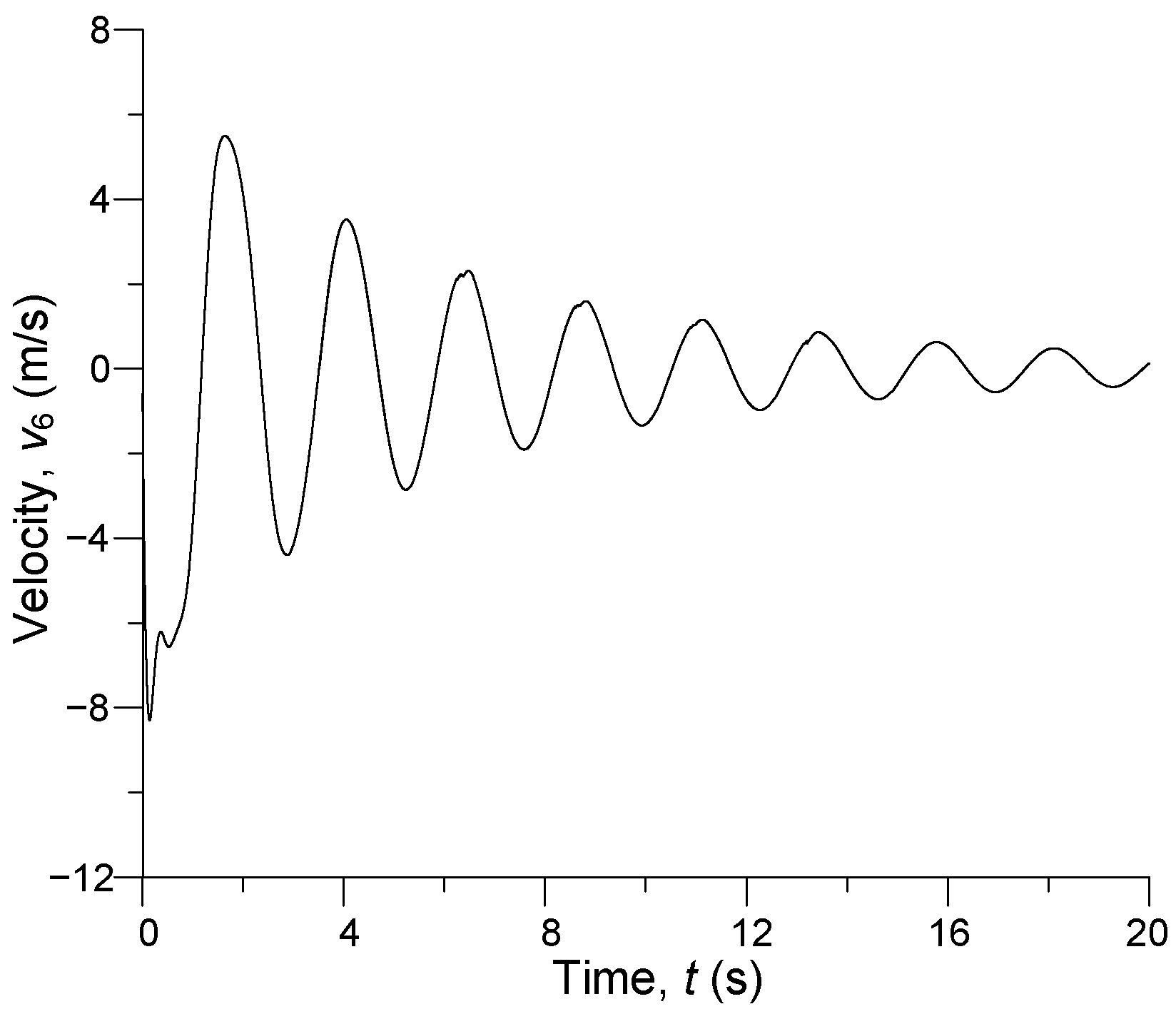

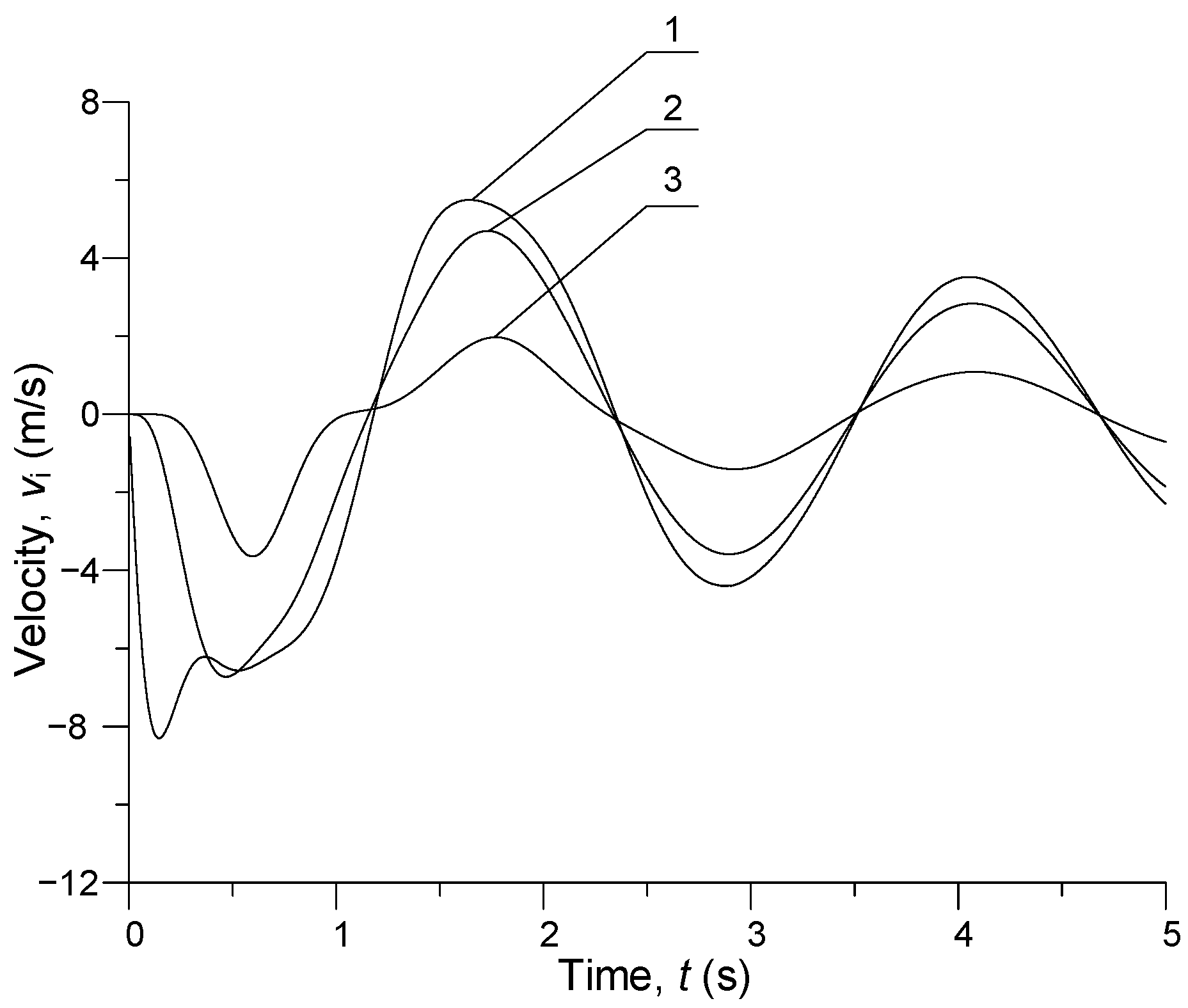
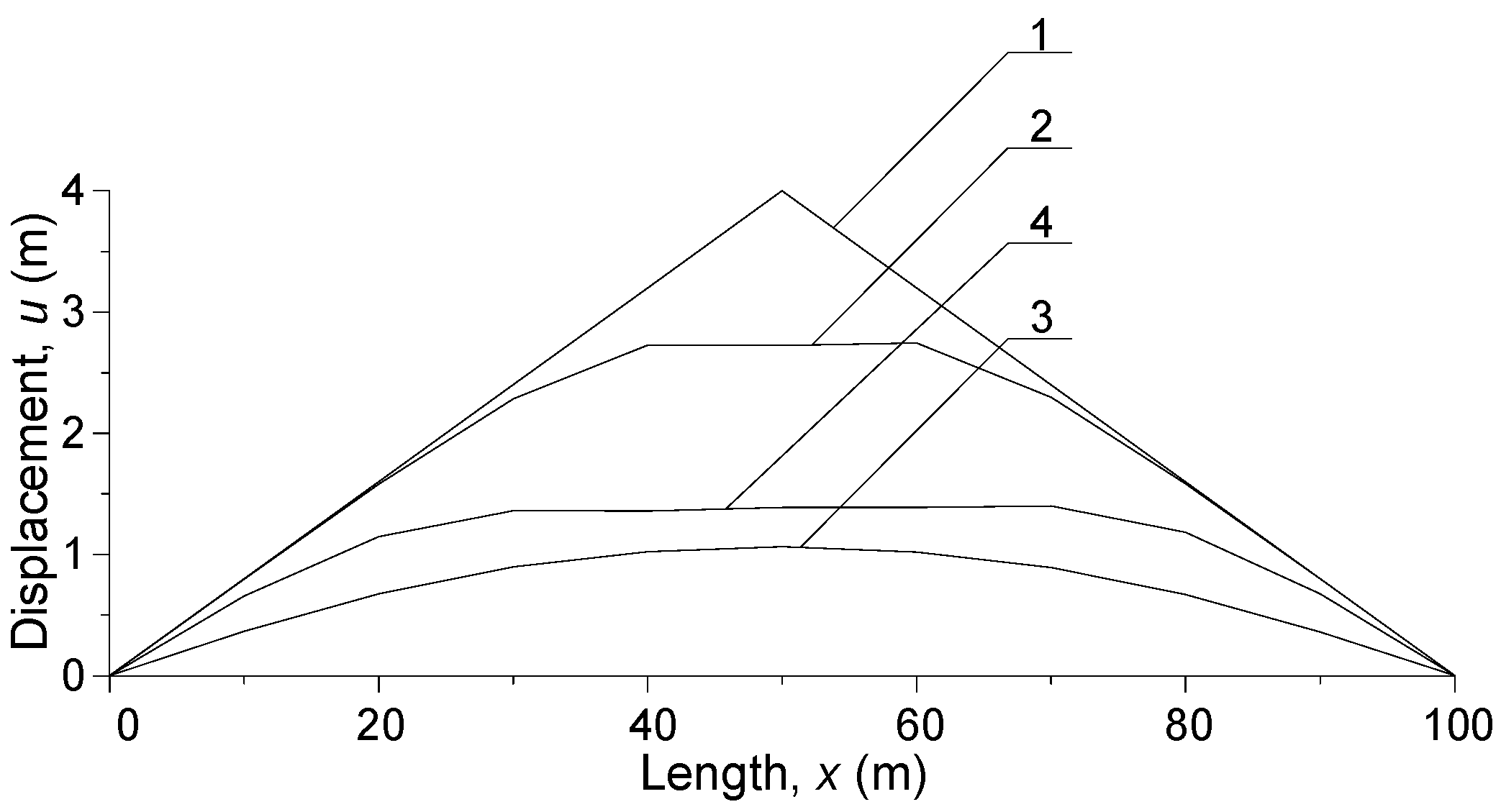


| u1 = u11, m | u2 = u10, m | u3 = u9, m | u4 = u8, m | u5 = u7, m | u6, m |
|---|---|---|---|---|---|
| 0.0 | 0.8 | 1.6 | 2.4 | 3.2 | 4.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chaban, A.; Pukach, P.; Perzyński, T.; Szafraniec, A.; Levoniuk, V.; Dydycz, A.; Arkanowicz, S. The Mathematical Modelling of Nonlinear String Oscillations in an Isotropic Viscoelastic Medium Using the Example of a Long Power Line. Energies 2025, 18, 6206. https://doi.org/10.3390/en18236206
Chaban A, Pukach P, Perzyński T, Szafraniec A, Levoniuk V, Dydycz A, Arkanowicz S. The Mathematical Modelling of Nonlinear String Oscillations in an Isotropic Viscoelastic Medium Using the Example of a Long Power Line. Energies. 2025; 18(23):6206. https://doi.org/10.3390/en18236206
Chicago/Turabian StyleChaban, Andriy, Petro Pukach, Tomasz Perzyński, Andrzej Szafraniec, Vitaliy Levoniuk, Aleksander Dydycz, and Szymon Arkanowicz. 2025. "The Mathematical Modelling of Nonlinear String Oscillations in an Isotropic Viscoelastic Medium Using the Example of a Long Power Line" Energies 18, no. 23: 6206. https://doi.org/10.3390/en18236206
APA StyleChaban, A., Pukach, P., Perzyński, T., Szafraniec, A., Levoniuk, V., Dydycz, A., & Arkanowicz, S. (2025). The Mathematical Modelling of Nonlinear String Oscillations in an Isotropic Viscoelastic Medium Using the Example of a Long Power Line. Energies, 18(23), 6206. https://doi.org/10.3390/en18236206








