A Si and SiC Hybrid Arms ANPC Converter Achieving Comprehensive Optimization of Power Quality, Efficiency, and Cost
Abstract
1. Introduction
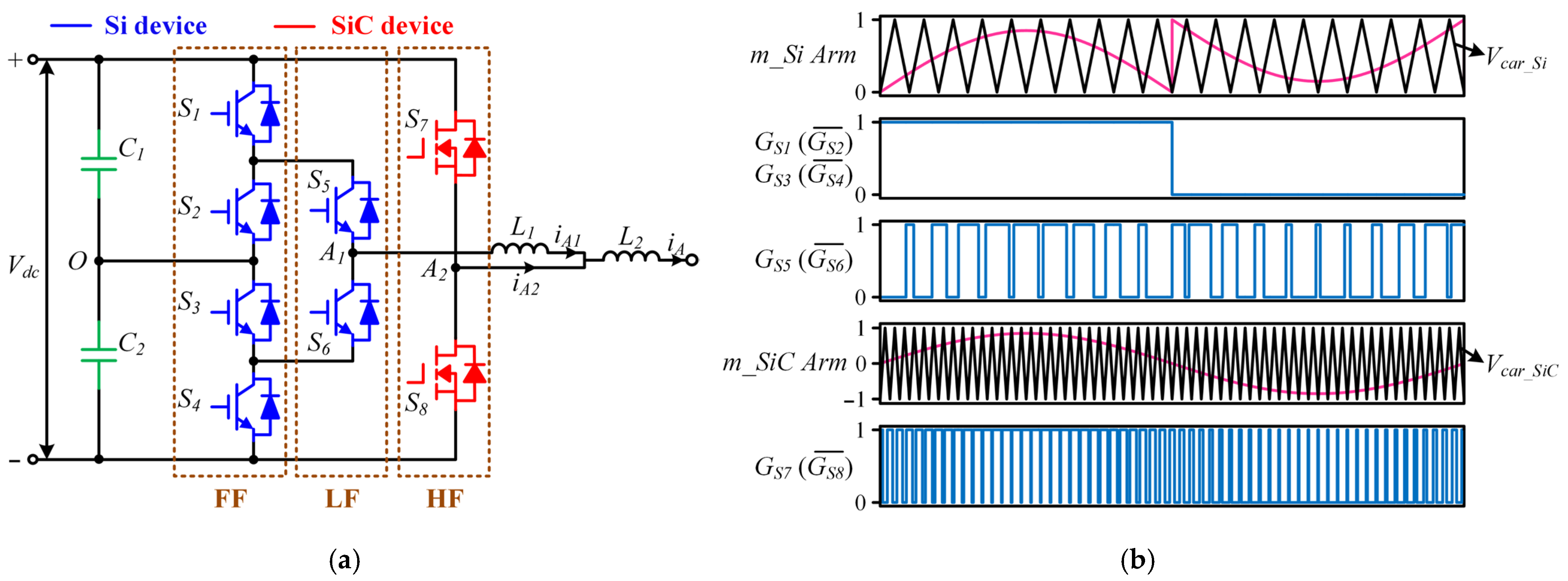
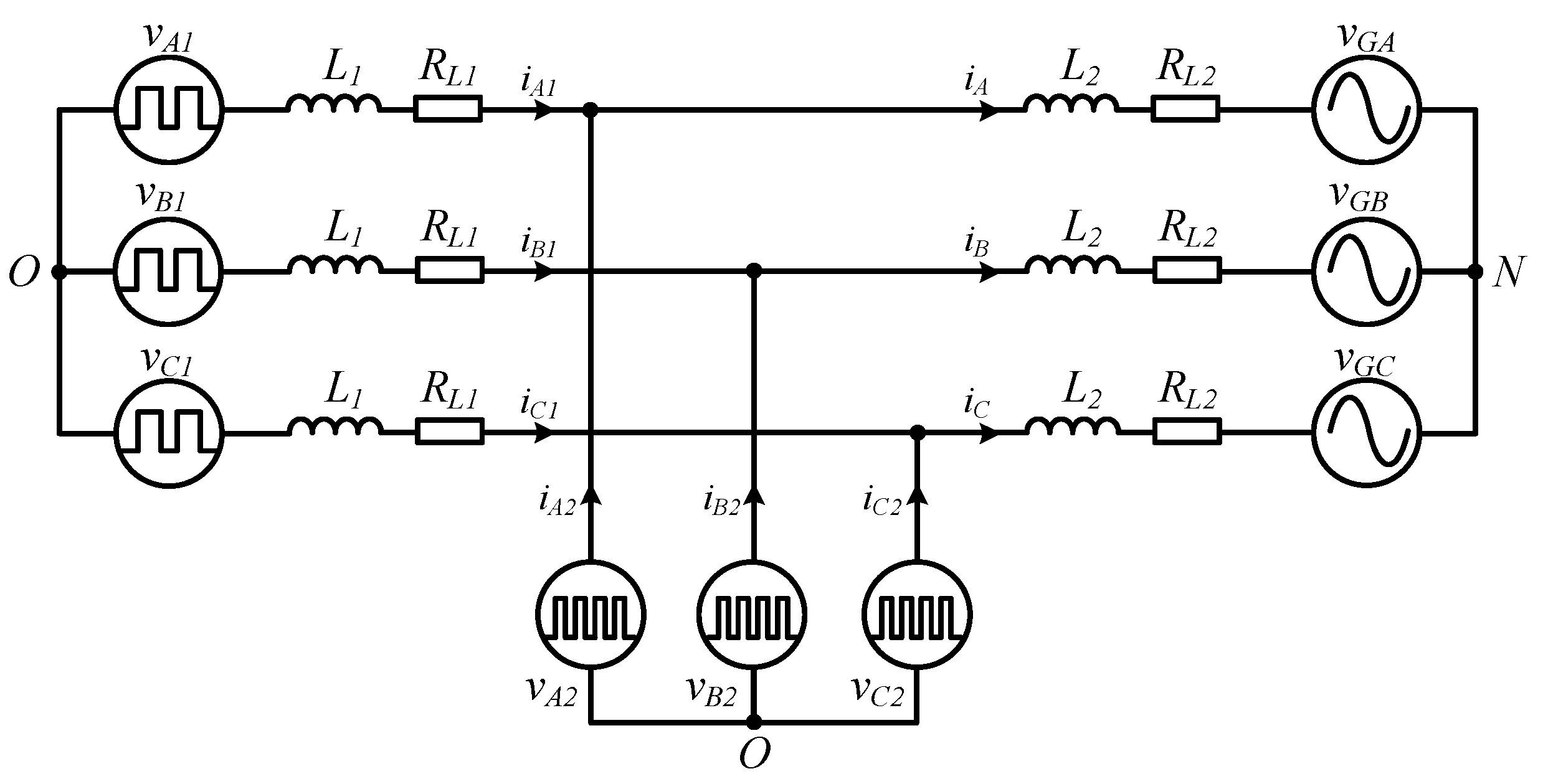
2. Proposed Hybrid Arms ANPC Converter
2.1. Topology and Modulation Scheme
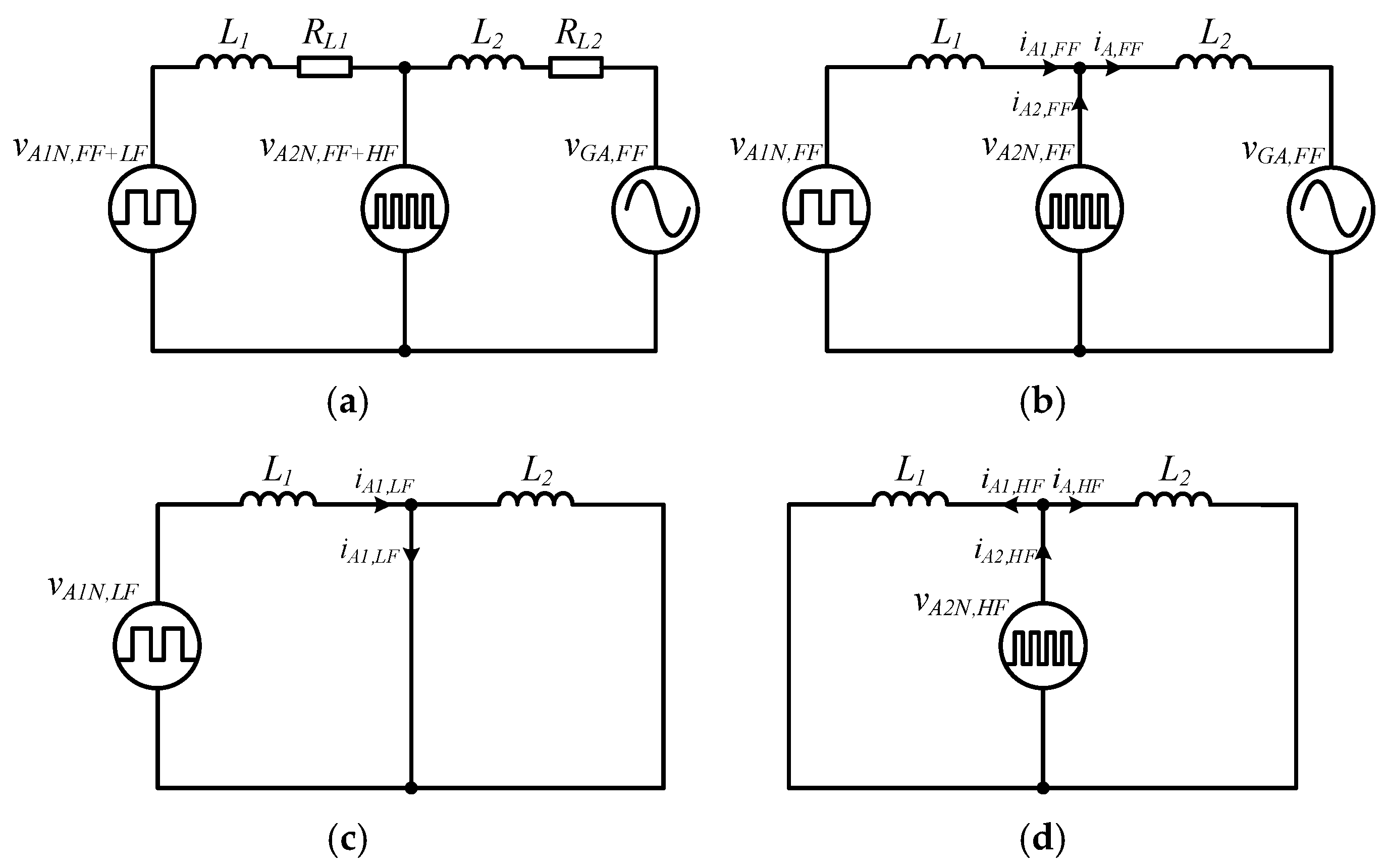
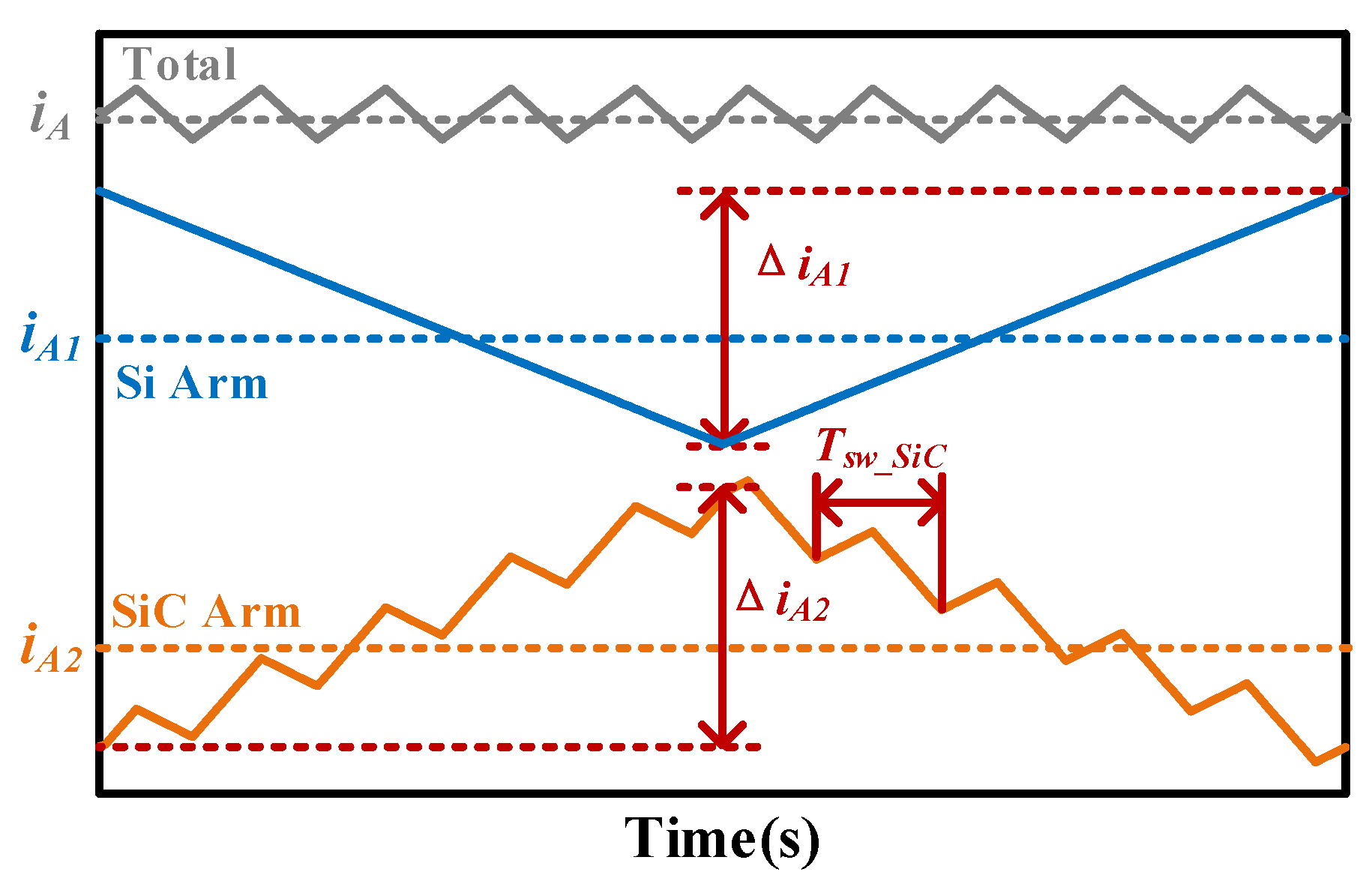
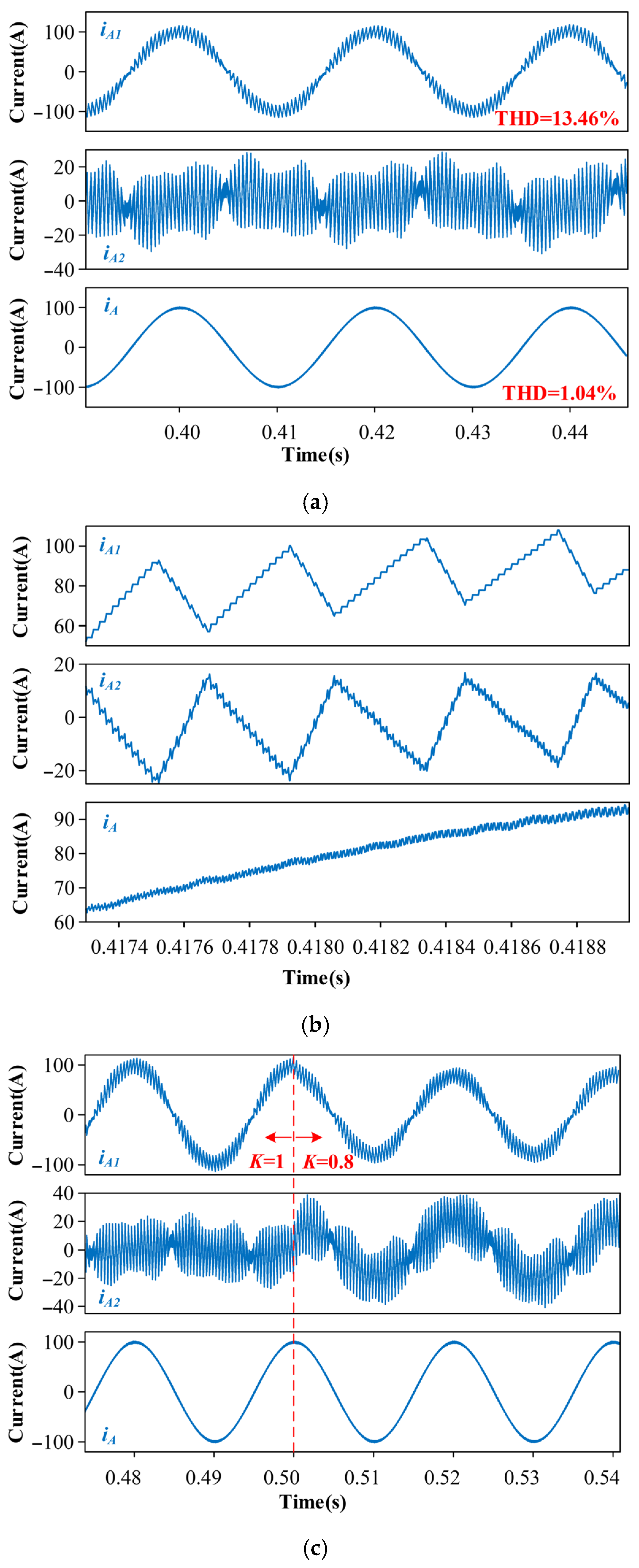
2.2. Operation Principle of Current Ripple Compensation
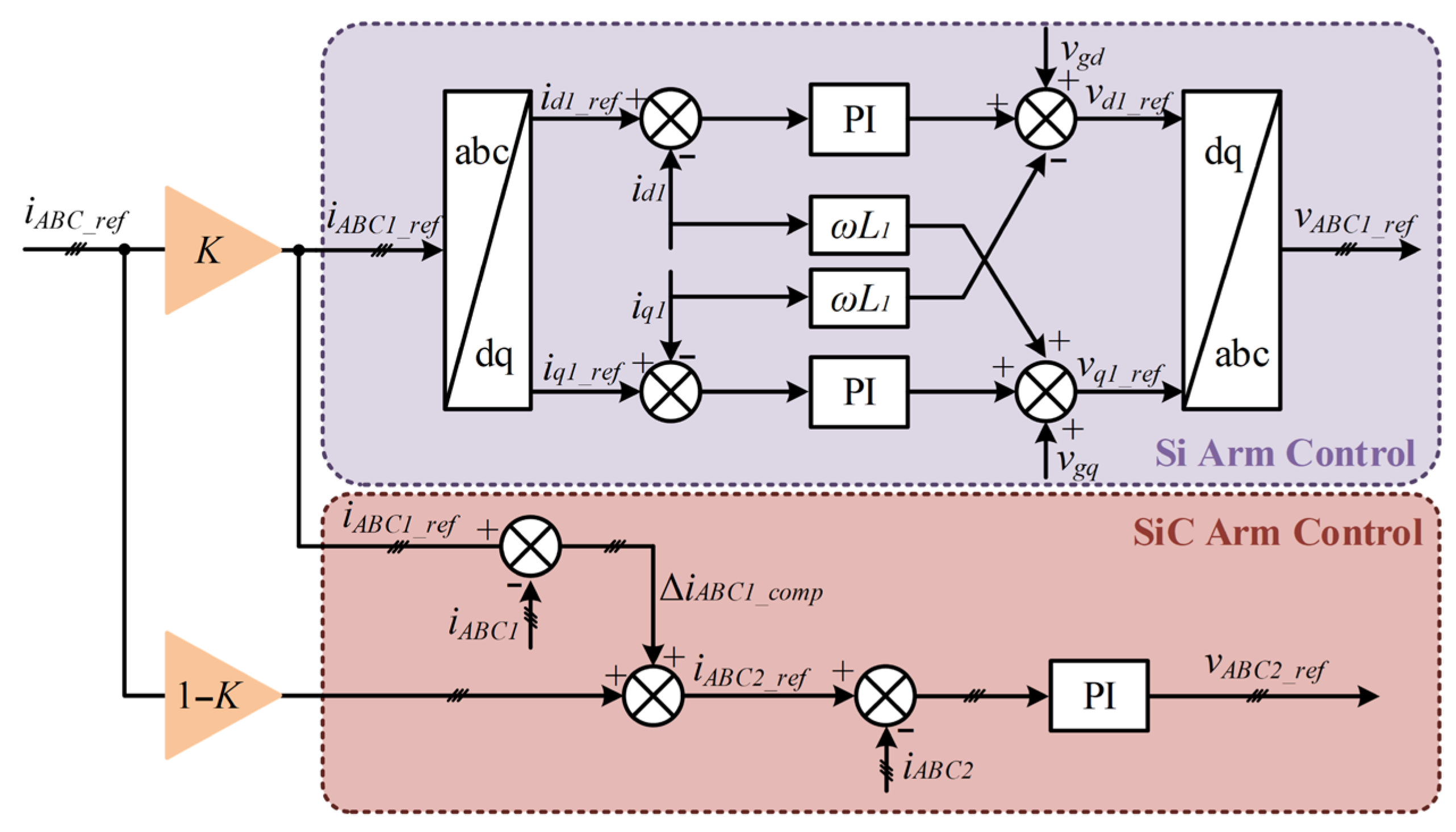
3. Proposed Current Control Strategy
3.1. Si Arm Current Control
3.2. SiC Arm Current Control
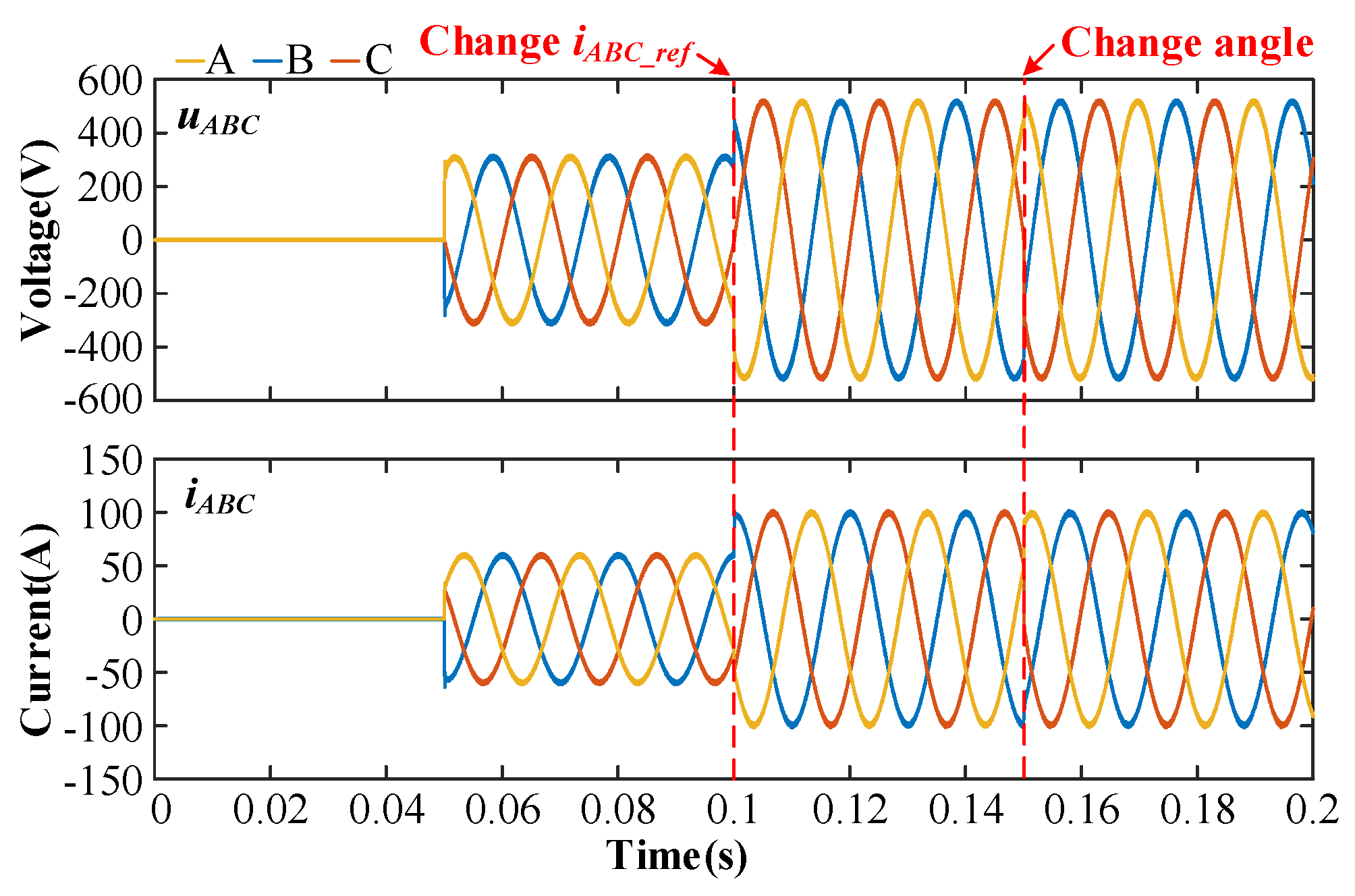
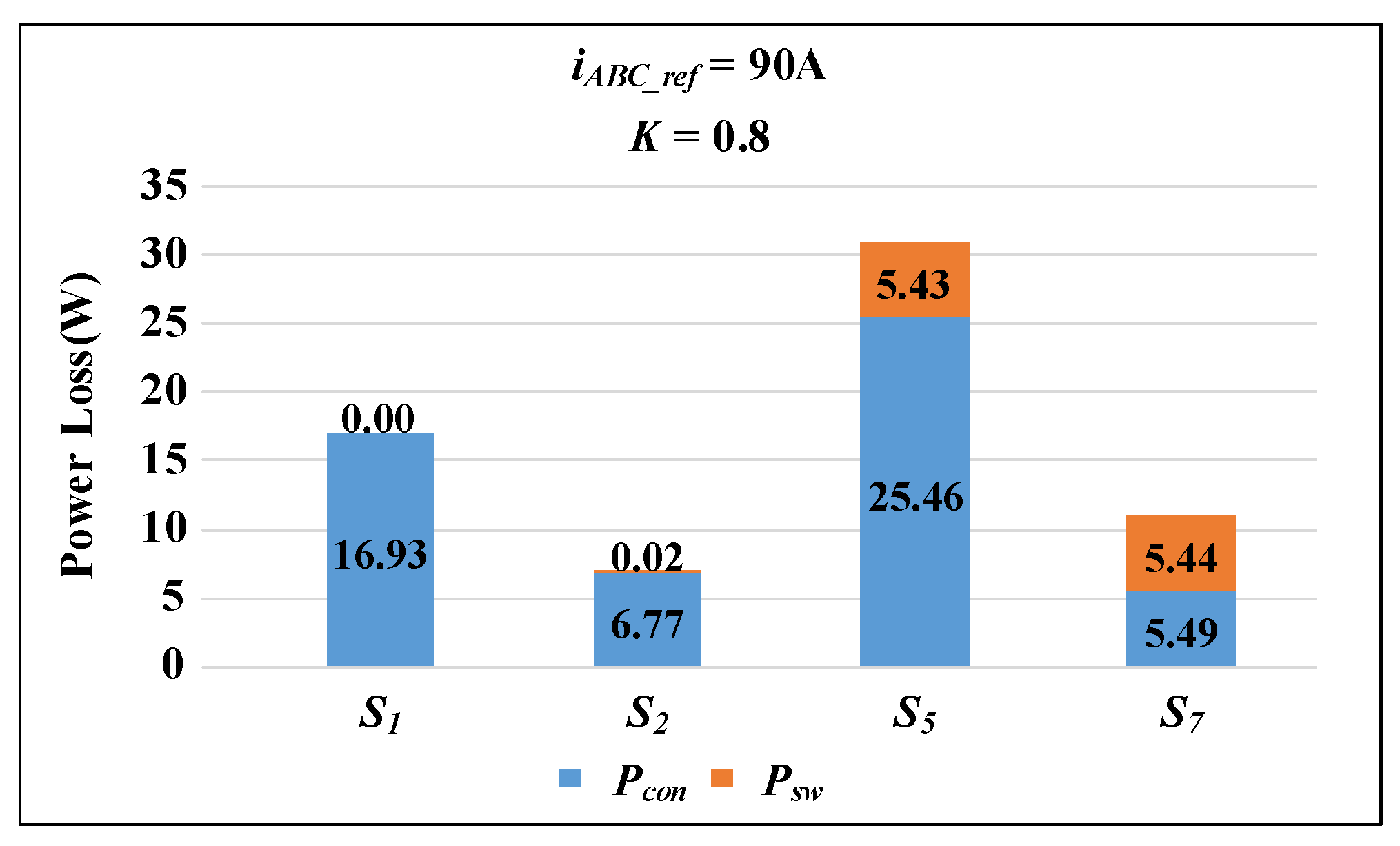
4. Simulation Verification
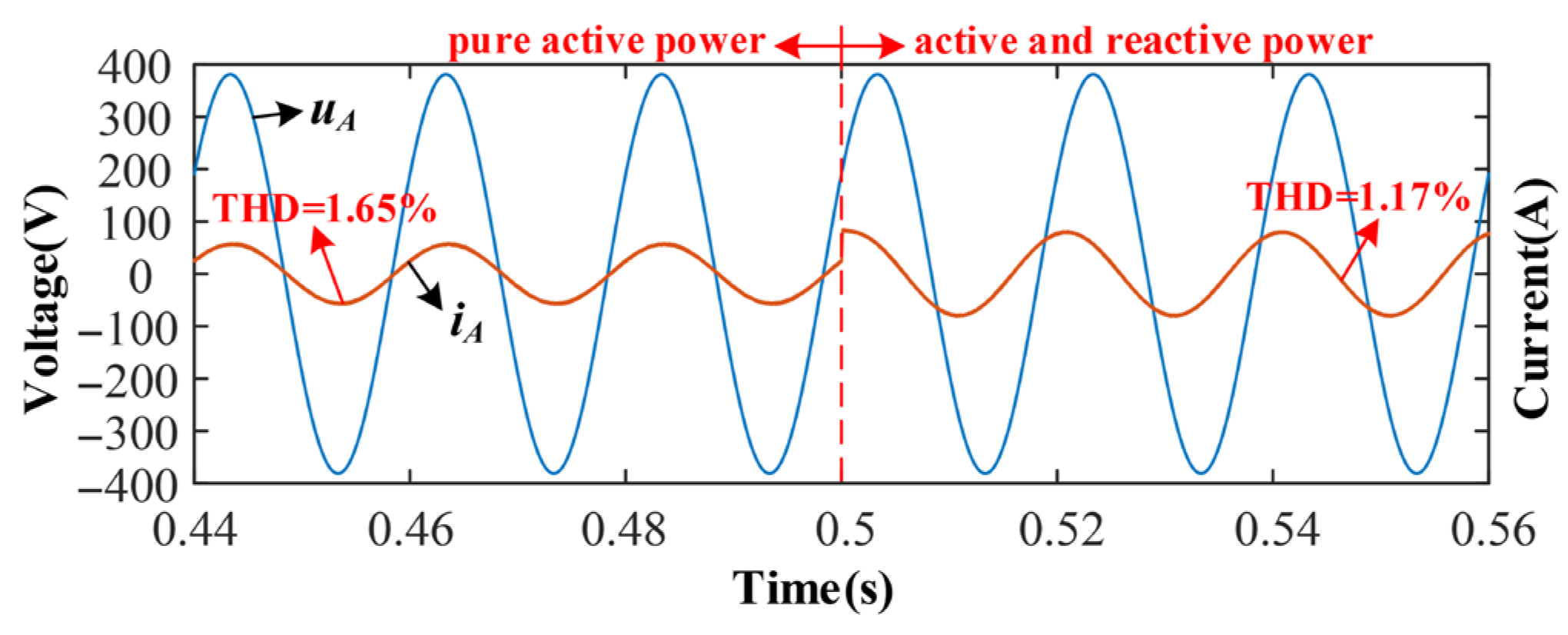
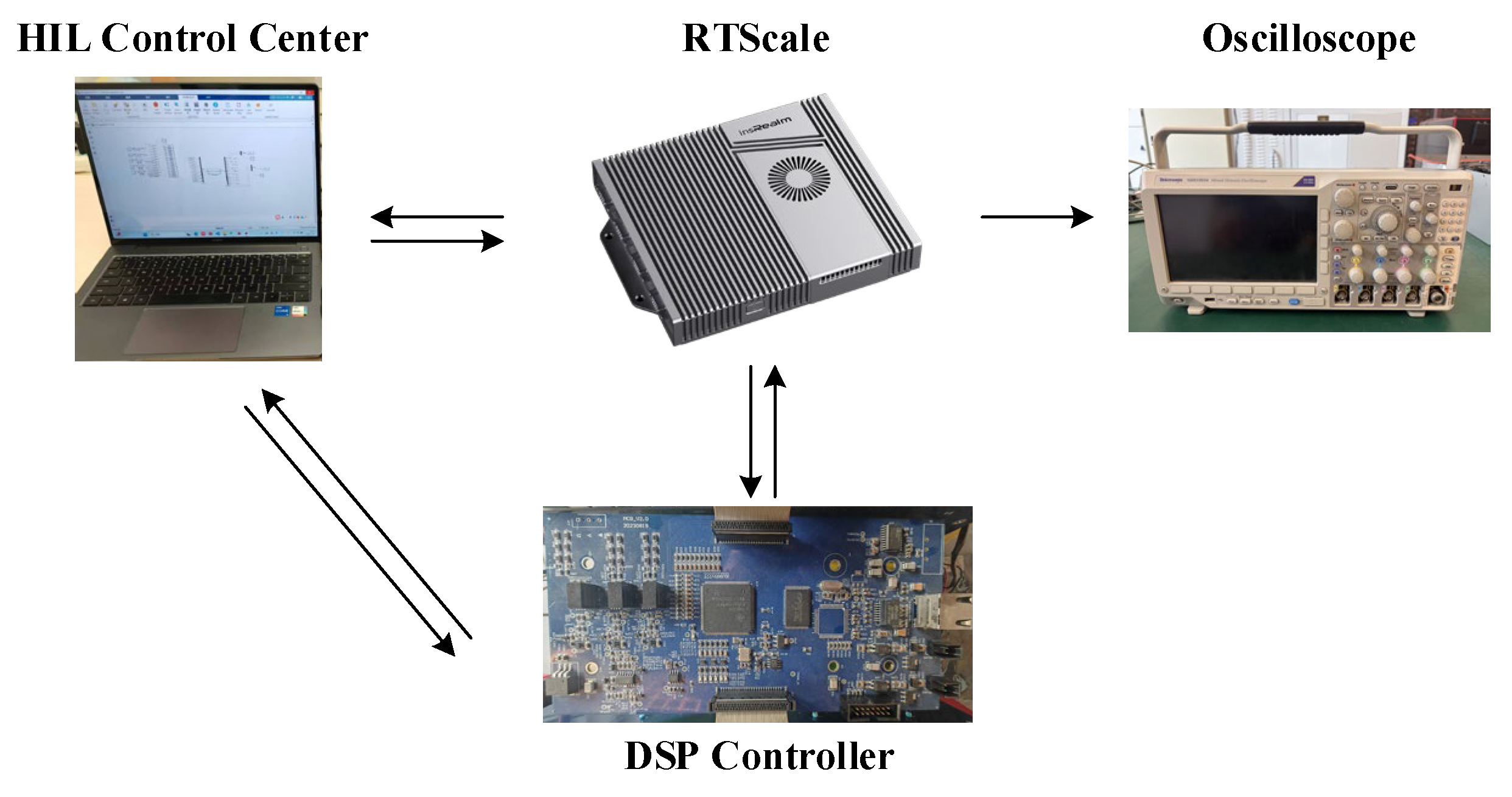
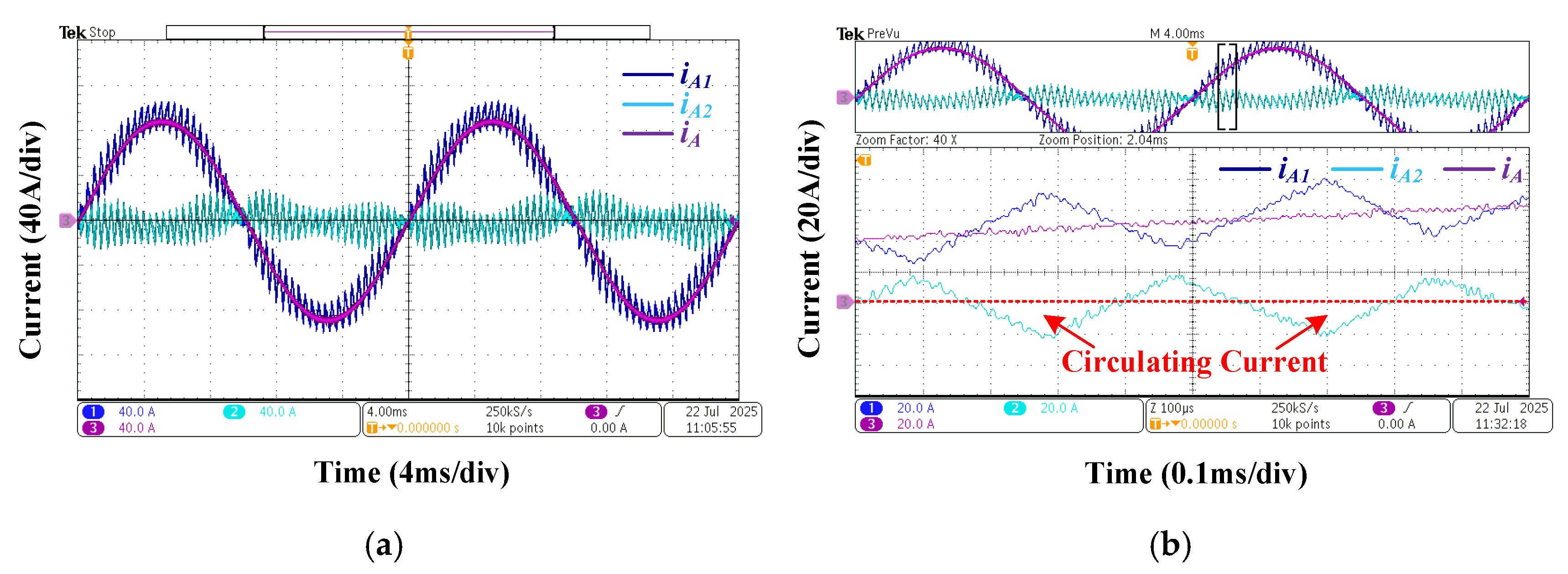
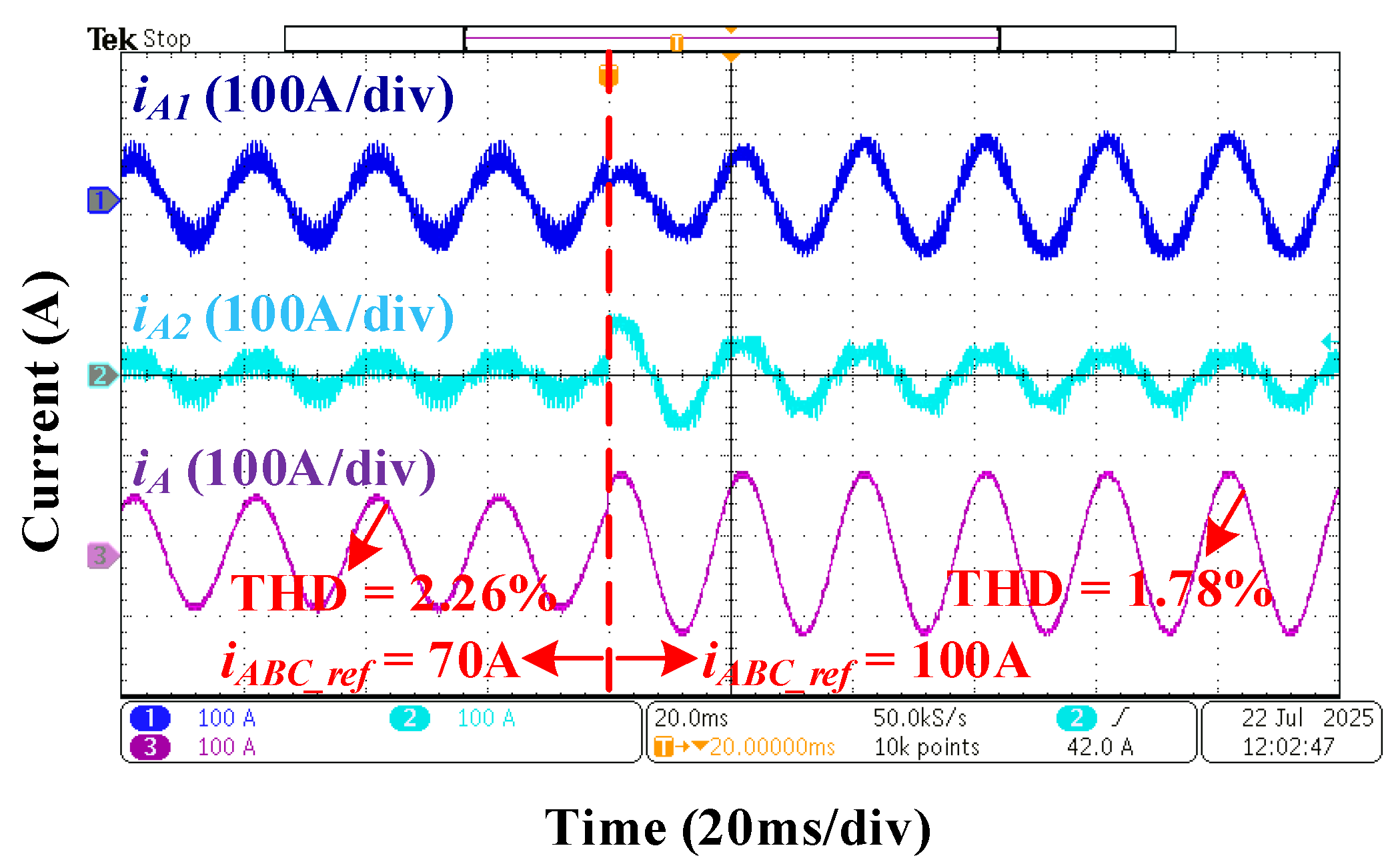
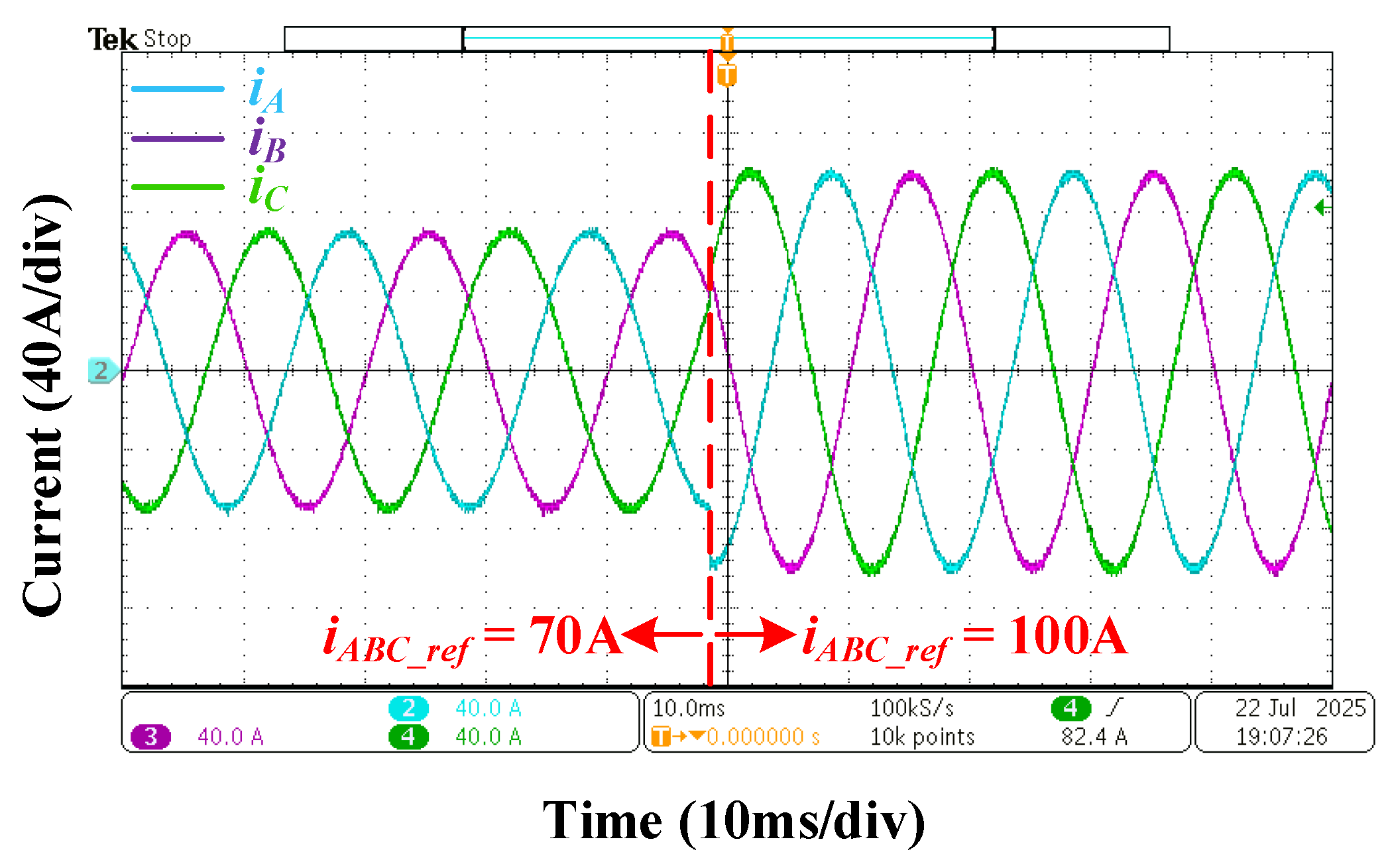
5. Experimental Results
6. Performance Comparison
6.1. Cost Comparison
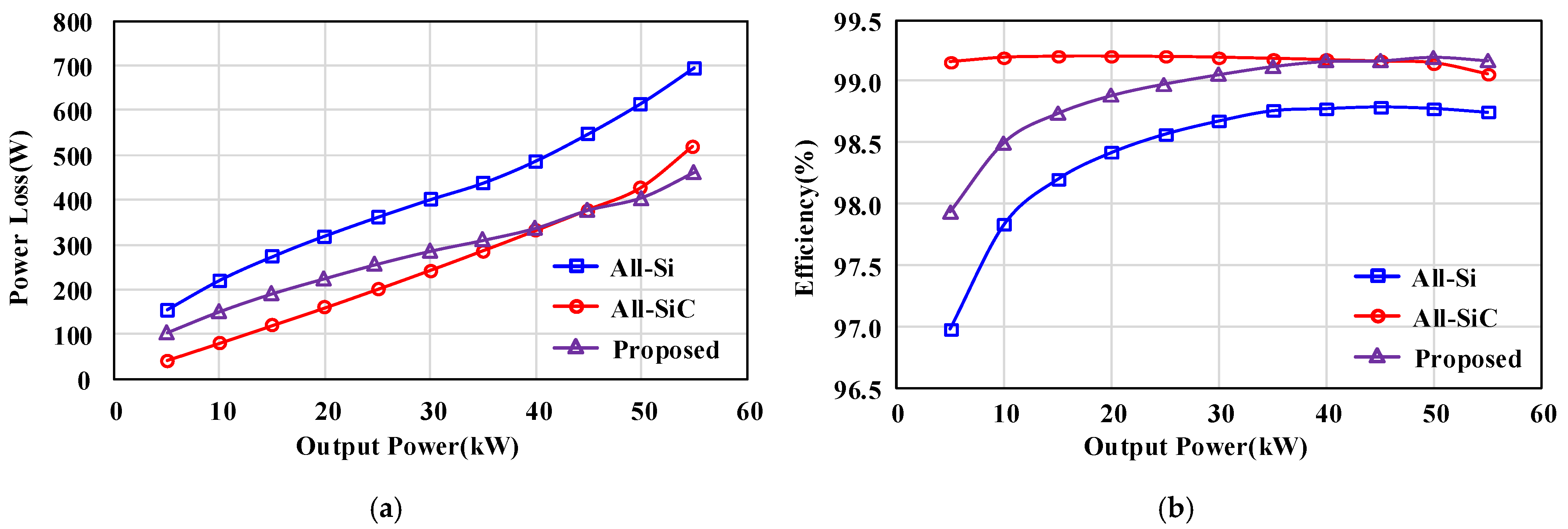
6.2. Efficiency Comparison
7. Conclusions
- (1)
- The proposed converter uses smaller current rating SiC devices, which can achieve more than 60% total cost reduction compared to the all-SiC 3L-ANPC converter.
- (2)
- Although the switching frequency of Si devices is decreased to reduce power losses, the equivalent switching frequency is equal to that of the all-SiC design. Thus, excellent power quality can be achieved.
- (3)
- By employing the hybrid-frequency modulation scheme and proposed current control strategy, the proposed converter can reduce 30–40% power losses compared to the all-Si converter in the full power range. Moreover, the efficiency under high-current conditions is higher than that of the all-SiC design.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| WBG | Wide bandgap |
| ANPC | Active neutral-point-clamped |
| FF | Fundamental frequency |
| LF | Low frequency |
| HF | High frequency |
| MEA | More electric aircraft |
| WFPP | WBG fractional power processing |
| HHB | Hybrid half-bridge |
| PFC | Power factor correction |
| 3L | Three-level |
| 5L | Five-level |
References
- Kouro, S.; Malinowski, M.; Gopakumar, K.; Pou, J.; Franquelo, L.G.; Wu, B.; Rodriguez, J.; Pérez, M.A.; Leon, J.I. Recent Advances and Industrial Applications of Multilevel Converters. IEEE Trans. Ind. Electron. 2010, 57, 2553–2580. [Google Scholar] [CrossRef]
- Blaabjerg, F.; Yang, Y.; Kim, K.A.; Rodriguez, J. Power Electronics Technology for Large-Scale Renewable Energy Generation. Proc. IEEE 2023, 111, 335–355. [Google Scholar] [CrossRef]
- Ali, A.; Mousa, H.H.H.; Shaaban, M.F.; Azzouz, M.A.; Awad, A.S.A. A Comprehensive Review on Charging Topologies and Power Electronic Converter Solutions for Electric Vehicles. J. Mod. Power Syst. Clean Energy 2024, 12, 675–694. [Google Scholar] [CrossRef]
- Wang, D.; Hemming, S.; Yang, Y.; Poorfakhraei, A.; Zhou, L.; Liu, C.; Emadi, A. Multilevel Inverters for Electric Aircraft Applications: Current Status and Future Trends. IEEE Trans. Transp. Electrif. 2024, 10, 3258–3282. [Google Scholar] [CrossRef]
- Kumar, R.; Singh, B.; Kant, P. Design and Analysis of a 54-Pulse Converter and 7-Level Hybrid Inverter for Medium Voltage Induction Motor Drive. IEEE Trans. Ind. Appl. 2023, 60, 560–572. [Google Scholar] [CrossRef]
- Millán, J.; Godignon, P.; Perpiñà, X.; Pérez-Tomás, A.; Rebollo, J. A Survey of Wide Bandgap Power Semiconductor Devices. IEEE Trans. Power Electron. 2014, 29, 2155–2163. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, C.; Li, C.; Xin, Z.; Chen, R.; Li, W.; He, X.; Ma, H. A SiC and Si Hybrid Five-Level Unidirectional Rectifier for Medium Voltage Applications. IEEE Trans. Ind. Electron. 2022, 69, 7537–7548. [Google Scholar] [CrossRef]
- Cai, Y.; Sun, P.; Chen, C.; Zhang, Y.; Zhao, Z.; Li, X.; Qi, L.; Chen, Z.; Nee, H.-P. Investigation on Gate Oxide Degradation of SiC MOSFET in Switching Operation. IEEE Trans. Power Electron. 2024, 39, 9565–9578. [Google Scholar] [CrossRef]
- Jiang, H.; Qi, X.; Qiu, G.; Zhong, X.; Tang, L.; Mao, H.; Wu, Z.; Chen, H.; Ran, L. A Physical Explanation of Threshold Voltage Drift of SiC MOSFET Induced by Gate Switching. IEEE Trans. Power Electron. 2022, 37, 8830–8834. [Google Scholar] [CrossRef]
- Kang, M.; Yu, S.; Xing, D.; Liu, T.; Salemi, A.; Booth, K.; Zhu, S.; White, M.H.; Agarwal, A.K. Body Diode Reliability of Commercial SiC Power MOSFETs. In Proceedings of the 2019 IEEE 7th Workshop on Wide Bandgap Power Devices and Applications (WiPDA), Raleigh, NC, USA, 29–31 October 2019; pp. 416–419. [Google Scholar]
- Zhang, D.; He, J.; Pan, D. A Megawatt-Scale Medium-Voltage High-Efficiency High Power Density “SiC+Si” Hybrid Three-Level ANPC Inverter for Aircraft Hybrid-Electric Propulsion Systems. IEEE Trans. Ind. Appl. 2019, 55, 5971–5980. [Google Scholar] [CrossRef]
- Lei, Z.; Zhuge, H.; Lou, X.; Zhang, L.; Tao, J. Performance Comparison of 4-SiC and 2-SiC Hybrid Three-Phase Three-Level ANPC Inverters. In Proceedings of the 2021 IEEE Sustainable Power and Energy Conference (iSPEC), Nanjing, China, 23–25 December 2021; pp. 3204–3209. [Google Scholar]
- Li, C.; Guan, Q.; Lei, J.; Li, C.; Zhang, Y.; Wang, S.; Xu, D.; Li, W.; Ma, H. An SiC MOSFET and Si Diode Hybrid Three-Phase High-Power Three-Level Rectifier. IEEE Trans. Power Electron. 2019, 34, 6076–6087. [Google Scholar] [CrossRef]
- Zhang, L.; Zheng, Z.; Li, C.; Ju, P.; Wu, F.; Gu, Y.; Chen, G. A Si/SiC Hybrid Five-Level Active NPC Inverter with Improved Modulation Scheme. IEEE Trans. Power Electron. 2020, 35, 4835–4846. [Google Scholar] [CrossRef]
- Zhang, Y.; He, J.; Padmanaban, S.; Ionel, D.M. Transistor-Clamped Multilevel H-Bridge Inverter in Si and SiC Hybrid Configuration for High-Efficiency Photovoltaic Applications. In Proceedings of the 2018 IEEE Energy Conversion Congress and Exposition (ECCE), Portland, OR, USA, 23–27 September 2018; pp. 2536–2542. [Google Scholar]
- Belkhode, S.; Shukla, A.; Doolla, S. Five-Level Hybrid Active-NPC H-Bridge Converter with Novel Space-Vector-Modulation Scheme. IEEE J. Emerg. Sel. Top. Power Electron. 2022, 10, 4146–4159. [Google Scholar] [CrossRef]
- Endres, J.; Ackva, A. A Parallel Three-Phase Converter System for Ripple Current Compensation and Passive Filter Reduction. In Proceedings of the 2015 17th European Conference on Power Electronics and Applications (EPE’15 ECCE-Europe), Geneva, Switzerland, 8–10 September 2015; pp. 1–9. [Google Scholar]
- Kundu, A.; Na, R.; Amir, A.; Zhou, Y.; Brown, I.P.; John Shen, Z. WBG Fractional Power Processing: A New Si-SiC Hybrid Voltage Source Inverter Design. In Proceedings of the 2020 IEEE Energy Conversion Congress and Exposition (ECCE), Detroit, MI, USA, 11–15 October 2020; pp. 6226–6231. [Google Scholar]
- Kundu, A.; Na, R.; Amir, A.; Shen, Z.J. Optimization Strategy of WBG Fractional Power Processing. In Proceedings of the 2021 IEEE Applied Power Electronics Conference and Exposition (APEC), Phoenix, AZ, USA, 14–17 June 2021; pp. 896–901. [Google Scholar]
- Zhang, C.; Wang, J.; Qu, K.; Hu, B.; Li, Z.; Yin, X.; Shen, Z.J. WBG and Si Hybrid Half-Bridge Power Processing Toward Optimal Efficiency, Power Quality, and Cost Tradeoff. IEEE Trans. Power Electron. 2022, 37, 6844–6856. [Google Scholar] [CrossRef]
- Zhang, C.; Qu, K.; Hu, B.; Wang, J.; Yin, X.; Shen, Z.J. A High-Frequency Dynamically Coordinated Hybrid Si/SiC Interleaved CCM Totem-Pole Bridgeless PFC Converter. IEEE J. Emerg. Sel. Top. Power Electron. 2022, 10, 2088–2100. [Google Scholar] [CrossRef]
- Zhang, C.; Yuan, X.; Wang, J.; Hu, B.; Yin, X.; Shen, Z.J. Optimization of Power Sharing and Switching Frequency in Si/WBG Hybrid Half-Bridge Converters Using Power Loss Models. IEEE J. Emerg. Sel. Top. Power Electron. 2023, 11, 2837–2849. [Google Scholar] [CrossRef]
- Zhang, C.; Yuan, X.; Wang, J.; Chen, W.; Hu, B.; Shen, Z.J. Adaptive Power Sharing and Switching Frequency Control for Power Loss Optimization in WBG/Si Hybrid Half-Bridge Converters. IEEE Trans. Power Electron. 2023, 38, 4440–4450. [Google Scholar] [CrossRef]




| Parameter | Value |
|---|---|
| DC Bus Voltage Vdc | 800 V |
| Fundamental Frequency fb | 50 Hz |
| Si Arm Switching Frequency fsw_Si | 2.5 kHz |
| SiC Arm Switching Frequency fsw_SiC | 50 kHz |
| Si Arm Filter Inductance L1 | 1 mH |
| SiC Arm Filter Inductance L2 | 500 μH |
| Load Resistor Rload | 3 Ω |
| Components | All-SiC | All-Si | Proposed |
|---|---|---|---|
| SiC MOSFET | C3M0015065K ($35.20 × 6) | / | C3M0040120K1 ($11.19 × 2) |
| Si IGBT | / | IKZ75N65EL5 ($4.01 × 6) | IKZ75N65EL5 ($4.01 × 6) |
| Driver IC | UCC21732 ($2.22 × 3) | UCC21732 ($2.22 × 3) | UCC21732 ($2.22 × 4) |
| Current Sensor | CASR 50-NP ($9.92 × 1) | CASR 50-NP ($9.92 × 1) | CASR 50-NP ($9.92 × 1) CASR 15-NP ($9.06 × 1) |
| Total Cost | $227.78 | $40.64 | $74.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xia, T.; Feng, X.; An, Z.; Li, M.; Li, C.; Luo, H.; Yang, H. A Si and SiC Hybrid Arms ANPC Converter Achieving Comprehensive Optimization of Power Quality, Efficiency, and Cost. Energies 2025, 18, 6198. https://doi.org/10.3390/en18236198
Xia T, Feng X, An Z, Li M, Li C, Luo H, Yang H. A Si and SiC Hybrid Arms ANPC Converter Achieving Comprehensive Optimization of Power Quality, Efficiency, and Cost. Energies. 2025; 18(23):6198. https://doi.org/10.3390/en18236198
Chicago/Turabian StyleXia, Tianlun, Xinchun Feng, Ziyang An, Meifang Li, Chushan Li, Haoze Luo, and Huan Yang. 2025. "A Si and SiC Hybrid Arms ANPC Converter Achieving Comprehensive Optimization of Power Quality, Efficiency, and Cost" Energies 18, no. 23: 6198. https://doi.org/10.3390/en18236198
APA StyleXia, T., Feng, X., An, Z., Li, M., Li, C., Luo, H., & Yang, H. (2025). A Si and SiC Hybrid Arms ANPC Converter Achieving Comprehensive Optimization of Power Quality, Efficiency, and Cost. Energies, 18(23), 6198. https://doi.org/10.3390/en18236198







