Design and Optimization of Current-Fed Dual Active Bridge Converter with Dual Coupled-Inductor Structure
Abstract
1. Introduction
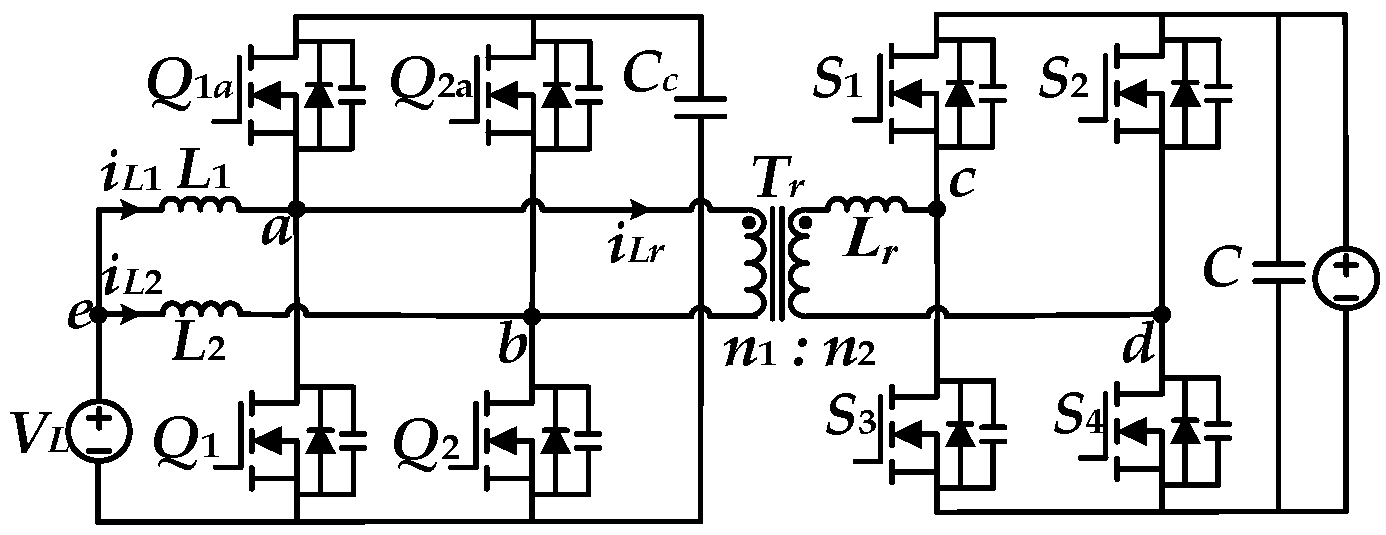
2. Current-Fed Dual Active Bridge Converter Modification Based on Magnetic Components Integration
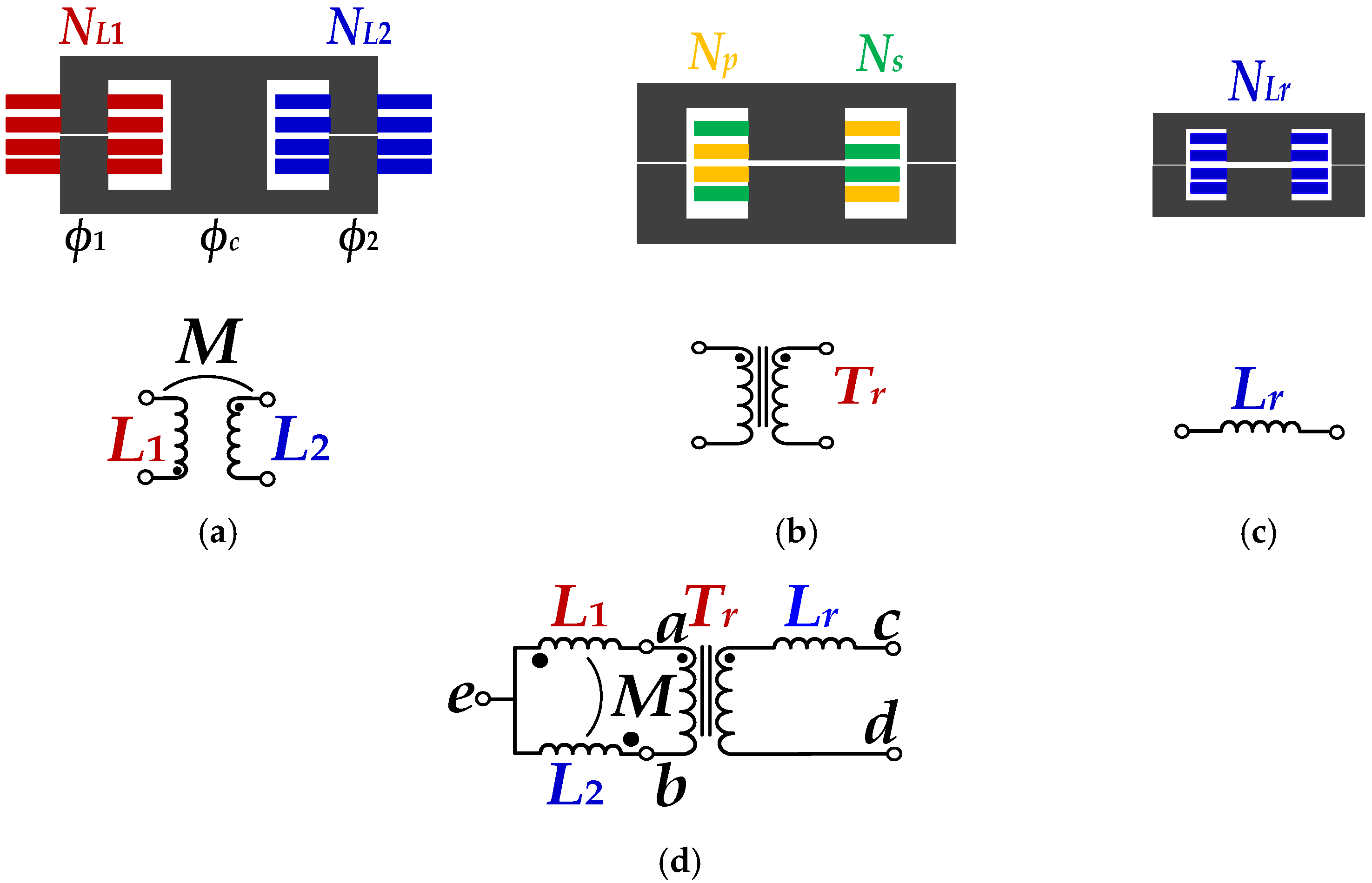
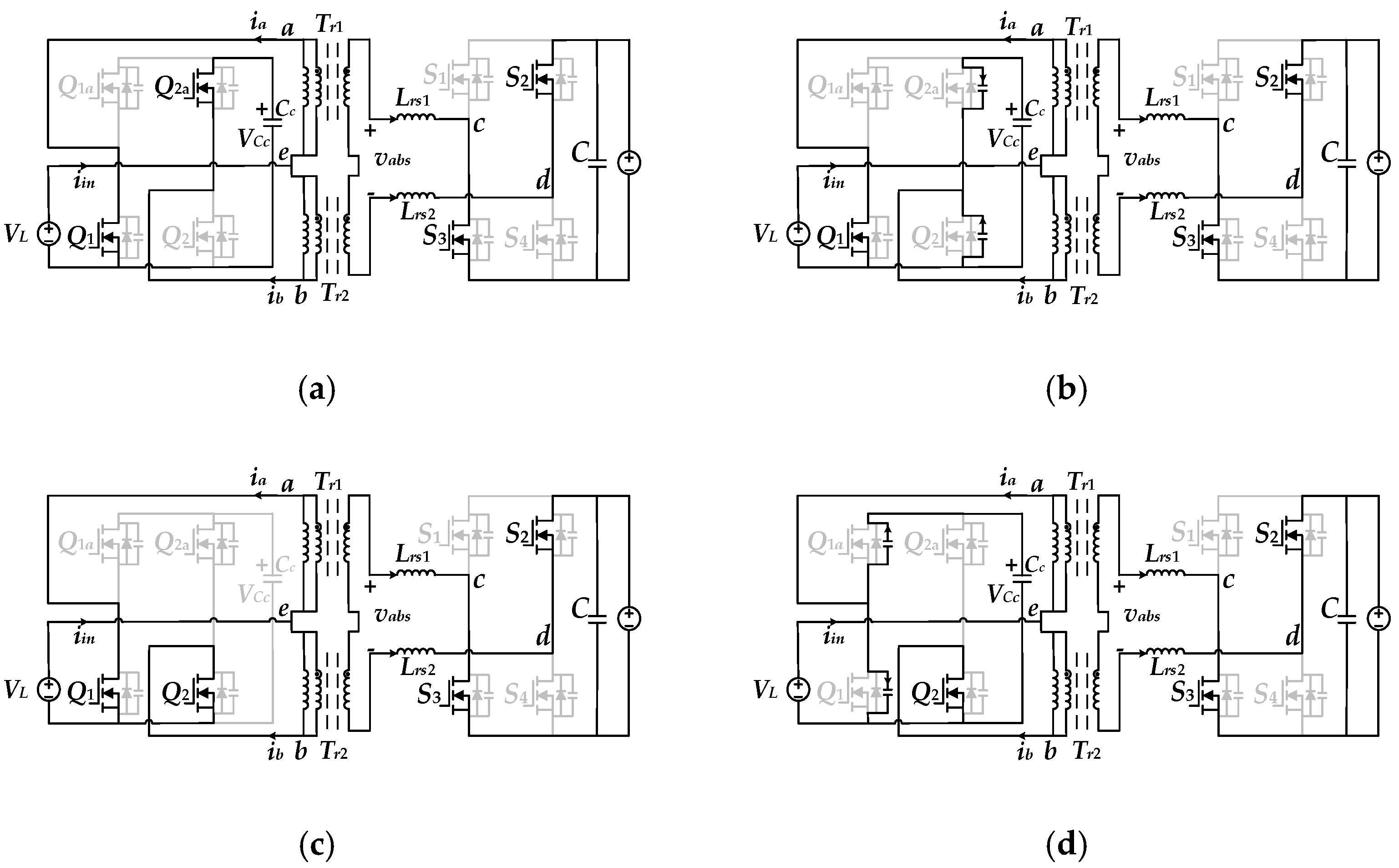
2.1. The Proposed Converter Derivation with DCI Structure
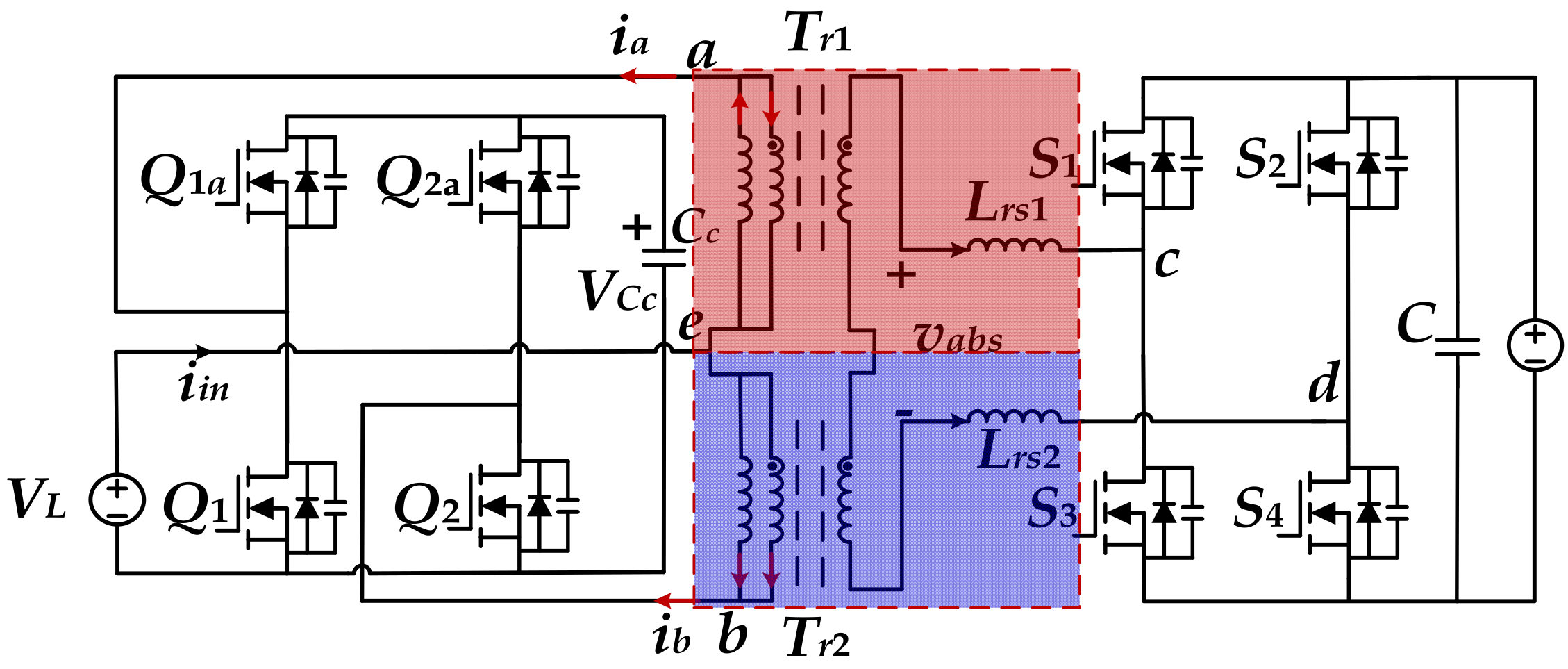
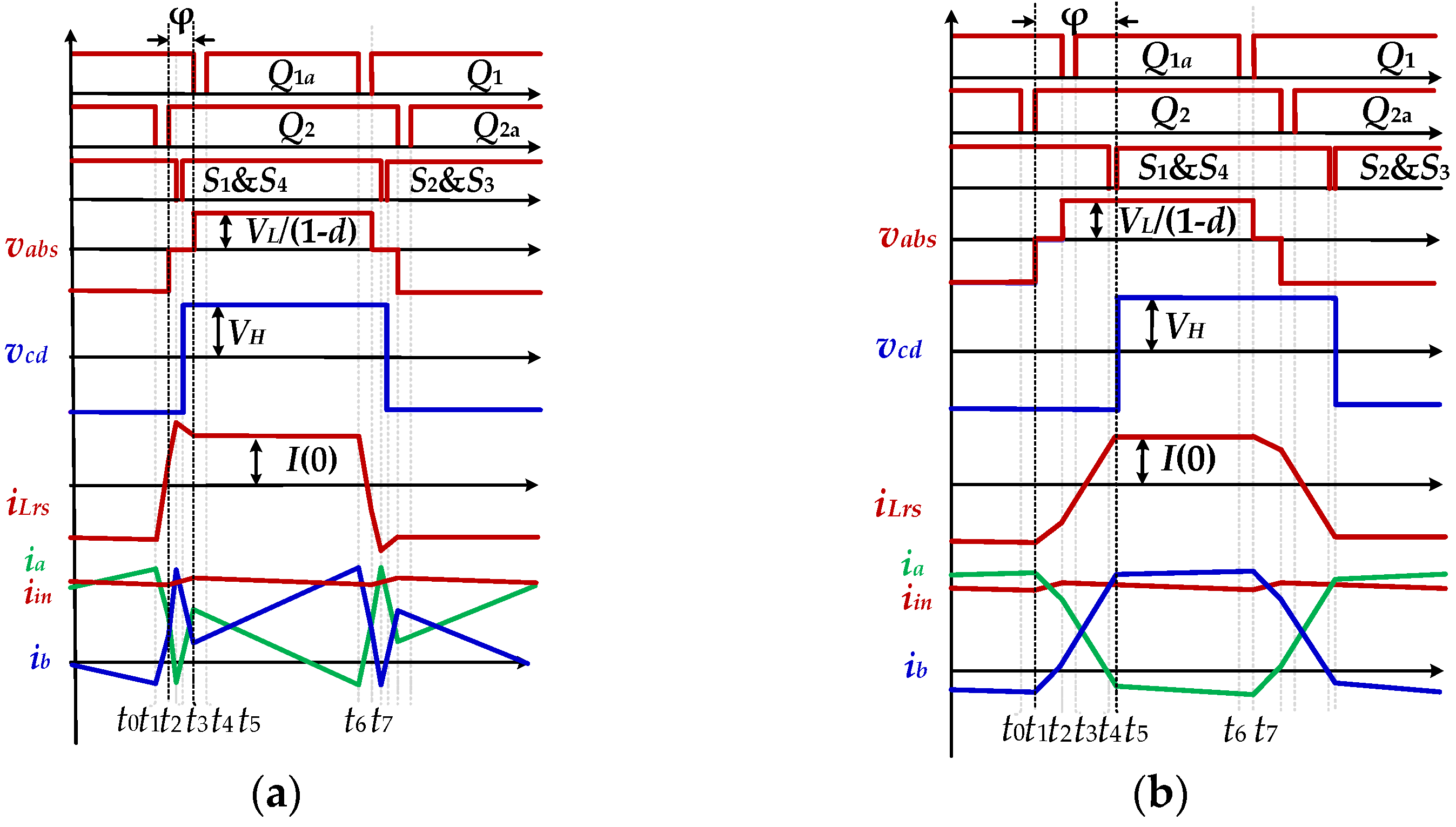
2.2. The Principle of the Proposed Converter with DCI Structure
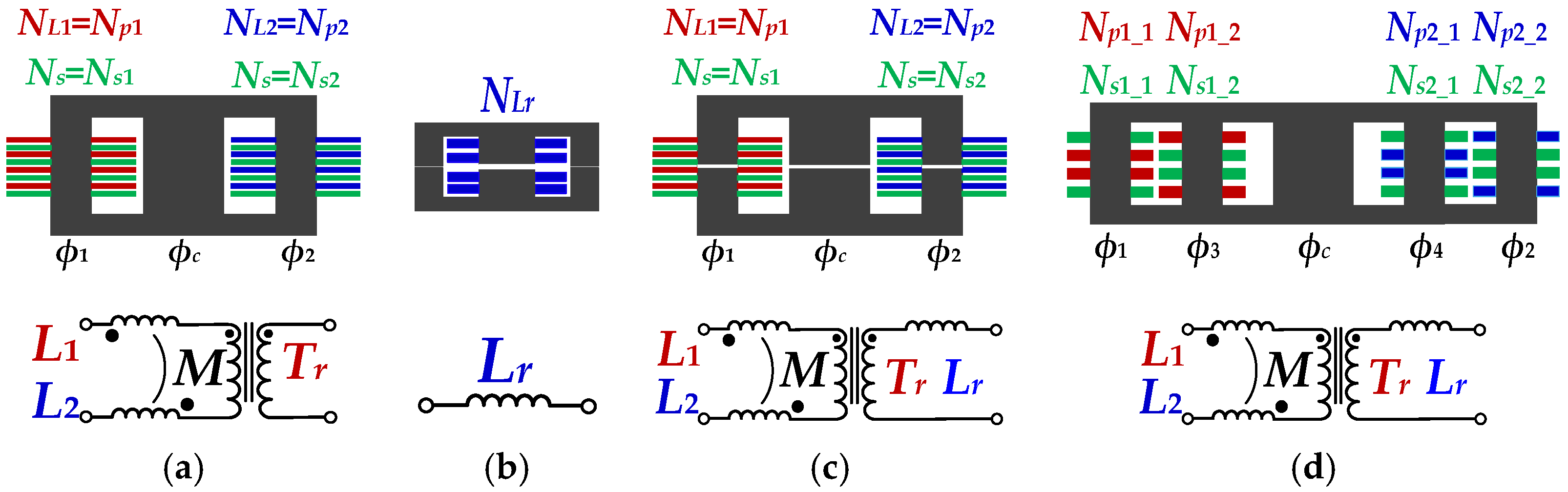
3. Design and Optimization of Planar Integrated DCI Structure
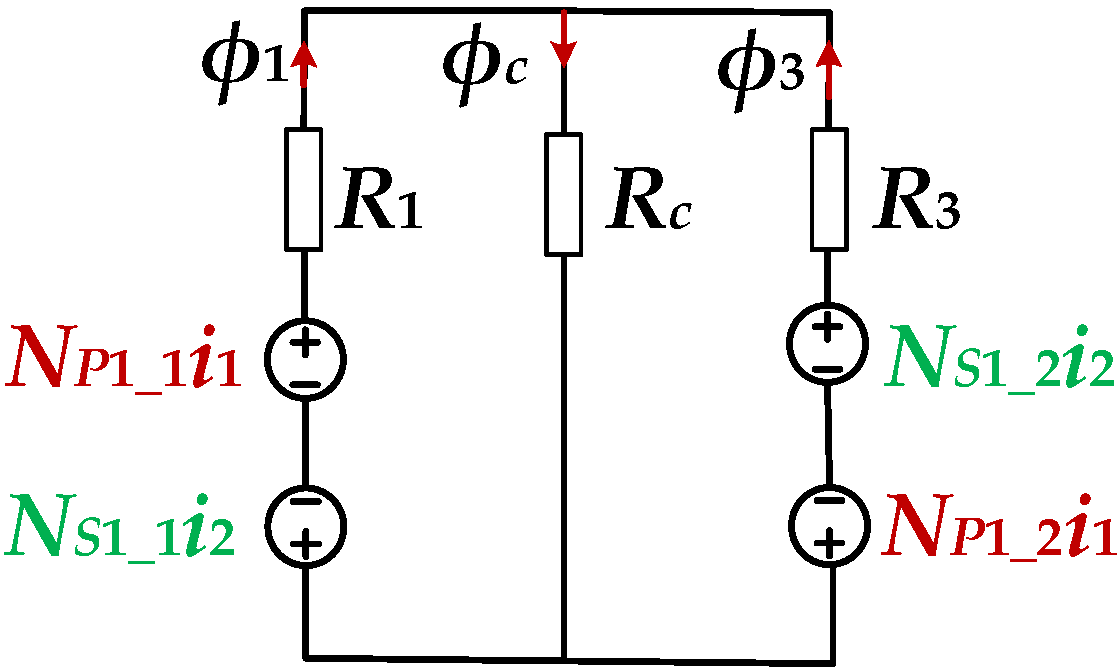
3.1. Design of Equal Air Gap Length
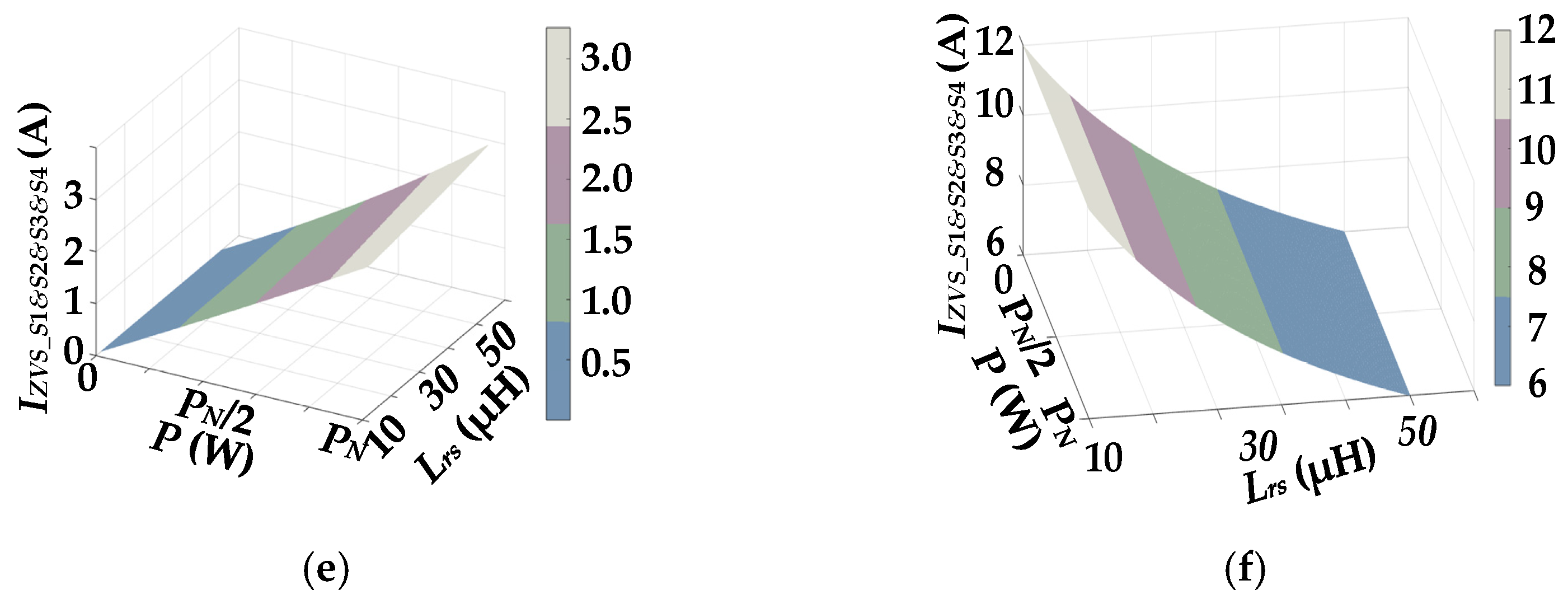
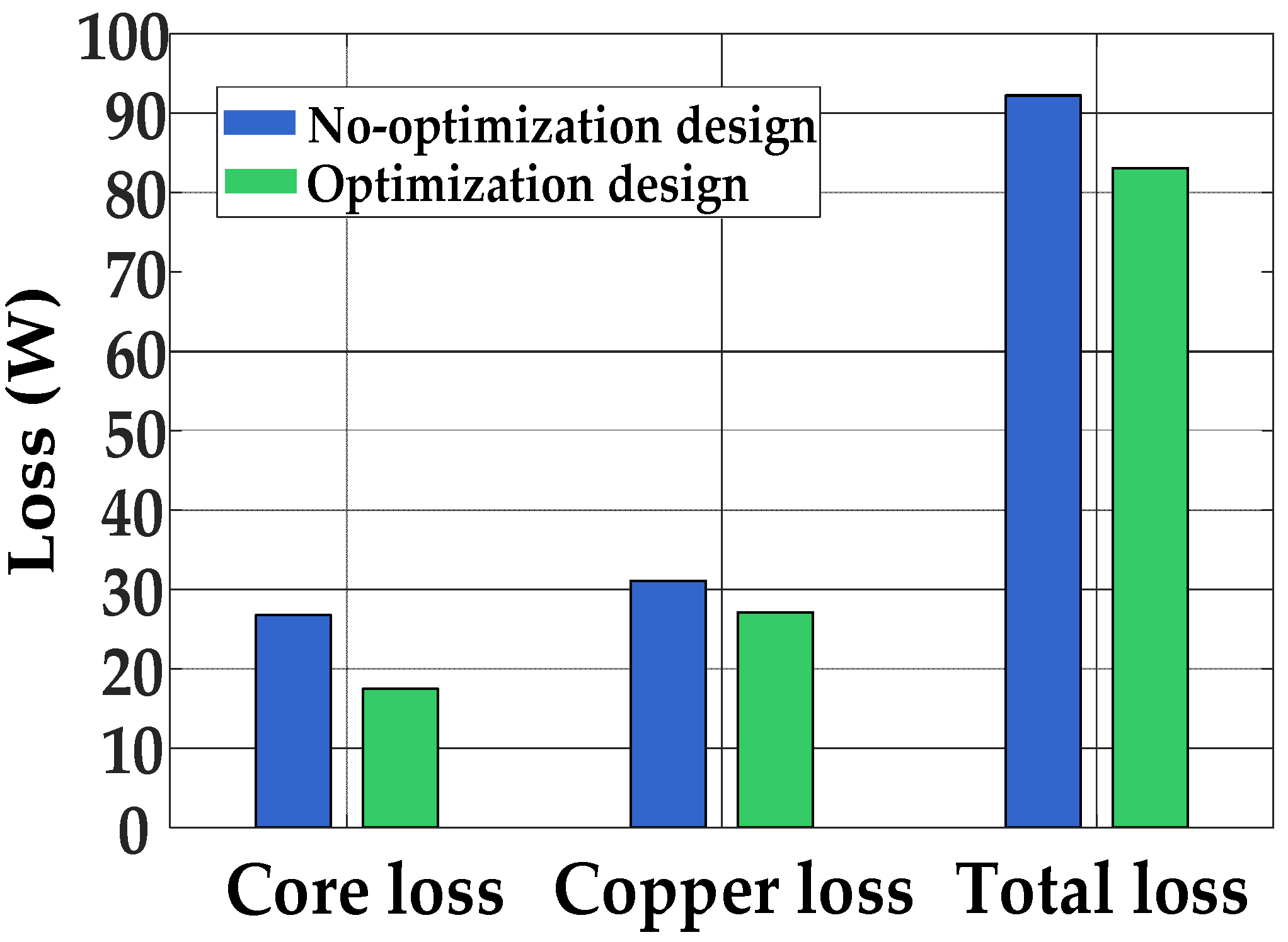
3.2. Loss Optimization Design
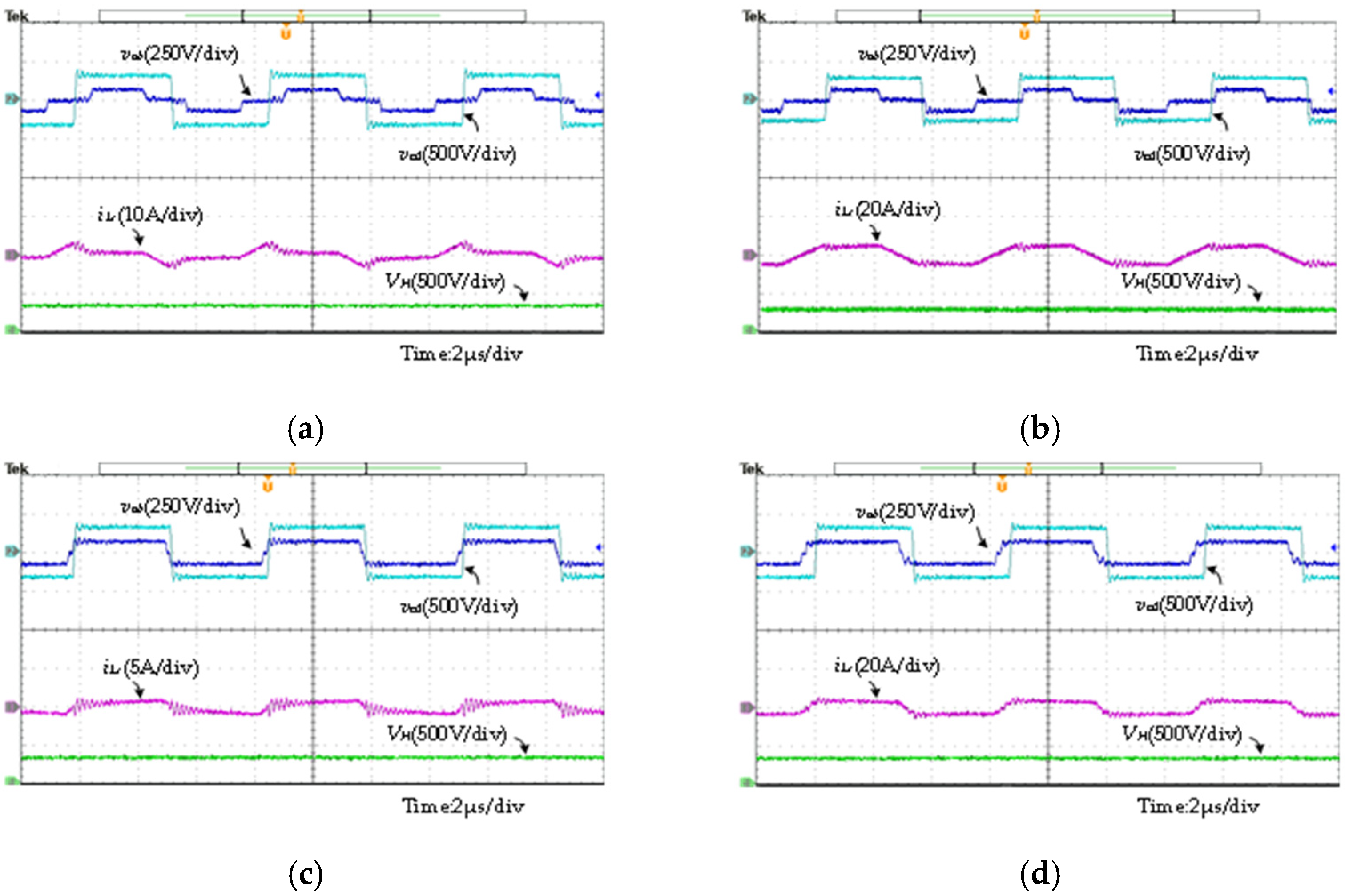
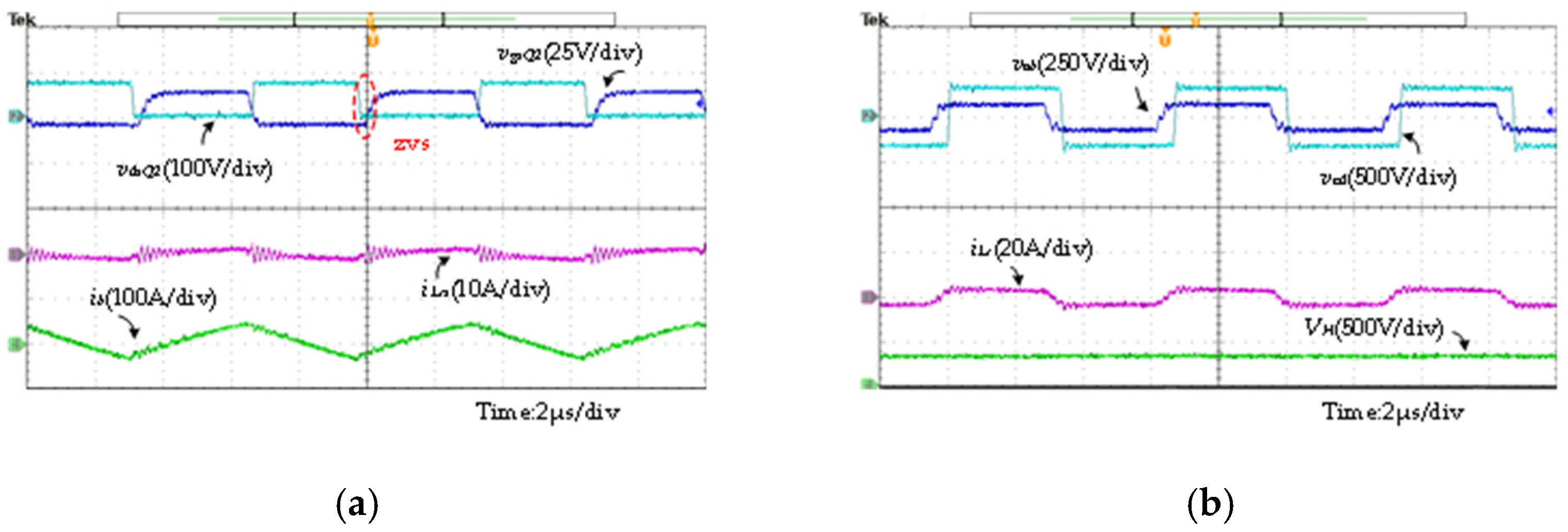
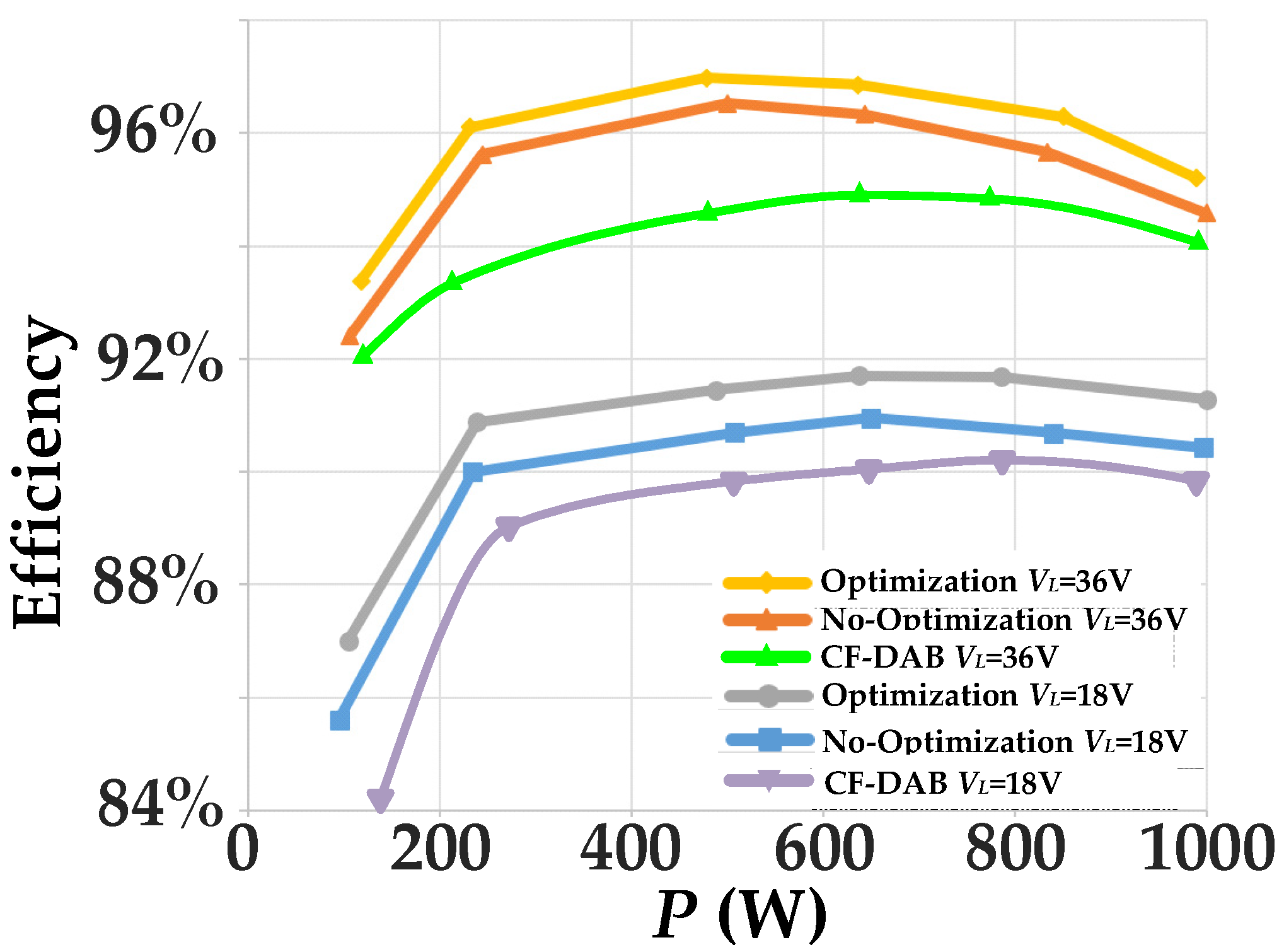
4. Experimental Verification
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ilyushin, Y.V.; Novozhilov, I.M. Methodology of Inspection of Absolute Stability of Pulse Distributed Control System. In Proceedings of the 2019 XXII International Conference on Soft Computing and Measurements (SCM), St. Petersburg, Russia, 23–25 May 2019. [Google Scholar]
- China Society of Automotive Engineers. Technology Roadmap for Energy Saving and New Energy Vehicles; China Machine Press: Ningbo, China, 2020; pp. 97–104. [Google Scholar]
- Guo, J.; Han, H.; Xu, G.; Cai, Z.; Wang, H.; Sun, Y. Design considerations for PPS controlled current-fed DAB converter to achieve full load range ZVS and low inductor current stress. IEEE Trans. Ind. Appl. 2021, 57, 6261–6276. [Google Scholar] [CrossRef]
- Spiazzi, G.; Rossetto, L.; Mattavelli, P.; Gallo, E.; Cvejic, F. An Isolated Bidirectional Soft-Switching DC-DC Converter for Wide Input/Output Voltage Range. Energies 2024, 17, 6121. [Google Scholar] [CrossRef]
- Carvalho, E.L.; Meneghetti, L.H.; Carati, E.G.; Costa, J.P.D.; Stein, C.M.D.O.; Cardoso, R. Asymmetrical Pulse-Width Modulation Strategy for Current-Fed Dual Active Bridge Bidirectional Isolated Converter Applied to Energy Storage Systems. Energies 2020, 13, 3475. [Google Scholar] [CrossRef]
- Bathala, K.; Kishan, D.; Harischandrappa, N. Soft Switched Current Fed Dual Active Bridge Isolated Bidirectional Series Resonant DC-DC Converter for Energy Storage Applications. Energies 2023, 16, 258. [Google Scholar] [CrossRef]
- Meneghetti, L.H.; Carvalho, E.L.; Carati, E.G.; Denardin, G.W.; da Costa, J.P.; de Oliveira Stein, C.M.; Cardoso, R. Hybrid Inverter and Control Strategy for Enabling the PV Generation Dispatch Using Extra-Low-Voltage Batteries. Energies 2022, 15, 7539. [Google Scholar] [CrossRef]
- Gu, Q.; Xie, B.; Li, R.; Zhu, Z.; Zhang, Y. A ZVS Implementation Method of a Current-fed Dual Active Bridge Converter within the Full Load Range. In Proceedings of the 2024 IEEE Applied Power Electronics Conference and Exposition (APEC), Long Beach, CA, USA, 25–29 February 2024; pp. 2059–2062. [Google Scholar]
- Liu, J.; Zheng, Z.; Li, C.; Wang, K.; Li, Y. Automatic current sharing of input-parallel output-parallel dual active bridge converters with coupled inductors. In Proceedings of the IEEE 13th International Conference on Power Electronics and Drive Systems, Toulouse, France, 9–12 July 2019; pp. 1–6. [Google Scholar]
- Liu, J.; Li, C.; Zheng, Z.; Wang, K.; Li, Y. Current discrepancy mitigation of input-parallel output-parallel dual active bridge converters using cou- pled inductors. IEEE Trans. Ind. Electron. 2021, 68, 8182–8192. [Google Scholar] [CrossRef]
- Guo, Z.; Sha, D. Dual-active-bridge converter with parallel-connected full bridges in low-voltage side for ZVS by using auxiliary coupling inductor. IEEE Trans. Ind. Electron. 2019, 66, 6856–6866. [Google Scholar] [CrossRef]
- Liu, Y.; Xu, J.; Shuai, Z.; Li, Y.; Peng, Y.; Liang, C.; Cui, G.; Hu, S.; Zhang, M.; Xie, B. A Novel Harmonic Suppression Traction Transformer with Integrated Filtering Inductors for Railway Systems. Energies 2020, 13, 473. [Google Scholar] [CrossRef]
- Yang, J.-W.; Han, S.-K. A Si-FET-Based High Switching Frequency Three-Level LLC Resonant Converter. Energies 2019, 12, 3082. [Google Scholar] [CrossRef]
- Sha, D.; Wang, X.; Liu, K.; Chen, C. A current-fed dual-active-bridgedc–dc converter using extended duty cycle control and magnetic-integrated inductors with optimized voltage mismatching control. IEEE Trans. Power Electron. 2019, 34, 462–473. [Google Scholar] [CrossRef]
- Jiang, C.; Liu, H. A novel interleaved parallel bidirectional dual- active-bridge dc–dc converter with coupled inductor for more-electric aircraft. IEEE Trans. Ind. Electron. 2021, 68, 1759–1768. [Google Scholar] [CrossRef]
- Wang, Z.; Li, C.; Zheng, Z. A high-step-up low-ripple and high- efficiency DC-DC converter for fuel-cell vehicles. IEEE Trans. Power Electron. 2022, 37, 3555–3569. [Google Scholar] [CrossRef]
- Han, H.; Guo, J.; Xu, G.; Xu, J.; Liu, D.; Su, M. Three winding coupled inductor-based dual active bridge DC-DC converter with full load range ZVS under wide voltage range. IEEE Trans. Ind. Electron. 2022, 69, 6935–6947. [Google Scholar] [CrossRef]
- Zhang, Z.; Liu, C.; Wang, M.; Si, Y.; Liu, Y.; Lei, Q. High-efficiency high-power-density CLLC resonant converter with low-stray-capacitance and well-heat-dissipated planar transformer for EV on-board charger. IEEE Trans. Power Electron. 2020, 35, 10831–10851. [Google Scholar] [CrossRef]
- Kolahian, P.; Grimm, F.; Baghdadi, M. A Comprehensive Review on Planar Magnetics and the Structures to Reduce the Parasitic Elements and Improve Efficiency. Energies 2023, 16, 3254. [Google Scholar] [CrossRef]
- Zhang, J.; Ouyang, Z.; Duffy, M.C.; Andesen, M.A.; Hurley, W.G. Leakage inductance calculation for planar transformers with a mag- netic shunt. IEEE Trans. Ind. Appl. 2014, 50, 4107–4112. [Google Scholar] [CrossRef]
- Mu, M.; Xue, L.; Boroyevich, D.; Hughes, B.; Mattavelli, P. Design of integrated transformer and inductor for high frequency dual active bridge GaN charge for PHEV. In Proceedings of the IEEE Applied Power Electronics Conference and Exposition, Charlotte, NC, USA, 15–19 March 2015; pp. 579–585. [Google Scholar]
- Li, B.; Li, Q.; Lee, F.C. High-frequency PCB winding transformer with integrated inductors for a bi-directional resonant converter. IEEE Trans. Power Electron. 2019, 34, 6123–6135. [Google Scholar] [CrossRef]
- Guo, J.; Wang, H.; Xu, G.; Li, X.; Sun, Y.; Su, M. Dual Coupled Inductors with Controllable Integrated Leakage Inductance and CM Noise Suppression for CF-DAB Converter. IEEE Trans. Power Electron. 2023, 38, 8033–8038. [Google Scholar] [CrossRef]
- Guo, J.; Wang, H.; Xu, G.; Han, H.; Su, M. Dual-Transformer-Based DAB Converter with Controllable Integrated Inductances. IEEE Trans. Power Electron. 2024, 39, 6376–6390. [Google Scholar] [CrossRef]



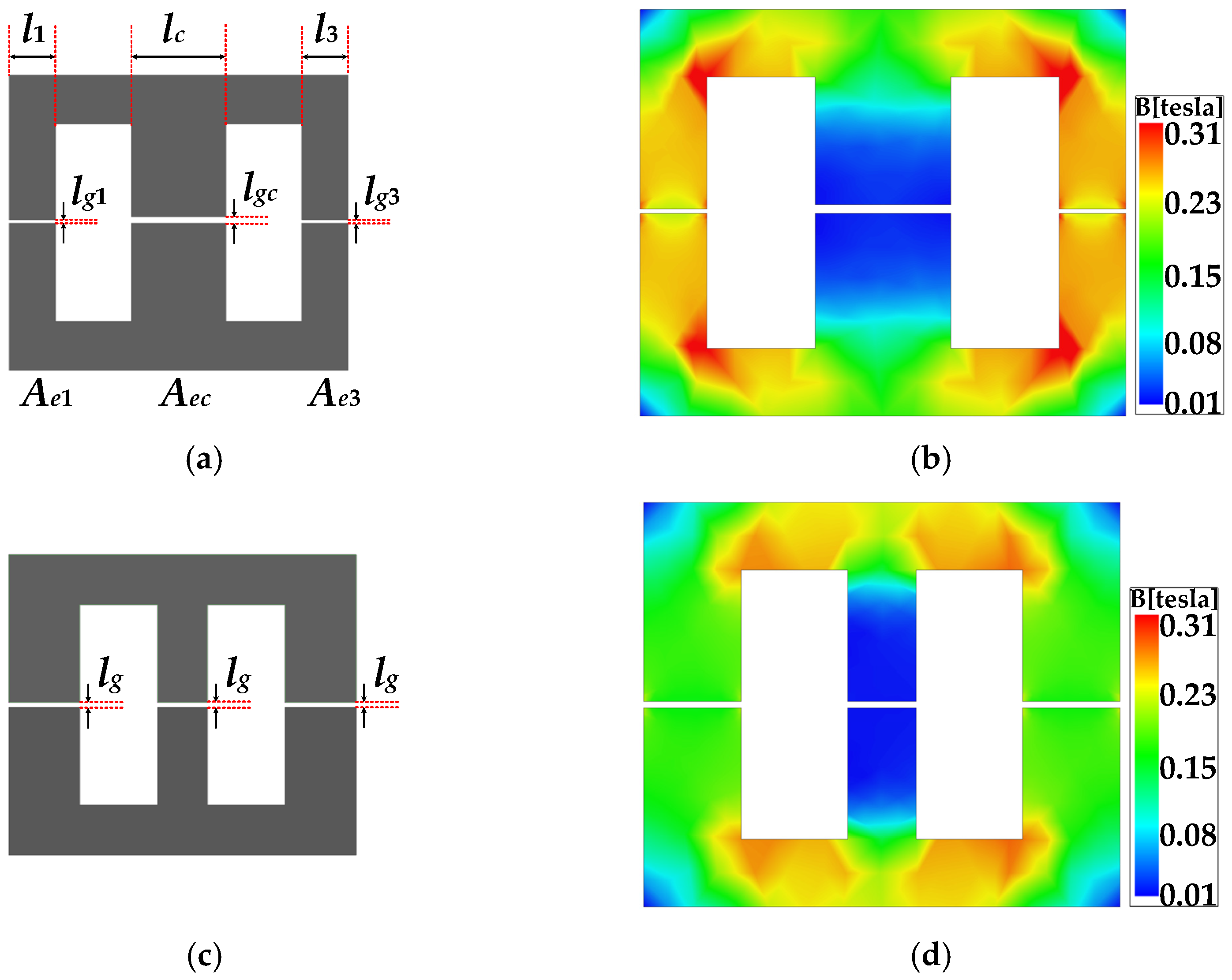
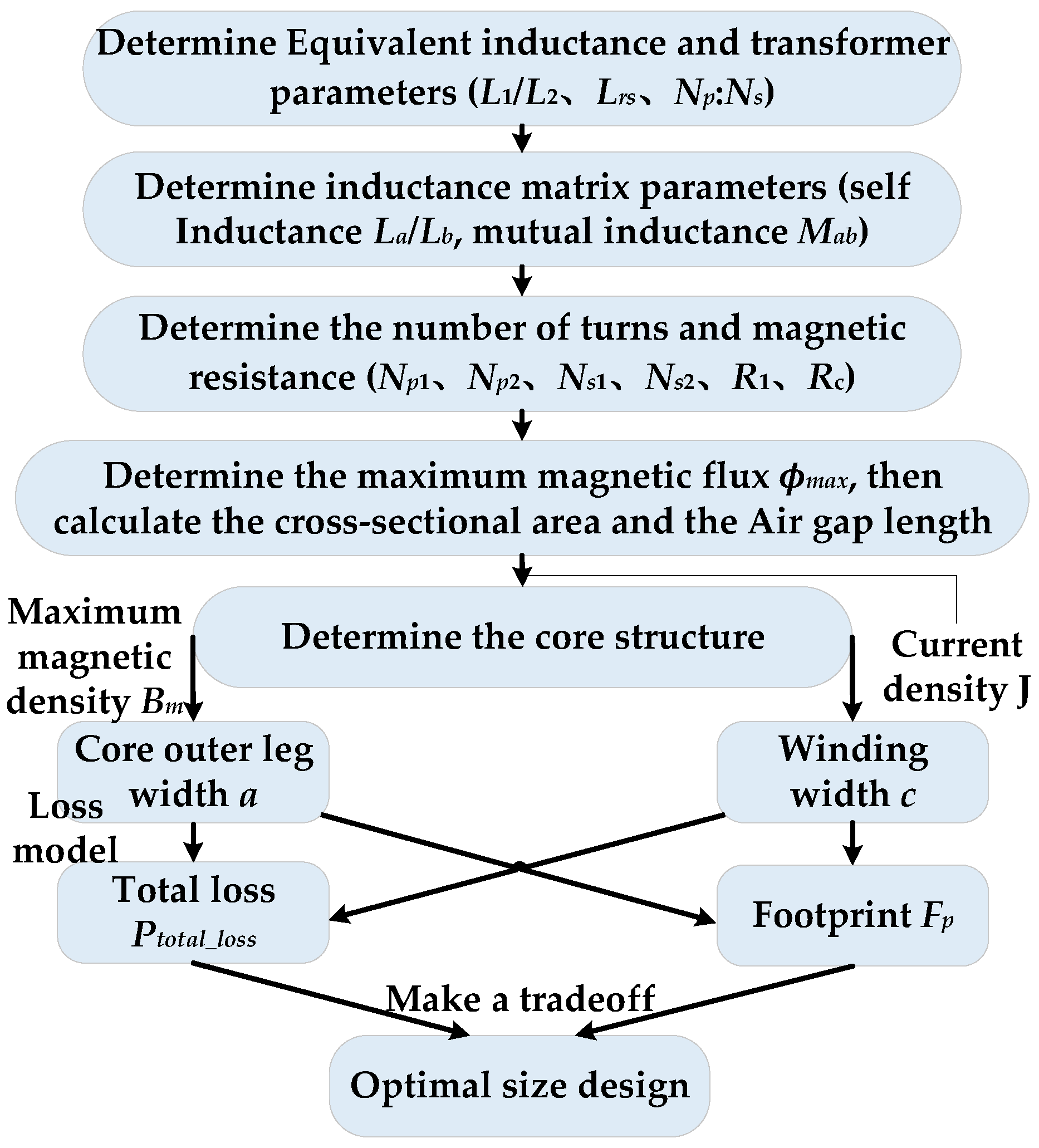
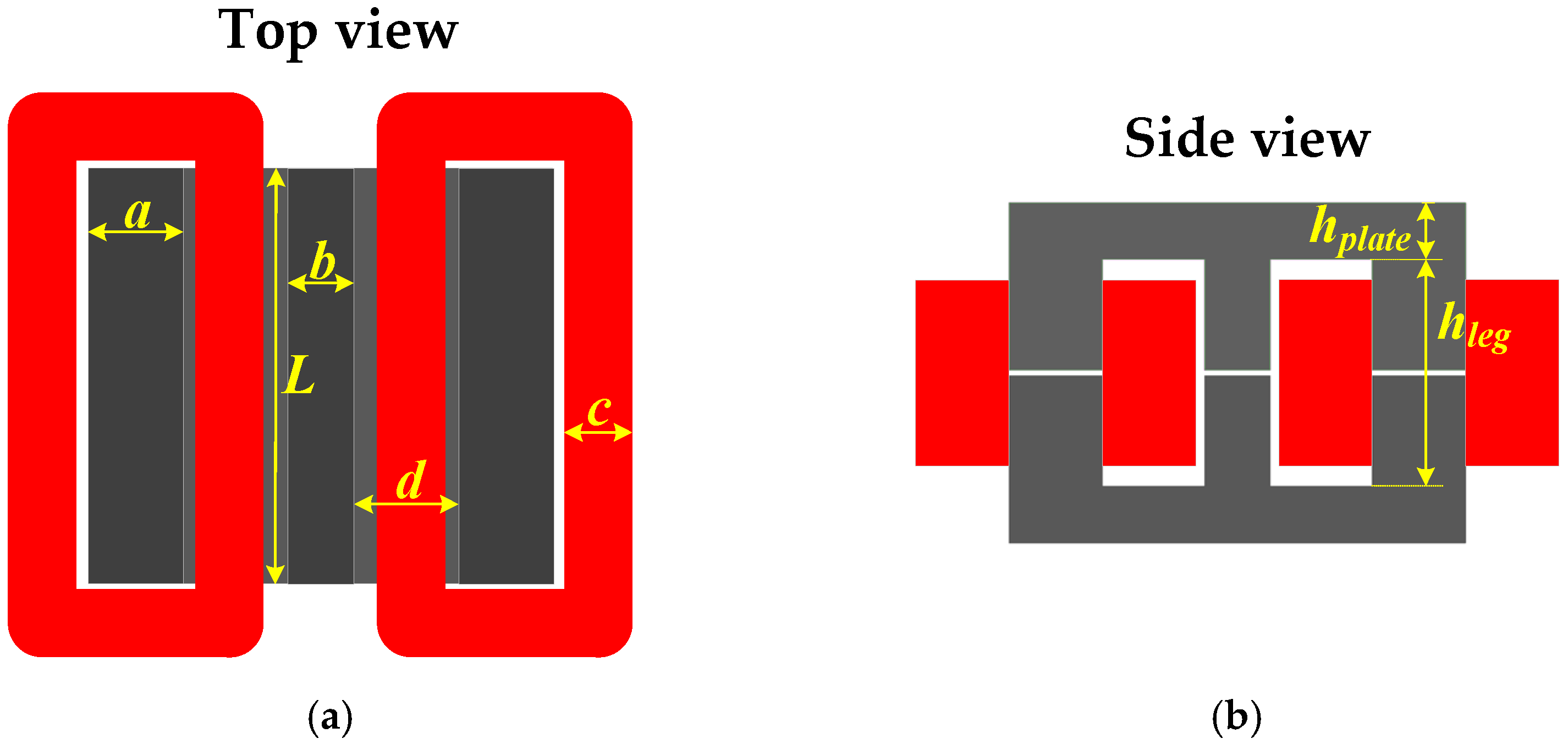
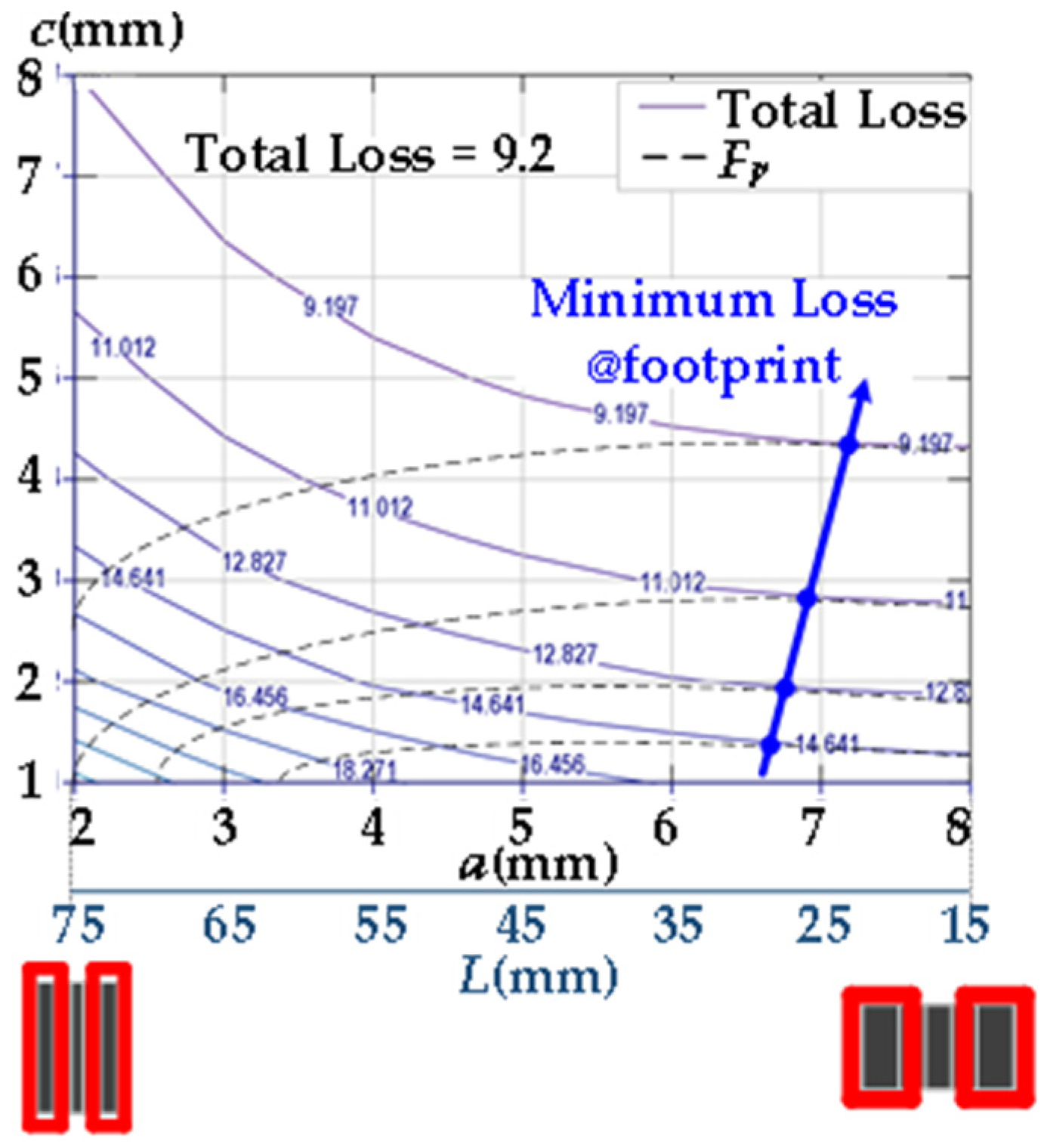

| Characteristic | Figure 2 | Figure 3a,b | Figure 3c | DCI Structure |
|---|---|---|---|---|
| Number of components | 3 | 2 | 1 | 1 |
| Power density/volume | Maximum | Medium | Minimum | Minimum |
| Magnetic integration | L1 and L2 | L1, L2 and Tr | L1, L2, Tr and Lrs | L1, L2, Tr and Lrs |
| Losses | / | Medium | Maximum | Minimum |
| Parameter | Value |
|---|---|
| Power (P/W) | 1000 |
| Switching frequency (f/kHz) | 150 |
| Input voltage (VL/V) | 18–36 |
| Output voltage (VH/V) | 360 |
| Leakage inductance (Lr/μH) | 1.44 |
| DC inductance (L1, L2/μH) | 6 |
| Transformation ratio (Np:Ns) | 1:5 |
| Clamp capacitor (Cc/μF) | 60 |
| Loss Component | No-Optimization Design | Proportion | Optimization Design | Proportion | Decrease |
|---|---|---|---|---|---|
| Total loss (W) | 92.235 | 100% | 83.086 | 90.1% | 9.1% |
| Core loss (W) | 26.747 | 29.0% | 17.444 | 18.9% | 10.1% |
| Copper loss (W) | 31.091 | 33.7% | 27.106 | 29.39% | 4.31% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, X.; Zhang, J.; Zhuang, Y.; Zhang, Y.; Guo, J. Design and Optimization of Current-Fed Dual Active Bridge Converter with Dual Coupled-Inductor Structure. Energies 2025, 18, 5722. https://doi.org/10.3390/en18215722
Chen X, Zhang J, Zhuang Y, Zhang Y, Guo J. Design and Optimization of Current-Fed Dual Active Bridge Converter with Dual Coupled-Inductor Structure. Energies. 2025; 18(21):5722. https://doi.org/10.3390/en18215722
Chicago/Turabian StyleChen, Xiaoying, Jun Zhang, Yizhan Zhuang, Yiming Zhang, and Jing Guo. 2025. "Design and Optimization of Current-Fed Dual Active Bridge Converter with Dual Coupled-Inductor Structure" Energies 18, no. 21: 5722. https://doi.org/10.3390/en18215722
APA StyleChen, X., Zhang, J., Zhuang, Y., Zhang, Y., & Guo, J. (2025). Design and Optimization of Current-Fed Dual Active Bridge Converter with Dual Coupled-Inductor Structure. Energies, 18(21), 5722. https://doi.org/10.3390/en18215722






