Multi-Physics LCA-Based Design Optimization of an Interior Permanent Magnet Motor for EVs
Abstract
1. Introduction
2. Methodology
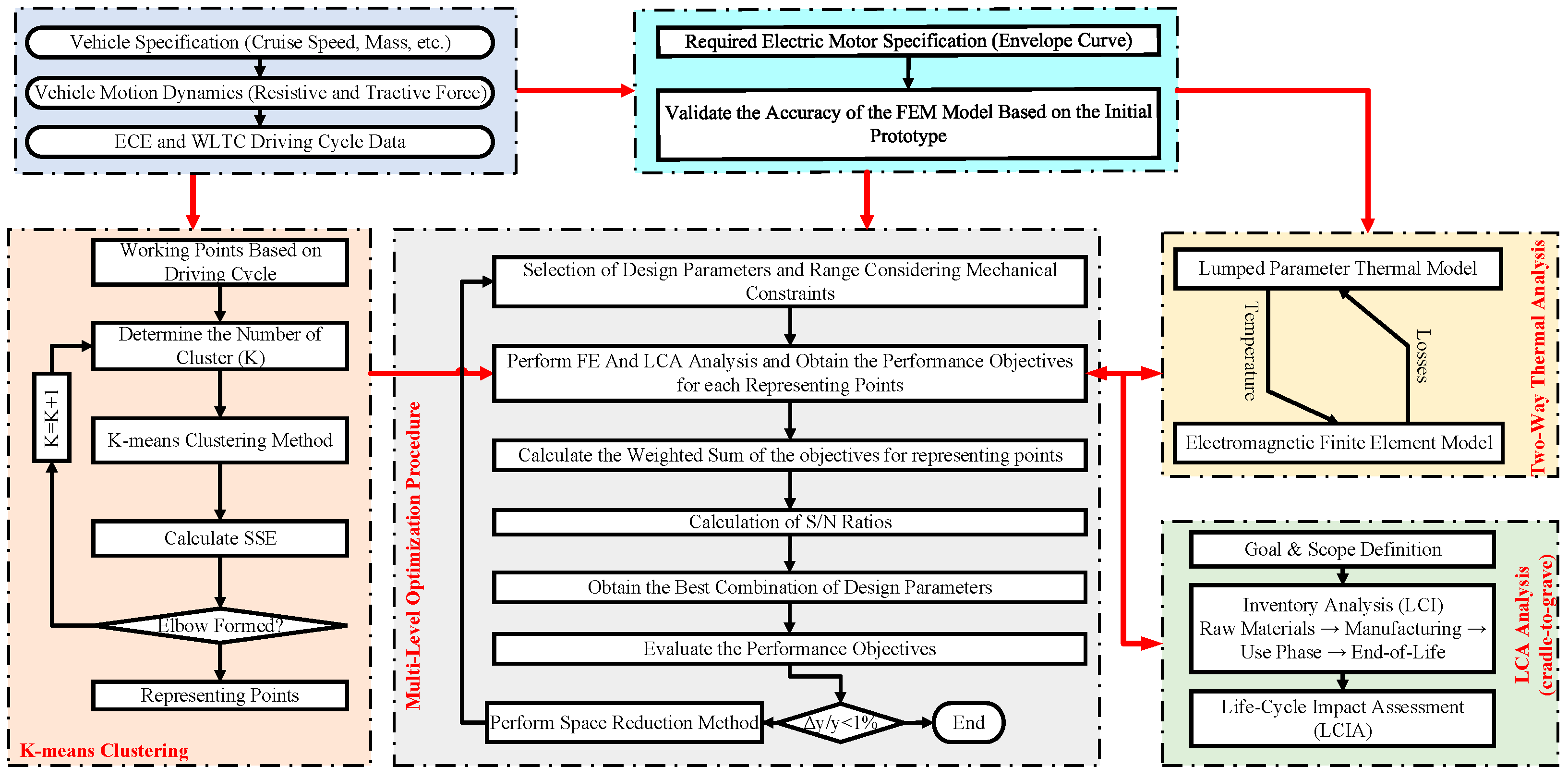
2.1. Methodological Flowchart
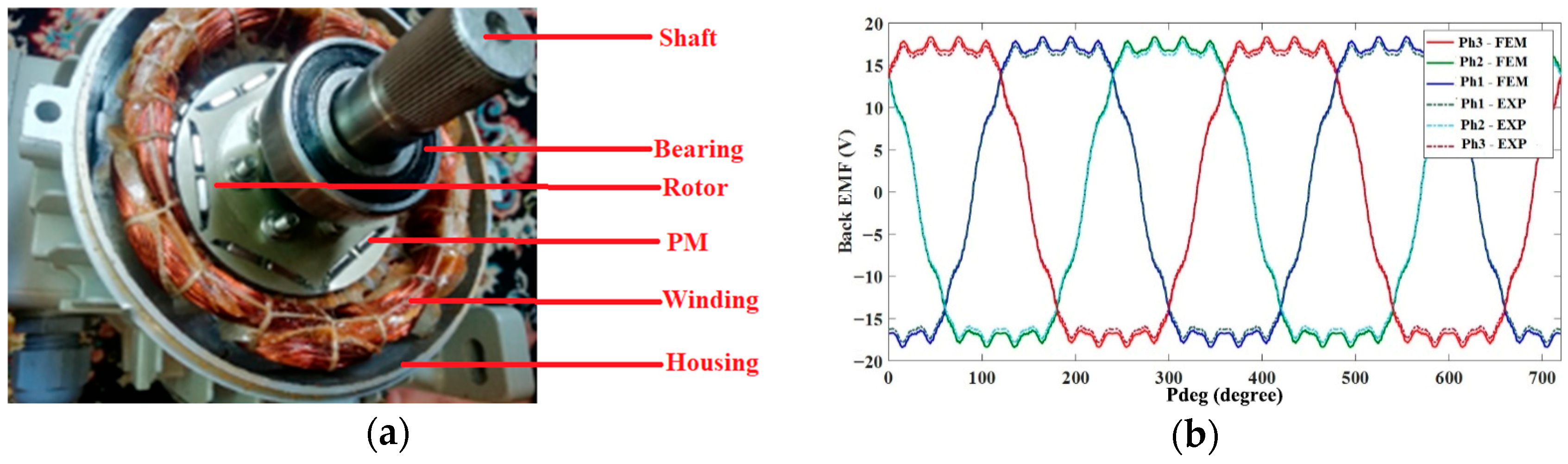
2.2. Motor Under Study
2.3. LCA Analysis
2.3.1. Goal and Scope Definition
2.3.2. Life Cycle Inventory (LCI)
Raw Material
Use Stage
End of Life
3. Design Optimization
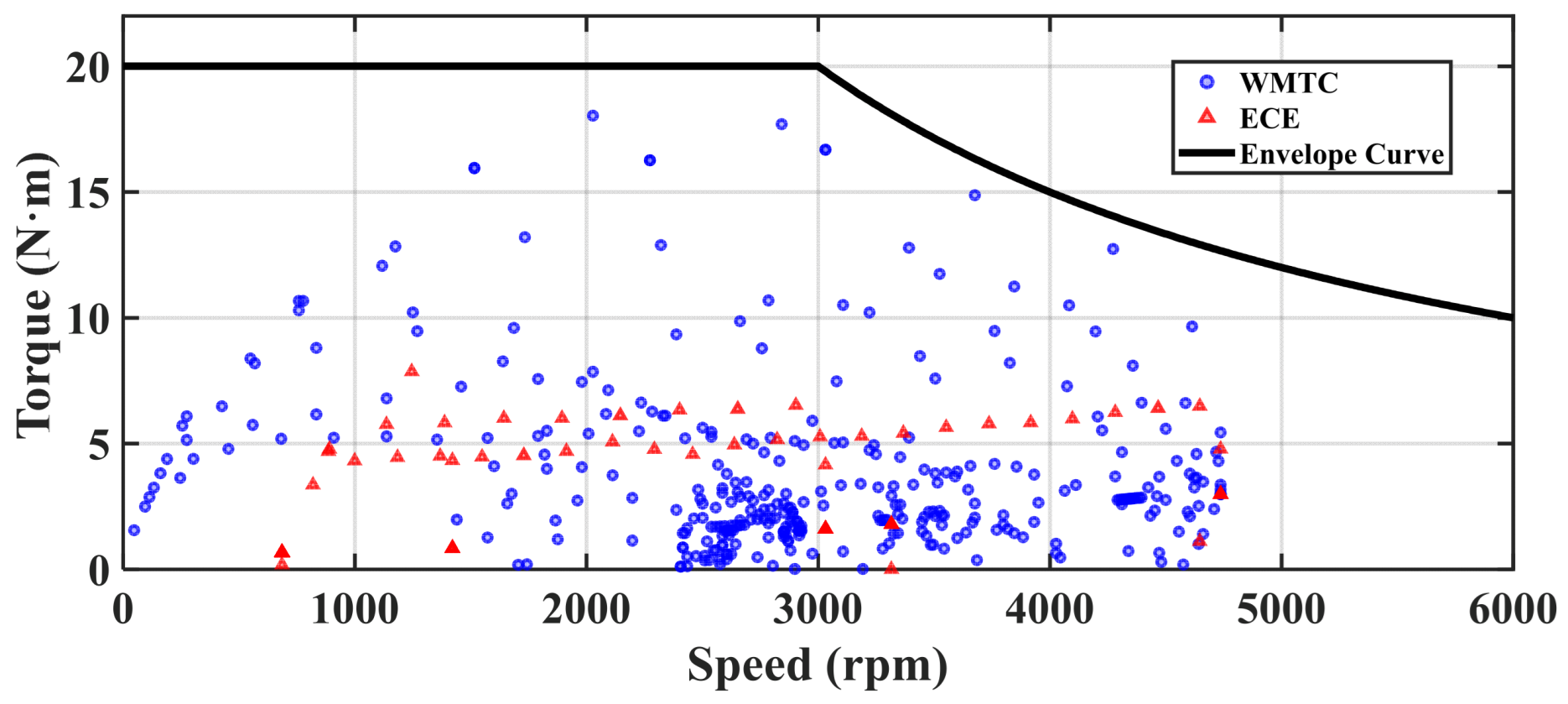
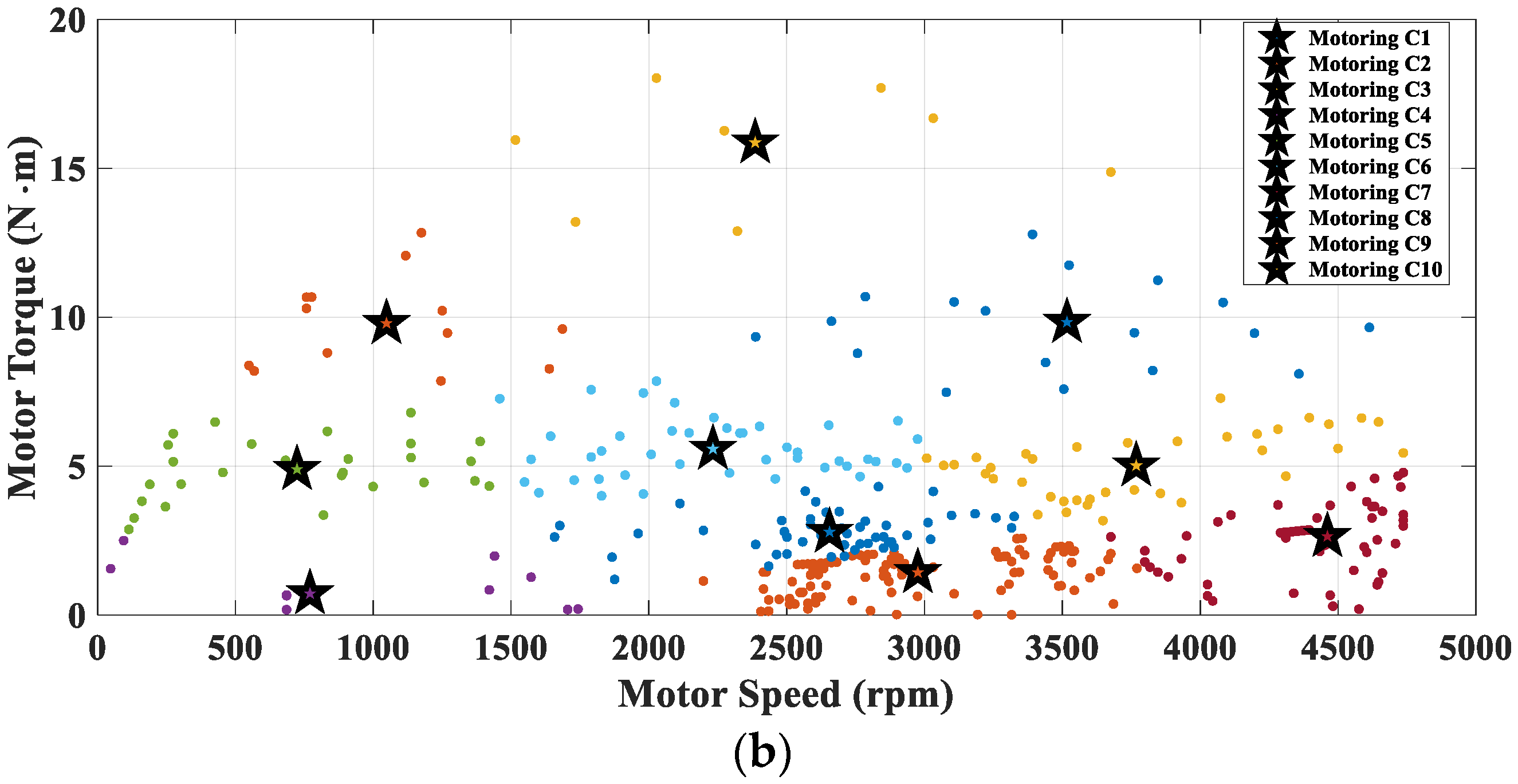
3.1. Driving Cycle Analysis
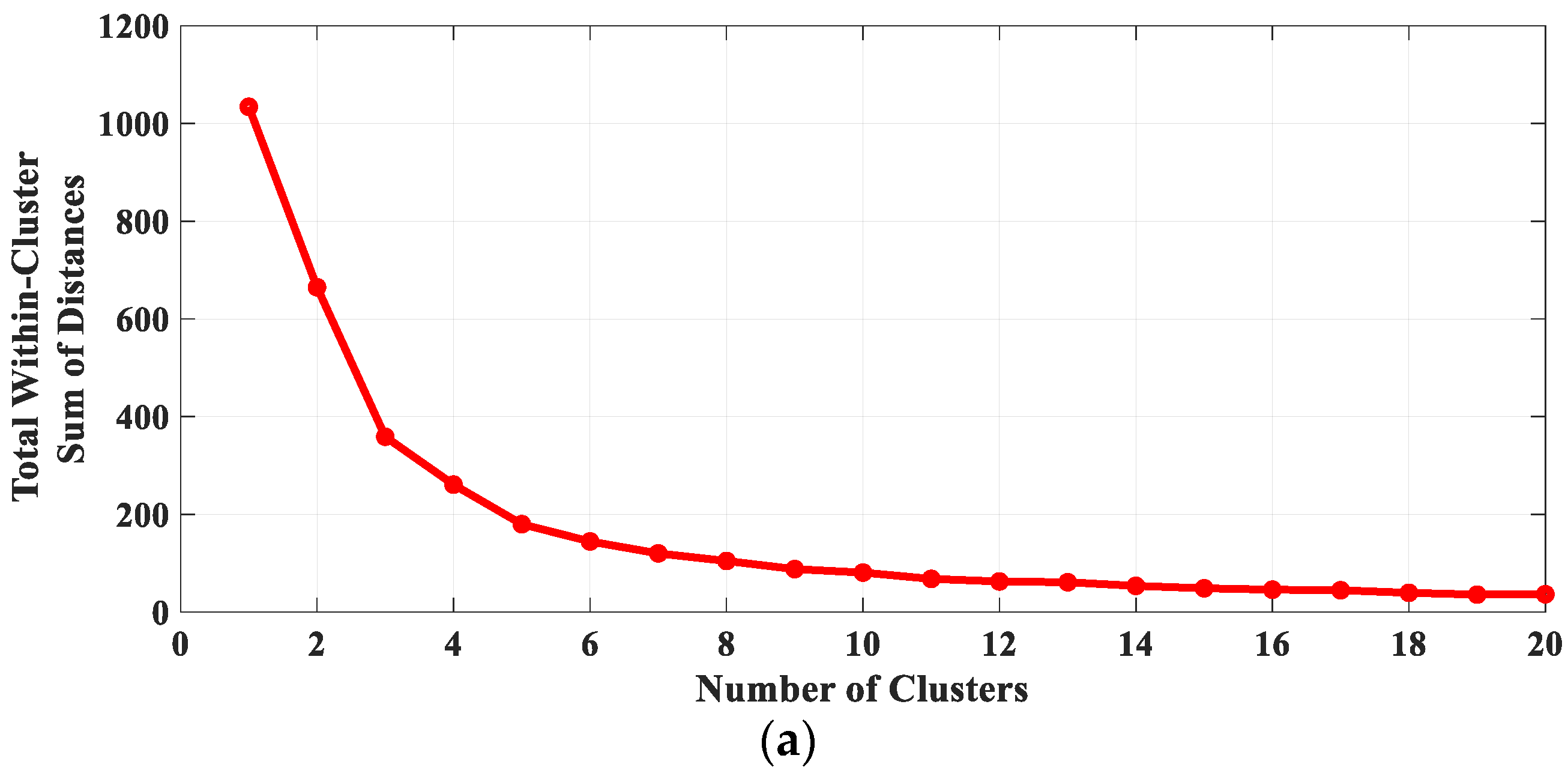
3.2. K-Means Clustering for Driving Cycle Representation
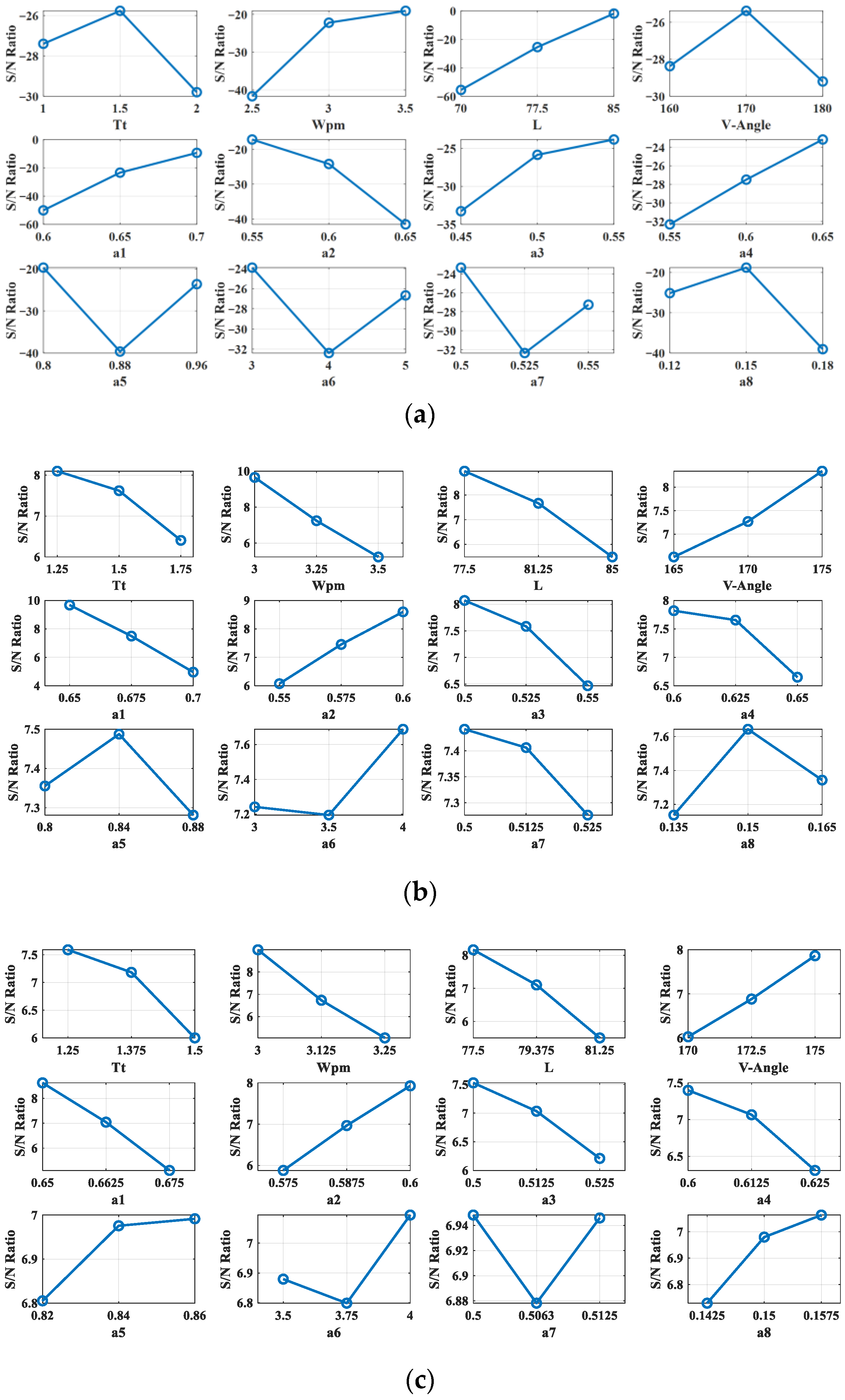
3.3. Optimization Algorithm
4. Results
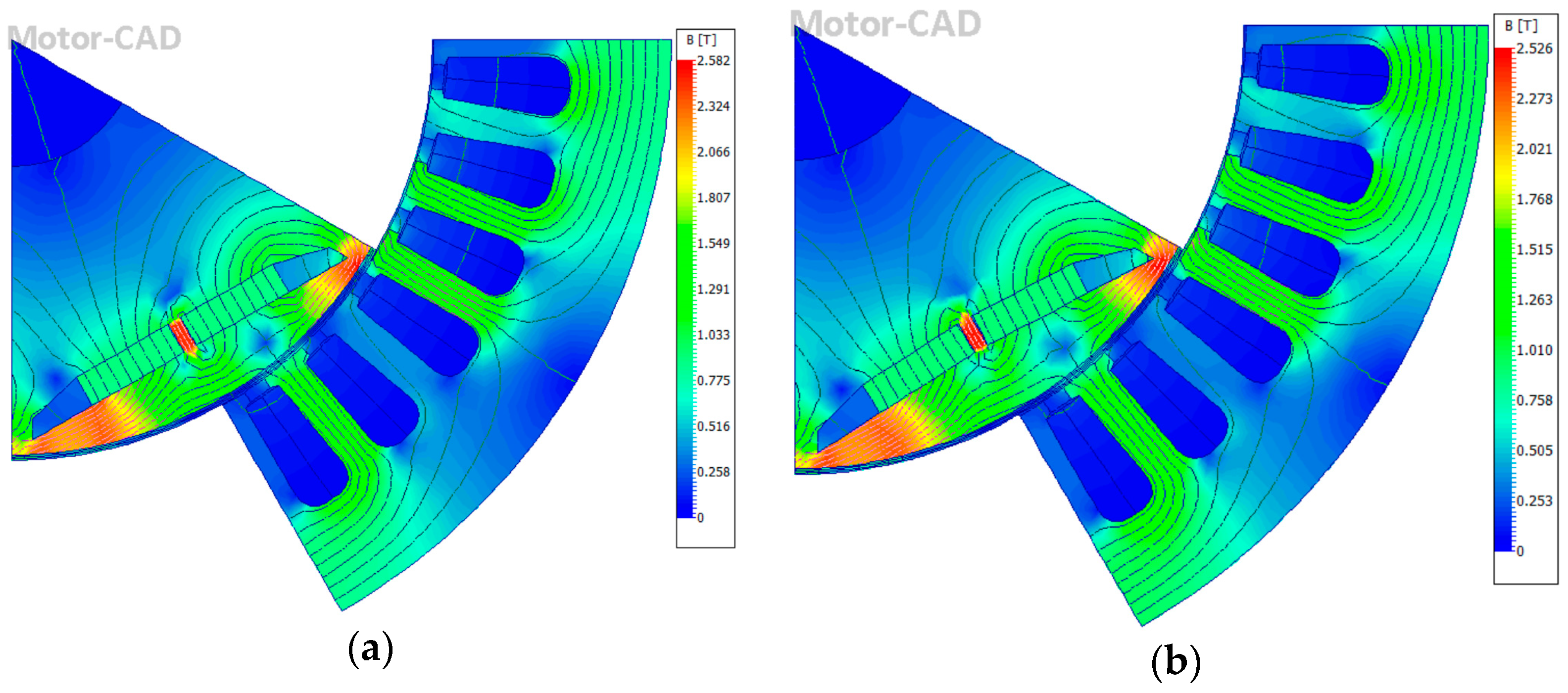
4.1. Magnetic Flux Density Distribution
4.2. Life Cycle Impact Assessment (LCIA) and Interpretation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ortega, A.J.P.; Das, S.; Islam, R.; Kouhshahi, M.B. High-Fidelity Analysis with Multiphysics Simulation for Performance Evaluation of Electric Motors Used in Traction Applications. IEEE Trans. Ind. Appl. 2023, 59, 1273–1282. [Google Scholar] [CrossRef]
- Ozer, K.; Yilmaz, M. Design and Optimization of IPMSM for Enhanced Efficiency, Cost Reduction, and Performance in Light Electric Vehicles. IEEE Access 2025, 13, 80621–80636. [Google Scholar] [CrossRef]
- Mahmouditabar, F.; Baker, N.J. Design Optimization of Induction Motors with Different Stator Slot Rotor Bar Combinations Considering Drive Cycle. Energies 2024, 17, 154. [Google Scholar] [CrossRef]
- Kim, T.K.; Kim, J.H.; Kim, J.H.; Kim, K.C.; Lee, J.H.; Yeo, C.G.; Jung, S.Y. Performance Comparison of Induction Motors and IPMSMs With Identical Stators for Use as Auxiliary Motors in EVs and HEVs. IEEE Trans. Ind. Appl. 2025, 1–11. [Google Scholar] [CrossRef]
- Mahmouditabar, F.; Baker, N.J. Robust Design of a Six-Phase Segmented Switch Reluctance Motor Considering Manufacturing Tolerances and Manufacturing Processes. IEEE Access 2024, 12, 160018–160029. [Google Scholar] [CrossRef]
- Ajamloo, A.M.; Ghaheri, A.; Ibrahim, M.N.; Sergeant, P. A New Hybrid Permanent Magnet-Assisted Synchronous Reluctance Motor With Efficient Utilization of Rare-Earth Permanent Magnets. IEEE Trans. Energy Convers. 2025, 40, 1325–1338. [Google Scholar] [CrossRef]
- Paulraj, T.; Obulesu, Y.P. Comprehensive Performance Evaluation of 60 KW PMSM, EESM, and SynRM for Electric Vehicle Traction Under Steady-State and Drive Cycle Conditions. IEEE Access 2025, 13, 155916–155939. [Google Scholar] [CrossRef]
- Sharma, A.; Banchhor, D.K.; Jain, A.K. Interior Permanent Magnet Rotor Notch Optimization for High-Speed Torque Enhancement in Brushless DC Motors. IEEE Trans. Energy Convers. 2025. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, X.; Wu, J.; Wang, M.; Hu, W.; Geng, H.; Pang, X. Multi-Objective Optimization Design of a Segmented Asymmetric V-Type Interior Permanent Magnet Synchronous Motor. IEEE Trans. Magn. 2025, 61, 8200312. [Google Scholar] [CrossRef]
- Gronwald, P.O.; Kern, T.A. Traction Motor Cooling Systems: A Literature Review and Comparative Study. IEEE Trans. Transp. Electrif. 2021, 7, 2892–2913. [Google Scholar] [CrossRef]
- Amini, A.; Farrokh, F.; Mahmouditabar, F.; Baker, N.J.; Vahedi, A. Enhanced Interior PMSM Design for Electric Vehicles Using Ship-Shaped Notching and Advanced Optimization Algorithms. Energies 2025, 18, 4527. [Google Scholar] [CrossRef]
- Li, S.; Tong, W.; Wu, S.; Tang, R. General Analytical Model and Experimental Verification for Mechanical Stress of High-Speed Interior Permanent Magnet Motors Considering Modified Rotor. IEEE Trans. Ind. Appl. 2025, 61, 67–76. [Google Scholar] [CrossRef]
- Yang, Y.; Sun, X.; Xu, N.; Wan, B.; Yao, M. Design Optimization of a 12/10 Switched Reluctance Motor Considering Target Driving Cycle and Driving Condition. IEEE J. Emerg. Sel. Top. Power Electron. 2025, 13, 5305–5316. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, C.; Guo, D.; Yang, F.; Zhang, Z.; Zhao, M. Drive-Cycle-Based Configuration Design and Energy Efficiency Analysis of Dual-Motor 4WD System With Two-Speed Transmission for Electric Vehicles. IEEE Trans. Transp. Electrif. 2024, 10, 1887–1899. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhang, Q.; Yu, B.; Yu, J. Online Identification of Parameters and Electromagnetic Torque for Permanent Magnet Synchronous Motors Based on Energy Analysis. In Proceedings of the Conference Record—IAS Annual Meeting (IEEE Industry Applications Society), Taipei, Taiwan, 15–20 June 2025. [Google Scholar] [CrossRef]
- Mahmouditabar, F.; Vahedi, A.; Takorabet, N. Design and Analysis of Interior Permanent Magnet Motor for Electric Vehicle Application Considering Irreversible Demagnetization. IEEE Trans. Ind. Appl. 2022, 58, 284–293. [Google Scholar] [CrossRef]
- Mahmouditabar, F.; Vahedi, A.; Takorabet, N. Robust Design of BLDC Motor Considering Driving Cycle. IEEE Trans. Transp. Electrif. 2023, 10, 1414–1424. [Google Scholar] [CrossRef]
- Fan, D.; Zhu, X.; Quan, L.; Han, P.; Xiang, Z.; Wu, J. Driving Cycle Design Optimization of Less-Rare-Earth PM Motor Using Dimension Reduction Method. IEEE Trans. Energy Convers. 2023, 38, 1614–1625. [Google Scholar] [CrossRef]
- Praslicka, B.; Ma, C.; Taran, N. A Computationally Efficient High-Fidelity Multi-Physics Design Optimization of Traction Motors for Drive Cycle Loss Minimization. IEEE Trans. Ind. Appl. 2023, 59, 1351–1360. [Google Scholar] [CrossRef]
- Cheng, Y.; Wang, Y.; Ma, J.; Liu, G.; Li, D.; Qu, R. Fast Evaluation of Driving Cycle Efficiency of Interior Permanent Magnet Synchronous Machines for Electric Vehicles Considering Step-Skewing. IEEE Trans. Ind. Appl. 2024, 60, 4396–4407. [Google Scholar] [CrossRef]
- Zhu, X.; Jiang, M.; Xiang, Z.; Xu, L.; Chen, Y.; Quan, L. Design and Optimization of a Multi-Region High-Efficiency Permanent Magnet Motor with Enhanced Energy Efficiency. IEEE Trans. Energy Convers. 2025, 40, 2169–2178. [Google Scholar] [CrossRef]
- Layek, K.; Nair, S.V.; Hatua, K. A Tapped Winding Interior Permanent Magnet Synchronous Machine for Medium-Duty Delivery Trucks. IEEE Trans. Transp. Electrif. 2024, 10, 7420–7430. [Google Scholar] [CrossRef]
- Hoang, K.D.; Yu, A.; Ullah, S.; Valente, G.; Shahaj, A.; Atallah, K. Design, Analysis and Experimental Evaluation of a Novel High-Speed High-Power Ferrite IPM Machine for Traction Applications. IEEE Trans. Ind. Appl. 2024, 60, 5998–6009. [Google Scholar] [CrossRef]
- Sahin, H.; Esen, H. Performance and Energy Analysis of a Fuel Cell Electric Vehicle. IEEE Access 2025, 13, 29206–29219. [Google Scholar] [CrossRef]
- Rassõlkin, A.; Belahcen, A.; Kallaste, A.; Vaimann, T.; Vyacheslavovich Lukichev, D.; Orlova, S.; Heidari, H.; Asad, B.; Pando Acedo, J. Life Cycle Analysis of Electrical Motor Drive System Based on Electrical Machine Type. Proc. Est. Acad. Sci. 2020, 69, 162–177. [Google Scholar] [CrossRef]
- Cassoret, B.; Manata, J.P.; Mallard, V.; Roger, D. Comparative Life Cycle Assessment of Induction Machines Made with Copper-Cage or Aluminium-Cage Rotors. IET Electr. Power Appl. 2019, 13, 712–719. [Google Scholar] [CrossRef]
- Keuter, R.J.; Melo, S.P.; Jois, P.K.; Cerdas, F.; Herrmann, C.; Ponick, B. Investigation of Electric Motors For All-Electric Aircraft with Different Material Combinations from an Environmental Perspective. In Proceedings of the 2023 IEEE International Conference on Electrical Systems for Aircraft, Railway, Ship Propulsion and Road Vehicles and International Transportation Electrification Conference, ESARS-ITEC 2023, Venice, Italy, 29–31 March 2023. [Google Scholar] [CrossRef]
- Mafrici, S.; Madonna, V.; Maria Meano, C.; Friis Hansen, K.; Tenconi, A. Switched Reluctance Machine for Transportation and Eco-Design: A Life Cycle Assessment. IEEE Access 2024, 12, 68334–68344. [Google Scholar] [CrossRef]
- Zhang, X.; Xu, Z.; Gerada, C.; Gerada, D. Carbon Emission Analysis of Electrical Machines. In Proceedings of the ICEMS 2021—2021 24th International Conference on Electrical Machines and Systems, Gyeongju, Republic of Korea, 31 October–3 November 2021; pp. 1678–1683. [Google Scholar] [CrossRef]
- Boughanmi, W.; Manata, J.P.; Roger, D. Contribution of LCA Approach to the Choice of Rotating Electrical Machines for Environmental Impact Minimization. In Proceedings of the 2012 20th International Conference on Electrical Machines, ICEM 2012, Marseille, France, 2–5 September 2012; pp. 122–128. [Google Scholar] [CrossRef]
- Schillingmann, H.; Gehler, S.; Henke, M. Life Cycle Assessment of Electrical Machine Production Considering Resource Requirements and Sustainability. In Proceedings of the 2021 11th International Electric Drives Production Conference, EDPC 2021, Erlangen, Germany, 7–9 December 2021. [Google Scholar] [CrossRef]
- Wrobel, R.; Rajaeifar, M.A.; Mecrow, B. Life Cycle Assessment of Electrical Machines—A Case Study. In Proceedings of the 2024 IEEE Energy Conversion Congress and Exposition, ECCE 2024, Phoenix, AZ, USA, 20–24 October 2024; pp. 5611–5618. [Google Scholar] [CrossRef]
- Zhang, X.; Xu, Z.; Zhang, F.; Darmani, M.A.; Jiang, J.; Gerada, C.; Gerada, D. Carbon Emission Evaluation and Comparison for Different Electric Machines. In Proceedings of the 2024 27th International Conference on Electrical Machines and Systems (ICEMS), Fukuoka, Japan, 26–29 November 2024; pp. 3158–3164. [Google Scholar] [CrossRef]
- Mahmouditabar, F.; Baker, N. A Review on the Effect of Electrical Steel Manufacturing Processes on the Performance of Electric Machines. Energies 2023, 16, 7954. [Google Scholar] [CrossRef]
- ISO 14040; Environmental Management—Life Cycle Assessment—Principles and Framework. International Organization for Standardization: Geneva, Switzerland, 2006.
- ISO 14044; Environmental Management—Life Cycle Assessment—Requirements and Guidelines. International Organization for Standardization: Geneva, Switzerland, 2006.
- Shenoy, A.A.; Miller, C.; Brunnert, D.; Verma, M. Enhancing Success in Carbon Capture Integration with Existing Industrial Facilities: Electrical Challenges and Strategies. IEEE Trans. Ind. Appl. 2025, 61, 6781–6789. [Google Scholar] [CrossRef]
- Ecoinvent—Data with Purpose. Available online: https://ecoinvent.org/ (accessed on 11 October 2025).
- What Are Emission Factors in Carbon Accounting? Available online: https://plana.earth/academy/emission-factors (accessed on 31 October 2025).
- GOV.UK Greenhouse Gas Reporting: Conversion Factors 2023. Available online: https://www.gov.uk/government/publications/greenhouse-gas-reporting-conversion-factors-2023 (accessed on 31 October 2025).
- Cao, J.; Zhu, W.; Yang, L.; Li, D.; He, X.; Jia, B.; Chen, S.; Yin, C. Electromagnetic Design and Taguchi Method Optimization of High-Speed Permanent Magnet Motors for Air Compressors. In Proceedings of the 2025 17th International Conference on Computer and Automation Engineering, ICCAE 2025, Perth, Australia, 20–22 March 2025; pp. 502–506. [Google Scholar] [CrossRef]
- Mahmouditabar, F.; Baker, N.J. Robust Design of Induction Machines for High-Speed Electric Freight Locomotive Applications. IEEE Access 2024, 12, 38786–38800. [Google Scholar] [CrossRef]
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Nominal power | 2 kW | Stator lamination | M800 |
| DC bus voltage | 72 V | Stator slot | 36 |
| Fill factor | 0.35 | Pole number | 6 |
| Magnet | N42 | Stator outer diameter | 124 |
| Axial length | 160 mm | Stator inner diameter | 80 mm |
| Magnet length | 3 mm | Magnet width | 10 mm |
| Component | Material | |||
|---|---|---|---|---|
| Stator | M800-50A | 2.2 | 0.9 | 0.92 |
| Rotor | M800-50A | 2.2 | 0.9 | 0.92 |
| Housing | Aluminum | 18.6 | 0.93 | 0.95 |
| End Caps | Aluminum | 18.6 | 0.93 | 0.95 |
| Stator Winding | Copper | 6 | 0.65 | 0.9 |
| Permanent Magnet | N42 | 31.4 | 0.01 | 0.5 |
| Insulation | Nomex | 6 | 0 | 0 |
| Shaft | CK45 | 1.37 | 0.95 | 0.95 |
| Impregnation | Epoxy | 5.09 | 0 | 0 |
| Bearing | Steel | 4.62 | 0.95 | 0.95 |
| Parameter | Symbol | Variation Range |
|---|---|---|
| Stator outer diameter (mm) | 125 | |
| Airgap (mm) | 0.65 | |
| Tooth Tip Depth | [1 2] | |
| Magnet thickness | M | [2.5 3.5] |
| Axial length (mm) | [75 85] | |
| V-angle | [160 180] | |
| The ratio of stator bore to stator diameter | [0.6 0.7] | |
| The ratio of slot depth to stator lam thickness | [0.55 0.65] | |
| The ratio of tooth width (radian) to slot pitch | [0.45 0.55] | |
| The ratio of slot opening to max slot opening | [0.55 0.65] | |
| The ratio of pole arc to max pole arc | [0.8 0.9] | |
| The ratio of web thickness to max web thickness | [0.8 1] | |
| The ratio of V web bar width to max V web bar width | [0.5 0.55] | |
| The ratio of Web length to max Web length | [0.12 0.18] |
| Cluster Number | Speed (rpm) | Torque (Nm.) | Cluster Weight |
|---|---|---|---|
| 1 | 3516 | 9.83 | 19 |
| 2 | 2975 | 1.43 | 150 |
| 3 | 3767 | 5.02 | 37 |
| 4 | 770 | 0.72 | 90 |
| 5 | 723 | 4.90 | 27 |
| 6 | 2232 | 5.58 | 44 |
| 7 | 4461 | 2.64 | 75 |
| 8 | 2655 | 2.79 | 52 |
| 9 | 1048 | 9.80 | 13 |
| 10 | 2385 | 15.86 | 11 |
| No. | ||||||||
|---|---|---|---|---|---|---|---|---|
| Initial | 62.6 | 74.1 | −46.98 | 20 | 0.0318 | 298.8 | 94.84 | 1 |
| 1 | 63.288 | 80.5 | −47.97 | 20 | 0.0316 | 296.324 | 120.68 | 1.039 |
| 2 | 59.344 | 72.5 | −46.1 | 20 | 0.0312 | 291.416 | 96.958 | 0.9768 |
| 3 | 59.344 | 72.5 | −46.1 | 20 | 0.0312 | 291.416 | 96.958 | 0.9768 |
| Design | Raw Material () | Use-Phase () | EoL () |
|---|---|---|---|
| Initial | 62.6 | 283.1 | −46.98 |
| Optimum | 59.3 | 278.1 | −46.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mahmouditabar, F.; Farmahini Farahani, E.; Pickert, V.; Kulan, M.C. Multi-Physics LCA-Based Design Optimization of an Interior Permanent Magnet Motor for EVs. Energies 2025, 18, 6167. https://doi.org/10.3390/en18236167
Mahmouditabar F, Farmahini Farahani E, Pickert V, Kulan MC. Multi-Physics LCA-Based Design Optimization of an Interior Permanent Magnet Motor for EVs. Energies. 2025; 18(23):6167. https://doi.org/10.3390/en18236167
Chicago/Turabian StyleMahmouditabar, Farshid, Ehsan Farmahini Farahani, Volker Pickert, and Mehmet C. Kulan. 2025. "Multi-Physics LCA-Based Design Optimization of an Interior Permanent Magnet Motor for EVs" Energies 18, no. 23: 6167. https://doi.org/10.3390/en18236167
APA StyleMahmouditabar, F., Farmahini Farahani, E., Pickert, V., & Kulan, M. C. (2025). Multi-Physics LCA-Based Design Optimization of an Interior Permanent Magnet Motor for EVs. Energies, 18(23), 6167. https://doi.org/10.3390/en18236167







