A Pattern-Guided CIM Vulnerability Diagnosis Framework for Multi-Sensor Thermal Management System in Energy Storage Stations

Abstract

The safe and reliable operation of energy storage stations critically depends on their thermal management systems, specifically the health states or working conditions of involved sensors, such as temperature, humidity, and pressure sensor. Impacted by several environmental factors, some indiscernible defects including signal drift, elevated noise, and response lag may affect the exact surveillance of batteries, leading to potential combustion or even explosion, which requires fault risk early-warning to support timely maintenance. These multi-sensor environmental factor data typically exhibit mixed characteristics, component coupling, and high uncertainty, thus impacting diagnostic accuracy and robustness. With this motivation, this study proposes a pattern-guided framework for vulnerability diagnosis using Component Importance Measure. A pattern-guided strategy is first designed to perform rule induction and fuzzy processing on discrete and continuous sensor data, respectively, to extract underlying vulnerability-related components. Subsequently, a component Importance Measure, which assesses the impact of individual risks on the whole reliability, is established to achieve unified integration and mapping of previous heterogeneous information, therefore providing multidimensional vulnerability representations. An empirical case study demonstrates the fault detection rate, false alarm control, and diagnostic stability of the proposed framework.

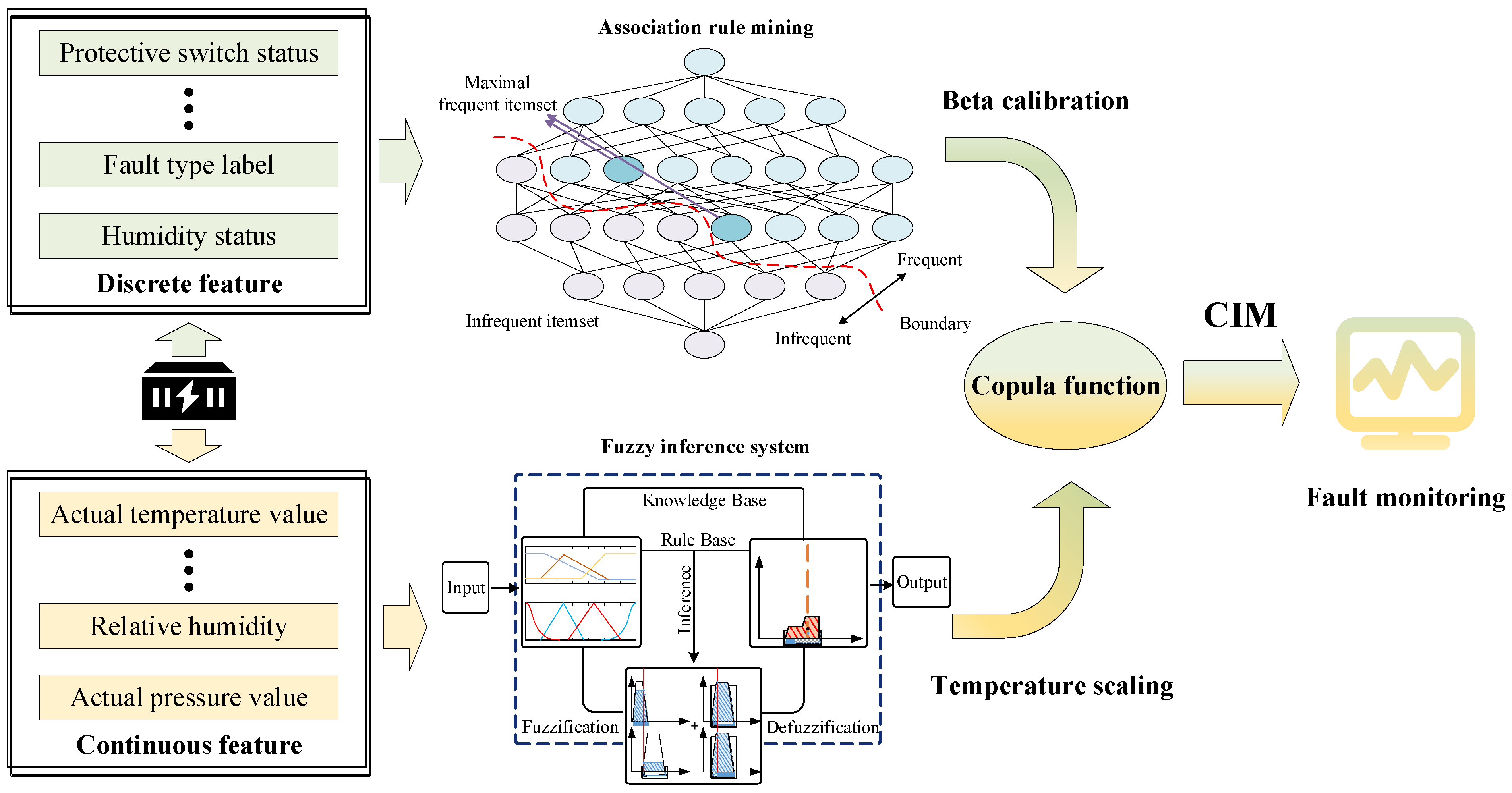
1. Introduction

With the large-scale integration of renewable energy sources, Battery Energy Storage Stations (BESS) have emerged as a vital support for enhancing grid regulation capability and operational security. The safety and reliability of BESSs are largely contingent upon their thermal management systems, within which environmental sensors—such as temperature, humidity, and pressure sensors—play a critical role in enabling condition monitoring and fault early warning [1,2,3,4]. Once these sensors undergo degradation or failure, the resulting distortion of monitoring data compromises the control accuracy of the thermal management system and may even trigger severe incidents such as thermal runaway. Consequently, ensuring the stable operation of environmental sensors under complex practical conditions has become a critical issue in both the research and application of battery energy storage stations [5]. Current studies on sensor risk assessment can be broadly categorized into three main approaches.

The first category comprises mechanism-driven approaches. These methods rely on electro–thermal coupling or control-theoretic models, where observers and residuals are constructed to achieve fault detection and isolation. Their primary advantages lie in strong interpretability and controllable thresholds, enabling diagnosis under small-sample or unlabeled conditions and thus offering high credibility in safety-critical scenarios. For instance, Lan et al. [6] developed an observer based on a battery electro–thermal coupling model to realize online fault estimation of current, voltage, and temperature sensors. Kim et al. [7] proposed a residual generation scheme that integrates a nonlinear state observer with disturbance estimation to achieve robust detection of current sensor faults in battery management systems. Park et al. [8] monitored temperature and humidity sensors in containerized energy storage systems and identified condensation and insulation degradation under high-humidity conditions as critical risks, further proposing corresponding control measures. Nevertheless, such methods exhibit high sensitivity to model parameters and operating-condition drifts, rendering them prone to failure in complex environments and thus limiting their applicability.

The second category corresponds to data-driven approaches. These methods leverage large-scale operational data to directly learn abnormal sensor patterns without relying on complex mechanistic models, thereby exhibiting favorable performance under noisy, nonlinear, and disturbance-prone conditions. Their advantages include broad applicability, high detection accuracy, and flexible extensibility through multimodal data integration. For instance, Shen et al. [9] proposed a multi-sensor, multi-mode diagnostic framework for battery systems capable of identifying diverse sensor faults under severe interference. Wu et al. [10] developed a Bayesian network that integrates data and knowledge to enable interpretable diagnostics of HVAC system sensors, demonstrating strong robustness against noise and nonstationary conditions. Fan et al. [11] introduced a diagnosis method combining relative entropy with state-of-charge estimation, which can simultaneously detect voltage and temperature sensor anomalies as well as potential short-circuit risks. Nevertheless, the performance of this category is constrained by its dependence on labeled samples, limited generalization capability, and insufficient interpretability.

The third category encompasses hybrid approaches. These methods integrate mechanistic constraints with data-driven learning, thereby exploiting physical models to enhance interpretability while leveraging data-driven techniques to improve robustness and adaptability. For example, Zheng et al. [12] employed stochastic hybrid systems combined with unscented particle filtering to diagnose battery voltage and current sensors, effectively mitigating the sensitivity to empirical thresholds. Jin et al. [13] incorporated a sliding-mode observer with data-driven discrimination under an event-triggered mechanism, achieving a balance between real-time performance and computational overhead. Such approaches offer a compromise between accuracy and interpretability, partially alleviating the limitations of purely mechanistic or data-driven methods. However, they are often associated with considerable computational cost and implementation complexity, posing ongoing challenges in terms of scalability and real-time applicability.

Overall, although the aforementioned studies have provided diverse perspectives on sensor risk assessment, most efforts remain confined to individual sensors and lack an integrated framework capable of jointly evaluating temperature, humidity, and pressure sensors within the thermal management systems of energy storage stations. When multiple types of sensors are simultaneously considered for holistic risk assessment, directly feeding multi-source heterogeneous data—including both continuous and discrete features—into complex neural networks or machine learning models often results in excessive parameter dimensionality, markedly increased computational complexity and storage overhead, and consequently degraded training and inference stability, which further constrains real-time deployment on edge nodes of storage stations. Moreover, the strong coupling and uncertainty inherent in multi-source data further compound the modeling challenge. Hence, developing sensor risk assessment methodologies that simultaneously achieve low complexity, interpretability, and robustness is of critical importance.

In the field of big data analytics, association rule mining (ARM) has demonstrated the capability to directly identify stable and interpretable patterns in large-scale databases, making it particularly effective for extracting strongly associated factors with high support and confidence from discrete features. In recent years, ARM has shown strong effectiveness in uncovering complex relationships among discrete events across various domains, including building energy consumption analysis [14], equipment reliability maintenance, and industrial IoT sensor diagnostics [15]. To enhance efficiency and scalability, algorithmic improvements to ARM have been widely adopted to address the computational burden posed by high feature dimensionality and the large number of frequent itemsets. The classical Apriori algorithm [16] has progressively evolved into advanced variants such as FP-Growth [17] and Eclat [18], achieving significant gains in both efficiency and scalability. A key advantage of ARM lies in its independence from predefined model structures, allowing it to directly reveal variable interactions while remaining effective under weakly labeled or even unlabeled conditions.

On the other hand, fuzzy inference is particularly suitable for handling continuous features, offering stable discrimination and multi-factor tradeoff capabilities under conditions of threshold drift, noise perturbations, and uncertainty. For instance, Syed Ahmad et al. [19] employed nonlinear fuzzy modeling to predict indoor environmental parameters in HVAC systems, demonstrating reliable discrimination under temperature/humidity fluctuations and boundary conditions. Gao et al. [20] combined kernel principal component analysis with a fuzzy genetic algorithm to improve HVAC sensor fault detection, thereby enhancing robustness against noise and nonlinear interactions. In resource-constrained or edge deployment scenarios, Quispe-Astorga et al. [21] and studies on heterogeneous TinyML architectures [22] explicitly examined the tradeoffs and engineering challenges associated with model compression, latency, and storage overhead. Within the context of environmental sensors in energy storage stations, ARM is more effective for mining discrete features, whereas FI provides robustness against gradual threshold variations and transient drifts in continuous features. The complementarity of these two approaches establishes a methodological foundation for developing interpretable and deployable risk assessment models that integrate multi-source heterogeneous inputs from temperature, humidity, and pressure sensors.

Building upon the above analysis, this study proposes a pattern-guided correlation integration model framework for vulnerability diagnosis. In the proposed framework, association rule mining is employed to induce patterns from discrete features, while fuzzy inference is utilized to model uncertainty in continuous features, thereby extracting potential vulnerability factors. The heterogeneous information is then unified and mapped through Component Importance Measure (CIM) to construct multidimensional vulnerability representations. Experimental results demonstrate that the framework outperforms conventional methods in terms of fault detection rate, false alarm control, and diagnostic stability, effectively identifying latent vulnerabilities in thermal management systems and enabling early warning, thereby enhancing the safety and resilience of battery energy storage stations.

2. Dual-Channel Risk Pattern Recognition Framework

2.1. Construction of the Input Mapping Matrix

In contrast to conventional approaches that model each sensor independently, this study jointly incorporates monitoring data from multiple sensor types—temperature, humidity, and pressure—at the input stage. An input mapping matrix is constructed to project heterogeneous sensor data into a unified space, thereby enabling consistent treatment of continuous and discrete features within a single framework. The multi-sensor input features are summarized in

Table 1. Examples of multi-sensor input features.

Sensor Category	Continuous Feature	Discrete Feature
Temperature sensor	Actual temperature value	Over-temperature alarm
	Output voltage signal	Thermostat switch status
	Temperature variation rate	Fan operation status
	Temperature fluctuation amplitude	Temperature sensor self-check flag
Humidity sensor	Relative humidity	Over-humidity alarm
	Humidity variation rate	Dehumidifier status
	Humidity fluctuation amplitude	Humidity sensor calibration flag
Pressure sensor	Actual pressure value	Over-pressure alarm
	Pressure variation rate	Safety valve status
	Pressure fluctuation amplitude	Protection switch status
	Output noise amplitude	Pressure sensor self-check flag

.

In risk modeling of complex systems, data collected from different stages often exhibit heterogeneous forms and diverse sources. Directly feeding such data into a model without distinction may lead to inconsistencies in information scales and metric standards, and may further introduce bias in subsequent computations, thereby undermining the reliability of risk assessment results. To address this issue, this study introduces the construction of an input mapping matrix, wherein fault records and associated feature factors are normalized to establish a unified mapping space.

Let the set of historical fault records be denoted as $\lambda ={\left\{{\lambda }_1,{\lambda }_2,\dots ,{\lambda }_i,\dots {\lambda }_m\right\}}^T$, where each event ${\lambda }_i$ represents one historical fault instance, with $i=1,\dots ,m$, Define the feature set as $F=\left\{f_1,f_2,\dots ,f_j,\dots f_n\right\}$, where each feature $f_j$ is composed of multiple feature factors $a_{k,j}$ such that $f_j={\left\{a_{1,j},a_{2,j},\dots ,a_{k,j},\dots a_{m,j}\right\}}^T$. The fault consequences are expressed as the target variable set $Y=\left\{y_1,y_2,\dots ,y_i,\dots y_m\right\}$, where $y_i$ denotes the outcome corresponding to fault event ${\lambda }_i$. By combining the sets of fault records ${\lambda }_i$ features $F$, and outcomes $Y$, an input mapping space $A$ is constructed and represented in the form of a mapping matrix as follows:

$$A=\left[\begin{array}{ccccccc}{\lambda }_1& a_{11}& \dots & a_{1j}& \dots & a_{1n}& y_1\\ ⋮& ⋮& \ddots & ⋮& \ddots & ⋮& ⋮\\ {\lambda }_i& a_{i1}& \dots & a_{ij}& \dots & a_{in}& y_i\\ ⋮& ⋮& \ddots & ⋮& \ddots & ⋮& ⋮\\ {\lambda }_m& a_{m1}& \dots & a_{mj}& \dots & a_{mn}& y_m\end{array}\right]$$

(1)

In this formulation, each row corresponds to a fault record, where ${\lambda }_i$ denotes the identifier of the $i-th$ record, $a_{i,1},a_{i,2},\dots ,a_{i,k},\dots a_{i,n}$ represent all feature factors associated with ${\lambda }_i$, and $y_i$ denotes the corresponding fault outcome.

2.2. Extraction of Coupling Relationships Among Discrete Features

Association rules represent a big data analytics technique designed to uncover implicit relationships among two or more entities. By employing association rule mining, potential coupling patterns and vulnerability relationships among features can be identified. The core idea lies in analyzing frequent itemsets to discover co-occurrence regularities among different features in operational data and expressing them through formalized logical rules.

In evaluating the operational status of multi-sensor systems in energy storage stations, the feature variables generally include both discrete and continuous attributes. The objective of association rule mining is to uncover dependencies and correlations among items in the dataset, where the items are typically represented as discrete itemsets. By mining large-scale data, valuable and meaningful relationships can be identified, enabling the prediction of certain events or attributes based on others. For example, if a dependency between a premise $a$ and a consequence $b$ is established, it can be formally expressed as an association rule of the form $a\to b$.

For the operational records of multi-sensor systems in energy storage stations, let $B=\left\{b_1,b_2,\dots ,b_j,\dots b_n\right\}$ denote the set containing all discrete input variables, where $b_j={[z_{1,j},z_{2,j},\dots ,z_{k,j},\dots ,z_{m,j}]}^T$. To construct an association rule, assume that $X$ is a subset of $B$ and $Y$ is a target variable set. If $X,Y\subseteq B$ and $X\cap Y=\varnothing$, then an association rule can be expressed as $X\to Y$. This implies that the occurrence of itemset $X$ indicates that itemset $Y$ will appear with a certain probability.

In the practical implementation, this study employs the FP-Growth algorithm as the tool for frequent itemset mining [23]. Unlike the traditional Apriori algorithm, FP-Growth eliminates the repeated generation of candidate itemsets by constructing a prefix tree to compress the transaction database and recursively mining frequent itemsets through conditional pattern bases. Using this approach, the observed features in the mapping matrix are transformed into transaction sets, while frequently co-occurring feature combinations are identified as candidate itemsets.

Building upon this, the study further evaluates the significance of rules from a quantitative perspective. Given the considerable variation in frequency and stability of different rules within the dataset, the absence of rigorous evaluation criteria may result in the erroneous retention of ineffective or noisy rules, thereby diminishing the overall modeling performance. To address this, support, all-confidence, imbalance ratio, and conviction are employed as the primary metrics for assessing rule importance.

In practical applications, support is employed to measure the frequency of a given rule within the entire dataset, thereby determining its statistical significance. As one of the most important and widely used metrics in association rule mining [24], support not only reflects the coverage of a rule but also helps filter out low-frequency rules that may arise from randomness. The mathematical formulation of support is given as:

$$Su\left(X\to Y\right)={\displaystyle \frac{num\left(X\cap Y\right)}{num\left(A\right)}}$$

(2)

All-confidence is employed to quantify the probability that the consequent occurs given the occurrence of the antecedent, thereby reflecting the reliability of a rule in conditional reasoning. Compared with traditional confidence, which is often insufficient to eliminate spurious rules when handling large-scale data, all-confidence possesses zero invariance and downward closure properties, enabling more accurate state assessment. The mathematical formulation of all-confidence is expressed as:

$$all-conf\left(X\to Y\right)={\displaystyle \frac{Su\left(X\cap Y\right)}{\max \left(Su\left(X\right),Su\left(Y\right)\right)}}$$

(3)

The imbalance ratio is employed to characterize the distributional disparity between two itemsets within an association rule [25]. In practical applications, imbalanced data are particularly prevalent due to the difficulty of acquiring labels or the scarcity of minority samples. A larger imbalance ratio indicates a stronger tendency toward uneven distributions. The mathematical formulation of the imbalance ratio can be expressed as:

$$IR\left(X\to Y\right)={\displaystyle \frac{\left(Su\left(X\right)-Su\left(Y\right)\right)}{\left(Su\left(X\right)+Su\left(Y\right)-Su\left(X\cap Y\right)\right)}}$$

(4)

Conviction is utilized to evaluate the degree of deviation between the observed probability that event $Y$ does not occur given the occurrence of $X$, and the expected probability under the independence assumption. The mathematical expression of conviction is given as:

$$Co\left(X\to Y\right)={\displaystyle \frac{1-Su\left(Y\right)}{1-[all-conf\left(X\to Y\right)]}}$$

(5)

2.3. Fuzzy Inference Approach

In contrast to discrete features, continuous features are represented as numerical intervals. Direct partitioning with absolute boundaries often introduces substantial subjectivity and leads to increased uncertainty. Fuzzy inference mitigates this issue by introducing overlapping boundaries and membership functions, thereby alleviating the rigidity of boundary partitioning and enabling smooth transitions of continuous variables across different risk levels [26]. In practical modeling, continuous features are typically divided into several fuzzy sets, each corresponding to a distinct risk level. The construction of fuzzy sets is generally based on either the value range of features or historical observations, ensuring that the inference results retain numerical clarity and enhanced interpretability. However, the value ranges of different features vary significantly, and the associated risk distributions may differ across operating scenarios. Consequently, the design of membership functions often requires feature-specific forms and parameters. While such feature dependency enhances the flexibility of the model, it also substantially increases the complexity of system construction and computation.

At the input layer of fuzzy inference, membership functions must first be constructed for each continuous feature. An input membership function assigns a degree of membership within the interval $\left[0,1\right]$ to each input variable, thereby enabling a smooth mapping from continuous values to fuzzy sets [27]. Overlapping membership functions are employed across adjacent value ranges to avoid information loss caused by rigid boundary partitions. Owing to their simplicity and computational efficiency, triangular and trapezoidal functions are most commonly used. 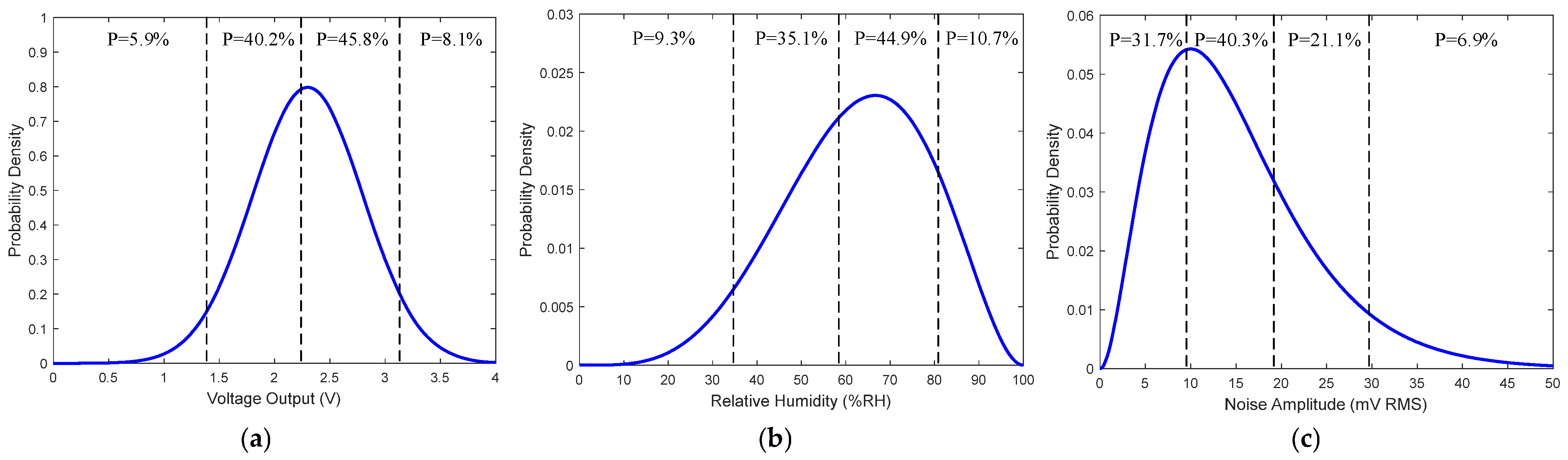In this paper, a Probability Distribution Function (PDF)-based approach is introduced to construct membership functions for more effective fuzzification of continuous features [28]. The occurrence frequency of feature values in the input database is represented by PDF curves, and based on these curves and the defined value intervals, the probability of each feature value falling within a given interval can be computed. As an illustrative example, Figure 1 presents the PDF curves and interval partitioning of output voltage signals, relative humidity, and output noise amplitude from the sensors in the thermal management system of an energy storage station.

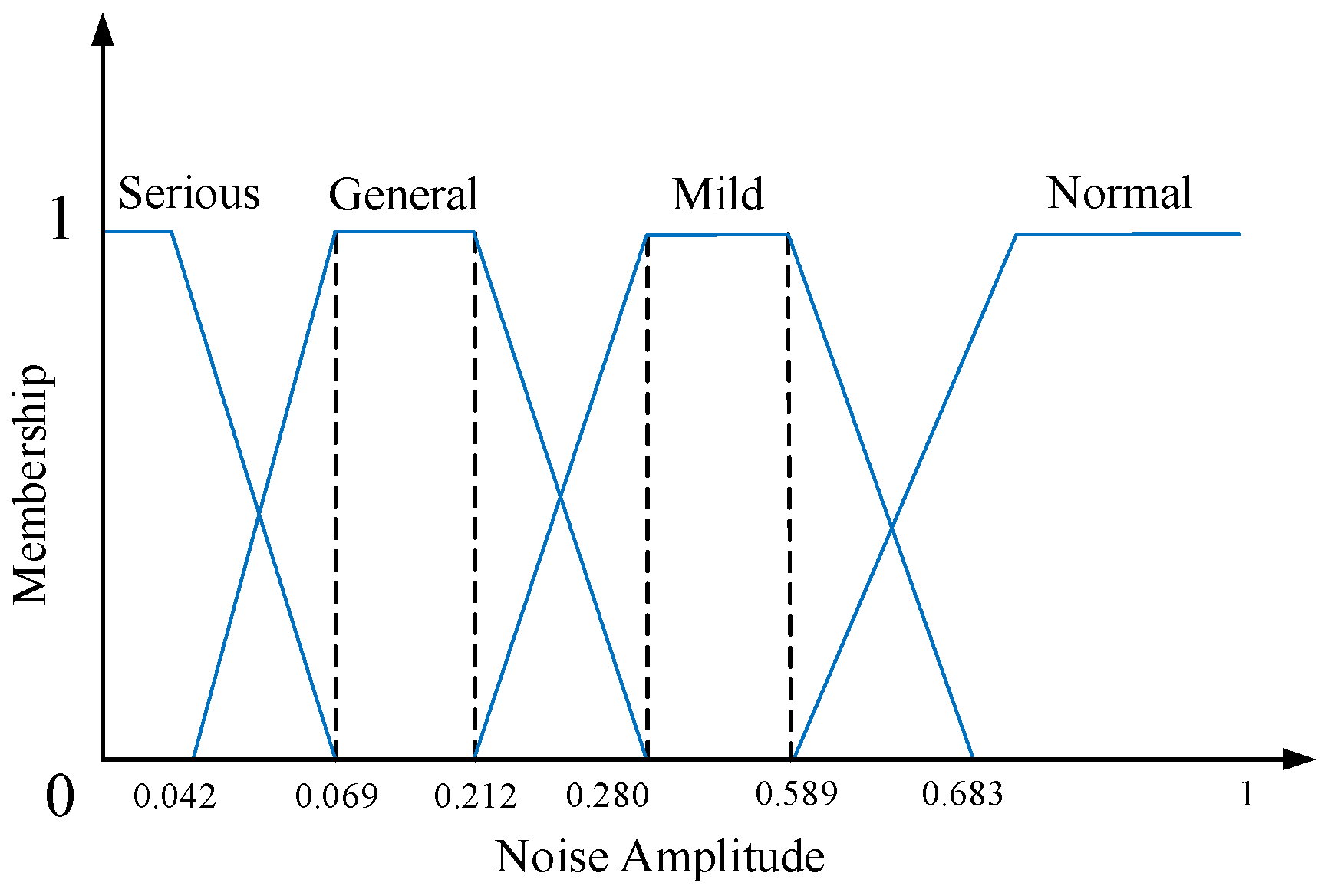
In constructing the input membership functions, continuous features are partitioned into four risk levels based on the empirical distribution of historical samples and field thresholds, corresponding to normal, mild, general, and serious. Data are drawn from long-term monitoring records, processed for missing values and robustly denoised, then summarized into empirical distributions and representative quantiles, with critical regions aligned to alarm and limit thresholds from operational guidelines. A unified protocol is adopted. The principal coverage of each level is determined by the empirical distribution so that the main probability mass falls within the designated level, and critical locations are aligned with operational thresholds to ensure procedural consistency. Boundaries between adjacent levels are placed at points where the two membership functions attain equal value, serving as the transition from lower to higher level. To soften boundaries and avoid abrupt changes near thresholds, narrow overlaps are introduced around each boundary. The overlap width is determined from historical statistics. A candidate range is set by local variability and data density, followed by back testing to compare the effects of different widths on false positives and false negatives, and the minimal feasible width is selected that preserves smoothness without expanding the high level coverage. Using relative humidity as an example, the boundary and overlap between normal and mild are placed near the upper edge of the normal regime, those between mild and general are placed near the high humidity alarm threshold, and those between general and serious are referenced to the upper edge of historical high humidity events, with the final width at each site determined by the same procedure. As the same type of input membership function is applied to all continuous features, only the input membership function for the continuous feature “output noise amplitude” is illustrated in Figure 2.

After obtaining the probability distribution curves and input membership functions, fuzzy rules and the corresponding hazard weights are further constructed to characterize the risk evolution logic of multiple sensors under varying operating conditions. For the inference mechanism, the Mamdani-type fuzzy inference method is adopted [29]. Specifically, the membership degrees of each input feature across different fuzzy sets are first computed. These values are then combined through the rule base to generate the membership distribution corresponding to each risk level. By enabling parallel activation of rules, the model is capable of capturing risk trends in the presence of coupling and uncertainty among the input conditions. The fuzzy inference rules are presented in

Table 2. Fuzzy inference rule table for feature–feature interactions.

Feature + Feature	Risk Level	Weight
S + S	=E	1
S + G	=E	1
S + M	=H	0.34
S + N	=H	0.34
G + S	=E	1
G + G	=H	0.34
G + M	=H	0.34
G + N	=Mo	0.22
M + S	=H	0.34
M + G	=Mo	0.22
M + M	=Mo	0.22
M + N	=L	0.11
N + S	=H	0.34
N + G	=Mo	0.22
N + M	=L	0.11
N + N	=L	0.11

and

Table 3. Fuzzy inference rule table for feature–risk interaction.

Feature + Risk	Risk Level	Weight
S + L	=Mo	0.22
S + Mo	=H	0.34
S + H	=E	1
S + E	=E	1
G + L	=Mo	0.22
G + Mo	=H	0.34
G + H	=H	0.34
G + E	=E	1
M + L	=L	0.11
M + Mo	=Mo	0.22
M + H	=Mo	0.22
M + E	=H	0.34
N + L	=L	0.11
N + Mo	=L	0.11
N + H	=Mo	0.22
N + E	=H	0.34

.

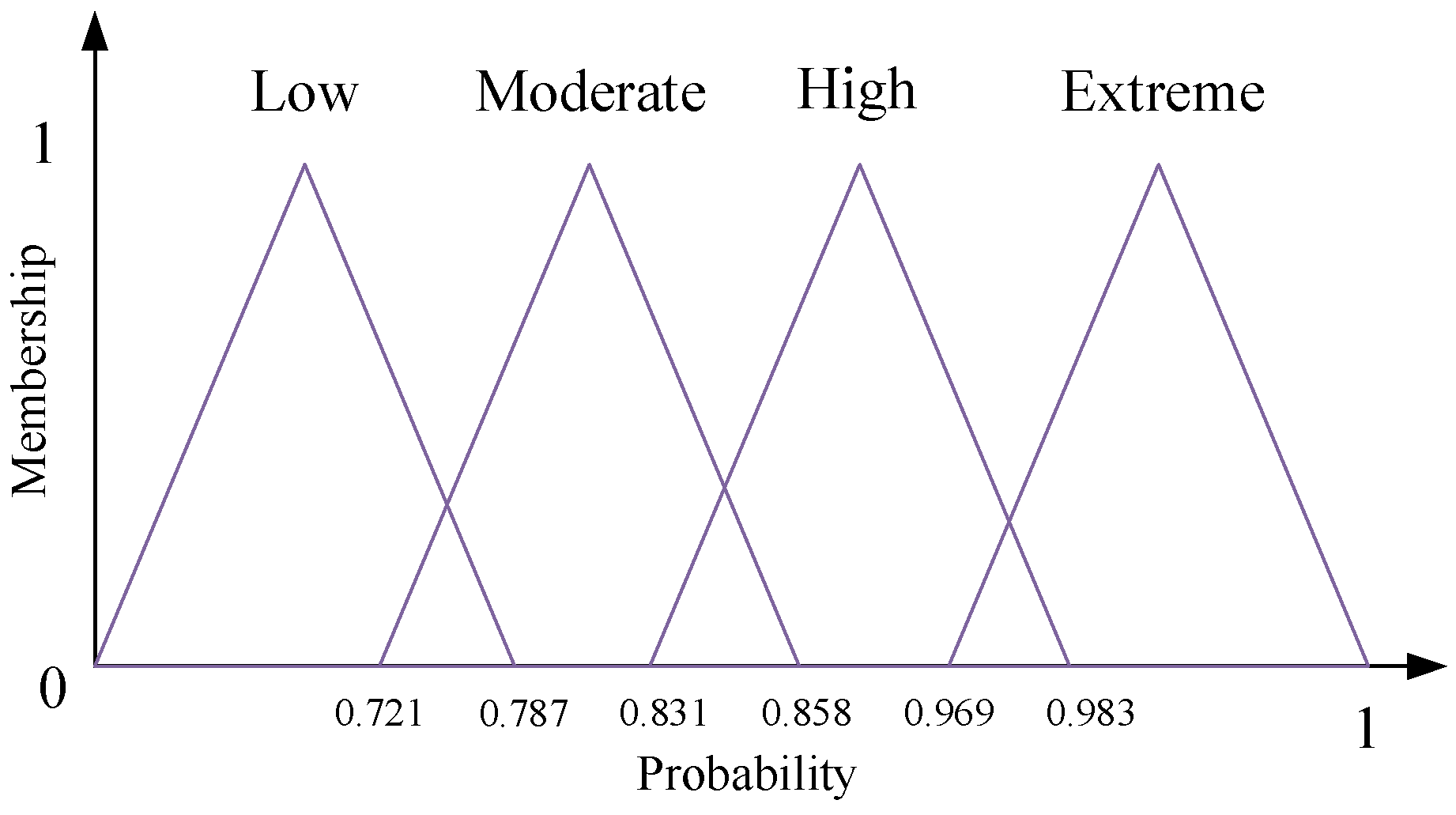
At the inference output layer, output membership functions must be constructed to represent different risk levels. In this work, four triangular functions are employed to define the output membership functions, corresponding to four levels: Low (L), Moderate (Mo), High (H), and Extreme (E). Based on the statistical distribution of data across these risk levels, the resulting output membership functions are illustrated in Figure 3.

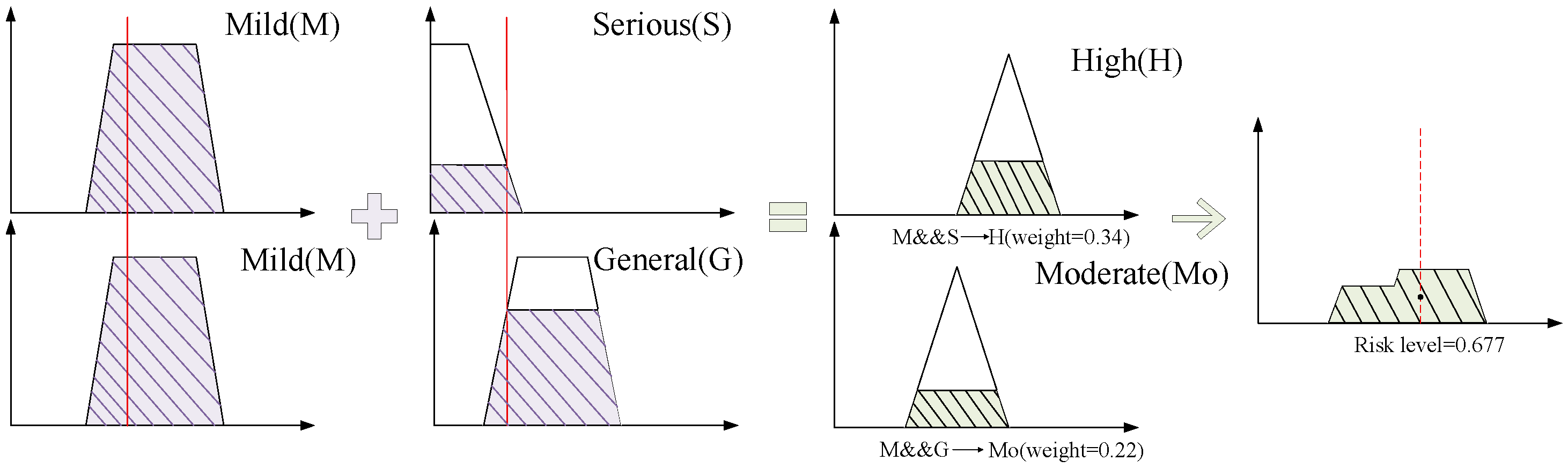
As an illustrative example, consider a fault record in which the output voltage signal is measured at 1.1 V and the relative humidity at 42.3%. Based on the probability distribution function (PDF) curves and the defined value intervals, the probabilities of the output voltage signal and relative humidity are calculated as 5.9% and 35.1%, respectively. According to the fuzzy rules in Table 2 and Table 3, the risk regions in the input membership functions are determined by the membership degrees associated with these probabilities. As shown in Figure 4, the fuzzy weights are 0.34 and 0.22, yielding a probabilistic fuzzy risk of 0.677. By aggregating and weighting these risk regions, the final probabilistic fuzzy risk is obtained through defuzzification in the output membership functions.

3. Unified Modeling of Multi-Source Risk Data

3.1. Construction of Dual-Channel Failure Probability

The CIM is a key tool in reliability analysis for quantifying the system’s sensitivity to individual components. Its fundamental principle is to compute the partial derivative of the system reliability function with respect to the reliability or failure probability of a component, thereby revealing the marginal impact of each component on overall system performance [30]. In the monitoring scenario of thermal management sensors in energy storage stations, the raw data simultaneously include both discrete and continuous features. To account for the structural differences in the data, association rule mining is employed for discrete features, while fuzzy inference is applied to continuous features. Since CIM cannot directly accommodate rule-based indices and fuzzy scores, both are mapped into a unified dimension of failure probability.

For the discrete data processed using the association rule method, this study employs the Beta Calibration approach to transform the multidimensional strength indices obtained from association rule mining into conditional failure probabilities. Let the rule strength vector of component $i$ at time $t$ be defined as $R_{AR}\left(i;t\right)=\left\{R_{Supp},R_{all-conf},R_{Imbat},R_{conv}\right\}$, where the elements correspond to support, all-confidence, imbalance ratio, and conviction, respectively. The raw score is then obtained through a linear combination of these components:

$$Z\left(i;t\right)={\omega }_0+{\displaystyle \sum }_{j=1}^4{\omega }_j\cdot R_{AR}\left(i;t\right)$$

(6)

Subsequently, the score is mapped into a probability:

$${\rho }_i^{AR}\left(t\right)=\sigma (\alpha \ln Z\left(i;t\right)+\beta \ln \left(1-Z\left(i;t\right)\right)+\gamma )$$

(7)

In this formulation, ${\omega }_0$ denotes the bias term, and ${\omega }_j$ represents the weight parameter associated with each rule strength index, quantifying the relative contribution of different indices to the component failure probability. Specifically, if a particular index exhibits stronger discriminative capability for actual fault occurrences, its corresponding weight ${\omega }_j$ is adjusted upward during training, thereby increasing its influence on the final probability output. The logistic function is defined as $\sigma \left(x\right)=1/\left(1+e^{-x}\right)$. The parameters $\alpha$, $\beta$, $\gamma$, as well as ${\omega }_0$ and ${\omega }_j$, are not manually assigned but are instead estimated from the training data through statistical learning methods. Compared with traditional Platt scaling, Beta Calibration offers greater flexibility and accuracy in handling imbalanced classes and fuzzy boundaries, thereby enabling a more reliable transformation of rule strengths into failure probabilities.

For the continuous data processed through fuzzy inference, the resulting risk score reflects the component’s risk level aggregated across different membership grades but does not directly correspond to a failure probability. To address this issue, this study applies the Temperature Scaling method for calibration, specifically [31]:

$${\rho }_i^{FZ}\left(t\right)=\sigma \left({\displaystyle \frac{R_{fuzzy}\left(i;t\right)}{T}}\right)$$

(8)

In this expression, $T>0$ denotes the temperature parameter, which is estimated by minimizing the negative log-likelihood on the validation set. While preserving monotonicity, this method improves the probabilistic interpretability of risk scores by adjusting the temperature parameter, thereby aligning them with the empirical fault frequency distribution and ensuring that the outputs of continuous features can serve as valid inputs for CIM.

3.2. Synthesis of Effective Probabilities at the Component Level

The monitoring data used in this study are derived from the same multivariate dataset, which includes both discrete attributes and continuous attributes represented as real values. Given the heterogeneous attribute structure, two complementary modeling pipelines are employed at the methodological level without performing sample-level partitioning. The quantities ${\rho }_i^{AR}\left(t\right)$ and ${\rho }_i^{FZ}\left(t\right)$ represent two statistical assessments of the failure likelihood of component $i$ at time $t$, obtained from the same observation. To ensure that both forms of evidence contribute consistently within the CIM, a probabilistic synthesis is performed, yielding an effective failure probability that can be directly incorporated into the system structure function.

This study employs the Gumbel Copula as the synthesis operator [32], where the two channels are denoted as $p={\rho }_i^{AR}\left(t\right)$ and $q={\rho }_i^{FZ}\left(t\right)$. According to Sklar’s theorem, the effective failure probability is defined as:

$${\rho }_i\left(t\right)=1-C\left(1-p,1-q,{\theta }_i\right)$$

(9)

where $C\left(\cdot ;\theta \right)$ denotes the Gumbel Copula:

$$C\left(l,v;\theta \right)=\exp \left\{-{\left[{\left(-\ln l\right)}^{\theta }+{\left(-\ln v\right)}^{\theta }\right]}^{{\displaystyle \frac{1}{\theta }}}\right\}$$

(10)

The Gumbel Copula is capable of characterizing upper-tail dependence, making it well suited for capturing the engineering semantics that discrete and continuous evidence are more likely to co-occur under extreme risk levels. The parameter ${\theta }_i$ is estimated and mapped from Kendall’s $\tau$ of historical samples:

$${\theta }_i={\displaystyle \frac{1}{1-{\tau }_i}}$$

(11)

where ${\tau }_i$ denotes the Kendall rank correlation coefficient of $\left({\rho }_i^{AR}\left(t\right),{\rho }_i^{FZ}\left(t\right)\right)$. To ensure numerical stability and reproducibility, ${\theta }_i$ is set to 1 when ${\tau }_i\le 0$ or when the sample size is insufficient, and an upper bound is imposed on ${\theta }_i$ to avoid extreme estimations.

3.3. Component Importance Measure

The component importance measure is a commonly used tool for evaluating the impact of each component on variations in overall system risk. The fundamental definition of Birnbaum importance is given as:

$$I=\rho \left(\phi \left(x\right)=1|x_i=1\right)-\rho \left(\phi \left(x\right)=1|x_i=0\right)$$

(12)

Here, φ denotes the system structure function, which maps component states to the system state, where 1 represents normal operation and 0 denotes system failure. The underlying interpretation of the formula is that the $i-th$ component is alternately forced into functioning or failed states, and the difference between the corresponding probabilities of system success is evaluated. A larger difference indicates a greater impact of component $i$ on overall system reliability.

In practical engineering environments, component failure processes exhibit pronounced temporal evolution. Evaluating sensitivity at a single time instant is insufficient to fully capture the contribution of a component to system reliability over the entire time horizon. Hence, it is necessary to extend Birnbaum importance to a time-dynamic framework. In the time domain, the importance of component $i$ can be interpreted as the impact on system reliability when the component experiences its first failure at any time $u$. Specifically, at time $u$, if component $i$ is forced into either an operational or failed state, the resulting system failure probabilities will differ. Moreover, the likelihood of component $i$ failing for the first time at time $u$ is not uniformly distributed but is instead governed by its underlying time-to-failure distribution.

To extend the static sensitivity measure into the time domain, the first-failure process of component $i$ along the time axis is considered. To transition from instantaneous effects to a full-time-domain measure, the interval $\left[0,t\right]$ is discretized into a set of partition nodes $\left\{k\right\}$, with $\Delta {\rho }_i\left(u_k\right)$ denoting the incremental probability of the first failure of component $i$ within the subinterval $[u_k,u_{k+1})$. At time $u$, if the state of component $i$ is switched from “operational” to “failed”, the instantaneous change in the system failure probability can be approximated by the difference $\rho \left(1_a,1-\rho \left(u\right)\right)-\rho \left(0_a,1-\rho \left(u\right)\right)$, which corresponds to the system failure probabilities when the $i-th$ component is fixed as functional or failed, respectively, while other components follow $1-\rho \left(u\right)$. Under any given partition, the cumulative contribution of component $i$ can then be expressed as a weighted summation of instantaneous impacts with first-failure weights. To ensure comparability across components, the weighted summations are further normalized over all components, yielding the discretized dynamic time-dependent importance measure:

$$I_c\approx {\displaystyle \frac{{{\displaystyle \sum }}_k\left[\rho \left(1_{ai},1-\rho \left(u_k\right)\right)-\rho \left(0_{ai},1-\rho \left(u_k\right)\right)\right]\mathsf{\Delta }{\rho }_i\left(u_k\right)}{{{\displaystyle \sum }}_{j=1}^n{{\displaystyle \sum }}_k\left[\rho \left(1_{aj},1-\rho \left(u_k\right)\right)-\rho \left(0_{aj},1-\rho \left(u_k\right)\right)\right]\mathsf{\Delta }{\rho }_j\left(u_k\right)}}$$

(13)

As the partition is refined, the above expression becomes insensitive to the discretization grid, and its limiting form defines the dynamic time-dependent component importance measure adopted in this study:

$$I_c\left(t\right)=\underset{\max \left|u_{k+1}-u_k\right|\to 0}{\lim }{\displaystyle \frac{{{\displaystyle \sum }}_k\left[\rho \left(1_{ai},1-\rho \left(u_k\right)\right)-\rho \left(0_{ai},1-\rho \left(u_k\right)\right)\right]\mathsf{\Delta }{\rho }_i\left(u_k\right)}{{{\displaystyle \sum }}_{j=1}^n{{\displaystyle \sum }}_k\left[\rho \left(1_{aj},1-\rho \left(u_k\right)\right)-\rho \left(0_{aj},1-\rho \left(u_k\right)\right)\right]\mathsf{\Delta }{\rho }_j\left(u_k\right)}}$$

(14)

Here, the numerator represents the weighted accumulation of the instantaneous impacts and first-failure weights of component $i$ over the interval $\left[0,t\right]$, while the denominator corresponds to the total weighted accumulation across all components. Consequently, $I_C(t)=\left[0,t\right]$, and at any given time $t$, the condition ${\displaystyle {\sum }_{i=1}^n{I}_C(t)=1}$ holds.

4. Overview of the Methodological Framework

This study proposes a Pattern-Guided CIM Vulnerability-Diagnosis framework (PG-CIM) for the multi-sensor thermal management system of an energy-storage station, focusing on heterogeneous data processing, risk-pattern extraction, unified probabilistic mapping, and system-importance quantification. First, to address discrepancies in dimensionality, scale, and sampling schemes across multi-source sensor data, an input mapping matrix is introduced to achieve a unified representation at the data level, thereby ensuring comparability and consistency in subsequent modeling. On this basis, discrete features are analyzed using an enhanced association rule mining approach to identify potential coupling patterns and vulnerability relationships, whereas continuous features are modeled through a fuzzy inference framework constructed from probability distributions, producing risk scores characterized by smooth transitions and high interpretability.

To overcome semantic discrepancies among results derived from different sources, the rule-based indices and fuzzy scores are transformed into conditional failure probabilities and jointly modeled through a Copula function, thereby yielding consistent risk representations within the probability space. Based on this unified probabilistic input, dynamic component-level importance measures are then computed to reveal the marginal effects and risk contributions of critical sensors over the operational timeline. Finally, by integrating the system structure function, global vulnerability diagnosis and early warning are achieved, enabling the transition from local information to an overall assessment of system security. The methodological workflow of this study is illustrated in Figure 5.

5. Case Study Analysis

5.1. Data Overview

In this study, a grid-connected battery energy storage station in a target region is adopted as the experimental testbed. The station employs a modular containerized layout of battery cabins. A representative battery unit consists of three battery cabins connected in parallel, providing a combined nominal energy capacity of approximately 2 MWh. Within each cabin, 336 tubular gel VRLA cells rated at 2 V/1000 Ah are series-connected to form a string with a nominal DC voltage of about 672 V and a string energy of roughly 672 kWh. A hierarchical battery management system (BMS) is deployed at the unit level to enable online monitoring and balancing control of key state variables, including voltages and temperatures at the cluster, module, and cell levels. The BMS adopts a modular acquisition architecture, where each acquisition module can monitor up to 24 cells; consequently, 14 acquisition modules are installed in each cabin to achieve cell-level supervision of all 336 series-connected cells. In accordance with the cabin layout, 14 temperature sensors, 14 pressure sensors, and 1 humidity sensor are instrumented in each cabin. The experimental setup consists of in situ sensor deployment inside the station, a data acquisition and time-synchronization subsystem, and a station-control data interface. Sensors are arranged along the battery cluster aisles and at critical heat-transfer locations, while the containerized cabins are installed in rows at the station level. The acquisition and synchronization subsystem assigns timestamps to all channels using a unified time reference and buffers the measurements to a local database. On the station-control side, operation records issued by the energy management system (EMS) and BMS are aligned with the measurement stream through dedicated data interfaces. The experiment is conducted under normal operating conditions without physical modification of the plant or additional loading. The dataset comprises long-term raw monitoring records and station-control logs with sampling intervals ranging from seconds to minutes. Prior to storage, the data undergo missing-value imputation, removal of sporadic spikes and plateau noise, unit and dimensional consistency checks, and resampling to a fixed time step. Multi-source signals are then aggregated by timestamp to form sensor-level time-series samples. Target labels indicate sensor faults and abnormal operating states, and are derived from station alarms and maintenance records, reconciled, and aligned with the corresponding sample windows. The resulting dataset is partitioned chronologically into training, validation, and test subsets with a 6:2:2 ratio; the training and validation subsets are used for model learning and threshold calibration, whereas the test subset is reserved solely for final performance evaluation. The overall experimental platform thus consists of the storage unit, sensing and acquisition modules, and data-recording infrastructure, with all relevant data automatically archived by the EMS/BMS and subsequently time-synchronized for analysis.

The operational data underpin the case analysis used to validate the proposed pattern guided CIM-based vulnerability diagnosis framework. The system is instrumented with temperature, humidity, and pressure sensors to capture multidimensional variations in the operating environment. The collected features comprise two categories. Continuous variables include temperature, relative humidity, and internal pressure. Discrete variables include alarm indicators, protection switch states, and fault type labels.

5.2. Validation Methodology

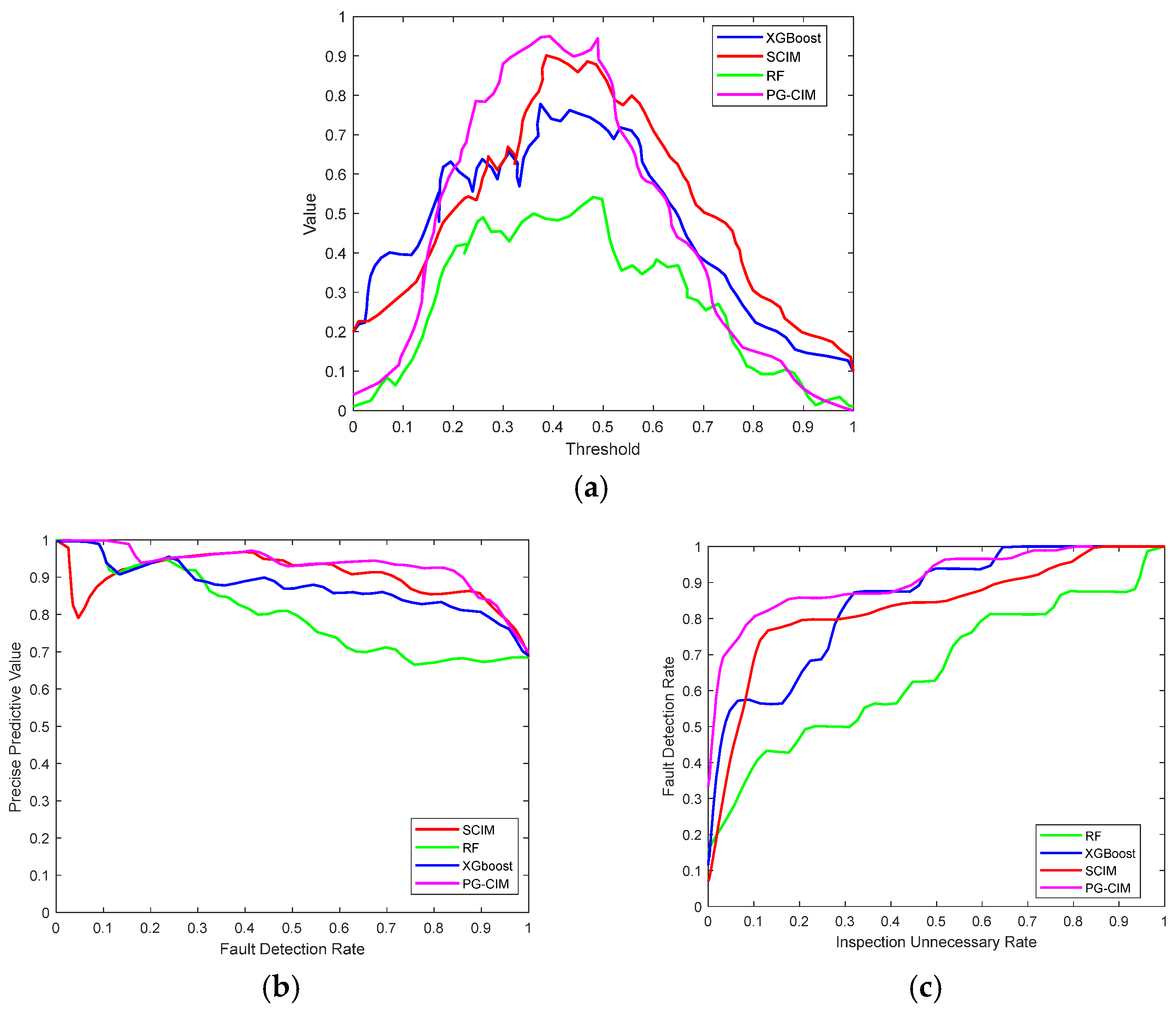
To accurately assess the performance of the proposed framework, the Kolmogorov–Smirnov (KS) statistic, the Receiver Operating Characteristic (ROC) curve, and the Precision–Recall (PR) curve are employed as the core evaluation metrics. The KS statistic quantifies the maximum difference between cumulative positive and negative instance rates, thereby reflecting the model’s discriminative capability at the optimal threshold. The ROC curve characterizes the overall detection capability and robustness of the model across varying decision thresholds, while the PR curve provides a more intuitive evaluation of performance on minority risk samples under class-imbalanced conditions.

For comparative evaluation, three baseline methods are considered. The first baseline maintains the two-channel probability extraction and calibration for discrete and continuous features but adopts the traditional static CIM rather than the proposed time-dynamic extension. This baseline, referred to as the Static CIM-based Framework (SCIM), is designed to examine the added value of dynamic CIM in capturing temporal evolution effects. The second baseline employs the ensemble learning method Random Forest (RF), which can efficiently model nonlinear relationships and variable interactions in multi-source feature spaces. RF has been widely applied in sensor diagnostics for power and energy storage systems, demonstrating broad acceptance and stable performance. The third baseline utilizes the gradient boosting decision tree model, exemplified by XGBoost, which has shown superior performance under imbalanced data conditions by effectively capturing nonlinear feature interactions. XGBoost has also gained widespread recognition in energy and industrial applications. Through comparisons with these three baselines, the proposed method highlights the temporal advantages of dynamic CIM as well as the performance improvements achieved by Copula-based fusion under complex coupling conditions.

5.3. Analysis of Test Results

Figure 6 presents the comparative KS, PR, and ROC curves of the four methods on the test set. As observed from the KS curves, the proposed PG-CIM framework consistently achieves the highest peak values and outperforms the other methods across the threshold interval of 0.3–0.6, indicating its superior capability to distinguish between positive and negative samples under varying decision conditions. In contrast, although the traditional SCIM method demonstrates a clear advantage over RF, it still fails to reach the peak performance level of PG-CIM, highlighting the limitations of static CIM in capturing temporal evolution effects.

5.4. Analysis of Empirical Case Study

An empirical case study is conducted using field operational data from a battery energy storage station equipped with temperature, pressure, and humidity sensors that continuously collect multi-source data from the battery compartments under varying operating conditions. Based on the proposed PG-CIM framework, two input scenarios are designed. In the first scenario, features from all three sensor types are jointly fed into the model to produce an integrated risk distribution of the storage station. In the second scenario, the features from temperature, pressure, and humidity sensors are individually input to derive dimension-specific risk distributions under the same framework. The results are visualized in the form of risk heatmaps, enabling intuitive representation of both the overall risk landscape and the sensor-specific risk characteristics. Figure 7 presents the overall risk heatmap of the station together with the heatmaps corresponding to temperature, pressure, and humidity sensors.

Guided by historical operating experience, this case study defines three graded intervals—normal, warning, and abnormal—for the internal temperature $T$, relative humidity $H$, and cabin pressure difference $\Delta P$, which are subsequently used to construct the corresponding fuzzy membership functions. For temperature, $T\le 30 °\mathrm{C}$ is classified as the normal range, $30 °\mathrm{C}<T\le 40 °\mathrm{C}$ as a temperature-warning range, and $T>40 °\mathrm{C}$ sustained over a period as the abnormal range. For relative humidity, $H\le 70\%$ is regarded as normal, $70\%<H\le 80\%$ as a humidity-warning range, and $H>80\%$ as abnormal. For the cabin pressure difference, $\left|\Delta P\right|\le 20 \mathrm{Pa}$ is treated as the normal fluctuation band, $20 \mathrm{Pa}<\left|\Delta P\right|\le 40 \mathrm{Pa}$ as mild deviation, and $\left|\Delta P\right|>40 \mathrm{Pa}$ as a significant abnormal condition.

In the case study, the input features consist of two parts, namely continuous measurement features and discrete operational features. The continuous features, including temperature, relative humidity and cabin pressure difference, are first modeled by constructing empirical probability distributions and corresponding fuzzy membership functions. A Mamdani-type fuzzy inference procedure is then applied to aggregate the membership degrees under different operating-condition combinations, and a defuzzification step is used to obtain a probabilistic fuzzy risk score in the range [0, 1], which characterizes the risk level implied by the joint continuous state. The discrete features, such as alarm logs, fault flags and operating-mode categories, are processed by an association-rule mining module that identifies stable co-occurrence patterns between typical discrete states and historical risk events, yielding a set of discrete risk factors that reflect fault susceptibility. Rather than being used in isolation, the outputs of these two branches are combined within a component-importance-based fusion framework, where the probabilistic fuzzy risk scores and the association-rule-based factors are jointly mapped to a single comprehensive risk score, which serves as the quantitative basis for the risk heatmap visualization.

The overall risk heatmap indicates that most battery compartments remain at low to moderate risk levels, reflecting generally stable operating conditions. Nevertheless, certain localized regions exhibit markedly elevated risk, with several units on the southern side forming distinct high-risk areas. In addition, scattered medium-risk units are observed in the central portion of the battery array, suggesting that sensors in this region may be influenced by environmental disturbances or load fluctuations. These results demonstrate that risk is not uniformly distributed in space but instead exhibits localized clustering characteristics.

A decomposition of risk distributions across different sensor dimensions provides more detailed insights. The risk heatmap of temperature sensors indicates generally low risk levels. In contrast, the pressure sensor heatmap reveals consistently higher risk levels than those of the temperature dimension, suggesting that pressure variations within the compartments are more likely to trigger unstable states. The humidity sensor heatmap displays multiple clustered medium-to-high risk regions, particularly in areas with densely arranged compartments. Field observations suggest that prolonged exposure to high-humidity environments can readily induce sensor signal drift, insulation degradation, and even condensation, thereby creating potential safety hazards.

For each risk region indicated in the multi-sensor overall risk block diagram, the corresponding values of temperature, relative humidity, and cabin pressure difference are collected and summarized in

Table 4. Example data for the risk block diagram.

Risk Region	Temperature/°C	Relative Humidity/%	Pressure Difference/Pa	Risk Score
Medium-risk region 1	26.3	72.5	26.7	0.52
Medium-risk region 2	29.8	76.6	40.1	0.58
High-risk region	38.6	85.3	8.2	0.73

.

As shown in Table 4, the temperature in medium-risk region 1 remains in the upper portion of the normal range, while the relative humidity has entered the warning band and the pressure difference is slightly above the normal fluctuation range. The corresponding risk score is 0.52, indicating that the medium risk level is primarily driven by elevated humidity combined with a mild pressure anomaly. In medium-risk region 2, temperature, humidity, and pressure difference all increase further and approach their respective abnormal intervals, yielding a higher risk score of 0.58, which reflects an upper-medium risk level. In the high-risk region, the temperature is close to the abnormal threshold, the humidity significantly exceeds its limit, and the pressure difference remains within the normal range. The resulting risk score reaches 0.73, suggesting that the high risk is mainly attributable to the combined effect of temperature rise and high humidity. This demonstrates that PG-CIM can capture such multi-factor coupled environmental hazards rather than relying solely on the limit violation of any single measured variable.

The combined analysis of overall and dimension-specific risks reveals a clear complementarity among different sensor types in risk characterization. Temperature-related risks primarily reflect the effects of load–cooling imbalances, pressure-related risks highlight hidden hazards arising from compartmental structural and interface fluctuations, and humidity-related risks emphasize the long-term influence of environmental conditions on sensor stability. The PG-CIM framework is capable of simultaneously capturing these heterogeneous characteristics across multiple dimensions and visualizing their spatial distribution through risk heatmaps, thereby enabling precise localization and early warning of potential hazards. These findings validate the diagnostic advantages of the framework under complex operating conditions and provide a reliable basis for risk management and differentiated operation and maintenance in energy storage stations.

6. Conclusions

This study addresses the complex characteristics of multi-source heterogeneous sensor data in the thermal management systems of energy storage stations and introduces PG-CIM for vulnerability diagnosis. The proposed framework incorporates three main innovations. First, a dual-channel modeling approach combining association rule mining and fuzzy inference is employed to mitigate uncertainties caused by mixed discrete and continuous features, near-threshold drift, and noise disturbances. Second, probabilistic calibration and Copula-based fusion are utilized to achieve unified mapping of multi-channel outputs, thereby overcoming semantic inconsistencies among different indices and ensuring probabilistic coherence in risk representation. Third, a time-dynamic extension of the component importance measure is developed to quantify the marginal risk contributions of critical sensors across operational timelines.

In the validation stage, the proposed PG-CIM framework was systematically evaluated against baseline models and an empirical case study. The results show that PG-CIM achieves significant improvements across key metrics, including KS, ROC, and PR, with particularly strong fault detection capability and diagnostic stability under conditions of class imbalance and complex coupling. Moreover, the empirical risk heatmaps demonstrate that the framework not only captures the overall risk distribution but also decomposes the risk sources and spatial variations in temperature, pressure, and humidity sensors, thereby enabling intuitive visualization and early warning of potential hazards.

Overall, the PG-CIM framework demonstrates improvements in reducing model complexity, enhancing interpretability, and strengthening robustness, thereby providing effective support for multidimensional risk diagnosis and the differentiated operation and maintenance of energy storage stations. Future research will focus on extending the adaptability of the framework to cross-station and multi-regional scenarios, and integrating it with edge computing and digital twin platforms to explore pathways for wide-area collaborative risk diagnosis and real-time early warning.