Multi-Objective Collaborative Optimization of Magnetic Gear Compound Machines Using Parameter Grouping and Kriging Surrogate Models
Abstract
1. Introduction
2. Magnetic Gear Compound Machine Structure and Parameters
3. Objective Functions and Constraints
4. Multi-Objective Optimization Design Methodology
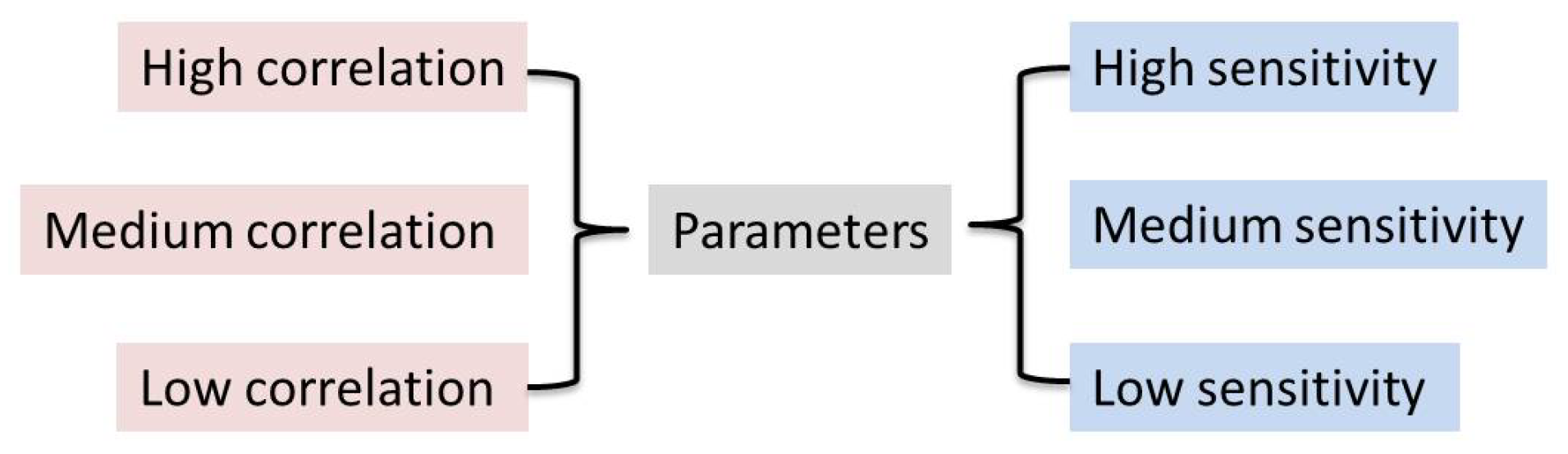
4.1. Parameter Grouping Strategy
4.2. Multi-Stage Optimization Process
- (1)
- Parameter Sampling:LHS [32] generates experimental designs that uniformly fill the design space of each parameter group. For the k-th optimization stage with parameter set , fixed parameters follow the assignment rule: if (), the optimized value is utilized; if (), the initial value is maintained. This procedure generates a representative sample set that ensures comprehensive exploration of the design space while respecting the sequential optimization structure.
- (2)
- Surrogate Model Construction: A Kriging metamodel [33] is constructed to approximate the input-output relationship. The model consists of two components: a deterministic global trend and a stochastic process capturing local variations:The Gaussian process term follows a normal distribution , where is the correlation matrix parameterized by . The model parameters are estimated via maximum likelihood estimation, and prediction accuracy is validated against hold-out samples, achieving R2 values consistent with reported electrical machine optimization studies [34].
- (3)
- Pareto Front Search: The NSGA-III algorithm is applied to solve the multi-objective optimization problem defined in (9), which considers four separate normalized objectives. The algorithm identifies the Pareto-optimal set representing the best trade-offs among the competing objectives without artificial scalarization [35,36].
- (4)
- Optimal Solution Decision: From the obtained Pareto front, the final design solution is selected using the weighted scoring approach in (10). This ensures that the selected solution aligns with specific application requirements while maintaining the diversity of the Pareto-optimal set.
5. Optimization Results and Analysis
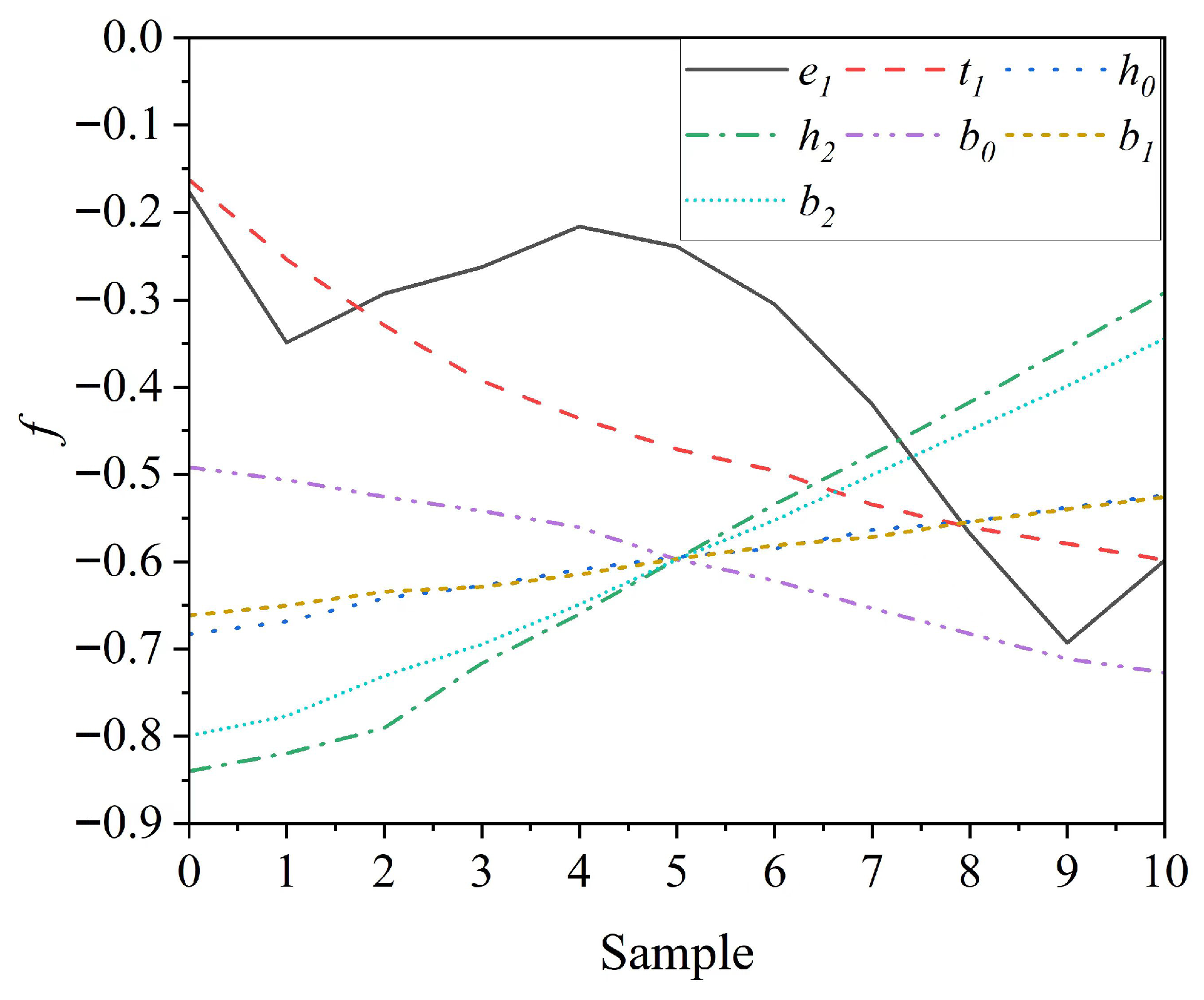
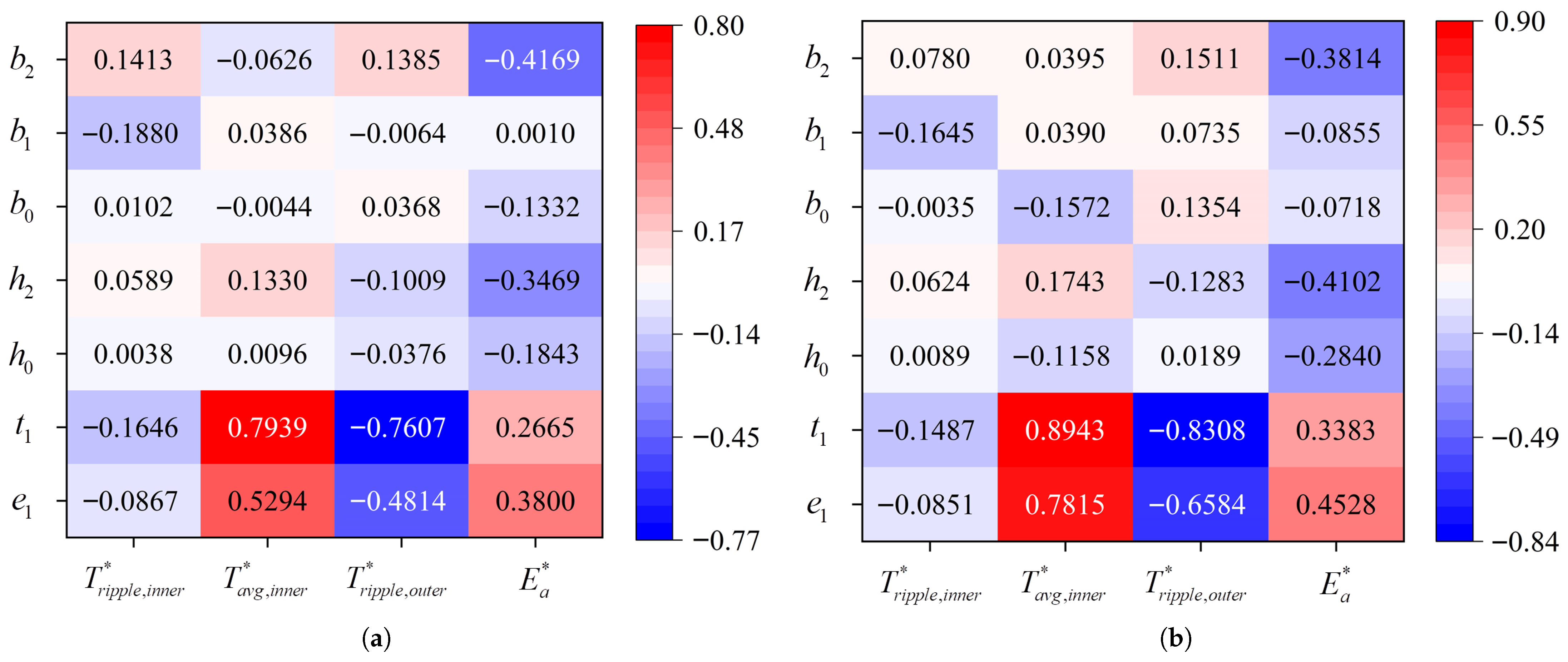
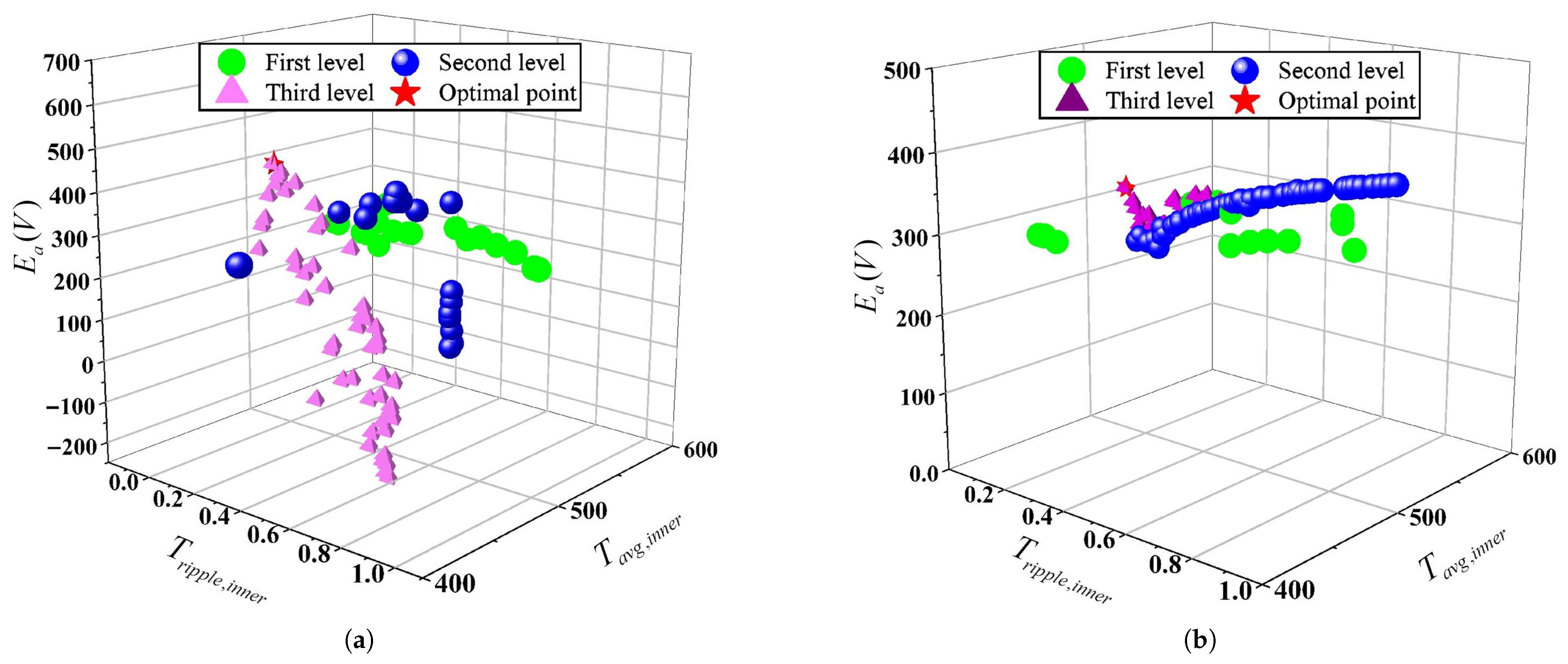
5.1. Parameter Grouping Results
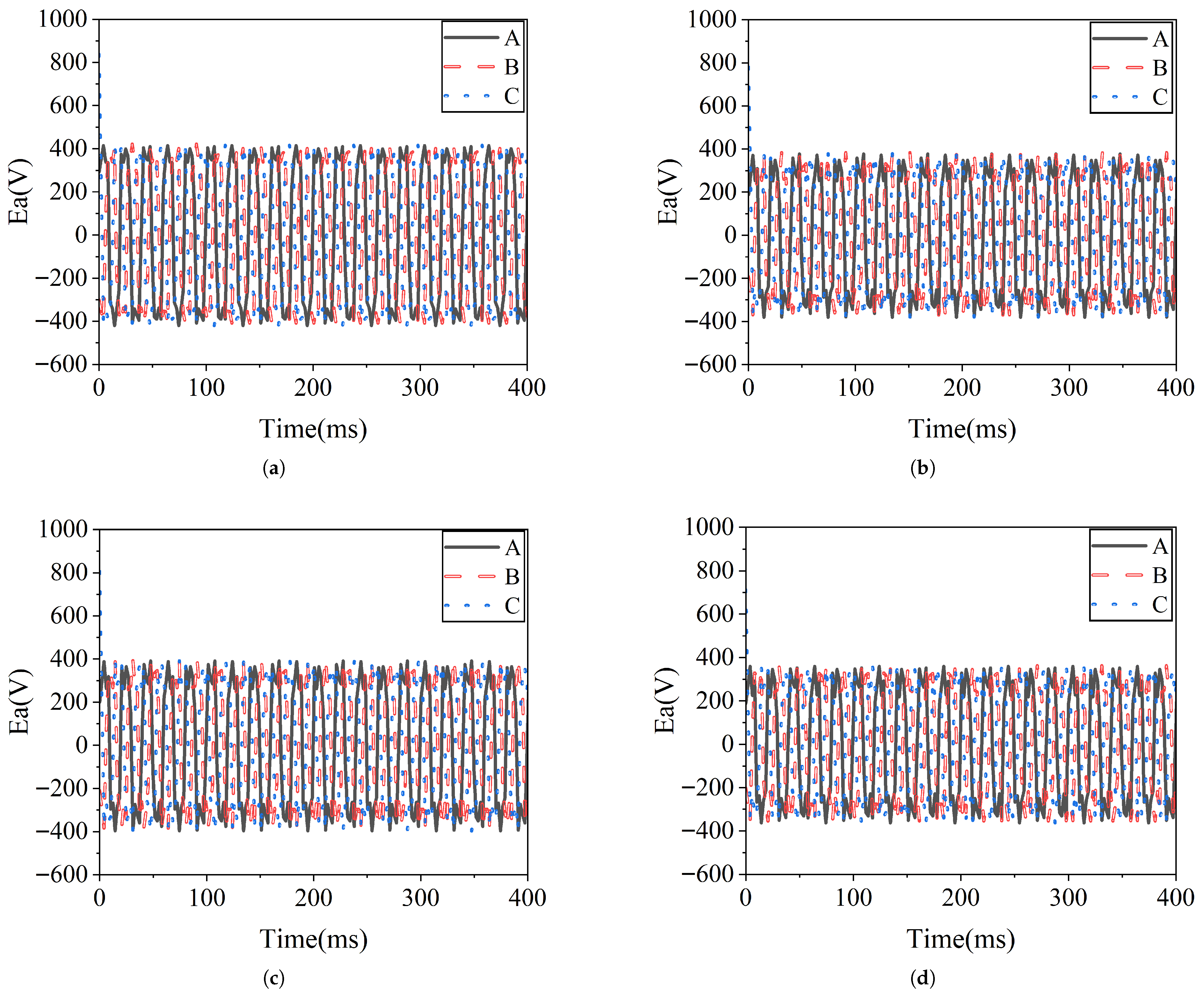
5.2. Optimization Result Analysis
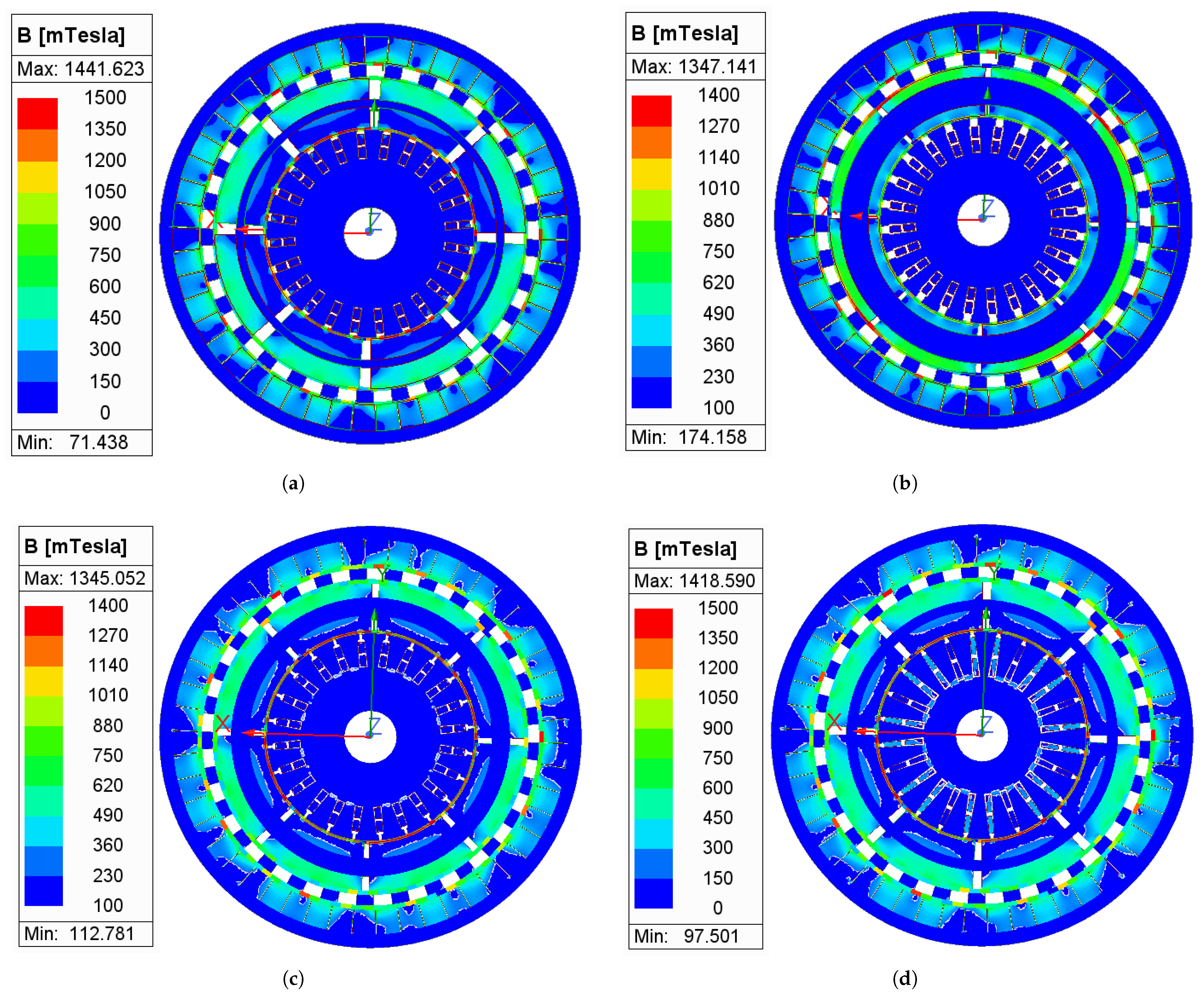
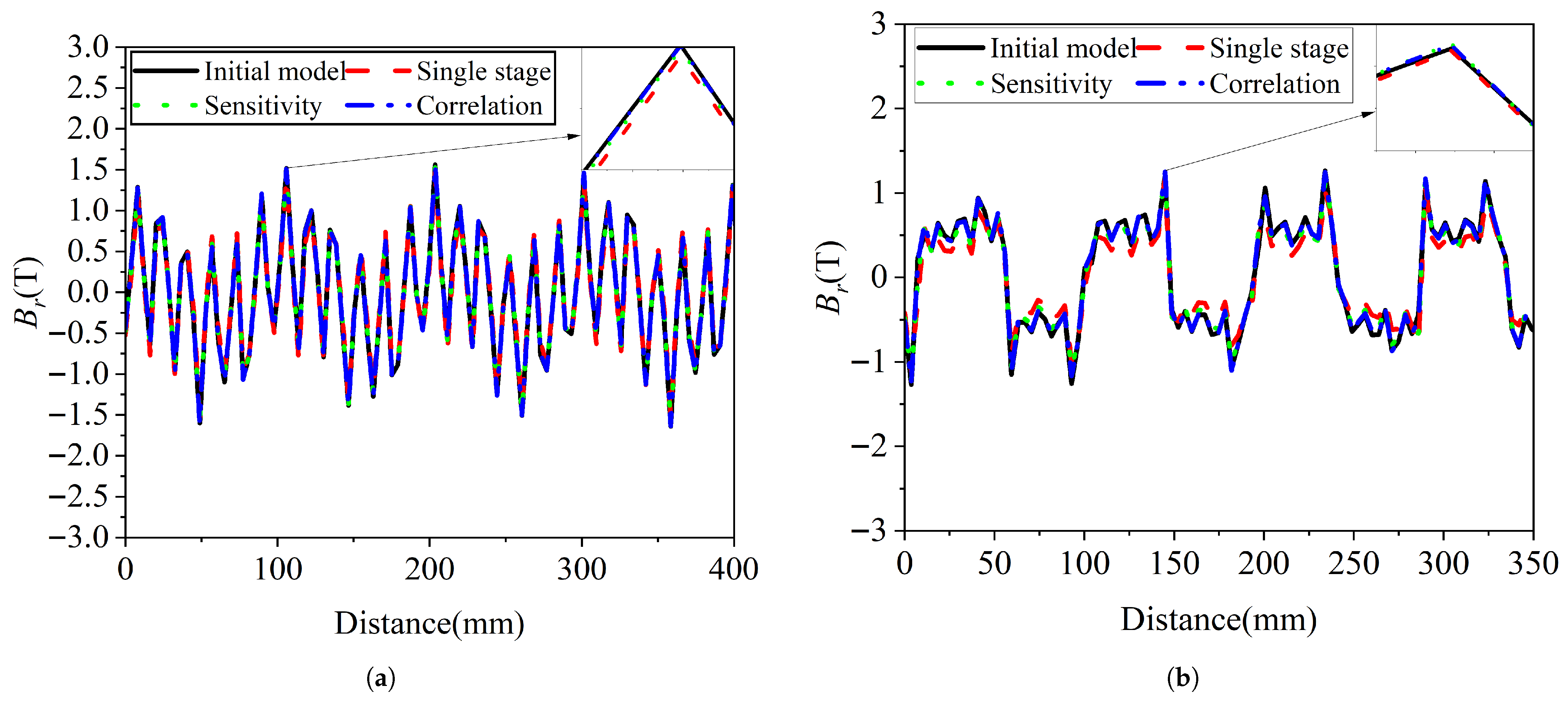
5.3. Magnetic Field Distribution and Radial Magnetic Field Analysis
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| MGCM | Magnetic Gear Compound Machine |
| MG | Magnetic Gear |
| PM | Permanent Magnet |
| PMSG | Permanent Magnet Synchronous Generator |
| PDD | Pseudo-Direct-Drive |
| EMF | Electromotive Force |
| LHS | Latin Hypercube Sampling |
| FEA | Finite Element Analysis |
| NSGA-III | Non-dominated Sorting Genetic Algorithm III |
References
- Wang, L.; Yu, S.; Liu, H.; Gao, X. Design of High Torque Density Magnetic Gear Composite Motor for Electric Vehicles. In Proceedings of the 2023 IEEE 6th Student Conference on Electrical Machines and Systems (SCEMS), Wuhan, China, 1–3 December 2023; pp. 1–5. [Google Scholar]
- Atallah, K.; Howe, D. A Novel High-Performance Magnetic Gear. IEEE Trans. Magn. 2001, 37, 2844–2846. [Google Scholar] [CrossRef]
- Tlali, P.M.; Wang, R.J.; Gerber, S. Magnetic Gear Technologies: A Review. In Proceedings of the International Conference on Electrical Machines (ICEM), Berlin, Germany, 2–5 September 2014; pp. 544–550. [Google Scholar]
- Chau, K.T.; Zhang, D.; Jiang, J.Z.; Liu, C.; Zhang, Y. Design of a Magnetic-Geared Outer-Rotor Permanent-Magnet Brushless Motor for Electric Vehicles. IEEE Trans. Magn. 2007, 43, 2504–2506. [Google Scholar] [CrossRef]
- Ito, K.; Kadomatsu, T.; Nakamura, K. Efficiency Improvement of In-Wheel Magnetic Geared Motor and Feasibility Study for Walking Support Machines. In Proceedings of the IEEE International Electric Machines and Drives Conference (IEMDC), San Diego, CA, USA, 12–15 May 2019; pp. 1818–1823. [Google Scholar]
- Jungmayr, G.; Marth, E.; Segon, G. Magnetic-Geared Motor in Side-by-Side Arrangement—Concept and Design. In Proceedings of the IEEE International Electric Machines and Drives Conference (IEMDC), San Diego, CA, USA, 12–15 May 2019; pp. 847–853. [Google Scholar]
- Jing, L.; Liu, W.; Tang, W.; Qu, R. Design and Optimization of Coaxial Magnetic Gear with Double-Layer PMs and Spoke Structure for Tidal Power Generation. IEEE/ASME Trans. Mechatronics 2023, 28, 3263–3271. [Google Scholar] [CrossRef]
- Jian, L.; Xu, G.; Gong, Y.; Song, J.; Liang, J.; Chang, M. Electromagnetic Design and Analysis of a Novel Magnetic-Gear-Integrated Wind Power Generator Using Time-Stepping Finite Element Method. Prog. Electromagn. Res. 2011, 113, 351–367. [Google Scholar] [CrossRef]
- Atallah, K.; Rens, J.; Mezani, S.; Howe, D. A Novel “Pseudo” Direct-Drive Brushless Permanent Magnet Machine. IEEE Trans. Magn. 2008, 44, 4349–4352. [Google Scholar] [CrossRef]
- Dragan, R.S.; Clark, R.E.; Hussain, E.K.; Atallah, K.; Odavic, M. Magnetically Geared Pseudo Direct Drive for Safety Critical Applications. IEEE Trans. Ind. Appl. 2019, 55, 1239–1249. [Google Scholar] [CrossRef]
- Magnomatics. Pseudo Direct Drive—Traction Motor. Available online: https://www.magnomatics.com/pdd-traction-motor (accessed on 1 January 2024).
- Gan, Q.; Fang, Y.; Pfister, P.D. A Novel Concentrated-Winding Vernier Pseudo-Direct-Drive Permanent-Magnet Machine. IEEE Trans. Magn. 2022, 58, 8201505. [Google Scholar] [CrossRef]
- Yin, X.; Fang, Y.; Pfister, P.D. High-Torque-Density Pseudo-Direct-Drive Permanent-Magnet Machine with Less Magnet. IEEE Trans. Ind. Electron. 2018, 65, 37–44. [Google Scholar] [CrossRef]
- Xu, X.; Zhang, W.; Cheng, J.; Zhao, J.; Qian, F. Design and Optimization of Axial Field Flux-Switching Magnetic Gear Composite Motor Based on Varying-Network Magnetic Circuit. IEEE Access 2023, 11, 53749–53759. [Google Scholar] [CrossRef]
- Xu, Z.; Zhu, Z.; Liu, R.; Chen, S. Design of an Eccentric Pole Type Magnetic Geared Composite Motor. In Proceedings of the 30th International Conference on Mechatronics and Machine Vision in Practice (M2VIP), Nanjing, China, 26–28 November 2024; pp. 1–5. [Google Scholar]
- Bramerdorfer, G.; Zăvoianu, A.C. Surrogate-Based Multi-Objective Optimization of Electrical Machine Designs Facilitating Tolerance Analysis. IEEE Trans. Magn. 2017, 53, 8203211. [Google Scholar] [CrossRef]
- Ma, Y.; Ching, T.W.; Fu, W.N.; Niu, S. Multi-Objective Optimization of a Direct-Drive Dual-Structure Permanent Magnet Machine. IEEE Trans. Magn. 2019, 55, 8203504. [Google Scholar] [CrossRef]
- Cui, X.; Li, Y.; Fan, J.; Wang, T.; Zheng, Y. A Hybrid Improved Dragonfly Algorithm for Feature Selection. IEEE Access 2020, 8, 155619–155629. [Google Scholar] [CrossRef]
- Shan, S.; Wang, G.G. Survey of Modeling and Optimization Strategies to Solve High-Dimensional Design Problems with Computationally-Expensive Black-Box Functions. Struct. Multidiscip. Optim. 2010, 41, 219–241. [Google Scholar] [CrossRef]
- Chau, K.T.; Chan, C.C.; Liu, C. Overview of Permanent-Magnet Brushless Drives for Electric and Hybrid Electric Vehicles. IEEE Trans. Ind. Electron. 2008, 55, 2246–2257. [Google Scholar] [CrossRef]
- Lee, J.I.; Kim, D.H.; Park, M.R.; Lim, M.S. Design and Analysis of the Coaxial Magnetic Gear Considering the Electromagnetic Performance and Mechanical Stress. IEEE Trans. Appl. Supercond. 2020, 30, 5203505. [Google Scholar] [CrossRef]
- Lee, J.I.; Kim, D.H.; Park, M.R.; Lim, M.S. Electromagnetic Performance Analysis and Experimental Verification Considering the End Effect of Linear Magnetic Gears Using Subdomain-Based Analytical Method. IEEE Trans. Magn. 2021, 57, 8203505. [Google Scholar] [CrossRef]
- Ling, Z.; Ji, J.; Zeng, T.; Zhao, W. Design Optimization and Comparison of Linear Magnetic Actuators under Different Topologies. Chin. J. Elect. Eng. 2020, 6, 41–51. [Google Scholar] [CrossRef]
- Zhu, Z.Q.; Howe, D. Electrical Machines and Drives for Electric, Hybrid, and Fuel Cell Vehicles. Proc. IEEE 2007, 95, 746–765. [Google Scholar] [CrossRef]
- Wu, Z.; Su, G.J. High-Performance Permanent Magnet Machine Drive for Electric Vehicle Applications Using a Current Source Inverter. In Proceedings of the 34th Annual Conference of IEEE Industrial Electronics, Orlando, FL, USA, 10–13 November 2008; pp. 2812–2817. [Google Scholar]
- Dai, L.; Gao, J.; Niu, S.; Huang, S. Multi-Electromagnetic Performance Optimization of Double-Layer Interior Permanent Magnet Synchronous Machine. IEEE Trans. Ind. Electron. 2024, 71, 14535–14545. [Google Scholar] [CrossRef]
- Jian, L.; Chau, K.T.; Gong, Y.; Jiang, J.Z.; Yu, C.; Li, W. Comparison of Coaxial Magnetic Gears with Different Topologies. IEEE Trans. Magn. 2009, 45, 4526–4529. [Google Scholar] [CrossRef]
- Lu, Y.; Kai, Y.; Songjun, S.; Yixiao, L.; Fei, X.; Cheng, L. Study on the Influence of a Combined-Halbach Array for the Axial Flux Permanent Magnet Electrical Machine with Yokeless and Segmented Armature. IEEE Trans. Magn. 2024, 60, 8201505. [Google Scholar] [CrossRef]
- Jara, E.C. Multi-Objective Optimization by Using Evolutionary Algorithms: The p-Optimality Criteria. IEEE Trans. Evol. Comput. 2014, 18, 167–179. [Google Scholar] [CrossRef]
- Simpson, T.; Poplinski, J.; Koch, P.; Allen, J. Metamodels for Computer-Based Engineering Design: Survey and Recommendations. Eng. Comput. 2001, 17, 129–150. [Google Scholar] [CrossRef]
- Zhang, B.; Zhao, J.; Xia, Y.; Zhu, X. Research on a Two-Stage Multi-Objective Optimization Design Method for Permanent Magnet Synchronous Motors Utilizing Partial Correlation Coefficients for Parameter Screening. IEEE Access 2025, 13, 143479–143488. [Google Scholar] [CrossRef]
- McKay, M.D.; Beckman, R.J.; Conover, W.J. A Comparison of Three Methods for Selecting Values of Input Variables in the Analysis of Output from a Computer Code. Technometrics 2000, 42, 55–61. [Google Scholar] [CrossRef]
- Jones, D.R.; Schonlau, M.; Welch, W.J. Efficient Global Optimization of Expensive Black-Box Functions. J. Glob. Optim. 1998, 13, 455–492. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, G.; Zhang, J.; Gao, Y.; Hua, W.; Wang, Y. An Improved Kriging Surrogate Model Method With High Robustness for Electrical Machine Optimization. IEEE Trans. Ind. Appl. 2024, 60, 6799–6810. [Google Scholar] [CrossRef]
- Deb, K.; Jain, H. An Evolutionary Many-Objective Optimization Algorithm Using Reference-Point-Based Nondominated Sorting Approach, Part I: Solving Problems with Box Constraints. IEEE Trans. Evol. Comput. 2014, 18, 577–601. [Google Scholar] [CrossRef]
- Marler, R.; Arora, J. Survey of Multi-Objective Optimization Methods for Engineering. Struct. Multidiscip. Optim. 2004, 26, 369–395. [Google Scholar] [CrossRef]
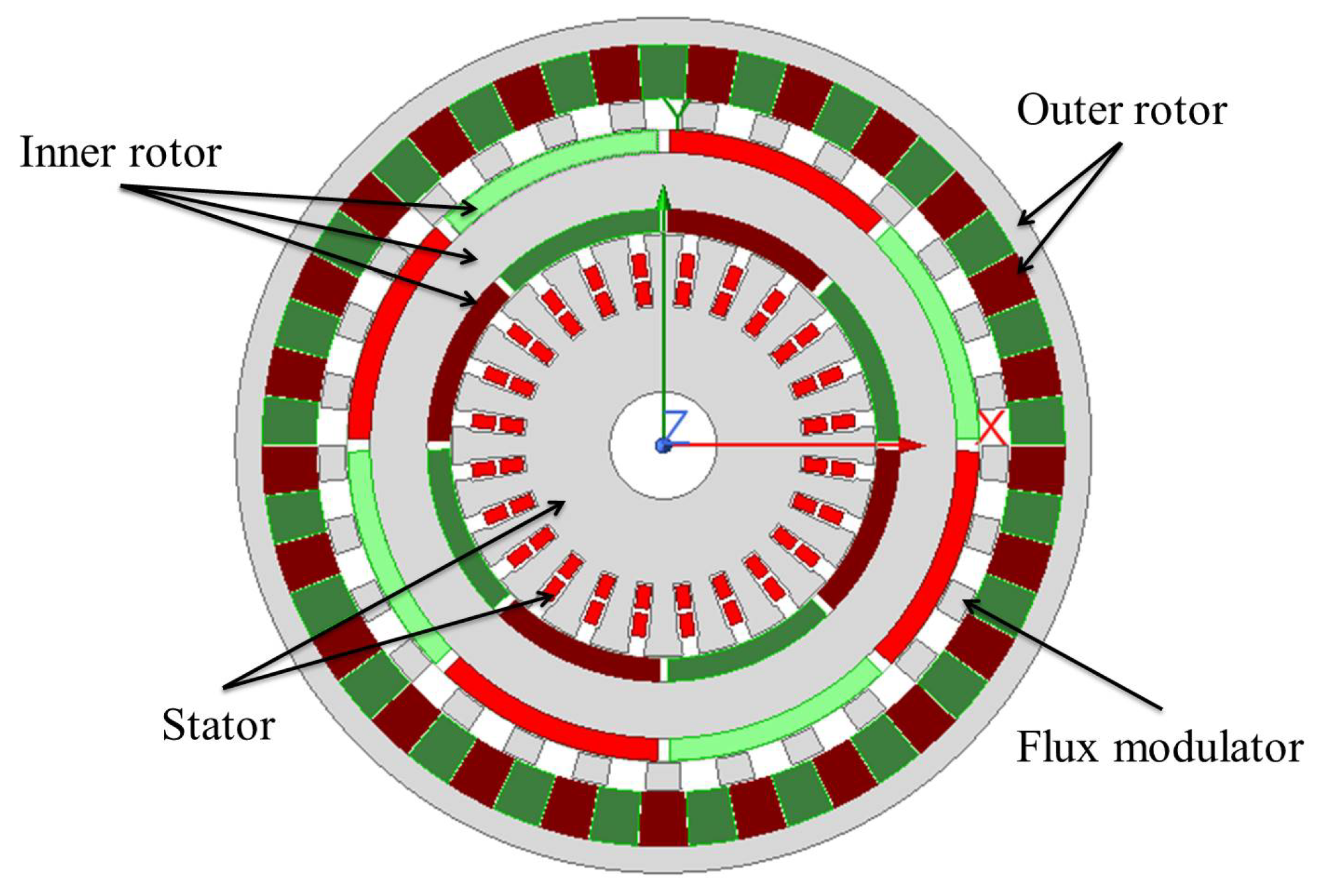



| Parameter | Value |
|---|---|
| Power (kW) | 6 |
| Outer radius of outer rotor (mm) | 80 |
| Inner radius of outer rotor (mm) | 65 |
| Outer radius of flux modulator (mm) | 64.5 |
| Inner radius of flux modulator (mm) | 59.5 |
| Outer radius of inner rotor (mm) | 59 |
| Inner radius of inner rotor (mm) | 40 |
| Radius of stator (mm) | 39.5 |
| Pole pairs of outer rotor | 25 |
| Number of modulation segments | 29 |
| Pole pairs of inner rotor | 4 |
| Number of stator slots | 24 |
| Variable | Initial Value | Variation Range |
|---|---|---|
| Embrace of inner rotor, | 0.7 | [0.45, 0.95] |
| Thickness of inner rotor, (mm) | 5 | [2, 8] |
| Slot opening height, (mm) | 2 | [1, 3] |
| Slot body height, (mm) | 15 | [10, 20] |
| Slot opening width, (mm) | 2 | [1, 3] |
| Maximum slot wedge width, (mm) | 3 | [2, 4] |
| Slot body bottom width, (mm) | 4 | [3, 5] |
| Parameter | |||||
|---|---|---|---|---|---|
| 6.0208 | 0.3668 | 1.4982 | 0.3188 | 1.0165 | |
| 0.1664 | 0.5268 | 1.0642 | 0.1786 | 0.3355 | |
| 0.4508 | 0.0023 | 0.2719 | 0.1438 | 0.1590 | |
| 1.7215 | 0.0105 | 0.2453 | 0.4909 | 0.4933 | |
| 1.0801 | 0.0102 | 0.2283 | 0.1146 | 0.2017 | |
| 0.4448 | 0.0036 | 0.1509 | 0.1168 | 0.1304 | |
| 1.7125 | 0.0112 | 0.2098 | 0.3274 | 0.3909 |
| Method | Group 1 | Group 2 | Group 3 |
|---|---|---|---|
| Sensitivity | |||
| Correlation |
| Model | Value Type | (N·m) | (V) | f | ||
|---|---|---|---|---|---|---|
| Initial Model | FEA Value | 0.627 | 526.237 | 0.016 | 421.716 | −0.811 |
| Single-stage | Predicted | −0.035 | 552.062 | 0.011 | 548.187 | −1.334 |
| FEA-Validated | 0.518 | 395.022 | 0.020 | 383.719 | −0.674 | |
| Sensitivity | Predicted | 0.095 | 474.939 | 0.014 | 425.586 | −0.974 |
| FEA-Validated | 0.091 | 475.100 | 0.016 | 399.578 | −0.901 | |
| Correlation | Predicted | 0.075 | 514.085 | 0.014 | 322.590 | −0.774 |
| FEA-Validated | 0.097 | 514.166 | 0.015 | 362.739 | −0.841 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, B.; Zhao, J.; Xia, Y.; Peng, X.; Shi, X.; Zhu, X.; Qu, B.; Yang, K. Multi-Objective Collaborative Optimization of Magnetic Gear Compound Machines Using Parameter Grouping and Kriging Surrogate Models. Energies 2025, 18, 6153. https://doi.org/10.3390/en18236153
Zhang B, Zhao J, Xia Y, Peng X, Shi X, Zhu X, Qu B, Yang K. Multi-Objective Collaborative Optimization of Magnetic Gear Compound Machines Using Parameter Grouping and Kriging Surrogate Models. Energies. 2025; 18(23):6153. https://doi.org/10.3390/en18236153
Chicago/Turabian StyleZhang, Bin, Jinghong Zhao, Yihui Xia, Xiang Peng, Xiaohua Shi, Xuedong Zhu, Baozhong Qu, and Keke Yang. 2025. "Multi-Objective Collaborative Optimization of Magnetic Gear Compound Machines Using Parameter Grouping and Kriging Surrogate Models" Energies 18, no. 23: 6153. https://doi.org/10.3390/en18236153
APA StyleZhang, B., Zhao, J., Xia, Y., Peng, X., Shi, X., Zhu, X., Qu, B., & Yang, K. (2025). Multi-Objective Collaborative Optimization of Magnetic Gear Compound Machines Using Parameter Grouping and Kriging Surrogate Models. Energies, 18(23), 6153. https://doi.org/10.3390/en18236153





